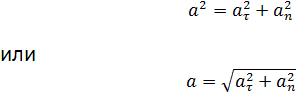Как найти ускорение — определение и формулы расчета в физике
Содержание:
-
Что такое ускорение
- Единица измерения
-
Как рассчитать ускорение: формулы
- Для прямолинейного движения
- Для равноускоренного движения
- Для равнозамедленного движения
- Нахождение ускорения через массу и силу
- Мгновенное ускорение
- Максимальное ускорение
- Среднее ускорение
- Проекция ускорения
Что такое ускорение
Ускорение (overrightarrow а) — векторная величина в физике, характеризующая быстроту изменения скорости тела.
Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.
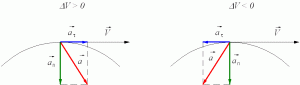
Единица измерения
В СИ (системе интернациональной) ускорение измеряется: ( begin{bmatrix}aend{bmatrix}=frac м{с^2})
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как рассчитать ускорение: формулы
Для прямолинейного движения
Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.
В этом случае ускорение находится по следующим формулам:
(a;=;frac{mathrm V}t)
(a;=;frac{2S}{t^2})
(a;=;frac{V^2}{2S})
Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.
Время отсчитывается от начала движения тела.
При прямолинейном равномерном движении ускорение по модулю равняется нулю.
Для равноускоренного движения
Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).
При таком виде движения ускорение определяется по формуле: (a;=;frac{V-V_0}t), где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.
Для равнозамедленного движения
Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).
При таком виде движения ускорение находим по формуле: (a;=-;frac{V-V_0}t), где V0 и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.
Нахождение ускорения через массу и силу
Принцип инерции Галилея:
Если не действовать на тело, то его скорость не будет меняться.
Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.
Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).
II закон Ньютона:
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
или
(overrightarrow a=frac{overrightarrow F}m)
Мгновенное ускорение
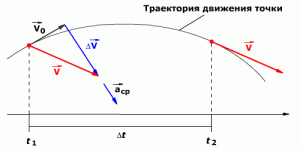
Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.
Выражается по формуле:
( overrightarrow a=lim_{trightarrow0}frac{triangleoverrightarrow V}{triangle t})
Максимальное ускорение
(a_{max}=omega v_{max},) где (a_{max}) — максимальное ускорение, (omega) — круговая (угловая, циклическая) частота, (v_{max}) — максимальная скорость.
Среднее ускорение
Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.
(overrightarrow{a_{ср}}=frac{triangleoverrightarrow V}{triangle t}), где (overrightarrow{a_{ср}}) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.
Проекция ускорения
Определение проекции ускорения на ось (х):
(a_x=frac{V_x-V_{0x}}t), где где (a_x) — проекция ускорения на ось (х), (V_x) — проекция текущей скорости на ось (х), (V_{0x}) — проекция начальной скорости на ось (х), (t) или (triangle t) — промежуток времени, за который произошло изменение проекции скорости.
Насколько полезной была для вас статья?
Рейтинг: 1.92 (Голосов: 36)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Загрузить PDF
Загрузить PDF
Ускорение характеризует быстроту изменения скорости движущегося тела.[1]
Если скорость тела остается постоянной, то оно не ускоряется. Ускорение имеет место только в том случае, когда скорость тела меняется. Если скорость тела увеличивается или уменьшается на некоторую постоянную величину, то такое тело движется с постоянным ускорением. [2]
Ускорение измеряется в метрах в секунду за секунду (м/с2) и вычисляется по значениям двух скоростей и времени или по значению силы, приложенной к телу.
-
1
Формула для вычисления среднего ускорения. Среднее ускорение тела вычисляется по его начальной и конечной скоростям (скорость – это быстрота передвижения в определенном направлении) и времени, которое необходимо телу для достижения конечной скорости. Формула для вычисления ускорения: a = Δv / Δt, где а – ускорение, Δv – изменение скорости, Δt – время, необходимое для достижения конечной скорости.[3]
- Единицами измерения ускорения являются метры в секунду за секунду, то есть м/с2.
- Ускорение является векторной величиной, то есть задается как значением, так и направлением.[4]
Значение – это числовая характеристика ускорения, а направление – это направление движения тела. Если тело замедляется, то ускорение будет отрицательным.
-
2
Определение переменных. Вы можете вычислить Δv и Δt следующим образом: Δv = vк — vн и Δt = tк — tн, где vк – конечная скорость, vн – начальная скорость, tк – конечное время, tн – начальное время.[5]
- Так как ускорение имеет направление, всегда вычитайте начальную скорость из конечной скорости; в противно случае направление вычисленного ускорения будет неверным.
- Если в задаче начальное время не дано, то подразумевается, что tн = 0.
-
3
Найдите ускорение при помощи формулы. Для начала напишите формулу и данные вам переменные. Формула: a = Δv / Δt = (vк — vн)/(tк — tн). Вычтите начальную скорость из конечной скорости, а затем разделите результат на промежуток времени (изменение времени). Вы получите среднее ускорение за данный промежуток времени.
- Если конечная скорость меньше начальной, то ускорение имеет отрицательное значение, то есть тело замедляется.
- Пример 1: автомобиль разгоняется с 18,5 м/с до 46,1 м/с за 2,47 с. Найдите среднее ускорение.
- Напишите формулу: a = Δv / Δt = (vк — vн)/(tк — tн)
- Напишите переменные: vк = 46,1 м/с, vн = 18,5 м/с, tк = 2,47 с, tн = 0 с.
- Вычисление: a = (46,1 — 18,5)/2,47 = 11,17 м/с2.
- Пример 2: мотоцикл начинает торможение при скорости 22,4 м/с и останавливается через 2,55 с. Найдите среднее ускорение.
- Напишите формулу: a = Δv / Δt = (vк — vн)/(tк — tн)
- Напишите переменные: vк = 0 м/с, vн = 22,4 м/с, tк = 2,55 с, tн = 0 с.
- Вычисление: а = (0 — 22,4)/2,55 = -8,78 м/с2.
Реклама
-
1
Второй закон Ньютона. Согласно второму закону Ньютона тело будет ускоряться, если силы, действующие на него, не уравновешивают друг друга. Такое ускорение зависит от результирующей силы, действующей на тело.[6]
Используя второй закон Ньютона, вы можете найти ускорение тела, если вам известна его масса и сила, действующая на это тело.- Второй закон Ньютона описывается формулой: Fрез = m x a, где Fрез – результирующая сила, действующая на тело, m – масса тела, a – ускорение тела.
- Работая с этой формулой, используйте единицы измерения метрической системы, в которой масса измеряется в килограммах (кг), сила в ньютонах (Н), а ускорение в метрах в секунду за секунду (м/с2).
-
2
Найдите массу тела. Для этого положите тело на весы и найдите его массу в граммах. Если вы рассматриваете очень большое тело, поищите его массу в справочниках или в интернете. Масса больших тел измеряется в килограммах.
- Для вычисления ускорения по приведенной формуле необходимо преобразовать граммы в килограммы. Разделите массу в граммах на 1000, чтобы получить массу в килограммах.
-
3
Найдите результирующую силу, действующую на тело. Результирующая сила не уравновешивается другими силами. Если на тело действуют две разнонаправленные силы, причем одна из них больше другой, то направление результирующей силы совпадает с направлением большей силы.[7]
Ускорение возникает тогда, когда на тело действует сила, которая не уравновешена другими силами и которая приводит к изменению скорости тела в направлении действия этой силы.- Например, вы с братом перетягиваете канат. Вы тянете канат с силой 5 Н, а ваш брат тянет канат (в противоположном направлении) с силой 7 Н. Результирующая сила равна 2 Н и направлена в сторону вашего брата.
- Помните, что 1 Н = 1 кг∙м/с2.[8]
-
4
Преобразуйте формулу F = ma так, чтобы вычислить ускорение. Для этого разделите обе стороны этой формулы на m (массу) и получите: a = F/m. Таким образом, для нахождения ускорения разделите силу на массу ускоряющегося тела.
- Сила прямо пропорциональна ускорению, то есть чем больше сила, действующая на тело, тем быстрее оно ускоряется.
- Масса обратно пропорциональна ускорению, то есть чем больше масса тела, тем медленнее оно ускоряется.
-
5
Вычислите ускорение по полученной формуле. Ускорение равно частному от деления результирующей силы, действующей на тело, на его массу. Подставьте данные вам значения в эту формулу, чтобы вычислить ускорение тела.
- Например: сила, равная 10 Н, действует на тело массой 2 кг. Найдите ускорение тела.
- a = F/m = 10/2 = 5 м/с2
Реклама
-
1
Направление ускорения. Научная концепция ускорения не всегда совпадает с использованием этой величины в повседневной жизни. Помните, что у ускорения есть направление; ускорение имеет положительное значение, если оно направлено вверх или вправо; ускорение имеет отрицательное значение, если оно направлено вниз или влево. Проверьте правильность вашего решения, основываясь на следующей таблице:
Движение автомобиля Изменение скорости Значение и направление ускорения Движется вправо (+) и ускоряется + → ++ (более положительное) Положительное Движется вправо (+) и замедляется ++ → + (менее положительное) Отрицательное Движется влево (-) и ускоряется — → — (более отрицательное) Отрицательное Движется влево (-) и замедляется — → — (менее отрицательное) Положительное Движется с постоянной скоростью Не меняется Равно 0 -
2
Направление силы. Помните, что ускорение всегда сонаправлено силе, действующей на тело. В некоторых задачах даются данные, цель которых заключается в том, чтобы ввести вас в заблуждение.
- Пример: игрушечная лодка массой 10 кг движется на север с ускорением 2 м/с2. Ветер, дующий в западном направлении, действует на лодку с силой 100 Н. Найдите ускорение лодки в северном направлении.
- Решение: так как сила перпендикулярна направлению движения, то она не влияет на движение в этом направлении. Поэтому ускорение лодки в северном направлении не изменится и будет равно 2 м/с2.
-
3
Результирующая сила. Если на тело действуют сразу несколько сил, найдите результирующую силу, а затем приступайте к вычислению ускорения. Рассмотрим следующую задачу (в двумерном пространстве):
Реклама
- Владимир тянет (справа) контейнер массой 400 кг с силой 150 Н. Дмитрий толкает (слева) контейнер с силой 200 Н. Ветер дует справа налево и действует на контейнер с силой 10 Н. Найдите ускорение контейнера.
- Решение: условие этой задачи составлено так, чтобы запутать вас. На самом деле все очень просто. Нарисуйте схему направления сил, так вы увидите, что сила в 150 Н направлена вправо, сила в 200 Н тоже направлена вправо, а вот сила в 10 Н направлена влево. Таким образом, результирующая сила равна: 150 + 200 — 10 = 340 Н. Ускорение равно: a = F/m = 340/400 = 0,85 м/с2.
Об этой статье
Эту страницу просматривали 190 509 раз.
Была ли эта статья полезной?
Искать «а» ради «ускорения»-пустое занятие. Искать надо F-Силу,которая вызывает движение,и изменяет его. S/tt=F/m. S,t,m можно измерить. F=?
Ошибка Ньютон: S=att/2. S=att ! (без /2).
«а»-это ЭНЕРГИЯ движения. Она НЕ зависит от графика движения, и численно = S/tt (V/t).
У падающего «яблока..» несколько скоростей: нач. скорость, кон.скорость,средняя скорость, at, 2at. «средняя скорость»-(S/t)-это та-же скорость at,но выраженная через ЭНЕРГИЮ и ВРЕМЯ: F/m*t.
ВСЕ расчёты на движение надо делать ТОЛЬКО из СРЕДНЕЙ скорости! (Энергия одинакова, и НЕ зависит от графика движения). И нет «надобности» в «интегралах». …Задачка: машина m=1165 кг, прошла 250 м. за 18 с.(набрала скорость от 0 до 27,7 м/с за 18 сек.) («Жигули»). Вопрос: какая мощность мотора?
Всякий механизм имеет КПД. КПД ДВС (у бензиновых двс=16%).Решение: S/tt=F/m. 250/324=F/1165, (или 13,9/18=F/1165). F=900 кг.м/сс. Это 12 л.с. при 100% КПД ! При 16% мощность=75 л.с. (а,Да! «ускорение»? оно =0,77 м/сс….). Но и без «а»не обойтись…
Грубая ошибка, находить «а»: Vo=0. V кон.=27,7. t=18 сек. а=(27,7-0)/18. а=1,5 м/сс. Мощность мотора=150 л.с.
То-же с «яблоком…» Vo=0, Vкон.=9,8. t=1 c. Правильно: (0+9,8)/2t. a=4,9 м/cc S=4,9 м.
«Если тело упало на Землю с высоты h, то S/tt ВСЕГДА !!! РАВНО числу 4,9… Это число 4,9 м/сс и ЕСТЬ «УСКОРЕНИЕ СВОБОДНОГО ПАДЕНИЯ»! Скорость: м/с. Ускорение-м/сек.сек. 9,8-это скорость,(но НЕ ускорение).
Сколько ошибок (и слёз) при решении задач:
Vo=5. t=10. a=2. S=? a=? V кон.=?
Решение: S=Vot+att. S=5/10+2*10*10. S=250. a=S/tt. a=2,5. V кон.=Vo+2at. Vкон.=5+2*2*10. V кон.=45. Проверка:S=att. 2,5*10*10=250. S=(v+V)/2*t. (5+45)/2*10. S=250 м.
По принятым формулам: S=(vo+att/2)*t. S=5*10+2*10/10/2=150 м. a=2S/tt. 300/100=3 м/сс
V кон.=v0+at. 5+20=25. S=(5+5+25)*10. S=350 м. («ОГОРОД!»)
Содержание материала
- Какое бывает ускорение
- Видео
- Формула ускорения в разных системах координат
- Среднее ускорение
- Тангенциальное ускорение
- Другие формы
- Перемещение и путь
- Как рассчитать ускорение: формулы
- Для прямолинейного движения
- Для равноускоренного движения
- Для равнозамедленного движения
- Нахождение ускорения через массу и силу
- Путь, скорость и ускорение
Какое бывает ускорение
Ускорение бывает равномерное, положительное и отрицательное.
- Если скорость изменяется (возрастает или убывает) равномерно, то ускорение называется равномерным;
- Если скорость возрастает, то ускорение положительно;
- Если скорость убывает, то ускорение отрицательно.
Формула для нахождения ускорения: a=v/t
Видео
Формула ускорения в разных системах координат
В декартовых координатах проекции ускорения (ax,ay,az) на оси (X,Y,Z)можно представить как:
Соответственно, имеем:
где $bar{i}, bar{j}, bar{k}$ – единичные орты по осям X,Y.Z. При этом модуль ускорения равен:
В цилиндрической системе координат имеем:
В сферической системе координат модуль ускорения можно найти как:
Среднее ускорение
Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.
(overrightarrow{a_{ср}}=frac{triangleoverrightarrow V}{triangle t}), где (overrightarrow{a_{ср}}) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения 
Другие формы
Можно взять материальный предмет, например, спутник, который вращается вокруг Земли. Он двигается по окружности и ускоряется, причина этого — изменение направления траектории движения. При этом его скоростной режим может не изменяться. В этом случае речь идёт о центростремительном (направленном к центру) ᾱ.
Ускорение тела относительно состояния свободного падения (ᾱ правильное) измеряется акселерометром. В механике для предмета с постоянной массой (m) ᾱ центра m тела пропорционально действующему на него вектору силы (суммы всех сил). Здесь действует второй закон Ньютона: F = m * ᾱ → ᾱ = F / m.
Скорость частицы, которая движется по криволинейной траектории, можно записать как функцию времени v(t) = v(t) * v(t) / v(t) = v(t) * ut(t), где единичный вектор касательной (ut) к траектории равен v(t) / v(t) и указывает направление движения в конкретный момент времени. Это и есть формула центростремительного ускорения, которое создаётся при круговом движении. Можно использовать цепное правило дифференцирования, чтобы записать формулу для произведения двух функций, если принять во внимание, что ᾱ частицы происходит по некой кривой проекции. Последовательность действий уравнения следующая:
- ᾱ = dv / dt;
- = dv / dt + v(t) * dut / dt;
- = dv / dt * ut + v² / r * un.
В уравнении un — единичный вектор нормали, r — мгновенный радиус кривизны, который основывается на колеблющемся круге в момент времени t. Все эти компоненты являются тангенциальным, радиальным или нормальным ускорением, формула которого может быть представлена в виде функции.
Перемещение и путь
Тело переместилось из точки А в точку Б. При этом перемещение тела – отрезок, соединяющий данные точки напрямую – векторная величина. Путь, пройденный телом – длина его траектории. Очевидно, перемещение и путь не стоит путать. Модуль вектора перемещения и длина пути совпадают лишь в случае прямолинейного движения.
В системе СИ перемещение и длина пути измеряются в метрах.
Перемещение равно разнице радиус-векторов в начальный и конечный моменты времени. Другими словами, это приращение радиус вектора.
Как рассчитать ускорение: формулы
Для прямолинейного движения
Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.
В этом случае ускорение находится по следующим формулам:
(a;=;frac{mathrm V}t)
(a;=;frac{2S}{t^2})
(a;=;frac{V^2}{2S})
Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.
Время отсчитывается от начала движения тела.
При прямолинейном равномерном движении ускорение по модулю равняется нулю.
Для равноускоренного движения
Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).
При таком виде движения ускорение определяется по формуле: (a;=;frac{V-V_0}t), где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.
Для равнозамедленного движения
Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).
При таком виде движения ускорение находим по формуле: (a;=-;frac{V-V_0}t), где V и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.
Нахождение ускорения через массу и силу
Принцип инерции Галилея:
Если не действовать на тело, то его скорость не будет меняться.
Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.
Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).
II закон Ньютона:
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
или
(overrightarrow a=frac{overrightarrow F}m)
Путь, скорость и ускорение
Формула v=at дает соотношение между скоростью, ускорением и временем, а формула S = at2/2 дает соотношение между путем, ускорением и временем. До сих пор, однако, мы не имели соотношения между путем S, скоростью и и ускорением а. Один из способов вывести это соотношение заключается в подстановке t2, выраженного через v и а, в формулу S = at2/2. Решая относительно t формулу v=at, мы получим t=v/a. Возведя обе части в квадрат: t2=v2/a2, подставляя v2/a2 вместо t2, имеем
v2 = 2aS
Задача:
Скорость автомобиля 90 см/сек. Через 3 сек его скорость равна нулю. Найдите его отрицательное ускорение (темп равномерного уменьшения скорости).
Решение:
a=-v/t
Подстановка значений:
a=-90/3=-30 см/сек. за 1 сек.
Ответ можно записать и так: 30 см/сек2, это будет означать, что автомобиль уменьшает свою скорость на 30 см/сек за каждую секунду.
Теги
Ускорение – это величина, которая характеризует быстроту изменения скорости.
Например, автомобиль, трогаясь с места, увеличивает скорость движения, то есть движется ускоренно. Вначале его скорость равна нулю. Тронувшись с места, автомобиль постепенно разгоняется до какой-то определённой скорости. Если на его пути загорится красный сигнал светофора, то автомобиль остановится. Но остановится он не сразу, а за какое-то время. То есть скорость его будет уменьшаться вплоть до нуля – автомобиль будет двигаться замедленно, пока совсем не остановится. Однако в физике нет термина «замедление». Если тело движется, замедляя скорость, то это тоже будет ускорение тела, только со знаком минус (как вы помните, скорость – это векторная величина).
Среднее ускорение
Среднее ускорение> – это отношение изменения скорости к промежутку времени, за который это изменении произошло. Определить среднее ускорение можно формулой:
Рис. 1.8. Среднее ускорение.В СИ единица ускорения – это 1 метр в секунду за секунду (или метр на секунду в квадрате), то есть
Метр на секунду в квадрате равен ускорению прямолинейно движущейся точки, при котором за одну секунду скорость этой точки увеличивается на 1 м/с. Иными словами, ускорение определяет, насколько изменяется скорость тела за одну секунду. Например, если ускорение равно 5 м/с2, то это означает, что скорость тела каждую секунду увеличивается на 5 м/с.
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени – это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Иными словами – это ускорение, которое развивает тело за очень короткий отрезок времени:
При ускоренном прямолинейном движении скорость тела возрастает по модулю, то есть
v2 > v1
а направление вектора ускорения совпадает с вектором скорости
Если скорость тела по модулю уменьшается, то есть
v2 < v1
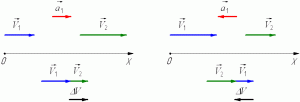
то направление вектора ускорения противоположно направлению вектора скорости Иначе говоря, в данном случае происходит замедление движения, при этом ускорение будет отрицательным (а < 0). На рис. 1.9 показано направление векторов ускорения при прямолинейном движении тела для случая ускорения и замедления.
Рис. 1.9. Мгновенное ускорение.
При движении по криволинейной траектории изменяется не только модуль скорости, но и её направление. В этом случае вектор ускорение представляют в виде двух составляющих (см. следующий раздел).
Тангенциальное ускорение
Тангенциальное (касательное) ускорение – это составляющая вектора ускорения, направленная вдоль касательной к траектории в данной точке траектории движения. Тангенциальное ускорение характеризует изменение скорости по модулю при криволинейном движении.
Рис. 1.10. Тангенциальное ускорение.
Направление вектора тангенциального ускорения (см. рис. 1.10) совпадает с направлением линейной скорости или противоположно ему. То есть вектор тангенциального ускорения лежит на одной оси с касательной окружности, которая является траекторией движения тела.
Нормальное ускорение
Нормальное ускорение – это составляющая вектора ускорения, направленная вдоль нормали к траектории движения в данной точке на траектории движения тела. То есть вектор нормального ускорения перпендикулярен линейной скорости движения (см. рис. 1.10). Нормальное ускорение характеризует изменение скорости по направлению и обозначается буквой Вектор нормального ускорения направлен по радиусу кривизны траектории.
Полное ускорение
Полное ускорение при криволинейном движении складывается из тангенциального и нормального ускорений по правилу сложения векторов и определяется формулой:
(согласно теореме Пифагора для прямоугольно прямоугольника).
Направление полного ускорения также определяется правилом сложения векторов: