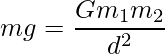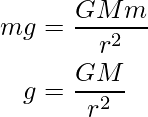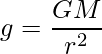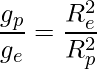Ускорение свободного падения характеризует то, как быстро будет увеличиваться скорость тела при свободном падении. Свободным падением называется ускоренное движение тела в безвоздушном пространстве, при котором на тело действует только сила тяжести. Из физики известно, что ускорение свободного падения на Земле составляет (9,8)
мс2
.
Вопрос, почему эта величина именно такая, мы рассмотрим в этой теме.
Ускорение свободного падения в упрощённом виде можно рассчитать по формуле
g=Fm
, которая получается из формулы
F=m⋅g
, где (F) — сила тяжести либо вес тела в состоянии покоя или равномерного прямолинейного движения, (m) — масса тела, которое притягивает планета, (g) — ускорение свободного падения.
Сила тяжести, действующая на тело, зависит от массы тела, массы планеты, притягивающей тело, и от расстояния, на котором находится тело от центра массы планеты.
(F) — сила тяжести, Н;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
(R) — расстояние между центрами планеты и объекта в метрах. Если притягиваемое тело находится на поверхности планеты, тогда (R) равен радиусу планеты (если планета имеет сферическую форму);
m1 и
m2
— масса планеты и притягиваемого тела, выраженные в кг.
Обрати внимание!
Если мы объединим обе формулы, тогда получим формулу
g=G⋅mR2
, с помощью которой можно вычислить ускорение свободного падения на любом космическом объекте — на планете или звезде.
Пример:
ускорение свободного падения у поверхности Земли вычисляют таким образом:
, где
(g) — ускорение свободного падения;
(G) — гравитационная постоянная,
G=6,6720⋅10−11Н⋅м2кг2
;
Практически на Земле ускорение свободного падения на полюсах немного больше ((9,832)
мс2
), чем на экваторе ((9,78)
мс2
), так как Земля не имеет форму идеального шара, а на экваторе скорость вращения больше, чем на полюсах. Среднее значение ускорения свободного падения у поверхности Земли равно (9,8)
мс2
.
Ускорение свободного падения у поверхности любого космического тела — на планете или звезде — зависит от массы этого тела и квадрата его радиуса. Таким образом, чем больше масса звезды и чем меньше её размеры, тем больше значение ускорения свободного падения у её поверхности.
При помощи формулы расчёта ускорения свободного падения и измерений, проведённых для удалённых объектов, учёные-физики могут определить величину ускорения свободного падения на любой планете или звезде.
Рис. (1). Планеты Солнечной системы: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун; и карликовые планеты: Церера, Плутон, Эрида ((2003) UB (313))
Таблица (1). Ускорение свободного падения и другие характеристики планет Солнечной системы и карликовых планет
|
Небесное тело |
Ускорение свободного падения, мс2 |
Диаметр, км |
Расстояние до Солнца, миллионы км |
Масса, кг |
Соотношение с массой Земли |
|
Меркурий |
(3,7) |
(4878) |
(58) |
(3,3*) 1023 |
(0,055) |
|
Венера |
(8,87) |
(12103) |
(108) |
(4,9*) 1024 |
(0,82) |
|
Земля |
(9,8) |
(12756,28) |
(150) |
(6,0*) 1024 |
(1) |
|
Марс |
(3,7) |
(6794) |
(228) |
(6,4*) 1023 |
(0,11) |
|
Юпитер |
(24,8) |
(142984) |
(778) |
(1,9*) 1027 |
(317,8) |
|
Сатурн |
(10,4) |
(120536) |
(1427) |
(5,7*) 1026 |
(95,0) |
|
Уран |
(8,87) |
(51118) |
(2871) |
(8,7*) 1025 |
(14,4) |
|
Нептун |
(10,15) |
(49532) |
(4498) |
(1,02*) 1026 |
(17,1) |
|
Плутон |
(0,66) |
(2390) |
(5906) |
(1,3*) 1022 |
(0,0022) |
|
Луна |
(1,62) |
(3473,8) |
(0,3844 ) (до Земли) |
(7,35*) 1022 |
(0,0123) |
|
Солнце |
(274,0) |
(1391000) |
— |
(2,0*) 1030 |
(332900) |
Нейтронные звёзды имеют малый диаметр — порядка десятков километров, — а масса их сопоставима с массой Солнца. Поэтому гравитационное поле у них очень сильное.
Пример:
если диаметр нейтронной звезды равен (20) км, а масса её в (1,4) раза больше массы Солнца, тогда ускорение свободного падения будет в (200000000000) раз больше, чем у поверхности Земли.
Его величина приблизительно равна
2⋅1012 мс2
. Значение ускорения свободного падения для нейтронной звезды может достигать значения
7⋅1012 мс2
.
Acceleration due to gravity (or acceleration of gravity) or gravity acceleration is the acceleration caused by the gravitational force of attraction of large bodies. As we know that the term acceleration is defined as the rate of change of velocity with respect to a given time. Scientists like Sir Isaac Newton and Lord Henry Cavendish soon discovered that this increase in speed, or acceleration, was caused by a different force known as gravity by studying objects falling to the Earth in a variety of circumstances. According to definitions, gravity is a force that pulls objects toward the center of mass, like the Earth. Conversely, acceleration describes how an object’s velocity or speed changes over time. Hence, the value of acceleration due to gravity is 9.8 m/s2 on earth.
What is Acceleration due to Gravity?
Acceleration due to Gravity is defined as the acceleration attained by an object due to the gravitational force of attraction. When a body is fallen toward the earth it experiences a change in its acceleration due to the gravitational pull (or force) of the Earth. This acceleration is called acceleration due to gravity. This is the acceleration that is attained by an object due to gravitational force.
The acceleration that an object experiences as a result of the gravitational force is known as acceleration due to gravity, ms-2 is its SI unit. It has a direction and a magnitude so it is a vector quantity as a result.
The symbol g represents the acceleration due by gravity. Its typical value at sea level on the surface of the earth is 9.8 ms-2. The second law of motion and the law of universal gravitation of Newton serve as the foundation for its calculation.
Acceleration due to Gravity Formula
Mathematically, the acceleration due to gravity is directly proportional to the mass of the object and inversely proportional to the distance from the center of mass, so given as:
or
where,
- g is the acceleration due to gravity,
- G is the Gravitational constant,
- m is the mass of the body and
- r is the distance from the center.
Units of Acceleration due to Gravity
- The SI unit of Acceleration due to Gravity is m/s2.
- The CGS unit of g is cm/s2.
- And the dimensional formula of Acceleration due to Gravity is [ML0T-2].
Derivation for the formula of acceleration due to gravity
According to the second law of motion:
F = ma
But, in case of a free-falling body, the force is equal to the product of the mass of the body and acceleration due to gravity.
F = mg ……(1)
But, according to the universal law of gravitation:
……(2)
Now, from the equation (1) and (2),
Consider for an ideal case the object is placed near to earth therefore the distance between earth and object will be radius of earth, so replace d with r and rearranging the above expression for g as:
Calculation of the Value of Acceleration due to Gravity
The acceleration due to gravity is stated as:
Here, substitute 6.67 × 10-11 Nm2 kg-2 for G, 6 × 1024 kg for M and 6.4 × 106 m for r in the above expression to calculate g at the surface of Earth.
Hence, the value of acceleration due to gravity on the surface of Earth is 9.8 m/s2.
Factor affecting Acceleration due to Gravity
- Shape of Earth: It is known that the shape of the earth is not spherical it’s quite oval so the gravitational force is different at different places. The force of attraction is maximum at the pole of the earth approximately 9.82 m/s2 as the radius of the earth is minimum at the pole. While the force of gravitation is minimum at the equator of the earth at approximately 9.78 m/s2 as the radius of the earth is maximum at the equator
- Altitude: When a body moves away from the surface of the earth the force of attraction decreases as the distance between the earth and the body increases.
- Depth: When a body is put inside the earth’s surface the acceleration due to gravity becomes less.
Effects on g due to Height (h)
Consider an object (of mass m) P at a height h from the surface of the earth, R be the radius of the earth as shown in the figure below:
The gravitational force F acting on the mass m is,
F = GMm/ (R+h)2
where, M is the mass of the Earth.
Since, F = mgh, where gh is the acceleration due to gravity at height h. Then the above equation becomes:
mgh = GMm/(R+h)2
gh = GM/r2 (1+h/r)2
= (GM/r2)/(1+h/r)2
Since, g = GM/r2
Therefore,
gh = g / (1+h/r)2
Now, if h is much lesser than the radius of the earth, the value of g at height h is given by:
gh = g/(1 – 2h/r)
Effects on g due to Depth D
Consider an object (of mass m) P at a depth d from the surface of the earth, R be the radius of the earth as shown in the figure below:
The acceleration due to gravity at the surface of Earth in terms of density is:
g = 4/3 x πρ x RG
At depth D,
gD = 4/3 x πρ x (R-D)G
On dividing both equations we get,
gd = g x πρ x (R-D)
Now two cases can be possible:
Case 1: If depth D is equal to the radius of the earth i.e. D = R, then:
gd = 0
Case 2: If depth D = 0, i.e. the object is at the surface of earth, then
gd = g
Effects on g due to Shape of Earth
The radius of the earth, an oblate spheroid, is greater towards the equator than it is farther from the poles. The acceleration caused by gravity changes with latitude due to the shape of the earth since it is inversely proportional to the square of the earth’s radius for a given mass.
where,
- Re and Rp are the radii of Earth at the equator and the poles, and
- ge and gp are the acceleration due to gravity at the equator and poles, respectively.
Hence, from the above-mentioned equation, it is obvious that the equator experiences less, and the poles have more gravitational acceleration. Therefore, when g lowers, a person’s weight falls as they move from the equator to the poles.
Effects on g due to the Rotation
The variation in g is due to the centrifugal force acting on the rotation of the earth. When the earth is rotating, all the objects tend to experience a centrifugal force that won’t act in the direction of gravity.
FAQs on Acceleration due to Gravity
Question 1: What do you mean by Acceleration due to Gravity?
Answer:
Acceleration due to Gravity is defined as the acceleration attained by an object due to the gravitational force of attraction. When a body is fallen toward the earth it experiences a change in its acceleration due to the gravitational pull (or force) of the Earth.
Question 2: What is the SI unit and dimensional formula of Acceleration due to Gravity?
Answer:
The SI unit of Acceleration due to Gravity is m/s2. And the dimensional formula of Acceleration due to Gravity is [ML0T-2].
Question 3: What is the acceleration due to gravity on the moon?
Answer:
The value of acceleration due to gravity on the moon is 1.625 m/s2.
Question 4: Does the mass of any object have an impact on the value of acceleration due to gravity?
Answer:
No, mass does not have any significant impact on the value of acceleration due to gravity.
Question 5: Write down the formula to calculate the attraction force between two objects.
Answer:
The formula to calculate the attraction force between two objects is given by,
F = GMm/ R2
where,
- m and M are the masses of the objects in contact,
- G is the Gravitational Constant and
- R is the distance between them.
Question 6: What do you understand by the term Free Fall?
Answer:
A body is said to be in free fall when it only moves with respect to the Earth’s gravity. An external force exerted on the ball will cause its motion to accelerate. Gravitational acceleration is another name for this rate of free fall.
Related Articles
- Factors affecting Acceleration due to Gravity
- Variation in Acceleration due to Gravity
- What is Gravity?
Last Updated :
18 Nov, 2022
Like Article
Save Article
Ускорение свободного падения
Ускорение свободного падения — движение объекта, который получает ускорение из-за действующей на него силы тяжести; обозначается буквой g и измеряется в м/с². На поверхности Земли ускорение свободного падения примерно равно 9,81 м/с².
На полюсах (Южном и Северном) ускорение свободного падения будет больше, а на экваторе — меньше. Это происходит из-за двух фактов:
- Земля — не идеальный круг, а приплюснутый шар и её радиус на полюсах меньше, чем на экваторе (ускорение зависит от радиуса),
- центробежные силы (при вращении Земли) минимально компенсируют гравитацию больше на экваторе, чем на полюсах.
В вакууме тела падают с одинаковой скоростью потому, что ускорение свободного падения не зависит от массы.
Таблица ускорения свободного падения небесных тел
| Небесное тело | g (в м/с²) |
|---|---|
| Луна | 1,62 |
| Солнце | 274 |
| Меркурий | 3,72 |
| Венера | 8,87 |
| Земля | 9,81 |
| Марс | 3,711 |
| Юпитер | 24,79 |
| Сатурн | 10,44 |
| Уран | 8,87 |
| Нептун | 11,15 |
От чего зависит ускорение свободного падения?
Ускорение свободного падения зависит от массы планеты и радиуса планеты — чем она тяжелее, тем сильнее притягивает тела (т.е. масса тела не влияет на ускорение).
Возможно для будущих вычислений нужны будут эти данные:
- Масса Земли = 5,98 × (10^24) кг (или 5,972E24 кг)
- Радиус Земли = 6 371 км = 6,37×(10^6) м.
Как найти ускорение свободного падения?
Формула ускорения свободного падения

g — ускорение свободного падения
G — гравитационная постоянная
M — масса планеты
R — радиус планеты
Гравитационная постоянная («G», не путайте с «g») — это фундаментальная физическая константа, которая примерно равна
и связывает силы гравитационного притяжения между двумя телами (G) с их массами (m1 и m2) и расстоянием между ними (R) в формуле:
Пример расчёта ускорения свободного падения (для Земли):
Вспомним формулу:

G — гравитационная постоянная
M — масса планеты
R — радиус планеты
Как узнать время падения тела?
Формула времени свободного падения (когда тело падает вертикально):
t = V / g = √(2h/g)
Где:
- t — время
- V — скорость тела
- g — ускорение ≈ 9,8 м/с²
- h — расстояние
Пример:
Высота (h) = 20 м
Нужно найти скорость и время падения.
Решение:
Формула скорости:
V0 = 0
g ≈ 9,8 м/с²
h = 20 м
V² = 0² + 2 × 9,8 м/с² × 20 м ⇔ V = √392 м/с ≈ 19,8 м/с
Зная скорость, применяем эту формулу:
t = V / g = (19,8 м/с) / (9,8 м/с²) ≈ 2,02 с
Либо используя только высоту и ускорение:
t = √(2h/g) = √(2 × 20 м / 9,8 м/с²) ≈ 2,02 с
Где нужны знания о свободном падении?
Они могут понадобиться:
- в авиации,
- в космонавтике,
- при поиске полезных ископаемых (там, где есть залежи тяжёлых ископаемых, g меняется),
- при разработке новых лыжных трамплинов и полос приземления,
- при разработке новых автомобилей (рассчитываются наилучшие показатели для экономии топлива).
Узнайте также про Закон сохранения энергии, Силу Архимеда, Законы Ньютона и Космологию.
Введение. Опыты Галилея по определению ускорения свободного падения
На предыдущем уроке мы обсудили вопрос, связанный с законом всемирного тяготения. Теперь перед нами стоит задача – рассмотреть, как этот закон связан с уже известным ускорением свободного падения. Ускорение свободного падения впервые определил итальянский ученый Галилео Галилей. Как вы помните, он измерял ускорение движения тел, которые двигались по наклонной плоскости, и ему удалось установить, что предельное ускорение таких тел (а это и есть ускорение свободного падения) составляет .
Вывод формулы для ускорения свободного падения на основании закона всемирного тяготения
Однако почему именно такое значение у этого ускорения, стало ясно только после открытия закона всемирного тяготения. Вспомним, что сила тяжести на Земле – это проявление действия закона всемирного тяготения для тел, которые находятся на поверхности Земли.
Рис. 1. Сила тяжести, действующая на тело на Земле
При этом вся масса Земли условно полагается сосредоточенной в ее центре. Радиус Земли – это расстояние между телами (рис. 1). Само тело, которое находится над поверхностью Земли, – то самое тело, которое притягивается. Запишем соответствующие формулы.
Сила тяжести на Земле:
, где
– масса тела, которое находится на поверхности Земли,
— ускорение свободного падения.
Закон всемирного тяготения в данном случае имеет вид:
Здесь – масса Земли,
– масса тела,
– радиус Земли,
– гравитационная постоянная. Если сравнить выражение для силы тяжести и для гравитационной силы, получим для ускорения свободного падения:
Обратите внимание: ускорение свободного падения зависит от массы Земли и от радиуса Земли. Если они будут изменяться, значит, будет изменяться и ускорение свободного падения.
Зависимость ускорения свободного падения от географической широты и других параметров. Искусственные спутники Земли
Как известно, Земля по форме не идеальный шар, а тело, которое немного сплюснуто с полюсов, поэтому полярный радиус несколько меньше, чем экваториальный (рис. 2). В этом случае надо понимать, что ускорение свободного падения на полюсе будет больше, а на экваторе – меньше. В общем случае ускорение свободного падения зависит от широты местности.
Рис. 2. Разность экваториального и полярного радиусов
Необходимо отметить еще вот что. Земля вращается, и вращательное движение Земли тоже влияет на ускорение свободного падения. Ускорение свободного падения на экваторе будет отличаться еще и по этой причине. Изменение ускорения свободного падения по всем вышеуказанным причинам достаточно незначительное, поэтому мы считаем, что ускорение свободного падения на Земле – величина постоянная и составляет .
Как видите, ускорение свободного падения зависит от радиуса Земли, значит, если увеличивать радиус, то ускорение свободного падения будет уменьшаться. Как такое может быть? Если мы поднимаем тело над поверхностью Земли (например, тот же спутник), то расстояние будет определяться суммой радиуса Земли и высоты над ее поверхностью (рис. 3).
Рис. 3. Тело, поднятое над поверхностью Земли.
В этом случае ускорение свободного падения тоже будет уменьшаться.
Ускорение свободного падения обратно пропорционально квадрату расстояния. Поэтому если высота будет равна радиусу Земли, то расстояние будет в 2 раза больше от центра Земли, чем для тела на поверхности. В этом случае ускорение свободного падения уменьшится в 4 раза.
Следует заметить, что многие спутники летают на небольшом расстоянии, приблизительно 200–300 км от поверхности Земли. На этом расстоянии ускорение свободного падения изменяется, но незначительно, поэтому мы будем считать, что в этом случае ускорение все-таки величина постоянная.
Обратите внимание на тот факт, что сила тяжести, как и ускорение свободного падения, с высотой будет убывать (по мере удаления от Земли сила тяжести будет убывать).
Как изменение  делает нас богаче
делает нас богаче
Дело в том, что измерение ускорения свободного падения в различных точках Земли является мощнейшим способом геологической разведки. Таким способом (без рытья шахт) можно определять наличие полезных ископаемых в толще земной коры. Первый способ: измерение при помощи пружинных весов (рис. 4). Они обладают феноменальной чувствительностью.
Рис. 4. Геологические весы
Второй способ: измерение при помощи математического маятника (груз, подвешенный на длинной нити). Оказывается, что период (время одного полного колебания) колебания такого маятника зависит от ускорения свободного падения.
Чем больше ускорение свободного падения, тем меньше период. То есть, измеряя период маятника в разных точках Земли, можно определить изменение ускорения свободного падения. Геологи используют очень точные маятники (рис. 5), которые позволяют измерять ускорение свободного падения с точностью до миллионных долей.
Рис. 5. Прибор с маятником для разведки полезных ископаемых
Что является нормой для величины ускорения свободного падения?
Как известно Земля имеет фору геоида (сплюснута у полюсов). Это значит, что значение ускорения свободного падания у полюсов больше чем на экваторе. Но на одной и той же географической широте ускорение свободного падения, при прочих равных условиях, должно быть одинаково. Измеряя в рамках одной широты ускорение свободного падения в разных точках, можно судит о наличии полезных ископаемых.
Представьте себе, что вы находитесь на широте Москвы. Допустим, норма ускорения свободного падения на этой широте равна . В рамках данной широты мы смещаемся западнее или севернее и замечаем, что
изменилось, теперь оно равно
.
Это означает, что мы наткнулись на место с залежами тяжелых ископаемых. Если же ускорение свободного падения уменьшилось, значит, там есть пустоты или залежи легких солей. Как правило, рядом с залежами легких солей находятся залежи нефти. Данный способ называется гравиметрической разведкой. Таким способом были обнаружены залежи нефти в Казахстане и Западной Сибири.
На рис. 6 изображены зоны, где ускорение свободного падения больше (красные области) или меньше (синие области).
Рис. 6. Области, где ускорение свободного падения отличается от
Залежи тяжелых веществ или наличие пустот оказывают влияние на направление ускорения свободного падения. Если вы проводите измерение вблизи большой горы, то это массивное тело будет оказывать влияние на направление
(рис. 7).
Рис. 7. Маятник в нормальных условиях и под воздействием массивного объекта
Ускорение свободного падения на других небесных телах на примере Луны
Теперь обсудим то, как определяется ускорение свободного падения на других телах.
Обратимся к уравнению, которое мы использовали для определения ускорения свободного падения на поверхности Земли: .
В этом уравнении вместо массы и радиуса Земли можно подставить массу и радиус любой другой планеты. Тогда мы получим ускорение свободного падения на любой из интересующих нас планет. В первую очередь нас интересует Луна. Ускорение свободного падения на Луне будет приблизительно равно: .
Как видно, ускорение свободного падения на Луне сильно отличается от ускорения свободного падения на Земле. Значит, если вдруг мы окажемся на Луне, мы почувствуем себя гораздо легче, чем на родной Земле. Например, у первых лунных космонавтов скафандр был массой .
Сила тяжести, действующая на скафандр на Земле:
Сила тяжести, действующая на скафандр на Луне:
Такую силу тяжести, как на Луне, на Земле бы имел скафандр массой :
 на разных небесных телах: сравнительная таблица
на разных небесных телах: сравнительная таблица
Значение величины ускорения свободного падения равное является самым комфортным для человека. Рассмотрим, какие значения принимает ускорение свободного падения на других небесных телах (Солнце, планеты, спутники).
Чем массивнее небесное тело, тем больше .
Рассмотрим таблицу для ускорения свободного падения для различных небесных тел.
|
Небесное тело |
|
|
Луна |
1,62 |
|
Солнце |
273,1 |
|
Меркурий |
3,72 |
|
Земля |
9,81 |
|
Уран |
8,86 |
|
Венера |
8,88 |
|
Сатурн |
10,44 |
Табл. 1. Ускорение свободного падения для различных небесных тел
Как видно, на Луне в 6 раз меньше, чем на Земле. Передвигаться на Луне гораздо легче, чем на Земле. На Солнце
в 30 раз больше, чем на Земле. Даже не учитывая больших температур, передвигаться на Солнце с учетом перегрузки в 30 раз невозможно. У Урана, Венеры и Сатурна более близкие значения
с Землей. На Уране и Сатурне достаточно холодно. А вот на Венере возможно существование каких-то форм жизни или возможно путешествие человека и организация базы для временного пребывания.
Зная ускорение свободного падения на небесных телах, можно посчитать и их среднюю плотность. Зная среднюю плотность, можно предсказывать то, из чего состоят небесные тела, и определять их строение.
Расчет массы Земли
При помощи полученной формулы мы можем определить массу тех планет и небесных объектов, которые нас интересуют. Посмотрим на формулу, которая позволяет это сделать. Рассмотрим это на примере Земли. Из формулы для ускорения свободного падения несложно получить: .
Эта формула позволяет определить массу Земли. Обычно всегда спрашивают, как удалось взвесить Землю?
Никто ее не взвешивал, а, воспользовавшись законом всемирного тяготения и, зная ускорение свободного падения на поверхности Земли, можно легко массу Земли вычислить.
Масса Земли все время уточняется. Все понимают, что эта величина является очень важной. Когда мы знаем массу Земли, то, пользуясь т. н. законами Кеплера, несложно определить массу других небесных тел. Если мы знаем расстояние между Землей и другой планетой, знаем, как они взаимодействуют друг с другом, мы можем легко определить массу других тел.
Поэтому в астрономии очень часто за единицу измерения принимают массу Земли, говорят, что масса Земли равна 1 единице, и все другие массы планет определяют уже в массах Земли.
Определение средней плотности Земли
Знание ускорения свободного падения на поверхности Земли и радиуса Земли дают возможность определить среднюю плотность вещества Земли.
Вспомним формулу для ускорения свободного падения:
Массу можно вычислить через плотность и объем тела:
Земля имеет форму шара, поэтому ее объем можно вычислить по формуле:
Из приведенных выше формул можно получить зависимость от плотности:
Выразим из данной формулы плотность и подставим все известные величины:
То есть кубик усредненного земного вещества размерами 1 см·1 см·1 см будет весить 5,5 грамм. Если взять вещество с поверхности Земли, то его плотность будет меньше усредненной (). Значит, внутри Земли (рис.

Рис.8 Строение Земли
По современным представлениям, в центре Земли находится раскаленное железное ядро. Считается, что Земля могла образоваться из метеоритов. Они сталкивались, постепенно образовывалось земное вещество, гравитационные силы стягивали наиболее тяжелые фракции к центру. В результате образовалось ядро. Более легкие фракции оказались на периферии.
Заключение
Закон всемирного тяготения и ускорение свободного падения имеют большое значение. В первую очередь для запуска искусственных спутников Земли.
Список дополнительной литературы
- Кикоин А. К. Вращение Земли и ускорение свободного падения //Квант. – 1984. – № 1. – С. 32–34.
- Кикоин И. К., Кикоин А. К. Физика: Учебник для 9 класса средней школы. – М.: Просвещение, 1992.
- Сивухин Д. В. Общий курс физики. – М.: Государственное издательство технико-теоретической литературы, 2005. – Т. 1. Механика. – С. 372.
- Смородинский Я. Закон всемирного тяготения //Квант. – 1990. – № 12. – С. 8–13; 51.
- Физика: Механика. 10 кл.: Учебник для углубленного изучения физики / под ред. Г. Я. Мякишева. – М.: Дрофа, 2002.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «class-fizika.narod.ru» (Источник)
- Интернет-портал «100ballov.kz» (Источник)
- Интернет-портал «eduspb.com» (Источник)
Домашнее задание
- Где на Земле ускорение свободного падения выше: на полюсах или на экваторе? Ответ обоснуйте.
- В чем заключались опыты Галилея по определению ускорения свободного падения?
- Определите, на какой высоте над Землей ускорение свободного падения в три раза меньше его значения на поверхности Земли.
- Известно, что Земля имеет определенную массу, но как удалось взвесить планету?
Выберем тело, например, камень. Расположим его не некотором расстоянии от поверхности земли. Расстояние от центра Земли до камня равно ( R = left( r + h right) ), как представлено на рисунке 1.
Рис. 1. Камень (черная точка), притягивается к планете (центральная окружность).
Пусть на камень действует только сила, с которой Земля притягивает его, а других сил нет (нет, например, силы сопротивления воздуха).
Свободное падение – это движение тела под действием только одной силы — силы притяжения.
Из законов Ньютона известно: если на тело действует сила, то тело получает ускорение.
Ускорение свободного падения – это ускорение, с которым движется тело, когда на него действует только сила тяжести.
Формула для расчета ускорения свободного падения
Ускорение свободного падения можно посчитать по формуле:
[ large boxed { g = G cdot frac{M}{left( r + h right)^{2}} }]
( g left( frac{text{м}}{c^{2}} right) ) (метры, деленные на секунду в квадрате) – ускорение свободного падения
( M left( text{кг} right) ) (килограммы) — масса планеты, которая притягивает
( r left( text{м} right) ) (метры) – радиус планеты
( h left( text{м} right) ) (метры) — расстояние от поверхности планеты до тела
(G = 6{,}67 cdot 10^{-11} left( text{Н} cdot frac{text{м}^2}{text{кг}^2} right)) — гравитационная постоянная
Интересные факты
У разных планет ускорение свободного падения различается.
- чем больше масса планеты (или звезды), тем больше будет ускорение свободного падения рядом с такой планетой (или звездой);
- чем дальше от планеты, тем меньше ускорение свободного падения;
- на полюсах ускорение свободного падения больше, чем на экваторе планеты;
Важно!
Все тела под действием силы тяжести падают с одинаковым ускорением! Это ускорение не зависит от массы тела.
Из житейского опыта мы знаем: чем больше площадь тела, тем больше времени ему нужно, чтобы упасть с какой-либо высоты. При своем падении тело опирается на воздух, поэтому, к примеру, лист бумаги будет падать дольше, чем шарик из пластилина, или гирька.
В безвоздушном пространстве опираться не на что. Поэтому гирька, лист бумаги, птичье перо и пластилиновый шарик, стартовав с одной и той же высоты одновременно, упадут на поверхность планеты тоже одновременно.
Ускорение свободного падения у поверхности некоторых небесных тел
- у поверхности Земли ( g = 9{,}8 left( frac{text{м}}{c^{2}} right) )
- у поверхности Луны ( g = 1{,}68 left( frac{text{м}}{c^{2}} right) )
- у поверхности Марса ( g = 3{,}86 left( frac{text{м}}{c^{2}} right) )
- у поверхности Солнца ( g = 273{,}1 left( frac{text{м}}{c^{2}} right) )
- у поверхности Юпитера ( g = 23{,}95 left( frac{text{м}}{c^{2}} right) )
Как вывести формулу ускорения свободного падения
Рассмотрим камень, находящийся на некотором расстоянии от Земли.
Земля и камень притягиваются, запишем закон притяжения между планетой и камнем
[ F = G cdot frac{mcdot M}{left( r + h right)^{2}} ]
С другой стороны, у камня есть вес, так как на него действует сила тяжести.
[ F_{text{тяж}} = m cdot g ]
Мы можем записать эти уравнения в виде системы.
[ begin{cases} displaystyle F = G cdot frac{mcdot M}{( r + h)^{2}} \ displaystyle F_{text{тяж}} = m cdot g end{cases} ]
Земля и камень притягиваются, благодаря этому на камень действует сила тяжести. На языке математики это запишется так:
[ F = F_{text{тяж}} ]
А если равны левые части уравнений, то будут равны и правые:
[ G cdot frac{mcdot M}{left( r + h right)^{2}} = m cdot g ]
Масса ( m ) камня встречается в обеих частях уравнения. Поделим обе части уравнения на массу камня.
[ G cdot frac{M}{ left( r + h right)^{2}} = g ]
Все)
Вам будет интересно почитать:
Закон всемирного тяготения
Законы Ньютона
Первая космическая скорость
Вторая космическая скорость



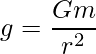
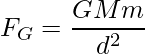 ……(2)
……(2)