From Wikipedia, the free encyclopedia
In probability theory and statistics, a conditional variance is the variance of a random variable given the value(s) of one or more other variables.
Particularly in econometrics, the conditional variance is also known as the scedastic function or skedastic function.[1] Conditional variances are important parts of autoregressive conditional heteroskedasticity (ARCH) models.
Definition[edit]
The conditional variance of a random variable Y given another random variable X is
The conditional variance tells us how much variance is left if we use 
Here, as usual, 
which we may recall, is a random variable itself (a function of X, determined up to probability one).
As a result, 
Explanation, relation to least-squares[edit]
Recall that variance is the expected squared deviation between a random variable (say, Y) and its expected value.
The expected value can be thought of as a reasonable prediction of the outcomes of the random experiment (in particular, the expected value is the best constant prediction when predictions are assessed by expected squared prediction error). Thus, one interpretation of variance is that it gives the smallest possible expected squared prediction error. If we have the knowledge of another random variable (X) that we can use to predict Y, we can potentially use this knowledge to reduce the expected squared error. As it turns out, the best prediction of Y given X is the conditional expectation. In particular, for any 
By selecting 
Here, the second equality used the law of total expectation.
We also see that the expected conditional variance of Y given X shows up as the irreducible error of predicting Y given only the knowledge of X.
Special cases, variations[edit]
Conditioning on discrete random variables[edit]
When X takes on countable many values 

where recall that 

An alternative notation for 

Note that here 

The connection of this definition to 
Let S be as above and define the function 


Definition using conditional distributions[edit]
The «conditional expectation of Y given X=x» can also be defined more generally
using the conditional distribution of Y given X (this exists in this case, as both here X and Y are real-valued).
In particular, letting 

![{displaystyle P_{Y|X}:{mathcal {B}}times mathbb {R} to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88ddda966175068cbdbbc030c735007ba9e68e13)


This can, of course, be specialized to when Y is discrete itself (replacing the integrals with sums), and also when the conditional density of Y given X=x with respect to some underlying distribution exists.
Components of variance[edit]
The law of total variance says

In words: the variance of Y is the sum of the expected conditional variance of Y given X and the variance of the conditional expectation of Y given X. The first term captures the variation left after «using X to predict Y«, while the second term captures the variation due to the mean of the prediction of Y due to the randomness of X.
See also[edit]
- Mixed model
- Random effects model
References[edit]
- ^ Spanos, Aris (1999). «Conditioning and regression». Probability Theory and Statistical Inference. New York: Cambridge University Press. pp. 339–356 [p. 342]. ISBN 0-521-42408-9.
Further reading[edit]
- Casella, George; Berger, Roger L. (2002). Statistical Inference (Second ed.). Wadsworth. pp. 151–52. ISBN 0-534-24312-6.
Для того чтобы
оценить насколько сильно отдельные
значения сл. величины могут отклоняться
от кривых регрессии, используют понятие
условной дисперсии:
(3.35)
Случайная величина
,
рассматриваемая
как функция η, носит название скедастика,
сами уравнения (3.35) называются
скедастическими
(терминология
справедлива и для сл. величины
.
Как и в случае
условного математического ожидания,
некоторые свойства условной дисперсии
аналогичны свойствам обычной дисперсии,
другие же присущи только условной
дисперсии. Первые только перечислим,
вторые приведем с доказательствами.
1.
2.
3.
4.
,
если
– независимые сл. величины при условии
η.
5.
Доказательство
приведем для непрерывной сл. величины.
Рассмотрим выражение
–
использовали
свойство 6 условного математического
ожидания. Далее используем формулу
(3.34).
6.
или
.
Согласно свойству
D4 дисперсии имеем
.
Применим к обеим частям полученного
равенства оператор математического
ожидания:
или, используя свойство 5 условного
математического ожидания в левой части
равенства,
.
Вычтем из обеих частей
:
.
В левой части получаем выражение для
дисперсии Dξ, правую же часть полученного
равенства преобразуем следующим образом.
Нетрудно показать, что
=
.
Действительно,
.
Тогда получаем равенство
Остается показать, что
Замечание. В
ходе доказательства получена формула,
имеющая самостоятельное значение
(3.36)
Пример 8. Пусть
(ξ,η) – двумерная сл. величина, имеющая
нормальное распределение. Известно
(см. предыдущий пример), что условная
плотность распределения
имеет вид
.
Но тогда
.
Аналогично,
.
Обе дисперсии
постоянны, т.е. не зависят от значений
сл. величин ξ и η соответственно. При |
ρ |=1
.
О том, как проинтерпретировать полученный
результат, см. п. 3.12.
Проверим свойство
6 условной дисперсии:
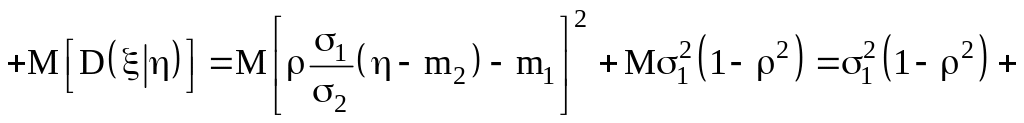
Мы
получили хорошо известный результат.
Упражнение.
Проверить
справедливость соотношений
1.
2.
3.
,
если ξ и η – независимые одинаково
распределенные сл. величины.
3.11. Ковариация случайных величин
Вышеописанные
характеристики связи сл. величин являются
функциями значений условия.
Одним числом
зависимость
между сл. величинами описывается
ковариацией или коэффициентом корреляции.
Определение.
Ковариацией скалярных сл. величин
и
называют
число, равное математическому ожиданию
произведения центрированных сл. величин
и
:
cov(,)=
(3.37)
Ковариацией
векторных случайных величин будет
квадратная матрица, элементами которой
служат ковариации между компонентами
векторов ξ и η –
и
n–размерность векторов ξ и η (см. также
п. 3.7).
(3.38)
Первая формула в
равенстве (3.38) справедлива для дискретного
распределения, вторая – для непрерывного.
Таким образом,

Если ξ=η, то

,
поскольку
диагональные элементы матрицы являются
дисперсиями сл. величин
по свойству 1 ковариаций сл. величин
(см. ниже). Поскольку
,
что следует из определения ковариации,
то матрица A – симметричная матрица.
Если cov(,)=0,
то сл. величины ξ и η называются
некоррелированными.
Ковариация сл.
величин обладает следующими свойствами:
1. cov
(,)
= D
cov (,)
= M(
– M)2
= D
2. Если
и
независимы, то cov(,)
= 0. Иначе говоря,
из независимости сл. величин следует
их некоррелируемость.
Cov(,)
= M(–
M)(
– M)
=(по свойству М4 математического ожидания
сл. величин)= M(–
M)M(
– M)=0.
Обратное утверждение
в общем случае места не имеет. Существуют
зависимые сл. величины, ковариация
которых равна нулю. Так, если ξ=sinν,
η=cosν, сл. величина ν распределена
равномерно на отрезке [0,2π], то cov(,)=
,
следовательно, по определению сл.
величины
и
не коррелированы. Однако между этими
сл. величинами существует функциональная
зависимость.
3. Пусть
.
Тогда
.
Действительно,
(по свойству М2
математического ожидания сл. величин).
Замечание.
Если в качестве ξ и η рассмотреть
двумерные сл. величины, то есть
,
при этом
,
где
– неслучайные матрицы порядка 2×2,
– двумерные неслучайные векторы, тогда
формула претерпевает очевидные изменения:
.
4.
.
Рассмотрим сл.
величину
= x
–
, x
– произвольное
число.
.
Квадратный трехчлен относительно x
неотрицателен
тогда и только тогда когда его дискриминант
не положителен, т.е.
.
В случае если ξ и
η – двумерные сл. величины, то неравенство
принимает вид
и
Это неравенство называют неравенством
Коши-Буняковского.
При выводе свойства
4 получен интересный результат, имеющий
самостоятельное значение:
.
(3.39)
Этот результат
может быть получен повторением
доказательства свойства 4 для сл. величины
=
+.
Полученное соотношение следует отнести
к свойствам дисперсии, в качестве 5
ее свойства.
Оно определяет дисперсию суммы
произвольных сл. величин.
5.
.
Пример 9. Рассмотрим
двумерную сл. величину, имеющую нормальное
распределение (см. пример 2). Вычислить
ковариацию между компонентами вектора.
Решение.


=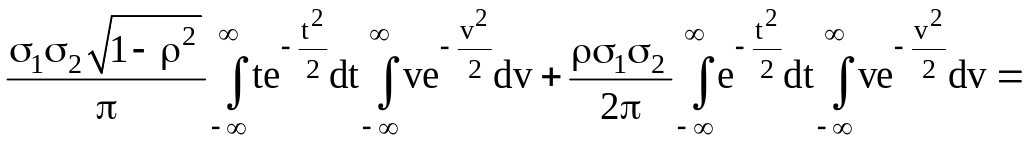
=
,
( последний интеграл вычислили по
частям).
Итак,
Поскольку
,
то ковариационная матрица A имеет вид
A=
.
Мы ввели этот термин “ковариационная
матрица” раньше (см. формулу 3.9 и пояснение
к ней) , чем выяснили смысл этого понятия.
Пример 10. Пусть
(
,)
– нормальный сл. вектор и матрица
ковариаций для него имеет вид A=
,
т.е. сл. величины
и
не коррелированны.
Запишем плотность
нормального распределения в этом
частном случае:

Итак,
сл. величины
и
независимы.
Этот пример имеет
принципиальное значение. Ранее мы
отметили, что из независимости сл.
величин следует их некоррелируемость.
Обратное утверждение в общем случае
места не имеет. Только для нормально
распределенных сл.
величин из некоррелируемости
случайных величин, следует
независимость сл.
величин ξ и η.
Пример 11. Докажем
свойство М4 математического ожидания
из п. 2.5:
,
если сл. величины ξ и η независимы. Для
простоты записи будем считать сл.
величины ξ и η непрерывными. По определению
математического ожидания функции
случайной величины имеем:
|по
определению независимых сл. величин
(3.23)|=
– по определению математического
ожидания сл. величины.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В этой статье условная дисперсия и прогнозы с использованием условного ожидания для различных типов случайных величин с некоторыми примерами, которые мы обсудим.
Условная дисперсия
Условная дисперсия случайной величины X, заданной Y, определяется аналогично условному ожиданию случайной величины X, заданной Y как
(Х|У)=Е[(ХЕ[Х|У])2|Г]
здесь дисперсия — это условное ожидание разницы между случайной величиной и квадратом условного ожидания X, заданного Y, когда задано значение Y.
Соотношение между условная дисперсия и условное ожидание is
(Х|У) = Е[Х2|Y] – (Е[X|Y])2
E[(X|Y)] = E[E[X2|Y]] – E[(E[X|Y])2]
= Е[Х2] – Е[(Е[ХУ])2]
поскольку E[E[X|Y]] = E[X], имеем
(Е[Х|У]) = Е[(Е[Х|У])2] — (БЫВШИЙ])2
это чем-то похоже на отношение безусловной дисперсии и ожидания, которое было
Var (X) = E [X2] — (БЫВШИЙ])2
и мы можем найти дисперсию с помощью условной дисперсии как
Var(X) = E[var(X|Y] + var(E[X|Y])
Пример условной дисперсии
Найдите среднее значение и дисперсию числа пассажиров, которые садятся в автобус, если люди, прибывшие на автобусную станцию, распределены по Пуассону со средним значением λt, а первоначальный автобус, прибывший на автобусную станцию, равномерно распределен в интервале (0, T) независимо от людей прибыл или нет.
Решение:
Чтобы найти среднее значение и дисперсию, позвольте для любого времени t, Y — случайная величина для времени прибытия автобуса, а N (t) — количество прибывших.
E[N(Y)|Y = t] = E[N(t)|Y = t]
в силу независимости Y и N (t)
=λt
поскольку N (t) пуассоновский со средним lambda t
следовательно
E[N(Y)|Y]=λY
поэтому принятие ожиданий дает
E[N(Y)] = λЭ[Г] = λТ / 2
Чтобы получить Var (N (Y)), воспользуемся формулой условной дисперсии
таким образом
(Н(Г)|Г) = λY
E[N(Y)|Y] = λY
Следовательно, из формулы условной дисперсии
Вар (N (Y)) = E [λГ]+(λY)
=λT/2 + λ2T2/ 12
где мы воспользовались тем, что Var (Y) = T2 / 12.
Дисперсия суммы случайного числа случайных величин
рассмотрим последовательность независимых и тождественных распределенный случайные величины X1,X2,X3,………. и другую случайную величину N, не зависящую от этой последовательности, найдем отклонение суммы этой последовательности как
через
что очевидно с определением дисперсии и условной дисперсии для отдельной случайной величины к сумме последовательности случайных величин, следовательно,
Прогноз
При прогнозировании значение одной случайной величины может быть предсказано на основе наблюдения другой случайной величины, для предсказания случайной величины Y, если наблюдаемая случайная величина равна X, мы используем g (X) как функцию, которая сообщает предсказанное значение, очевидно, что мы попробуйте выбрать g (X), близкую к Y, для этого наилучшим g является g (X) = E (Y | X), для этого мы должны минимизировать значение g, используя неравенство
Это неравенство можно получить как
Однако, учитывая X, E [Y | X] -g (X), будучи функцией X, можно рассматривать как константу. Таким образом,
что дает требуемое неравенство
Примеры прогнозирования
1. Замечено, что рост человека составляет шесть футов, каково было бы предсказание роста его сына после того, как он вырастет, если рост сына, который сейчас составляет x дюймов, нормально распределен со средним значением x + 1 и дисперсией 4.
Решение: пусть X будет случайной величиной, обозначающей рост человека, а Y — случайной величиной для роста сына, тогда случайная величина Y будет
Y = X + e + 1
здесь e представляет собой нормальную случайную величину, не зависящую от случайной величины X, со средним нулевым и четырехкратной дисперсией.
так что прогноз для роста сына
так что рост сына будет 73 дюйма после роста.
2. Рассмотрим пример отправки сигналов из местоположения A и местоположения B, если из местоположения A отправлено значение сигнала s, которое в местоположении B получено по нормальному распределению со средним значением s и дисперсией 1, тогда как если сигнал S, отправленный в A, нормально распределен со средним значением mu и дисперсией sigma ^ 2, как мы можем предсказать, что значение сигнала R, отправленное из местоположения A, будет получено как r в местоположении B?
Решение: значения сигналов S и R обозначают здесь случайные величины, распределенные нормально, сначала мы находим условную функцию плотности S для R как
этот K не зависит от S, теперь
здесь также C1 и C2 не зависят от S, поэтому значение условной функции плотности равно
C также не зависит от s. Таким образом, сигнал, отправленный из местоположения A как R и принятый в местоположении B как r, является нормальным со средним значением и дисперсией
и среднеквадратичная ошибка для этой ситуации равна
Линейный предсказатель
Каждый раз, когда мы не можем найти совместную функцию плотности вероятности, даже если известно среднее значение, дисперсия и корреляция между двумя случайными величинами, в такой ситуации очень полезен линейный предиктор одной случайной величины по отношению к другой случайной величине, который может предсказать минимум , поэтому для линейного предиктора случайной величины Y относительно случайной величины X мы берем a и b, чтобы минимизировать
Теперь частично дифференцируя по a и b, мы получим
решая эти два уравнения относительно и b, мы получим
таким образом минимизация этого ожидания дает линейный предсказатель как
где средние значения являются соответствующими средними значениями случайных величин X и Y, ошибка для линейного предиктора будет получена с математическим ожиданием
Эта ошибка будет ближе к нулю, если корреляция абсолютно положительная или совершенно отрицательная, то есть коэффициент корреляции равен +1 или -1.
Заключение
Обсуждалась условная дисперсия для дискретной и непрерывной случайной величины с различными примерами, одно из важных применений условного ожидания в прогнозировании также объясняется с помощью подходящих примеров и лучшего линейного предиктора, если вам требуется дальнейшее чтение, перейдите по ссылкам ниже.
Дополнительную информацию о математике см. В нашем Страница математики
Первый курс вероятности Шелдона Росс
Очерки вероятности и статистики Шаума
Введение в вероятность и статистику от ROHATGI и SALEH
В теории вероятностей и статистике условная дисперсия — дисперсия случайной величины с учетом значения (значений) одной или нескольких других переменных. В частности, в эконометрике условная дисперсия также известна как скедастическая функция или скедастическая функция . Условные дисперсии являются важной частью моделей авторегрессионной условной гетероскедастичности (ARCH).
Содержание
- 1 Определение
- 2 Объяснение, отношение к методу наименьших квадратов
- 3 Особые случаи, варианты
- 3.1 Условие для дискретных случайных величин
- 3.2 Определение с использованием условных распределений
- 4 Компоненты дисперсии
- 5 См. также
- 6 Ссылки
- 7 Дополнительная литература
Определение
Условная дисперсия случайной величины Y для другой случайной величины X равна
- Var (Y | X) = E ((Y — E (Y ∣ X)) 2 ∣ X). { displaystyle operatorname {Var} (Y | X) = Operatorname {E} { Big (} { big (} Y- operatorname {E} (Y mid X) { big)} ^ {2 } mid X { Big)}.}
Условная дисперсия сообщает нам, сколько дисперсии остается, если мы используем E (Y ∣ X) { displaystyle operatorname {E} (Y mid X)}


Объяснение, отношение к методу наименьших квадратов
Напомним, что дисперсия — это ожидаемое квадратичное отклонение между случайной величиной (скажем, Y) и ее ожидаемым значением. Ожидаемое значение можно рассматривать как разумное предсказание результатов случайного эксперимента (в частности, ожидаемое значение является лучшим постоянным предсказанием, когда предсказания оцениваются с помощью ожидаемой квадратичной ошибки предсказания). Таким образом, одна интерпретация дисперсии состоит в том, что она дает наименьшую возможную квадратичную ошибку предсказания. Если у нас есть сведения о другой случайной величине (X), которую мы можем использовать для прогнозирования Y, мы потенциально можем использовать это знание для уменьшения ожидаемой квадратичной ошибки. Оказывается, лучший прогноз Y с учетом X — это условное ожидание. В частности, для любого f: R → R { displaystyle f: mathbb {R} to mathbb {R}}
- E [(Y — f ( X)) 2] = E [(Y — E (Y | X) + E (Y | X) — f (X)) 2] = E [E {(Y — E (Y | X) + E (Y | X) — f (X)) 2 | X}] = E [Var (Y | X)] + E [(E (Y | X) — f (X)) 2]. { displaystyle { begin {align} operatorname {E} [(Yf (X)) ^ {2}] = operatorname {E} [(Y- operatorname {E} (Y | X) , , + , , operatorname {E} (Y | X) -f (X)) ^ {2}] \ = operatorname {E} [ operatorname {E} {(Y- operatorname { E} (Y | X) , , + , , operatorname {E} (Y | X) -f (X)) ^ {2} | X }] \ = operatorname {E} [ operatorname {Var} (Y | X)] + operatorname {E} [( operatorname {E} (Y | X) -f (X)) ^ {2}] ,. end {выровнено}} }
Выбрав f (X) = E (Y | X) { displaystyle f (X) = operatorname {E} (Y | X)} 
Особые случаи, вариации
Условие для дискретных случайных величин
Когда X принимает счетное множество значений S = {x 1, x 1,…} { displaystyle S = {x_ {1}, x_ {1}, dots }}

- Var (Y | X = x) = E ((Y — E (Y ∣ Икс = Икс)) 2 ∣ Икс = Икс), { Displaystyle OperatorName {Var} (Y | X = x) = OperatorName {E} ((Y- OperatorName {E} (Y mid X = x)) ^ {2} mid X = x),}
где напомним, что E (Z ∣ X = x) { displaystyle operatorname {E} (Z mid X = x) }


Обратите внимание, что здесь Var (Y | X = x) { displaystyle operatorname {Var} (Y | X = x)}

Связь этого определения с Var (Y | X) { displaystyle operatorname {Var} (Y | X)} 



Определение с использованием условных распределений
«Условное ожидание Y при X = x» также может быть определено в более общем плане с помощью условного распределения Y при X (это существует в данном случае, поскольку оба здесь X и Y являются действительными -значен).
В частности, если P Y | X { displaystyle P_ {Y | X}}

![{ displaystyle P_ {Y | X}: { mathcal {B}} times mathbb {R} to [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/88ddda966175068cbdbbc030c735007ba9e68e13)

Var (Y | X = x) = ∫ (y — ∫ y ′ PY | X (dy ′ | x)) 2 ПГ | Х (д у | х). { displaystyle operatorname {Var} (Y | X = x) = int (y- int y’P_ {Y | X} (dy ‘| x)) ^ {2} P_ {Y | X} (dy | x).}
Это, конечно, может быть специализировано для случая, когда Y сам по себе дискретен (заменяя интегралы суммами), а также когда условная плотность Y при X = x относительно к некоторому базовому дистрибутиву.
Компоненты дисперсии
Закон полной дисперсии гласит, что
Var (Y) = E (Var (Y ∣ X)) + Var (E (Y ∣ X)). { displaystyle operatorname {Var} (Y) = operatorname {E} ( operatorname {Var} (Y mid X)) + operatorname {Var} ( operatorname {E} (Y mid X)). }
На словах: дисперсия Y — это сумма ожидаемой условной дисперсии Y для данного X и дисперсии условного ожидания Y для X. Первый член отражает вариацию, оставшуюся после «использования X для прогнозирования Y», в то время как второй член отражает вариацию из-за среднего значения предсказания Y из-за случайности X.
См. также
Ссылки
Дополнительная литература
- Казелла, Джордж; Бергер, Роджер Л. (2002). Статистический вывод (Второе изд.). Уодсворт. С. 151–52. ISBN 0-534-24312-6.
В теории вероятностей и статистике , А условная дисперсия является дисперсией из случайной величины заданного значения (ов) из одного или более других переменных. В частности, в эконометрике условная дисперсия также известна как скедастическая функция или скедастическая функция . Условные дисперсии являются важной частью моделей авторегрессионной условной гетероскедастичности (ARCH).
Определение
Условная дисперсия случайной величины Y для другой случайной величины X равна
Условная дисперсия говорит нам , сколько разница остается , если мы используем «предсказать» Y . Здесь, как обычно, обозначает условное математическое ожидание из Y данного Х , который мы можем вспомнить, сама по себе является случайной величина (функция X , определяется с точностью до одной вероятности). В результате сама является случайной величиной (и является функцией X ).
Объяснение, отношение к методу наименьших квадратов
Напомним, что дисперсия — это ожидаемое квадратичное отклонение между случайной величиной (скажем, Y ) и ее ожидаемым значением. Ожидаемое значение можно рассматривать как разумное предсказание результатов случайного эксперимента (в частности, ожидаемое значение является лучшим постоянным предсказанием, когда предсказания оцениваются с помощью ожидаемой квадратичной ошибки предсказания). Таким образом, одна интерпретация дисперсии заключается в том, что она дает наименьшую возможную квадратичную ошибку предсказания. Если у нас есть сведения о другой случайной величине ( X ), которую мы можем использовать для прогнозирования Y , мы потенциально можем использовать это знание для уменьшения ожидаемой квадратичной ошибки. Как оказалось, наилучшее предсказание Y с учетом X — это условное ожидание. В частности, для любого измеримого
При выборе второй неотрицательный член становится равным нулю, показывая претензию. Здесь во втором равенстве использован закон полного ожидания . Мы также видим , что ожидаемая условная дисперсию Y данной X показывает, как неприводимая погрешность прогнозирования Y заданной только знание X .
Особые случаи, вариации
Обусловленность дискретными случайными величинами
Когда X принимает счетное множество значений с положительной вероятностью, то есть это дискретная случайная величина , мы можем ввести условную дисперсию Y при условии, что X = x для любого x из S следующим образом:
где напомним, что это условное ожидание Z при условии, что X = x , что хорошо определено для . Альтернативное обозначение для is
Заметим , что здесь определяет константу для возможных значений х , и , в частности, является не случайной величиной.
Связь этого определения с следующим образом: Пусть S такое же, как указано выше, и определим функцию как . Тогда почти наверняка .

Определение с использованием условных распределений
«Условное математическое ожидание Y дано X = X » , также может быть определенно в более общем случае, используя условное распределение по Y данного X (это существует в этом случае, как и здесь , Х и Y являются вещественными).
В частности, позволяя быть (регулярное) условное распределение по Y данного X , то есть (намерение , что почти наверняка за поддержку X ), мы можем определить


Это может, конечно, быть специализированы, когда Y является дискретным самим по себе (заменяя интегралы сумм), а также когда условная плотность по Y с учетом X = X относительно некоторого базового распределения существует.
Компоненты дисперсии
Закон общей дисперсии говорит

На словах: дисперсия Y представляет собой сумма ожидаемой условной дисперсии Y с учетом X и дисперсий условного математического ожидания Y данного X . Первый член захватывает изменение влево после того, как « с помощью X предсказать Y », а второе слагаемое фиксирует вариации , обусловленные среднее значение предсказания Y из — за случайности X .
Смотрите также
- Смешанная модель
- Модель случайных эффектов
Рекомендации
дальнейшее чтение
- Казелла, Джордж; Бергер, Роджер Л. (2002). Статистический вывод (второе изд.). Уодсворт. С. 151–52. ISBN 0-534-24312-6 .


![{displaystyle {begin{aligned}operatorname {E} [(Y-f(X))^{2}]&=operatorname {E} [(Y-operatorname {E} (Y|X),,+,,operatorname {E} (Y|X)-f(X))^{2}]\&=operatorname {E} [operatorname {E} {(Y-operatorname {E} (Y|X),,+,,operatorname {E} (Y|X)-f(X))^{2}|X}]\&=operatorname {E} [operatorname {Var} (Y|X)]+operatorname {E} [(operatorname {E} (Y|X)-f(X))^{2}],.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/53a7661b7f329003e656ea07186194e23e37ec09)






























