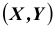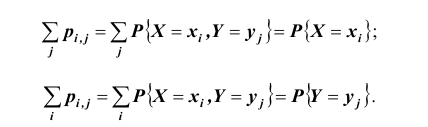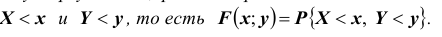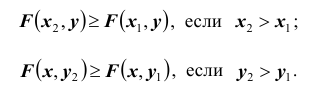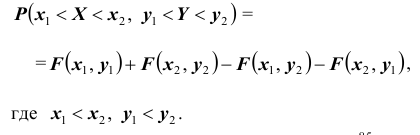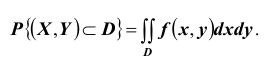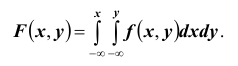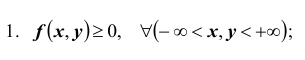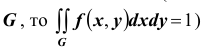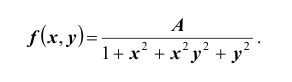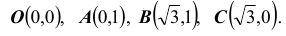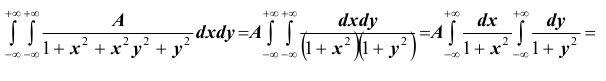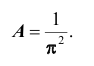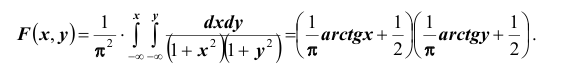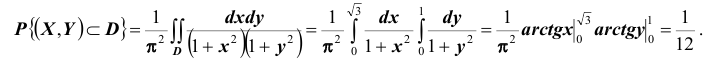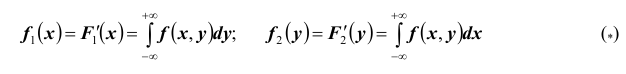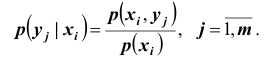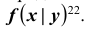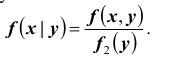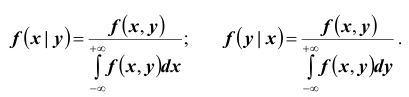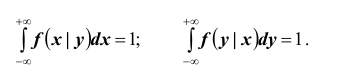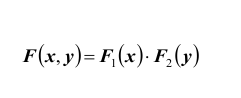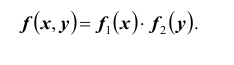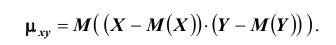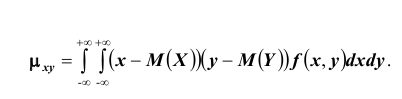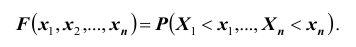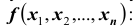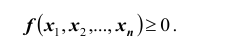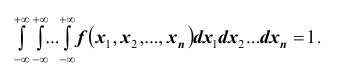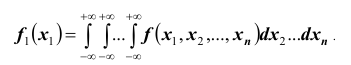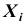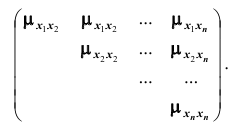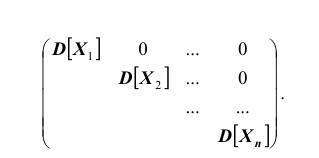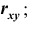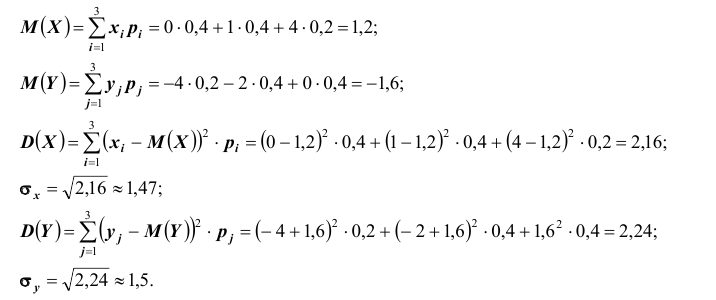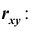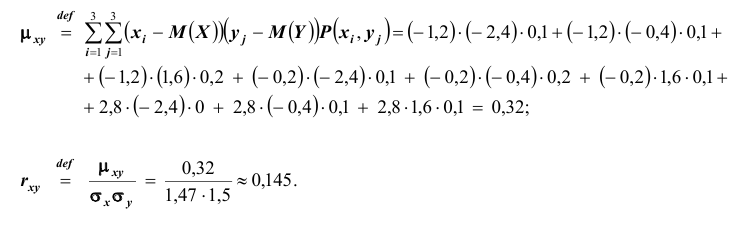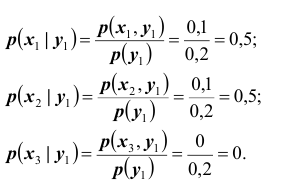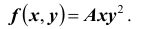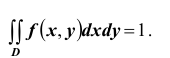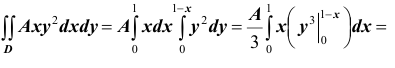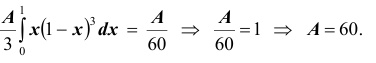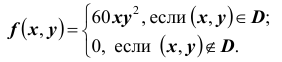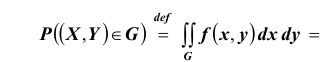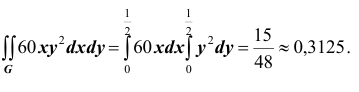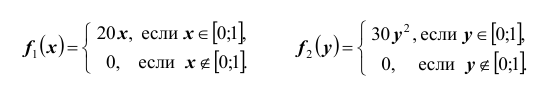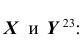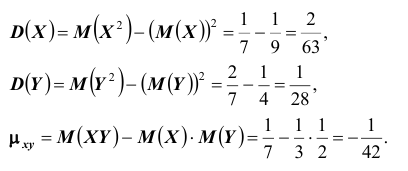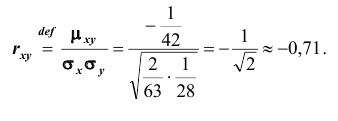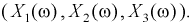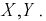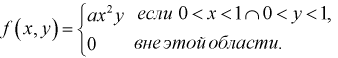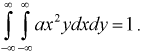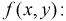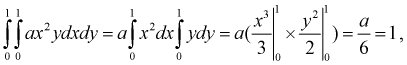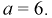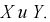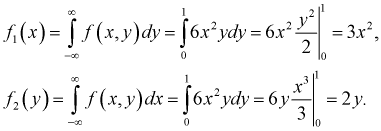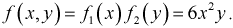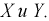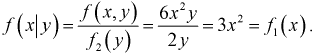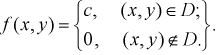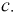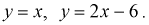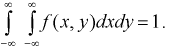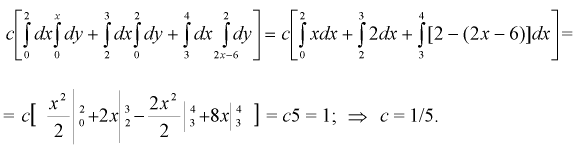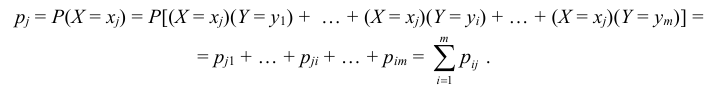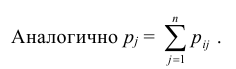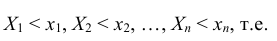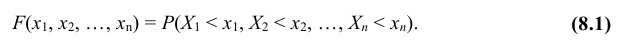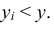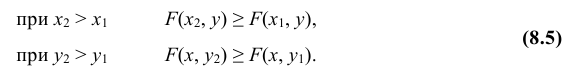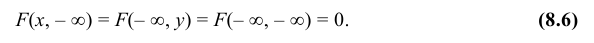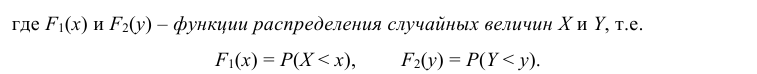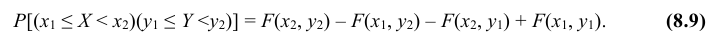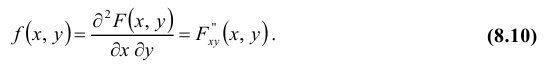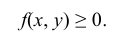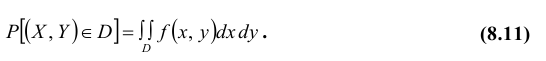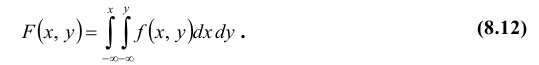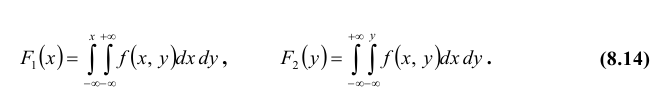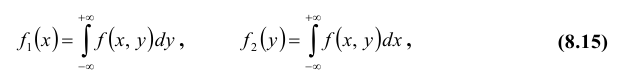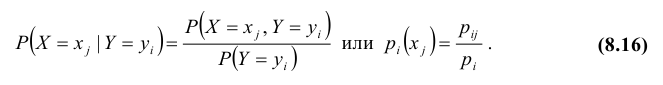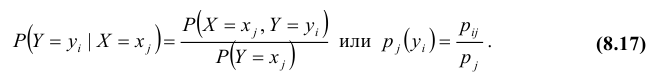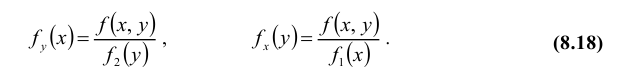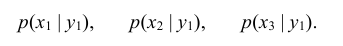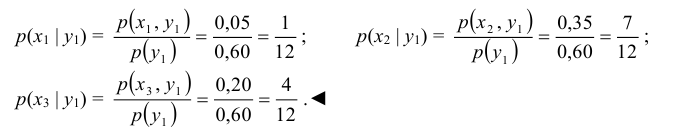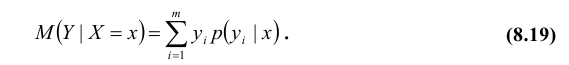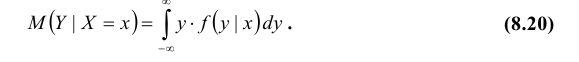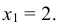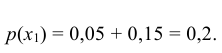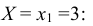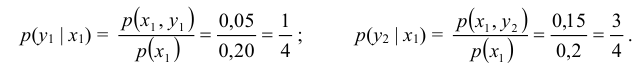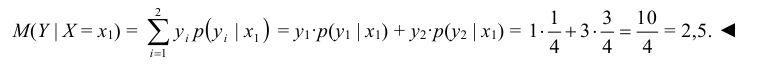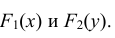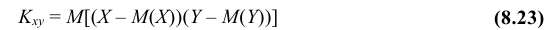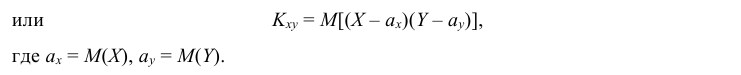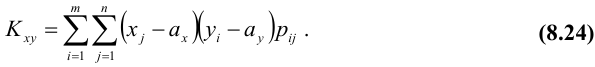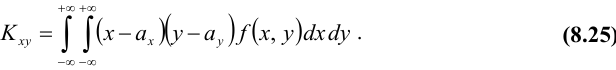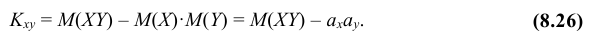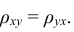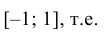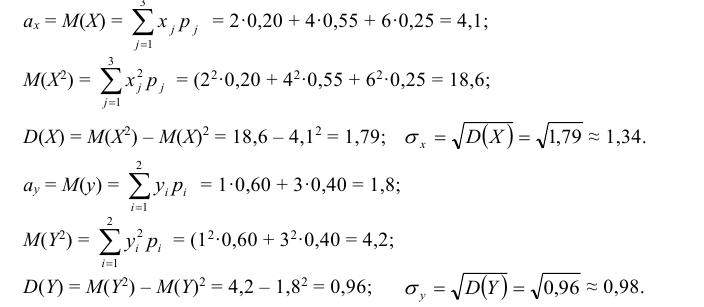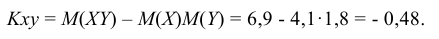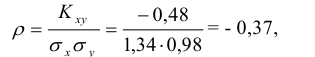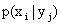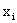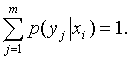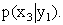Как найти условную вероятность дискретные величины - Исправление недочетов и поиск решений вместе с Examum.ru

Обратимся
теперь к зависимым величинам. Вероятностная
зависимость между случайными величинами
часто встречается на практике. Если
случайные величины X
и Y
находятся в вероятностной зависимости,
это не означает, что с изменением величины
X
величина Y
изменяется вполне определенным образом;
это лишь означает, что с изменением
величины X
величина Y
имеет тенденцию также изменяться
(например, возрастать или убывать с
ростом X).
Эта тенденция соблюдается лишь в общих
чертах, и в каком-то отдельном случае
от неё возможны отступления. Примеры
случайных величин, находящихся в
вероятностной зависимости: рост и
возраст ребенка; затраты и прибыль при
производстве определенной продукции;
затраты на рекламу и объем продаваемой
продукции.

Для
того, чтобы полностью описать систему,
недостаточно знать распределение каждой
из составляющих; нужно ещё знать
зависимость между величинами, входящими
в систему. Эта зависимость характеризуется
с помощью условных
законов распределения.

Условным
законом распределения одной из случайных
величин,
входящих в систему (X,Y),
называется её закон распределения,
найденный при условии, что другая
случайная величина приняла определённое
значение (или попала в какой-то интервал).

Пусть
(X,Y)
– дискретная двумерная случайная
величина и

В
соответствии с определением условных
вероятностей событий^*),
условная вероятность того, что случайная
величина Х примет значение
при условии,
определяется равенством

(34)

Совокупность
вероятностей (34), то есть
,
представляет собой условный закон
распределения случайной величины Х при
условии.
Сумма условных вероятностей

Аналогично
определяются условная вероятность и
условный закон распределения случайной
величины Y
при условии
:

(35)

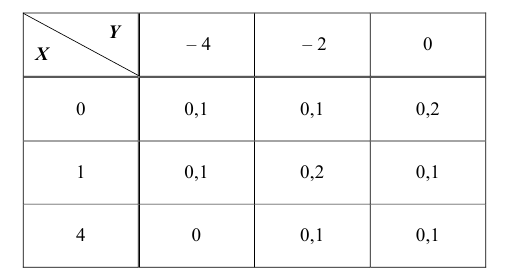
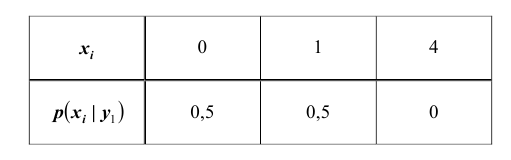
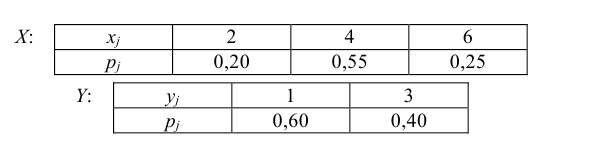
Пример
8. Пусть закон
распределения двумерного случайного
вектора (X,Y)
задан таблицей 2 (стр. 8). Найти условный
закон распределения случайной величины
Х при Y
=0,1.

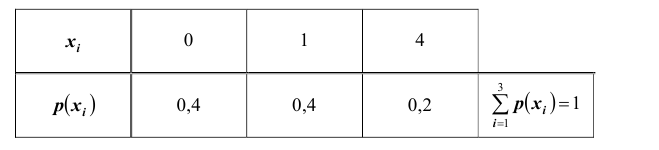
Решение.
С учетом
формулы (34) имеем:

(значение
взято из безусловного закона распределения
случайной величиныY,
приведенного в таблице 4 на стр. 9).

^*)Пусть А и
В – случайные события. Тогда вероятность
их совместного появления равна
,
где— условная вероятность события В при
условии, что событие А произошло;— условная вероятность события А при
условии, что событие В произошло. Тогда,.

Таким
образом, условный закон распределения
случайной величины Х при Y
=0,1 таков:

Таблица 5

Х	5	6	7
	0,4	0,6	0

Сравнивая
найденный условный закон распределения
случайной величины Х с безусловным
законом её распределения (таблица 3 на
стр. 8), видим, что они различны.
Следовательно, случайные величины X
и Y
находятся в
вероятностной зависимости.

Пусть
теперь (X,Y)
– непрерывная двумерная случайная
величина с плотностью
;и—
плотности распределения соответственно
случайной величины Х и случайной величиныY.

Условной
плотностью распределения составляющей
X
при условии Y=y
называют отношение плотности совместного
распределения к плотности распределения
составляющей Y:

(36)

Аналогично
определяется условная плотность
распределения составляющей Y
при условии X=x:

(37)

Из
(36) и (37) получим:

.
(38)

Таким
образом, плотность распределения системы
двух непрерывных случайных величин
равна произведению плотности одной
составляющей на условную плотность
другой составляющей.

Как
и любая плотность распределения, условные
плотности обладают следующими свойствами:

(39)

Пример
9. Непрерывный
вектор (X,Y)
равномерно распределен в круге с
радиусом 1, то есть

Найти
условные плотности распределения
компонент этого вектора.

Решение

Условную
плотность составляющей Х при
найдём по формуле (36):

Так
как
при,
топри.

Аналогично находим:

;

при

Итак,
искомые условные плотности распределения
составляющих системы (X,Y)
имеют вид:

Для
независимых случайных величин условная
плотность распределения совпадает с
безусловной плотностью распределения.
Действительно,

(40)

Аналогично
(41)

Степень
зависимости между случайными величинами
обычно оценивают с помощью числовых
характеристик зависимости.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Сергей Евгеньевич Грамотинский

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Определение 1

Условным законом распределения одной из составляющих двумерной случайной величины $(X,Y)$ называется её закон распределения, вычисленный при условии, что другая составляющая принимает определенное значение или попадает в определенный интеграл.

Введем теперь по отдельности определения условного закона распределения для составляющей $X$ и для составляющей $Y$.

Условные законы распределения составляющих дискретной двумерной случайной величины

Пусть $(X,Y)$ — дискретная двумерная случайная величина.

Определение 2

Условным распределением составляющей $X$ при $Y=y$ называется совокупность условных вероятностей $pleft(x_1,yright), pleft(x_2,yright),..,pleft(x_n,yright)$ при условии, что событие $Y=y$ уже произошло.

Если известен закон распределения двумерной случайной величины $(X,Y)$, то условная составляющая $X$ представляется в виде

Определение 3

Условным распределением составляющей $Y$ при $X=x$ называется совокупность условных вероятностей $pleft(x,y_1right), pleft(x,y_2right),..,pleft(x,y_mright)$ при условии, что событие $X=x$ уже произошло.

Условные законы распределения составляющих непрерывной двумерной случайной величины

Пусть $(X,Y)$ — непрерывная двумерная случайная величина.

Напомним, что для непрерывной случайной величины существует понятие плотности распределения случайной величины.

Определение 4

Условной плотностью $varphi (x/y)$ распределения составляющей $X$ при $Y=y$ называется отношение плотности $varphi (x,y)$ двумерной случайной величины $(X,Y)$ к плотности распределения $varphi (y)$ при условии, что составляющая $Y$ приняла конкретное значение или попала в заданный интервал. То есть

[varphi (x/y)=frac{varphi (x,y)}{varphi (y)}]

«Условные законы распределения составляющих системы» 👇

Определение 5

Условной плотностью $varphi (y/x)$ распределения составляющей $Y$ при $X=x$ называется отношение плотности $varphi (x,y)$ двумерной случайной величины $(X,Y)$ к плотности распределения $varphi (x)$ при условии, что составляющая $X$ приняла конкретное значение или попала в заданный интервал. То есть

[varphi (y/x)=frac{varphi (x,y)}{varphi (x)}]

Приведем еще две формулы для вычисления условных плотностей распределения. Если известна плотность совместного распределения, то условные плотности по составляющей $X$ и по составляющей $Y$ можно найти по формулам:

Введем несколько свойств для функций условной плотности распределения.

Свойство 1: Функции условной плотности распределения неотрицательны на всей области определения, то есть:

Свойство 2: Выполняются следующие равенства:

Условное математическое ожидание

Введем формулы для вычисления условных математических ожиданий для различных случаев.

Условное математическое ожидание дискретной случайной величины $Y$ при $X=x$:

Условное математическое ожидание дискретной случайной величины $X$ при $Y=y$:

Условное математическое ожидание непрерывной случайной величины $Y$ при $X=x$:

Условное математическое ожидание непрерывной случайной величины $X$ при $Y=y$:

Определение 7

Условное математическое ожидание $M(X/Y)$ называется функцией регрессии $Y$ на $X$.

Пример задачи на условное распределение

Пример 1

Распределение случайной величины задано таблицей.

Рисунок 1.

Найти для этой двумерной случайной величины условное распределение по составляющей $X$, если $Y=10$.

Решение.

Для нахождения условного распределения по составляющей $X$, будем использовать следующую формулу:

[pleft(x_i/yright)=frac{pleft(x_i,yright)}{p(y)}]

Для начала необходимо найти ряд распределения случайной величины $Y$.

С помощью простейших вычислений, получим:

Рисунок 2.

Для нахождения условного распределения по составляющей $X$, будем использовать следующую формулу:

[pleft(x_i/yright)=frac{pleft(x_i,yright)}{p(y)}]

Y=10

[pleft(x_1/Y=10right)=frac{0,02}{0,06}=frac{1}{3}] [pleft(x_2/Y=10right)=frac{0,04}{0,06}=frac{2}{3}] [pleft(x_3/Y=10right)=frac{0}{0,06}=0] [pleft(x_4/Y=10right)=frac{0}{0,06}=0] [pleft(x_5/Y=10right)=frac{0}{0,06}=0] [pleft(x_6/Y=10right)=frac{0}{0,06}=0]

Получаем следующий ряд условного распределения по составляющей $X$:

Рисунок 3.

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

In probability theory, conditional probability is a measure of the probability of an event occurring, given that another event (by assumption, presumption, assertion or evidence) has already occurred.^[1] This particular method relies on event B occurring with some sort of relationship with another event A. In this event, the event B can be analyzed by a conditional probability with respect to A. If the event of interest is A and the event B is known or assumed to have occurred, «the conditional probability of A given B«, or «the probability of A under the condition B«, is usually written as P(A|B)^[2] or occasionally P_B(A). This can also be understood as the fraction of probability B that intersects with A: ${displaystyle P(Amid B)={frac {P(Acap B)}{P(B)}}}$ .^[3]

For example, the probability that any given person has a cough on any given day may be only 5%. But if we know or assume that the person is sick, then they are much more likely to be coughing. For example, the conditional probability that someone unwell (sick) is coughing might be 75%, in which case we would have that P(Cough) = 5% and P(Cough|Sick) = 75 %. Although there is a relationship between A and B in this example, such a relationship or dependence between A and B is not necessary, nor do they have to occur simultaneously.

P(A|B) may or may not be equal to P(A) (the unconditional probability of A). If P(A|B) = P(A), then events A and B are said to be independent: in such a case, knowledge about either event does not alter the likelihood of each other. P(A|B) (the conditional probability of A given B) typically differs from P(B|A). For example, if a person has dengue fever, the person might have a 90% chance of being tested as positive for the disease. In this case, what is being measured is that if event B (having dengue) has occurred, the probability of A (tested as positive) given that B occurred is 90%, simply writing P(A|B) = 90%. Alternatively, if a person is tested as positive for dengue fever, they may have only a 15% chance of actually having this rare disease due to high false positive rates. In this case, the probability of the event B (having dengue) given that the event A (testing positive) has occurred is 15% or P(B|A) = 15%. It should be apparent now that falsely equating the two probabilities can lead to various errors of reasoning, which is commonly seen through base rate fallacies.

While conditional probabilities can provide extremely useful information, limited information is often supplied or at hand. Therefore, it can be useful to reverse or convert a conditional probability using Bayes’ theorem: .^[4] Another option is to display conditional probabilities in conditional probability table to illuminate the relationship between events.

Definition[edit]

Illustration of conditional probabilities with an Euler diagram. The unconditional probability P(A) = 0.30 + 0.10 + 0.12 = 0.52. However, the conditional probability P(A|B₁) = 1, P(A|B₂) = 0.12 ÷ (0.12 + 0.04) = 0.75, and P(A|B₃) = 0.

On a tree diagram, branch probabilities are conditional on the event associated with the parent node. (Here, the overbars indicate that the event does not occur.)

Venn Pie Chart describing conditional probabilities

Conditioning on an event[edit]

Kolmogorov definition[edit]

Given two events A and B from the sigma-field of a probability space, with the unconditional probability of B being greater than zero (i.e., P(B) > 0), the conditional probability of A given B () is the probability of A occurring if B has or is assumed to have happened.^[5] A is assumed to be the set of all possible outcomes of an experiment or random trial that has a restricted or reduced sample space. The conditional probability can be found by the quotient of the probability of the joint intersection of events A and B ()—the probability at which A and B occur together, although not necessarily occurring at the same time—and the probability of B:^[2]^[6]^[7]

${displaystyle P(Amid B)={frac {P(Acap B)}{P(B)}}}$

For a sample space consisting of equal likelihood outcomes, the probability of the event A is understood as the fraction of the number of outcomes in A to the number of all outcomes in the sample space. Then, this equation is understood as the fraction of the set Acap B to the set B. Note that the above equation is a definition, not just a theoretical result. We denote the quantity ${displaystyle {frac {P(Acap B)}{P(B)}}}$ as and call it the «conditional probability of A given B.»

As an axiom of probability[edit]

Some authors, such as de Finetti, prefer to introduce conditional probability as an axiom of probability:

This equation for a conditional probability, although mathematically equivalent, may be intuitively easier to understand. It can be interpreted as «the probability of B occurring multiplied by the probability of A occurring, provided that B has occurred, is equal to the probability of the A and B occurrences together, although not necessarily occurring at the same time». Additionally, this may be preferred philosophically; under major probability interpretations, such as the subjective theory, conditional probability is considered a primitive entity. Moreover, this «multiplication rule» can be practically useful in computing the probability of Acap B and introduces a symmetry with the summation axiom for Poincaré Formula:

{displaystyle P(Acup B)=P(A)+P(B)-P(Acap B)}

Thus the equations can be combined to find a new representation of the :

{displaystyle P(Acap B)=P(A)+P(B)-P(Acup B)=P(Amid B)P(B)}

{displaystyle P(Acup B)={P(A)+P(B)-P(Amid B){P(B)}}}

As the probability of a conditional event[edit]

Conditional probability can be defined as the probability of a conditional event A_B . The Goodman–Nguyen–Van Fraassen conditional event can be defined as:

${displaystyle A_{B}=bigcup _{igeq 1}left(bigcap _{j<i}{overline {B}}_{j},A_{i}B_{i}right)}$

, where ${displaystyle A_{i}}$

and ${displaystyle B_{i}}$

represent states or elements of A or B. ^[8]

It can be shown that

${displaystyle P(A_{B})={frac {P(Acap B)}{P(B)}}}$

which meets the Kolmogorov definition of conditional probability.^[9]

Conditioning on an event of probability zero[edit]

If , then according to the definition, is undefined.

The case of greatest interest is that of a random variable Y, conditioned on a continuous random variable X resulting in a particular outcome x. The event has probability zero and, as such, cannot be conditioned on.

Instead of conditioning on X being exactly x, we could condition on it being closer than distance epsilon away from x. The event will generally have nonzero probability and hence, can be conditioned on.
We can then take the limit

${displaystyle lim _{epsilon to 0}P(Amid x-epsilon <X<x+epsilon ).}$

For example, if two continuous random variables X and Y have a joint density $f_{{X,Y}}(x,y)$ , then by L’Hôpital’s rule and Leibniz integral rule, upon differentiation with respect to epsilon :

${displaystyle {begin{aligned}lim _{epsilon to 0}P(Yin Umid x_{0}-epsilon <X<x_{0}+epsilon )&=lim _{epsilon to 0}{frac {int _{x_{0}-epsilon }^{x_{0}+epsilon }int _{U}f_{X,Y}(x,y)mathrm {d} ymathrm {d} x}{int _{x_{0}-epsilon }^{x_{0}+epsilon }int _{mathbb {R} }f_{X,Y}(x,y)mathrm {d} ymathrm {d} x}}\&={frac {int _{U}f_{X,Y}(x_{0},y)mathrm {d} y}{int _{mathbb {R} }f_{X,Y}(x_{0},y)mathrm {d} y}}.end{aligned}}}$

The resulting limit is the conditional probability distribution of Y given X and exists when the denominator, the probability density ${displaystyle f_{X}(x_{0})}$ , is strictly positive.

It is tempting to define the undefined probability using this limit, but this cannot be done in a consistent manner. In particular, it is possible to find random variables X and W and values x, w such that the events and are identical but the resulting limits are not:^[10]

${displaystyle lim _{epsilon to 0}P(Amid x-epsilon leq Xleq x+epsilon )neq lim _{epsilon to 0}P(Amid w-epsilon leq Wleq w+epsilon ).}$

The Borel–Kolmogorov paradox demonstrates this with a geometrical argument.

Conditioning on a discrete random variable[edit]

Let X be a discrete random variable and its possible outcomes denoted V. For example, if X represents the value of a rolled die then V is the set . Let us assume for the sake of presentation that X is a discrete random variable, so that each value in V has a nonzero probability.

For a value x in V and an event A, the conditional probability
is given by .
Writing

for short, we see that it is a function of two variables, x and A.

For a fixed A, we can form the random variable . It represents an outcome of whenever a value x of X is observed.

The conditional probability of A given X can thus be treated as a random variable Y with outcomes in the interval [0,1] . From the law of total probability, its expected value is equal to the unconditional probability of A.

Partial conditional probability[edit]

The partial conditional probability
${displaystyle P(Amid B_{1}equiv b_{1},ldots ,B_{m}equiv b_{m})}$
is about the probability of event
given that each of the condition events
$B_{i}$ has occurred to a degree
$b_{i}$ (degree of belief, degree of experience) that might be different from 100%. Frequentistically, partial conditional probability makes sense, if the conditions are tested in experiment repetitions of appropriate length
.^[11] Such
-bounded partial conditional probability can be defined as the conditionally expected average occurrence of event
in testbeds of length
that adhere to all of the probability specifications
${displaystyle B_{i}equiv b_{i}}$ , i.e.:

${displaystyle P^{n}(Amid B_{1}equiv b_{1},ldots ,B_{m}equiv b_{m})=operatorname {E} ({overline {A}}^{n}mid {overline {B}}_{1}^{n}=b_{1},ldots ,{overline {B}}_{m}^{n}=b_{m})}$

^[11]

Based on that, partial conditional probability can be defined as

${displaystyle P(Amid B_{1}equiv b_{1},ldots ,B_{m}equiv b_{m})=lim _{nto infty }P^{n}(Amid B_{1}equiv b_{1},ldots ,B_{m}equiv b_{m}),}$

where ${displaystyle b_{i}nin mathbb {N} }$ ^[11]

Jeffrey conditionalization^[12]^[13]
is a special case of partial conditional probability, in which the condition events must form a partition:

${displaystyle P(Amid B_{1}equiv b_{1},ldots ,B_{m}equiv b_{m})=sum _{i=1}^{m}b_{i}P(Amid B_{i})}$

Example[edit]

Suppose that somebody secretly rolls two fair six-sided dice, and we wish to compute the probability that the face-up value of the first one is 2, given the information that their sum is no greater than 5.

Let D₁ be the value rolled on die 1.
Let D₂ be the value rolled on die 2.

Probability that D₁ = 2

Table 1 shows the sample space of 36 combinations of rolled values of the two dice, each of which occurs with probability 1/36, with the numbers displayed in the red and dark gray cells being D₁ + D₂.

D₁ = 2 in exactly 6 of the 36 outcomes; thus P(D₁ = 2) = 6⁄36 = 1⁄6:

Table 1

+	D₂
1	2	3	4	5	6
D₁	1	2	3	4	5	6	7
2	3	4	5	6	7	8
3	4	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

Probability that D₁ + D₂ ≤ 5

Table 2 shows that D₁ + D₂ ≤ 5 for exactly 10 of the 36 outcomes, thus P(D₁ + D₂ ≤ 5) = 10⁄36:

Table 2

+	D₂
1	2	3	4	5	6
D₁	1	2	3	4	5	6	7
2	3	4	5	6	7	8
3	4	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

Probability that D₁ = 2 given that D₁ + D₂ ≤ 5

Table 3 shows that for 3 of these 10 outcomes, D₁ = 2.

Thus, the conditional probability P(D₁ = 2 | D₁+D₂ ≤ 5) = 3⁄10 = 0.3:

Table 3

+	D₂
1	2	3	4	5	6
D₁	1	2	3	4	5	6	7
2	3	4	5	6	7	8
3	4	5	6	7	8	9
4	5	6	7	8	9	10
5	6	7	8	9	10	11
6	7	8	9	10	11	12

Here, in the earlier notation for the definition of conditional probability, the conditioning event B is that D₁ + D₂ ≤ 5, and the event A is D₁ = 2. We have ${displaystyle P(Amid B)={tfrac {P(Acap B)}{P(B)}}={tfrac {3/36}{10/36}}={tfrac {3}{10}},}$ as seen in the table.

Use in inference[edit]

In statistical inference, the conditional probability is an update of the probability of an event based on new information.^[14] The new information can be incorporated as follows:^[1]

This approach results in a probability measure that is consistent with the original probability measure and satisfies all the Kolmogorov axioms. This conditional probability measure also could have resulted by assuming that the relative magnitude of the probability of A with respect to X will be preserved with respect to B (cf. a Formal Derivation below).

The wording «evidence» or «information» is generally used in the Bayesian interpretation of probability. The conditioning event is interpreted as evidence for the conditioned event. That is, P(A) is the probability of A before accounting for evidence E, and P(A|E) is the probability of A after having accounted for evidence E or after having updated P(A). This is consistent with the frequentist interpretation, which is the first definition given above.

Example[edit]

When Morse code is transmitted, there is a certain probability that the «dot» or «dash» that was received is erroneous. This is often taken as interference in the transmission of a message. Therefore, it is important to consider when sending a «dot», for example, the probability that a «dot» was received. This is represented by: ${displaystyle P(dot sentmid dot received)=P(dot receivedmid dot sent){frac {P(dot sent)}{P(dot received)}}.}$ In Morse code, the ratio of dots to dashes is 3:4 at the point of sending, so the probability of a «dot» and «dash» are ${displaystyle P(dot sent)={frac {3}{7}} and P(dash sent)={frac {4}{7}}}$ . If it is assumed that the probability that a dot is transmitted as a dash is 1/10, and that the probability that a dash is transmitted as a dot is likewise 1/10, then Bayes’s rule can be used to calculate .

${displaystyle P(dot received)={frac {9}{10}}times {frac {3}{7}}+{frac {1}{10}}times {frac {4}{7}}={frac {31}{70}}}$

Now, can be calculated:

${displaystyle P(dot sentmid dot received)=P(dot receivedmid dot sent){frac {P(dot sent)}{P(dot received)}}={frac {9}{10}}times {frac {frac {3}{7}}{frac {31}{70}}}={frac {27}{31}}}$ ^[15]

Statistical independence[edit]

Events A and B are defined to be statistically independent if the probability of the intersection of A and B is equal to the product of the probabilities of A and B:

If P(B) is not zero, then this is equivalent to the statement that

Similarly, if P(A) is not zero, then

is also equivalent. Although the derived forms may seem more intuitive, they are not the preferred definition as the conditional probabilities may be undefined, and the preferred definition is symmetrical in A and B. Independence does not refer to a disjoint event.^[16]

It should also be noted that given the independent event pair [A B] and an event C, the pair is defined to be conditionally independent if the product holds true:^[17]

This theorem could be useful in applications where multiple independent events are being observed.

Independent events vs. mutually exclusive events

The concepts of mutually independent events and mutually exclusive events are separate and distinct. The following table contrasts results for the two cases (provided that the probability of the conditioning event is not zero).

	If statistically independent	If mutually exclusive
		0
		0
		0

In fact, mutually exclusive events cannot be statistically independent (unless both of them are impossible), since knowing that one occurs gives information about the other (in particular, that the latter will certainly not occur).

Common fallacies[edit]

These fallacies should not be confused with Robert K. Shope’s 1978 «conditional fallacy», which deals with counterfactual examples that beg the question.

Assuming conditional probability is of similar size to its inverse[edit]

A geometric visualisation of Bayes’ theorem. In the table, the values 3, 1, 2 and 6 give the relative weights of each corresponding condition and case. The figures denote the cells of the table involved in each metric, the probability being the fraction of each figure that is shaded. This shows that P(A|B) P(B) = P(B|A) P(A) i.e. P(A|B) = P(B|A) P(A)/P(B) . Similar reasoning can be used to show that P(Ā|B) =

P(B|Ā) P(Ā)/P(B) etc.

In general, it cannot be assumed that P(A|B) ≈ P(B|A). This can be an insidious error, even for those who are highly conversant with statistics.^[18] The relationship between P(A|B) and P(B|A) is given by Bayes’ theorem:

${displaystyle {begin{aligned}P(Bmid A)&={frac {P(Amid B)P(B)}{P(A)}}\Leftrightarrow {frac {P(Bmid A)}{P(Amid B)}}&={frac {P(B)}{P(A)}}end{aligned}}}$

That is, P(A|B) ≈ P(B|A) only if P(B)/P(A) ≈ 1, or equivalently, P(A) ≈ P(B).

Assuming marginal and conditional probabilities are of similar size[edit]

In general, it cannot be assumed that P(A) ≈ P(A|B). These probabilities are linked through the law of total probability:

${displaystyle P(A)=sum _{n}P(Acap B_{n})=sum _{n}P(Amid B_{n})P(B_{n}).}$

where the events $(B_{n})$ form a countable partition of Omega .

This fallacy may arise through selection bias.^[19] For example, in the context of a medical claim, let S_C be the event that a sequela (chronic disease) S occurs as a consequence of circumstance (acute condition) C. Let H be the event that an individual seeks medical help. Suppose that in most cases, C does not cause S (so that P(S_C) is low). Suppose also that medical attention is only sought if S has occurred due to C. From experience of patients, a doctor may therefore erroneously conclude that P(S_C) is high. The actual probability observed by the doctor is P(S_C|H).

Over- or under-weighting priors[edit]

Not taking prior probability into account partially or completely is called base rate neglect. The reverse, insufficient adjustment from the prior probability is conservatism.

Formal derivation[edit]

Formally, P(A | B) is defined as the probability of A according to a new probability function on the sample space, such that outcomes not in B have probability 0 and that it is consistent with all original probability measures.^[20]^[21]

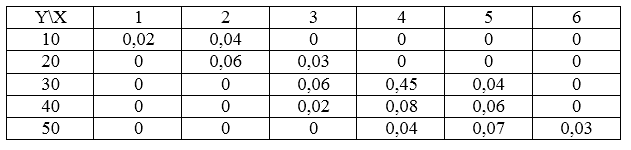
Let Ω be a discrete sample space with elementary events {ω}, and let P be the probability measure with respect to the σ-algebra of Ω. Suppose we are told that the event B ⊆ Ω has occurred. A new probability distribution (denoted by the conditional notation) is to be assigned on {ω} to reflect this. All events that are not in B will have null probability in the new distribution. For events in B, two conditions must be met: the probability of B is one and the relative magnitudes of the probabilities must be preserved. The former is required by the axioms of probability, and the latter stems from the fact that the new probability measure has to be the analog of P in which the probability of B is one — and every event that is not in B, therefore, has a null probability. Hence, for some scale factor α, the new distribution must satisfy:

${displaystyle sum _{omega in Omega }{P(omega mid B)}=1.}$

Substituting 1 and 2 into 3 to select α:

${displaystyle {begin{aligned}1&=sum _{omega in Omega }{P(omega mid B)}\&=sum _{omega in B}{P(omega mid B)}+{cancelto {0}{sum _{omega notin B}P(omega mid B)}}\&=alpha sum _{omega in B}{P(omega )}\[5pt]&=alpha cdot P(B)\[5pt]Rightarrow alpha &={frac {1}{P(B)}}end{aligned}}}$

So the new probability distribution is

${displaystyle omega in B:P(omega mid B)={frac {P(omega )}{P(B)}}}$

Now for a general event A,

${displaystyle {begin{aligned}P(Amid B)&=sum _{omega in Acap B}{P(omega mid B)}+{cancelto {0}{sum _{omega in Acap B^{c}}P(omega mid B)}}\&=sum _{omega in Acap B}{frac {P(omega )}{P(B)}}\[5pt]&={frac {P(Acap B)}{P(B)}}end{aligned}}}$

References[edit]

^ ^a ^b Gut, Allan (2013). Probability: A Graduate Course (Second ed.). New York, NY: Springer. ISBN 978-1-4614-4707-8.
^ ^a ^b «Conditional Probability». www.mathsisfun.com. Retrieved 2020-09-11.
^ Dekking, Frederik Michel; Kraaikamp, Cornelis; Lopuhaä, Hendrik Paul; Meester, Ludolf Erwin (2005). «A Modern Introduction to Probability and Statistics». Springer Texts in Statistics: 26. doi:10.1007/1-84628-168-7. ISBN 978-1-85233-896-1. ISSN 1431-875X.
^ Dekking, Frederik Michel; Kraaikamp, Cornelis; Lopuhaä, Hendrik Paul; Meester, Ludolf Erwin (2005). «A Modern Introduction to Probability and Statistics». Springer Texts in Statistics: 25–40. doi:10.1007/1-84628-168-7. ISBN 978-1-85233-896-1. ISSN 1431-875X.
^ Reichl, Linda Elizabeth (2016). «2.3 Probability». A Modern Course in Statistical Physics (4th revised and updated ed.). WILEY-VCH. ISBN 978-3-527-69049-7.
^ Kolmogorov, Andrey (1956), Foundations of the Theory of Probability, Chelsea
^ «Conditional Probability». www.stat.yale.edu. Retrieved 2020-09-11.
^ Flaminio, Tommaso; Godo, Lluis; Hosni, Hykel (2020-09-01). «Boolean algebras of conditionals, probability and logic». Artificial Intelligence. 286: 103347. arXiv:2006.04673. doi:10.1016/j.artint.2020.103347. ISSN 0004-3702. S2CID 214584872.
^ Van Fraassen, Bas C. (1976), Harper, William L.; Hooker, Clifford Alan (eds.), «Probabilities of Conditionals», Foundations of Probability Theory, Statistical Inference, and Statistical Theories of Science: Volume I Foundations and Philosophy of Epistemic Applications of Probability Theory, The University of Western Ontario Series in Philosophy of Science, Dordrecht: Springer Netherlands, pp. 261–308, doi:10.1007/978-94-010-1853-1_10, ISBN 978-94-010-1853-1, retrieved 2021-12-04
^ Gal, Yarin. «The Borel–Kolmogorov paradox» (PDF).
^ ^a ^b ^c Draheim, Dirk (2017). «Generalized Jeffrey Conditionalization (A Frequentist Semantics of Partial Conditionalization)». Springer. Retrieved December 19, 2017.
^ Jeffrey, Richard C. (1983), The Logic of Decision, 2nd edition, University of Chicago Press, ISBN 9780226395821
^ «Bayesian Epistemology». Stanford Encyclopedia of Philosophy. 2017. Retrieved December 29, 2017.
^ Casella, George; Berger, Roger L. (2002). Statistical Inference. Duxbury Press. ISBN 0-534-24312-6.
^ «Conditional Probability and Independence» (PDF). Retrieved 2021-12-22.
^ Tijms, Henk (2012). Understanding Probability (3 ed.). Cambridge: Cambridge University Press. doi:10.1017/cbo9781139206990. ISBN 978-1-107-65856-1.
^ Pfeiffer, Paul E. (1978). Conditional Independence in Applied Probability. Boston, MA: Birkhäuser Boston. ISBN 978-1-4612-6335-7. OCLC 858880328.
^ Paulos, J.A. (1988) Innumeracy: Mathematical Illiteracy and its Consequences, Hill and Wang. ISBN 0-8090-7447-8 (p. 63 et seq.)
^ F. Thomas Bruss Der Wyatt-Earp-Effekt oder die betörende Macht kleiner Wahrscheinlichkeiten (in German), Spektrum der Wissenschaft (German Edition of Scientific American), Vol 2, 110–113, (2007).
^ George Casella and Roger L. Berger (1990), Statistical Inference, Duxbury Press, ISBN 0-534-11958-1 (p. 18 et seq.)
^ Grinstead and Snell’s Introduction to Probability, p. 134

External links[edit]

Weisstein, Eric W. «Conditional Probability». MathWorld.
Visual explanation of conditional probability

Источник

Содержание:

Многомерные случайные величины:

До сих пор рассматривались случайные величины, возможные значения которых определялись одним числом. Такие величины называют одномерными. Например, число очков, которое может выпасть при бросании игральной кости – дискретная одномерная величина; расстояние от орудия до места падения снаряда – непрерывная одномерная случайная величина. Однако, при изучении случайных явлений в зависимости от их сложности иногда приходится использовать две, три и более случайных величин. Например, точка попадания снаряда определяется не одной, а двумя случайными величинами – абсциссой и ординатой. При различных измерениях очень часто имеем дело с двумя или тремя случайными величинами. Совместное рассмотрение двух или нескольких случайных величин приводит к понятию системы случайных величин. Условимся систему нескольких случайных величин X ,Y , . . . , W обозначать (X ,Y , . . . , W) Такая система называется также многомерной случайной величиной. При изучении системы случайных величин недостаточно изучить отдельно случайные величины, составляющие систему, а необходимо учитывать связи или зависимости между этими величинами.

При рассмотрении системы случайных величин удобно пользоваться геометрической интерпретацией системы. Например, систему двух случайных величин

В дальнейшем, при изучении системы случайных величин ограничимся подробным рассмотрением системы двух случайных величин.

Закон распределения вероятностей системы случайных величин

Законом распределения вероятностей системы случайных величин называется соответствие, устанавливающее связь между областями возможных значений данной системы случайных величин и вероятностями появления системы в этих областях.

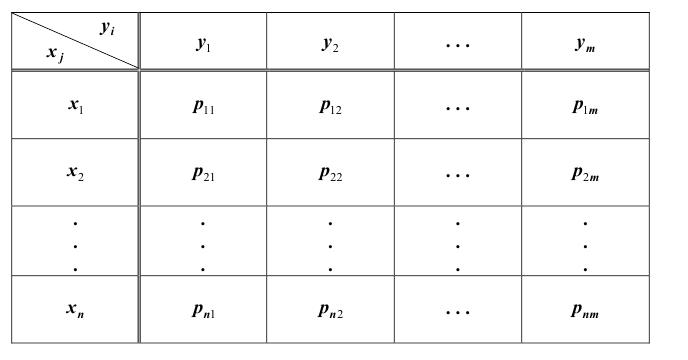
Так же, как и для одной случайной величины, закон распределения системы случайных величин может быть задан в различных формах. Рассмотрим таблицу распределения вероятностей системы двух дискретных случайных величин. Пусть

Одномерную случайную величину иногда называют скалярной случайной величиной.

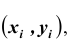
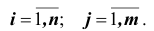
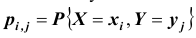
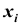
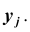
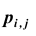
X и Y – дискретные случайные величины, возможные значения которых где Тогда распределение системы таких случайных величин может быть охарактеризовано указанием вероятностей y того, что случайная величина X примет значение и одновременно с этим случайная величина Y примет значение . Вероятности фиксируются в таблице

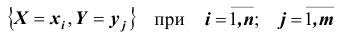
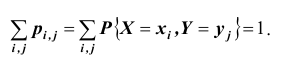
Такая таблица называется таблицей распределения вероятностей системы двух дискретных случайных величин с конечным числом возможных значений. Все возможные события составляют полную группу несовместных событий, поэтомупри этом

Функцией распределения вероятностей системы двух случайных величин называется функция 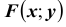двух аргументов, равная вероятности совместного выполнения двух неравенств

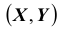
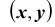
Геометрически функцию распределения системы двух случайных величин можно интерпретировать как вероятность попадания случайной точки в левый нижний бесконечный квадрант с вершиной в точке плоскости XOY (см. рис.).

5. Функция распределения является неубывающей функцией по каждому из своих аргументов, то есть:

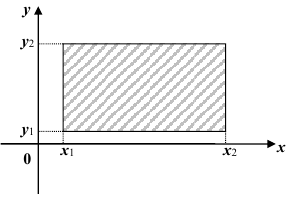
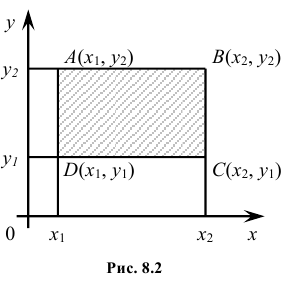
6. Вероятность попадания случайной точки (X,Y ) в произвольный прямоугольник со сторонами, параллельными координатным осям (см. рис.) вычисляется по формуле:

Плотность распределения вероятностей системы двух случайных величин

Предположим, что функция распределения F(x, y) всюду непрерывна и дважды дифференцируема21 (за исключением, быть может, конечного числа кривых). Тогда, смешанная частная производная функции F(x, y)

Функция называется плотностью распределения (или, дифференциальной функцией распределения) системы непрерывных случайных величин .
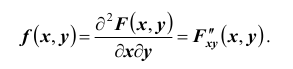
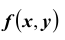
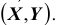
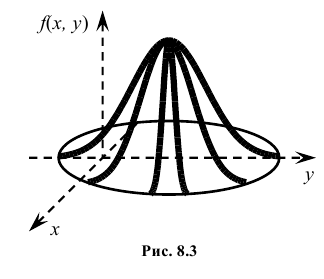
Геометрически эту функцию можно истолковать как поверхность, которую называют поверхностью распределения.
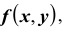
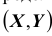
Зная плотность распределения можно определить вероятность попадания случайной точки в произвольную область D:

Используя последнюю формулу, выразим интегральную функцию F(x, y) распределения вероятностей системы двух непрерывных случайных величин через плотность распределения f (x, y):

Рассмотрим некоторые свойства плотности распределения системы двух непрерывных случайных величин:

Предполагается, что интегральная функция распределения вероятностей имеет непрерывную
смешанную частную производную второго порядка

если случайная величина (X,Y ) распределена на всей координатной плоскости (если же (X,Y ) распределена в некоторой плоской области

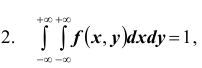
Пример №1

Пусть плотность распределения системы двух случайных величин (X,Y ) задана выражением:

Найти параметр А. Определить функцию распределения F(x, y) и вероятность попадания случайной точки (X,Y ) в прямоугольник D с вершинами:

Решение. Использовав свойство 2 плотности распределения, найдём постоянную величину А:

Следовательно

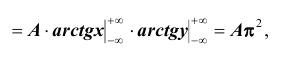
Определим теперь интегральную функцию распределения:

Таким образом, нетрудно теперь найти вероятность попадания случайной точки (X,Y ) в заданный прямоугольник D:

Условные законы распределения

Пусть известна плотность распределения системы двух случайных величин. Используя свойства функций распределения, можно вывести формулы для нахождения плотности распределения одной величины, входящей в систему:

Перейдём теперь к решению обратной задачи: по известным законам распределения отдельных случайных величин, входящих в систему, найти закон распределения системы. Легко увидеть, что в общем случае эта задача неразрешима. Действительно, с одной стороны, законы распределения отдельных случайных величин, входящих в систему, характеризуют каждую из случайных величин в отдельности, но ничего не говорят о том, как они взаимосвязаны. С другой стороны, искомый закон распределения системы должен содержать все сведения о случайных величинах системы, в том числе и о характере связей между ними. Таким образом, если случайные величины X ,Y взаимозависимы, то закон распределения системы не может быть выражен через законы распределения отдельных случайных величин, входящих в систему. Это приводит к необходимости введения условных законов распределения. Распределение одной случайной величины, входящей в систему, найденное при условии, что другая случайная величина, входящая в систему, приняла определённое значение, называется условным законом распределения.

Для дискретных случайных величин условным распределением составляющей
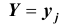
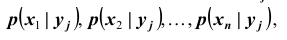
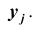
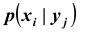
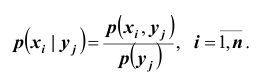
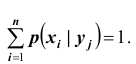
X при условии, чтоназывается совокупность условных вероятностей вычисленных в предположен, что случайная величина Y уже приняла значение Для нахождения пользуются формулой Заметим что Аналогично находим

Условный закон распределения можно задавать как функцией распределения, так и плотностью распределения. Условная функция распределения обозначается F(x | y); условная плотность распределения обозначается

Плотностью распределения для случайной величины X при условии, что случайная величина Y приняла определённое значение (условной плотностью распределения), назовём величину

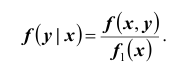
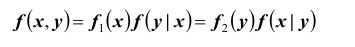
Аналогично, плотностью распределения для случайной величины Y при условии, что случайная величина X приняла определённое значение, назовём величинуОтсюда получаем или, с учётом формул (*)

Условная плотность распределения обладает всеми свойствами безусловной плотности распределения. В частности,

Числовые характеристики условных законов распределения

Для описания условных законов распределения можно использовать различные характеристики подобно тому, как для одномерных распределений. Наиболее важной характеристикой является условное математическое ожидание. Условным математическим ожиданием дискретной случайной величины X при Y = y ( y – определённое возможное значение случайной величины Y )

Мы записали условные законы распределения случайной величины X при условии, что другая случайная величина Y приняла определённое значение.

называется сумма произведений возможных значений X на их условные вероятности:

Для непрерывных случайных величин:где f x | y – условная плотность распределения случайной величины X приY = y . Аналогично, условным математическим ожиданием дискретной случайной величины Y при X = x ( x – определённое возможное значение случайной величины X ) называется сумма произведений возможных значений Y на их условные вероятности:Для непрерывных случайных величин:где – условная плотность распределения случайной величины Y при X = x. Аналогично вводятся условные дисперсии и условные моменты более высоких порядков (предлагаем это сделать самостоятельно).

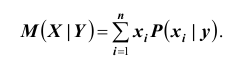
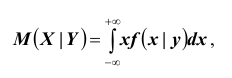
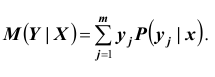
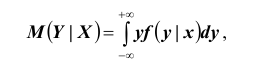
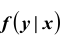
Числовые характеристики системы двух случайных величин

Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Из этого определения следует, что условные распределения независимых случайных величин равны их безусловным распределениям. Укажем необходимые и достаточные условия независимости случайных величин.

ТЕОРЕМА 1: Для того чтобы случайные величины X и Y были независимыми, необходимо и достаточно, чтобы функция распределения
системы (X ,Y ) была равна произведению функций распределения составляющих:

ТЕОРЕМА 2: Для того чтобы случайные величины X и Y были независимыми, необходимо и достаточно, чтобы плотность вероятности
системы (X ,Y ) была равна произведению плотностей вероятностей составляющих:

Для описания системы двух случайных величин кроме математических ожиданий и дисперсий составляющих используют и другие характеристики, к которым относятся корреляционный момент и коэффициент корреляции. Корреляционным моментом 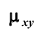случайных величин X и Y называют математическое ожидание произведения отклонений этих величин:

Для вычисления корреляционного момента дискретных величин используют формулу: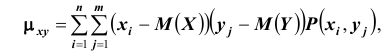а для непрерывных величин:

Корреляционный момент служит для характеристики связи между величинами X и Y .

ТЕОРЕМА 3: Корреляционный момент двух независимых случайных величин X и Y равен нулю.

Замечание: из теоремы 3 следует, что если корреляционный момент двух случайных величин X и Y не равен нулю, то X и Y – зависимые случайные величины.

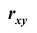
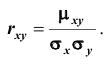
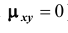
Коэффициентом корреляции случайных величин X и Y называют отношение корреляционного момента к произведению средних квадратических отклонений этих величин:Очевидно, коэффициент корреляции двух независимых случайных величин равен нулю (так как ).

Коррелированность и зависимость случайных величин

Две случайные величины X и Y называются коррелированными, если их корреляционный момент (или коэффициент корреляции) отличен от нуля; X и Y называют некоррелированными величинами, если их корреляционный момент равен нулю. Две коррелированные величины также и зависимы. Обратное утверждение не всегда имеет место, то есть если две величины зависимы, то они могут быть как коррелированными, так и некоррелированными. Другими словами, корреляционный момент двух зависимых величин может быть не равным нулю, но может и равняться нулю.

Заметим, что для нормально распределённых составляющих двумерной случайной величины понятия независимости и некоррелированности равносильны.

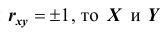
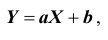
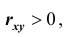
Если связаны линейной зависимостью Если , то говорят о положительной (или прямой) корреляции между
X и Y , то есть с возрастанием одной случайной величины другая случайная величина также возрастает.
Если 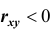, то говорят об отрицательной корреляции между X и Y , то есть с возрастанием одной случайной величины другая случайная величина убывает.

Функция и плотность распределения системы случайных величин

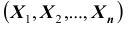
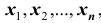
На практике очень часто приходится рассматривать системы более чем двух случайных величин. Функция распределения системы нескольких (более двух) случайных величин вводится как обобщение функции распределения системы двух случайных величин. Так, функцией распределения системы n случайных величин называется функция n аргументов , равная вероятности
совместного выполнения n неравенств 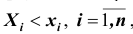, то есть:

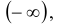
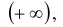
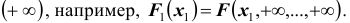
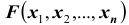
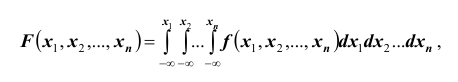
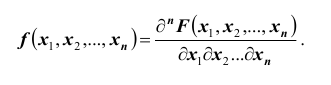
Эта функция является неубывающей функцией каждой переменной при фиксированных значениях других переменных. Если хотя бы одна из переменных стремится к , то функция распределения стремится к нулю. Если все переменные стремятся к, то функция распределения стремится к единице. Функция распределения каждой из величин, входящих в систему, получится, если в функции распределения системы все остальные аргументы положить равнымиАналогично одномерному случаю можно вывести формулу, связывающую функцию распределенияи плотность вероятности

или что тоже самое Плотность распределения системы не может быть отрицательной:

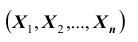
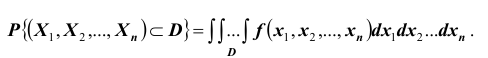
Вероятность попадания случайной точки с координатамив n – мерную область Dвыражается интегралом Используя свойства функции распределения, получаем

Плотность распределения каждой из величин, входящих в систему, получится, если плотность распределения системы проинтегрировать в бесконечных пределах по всем остальным аргументам. Например,

Числовые характеристики произвольного числа случайных величин

Основными числовыми характеристиками, с помощью которых может быть охарактеризована система n случайных величин 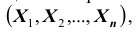являются следующие:

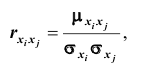
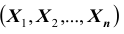
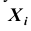
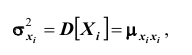
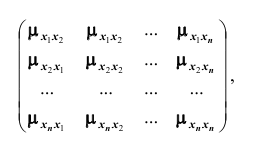
Зная корреляционные моменты, можно найти коэффициенты корреляции которые характеризуют степень связи между каждой парой случайных величин. Так как дисперсия каждой из случайных величин системы есть не что иное, как частный случай корреляционного момента, а именно: корреляционный момент величины и той же величины

то все корреляционные моменты и дисперсии располагают в виде прямоугольной таблицы (матрицы)

которая называется корреляционной матрицей системы n случайных величин.

Из определения корреляционного момента следует, что 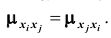. Это означает, что элементы корреляционной матрицы, расположенные симметрично по отношению к главной диагонали, равны. В этой связи часто для простоты в корреляционной матрице заполняют только её половину (правый верхний треугольник):

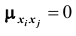
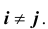
Если случайные величины системы некоррелированы, имеемпри Следовательно, корреляционная матрица системы некоррелированных случайных величин имеет вид:

Такая матрица, как вам известно, называется диагональной. Вместо
корреляционной матрицы часто используют нормированную корреляционную матрицу. Матрица, элементами которой являются коэффициенты корреляции, называется нормированной корреляционной матрицей. Все элементы главной диагонали нормированной корреляционной матрицы равны единице. Нормированная корреляционная матрица имеет вид:

Задача 1.

Закон распределения двумерной дискретной случайной величины (X ,Y ) задан таблицей

Найти:
— собственные законы распределения случайных величин X и Y ;
— математические ожидания M(X) M(Y );
— дисперсии D(X), D(Y );
— корреляционный момент ;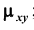
— коэффициент корреляции
— закон распределения случайной величины X при условии, что случайная
величина Y принимает своё наименьшее значение.

Решение. Складывая вероятности по строкам, получим закон распределения случайной величины X в виде ряда распределения

Складывая вероятности по столбцам, получим закон распределения случайной величины Y в виде ряда распределения

Найдём математические ожидания и дисперсии составляющих:

Найдём корреляционный момент 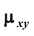и коэффициент корреляции

Найдём закон распределения случайной величины X при условии, что случайная величина Y принимает своё наименьшее значение, то есть при условии, что 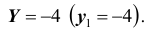Искомый закон распределения, как ранее отмечалось,
определяется совокупностью условных вероятностей 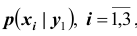где

Следовательно, искомый закон распределения имеет вид:

Задача 2.

Вне области 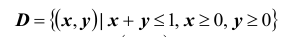плотность распределения двумерной случайной величины (X ,Y ) равна 0; в области D
плотность распределения

Найти:

Решение. Для нахождения параметра А воспользуемся формулой

тогда

Получим

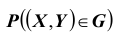
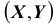
Найдём теперь вероятность попадания двумерной случайной величины в плоскую область G:

Далее, найдём одномерные плотности распределения:

Итак

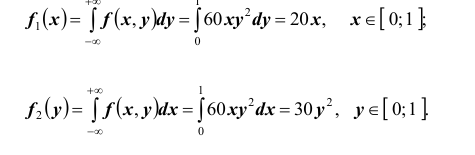
Найдём математические ожидания и дисперсии составляющих

далее тогда

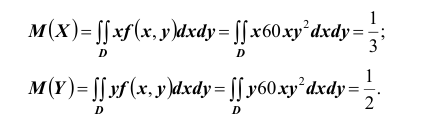
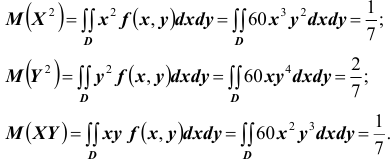
Так как 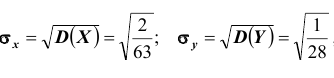, то нетрудно вычислить

Что такое многомерные случайные величины

Ранее мы рассматривали случайные величины, возможные значения которой определялись одним числом. Такие величины называют одномерными. Однако часто результат испытания характеризуется не одной случайной величиной, а некоторой системой случайных величин, которую называют многомерной случайной величиной или случайным вектором.

Понятие многомерной случайной величины

Многомерная случайная величина, случайный вектор, система случайных величин – это все различные интерпретации одного и того же математического объекта. В зависимости от удобства изложения мы будем пользоваться той или иной интерпретацией.

Так же, как и в случае одномерных случайных величин, случайные величины входящие в систему, могут быть как дискретными, так и непрерывными. Например, успеваемость студентов вуза, которая характеризуется системой n случайных величин 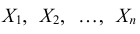– оценками по различным дисциплинам, проставленными в зачетной книжке – является дискретной многомерной величиной. А размер деталей, который характеризуются длиной (X), шириной (Y) и высотой (Z) – является непрерывной трехмерной величиной.

Геометрически двумерную (X, Y) и трехмерную (X, Y, Z) случайные величины можно изобразить случайной точкой плоскости Oxy или трехмерного пространства Oxyz. При этом случайные величины X, Y или X, Y, Z являются составляющими этих векторов. В случае n-мерного пространства (n > 3) также говорят о случайной точке этого пространства, хотя геометрическая интерпретация в этом случае теряет свою наглядность.

Пример №2

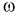
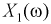
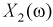
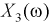
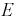
Пусть вероятностный эксперимент состоит в рождении ребенка. Тогда каждому элементарному событию (каждому новорожденному) можно поставить в соответствие следующие числа: — рост, — вес, — пол (0 или 1). Таким образом , эксперимент описывается трехмерной случайной величиной, или системой трех случайных величин, или трехмерным вектором

Пример №3

Пусть эксперимент состоит в измерении коэффициента усиления транзистора на высокой частоте. Тогда элементарное событие — это одного транзистора и ему можно поставить в соответствие следующие случайные величины: — коэффициент передачи тока на высокой частоте, — обратный ток коллекторного перехода, — входная проводимость, — емкость эмиттерного перехода, — емкость коллекторного перехода, — выходная проводимость. 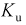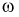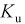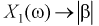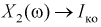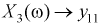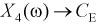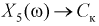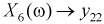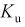Все перечисленные параметры для каждого транзистора при массовом производстве полупроводниковых приборов имеют отклонения от некоторого среднего значения (ввиду сложности поддержания технологического процесса стабильным для каждого кристалла при напылении, диффузии, травлении и т. д.). Поэтому их можно считать случайными величинами, и от значения каждого из них зависит коэффициент усиления транзистора на высокой частоте. Тогда в данном случае эксперимент описывается шестимерной случайной величиной, или шестимерным вектором, или системой шести случайных величин.

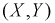
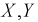
При изучении многомерных случайных величин удобно пользоваться следующей геометрической интерпретацией. Например (рис. 3.1), систему двух случайных величин можно рассматривать как случайную точку на плоскости с координатами или как случайный вектор на плоскости со случайными составляющими

Пример №4

Пусть двумерная случайная величина 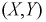задана плотностью распределения.

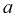
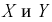
Найти коэффициент и показать, что случайные величины независимые.

Решение.

Для определения коэффициента 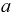используем условие нормировки

Учтем область определения

откуда

1-й способ проверки независимости

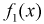
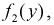
Найдем плотности распределений отдельных составляющих и применяя (3.4):

Подставим эти выражения в условие (3.13):

Значит случайные величины 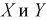независимы.

2-й способ проверки независимости

Найдем условную плотность распределения:

Видим, что выполняется условие (3.12), значит случайные величины 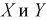независимы.

3-й способ проверки независимости

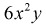
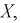
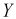
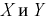
Все предыдущие вычисления можно не делать, а сослаться на следствие к доказанной выше теореме. Видим, что двумерная плотность представима в виде произведения двух сомножителей, один из которых содержит только а другой только составляющие. Тогда на основании следствия из доказанной выше теоремы случайные величины независимы.

Пример №5

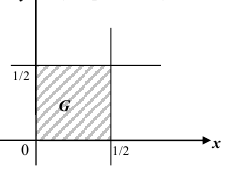
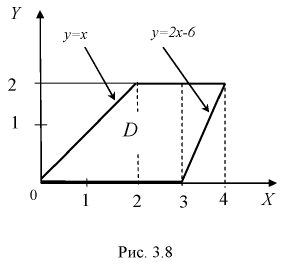
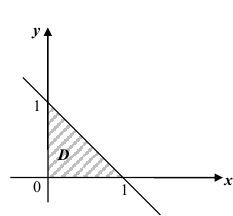
Двумерная случайная величина равномерно распределена внутри области 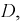выделенной на рис. 3.8 жирными прямыми:

Найти константу

Решение.

Запишем уравнения прямых (см. рис. 3.7):

Используем условие нормировки

Этот интеграл вычислим в виде суммы трех интегралов, разбивая область 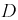на три части (пунктирные прямые на рис. 3.8):

Закон распределения вероятностей двумерной дискретной случайной величины

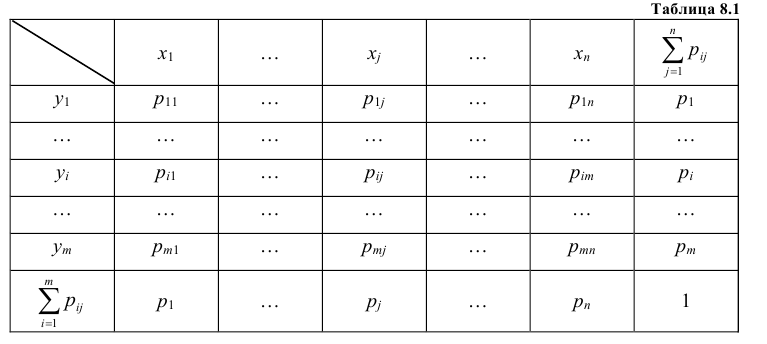
Так же как и для одномерной случайной величины наиболее полным, исчерпывающим описанием многомерной случайной величины является закон ее распределения. При конечном множестве возможных значений многомерной случайной величины такой закон может быть задан в виде таблицы (матрицы), содержащей все возможные сочетания значений каждой из одномерных величин, входящих в систему, и соответствующие им вероятности. Так, если рассматривается двумерная дискретная случайная величина (X, Y), то ее двумерное распределение можно представить в виде таблицы распределения (табл. 8.1), в каждой клетке (i, j) которой располагаются вероятности произведения событий

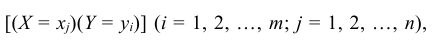
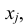
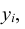
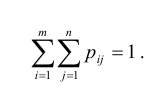
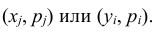
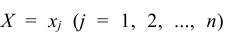
Так как события состоящие в том, что случайная величина Х примет значение , а случайная величина Y – значение , несовместны и единственно возможны, то сумма их вероятностей равна единице, т.е. Итоговые столбцы или строки таблицы распределения (X, Y) представляют соответственно распределение одномерных составляющих Действительно, распределение одномерной случайной величины Х можно получить, вычислив вероятность события как сумму вероятностей несовместных событий

Таким образом, чтобы по таблице распределения (табл. 8.1) найти вероятность того, что одномерная случайная величина примет определенное значение, надо просуммировать вероятности pij из соответствующего этому значению строки (столбца) данной таблицы.

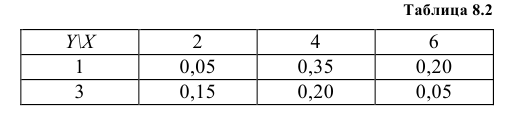
Пример №6

Закон распределения дискретной двумерной случайной величины (X, Y) задан в табл. 8.2. Найти законы распределения одномерных случайных величин X и Y.

Решение:

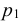
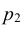
Случайная величина Х может принять значения: Х = 2 с вероятностью = 0,05 + 0,15 = 0,20; Х = 4 с вероятностью = 0,35 + 0,20 = 0,55; Х = 6 с вероятностью = 0,20 + 0,05 = 0,25. т.е. ее закон распределения

Аналогично закон распределения Y

Функция распределения многомерной случайной величины

При изучении одномерных случайных величин уже говорилось, что самой универсальной характеристикой случайной величины является функция распределения. Она существует для всех случайных величин: как дискретных, так и непрерывных. Точно также функция распределения полностью характеризует и многомерную случайную величину.

Определение: Функцией распределения n-мерной случайной величины 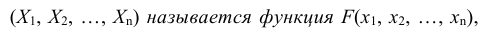выражающая вероятность

совместного выполнения n неравенств

В случае двумерной случайной величины XY функция распределения определяется неравенством

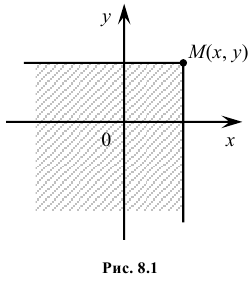
Геометрически функция распределения F(x, y) означает вероятность попадания случайной точки (X, Y) в заштрихованную область – бесконечный квадрант, лежащий левее и ниже точки M(x, y). Правая и верхняя границы области в квадрант не включаются – это означает, что функция непрерывна с л е в а по каждому аргументу. В случае двумерной дискретной случайной величины ее функция распределения определяется по формуле: где суммирование вероятностей распространяется на все j, для которых и все i, для которых

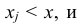
Отметим свойства функции распределения двумерной случайной величины.

1. Функция распределения есть неотрицательная функция, заключенная между нулем и единицей, т.е.

2. Функция распределения есть неубывающая функция по каждому из аргументов, т.е.

3. Если хотя бы один из аргументов обращается в – ∞, то функция распределения равна нулю, т.е.

4. Если один из аргументов обращается в + ∞, то функция распределения становится равной функции распределения случайной величины, соответствующей другому аргументу, т.е.

5. Если оба аргумента равны + ∞, то функция распределения равна единице:

Геометрически функция распределения есть некоторая поверхность, обладающая перечисленными свойствами. Для дискретной двумерной случайной величины (X, Y) ее функция распределения представляет собой некоторую ступенчатую поверхность, ступени которой соответствуют скачкам функции F(x, y). Зная функцию распределения F(x, y) можно найти вероятность попадания случайной точки (X, Y) в пределы прямоугольника ABCD (рис. 8.2). 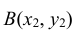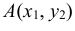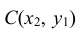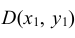Эта вероятность равна вероятности попадания в бесконечный квадрант с вершиной минус вероятность попадания в квадранты с вершинами в точкахиплюс вероятность попадания в квадрант с вершиной в точке (так как эта вероятность вычиталась дважды), т.е.

Плотность вероятности двумерной случайной величины

Для непрерывной двумерной случайной величины, так же как и для одномерной, существует понятие плотности вероятности.

Определение: Плотностью вероятности (или совместной плотностью) непрерывной двумерной случайной величины XY называется вторая смешанная частная производная ее функции распределения, т.е.

Геометрически плотность вероятности двумерной случайной величины XY представляет собой поверхность распределения в пространстве Oxyz.

Отметим свойства плотности вероятности двумерной случайной величины.

1. Плотность вероятности двумерной случайной величины есть неотрицательная функция, т.е.

2. Вероятность попадания непрерывной случайной величины XY в область D равна

3. Функция распределения непрерывной случайной величины может быть выражена через ее плотность вероятности по формуле:

4. Двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной случайной величины равен единице: Зная плотность вероятности двумерной случайной величины (X, Y) можно найти функции распределения и плотность вероятностей ее одномерных составляющих X и Y.

Так как в соответствии с (8.7) 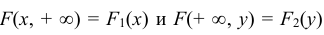то взяв в формуле (8.12) соответственно x = + ∞ и y = + ∞, получим функции распределения одномерных случайных величин X и Y:

Дифференцируя функции распределения 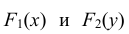соответственно по аргументам x и y, получим плотности вероятности одномерных случайных величин X и Y:

т.е. несобственный интеграл в бесконечных пределах от совместной плотности двумерной случайной величины по аргументу x дает плотность вероятности , а по аргументу y – плотность вероятности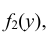

Условные законы распределения двумерной случайной величины

Итак, мы выяснили, как по известному закону распределения системы двух случайных величин определить законы распределения одномерных величин, входящих в систему.

Естественно возникает вопрос: нельзя ли по законам распределения одномерных величин, входящих в систему, найти закон распределения системы в целом? Оказывается, в общем случае этого сделать нельзя. Для того, чтобы полностью описать систему случайных величин, недостаточно знать распределение каждой из ее составляющих. Нужно еще знать зависимость между величинами, входящими в систему. Эта зависимость характеризуется с помощью условных законов распределения.

Определение: Условным законом распределения одной из одномерных составляющих двумерной случайной величины XY называется ее закон распределения, вычисленный при условии, что другая составляющая приняла определенное значение (или попала в определенный интервал).

Для дискретных случайных величин условные вероятности находятся по формулам:

В случае непрерывных случайных величин необходимо определить плотность вероятности условных распределений. Заменяя в формулах для дискретных величин вероятности событий «элементами вероятностей», получим:

т.е. условная плотность вероятности одной из одномерных составляющих двумерной случайной величины равно отношению ее совместной плотности к плотности вероятности другой составляющей.

Пример №7

По данным примера 8.1 найти условный закон распределения составляющей Х при условии, сто составляющая Y приняла значение y1 =1.

Решение:

Искомый закон определяется следующей совокупностью условных вероятностей

Воспользовавшись формулой (8.16) и учитывая, что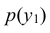= 0,6 (пример 8.1), получаем:

Важной характеристикой условного распределения вероятностей является условное математическое ожидание. Условным математическим ожиданием дискретной случайной величины Y при Х = х (х – определенное возможное значение Х) называют произведение возможных значений Y на их условные вероятности:

Для непрерывных величин

Аналогично определяется условное математическое ожидание случайной величины Х.

Пример №8

Найти условное математическое ожидание составляющей Y при условии, что составляющая Х примет значение

Решение:

Найдем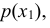, для чего сложим вероятности, помещенные в первом столбце табл. 8.2

Найдем условное распределение вероятностей величины Y при при

Найдем условное математическое ожидание по формуле (8.19):

Условное математическое ожидание случайной величины Y при Х = х, т.е. Mx(Y), есть функция от х, называемая функцией регрессии или просто регрессией Y по Х. Аналогично My(X) называется функцией регрессии или регрессией X по Y. Графики этих функций называются соответственно линиями регрессии (или кривыми регрессии) Y по Х и Х по Y.

Зависимые и независимые случайные величины

Ранее мы назвали две случайные величины независимыми, если закон распределения одной из них не зависит от того, какие возможные значения приняла другая величина. Теперь можно дать общее определение независимости случайных величин, основанное на независимости событий X < x и Y < y, т.е. функций распределения

Определение: Случайные величины X и Y называются независимыми, если их совместная функция распределения F(x, y) представляется в виде произведения функций 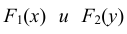этих случайных величин, т.е.

При невыполнении этого равенства случайные величины называются зависимыми. Дифференцируя дважды равенство (8.19) по аргументам x и y, получим

т.е. для независимых непрерывных случайных величин их совместная плотность равна произведению плотностей вероятностей этих случайных величин.

Другими словами, независимость двух случайных величин, что условные вероятности каждой из них совпадают с соответствующими безусловными плотностями вероятностей.

Числовые характеристики двумерной случайной величины

Для описания системы двух случайных величин, кроме математических ожиданий и дисперсий составляющих, используются и другие характеристики, к числу которых относятся ковариация и коэффициент корреляции.

Определение: Ковариацией (или корреляционным моментом) случайных величин X и Y называется математическое ожидание произведения отклонений этих величин от своих математических ожиданий, т.е.

Из определения следует, что Kxy = Kyx.

Для дискретных случайных величин

Для непрерывных случайных величин

Ковариация двух случайных величин характеризует как степень зависимости случайных величин, так и их рассеяние вокруг точки (ax, ay).

Отметим свойства ковариации:

1. Ковариация двух независимых случайных величин равна нулю.

2. Ковариация двух случайных величин равна математическому ожиданию их произведения минус произведение математических ожиданий, т.е.

3. Ковариация двух случайных величин по абсолютной величине не превосходит произведения их средних квадратических отклонений, т.е.

Не трудно заметить, что ковариация имеет размерность, равную произведению размерностей величин X и Y. Другими словами, величина ковариации зависит от единиц измерения случайных величин. Такая особенность затрудняет сравнение ковариаций различных систем случайных величин. Для устранения этого недостатка вводится безразмерная характеристика – коэффициент корреляции.

Определение: Коэффициентом корреляции двух случайных величин называется отношение их ковариации к произведению средних квадратических отношений этих величин, т.е.

Из определения следует, что

Отметим свойства коэффициента корреляции.

1. Коэффициент корреляции принимает значения на отрезке

2. Если случайные величины независимы, то их коэффициент корреляции равен нулю, т.е. ρ = 0.

3. Если коэффициент корреляции двух случайных величин равен (по абсолютной величине) единице, то между этими случайными величинами существует линейная функциональная зависимость.

Пример №9

Определить ковариацию и корреляционный момент случайных величин Х и Y.

Решение:

В примере были получены следующие распределения одномерных случайных величин

Найдем математические ожидания и средние квадратические отклонения этих случайных величин:

Для нахождения математического ожидания M(XY) произведения случайных величин Х и Y можно составить закон распределения произведения двух дискретных случайных величин, а затем по нему найти M(XY). Однако M(XY) можно найти непосредственно по табл. 8.2 распределения двумерной случайной величины (X, Y) по формуле:

где двойная сумма означает суммирование по всем mn клеткам таблицы (m – число строк, n – число столбцов):

Вычисляем ковариацию по формуле (8.26):

Вычисляем коэффициент корреляции по формуле (8.28):

т.е. между случайными величинами Х и Y существует отрицательная линейная зависимость.

Случайные события — определение и вычисление
Системы случайных величин
Вероятность и риск
Определения вероятности событий
Генеральная и выборочная совокупности
Интервальные оценки параметров распределения
Алгебра событий — определение и вычисление
Свойства вероятности

Источник

Известно, что если события A и B зависимы, то условная вероятность события B отличается от его безусловной вероятности. В этом случае

. (13.1.43)

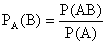
Аналогичное положение имеет место и для случайных величин. Для того, чтобы охарактеризовать зависимость между составляющими двумерной случайной величины, введем понятие условного распределения.

Рассмотрим дискретную двумерную случайную величину (X,Y). Пусть возможные значения составляющих таковы: .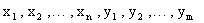

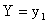
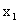
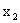
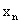
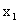
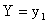
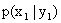
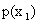
Допустим, что в результате испытания величина Y приняла значение ; при этом X примет одно из своих возможных значений: , или , …, или . Обозначим условную вероятность того, что X примет, например, значение при условии, что , через . Эта вероятность, вообще говоря, не будет равна безусловной вероятности .

В общем случае условные вероятности составляющей будем обозначать так:
(i=1, 2, …, n; j=1, 2, …, m).

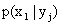
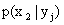
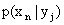
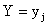
Условным распределением составляющей X при называют совокупность условных вероятностей , , …, , вычисленных в предположении, что событие (j имеет одно и то же значение при всех значениях X) уже наступило. Аналогично определяется условное распределение составляющей Y.

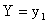
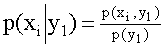
Зная закон распределения двумерной дискретной случайной величины, можно, пользуясь формулой (13.1.43), вычислить условные законы распределения составляющих. Например, условный закон распределения X в предположении, что событие уже произошло, может быть найден по формуле

(i = 1, 2, … , n).

В общем случае условные законы распределения составляющей X определяются соотношением

(13.1.44)

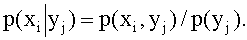
Аналогично находят условные законы распределения составляющей Y:

(13.1.45)

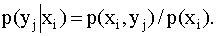
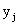
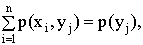
Замечание. Сумма вероятностей условного распределения равна единице. Действительно, так как при фиксированном имеем

то .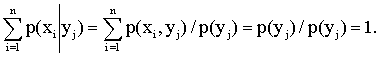

Аналогично доказывается, что при фиксированном

Это свойство условных распределений используют для контроля вычислений.

ПРИМЕР 13.1.56 Дискретная двумерная случайная величина задана таблицей

Найти условный закон распределения составляющей X при условии, что составляющая Y приняла значение .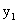

Решение. Искомый закон определяется совокупностью следующих условных вероятностей: , ,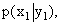

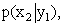
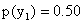
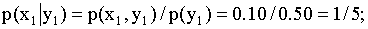
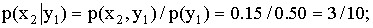
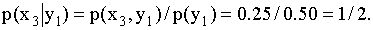
Воспользовавшись формулой (13.1.44) и приняв во внимание, что , имеем:

Сложив для контроля найденные условные вероятности, убедимся, что их сумма равна единице, как и должно быть, в соответствии с замечанием, помещенным выше: 1/5+3/10+1/2=1.

Онлайн помощь по математике >
Лекции по высшей математике >
Примеры решения задач >

Источник

Условные законы распределения составляющих дискретной двумерной случайной величины

Условные законы распределения составляющих непрерывной двумерной случайной величины

Условное математическое ожидание

Пример задачи на условное распределение

Definition[edit]

Conditioning on an event[edit]

Kolmogorov definition[edit]

As an axiom of probability[edit]

As the probability of a conditional event[edit]

Conditioning on an event of probability zero[edit]

Conditioning on a discrete random variable[edit]

Partial conditional probability[edit]

Example[edit]

Use in inference[edit]

Example[edit]

Statistical independence[edit]

Common fallacies[edit]

Assuming conditional probability is of similar size to its inverse[edit]

Assuming marginal and conditional probabilities are of similar size[edit]

Over- or under-weighting priors[edit]

Formal derivation[edit]

See also[edit]

References[edit]

External links[edit]

Закон распределения вероятностей системы случайных величин

Плотность распределения вероятностей системы двух случайных величин

Пример №1

Условные законы распределения

Числовые характеристики условных законов распределения

Числовые характеристики системы двух случайных величин

Коррелированность и зависимость случайных величин

Функция и плотность распределения системы случайных величин

Числовые характеристики произвольного числа случайных величин

Что такое многомерные случайные величины

Понятие многомерной случайной величины

Пример №2

Пример №3

Пример №4

Пример №5

Закон распределения вероятностей двумерной дискретной случайной величины

Пример №6

Функция распределения многомерной случайной величины

Плотность вероятности двумерной случайной величины

Условные законы распределения двумерной случайной величины

Пример №7

Пример №8

Зависимые и независимые случайные величины

Числовые характеристики двумерной случайной величины

Пример №9