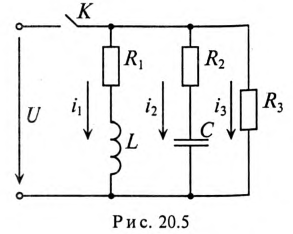
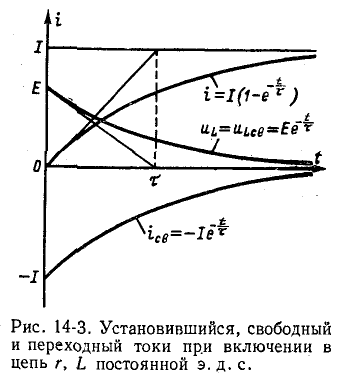
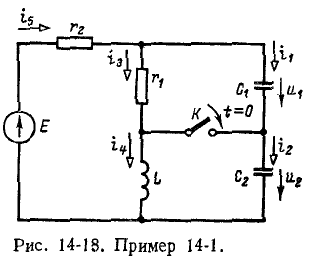
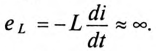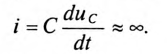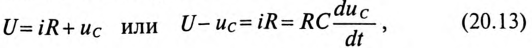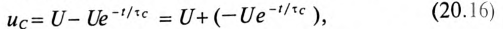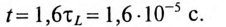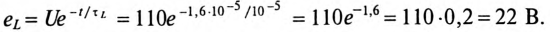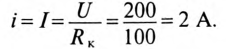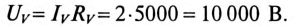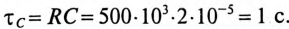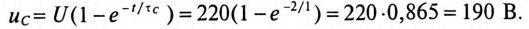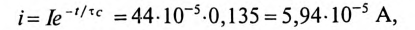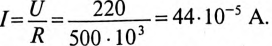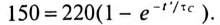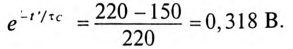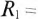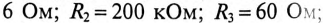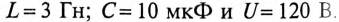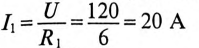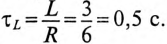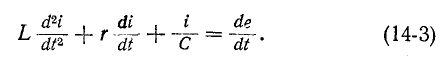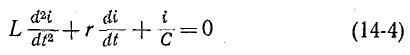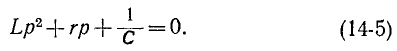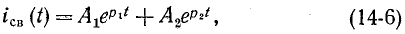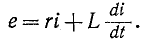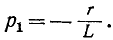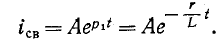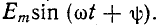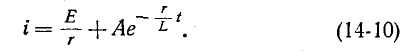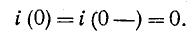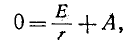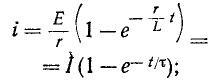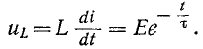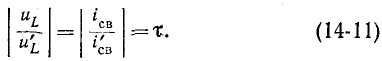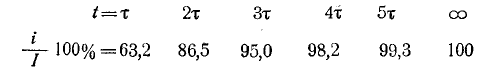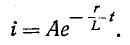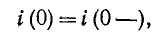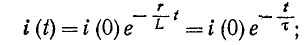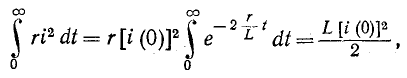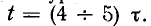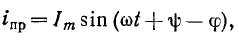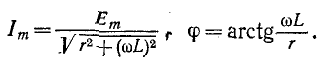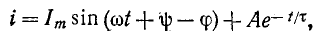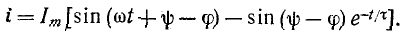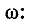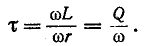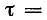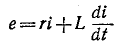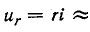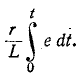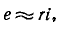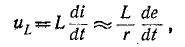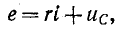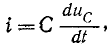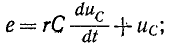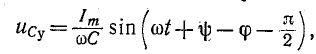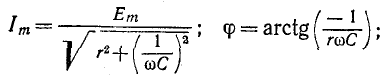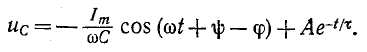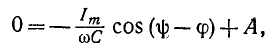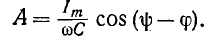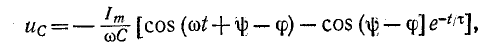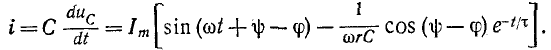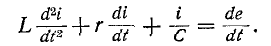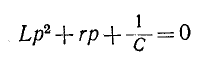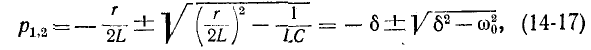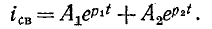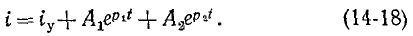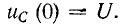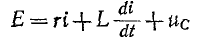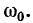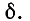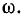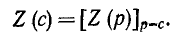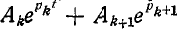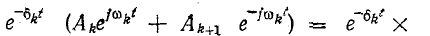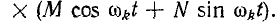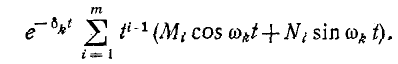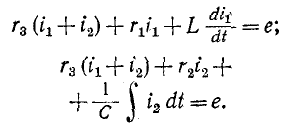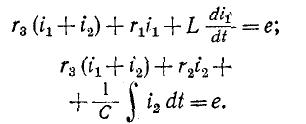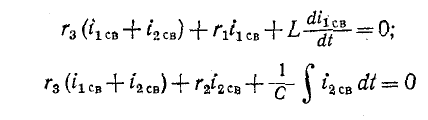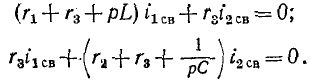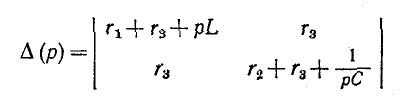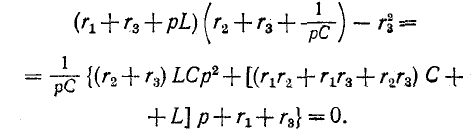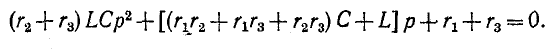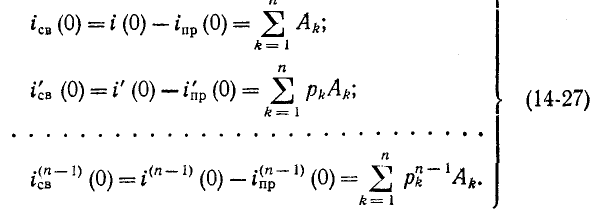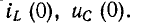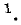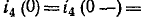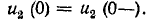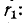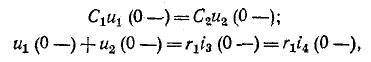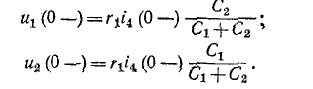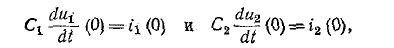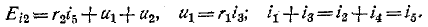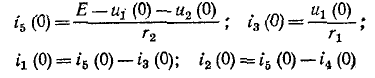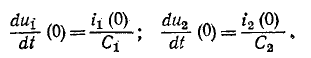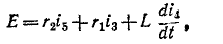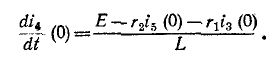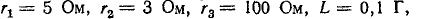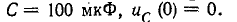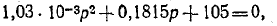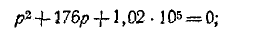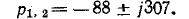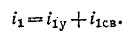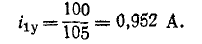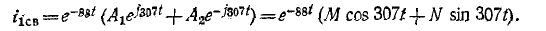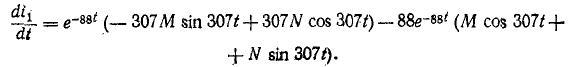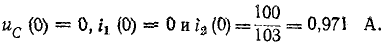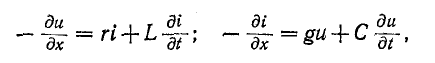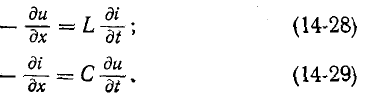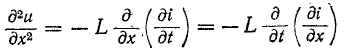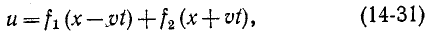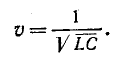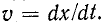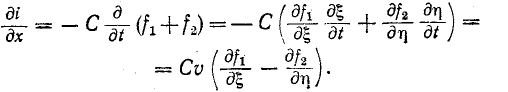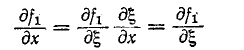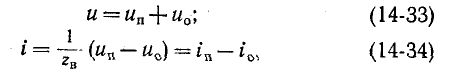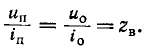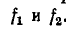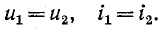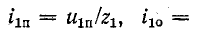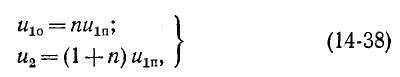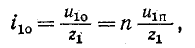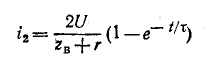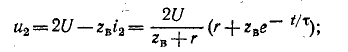3 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Приведено полное решение, включающее следующие элементы:
I) Записаны положения теории и физические законы, закономерности, применение которых
необходимо для решения задачи выбранным способом (в данном случае: записан закон Ома для участка
цепи и для полно цепи, формула расчета напряжения при последовательном соединении элементов,
формула расчета сопротивления участка цепи, состоящего из параллельно соединенных
элементов)
II) Описаны все вводимые буквенные обозначения величин, кроме тех, которые приведены в
условии задачи или представлены в виде констант в КИМ, стандартных обозначений величин,
используемых при написании физических законов.(Введены обозначения для величин не входящих в
КИМы)
III) Проведены необходимые математические преобразования и расчёты, приводящие
к правильному числовому ответу (допускается решение «по частям» с промежуточными
вычислениями).
IV) Представлен правильный ответ с указанием единиц измерения искомой величины.
2 балла ставится за задачу если:
_________________________________________________________________________________________________________________
Верно записаны все положения теории, физические законы, закономерности, и проведены необходимые
преобразования, но имеются один или несколько из следующих недостатков:
Записи, соответствующие одному или обоим пунктам: II и III, – представлены не в полном объёме
или отсутствуют.
При ПОЛНОМ правильном решении лишние записи, не входящие в решение (возможно, неверные), не
отделены от решения (не зачёркнуты; не заключены в скобки, рамку и т. п.).
При ПОЛНОМ решении в необходимых математических преобразованиях или вычислениях допущены
ошибки, и (или) преобразования/вычисления не доведены до конца.
При ПОЛНОМ решении отсутствует пункт IV, или в нём допущена ошибка. (В ответе обязательны единицы
измерений)
1 балл ставится за задачу если:
_________________________________________________________________________________________________________________
Представлены записи, соответствующие одному из следующих случаев.
Записаны только положения и формулы, выражающие физические законы, применение которых
необходимо и достаточно для решения данной задачи, без каких-либо преобразований с их
использованием, направленных на решение задачи.
В решении отсутствует ОДНА из исходных формул, необходимая для решении задачи (или утверждение,
лежащее в основе решения), но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
В ОДНОЙ из исходных формул, необходимых для решения данной задачи (или в утверждении, лежащем в
основе решения), допущена ошибка, но присутствуют логически верные преобразования с имеющимися
формулами, направленные на решение задачи.
Во всех остальных случаях за задачу выставляется 0 баллов.
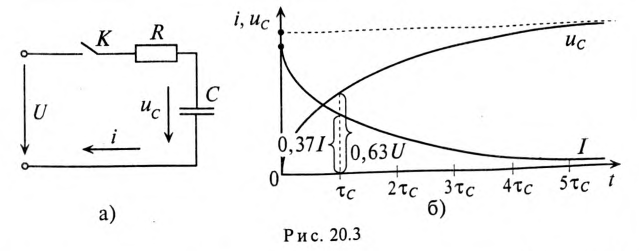
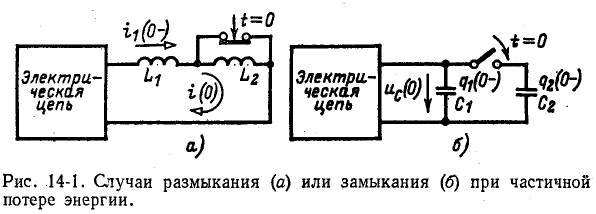
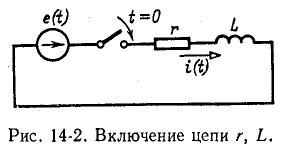
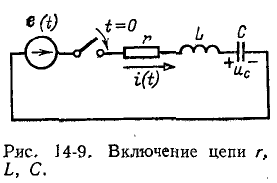
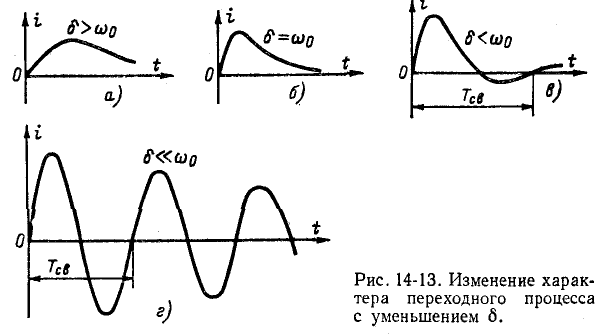
5.5.1. Разряд конденсатора на резистор
Рассмотрим
переходный процесс при коротком замыкании
в цепи с конденсатором и резистором
(рис. 5.8), если предварительно конденсатор
был заряжен до напряжения
uC(0+)
= U0 =
Е.
Рис.
5.8
Установившийся
ток через конденсатор и установившееся
напряжение на конденсаторе равны нулю.
Для построения характеристического
уравнения запишем по второму закону
Кирхгофа уравнение для вновь образованного
контура
R
i + uC =
0.
При
расчете переходных процессов в цепях
с конденсатором часто удобнее отыскать
сначала не ток, а напряжение на конденсаторе
uC ,
а затем учитывая, что ,
найти ток через конденсатор. Поэтому
запишем уравнение по второму закону
Кирхгофа в виде:
.
Характеристическое
уравнение имеет вид:
RCp
+ 1 = 0.
Общее
решение для свободной составляющей
напряжения:
uCсв =
A ept =
A e-t/τ,
где:
А = U0 –
постоянная интегрирования;
p = — 1 / (RC)
– корень характеристического уравнения;
τ
= RC – постоянная времени цепи.
С
учетом нулевого значения установившегося
напряжения получим напряжение на
конденсаторе:
uC =
U0 e-t/τ.
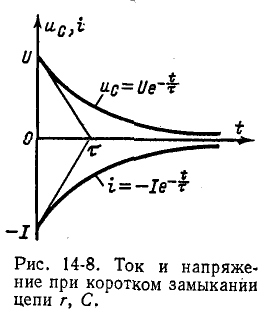
Переходный
ток в цепи

Рис.
5.9
Кривые
изменения напряжения на конденсаторе
и тока в цепи во времени имеют вид
экспонент (рис. 5.9).
С
энергетической точки зрения переходный
процесс характеризуется переходом
энергии электрического поля конденсатора
в тепловую энергию в резисторе. Следует
отметить; что сопротивление резистора
влияет не на количество выделенной
теплоты, а на начальное значение тока
и длительность разряда. В самом деле
5.5.2. Включение цепи с резистором и конденсатором на постоянное напряжение (заряд конденсатора)
Из
схемы, приведенной на рис. 5.10, следует,
что установившаяся составляющая
напряжения на конденсаторе uCу = U,
а свободная составляющая, очевидно,
равна
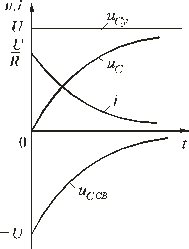
5.10
uCсв =
A e-t/τ,
τ
= RC.
Полагаем,
что до замыкания ключа конденсатор не
был заряжен (Uс(0—) = 0).
На основании законов коммутации
uC(0—) = uC(0+) = 0,
при t = 0; следовательно:
uC(0)
= uCу(0)
+ uCсв(0)
или 0 = U + A, откуда А = -U.
Тогда
переходное напряжение на конденсаторе
uC =
U (1 — e-t/τ),
а
переходный ток в цепи
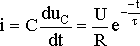
Зависимости
напряжений и токов от времени показаны
на рис. 5.10. Из них видно, что напряжение
на конденсаторе возрастает по
экспоненциальному закону от нуля до
напряжения источника, а ток уменьшается
от начального значения до нуля также
по экспоненте. Длительность их изменения
определяется постоянной времени τ = RC.
Здесь как и в п. 5.5.1 время переходного
процесса принимается равным t ≈ (3 ÷ 5)τ.
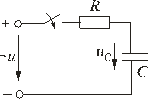
5.5.3. Включение цепи с резистором и конденсатором на синусоидальное напряжение
Рис.
5.11
Пусть
напряжение источника изменяется по
закону
u
= Um sin(ωt
+ ψ).
Установившаяся
составляющая напряжения на конденсаторе
(см. рис. 5.11) равна:
uCу =
-Um XC /
Z sin(ωt + ψ – φ – π / 2).
где: —
полное сопротивление цепи;
XC =
1 / (ωC) – емкостное сопротивление;
φ = -arctg(XC / R)
– угол сдвига фаз между установившимся
током в цепи и приложенным синусоидальным
напряжением.
Свободная
составляющая напряжения на конденсаторе
uCсв =
A e-t/τ,
τ = RC.
Переходное
напряжение на конденсаторе
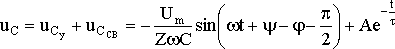
Рис.
5.12
Полагая,
что uC(0—) = 0,
для постоянной интегрирования получим

Окончательно
напряжение на конденсаторе можно
записать в виде
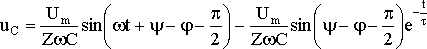
Ток
в цепи
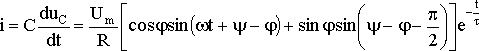
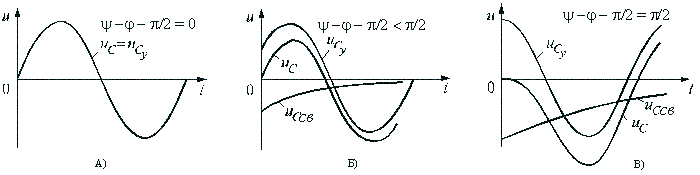
Зависимости
переходного напряжения на конденсаторе
от времени при различных значениях
разностей ψ — φ показаны на рис. 5.12.
Их анализ позволяет сделать следующие
выводы.
Если
в момент включения мгновенное значение
установившегося напряжение на конденсаторе
равно нулю (ψ – φ – π / 2 = 0),
то и свободная составляющая напряжения
равна нулю. В цепи сразу устанавливается
режим (рис. 5.12 а).
Если
в момент включения мгновенное значение
установившегося напряжение на конденсаторе
имеет наибольшее значение
(ψ – φ – π / 2 = π / 2),
то переходное напряжение достигает
максимального значения приблизительно
через половину периода и может приблизиться
к удвоенной амплитуде установившегося
напряжения, но не превысит его
(рис. 5.12 в).
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Государственное учреждение образования
“Средняя школа №16 г. Пинска”
Конденсаторы
в переходных процессах: до, во время, и после…
Методическое пособие для подготовки к олимпиадам по физике
Пинск 2018
ББК 22.3 Ф 57
УДК 53(075)
Ф57 Конденсаторы
в переходных процессах: до, во время и после… — Методическое
пособие для подготовки к ЦТ и олимпиадам по физике. Пинск: Учебное издание
кафедры довузовской подготовки государственного учреждения образования «Средняя
школа № 16 г. Пинска» г. Пинск, 2018. — 100 с.
Составитель:
учитель высшей категории в ГУО
СШ № 16, отличник образования Федорино Сергей Иванович
Рецензент:
учащаяся
профильного физико-математического класса в ГУО СШ № 16, победитель и
дипломант олимпиад по физике Троцкая Дарина Витальевна
В пособии представлены решения более 50
избранных задач по физике, предложенных на вступительных экзаменах в
Московский физико-технический институт (Государственный университет). Выбранная
тема касается поведения конденсаторов в цепи постоянного тока в моменты
коммутации. Решения всех задач оформлены составителем пособия, при этом
формулировки задач частично изменены.
Пособие предназначено
для учащихся 10 – 11 классов средних школ, гимназий и лицеев, и будет полезно
при подготовке к олимпиадам по физике различного уровня и сдаче ЦТ повышенной
сложности. Представленное пособие может вызвать интерес учителей и
преподавателей физики, студентов младших курсов технических вузов, а также всех
тех, кто увлекается физикой и занимается самообразованием.
Компьютерный набор и вёрстка материалов
пособия: — Троцкая Д.В.
ISBN 978-985-533-561-1
© Федорино С.И., Троцкая Д.В., 2018 Слово к читателю
Физика – безгранично увлекательная
наука, открывающая новые горизонты. Но как это обычно бывает, чем больше ты
узнаешь, тем больше возникает новых вопросов. И если в вас горит желание искать
на их ответы, каждый раз смело затрагивая совершенно незнакомую или не до конца
понятную вам тему, то это пособие станет отличным помощником. Возможно, раньше
вас не особо интересовала тема связанная с поведением конденсатора в цепи
постоянного тока и знаний, которые предоставляет обычный школьный учебник,
казалось вполне достаточно, то после прочтения нескольких страниц вы, скорее
всего, переубедитесь в этом.
Не трудно предположить, что у читателя
мог возникнуть вопрос: чем еще, кроме теории, позволяющей глубже понимать
предложенную тему, мне может быть полезно данное пособие? Стоит отметить, что
книга содержит подробный разбор разнообразных задач, которые могут предлагаться
на олимпиадах и профильных экзаменах. Кроме того формулировки пояснений к
задачам отличаются своей доступностью для понимания, поэтому учащийся 10-11
класса, при наличии базовых знаний, касающихся данной темы, не будет
обескуражен обилием замысловатых фраз или неожиданных математических
преобразований.
Надеемся, что изучение данного пособия
станет для вас приятным и увлекательным, ответы на возникшие вопросы будут
получены, а желание глубже окунуться в мир, который открывает нам физика,
станет в несколько раз сильнее.
Содержание
Глава 1
Коротко о главном………………………………………………………………………………………. 5
Глава 2 ………………………………………………………………………………………………………..
Сразу после коммутации…………………………………………………………………………….. 11
Глава 3
Переходный процесс
…………………………………………………………………………………………….
33
Глава 4
Установившийся режим
………………………………………………………………………………………
49
Глава 5
До и после коммутации
………………………………………………………………………………………..
75
Глава 1
Коротко о главном
В упрощенном виде конденсатор
представляет собой систему двух проводников, разделенных диэлектриком, толщина
которого мала по сравнению с размерами проводников. Такая система проводников
обладает способностью накапливать электрический заряд: на одной обкладке
положительный, а на другой отрицательный, в целом же конденсатор остается
электрически нейтральным. Количественной характеристикой накопительной
способности таких систем является электроёмкость. Для ориентировки в величинах
электроемкости приведем два примера: электроемкость уединенного проводящего
шара радиусом, равным радиусу нашей планеты (R ~ 6371 км), составляет
примерно 10–3 Ф, а электроемкость уединенного куска провода
диаметром 2 мм и длиной 1 м равна приблизительно 10–12 Ф. (В этих
примерах вторая обкладка уединенных проводников находится в бесконечности, т.
е. силовые линии электрического поля уходят с данных проводников на
бесконечность.)
Основное внимание в статье будет уделено
поведению конденсаторов в электрических цепях с источниками постоянного тока.
Помимо конденсаторов, в таких цепях обычно присутствуют и резисторы. Весь
промежуток времени с момента замыкания цепи и до момента установления
стационарного состояния можно разбить на три этапа.
Первый этап — это очень короткий
промежуток времени (его можно оценить, разделив линейный размер схемы на
скорость света) сразу после замыкания ключа. За это время в цепи установится
некоторый начальный ток, но, поскольку в реальных схемах величина этого тока
конечна, за бесконечно малое время во всех участках цепи протекут бесконечно
малые заряды и изменения зарядов и напряжений на конденсаторах можно будет
пренебречь. Итак, на первом этапе, сразу после замыкания цепи, сохраняются
напряжения на конденсаторах, которые были до замыкания, и устанавливаются
начальные токи, величины которых определяются законом Ома для замкнутых цепей и
не зависят от ёмкостей конденсаторов.
На втором этапе идет переходной процесс
— выход на стационарным режим, во время которого в участках цепи текут
переменные токи и происходит разрядка или подзарядка конденсаторов. Скорость
нарастания напряжения во время зарядки (или убыли во время разрядки) измеряется
величиной произведения RC, которое выражает постоянную времени ёмкостной
цепи: τ = RC
Легко убедиться, что произведение RC
имеет размерность времени. Постоянная времени RC-цепи характеризует
степень заряда и разряда конденсатора. При заряде τ показывает время,
необходимое для того, чтобы конденсатор зарядился до 63% приложенного
напряжения. При разряде τ показывает время, в течение которого конденсатор
успевает разрядится до 37% первоначального напряжения на его зажимах. Принято
считать, что после 5τ конденсатор практически полностью заряжается или
полностью разряжается.
Таким образом, постоянная времени τ
имеет смысл: если время, прошедшее после замыкания цепи, много меньше, можно
считать, что переходной процесс и не начался, а если время много больше, то
переходное процесс закончился и установился стационарный режим. Как в первом,
так и во втором процессах через конденсаторы текут переменные токи, но в первом
случае это очень быстро изменяющиеся токи и поэтому реактивные сопротивления
конденсаторов практически равны нулю, а во втором случае скоро-
Глава 1: Коротко о главном
сти изменения тока существенно меньше и зависят как от
омического сопротивления цепи, так и от её ёмкости.
И наконец, третий (и последний) этап,
когда устанавливается стационарный режим. Здесь реактивные сопротивления
конденсаторов равны бесконечности, токи через конденсаторы равны нулю,
напряжения на конденсаторах равны установившимся значениям, которые
определяются законом Ома для замкнутой цепи.
Задача 0. В
электрической схеме, изображенной на рисунке 0а, в начальный момент ключ К
разомкнут, а конденсатор не заряжен. Параметры схемы указаны на рисунке.
Найдите зависимость от времени тока через батарею после замыкания ключа.
Внутренним сопротивлением батареи пренебречь.
Рис. 0а
Рис. 0б
1) Рассмотрим момент сразу после замыкания ключа. За
очень малое время установления начальных токов заряд на конденсаторе не
изменится и разность потенциалов на нём останется такой, какой она была
замыкания ключа (до коммутации). То есть, согласно закону коммутации:
UC(0–) = UC(0+)
Эквивалентная схема для этого промежутка
времени будет иметь вид, изображенный на рисунке 0б. Так как до коммутации
конденсатор не был заряжен, то в момент после коммутации напряжение на
конденсаторе равно нулю:
UC = 0
Такая схема позволяет с помощью законов
Кирхгофа определить начальный ток через батарею:
I =
I1 +
I2
E =
I1 ⋅R1
E −UC =
I2 ⋅R2
Выражая из двух последних уравнений токи I1,
I2 и подставляя в верхнее уравнение, окончательно получим:
I1 = RE1
I2 = E −RU2 C =
RE2
I E E ( R +
R )⋅E
3) Рассмотрим электрическую схему через длительный
промежуток времени, когда установится стационарный режим. При этом ветвь,
содержащую конденсатор можно удалить, так как он через себя не пропускает
постоянный ток. В этом случае (см. рис. 0в) в цепи через батарею протекает
ток:
I =
E
R1
Рис.
0в Рис.
0г
2) Рассмотрим переходный процесс, при котором
происходит выход на стационарный режим. Сразу оговоримся, что решение этой
задачи выходит за рамки школьной программы, но интерес представляет не само
решение, а физическая сторона переходных процессов и та роль, которую выполняют
конденсаторы в подобных цепях. Рассмотрим произвольный момент времени после
замыкания ключа, причём за начало отсчёта времени возьмём момент окончания
первого этапа — установления начальных значений токов и напряжений. Именно
начиная с этого момента, в цепи будет идти квазистационарный процесс. Согласно
рисунку 0б, для произвольного момента времени можно записать законы Кирхгофа:
I =
I1 +
I2
E =
I1 ⋅R1
Глава 1: Коротко о главном
E −UC =
I2 ⋅R2
Сила тока, протекающая через конденсатор —
это связь между током в конденсаторе и изменением напряжения на конденсаторе:
I2 = dqdt = C dUdtC
Продифференцировав третье уравнение по времени и решая его
совместно с остальными тремя уравнениями, получим дифференциальное уравнение
относительно тока через батарею:
dI +
1 ⋅I = E
dt R2C R1R2C
Общее решение этого дифференциального уравнения имеет вид:
I(t ) =
A⋅e−tt +
E ,
R1
где τ = R2C —
постоянная времени. Постоянную интегрирования А можно определить по
начальным условиям (при t = 0), которые мы уже находили ранее в пункте 1):
I E .
 1 2
1 2
И тогда, частное решение дифференциального
уравнения, а именно зависимость тока через батарею от времени примет вид:
E
I(t ) = ⋅1+ R1 ⋅e−R2tC .
R1 R2
Постоянная времени τ = R2C
является характерным временем данного переходного процесса. При t
<< τ ток через батарею практически не успевает заметно измениться, а при t
>> τ можно считать, что переходный процесс закончился и через батарею
течёт постоянный ток, рассчитанный выше в пункте 3):
I =
E .
R1
График зависимости силы тока через батарею от времени I(t),
показан на рисунке 0г. На примере разобранной схемы мы рассмотрели все три
процесса. До замыкания ключа ток через батарею равен нулю:
I(0− ) = 0.
Сразу после замыкания ток скачком возрастает до значения:
I  E
E
,
1 2
затем по экспоненте спадает до установившегося значения:
I(∞ ) = E
R1
Глава 2
Сразу после коммутации
Задача 1. В
электрической схеме, изображенной на рисунке 1а, в начальный момент ключ К
разомкнут, а конденсатор не заряжен. Параметры схемы указаны на рисунке.
Определите начальные токи через резисторы и через батарею сразу после замыкания

Рис.
1а Рис. 1б
Решение. За очень малое время установления начальных
токов (не путать с установившимися стационарными токами) заряд на конденсаторе
не изменится и разность потенциалов на нём останется равной нулю. Эквивалентная
схема для этого промежутка времени будет иметь вид, изображенный на рисунке 1б.
Такая схема позволяет с помощью закона Ома для замкнутой цепи определить
начальные токи. Начальный ток через батарею:
I = R1 ⋅ RE2 + r = r ⋅( R(1R+1 +R2R)2+)⋅RE1 ⋅ R2 R1 +
R2
а начальные токи через резисторы, соединённые параллельно:
I1 =
I ⋅
R1R+2R2 =
r ⋅( R1 +RR22⋅)E+ R1 ⋅ R2
и
I2 =
I ⋅
R1R+1R2 =
r ⋅(R1 +RR12⋅)E+ R1 ⋅ R2
Следует отметить, что полученные значения
начальных токов не зависят от ёмкости конденсатора С.
Задача 2. В
электрической схеме, изображённой на рисунке 2а, в начальный момент ключ К
разомкнут, а конденсатор не заряжен. Параметры схемы указаны на рисунке.
Определите начальные токи через ключ и через батарею сразу после замыкания
ключа.
Решение. Сразу после замыкания ключа
К напряжение на конденсаторе остаётся равным нулю, поэтому начальный ток
через резистор сопротивлением 3R будет равен нулю.
UC = I3 ⋅R3
Эквивалентная схема для этого момента времени изображена на
рисунке 2б.
Рис.
2а Рис. 2б
Начальный ток через батарею, очевидно, будет равен:
I =
R⋅2ER r =
3r3+E2R
+
R +
2R
Такой же ток течёт и через конденсатор. А начальный ток
через ключ равен начальному току, протекающему через резистор сопротивлением 2R:
I2 = I = r +E2R
3 3
“Очевидные” рассуждения можно заменить классическими
методами решения данной задачи, применив закон коммутации. Напряжение на
конденсаторе после замыкания ключа К скачком изменится не может. По
условию задачи до замыкания конденсатор не был заряжен, следовательно, после
замыкания напряжение на конденсаторе остаётся равным нулю:
UC(0–) = UC(0+)
= 0
Изобразим цепь и направим соответствующие токи: ток I
— в ветви с батареей Е; ток I1
— через резистор сопротивлением R,
ток I2 — через резистор сопротивлением 2R; ток I3
— через резистор сопротивлением 3R; IC — ток через
конденсатор в момент замыкания ключа К (рис. 2в). Запишем первый закон
Кирхгофа для верхнего узла:
I =
I1 +
I2 .
Запишем первый закон Кирхгофа для нижнего узла:
I =
IC +
I3.

2R
3R
Рис. 2в
Теперь запишем второй закон Кирхгофа для верхнего маленького
контура:
0 = −I1R + I2
⋅2R,
откуда
I1 =2I2
и для нижнего маленького контура:
UC =
I3 ⋅3R = 0,
откуда
I3 =
0
Тогда сила тока через батарею равна:
I =
2I2 +
I2 =
3I2
I2 = I , 3
а ток через конденсатор
IC =
I
Записав второй закон Кирхгофа для внешнего контура,
окончательно получим:
E =
I ⋅r + I2 ⋅2R +
I3 ⋅3R
E =
I ⋅r + I ⋅2R +
0
3
E =
I ⋅(3r + 2R)
3
Ток, протекающий через батарею в момент сразу после
замыкания ключа:
I =
3E
3r +
2R
и равен току, протекающему через конденсатор. Если ток через
резистор сопротивлением 3R не протекает, то ключ К оказывается в
цепи резистора сопротивлением 2R. Применяя законы параллельного
соединения, определим ток через резистор сопротивлением
2R:
I2 = I ⋅ R +R2R =
3r +E2R
Задача 3. В
электрической схеме, состоящей из батареи с ЭДС Е = 15 В, резисторов R1
= 10 Ом, R2
= 30 Ом и конденсатора (см. рис. 3а), замыкают ключ К. Найти ток I0
через резистор R2 сразу после замыкания ключа. Внутренним
сопротивлением батареи пренебречь.
Рис.
3а
Рис. 3б
Решение. За очень малое время установления начальных
токов заряд на конденсаторе не изменится и разность потенциалов на нём останется
равной нулю. Эквивалентная схема для этого промежутка времени будет иметь вид,
изображенный на рисунке 3б. Такая схема позволяет с помощью закона Ома для
замкнутой цепи определить начальные токи.
Начальный ток через батарею:
I E (R +R )⋅E
Начальный ток через резистор сопротивлением
R2 (он же и через конденсатор) можно определить, используя
законы параллельного соединения проводников:
I0 =
I ⋅
R1R+1R2 =
RE2 = 1530 = 0,5 А
Задача 4. В
электрической схеме, состоящей из батареи с ЭДС Е = 30 В, резисторов R1
= 10 Ом, R2 = 20 Ом, R3 = 30 Ом и конденсатора (см. рис.
4а), замыкают ключ К. Найти ток I0 через резистор R2
сразу после замыкания ключа. Внутренним сопротивлением батареи пренебречь.
Решение. За очень малое время установления начальных
токов заряд на конденсаторе не изменится и разность потенциалов на нём
останется равной нулю. Схема для этого промежутка времени с токами будет иметь
вид, изображенный на рисунке 4б.
Рис.
4а Рис.
4б
Согласно закону коммутации: UC(0–)
= UC(0+) = 0
Запишем первый закон Кирхгофа для узла а:
I =
I1 +
I0.
Запишем первый закон Кирхгофа для узла б:
I0 = IC + I3.
Запишем второй закон Кирхгофа для крайнего правого контура:
UC =
I3 ⋅
R3 = 0,
откуда
I3 =
0
Тогда сила тока через резистор, сопротивлением R2
равна:
I0 = IC
Записав второй закон Кирхгофа для внешнего контура,
окончательно получим:
E =
I0 ⋅R2
I0 =
E =
30
= 1,5 А
R2 20
Задача 5. В электрической схеме, состоящей
из батареи с ЭДС Е = 20 В, резисторов R1 = 10 Ом, R2 = 20
Ом, R3 = 30 Ом и конденсатора (см. рис. 5а), замыкают ключ К. Найти
ток I0 через резистор R3 сразу после замыкания ключа.
Внутренним сопротивлением батареи пренебречь.
Решение. За очень малое время установления начальных
токов заряд на конденсаторе не изменится и разность потенциалов на нём
останется такой, какой она была до замыкания ключа:
Рис.
5а
Рис. 5б
Определим напряжение на конденсаторе до коммутации:
UC =
IБ ⋅R2,
где IБ — ток через
батарею и двух последовательно соединенных резистора с сопротивлениями R1
и R2 (ток в ветви с конденсатором и резистором сопротивлением
R3 отсутствует). По закону Ома для замкнутой цепи:
IБ = E
R1 + R2
и тогда
UC =
E ⋅R2
R1 + R2
После коммутации, схема для этого промежутка времени с
токами будет иметь вид, изображенный на рисунке 5б. Запишем второй закон
Кирхгофа для крайнего правого контура, содержащего конденсатор:
UC =
I0 ⋅R3,
откуда
I U
E ⋅R
3 1 +
2 ⋅
3
I = 0,44 А
Задача 6. В электрической схеме, изображенной на
рисунке, в K2 K1
начальный момент
времени ключи К1 и К2 разомкнуты, а конденсатор С
(большой ёмкости) не заряжен. После замыкания ключа К1 амперметр А
показывает постоянный ток силой I1

замыкают ключ К2. Чему будет равно R1 показание
амперметра сразу после замыкания ключа К2, если известно, что R2/R1
= 2? Внутренним сопротивлением амперметра пренебречь.
Решение. Рассмотрим электрическую цепь, в которой
ключ К1 замкнут. За очень малое время установления начальных
токов заряд на конденсаторе не изменится и разность потенциалов на нём
останется такой, какой она была до замыкания ключа:
Рис.
6а Рис. 6б
Выразим силу тока I1,
которую показывает амперметр, записав закон Ома для полной цепи (см. рис. 6а):
I1 = R1 +ER2
откуда E =
I ⋅( R1 +
R2 )
Теперь замкнём ключ К2.
Схема для этого промежутка времени с токами будет иметь вид, изображенный на
рисунке 6б. Для нижнего узла запишем первый закон Кирхгофа:
I =
IC +
I2.
Теперь запишем второй закон Кирхгофа для левого контура,
содержащего конденсатор:
UC =
I2 ⋅R2 = 0,
откуда
следует, что I2 =0 и I = IC
Значит для внешнего контура, как это следует из второго
закона Кирхгофа, искомый ток через резистор сопротивлением R1
будет равен:
E =
I ⋅
R1
I =
E
R1
или
I
= 9 мкА
R1 R1
Задача 7. В
электрической схеме, изображенной на рисунке 7а, ключ К разомкнут, а
конденсатор заряжен до некоторого значения UC. Параметры схемы
указаны на рисунке 7а. Определите величину напряжения UC, при
которой ток через батарею сразу после замыкания ключа останется неизменным.
Решение. За очень малое время установления начальных
токов заряд на конденсаторе не изменится и разность потенциалов на нём
останется такой, какой она была до замыкания ключа:
Рис.
7а Рис.7б
До замыкания ключа через батарею течёт ток, силой:
I = E
R1 +
r
Сразу после замыкания ключа напряжение на
конденсаторе остаётся неизменным и равным UC. Пусть в этот
момент текут токи, как показано на рисунке 7б. Запишем второй закон Кирхгофа
для левого контура, содержащего резистор сопротивлением R1:
E =
I ⋅r + I1 ⋅
R1
E =
RE1 +⋅rr + I1 ⋅ R1
RE1 = R1(ER1⋅r+ r) + I1,
откуда
I1 = RE1 − R1(ER1⋅r+ r ) =
RE1 ⋅1− R1r+ r = RE1 R1R+1 r = R1E+ r и равен току I !!!
Так как сила тока через резистор
сопротивлением R1 равна силе тока через батарею, то по
первому закону Кирхгофа ток I2 = 0. Записав второй закон
Кирхгофа для правого контура, содержащего конденсатор:
UC =
I1 ⋅
R1 −
I2 ⋅
R2,
окончательно получим:
UC = I1 ⋅ R1 = RE1⋅+Rr1

рисунке, в Е R
начальный момент
времени ключи К1 и К2 разомкнуты, а конденсатор С
(большой ёмкости) не заряжен. Через некоторое время после замыкания ключа К1
амперметр А показывает постоянный ток силой I1 = 1 мкА. В этот
момент замыкают ключ К2. Какую величину силы тока покажет амперметр
сразу после замыкания ключа К2, если известно, что R2 = 2
R1 = 100 МОм, а ЭДС батареи Е = 100 В? Внутренними сопротивлениями
амперметра и батареи пренебречь. R2
Решение. Рассмотрим электрическую цепь, в которой
ключ К1 замкнут, а ключ К2 разомкнут. За
очень малое время установления начальных токов заряд на конденсаторе не
изменится и разность потенциалов на нём останется такой, какой она была до
замыкания ключа К2:
UC(0–) = UC(0+)
Рис. 8а Рис. 8б
Выразим напряжение на конденсаторе до
коммутации через силу тока I1, которую показывает амперметр,
записав второй закон Кирхгофа (см. рис. 8а):
E −UC =
I1 ⋅
R1
откуда
UC =
E −
I1 ⋅
R1
Теперь замкнём ключ К2.
Схема для этого промежутка времени с токами будет иметь вид, изображенный на
рисунке 8б. Для правого узла запишем первый закон Кирхгофа:
IA =
I −
I2 .
Теперь запишем второй закон Кирхгофа для внешнего контура:
E =
I ⋅
R1 +
I2 ⋅
R2,
откуда следует, что
I =
E −
I2 ⋅ R2
R1
Далее, запишем второй закон Кирхгофа для нижнего контура:
UC =
I2 ⋅
R2,
откуда следует, что
I2 = URC2
И тогда, искомый ток IA,
протекающий через амперметр, сразу после замыкания ключа К2,
будет равен:
IA = I − I2 = E −RI2 ⋅ R2 − URC2 = RE1 − I2 ⋅ RR12 − URC2 = RE1 − URC2 ⋅ RR12 − URC2
1
IA = RE1 − URC1 − URC2
IA = RE1 −
( E −RI11 ⋅
R1 ) −
( E −RI12 ⋅
R1 ) =
RE1 −
RE1 +
I1 − RE2 +
I1 ⋅ RR12
IA = I1 − RE2 + I1 ⋅ RR12 = I1 ⋅1+ RR12 − RE2
IA =1⋅10−6 ⋅1+ 1 − 100 6 = 0,5⋅10−6 = 0,5 мкА
2 100⋅10

электрической схеме, изображенной на рисунке, в Е R1 начальный момент времени
ключи К1 и К2 разомкнуты, а кон-
денсатор С (большой
ёмкости) не заряжен. Через некоторое K1
время после
замыкания ключа К1 амперметр А показывает величину силы тока I = 2
мкА. В этот момент замыкают
ключ К2.
Сразу после замыкания ключа К2 амперметр K2
показывает
нулевое значение силы тока. Чему равна ЭДС батареи, если известно, что R1 = R2 = 108
Ом? Внутренними
сопротивлениями амперметра и батареи пренебречь. R2
Решение. Рассмотрим электрическую цепь, в которой
ключ К1 замкнут, а ключ К2 разомкнут. За
очень малое время установления начальных токов заряд на конденсаторе не
изменится и разность потенциалов на нём останется такой, какой она была до
замыкания ключа К2:
UC(0–) = UC(0+)
= 0
Выразим искомое ЭДС батареи, записав второй закон Кирхгофа
для замкнутого контура (см. рис. 9а):
E −UC =
I ⋅
R1,
откуда
Рис.
9а Рис. 9б
Теперь замкнём ключ К2. Схема для этого
промежутка времени с токами будет иметь вид, изображенный на рисунке 9б. Так
как по условию задачи, ток через амперметр не проходит, то по первому закону
Кирхгофа, ток идёт по внешнему контуру и его величина:
I2 = R1 +ER2 .
Теперь запишем второй закон Кирхгофа для нижнего контура, из
которого определим напряжение на конденсаторе:
UC = I2 ⋅ R2 = RE1 +⋅ RR22 . И тогда, окончательно:
E =
I ⋅
R1 + RE1 +⋅ RR22
E −
RE1 +⋅ RR22 = I ⋅ R1
E ⋅1− R1R+2R2 = I ⋅ R1
E ⋅ R1R+1R2 = I ⋅ R1
E =
I ⋅( R1 +
R2 )
E =
2⋅10−6 ⋅(108 +108 )
= 400 В
Задача 10. Две
батареи с ЭДС Е1 и Е2 включены в схему, параметры которой
указаны на рисунке 10а, причём R1 = R2 = R3 =
R. В начальный момент времени ключи К1 и К2 разомкнуты, а конденсаторы не заряжены. Ключи одновременно
замыкают. Найдите ток через резистор R1.
Решение. За очень малое время установления начальных
токов заряды на конденсаторах не изменяются и разность потенциалов на них
останется такой, какой она была до замыкания ключа:
UC(0–) = UC(0+)
= 0
Рис. 10а Рис.10б
Теперь замкнём ключи. Схема для этого промежутка времени с
токами будет иметь вид, изображенный на рисунке 10б. По двум законам Кирхгофа,
составим систему из трёх уравнений:
I1 =
I2 + I3
E1 =
I1 ⋅ R1 + I2 ⋅ R2
E2 =
I1 ⋅ R1 + I3 ⋅ R3
Выразим из второго уравнения системы ток I2,
из третьего уравнений системы — ток I3 и подставим в первое
уравнение:
I2 = E1 −RI21 ⋅
R1 = RE21 −
I1 ⋅ RR12
I3 = E2 −RI31 ⋅R1 = ER32 − I1 ⋅ RR13
I1 = RE21 −
I1 ⋅ RR12 + ER32 − I1 ⋅ RR13
I1 ⋅1+ RR12 + RR13 = RE21 +
ER32
Учитывая, что все резисторы одинакового сопротивления,
окончательно получим:
I
I1 = E13+RE2
Задача 11. В
электрической схеме, изображённой на рисунке 11а, в начальный момент времени
ключ К разомкнут, а в замкнутом контуре течёт установившийся ток. Определите
величину и направление тока через конденсатор С сразу после замыкания ключа.
Параметры схемы: ЭДС первой батареи Е1 = 40 В, её внутреннее
сопротивление r1 = 200 Ом, ЭДС второй батареи Е2 = 80 В,
её внутреннее сопротивление r2 = 50 Ом, сопротивление резистора R =
150 Ом.
Решение. За очень малое время установления начальных
токов заряд на конденсаторе не изменится и разность потенциалов на нём
останется такой, какой она была до замыкания ключа К:
UC(0–) = UC(0+)
Рис.
11а Рис. 11б
До замыкания ключа через батарею Е2 и
резистор сопротивлением R течёт ток, силой:
I = E2 =
80 = 0,4 А
R +
r2 150+50
Тогда напряжение на конденсаторе будет равно разности
потенциалов на резисторе:
UC E ⋅ R 80⋅150 = 60 В
Сразу после замыкания ключа напряжение на
конденсаторе остаётся неизменным и равным UC. Пусть в этот
момент текут токи, как показано на рисунке 11б. Запишем первый закон Кирхгофа
для правого узла:
IC = I1 + I2 − IR
Запишем второй закон Кирхгофа среднего контура, содержащего
резистор и конденсатор:
UC =
IR ⋅
R,
откуда
IR = URC =
RE2+⋅rR2 R1 = RE+2r2 =
15080+ 50 = 0,4 А
То есть, в момент сразу после замыкания ключа ток через
резистор не изменился! Теперь запишем второй закон Кирхгофа для нижнего
контура:
E2 = I2 ⋅r2 + IR ⋅ R
или
E2 E R,
откуда
I2 = E2 −rRE2 2+⋅rR2 = (RE+2r⋅2r)2⋅r2 = RE+2r2 = 150
80+
50 = 0,4 А
Таким образом, ток через конденсатор в момент замыкания
ключа равен току через батарею с ЭДС Е2, то есть этот ток
тоже не изменился! И наконец, записывая второй закон Кирхгофа для внешнего
контура, получим выражение для тока I1:
E2 − E1 = I2 ⋅r2 − I1 ⋅r1
E2 E r1
I1 E E1
I = –
0,1 А
2 1 1 1
То есть ток через батарею с ЭДС Е1
течёт противоположно показанному на рисунке 11б. и тогда окончательно, ток
через конденсатор:
IC = I1 + I2 − IR = RE+2r2 ⋅
rr12 − Er12 + Er11 + RE+2r2 −
RE+2r2
IC = RE+2r2 ⋅
rr12 − Er12 + Er11 = I1 = – 0,1 А
Это означает, что ток через конденсатор в
момент замыкания ключа К равен току через батарею с ЭДС Е1:
IC = I1 = – 0,1 А
и направлен слева направо.
Задача 12. Батарея
с ЭДС Е и внутренним сопротивлением r включена через ключ К в схему, параметры
которой указаны на рисунке 12а. В начальный момент времени ключ разомкнут, а
конденсаторы не заряжены. Ключ замыкают. Определите начальный ток (сразу после
замыкания ключа) через батарею.
Решение. За очень малое время
установления начальных токов заряды на конденсаторах не изменяются и разность
потенциалов на них останется такой, какой она была до замыкания ключа К:
UC(0–) = UC(0+)
= 0

Рис.
12а Рис. 12б
Теперь замкнём ключ К. Схема для
этого промежутка времени с токами будет иметь вид, изображенный на рисунке 12б.
По второму закону Кирхгофа, какой бы мы ни взяли замкнутый контур в мостовой
схеме, получим:
UC =
I1 ⋅
R1 =
0 и UC =
I2 ⋅
R2 =
0,
откуда следует, что токи через резисторы не
протекают. Тогда по первому закону Кирхгофа следует, что IC =
I. Записав второй закон Кирхгофа для внешнего контура, окончательно
получим:
E =
I ⋅r
откуда
I =
E
r
Задача 13. В
электрической схеме, представленной на рисунке 13а, в начальный момент времени
ключи К1 и К2 разомкнуты. Ключ К1 замыкают и,
когда ток через резистор с сопротивлением R достигает значения I0,
замыкают ключ К2. Найдите ток через конденсатор ёмкостью С сразу
после замыкания ключа К2. ЭДС батарей Е1 и Е2
и их внутренние сопротивления r1 и r2 известны.
Решение. За очень малое время установления начальных
токов заряд на конденсаторе не изменится и разность потенциалов на нём
останется такой, какой она была до замыкания ключа К2:
UC(0–) = UC(0+)
Рис.
13а Рис. 13б
До замыкания ключа К2
через резистор сопротивлением R течёт ток силой I0.
Следовательно в момент замыкания ключа К2 напряжение скачком
на конденсаторе не изменяется и будет равно:
UC =
I0 ⋅
R
Запишем первый закон Кирхгофа для верхнего узла
электрической схемы:
I1 + I2 − IC − I0 = 0
откуда
IC =
I1 +
I2 −
I0
( 1 )
Запишем второй закон Кирхгофа для крайнего левого контура:
E1 −UC = I1 ⋅r1
откуда выразим ток I1:
I1 =
E1 −r1UC =
E1 −r1I0 ⋅
R
( 2 )
Запишем второй закон Кирхгофа для контура, содержащего
конденсатор и батарею с ЭДС Е2:
E2 −UC = I2 ⋅r2
откуда выразим ток I2:
I2 =
E2 −r2UC =
E2 −r2I0 ⋅
R
( 3 )
Подставляя выражения (2), (3) для токов I1
и I2 в равенство (1), окончательно получим:
IC = E1 −r1I0 ⋅
R +
E2 −r2I0 ⋅
R −
I0
IC = Er11 + Er22 − I0 ⋅1+ rR1 + rR2
Задача 14. Определите
ток I, текущий через резистор с сопротивлением R1 в схеме, параметры
которой даны на рисунке 14а, в первый момент после замыкания ключа, если до
этого напряжение на конденсаторе было постоянным.
Рис.
14а Рис. 14б
Решение. За очень малое время установления начальных
токов заряд на конденсаторе не изменится и разность потенциалов на нём
останется такой, какой она была до замыкания ключа К:
UC(0–) = UC(0+)
До коммутации (см. рис. 14а) ток в цепи отсутствовал,
поэтому напряжение на конденсаторе равно ЭДС источника тока:
UC = E
Сразу после замыкания ключа напряжение на
конденсаторе остаётся неизменным и равным UC. Пусть в этот
момент текут токи, как показано на рисунке 14б. Запишем первый закон Кирхгофа
для правого узла:
I =
I2 + IC
Запишем второй закон Кирхгофа для контура, содержащего
батарею и конденсатор:
E −UC =
I2 ⋅
R2,
E −
E =
I2 ⋅
R2 = 0,
откуда следует, что ток через батарею сразу после замыкания
ключа не протекает:
I2 = 0
Следовательно, ток через резистор
сопротивлением R1 равен току через конденсатор. Записав
второй закон Кирхгофа для внешнего контура, окончательно получим:
E =
I2 ⋅
R2 +
I ⋅
R1
E =
0 +
I ⋅
R1
I =
E
R1
Задача 15. В
электрической схеме, представленной на рисунке 15а, в начальный момент времени
ключи К1 и К2 разомкнуты. Ключ К1 замыкают и,
когда ток через конденсатор ёмкостью С достигает значения I0,
замыкают ключ К2. Найдите ток через конденсатор сразу после
замыкания ключа К2. ЭДС батарей Е1 и Е2, их
внутренние сопротивления r1 и r2, а также сопротивление R
резистора известны.
Решение. За очень малое время установления начальных
токов заряд на конденсаторе не изменится и разность потенциалов на нём
останется такой, какой она была до замыкания ключа К:
UC(0–) = UC(0+)
K1 K2
I
Рис. 15а Рис. 15б
До замыкания ключа К2, по условию задачи,
через конденсатор ёмкостью С протекает ток силой I0.
Определим силу тока IR, проходящего через резистор
сопротивлением R. Для этого рассмотрим электрическую цепь (см. рис.
15б), в которой расставим соответствующие токи. Запишем первый закон Кирхгофа
для верхнего узла электрической схемы:
I =
I0 + IR
Так как до замыкания ключа К2
через резистор сопротивлением R протекает ток, то на конденсаторе будет
начальное напряжение UC0. Поэтому запишем второй закон
Кирхгофа для внешнего контура электрической схемы (см. рис. 15б):
E1 =
I ⋅r1 +
IR ⋅
R
E1 =
(I0 +
IR )⋅r1 +
IR ⋅
R
E1 = I0 ⋅r1 + IR ⋅r1 + IR ⋅ R
откуда
IR = E1r1−+I0R⋅r1
За очень малое время установления начальных токов заряд на
конденсаторе не изменится и разность потенциалов на нём останется такой, какой
она была до замыкания ключа К2:
UC(0–) = UC(0+)
Следовательно в момент замыкания ключа К2
напряжение скачком на конденсаторе не изменяется и будет равно:
UC = IR ⋅ R = E1r1−+I0R⋅r1 ⋅ R
Сразу после замыкания ключа напряжение на
конденсаторе остаётся неизменным и равным UC. Тогда, записав
второй закон Кирхгофа для внутреннего контура, можно показать, что ток через
резистор сопротивлением R не изменился:
UC = IR ⋅ R = E1r1−+I0R⋅r1 ⋅ R ,
откуда
IR =
URC =
E1r1−+I0R⋅r1
( 1 )
Пусть в этот момент текут токи, как показано на рисунке 15в.
I1
I2
Запишем первый закон Кирхгофа для верхнего узла:
I1 + I2 − IC − IR = 0
откуда
IC =
I1 +
I2 −
IR
( 2 )
Запишем второй закон Кирхгофа для крайнего левого контура:
E1 −UC = I1 ⋅r1
откуда выразим ток I1:
I1 =
E1 −r1UC =
E1 −rI1R ⋅
R
( 3 )
Запишем второй закон Кирхгофа для контура, содержащего
конденсатор и батарею с ЭДС Е2:
E2 −UC = I2 ⋅r2
откуда выразим ток I2:
I2 =
E2 −r2UC =
E2 −r2IR ⋅
R
( 4 )
Подставляя выражения (3), (4) для токов I1
и I2 в равенство (2), окончательно получим:
IC = E1 −rI1R ⋅
R +
E2 −r2IR ⋅
R −
IR
IC = Er11 − IRr1⋅ R +
Er22 − IRr2⋅ R −
IR
IC = Er11 + Er22 − IR ⋅1+ rR1 + rR2
Учитывая выражение (1), окончательно получим:
IC = Er11 + Er22 − E1r1−+I0R⋅r1 ⋅1+ rR1 + rR2
Глава 3
Переходный процесс
Задача 16. В
электрической схеме, изображенной на рисунке 16а, ключ К разомкнут, а
конденсатор не заряжен. ЭДС источника равна Е, внутреннее сопротивление r,
ёмкость конденсатора С. Ключ замыкают. Найдите силу тока в цепи в тот момент,
когда заряд на конденсаторе составляет треть от максимально возможного заряда кон-

Рис.
16а Рис. 16б
Решение. Максимально возможный
заряд, который может получить конденсатор, очевидно равен:
Q =
E ⋅C
Это произойдёт через бесконечно длительный промежуток
времени после замыкания ключа, когда электрический ток в цепи прекратиться. В
этом случае, после полной зарядки конденсатора, напряжение на его обкладках
будет равно ЭДС батареи.
Теперь рассмотрим
переходный процесс, когда в цепи протекает электрический ток силой I и
происходит зарядка конденсатора. В этот момент времени заряд конденсатора
равен:
q C ,
а напряжение на его обкладках:
UC = Cq =
E3
Эквивалентная схема для этого промежутка
времени будет иметь вид, изображенный на рисунке 16б. Такая схема позволяет с
помощью закона Кирхгофа для замкнутой цепи определить искомую силу тока:
E −UC =
I ⋅r
E r
r
I E
Задача 17. В
электрической схеме, состоящей из батареи с ЭДС Е = 1 В, резисторов R1
= 30 Ом, R2 = 10 Ом и конденсатора (см. рис. 17а), замыкают ключ К.
Найти ток IБ через батарею в тот момент, когда напряжение на
конденсаторе равно Е/3. Внутренним сопротивлением батареи пренебречь.
Рис.
17а Рис. 17б
Решение. Эквивалентная схема с
электрическими токами для этого промежутка времени будет иметь вид,
изображенный на рисунке 17б. Запишем первый закон Кирхгофа для верхнего узла:
IБ = I1 + I2
Запишем второй закон Кирхгофа для контуров, содержащих ток
через батарею и и неизвестные токи I1, I2:
E =
I1 ⋅
R1
E −UC =
I2 ⋅
R2
Выразим токи I1, I2 и
подставим в верхнее уравнение:
I1 = RE1 и I2 = E −RU2 C
IБ E E −U E E −
E / 3 =
E +
2E = ⋅
2R +
3R
1 2 1 2 1 2 1
2
IБ =
E ⋅
Подставив числовые значения заданных величин, окончательно
получим:
IБ 
Задача 18. В электрической схеме, состоящей
из батареи с ЭДС Е = 10 В, резисторов R1 = 50 Ом, R2 =
100 Ом и конденсатора (см. рис. 18а), замыкают ключ К. Найдите ток через
батарею в тот момент, когда напряжение на конденсаторе достигло значения Е/2.
Внутренним сопротивлением батареи пренебречь.

Рис.
18а Рис. 18б
Решение. Эквивалентная схема с
электрическими токами для этого промежутка времени будет иметь вид,
изображенный на рисунке 18б. Для решения задачи достаточно записать второй
закон Кирхгофа для внешнего контура:
E −UC =
I ⋅
R1
E
I =
E
2R1
Подставим числовые значения всех заданных величин и
произведём вычисление:
I = 0,1 А
Задача 19. В
электрической схеме, состоящей из батареи с ЭДС Е = 30 В, резисторов R1
= 10 Ом, R2 = 20 Ом, R3 = 30 Ом и конденсатора (см. рис.
19а), замыкают ключ К. Найдите ток IБ через батарею в тот момент
времени, когда ток через резистор R3 равен I = 0,3А. Внутренним
сопротивлением батареи пренебречь.
Решение. Схема с электрическими
токами для этого промежутка времени будет иметь вид, изображенный на рисунке
19б.
Рис. 19а
Рис. 19б
Запишем первый закон Кирхгофа для верхнего левого узла:
IБ = I1 + I2
Запишем второй закон Кирхгофа для крайнего левого контура,
содержащего батарею:
E =
I1 ⋅
R1,
откуда
I1 = RE1
Ток I2 выразим, записав
второй закон Кирхгофа для крайнего левого и среднего контуров:
E =
I2 ⋅
R2 +
I ⋅
R3,
откуда
I2 =
E −RI2⋅
R3
В результате будем иметь:
I1 = RE1 и I2 = E −RI2⋅ R3
Подставив найденные значения токов I1 и I2
в верхнее уравнение, окончательно получим:
IБ = E +
E −
I ⋅
R3
R1 R2
IБ = 4,05 А
Задача 20. В
электрической схеме, состоящей из батареи с ЭДС Е = 20 В, резисторов R1
= 10 Ом, R2 = 20 Ом, R3 = 30 Ом и конденсатора (см. рис.
20а), замыкают ключ К.
Найдите ток IБ
через батарею в тот момент времени, когда напряжение на конденсаторе равно
0,6Е. Внутренним сопротивлением батареи пренебречь.
Рис.
20а Рис.
20б
Решение. Сначала необходимо выяснить, в каком режиме
находится наша схема в заданный момент времени: то ли это будет переходный
процесс, то ли стационарный режим. Для этого найдём установившееся напряжение
на конденсаторе в стационарном режиме. Схема, соответствующая этому случаю,
будет иметь вид, изображённый на рисунке 20б. При этом эквивалентное
сопротивление цепи будет равно:
RЭ = R1 + RR22+⋅RR33
Через резистор R1, равно, как и через
батарею, течёт ток силой:
I = REЭ = R ER2R3 = R1 ⋅(ER⋅2(+R2R+3 )R+3R)2R3
1 +
R2 + R3
Зная ток в неразветвленной части цепи, можно найти токи в
параллельных её ветвях:
I2 = I ⋅ R2R+3R3 = R1 ⋅(R2 E+⋅RR33)+ R2R3
I3 = I ⋅ R2R+2R3 = R1 ⋅(R2E+⋅RR32)+ R2R3
Напряжение на резисторах R2
и R3 такое же, как на конденсаторе в установившемся режиме:
U3 =U3 =UC = R1 ⋅(R2E+⋅ RR23R)3+ R2R3
После подстановки числовых значений, получим:
UC = 10,9 В
Поскольку в задаче речь идёт о напряжении
на конденсаторе, равном 0,6Е = 12В, то очевидно, что состояние системы
соответствует переходному процессу. Рассмотрим в этот момент времени
электрическую цепь, представленную на рисунке 20в.
R1 IБ 3
R3
I3
Рис. 20в
Для решения задачи достаточно записать второй закон Кирхгофа
для контура, содержащего батарею и конденсатор:
E −UC =
IБ ⋅
R1,
E −
0,6E =
IБ ⋅
R1
0,4E
=
IБ ⋅
R1
откуда
IБ = 0,8 А
Задача 21. Электрическая
цепь состоит из батареи с ЭДС Е, конденсатора ёмкости С и переменного
резистора, начальное значение сопротивления которого равно R0 (см.
рис. 21а). Через некоторое время после замыкания ключа К в цепи течёт ток силой
I0. Начиная с этого момента времени сопротивление R изменяется таким
образом, что ток в цепи остаётся постоянным и равным I0. 1)
Определите ток в цепи сразу после замыкания ключа К. 2) Найдите зависимость
сопротивления от времени. Внутреннее сопротивление батареи не учитывать.
Решение. Ток в цепи сразу после замыкания ключа имеет
максимальное значение, так как на конденсаторе напряжение отсутствует.
Следовательно, по второму закону Кирхгофа можно определить его значение:
E −UC =
I ⋅R0,
I =
E
R0
Рис.
21а Рис. 21б
Рассмотрим момент времени, когда в цепи
протекает ток, силой I0 (см. рис. 21б). Согласно второму
закону Кирхгофа:
E −UC =
I0 ⋅
R,
E =
I0 ⋅
R +UC
Напряжение на конденсаторе для этого момента времени можно
выразить через заряд:
E =
I0 ⋅
R +
Cq ,
который изменяется с течением времени:
E =
I0 ⋅ R + I0C⋅t
E =
R +
t
I0 C
Но по условию задачи в начальный момент
времени сопротивление переменного резистора равно R0,
следовательно:
R0 =
R +
Ct ,
откуда, окончательно:
R(t ) =
R0 −
Ct
Задача 22 В
цепи, изображённой на рисунке 22а первоначально ключ К замкнут и в ней течёт
постоянный ток. Ключ размыкают. Через какое приблизительно время заряд на
конденсаторе уменьшится на 1/1000 своей первоначальной величины? ЭДС батареи Е
= 4,5 В, её внутреннее сопротивление r = 1 Ом, ёмкость конденсатора С = 12 мкФ,
сопротивление резистора R = 500 кОм.
Рис.
22а Рис. 22б
Решение: сразу после размыкания
ключа, по резистору сопротивлением R потечёт ток, мгновенное значение
которого будет равно:
i =
UC ,
R
где UC — разность потенциалов на
конденсаторе, которая равна:
UC = Cq
Так как в задаче речь идёт об изменении очень малых зарядов,
то мы не будем учитывать, что и ток, и разность потенциалов зависит от времени.
Таким образом, за бесконечно малый интервал времени Δt заряд на
конденсаторе уменьшится на величину:
∆q = i⋅∆t
Тогда: ∆q = i⋅∆t = UC ⋅∆t = q ⋅∆t ,
R RC
Откуда:
RC
Подставив числовые значения заданных величин, окончательно
получим:
= 0,006 с = 6 мс
Задача 23 Электрическая
цепь состоит из батареи с ЭДС Е, резистора, сопротивлением R и конденсатора
переменной ёмкости, начальное значение которой равно С0 (см. рис.
23а). Через некоторое время после замыкания ключа К в цепи течёт ток силой I0.
Начиная с этого момента времени ёмкость конденсатора изменяется таким образом,
что ток в цепи остаётся постоянным и равным I0. 1) Определите ток в
цепи сразу после замыкания ключа К. 2) Найдите зависимость ёмкости конденсатора
от времени. Внутреннее сопротивление батареи не учитывать. Конденсатор вначале
не заряжен.
Решение. Ток в цепи сразу после замыкания ключа имеет
максимальное значение, так как на конденсаторе напряжение отсутствует.
Следовательно, по второму закону Кирхгофа можно определить его значение:
E −UC =
I ⋅
R,
Рис.
23а Рис. 23б
Рассмотрим момент времени, когда в цепи
протекает ток, силой I0 (см. рис. 23б). Согласно второму
закону Кирхгофа:
E −UC =
I0 ⋅
R,
E =
I0 ⋅
R +UC
Напряжение на конденсаторе для этого момента времени можно
выразить через заряд:
E =
I0 ⋅
R +
Cq ,
который изменяется с течением времени:
E =
I0 ⋅ R + I0C⋅t ,
откуда
I0C⋅t =
E −
I0 ⋅ R
C = I0 ⋅t
E −
I0 ⋅
R
Но по условию задачи в начальный момент времени ёмкость
переменного конденсатора равна С0, следовательно:
C(t ) =
C0 + E −II00 ⋅ R ⋅t
Задача 24 В изображённой
на рисунке 24а цепи конденсаторы одинаковые, ёмкость каждого С = 100 мкФ,
резистор имеет сопротивление R = 100 кОм, батарея с ЭДС Е = 10 В обладает
внутренним сопротивлением r = 1 Ом. Ключ К замыкают. Какой ток течёт по
резистору через время τ = 0,1 с после замыкания ключа К?
Решение. После замыкания цепи конденсаторы очень
быстро заряжаются, а ток через резистор очень мал. Покажем это. Токи заряда в
самом начале определяются маленьким внутренним сопротивлением батареи.
Характерное время заряда цепи равно произведению эквивалентной ёмкости батареи
и внутреннего сопротивления источника тока:
tr = r ⋅CЭКВ =
r ⋅0,6C =1⋅0,6⋅100⋅10−6 = 6.10–5
с,
что намного меньше заданного времени τ = 0,1 с в условии
задачи. С другой стороны, постоянная времени заданной цепи:
tR = R⋅CЭКВ =
R⋅0,6C =100⋅103 ⋅0,6⋅100⋅10−6 = 6 с,
что намного больше заданного интервала времени τ = 0,1.
Рис.
24а Рис. 24б
Обозначим на схеме потенциалы всех обкладок конденсаторов и
их заряды. Потенциал точки о примем за нуль, тогда потенциал точки е
будет равен ЭДС батареи:
ϕo = 0 и ϕe =
E
Пусть через резистор протёк заряд qR от
точки с потенциалом е к точке с потенциалом b.
Тогда для узла b можно записать:
−
q3 −
qR +
q4 =
0 Откуда:
−C(ϕa −ϕb )+ C(ϕb −ϕo ) = qR
qR
−ϕa +ϕb +ϕb =
C
Следовательно, потенциал точки а:
ϕa = 2ϕb −
qCR
Суммарный заряд обкладок конденсаторов, соединённых в точке а
равен нулю:
− q1 + q2 + q3 = 0
−C(ϕe −ϕa )+ C(ϕa −ϕo )+ C(ϕa −ϕb ) = 0
− E +ϕa +ϕa +ϕa −ϕb =
0
ϕb = 3ϕa −
E
С учётом найденного выражения для потенциала точки а,
будем иметь:
ϕb = 3⋅2ϕb −
qCR
−
E
ϕb = 6ϕb −
3CqR −
E
5ϕb =
E +
3CqR
E 3qR ϕb =
5 +
5C
Из последнего выражения видно, что в момент
времени τ = 0,1 с, т.е. когда qR = 0, потенциал точки b
будет равен:
E , ϕb =
5
а разность потенциалов на резисторе:
U R =ϕe −ϕb =
E −
E5 = 45E
Таким образом, ток через резистор в заданный момент времени
будет равен:
IR = URR =
45RE =
5⋅1004⋅10⋅103 = 8·10–5
А
Ответ: IR = 80 мкА.
Задача 25. В
плоский конденсатор, закороченный на резистор сопротивлением R, помещена
аналогичная проводящая пластина, имеющая заряд q (см. рис. 25а) на расстоянии а
от левой пластины (а < d/2). Где d — расстояние между обкладками
конденсатора. Какой ток потечёт через резистор, если пластину двигать с
постоянной скоростью υ?
Решение. При движении заряженной пластины с
постоянной скоростью на обкладках конденсатора появляются заряды,
обеспечивающие такую разность потенциалов между пластинами, чтобы ток в цепи а,
следовательно, и напряжение на резисторе оставались постоянными.
Рис.
25а Рис. 25б
Пусть в некоторый момент времени расстояние между
перемещаемой заряженной пластиной и левой пластиной конденсатора равно х.
Обозначим заряды левой и правой обкладок конденсатора в этот момент через q1
и q2. В силу закона сохранения электрического заряда: q1
+ q2 = 0,
или q1 = – q2.
Эти заряды создают внутри конденсатора электрическое поле,
напряженность которого равна:
E,
а заряд q уединённой пластины создаёт поле
напряжённостью:
E ,
0 0
где S — площадь обкладок конденсатора и внесённой в
него пластины (по условию задачи они равны). Согласно принципу суперпозиции
электрических полей (см. рис 25б), разность потенциалов на обкладках
конденсатора равна:
UC =
( E1 +
E )⋅
x +( E1 −
E )⋅(d − x).
Положив х = а + υt,
найдём временную зависимость зарядов, возникающих на обкладках конденсатора:
UC =
E1 ⋅
x +
E ⋅
x −
E1 ⋅
x +
E ⋅
x +
E1 ⋅d − E ⋅d
UC =
d ⋅( E1 −
E )+
2E ⋅
x
Напряжение на плоском конденсаторе будет изменяться со
временем по закону
UC =qCC(t) .
Воспользуемся формулой для плоского конденсатора:
C=εε0 ⋅S
d
Учитывая взаимодействия, происходящие в воздухе (ε = 1),
получим зависимость напряжения от времени:
UC =
qCε(0t⋅)S⋅d
Приравнивая между собой правые части двух зависимостей
напряжения от времени и от координаты, получим:
qC (t)S⋅d =d⋅(E1 −E)+2E⋅x
ε0 ⋅
qC(t ) =ε0 ⋅S ⋅( E1 −
E )+ε0 ⋅S ⋅ 2dE ⋅
x
qC(t ) =ε0 ⋅S ⋅ε0q⋅1S − 2ε0q⋅S +ε0 ⋅S ⋅
2ε0q⋅S d2 ⋅ x
qC 2 d x
При этом координата х зависит от скорости движения пластины,
поэтому
qC(t ) =
q1 − q2
+
dq ⋅(a +υt )
qC (t ) =
q1 − q2 + qad + qdυt
Видно, что окончательная зависимость представляет собой
линейную зависимость, так как величины, стоящие в круглых скобках являются
постоянными и не зависят от времени. Взяв производную электрического заряда по
времени, определим искомую силу тока через резистор:
I =
dqdt = qC/ (t ) =
q1 − q2 + qad
+
qdυt/ =
q1 − q2 + qad / +
qdυt/
I = qυ
d
Ответ: I = qυ.
d
Глава 4
Установившийся режим
Задача 26. Определите
заряды конденсаторов в установившемся режиме в цепи, изображенной на рисунке
26а: 2С
Рис. 26а
Решение. На примере, достаточно
простой задачи покажем несколько способов её решения.
I
способ, назовём его, школьный. Находим
эквивалентную ёмкость батареи конденсаторов, подключенных к источнику тока:
CЭКВ 2C ⋅(C +C) = С
2C (C
C)
Тогда электрический заряд, накопленный батареей
конденсаторов, будет равен:
Q =
C ⋅E
Очевидно, что заряд на конденсаторе ёмкостью 2С равен
заряду батареи:
q1 =
Q =
CE
На двух параллельно соединённых конденсаторах равной
ёмкости, очевидно, заряды будут одинаковыми и равными половине заряда батареи:
q2 = q3 = Q =
CE
2 2
Ответ: q1 =
Q =
CE, q2 =
q3 =
Q2 =
CE2 .
II
способ, назовём его, потенциальный. Этот способ
очень удобен, если необходимо определить разность потенциалов между любыми
двумя точками цепи. Для этого:
1)
Расставляем произвольным образом заряды на обкладках
конденсаторов (см. рис. 26б).
2) Обозначаем
дополнительные точки на схеме между обкладками конденсаторов.
C1
B
C3
Рис. 26б
3) Принимаем
потенциал точки А равным нулю:
ϕA = 0 и тогда ϕB =
E
4)
Для связанных зарядов (точка О — узел — точка соединения
трёх пластин конденсаторов) выполним закон сохранения электрического заряда, а
именно:
− q1 + q2 + q3 = 0
5)
Подставляем в последнее равенство заряды, выраженные через
разность потенциалов (по рисунку вычитают от большего потенциала меньший
потенциал):
−C1(ϕB −ϕO )+C2(ϕO −ϕA )+C3(ϕO −ϕA )= 0
−C1 ⋅ϕB +C1 ⋅ϕO +C2 ⋅ϕO +C3 ⋅ϕO =
0
откуда
ϕO = C1 +C1C⋅ϕ2 +B C3 = C1 +CC1 ⋅2E+C3
или
2C ⋅E E
ϕO = C +C +C = 2
2
Теперь, зная потенциалы все точек легко определить заряды на
конденсаторах:
q1 =
C1 ⋅(ϕB −ϕO )= 2C ⋅E − E
= CE
2
q2 =
C2 ⋅(ϕO −ϕA )= C ⋅
E −0
=
CE
2
2
q3 =
C3 ⋅(ϕO −ϕA )= C ⋅
E −0
=
CE
2
2
Так как заряды получились положительными, то с расстановкой
знаков угадали.
Ответ: q1 =
CE ,
q2 =
q3 =
CE2 .
Способ достаточно громоздкий по сравнению
со школьным, но очень надёжный — всегда найдены потенциалы обкладок
конденсаторов.
III способ, назовём его, кирхгофный.
Очень удобен, особенно, когда цепь с конденсаторами содержит несколько
источников ЭДС. Для этого:
1) Расставляем
произвольным образом заряды на обкладках конденсаторов (см. рис.
26в).
2)
Пользуемся правилом направление ЭДС r Е и
напряжённости электростатического поля заряженного конденсатора E :
Е Er
3)
Выбираем положительный обход замкнутых контуров, например, по
ходу часовой стрелки. Записываем закон Кирхгофа для выбранного контура:
ΣEi =ΣUCi
Для левого замкнутого контура:
E =UC1 +UC2 = Cq11 + Cq22 ,
откуда
Cq22 = E − Cq11 или q2 =
EC2 −
q1 CC12
Для общего внешнего замкнутого контура:
E =UC1 +UC3 = Cq11 + Cq33 ,
откуда
Cq33 = E − Cq11 или q3 =
EC3 −
q1 CC13
Для узла — точки соединения трёх пластин
конденсаторов, запишем закон сохранения электрического заряда:
− q1 + q2 + q3 = 0
Или с учётом полученных выражений:
− q1 +
EC2 − q1 CC12 +
EC3 − q1 CC13 =
0
EC2 + EC3 = q1 + q1 CC12 +
q1 CC13
E ⋅(C2 +C3 )= q1 ⋅C1 +CC21 +C3
q1 = EC1 ⋅C1C+2C+2C+3C3
или
q1 = E ⋅2C ⋅
2CC++CC+C = EC
И тогда: q2 =
EC2 −
q1 CC12 = EC − EC ⋅ 2CC = EC2
q3 =
EC3 −
q1 CC13 = EC − EC ⋅ 2CC = EC2
Ответ: q1 =
CE ,
q2 =
q3 =
CE2 .
Задача 27. Определите
заряды конденсаторов в установившемся режиме в цепи, изображенной на рисунке
27а.
Рис.
27а Рис. 27б
Решение. Расставляем знаки зарядов на пластинах
конденсаторов, а так же указываем направление ЭДС и направление векторов
напряженности электрических полей в конденсаторах (см. рис. 27б). Запишем для
нижнего узла закон сохранения электрического заряда:
q1 +
q2 −
q3 =
0
Для внешнего замкнутого контура:
E1 − E2 = Cq11 − Cq22 ,
откуда
Cq2 = Cq1 + E2 − E1 или q2 =
q1 CC12
+
C2E2 −C2E1
2 1
Для левого замкнутого контура:
E1 = Cq11 +
Cq33 ,
откуда
Cq33 = E1 −
Cq11 или q3 =
C3E1 −
q1 CC13
Подставим в первое уравнение и определим заряд на первом
конденсаторе:
q1 + q1 CC12 +
C2E2 −C2E1 −C3E1 +
q1 CC13
=
0
q1 C + C +
C C2E2
q1 = C1 ⋅ E1 ⋅(CC12++CC23+)−C3C2E2
С учётом последнего выражения, определятся заряды на
оставшихся конденсаторах:
q2 = q1 CC12 +
C2E2 −C2E1 =
C1 ⋅ E1 ⋅(CC12++CC23+)−C3C2E2 ⋅ CC12 + C2E2 −C2E1
q2 = E1 ⋅(CC12++CC23+)−C3C2E2 ⋅C2 + C2E2 ⋅(C1 + C2(+CC1 +3 )C−2C+2CE31 ⋅)(C1 + C2 + C3 )
q2 = C2C2E1 +C2C3E1 −C2C2E2 −C1C2E1C−1C+2CC22E+1C−3C2C3E1 +C1C2E2 +C2C2E2 +C2C3E2
q2 = −C1C2E1C+1 +C1CC22+E2C+3 C2C3E2 = C2 ⋅ C1EC21++CC3E2 +2 −CC3 1E1
q2 = C2 ⋅ E2 ⋅(CC11++CC23+)C−3C1E1
q3 = C3E1 −q1 CC13 =
C3E1 −C1⋅ E1⋅(CC12++CC23+)−C3C2E2 ⋅ CC13
q3 = C1C3E1C+1C+2CC23E+1C+3C3C3E1 − E1 ⋅(C2C+1C+3C)2⋅C+3C−3C2C3E2 = C1CC13E+1C+2C+2CC33E2
q3 = C3 ⋅ CC11E+1C+2C+2EC23
Ответ: q1 =
C1 ⋅ E1 ⋅(CC12++CC23+)−C3C2E2 ; q2 = C2 ⋅ E2 ⋅(CC11++CC23+)C−3C1E1 ;
q3 = C3 ⋅ CC11E+1C+2C+2EC23 .
Ответы, представленные в первоисточнике: Горбунов А.К.,
Панаиотти Э.Д. «Сборник задач по физике для поступающих в ВУЗ» Издательство
МГТУ им. Н.Э. Баумана, имеют следующие выражения:
q1 = C1 ⋅ C2E2C−1 +E1C⋅2(+C2C+3 C3 ) ; q2 = C2 ⋅ C1E1C−1 +E2C⋅2(+C1C+3 C3 ) ; q3 = C3 ⋅ CC11E+1C+2C+2EC23 .
Как видно, отличаются знаками. В связи с этим следующая
задача…
Задача 28. Определите
заряд и напряжение конденсаторов в установившемся режиме в цепи, изображенной
на рисунке 28а. Ёмкости конденсаторов: С1 = 5 мкФ, С2 = 4
мкФ, С3 = 3 мкФ, ЭДС источников тока: Е1 = 20 В, Е2
= 5 В.
Рис.
28а Рис.
28б
Решение. Расставляем знаки зарядов на пластинах
конденсаторов, а так же указываем направление ЭДС и направление напряженностей
электрических полей в конденсаторах (см. рис. 28б). Запишем для нижнего узла
закон сохранения электрического заряда:
− q1 − q2 + q3 = 0
Для внешнего замкнутого контура:
E1 − E2 = Cq11 − Cq22 ,
откуда
Cq2 = Cq1 + E2 − E1 или q2 =
q1 CC12
+
C2E2 −C2E1
2 1
Для левого замкнутого контура:
E1 = Cq11 +
Cq33 ,
откуда
Cq33 =
E1 − Cq11 или q3 =
C3E1 −
q1 CC13
Подставим в первое уравнение и определим заряд на первом
конденсаторе (см. решение задачи № 27):
q1 = C1 ⋅ E1 ⋅(CC12++CC23+)−C3C2E2
q1 = 5⋅ 20⋅(54++43+)−34⋅5 = 50 мкКл; U1 = Cq11 = 505 = 10 В
q2 = q1 CC12 +
C2E2 −C2E1
q2 =
50⋅
54 +
4⋅5− 4⋅20 = – 20 мкКл; U2 =
Cq22 = 204 = 5
q3 = C3E1 −
q1 CC13
q3 =
3⋅20 −50⋅ 53 = 30 мкКл;
U3 =
Cq33 =
303 = 10 В.
Таким образом, в зависимости от значений ЭДС источников
тока, возможны любые распределения зарядов на конденсаторах, как, например,
невозможно сразу предугадать направление сил токов в цепях с несколькими
источниками ЭДС.
Задача 29. В
некоторой цепи имеется участок АВ, показанный на рисунке 29а. ЭДС источника Е =
10 В, ёмкости конденсаторов С1 = 1,0 мкФ, С2 = 2,0 мкФ и
разность потенциалов φА – φВ = 5,0 В. Найдите напряжение
на каждом конденсаторе.
Е С1 Е С2 В
С1 С2 q1 q2
Рис.
29а Рис. 29б
Решение. Если пластины нескольких конденсаторов
соединены в один узел, не связанный непосредственно с источником тока, то алгебраическая
сумма зарядов на этих пластинах равна нулю (закон сохранения электрического
заряда).
Рис.
29в Рис. 29г
Например, для цепи, представленной на рисунке 29в: –q1
+ q2 + q3 = 0. Это соотношение справедливо
и тогда, когда перед конденсаторами имеются источники ЭДС (см. рис. 29г): –q1
+ q2 + q3 = 0. Для нашей заданной схемы
(см. рис. 29б), согласно записанной теории, тоже будет выполняться закон
сохранения электрического заряда: –q1 + q2
= 0. Откуда следует, что: q1 =
q2 =
q
Принимая потенциал точки В равным
нулю, можно записать чему будет равен потенциал точки А:
ϕA −ϕB =UC2 − E +UC1
или
ϕA −ϕB = Cq2 − E + Cq1
Откуда можно определить заряд на конденсаторах:
1 1
q =
(ϕAC−1ϕ+BC)2+ E ⋅C1C2
Тогда искомые напряжения на конденсаторах будут равны:
U1 = Cq1 =
(ϕAC−1ϕ+BC)2+ E ⋅C2 = 51++102 ⋅2 = 10 В
U2 = Cq2 =
(ϕAC−1ϕ+BC)2+
E ⋅C1 = 51++102 ⋅1 = 5 В
Задача 30. Определите
заряды конденсаторов в установившемся режиме в цепи, изображенной на рисунке
30а.
Если решение задач № 27 и № 28 законами Кирхгофа весьма
громоздкое по сравнению с потенциальным способом, то представленная задача
решается “почти устно”.
Решение. Расставляем знаки зарядов на пластинах
конденсаторов, а так же указываем направление вектора напряженности
электростатического поля конденсаторов (см. рис 30б).
Рис. 30а Рис. 30б
Обходим контуры по ходу часовой стрелки, содержащие
источники тока и только один из конденсаторов:
E1 =
Cq11 , откуда q1 =E1C1
E1 +
E2 =
Cq22 , откуда q2 =(E1 +E2 )⋅C2
E1 +
E2 −
E3 =
Cq33 , откуда q3 =
(E1 +
E2 −
E3 )⋅C3
Задача 31. Найдите
заряды конденсаторов в установившемся режиме в цепи, изображенной на рисунке
31а. Ёмкость каждого конденсатора равна С.
Решение. Расставляем знаки зарядов на пластинах
конденсаторов, а так же указываем направление вектора напряженности
электростатического поля конденсаторов (см. рис 31б).
Рис.
31а Рис. 31б Воспользуемся
тем, то если пластины нескольких конденсаторов соединены в один узел, не
связанный непосредственно с источником ЭДС (это соотношение справедливо и
тогда, когда перед конденсаторами имеются источники ЭДС — см. решение зад. №
29), то алгебраическая сумма зарядов равна нулю:
q1 −
q2 −
q3 −
q4 =
0
Составим по второму закону Кирхгофа такие уравнения,
чтобы при обходе контура всегда присутствовал заряд на конденсаторе 1:
E1 =qC1 +qC2 ,
откуда
qC2 =
E1 −
qC1 или q2 =
CE1 −
q1
E1 + E2 = qC1 + qC3 ,
откуда
qC3 =
E1 +
E2 −
qC1 или q3 =
CE1 +
CE2 −
q1
E1 + E2 + E3 = qC1 + qC4 ,
откуда
qC4 =E1 +E2 +E3 −qC1 или q4 =
CE1 +
CE2 +
CE3 −
q1
Подставляем выражения для зарядов в первое уравнение:
q1 −CE1 +
q1 −CE1 −CE2 +
q1 −CE1 −CE2 −CE3 +
q1 =
0
4q1 =
3CE1 +
2CE2 +
CE3
q
И тогда, окончательно:
q2 = CE1 − q1 = CE1 − 3CE4 1 − −
CE43
q2 = 4CE1 −3CE14− 2CE2 −CE3
q
q3 = CE1 + CE2 − q1 = CE1 + CE2 − 3CE4 1 − −
CE43
q3 = 4CE1 + 4CE2 −3CE4 1 − 2CE2 −CE3
q
q4 = CE1 + CE2 + CE3 − q1 = CE1 + CE2 + CE3 − 3CE4 1 − −
CE43
q4 = 4CE1 +
4CE2 +
4CE34−3CE1 −
2CE2 −CE3
q
Ответ: q; q
;
q; q
.
Задача 32. В
цепи, изображенной на рисунке 32а известны ёмкости конденсаторов С1,
С2, С3 и ЭДС источника тока Е. Кроме того, известно, что
заряд первого конденсатора равен Q1. Найдите ЭДС Е2
второго источника тока в установившемся режиме.
Рис.
32а Рис. 32б
Решение. Расставляем знаки зарядов на пластинах
конденсаторов, а так же указываем направление ЭДС и направление напряженностей
электрических полей в конденсаторах (см. рис. 32б). Запишем для правого узла
закон сохранения электрического заряда:
−Q1 − q2 + q3 = 0,
откуда
q3 =
Q1 +
q2
Для верхнего замкнутого контура:
E = q2 − Q1 , C2 C1
откуда
Cq22 = E + QC11 или q2 = EC2 +
Q1 CC12
Для внешнего замкнутого контура:
E2 = QC11 + Cq33 ,
Подставляем в последнее выражение заряды q2
и q3:
E2 = QC11 + Q1C+3q2 = QC11 + CQ13 +
Cq23
E2 = QC11 + CQ13 + C13 ⋅EC2 + Q1 CC12
= CC13CQ31 + CC11CQ13 + ECC32 + CC12CQ31
E2 = E CC23 +
Q1 C1 +CC1C23+
C3
Задача 33. В
цепи, изображенной на рисунке 33а известны ёмкости конденсаторов С, С1,
С2 и ЭДС источника тока Е. Определите разность потенциалов между
точками а и b в установившемся режиме.
С С
1 3
o
Рис.
33а Рис. 33б
Решение. Расставляем знаки зарядов
на пластинах конденсаторов (см. рис. 33б). Для узлов а и b можно
записать закон сохранения электрического заряда:
−q1 + q3 = 0 и − q2 +
q4 =
0,
откуда
q1 =
q3 и q2 =
q4
C1 ⋅(ϕf −ϕa ) = C ⋅(ϕa −ϕo ) и C2 ⋅(ϕf −ϕb )= C ⋅(ϕb −ϕo )
Примем потенциал точки о равным нулю, тогда потенциал
точки f будет равен Е:
C1 ⋅(ϕf −ϕa )= C ⋅ϕa и C2 ⋅(ϕf −ϕb ) = C ⋅ϕb
C1 ⋅(E −ϕa ) = C ⋅ϕa и C2 ⋅(E −ϕb )= C ⋅ϕb
C1 ⋅E = C ⋅ϕa +C1 ⋅ϕa и C2 ⋅
E =
C ⋅ϕb +
C2 ⋅ϕb
ϕa = CC1 1+EC и ϕb =
CC22+EC
И тогда окончательно:
C1E −
C2E = C1C −C2C
ϕa −ϕb = C1 +C C2 +C (C1 +C)(C2 +C)
Ответ:
ϕa −ϕb =
(C1C+1CC)(−
CC22C+
C)
Задача 34. В
цепи, изображенной на рисунке 34а известны ёмкости конденсаторов С1,
С2 и ЭДС источников тока Е1, Е2. Определите
разность потенциалов между точками а и b в установившемся режиме.
С1 С2 С1 С2
е
Рис. 34а Рис. 34б
Решение. Расставляем знаки зарядов
на пластинах конденсаторов (см. рис. 34б). Пусть потенциал точки а будет
равен нулю, тогда искомая разность потенциалов φb – φа
= φb.
Для узла а можно записать закон сохранения
электрического заряда:
− q1 + q2 = 0,
откуда q1 =
q2
или
C1 ⋅(ϕf −ϕa ) = C2 ⋅(ϕa −ϕe )
C1 ⋅ϕf =
−C2 ⋅ϕe
С другой
стороны, ϕf −ϕb =
E1 и ϕb −ϕe =
E2,
откуда ϕf =
E1 +ϕb и ϕe =ϕb −
E2.
Подставим полученные выражения в равенство, записанное выше:
C1 ⋅(E1 +ϕb ) = −C2 ⋅(ϕb −
E2 )
C1 ⋅E1 +C1 ⋅ϕb =
−C2 ⋅ϕb +C2 ⋅E2
C1⋅ϕb +C2 ⋅ϕb =
C2 ⋅E2 −C1⋅E1
ϕb =Uab = C2CE12+−CC21E1
Задача 35. В
цепи, изображенной на рисунке 35а известны ёмкости конденсаторов С1,
С2, С3 и ЭДС источников тока Е1, Е2.
Определите разность потенциалов между точками b и k в установившемся режиме.
С1
f
Рис.
35а Рис. 35б
Решение. Расставляем знаки зарядов
на пластинах конденсаторов (см. рис. 35б). Пусть потенциал точки b будет
равен нулю, тогда искомая разность потенциалов φk – φb
= φk и Е1 > Е2. Для
узла b можно записать закон сохранения электрического заряда:
q12 −
q3 =
0,
откуда
q21 = q3
или
(C1 +C2 )⋅(ϕb −ϕe ) = C3 ⋅(ϕf −ϕb )
−(C1 +C2 )⋅ϕe =
C3 ⋅ϕf
С другой
стороны, ϕk −ϕe =
E1 и ϕk −ϕf =
E2,
откуда ϕe =ϕk −
E1 и ϕf =ϕk −
E2.
Подставим полученные выражения в равенство, записанное выше:
−(C1 +C2 )⋅(ϕk −
E1 ) = C3 ⋅(ϕk −
E2 )
−C1ϕk +C1E1 −C2ϕk +C2E1 =
C3ϕk −C3E2
C1E1 +C2E1 +C3E2 =
C1ϕk +C2ϕk +C3ϕk
ϕk =Ukb = E1(CC11 ++CC22 )++CC33E2
Задача 36. Найдите
силу притяжения между пластинами плоского конденсатора С1 в схеме,
изображенной на рисунке 36а в установившемся режиме. Ёмкости конденсаторов С1
= С0, С2 = 2С0, и ЭДС источников тока Е1
= Е0, Е2 = 2Е0, а расстояние между пластинами
конденсатора С1 равно d.
Решение. Электрический заряд q1 rодной
пластины конденсатора С1 находится в однородном
электростатическом поле E
второй пластины этого же конденсатора (см. рис. 36б).
Рис.
36а Рис. 36б
Поэтому:
F σ q
Электрическая ёмкость плоского конденсатора определяется
выражением:
C1 = ε0dεS ,
откуда ε0εS = C1d
И тогда искомая сила притяжения между пластинами
конденсатора сводится к нахождению электрического заряда на этом конденсаторе:
F = q12
2C1d
Расставляем знаки зарядов на пластинах конденсаторов (см.
рис. 36в).
Е1
С1 С2
2
Рис. 36в По
второму закону Кирхгофа:
E1 + E2 −UC1 −UC2 = 0,
или
E1 + E2 = Cq11 + Cq22
Но так как заряды на обкладках обоих конденсаторов
одинаковые, то:
E1 + E2 = q1⋅C11 +
C12 = q1⋅ CC11+CC22
q
Последнюю формулу можно было получить и школьным способом — это
заряд эквивалентной батареи конденсаторов, соединённых последовательно. И
тогда, окончательно, искомая сила будет равна:
F = (E1 +C1E+2 C)⋅2C1C2 2C1d = 2(C1 +C2 )2d
F
Ответ: F = 2C0E02 . d
Задача 37. В
схеме, изображенной на рисунке 37а в установившемся режиме, сила притяжения
между пластинами плоского конденсатора С1 равна F. Найдите
расстояние между пластинами этого конденсатора, если С1 = 2С0,
С2 = С0, и ЭДС источников тока Е1 = 2Е0,
Е2 = Е0.
Решение. Рассуждения, описанные в
задаче № 36, могут быть использованы при решении данной задачи:
F = q12 ,
2C1d
откуда
d =
q12
2C1F
С1 С2 С1 С2
Рис.
37а Рис. 37б
Расставляем знаки зарядов на пластинах
конденсаторов (см. рис. 37б). По второму закону Кирхгофа:
E1 − E2 −UC1 −UC2 = 0,
или
E1 − E2 = Cq11 + Cq22
Но так как заряды на обкладках обоих конденсаторов
одинаковые, то:
E1 − E2 = q1 ⋅C11 + C12 = q1 ⋅ CC11+CC22
q
d =
(E1 −C1E+2 )C⋅2C1C2 2 2C11F =
(E21(C−1E+2C)22⋅)C21FC22
d
Ответ: d
=
C E2 .
Задача 38. В
цепи, изображенной на рисунке 38а известны ёмкости конденсаторов С1,
С2, С3 и ЭДС источников тока Е1, Е2,
Е3. Определите разность потенциалов между точками а и b в
установившемся режиме.
1
b
Рис.
38а Рис. 38б
Решение. Пусть Е1
> E2 > Е3. В связи с этим расставляем
знаки зарядов на пластинах конденсаторов (см. рис. 38б). Пусть потенциал точки b
будет равен нулю, тогда искомая разность потенциалов φa – φb
= φa. Для узла b можно записать закон сохранения
электрического заряда:
− q1 − q2 + q3 = 0,
откуда q3 = q1 + q2
или
C3 ⋅(ϕb −ϕf ) = C1 ⋅(ϕa −ϕb )+C2 ⋅(ϕm −ϕb )
−C3 ⋅ϕf =
C1 ⋅ϕa +C2 ⋅ϕm
С другой стороны, ϕa −ϕd =
E1, откуда ϕa =
E1 +ϕd
ϕm −ϕd =
E2, откуда ϕm =
E2 +ϕd
ϕf −ϕd =
E3, откуда ϕf =
E3 +ϕd
Подставим полученные выражения в равенство, записанное выше:
−C3 ⋅(E3 +ϕd ) = C1 ⋅(E1 +ϕd )+C2 ⋅(E2 +ϕd )
−C3 ⋅E3 −C3 ⋅ϕd =
C1 ⋅E1 +C1 ⋅ϕd +C2 ⋅E2 +C2 ⋅ϕd
−C1⋅E1 −C2 ⋅E2 −C3 ⋅E3 = C1⋅ϕd +C2 ⋅ϕd +C3 ⋅ϕd
ϕd = − C1 ⋅E1C+1C+2C⋅2E+2 C+3C3 ⋅E3
Очевидно, что φа – φd = E1,
поэтому, окончательно будем иметь:
ϕa =Uab = E1 −
C1⋅E1C+1C+2C⋅2E+2 C+3C3 ⋅E3
Кроме этого, можно записать:
ϕm =Umb = E2 −
C1 ⋅E1C+1C+2C⋅2E+2 C+3C3 ⋅E3 ,
и
,
1 2 3
что соответствует решению задачи № 3.125, представленному в
сборнике задач по общей физике И.Е. Иродов — 1979 год.
Задача 39. Найдите
эквивалентную ёмкость батареи конденсаторов изображенных на рисунке 39а.
Ёмкости всех конденсаторов известна.
Решение. Очевидно, что задача решается устно, так как
выполняется равенство произведения плеч мостовой схемы: ЭКВ 3С
С =
2

Рис. 39а Рис.
39б
Однако рассмотрим способ, при помощи которого можно
определить эквивалентную ёмкость батареи при любых соотношениях ёмкостей
конденсаторов. Для этого мысленно подключим к батарее конденсаторов источник
тока так, чтобы потенциал левой клеммы был положительным и равным φ, а
потенциал правой клеммы (точка о) примем равным нулю. Расставим знаки
зарядов на пластинах конденсаторов (см. рис. 39б). Тогда, очевидно, что: CЭКВ =
q ϕ
Заряд q всей батареи конденсаторов равен сумме
зарядов:
q = q1 + q3
(или q = q2 + q4).
Как в случае общего тока I, который расходится из ветви, содержащей
источник, в параллельные ветви, выражаем заряды на всех конденсаторах, через
ёмкости и разность потенциалов: q1 =
C1(ϕ−ϕa ) = C(ϕ−ϕa )
q2 =
C2(ϕa −ϕo ) = Cϕa
q3 =
C3(ϕ−ϕb ) = 2C(ϕ−ϕb )
q4 =
C4(ϕb −ϕo ) = 2Cϕb
q5 =
C5(ϕa −ϕb ) = 3C(ϕa −ϕb )
Запишем закон сохранения электрического заряда для узлов а
и b:
− q1 + q2 + q5 = 0 или q1 = q2 + q5
−q3 + q4 −q5 = 0 или q4 = q3 + q5
С учётом верхних выражений, можно составить систему
уравнений:
C(ϕ−ϕa ) = Cϕa +3C(ϕa −ϕb )
2Cϕb =
2C(ϕ−ϕb )+3C(ϕa −ϕb )
ϕ−ϕa =ϕa +3ϕa −3ϕb
2ϕb =
2ϕ−
2ϕb +3ϕa −3ϕb
ϕ=
5ϕa −3ϕb
7ϕb =
2ϕ+3ϕa
ϕ7ϕa b== 2ϕ+ϕ3bϕ5 + 53ϕb
ϕa =ϕb
7ϕb =
2ϕ+
ϕ+
ϕb
ϕa =ϕb
26ϕb =
135 ϕ
5
ϕ ϕ ϕ
ϕb =
ϕa =ϕb =
Что вытекает из равенства произведения плеч мостовой схемы.
И тогда, окончательно:
CЭКВ = q1 + q3 = C(ϕ−ϕa )+
2C(ϕ−ϕb ) =
C(ϕ− (ϕ−
ϕ ϕ
CЭКВ = C
Ответ: CЭКВ =
3C
2
Задача 40. Найдите
эквивалентную ёмкость батареи конденсаторов изображенных на рисунке 40а.
Ёмкость каждого конденсатора равна С.
Решение. Преобразуем электрическую цепь, удалив из
неё “недоветви”. Мысленно подключим к батарее конденсаторов источник тока так,
чтобы потенциал левой клеммы был положительным и равным φ, а потенциал нижней
клеммы (точка о) примем равным нулю. Расставим знаки зарядов на
пластинах конденсаторов (см. рис. 40б):
Рис.
40а Рис. 40б
Тогда, очевидно, что:
СЭКВ = q =
q4 + q5 + q6 ϕ ϕ
Выражаем заряды на всех конденсаторах, через ёмкости и
разность потенциалов:
q1 =
C1(ϕ−ϕp )= C(ϕ−ϕp )
q2 =
C2(ϕ−ϕn ) = C(ϕ−ϕn )
q3 =
C3(ϕn −ϕp ) = C(ϕn −ϕp )
q4 =
C4(ϕ−ϕo ) = Cϕ
q5 =
C5(ϕn −ϕo ) = Cϕn
q6 =
C6(ϕp −ϕo ) = Cϕp
Запишем закон сохранения электрического заряда для узлов n
и р:
− q2 + q3 + q5 = 0 или q2 = q3 + q5
− q1 − q3 + q6 = 0 или q6 = q1 + q3
С учётом верхних выражений, можно составить систему
уравнений:
C(ϕ−ϕn ) = C(ϕn −ϕp )+Cϕn
Cϕp =
C(ϕ−ϕp )+C(ϕn −ϕp )
ϕ−ϕn =ϕn −ϕp +ϕn
ϕp =ϕ−ϕp +ϕn −ϕp
ϕ=
3ϕn −ϕp
3ϕp =ϕ+ϕn
ϕp =
3ϕn −ϕ
3⋅(3ϕn −ϕ) =ϕ+ϕn
ϕp =
3ϕn −ϕ
9ϕn −3ϕ=ϕ+ϕn
ϕp = 3⋅ϕ2 −ϕ
ϕn =
ϕ2
ϕn =ϕp =
И тогда, окончательно:
ϕ
CЭКВ = q4 + q5 + q6 = Cϕ+Cϕn +Cϕp = Cϕ+C +C 2 = 2C ϕ ϕ ϕ
Ответ: CЭКВ =
2C
Глава 5
До и после коммутации
Задача 41. При
замкнутом ключе К (рис. 41а) установившееся напряжение на конденсаторе U1
= 27 В. Найдите ЭДС источника тока, если его внутреннее сопротивление r = R.
Определите также установившееся напряжение на конденсаторе U2 после
размыкания ключа.
2R
3R
Рис. 41а
Решение. Очевидно, что
установившееся напряжение на конденсаторе равно напряжению на резисторе
сопротивлением 3R. Кроме того, резистор сопротивлением 3R
находится в цепи с батареей, поэтому ток через него равен току через батарею
(см. рис. 41б):
Рис.
41б Рис. 41в
Откуда:
I1 =
UR1
3
С другой стороны, силу тока в цепи, содержащей батарею,
можно выразить по закону
Ома для полной цепи
I1 = E ,
RЭКВ + r
где
RЭКВ R
И тогда: I1 = 11RE R =
143ER
+
3
Таким образом, приравнивая левые части равенств, получим:
E = 42 В
После размыкания ключа и установления
стационарного режима ток через резистор сопротивлением R прекращается и
разность потенциалов на обкладках конденсатора ёмкостью С становится
равной разности потенциалов на клеммах батареи. Следовательно, ток течёт только
через резисторы сопротивлениями 2R и 3R. По закону Ома для полной
цепи находим ток проходящий через батарею после размыкания цепи:
I2 = E = E
2R +
3R +
R 6R
И установившееся новое напряжение на конденсаторе:
U2
=
35 В
6
Задача 42. При
разомкнутом ключе К (рис. 42а) на конденсаторе устанавливается напряжение U1
= 12 В. Найдите ЭДС источника тока, если его внутреннее сопротивление r = R.
Определите также установившееся напряжение на конденсаторе U2 после
размыкания ключа.
Рис. 42а
Решение. В ветви, содержащей конденсатор,
электрический ток отсутствует, поэтому напряжение до коммутации равно падению
напряжения на резисторах сопротивлениями R и 2R (см. рис. 42б):
Рис.
42б Рис. 42в
Силу тока в цепи, содержащей
батарею, можно выразить по закону Ома для полной цепи
I1 =
RЭКВE+ r ,
где
RЭКВ =
R +
2R =
3R
И тогда:
I1 = 3RE+
R =
4ER
Подставляя полученное выражение в верхнее равенство,
получим:
U1 =
(R +
2R)⋅
4ER = 34 E
Откуда
E = 16 В
После коммутации (замыкания ключа К) и установления
стационарного режима ток в ветви, содержащей конденсатор отсутствует и
принципиальная схема соединения резисторов представлена на рисунке 42в.
Очевидно, что установившееся напряжение на конденсаторе U2
будет равно падению напряжения на резисторе сопротивлением R. А он, в
свою очередь, находится в цепи с батареей, поэтому:
U2 =
R⋅I2
Силу тока в цепи, содержащей батарею, можно выразить по
закону Ома для полной цепи
I2 =
RЭКВE+ r ,
где
RЭКВ =
R +
2R⋅3R =
R +
6 R =
11R
2R +3R 5 5
И тогда:
I2 =
11RE+
R =
165ER
5
Подставляя полученное выражение в верхнее равенство для силы
тока после коммутации, получим:
U
= ⋅ = E
Откуда
U = 5 В
Задача 43. В
схеме, представленной на рисунке 43а ключи К1 и К2 разомкнуты,
а конденсаторы не заряжены. Ключ К1 замыкают, оставляя ключ К2
разомкнутым. 1) Какие напряжения установятся на конденсаторах? 2) Какой заряд
протечёт через ключ К2, если его замкнуть (при замкнутом ключе К1)?
Параметры схемы указаны на рисунке.
Рис. 43а
Решение. В установившемся режиме после замыкания
ключа К1 общее напряжение на конденсаторах будет равно
суммарному падению напряжения на последовательно соединенных резисторах (см.
рис. 43б). В ветви, содержащей конденсатор, электрический ток отсутствует,
поэтому:
U0 =
( R +
2R)⋅I
Силу тока в цепи, содержащей батарею, можно выразить по
закону Ома для полной цепи
 I
I
= E ,
RЭКВ + r
где
RЭКВ = 3R
Рис.
43б Рис. 43в
И тогда:
I = E
3R +
r
Подставляя полученное выражение в верхнее равенство,
получим:
U0 =
(R +
2R)⋅
3RE+
r =
3R3R+
r E
Поскольку общая ёмкость батареи конденсаторов при их
последовательном соединении
C0 = CC+⋅22CC = 32C ,
заряды на конденсаторах:
q1 = q2 =U0C0 =
33RRE+
r ⋅
23C =
32RREC+
r .
А напряжения составляют:
U1 = qC1 =3R2R+r E
U2 =2qC2 =3RR+r E
До коммутации (замыкания ключа К2)
на правой пластине (ближней к ключу К2) конденсатора ёмкостью
С, находился отрицательный заряд:
−
q1 − 32RREC+
r ,
а на левой пластине (ближней к ключу К2)
конденсатора ёмкостью 2С, находился положительный заряд:
+ q2 =
+ 32RREC+
r .
После коммутации (замыкания ключа К2)
и установления нового стационарного состояния напряжения на конденсаторах
поменяются и будут равны:
U1/ =
RI =
R⋅
3RE+
r =
3RR+
r E
U2/ =
2RI =
2R⋅
3RE+
r =
3R2R+
r E
Тогда новый заряд на правой пластине
(ближней к ключу К2) конденсатора ёмкостью С, станет
равным:
−
q / R E ⋅C
= − REC ,
3R +
r 3R +
r
а на левой пластине (ближней к ключу К2)
конденсатора ёмкостью 2С, станет положительный заряд:
R E
.
3R +
r
При этом, заряд на конденсаторе ёмкостью С изменился
на величину:
∆q1 =
q1/ −
q1 = − 3RECR +
r −−
32RREC+
r
=
3RECR +
r ,
а на конденсаторе ёмкостью 2С заряд изменился на
величину:
∆q2 =
q2/ −
q2 = 34RREC+
r −
32RREC+
r =
32RREC+
r
Очевидно, что общий заряд, прошедший через ключ К2
будет равен:
q =
∆q1 + ∆q2 = 32RREC+
r +
3RECR +
r =
33RREC+
r
Так как заряды на конденсаторах увеличились, то заряд через
ключ К2 прошёл вверх (см.
рис. 43а)
Ответ: q = 3R EC.
3R +
r
Задача 44. В
схеме, изображённой на рисунке 44а, в начальный момент ключ К разомкнут, а
конденсаторы не заряжены. Какой заряд протечёт через перемычку аb после
замыкания ключа К? Сопротивлением перемычки пренебречь. Параметры схемы указа-
ны на рисунке. К
2R
С
Рис. 44а
Решение. Сразу после замыкания ключа К в
участках цепи текут токи, которые для произвольного момента времени Δt =
t показаны на рисунке 44б. Очевидно, что токи возникают до некоторого
установившегося режима, когда произойдёт полная зарядка конденсаторов.
Рис.
44б Рис. 44в
Выразим силы токов через резисторы, записав второй закон
Кирхгофа для двух контуров, содержащих батарею ЭДС и резисторы:
E −UC =
R ⋅
I1, откуда I1 =
ER
E −UC =
2R ⋅
I2, откуда I2 =
2ER
Здесь по закону коммутации учтено, что напряжение на
конденсаторах до и после замыкания ключа моментально не изменяется и равно нулю
(по условию задачи конденсаторы до коммутации не были заряжены). Тогда общий
ток цепи, прошедший через батарею:
I = I1 + I1 ER + 2ER = 32ER
А заряд, прошедший за время установки стационарного режима,
через батарею ЭДС:
q =
I ⋅t = 3E ⋅t
2R
численно равен полному заряду батареи конденсаторов (см.
рис. 44в), электрическая ёмкость которых при параллельном соединении равна 2С.
Следовательно,
E t ,
Откуда время установившегося режима:
t =
4RC
3
Определим силу тока, прошедшую через
перемычку ab, записав первый закон Кирхгофа для узлов а и b:
I1 − IП − IC = 0 I2 +
IП − IC = 0
Вычитая из нижнего выражения верхнее выражение, получим:
I2 − I1 + 2IП = 0
E −
E +
2IП = 0
2R R
IП = E =
qП ,
4R t
Откуда искомый заряд:
qП =
E t .
4R
qП =
E ⋅
4RC =
EC
4R 3 3
Ответ: qП =
EC .
3
Задача 45. В
схеме, изображённой на рисунке 45а, в начальный момент конденсаторы не
заряжены. Параметры элементов указаны на рисунке. Сначала замыкают ключ К1
и дожидаются установившегося режима. Затем замыкают ключ К2, причём
ток через него сразу после этого оказался равным Е/R и направленным слева
направо. 1) Найдите ЭДС левой батареи. 2) Найдите величину заряда, протекшего
через ключ К2 после его замыкания.
К1
Рис. 45а
Решение. В установившемся режиме
после замыкания ключа К1 общее напряжение на конденсаторах
будет равно ЭДС левой батареи (обозначим её через U) на последовательно
соединенных конденсаторах (см. рис. 45б). Очевидно, что:
Рис.
45б Рис. 45в
Так как общая ёмкость батареи конденсаторов равна 2С/3,
а заряд на них одинаковый, и равный:
q1 UC ,
то можно определить установившиеся напряжения на
конденсаторах после замыкания ключа К1:
UC1 = qC1 = 23U
UC2 2qC2
=
U3
Теперь рассмотрим схему сразу после замыкания ключа К2
(см. рис. 45в). запишем второй закон Кирхгофа для крайнего правого контура,
учитывая, что ток течёт слева направо — напряжение на конденсаторе ёмкостью С
больше ЭДС батареи Е:
UC1 −
E =
I ⋅
R
2U −
E =
E ⋅
R
3 R
E,
откуда ответ на первый пункт:
U = 3E
Теперь определим установившиеся напряжения на конденсаторах
после замыкания ключа К2. Для этого запишем второй закон
Кирхгофа для левого и правого контуров в установившемся режиме:
3E −UC/ 2 −UC/1 = 0
E −UC/1 =
0,
откуда:
UC/1 =
E , а
заряд конденсатора q1/ =UC/1 ⋅C = EC
UC/ 2 =
2E, а
заряд конденсатора q2/ =UC/ 2 ⋅2C =
4EC
Таким образом, до коммутации (замыкания
ключа К2) на верхней пластине (ближней к ключу К2)
конденсатора ёмкостью С, находился положительный заряд:
ЕС,
а на нижней пластине (ближней к ключу К2)
конденсатора ёмкостью 2С, находился отрицательный заряд:
ЕС.
После коммутации (замыкания ключа К2) и
установления нового стационарного состояния заряды на конденсаторах поменяются.
Так, новый заряд на верхней пластине (ближней к ключу К2)
конденсатора ёмкостью С, станет положительным и равным:
+ q1/ =
+EC ,
а на нижней пластине (ближней к ключу К2)
конденсатора ёмкостью 2С, станет отрицательный заряд:
− q2/ =
−4EC .
При этом, заряд на конденсаторе ёмкостью С изменился
на величину:
∆q1 = q1/ −
q =
EC −
2EC =
−EC ,
а на конденсаторе ёмкостью 2С заряд изменился на
величину:
∆q2 = q2/ −
q2 =
−4EC −(−2EC ) =
−2EC
Очевидно, что общий заряд, прошедший через ключ К2
будет равен:
q =
∆q1 +
∆q2
= EC +
2EC =
3EC
Так как заряды на конденсаторах
уменьшились, то заряд через ключ К2 прошёл слева направо.
Ответ: Δq = 3ЕС.
Задача 46. В
схеме, изображённой на рисунке 46а, в начальный момент конденсаторы находятся в
установившемся режиме. Какой заряд протечёт через гальванометр Г после
замыкания ключа К? Какое количество теплоты выделится на резисторе
сопротивлением R? Величины Е и С известны, внутренним сопротивлением батареи
пренебречь.
Рис. 46а
Решение. В установившемся режиме после до замыкания
ключа К общее напряжение на конденсаторах будет равно ЭДС батареи на
последовательно соединенных конденсаторах (см. рис. 46б). Очевидно, что:
Рис.
46б Рис. 46в
Так как общая ёмкость батареи конденсаторов равна С/2,
а заряд на них одинаковый, и равный:
q1 EC ,
то можно определить установившиеся напряжения на
конденсаторах до замыкания ключа К:
UC1 =UC2 =
qC1 =
E2
и энергию системы в первом состоянии:
W1 = 2⋅ CU2C21 = CE4 2
Теперь определим установившиеся напряжения
на конденсаторах после замыкания ключа К (см. рис. 46в). Для этого
запишем второй закон Кирхгофа для левого и правого контуров в установившемся
режиме:
E −UC/ 2 −UC/1 = 0
UC/ 2 = 0,
откуда:
UC/1 =
E , а
заряд конденсатора q1/ =UC/1 ⋅C = EC
UC/ 2 =
0, а заряд
конденсатора q2/ =UC/ 2 ⋅C = 0
Таким образом, до коммутации (замыкания ключа К) на
правой пластине (ближней к ключу К) верхнего конденсатора ёмкостью С,
находился положительный заряд:
+ q1 = + EC2 ,
а на верхней пластине (ближней к ключу К)
центрального конденсатора ёмкостью С, находился отрицательный заряд: −
q2 =
−
EC .
2
После коммутации (замыкания ключа К) и установления
нового стационарного состояния заряды на конденсаторах поменяются. Так, новый
заряд на правой пластине (ближней к ключу К) конденсатора ёмкостью С,
станет положительным и равным:
+ q1/ =
+EC ,
а на нижней пластине (ближней к ключу К)
центрального конденсатора ёмкостью С электрический заряд будет
отсутствовать:
q2/ =
0.
При этом, заряд на верхнем конденсаторе изменился на
величину:
∆q1 = q1/ −
q =
EC −
EC2 = EC2 ,
а на центральном конденсаторе заряд изменился на величину:
∆q2 = q2/ −q2 =
0−−
EC2
=
EC2
Очевидно, что общий заряд, прошедший через гальванометр Г
будет равен:
∆q = ∆q1 + ∆q2 =
EC2 + EC2 = EC
Потенциальная энергия во втором состоянии системы (после
коммутации) определится энергией только верхнего заряженного конденсатора:
W2 =
CE2 2
Для вычисления выделившейся на сопротивлении теплоты
воспользуемся законом сохранения энергии:
E ⋅∆q = ∆W +Q
E⋅∆q =W2 −W1 +Q Откуда:
Q =
E ⋅∆q +W1 −W2
С учётом выполненных вычислений, окончательно получим:
Q =
E ⋅EC + CE2 − CE2 = CE2
4 2 2
Ответ: заряд, прошедший через гальванометр Δq = ЕС;
количество теплоты Q =
CE2 . 2
Задача 47. Какое
количество теплоты выделится на резисторе сопротивлением R2 в схеме,
изображённой на рисунке 47а, после перемещения ключа К из положения 1 в
положение 2?Внутренним сопротивлением батареи пренебречь.
R1
С
Рис. 47а
Решение. Определяем параметры схемы до коммутации:
напряжение на конденсаторе, заряд, накопленный конденсатором в установившемся
режиме и энергию заряженного конденсатора. Когда ключ К находится в
положении 1 в цепи идёт ток, сила которого определится по закону Ома (см. рис.
47б):
I = E
R1 + R2
Рис.
47б Рис. 47в
Тогда напряжение на конденсаторе до коммутации:
UC1 = I ⋅R2 = RE1 +⋅RR22 ,
заряд, накопленный конденсатором:
q1 =UC1 ⋅C = CER1 +⋅RR22
Обязательно обращаем внимание на знаки обкладок заряженного
конденсатора. Энергия системы в первом положении:
CUC21 q2 CE2
W1 = 2 = 2C1 = 2 R1R+2R2 2
После коммутации (переведения ключа К из положения 1
в положение 2) конденсатор оказывается подключённым к двум параллельно
соединённым резисторам (см. рис. 47в). При этом он оказывается полностью
разряженным. Следовательно, напряжение, заряд и энергия во втором состоянии
системы отсутствуют:
q2 =UC2 =W2 = 0
Запишем закон сохранения энергии:
E⋅∆q =∆W +Q
или
E⋅(q2 −q1 ) = (W2 −W1 )+Q
Так как после коммутации батарея была отключена и через неё
не протекал электрический заряд, то
0 =
(0−W1 )+Q
Q =W1 = CE2 2 R1R+2R2 2
Это общее количество теплоты, выделившееся
в цепи после коммутации. Для определения количества теплоты, выделившееся
именно в резисторе сопротивлением R2, воспользуемся законом
Джоуля-Ленца для параллельно соединённых проводников:
U12
Q1 = R t,
Q2 = UR222t и Q1 +Q2 = Q
1
Откуда получим систему уравнений:
Q1 = R2
Q2 R1
Q1 +Q2 = Q
Решая её относительно резистора, сопротивлением R2,
окончательно получим:
Q2 =
Q⋅
R1R+1R2 =
CE2 2 (
R1R+1RR222 )3
Задача 48. В
схеме, представленной на рисунке 48а, сопротивления резисторов R1 =
250 Ом, R2 = 100 Ом, электрическая ёмкость конденсатора С = 10 мкФ.
Источник постоянного тока с ЭДС Е = 480 В и внутренним сопротивлением r = 50
Ом. Вначале ключ К замкнут. Определите, какое количество теплоты выделится на
резисторе сопротивлением R1 после размыкания ключа К в
установившемся режиме.
R2
R
Рис. 48а
Решение. Определяем параметры схемы до коммутации:
напряжение на конденсаторе, заряд, накопленный конденсатором в установившемся
режиме и энергию заряженного конденсатора. Когда ключ К замкнут, в цепи
идёт ток, сила которого определится по закону Ома (см. рис. 48б):
I = E
R1 +
R2 +
r
R I C
I
R1 I R1
Рис.
48б Рис. 48в
Тогда напряжение на конденсаторе до коммутации:
UC1 = I ⋅R2 = R1E+⋅RR22+
r ,
заряд, накопленный конденсатором:
q1 =UC1 ⋅C = R1CE+
R⋅2R+2 r
Обязательно обращаем внимание на знаки обкладок заряженного
конденсатора. Энергия системы в первом положении:
W1 = CU2C21 = 2qC12 =
CE2 2 R1 +RR22 + r 2
После коммутации (размыкания ключа К)
конденсатор оказывается последовательно подключённым к резистору сопротивлением
R1 и батарее (см. рис. 48в). При этом новое напряжение на
конденсаторе станет равным ЭДС батареи:
UC2 =
E
заряд, накопленный конденсатором:
q2 =UC2 ⋅C = CE
Обязательно обращаем внимание на то, что знаки обкладок
заряженного конденсатора не изменились. Энергия системы во втором положении:
W2 =CU2C22 =2qC22 =CE2 2
Запишем закон сохранения энергии:
E⋅∆q =∆W +Q
или
E⋅(q2 −q1 ) = (W2 −W1 )+Q
E ⋅CE − R1CE+ R⋅2R+2 r = CE2 2 − CE2 2 R1 +RR22 + r 2 +Q
⋅
CE2
1− R1 +RR22 + r = CE2 2 ⋅1− R1 +RR22 + r 2 +Q
CE2
⋅
R1R+1R+2r+
r
= CE2 2 ⋅1− R1 +RR22 + r 2 +Q
Q = CE2 ⋅
R1R+1R+2r+
r −
CE2 2 ⋅1− R1 +RR22 + r 2
Подставив числовые значения, получим:
Q =10⋅10−6 ⋅4802 ⋅ 250250100+5050 −10⋅10−26 ⋅4802 ⋅1−
250+100100+502 = 0,648
Дж
+ +
Это общее количество теплоты, выделившееся
в цепи после коммутации. Для определения количества теплоты, выделившееся
именно в резисторе сопротивлением R1, воспользуемся законом
Джоуля-Ленца для последовательно соединённых проводников:
Qt,
Qrt
и Q1 +Q2 =
Q
Откуда получим систему уравнений:
QQ12 = Rr1
Q1 +Q2 = Q
Решая её относительно резистора, сопротивлением R1,
окончательно получим:
Q1 = Q⋅ R1 = 0,648⋅
250 = 0,54 Дж
R1 +
r 250+50
Ответ: Q1 = 540 мДж.
Задача 49. Какое
количество теплоты выделится в цепи, изображённой на рисунке 49а, после
перемещения ключа К из положения 1 в положение 2?Внутренними сопротивлениями
батарей пренебречь.
1
С
R
Рис. 49а
Решение. Определяем параметры схемы до коммутации:
напряжение на конденсаторе, заряд, накопленный конденсатором в установившемся
режиме и энергию заряженного конденсатора. Когда ключ К находится в
положении 1 (см. рис. 49б):
C C
Рис. 49б
Рис. 49в
UC1 =
2E −
E =
E ,
При этом батарея с ЭДС 2Е создаёт на обкладках
конденсатора заряд, равный:
q1 =UC1 ⋅C = CE
Обязательно обращаем внимание на знаки обкладок заряженного
конденсатора. Энергия системы в первом положении:
W1 = CU2C21 = 2qC12 =
CE2 2
После коммутации (переключение ключа К в
положение 2) конденсатор оказывается последовательно подключённым к резистору
сопротивлением R и батарее (см. рис. 49в) с ЭДС Е. При этом новое
напряжение на конденсаторе станет равным ЭДС батареи:
UC2 =
E ,
При этом батарея с ЭДС Е создаёт на
обкладках конденсатора заряд противоположной полярности, равный: q2 =UC2 ⋅C = CE
Обязательно обращаем внимание на знаки обкладок заряженного
конденсатора. Энергия системы во втором положении:
W2 =CU2C22 =2qC22 =CE2 2
Запишем закон сохранения энергии:
E⋅∆q =∆W +Q
или
E ⋅(q2 −(−q1 )) = (W2 −W1 )+ Q
E ⋅(CE + CE)=
CE2 2 − CE2 2 + Q
Q =
2CE2
Задача 50. В
электрической цепи, схема которой представлена на рисунке 50а, ёмкости
конденсаторов С1 = 100 мкФ, С2 = 300 мкФ, ЭДС источника
тока Е = 60 В. Сопротивление резистора R2 в два раза больше, чем
сопротивление резистора R1, то есть R2 = 2R1.
В начальный момент времени ключ К замкнут и через резисторы протекает
постоянный ток. Какое количество теплоты выделится в резисторе R2
после размыкания ключа? Внутренними сопротивлениями батарей пренебречь.
R1
С2
Рис. 50а
Решение. Определяем параметры схемы до коммутации:
напряжения на конденсаторах, заряды, накопленные конденсаторами в
установившемся режиме и энергию заряженных конденсаторов. Когда ключ К
замкнут, в цепи идёт ток, сила которого определится по закону Ома (см. рис. 50б):
I = E
R1 + R2
Тогда напряжения на конденсаторах до коммутации:
UC1 = I ⋅ R1 = RE1 +⋅ RR12 = R1E+⋅ R21R1 =
E3 ,
UC2 = I ⋅ R2 = RE1 +⋅ RR22 = RE1 +⋅22RR11 =
23E
R1 I R2 R2

Рис.
50б Рис. 50в
заряды, накопленные конденсаторами:
q C E
qE
Обязательно обращаем внимание на знаки обкладок заряженных
конденсаторов. Энергия системы в первом положении:
W
1
W C U2 q2 4C E2
2
WI
После коммутации (размыкания ключа К) ток через
некоторое время прекратиться, пока шла перезарядка конденсаторов. В
установившемся режиме напряжение на конденсаторе ёмкостью С1
будет равно ЭДС батареи, а напряжение на резисторе сопротивлением R2
и на конденсаторе С2 станет равным нулю, так как этот
конденсатор полностью разрядится на резистор, подключенный параллельно (см.
рис. 50в). Тогда напряжения на конденсаторах после коммутации:
UC/1 = E ,
UC/ 2 = 0
заряды, накопленные конденсаторами после коммутации:
q1/ =UC1 ⋅C1 = C1E
q2/ =UC2 ⋅C2 = 0
Обязательно обращаем внимание на знаки обкладок заряженных
конденсаторов. Энергия системы во втором положении:
W1/ = C12E2
W2/ =
0
C1E2
WII =W1/ +W2/ = +
0 =
E2 C1
2 2
Запишем закон сохранения энергии с учётом
работы источника тока (работа сторонних сил) и потерь энергии в виде джоулевого
тепла на резисторе сопротивлением R2. При этом будем считать,
что увеличение электрического заряда на конденсаторе ёмкостью С1
произошло за счёт работы сторонних сил (конденсатор ёмкостью С1
“приобрёл” дополнительный заряд от источника), а конденсатор ёмкостью С2
“израсходовал” свой заряд на тепловые потери:
E⋅∆q =∆W +Q
или
E Q
E ⋅C C E = E22 C1 − 18E2 (C1 +
4C2 ) + Q
Q =
2C1E2 − C1E2 + C1E2 + 4C2E2
3 2 18 18
Q =
2C1E2 − C1E2 + C1E2 + 4C2E2
3 2 18 18
Q =
4C1E218+ 4C2E2 =
2E92 (C1 + C2 )
Q = 0,32 Дж
Ответ: Q = 320 мДж
Используемые цифровые ресурсы
1.
http://mathus.ru/ —
Олимпиады по математике и физике. Сайт Яковлева Игоря Вячеславовича.
2.
http://olymp.mipt.ru/ —
Физико-математическая олимпиада «Физтех».
3.
http://trushinbv.ru/shkolnikam/ — Физико-математические олимпиады «Физтех» прошлых лет. Сайт
Бориса Трушина.
4.
http://kvant.mccme.ru/ —
Электронная библиотека журнала «Квант»: задачи по физике.
Содержание:
Переходные процессы в электрических цепях:
Переходный процесс в электрической цепи — это электромагнитный процесс, возникающий в электрической цепи при переходе от одного установившегося (принужденного) режима к другому. Установившимся (принужденным) называется режим работы электрической цепи, при котором напряжение и токи цепи в течение длительного времени остаются неизменными.
Такой режим в электрической цепи устанавливается при длительном действии источников постоянной или переменной ЭДС при неизменных параметрах этой цепи R, L и С.
Переходный процесс вызывается коммутацией в цепи. Коммутацией называется процесс замыкания или размыкания рубильников или выключателей. Переходный процесс может быть вызван изменением параметров электрической цепи R, L или С.
Переходный процесс базируется на двух законах коммутации:
- ток в индуктивности не может изменяться скачком;
- напряжение на емкости не может изменяться скачком.
Действительно, если ток в индуктивности L изменяется скачком, т. е. мгновенно, то ЭДС самоиндукции eL становится бесконечно большой (при
В реальных цепях ЭДС самоиндукции может иметь только конечные значения.
Если в цепи с емкостью С напряжение на ее обкладках изменяется скачком, т. е. мгновенно, то появляется бесконечно большой зарядный (или разрядный) ток (при 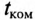
Ток в электрических цепях может иметь только конечные значения.
Переходный процесс является быстропротекающим процессом, длительность которого обычно составляет десятые, сотые и даже миллионные доли секунды и сравнительно редко — секунды и даже десятки секунд.
Таким образом, один установившийся режим цепи отделяется от другого некоторым промежутком времени, в течение которого происходит постепенный переход от прежнего состояния цепи к новому.
Переходный процесс в линейных цепях можно рассматривать как результат наложения двух процессов:
- нового установившегося режима, который наступает после коммутации;
- свободного процесса, обеспечивающего переход цепи от прежнего установившегося режима к новому установившемуся режиму.
Таким образом, ток i цепи в течение переходного процесса можно представить суммой двух токов: нового установившегося 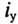
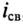
Аналогично напряжение в течение переходного процесса равно
В результате переходного процесса происходят изменения тока, напряжения, фазы, частоты и т.д.
Изучение переходных процессов очень важно, так как оно позволяет выявить возможные превышения напряжения на отдельных участках цепи, которые могут оказаться опасными для изоляции установки, позволяет выявить возможные броски токов, величина которых в десятки раз превышает установившийся. Изучение переходных процессов позволяет выявить ситуации, возникающие в электрических цепях при коротком замыкании, резком включении и выключении рубильников, и прочие режимы работы цепи.
Переходный процесс в электрической цепи
Переходный процесс в электрической цепи — это процесс, возникающий в электрической цепи при различных воздействиях, приводящих их из стационарного состояния в новое стационарное состояние, когда при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приёмника энергии, при обрывах в цепи, при коротких замыканиях отдельных участков цепи и т. д.
Подключение катушки индуктивности к источнику с постоянным напряжением
Если катушку индуктивности (RL) подключить к источнику с постоянным напряжением U (замыкание ключа К), то ток i в не-разветвленной цепи (рис. 20.1а) будет увеличиваться от нуля (в начале переходного процесса) до установившегося значения
Установившийся, т.е. постоянный, ток I не индуктирует в катушке ЭДС самоиндукции, поэтому индуктивное сопротивление в установившемся режиме при условии (20.3) отсутствует.
Этот увеличивающийся ток i индуктирует в индуктивности L катушки ЭДС самоиндукции (см. (9.11))
Следовательно, для любого момента времени переходного процесса по второму закону Кирхгофа можно записать
Разделив уравнение (20.4) на R, получают
В уравнении (20.5) 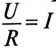
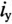
Отношение — 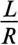
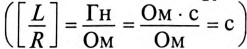
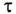
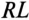
Тогда уравнение (20.5) можно записать в виде
Если это уравнение проинтегрировать, предварительно разделив переменные (ток и время), а затем спотенцировать, то получим выражение
где е — основание натурального логарифма (е=2,71); I — установившийся ток (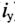
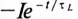
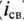
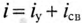
Таким образом, уравнение, которое позволяет определить вели-шу тока в цепи с индуктивностью L в любой момент переходно-процесса RL-цепи при подключении реальной катушки индук-1Вности к источнику с постоянным напряжением U, записывается в виде
Воспользовавшись Приложением 9, по выражению (20.10) можно определить, что за время t=
Теоретически переходный процесс происходит бесконечно долго. Практически переходный процесс в рассматриваемой цепи считается законченным, когда ток i увеличивается до 99 % установившегося тока I.
Как видим, чем больше xL, тем больше времени t длится перечный процесс.
Таким образом, постоянная времени xL определяет скорость греховного процесса или его длительность.
ЭДС самоиндукции в рассматриваемой цепи, вызванная свободным током 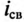
Таким образом, ЭДС самоиндукции в 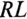
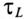
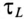
Увеличение тока и уменьшение ЭДС самоиндукции катушки при подключении катушки к источнику с постоянным напряжением U показаны на графике рис. 20.1б.
Отключение и замыкание RL-цепи
Если цепь с катушкой, в которой проходит установившийся ток I (рис. 20.1а), разомкнуть, то ток i в такой цепи с большой скоростью уменьшается до нуля и в катушке индуктируется большая ЭДС самоиндукции eL
Эта ЭДС полностью приложена к клеммам ключа, так как при размыкании сопротивление ключа становится бесконечно большим. Эта ЭДС вызывает значительное увеличение электрического поля между контактами ключа, а следовательно, и напряженности поля. Большая напряженность электрического поля может вызвать искровой и даже дуговой разряд между размыкающимися контактами ключа, в результате чего обгорают контакты ключа.
Поэтому рубильники в RL-цепях шунтируются специальными устройствами, которые обеспечивают гашение дугового разряда. Для гашения дугового разряда необходимо одновременно с отключением катушки индуктивности от источника замкнуть ее на разрядное сопротивление R0 (рис. 20.2а).
Уменьшение тока 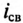
Наглядно это уменьшение можно наблюдать на рис. 20.1б, если кривую изменения eL считать кривой уменьшения тока 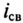
Постоянная времени при отключении катушки от источника с постоянным напряжением U определяется как и при включении катушки на это напряжение, т.е.
Если катушку с установившимся током I, зашунтированную сопротивлением Ro (рис. 20.2а), отключить от источника (разомкнуть ключ К), то в замкнутом контуре ABCD в начальный момент коммутации 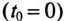
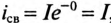
Для определения активного сопротивления катушки 
Как видно, за счет переходных процессов в цепях с индуктивностью возникают большие токи и напряжения. С этим необходимо считаться и учитывать при проектировании и эксплуатации цепей с индуктивностью.
Зарядка, разрядка и саморазрядка конденсатора
Если конденсатор с сопротивлением (утечки) R и емкостью С подключить к источнику с постоянным напряжением U (замыканием ключа К), то в цепи (рис. 20.3а) появится ток зарядки конденсатора (см. (11.16)):
где 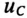
По второму закону Кирхгофа для цепи зарядки конденсатора (рис. 20.3а) можно записать уравнение
где произведение RC имеет размерность времени, обозначается буквой 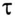
Уравнение (20.13) можно записать в виде
Если в уравнении (20.15) разделить переменные, проинтегрировать, а затем спотенцировать, то получится выражение
где U — установившееся напряжение 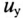
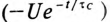
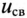
Следовательно, напряжение на заряжающемся конденсаторе в любой момент времени t переходного процесса определяется выражением
По (20.17), пользуясь Приложением 9, можно определить, что за время t= 
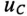

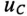
Теоретически зарядка конденсатора длится бесконечно долю а практически конденсатор считается заряженным, когда напряжение на нем достигает 99 % напряжения источника U.
Таким образом, и в RC-цепи, чем больше постоянная времени 

Ток i при зарядке конденсатора (см. (20.13)) уменьшается по за кону
(20. IS)
где 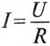
За время t=

Графики изменения напряжения на конденсаторе и тока в цепи арядки конденсатора изображены на рис. 20.36.
Если конденсатор емкостью С, заряженный предварительно до напряжения U, разряжать через резистор с сопротивлением R рис. 20.4а), то напряжение 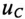
где U — напряжение на конденсаторе до начала разрядки (при t= 0), а 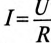

За время t= 
Если конденсатор емкостью С, заряженный до напряжения U, отсоединить от источника, то он будет разряжаться через свой диэлектрик. Напряжение на нем будет уменьшаться по закону 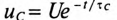
Постоянная времени саморазряда зависит от физических свойств диэлектрика
где р — удельное сопротивление диэлектрика; 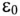
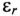
Для определения напряжения, тока, ЭДС в любой момент переходного процесса 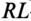
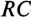
Пример 20.1
Катушка электромагнита с параметрами 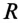
Решение
Установившийся ток
Постоянная времени для катушки
Подставляем значение величин в (20.10):
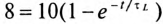
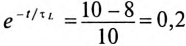
По Приложению 9 определяется 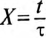
ЭДС самоиндукции за время 
Пример 20.2
К зажимам катушки индуктивности с параметрами 
Определить напряжение на зажимах вольтметра и ток в обмотках прибора (обмотки соединены последовательно) при t=0, если размыкание рубильника К произойдет мгновенно и дуги не возникнет.
Решение
До размыкания рубильника через катушку проходил ток
В момент размыкания рубильника (t = 0) весь этот ток проходит обмоткам вольтметра. При этом на вольтметре напряжение cтанет равным
Такого напряжения (10 кВ) и такого тока (2 А) обмотка вольтметра (обычно подвижная обмотка электродинамического прибора рассчитана на ток порядка десятков, максимум, сотен миллиампер) не выдержит и сгорит.
При размыкании рубильника с конечной скоростью между расходящимися контактами рубильника К (рис. 20.26) возникнет электрическая дуга. Это приведет к тому, что увеличение напряжения на вольтметре и тока через обмотки вольтметра будет меньше, чем в рассмотренном выше случае (мгновенное размыкание рубильника). Однако меры предосторожности для сохранения вольтметра и рубильника, описанные выше, нужно соблюдать.
Пример 20.3
Конденсатор емкостью С= 2 мкФ через сопротивление R= 500 кОм подключается к источнику с постоянным напряжением U= 220 В.
Определить напряжение на конденсаторе 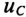
Решение
Постоянная времени заряда конденсатора
Напряжение на конденсаторе через 2 с от начала заряда
Ток в цепи заряда конденсатора через 2 с от начала заряда
так как
Время t’ заряда конденсатора до напряжения 150 В определяется по формуле (20.17):
Откуда
Из таблицы показательных функций (Приложение 9) находят t’= 1,14 с.
Пример 20.4
Параметры цепи, изображенной на рис. 20.5, следующие:
Определить значение токов в ветвях через время t= 2 с после замыкания ключа К.
Решение
Для ветви (1) с индуктивностью определяются:
установившийся ток
и постоянная времени
Тогда ток через 2 с будет равен
Для ветви (2) с емкостью определяются:
максимальный установившийся ток по окончании переходного процесса
и постоянная времени 
Тогда ток зарядки через 2 с будет равен
Для ветви (3) с активным сопротивлением 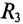
Постоянная времени 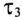
Через 2 с значение тока будет таким же, т. е.
Переходные процессы в электрических цепях. Классический метод расчета
Возникновение переходных процессов:
В предыдущих главах рассматривались установившиеся процессы в линейных электрических цепях, т. е. такие процессы, при которых напряжения и токи либо неизменны во времени (цепи постоянного тока), либо представляют собой периодические функции времени (цепи переменного тока).
Наступлению установившегося процесса, отличного от первоначального режима работы цепи, предшествует, как правило, переходный процесс, при котором напряжения и токи изменяются непериодически.
Переход от одного режима работы цепи к другому может быть вызван изменением параметров или схемы цепи, называемым в общем случае в электротехнике коммутацией.
Можно теоретически считать, что коммутация цепи производится мгновенно, т. е. на включение, выключение или переключение цепи время не расходуется. Тем не менее переход от исходного режима работы цепи к последующему установившемуся процессу происходит не мгновенно, а в течение некоторого времени. Объясняется это тем, что каждому состоянию цепи соответствует определенный запас энергии электрических и магнитных полей. Переход к новому режиму связан с нарастанием или убыванием энергии этих полей. Энергия 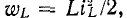
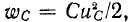
Если исключить случаи размыкания индуктивности и замыкания накоротко емкости и рассматривать цепи, в которых энергия, накапливаемая в магнитном или электрическом поле, может рассеиваться в виде теплоты в сопротивлениях, то, считая, что коммутация происходит мгновенно, можно искрообразование не учитывать.
Для завершения переходного и наступления установившегося процессов теоретически требуется бесконечно большое время. Практически, однако, время переходного процесса определяется малым интервалом, по истечении которого токи и напряжения настолько приближаются к установившимся значениям, что разница оказывается практически неощутимой. Чем интенсивнее происходит рассеяние энергии в сопротивлениях, тем быстрее протекает переходный процесс.
Если бы электрическая цепь состояла только из сопротивлений и не содержала индуктивностей и емкостей, то переход от одного установившегося состояния к другому совершался бы мгновенно, без затраты времени. В реальных электротехнических устройствах тепловые потери, обусловленные током, магнитные и электрические поля сопутствуют друг другу. Применяя специальные схемы и подбирая соответствующие параметры цепи, можно в зависимости от необходимости ускорить или замедлить переходный процесс.
В одних случаях переходные процессы в электрических цепях нежелательны и опасны (например, при коротких замыканиях в энергетических системах). В других случаях переходный процесс представляет собой естественный, нормальный режим работы цепи, как это, например, имеет место в радиопередающих и радиоприемных устройствах, системах автоматического регулирования и других цепях.
Существуют различные методы расчета переходных процессов в линейных электрических цепях. Настоящая глава посвящена классическому методу решения дифференциальных уравнений, описывающих переходные процессы.
Законы коммутации и начальные условия
Высказанные выше положения о том, что запас энергии магнитного или электрического поля может изменяться только плавно, без скачков, выражают принцип непрерывности во времени потокосцепления индуктивности и электрического заряда емкости и называются законами коммутации.
Невозможность скачкообразного изменения потокосцепления следует из того, что в противном случае на индуктивности появилось бы бесконечно большое напряжение 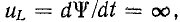
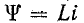
Аналогично невозможность скачкообразного изменения электрического заряда q следует из того, что в противном случае через емкость проходил бы бесконечно большой ток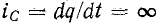
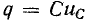
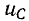
При этом следует отметить, что в цепях с идеализированными сосредоточенными параметрами скачкообразно могут изменяться: 1) токи в сопротивлениях и емкостях и 2) напряжения на сопротивлениях и индуктивностях.
Значения тока в индуктивности и напряжения на емкости в момент коммутации называются независимыми начальными условиями.
Обычно принимают, что коммутация происходит в момент времени t= 0; тогда ток в индуктивности и напряжение на емкости в момент времени непосредственно перед коммутацией обозначаются через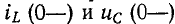
На основании законов коммутации:
Эти равенства выражают начальные условия цепи, в которых происходит коммутация.
При нулевых начальных условиях, т. е. косца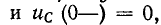
В случае ненулевых начальных условий, т. е. когда 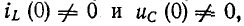
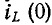
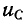
Независимые начальные условия характеризуют энергию магнитного и электрического полей, запасенную к моменту коммутации, и для расчета переходного процесса обязательно требуется знание этих начальных условий, причем совершенно безразлично, каким образом эти условия в цепи были созданы.
При расчете переходных процессов в разветвленных электрических цепях наряду с независимыми начальными условиями используются так называемые зависимые начальные условия, а именно: значения токов, напряжений и их производных в начальный момент времени (t = 0).
До сих пор нами исключались из рассмотрения случаи коммутации, при которых неизбежно между контактами возникает искра или дуга. Один из таких случаев показан на рис. 14-1, а. До коммутации ток проходит через индуктивность 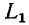
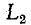
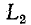
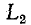
замкнуться и через межвитковую емкость. После быстрого погасания дуги токи в 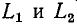
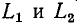
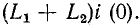
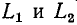
Найденный таким образом ток 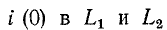
При коммутациях в цепях с емкостями при отсутствии сопротивлений также возможны весьма быстрые перераспределения зарядов, условно рассматриваемые как мгновенные. В этом случае применим принцип непрерывности суммарного заряда. Полученные при этом значения зарядов и напряжений на отдельных емкостях используются в расчете последующего переходного процесса как независимые начальные условия.
Например, в случае схемы на рис. 14-1, б принцип непрерывности суммарного заряда до и после коммутации выражается равенством
При сделанном допущении в остальной электрической цепи, соединенной с емкостями, не возникает бесконечно большого тока, так как суммарный заряд не изменяется скачкообразно при t=0.
В процессе рассматриваемой коммутации энергия электрического поля уменьшится, так как часть ее превратится в тепло в очень малом сопротивлении проводника при очень большом токе, а также сможет выделиться в искре и излучиться.
Установившийся и свободный режимы
В общем случае анализ переходного процесса в линейной цепи с сосредоточенными параметрами r, L, С и М сводится к решению обыкновенных линейных неоднородных дифференциальных уравнений, выражаюших законы Кирхгофа. Эти уравнения представляют собой линейную комбинацию напряжений, токов, их первых производных и интегралов по времени.
Например, если какая-нибудь э. д. с. е (t) включается в цепь, состоящую из последовательно соединенных r, L и С, то интегродифференциальное уравнение имеет вид:
Это уравнение после дифференцирования приводится к неоднородному дифференциальному уравнению второго
порядка
Как известно, общий интеграл такого^ уравнения равен сумме частного решения неоднородного уравнения и общего решения однородного уравнения.
Частное решение выражает установившийся режим, задаваемый источником.
Расчеты установившихся токов рассмотрены в предыдущих главах.
Общее решение физически определяет поведение цепи при отсутствии внешних источников электрической энергии и заданных начальных условиях. Функции, определяемые общим решением, называются свободными составляющими (токов, напряжений и пр.).
В случае, рассмотренном выше, однородное уравнение имеет вид:
и соответствующее ему характеристическое уравнение
Если корни характеристического уравнения обозначить через 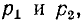
где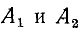
Полный переходный ток в цепи равен сумме установившегося и свободного токов:
Аналогично напряжение, заряд, магнитный поток и другие функции на любом участке цепи в переходном режиме состоят из установившейся и свободной составляющих.
На основании законов коммутации можно найти начальные независимые условия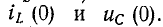
откуда
Итак, начальные значения свободных функций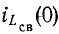
В частном случае при нулевых начальных условиях:
В зависимости от порядка дифференциальных уравнений, описывающих исследуемые переходные процессы, различают цепи первого, второго и более высокого порядков.
В цепях первого порядка накопление энергии происходит только в одном элементе, L или С в форме магнитной энергии, или электрической энергии . Одноконтурная цепь, содержащая элементы, в которых накапливается энергия обоих видов — магнитная « электрическая, представляет собой цепь второго порядка . Разветвленные цепи могут быть более высокого порядка.
Переходный процесс в цепи r, L
Положим, что в момент t = 0 цепь, состоящая из сопротивления r и индуктивности L, включенных последовательно, присоединяется к источнику э. д. с. е (t) (рис. 14-2).
Дифференциальное уравнение для времени
Характеристическое уравнение имеет вид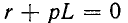
Отсюда свободный ток
Переходный ток в цепи определится суммой установившегося и свободного токов:
Установившийся ток может быть найден, если задана э. д. с. е (t).
Рассмотрим три случая:
1) включение в цепь г, L постоянной э. д. с. £;
2) короткое замыкание цепи г, L
3) включение в цепь г, L синусоидальной э. д. с.
1. Включение в цепь г, L постоянной э. д. с.
При включении в цепь г, L постоянной э. д. с. Е установившийся ток равен Е’/г. Поэтому согласно (14-9)
Постоянная интегрирования А находится по начальному условию
Согласно уравнению (14-10) при t — 0
откуда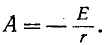
здесь 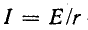
В начальный момент t = 0 э. д. с. самоиндукции 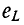
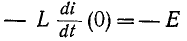
С течением времени э. д. с. самоиндукции убывает, а ток в цепи возрастает, асимптотически приближаясь к установившемуся значению.
На рис. 14-3 показаны кривые установившегося, свободного и переходного токов; на том же рисунке изображена кривая напряжения на индуктивности
Из курса математического анализа известно, что если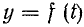
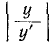
Величина 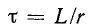
Выражение (14-11) показывает, что постоянная времени графически определяется длиной подкасательной к кривой
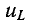
Нарастание тока происходит тем быстрее, чем меньше постоянная времени и соответственно чем быстрее убывает э. д. с. самоиндукции. Для различных моментов времени ток в цепи, выраженный в процентах конечного (установившегося) значения составляет:
Следовательно, постоянная времени цепи г, L равна промежутку времени, в течение которого свободная составляющая тока убывает в е = 2,718 раза и соответственно ток в этой цепи, включенной на постоянное напряжение, достигает 63,2% своего установившегося значения.
Как видно из рис. 14-3 и приведенной выше таблицы», переходный процесс теоретически длится бесконечно долго. Практически же можно считать, что он заканчивается спустя
2. Короткое замыкание цепи r, L.
Положим, что цепь r, L, присоединенная к источнику постоянного или переменного напряжения, замыкается при t = 0 накоротко (рис. 14-4, а). В образовавшемся при этом контуре r, L благодаря наличию магнитного поля индуктивной катушки ток исчезает не мгновенно: э. д. с. самоиндукции, обусловленная убыванием магнитного потока, стремится поддержать ток в контуре за счет энергии исчезающего магнитного поля.
По мере того как энергия магнитного поля постепенно рассеивается, превращаясь в сопротивлении г в тепло, ток в контуре приближается к нулю.
Процесс, происходящий в короткозамкнутом контуре г, L, является свободным; установившийся ток в данном случае равен нулю.
Положив в (14-9)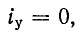
Постоянная интегрирования А находится из начального условия
откуда
здесь i (0—) — значение тока в индуктивности в момент, непосредственно предшествовавший короткому замыканию; оно может быть положительным или отрицательным.
На рис. 14-4, б изображены кривые спада тока в короткозамкнутом контуре и кривая напряжения на индуктивности

Постоянная времени контура 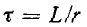
Переходный процесс в короткозамкнутом контуре заканчивается теоретически при 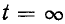
т. е. вся энергия, запасенная в магнитном поле катушки до коммутации.
Так же как и в предыдущем случае, переходный процесс в короткозамкнутом контуре можно практически считать законченным спустя
3. Включение в цепь r, L синусоидальной э. д. с.
При включении в цепь r, L синусоидальной э. д. с. 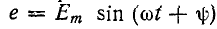
где
На основании (14-9)
где
Постоянная интегрирования определяется по начальному условию
Следовательно, 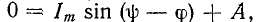
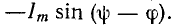
На рис. 14-5, а изображены кривые 
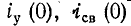
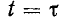
контура Q и обратно пропорциональна частоте
Если в момент коммутации (t = 0) ток 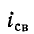
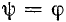
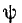
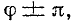
Если же коммутация происходит при 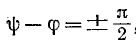
а именно 
гает экстремального значения (положительного или отрицательного) в конце первого полупёриода. Однако даже в предельном случае, когда r= 0 и, следовательно, 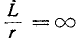
При достаточно большой постоянной времени 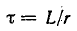
можно пренебречь по сравнению со вторым слагаемым, приняв приближенно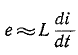
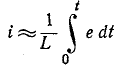
Следовательно, цепь с последовательно соединенными сопротивлением и индуктивностью при большой постоянной времени можно рассматривать как интегрирующее звено.
В свою очередь при достаточно малой постоянной времени, пренебрегая вторым слагаемым уравнения, приближенно получаем:
откуда
.
т. e. цепь с последовательно соединенными сопротивлением и индуктивностью при малой постоянной времени представляет собой дифференцирующее звено.
В обоих случаях функция е(t) может быть произвольной.
Интегрирующие и дифференцирующие звенья входят в качестве элементов в системы автоматического управления и регулирования.
Переходный процесс в цепи r, С
Положим, что в момент t = О цепь, состоящая из сопротивления г и емкости С, включенных последовательно, присоединяется к источнику э. д. с. е (t) (рис. 14-6).
На основании второго закона Кирхгофа уравнение для времени t
где 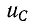
С учетом того, что
получим:
здесь искомой величиной является напряжение на емкости.
Характеристическое уравнение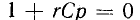
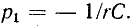
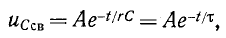
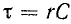
Переходное напряжение на емкости равно сумме принужденного и свободного напряжений:
В свою очередь ток в контуре
Рассмотрим три случая:
1) включение в цепь г, С постоянной э. д. с.
2) короткое замыкание цепи r, С
3) включение в цепь r, С синусоидальной э. д. с.
Включение в цепь r, С постоянной э. д. с.
Включим постоянную э. д. с. Е в цепь с сопротивлением г и предварительно заряженной емкостью С (полярности заряженной емкости указаны на рис. 14-6 знаками + и —); начальное напряжение на емкости
(0) обозначим для простоты через U.
Установившееся напряжение на емкости равно э. д. с. источника. Поэтому согласно (14-12)
Постоянная интегрирования А, входящая в (14-14), находится по начальному условию:
При t = 0 имеем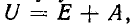
Согласно (14-13) ток в контуре
Если Е > U, то с течением времени напряжение на емкости возрастает, стремясь к установившемуся значению Е, а ток убывает, стремясь в пределе к нулю; на рис. 14-7, а изображены кривые нарастания 
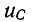
Если Е < U, то кривые 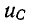
Постоянная времени 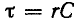
Закон изменения напряжения на емкости и тока в данной цепи аналогичен закону изменения тока и напряжения 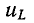
Короткое замыкание цепи r, С
Замыкание накоротко цепи, состоящей из последовательно соединенных г и С, равносильно принятию в предыдущем случае э. д. с., равной нулю. Предполагается, что емкость С заряжена, т. е. в момент включения на выводах имеется напряжение U.
Положив в (14-15) и (14-16) э. д. с. Е равной нулю, получим:
где
При коротком замыкании цепи r, С электрический ток идет от вывода + к выводу — Следовательно, при выбранной на рис. 14-6 полярности емкости ток проходит через сопротивление r в направлении, противоположном тому, которое принято на рис. 14-6 за положительное. Поэтому в выражении для тока стоит знак минус. На рис. 14-8 изображены кривые спала 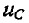
В отличие от напряжения на емкости, которое изменяется непрерывно, ток в контуре r, С, пропорциональный скорости изменения 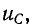
Энергия, рассеиваемая в сопротивлении г в течение всего переходного процесса, равна энергии, запасенной в электрическом поле до коммутации:
Так же как и в случае цепи r, L, переходный процесс может считаться законченным спустя 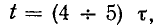
к этому времени емкость разрядится на 98,2—99,3% и напряжение на емкости снизится до 1,8—0,7% первоначального.
Включение в цепь г, С синусоидальной э. д. с.
При включении в цепь r, С синусоидальной э. д. с. установившееся напряжение на емкости
на основании (14-12)
Если предполагать, что конденсатор не был заряжен, то постоянная интегрирования определится по начальному условию 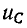
откуда
Тогда искомое напряжение на емкости будет:
а ток в цепи
Из написанных выражений видно, что если включение цепи r, С происходит в момент, когда установившийся ток должен достигать максимума — положительного или
отрицательного (т. е. 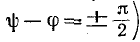
напряжение на емкости должно быть равно нулю, то свободной слагающей напряжения на емкости не возникает и в цепи сразу же без переходного процесса наступает установившийся режим.
Так как цепь г, С по протеканию переходного процесса подобна цепи г, L, то при соответствующем подборе параметров г и С она также может служить дифференцирующим и интегрирующим звеном.
Переходный процесс в цепи r, L, С
При включении в цепь г, L, С э. д. с. е (t) (рис. 14-9) переходный процесс исследуется с помощью дифференциального уравнения (14-3):
Соответствующее ему характеристическое уравнение (14-5)
имеет корни
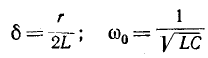
Свободный ток согласно (14-6) равен:
Ток в цепи определяется суммой установившегося и свободного токов:
Установившийся ток находится в соответствии с заданной э. д. с. е (t). Что касается свободного тока, то его характер зависит от знака подкоренного выражения (14-17).
Включение в цепь г, L, С постоянной э. д. с.
Рассмотрим сначала случай, когда э. д. с. источника постоянна: е = Е, и емкость имеет начальное напряжение
Ввиду наличия индуктивности начальное значение тока i (0) = 0.
Исходное уравнение
для начального момента записывается в виде
откуда находится начальное значение производной
которое является зависимым начальным условием, необходимым для вычисления 
При установившемся режиме ток будет равен нулю, что следует как из физического смысла, так и из вида правой части дифференциального уравнения (14-3). Продифференцировав (14-18) с учетом того, что 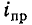
Подставляя в (14-18) и (14-20) t = 0 и используя (14-19), получаем:
Из этих уравнений следует:
поэтому
Рассмотрим возможные три случая.
Случай 1. 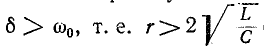
Согласно (14-17) корни характеристического уравнения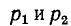
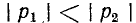
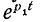
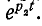
При больших значениях С влияние емкости мало и кривая тока приближается к кривой тока в цепи r, L (см. рис. 14-3); при малых значениях L влияние индуктивности незначительно и кривая тока близка к кривой тока в цепи г, С (рис. 14-7).
Выражение (14-21) может быть преобразовано в гиперболическую форму
Следует заметить, что при коротком замыкании цепи г, L, С, т. е. при Е = О, ток в цепи обусловливается разрядом емкости.
Случай 2.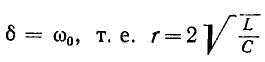
Согласно (14-17) корни характеристического уравнения одинаковы:
(см. рис. 14-10, б).
Выражение (14-21) приводит в этом случае к неопределенности вида 0/0.
Раскрывая неопределенность по правилу Лопиталя дифференцированием числителя и знаменателя по 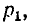
To же выражение получится, если воспользоваться общим решением однородного дифференциального уравнения с кратными корнями:
В рассматриваемом случае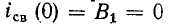
Следовательно,
Кривая тока аналогична кривой i на рис. 14-11.
Случай 3. 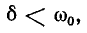
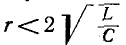
Корни характеристического уравнения комплексные и сопряженные:
Согласно (14-24)
Корни характеристического уравнения располагаются симметрично относительно действительной оси в левой полуплоскости, на полуокружности, центр которой совпадает с началом координат, а радиус равен 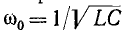
Сопоставление рис. 14-10, а, б к в показывает, что о характере переходного процесса в цени г, L, С можно судить по расположению корней характеристического уравнения, т. е. нулей функции Z (р), на комплексной плоскости.
Если расположенные в левой полуплоскости нули функции Z (р) лежат на действительной оси, то имеет место апериодический процесс: совмещению нулей в одной точке отвечает критический случай; наконец, если нули функции Z (р) являются комплексно-сопряженными, то имеет место колебательный процесс.
Величина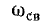
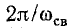
Полученное выражение показывает, что при включении цепи г, L, С на постоянное напряжение, когда 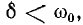
(рис. 14-12). Колебания возникают вследствие периодического преобразования энергии электрического поля в энергию
* Тот же результат получится, если исходить из общего решения однородного дифференциального уравнения с комплексно-сопряженными корнями:
магнитного поля и обратно, причем эти колебания сопровождаются потерей энергии в сопротивлении.
При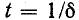
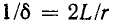
На рис. 14-12 показана также кривая напряжения 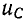
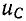
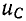
Как видно из (14-23) и рис. 14-10, в, угловая частота этих колебаний 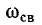
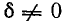
Чем меньше 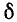
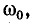
В пределе, при 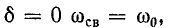
О быстроте затухания колебательного процесса судят по величине 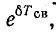
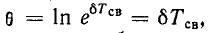
На рис. 14-13, а—г показано изменение характера переходного процесса при уменьшении
Приведенные выше величины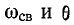
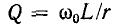
При достаточно высокой добротности 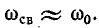
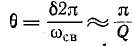
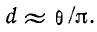
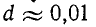
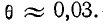
Включение в цепь г, L, С синусоидальной э. д. с.
Если цепь г, L, С присоединяется к источнику синусоидальной э. д. с.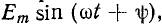
ток равен:
и переходный ток согласно (14-18) равен:
Кривые установившегося, свободного и- переходного токов при апериодическом и колебательном процессах показаны в виде примера на рис. 14-14.
Частота установившегося тока равна частоте источника синусоидального напряжения, свободный же ток при 
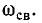
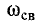
Свободные колебания тока накладываются на установившийся ток и затухают пропорционально множителю 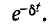
Та из двух слагающих тока i, частота которой меньше, служит как бы криволинейной осью для другой слагающей, колеблющейся относительно нее (рис. 14-14, б). При близком совпадении частот 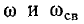
Расчет переходного процесса в разветвленной цепи
Переходный процесс в разветвленной линейной электрической цепи описывается системой линейных дифференциальных уравнений с постоянными коэффициентами, общее решение которых находится как сумма установившейся и свободной составляющих.
Рассмотрим сначала методику расчета установившегося режима.
Во многих случаях воздействующая функция, например
э. д. с. источника, может быть представлена в обобщенной форме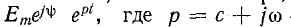
Условие 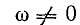
Условие 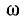
Задавшись э. д. с. 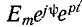
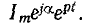
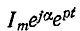
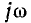
В зависимости от схемы и постановки задачи Z (р) означает обобщенное входное сопротивление или величину, обратную обобщенной передаточной проводимости;Z (р) получается из соответствующего комплексного сопротивления заменой
Мгновенные значения тока определяются мнимой или действительной частью
В случае синусоидальной э. д. с. (с = 0; р 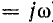
Если э. д. с. есть показательная функция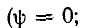
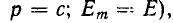
где
При постоянной э. д. с. 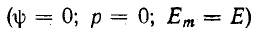
где z (0) — сопротивление при постоянном токе.
Перейдем теперь к рассмотрению свободного режима.
Свободные составляющие представляют собой общее решение системы однородных линейных дифференциальных уравнений. Для заданной цепи степень характеристического уравнения не зависит от выбора контуров, для которых составляются уравнения по второму закону Кирхгофа. Однако если выбрать контуры так, чтобы порядок дифференциальных уравнений был наименьшим, то степень характеристического уравнения не будет превышать суммы порядков исходных дифференциальных уравнений системы. При этом, как будет показано ниже, для получения характеристического уравнения отнюдь не обязательно приводить систему дифференциальных уравнений к одному уравнению относительно одной неизвестной функции.
Корни характеристического уравнения могут быть действительными или комплексными. Если корни комплексные, то они всегда образуют комплексно сопряженные пары. В связи с этим характеристическое уравнение нечетной степени всегда имеет хотя бы один действительный корень, остальные же корни могут быть действительными или комплексно-сопряженными; характеристическое уравнение четной степени имеет четное число действительных или комплексно-сопряженных корней. Действительные части всех корней характеристического уравнения всегда отрицательны, что физически обусловлено затуханием свободных составляющих в пассивных цепях с течением времени. При этом все коэффициенты характеристического уравнения должны быть действительными и положительными.
Корни единого характеристического уравнения используются для нахождения в данной цепи свободных составляющих как токов, так и напряжений.
Допустим, что характеристическое уравнение имеет п корней. Тогда свободный ток в любой ветви
здесь 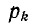
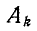
Аналогичная структура решения получается и для свободных составляющих напряжений.
В случае, когда 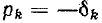
Если имеются сопряженные комплексные корни, например 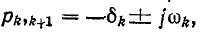
преобразуется в
Для m-кратных сопряженных комплексных корней решение принимает вид:
Методика получения характеристического уравнения иллюстрирована ниже на примере двухконтурной схемы, изображенной на рис. 14-17.
Первый контур содержит сопротивления 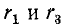
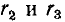
Соответственно степень характеристического уравнения равна 2.
Для получения характеристического уравнения применяется следующий прием. Система дифференциальных уравнений для свободных слагающих токов
записывается в символической алгебраической форме, при которой символ р заменяет операцию дифференцирования, а символ 1/р — операцию интегрирования:
Данная система уравнений имеет решение, отличное от нулевого, если определитель системы равен нулю, т. е.
или
Таким образом, получается характеристическое уравнение второй степени
Ввиду прямой пропорциональности, существующей между входным сопротивлением цепи Z (р) и определителем системы 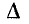
Операторное сопротивление Z (р) получается из комплексного сопротивления 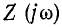
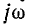
Если характеристическое уравнение имеет степень л, то искомыми являются п постоянных интегрирования 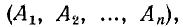
(n — 1)-кратного дифференцирования уравнения (14-26):
Значения свободного тока и его производных при t =0, входящие в (14-27), находятся предварительно на основании законов коммутациии уравнений Кирхгофа.
Для определения начальных значений токов и напряжений в цепи можно для наглядности воспользоваться схемой замещения, которая составляется из исходной схемы после коммутации, если заменить индуктивности идеальными источниками тока с токами, равными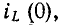
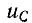
При нулевых начальных условиях индуктивность равносильна разрыву ветви, а емкость — короткому замыканию.
По этой схеме замещения можно найти другие токи и напряжения в момент t=0, если воспользоваться уравнениями Кирхгофа или правилами преобразования схем.
Итак, в соответствии со сказанным выше расчет переходного процесса классическим методом проводится в следующем порядке:
- Производится расчет режима до коммутации, из которого определяются конечные значения (т. е. при t=0—) функций, не меняющихся скачком (токов в индуктивностях, напряжений на емкостях). Далее с использованием законов коммутации находятся независимые начальные условия, т. е.
- Составляется система дифференциальных уравнений Кирхгофа, описывающая процесс в цепи после коммутации.
- Находится общее решение системы однородных дифференциальных уравнений.
- Находится тем или иным методом частное решение системы неоднородных дифференциальных уравнений, указанных в n. 2, соответствующее принужденному режиму цепи.
- Определяются зависимые начальные условия для искомых функций на основании найденных в п. 1 независимых начальных условий и уравнений Кирхгофа из п. 2, примененных для t = 0.
- По начальным условиям определяются постоянные интегрирования, содержащиеся в общем решении.
- Найденные установившиеся и свободные токи и напряжения складываются
Приведенный ниже пример 14-1 иллюстрирует нахождение начальных условий; в примере 14-2 дан численный расчет переходного процесса в цепи на рис. 14-17.
Пример 14-1. В цепи, изображенной на рис. 14-18, моменту t= 0 предшествовал установившийся режим постоянного тока. При t = 0 замкнулся контакт К. Найти начальные значения тока в.индук- is & тивности и напряжений на емкостях и их первых производных.
Независимыми начальными условиями будут ток в индуктивности 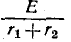
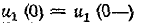
Напряжения на емкостях до коммутации находятся из условий равенства их зарядов (так как емкости соединены последовательно) и равенства суммарного напряжения на емкостях напряжению на сопротивлении
откуда
Требуемые зависимые начальные условия определятся из уравнений
1В случае, когда э. д. с. изменяется в виде импульса, имеющего кусочно-аналитическую форму, представляется часто целесообразным применять интеграл Дюамеля
токи же 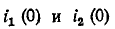
Подстановка в эти уравнения найденных значений 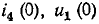
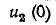
и далее
Начальное значение производной тока в индуктивности определяется также из уравнения Кирхгофа:
откуда при t = О
Пример (4-2. Определить ток i в иепи на рис. 14-17, если известно, что е = E = 100 В,
Подстановка заданных значений в приведенное выше характеристическое уравнение дает:
или
корни характеристического уравнения комплексные:
Искомый ток
Установившийся ток
Свободный ток
В начальный момент 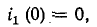
Производная тока по времени
В начальный момент
Следовательно, в начальный момент напряжение на ветви
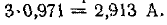
производной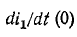
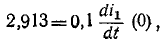
Следовательно, подставляя значение 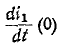
откуда
Итак,
Переходные процессы в цепях с распределенными параметрами
Переходные процессы в цепях с распределенными параметрами (в линиях, обмотках электрических машин и т. п.) возникают при коммутациях, передаче непериодических сигналов или под влиянием внешнего электромагнитного поля (например, при грозовых разрядах). Для исследования переходных процессов в однородных цепях с распределенными параметрами пользуются дифференциальными уравнениями (11-2) в частных производных:
где r, L, g и С — параметры цепи на единицу длины; х — координата рассматриваемой точки, отсчитываемая от начала цепи.
В общем виде решение этих дифференциальных уравнений достаточно сложно. Решение упрощается, если пренебречь потерями В этом случае
е. считать, что r и g равны нулю.
В этом случае
Дифференцируя (14-28) по х:
и используя (14-29), получаем:
Дифференциальное уравнение (14-30) известно в математической физике под названием уравнения ко—лебаний струны. Его решение дано Даламбером и имеет вид:
где
Первая слагающая представляет собой одиночную прямую волну напряжения, которая без изменения перемещается в сторону возрастающих х, т. е. от начала к концу цепи. Для всех значений х, при которых 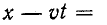
Вторая слагающая представляет собой одиночную о б -ратную волну напряжения, которая без изменения перемещается в противоположном направлении.
Для нахождения тока произведем замену переменных, обозначив 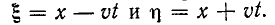
Но
и
Следовательно,
Интегрирование последнего уравнения дает
Выражения (14-31) и (14-32) записываются сокращенно:
здесь
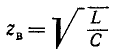
Следовательно, напряжение и ток прямой и соответственно обратной волн связаны законом
Аналогичный результат был получен для установившихся прямой и обратной волн при рассмотрении синусоидального режима в однородной линии. Физически установившиеся волны представляют собой бесконечные суммы прямых и обратных одиночных волн, отраженных от обоих концов линии.
Итак, при отсутствии потерь в однородной цепи с распределенными параметрами напряжение и ток могут быть представлены как сумма и разность двух волн, движущихся с одинаковой скоростью 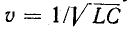
Если на пути распространения волны встречается неоднородность, например воздушная линия переходит в кабельную или волна достигает конца линии (разомкнутого или замкнутого через сопротивление или на короткое), происходит отражение волны. В зависимости от характера неоднородности отражение может быть частичным или полным. В первом случае наряду с отраженной волной возникает преломленная волна, распространяющаяся за место нарушения однородности; во втором случае преломленная волна отсутствует.
Обозначим 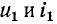
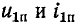
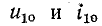
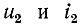
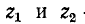
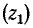
В месте неоднородности выполняется условие равенства
напряжений и токов:
Следовательно,
Подстановка в (14-36) значений 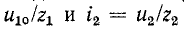
В результате совместного решения уравнений (14-35) — (14-37) находятся отраженная 
где 
Соответственно ток отраженной волны
а ток преломленной волны
Последнее выражение показывает, что ток в конце линии после отражения можно найти как ток в эквивалентной цепи, в которую включается напряжение, равное двойному напряжению падающей волны, и которая состоит из волнового сопротивления первой линии 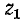
Опишем процесс включения однородной линии без потерь. После присоединения линии к источнику э. д. с. по линии начнет распространяться зарядная волна, создающая напряжение и ток. Если в конце линии присоединена нагрузка, равная волновому сопротивлению линии,
то падающая волна, достигнув ее, не отразится и в линии сразу наступит установившийся режим. Если же нагрузка с линией не согласована, то падающая зарядная волна, достигнув конца линии, претерпит отражение. Распространяясь в обратную сторону, отраженная волна сложится с падающей, причем напряжения волн суммируются, а токи вычитаются (алгебраически). Достигнув начала линии, обратная волна снова отразится от источника э. д. с., как от короткозамкнутого конца; появится новая прямая волна напряжения и тока, которая также отразится от конца, и т. д. Процесс будет продолжаться до наступления установившегося режима. Теоретически в идеальной линии без потерь при чисто реактивной нагрузке процесс колебаний будет продолжаться бесконечно долго. В реальной линии при наличии потерь волны напряжения и тока будут постепенно затухать в направлении распространения.
Напряжение и ток в линии в произвольный момент времени определятся как алгебраические суммы и соответственно разности напряжений и токов прямых и обратных волн.
Пользуясь формулами и схемой замещения, описанной выше, можно найти напряжение и ток, возникающие в месте присоединения сосредоточенной нагрузки или перехода одной линии в другую (см. пример 14-3).
Следует отметить что индуктивность, включенная последовательно в линию, или емкость, включенная параллельно проводам линии, сглаживает фронт преломленных волн; активное сопротивление, включенное в линию параллельно, уменьшает преломленную волну.
Пример 14-3. К концу линии, имеющей волновое сопротивление 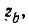
запишите так:
откуда
и
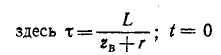
- Переходные процессы в линейных цепях
- Переходные процессы в нелинейных цепях
- Переходные процессы в электрических цепях с сосредоточенными параметрами
- Переходные процессы в колебательных контурах
- Цепи с взаимной индукцией
- Трехфазные цепи
- Периодические несинусоидальные напряжения и токи в линейных цепях
- Нелинейные цепи переменного тока