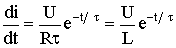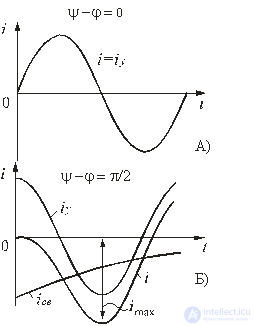L.
511.
«Электротехника» Аксютин В.А.
Основные
определения, расчет переходных процессов
классическим методом.
Установившимся
процессом
электрической
цепи называется
процесс, создаваемый
источниками ЭДС и тока постоянными или
изменяющимися во времени по периодическому
закону, который продолжается в течение
любого заданного времени.
Переходным
процессом
в электрической цепи называется процесс
изменения во времени токов в ветвях и
напряжений на элементах цепи, вызванный
коммутацией.
Коммутация
— это
включение,
отключение, переключение элементов
цепи (источников ЭДС и тока, резисторов,
катушек индуктивности и конденсаторов),
изменение параметров элементов цепи и
т. п. Считается, что коммутация происходит
мгновенно.
а
б
Рис. 1
Переходный
процесс может возникнуть в цепи только
при наличии в ней таких элементов, как
катушки индуктивности
и конденсаторы,
и определяет после коммутации
перераспределение энергии между
источником, катушками индуктивности и
конденсаторами. Такие элементы называют
независимые
накопители энергии.
Если цепь состоит только из резисторов,
то после коммутации сразу возникает
установившийся режим. Переходный процесс
начинается с момента возникновения
коммутации (время t = 0) и протекает между
установившимся
процессом до
коммутации
и установившимся
процессом
после коммутации.
Момент времени непосредственно перед
коммутацией обозначается t = 0,
а сразу после коммутации – t = 0+
или t = 0. Длительность переходного
процесса равна бесконечности, но для
большинства практических задач можно
принять, что переходный процесс
заканчивается, если искомая величина
переходного тока или напряжения
отличается от установившегося значения
менее чем на 5%. Так определяется,
приближённо, время переходного процесса
tПП.
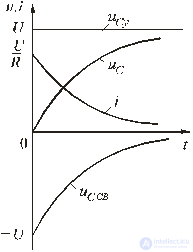
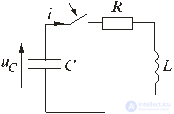
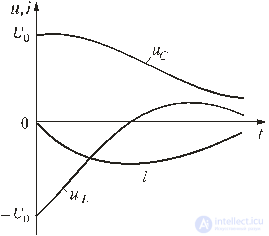
Рассмотрим,
например, изменение напряжения на
конденсаторе uC(t)
и тока в цепи
i(t)
при переключении ветви с последовательным
соединением резистора индуктивности
и ёмкости с источника постоянного
напряжения E1
на источник E2
(рис. 2).
Рис. 2
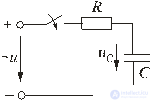
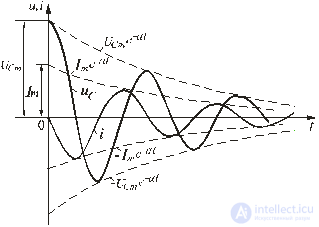
Рис.
3
На рис. 3 изображены
графики изменения напряжения на
конденсаторе
uC(t)
и тока ветви i(t).
Колебательный характер процесса
получается при определённом сочетании
значений сопротивления, индуктивности
и ёмкости. На графиках показаны области:
установившийся до коммутационный
процесс t
= (–∞, 0–)
переходный процесс t
= (0+,
tПП)
и установившегося после коммутационного
процесс (принуждённый режим) t
= (tПП,
∞).
На рисунке:
— длительность
импульса (u(t) = U);
— длительность
паузы (u(t) = 0);
—
период следования импульсов;
— частота генератора.
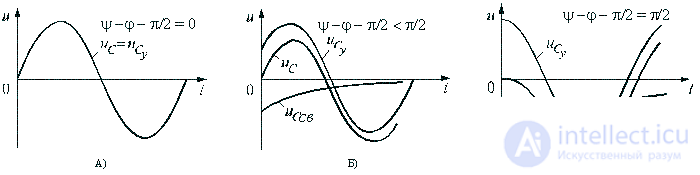
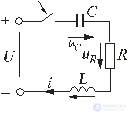
Рис. 4
Переходные
процессы в большинстве случаев являются
кратковременными и однократными. Расчет
и непосредственное наблюдение переходных
процессов на мониторе или экране
осциллографа удобно проводить, если
подключить цепь к источнику периодических
сигналов прямоугольной формы (рис. 4).
Длительность импульса должна выбираться
такой, чтобы переходный процесс
заканчивался за время
.
Передний фронт импульса соответствует
включению цепи на постоянное напряжение,
а задний – уменьшению напряжения
источника до нуля. Длительность паузы
должна выбираться так, чтобы в исследуемых
схемах значения токов в катушках
индуктивности и напряжения на конденсаторах
уменьшились до нуля. Это обстоятельство
позволяет наблюдать на экране монитора
переходный процесс при включении или
отключения цепи на постоянное напряжение,
а также найти установившиеся значения
исследуемых токов и напряжений до и
после коммутации.
Соседние файлы в папке UE_mod_5
- #
- #
- #
- #
- #
- #
Содержание:
Классический метод расчета переходных процессов:
В работе электрических цепей различают два режима процессов: переходный и установившийся.
Переходной процесс
Переходным процессом в электрической цепи называют электромагнитный процесс, возникающий в цепи при переходе от одного установившегося режима к другому. Этот процесс возникает в электрических цепях при подключении к ним или отключении от них источников электрической энергии, а также при скачкообразном изменении схемы цепи или параметров входящих в нее элементов. Установившимся называют такой режим, при котором токи, напряжения и ЭДС в цепи являются постоянными функциями времени [I4].
В цепях, не содержащих энергоемких элементов (индуктивностей и емкостей), новый установившийся режим наступает непосредственно за моментом коммутации. Поэтому можно считать, что в таких цепях переходные процессы отсутствуют.
В цепях с энергоемкими элементами переходные процессы продолжаются некоторое время, так как энергии электрических полей конденсаторов
При анализе переходных процессов в электрических цепях классическим методом составляется система уравнений для мгновенных значений токов и напряжений. Эти уравнения составляются непосредственно по законам Кирхгофа или с помощью других методов расчет цепей, например метода контурных токов или метода узловых потенциалов. При этом используются соотношения между токами и напряжениями в элементах цепи
В полученной таким образом системе уравнений выбирается основная переменная, и исключением других переменных из системы уравнений получают одно уравнение, содержащее только основную переменную. В общем случае для линейных электрических цепей с сосредоточенными параметрами, содержащих элементы 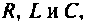
где 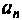
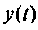
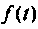
Порядок высшей производной дифференциального уравнения определяет порядок цепи. Так, например, если этот порядок будет первым, то и цепь называют цепью первого порядка и т. д.
Решение уравнения (6.2) ищется в виде
где 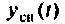
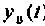
Свободная составляющая 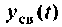
Вынужденная составляющая 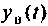
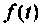
Решение однородного дифференциального уравнения имеет вид
где 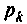
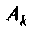
Корни характеристического уравнения 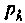
Особенностью метода является необходимость определения постоянных интегрирования и корней характеристического уравнения.
Число постоянных интегрирования и корней характеристического уравнения зависит от порядка цепи. Постоянные интегрирования находят из начальных условий искомой функции и ее производных.
Законы коммутации
Начальные условия — значения токов и напряжений при t = 0.
Независимые начальные условия — это величины, которые согласно законам коммутации не изменяются скачком. Они определяются из расчета установившегося режима до коммутации:
Зависимые начальные условия — это значения токов и напряжений в момент коммутации 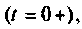
Пример расчета начальных условий
Независимые начальные условия (рис. 6.1) определяют по второму закону коммутации, используя соотношение (6.2)
Зависимые начальные условия находят для после коммутационной схемы (рис. 6.2), записав уравнения в соответствии с законами Кирхгофа с учетом того, что 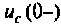
Выразим из первого уравнения системы уравнений (6.10) 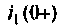
Тогда
В матричной форме система уравнений (6.11) принимает вид:
Решении системы уравнений (6.12), согласно формулам Крамера имеют вид:
где
Определение корней характеристического уравнения
Определение корней по однородному уравнению:
Записывают неоднородное дифференциальное уравнение относительно тока
Преобразуя однородное уравнение, получают характеристическое
откуда корень характеристического уравнения
Определение корней по входному комплексному сопротивлению после коммутационной схемы
Запишем выражение для входною комплексного сопротивления, приравняем его к нулю (для схемы с источником ЭДС) или комплексную проводимость (для схемы с источником тока) заменив 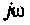
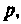
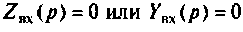
Переходя от исследуемой схемы (рис. 6.3, a) к комплексной схеме замещения {рис. 6.3, б), определяют
Заменив 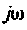
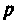
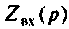
откуда корень полученного уравнения
Определение корней по постоянной времени цепи
Известно [4, 14], что 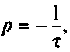

Для цепи с одним индуктивным элементом постоянная времени 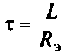
Для определения 
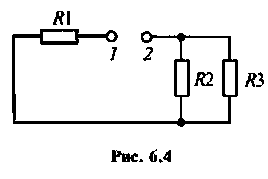
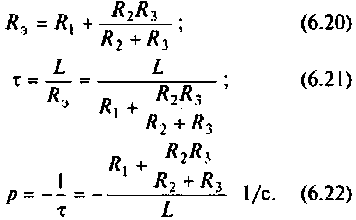
Для последовательного колебательного контура
Определение корней по определителю матрицы комплексных контурных сопротивлений (узловых проводимостей)
Определитель матрицы комплексных контурных сопротивлений (узловых проводимостей) приравнивают к нулю и, заменив 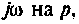
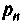
Порядок расчета переходных процессов. Составляют дифференциальные уравнения для послекоммутационной схемы относительно величин, которые согласно законам коммутации не изменяются скачком. Решение уравнений представляют в виде суммы вынужденной 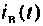
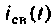
Определяют вынужденную составляющую тока (напряжения), используя методы расчета цепи в установившемся режиме, т.е. в цепи после окончания переходного процесса
Определяют свободную составляющую.
Вычисляют постоянные интегрирования.
Рассчитывают корни характеристического уравнения р„.
Записывают решение, строят графики.
Проверяют решение, изображают схему при
Качественный анализ переходных процессов
В цепях с одним реактивным элементом можно провести качественный анализ переходных процессов без составления и решения дифференциальных уравнений, применив законы Кирхгофа и учитывая законы коммутации. Для этого используют два положения:
- в цепях 1-го порядка свободная составляющая затухает но экспоненциальному закону
;
- закон изменения вынужденной составляющей определяется характером воздействующих на цепь напряжений.
Порядок расчета переходных процессов в цепях первого порядка:
Примеры решения типовых задач
Пример 6.5.1.
Накопительная емкость импульсного модулятора передающего устройства РЛС (рис. 6.5) после включения разряжается через разрядное сопротивление. Определить время, через которое напряжение на емкости уменьшится до уровня
Решение
Составляют дифференциальное уравнение для послекоммутационной схемы относительно напряжения
где
Решением дифференциального уравнения служит напряжение на емкости в переходном и установившемся режимах и имеет вид
Вынужденная составляющая напряжения (в послекоммутационной схеме при 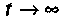
Свободная составляющая напряжения
Рассчитывают постоянную интегрирования А из начальных условий |при /(0+)].
откуда
Определяют постоянную времени, используя соотношение
Находят напряжение в переходном режиме
Вычисляют время разряда накопительной емкости из уравнений
После логарифмирования получаем:
Строят, например, в среде Mathcad, графики изменения напряжения на емкости в переходном режиме (рис. 6.6).
Определяют длительность переходного процесса
Вывод. Для регулирования длительности переходного процесса необходимо изменять в цепи постоянную времени 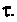
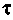
Пример 6.5.2.
Обмотка электромагнитного реле подключается к источнику постоянной ЭДС 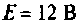
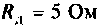
Найти время, через которое срабатывает реле, если ток срабатывания 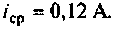
Решение
Составляют дифференциальное уравнение для послекоммутационной схемы относительно тока
Решив полученное дифференциальное уравнение, получают ток переходного процесса
Определяют вынужденную составляющую тока (в послекоммутационной схеме при 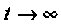
Определяет свободную составляющую тока
Определяют постоянную интегрирования А из начальных условий. Независимые начальные условия находят по первому закону коммутации
откуда
Определяют постоянную времени электрической цепи
Определяют ток в переходном режиме
Определяют время срабатывания реле из уравнения
в результате следующих преобразований которого
получаем
В среде Mathcad график функции i(t) имеет вид, приведенный на рис. 6.8.
Выводы. 1. Подбирая различное по значению добавочное сопротивление 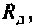
2.Приведенный порядок расчета можно применить в интегрирующих и дифференцирующих цепях, используемых для коррекции динамических свойств систем автоматического управления.
Пример 6.5.3.
Параллельный колебательный контур (рис. 6.9) подключается к источнику ЭДС
Определить закон изменения напряжении 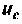
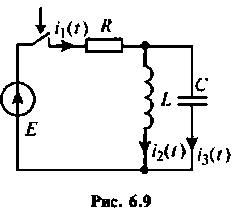
Решение
Определяют напряжение на конденсаторе в переходном режиме как сумму вынужденной и свободной составляющей
Определяют вынужденную составляющую напряжения
При установившемся режиме 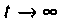
Определяют корни характеристического уравнения 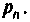
откуда
Для трех заданных значений параметров определяют вид корней:
а после вычислений получаем
Корни действительные и различные, поэтому свободная составляющая напряжения на конденсаторе имеет вид
2)
Корни действительные, равные, следовательно,
3)
Корни комплексные, сопряженные, тогда
Определяют постоянные интегрирования 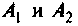
Решают уравнения, составленные по законам Кирхгофа для
Далее находят 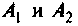
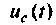
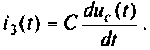
Рассчитаем 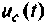
1) корни действительные и различные (рис. 6.10): 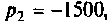
При t = (0+)
отсюда
Графики напряжения 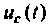
2) корни действительные и равные (рис. 6.11): 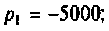
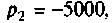
При t = (0+)
отсюда
тогда
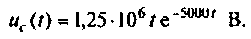
Компьютерный график напряжения 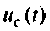
3) корни комплексные, сопряженные (рис. 6.12): 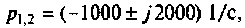
При t=(0+)
отсюда
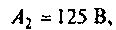
тогда
Компьютерный график напряжения 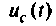
Выводы
1. Напряжение 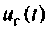
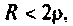
2. Переходной процесс в параллельном колебательном контуре при R < 2р используют в автоколебательных системах, где контур является нагрузочной цепью.
Пример 6.5.4. Интегрирующая цепь (рис. 6.13) с параметрами 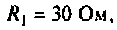
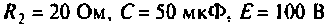
Произвести качественный анализ изменении напряжения на конденсаторе и токов в ветвях в переходном режиме.
Решение
Определяют значение переходных токов и напряжений для 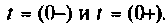
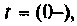
Эквивалентная схема для 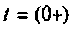
Для этой схемы составляют систему уравнений по законам Кирхгофа:
Определяют значение переходных токов и напряжений для 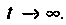
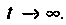
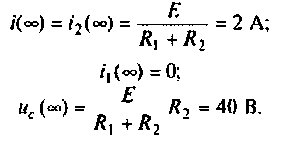
Определяют 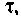
Записывают аналитические выражения для переходных токов и напряжений:
Строят графики напряжений и токов, например, в среде Mathcad (рис. 6.17, 6.18).
Цепи в виде резисторно-конденсаторного делителя нашли широкое применение и импульсных устройствах РЭТ.
- Анализ переходных и установившихся процессов методом интеграла свертки
- Операторный метод расчета переходных процессов
- Метод пространства состояний электрических цепей
- Синтез электрических цепей
- Переходные процессы в нелинейных цепях
- Переходные процессы в электрических цепях с сосредоточенными параметрами
- Переходные процессы в колебательных контурах
- Расчет переходных процессов
Рассмотрим сначала некоторые общие вопросы расчета переходных процессов на достаточно простом примере — включении последовательного контура (rLC-цепи) к источнику ЭДС е, которая изменяется во времени непрерывно и задана каким-либо аналитическим выражением.
Запишем второй закон Кирхгофа для произвольного момента времени
где i — ток переходного процесса, который в дальнейшем будем называть переходным током, или просто током;
Когда с переходным процессом можно уже не считаться, наступает принужденный режим. Принужденный режим, создаваемый источником произвольной периодически изменяющейся ЭДС (или тока), называют установившимся. После окончания переходного процесса источник ЭДС, изменяющейся, например, по экспоненциальному закону, создает принужденный режим. Источники постоянной и изменяющейся по гармоническому закону ЭДС (или тока) создают принужденный, или установившийся, режим.
Когда наступит установившийся режим, уравнение (14.1) примет вид
где и
— ток и напряжение установившегося режима, или просто установившиеся ток и напряжение.
Вычитая почленно уравнение (14.2) из уравнения (14.1) и обозначая
получаем
или
Разности токов и напряжений переходного процесса и принужденного режимов называются соответственно тока и напряжением свободного процесса, или просто свободными током и напряжением.
Уравнения (14.4) показывают, что при переходе цепи от одного установившегося состояния к другому напряжения на всех элементах, создаваемые свободными составляющими токов, взаимно уравновешиваются, но свободные напряжения зависят, конечно, от ЭДС е источника.
Уравнение (14.3) показывает, что процесс, происходящий в цепи, можно рассматривать состоящим из двух накладывающихся друг на друга процессов — установившегося, который как бы наступил сразу, и свободного, имеющего место только во время переходного процесса. Благодаря свободным составляющим и достигается в переходном процессе непрерывное приближение к установившемуся режиму. Следовательно, во время переходного процесса токи и напряжения могут быть разложены на слагающие в общем случае принужденного, а при постоянных и периодических ЭДС или токах источников установившегося режима и свободного процесса:
Так как принцип наложения применим лишь к линейным цепям, то это разложение допустимо для линейных цепей. Конечно, физически существуют только переходные токи и напряжения, и разложение их на установившиеся и свободные составляющие является удобным математическим приемом, облегчающим расчет переходных процессов в линейных цепях. Разложение переходных токов и напряжений соответствует правилу решения линейных неоднородных дифференциальных уравнений, согласно которому общее решение таких уравнений равно сумме частного решения неоднородного уравнения и общего решения однородного уравнения.
Действительно, свободный ток представляет собой общее решение однородного дифференциального уравнения (14.4а), и, следовательно, в его выражении должны быть постоянные интегрирования, число которых равно порядку дифференциального уравнения. Установившийся ток представляет собой частное решение неоднородного дифференциального уравнения (14.1), а именно такое, которое получается из общего решения неоднородного дифференциального уравнения при равных нулю постоянных интегрирования. Иными словами, в составе принужденного тока не должно быть слагающих свободного тока. Поэтому переходный ток и будет общим решением того же самого неоднородного дифференциального уравнения.
Начнем изучение переходных процессов с исследования процессов в простейших цепях так называемым классическим методом. Этот метод заключается в интегрировании дифференциальных уравнений, связывающих токи и напряжения цепи, в результате чего появляются постоянные, и в определении постоянных из начальных условий, вытекающих из законов коммутации.
Начальными условиями назовем значения переходных токов в индуктивных элементах и напряжений на емкостных элементах при t = О, т. е. те значения, которые в момент коммутации не изменяются скачком. Иногда эти условия называются еще независимыми начальными условиями. В отличие от них начальные значения всех остальных токов и напряжений называют зависимыми начальными условиями. Зависимые начальные условия определяются по независимым начальным условиям при помощи уравнений, составленных по первому и второму законам Кирхгофа. Отметим, что основная трудность классического метода исследования переходных процессов в сложных цепях как раз и состоит в определении зависимых начальных условий.
6.1. Переходный режим электрических цепей. Законы коммутации
6.2. Классический метод расчета переходных процессов
6.3. Переходные процессы в цепях первого порядка
6.4. Переходные процессы в цепях второго порядка
6.5. Включение RLC-контура на постоянное и гармоническое напряжение
6.6. Переходные процессы в разветвленных цепях
6.7. Метод переменных состояния
6.8. Вопросы и задания для самопроверки
6.1. Переходный режим электрических цепей. Законы коммутации
В предыдущих главах рассматривались процессы в электрических цепях и методы их расчета в установившемся режиме, т. е. в режиме, при котором напряжения и токи в цепях либо не зависят от времени, либо являются периодическими функциями времени в зависимости от вида приложенного воздействия. Установившийся режим в цепи достигается обычно через определенный промежуток времени после начала воздействия, поэтому рассмотренные ранее методы анализа не охватывают так называемый переходный режим от начала воздействия до установившегося состояния цепи. Переходной режим работы цепи обусловлен наличием в ней реактивных элементов (индуктивности, емкости), в которых накапливается энергия магнитного и электрического полей. При различного рода воздействиях (подключении к цепи или исключении источников электрической энергии, изменении параметров цепи) изменяется энергетический режим работы цепи, причем эти изменения не могут осуществляться мгновенно в силу непрерывности изменения энергии электрического и магнитного полей (принцип непрерывности), что и приводит к возникновению переходных процессов. Следует подчеркнуть, что переходные процессы во многих устройствах и системах связи являются составной «нормальной» частью режима их работы. В то же время в ряде случаев переходные процессы могут приводить к таким нежелательным явлениям, как возникновение сверхтоков и перенапряжений. Все это определяет важность рассмотрения методов анализа переходных процессов в электрических цепях.
В основе методов расчета переходных процессов лежат законы коммутации. Коммутацией принято называть любое изменение параметров цепи, ее конфигурации, подключение или отключение источников, приводящее к возникновению переходных процессов. Коммутацию будем считать мгновенной, однако переходный процесс, как было отмечено выше, будет протекать определенное время. Теоретически для завершения переходного процесса требуется бесконечно большое время, но на практике его принимают конечным, зависящим от параметров цепи. Будем считать, что коммутация осуществляется с помощью идеального ключа К (рис. 6.1), сопротивление которого в разомкнутом состоянии бесконечно велико, а в замкнутом равно нулю. Направление замыкания или размыкания ключа будем показывать стрелкой. Будем также считать, если не оговорено иное, что коммутация осуществляется в момент t = 0.
Различают первый и второй законы коммутации. Первый закон коммутации связан с непрерывностью изменения магнитного поля катушки индуктивности WL = Li2/2 и гласит: в начальный момент t = 0+ непосредственно после коммутации ток в индуктивности имеет то же значение, что и в момент t = 0– до коммутации и с этого момента плавно изменяется (здесь и далее под f(0— ) понимается левосторонний предел функции f(t) при t 0— , а под f(0+ ) — правосторонний предел f(t) при t
0+ )
(6.1)
Второй закон коммутации связан с непрерывностью изменения электрического поля емкости WC = Cu2/2: в начальный момент t = 0+ непосредственно после коммутации напряжение на емкости имеет то же значение, что и в момент t = 0– до коммутации и с этого момента плавно изменяется: (6.2)
В отличие от тока в индуктивности iL и напряжения на емкости uC напряжение на индуктивности uL и ток в емкости iC могут изменяться скачком, так как согласно (1.9) и (1.12) они являются производными от iL и uC и с ними непосредственно не связана энергия магнитного и электрического полей. Значения токов в индуктивности iL(0+) и напряжений на емкостях uC(0+) образуют начальные условия задачи. В зависимости от начального энергетического состояния цепи различают два типа задач расчета переходных процессов: задачи с нулевыми начальными условиями, когда непосредственно после коммутации (при t = 0+) iL(0+) = 0; uC(0+) = 0 (т. е. WL(0+) + WC(0+) = 0) и задачи с ненулевыми начальными условиями, когда iL(0+) 0 и (или) uC(0+)
0 (т. е. WL(0+) + WC(0+)
0). Нулевые и ненулевые значения начальных условий для iL и uC называются независимыми, а начальные условия остальных токов и напряжений зависимыми. Независимые начальные условия определяются с помощью законов коммутации (6.1) и (6.2).
6.2. Классический метод расчета переходных процессов
В основе классического метода расчета переходных процессов в электрических цепях лежит составление интегрально-дифференциальных уравнений для мгновенных значений токов и напряжений. Эти уравнения составляются на основе законов Кирхгофа, методов контурных токов, узловых напряжений и могут содержать как независимые, так и зависимые переменные. Для удобства решения обычно принято составлять дифференциальные уравнения относительно независимой переменной, в качестве которой может служить iL или uC. Решение полученных дифференциальных уравнений относительно выбранной переменной и составляет сущность классического метода.
Учитывая, что в ряде случаев решение дифференциальных уравнений проще интегрально-дифференциальных, полученную систему сводят к одному дифференциальному уравнению соответствующего порядка относительно выбранной независимой переменной iL или uC. Порядок дифференциального уравнения определяется числом независимых накопителей энергии электрического и магнитного полей.
Обозначим независимую переменную (iL или uC) через x = x(t).
Дифференциальное уравнение m-гo порядка, описывающее переходный процесс в электрической цепи, находящейся под воздействием источника w(t), описывается уравнением: (6.3) где b0, b1, …, bm–1, bm — коэффициенты параметров цепи; w(t) — функция, описывающая характер воздействия на цепь.
Цепь, параметры которой b0, b1, …, bm–1, bm – неизменны, называют цепью с постоянными параметрами. Если же какой-либо из коэффициентов b0, b1, …, bm–1, bm — переменен, то цепь называют параметрической. В дальнейшем будем рассматривать цепи с постоянными параметрами.
Дифференциальное уравнение (6.3) относится к линейным неоднородным уравнениям m-го порядка. Как известно, его решение находится как сумма общего решения xсв однородного дифференциального уравнения m-го порядка: (6.4) и частного решения xпр уравнения (6.3):
(6.4) где xсв и xпр — общее и частное решения. Общее решение xсв определяет свободные процессы, которые протекают в цепи без участия источника w(t) (отсюда индекс «св»). Частное решение xпр определяет принудительный процесс (отсюда индекс «пр»), который протекает в цепи под влиянием w(t). В теории цепей xпр обычно находят одним из ранее рассмотренных методов расчета цепей в установившемся режиме.
Свободная составляющая переходного процесса xсв будет зависеть от характера корней характеристического уравнения: (6.6)
В случае, когда корни p1, p2, …, рm характеристического уравнения (6.6) вещественные и различные, решение (6.4) имеет вид (6.7) где A1, A2, …, Am — постоянные интегрирования, которые находятся из начальных условий.
В случае, когда корни уравнения (6.6) вещественные и равные, т. е. p1 = p2 = … = рm = p, свободная составляющая определяется уравнением (6.8)
Представляет практический интерес и случай, когда корни попарно комплексно-сопряженные рk,k–1= —a ± jс. При этом в формуле (6.7) соответствующая пара корней рk,k–1заменяется слагаемыми вида
(6.9) где A,
— постоянные интегрирования, определяемые также из начальных условий.
6.3. Переходные процессы в цепях первого порядка
Рассмотрим применение классического метода к расчету переходных процессов в цепях первого порядка. Это цепи, содержащие только однотипные реактивные элементы (емкости или индуктивности), процессы, в которых описываются дифференциальными уравнениями первого порядка (6.10)
Примером цепей первого порядка являются простейшие RL и RC цепи.
Переходные процессы в RL-цепях
Рассмотрим включение RL-цепи к источнику напряжения u(t) (рис. 6.1).
Из рис. 6.1 следует, что до коммутации ключ К разомкнут, поэтому ток iL(0–) = 0 и цепь находится при нулевых начальных условиях. В момент t = 0 ключом К замыкаем (осуществим коммутацию) цепь, подключив ее к источнику напряжения u(t). После замыкания ключа К в цепи начнется переходный процесс. Для его математического описания выберем в качестве независимой переменной iL = i и составим относительно нее дифференциальное уравнение по ЗНК: (6.11)
Уравнение (6.11) относится к линейным неоднородным дифференциальным уравнениям первого порядка типа (6.3), решение которого можно записать согласно (6.5) в форме (6.12) где iсв — свободная составляющая тока, обусловленная свободными процессами, протекающими в цепи без участия источника u(t); inp — принужденная составляющая тока, обусловленная действием источника напряжения u(t).
Свободная составляющая тока iсв есть общее решение однородного дифференциального уравнения (6.13) и согласно (6.7)
(6.14) где А — постоянная интегрирования; р — корень характеристического уравнения типа (6.6);
(6.15)
Отсюда p = —R/L. Величина 1/|р| носит название постоянной времени цепи. В неразветвленной RL-цепи = L/R.
Принужденная составляющая iпp может быть определена как частное решение уравнения (6.11). Однако, как было указано выше, iпp можно найти более просто методами расчета установившегося режима цепи. Рассмотрим два частных случая:
В первом случае принужденная составляющая может быть определена из установившегося режима: iпp = U/R. Для нахождения постоянной интегрирования A перепишем (6.12) в форме i = Ае–t / + U/R и учтем начальные условия для i, а также первый закон коммутации (6.1):
Отсюда А = —U/R. Таким образом, закон изменения тока в RL-цепи определяется уравнением (6.16)
Напряжение на индуктивности согласно (1.9) (6.17)
На рис. 6.2 изображены графики зависимости i(t) и uL(t). Анализ полученных уравнений (6.16) и (6.17) показывает, что чем больше постоянная времени цепи , тем медленнее затухает переходной процесс. На практике принято считать переходной процесс законченным при t = (3…5)
, при t = 3
ток достигает 95% своего установившегося значения, а при t = 5
— более 99%. Графически постоянная времени
может определиться как интервал времени на оси t от t = 0 до точки пересечения касательной к uL (рис. 6.2), в указанный момент напряжение на uL уменьшается в е раз по сравнению с начальным.
Анализ полученных результатов показывает, что при нулевых начальных условиях в момент t = 0+ индуктивность ведет себя как бесконечно большое сопротивление (разрыв цепи), а при t = как бесконечно малое сопротивление (короткое замыкание цепи).
Для второго случая принужденная составляющая тока где
,
= arctg(
L/R). Постоянная интегрирования определяется из уравнения
Откуда . Следовательно, закон изменения тока в цепи в этом случае будет
(6.18)
На рис. 6.3 изображена временная зависимость тока (6.18). Напряжение на индуктивности 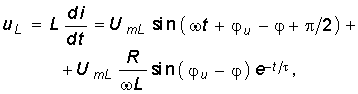
LIm.
Анализ уравнения (6.18) показывает, что в случае подключения цепи к источнику u(t) в момент, когда u =
±
/2 в последней могут возникать сверхтоки. Если постоянная времени цепи
достаточно велика, то скачок тока в начальный период может достигать imax
2Im. Напротив, при включении цепи в момент, когда
u =
, в ней сразу наступает установившийся режим. Аналогичная картина наблюдается и с напряжением на индуктивности (6.19).
В качестве второго примера расчета рассмотрим случай ненулевых начальных условий в RL-цепи (рис. 6.4). К моменту коммутации в данной цепи была запасена энергия магнитного поля, равная WL = Li2(0– )/2, где i(0– ) = U/(R0 + R). После коммутации в RL-цепи возникает переходный процесс, описываемый уравнением: (6.20) т. е. iпp = 0. Решая уравнение (6.20), находим с учетом (6.13) – (6.15):
Постоянную А находим из начального условия i(0– ) и закона коммутации (6.1):
Окончательно закон изменения тока в переходном режиме описывается уравнением 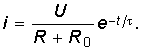
Напряжение uL определяется как 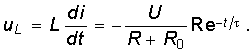
На рис. 6.5 изображены графики i и uL. Следует отметить, что вся энергия WL, запасенная в индуктивности с течением времени, расходуется на тепловые потери в R. При ненулевых начальных условиях L ведет себя как источник тока.
Переходные процессы в RС-цепях
При расчете переходных процессов в RС-цепях в качестве независимой переменной выбирают uC. Затем также составляют дифференциальное уравнение для заданной RС-цепи, решение которого с учетом начальных условий для uC(0) и определяет закон изменения напряжения на емкости.
Рассмотрим вначале RC-цепь при нулевых начальных условиях (рис. 6.6), которая подключается в момент t = 0 к источнику постоянного и(t) = U или синусоидального и(t) = Umsin(t +
u ) напряжения. Переходный процесс в данной цепи описывается дифференциальным уравнением
(6.23) решение которого ищем также в форме суммы общего и частного решений, определяющих свободную и принужденную составляющие:
(6.24)
Свободная составляющая является решением однородного дифференциального уравнения 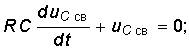
(6.26) где р определяется из характеристического уравнения
Величина RC носит название постоянной времени RC-цепи и обозначается через .
Определим принужденную составляющую uC пp для случая, когда u(t) = U = const. Из рис. 6.6 следует, что в установившемся режиме uC пp = U. Следовательно, с учетом (6.24) и (6.26) уравнение для иC примет вид иC = Ae–t / + U. Для нахождения постоянной интегрирования А учтем нулевые начальные условия для uC(0–) и второй закон коммутации (6.2): uC(0–) = uC(0+) = 0 = A + U, откуда А = —U. Таким образом, получаем окончательно:
(6.27)
Ток в цепи определяется согласно (1.12): (6.28)
На рис. 6.7 изображены графические зависимости uС(t) и i(t).
Анализ полученных результатов показывает, что в момент t = 0+ емкость С (при нулевых начальных условиях) ведет себя как короткозамкнутый участок. Напротив, при t = емкость представляет собой бесконечно большое сопротивление (разрыв цепи для постоянного тока).
Рассмотрим случай гармонического воздействия. Нетрудно видеть что при этом (6.29) где
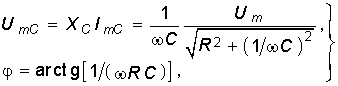
Постоянная А находится из начальных условий для uC(0+) при t = 0+:
Окончательно закон изменения напряжения 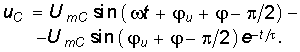
На рис. 6.8 изображен график зависимости uC(t). Анализ уравнения (6.31) показывает, что в случае неудачного включения при u =
–
и большой
в цепи могут возникать перенапряжения, достигающие на емкости величины uCmax
2UmC. В случае удачного включения, когда
u =
/2 –
, в цепи сразу наступает установившийся режим.
Ток в цепи 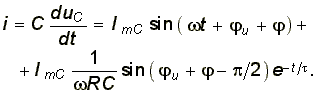
Рассмотрим теперь случай ненулевых начальных условий, когда емкость С, заряженная до напряжения U, разряжается на сопротивление R (рис. 6.9). К моменту коммутации в емкости была запасена энергия WC = CU2/2. После коммутации возникает переходный процесс, определяемый уравнением (6.33) т. е. имеет место свободный режим разряда (емкости):
(6.34)
Постоянную интегрирования А находим из начального условия для uC(0+) = U и закона коммутации (6.2):
Таким образом, получаем закон изменения напряжения на емкости (6.35) и тока в цепи
(6.36)
Знак «–» в уравнении (6.36) для тока свидетельствует о том, что ток разряда направлен противоположно опорному направлению напряжения иС в емкости. На рис. 6.10 приведены графики изменения напряжения иС(t) и тока i(t) данной RС-цепи. Следует подчеркнуть, что вся запасенная энергия WC емкости с течением времени преобразуется в элементе R в тепло. При ненулевых начальных условиях С ведет себя как источник напряжения.
6.4. Переходные процессы в цепях второго порядка
Ранее рассматривались переходные процессы в RL- и RС-цепях, которые относятся к цепям первого порядка, так как описываются дифференциальными уравнениями первого порядка (6.11), (6.23). При наличии в цепи двух независимых накопителей энергии переходные процессы в них описываются уравнением второго порядка. Простейшим примером такой цепи является последовательный колебательный контур (рис. 6.11).
Для этого контура можно по аналогии с RL- и RС-цепью составить дифференциальное уравнение второго порядка, выбрав в качестве независимой переменной напряжение на емкости
Учитывая, что i = CduC/dt окончательно получаем (6.37)
Решение дифференциального уравнения (6.37) ищется согласно (6.5) в форме суммы свободной uCсв и принужденной uCпр составляющих: (6.38)
Вид uCпр зависит от характера приложенного напряжения, а uCсв определится решением однородного дифференциального уравнения второго порядка: 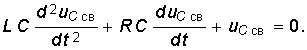
Решение уравнения (6.39) зависит от вида корней характеристического уравнения (6.40)
Корни уравнения (6.40) определяются только параметрами цепи независимо от выбранной переменной: 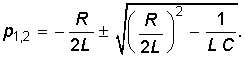
Величина a = R/2L носит название коэффициента затухания контура, а есть резонансная частота контура (см. § 4.2). Таким образом, уравнение (6.41) можно переписать в виде
(6.42)
Характер переходного процесса существенным образом зависит от вида корней р1, р2, которые могут быть: 1) вещественными и различными (при R > 2); 2) комплексно-сопряженными (при R < 2
); 3) вещественными и равными (при R = 2
).
Здесь =
— характеристическое сопротивление контура (см. формулу (4.22)).
Разряд емкости на RL-цепь
Для исследования характера переходного процесса во всех этих случаях рассмотрим разряд емкости С на цепь RL (см. рис. 6.11). Так как до коммутации емкость С была заряжена до напряжения U, то имеем ненулевые начальные условия:
После коммутации (переключение ключа К из положения 1 в положение 2 емкость начнет разряжаться и в цепи возникнет свободный переходный процесс. Найдем закон изменения тока и напряжений на отдельных элементах цепи для случая 1)—3).
В первом случае, когда R > 2, корни p1 и р2 в (6.41) будут вещественными и различными, и решение уравнения определится согласно (6.7):
(6.43) где A1 и A2 — постоянные интегрирования. Для определения A1 и A2 запишем еще уравнение для тока в цепи:
(6.44)
Постоянные A1 и A2 можно найти из начальных условий для uC(0–) = U и i(0–) = 0 (при t = 0–) и законов коммутации (6.1), (6.2): (6.45)
Из решения системы уравнение (6.45)
В результате получаем уравнения для напряжения UC и тока i: 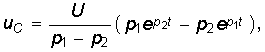
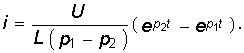
Закон изменения напряжения на индуктивности определяется при этом уравнением 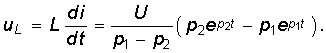
Из уравнений (6.46)—(6.48) следует, что каждая из найденных величин uC, i, uL состоит из двух слагаемых, затухающих по экспоненте с коэффициентами p1 < 0 и p2 < 0. На рис. 6.12 показан характер зависимостей (6.46)—(6.48). Момент времени t1, соответствующий точке перегиба uC, максимуму | i | и нулевому значению uL определяется из решения уравнения di / dt = 0, а момент t2 из решения уравнения duL / dt = 0: 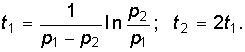
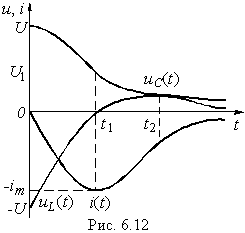
Анализ полученных кривых показывает, что в рассматриваемом случае происходит апериодический разряд емкости С, причем в интервале от 0 до t1 энергия WC расходуется на покрытие тепловых потерь в резистивном сопротивлении R и создание магнитного поля в индуктивности ( pC = uC i < 0; pL = uL i > 0). В дальнейшем (при t > t1) как энергия электрического поля емкости WC, так и запасенная к моменту t = t1 магнитная энергия индуктивности WL расходуется на покрытие тепловых потерь в сопротивлении R. Отрицательное значение тока свидетельствует о противоположном направлении тока разряда относительно опорного направления.
Во втором случае при R < 2, когда корни p1 и p2 носят комплексно-сопряженный характер,
(6.50) где
называют частотой собственных затухающих колебаний. Решение уравнения (6.39) имеет вид (6.9)
(6.51) где A и
— постоянные интегрирования. Закон изменения тока в цепи
(6.52)
Постоянные A и определяются из начальных условий для uC и i и законов коммутации (6.1), (6.2):
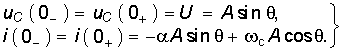
Отсюда
Окончательно уравнения для uC, i и и принимают вид 
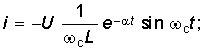
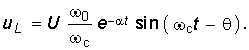
Полученные уравнения показывают, что в данном случае имеет место колебательный разряд емкости с частотой с, зависящей только от параметров R, L, С цепи. Интервал времени Тc = 2
/
с носит название квазипериода. На рис. 6.13 изображены графики зависимостей uC(t) и i(t) определяемых уравнениями (6.54) и (6.55). Скорость затухания периодического процесса принято характеризовать декрементом затухания, который определяют как отношение двух соседних амплитуд тока или напряжения одного знака (см. рис. 6.13):
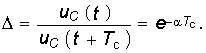
На практике чаще используется логарифмический декремент затухания 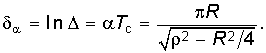
Из уравнений (6.57) и (6.58) следует, что затухание тем больше, чем больше R. При R = 2 колебания прекращаются и переходной процесс становится апериодическим. При R = 0 оказываются незатухающие гармонические колебания с частотой
с =
0 =
. Очевидно, что этот случай представляет чисто теоретический интерес, так как в любом реальном контуре имеются потери. В процессе колебательного разряда емкости (свободных колебаний в RLC-контуре) имеет место попеременное запасание энергии WC в электрическом поле емкости и магнитном поле индуктивности WL: в начале энергия WC расходуется на создание магнитного поля WL индуктивности и покрытие тепловых потерь сопротивления R, затем запасенная энергия WL, расходуется на перезаряд емкости и покрытие потерь в R и т. д. до полного перехода первоначальной энергии Wc(0) в тепловые потери в резисторе R.
Третий случай R = 2 является пограничным между колебательным и апериодическим и соответствует критическому разряду емкости. Решение уравнения (6.39) при этом имеет вид (6.8)
(6.59)
Ток определяется уравнением (6.60) где p1 = p2 = p = -a — корни характеристического уравнения (6.40); А1, А2 — постоянные интегрирования, определяемые из начальных условий для uC и i и законов коммутации (6.1), (6.2):
Отсюда А2 = aU. Окончательные выражения для напряжения и тока принимают вид (6.61)
(6.62)
(6.63)
По своей форме графики зависимостей (6.61)—(6.63) аналогичны кривым, изображенным на рис. 6.12 с той лишь разницей, что их скорость изменения больше, чем при R > 2. Значение R = 2
носит название критического сопротивления контура.
6.5. Включение RLC-контура на постоянное и гармоническое напряжение
Включение RLC-контура на постоянное напряжение
Рассмотрим случай нулевых начальных условий uC(0–) = 0, i(0–) = 0, когда RLC-контур включается на постоянное напряжение (рис. 6.14).
Отличие данного случая от рассмотренного выше заключается в нулевых начальных условиях и наличии принужденной составляю щей uCпр = U. Свободная составляющая uCсв определяется, как и ранее, уравнениями (6.43), (6.51) или (6.59) в зависимости от вида корней р1 и р2. Постоянные интегрирования А1 и А2 находятся при этом из начальных условий i(0–) = 0, uC(0–) = 0 и законов коммутации для i и uC. Определим, например, закон изменения uC, i и uL в случае, когда корни р1 и р2 — вещественные и различные. При этом uC св определяются уравнением (6.43), а напряжение uC и ток i имеют следующий вид: 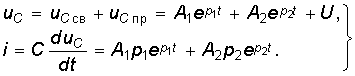
Для нахождения коэффициентов А1 и А2 используем начальные условия uC(0– ) = 0 и i(0– ) = 0, а также законы коммутации, определяемые выражениями (6.1),(6.2): (6.65)
Тогда (6.66)
Окончательные уравнения для иС, i, иL имеют вид 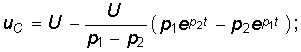
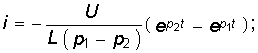
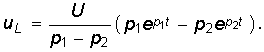
На рис. 6.15 изображены графики зависимостей (6.67)—(6.69), где моменты времени t1 и t2 определяются уравнениями (6.49). Сравнение формул (6.67)—(6.69) с (6.46)—(6.48) показывает, что ток i и напряжение иL отличаются только знаком, а напряжение иС — наличием постоянной составляющей U.
Аналогичным можно найти уравнения напряжений и тока для случая R < 2:
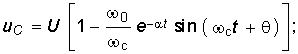
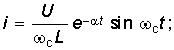
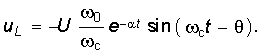
На рис. 6.15 штриховой линией показана зависимость (6.70), которая свидетельствует о колебательном характере заряда емкости. Таким же образом можно получить уравнения для uC, i и uL для случая критического заряда емкости С при R = 2.
Включение RLC-контура на гармоническое напряжение
При включении RLC-контура на гармоническое напряжение u = Umsin(t +
u ) принужденная составляющая напряжения на емкости
(6.73) где
C =
u +
—
/2. Здесь фазовый сдвиг между током в контуре и приложенным напряжением
(6.74) а амплитуда принужденного напряжения на емкости
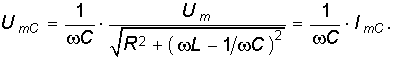
Учитывая, что колебательный контур в радиотехнических устройствах, как правило имеет высокую добротность, т. е. выполняется условие R 2
, то свободная составляющая uCсв определяется уравнением (6.51), и закон изменения напряжения на емкости будет иметь вид
(6.76)
Взяв производную от выражения (6.76), и учтя, что для заданного контура , получим уравнение тока
(6.77)
Постоянные интегрирования A и находим из начальных условий и законов коммутации:

Откуда 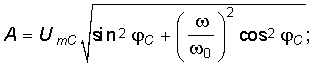
(6.80)
Подставив значения А и из уравнений (6.79), (6.80) в (6.76) и (6.77), получим окончательный закон изменения напряжения на емкости и тока в RLC-контуре:
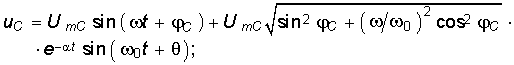
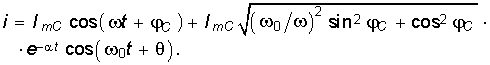
Анализ уравнений (6.81), (6.82) показывает, что в случае, когда частота приложенного напряжения существенно превышает резонансную частоту контура
0 при
C
0 в цепи могут возникнуть сверхнапряжения, а в случае
и
C
/2 — сверхтоки.
Если частота задающего напряжения =
0, то при этом в цепи возникают явления изохронизма, когда напряжение на емкости и ток в контуре плавно изменяется в соответствии с уравнениями:
(6.83)
(6.84)
При этом переходный процесс протекает без перенапряжений и сверхтоков (рис. 6.16, а).
В случае, когда частота заданного напряжения и резонансная частота контура
0 близки между собой, то в контуре возникают явления биений. Положим, что a = 0, тогда
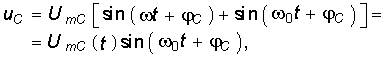
t — амплитуда биений с угловой частотой
= (
—
0 )/2. На рис. 6.16, б, показан график изменения напряжений биений (6.85).
При расчете переходных процессов в разветвленных цепях классическим методом составляется система уравнений для мгновенных значений токов и напряжений по ЗТК и ЗНК. Затем полученная система сводится к дифференциальному уравнению соответствующего порядка относительно выбранной независимой переменной (иС или iL). После этого полученное уравнение решается по аналогии с уравнениями, рассмотренными в 6.2. Классический метод расчета переходных процессов, 6.3. Переходные процессы в цепях первого порядка, 6.4. Переходные процессы в цепях второго порядка, 6.5. Включение RLC-контура на постоянное и гармоническое напряжение.
В качестве примера рассмотрим разветвленную цепь второго порядка, изображенную на рис. 6.17. Для данной цепи имеем ненулевые начальные условия: uC(0– ) = U; iL(0– ) = 0. Составим для нее систему уравнений по законам Кирхгофа: 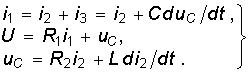
Выберем в качестве независимой переменной i2 = iL и, решая (6.86) относительно i2, получаем: 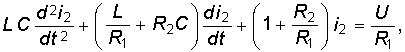
(6.88) где i2np = U/(R1 + R2), а i2св определим из решения однородного дифференциального уравнения
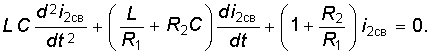
Решение последнего имеет вид, аналогичный (6.43), (6.51) или (6.59) в зависимости от вида корней характеристического уравнения 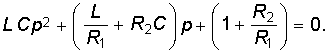
Постоянные интегрирования определяются из начальных условий и законов коммутации, причем для нахождения иС используется система уравнений (6.86). Например, для случая вещественных и различных корней при R1 = R2 = R получим 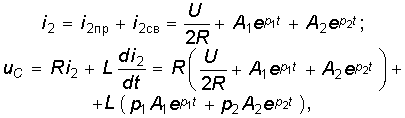
откуда
На рис. 6.18 изображены графики uC(t) и i2(t).
Как следует из вышеуказанного, для определения характера переходного процесса и записи уравнения свободной составляющей независимой переменной необходимо располагать характеристическим уравнением цепи. Это уравнение может быть получено из соответствующего дифференциального уравнения цепи или из анализа ее операторного сопротивления. Последнее может быть получено, если в уравнении для комплексного сопротивления цепи Z = Z(j) заменить оператор j
на р и приравнять его к нулю:
(6.91)
Например для цепи, изображенной на рис. 6.17, имеем:
Отсюда 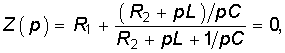
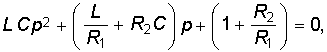
Таким образом, отпадает необходимость преобразовывать систему уравнений к одному уравнению для выбранной независимой переменной.
В заключение следует отметить, что применение классического метода расчета к цепям более высокого порядка встречает определенные трудности. Главное из них резко возрастающий объем необходимых вычислений, связанных с решением задач уравнений высокого порядка. В этой связи в последнее время все большее применение находят другие методы расчета переходных процессов: метод переменных состояний, операторный и частотные методы, которые будут рассмотрены ниже.
6.7. Метод переменных состояния
В настоящее время для анализа переходных процессов в цепях широкое применение находит метод переменных состояния, позволяющий при расчетах эффективно использовать ЭВМ. Суть метода заключается в том, что переходный процесс в цепи рассматривается как траектория в m-мерном пространстве (где т — порядок цепи) с начальной точкой при t = 0 (начальное состояние) и конечной при t = . Например, переходный процесс в последовательном RLC-контуре (см. 6.4. Переходные процессы в цепях второго порядка, апериодический разряд и рис. 6.12) можно в пространстве состояний представить кривой, изображенной на рис. 6.19, где iL(0) = 0 и uC(0) = U характеризуют начальное состояние цепи, а iL(t) и uC(t) определяют состояние цепи в любой заданный момент времени. Достоинства этого метода — наглядность, простота, удобство программирования на ЭВМ, возможность анализа как линейных, так и нелинейных цепей, а также цепей с переменными параметрами.
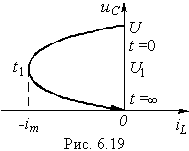
Поясним сущность данного метода на примере цепи, находящейся при ненулевых начальных условиях: iL(0) = i0, uC(0) = u0 (рис. 6.20). Для этой цепи при t 0 можно записать:
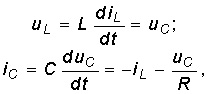
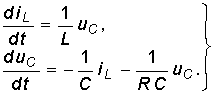
Уравнения (6.92) называются уравнениями состояния цепи, а iL и uC — переменными состояния. Начальные условия iL(0) = i0 и uC(0) = u0 определяют с помощью (6.92) состояния цепи в любой момент t 0. Величины iL и uC можно считать компонентами вектора состояния х:
Тогда (6.92) можно переписать в матричной форме: (6.93) где
В случае, если цепь находится после коммутации под воздействием источников, уравнение состояния принимает вид (6.94) где w(t) — вектор воздействий источников; В — матрица параметров цепи.
Например, для случая включения RLC-контура на постоянное напряжение уравнение состояния имеет вид (6.94), где
Зная состояние цепи х(t), реакцию цепи y(t) (токи и напряжения в любой ветви) можно найти как линейную комбинацию векторов состояния х(t) и входных воздействий w(t): (6.95) где у(t) — вектор искомых реакций цепи; С, D — матрицы, зависящие только от параметров цепи. Уравнение (6.95) называют уравнением реакции цепи.
Так, если в качестве компонентов вектора у(t) в предыдущем примере RLC-контура взять uR и uL, то искомые реакции цепи (uR и uL) определяются согласно системе уравнений: которую можно переписать в форме (6.95), где
Следует подчеркнуть, что уравнения (6.93)—(6.95) справедливы для линейных цепей с постоянными параметрами (матрицы А, В, С, D не зависят от t). Для цепей с переменными параметрами (параметрические цепи) матрицы А(t), B(t), C(t), D(t) являются функциями времени.
Уравнения (6.94), (6.95) — основные в методе переменных состояний. Для решения уравнений состояния могут использоваться как аналитические, так и численные методы. Аналитически уравнение (6.94) может быть решено в области как действительного переменного t, так и комплексного переменного р. Рассмотрим некоторые основные методы решения уравнения состояния.
Метод матричных экспонент
Решение этим методом ищут в форме 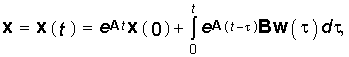
Для вычисления е At обычно используют разложение (6.97)
Пример. Найдем матрицу перехода для схемы, изображенной на рис. 6.21.
Матрицы А и В для данной схемы имеют следующий вид:
Примем L = 0,55 Гн, С = 0,5 Ф, R1 = 1 Ом, R2 = 3,5 Ом, е(t) = 1 В, iL = 0, uC = 1 В. Тогда
Согласно (6.97) матрица перехода примет вид
Таким образом, матрица перехода представляет собой квадратную матрицу порядка п с элементами в форме рядов от t. Подставив значение е At в уравнение (6.96), можно определить после интегрирования искомое решение x(t).
Следует, однако, отметить, что ряд (6.97) сходится медленно и использование уравнения (6.96) требует большого объема вычислений, поэтому вместо (6.96) обычно используют итерационную процедуру для дискретных моментов времени tn = nt = nh, где h =
t достаточно малый шаг:
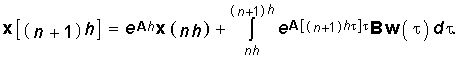
Интеграл в (6.98) вычисляется численными методами (методом прямоугольников, трапеций, Симпсона и др.). Так, при использовании метода прямоугольников алгоритм (6.98) приобретает вид (6.99)
При нулевом входном сигнале w = 0 (свободные колебания) (6.100)
Если ограничиться в разложении (6.97) только первыми двумя членами e Ah I + Ah, то получим
(6.101)
Алгоритм (6.101) легко программируется на ЭВМ и имеет ясный физический смысл. Он определяет положение точки в пространстве состояний на (n + 1)-м шаге, исходя из ее состояния на n-м шаге при аппроксимации траектории на участке h прямолинейным отрезком с постоянной скоростью (h).
Пример. Рассчитать траекторию состояний, изображенную на рис. 6.19, используя аппроксимацию ее на каждом из m участков величины h в форме прямолинейных отрезков. Скорость изменения состояния (h) на каждом из выделенных участков остается постоянной.
На основании уравнения состояния (6.93) имеем: для момента t = 0; (0) = Ах(0); для момента t = h
для момента t = 2h
для момента t = (n + 1)h
т. е. полученное уравнение полностью совпадает с (6.101).
Метод Рунге—Кутта — метод численного решения уравнения состояния (6.94), при котором интервал 0…t разбивается на » т » малых участков t = h, на каждом из которых значение переменной х определяется с помощью линейной комбинации некоторых вспомогательных функций ki (h) с постоянными коэффициентами. В зависимости от способа выбора коэффициентов и требуемой точности решения существуют различные модификации алгоритмов Рунге — Кутта.
Проиллюстрируем суть метода Рунге—Кутта на примере скалярного уравнения состояния (6.102)
Наиболее распространенный алгоритм Рунге—Кутта имеет вид 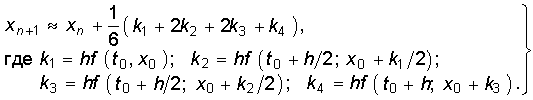
При этом порядок погрешности составляет h 5.
Пример. Решить скалярное уравнение состояния (6.102) на интервале [0; t ] методом Рунге—Кутта при условии A = 1; х(0) = 1.
Разобьем интервал [0; t ] на 10 участков с шагом h = 0,1. Тогда в соответствии с алгоритмами (6.103) можем получить для t = 0, х(0) = 1 (первый шаг):
Аналогично на втором шаге
Как следует из (6.103), для определения х необходимо вычислить f (t, x) в четырех точках.
Аналогично записывается алгоритм Рунге—Кутта для системы уравнений типа (6.102). Например, для случая системы из двух уравнений 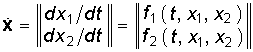
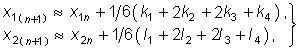
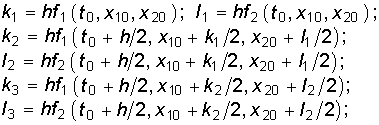
Частным случаем метода Рунге—Кутта является прямой алгоритм Эйлера (при k2 = k3 = k4 = 0). Однако он имеет малую точность и не нашел широкого применения.
Разностные методы
Существенным недостатком метода Рунге—Кутта является то, что для получения каждого значения решения х необходимо вычислять правую часть уравнения (6.94) в нескольких точках (для алгоритма (6.103) — в четырех точках). Это приводит к большому объему вычислений, особенно для сложной правой части. Применение разностных методов позволяет существенно сократить объем вычислений и затраты машинного времени, так как на каждом шаге правая часть вычисляется только один раз.
В основе разностных методов лежит использование различных интерполяционных алгебраических многочленов (многочлены Ньютона, Стирлинга, Эрмита и др.). При этом решение x на (n + 1) шаге определяется алгоритмом 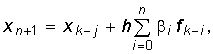
i — постоянные коэффициенты; fk — значение алгебраического многочлена в точке k. Как следует из (6.105) для определения решения хk+j; необходимо знать значения х1, х2, …, хj — они находятся обычно либо аналитически, либо методом Рунге—Кутта.
6.8. Вопросы и задания для самопроверки
- Каковы причины возникновения переходных процессов?
- Сформулировать законы коммутации.
- Дать понятия переходного, установившегося и свободного режимов в электрических цепях.
- Что такое нулевые и ненулевые начальные условия?
- Какой вид имеет свободная составляющая переходных колебаний в цепях первого порядка?
- Что представляет собой принужденная составляющая?
- Как рассчитываются постоянные интегрирования в цепях первого порядка?
- Что такое постоянная времени цепи?
- Для схемы, изображенной на рис. 6.22, определить ток i(t) и напряжение на катушке индуктивности uL(t), если U = 90 В; L = 0,25 Гн; R1 = 20 Ом; R2 = R3 = 5 Ом.
Ответ: i(t) = 3,6 – 1,6е–100t, А; uL(t) = 40е–j100t, В.
- Для схемы, изображенной на рис. 6.23, найти uС(t), если U = 60 В; R1 = R2 = R3 = 5 кОм; С = 2,5 мкФ.
Ответ: uС(t) = 60 – 30е–40t, В.
- Как зависит характер свободных колебаний в RLC-контуре от расположения на комплексной плоскости корней характеристического уравнения?
- Как определяются частота и период свободных колебаний?
- Что такое логарифмический декремент затухания?
- Какова последовательность анализа переходных процессов в разветвленных цепях второго порядка?
- Для схемы, приведенной на рис. 6.24, найти iL(t) и uС(t), если U = 100 В; L = 50 мГн; С = 5 мкФ; R = 25 Ом.
Ответ: iL(t) = 0,29е–540t – 0,29е–7460t, А; uС(t) = 100 + 8е–540t – 108е–7460t, В.
- Для схемы, приведенной на рис. 6.25, найти i(t) и uС(t), если U = 60 В; R1 = 250 Ом; R2 = 50 Ом; L = 50 мГн; C = 0,5 мкФ.
Ответ: i(t) = 0,22е–2500tsin(5800t + 67°), А; uС(t) = 60 + 69е–2500tsin(5800t – 46,5°), В.
- В чем заключается суть метода переменных состояния? Что понимают под переменными состояния?
- Что такое уравнения состояния цепи? Какова его матричная форма записи?
- В чем сущность метода матричных экспонент?
- Суть метода Рунге-Кутта.
- Что лежит в основе методов решения уравнения состояния цепи?
Сразу хочу сказать, что здесь никакой воды про переходные процессы, и только нужная информация. Для того чтобы лучше понимать что такое
переходные процессы, расчет переходного процесса классическим методом, переходные процессы с последовательно соединенными резисторами и катушками, разряд конденсатора на резистор, заряд конденсатора, определение собственных частот цепи, контур из конденсатора резистора и катушки на постоянное напряжение , настоятельно рекомендую прочитать все из категории Электротехника, Схемотехника, Аналоговые устройства.
Под переходным (динамическим, нестационарным) процессом или режимом в электрических цепях понимается процесс перехода цепи из одного установившегося состояния (режима) в другое. При установившихся, или стационарных, режимах в цепях постоянного тока напряжения и токи неизменны во времени, а в цепях переменного тока они представляют собой периодические функции времени. Установившиеся режимы при заданных и неизменных параметрах цепи полностью определяются только источником энергии. Следовательно, источники постоянного напряжения (или тока) создают в цепи постоянный ток, а источники переменного напряжения (или тока) – переменный ток той же частоты, что и частота источника энергии.
переходные процессы — процессы, возникающие в электрических цепях при различных воздействиях, приводящих к изменению их режима работы, то есть при действии различного рода коммутационной аппаратуры, например, ключей, переключателей для включения или отключения источника или приемника энергии, при обрывах в цепи, при коротких замыканиях отдельных участков цепи и т. д.
Физическая причина возникновения переходных процессов в цепях — наличие в них катушек индуктивности и конденсаторов, то есть индуктивных и емкостных элементов в соответствующих схемах замещения. Объясняется это тем, что энергия магнитного иэлектрического полей этих элементов не может изменяться скачком при коммутации (процесс замыкания или размыкания выключателей) в цепи.
Переходный процесс в цепи описывается дифференциальным уравнением
- неоднородным (однородным), если схема замещения цепи содержит (не содержит) источники ЭДС и тока,
- линейным (нелинейным) для линейной (нелинейной) цепи.
Переходные процессы возникают при любых изменениях режима электрической цепи: при подключении и отключении цепи, при изменении нагрузки, при возникновении аварийных режимов (короткое замыкание, обрыв провода и т.д.). Изменения в электрической цепи можно представить в виде тех или иных переключений, называемых в общем случае коммутацией. Физически переходные процессы представляют собой процессы перехода от энергетического состояния, соответствующего до коммутационному режиму, к энергетическому состоянию, соответствующему после коммутационному режиму.
Переходные процессы обычно быстро протекающие: длительность их составляет десятые, сотые, а иногда и миллиардные доли секунды. Сравнительно редко длительность переходных процессов достигает секунд и десятков секунд. Тем не менее изучение переходных процессов весьма важно, так как позволяет установить, как деформируется по форме и амплитуде сигнал, выявить превышения напряжения на отдельных участках цепи, которые могут оказаться опасными для изоляции установки, увеличения амплитуд токов, которые могут в десятки раз превышать амплитуду тока установившегося периодического процесса, а также определять продолжительность переходного процесса. С другой стороны, работа многих электротехнических устройств, особенно устройств промышленной электроники, основана на переходных процессах. Например, в электрических нагревательных печах качество выпускаемого материала зависит от характера протекания переходного процесса. Чрезмерно быстрое нагревание может стать причиной брака, а чрезмерно медленное отрицательно оказывается на качестве материала и приводит к снижению производительности.
сновные методы анализа переходных процессов в линейных цепях:
- Классический метод, заключающийся в непосредственном интегрировании дифференциальных уравнений, описывающих электромагнитное состояние цепи.
- Операторный метод, заключающийся в решении системы алгебраических уравнений относительно изображений искомых переменных с последующим переходом от найденных изображений к оригиналам.
- Частотный метод, основанный на преобразовании Фурье и находящий широкое применение при решении задач синтеза.
- Метод расчета с помощью интеграла Дюамеля, используемый при сложной форме кривой возмущающего воздействия.
- Метод переменных состояния, представляющий собой упорядоченный способ определения электромагнитного состояния цепи на основе решения системы дифференциальных уравнений первого прядка, записанных в нормальной форме (форме Коши).
5.1 Причины возникновения переходных процессов.
Законы коммутации
В общем случае в электрической цепи переходные процессы могут возникать, если в цепи имеются индуктивные и емкостные элементы, обладающие способностью накапливать или отдавать энергию магнитного или электрического поля. В момент коммутации, когда начинается переходный процесс, происходит перераспределение энергии между индуктивными, емкостными элементами цепи и внешними источниками энергии, подключенными к цепи. При этом часть энергия безвозвратно преобразуется в другие виды энергий (например, в тепловую на активном сопротивлении).
После окончания переходного процесса устанавливается новый установившийся режим, который определяется только внешними источниками энергии. При отключении внешних источников энергии переходный процесс может возникать за счет энергии электромагнитного поля, накопленной до начала переходного режима в индуктивных и емкостных элементах цепи.
Изменения энергии магнитного и электрического полей не могут происходить мгновенно, и, следовательно, не могут мгновенно протекать процессы в момент коммутации. В самом деле, скачкообразное (мгновенное) изменение энергии в индуктивном и емкостном элементе приводит к необходимости иметь бесконечно большие мощности p = dW/dt, что практически невозможно, ибо в реальных электрических цепях бесконечно большой мощности не существует.
Таким образом, переходные процессы не могут протекать мгновенно, так как невозможно в принципе мгновенно изменять энергию, накопленную в электромагнитном поле цепи. Теоретически переходные процессы заканчиваются за время t→∞. Практически же переходные процессы являются быстропротекающими, и их длительность обычно составляет доли секунды. Так как энергия магнитного WМ и электрического полей WЭ описывается выражениями
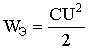
то ток в индуктивности и напряжение на емкости не могут изменяться мгновенно. На этом основаны законы коммутации.
Первый закон коммутации состоит в том, что ток в ветви с индуктивным элементом в начальный момент времени после коммутации имеет то же значение, какое он имел непосредственно перед коммутацией, а затем с этого значения он начинает плавно изменяться. Сказанное обычно записывают в виде iL(0-) = iL(0+), считая, что коммутация происходит мгновенно в момент t = 0.
Второй закон коммутации состоит в том, что напряжение на емкостном элементе в начальный момент после коммутации имеет то же значение, какое оно имело непосредственно перед коммутацией, а затем с этого значения оно начинает плавно изменяться: UC(0-) = UC(0+).
Следовательно, наличие ветви, содержащей индуктивность, в цепи, включаемой под напряжение, равносильно разрыву цепи в этом месте в момент коммутации, так как iL(0-) = iL(0+). Наличие в цепи, включаемой под напряжение, ветви, содержащей разряженный конденсатор, равносильно короткому замыканию в этом месте в момент коммутации, так как UC(0-) = UC(0+).
Однако в электрической цепи возможны скачки напряжений на индуктивностях и токов на емкостях.
В электрических цепях с резистивными элементами энергия электромагнитного поля не запасается, вследствие чего в них переходные процессы не возникают, т.е. в таких цепях стационарные режимы устанавливаются мгновенно, скачком.
В действительности любой элемент цепи обладает каким-то сопротивлением r, индуктивностью L и емкостью С, т.е. в реальных электротехнических устройствах существуют тепловые потери, обусловленные прохождением тока и наличием сопротивления r, а также магнитные и электрические поля.
Переходные процессы в реальных электротехнических устройствах можно ускорять или замедлять путем подбора соответствующих параметров элементов цепей, а также за счет применения специальных устройств.
5.2. Математические основы анализа переходных процессов
Задача исследования переходных процессов заключается в том, чтобы выяснить, по какому закону и как долго будет наблюдаться заметное отклонение токов в ветвях и напряжений на участках цепи от их установившихся значений. Так, например, если в исследуемой ветви некоторой цепи до коммутации существовал постоянный ток I1, а в установившемся режиме после коммутации он стал I2, то нас будет интересовать закон изменения переходного тока i между моментом коммутации (t=0) и тем неизвестным нам моментом времени t1, когда переходный процесс можно считать закончившимся.
При анализе переходных процессов в электрических цепях считается, что:
- рубильники включаются и размыкаются мгновенно, без возникновения электрической дуги;
- время переходного процесса, теоретически бесконечно длительное, (переходный режим асимптотически приближается к новому установившемуся режиму), ограничивают условным пределом – длительностью переходного процесса;
- установившийся режим после коммутации рассчитывают при теоретическом условии t→∞, т.е. когда после коммутации прошло бесконечно большое время.
Установившийся режим до коммутации рассчитывают обычно в предположении, что к моменту коммутации в цепи закончился предыдущий переходный процесс. Хотя иногда приходится анализировать переходные процессы, возникающие в цепи, когда предыдущий переходный процесс, вызванный прежними коммутациями, еще не закончился. Но это не изменяет теоретическую постановку задачи.
Анализ переходных процессов производят путем решения дифференциальных уравнений, составленных для исследуемой электрической цепи на основе законов Кирхгофа или метода контурных токов.
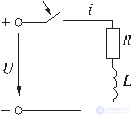
Рис. 5.1
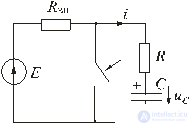
Пусть в некоторой цепи (рис. 5.1 а) внезапно изменяется сопротивление. До коммутации в цепи существовали сопротивления R0 и R, после коммутации остается только R. Требуется определить переходный ток i. Электрическое состояние схемы после коммутации описывается интегродифференциальным уравнением, записанным на основании II закона Кирхгофа для мгновенных значений токов и напряжений:
(5.1)
Если это уравнение продифференцировать по времени получим линейное дифференциальное уравнение второго порядка, у которого в качестве постоянных коэффициентов выступают параметры цепи или их комбинации:
(5.2)
Из математики известно, что полное решение линейного дифференциального уравнения с постоянными коэффициентами находят в виде суммы частного решения неоднородного и общего решения соответствующего однородного уравнения.
Поскольку в правой части дифференциальных уравнений, описывающих электрическое состояние цепей, обычно находится напряжение (или ток) источника (внешняя вынуждающая сила), то частное решение находят из анализа установившегося режима после коммутации. Отсюда этот режим называют принужденным и соответственно токи или напряжения, найденные в данном режиме, называют принужденными. Расчет принужденного режима, когда внешние источники вырабатывают постоянную или синусоидальную э.д.с. (ток), не представляет трудностей и может быть осуществлен любым известным методом.
Однородное дифференциальное уравнение получают из выражения (5.2) путем «освобождения» его от правой части. Физически это означает, что исследуемая цепь «освобождается» от внешней вынуждающей силы. Токи или напряжения, найденные при решении однородного дифференциального уравнения, называются свободными. Свободные токи и напряжения являются результатом действия внутренних источников схемы: э.д.с. самоиндукции, возникающих в катушках, и напряжений на конденсаторах, когда и те, и другие не уравновешены внешними источниками.
Схематически анализ переходного процесса может быть представлен как результат наложения двух режимов: принужденного и свободного. Схема на рис. 5.1 б должна быть рассчитана в установившемся (принужденном) режиме, а схема на рис. 5.1 в — в режиме, когда цепь освобождена от внешних источников. Действительный (переходный) ток в соответствии с принципом суперпозиции равен сумме установившегося (принужденного) и свободного токов:
i = iу + iсв.
Заметим, что физически существует только переходные токи и напряжения, а разложение их на свободные и принужденные составляющие является математическим приемом, позволяющим упростить расчет переходных процессов в линейных цепях. Напомним, что принцип суперпозиции применим лишь к линейным цепям.
Существуют различные методы решения однородного дифференциального уравнения, полученного из выражения (5.2):
(5.3)
Классический метод анализа переходных процессов заключается в непосредственном интегрировании дифференциальных уравнений . Об этом говорит сайт https://intellect.icu . Решение находят в виде суммы экспонент:
(5.4)
iсв = A1 · ep1t + A2 · ep2t,
где число слагаемых равно порядку дифференциального уравнения.
После подстановки экспонент Ak · epkt в исходное уравнение (5.3) и дифференцирования можно получить характеристическое уравнение, из которого определяют корни p1, p2. Если встречаются кратные корни (например, p1 = p2 = P), решение имеет вид A1 · ePt + A2 · ePt.
Постоянные интегрирования A1, A2 находят из начальных условий, которые определяют с помощью законов коммутации. Различают независимые и зависимые (после коммутационные) начальные условия. К первым относят значения токов через индуктивности и значения напряжений на емкостях, известные из до коммутационного режима работы цепи.
Значения остальных токов и напряжений при t = 0 в после коммутационной схеме, определяемые по независимым начальным значениям из законов Кирхгофа для схемы после коммутации, называют зависимыми начальными значениями.
Классический метод анализа применяют обычно для анализа процессов в несложных электрических цепях.
5.3. Алгоритм расчета переходного процесса классическим методом
Для анализа переходного процесса предварительно следует привести схему к минимальному числу накопителей энергии, исключив параллельные и последовательные соединения однотипных реактивных элементов (индуктивностей или емкостей). Система интегродифференциальных уравнений, составленных в соответствии с законами Кирхгофа или методом контурных токов, может быть сведена путем подстановки к одному дифференциальному уравнению, которое используется для составления характеристического уравнения.
Порядок дифференциального, следовательно, и характеристического уравнения зависит от числа реактивных элементов приведенной схемы. Главная трудность в решения задачи классическим методом для уравнений высоких порядков состоит в отыскании корней характеристического уравнения и постоянных интегрирования. Поэтому для решения уравнений порядка выше второго применяют другие методы, в частности операторный метод, основанный на применении преобразования Лапласа и исключающий трудоемкую процедуру отыскания постоянных интегрирования.
Для практических целей при анализе переходных процессов в любой схеме классическим методом может быть рекомендован следующий алгоритм.
- Рассчитать принужденный (установившийся) режим при t→∞. Определить принужденные токи и напряжения.
- Рассчитать режим до коммутации. Определить токи в ветвях с индуктивностью и напряжения на конденсаторах. Значения этих величин в момент коммутации является независимыми начальными условиями.
- Составить дифференциальные уравнения для свободного процесса (Е = 0) в схеме после коммутации по законам Кирхгофа или по методу контурных токов. Алгебраизировать данные уравнения, получить характеристическое уравнение и найти его корни. Существуют приемы, упрощающие операцию отыскания корней характеристического уравнения, например, приравнивание нулю входного операторного сопротивления цепи, которое получается путем замены в выражении комплексного сопротивления цепи множителя «jω» на оператор «р».
- Записать общие выражения для искомых напряжений и токов в соответствии с видом корней характеристического уравнения.
- Переписать величины, полученные в п. 4, и производные от них при t = 0.
- Определить необходимые зависимые начальные условия, используя независимые начальные условия.
- Подставив начальные условия в уравнения п. 5, найти постоянные интегрирования.
- Записать законы изменения искомых токов и напряжений.
5.4. Переходные процессы в электрических цепях с последовательно соединенными резисторами и катушками
В данном разделе предполагается не только практическое знакомство с классическим методом расчета переходных процессов, но и с особенностями самих процессов в рассматриваемых задачах.
5.4.1. Короткое замыкание в цепи с резистором и катушкой
Рис. 5.2
Исследуем электромагнитные процессы в цепи, изображенной на рис. 5.2, происходящие после замыкания ключа.
Рассчитаем установившийся режим в цепи до коммутации (до замыкания ключа) и определим из него независимое начальное условие — ток в катушке в момент t = 0-, непосредственно предшествующий коммутации
i(0-) = i(0+) = E / (Rвн + R).
Найдем установившийся ток i после коммутации. Так как во вновь образованном контуре из катушки L и резистора R нет источника, то iy = 0.
Для определения свободной составляющей тока запишем по второму закону Кирхгофа уравнение электрического состояния цепи после коммутации:
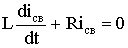
Характеристическое уравнение имеет вид:
pL + R = 0.
Общее решение уравнения для свободной составляющей:
iсв = A ept,
где: А – постоянная интегрирования;
p = — R/L, c-1 – корень характеристического уравнения.
Записав общий вид переходного тока катушки
i = iу + iсв = A ept,
приравниваем его значение i(0+) = A в точке t = 0+ к значению i(0-), найденному в п. 1. Получаем искомую константу
A = E / (Rвн + R) = I0.
Переходный ток i = iу + iсв при этом равен
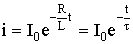
где τ = L / R – постоянная времени цепи.
Постоянная времени – это время, в течение которого свободная составляющая процесса уменьшается в е = 2,72 раза по сравнению с начальным значением.
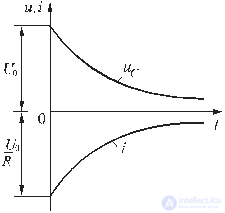
Рис. 5.3
График изменения переходного тока показан на рис. 5.3.
Определим э.д.с. самоиндукции катушки
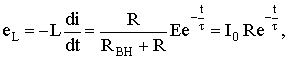
В момент коммутации эта э.д.с. равна напряжению на сопротивлении R, а в дальнейшем уменьшается по экспоненциальному закону. На основании изложенного можно сделать следующие выводы.
- При коротком замыкании в рассматриваемой цепи ток в ней изменяется по экспоненциальному закону, уменьшаясь от начального значения до нуля.
- Скорость изменения тока определяется постоянной времени цепи, которая равна индуктивности катушки, деленной на активное сопротивление цепи.
- Практически можно считать, что переходный процесс заканчивается при t ≈ (3…5)τ , когда первоначальное значение тока уменьшается по модулю на порядок.
- Напряжение на катушке в начальный момент времени равно напряжению на активном сопротивлении:
uL(0+) = I0R.
- С энергетической точки зрения рассматриваемый переходный процесс характеризуется расходом энергии магнитного поля катушки на тепловые потери в резисторе. Следует отметить, что сопротивление резистора влияет не на количество выделенной теплоты W, а на начальное значение напряжения катушки и длительность процесса. В самом деле
.
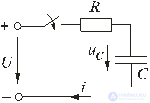
5.4.2. Включение цепи с резистором и катушкой на постоянное напряжение
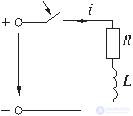
Рис. 5.4
Переходный ток в цепи, изображенной на рис. 5.4, представим в виде
i = iу + iсв.
1. До коммутации тока в катушке не было, следовательно,
iL(0-) = 0.
2. Установившаяся составляющая тока после коммутации
iу = U / R.
3. Свободная составляющая тока для цепи, описываемой дифференциальным уравнением первого порядка
iсв = A e-t/τ =A ept , p = — R / L.
4. По начальным условиям определим постоянную интегрирования А и свободную составляющую тока:
i(0) = iу(0) + iсв(0); i(0) = iу(0+) + iсв(0-);
или
0 = U / R + A; A = -U / R; iсв = -U / R · e-t/τ.
Переходный ток получается в виде
i = U / R (1 — e-t/τ).
Рис. 5.5
Напряжение на катушке
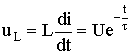
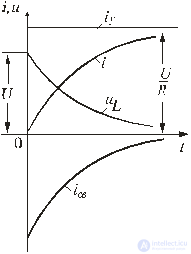
Кривые изменения токов i, iy, iсв и напряжения на катушке uL показаны на рис. 5.5.
При включении рассматриваемого контура под постоянное напряжение ток в нем нарастает от нуля до установившегося значения. Скорость нарастания тока
изменяется по экспоненте с отрицательным показателем. В момент t = 0 эта скорость максимальна и равна U / L [А/с], со временем она падает практически до нуля, процесс выходит на установившийся режим.
В первый после коммутации момент t = 0+ ток в цепи еще равен нулю, и напряжение на катушке максимально uL = U, далее оно экспоненциально снижается до нуля.
5.4.3. Включение цепи с резистором и катушкой на синусоидальное напряжение
Рис. 5.6
Если напряжение источника цепи (рис. 5.6)
u = Umsin(ωt + ψ),
то установившийся ток
iу = Um / Z sin(ωt + ψ — φ),
где: 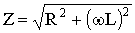
φ = arctg(ω L/R) — угол сдвига фаз между напряжением и током.
Свободный ток определяется
iсв = A e-t/τ.
Суммируя установившуюся и свободную составляющие, получим выражение для переходного тока:
i = iу + iсв = Um / Z sin(ωt + ψ — φ) + A e-t/τ.
Рис. 5.7
используя независимые начальные условия при t = 0
i(0-) = i(0+) = 0,
находим постоянную интегрирования:
A = -Um / Z sin(ψ — φ).
Тогда переходный ток:
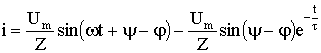
Зависимости переходного тока от времени при различных значениях разностей ψ — φ показаны на рис. 5.7. Их анализ позволяет сделать следующие выводы.
- Если в момент включения установившийся ток равен нулю (ψ — φ = 0 или ψ — φ = π), то свободной составляющей тока не возникает и в цепи сразу возникает установившийся режим:
i = iу = Im sin(ωt) = Um / Z sin(ωt).
- Если в момент включения установившийся ток имеет наибольшее значение (ψ — φ = π / 2), свободный ток достигает максимального по модулю значения приблизительно через половину периода, однако ни при каких условиях он не может превышать удвоенной амплитуды установившегося тока (рис. 5.7 б).
5.5 Переходные процессы в цепи с последовательно включенными резисторами и конденсатором
5.5.1.
разряд конденсатора на резистор
Рассмотрим переходный процесс при коротком замыкании в цепи с конденсатором и резистором (рис. 5.8), если предварительно конденсатор был заряжен до напряжения
uC(0+) = U0 = Е.
Рис. 5.8
Установившийся ток через конденсатор и установившееся напряжение на конденсаторе равны нулю. Для построения характеристического уравнения запишем по второму закону Кирхгофа уравнение для вновь образованного контура
R i + uC = 0.
При расчете переходных процессов в цепях с конденсатором часто удобнее отыскать сначала не ток, а напряжение на конденсаторе uC , а затем учитывая, что 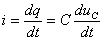
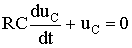
Характеристическое уравнение имеет вид:
RCp + 1 = 0.
Общее решение для свободной составляющей напряжения:
uCсв = A ept = A e-t/τ,
где: А = U0 – постоянная интегрирования;
p = — 1 / (RC) – корень характеристического уравнения;
τ = RC – постоянная времени цепи.
С учетом нулевого значения установившегося напряжения получим напряжение на конденсаторе:
uC = U0 e-t/τ.
Переходный ток в цепи
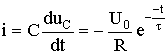
Рис. 5.9
Кривые изменения напряжения на конденсаторе и тока в цепи во времени имеют вид экспонент (рис. 5.9).
С энергетической точки зрения переходный процесс характеризуется переходом энергии электрического поля конденсатора в тепловую энергию в резисторе. Следует отметить; что сопротивление резистора влияет не на количество выделенной теплоты, а на начальное значение тока и длительность разряда. В самом деле
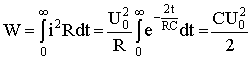
5.5.2. Включение цепи с резистором и конденсатором на постоянное напряжение (
заряд конденсатора )
Из схемы, приведенной на рис. 5.10, следует, что установившаяся составляющая напряжения на конденсаторе uCу = U, а свободная составляющая, очевидно, равна
Рис. 5.10
uCсв = A e-t/τ, τ = RC.
Полагаем, что до замыкания ключа конденсатор не был заряжен (Uс(0-) = 0). На основании законов коммутации uC(0-) = uC(0+) = 0, при t = 0; следовательно:
uC(0) = uCу(0) + uCсв(0) или 0 = U + A, откуда А = -U.
Тогда переходное напряжение на конденсаторе
uC = U (1 — e-t/τ),
а переходный ток в цепи
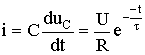
Зависимости напряжений и токов от времени показаны на рис. 5.10. Из них видно, что напряжение на конденсаторе возрастает по экспоненциальному закону от нуля до напряжения источника, а ток уменьшается от начального значения до нуля также по экспоненте. Длительность их изменения определяется постоянной времени τ = RC. Здесь как и в п. 5.5.1 время переходного процесса принимается равным t ≈ (3 ÷ 5)τ.
5.5.3. Включение цепи с резистором и конденсатором на синусоидальное напряжение
Рис. 5.11
Пусть напряжение источника изменяется по закону
u = Um sin(ωt + ψ).
Установившаяся составляющая напряжения на конденсаторе (см. рис. 5.11) равна:
uCу = -Um XC / Z sin(ωt + ψ – φ – π / 2).
где: 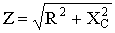
XC = 1 / (ωC) – емкостное сопротивление;
φ = -arctg(XC / R) – угол сдвига фаз между установившимся током в цепи и приложенным синусоидальным напряжением.
Свободная составляющая напряжения на конденсаторе
uCсв = A e-t/τ, τ = RC.
Переходное напряжение на конденсаторе
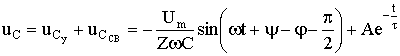
Рис. 5.12
Полагая, что uC(0-) = 0, для постоянной интегрирования получим
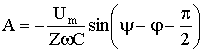
Окончательно напряжение на конденсаторе можно записать в виде
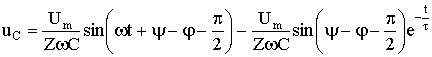
Ток в цепи
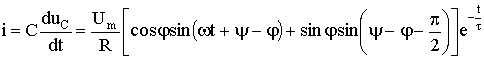
Зависимости переходного напряжения на конденсаторе от времени при различных значениях разностей ψ — φ показаны на рис. 5.12. Их анализ позволяет сделать следующие выводы.
Если в момент включения мгновенное значение установившегося напряжение на конденсаторе равно нулю (ψ – φ – π / 2 = 0), то и свободная составляющая напряжения равна нулю. В цепи сразу устанавливается режим (рис. 5.12 а).
Если в момент включения мгновенное значение установившегося напряжение на конденсаторе имеет наибольшее значение (ψ – φ – π / 2 = π / 2), то переходное напряжение достигает максимального значения приблизительно через половину периода и может приблизиться к удвоенной амплитуде установившегося напряжения, но не превысит его (рис. 5.12 в).
5.6. Разряд конденсатора на цепь с резистором и катушкой
Рис. 5.13
Пусть в цепи, изображенной на рис. 5.13, конденсатор был заряжен до напряжения uC(0-) = U0. Исследуем процессы в контуре, образованном резистором, конденсатором и катушкой после замыкания в момент t = 0 ключа. Так как источники в цепи отсутствуют, то установившиеся составляющие решений равны нулю. Решение будет состоять из одной свободной составляющей.
5.6.1. Составление характеристического уравнения.
определение собственных частот цепи
По второму закону Кирхгофа t ≥ 0 имеем:
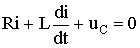
Учитывая, что 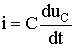
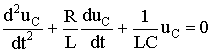
Характеристическое уравнение при этом имеет вид:
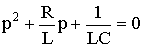
Характер электромагнитных процессов в контуре зависит от соотношения параметров R, L, С, входящих в выражение для корней характеристического уравнения
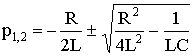
В зависимости от знака подкоренного выражения корни могут быть вещественными или комплексно-сопряженными. Они определяют характер свободных составляющих переходных токов и напряжений.
5.6.2. Апериодический разряд конденсатора на катушку и резистор
Рассмотрим процесс разряда конденсатора на резистор R и катушку L. Если параметры контура из резистора, катушки и конденсатора удовлетворяют условию 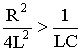
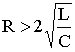
uC = uCсв = A1 · ep1t + A2 · ep2t,
где А1 и А2 – постоянные интегрирования, определяемые из начальных, условий.
Свободный ток равен
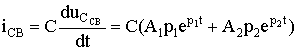
Установившиеся составляющие напряжения на конденсаторе и тока равны нулю. Поэтому их переходные значения равны свободным составляющим:
uC = uCсв; i = iсв.
Определим из начальных условий постоянные интегрирования А1 и А2. При t = 0, uC(0) = U0 и i(0) = 0. Подставив их в выражения для переходных напряжений и токов при t = 0 имеем
U0 = A1 + A2; 0 = A1 p1 + A2 p2.
Отсюда
A1 = U0 p2 / (p2 — p1); A2 = -U0 p1 / (p2 — p1);
С учетом начальных условий запишем
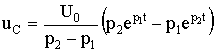
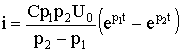
Рис. 5.14
Произведение корней по теореме Виета: p1 p2 = 1 / (LC), следовательно, ток
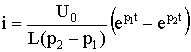
Напряжение на катушке
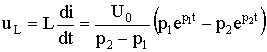
Графики зависимости тока и напряжения от времени, показанные на рис. 5.14 позволяют говорить об апериодическом разряде конденсатора. Апериодическим называется такой разряд, при котором конденсатор все время разряжается, т.е. функция uC(t) — убывающая, а ток i не меняет своего направления, в нашем случае он отрицателен. Сделаем некоторые выводы.
- Апериодический разряд конденсатора в цепи R, L, С возникает при вещественных, отрицательных и неравных корнях характеристического уравнения.
- При апериодическом разряде напряжение на конденсаторе уменьшается от начального значения до нуля, а ток сначала возрастает по модулю, затем уменьшается, проходя через максимальное значение.
- Напряжение на катушке уменьшается от начального значения, проходит через нулевое значение, изменяя знак и, достигнув наибольшего значения, уменьшается до нуля.
5.6.3. Предельный апериодический разряд конденсатора на катушку и резистор
При соотношении параметров контура из конденсатора, катушки и резистора
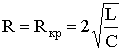
где RКР — критическое сопротивление резистора R, корни характеристического уравнения контура вещественные, равные и отрицательные:
p1 = p2 = p = -R / (2L).
Переходный процесс получается апериодическим, но граничным с колебательным процессом. Переходный ток и переходное напряжение в этом случае имеют вид:
uC = (A1 + A2 t) ept;
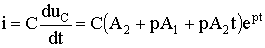
При начальных условиях uC(0) = U0; i(0) = 0 находим: А1 = U0; A2 = -p U0. С учетом найденных постоянных интегрирования получаем решения:
uC = U0 (1 — pt) ept;
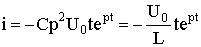
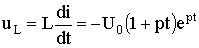
Зависимости i, uC, uL такие же, как для апериодического разряда.
5.6.4. Периодический (колебательный) разряд конденсатора на цепь с резистором и катушкой
При соотношении параметров контура из конденсатора, катушки и резистора 
p1,2 = -α ± jω,
где α = R / (2L) – коэффициент затухания свободной составляющей;
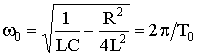
Т0 – период собственных колебаний.
Поскольку 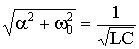
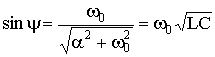
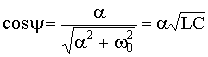
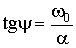
Свободная составляющая переходного напряжения при комплексно-сопряженных корнях (см. п.п. 5.2.1)
uCсв = A e-αt sin(ω0t + ψ),
Для свободной составляющей тока 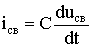
iсв = C A e-αt (-α sin(ω0t + ψ) + ω0 cos(ω0t + ψ)).
С учетом начальных условий при t = 0, uC = U0 , i = 0 из последних двух уравнений находим константы интегрирования:
U0 = A sin ψ; 0 = C A (-α sin ψ + ω0 cos ψ).
и далее
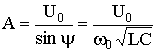
Запишем переходные напряжения и ток:
uC = UCm e-αt sin(ω0t + ψ);
i = -Im e-αt sin(ω0t + π);
uL= ULm e-αt sin(ω0t — ψ),
где 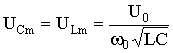
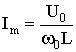
Рис. 5.15
Зависимости переходных напряжения и тока uC, i показаны на рис. 5.15. Они представляют собой затухающие синусоиды. Скорость затухания колебаний оценивают декрементом колебаний. Декремент колебания — это постоянная, зависящая от параметров R, L, С и равная отношению амплитуд переходных параметров, отстающих друг от друга на период колебания Т0, например:
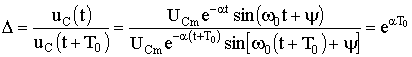
Часто пользуются логарифмическим декрементом колебания:
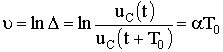
В предельном случае чисто консервативной системы (R = 0) Δ = 1 колебания в параллельно соединенных конденсаторе и катушке носят незатухающий характер. Период этих колебаний дается формулой Томпсона 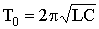
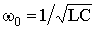
5.7. Включение контура из конденсатора, резистора, катушки на постоянное напряжение
Рис. 5.16
Рассмотрим электромагнитные процессы, возникающие после замыкания ключа в цепи, изображенной на рис. 5.16 в предположении, что конденсатор был предварительно не заряжен, т.е. uC(0-) = 0. Характеристическое уравнение и вид его корней будут такими же, как и в цепи, рассмотренной в п. 5.6.
5.7.1. Апериодический процесс
Между разрядом конденсатора на резистор с катушкой и включением на постоянное напряжение контура (см. рис. 5.16) существует аналогия. Так же, как при разряде конденсатора, установившаяся составляющая тока равна нулю. Установившееся напряжение на конденсаторе uCу = U. Следовательно, начальное значение свободной составляющей напряжения на конденсаторе
Рис. 5.17
uCсв(0+) = uC(0+) — uCу(0-)
равно uCсв(0+) = -U. То есть знаки постоянных интегрирования А1 и А2 в отличие от рассмотренного в п. 5.6 случая изменяются на противоположные. В этом случае переходное напряжение на конденсаторе, ток и напряжение на катушке определяются по формулам:
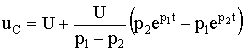
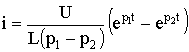
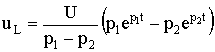
Кривые uC(t), uL(t) и i(t) приведены на рис. 5.17.
5.7.2. Колебательный процесс
Включение рассматриваемого контура на постоянное напряжение может сопровождаться колебательным переходным процессом. При этом в отличие от процесса разряда конденсатора (см. п. 5.6) знак начального значения преходящего напряжения, следовательно, и коэффициента А, изменится на противоположный. Переходные напряжения и ток приобретут вид:
Рис. 5.18
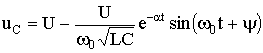
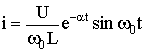
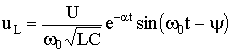
Кривые uC(t) и i(t) показаны на рис. 5.18. Кривая тока отображает затухающие колебания относительно нулевого значения, а напряжения на конденсаторе – относительно установившегося значения. Следует отметить, что за время переходного процесса контура часть энергии источника переходит в тепло, а другая часть запасается в электрическом поле конденсатора в виде:
т.е. 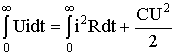
См. также
- первый закон коммутации , коммутация в цепи ,
- переходные процессы , виды коротких замыканий ,
- второй закон коммутации ,
- Интеграл Дюамеля
- Время релаксации
- Бифуркационная память
- Время изодрома
- Зона нечувствительности
- Коэффициент демпфирования
- Бифуркация
- расчет переходных процессов в электрических цепях классическим методом ,
- переходные процессы в линейных электрических цепях с сосредоточенными параметрами ,
- операторный метод расчета переходных процессов ,
Статью про переходные процессы я написал специально для тебя. Если ты хотел бы внести свой вклад в развии теории и практики,
ты можешь написать коммент или статью отправив на мою почту в разделе контакты.
Этим ты поможешь другим читателям, ведь ты хочешь это сделать? Надеюсь, что теперь ты понял что такое переходные процессы, расчет переходного процесса классическим методом, переходные процессы с последовательно соединенными резисторами и катушками, разряд конденсатора на резистор, заряд конденсатора, определение собственных частот цепи, контур из конденсатора резистора и катушки на постоянное напряжение
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
Электротехника, Схемотехника, Аналоговые устройства




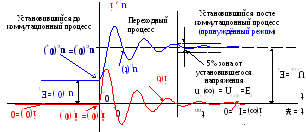

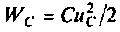
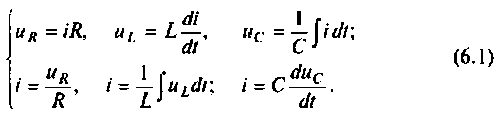
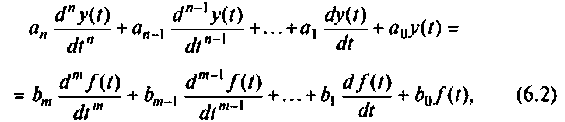

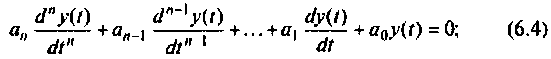
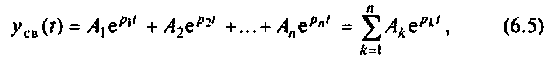
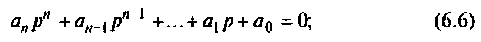


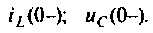

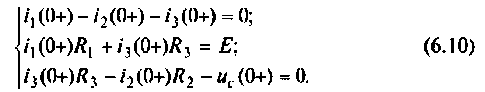
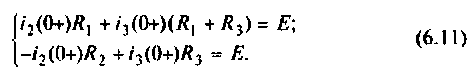
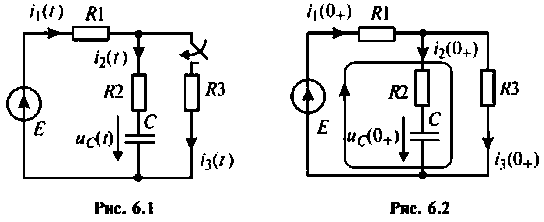
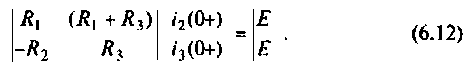
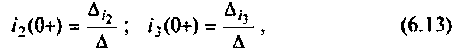
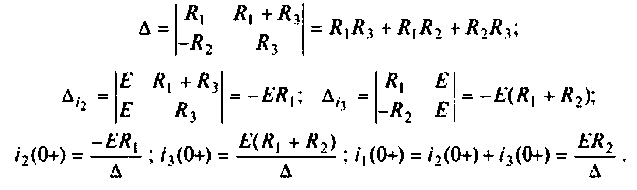
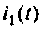
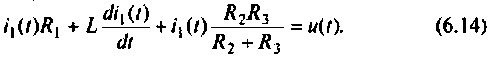
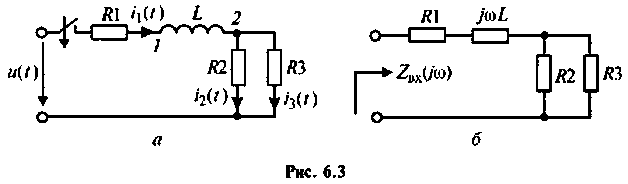
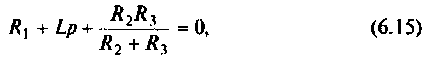
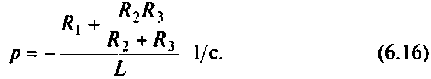
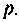
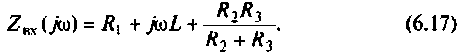
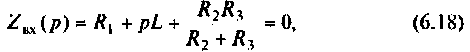
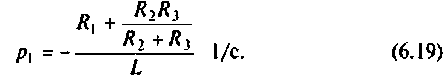
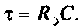

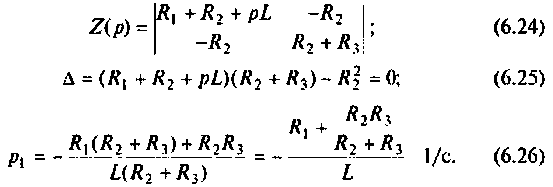
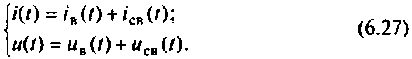
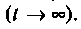
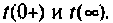
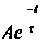 ;
;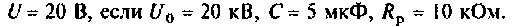
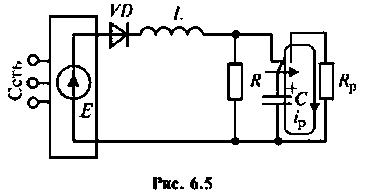
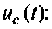
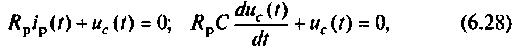
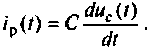
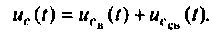
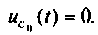
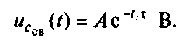
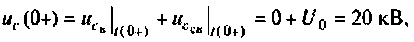
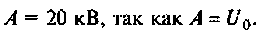
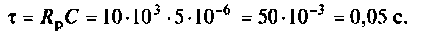
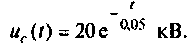
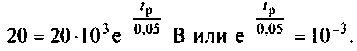
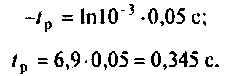
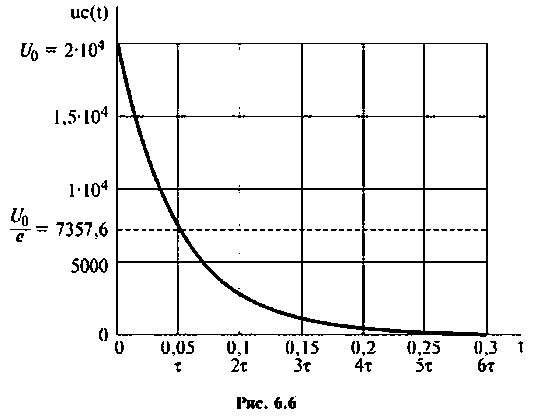
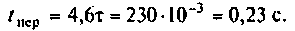
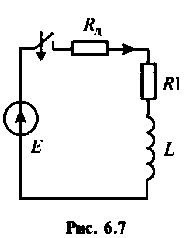
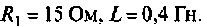
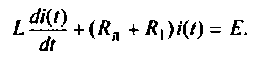
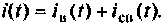
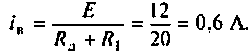
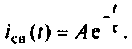
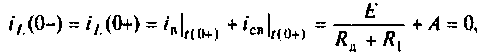
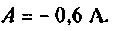
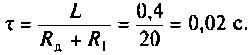
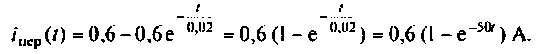
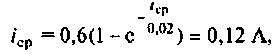
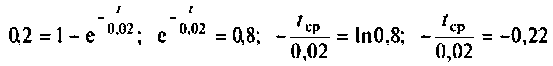
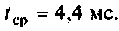
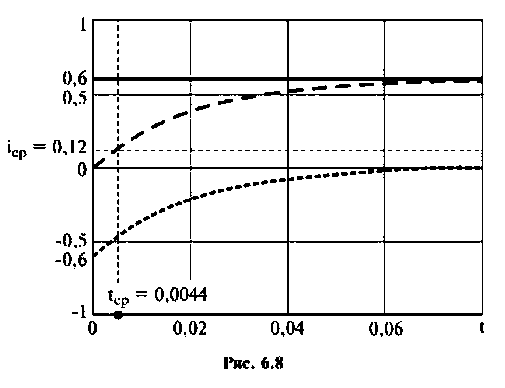
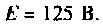
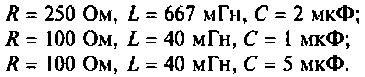
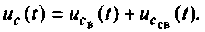
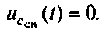
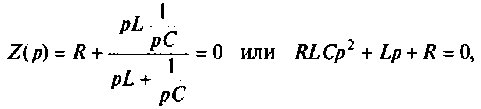
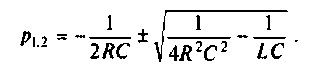
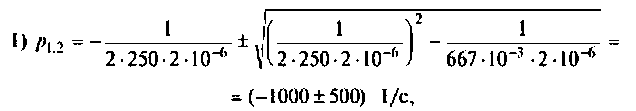
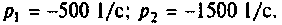
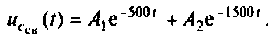

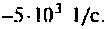
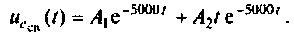
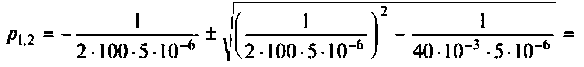
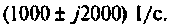
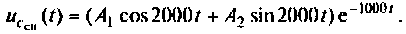
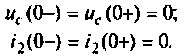
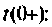
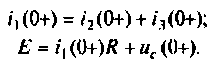
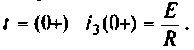
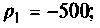
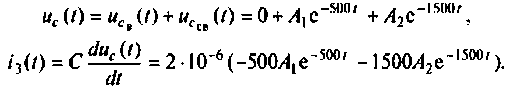
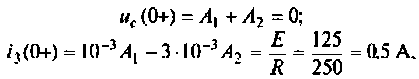
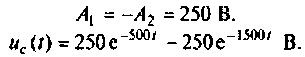
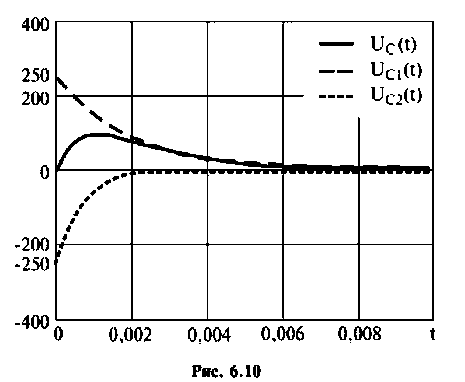
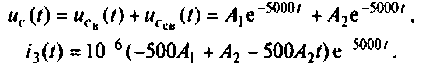
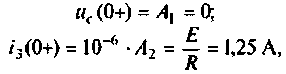
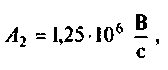
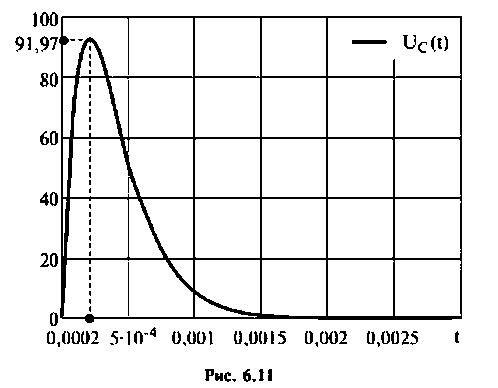
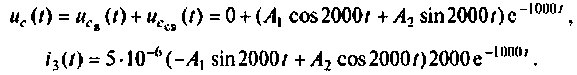
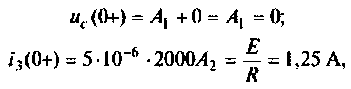
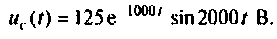
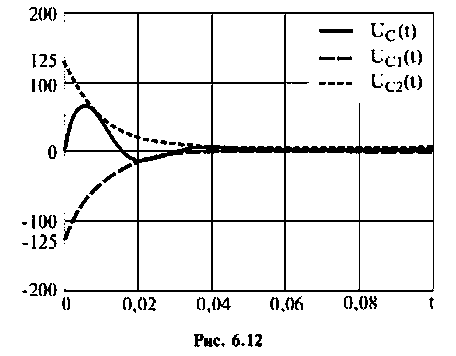
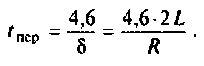
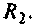
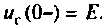
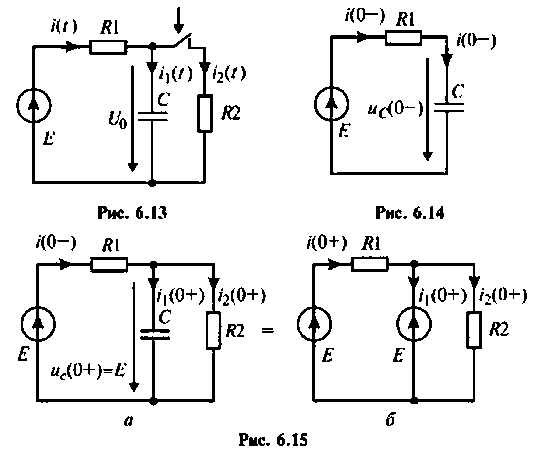
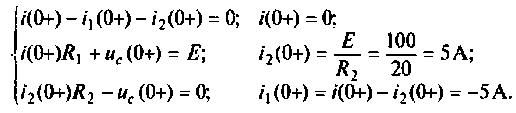
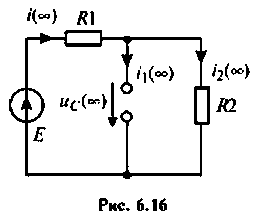
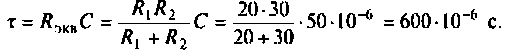
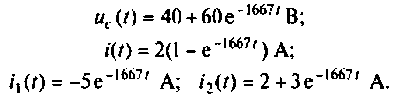
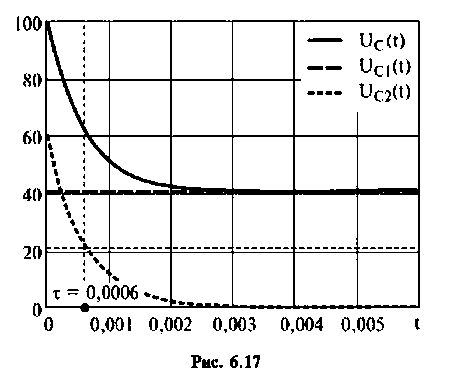
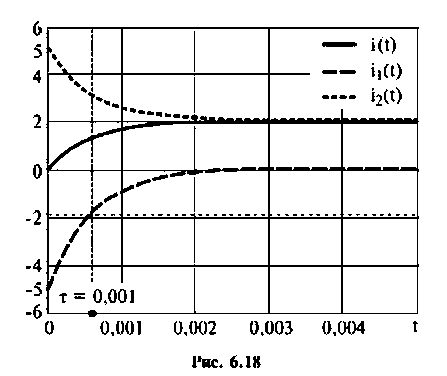
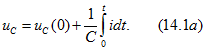
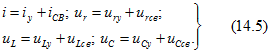
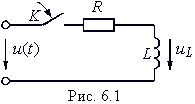
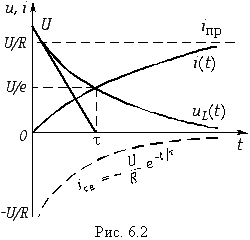
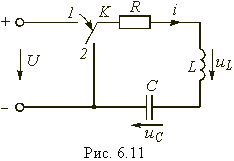
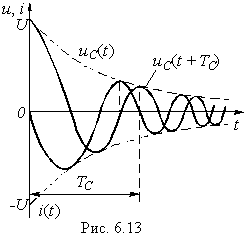
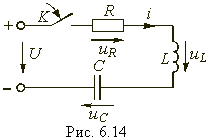
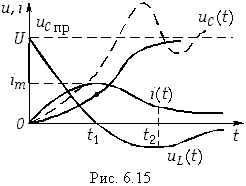
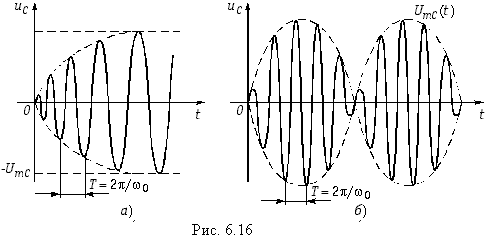
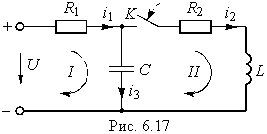
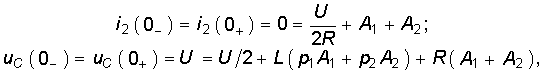
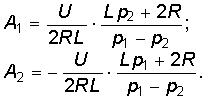
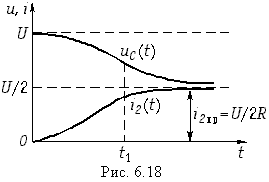
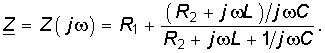
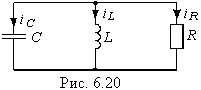
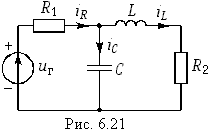
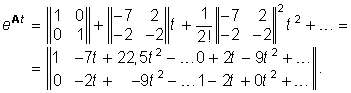
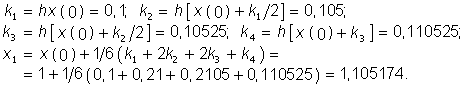
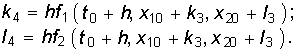
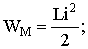
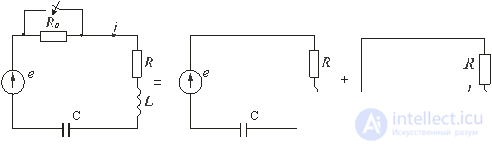
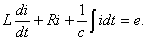
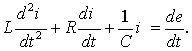
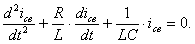
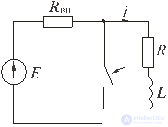
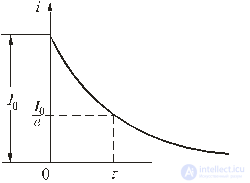
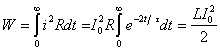 .
.