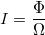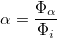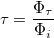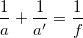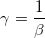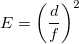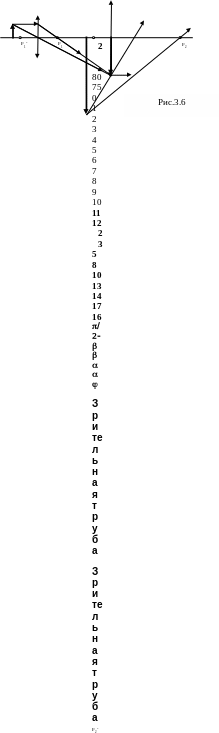Как найти увеличение лупы формулы - Исправление недочетов и поиск решений вместе с Examum.ru

Оптические приборы.

Невооружённый глаз.
Лупа.
Микроскоп.
Труба Кеплера.
Труба Галилея.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: оптические приборы.

Как мы знаем из предыдущей темы, для более подробного разглядывания объекта нужно увеличить угол зрения. Тогда изображение объекта на сетчатке будет крупнее, и это приведёт к раздражению большего числа нервных окончаний зрительного нерва; в мозг направится большее количество визуальной информации, и мы сможем увидеть новые детали рассматриваемого объекта.

Почему угол зрения бывает малым? На то есть две причины: 1) объект сам по себе имеет малый размер; 2) объект, хотя и достаточно велик по размерам, но расположен далеко.

Оптические приборы — это приспособления для увеличения угла зрения. Для рассматривания малых объектов используются лупа и микроскоп. Для рассматривания далёких объектов применяются зрительные трубы (а также бинокли, телескопы и т. д.)

к оглавлению ▴

Невооружённый глаз.

Начинаем с рассматривания мелких объектов невооружённым глазом. Здесь и далее глаз считается нормальным. Напомним, что нормальный глаз в ненапряжённом состоянии фокусирует на сетчатке параллельный пучок света, а расстояние наилучшего зрения для нормального глаза равно $d_{0}=25$ см.

Пусть небольшой предмет размером находится на расстоянии наилучшего зрения $d_{0}$ от глаза (рис. 1). На сетчатке возникает перевёрнутое изображение предмета, но, как вы помните, это изображение затем вторично переворачивается в коре головного мозга, и в результате мы видим предмет нормально — не вверх ногами.

Рис. 1. Рассматривание мелкого предмета невооружённым глазом

Ввиду малости предмета угол зрения $varphi _{0}$ также является малым. Напомним, что малый угол (в радианах) почти не отличается от своего тангенса: $varphi _{0}approx tg varphi _{0}$ . Поэтому:

$varphi _{0}=frac{displaystyle h}{displaystyle d_{0}}$ . (1)

Если r расстояние от оптического центра глаза до сетчатки, то размер изображения на сетчатке будет равен:

$l_{0}=rvarphi _{0}$ . (2)

Из (1) и (2) имеем также:

$l_{0}=frac{displaystyle rh}{displaystyle d_{0}}$ . (3)

Как известно, диаметр глаза составляет около 2,5 см, так что $l/d_{0}approx 0,1$ . Поэтому из (3) следует, что при рассматривании мелкого предмета невооружённым глазом изображение предмета на сетчатке примерно в 10 раз меньше самого предмета.

к оглавлению ▴

Лупа.

Укрупнить изображение объекта на сетчатке можно с помощью лупы (увеличительного стекла).

Лупа — это просто собирающая линза (или система линз); фокусное расстояние лупы обычно находится в диапазоне от 5 до 125 мм. Предмет, разглядываемый через лупу, помещается в её фокальной плоскости (рис. 2). В таком случае лучи, исходящие из каждой точки предмета, после прохождения лупы становятся параллельными, и глаз фокусирует их на сетчатке, не испытывая напряжения.

Рис. 2. Рассматривание предмета через лупу

Теперь, как видим, угол зрения равен varphi . Он также мал и приблизительно равен своему тангенсу:

$varphi=frac{displaystyle h}{displaystyle f}$ . (4)

Размер l изображения на сетчатке теперь равен:

. (5)

или, с учётом (4):

$l=frac{displaystyle rh}{displaystyle f}$ . (6)

Как и на рис. 1, красная стрелочка на сетчатке также направлена вниз. Это означает, что (с учётом вторичного переворачивания изображения нашим сознанием) в лупу мы видим неперевёрнутое изображение предмета.

Увеличение лупы — это отношение размера изображения при использовании лупы к размеру изображения при рассматривании предмета невооружённым глазом:

$Gamma = frac{displaystyle l}{displaystyle l_{0}}$ . (7)

Подставляя сюда выражения (6) и (3), получим:

$Gamma = frac{displaystyle d_{0}}{displaystyle f}$ . (8)

Например, если фокусное расстояние лупы равно 5 см, то её увеличение . При рассматривании через такую лупу объект кажется в пять раз больше, чем при рассматривании его невооружённым глазом.
Подставим также в формулу (7) соотношения (5) и (2):

$Gamma = frac{displaystyle rvarphi }{displaystyle rvarphi _{0}}=frac{displaystyle varphi }{displaystyle varphi _{0}}$ .

Таким образом, увеличение лупы есть угловое увеличение: оно равно отношению угла зрения при рассматривании объекта через лупу к углу зрения при рассматривании этого объекта невооружённым глазом.

Отметим, что увеличение лупы есть величина субъективная — ведь величина $d_{0}$ в формуле (8) есть расстояние наилучшего зрения для нормального глаза. В случае близорукого или дальнозоркого глаза расстояние наилучшего зрения будет соответственно меньше или больше.

Из формулы (8) следует, что увеличение лупы тем больше, чем меньше её фокусное расстояние. Уменьшение фокусного расстояния собирающей линзы достигается за счёт увеличения кривизны преломляющих поверхностей: линзу надо делать более выпуклой и тем самым уменьшать её размеры. Когда увеличение Gamma достигает 40–50, размер лупы становится равным нескольким миллиметрам. При ещё меньших размерах лупы пользоваться ей станет невозможно, поэтому считается верхней границей увеличения лупы.

к оглавлению ▴

Микроскоп.

Во многих случаях (например, в биологии, медицине и т. д.) нужно наблюдать мелкие объекты с увеличением в несколько сотен. Лупой тут не обойдёшься, и люди прибегают к помощи микроскопа.

Микроскоп содержит две собирающие линзы (или две системы таких линз) — объектив и окуляр. Запомнить это просто: объектив обращён к объекту, а окуляр — к глазу (к оку).

Идея микроскопа проста. Рассматриваемый объект находится между фокусом и двойным фокусом объектива, так что объектив даёт увеличенное (действительное перевёрнутое) изображение объекта. Это изображение располагается в фокальной плоскости окуляра и затем рассматривается в окуляр как в лупу. В результате удаётся достичь итогового увеличения, гораздо большего 50.

Ход лучей в микроскопе показан на рис. 3.

Рис. 3. Ход лучей в микроскопе

Обозначения на рисунке понятны: $f_{1}$ — фокусное расстояние объектива $Ob; f_{2}$ — фокусное расстояние окуляра Ok; h — размер объекта; — размер изображения объекта, даваемого объективом. Расстояние $delta =F_{1}F_{2}$ между фокальными плоскостями объектива и окуляра называется оптической длиной тубуса микроскопа.

Обратите внимание, что красная стрелочка на сетчатке направлена вверх. Мозг вторично перевернёт её, и в результате объект при рассмотрении в микроскоп будет казаться перевёрнутым. Чтобы этого не происходило, в микроскопе используются промежуточные линзы, дополнительно переворачивающие изображение.

Увеличение микроскопа определяется точно так же, как и для лупы: $Gamma= l/l_{0}=varphi /varphi _{0}$ . Здесь, как и выше, и varphi — размер изображения на сетчатке и угол зрения при рассматривании объекта в микроскоп, $l_{0}$ и $varphi_{0}$ — те же величины при рассматривании объекта невооружённым глазом.

Имеем по-прежнему $varphi_{0}=h/d_{0}$ , а угол varphi , как видно из рис. 3, равен:

$varphi =frac{displaystyle H}{displaystyle f_{displaystyle 2}}$ .

Деля varphi на $varphi_{0}$ , получим для увеличения микроскопа:

$Gamma =frac{displaystyle Hd_{displaystyle 0}}{displaystyle hf_{displaystyle 2}}$ . (9)

Это, разумеется, не окончательная формула: в ней присутствуют и (величины, относящиеся к объекту), а хотелось бы видеть характеристики микроскопа. Ненужное нам отношение H/h мы устраним с помощью формулы линзы.
Для начала ещё раз посмотрим на рис. 3 и используем подобие прямоугольных треугольников с красными катетами и :

$frac{displaystyle H}{displaystyle h}=frac{displaystyle b}{displaystyle a}$ .

Здесь $b=f_{1}+delta$ — расстояние от изображения до объектива, — a — расстояние от объекта h до объектива. Теперь привлекаем формулу линзы для объектива:

$frac{displaystyle 1}{displaystyle a}+frac{displaystyle 1}{displaystyle b}=frac{displaystyle 1}{f_{displaystyle 1}}$ ,

из которой получаем:

$frac{displaystyle b}{displaystyle a}=frac{displaystyle b - f_{displaystyle 1}}{displaystyle f_{displaystyle 1}}$ .

Итак,

$frac{displaystyle H}{displaystyle h}=frac{displaystyle b - f_{displaystyle 1}}{displaystyle f_{displaystyle 1}}=frac{delta }{displaystyle f_{displaystyle 1}}$ ,

и это выражение мы подставляем в (9):

$Gamma =frac{displaystyle delta d_{displaystyle 0}}{displaystyle f_{displaystyle 1}displaystyle f_{displaystyle 2}}$ . (10)

Вот это и есть окончательное выражение для увеличения, даваемого микроскопом. Например, если фокусное расстояние объектива равно $f_{1}=1$ см, фокусное расстояние окуляра $f_{2}=2$ , а оптическая длина тубуса см, то согласно формуле (10)

$Gamma =frac{displaystyle 20cdot25}{displaystyle 1cdot2}=250$ см.

Сравните это с увеличением одного только объектива, которое вычисляется по формуле (8):

$Gamma _{1}=frac{displaystyle d_{displaystyle 0}}{displaystyle f_{displaystyle 1}}=frac{displaystyle 25}{displaystyle 1}=25$ см.

Увеличение микроскопа в 10 раз больше!

Теперь мы переходим к объектам, которые достаточно крупны, но находятся слишком далеко от нас. Чтобы рассматривать их получше, применяются зрительные трубы — подзорные трубы, бинокли, телескопы и т. д.

Объективом зрительной трубы служит собирающая линза (или система линз) с достаточно большим фокусным расстоянием. А вот окуляром может быть как собирающая, так и рассеивающая линза. Соответственно имеются два вида зрительных труб:

-труба Кеплера — если окуляр является собирающей линзой;
-труба Галилея — если окуляр является рассеивающей линзой.

Рассмотрим подробнее, как работают эти зрительные трубы.

к оглавлению ▴

Труба Кеплера.

Принцип действия трубы Кеплера очень прост: объектив даёт изображение удалённого обекта в своей фокальной плоскости, а затем это изображение рассматривается в окуляр как в лупу. Таким образом, задняя фокальная плоскость объектива совпадает с передней фокальной плоскостью окуляра.

Ход лучей в трубе Кеплера изображён на рис. 4.

Рис. 4

Объектом служит далеко расположенная стрелка , направленная вертикально вверх; она не показана на рисунке. Луч из точки идёт вдоль главной оптической оси объектива и окуляра. Из точки идут два луча, которые ввиду удалённости объекта можно считать параллельными.

В результате изображение A{} нашего объекта, даваемое объективом, расположено в фокальной плоскости объектива и является действительным, перевёрнутым и уменьшенным. Размер изображения обозначим .

Невооружённым глазом объект виден под углом $varphi _{0}$ . Согласно рис. 4:

$varphi _{0}=frac{displaystyle H}{displaystyle f_{displaystyle 1}}$ , (11)

где $f_{1}$ — фокусное расстояние объектива.

Изображение объекта мы видим в окуляр под углом varphi , который равен:

$varphi =frac{displaystyle H}{displaystyle f_{displaystyle 2}}$ , (12)

где $f_{2}$ — фокусное расстояние окуляра.

Увеличение зрительной трубы — это отношение угла зрения при наблюдении в трубу к углу зрения при наблюдении невооружённым глазом:

$Gamma =frac{displaystyle varphi }{displaystyle varphi _{displaystyle 0}}.$

Согласно формулам (12) и (11) получаем:

$Gamma =frac{displaystyle f_{displaystyle 1}}{displaystyle f_{displaystyle 2}}.$ (13)

Например, если фокусное расстояние объектива равно 1 м, а фокусное расстояние окуляра равно 2 см, то увеличение зрительной трубы окажется равным: .

Ход лучей в трубе Кеплера принципиально тот же, что и в микроскопе. Изображением объекта на сетчатке также будет стрелочка, направленная вверх, и поэтому в трубе Кеплера мы увидим объект перевёрнутым. Во избежании этого в пространстве между объективом и окуляром ставят специальные оборачивающие системы линз или призм, которые ещё раз переворачивают изображение.

к оглавлению ▴

Труба Галилея.

Галилей изобрёл свой телескоп в 1609 году, и его астрономические открытия потрясли современников. Он обнаружил спутники Юпитера и фазы Венеры, разглядел лунный рельеф (горы, впадины, долины) и пятна на Солнце, а сплошной с виду Млечный Путь оказался скоплением звёзд.

Окуляром трубы Галилея служит рассеивающая линза; задняя фокальная плоскость объектива совпадает с задней фокальной плоскостью окуляра (рис. 5).

Рис. 5.

Если бы окуляра не было, то изображение A{} удалённой стрелки находилось бы в
фокальной плоскости объектива. На рисунке это изображение показано пунктиром — ведь в реальности его там нет!

А нет его там потому, что лучи от точки , которые после прохождения объектива стали сходящимися к точке B{} , не доходят до B{} и попадают на окуляр. После окуляра они вновь становятся параллельными и поэтому воспринимаются глазом без напряжения. Но теперь мы видим изображение объекта под углом varphi , который больше угла зрения $varphi _{0}$ при рассматривании объекта невооружённым глазом.

Из рис. 5 имеем

$varphi =frac{displaystyle H}{displaystyle f_{displaystyle 2}}, varphi _{0}=frac{displaystyle H}{displaystyle f_{displaystyle 2}}$ ,

и для увеличения трубы Галилея мы получаем ту же формулу (13), что и для трубы Кеплера:

$Gamma =frac{displaystyle varphi }{displaystyle varphi _{displaystyle 0}}=frac{displaystyle f_{displaystyle 1}}{displaystyle f_{displaystyle 2}}.$

Заметьте, что при том же увеличении труба Галилея меньше размером, чем труба Кеплера. Поэтому одно из основных применений трубы Галилея — театральные бинокли.

В отличие от микроскопа и трубы Кеплера, в трубе Галилея мы видим объекты неперевёрнутыми. Почему?

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Оптические приборы.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

Оптика Основные формулы

1. Фотометрия и светотехника

1.1 Поток излучения

Φ — поток излучения,
W — энергия излучения,
t — время прохождения энергии излучения.

1.2 Сила света

I — сила света,
Φ — поток излучения,
Ω — телесный угол, через который проходит поток излучения.

1.3 Освещенность

E — освещенность,
Φ — поток излучения,
σ — площадь, через которую проходит поток излучения.

1.4 Яркость источника света

L — яркость источника света,
I — сила света,
σ — площадь видимой светящейся поверхности.

1.5 Коэффициент поглощения

α — коэффициент поглощения,
Φ_α — световой поток, поглощенный телом,
Φ_i — световой поток, падающий на тело.

1.6 Коэффициент отражения

ρ — коэффициент отражения,
Φ_ρ — световой поток, отраженный телом,
Φ_i — световой поток, падающий на тело.

1.7 Коэффициент пропускания

τ — коэффициент пропускания,
Φ_τ — световой поток, пропущенный телом,
Φ_i — световой поток, падающий на тело.

2. Геометрическая оптика

2.1 Относительный показатель преломления

n — относительный показатель преломления для граничащих сред
n₂ — абсолютный показатель преломления для второй среды,
n₁ — абсолютный показатель преломления для первой среды.

2.2 Закон преломления света

i — угол отражения,
r — угол преломления,
n — относительный показатель преломления для граничащих сред.

2.3 Предельный угол полного внутреннего отражения

i_пр — предельный угол полного внутреннего отражения,
n — относительный показатель преломления для граничащих сред.

2.4 Основная формула тонкой линзы

a — расстояние от источника света до линзы,
a’ — расстояние от линзы до изображения источника света,
f — фокусное расстояние линзы.

2.5 Основная формула сферического зеркала

a — расстояние от источника света до зеркала,
a’ — расстояние от зеркала до изображения источника света,
R — радиус кривизны зеркала,
f — фокусное расстояние зеркала.

2.6 Линейное увеличение

β — линейное увеличение линзы или зеркала,
h — высота источника света,
h’ — высота изображения источника света,
a — расстояние от источника света до линзы или зеркала,
a’ — расстояние от линзы или зеркала до изображения источника света.

2.7 Угловое увеличение

γ — угловое увеличение линзы или зеркала,
β — линейное увеличение линзы или зеркала.

2.8 Оптическая сила линзы

D — оптическая сила линзы,
f — фокусное расстояние.

2.9 Светосила линзы

E — светосила линзы,
d — диаметр линзы или диафрагмы, закрывающей линзу,
f — фокусное расстояние.

3. Оптические приборы

3.1 Увеличение лупы

N — увеличение лупы,
D — расстояние наилучшего видения человеческого глаза, обычно D=250 мм, при этом f также должно быть выражено в мм,
f — фокусное расстояние лупы.

3.2 Увеличение микроскопа

N — увеличение микроскопа,
N₁ — увеличение окуляра микроскопа,
N₂ — увеличение объектива микроскопа,
D — расстояние наилучшего видения человеческого глаза, обычно D=250 мм, при этом f также должно быть выражено в мм,
f — фокусное расстояние системы линз микроскопа: окуляра и объектива.

3.3 Увеличение зрительной (подзорной) трубы

N — увеличение зрительной (подзорной) трубы,
f₁ — фокусное расстояние объектива,
f₂ — фокусное расстояние окуляра.

Источник

Л
у п а —
простая система (одна или несколько
линз) с небольшим фокусным расстоянием
(примерно от 100 до 10 мм), располагаемая
между рассматриваемым предметом и
глазом.
Мнимое увеличенное изображение предмета
получается на расстоянии наилучшего
зрения (250 мм для нормального глаза) или
в бесконечности, т. е. рассматривается
глазом без усилия аккомодации. При обоих
способах применения лупы видимое
увеличение, ею даваемое, практически
одно и то же и равно

N
= tgφ’/tgφ
= D/ƒ

(3.1)

где
D
— расстояние
наилучшего зрения и f
— фокусное
расстояние лупы. Так как D
= 250мм, то
обычно применяемые лупы дают увеличение
от 2,5 до 25 раз. Для близорукого глаза D
меньше и,
следовательно, лупа оказывает меньшую
помощь в распознавании деталей.

Увеличение
лупы.

Применяя формулу
простой линзы, найдем:

(3.2),

где
φ’ – угол зрения изображения; tgφ=l/D,
где φ
— угол зрения предмета, помещенного на
расстоянии D
от невооруженного
глаза (рис.3.4).

Увеличение
N
равно

(3.3);

при
а’ = — ∞ имеем N
= D/ƒ
, при d
— а’ = D
получим

N
=
D/f
+
1— d/ƒ
(3.4),

т.
е. увеличение несколько зависит от
положения глаза (d).
Когда глаз
помещен вблизи главного фокуса (d
= ƒ), что
практически имеет
место, то

N
= D/f.

3. Микроскоп. Ход лучей в микроскопе. Вывести формулу увеличения микроскопа

Микроскоп.
Для получения больших увеличений
применяют микроскоп, представляющий в
принципе комбинацию двух оптических
систем – объектива и окуляра, –
разделенных значительным расстоянием.
Они помещены в тубус. Если фокусные
расстояния объектива и окуляра
соответственно f₁
и f₂,
то фокусное расстояние всей системы
можно вычислить по формуле:

(3.5),

где
d
– расстояние между линзами. Отсюда

(3.6),

где

—
расстояние между фокусами обеих линз.
Увеличение, даваемое микроскопом можно
получить, воспользовавшись формулой
увеличения лупы:

.

В дальнейшем будем
говорить об абсолютном значении
увеличения

(3.7).

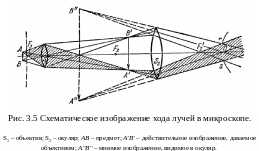
Схема
оптической системы микроскопа показана
на рис. 3.5. Малый объект АВ
помещается
вблизи главного фокуса F₁
объектива
S₁, дающего
его увеличенное действительное
изображение А’В’,
которое
рассматривают через окуляр S₂
так, чтобы увеличенное мнимое
изображение А»В»
получалось
на расстоянии наилучшего зрения от
глаза или в бесконечности (наблюдение
спокойным глазом). Оба способа наблюдения
одинаково пригодны.

От
предмета к объективу свет поступает
широкими
пучками, что
важно для использования больших световых
потоков и улучшения разрешающей
способности микроскопа. Так как обычно
в микроскопе наблюдаются несветящиеся
объекты, то для обеспечения широких
пучков важно иметь специальное
осветительное устройство (конденсор).
Объектив микроскопа, работающий с
широкими пучками, должен удовлетворять
условию апланатизма для точки вблизи
фокуса; требуется также высокая
ахроматизация (ахроматы и апохроматы).
Хороший объектив состоит из многих линз
(иногда свыше 10). Построение изображения
по принципам геометрической оптики
представлено на рис.3.6.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Загрузить PDF

Оптическое увеличение – это отношение линейных или угловых размеров изображения и предмета.^[1] Например, линза, увеличивающая размеры предмета, имеет большое увеличение, а линза, уменьшающая размеры предмета, имеет малое увеличение. Увеличение, как правило, вычисляется по формуле M = (h_i/h_o) = -(d_i/d_o), где М – увеличение, h_i – высота изображения, h_o – высота объекта, d_i и d_o – расстояние до изображения и предмета.

Примечание: собирающая линза широкая посередине и узкая по краям; рассеивающая линза широкая по краям и узкая посередине.^[2] Процесс вычисления увеличения одинаков для обеих линз за одним исключением в случае рассеивающей линзы.

1
Напишите формулу. Теперь определите, какие переменные вам даны. По формуле вы можете найти любую переменную, входящую в формулу (а не только увеличение).
- Например, рассмотрим фигурку высотой 6 см, которая находится на расстоянии 50 см от собирающей линзы с фокусным расстоянием 20 см. Здесь вы должны найти увеличение, размер изображения и расстояние до изображения. Запишите формулу так:
  
  M = (h_i/h_o) = -(d_i/d_o)
- В задаче даны h_o (высота фигурки) и d_o (расстояние от фигурки до линзы). Вы также знаете фокусное расстояние линзы, которое не входит в формулу. Вы должны найти h_i, d_i и M.
2
Используйте формулу линзы для вычисления d_i, если вы знаете расстояние от линзы до предмета и фокусное расстояние линзы. Формула линзы: 1/f = 1/d_o + 1/d_i, где f = фокусное расстояние линзы.
- В нашем примере:
  
  1/f = 1/d_o + 1/d_i
  
  1/20 = 1/50 + 1/d_i
  
  5/100 — 2/100 = 1/d_i
  
  3/100 = 1/d_i
  
  100/3 = d_i = 33,3 см
- Фокусное расстояние линзы – это расстояние от центра объектива до точки, в которой сходятся лучи света. В задачах фокусное расстояние, как правило, дано. В реальной жизни фокусное расстояние наносится на оправу линзы.^[3]
3
Теперь вы знаете d_o и d_i и можете найти высоту увеличенного изображения и увеличение линзы. Обратите внимание, что формула для вычисления увеличения включает два знака равенства (M = (h_i/h_o) = -(d_i/d_o)), то есть оба отношения равны, и вы можете воспользоваться этим фактом при вычислении M и h_i.
- В нашем примере найдите h_i следующим образом:
  
  (h_i/h_o) = -(d_i/d_o)
  
  (h_i/6) = -(33,3/50)
  
  h_i = -(33,3/50) × 6
  
  h_i = -3,996 см
- Обратите внимание, что отрицательная высота означает, что изображение будет перевернутым.
4
Для вычисления М используйте либо –(d_i/d_o), либо (h_i/h_o).
- В нашем примере:
  
  M = (h_i/h_o)
  
  M = (-3,996/6) = -0,666
- Вы получите тот же результат, используя значения d:
  
  M = -(d_i/d_o)
  
  M = -(33,3/50) = -0,666
- Обратите внимание, что увеличение не имеет единиц измерения.
5
Если у вас есть значение увеличения, вы можете предположить некоторые свойства изображения.
- Размер изображения. Чем больше значение М, тем больше изображение. Значения M между 1 и 0 свидетельствуют о том, что предмет через линзу будет выглядеть меньше.
- Ориентация изображения. Отрицательные значения М указывают на то, что изображение предмета будет перевернутым.
- В нашем примере М = -0,666, то есть изображение фигурки будет перевернутым и составлять две трети высоты фигурки.
6
В случае рассеивающей линзы используйте отрицательное значение фокусного расстояния. Это единственное отличие вычисления увеличения рассеивающей линзы от вычисления увеличения собирающей линзы (все формулы остаются теми же). В нашем примере этот факт повлияет на значение d_i.
- Проделаем вычисления для нашего примера еще раз, но при условии, что мы используем рассеивающую линзу с фокусным расстоянием -20 см. Все другие значениями остаются такими же.
- Во-первых, найдем d_i через формулу линзы:
  
  1/f = 1/d_o + 1/d_i
  
  1/-20 = 1/50 + 1/d_i
  
  -5/100 — 2/100 = 1/d_i
  
  -7/100 = 1/d_i
  
  -100/7 = d_i = -14,29 см
- Теперь найдем h_i и M.
  
  (h_i/h_o) = -(d_i/d_o)
  
  (h_i/6) = -(-14,29/50)
  
  h_i = -(-14,29/50) × 6
  
  h_i = 1,71 см
  
  M = (h_i/h_o)
  
  M = (1,71/6) = 0,285
Реклама

Две линзы

1
Найдите фокусное расстояние обеих линз. Когда вы имеете дело с системой, состоящей из двух линз, которые расположены параллельно друг другу (например, как в телескопе), вам нужно определить фокусное расстояние обеих линз, чтобы найти увеличение такой системы. Это можно сделать по формуле M = f_o/f_e.^[4]
- В формуле f_o – это фокусное расстояние линзы объектива, f_o – это фокусное расстояние линзы окуляра (к окуляру вы прикладываете глаз).
2
Подставьте значения фокусных расстояний в формулу, и вы найдете увеличение системы из двух линз.
- Например, рассмотрим телескоп, в котором фокусное расстояние линзы объектива равно 10 см, а фокусное расстояние линзы окуляра равно 5 см. М = 10/5 = 2.
Реклама

Детальный метод

1
Найдите расстояние между линзами и предметом. Если перед предметом расположены две линзы, можно вычислить увеличение конечного изображения, зная расстояния от предмета до линз, высоту предмета и фокусные расстояния обеих линз.
- Рассмотрим предыдущий пример – фигурку высотой 6 см, которая находится на расстоянии 50 см от собирающей линзы с фокусным расстоянием 20 см и на расстоянии 100 см от второй линзы с фокусным расстоянием 5 см. Найдите увеличение такой системы линз.
2
Найдите расстояние до изображения, его высоту и увеличение первой линзы. Начните с ближайшей к фигурке линзы и по формуле линзы найдите расстояние до изображения, а затем по формуле для вычисления увеличения найдите высоту изображения и увеличение.
- В предыдущем разделе мы выяснили, что первая линза дает изображение высотой -3,996 см, расстояние до изображения равно 33,3 см, а увеличение равно -0,666.
3
Используйте изображение от первой линзы в качестве предмета для второй линзы. Теперь вы можете найти увеличение второй линзы, высоту изображения и расстояние до него; для этого используйте те же методы, которые вы использовали для первой линзы, только в этот раз вместо фигурки воспользуйтесь изображением от первой линзы.
- В нашем примере изображение находится на расстоянии 33,3 см от первой линзы, поэтому находится на расстоянии 50-33,3 = 16,7 см от второй линзы. Найдем расстояние до изображения от второй линзы, используя найденное расстояние до предмета и фокусное расстояние второй линзы.
  
  1/f = 1/d_o + 1/d_i
  
  1/5 = 1/16,7 + 1/d_i
  
  0,2 — 0,0599 = 1/d_i
  
  0,14 = 1/d_i
  
  d_i = 7,14 см
- Теперь мы можем найти h_i и M для второй линзы:
  
  (h_i/h_o) = -(d_i/d_o)
  
  (h_i/-3,996) = -(7,14/16,7)
  
  h_i = -(0,427) × -3,996
  
  h_i = 1,71 см
  
  M = (h_i/h_o)
  
  M = (1,71/-3,996) = -0,428
4
Продолжайте описанный процесс вычислений для любого числа дополнительных линз. Для каждой последующей линзы предметом считайте изображение от предыдущей линзы и используйте формулу линзы и формулу для вычисления увеличения.
- Имейте в виду, что последующие линзы могут переворачивать изображение. Например, полученное выше значение увеличения (-0,428) свидетельствует о том, что изображение от второй линзы будет составлять 4/10 размера изображения предмета от первой линзы, но теперь изображение фигурки не будет перевернутым (вторая линза перевернет «перевернутое» изображение от первой линзы).
Реклама

Советы

На биноклях, как правило, стоит такая маркировка: число х число, например, 8×25 или 8×40. В этом случае первое число – это увеличение бинокля. Второе число относится к четкости изображения.
Заметьте, что для системы, состоящей из одной линзы, увеличение будет отрицательным в случае, если расстояние до предмета превышает фокусное расстояние линзы. Это не означает, что изображение предмета будет меньше его действительной высоты. Просто в данном случае изображение будет перевернутым.

Об этой статье

Эту страницу просматривали 32 013 раз.

Была ли эта статья полезной?

Источник