17 авг. 2022 г.
читать 3 мин
Выброс — это наблюдение, которое лежит аномально далеко от других значений в наборе данных. Выбросы могут быть проблематичными, поскольку они могут повлиять на результаты анализа.
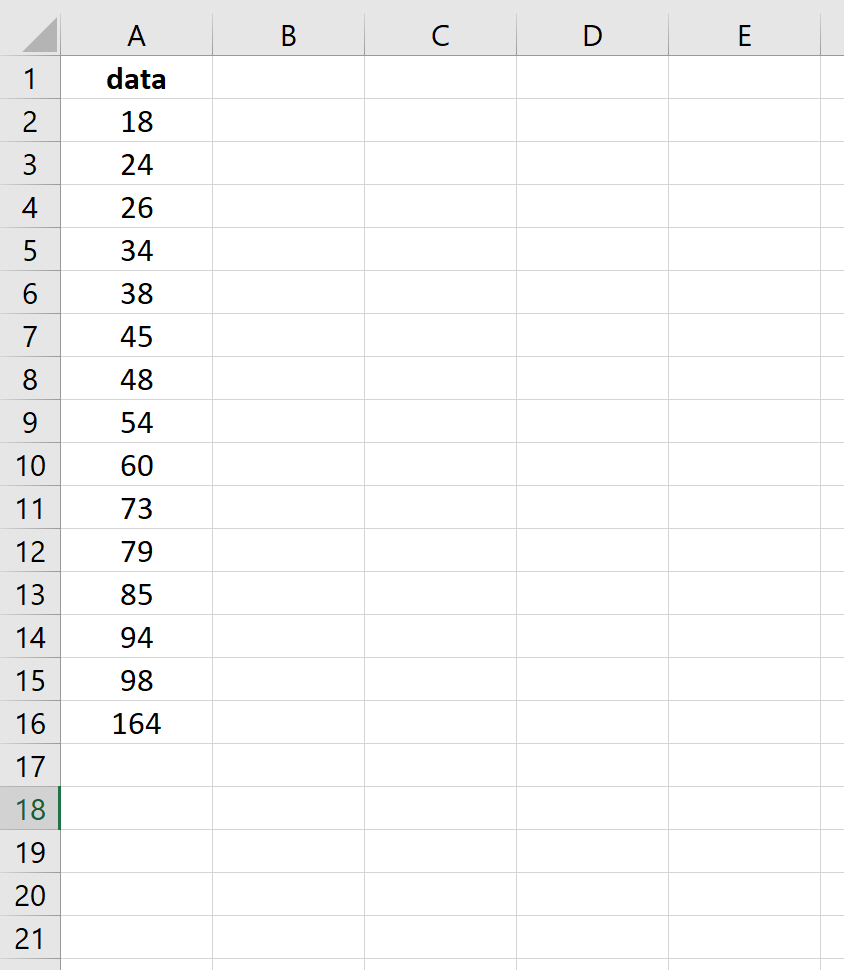
Мы будем использовать следующий набор данных в Excel, чтобы проиллюстрировать два метода поиска выбросов:
Связанный: Как рассчитать среднее значение, исключая выбросы в Excel
Метод 1: используйте межквартильный диапазон
Межквартильный размах (IQR) — это разница между 75-м процентилем (Q3) и 25-м процентилем (Q1) в наборе данных. Он измеряет разброс средних 50% значений.
Мы можем определить наблюдение как выброс, если оно в 1,5 раза превышает межквартильный размах, превышающий третий квартиль (Q3), или в 1,5 раза превышает межквартильный размах меньше, чем первый квартиль (Q1).
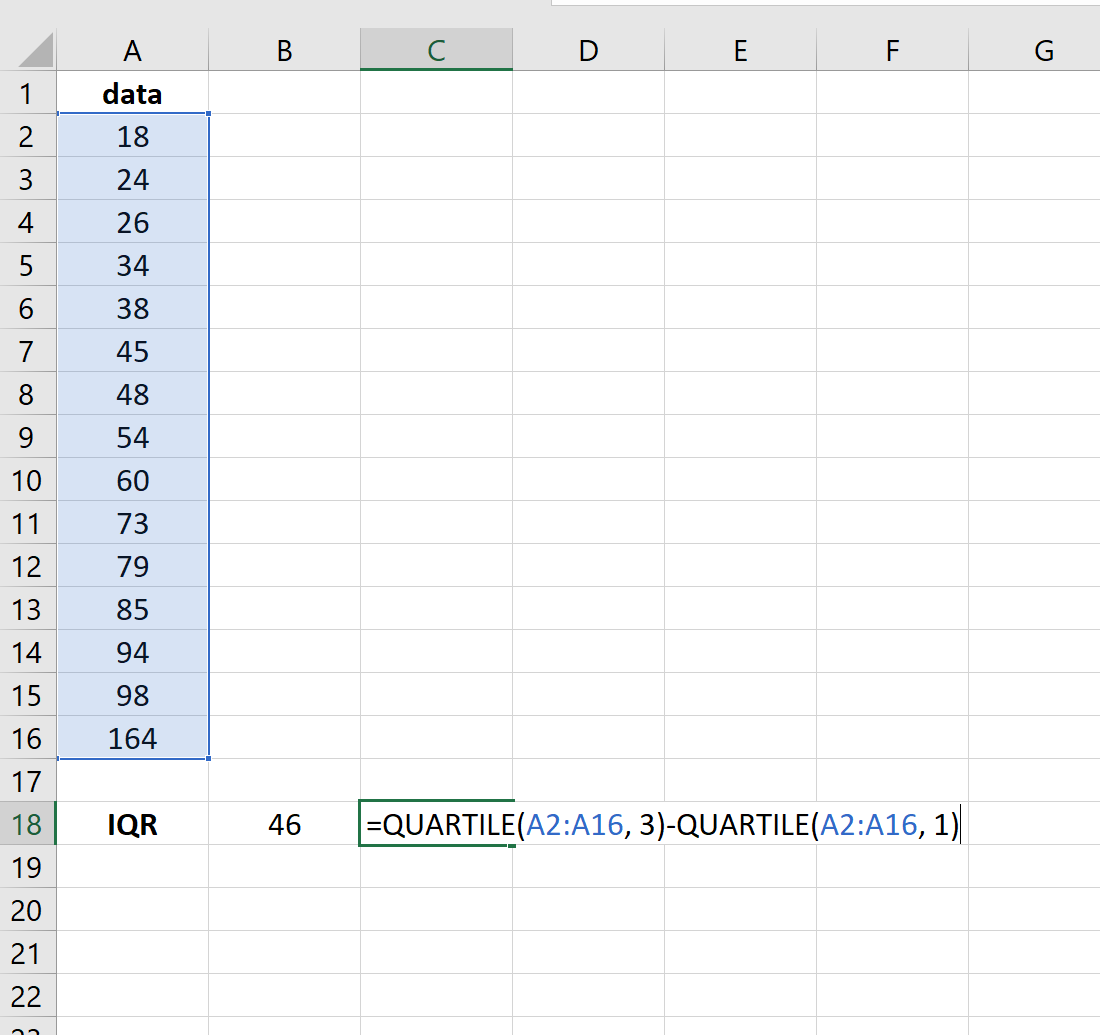
На следующем изображении показано, как рассчитать межквартильный диапазон в Excel:
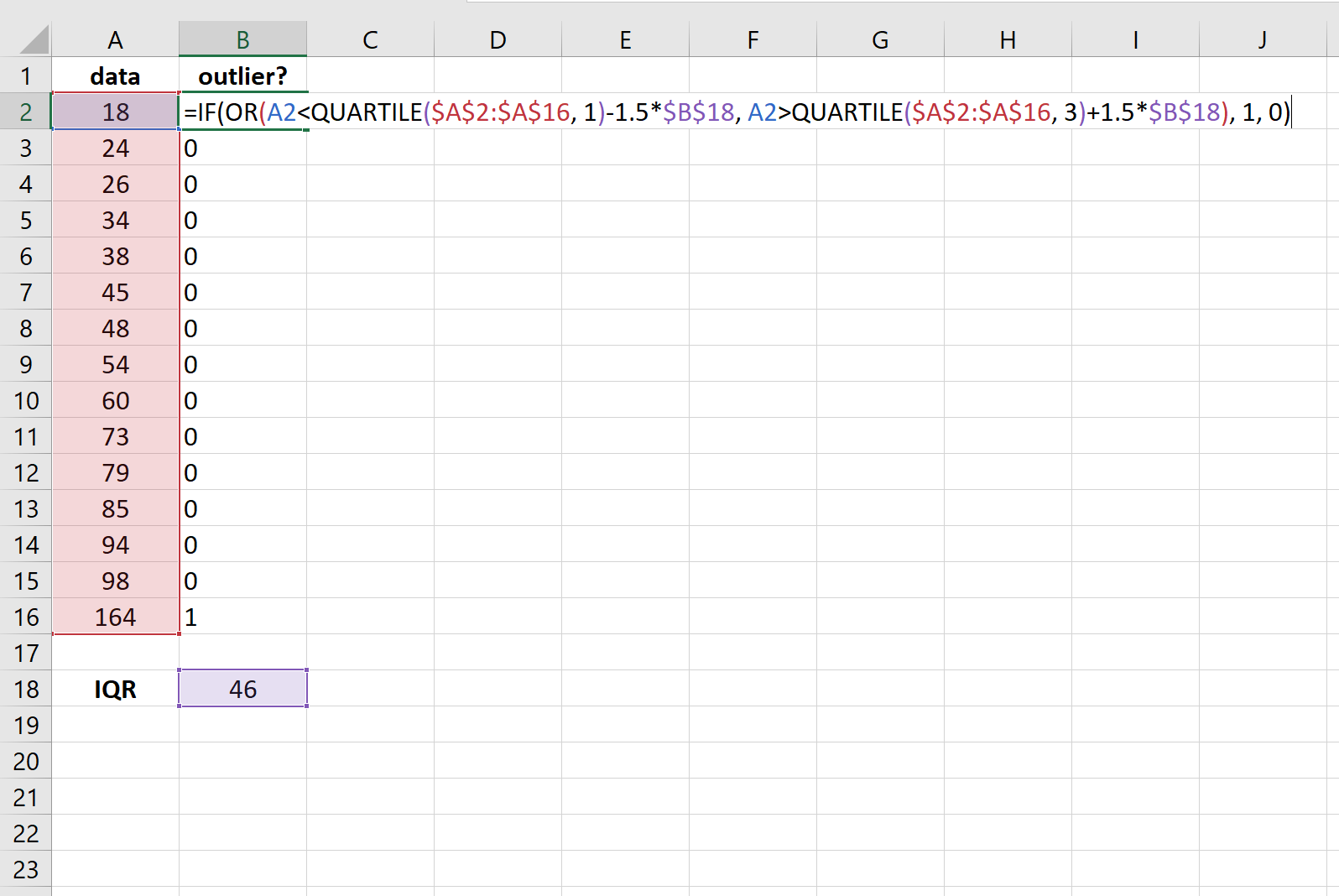
Затем мы можем использовать формулу, упомянутую выше, чтобы присвоить «1» любому значению, которое является выбросом в наборе данных:
Мы видим, что только одно значение — 164 — оказывается выбросом в этом наборе данных.
Способ 2: использовать z-показатели
Z-оценка показывает, сколько стандартных отклонений данного значения от среднего. Мы используем следующую формулу для расчета z-показателя:
z = (X — μ) / σ
куда:
- X — это одно необработанное значение данных.
- μ — среднее значение населения
- σ — стандартное отклонение населения
Мы можем определить наблюдение как выброс, если его z-оценка меньше -3 или больше 3.
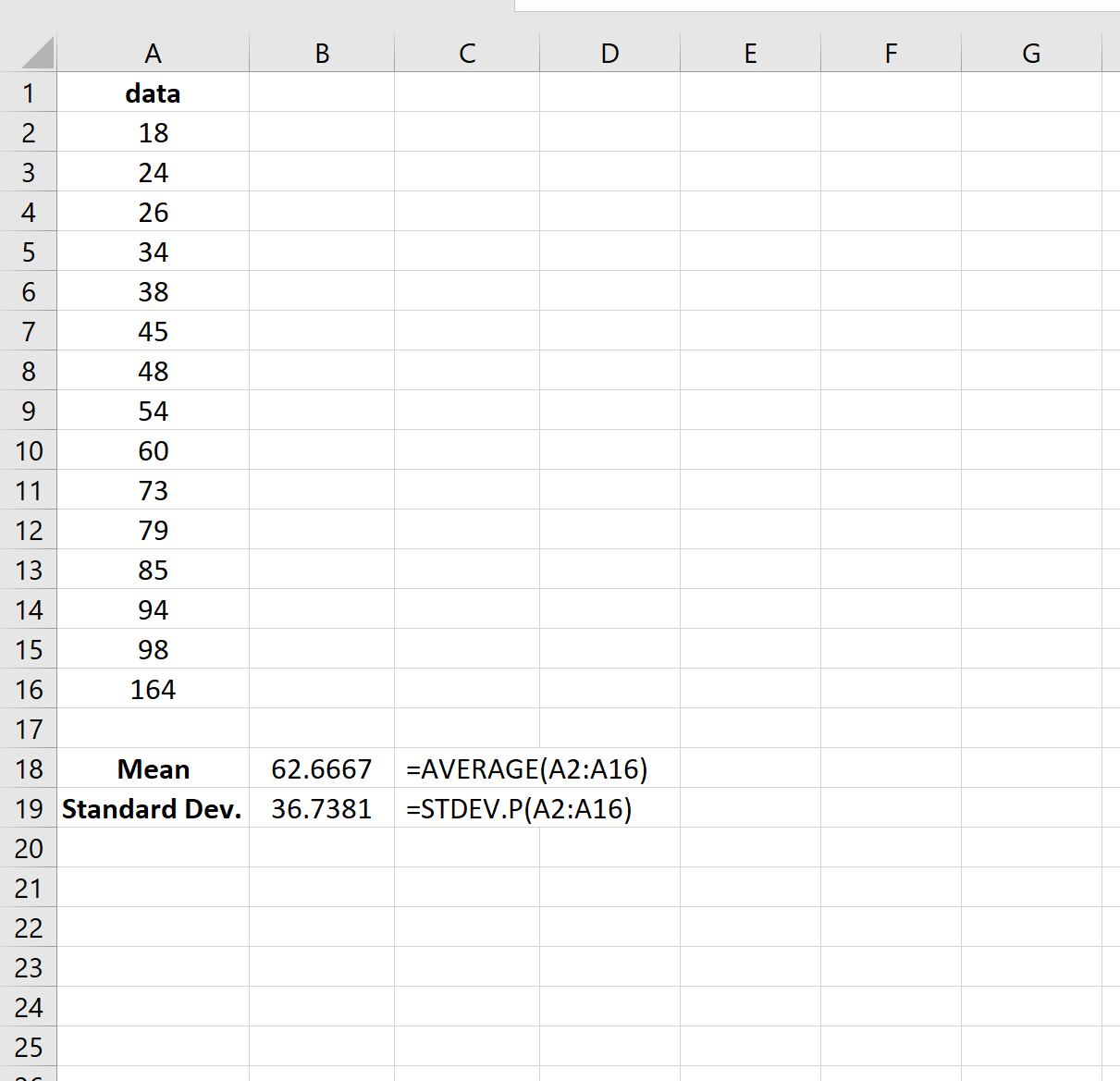
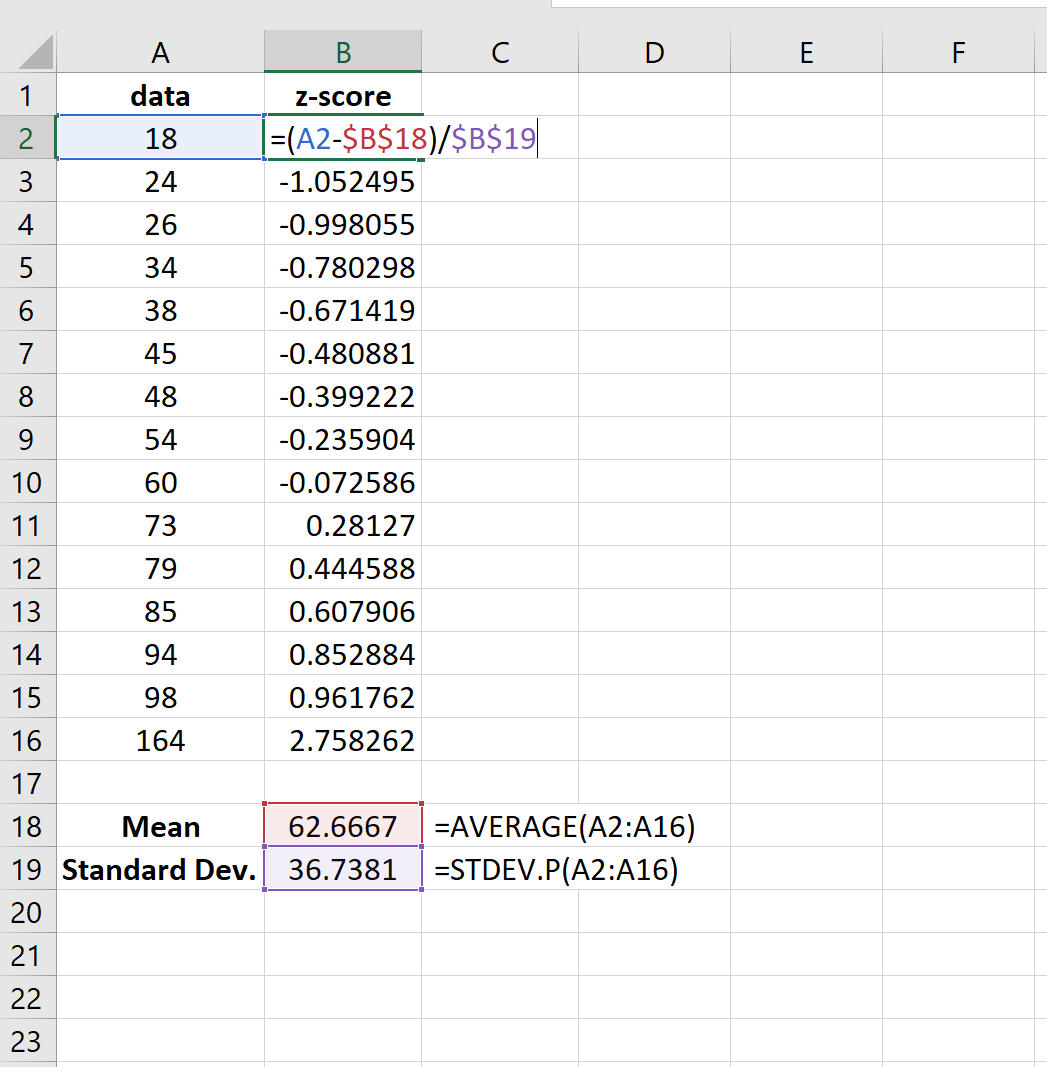
На следующем изображении показано, как рассчитать среднее значение и стандартное отклонение для набора данных в Excel:
Затем мы можем использовать среднее значение и стандартное отклонение, чтобы найти z-оценку для каждого отдельного значения в наборе данных:
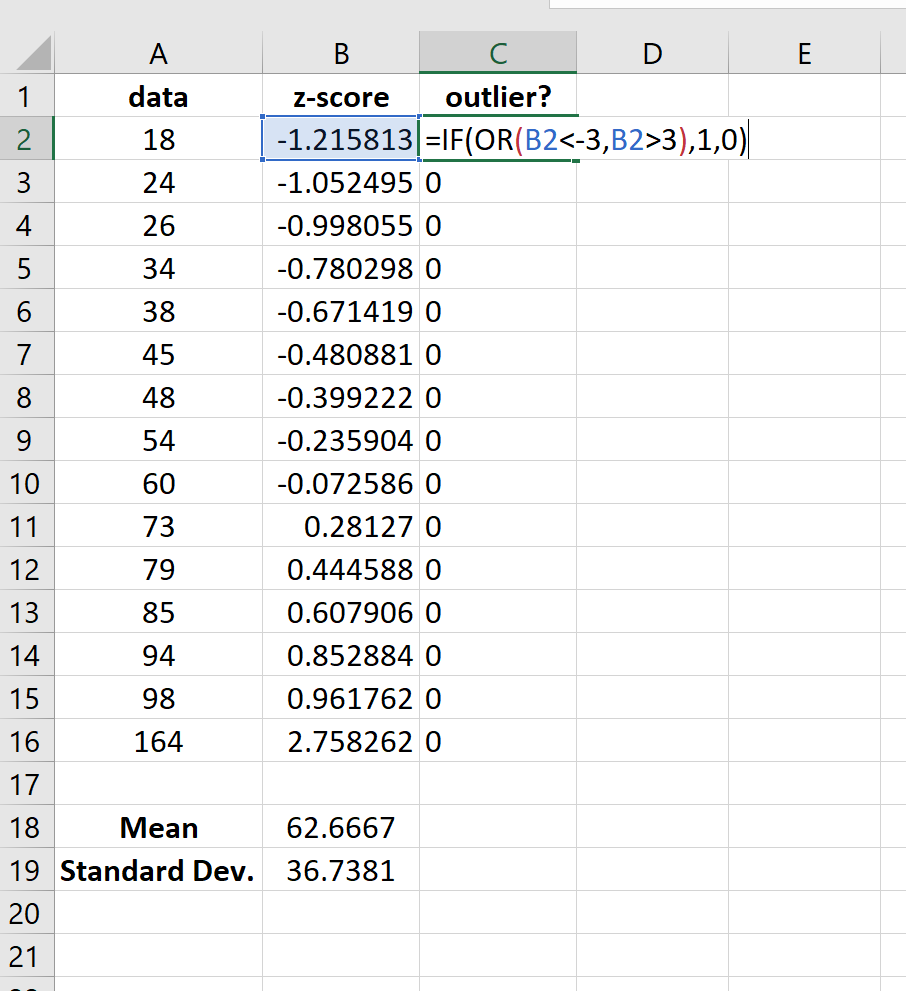
Затем мы можем присвоить «1» любому значению, которое имеет z-оценку меньше -3 или больше 3:
Используя этот метод, мы видим, что в наборе данных нет выбросов.
Примечание. Иногда вместо 3 используется z-показатель 2,5. В этом случае отдельное значение 164 будет считаться выбросом, поскольку его z-показатель больше 2,5. При использовании метода z-показателя руководствуйтесь своим здравым смыслом, какое значение z-показателя вы считаете выбросом.
Как обращаться с выбросами
Если в ваших данных присутствует выброс, у вас есть несколько вариантов:
1. Убедитесь, что выброс не является результатом ошибки ввода данных.
Иногда человек просто вводит неправильное значение данных при записи данных. Если присутствует выброс, сначала убедитесь, что значение было введено правильно и что это не ошибка.
2. Удалите выброс.
Если значение является истинным выбросом, вы можете удалить его, если оно окажет значительное влияние на общий анализ. Просто не забудьте упомянуть в своем окончательном отчете или анализе, что вы удалили выброс.
3. Присвойте новое значение выбросу .
Если выброс является результатом ошибки ввода данных, вы можете решить присвоить ему новое значение, такое как среднее или медиана набора данных.
Содержание:
- Что такое выбросы и почему их важно найти?
- Найдите выбросы путем сортировки данных
- Поиск выбросов с помощью квартильных функций
- Поиск выбросов с помощью функций НАИБОЛЬШИЙ / МАЛЕНЬКИЙ
- Как правильно обращаться с выбросами
- Удалить выбросы
- Нормализовать выбросы (отрегулировать значение)
При работе с данными в Excel у вас часто возникают проблемы с обработкой выбросов в наборе данных.
Выбросы довольно часто встречаются во всех видах данных, и важно идентифицировать и обрабатывать эти выбросы, чтобы убедиться, что ваш анализ правильный и значимый.
В этом уроке я покажу вам как найти выбросы в Excel, а также некоторые методы, которые я использовал в своей работе для обработки этих выбросов.
Что такое выбросы и почему их важно найти?
Выброс — это точка данных, которая выходит за рамки других точек данных в наборе данных. Если у вас есть выброс в данных, это может исказить ваши данные, что может привести к неверным выводам.
Приведу простой пример.
Допустим, 30 человек едут на автобусе из пункта назначения A в пункт назначения B. Все люди относятся к одной весовой группе и группе доходов. Для целей этого руководства давайте предположим, что средний вес составляет 220 фунтов, а средний годовой доход — 70 000 долларов.
Сейчас где-то посередине нашего маршрута автобус останавливается, и в него садится Билл Гейтс.
Как вы думаете, как это повлияет на средний вес и средний доход людей в автобусе?
Хотя средний вес вряд ли сильно изменится, средний доход пассажиров автобуса резко вырастет.
Это связано с тем, что доход Билла Гейтса является исключением в нашей группе, и это дает нам неправильную интерпретацию данных. Средний доход каждого пассажира автобуса составит несколько миллиардов долларов, что намного превышает реальную стоимость.
При работе с фактическими наборами данных в Excel вы можете иметь выбросы в любом направлении (например, положительный выброс или отрицательный выброс).
И чтобы убедиться, что ваш анализ верен, вам нужно каким-то образом идентифицировать эти выбросы, а затем решить, как лучше всего их лечить.
Теперь давайте рассмотрим несколько способов найти выбросы в Excel.
Найдите выбросы путем сортировки данных
С небольшими наборами данных быстрый способ определить выбросы — просто отсортировать данные и вручную просмотреть некоторые значения в верхней части отсортированных данных.
А так как выбросы могут быть в обоих направлениях, убедитесь, что вы сначала отсортировали данные в порядке возрастания, а затем в порядке убывания, а затем перебрали самые верхние значения.
Позвольте мне показать вам пример.
Ниже у меня есть набор данных, в котором у меня есть продолжительность звонков (в секундах) для 15 звонков в службу поддержки.
Ниже приведены шаги по сортировке этих данных, чтобы мы могли идентифицировать выбросы в наборе данных:
- Выберите заголовок столбца, который вы хотите отсортировать (в этом примере ячейка B1).
- Перейдите на вкладку «Главная«
- В группе «Редактирование» щелкните значок «Сортировка и фильтр».
- Щелкните Custom Sort (Пользовательская сортировка).
- В диалоговом окне «Сортировка» выберите «Продолжительность» в раскрывающемся списке «Сортировка по» и «От наибольшего к наименьшему» в раскрывающемся списке «Порядок».
- Нажмите ОК
Вышеупомянутые шаги сортируют столбец продолжительности звонка с наивысшими значениями вверху. Теперь вы можете вручную просмотреть данные и посмотреть, есть ли выбросы.
В нашем примере я вижу, что первые два значения намного выше остальных значений (а два нижних намного ниже).
Примечание. Этот метод работает с небольшими наборами данных, где вы можете вручную сканировать данные. Это не научный метод, но он хорошо работает
Поиск выбросов с помощью квартильных функций
Теперь давайте поговорим о более научном решении, которое поможет вам определить, есть ли какие-то выбросы.
В статистике квартиль составляет четверть набора данных. Например, если у вас есть 12 точек данных, то первый квартиль будет тремя нижними точками данных, второй квартиль будет следующими тремя точками данных и так далее.
Ниже приведен набор данных, по которому я хочу найти выбросы. Для этого мне нужно будет вычислить 1-й и 3-й квартили, а затем с его помощью вычислить верхний и нижний предел.
Ниже приведена формула для вычисления первого квартиля в ячейке E2:
= QUARTILE.INC ($ B $ 2: $ B $ 15,1)
и вот тот, который вычисляет третий квартиль в ячейке E3:
= QUARTILE.INC ($ B $ 2: $ B $ 15,3)
Теперь я могу использовать два вышеупомянутых вычисления, чтобы получить межквартильный размах (который составляет 50% наших данных в пределах 1-го и 3-го квартилей).
= F3-F2
Теперь мы будем использовать межквартильный диапазон, чтобы найти нижний и верхний предел, который будет содержать большую часть наших данных.
Все, что выходит за эти нижние и верхние пределы, будет считаться выбросом.
Ниже приведена формула для расчета нижнего предела:
= Квартиль1 - 1,5 * (Межквартильный диапазон)
который в нашем примере становится:
= F2-1,5 * F4
И формула для расчета верхнего предела:
= Квартиль3 + 1,5 * (Межквартильный диапазон)
который в нашем примере становится:
= F3 + 1,5 * F4
Теперь, когда у нас есть верхний и нижний предел в нашем наборе данных, мы можем вернуться к исходным данным и быстро определить те значения, которые не лежат в этом диапазоне.
Быстрый способ сделать это — проверить каждое значение и вернуть ИСТИНА или ЛОЖЬ в новом столбце.
Я использовал приведенную ниже формулу ИЛИ, чтобы получить ИСТИНА для тех значений, которые являются выбросами.
= ИЛИ (B2 $ F $ 6)
Теперь вы можете фильтровать столбец Outlier и отображать только те записи, для которых значение TRUE.
Кроме того, вы также можете использовать условное форматирование, чтобы выделить все ячейки, в которых значение TRUE.
Примечание: Хотя это более распространенный метод поиска выбросов в статистике. Я считаю, что этот метод немного непригоден для использования в реальных сценариях. В приведенном выше примере нижний предел, рассчитанный по формуле, равен -103, в то время как набор данных, который у нас есть, может быть только положительным. Таким образом, этот метод может помочь нам найти выбросы в одном направлении (высокие значения), он бесполезен при выявлении выбросов в другом направлении.
Поиск выбросов с помощью функций НАИБОЛЬШИЙ / МАЛЕНЬКИЙ
Если вы работаете с большим количеством данных (значения в нескольких столбцах), вы можете извлечь 5 или 7 наибольших и наименьших значений и посмотреть, есть ли в них выбросы.
Если есть какие-либо выбросы, вы сможете их идентифицировать, не просматривая все данные в обоих направлениях.
Предположим, у нас есть приведенный ниже набор данных, и мы хотим знать, есть ли какие-либо выбросы.
Ниже приведена формула, которая даст вам наибольшее значение в наборе данных:
= БОЛЬШОЙ ($ B $ 2: $ B $ 16,1)
Точно так же второе по величине значение будет равно
= БОЛЬШОЙ ($ B $ 2: $ B $ 16,1)
Если вы не используете Microsoft 365, в которой есть динамические массивы, вы можете использовать приведенную ниже формулу, и она даст вам пять наибольших значений из набора данных с помощью одной формулы:
= БОЛЬШОЙ ($ B $ 2: $ B $ 16; СТРОКА ($ 1: 5))
Точно так же, если вам нужны 5 наименьших значений, используйте следующую формулу:
= МАЛЕНЬКИЙ ($ B $ 2: $ B $ 16; СТРОКА ($ 1: 5))
или следующее, если у вас нет динамических массивов:
= МАЛЕНЬКИЙ ($ B $ 2: $ B $ 16,1)
Когда у вас есть эти значения, очень легко обнаружить любые выбросы в наборе данных.
Хотя я решил извлечь 5 наибольших и наименьших значений, вы можете выбрать 7 или 10 в зависимости от размера вашего набора данных.
Я не уверен, является ли это приемлемым методом для поиска выбросов в Excel или нет, но это метод, который я использовал, когда мне приходилось работать с большим количеством финансовых данных на моей работе несколько лет назад. По сравнению со всеми другими методами, описанными в этом руководстве, я считаю этот наиболее эффективным.
Как правильно обращаться с выбросами
До сих пор мы видели методы, которые помогут нам найти выбросы в нашем наборе данных. Но что делать, если вы знаете, что есть выбросы.
Вот несколько методов, которые вы можете использовать для обработки выбросов, чтобы ваш анализ данных был правильным.
Удалить выбросы
Самый простой способ удалить выбросы из набора данных — просто удалить их. Таким образом, это не исказит ваш анализ.
Это более жизнеспособное решение, когда у вас большие наборы данных и удаление пары выбросов не повлияет на общий анализ. И, конечно же, перед удалением данных обязательно создайте копию и выясните, что вызывает эти выбросы.
Нормализовать выбросы (отрегулировать значение)
Нормализация выбросов — это то, что я делал, когда работал полный рабочий день. Для всех значений выбросов я бы просто изменил их на значение, немного превышающее максимальное значение в наборе данных.
Это гарантирует, что я не удаляю данные, но в то же время не позволяю им искажать мои данные.
Чтобы дать вам реальный пример, если вы анализируете маржу чистой прибыли компаний, где большинство компаний находится в пределах от -10% до 30%, а есть несколько значений, превышающих 100%, я просто изменит эти выбросы на 30% или 35%.
Итак, вот некоторые из методов, которые вы можете использовать в Excel, чтобы найти выбросы.
После того, как вы определили выбросы, вы можете углубиться в данные и посмотреть, что их вызывает, и в то же время выбрать один из методов обработки этих выбросов (который может удалить их или нормализовать, изменив значение)
Надеюсь, вы нашли этот урок полезным.
В процессе анализ данных обычно прослеживается закономерность в том, что все значения колеблются возле определенного центрального уровня – медианы. Хотя очень часто некоторые из них выпадают далеко от центра. Такие значения называются статистическими выбросами (находятся далеко за прогнозируемым диапазоном). Статистические выбросы могут запачкать результаты статистического анализа, что может приводить к фальшивым или ошибочным выводам касающихся данных.
Как определить статистические выбросы и сделать выборку для их удаления в Excel
Для экспонирования и выделения цветом значений статистических выбросов от медианы можно использовать несколько простых формул и условное форматирование.
Первым шагом в поиске значений выбросов статистики является определение статистического центра диапазона данных. С этой целью необходимо сначала определить границы первого и третьего квартала. Определение границ квартала – значит разделение данных на 4 равные группы, которые содержат по 25% данных каждая. Группа, содержащая 25% наибольших значений, называется первым квартилем.
Границы квартилей в Excel можно легко определить с помощью простой функции КВАРТИЛЬ. Данная функция имеет 2 аргумента: диапазон данных и номер для получения желаемого квартиля.
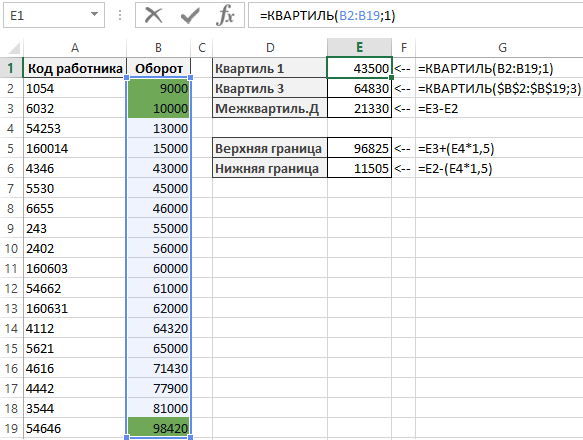
В примере показанному на рисунке ниже значения в ячейках E1 и E2 содержат показатели первого и третьего квартиля данных в диапазоне ячеек B2:B19:
Вычитая от значения первого квартиля третьего, можно определить набор 50% статистических данных, который называется межквартильным диапазоном. В ячейке E3 определен размер межквартильного диапазона.
В этом месте возникает вопрос, как сильно данное значение может отличаться от среднего значения 50% данных и оставаться все еще в пределах нормы? Статистические аналитики соглашаются с тем, что для определения нижней и верхней границы диапазона данных можно смело использовать коэффициент расширения 1,5 умножив на значение межквартильного диапазона. То есть:
- Нижняя граница диапазона данных равна: значение первого квартиля – межкваритльный диапазон * 1,5.
- Верхняя граница диапазона данных равна: значение третьего квартиля + расширенных диапазон * 1,5.
Как показано на рисунке ячейки E5 и E6 содержат вычисленные значения верхней и нижней границы диапазона данных. Каждое значение, которое больше верхней границы нормы или меньше нижней границы нормы считается значением статистического выброса.
Чтобы выделить цветом для улучшения визуального анализа данных можно создать простое правило для условного форматирования.
Выборка статистических выбросов с помощью квартилей в Excel
Чтобы создать правило для условного форматирования по выше описанным инструкциям, сделайте следующее:
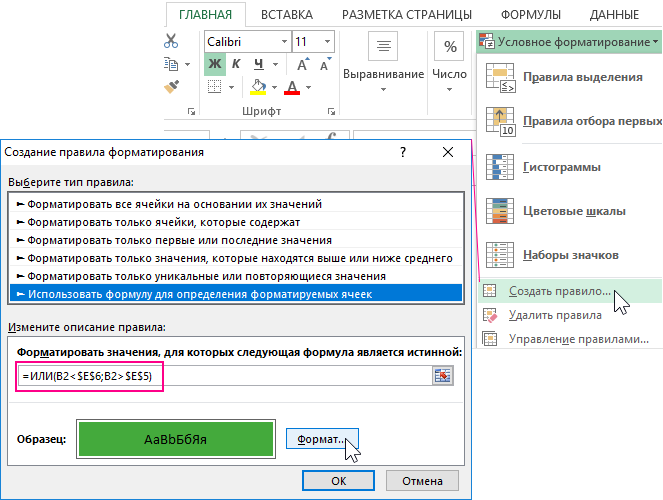
- Выделите целевой диапазон ячеек (в данном примере B2:B19) и выберите инструмент «ГЛАВНАЯ»-«Условное форматирование»-«Создать правило». Появится окно «Создание правила форматирования ячеек», как показано ниже на рисунке:
- Из списка в верхней части окна выберите опцию «Использовать формулу для определения форматируемых ячеек». Данная опция служит для анализа значений в ячейках выделенного диапазона, с помощью определенной формулы с логическим выражением. Если в результате вычислений формулой, по какому-то из значений будет возвращено логическое значение ИСТИНА, тогда в этой ячейке будет применятся условное форматирование.
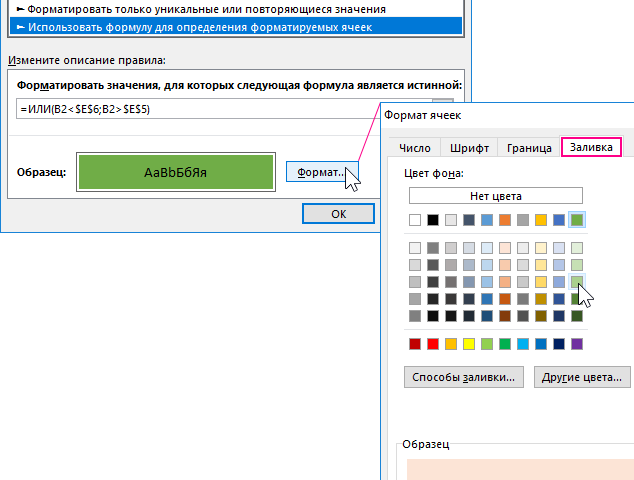
- В полю для введения формулы введите логическое выражение представленное на данном шаге. Обратите внимание на то, что в формуле используется относительная ссылка на целевую ячейку B2. А ссылки на верхнюю и нижнюю границу в ячейках $E$5 и $E$6 являются абсолютными. Два логических выражения помещены внутрь логической функции ИЛИ в качестве аргументов. Если значение целевой ячейки будет больше, чем верхняя граница или же меньше чем нижняя граница, тогда формула возвращает значение ИСТИНА и автоматически применяется условное форматирование.
=ИЛИ(B2<$E$6;B2>$E$5)
- Нажмите на кнопку «Формат» и появится окно «Формат ячеек», в котором находятся все опции для форматирования шрифтов, границ и заливки ячеек. После указания необходимых опций форматирования подтвердите их нажатием на кнопку «ОК» на всех открытых окнах, чтобы получить готовый результат.
В результате выделены цветом все ячейки, которые содержат значение статистического выброса от медианы.
На чтение 5 мин. Просмотров 4.1k. Опубликовано 21.06.2019
Содержание
- Быстрый пример
- Как найти выбросы в ваших данных
- Шаг первый: вычислите квартили
- Шаг второй: оценка межквартильного диапазона
- Шаг третий: вернуть нижнюю и верхнюю границы
- Шаг четвертый: выявить выбросы
- Игнорирование выбросов при расчете среднего значения
Выброс – это значение, которое значительно выше или ниже, чем большинство значений в ваших данных. При использовании Excel для анализа данных выбросы могут искажать результаты. Например, среднее значение набора данных может действительно отражать ваши значения. Excel предоставляет несколько полезных функций, которые помогут вам управлять своими выбросами, поэтому давайте взглянем.
Быстрый пример
На изображении ниже достаточно легко определить выбросы – значение двух, присвоенное Эрику, и значение 173, присвоенное Райану. В таком наборе данных достаточно легко определить и устранить эти выбросы вручную.

В большем наборе данных это не будет иметь место. Очень важно уметь определять выбросы и исключать их из статистических расчетов, и именно это мы и рассмотрим, как это сделать в этой статье.
Как найти выбросы в ваших данных
Чтобы найти выбросы в наборе данных, мы используем следующие шаги:
- Вычислите 1-й и 3-й квартили (мы немного поговорим о том, что это такое).
- Оцените межквартильный диапазон (мы также объясним это чуть ниже).
- Вернуть верхнюю и нижнюю границы нашего диапазона данных.
- Используйте эти границы для определения удаленных точек данных.
Диапазон ячеек справа от набора данных, показанного на рисунке ниже, будет использоваться для хранения этих значений.

Давайте начнем.
Шаг первый: вычислите квартили
Если вы разделите свои данные на кварталы, каждый из этих наборов называется квартилем. Самые низкие 25% чисел в диапазоне составляют 1-й квартиль, следующие 25% – 2-й квартиль и так далее. Сначала мы сделаем этот шаг, потому что наиболее широко используемое определение выброса – это точка данных, которая находится на расстоянии более 1,5 межквартильных диапазонов (IQR) ниже 1-го квартиля и 1,5 межквартильных диапазонов выше 3-го квартиля. Чтобы определить эти значения, мы сначала должны выяснить, что такое квартили.
Excel предоставляет функцию QUARTILE для расчета квартилей. Требуется две части информации: массив и кварт.
= QUARTILE (массив, кварт)
массив – это диапазон значений, которые вы оцениваете. И кварта – это число, представляющее квартиль, который вы хотите вернуть (например, 1 для 1-го квартиля, 2 для 2-го квартиля и т. Д.).
Примечание. В Excel 2010 Microsoft выпустила функции QUARTILE.INC и QUARTILE.EXC в качестве улучшений функции QUARTILE. QUARTILE более обратно совместим при работе с несколькими версиями Excel.
Давайте вернемся к нашему примеру таблицы.

Для вычисления 1-го квартиля мы можем использовать следующую формулу в ячейке F2.
= КВАРТИЛЬ (В2: B14,1)
При вводе формулы Excel предоставляет список параметров для аргумента кварта.

Чтобы вычислить третий квартиль, мы можем ввести формулу, аналогичную предыдущей, в ячейку F3, но используя три вместо одного.
= КВАРТИЛЬ (В2: B14,3)
Теперь у нас есть квартильные точки данных, отображаемые в ячейках.

Шаг второй: оценка межквартильного диапазона
Межквартильный диапазон (или IQR) – это средние 50% значений в ваших данных. Он рассчитывается как разница между значением 1-го квартиля и 3-го квартиля.
Мы собираемся использовать простую формулу в ячейке F4, которая вычитает 1-й квартиль из 3-го квартиля:
= F3-F2
Теперь мы можем видеть наш межквартильный диапазон.

Шаг третий: вернуть нижнюю и верхнюю границы
Нижние и верхние границы – это самые маленькие и самые большие значения диапазона данных, которые мы хотим использовать. Любые значения, меньшие или большие, чем эти связанные значения, являются выбросами.
Мы рассчитаем нижний предел границы в ячейке F5, умножив значение IQR на 1,5, а затем вычтя его из точки данных Q1:
= F2- (1,5 * F4)

Примечание . В этой формуле скобки не обязательны, так как часть умножения будет рассчитываться до части вычитания, но она облегчает чтение формулы.
Чтобы вычислить верхнюю границу в ячейке F6, мы снова умножим IQR на 1,5, но на этот раз добавим его в точку данных Q3:
= F3 + (1,5 * F4)

Шаг четвертый: выявить выбросы
Теперь, когда мы настроили все наши базовые данные, пришло время идентифицировать наши отдаленные точки данных – те, которые ниже, чем нижнее граничное значение, или выше, чем верхнее граничное значение.
Мы будем использовать функцию ИЛИ, чтобы выполнить этот логический тест и показать значения, которые соответствуют этим критериям, введя следующую формулу в ячейку C2:
= ИЛИ (В2 $ F $ 6)

Затем мы скопируем это значение в наши ячейки C3-C14. Значение TRUE указывает на выброс, и, как вы можете видеть, у нас есть два в наших данных.

Игнорирование выбросов при расчете среднего значения
Используя функцию QUARTILE, мы рассчитаем IQR и работаем с наиболее широко используемым определением выброса. Однако при расчете среднего значения для диапазона значений и игнорировании выбросов существует более быстрая и простая функция для использования. Этот метод не будет идентифицировать выброс как прежде, но он позволит нам быть гибкими с тем, что мы могли бы считать нашей частью выброса.
Функция, которая нам нужна, называется TRIMMEAN, и вы можете увидеть ее синтаксис ниже:
= TRIMMEAN (массив, проценты)
массив – это диапазон значений, которые вы хотите усреднить. процент – это процент точек данных, которые нужно исключить из верхней и нижней частей набора данных (вы можете ввести его в процентах или десятичном значении).
Мы ввели формулу ниже в ячейку D3 в нашем примере, чтобы вычислить среднее значение и исключить 20% выбросов.
= TRIMMEAN (B2: B14, 20%)

Там у вас есть две разные функции для обработки выбросов. Независимо от того, хотите ли вы определить их для каких-либо потребностей в отчетности или исключить их из вычислений, таких как средние значения, в Excel есть функция, отвечающая вашим потребностям.
Outliers as the name suggest are something that doesn’t fall in the required/given range. Outliers in statistics need to be removed because they affect the decision that is to be made after performing the required calculations. Outliers generally make the decision skewed i.e they move the decision in a positive or negative direction. Sometimes it is easy to find an outlier by looking at the data but it is difficult to find an outlier when the data is large. We’ll see this with the help of an example, given a dataset and you need to perform the average of the dataset 1, 89, 57, 100, 150, 139, 49, 87, 200, 250. So, the average of the given data set is 112.2. But, it is clearly visible that 1, 200, and 250 are ranges that are too small or too large to be a part of the dataset. These ranges are known as outliers in data. After removing the outliers, the average becomes 95.85. It is evidently seen from the above example that an outlier will make decisions based.
Finding Outliers using Sorting in Excel
This is one of the easiest ways to find outliers in MS excel when your data is not huge because by having a look at the data you’ll get to know about the values that are far away from the originally recorded values.
From the above image, we can clearly tell that the data is not sorted and hence it would take some time for us to identify outliers.
While looking at Img. 2, we can clearly say that the numbers 1, 200, and 250 are outliers.
Finding Outliers using LARGE/SMALL Excel Function
Another way to find outlier is by using built-in MS Excel functions known as LARGE and SMALL. The LARGE function will return the largest value from the array of data and the SMALL function will return the smallest value. Here, we will be using a LARGE and SMALL function which is an in-built function in Microsoft excel. Consider the example used above:
LARGE Function Syntax:
LARGE($B$1:$B$12, 1)
Here, we are passing an array and a number. The array has the dataset for which we have to find the outlier and the number, 1, represents the first largest number from the array. If we use 2, it will return the second largest value from the array. Now when we use this function in the above example, we will get the following output:
SMALL Function Syntax:
SMALL($B$1:$B$12, 1)
The syntax and pass-on value are the same. Now when we use this function in the above example, we will get the following output:
Note: If there are multiple outliers in the data then you have to use the function again and again.
Finding Outliers using Inter Quartile Range(IQR)
The data presented in the above example has a small sample size but when it comes to a real-life situation, the data can be huge, and that’s where the original problem arrives. As per IQR, An outlier is any point of data that lies over 1.5 times IQRs below the first quartile (Q1) and 1.5 times IQR above the third quartile (Q3)in a data set.
Formula is
High = Q3 + 1.5 * IQR
Low = Q1 – 1.5 * IQR
Finding Outliers using the following steps:
Step 1: Open the worksheet where the data to find outlier is stored.
Step 2: Add the function QUARTILE(array, quart), where an array is the data set for which the quartile is being calculated and a quart is the quartile number. In our case, the quart is 1 because we wish to calculate the 1st quartile to calculate the lowest outlier.
| Quart Number | Quartile Returns |
| 0 | Minimum Value |
| 1 | First quartile(25th percentile) |
| 2 | Median Value(50th percentile) |
| 3 | Third Quartile(75th percentile) |
| 4 | Maximum Value |
Step 3: Similar to step 2 add the quartile formula under Q3 and write 3 as quart number because we wish to calculate the 3rd quartile i.e 75th percentile to calculate the highest quartile value.
Step 4: Inter Quartile Range or IQR is Q3-Q1, put the formula to get the IQR value.
Step 5: To find the High value, the formula is Q3+(1.5*IQR). Similarly, for Low value, the formula is Q1-(1.5*IQR)
Step 6: To find whether the number in the data set is an outlier or not, we need to check whether the data entry is higher than the High value or lower than the Low value. To perform this we will use the OR function. The formula will be OR(B3>$G$3, B3<$H$3). Put the formula in the required cell and drag down the cell adjacent to the last data set, if the value returns TRUE, then the data is an outlier otherwise not.
Since you’ve checked for the outlier data. Now you can remove the outliers and use the rest data for calculations and get unbiased results.
Last Updated :
28 Mar, 2022
Like Article
Save Article