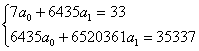Вариант
6 задача 1.
Имеются следующие отчетные данные 30
предприятий отрасли:
|
Номер |
Среднесписочная |
Объем |
Номер |
Среднесписочная |
Объем |
|
1 |
1595 |
100454 |
16 |
846 |
45654 |
|
2 |
1284 |
75156 |
17 |
2388 |
167129 |
|
3 |
1323 |
79208 |
18 |
1868 |
124823 |
|
4 |
2028 |
135876 |
19 |
1161 |
64836 |
|
5 |
1025 |
57372 |
20 |
1298 |
76553 |
|
6 |
1731 |
109203 |
21 |
1244 |
73491 |
|
7 |
1427 |
84164 |
22 |
921 |
51392 |
|
8 |
1923 |
129141 |
23 |
2400 |
168032 |
|
9 |
600 |
32430 |
24 |
1394 |
82380 |
|
10 |
1538 |
96863 |
25 |
1122 |
63084 |
|
11 |
2169 |
151830 |
26 |
1191 |
66929 |
|
12 |
2078 |
139463 |
27 |
1688 |
106310 |
|
13 |
1454 |
85757 |
28 |
1278 |
75564 |
|
14 |
1097 |
61254 |
29 |
1626 |
102438 |
|
15 |
1499 |
88562 |
30 |
1796 |
112970 |
С целью изучения зависимости между
среднесписочной численностью
промышленно-производственного персонала
и объемом производства продукции
произвести группировку предприятий по
среднесписочной численности
промышленно-производственного персонала,
образовав шесть групп с равными
интервалами.
По каждой группе и по совокупности
предприятия в целом посчитайте:
1) число предприятий;
2) среднесписочную численность
промышленно-производственного персонала
(всего и в среднем на одно предприятие);
3) объем производства продукции (всего
и в среднем на одно предприятие);
4) объем производства продукции на одного
среднесписочного работника
(производительность труда).
Результаты представить в виде групповой
таблицы. Сделать выводы.
Решение:
1)
Для группировки предприятий по
среднесписочной численности
промышленно-производственного персонала
определим границы групп (интервалов).
Величину
равного интервала i
найдем по формуле:

где
Xmax,
Xmin,
— соответственно максимальное и
минимальное значения группировочного
признака;
n
– число групп (интервалов).
Верхнюю
границу интервала очередной группы
определим путем прибавления к нижней
ее границе величины интервала:
Xнижн+i=Xверхн;
(чел.)
Результаты
аналитической группировки статистических
данных занесем в итоговую таблицу 2.
Таблица
2 – Аналитическая группировка
статистических данных
|
Среднесписочная |
Количество |
|
600-900 |
2 |
|
900-1200 |
6 |
|
1200-1500 |
9 |
|
1500-1800 |
6 |
|
1800-2100 |
4 |
|
2100-2400 |
3 |
|
Итого |
30 |
Таким образом, как видно из данных
таблицы 2, наибольшее количество
предприятий – 9 принадлежит к третьей
группе со среднесписочной численностью
промышленно-производственного персонала
от 1200 до 1500 чел., наименьшее количество
предприятий – 2 со среднесписочной
численностью промышленно-производственного
персонала 600-900 чел.
Таблица 3 — Сводная таблица расчета
среднесписочной численности
промышленно-производственного персонала
|
№ группы |
Количество |
Среднесписочная |
Объем |
|
1 |
2 |
3 |
4 |
|
1 |
2 |
600 |
32430 |
|
846 |
45654 |
||
|
Итого |
1446 |
78084 |
|
|
2 |
6 |
921 |
51392 |
|
1025 |
57372 |
||
|
1097 |
61254 |
||
|
1122 |
63084 |
||
|
1161 |
64836 |
||
|
1191 |
66929 |
||
|
Итого |
6517 |
364867 |
|
|
Продолжение |
|||
|
3 |
9 |
1244 |
73491 |
|
1278 |
75564 |
||
|
1284 |
75156 |
||
|
1298 |
76553 |
||
|
1323 |
79208 |
||
|
1394 |
82380 |
||
|
1427 |
84164 |
||
|
1454 |
85757 |
||
|
1499 |
88562 |
||
|
Итого |
12201 |
720835 |
|
|
4 |
6 |
1538 |
96863 |
|
1595 |
100454 |
||
|
1626 |
102438 |
||
|
1688 |
106310 |
||
|
1731 |
109203 |
||
|
1796 |
112970 |
||
|
Итого |
9974 |
628328 |
|
|
5 |
4 |
1868 |
124823 |
|
1923 |
129141 |
||
|
2028 |
135876 |
||
|
2078 |
139463 |
||
|
Итого |
7897 |
529303 |
|
|
6 |
3 |
2169 |
151830 |
|
2388 |
167129 |
||
|
2400 |
168032 |
||
|
Итого |
6957 |
486991 |
|
|
Всего |
44992 |
2808318 |
Как видно из таблицы 3, среднесписочная
численность промышленно-производственного
персонала за отчетный период в целом
по совокупности составляет 44992 человека,
при этом, по первой группе предприятий
– 1446 чел., второй – 6517 чел., третьей –
12201 чел., четвертой – 9974, пятой – 7897 чел.,
по шестой – 6957 чел.
Среднесписочную численность
промышленно-производственного персонала
в среднем на одно предприятие, найдем:
чел.
Среднесписочная численность
промышленно-производственного персонала
(чел.) по группам:
1 группа –
чел.
2 группа –
чел.
3 группа –
чел.
4 группа –
чел.
5 группа –
чел.
6 группа –
чел.
3) Объем производства продукции на одного
среднесписочного работника
(производительность труда) в целом:
млн. руб./чел.
млн. руб./чел.
Объем производства продукции на одного
среднесписочного работника
(производительность труда) по каждой
группе (млн. руб./чел):
1 группа –
млн. руб./чел
2 группа –
млн. руб./чел
3 группа –
млн. руб./чел
4 группа –
млн. руб./чел
5 группа –
млн. руб./чел
5 группа –
млн. руб./чел
Представим полученные результаты в
виде групповой таблицы.
Таблица 4 – Итоговая групповая таблица
|
Среднесписочная |
Количество |
Среднесписочная |
Объем |
|
600-900 |
2 |
1446 |
54,0 |
|
900-1200 |
6 |
6517 |
56.0 |
|
1200-1500 |
9 |
12201 |
59,1 |
|
1500-1800 |
6 |
9974 |
63,0 |
|
1800-2100 |
4 |
7897 |
67,0 |
|
2100-2400 |
3 |
6957 |
70,0 |
|
Итого |
30 |
1500 |
62.4 |
Итак, наибольшее количество предприятий
(9) по среднесписочной численности
промышленно-производственного персонала
в общем количестве предприятий (30) имеет
третья группа, в которой работает 12201
человек.
Напротив, наименьшее количество
предприятий (2) с количеством работающих
(1446 чел.) имеет первая группа с объемом
произведенной продукции 78084 млн. руб.,
здесь наблюдается самая низкая по всей
совокупности производительность труда
– 54 млн. руб./чел.
Среднесписочная численность
промышленно-производственного персонала
за отчетный период в целом по совокупности
составляет 44992 человек, а в среднем на
одно предприятие – 1500 чел.
Объем производства продукции на одного
среднесписочного работника
(производительность труда) в целом
составил 50 млн. руб./чел. При этом
наблюдается зависимость, что чем больше
работников сосредоточено на одном
предприятии, тем выше производительность
труда.
Вариант 1 задача 2.
Имеются следующие данные о распределении
работников предприятия по длительности
производственного стажа:
|
Группы |
Число |
||
|
Всего |
В |
||
|
цех |
цех |
||
|
Менее |
18 |
8 |
10 |
|
От 1 |
34 |
16 |
18 |
|
От 3 |
76 |
34 |
42 |
|
От 6 |
48 |
28 |
20 |
|
От 11 |
24 |
14 |
10 |
|
Итого |
200 |
100 |
100 |
На основании имеющихся данных
определите по цехам предприятия и по
предприятию в целом:
1) средний производственный стаж
работников;
2) модальные и медианные значения
производственного стажа работников.
Поясните экономическое содержание этих
показателей;
3) абсолютные показатели вариации
производственного стажа работников;
4) относительные показатели вариации
производственного стажа работников.
Сравните вариацию стажа работников по
цехам предприятия и по предприятию в
целом.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Определение средней численности работников на одно предприятие. Расчет дисперсии и среднего квадратического отклонения
Страницы работы
Фрагмент текста работы
Содержание
Задача 1. 3
Задача 2. 5
Задача 3. 6
Задача 4. 8
Задача 5. 10
Задача 6. 11
Задача 7. 13
Список литература. 15
Задача 1
Распределение предприятий
по численности работников:
|
Группы |
Число |
|
До 2 |
14 |
|
2-4 |
28 |
|
4-6 |
31 |
|
6-8 |
18 |
|
8 и |
9 |
Определите:
1) среднюю численность работников
на одно предприятие;
2) дисперсию и среднее
квадратическое отклонение;
3) коэффициент вариации;
4)
модальную численность работников
предприятий.
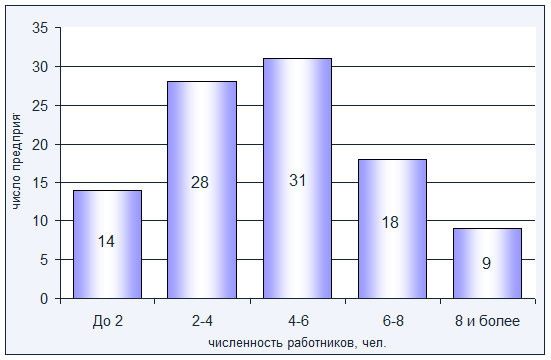
Постройте
график распределения предприятий по численности работников. Сделайте выводы.
Решение:
1)
Рассчитаем среднюю численность работников на предприятии используя формулу:
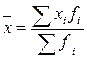
где –
среднее значение признака;
– значение признака у
отдельных единиц совокупности, ;
– частота признака.
Вспомогательные
вычисления занесем в таблицу:
|
Группы |
Число |
Середина хi |
хi |
|
( |
( |
|
До 2 |
14 |
1 |
14 |
-3,6 |
12,96 |
181,44 |
|
2-4 |
28 |
3 |
84 |
-1,6 |
2,56 |
71,68 |
|
4-6 |
31 |
5 |
155 |
0,4 |
0,16 |
4,96 |
|
6-8 |
18 |
7 |
126 |
2,4 |
5,76 |
103,68 |
|
8 и |
9 |
9 |
81 |
4,4 |
19,36 |
174,24 |
|
Сумма |
100 |
– |
460 |
– |
– |
536 |
Используя
полученные данные, рассчитаем значение средней численности работников на
предприятии:
чел.
2) Определим
показатели вариации – дисперсию и среднее квадратическое отклонение:
Дисперсия равна:
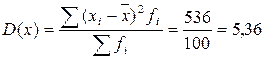
Среднее
квадратическое отклонение:
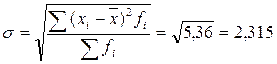
3) Определим
степень отклонения индивидуальных значений признака от среднего уровня:
4) Значение
моды определяем по формуле:
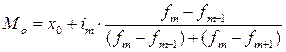
где –
начало модального интервала (минимальное значение признака в модальном
интервале);
– величина соответственно
модального интервала;
– частота модального, до и
послемодального интервалов соответственно.
Модальный
интервал – интервал с наибольшей частотой признака, в нашей задаче это интервал
от 4 до 6 чел. Подставляем исходные значения и получаем:
чел.
Построим
гистограмму распределения численности работников по предприятиям, для этого по
оси абсцисс отложим значения численности работников, а по оси ординат –
частоты:
Выводы:
1)
средняя
численность работников на предприятии составляет 4,6 чел.;
2)
отклонение
от средней численности составляет 2,315 чел. или 50,33%, вариация признака
сильная;
3)
наиболее
часто встречается численность работников, равная 4,375 чел.
Задача 2
Для определения среднего
размера кредита по одному из банков с общим числом заемщиков 5000, необходимо
провести выборку счетов методом механического отбора. Предварительно
установлено, что среднее квадратическое отклонение размера кредита составляет
10000 руб.
Определите
необходимую численность выборки при условии, что с вероятностью 0,954 ошибка выборки
не превысит 1000 рублей.
Решение:
Необходимый объем
бесповторной выборки для механического отбора можно определить при помощи
формулы:
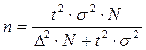
предельная ошибка выборки;
σ2 – выборочная дисперсия;
t – коэффициент доверия, который
вычисляется при помощи таблицы;
N– объем генеральной совокупности;
n – численность выборки.
Коэффициент
доверия при вероятности Р = 0,954 составляет t = 2.
Подставив
исходные данные получим:
Вывод: для того, чтобы ошибка выборки при проведении исследования не
превысила 1000 руб. с вероятностью 0,954, необходимо исследовать не менее 371
заемщика.
Задача 3
Ежегодные темпы
прироста реализации товара «А» составили в % к предыдущему году: 1998 – 5,5;
1999 – 6,2; 2000 – 8,4; 2001 – 10,5; 2002 – 9,2.
Исчислите
за приведенные годы базисные темпы динамики по отношению к 1997 году и
среднегодовой темп прироста за 1998-2002 гг.
Решение:
Вычислим
коэффициенты цепные коэффициенты роста для каждого года:
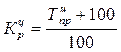
где – цепной темп прироста.
Далее
вычислим базисные коэффициенты роста, используя связь цепных и базисных
показателей:
Соответственно темпы роста
и прироста составят:
Занесем
показатели в таблицу:
|
Год |
Коэффициент |
Темп |
Темп |
|||
|
цепные |
базисные |
цепные |
базисные |
цепные |
базисные |
|
|
1998 |
1,055 |
1,055 |
105,5 |
105,5 |
5,5 |
5,5 |
|
1999 |
1,062 |
1,12 |
106,2 |
112 |
6,2 |
12 |
|
2000 |
1,084 |
1,215 |
108,4 |
121,5 |
8,4 |
21,5 |
|
2001 |
1,105 |
1,342 |
110,5 |
134,2 |
10,5 |
34,2 |
|
2002 |
1,092 |
1,465 |
109,2 |
146,5 |
9,2 |
46,5 |
Определим
среднегодовой темп роста:
Среднегодовой
темп прироста:
Задача 4
Имеются данные о
спросе на книжную продукцию и структуре оборота книжного издательства в
отчетном году:
|
Стратегическая единица |
Спрос на продукцию, тыс. экз. |
Доля в общем обороте издательства, % |
|
Классика |
20 |
0 |
|
Детская литература |
100 |
1,0 |
|
Зарубежный детектив |
60 |
49,5 |
|
Российский детектив |
120 |
20,5 |
|
Женский роман |
90 |
6,8 |
|
Фантастика |
50 |
0 |
|
Приключения |
30 |
1,0 |
|
Специальная литература |
110 |
14,3 |
|
Рекламная продукция |
60 |
4,9 |
|
Прочая литература |
80 |
2,0 |
Определите уровень
согласованности между спросом на книжную продукцию и структурой оборота
издательства с помощью коэффициентов корреляции Спирмена и Фехнера.
Решение:
Коэффициент
ранговой корреляции Спирмена рассчитывается следующим образом:
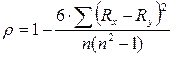
где Rx – ранг признака Х;
Ry – ранг признака У;
n– число наблюдений.
Составим
вспомогательную таблицу:
|
Стратегическая |
Спрос |
Доля |
Rx |
Ry |
|
|
|
Классика |
20 |
0 |
1 |
1,5 |
-0,5 |
0,25 |
|
Фантастика |
50 |
0 |
3 |
1,5 |
1,5 |
2,25 |
|
Приключения |
30 |
1 |
2 |
3,5 |
-1,5 |
2,25 |
|
Детская литература |
100 |
1 |
8 |
3,5 |
4,5 |
20,25 |
|
Прочая литература |
80 |
2 |
6 |
5 |
1 |
1 |
|
Рекламная |
60 |
4,9 |
4,5 |
6 |
-1,5 |
2,25 |
|
Женский роман |
90 |
6,8 |
7 |
7 |
0 |
0 |
|
Специальная литература |
110 |
14,3 |
9 |
8 |
1 |
1 |
|
Российский |
120 |
20,5 |
10 |
9 |
1 |
1 |
|
Зарубежный |
60 |
49,5 |
4,5 |
10 |
-5,5 |
30,25 |
|
Сумма |
– |
– |
– |
– |
– |
60,5 |
Подставляя полученные значения в
формулу, получаем:
Коэффициент
корреляции рангов Фехнера равен:
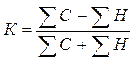
знаков отклонений от среднего ранга;
Н – ситуация несовпадений
знаков отклонений от среднего ранга.
Средний ранг
равен: .
Составим
вспомогательную таблицу для расчета коэффициента Фехнера:
|
Стратегическая |
Спрос |
Доля |
Rx |
Ry |
Rx— |
Ry — |
|
Классика |
20 |
0 |
1 |
1,5 |
– |
– |
|
Фантастика |
50 |
0 |
3 |
1,5 |
– |
– |
|
Приключения |
30 |
1 |
2 |
3,5 |
– |
– |
|
Детская литература |
100 |
1 |
8 |
3,5 |
+ |
– |
|
Прочая литература |
80 |
2 |
6 |
5 |
+ |
– |
|
Рекламная |
60 |
4,9 |
4,5 |
6 |
– |
+ |
|
Женский роман |
90 |
6,8 |
7 |
7 |
+ |
+ |
|
Специальная |
110 |
14,3 |
9 |
8 |
+ |
+ |
|
Российский |
120 |
20,5 |
10 |
9 |
+ |
+ |
|
Зарубежный |
60 |
49,5 |
4,5 |
10 |
– |
+ |
Итак,
Рассчитанные коэффициенты
позволяют говорить о слабой зависимости
Похожие материалы
- Предмет, метод, задачи статистики. Статистическое наблюдение. Сводка и группировка статистических данных
- Порядок построения взвешенных средних величин
- Характеристика статистического распределения. Мода. Медиана. Порядок построения динамических рядов. Сопоставимость уровней ряда. Аналитическое выравнивание динамических рядов
Информация о работе
На основе данных приведенной ниже таблицы необходимо произвести группировку торговых предприятий по скорости оборота товарных запасов (расчет произвести с точностью до 0,1).
Результаты группировки изложите в табличной форме. Каждую группу и совокупность предприятий в целом охарактеризуйте:
1) количеством предприятий в абсолютном и относительном выражении;
2) числом оборотов в среднем на 1 предприятие;
3) объемом товарооборота всего и в среднем на 1 предприятие, млн. руб.;
4) суммой прибыли всего и в среднем на 1 предприятие, млн. руб.
5) сделайте выводы в целом, а также охарактеризуйте зависимость прибыли от числа оборотов средних товарных запасов.
| № п/п | Объем товарооборота, млн. руб. | Средние остатки товарных запасов, млн. руб. | Прибыль, млн. руб. | № п/п | Объем товарооборота, млн. руб. | Средние остатки товарных запасов, млн. руб. | Прибыль, млн. руб. |
|---|---|---|---|---|---|---|---|
| 1 | 1339 | 194 | 378 | 14 | 1102 | 173 | 270 |
| 2 | 1512 | 216 | 416 | 15 | 1123 | 184 | 281 |
| 3 | 1080 | 162 | 356 | 16 | 2236 | 248 | 670 |
| 4 | 1534 | 173 | 460 | 17 | 648 | 130 | 130 |
| 5 | 1382 | 216 | 346 | 18 | 378 | 76 | 78 |
| 6 | 367 | 65 | 92 | 19 | 1944 | 216 | 583 |
| 7 | 173 | 32 | 35 | 20 | 1037 | 173 | 324 |
| 8 | 378 | 76 | 86 | 21 | 1145 | 162 | 313 |
| 9 | 216 | 43 | 43 | 22 | 389 | 97 | 108 |
| 10 | 238 | 43 | 54 | 23 | 486 | 97 | 114 |
Решение:
Произведём группировку торговых предприятий по скорости оборота товарных запасов. Рассчитаем число оборотов по формуле:
Результаты вычислений занесём в таблицу:
| № п/п | Объем товарооборота, млн. руб. | Средние остатки товарных запасов, млн. руб. | Прибыль, млн. руб. | Число оборотов средних товарных запасов | № п/п | Объем товарооборота, млн. руб. | Средние остатки товарных запасов, млн. руб. | Прибыль, млн. руб. | Число оборотов средних товарных запасов |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 1339 | 194 | 378 | 6,9 | 14 | 1102 | 173 | 270 | 6,4 |
| 2 | 1512 | 216 | 416 | 7,0 | 15 | 1123 | 184 | 281 | 6,1 |
| 3 | 1080 | 162 | 356 | 6,7 | 16 | 2236 | 248 | 670 | 9,0 |
| 4 | 1534 | 173 | 460 | 8,9 | 17 | 648 | 130 | 130 | 5,0 |
| 5 | 1382 | 216 | 346 | 6,4 | 18 | 378 | 76 | 78 | 5,0 |
| 6 | 367 | 65 | 92 | 5,6 | 19 | 1944 | 216 | 583 | 9,0 |
| 7 | 173 | 32 | 35 | 5,4 | 20 | 1037 | 173 | 324 | 6,0 |
| 8 | 378 | 76 | 86 | 5,0 | 21 | 1145 | 162 | 313 | 7,1 |
| 9 | 216 | 43 | 43 | 5,0 | 22 | 389 | 97 | 108 | 4,0 |
| 10 | 238 | 43 | 54 | 5,5 | 23 | 486 | 97 | 114 | 5,0 |
Определим число образуемых интервалов группировки с помощью математического правила Стерджесса:
n = 1 + 3,322 × lgN
где
N – число наблюдений.
n = 1 + 3,322 × lg20 = 5,32
Образуем пять групп торговых предприятий.
Величину интервалов определим по формуле:
Для исключения двойного счёта введём правило:
при отнесении крайних значений в ту или иную группу будем считать, что нижняя граница, кроме первого интервала будет закрытой, а верхняя граница интервала будет открытой. Так, например, предприятие, имеющее скорость оборота равную 5 попадёт в первый интервал, во второй интервал оно уже не включается.
Построим вспомогательную таблицу:
| № п/п | Объем товарооборота, млн. руб. | Средние остатки товарных запасов, млн. руб. | Прибыль, млн. руб. | Число оборотов средних товарных запасов |
|---|---|---|---|---|
| I группа 4 – 5 | ||||
| 8 | 378 | 76 | 86 | 5,0 |
| 9 | 216 | 43 | 43 | 5,0 |
| 17 | 648 | 130 | 130 | 5,0 |
| 18 | 378 | 76 | 78 | 5,0 |
| 22 | 389 | 97 | 108 | 4,0 |
| 23 | 486 | 97 | 114 | 5,0 |
| Итого | 2495 | 519 | 559 | 29 |
| Среднее | 415,833333 | 86,5 | 93,167 | 4,83333 |
| II группа 5 – 6 | ||||
| 6 | 367 | 65 | 92 | 5,6 |
| 7 | 173 | 32 | 35 | 5,4 |
| 10 | 238 | 43 | 54 | 5,5 |
| 20 | 1037 | 173 | 324 | 6,0 |
| Итого | 1815 | 313 | 505 | 22,5 |
| Среднее | 453,75 | 78,25 | 126,25 | 5,625 |
| III группа 6 – 7 | ||||
| 1 | 1339 | 194 | 378 | 6,9 |
| 2 | 1512 | 216 | 416 | 7,0 |
| 3 | 1080 | 162 | 356 | 6,7 |
| 5 | 1382 | 216 | 346 | 6,4 |
| 14 | 1102 | 173 | 270 | 6,4 |
| 15 | 1123 | 184 | 281 | 6,1 |
| Итого | 7538 | 1145 | 2047 | 39,5 |
| Среднее | 1256,33333 | 190,83 | 341,17 | 6,58333 |
| IV группа 7 – 8 | ||||
| 21 | 1145 | 162 | 313 | 7,1 |
| Итого | 1145 | 162 | 313 | 7,1 |
| Среднее | 1145 | 162 | 313 | 7,1 |
| V группа 8 – 9 | ||||
| 4 | 1534 | 173 | 460 | 8,9 |
| 16 | 2236 | 248 | 670 | 9,0 |
| 19 | 1944 | 216 | 583 | 9,0 |
| Итого | 5714 | 637 | 1713 | 26,9 |
| Среднее | 1904,66667 | 212,33 | 571 | 8,96667 |
Сведём результирующие строки вспомогательной таблицы в аналитическую группировку.
| Группы предприятий по скорости оборота товарных запасов | Число предприятий | Удельный вес в % к итогу | Число оборотов средних товарных запасов | Объем товарооборота, млн. руб. | Прибыль, млн. руб. | |||
|---|---|---|---|---|---|---|---|---|
| Всего по группе | В среднем на одно предприятие | Всего по группе | В среднем на одно предприятие | Всего по группе | В среднем на одно предприятие | |||
| 4 – 5 | 6 | 30 | 29,0 | 4,82931 | 2495 | 415,8333 | 559 | 93,16667 |
| 5 – 6 | 4 | 20 | 22,6 | 5,645377 | 1815 | 453,75 | 505 | 126,25 |
| 6 – 7 | 6 | 30 | 39,4 | 6,573347 | 7538 | 1256,333 | 2047 | 341,1667 |
| 7 – 8 | 1 | 5 | 7,1 | 7,067901 | 1145 | 1145 | 313 | 313 |
| 8 – 9 | 3 | 15 | 26,9 | 8,96106 | 5714 | 1904,667 | 1713 | 571 |
| Итого | 20 | 100 | 124,9 | 6,247426 | 18707 | 935,35 | 5137 | 256,85 |
Из таблицы видно, что наибольший удельный вес (30%) в общем итоге занимают торговые предприятия со скоростью оборота от 4 до 5 и со скоростью оборота от 5 до 6.
Кроме этого построенная аналитическая группировка позволяет сделать вывод, что зависимость объёма товарооборота и величины прибыли от скорости оборота товарных запасов прямая. Чем больше скорость оборота товарных запасов, тем больше величина прибыли торгового предприятия.
Задачи по статистике с решением — Средние величины
Решаем проверочные задачи по статистике
Тема: «Средние величины»
1. Задача на определение средней арифметической
Рассчитать средний возраст студентов в группе из 20 человек:


|
№ пп |
Возраст (лет) |
№ пп |
Возраст (лет) |
№ пп |
Возраст (лет) |
№ пп |
Возраст (лет) |
|
1 2 3 4 5 |
18 18 19 20 19 |
6 7 8 9 10 |
20 19 19 19 20 |
11 12 13 14 15 |
22 19 19 20 20 |
16 17 18 19 20 |
21 19 19 19 19 |
Если сгруппировать данные, то получим ряд распределения:


2. Задача на нахождение средней арифметической взвешенной
Распределение рабочих по выработке деталей
|
Выработка деталей за смену одним рабочим, шт., Хi |
18 |
19 |
20 |
21 |
22 |
Всего |
|
Число рабочих, fi |
2 |
11 |
5 |
1 |
1 |
20 |


3. Задача на вычисление средней по групповым средним или по частным средним.
Распределение рабочих по среднему стажу работы
|
Номер цеха |
Средний стаж работы, лет. |
Число рабочих, чел., fi |
|
1-й 2-й 3-й |
5 7 10 |
90 60 50 |
|
ИТОГО: |
200 |


4. Задача на вычисление средних в рядах распределения (интервальный ряд).
Распределение рабочих АО по уровню ежемесячной оплаты труда
|
Группы рабочих по оплате труда у.е. |
Число рабочих, чел. |
Середина интервала, хi |
|
До 500 |
5 |
450 |
|
500-600 |
15 |
550 |
|
600-700 |
20 |
650 |
|
700-800 |
30 |
750 |
|
800-900 |
16 |
850 |
|
900 и более |
14 |
950 |
|
Итого: |
100 |
— |

Задача 5. Вычисление средних в интервальных рядах методом моментов
Распределение малых предприятий региона по стоимости основных производственных фондов
|
Группы предприятий по стоимости ОПФ, у.е. |
Число предприятий |
Середина интервалов, х |
|
Хi*f |
|
14-16 16-18 18-20 20-22 22-24 |
2 6 10 4 3 |
15 17 19 21 22 |
-2 -1 0 1 2 |
-4 -6 0 4 6 |
|
Итого: |
25 |
— |
— |
0 |
Для упрощения расчетов средней идут по пути уменьшения значений вариантов и частот.
Один из вариантов, обладающий наибольшей частотой принимают за А, i— величина интервала.
А- начало отсчета «способ отсчета от условного нуля», «способ моментов». Все варианты уменьшим на А, затем разделим на I, получим новый вариационный ряд распределения новых вариантов хi. Средняя арифметическая их новых вариантов- момент первого порядка m i= 

Задача 6 на определение Средней гармонической.
Заработная плата предприятий АО
|
Предприятие |
Численность промышленно- производственного персонала, чел |
Месячный фонд заработной платы, тыс руб. |
Средняя заработная плата, руб. |
|
А |
1 |
2 |
3 |
|
1 2 3 |
540 275 458 |
564,84 332,75 517,54 |
1046 1210 1130 |
|
ИТОГО: |
1 273 |
1415,13 |
? |
Определить среднюю з/п по всем предприятиям.
Решение:
Составим логическую формулу средней: средняя з/п по всем предприятиям =
1) Пусть мы располагаем данными гр.1 и 2. Нам известен числитель и знаменатель логической формулы.
Искомая средняя величина определяется по средней агрегатной:

2) Пусть мы располагаем данными гр.1 и 3 , нам известен числитель логической формулы, а знаменатель числитель не известен, но может быть найден путем умножения средней з/п на численность ППП. Искомая средняя определяется по средней арифметической взвешенной.


3) Пусть мы располагаем данными гр.2 и 3 , нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления фонда з/п на среднюю з/п логической формулы. Искомая средняя определяется по средней гармонической взвешенной:
Все ответы верны.
Задача 7. Определить среднюю цену моркови по всем магазинам.
Цена и выручка от реализации по трем коммерческим магазинам.
|
№ магазина |
Цена моркови., руб за кг. |
Выручка от реализации, руб. |
|
1 2 3 |
17 20 24 |
3060 2800 1920 |
|
Итого: |
— |
7780 |
Решение.
Логическая формула средней: средняя цена моркови =
нам известен числитель логической формулы, а знаменатель не известен, но может быть найден путем деления выручки от реализации на цену моркови.
Искомая средняя определяется по средней гармонической взвешенной:
Задача 8 по статистике с решением: средние величины.
Информация о вкладах в банке
|
Вид вклада |
Октябрь |
Ноябрь |
||
|
Число вкладов, тыс., f |
Средний размер вклада, руб., x |
Сумма вкладов, млн. руб., F |
Средний размер вклада, x |
|
|
До востребования Срочный |
10 8 |
350 400 |
4,07 3,87 |
370 430 |
Определить средний размер вклада по двум видам.
1) Пусть в октябре известен средний размер вкладов каждого вида и число вкладов. По формуле средней арифметической взвешенной:


2) Пусть в ноябре известен средний размер вкладов каждого вида и сумма вкладов. По формуле средней гармонической взвешенной:
Задача 9: Удельная материалоемкость по двум предприятиям, изготавливающим один и тот же вид продукции составила соответственно 2,5 и 3 кг. Вычислить среднюю удельную материалоемкость изделия по двум предприятиям при условии, что каждым предприятием израсходовано на изготовления одного изделия по 60 тонн стали.
1) Решение задачи по средней арифметической простой:


2) решение по средней арифметической взвешенной



Оба решения не имеют логического смысла, чтобы правильно выбрать формулу средней величины необходимо составить логическую формулу задачи, отражающую ее смысл.
Логическая формула: средняя удельная материалоемкость по двум предприятиям = общему расходу материала на двух предприятиях/ на количество произведенных изделий→ средняя гармоническая взвешенная
3)
Решение статистических задач
Содержание
ЗАДАЧА 1
ЗАДАЧА 2
ЗАДАЧА 3
ЗАДАЧА 4
ЗАДАЧА 5
ЗАДАЧА 6
ЗАДАЧА 7
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
Задача 1
Уточнение
величины валового внутреннего продукта региона провели с использованием
распределения малых предприятий по объему выпуска продукции (товаров, работ,
услуг), полученного на основе 10-процентного выборочного наблюдения:
|
Группы предприятий по |
Количество предприятий |
|
До 100,0 |
80 |
|
100,0-200,0 |
160 |
|
200,0-300,0 |
490 |
|
300,0-400,0 |
326 |
|
400,0-500,0 |
100 |
|
500,0 и более |
44 |
|
Итого: |
1200 |
Определите по
предприятиям, включенным в выборку:
а) средний размер
произведенной продукции (товаров, работ, услуг) на одно предприятие;
б) долю
предприятий с объемом производства продукции более 400 тыс. руб.;
в) средние ошибки
показателей объема произведенной продукции и доли предприятий с объемом
производства продукции свыше 400 тыс. руб. (с вероятностью 0,954).
Сделайте выводы.
Решение
Закроем
интервалы, определим центры интервалов, рассчитаем размер кредитов во всех
договорах и занесем расчетные показатели в таблицу:
|
Группы предприятий по |
Середина интервала (x) |
Количество предприятий (f) |
xf |
x2f |
|
0,0-100,0 |
50 |
80 |
4000 |
200000 |
|
100,0-200,0 |
150 |
160 |
24000 |
3600000 |
|
200,0-300,0 |
250 |
490 |
122500 |
30625000 |
|
300,0-400,0 |
350 |
326 |
114100 |
39935000 |
|
400,0-500,0 |
450 |
100 |
45000 |
20250000 |
|
500,0 -600,0 |
550 |
44 |
24200 |
|
|
Итого: |
— |
1200 |
333800 |
107920000 |
а) для определения среднего размера в произведенной
продукции (товаров, работ, услуг) на одно предприятие воспользуемся формулой
средней арифметической взвешенной:
 тыс. руб.
тыс. руб.
б) долю
предприятий с объемом производства продукции более 400 тыс. руб. равна:
 или 83%.
или 83%.
Дисперсия
рассчитывается по формуле:
Средняя ошибка
выборки составит:
t=2
тыс. руб.
Установим
границы: 218.7-6.47≤≤218.7+6.47 212.23≤
≤225.17
На основании
проведенного обследования с вероятностью 0,954 можно заключить, что средний объем
произведенной продукции свыше 400 тыс. руб., в целом по предприятиям лежит в
пределах от 212,23 до 225,17 тыс. руб.
Задача 2
Имеются следующие
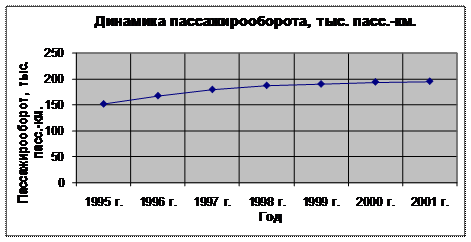
данные о пассажирообороте по одному из регионов:
|
Показатель |
1995 |
1996 |
1997 |
1998 |
1999 |
2000 |
2001 |
|
Пассажирооборот, тыс. |
152,4 |
167,9 |
179,8 |
187,5 |
190,2 |
194,1 |
195,4 |
Определите:
1. Цепные
показатели:
а) абсолютного
прироста;
б) темпа роста и
прироста;
в) абсолютное
значение 1% прироста.
(Результаты расчетов
представьте в таблице)
2. Среднегодовой
пассажирооборот.
3. Среднегодовой
абсолютный прирост.
Изобразите
динамику пассажирооборота на графике. Сделайте выводы.
Решение
1.
Заданные показатели
рассчитываются по следующим формулам:
·
Абсолютный прирост:
·
Темп роста:
·
Темп прироста:
·
Абсолютное содержание
1% прироста:
Полученные данные
представим в таблице:
|
Год |
Пассажирооборот, тыс. |
Абсолютный прирост, |
Темпы роста, % |
Темпы прироста, % |
Абсолютное содержание |
|
1995 |
152,4 |
— |
— |
— |
— |
|
1996 |
167,9 |
15,5 |
110,17 |
10,17 |
1,52 |
|
1997 |
179,8 |
11,9 |
107,09 |
1,68 |
|
|
1998 |
187,5 |
7,7 |
104,28 |
4,28 |
1,8 |
|
1999 |
190,2 |
2,7 |
101,44 |
1,44 |
1,88 |
|
2000 |
194,1 |
3,9 |
102,05 |
2,05 |
1,9 |
|
2001 |
195,4 |
1,3 |
100,67 |
0,67 |
1,94 |
|
Итого |
1267,3 |
43 |
2.
Данный динамический
ряд является интервальным. Поэтому среднегодовой пассажирооборот исчислим по
формуле средней арифметической простой:
пасс.-км.
3. Среднегодовой
абсолютный прирост определим по формуле:
пасс.-км.
То есть ежегодно
уровни ряда в среднем возрастали на 7,17 пасс.-км.
Представим
динамический ряд на графике:
Задача
3
Имеются данные по
плательщикам налога на прибыль:
|
Налогоплательщики |
Размер прибыли, тыс. |
Ставка налога на |
||
|
Базисный период |
Отчетный период |
Базисный период |
Отчетный период |
|
|
1 |
42000 |
40000 |
30 |
32 |
|
2 |
83000 |
50000 |
32 |
28 |
|
3 |
35000 |
48000 |
28 |
30 |
Проанализируйте
динамику общей суммы налога на прибыль в форме индексов, выявив:
а) влияние
фактора изменения среднего размера прибыли;
б) влияние
фактора изменения ставки налога на прибыль.
Решение
Общее изменение
суммы налогов:
,
то есть сумма
налога на прибыль уменьшилась на 16% или на 776000 тыс. руб. (4120000-4896000).
а) Определим
влияние первого фактора:
б) определим
влияние второго фактора:
.
То есть общая
сумма налогов уменьшилась на 16%, в том числе за счет уменьшения среднего
размера прибыли – на 15%, и за счет уменьшения ставки налога на прибыль – на
4%.
|
Группы семей |
Месячный доход в |
Оплата услуг в |
|
1 |
542 |
2 |
|
2 |
683 |
2 |
|
3 |
753 |
3 |
|
4 |
859 |
4 |
|
5 |
956 |
6 |
|
6 |
1161 |
7 |
|
7 |
1481 |
9 |
Определите
коэффициент эластичности оплаты услуг в учреждениях образования с ростом
доходов населения, когда связь между доходом и потреблением услуг образования
выражается уравнением прямой линии. Оцените возможный уровень расходов семей,
если доходы увеличатся до 1500 руб.
Решение
Для определения
коэффициента эластичности произведем необходимые расчеты и занесем полученные
результаты в таблицу:
|
Группы семей |
Месячный доход в (x) |
Оплата услуг в (y) |
x2 |
xy |
yx |
Э = |
|
1 |
542 |
2 |
293764 |
1084 |
1,57 |
2,87 |
|
2 |
683 |
2 |
466489 |
1366 |
2,74 |
2,07 |
|
3 |
753 |
3 |
567009 |
2259 |
3,32 |
1,88 |
|
4 |
859 |
4 |
737881 |
3436 |
4,2 |
1,7 |
|
5 |
956 |
6 |
913936 |
5736 |
5 |
|
|
6 |
1161 |
7 |
1347921 |
8127 |
6,71 |
1,44 |
|
7 |
1481 |
9 |
2193361 |
13329 |
9,36 |
1,31 |
|
Итого |
6435 |
33 |
6520361 |
35337 |
32,9 |
1,62 |
Для определения
коэффициента эластичности применим формулу
Э = .
Изменение в
оплате услуг в учреждениях образования с повышением месячного дохода в расчете
на одного члена семьи представим уравнением прямой y = a0+a1x. Для решения уравнения необходимо определить параметры a0 b a1 по
системе нормальных уравнений:
В результате
получим: a0 = -2.93; a1 = 0.0083.
y = -2.93+0.0083x.
Параметр a1 показывает, что при увеличении месячного дохода в расчете на
1 члена семьи на 1 рубль потребление услуг растет в среднем на 0,0083.
Таким образом, с ростом месячного дохода
на 1% потребление услуг растет в среднем на 1,62%.
Если доходы
увеличатся до 1500 руб., то потребление данных услуг составит: yx = -2.93+0.0083*1500 = 9.52.
Задача
5
Имеются следующие
данные о распределении доходов в экономике (млрд. руб.):
|
Валовая прибыль |
8200 |
|
Оплата труда работников-резидентов |
4500 |
|
Чистые налоги на |
950 |
|
Другие налоги на |
620 |
|
Субсидии на |
370 |
|
Доходы от |
20 |
|
Доходы от |
290 |
|
Текущие трансферты, |
110 |
|
Текущие трансферты, |
75 |
Определите:
1.
Сальдо первичных
доходов экономики.
2.
Валовой располагаемый
доход государства.
Решение
1.
Сальдо первичных
доходов = Валовая прибыль + Оплата труда работников-резидентов + Чистые налоги
на продукты + Другие налоги на производство + Доходы от собственности,
полученные из-за границы — Доходы от собственности, переданные за границу —
Субсидии на производство = 8200+4500+620+20+950-290-370 = 13630 млрд. руб.
2.
Валовой располагаемый
доход государства = Сальдо первичных доходов экономики + Текущие трансферты,
полученные из-за границы — Текущие трансферты, переданные за границу =
13630+110-75 = 13665 млрд. руб.
Задача 6
Имеются следующие
данные о численности и движении безработных по отделению службы занятости
города, чел:
|
Численность безработных |
26774 |
|
В течение текущего периода: |
|
|
Поставлено на учет |
5334 |
|
Признано безработными |
3550 |
|
Снято с учета |
6934 |
|
В том числе: |
|
|
Нашли работу (доходное |
3022 |
|
Оформлено на досрочную |
170 |
|
Направлено на |
|
|
По другим причинам |
2446 |
Определите:
— численность
безработных по отделению службы занятости на конец текущего периода;
— коэффициент
пополнения безработных;
-коэффициент
снятия с учета безработных;
— структуру
снятых с учета безработных;
— уровень
безработицы, если известно, что численность занятых в экономике на начало года
– 1051 тыс. чел, на конец года – 1024 тыс. чел.
Решение
Рассчитаем
численность безработных по отделению службы занятости на конец текущего периода
= 26774+5334+3550 = 35658 чел.
Рассчитаем
коэффициент пополнения безработных:
.
Рассчитаем
коэффициент снятия с учета безработных:
.
Рассчитаем
структуру снятых с учета безработных:
|
Нашли работу (доходное |
|
|
Оформлено на досрочную |
|
|
Направлено на |
|
|
По другим причинам |
|
Рассчитаем
уровень безработицы:
— на начало
года: ;
— на конец года:
.
Задача 7
По предприятию
имеются следующие данные:
|
Показатели |
Базисный период |
Отчетный период |
|
Выпуск товаров (услуг) |
1966 |
2100 |
|
Средняя годовая |
2028 |
2142 |
|
Среднесписочная |
200 |
210 |
Определите:
— фондоотдачу,
фондовооруженность и производительность труда за каждый период;
— темпы роста
исчисленных показателей (двумя способами);
— изменение
производительности труда за счет фондоотдачи и фондовооруженности труда.
Сделайте выводы.
Решение
1.
Определим фондоотдачу:
Определим
фондовооруженность:
Производительность
труда:
3.
Исчислим темпы роста
фондоотдачи: ; фондовооруженности:
; производительности труда:
.
4.
Общий прирост
производительности труда составляет: .
Прирост
производительности труда происходит под влиянием:
— изменения
фондоотдачи: ;
— изменения фондовооруженности:
.
Итак,
производительность труда возросла на 0,16, в том числе за счет увеличения
фондоотдачи – на 0,102 и за счет увеличения фондовооруженности – на 0,058.
Список
использованной литературы
1. Гусаров В.М. Статистика: Учебное пособие
для вузов. — М.: ЮНИТИ-ДАНА, 2001.
2. Октябрьский П. Я.
Статистика: учеб. – М.: ТК Велби, Изд-во Проспект, 2005
3. Статистика: Учебное пособие/Харченко Л-П.,
Долженкова В.Г., Ионин В.Г. и др., Под ред. В.Г.Ионина. — Изд. 2-е, перераб. и
доп. — М.: ИНФРА-М.2003.
4. Статистика: Учебник. – М.: ТК Велби,
Изд-во Проспект, 2005
5. Теория статистики:
Учебник/Р. А. Шмойлова – 4-е изд, перераб. и доп. – М.: Финансы и статистика,
2005


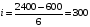
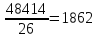
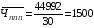


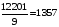
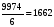
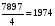

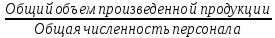

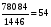
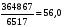
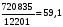


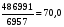
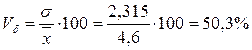
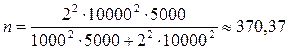
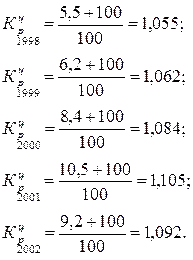
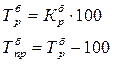
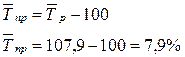
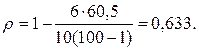
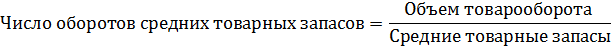
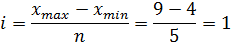









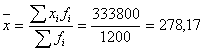 тыс. руб.
тыс. руб.