Задача планирования производства
Задача планирования
производства (или задача об использовании
ресурсов) является одной из разновидностей
задачи линейного программирования.
Рассмотрим пример
подобной задачи.
Для изготовления
двух видов продукции
и
используют четыре вида ресурсов
,
,
и
.
Запасы ресурсов, число единиц ресурсов,
затрачиваемых на изготовление единицы
продукции, приведены в следующей таблице
(цифры условные):
|
Вид |
Запас |
Число |
|
|
|
|
||
|
|
18 |
1 |
3 |
|
|
16 |
2 |
1 |
|
|
5 |
– |
1 |
|
|
2 |
3 |
– |
Прибыль, получаемая
от единицы продукции
и
,
– соответственно 2 и 3 руб.
Необходимо составить
такой план производства продукции, при
котором прибыль от ее реализации будет
максимальной.
Решение. Составим
экономико-математическую модель задачи.
Обозначим
,
– число единиц продукции соответственно
и
,
запланированных к производству. Для их
изготовления потребуетсяединиц ресурса
,
единиц ресурса
,
единиц ресурса
и
единиц ресурса
.
Так как потребление ресурсов,
,
и
не должно превышать их запасов,
соответственно 18, 16, 5 и 21 единицы, то
связь между потреблением ресурсов и их
запасами выразится системой неравенств:

По смыслу задачи
переменные
(1.9)
Суммарная прибыль
составит
руб. от реализации продукции
и
руб.–
от реализации продукции,
т.е.
. (1.10)
Итак,
экономико-математическая модель задачи:
найти такой план выпуска продукции
,
удовлетворяющий системе (1.8) и условию
(1.9), при котором функция (1.10) принимает
максимальное значение.
Задачу легко
обобщить на случай выпуска
видов продукции с использованием
видов ресурсов.
Обозначим
– число единиц продукции
,
запланированной к производству;– запас ресурса
,
– число единиц ресурса
,
затрачиваемого на изготовление единицы
продукции(числа
часто называюттехнологическими
коэффициентами);
– прибыль от реализации единицы продукции
.
Тогда
экономико-математическая модель задачи
об использовании ресурсов в общей
постановке примет вид: найти
такой план
выпуска
продукции, удовлетворяющий системе

и условию
(1.12)
при котором функция
(1.13)
принимает
максимальное значение.
Решение типового примера
Задание 1
Предприятию
ООО «ТИТАН», одним из видов деятельности
которого является выполнение токарных,
фрезерных и сверлильных работ, поступил
заказ на производство гаек стремянки,
гаек штанги, гаек МОД и колец шкворня в
количестве соответственно
шт.
Производство заказанной токарной
продукции в полном объеме ограничено
запасами имеющихся ресурсов (трудозатратами
–чел.-час.,
запасом стали –кг,
а также выделенными денежными средствами
на оплату труда рабочих и последующую
обработку токарной продукции –руб.).
Кроме того, известно, что для производства
единицы продукции каждого вида требуется
соответственнокг
стали, трудозатраты при этом составляют
соответственночел.-час.
За каждую изготовленную деталь рабочий
предприятия получаетруб.,
последующая обработка единицы изделия
каждого вида требует затрат денежных
средств в размереруб.
соответственно.
Задача оптимизации
производства для ООО «ТИТАН» ставится
в форме максимизации дополнительной
прибыли предприятия при заданных
ассортименте выпускаемой продукции и
ограничениях на имеющиеся запасы
ресурсов, при условии, что прибыль от
реализации единицы продукции каждого
вида составляет соответственно
руб.
Исходные данные
задачи представлены в таблице:
|
Показатель |
Ассортимент |
|||
|
Гайка |
Гайка |
Гайка |
Кольцо |
|
|
|
1300 |
950 |
500 |
600 |
|
|
0,21 |
0,18 |
0,42 |
1,35 |
|
|
0,11 |
0,125 |
0,4 |
0,225 |
|
|
5 |
6 |
14 |
7 |
|
|
2 |
2 |
3 |
4 |
|
|
7 |
10 |
17 |
11 |
|
|
440 |
|||
|
|
1000 |
|||
|
|
30900 |
Необходимо:
1. Построить
экономико-математическую модель
представленной задачи линейного
программирования (с учетом условия
целочисленности).
2. Определить с
помощью надстройки «Поиск решения» в
Microsoft Excel оптимальный план производства
продукции ООО «ТИТАН» (количество гаек
стремянки, гаек штанги, гаек МОД и колец
шкворня).
3. Дать экономическую
интерпретацию полученного решения.
Сформулировать оптимальное управленческое
решение в описанных условиях.
Решение.
1. Построим
экономико-математическую модель
представленной задачи линейного
программирования (с учетом условия
целочисленности).
Обозначим через
(где
)
– объём производства продукции ООО
«ТИТАН» (количество гаек стремянки,
гаек штанги, гаек МОД и колец шкворня).
Тогда дополнительная
прибыль предприятия при заданном
ассортименте выпускаемой продукции
составит:
Ограничения по
запасам имеющихся ресурсов:
Ограничения по
объему производства:
Условия
неотрицательности объемов производства:
Условия целочисленности
объемов производства:
.
Экономико-математическая
модель представленной задачи планирования
производства составлена.
2. Определим с
помощью надстройки «Поиск решения» в
Microsoft Excel оптимальный план производства
продукции ООО «ТИТАН» (количество гаек
стремянки, гаек штанги, гаек МОД и колец
шкворня).
На листе 1 новой
книги Microsoft Excel,
названной «Задача планирования
производства», в ячейки А3:F12
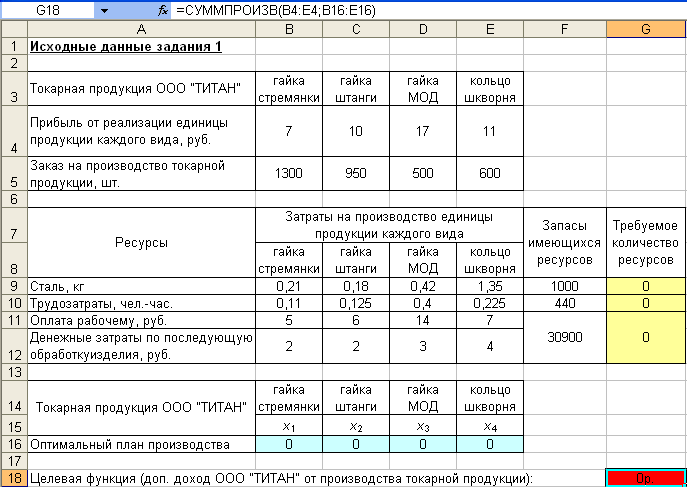
введем исходные данные как на рис. 1.
Рис. 1. Ввод
исходных данных задания 1
В ячейках А14:Е16
сформируем таблицу оптимального плана
производства токарной продукции ООО
«ТИТАН», причем ячейки В16:Е16 заполняем
нулями (см. рис. 2).
Ячейки G7:G8
объединим и введем «Требуемое количество
ресурсов», а в ячейку G9
формулу, определяющую общее количество
стали, необходимое для производства
всего объема токарной продукции:
«=СУММПРОИЗВ(B9:E9;$B$16:$E$16)» (Для вставки
функции «СУММПРОИЗВ» необходимо
выполнить команду «Вставка»/«Функция»,
в открывшемся окне Мастера функции
выбрать категорию «Математические»,
функцию СУММПРОИЗВ(). Данная функция
возвращает сумму произведений
соответствующих элементов массивов и
диапазонов. Далее необходимо заполнить
поля функции СУММПРОИЗВ согласно рис. 3:
в поле «Массив 1» указываются ячейки
B9:Е9, содержащие нормы затрат стали на
производство единицы продукции каждого
вида, в поле «Массив 2» – ячейки
$B$16:$E$16, содержащие оптимальный план
производства токарной продукции, причем
ссылки на эти ячейки должны быть
абсолютными, для чего после выбора этих
ячеек нажимаем клавишу F4
на клавиатуре). Далее копируем формулу
из ячейки G9
в ячейку G10,
как на рис. 2.
Ячейки G11
и G12
объединим и введем формулу, определяющую
общее количество денежных средств,
необходимых для оплаты труда рабочих
и последующую обработку произведенной
продукции (рис. 2):
=СУММПРОИЗВ(B11:E11;$B$16:$E$16)+СУММПРОИЗВ(B12:E12;$B$16:$E$16)».
Рис. 2. Ввод
формул
Рис. 3. Ввод
аргументов функции СУММПРОИЗВ()
Затем в ячейку А18
введем «Целевая функция (доп. доход ООО
«ТИТАН» от производства токарной
продукции):», а в ячейку G18
– формулу: =СУММПРОИЗВ(B4:E4;B16:E16)» (в поле
«Массив 1» окна аргументов функции
СУММПРОИЗВ указываются ячейки B4:E4,
содержащие прибыль от реализации единицы
продукции каждого вида, в поле «Массив 2»
– ячейки B16:E16, содержащие оптимальный
план производства токарной продукции
ООО «ТИТАН»).
Результатом расчета
дополнительной прибыли предприятия от
производства токарной продукции в
Microsoft Excel
на данном этапе выполнения задания
является значение, равное нулю (рис. 4).
В дальнейшем (после выполнения некоторых
манипуляций) в ячейке G18
будет рассчитана максимальная
дополнительная прибыль ООО «ТИТАН».
Рис. 4. Результат
вычисления введенных формул
Теперь определим
с помощью надстройки «Поиск решения»
в Microsoft Excel оптимальный план производства
продукции ООО «ТИТАН» (количество гаек
стремянки, гаек штанги, гаек МОД и колец
шкворня), при котором предприятие получит
дополнительный доход.
Для этого необходимо
выделить ячейку, содержащую значение
целевой функции (ячейку G18),
и выполнить команду «Сервис»/ «Поиск
решения…»1.
В открывшемся окне надстройки «Поиск
решения…» в поле «Целевая ячейка» уже
будет указано: «$G$18»
(т.е. ячейка, содержащая значение
дополнительной прибыли рассматриваемого
предприятия от производства токарной
продукции), необходимо установить флажок
«Равной максимальному значению», в поле
«Изменяя ячейки» – выбрать «$В$16:$Е$16»,
т.е. ячейки, содержащие оптимальный план
производства гаек стремянки, гаек
штанги, гаек МОД и колец шкворня (рис. 5).
Далее указываем ограничения следующим
образом: нажимаем кнопку «Добавить», и
в открывшемся окне вводим ограничение
по запасам имеющихся ресурсов (стали и
трудозатрат) (рис. 6), нажимаем «ОК»,
еще раз нажимаем кнопку «Добавить» и
вводим ограничение по имеющимся денежным
средствам на оплату труда рабочих и
последующую обработку токарной продукции
(рис. 7). Аналогично добавляем ограничение
по объему производства (рис. 8), условие
неотрицательности объема производства
(рис. 9), а также условие целочисленности
объема производства (рис. 10).
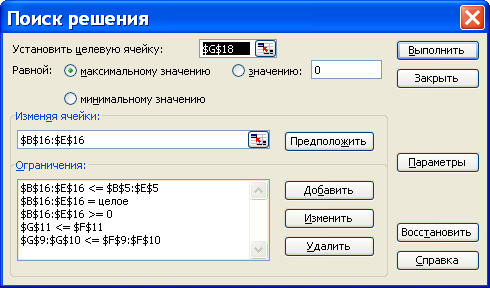
Рис. 5. Окно
«Поиск решений» задания 1
Рис. 6. Ввод
ограничения по запасам имеющихся
ресурсов (стали и трудозатрат)
Рис. 7. Ввод
ограничения по имеющимся денежным
средствам
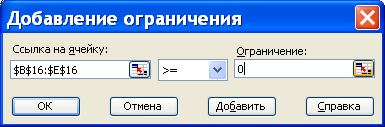
Рис. 8. Ввод
ограничения по объему производства
Рис. 9. Ввод
условия неотрицательности
Рис. 10. Ввод
условия целочисленности
Далее в окне поиска
решений (рис.5)нажимаем
кнопку «Параметры», в открывшемся окне
«Параметры поиска решения» устанавливаем
флажок «Линейная модель» (рис. 11),
нажимаем «ОК». В окне поиска решений
(рис.5)нажимаем
«Выполнить».
Рис. 11. Окно
«Параметры поиска решения»
В результате
получим такой план производства гаек
стремянки, гаек штанги, гаек МОД и колец
шкворня ООО «ТИТАН» (ячейки В16:Е16), при
котором дополнительный доход предприятия
примет максимальное значение, равное
26 650 руб. (ячейка G18)
(рис. 12).
Рис. 12.
Результат поиска решения (оптимального
плана производства)
3. Дадим
экономическую интерпретацию полученного
решения. Сформулируем оптимальное
управленческое решение в описанных
условиях.
Для обеспечения
максимальной дополнительной прибыли
в размере 26 650 рублей предприятию
ООО «ТИТАН» следует производить гайки
стремянки в количестве 1300 шт., гайки
штанги – 950 шт., гайки МОД – 260 шт. и
кольца шкворня – 330 шт. в месяц.
Дефицитным ресурсом
при этом являются трудозатраты, поскольку
его остатки равны нулю. Увеличение
недефицитных ресурсов: запаса стали,
денежных средств на оплату труда рабочих
и последующую обработку изделий, не
может влиять на оптимальный план
производства токарной продукции ООО
«ТИТАН».
Уважаемые коллеги!
Целями данного урока является не изложение теории из курса матпрограммирования, а более простая цель — показать практическое применение знаний, которые Вы получаете в процессе изучения раздела «математическое программирование» в курсе высшей математики. Поэтому изложение будет максимально простым, но не совсем «каноническим».
Задача
Предприятие планирует выпускать четыре вида продукции. Объемы ресурсов трех видов (в расчете на трудовую неделю), затраты каждого ресурса на изготовление единицы продукции и цена единицы продукции приведены в таблице. Найти, сколько продукции и какого вида необходимо производить, чтобы общая выручка от реализации всей выпущенной продукции была бы наибольшей. Построить модель прямой и двойственной задач. Найти оптимальные планы для обеих задач и экстремальные значения целевых функций. Дать экономическую интерпретацию основным и дополнительным переменным исходной и двойственной задач. Проанализировать рациональность расширения ассортимента продукции за счет включения новой продукции (П5).
| П1 | П2 | П3 | П4 | Объем | П5 | |
| Р1 | 8 | 10 | 8 | 10 | 3600 | 9 |
| Р2 | 4 | 7 | 4 | 6 | 1850 | 5 |
| Р3 | 4 | 3 | 3 | 5 | 1500 | 3 |
| Цена | 25 | 30 | 40 | 35 | 33 |
Решение.
Обозначим через x1..x4 число изготавливаемых продуктов. Тогда условие задачи может быть записано в следующем виде:
25x1 + 30x2 + 40x3 + 35x4 → max
8x1 + 10x2 + 8x3 + 10x4 ≤ 3600
4x1 + 7x2 + 4x3 + 6x4 ≤ 1850
4x1 + 3x2 + 3x3 + 5x4 ≤ 1500
x1 ≥ 0
x2 ≥ 0
x3 ≥ 0
x4 ≥ 0
Припишем каждому из видов сырья, используемых для производства продукции, двойственную оценку, соответственно равную y1, y2 и у3. Тогда общая оценка сырья, используемого на производство продукции, составит
3600y1 + 1850y2+ 1500y3 → min
Согласно условию, двойственные оценки должны быть такими, чтобы общая оценка сырья, используемого на производство единицы продукции каждого вида, была не меньше цены единицы продукции данного вида, т. е. y1, y2 и у3 должны удовлетворять следующей системе неравенств:
8y1 + 4y2+ 4y3 ≥ 25
10y1 + 7y2+ 3y3 ≥ 30
8y1 + 4y2+ 3y3 ≥ 40
10y1 + 6y2+ 5y3 ≥ 35
y1 ≥ 0
y2 ≥ 0
y3 ≥ 0
Как видно, данные задачи образуют симметричную пару двойственных задач. Решение прямой задачи дает оптимальный план производства изделий, а решение двойственной – оптимальную систему оценок сырья, используемого для производства этих изделий. Чтобы найти решение этих задач, следует сначала отыскать решение какой–либо одной из них.
Приведем математическую модель задачи к каноническому виду.Для этого избавимся от знаков неравенств посредством ввода дополнительных переменных и замены знака неравенства на знак равенства. Дополнительная переменная добавляется для каждого неравенства, причем эта переменная указывается в целевой функции с нулевым коэффициентом. Правило ввода дополнительных переменных: при «>=» — переменная вводится в неравенство с коэффициентом (-1); при «<=» — с коэффициентом (+1).
25x1 + 30x2 + 40x3 + 35x4 — 0x5 — 0x6 — 0x7 → max
8x1 + 10x2 + 8x3 + 10x4 + x5 = 3600
4x1 + 7x2 + 4x3 + 6x4 + x6 = 1850
4x1 + 3x2 + 3x3 + 5x4 + x7 = 1500
Экономический смысл введенных дополнительных переменных — остатки соответствующих ресурсов каждого вида. Для решения задачи составим симплекс-таблицу.
Симплекс-таблица составляется так:
В графе «Базис» записываются вектора переменных, принимаемые за базисные. На первом этапе это – A5, A6, A7. Базисными будут переменные, каждая из которых входит только в одно уравнение системы, и нет такого уравнения, в которое не входила бы хотя бы одна из базисных переменных.
В следующий столбец записываются коэффициенты целевой функции, соответствующие каждой переменной. Столбец В – столбец свободных членов. Далее идут столбцы коэффициентов Аi при i –й переменной.
| 25 | 30 | 40 | 35 | 0 | 0 | 0 | ||||
| i | Базис | C | B | A1 | A2 | A3 | A4 | A5 | A6 | A7 |
| 1 | A5 | 0 | 3600 | 8 | 10 | 8 | 10 | 1 | 0 | 0 |
| 2 | A6 | 0 | 1850 | 4 | 7 | 4 | 6 | 0 | 1 | 0 |
| 3 | A7 | 0 | 1500 | 4 | 3 | 3 | 5 | 0 | 0 | 1 |
| 4 | Fi-Ci | 0 | -25 | -30 | -40 | -35 | 0 | 0 | 0 | |
Под столбцом свободных членов записывается начальная оценка F0 = CiBi = 0*3600+0*1850+0*1500=0 .
Остальные оценки записываются под столбцами соответствующих векторов:
F1 — C1 = 0*8 + 0*4 + 0*4 — 25 = -25
F2 — C2 = 0*10 + 0*7 + 0*3 — 30 = -30
F3 — C3 = 0*8 + 0*4 + 0*3 — 40 = -40
F4 — C4 = 0*10 + 0*6 + 0*5 — 35 = -35
Следует отметить, что оценки для базисных векторов всегда равны нулю.
Преобразование симплекс-таблицы ведется следующим образом:
Шаг 1: Проверяется критерий оптимальности, суть которого состоит в том, что все оценки должны быть неотрицательны. В нашем случае этот критерий не выполнен, поэтому переходим ко второму шагу.
Шаг 2: Для отрицательных оценок вычисляются величины:
Θ1 = min{ Bi / Ai }= min{ 3600/8 ; 1850/4; 1500/4 } = min{450; 462.5; 375} = 375
Θ2 = min{ Bi / Ai }= min{ 3600/10 ; 1850/7; 1500/3 } = min{360; 264.29; 500} = 1850/7
Θ3 = min{ Bi / Ai }= min{ 3600/8 ; 1850/4; 1500/3 } = min{450; 462.5; 500} = 450
Θ4 = min{ Bi / Ai }= min{ 3600/10 ; 1850/6; 1500/5 } = min{360; 308.33; 300} = 300
Θ1 (F1 — C1 ) = 375 * (-25) = — 9375
Θ2 (F2 — C2 ) = 1850/7 * (-30) = — 55500/7
Θ3 (F3 — C3 ) = 450 * (-40) = — 18000
Θ4 (F4 — C4 ) = 300 * (-35) = — 10500
Из этих элементов выбирается тот, для которого вычисленное произведение минимально, в нашем случае минимально -18000, поэтому выбираем третий столбец, а в качестве так называемого разрешающего элемента выбирается первый элемент третьего столбца (по значению Θ3 ) – 8 (выделен в таблице).
Шаг 3: Третья строка таблицы делится на 8 и вычитается из остальных строк с коэффициентами, позволяющими ввести в базис третий столбец. В сущности, применяется метод исключения неизвестных, известный как метод Жордана – Гаусса..
| 25 | 30 | 40 | 35 | 0 | 0 | 0 | ||||
| i | Базис | C | B | A1 | A2 | A3 | A4 | A5 | A6 | A7 |
| 1 | A3 | 40 |
450 | 1 | 1,25 | 1 | 1,25 | 1/8 | 0 | 0 |
| 2 | A6 | 0 | 12.5 |
0 |
0.5 |
0 |
0.25 |
-1/8 |
0.25 |
0 |
| 3 | A7 | 0 | 50 | 1/3 |
-0,25 |
0 |
5/12 | -1/8 |
0 | 1/3 |
| 4 | Fi-Ci | 0 | 15 | 20 | 0 | 15 | 5 | 0 | 0 | |
В итоге получаем все положительные оценки Fi — Ci, что означает оптимальность полученного плана. То есть необходимо выпускать 450 единиц продукции третьего вида, чтобы выручка была максимальной и составляла 18 тысяч.
Проанализируем, что будет, если включить в ассортимент пятый вид товара.
25x1 + 30x2 + 40x3 + 35x4 + 33x5 → max
8x1 + 10x2 + 8x3 + 10x4 + 9x5 ≤ 3600
4x1 + 7x2 + 4x3 + 6x4 + 5x5 ≤ 1850
4x1 + 3x2 + 3x3 + 5x4 + 3x5 ≤ 1500
x1 ≥ 0
x2 ≥ 0
x3 ≥ 0
x4 ≥ 0
x5 ≥ 0
Приведем математическую модель задачи к каноническому виду.
25x1 + 30x2 + 40x3 + 35x4 + 33x5 — 0x6 — 0x7 — 0x8 → max
8x1 + 10x2 + 8x3 + 10x4 + 9x5 + x6 = 3600
4x1 + 7x2 + 4x3 + 6x4 + 5x5 + x7 = 1850
4x1 + 3x2 + 3x3 + 5x4 + 3x5 + x8 = 1500
| 25 | 30 | 40 | 35 | 33 | 0 | 0 | 0 | ||||
| i | Базис | C | B | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 |
| 1 | A6 | 0 | 3600 | 8 | 10 | 8 | 10 | 9 |
1 | 0 | 0 |
| 2 | A7 | 0 | 1850 | 4 | 7 | 4 | 6 | 5 | 0 |
1 | 0 |
| 3 | A8 | 0 | 1500 | 4 | 3 | 3 | 5 | 3 | 0 | 0 |
1 |
| 4 | Fi-Ci | 0 | -25 | -30 | -40 | -35 | -33 | 0 | 0 | 0 | |
Θ1 = min{ Bi / Ai }= min{ 3600/8 ; 1850/4; 1500/4 } = min{450; 462.5; 375} = 375
Θ2 = min{ Bi / Ai }= min{ 3600/10 ; 1850/7; 1500/3 } = min{360; 264.29; 500} = 1850/7
Θ3 = min{ Bi / Ai }= min{ 3600/8 ; 1850/4; 1500/3 } = min{450; 462.5; 500} = 450
Θ4 = min{ Bi / Ai }= min{ 3600/10 ; 1850/6; 1500/5 } = min{360; 308.33; 300} = 300
Θ5 = min{ Bi / Ai }= min{ 3600/9 ; 1850/5; 1500/3 } = min{400; 370; 500} = 370
Θ1 (F1 — C1 ) = 375 * (-25) = — 9375
Θ2 (F2 — C2 ) = 1850/7 * (-30) = — 55500/7
Θ3 (F3 — C3 ) = 450 * (-40) = — 18000
Θ4 (F4 — C4 ) = 300 * (-35) = — 10500
Θ5 (F5 — C5 ) = 370 * (-33) = — 12210
Из этих элементов выбирается тот, для которого вычисленное произведение минимально, в нашем случае минимально -18000, поэтому выбираем третий столбец, а в качестве так называемого разрешающего элемента выбирается первый элемент третьего столбца (по значению Θ3 ) – 8 (выделен в таблице).
| 25 | 30 | 40 | 35 | 33 | 0 | 0 | 0 |
||||
| i | Базис | C | B | A1 | A2 | A3 | A4 | A5 | A6 | A7 | A8 |
| 1 | A3 | 40 | 450 | 1 | 1.25 | 1 | 1,25 | 1,125 |
1/8 | 0 | 0 |
| 2 | A7 | 0 | 12,5 |
0 |
0,5 |
0 |
0,25 |
1/8 |
-1/8 |
1/4 | 0 |
| 3 | A8 | 0 | 50 | 1/3 |
-0,25 |
0 |
5/12 | -1/8 |
-1/8 |
0 |
1/3 |
| 4 | Fi-Ci | 0 | 15 | 20 | 0 | 15 | 12 |
5 |
0 | 0 |
|
В итоге получаем все положительные оценки Fi — Ci, что означает оптимальность полученного плана. То есть необходимо выпускать 450 единиц продукции третьего вида, чтобы выручка была максимальной и составляла 18 тысяч.
Таким образом, введение нового продукта никак не повлияет на стратегию предприятия по максимизации выручки.
0
Транспортная задача |
Описание курса
| Теория вероятности
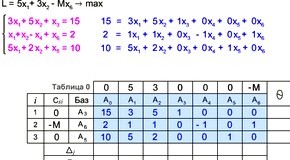
Рассмотрим алгоритм табличного симплекс-метода на примере решения производственной задачи, которая сводится к нахождению производственного плана обеспечивающего максимальную прибыль.
Решение задачи табличным симплекс-методом
Решение задачи происходит в несколько последовательных этапов. Разберем их на небольшом примере производственной задачи.
1. Определение исходных данных
В нашем примере, по условиям задачи предприятие выпускает 4 вида изделий, обрабатывая их на 3 станках.
Исходные данные для производственной задачи запишем в формате матриц:
- Матрица A — нормы времени на обработку изделий;
- Матрица B — фонд времени работы станков;
- Матрица C — продажи производимых изделий.
Таким образом, нормы времени (мин./шт.) на обработку изделий на станках, заданы матрицей A:
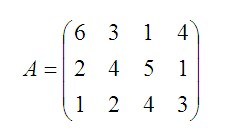
Фонд времени работы станков (мин.) задан в матрице B:
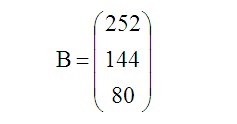
Прибыль от продажи каждой единицы изделия (руб./шт.) задана матрицей C:
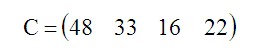
Кроме того, обозначим через Xi планируемое количество изделий каждого вида. Тогда искомый план: X1, X2, X3, X4.
2. Запись ограничений плана в виде системы неравенств
Запишем ограничения плана в виде системы неравенств:
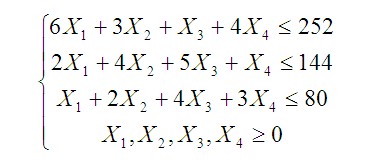
Коэффициенты при переменных в левой части системы неравенств берем из матрицы A, значения из правой части — из матрицы B.
Неравенства задают для каждого станка ограничение на суммарное время обработки им всех видов изделий, которое не должно превышать соответствующий ему фонд времени (т. к. станок чисто физически не может проработать ни минутой больше).
Также добавляем условие, согласно которому переменные не могут быть меньше нуля, так как произвести отрицательное количество изделий невозможно.
3. Определение целевого показателя
В нашей задаче целевой показатель — прибыль, которую следует максимизировать путем составления оптимального плана производства.
Тогда целевая прибыль может быть записана через следующее равенство:
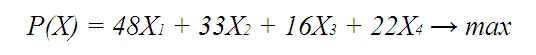
Коэффициенты при переменных берем из матрицы C. То есть мы перемножаем прибыль от производства единицы изделия каждого вида на их планируемое количество, для получения значения суммарной прибыли (которая должна быть максимальной).
4. Приведение системы неравенств к системе линейных уравнений
Для решения получившейся задачи на условный экстремум, заменим систему неравенств системой линейных уравнений путем ввода в нее дополнительных неотрицательных переменных (X5, X6, X7).
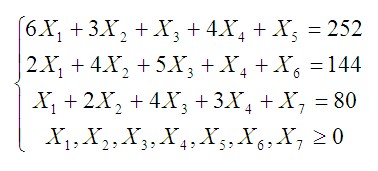
Эти переменные являются фиктивными изделиями, на которые мы списываем неиспользованные остатки фондов времени работы станков.
5. Формирование опорного плана
Примем следующий опорный план (предварительный вариант, который в процессе решения задачи будет итерационно улучшаться):
X1 = 0, X2 = 0, X3 = 0, X4 = 0, X5 = 252, X6 = 144, X7 = 80.
Здесь основным переменным (количеству изделий производимых в рамках плана) сопоставляем нулевые значения, а дополнительным (фиктивным) переменным — соответствующие величины фондов времени работы станков.
6. Составление симплекс-таблицы
Занесем исходные данные в специальную симплекс-таблицу.
В столбец Базис выписываем дополнительные переменные (X5..X7). В колонку H вносим величины фонда времени работы станков. В столбцы X1..X7 помещаем коэффициенты при этих переменных из составленной ранее системы уравнений (если переменных в уравнении нет, как например, X6 и X7 в первом равенстве, то коэффициенты будут равны 0). Кроме того, следует предусмотреть дополнительный столбец (b) для показателя, который мы будем рассчитывать на следующем этапе.
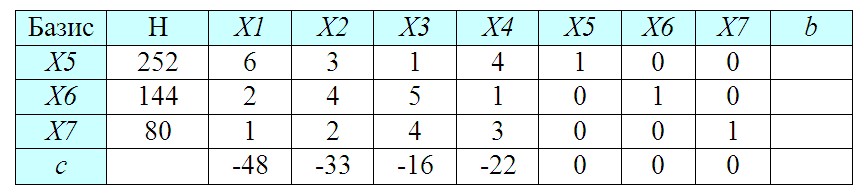
Количество строк в таблице соответствует числу дополнительных переменных (X5..X7). В последнюю строку (c) заносим коэффициенты при целевой функции с обратным знаком (коэффициенты при дополнительных переменных X5..X7 будут нулевыми).
7. Вычисление показателя b
Выбираем в последней строке наибольшее (по модулю!) отрицательное число.
В нашем примере это -48 (еще раз подчеркнем, что отрицательные числа сравниваем без учета знака).
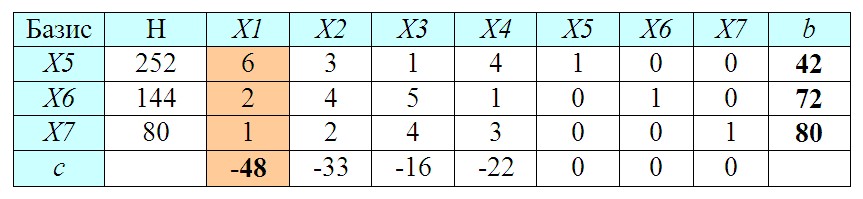
Далее вычислим для столбца, которому соответствует выбранное число, специальный показатель bi = Нi / ai, где ai — значение ячейки выбранного столбца и соответствующей строки.
8. Нахождение разрешающего элемента
Среди вычисленных значений b выбираем наименьшее.
Пересечение выбранных столбца и строки даст нам разрешающий элемент (РЭ). Меняем базисную переменную (из первой колонки в выбранной строке) на переменную соответствующую разрешающему элементу (X5 на X1).
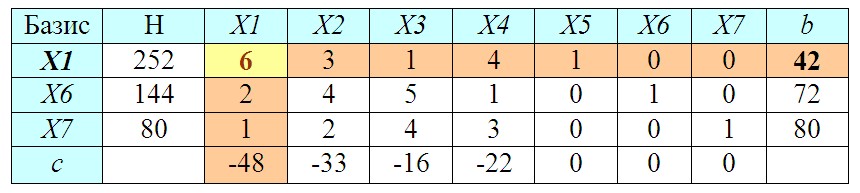
9. Перерасчет элементов симплекс-таблицы
Теперь необходимо пересчитать все элементы симплекс-таблицы, кроме столбца b (который очищается).
При перерасчете элементов симплекс-таблицы следует придерживаться следующих правил:
- Сам разрешающий элемент (РЭ) обращается в единицу;
- Для элементов разрешающей строки применяется формула: aij* = aij / РЭ (то есть каждый элемент делим на значение разрешающего элемента и получаем новые данные);
- Для элементов разрешающего столбца — они просто обнуляются;
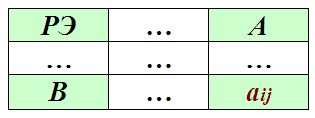
- Остальные элементы таблицы пересчитываем по правилу прямоугольника:
Формула здесь следующая: aij* = aij — ( A × B / РЭ )
Как видите, мы берем пересчитываемую ячейку и ячейку с разрешающим элементом. Они образуют противоположные углы прямоугольника. Далее перемножаем значения из ячеек 2-х других углов этого прямоугольника. Это произведение (A × B) делим на разрешающий элемент (РЭ) и вычитаем из текущей пересчитываемой ячейки (aij) то, что получилось. В итоге имеем новое значение — aij*.
Полученные в результате перерасчета значения заносим в новую симплекс-таблицу:
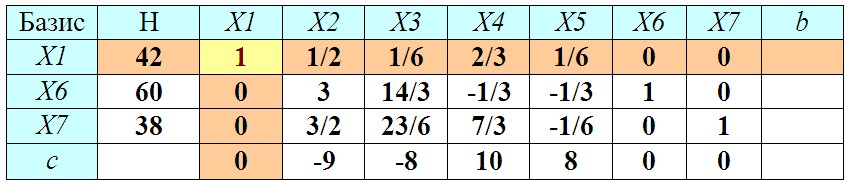
10. Проверяем последнюю строку симплекс-таблицы на наличие отрицательных чисел: если их нет — оптимальный план найден (п. 11), если есть — план требует улучшения (п. 7)
Вновь проверяем последнюю строку (c) на наличие отрицательных чисел. Если их нет — оптимальный план найден, переходим к последнему этапу решения задачи (пункт 11). Если есть — план еще не оптимален, и симплекс-таблицу вновь нужно пересчитать.
Так как у нас в последней строке снова имеются отрицательные числа, начинаем новую итерацию (повторение) вычислений с пункта 7.
В нашем примере мы снова ищем в последней строке наибольшее по модулю отрицательное число, вычисляем для соответствующего ему столбца показатель b, определяем разрешающий элемент, меняем базис и пересчитываем элементы симплекс-таблицы.
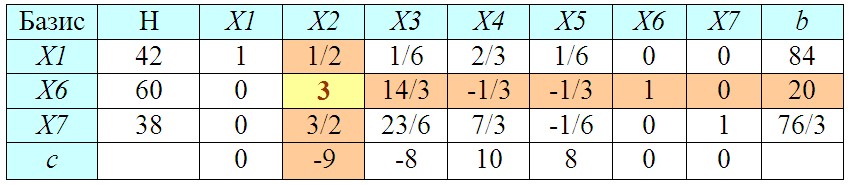
Пересчитав таблицу мы видим, что на сей раз в последней строке нет отрицательных чисел, следовательно оптимальный план (позволяющий получить максимальную прибыль) найден и можно переходить к завершающему пункту решения.
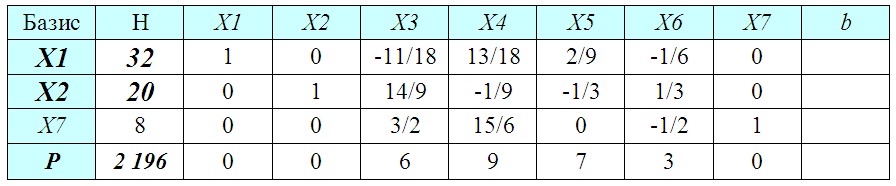
Еще раз обращаю ваше внимание, что отсутствие в последней строке отрицательных элементов указывает на то, что нами найден оптимальный план производства позволяющий получить максимально возможную прибыль при заданных условиях.
11. Определение производственного плана и вычисление общей прибыли
В соответствии с найденным планом (смотрим какие переменные перешли в колонку «Базис») выпускать мы будем изделия X1 и X2 (X7 не учитываем, т. к. это фиктивное изделие, не производимое на предприятии и введенное для приведения системы неравенств к системе уравнений).
Прибыль от производства каждой единицы продукции нам известна (матрица C). Остается перемножить ее с найденными объемами выпуска изделий X1 и X2 (значения X3 и X4 нулевые, т. к. эти изделия производить оказалось невыгодно), для получения общей (максимально возможной!) прибыли.
Ответ План производства: X1 = 32 шт., X2 = 20 шт., X3 = 0 шт., X4 = 0 шт., общая прибыль: P = 48 × 32 + 33 × 20 = 2 196 руб.
Источники
- Галяутдинов Р. Р. Курс лекций по логистике
- Симплекс-метод // Википедия. URL: http://ru.wikipedia.org/wiki/Симплекс-метод (дата обращения: 25.11.2013)
Статья дополнена и доработана автором 5 ноя 2020 г.
© Копирование любых материалов статьи допустимо только при указании прямой индексируемой ссылки на источник: Галяутдинов Р.Р.
Скачать материал

Скачать материал




- Сейчас обучается 97 человек из 41 региона


- Сейчас обучается 32 человека из 16 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Математическое моделирование
-
2 слайд
1. Задача об использовании ресурсов (задача планирования производства). Для изготовления двух видов продукции P1 и P2 используют четыре вида ресурсов S1, S2, S3, и S4. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, приведены в таблице (цифры условные).
Прибыль от получаемого продукта: P1 = 6 рублей , P2 = 8 рублей -
3 слайд
Составим план производства продукции, при котором прибыль от ее реализации будет максимальной!
Для этого составим математическую модель и запишем обозначения:
1) X1 и X2 – это число единицы продукции
2) P1 и P2 – это продукция -
4 слайд
ПРИСТУПИМ К ИЗГОТОВЛЕНИЮ ПРОДУКЦИИ!!! ( X1, X2 )
Сейчас мы составим математическое уравнение для каждого ресурса ( S1 , S2, S3, S4 )
S1 = P1 + P2 ≤ S
P1 (продукция) в паре с x1 (продукция = неизвестная), а P2 (продукция) в паре с x2 (продукции = неизвестная)
= вот данные взятые из таблицы
Запас ресурса
Теперь подставляем значения формулы S1 = P1 + P2 ≤ S = S1 = 7 (x1) + 2 (x2) ≤ 20 -
5 слайд
ПРИСТУПИМ К ИЗГОТОВЛЕНИЮ ПРОДУКЦИИ!!! ( X1, X2 )
Сейчас мы составим математическое уравнение для каждого ресурса ( S1 , S2, S3, S4 )
S2 = P1 + P2 ≤ S
P1 (продукция) в паре с x1 (продукция = неизвестная), а P2 (продукция) в паре с x2 (продукции = неизвестная)
= вот данные взятые из таблицы
Запас ресурса
Теперь подставляем значения формулы S2 = P1 + P2 ≤ S = S2 = 4 (x1) + 5 (x2) ≤ 14 -
6 слайд
ПРИСТУПИМ К ИЗГОТОВЛЕНИЮ ПРОДУКЦИИ!!! ( X1, X2 )
Сейчас мы составим математическое уравнение для каждого ресурса ( S1 , S2, S3, S4 )
S3 = P1 + P2 ≤ S
P1 (продукция) в паре с x1 (продукция = неизвестная), а P2 (продукция) в паре с x2 (продукции = неизвестная)
= вот данные взятые из таблицы
Запас ресурса
Теперь подставляем значения формулы S3 = P1 + P2 ≤ S = S3 = ? (x1) + 3 (x2) ≤ 7 -
7 слайд
ПРИСТУПИМ К ИЗГОТОВЛЕНИЮ ПРОДУКЦИИ!!! ( X1, X2 )
Сейчас мы составим математическое уравнение для каждого ресурса ( S1 , S2, S3, S4 )
S4 = P1 + P2 ≤ S
P1 (продукция) в паре с x1 (продукция = неизвестная), а P2 (продукция) в паре с x2 (продукции = неизвестная)
= вот данные взятые из таблицы
Запас ресурса
Теперь подставляем значения формулы S4 = P1 + P2 ≤ S = S4 = 5 (x1) + ? (x2) ≤ 34 -
8 слайд
= S1 = 7 (x1) + 2 (x2) ≤ 20
= S2 = 4 (x1) + 5 (x2) ≤ 14
= S3 = ? (x1) + 3 (x2) ≤ 7
= S4 = 5 (x1) + ? (x2) ≤ 34
По смыслу задачи переменные: x1 ≥ 0, x2 ≥ 0 -
9 слайд
F – это суммарная прибыль.
F = 6 (x1) + 8 (x2)
F = P1 (x1) + P2 (x2) -
10 слайд
Экономико-математическая модель задачи: найти такой план выпуска продукции Х=(x1,x2), удовлетворяющий системе (1.1) и условию (1.2), при котором функция (1.3) принимает максимальное значение.
(1.1)
X1 ≥ 0, x2 ≥ 0
(1.2)
(1.3)
F = 6 (x1) + 8 (x2)
Задачу легко обобщить на случай выпуска n видов продукции с
использованием m видов ресурсов.
Предприятие для производства n видов продукции использует m видов ресурсов.
Известно, нормы затрат ресурсов для производства единицы продукции каждого вида:
a (ij) — норма затрат,
i – ого ресурса для производства единицы продукции,
j – ого вида. -
11 слайд
m видов ресурсов
a (ij) — норма затрат
i – одного ресурса для производства единицы продукции
j – одного вида продукции
B – объём ресурсов у предприятия
Cj – производимая продукция реализуемая в цене
N – виды продукции
Составим экономико-математическую модель задачи:
Вид продукции = 1, вид продукции
Прибыль = вид продукции * (х1) + (прибыль от единицы продукта) (х2) + …
(прибыль от единицы продукта) вид продукции х вид продукции =
(прибыль от единицы продукта) вид продукции * х вид продукции -
12 слайд
норма затрат * неизвестный вид продукции ≤ ограниченный вид ресурс,
Одного ресурса на единицу ресурса = 1, видов ресурсаТак как при решении результат может получиться отрицательным, то для решения необходимо обязательно использовать условия не отрицательности проектных параметров х. Нужно для избежание ошибки!
неизвестный вид продукции ≥ 0, вид продукции = 1, вида продукции. -
13 слайд
Замечания:
1. В модели не учтены емкость рынка и объем поступивших заказов.
Учет этих факторов рынка можно записать в виде ограничений , где
dj- объем заказов
Dj — предельная емкость рынка
j — ой продукции.
2. Оптимальный объем и номенклатура производства могут определяться не только первоначальными запасами ресурсов , но и объемом выделенных финансов на производство Q . Тогда ограничения на ресурсы и финансы запишутся в виде следующих неравенств:
— цены на ресурсы -
14 слайд
Таким образом, был рассмотрен план производство продукции, изготовление продукции, вычитывали максимальную прибыль и учёт с отрицательным значением
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 268 708 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 08.12.2022
- 98
- 5

- 08.12.2022
- 577
- 9
- 08.12.2022
- 244
- 7
- 08.12.2022
- 211
- 7
- 08.12.2022
- 79
- 3
- 08.12.2022
- 228
- 37
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Облачные технологии в образовании»
-
Курс повышения квалификации «Сетевые и дистанционные (электронные) формы обучения в условиях реализации ФГОС по ТОП-50»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»
-
Курс повышения квалификации «Введение в программирование на языке С (СИ)»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания дисциплины «Информационные технологии» в условиях реализации ФГОС СПО по ТОП-50»
-
Курс повышения квалификации «Современные языки программирования интегрированной оболочки Microsoft Visual Studio C# NET., C++. NET, VB.NET. с использованием структурного и объектно-ориентированного методов разработки корпоративных систем»
-
Курс повышения квалификации «Применение интерактивных образовательных платформ на примере платформы Moodle»
Пример №4. Задача планирования производства.
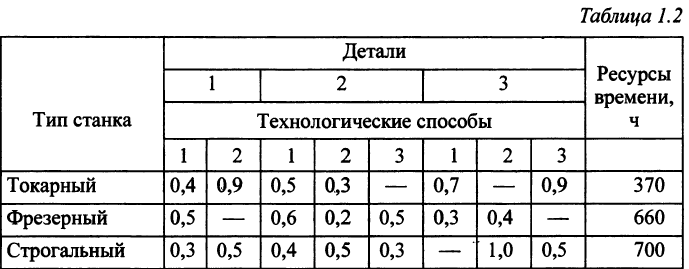
Для производства трех различных видов деталей используют токарные, фрезерные и строгальные станки. Обработку каждой детали можно вести тремя различными технологическими способами. В табл. 1.2 указаны ресурсы (ч) каждой группы станков и время (ч), затрачиваемые на обработку детали по соответствующему технологическому способу. Прибыль от продажи деталей не зависит от способа производства и составляет 16, 18, 30 единиц за одну деталь первого, второго и третьего вида соответственно. Спланировать производство деталей, обеспечивающее максимум прибыли.
Описание неизвестных. Нужно определить, сколько деталей необходимо изготовить по каждому технологическому способу. Для описания неизвестных мало одного индекса. Нужно указать, во-первых, номер детали, и, во-вторых, номер технологического способа, по которому деталь изготовляется. Обозначим через 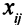
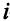
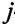
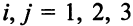
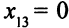
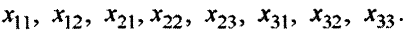
Описание целевой функции. Требуется обеспечить максимум суммарной прибыли. Целевая функция
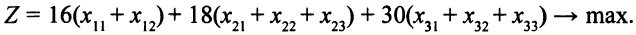
Описание системы ограничений. Необходимо вычислить время, затраченное на обработку на каждом из типов станков всех видов деталей, и потребовать, чтобы это время не превысило имеющихся ресурсов. Например, на производство 

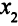
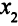
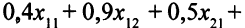
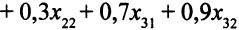
часов. Ограничение по ресурсам времени токарных станков таково:
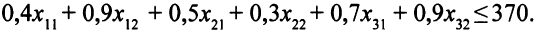
Аналогично строятся ограничения по ресурсам времени фрезерных и строгальных станков:
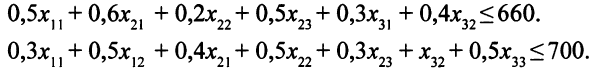
И здесь все переменные не могут быть меньше нуля:
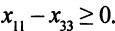
Кроме того, нужно ввести требование целочисленности переменных.
Эта задача взята со страницы решения задач по предмету «линейное программирование»:
Решение задач по линейному программированию
Возможно эти страницы вам будут полезны: