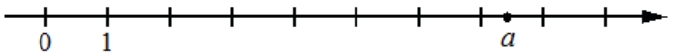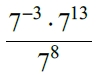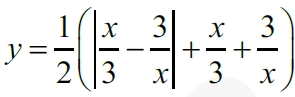Как найти вариант огэ по варианту - Исправление недочетов и поиск решений вместе с Examum.ru

В данном разделе представлены все необходимые материалы для подготовки к ОГЭ по математике 2022. Мы предоставляем как разобранные варианты с теорией по заданиям, так и тестовые варианты для самоподготовки. Пройдя курс подготовки к ОГЭ на нашем сайте, вы уверенно напишете экзамен в 9 классе в 2022 году!

Решение образца реального варианта с ответами ОГЭ по математике от сайта Ягубов.рф 27 мая 2021 года. КИМ 9 класс 27.05.21.

Все материалы получены из открытых источников и публикуются после окончания экзамена в ознакомительных целях.

ЧАСТЬ 1

Задание 1-5.
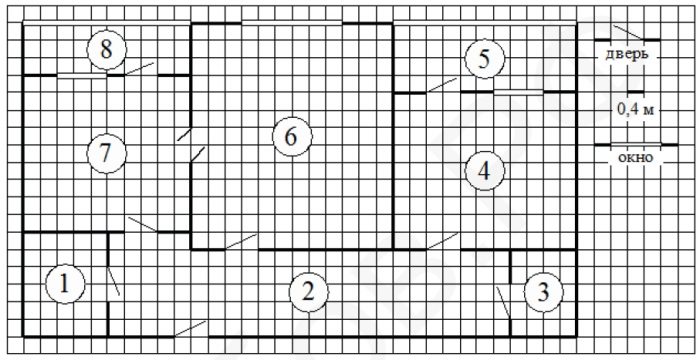
На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка. Вход в квартиру находится в коридоре. Слева от входа в квартиру находится санузел, а в противоположном конце коридора – дверь в кладовую. Рядом с кладовой находится спальня, из которой можно пройти на одну из застеклённых лоджий. Самое большое по площади помещение – гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застеклённую лоджию.

Задание 6.
Найдите значение выражения 5,7 – 7,6.

Задание 7.
На координатной прямой отмечено число а. Какое из утверждений для этого числа является верным?

1) а – 6 < 0
2) a – 7 > 0
3) 6 – a > 0
4) 8 – a < 0

Задание 8.
Найдите значение выражения

Задание 9.
Решите уравнение х² – 121 = 0. Если уравнение имеет более одного корня, в ответ запишите больший из корней.

Задание 10.
На экзамене 25 билетов, Костя не выучил 4 из них. Найдите вероятность того, что ему попадётся выученный билет.

Задание 11.
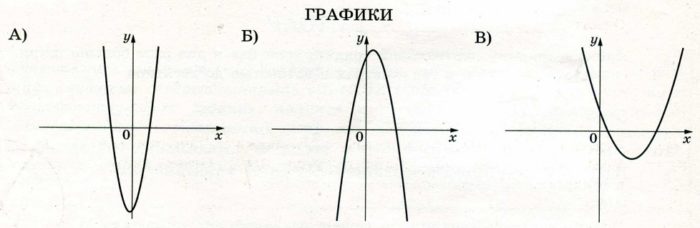
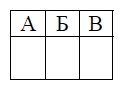
На рисунках изображены графики функций вида у = ах² + bх + c. Установите соответствие между графиками функций и знаками коэффициентов а и с.

КОЭФФИЦИЕНТЫ

1) а>0‚ с>0 2) а>0, с<0 3) а<0, с>0

В таблице под каждой буквой укажите соответствующий номер.

Задание 12.
Площадь четырёхугольника можно вычислить по формуле , где d₁ и d₂ – длины диагоналей четырёхугольника, α – угол между диагоналями. Пользуясь этой формулой, найдите длину диагонали d₂, если d₁ = 14, sinα = , S = 8,75.

Задание 13.
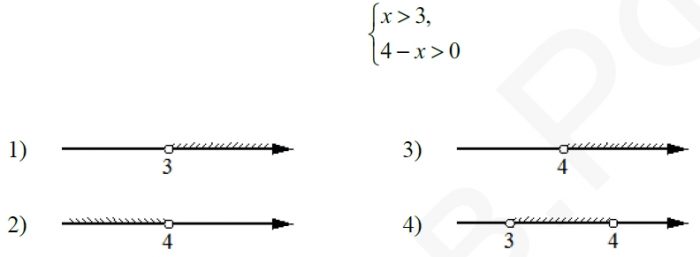
Укажите решение системы неравенств

Задание 14.
В амфитеатре 15 рядов. В первом ряду 20 мест, а в каждом следующем на 2 места больше, чем в предыдущем. Сколько мест в десятом ряду амфитеатра?

Задание 15.
Один из острых углов прямоугольного треугольника равен 63°. Найдите его другой острый угол. Ответ дайте в градусах.

Задание 16.
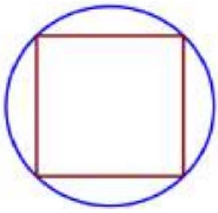
Радиус окружности, описанной около квадрата, равен 32√2. Найдите длину стороны этого квадрата.

Задание 17.
Площадь параллелограмма равна 60, а две его стороны равны 4 и 20. Найдите его высоты. В ответе укажите большую высоту.

Задание 18.
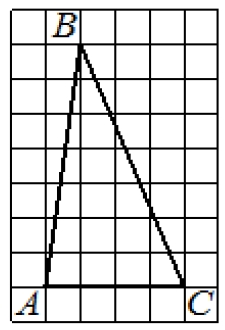
На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

Задание 19.
Какие из следующих утверждений верны?

1) Центр описанной около треугольника окружности всегда лежит внутри этого треугольника.
2) Сумма углов равнобедренного треугольника равна 180 градусам.
3) Касательная к окружности перпендикулярна радиусу, проведённому в точку касания.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

ЧАСТЬ 2

Задание 20.
Решите уравнение (x² – 49)² + (x² + 4x – 21)² = 0

Задание 21.
Поезд, двигаясь равномерно со скоростью 57 км/ч, проезжает мимо пешехода, идущего по платформе параллельно путям со скоростью 3 км/ч навстречу поезду, за 36 секунд. Найдите длину поезда в метрах.

Задание 22.
Постройте график функции

Определите, при каких значениях m прямая y = m имеет с графиком ровно одну общую точку.

Задание 23.
Точка H является основанием высоты, проведённой из вершины прямого угла В треугольника ABС к гипотенузе АС. Найдите АВ, если AH = 5, AC = 45.

Задание 24.
Через точку О пересечения диагоналей параллелограмма АВСD проведена прямая, пересекающая стороны АВ и CD в точках E и F соответственно. Докажите, что отрезки АЕ и CF равны.

Задание 25.
Четырёхугольника ABCD со сторонами AB = 25 и CD = 16 вписан в окружность. Диагонали АС и BD пересекаются в точке K, причём ∠AKB = 60°. Найдите радиус окружности, описанной около этого четырёхугольника.

Источник варианта: Ягубов.рф

Есть три секунды времени? Для меня важно твоё мнение!

Насколько понятно решение?

Средняя оценка: 5 / 5. Количество оценок: 1

Оценок пока нет. Поставь оценку первым.

Новости о решённых вариантах ЕГЭ и ОГЭ на сайте ↙️

Вступай в группу vk.com 😉

Расскажи, что не так? Я исправлю в ближайшее время

В отзыве оставь контакт для связи, если хочешь, что бы я тебе ответил.

Решайте и скачайте пробные тренировочные варианты ОГЭ по информатике — тесты и варианты за 2022 год (с ответами и решениями заданий) с сайта (не Гущина) — сдам ГИА, решу ОГЭ. Тесты за 9 класс можно смотреть онлайн, а можно распечатать в формате pdf. Многие задачи (упражнения) взяты из КИМов (реальных вариантов) и открытого банка заданий ОГЭ.

Пробный тренировочный вариант ОГЭ по информатике.

Часть 1

Задание №1

Задание №2

Задание №3

Задание №4

Задание №5

Задание №6

Задание №7

Задание №8

Задание №9

Задание №10

Задание №11

Задание №12

Задание №13

Задание №14

Задание №15

Задание №16

Задание №17

Задание №18

Часть 2

Задание №19

Задание №20

Задание №21

Каталог заданий.
Действия с обыкновенными дробями

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Задание 6 № 314127

Найдите значение выражения

Аналоги к заданию № 311234: 314127 32 311235 314128 314173 314175 314176 314177 314184 314186 … Все

Источник: Банк заданий ФИПИ

Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.

Решение

Сообщить об ошибке · Помощь

Задание 6 № 314264

Вычислите: 

Аналоги к заданию № 314262: 314264 314265 383596 314263 314266 314267 314268 314269 314270 314271 … Все

Источник: Банк заданий ФИПИ

Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.

Решение

Сообщить об ошибке · Помощь

Задание 6 № 314265

Вычислите: 

Аналоги к заданию № 314262: 314264 314265 383596 314263 314266 314267 314268 314269 314270 314271 … Все

Источник: Банк заданий ФИПИ

Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.

Решение

Сообщить об ошибке · Помощь

Задание 6 № 314288

Найдите значение выражения

Аналоги к заданию № 314282: 314288 333111 314283 314284 314285 314286 314287 314289 314290 314291 … Все

Источник: Банк заданий ФИПИ

Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.

Решение

Сообщить об ошибке · Помощь

Задание 6 № 333006

Найдите значение выражения .

Аналоги к заданию № 333006: 337375 353450 Все

Раздел кодификатора ФИПИ: 1.1 Действия с числами, сравнение чисел.

Решение

Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Решаем ОГЭ 208 вариант Ларина. Подробное решение 1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20 заданий тренировочного варианта ОГЭ Ларина № 208 (alexlarin.com)

Решаем ОГЭ 208 вариант Ларина. Подробное решение 21,22,23,24,25,26 заданий тренировочного варианта ОГЭ Ларина № 208 (alexlarin.com)

Задание 1

Найдите значение выражения $$(frac{3}{16}-frac{5}{12})*2frac{2}{11}$$

Ответ: -0,5

Скрыть

$$(frac{3}{16}-frac{5}{12})*2frac{2}{11}=$$$$frac{9-20}{48}*frac{24}{11}=$$$$frac{-11*24}{48*11}=-0,5$$

Задание 2

В таблице даны результаты забега мальчиков 6-го класса на дистанцию 30 м.

Номер дорожки	1	2	3	4
Время (с)	6,1	5,8	6,8	6,0

Зачёт выставляется, если показано время не хуже 5,9 с. Выпишите номера дорожек, по которым бежали мальчики, получившие зачёт.

Ответ: 2

Скрыть

Зачет получит только если время меньше или равно 5,9 секундам, следовательно, получит мальчик на 2 дороже , т.к. 5,8<5,9

Задание 3

Одна из точек, отмеченных на координатной прямой, соответствует числу $$sqrt{60}$$ . Какая это точка?

Варианты ответа

точка M
точка N
точка P
точка Q

Ответ: 4

Скрыть

$$sqrt{60} in [sqrt{49};sqrt{64}]Rightarrow$$ $$7<sqrt{60}<8$$. При этом $$sqrt{60}$$ ближе к $$sqrt{64}Rightarrow$$ точка Q или 4 вариант ответа.

Задание 4

Найдите значение выражения $$sqrt{24*5}sqrt{30}$$

Ответ: 60

Скрыть

$$sqrt{24*5}*sqrt{30}=$$$$sqrt{2^{3}*3*5*2*3*5}=$$$$sqrt{2^{4}*3^{2}*5^{2}}=$$$$2^{2}*3*5=60$$

Задание 5

На диаграмме показано количество SMS, присланных слушателями за каждый час четырёхчасового эфира программы по заявкам на радио. Определите, на сколько больше сообщений было прислано за первые два часа программы по сравнению с последними двумя часами этой программы.

Ответ: 15

Скрыть

За первые два часа: 40+20=60 сообщений, за последние: 15+30=45. Разница: 60-45=15 сообщений

Задание 6

При каком значении x значения выражений –1 – 5x и 5 – 8х равны?

Ответ: 2

Скрыть

Приравняем выражение: $$-1-5x=5-8xLeftrightarrow$$ $$-1-5=-8x+5xLeftrightarrow$$ $$-3x=-6Leftrightarrow$$ $$x=2$$

Задание 7

Поступивший в продажу в июле электрический чайник стоил 5400 рублей. В декабре он стал стоить 4590 рублей. На сколько процентов снизилась цена на чайник в период с июля по декабрь?

Ответ: 15

Скрыть

Первоначальную цену примем за 100% :

5400-100%

4590-x%

Тогда $$x=frac{4590*100}{5400}=85$$% , следовательно , понижение на: $$100-85=15$$%

Задание 8

На диаграмме показан возрастной состав населения Австрии. Определите по диаграмме, население какого возраста преобладает.

0–14 лет
15–50 лет
51–64 лет
65 лет и более

В ответе запишите номер выбранного варианта ответа.

Ответ: 2

Скрыть

В Австрии преобладает население возрастной группы 15-50 лет, что соответствует 2 варианту ответа.

Задание 9

В каждом двадцать пятом пакете сока согласно условиям акции под крышкой есть приз. Призы распределены случайно. Ася покупает пакет сока. Найдите вероятность того, что Ася не найдёт приз в своём пакете.

Ответ: 0,96

Скрыть

В 24 из 25 приза нет, следовательно, вероятность не выиграть приз $$P=frac{24}{25}=0,96$$

Задание 10

Установите соответствие между функциями и их графиками.

ФУНКЦИИ

$$y=-frac{1}{2}x-2$$
$$y=frac{1}{2}x+2$$
$$y=frac{1}{2}x-2$$

В таблице под каждой буквой укажите соответствующий номер.

Ответ: 231

Скрыть

A) $$k=-frac{1}{2}<0 Rightarrow$$ прямая располагается во 2 и 4 четвертях , $$b=-2<0Rightarrow$$ прямая пересекает Oy под Ox $$Rightarrow$$ 2

Б) $$k>0; b>0=$$3

B) $$k>0; b<0 Rightarrow$$ 1

Задание 11

Дана арифметическая прогрессия: 102, 95, 88, … . Какое число стоит в этой последовательности на 36-м месте?

Ответ: -143

Скрыть

Найдем разность арифметической прогрессии: $$d=a_{n+1}-a_{n}=95-102=-7$$

Найдем 36-й член: $$a_{n}=a_{1}+d(n-1)Rightarrow$$$$a_{36}=102 -7(36-1)=-143$$

Задание 12

Найдите значение выражения $$(frac{a+3b}{a^{2}-3ab}-frac{1}{a}):frac{b}{3b-a}$$, при $$a=1,5, b=sqrt{5}$$

Ответ: -4

Скрыть

$$(frac{a+3b}{a^{2}-3ab}-frac{1}{a}):frac{b}{3b-a}=$$$$frac{a+3b-a+3b}{a(a-3b)}*frac{-(a-3b)}{b}=$$$$-frac{6b}{ab}=-frac{6}{a}=$$$$-frac{6}{1,5}=-4$$

Задание 13

Расстояние s (в метрах) до места удара молнии можно приближенно вычислить по формуле s = 330t, где t – количество секунд, прошедших между вспышкой молнии и ударом грома. Определите, на каком расстоянии от места удара молнии находится наблюдатель, если t = 6. Ответ дайте в километрах, округлив его до целых.

Ответ: 2

Скрыть

Найдем расстояние в метрах: $$S=330*6=1980 Rightarrow$$ $$S=1,98$$ км $$approx 2$$ км

Задание 14

Укажите решение неравенства $$121-x^{2} geq 0$$

Варианты ответа

$$(-infty;+infty)$$
$$(-infty;-11]cup [11;+infty)$$
$$[-11;11]$$
нет решений

Ответ: 2

Скрыть

$$121-x^{2}leq 0Leftrightarrow$$ $$(11-x)(11+x)leq 0Leftrightarrow$$ $$left[begin{matrix}x leq -11xgeq 11end{matrix}right.$$, что соответствует 2 варианту ответа

Задание 15

Пол кухни размера 4 м x 3 м нужно застелить линолеумом, состоящим из плиток формы правильных шестиугольников. Сколько потребуется плиток, если их стороны равны 20 см?

Ответ: 30

Скрыть

Площадь одной плитки в м² : 0,2*0,2=0,04 м². Площадь пола в м² : 4*3=12 м², когда количество плиток составляет : $$frac{12}{0,04}=300$$ шт .

Задание 16

Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке К. Найдите периметр параллелограмма, если BК = 10, CК = 3.

Ответ: 52

Скрыть

1) $$BC=BK+KC=13$$

2) $$angle BAK=angle KAD$$(AK-биссектриса ); $$angle KAD=angle AKB$$ (накрест лежащие )$$Rightarrow$$ $$angle BAK=angle BKA$$$$Rightarrow$$ $$AB=BK=10$$

3) $$P_{ABCD}=(13+10)*2=52$$

Задание 17

Найдите периметр прямоугольника, если в него вписана окружность радиуса 6

Ответ: 48

Скрыть

Если в него вписана окружность, то это квадрат , тогда его сторона в 2 раза больше радиуса окружности $$Rightarrow$$ $$P=2*6*4=48$$

Задание 18

На клетчатой бумаге с размером клетки 1×1 изображен параллелограмм. Найдите его площадь.

Ответ: 36

Скрыть

Сторона a=6; высота: h=6. Тогда площадь: S=ah=6*6=36

Задание 19

Катеты прямоугольного треугольника равны $$5sqrt{3}$$ и 5 . Найдите наименьший угол этого треугольника.

Ответ: 30

Скрыть

Меньший угол напротив меньшей стороны . Пусть $$BC=5Rightarrow$$ $$angle A$$-меньший

$$tgangle A=frac{BC}{AB}=$$$$frac{1}{sqrt{3}}=$$$$frac{sqrt{3}}{3}Rightarrow$$ $$angle A=30$$

Задание 20

Какие из следующих утверждений верны?

Центр вписанной в треугольник окружности всегда лежит внутри этого треугольника.
Любые два равнобедренных треугольника подобны
Диагонали прямоугольника взаимно перпендикулярны.

В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов

Ответ: 1

Скрыть

Верно
Нет, зависит от углов
Нет, у ромба и квадрата.

Задание 21

Решите неравенство $$x geq frac{5x-14}{25}+frac{3x-5}{20}-9frac{3}{4}$$

Ответ: $$(-infty; -frac{1056}{65})$$

Скрыть

$$xgeq frac{5x-14}{25}+frac{3x-5}{20}-9frac{4}{5}|*100Leftrightarrow$$ $$100xgeq 20x-56+15x-25-975Leftrightarrow$$$$100x-35xgeq -1056Leftrightarrow$$$$65xgeq -1056Leftrightarrow$$$$xgeq -frac{1056}{65}Leftrightarrow$$

Задание 22

Имеются три куска сплава меди с никелем в отношениях 2 : 1, 3 : 1 и 5 : 1 по массе. Из них сплавлен кусок массой 12 кг с отношением содержания меди и никеля 4 : 1. Найдите массу каждого исходного куска, если масса первого из них вдвое больше массы второго

Ответ: 1,92; 0,96; 9,12

Скрыть

Пусть x кг-масса второго, тогда 2x кг-масса первого, y кг-третьего. Тогда x+2x+y=12 . В первом $$frac{2}{3}$$ меди и $$frac{1}{3}$$ никеля $$Rightarrow$$ $$frac{4x}{3}$$ кг и $$frac{2x}{3}$$ кг, во втором $$frac{3}{4}$$ меди и $$frac{1}{4}$$ никеля $$Rightarrow$$ $$frac{3x}{4}$$ кг и $$frac{x}{4}$$ кг, в третьем $$frac{5}{6}$$ меди и $$frac{1}{6}$$ никеля $$Rightarrow$$ $$frac{5y}{6}$$ и $$frac{y}{6}$$. В итоговом $$frac{4}{5}$$ меди и $$frac{1}{5}$$ никеля $$Rightarrow$$ 9,6 кг. меди и 2,4 кг. никеля. Тогда:

$$left{begin{matrix}frac{4x}{3}+frac{3x}{4}+frac{5y}{6}=9,6|*60frac{2x}{3}+frac{x}{4}+frac{y}{6}=2,4 |*603x+y=12end{matrix}right.Leftrightarrow$$ $$left{begin{matrix}16x+9x+10y=115,2y=12-3xend{matrix}right.Leftrightarrow$$$$left{begin{matrix}25x+10y=115,2y=12-3xend{matrix}right.Leftrightarrow$$$$25x+120-30x=115,2Leftrightarrow$$$$-5x=-4,8Rightarrow$$ $$x=0,96Rightarrow$$ $$2x=1,92$$ — масса первого и $$y=9,12$$ — масса третьего

Задание 23

Постройте график функции $$y=-1-frac{x-1}{x^{2}-x}$$ и определите, при каких значениях а прямая y=а не имеет с графиком ни одной общей точки

Ответ: -2 ; -1

Скрыть

Упростим формулу: $$y_{1}=-1-frac{x-1}{x(x-1)}=-1-frac{1}{x}$$ . Следовательно , график функции $$y_{1}$$ совпадает с $$y$$ при учете , что $$xneq 1$$.

Не имеет при $$a=-2$$ и при $$a=-1$$.

Задание 24

В треугольнике АВС проведена медиана ВК и средняя линия КЕ, параллельная стороне АВ. Площадь треугольника ВКЕ равна 1. Найдите площадь треугольника АВС.

Ответ: 4

Скрыть

1) $$S_{BKE}=S_{EKC}$$ (BE=EC,общая вершина ) $$Rightarrow$$ $$S_{ERC}=1$$

2) $$frac{S_{EKC}}{S_{ABC}}=(frac{EK}{AB})^{2}=$$$$frac{1}{4}Rightarrow$$ $$S_{ABC} =4$$ (средняя линия равна половине стороны)

Задание 25

В треугольнике АВС прямая, проходящая через вершину А, делит медиану ВМ пополам. Докажите, что эта прямая делит сторону ВС в отношении 1 : 2.

Ответ:

Скрыть

1) Построим $$MKleft | right |AM$$. По т. Фалеса : $$frac{CM}{MA}=frac{CK}{KM}Rightarrow$$ $$frac{CK}{KM}=frac{1}{1}Rightarrow$$ $$CK=KM$$

2) Аналогично : $$frac{BH}{HM}=frac{BM}{MK}=frac{1}{1}Rightarrow$$ $$CK=KM=MBRightarrow$$ $$CM:MB=2:1$$

Задание 26

На плоскости дан прямой угол. Окружность с центром внутри этого угла касается одной стороны угла, пересекает другую в точках А и В, а биссектрису угла – в точках С и D. Найдите радиус окружности, если $$AB=sqrt{6}$$ см, $$CD=sqrt{7}$$ см.

Ответ: $$sqrt{2}$$

Скрыть

1) Пусть O – центр окружности,K-вершина, M-точка касания, $$OMperp KM$$; $$ORperp AB$$; x –радиус . $$RA=frac{AB}{2}=frac{sqrt{6}}{2}$$; $$HC=frac{DC}{2}=frac{sqrt{7}}{2}$$.

2) из $$Delta ORA$$: $$OR=sqrt{OA^{2}-RA^{2}}=sqrt{x^{2}-frac{3}{2}}$$

3) $$Delta OHN sim Delta NMK$$ (прямоугольные, $$angle ONH=angle MNK$$)$$Rightarrow$$ $$OH=HN=frac{ON}{sqrt{2}}=$$$$frac{OM-NM}{sqrt{2}}=frac{x-NM}{sqrt{2}}=$$$$frac{x-MK}{sqrt{2}}=frac{x-OR}{sqrt{2}}=$$$$frac{x-sqrt{x^{2}-frac{3}{2}}}{sqrt{2}}$$

4) из $$Delta OHC$$: $$OC^{2}=OH^{2}+HC^{2}Leftrightarrow$$ $$x^{2}=(frac{x-sqrt{x^{2}-frac{3}{2}}}{2})^{2}+frac{7}{4}Leftrightarrow$$ $$x^{2} =frac{1}{2} (x^{2}+x^{2}-frac{3}{2}-2xsqrt{x^{2}-frac{3}{2}}) +frac{7}{4} Leftrightarrow$$ $$2x^{2}=2x^{2}-frac{3}{2}+frac{7}{2}-2xsqrt{x^{2}-frac{3}{2}}Leftrightarrow$$ $$xsqrt{x^{2}-frac{3}{2}}=1Leftrightarrow$$ $$x^{4}-frac{3}{2}x^{2}-1=0Leftrightarrow$$ $$left[begin{matrix}x^{2}=2 & & x^{2}=-frac{1}{2} & &end{matrix}right.Leftrightarrow$$ $$x=sqrt{2}$$

Источник

3 тренировочных варианта ОГЭ 2023 по математике 9 класс пробник формата реального экзамена с ответами и решением. Каждый вариант состоит из двух частей, включающих в себя 25 заданий. Часть 1 содержит 19 заданий, часть 2 содержит 6 заданий с развёрнутым ответом.

Скачать 1 тренировочный вариант
Скачать 2 тренировочный вариант
Скачать 3 тренировочный вариант
Скачать ответы и решения

1variant_oge2023_mat_9klass

2 тренировочный вариант ОГЭ 2023 по математике 9 класс

2variant_oge2023_mat_9klass

3 тренировочный вариант ОГЭ 2023 по математике 9 класс

3variant_oge2023_mat_9klass

1 вариант заданий с ответами

На рисунке изображён план двухкомнатной квартиры в многоэтажном жилом доме. Сторона одной клетки на плане соответствует 0,4 м, а условные обозначения двери и окна приведены в правой части рисунка. Вход в квартиру находится в коридоре. Справа от входа в квартиру находится санузел, а в противоположном конце коридора – дверь в кладовую. Рядом с кладовой находится спальня, из которой можно пройти на одну из застеклённых лоджий. Самое большое по площади помещение – гостиная, откуда можно попасть в коридор и на кухню. Из кухни также можно попасть на застеклённую лоджию.

1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк перенесите последовательность четырёх цифр без пробелов, запятых и других дополнительных символов.

2. Найдите площадь гостиной. Ответ дайте в квадратных метрах.

3. Плитка для пола размером 40 см на 40 см продаётся в упаковках по 12 штук. Сколько упаковок плитки понадобилось, чтобы выложить пол обеих лоджий?

4. На сколько процентов площадь санузла больше площади кладовой?

5. В квартире планируется установить стиральную машину. Характеристики стиральных машин, условия подключения и доставки приведены в таблице. Планируется купить стиральную машину с вертикальной загрузкой вместимостью не менее 6 кг. Сколько рублей будет стоить наиболее дешёвый подходящий вариант вместе с подключением и доставкой?

7. На координатной прямой отмечено число a. Какое из утверждений для этого числа является верным?

10. На экзамене 40 билетов, Серёжа не выучил 6 из них. Найдите вероятность того, что ему попадётся выученный билет.

14. Камень бросают в глубокое ущелье. При этом в первую секунду он пролетает 13 метров, а в каждую следующую секунду на 10 метров больше, чем в предыдущую, до тех пор, пока не достигнет дна ущелья. Сколько метров пролетит камень за первые пять секунд?

15. В треугольнике одна из сторон равна 18, а опущенная на нее высота -12. Найдите площадь треугольника.

16. На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что угол NBA=34°. Найдите угол NMB. Ответ дайте в градусах.

17. Диагональ прямоугольника образует угол 69° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

18. На клетчатой бумаге с размером клетки 1×1 изображён треугольник ABC. Найдите длину его средней линии, параллельной стороне AC.

19. Какие из следующих утверждений верны? 1)В параллелограмме есть два равных угла. 2)Площадь треугольника меньше произведения двух его сторон. 3) Средняя линия трапеции равна сумме её оснований. В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.

21. Первый велосипедист выехал из посёлка по шоссе со скоростью 21 км/ч. Через час после него со скоростью 15 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час – третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 9 часов после этого догнал первого.

23.Отрезки АВ и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке М. Найдите МС, если АВ = 12, DC = 48, АС = 35.

24. В выпуклом четырехугольнике АВСD углы DAC и DBC равны. Докажите, что углы CDB и CAB также равны.

25. В треугольнике АВС биссектриса ВЕ и медиана AD перпендикулярны и имеют одинаковую длину, равную 24. Найдите стороны треугольника АВС.

2 вариант заданий с ответами

Серёжа летом отдыхает с папой в деревне Пирожки. В среду они собираются съездить на машине в село Княжеское. Из деревни Пирожки в село Княжеское можно проехать по прямой грунтовой дороге. Есть более длинный путь: по прямолинейному шоссе через деревню Васильево до деревни Рябиновка, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в село Княжеское. Есть и третий маршрут: в деревне Васильево можно свернуть на прямую грунтовую дорогу в село Княжеское, которая идёт мимо пруда. Шоссе и грунтовые дороги образуют прямоугольные треугольники.

По шоссе Серёжа с папой едут со скоростью 60 км/ч, а по грунтовой дороге – со скоростью 40 км/ч. На плане изображено взаимное расположение населённых пунктов, длина стороны каждой клетки равна 2 км.

1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. Заполните таблицу, в бланк ответов перенесите последовательность трёх цифр без пробелов, запятых и других дополнительных символов.

2. Сколько километров проедут Серёжа с папой от деревни Васильево до села Княжеское, если они поедут по шоссе через деревню Рябиновка?

3. Найдите расстояние от деревни Васильево до села Княжеское по прямой. Ответ дайте в километрах.

4. Сколько минут затратят на дорогу из деревни Пирожки в село Княжеское Серёжа с папой, если они поедут по прямой грунтовой дороге?

5. В таблице указана стоимость (в рублях) некоторых продуктов в четырёх магазинах, расположенных в деревне Пирожки, селе Княжеское, деревне Васильево и деревне Рябиновка. Серёжа с папой хотят купить 2 л молока, 3 батона хлеба и 1,5 кг сыра «Российский». В каком магазине такой набор продуктов будет стоить дешевле всего? В ответ запишите стоимость данного набора в этом магазине.

7. На координатной прямой отмечены точки A, B, C, и D. Одна из них соответствует числу 60 Какая это точка?

10. В лыжных гонках участвуют 13 спортсменов из России, 4 спортсмена из Норвегии и 3 спортсмена из Швеции. Порядок, в котором спортсмены стартуют, определяется жребием. Найдите вероятность того, что первым будет стартовать спортсмен не из Норвегии.

14. В амфитеатре 16 рядов, причём в каждом следующем ряду на одно и то же число мест больше, чем в предыдущем. В четвёртом ряду 23 места, а в восьмом ряду 35 мест. Сколько мест в последнем ряду амфитеатра?

15. Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 31, сторона BC равна 37, сторона AC равна 50. Найдите MN.

16. На окружности отмечены точки A и B так, что меньшая дуга AB равна 134°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.

17. Площадь параллелограмма ABCD равна 148. Точка M – середина стороны CD. Найдите площадь трапеции ABMD.

18. На клетчатой бумаге с размером клетки 1 см × 1 см отмечены точки А, В и С. Найдите расстояние от точки А до прямой ВС. Ответ выразите в сантиметрах.

19. Какое из следующих утверждений верно? 1) Внешний угол треугольника равен сумме его внутренних углов. 2) В любой четырёхугольник можно вписать окружность. 3) Площадь ромба равна произведению его стороны на высоту, проведённую к этой стороне. В ответ запишите номер выбранного утверждения.

21. Из двух городов одновременно навстречу друг другу отправились два велосипедиста. Проехав некоторую часть пути, первый велосипедист сделал остановку на 36 минут, а затем продолжил движение до встречи со вторым велосипедистом. Расстояние между городами составляет 82 км, скорость первого велосипедиста равна 28 км/ч, скорость второго — 10 км/ч. Определите расстояние от города, из которого выехал второй велосипедист, до места встречи.

23. Биссектриса угла A параллелограмма ABCD пересекает сторону BC в точке K. Найдите периметр параллелограмма, если BK = 7 , CK =12 .

24. Известно, что около четырёхугольника ABCD можно описать окружность и что продолжения сторон AD и BC четырёхугольника пересекаются в точке K. . Докажите, что треугольники KAB и KCD подобны.

25. Четырёхугольник ABCD со сторонами AB = 34 и CD = 22 вписан в окружность. Диагонали AC и BD пересекаются в точке K , причём ∠AKB = 60° . Найдите радиус окружности, описанной около этого четырёхугольника.

Статград ОГЭ 2023 математика 9 класс варианты с ответами

Работа статград ОГЭ 2023 математика 9 класс варианты с ответами

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

+ Реальные варианты ОГЭ

Решение Реального Варианта ОГЭ 2022 от 23.05-24.05 Математика

Решение образца реального варианта с ответами ОГЭ по математике. КИМ 9 класс 23.05 24.05.

Продолжить чтение Решение Реального Варианта ОГЭ 2022 от 23.05-24.05 Математика

Решение Реального Варианта ОГЭ 2021 от 27.05 Математика

Решение образца реального варианта ОГЭ по математике от сайта Ягубов.рф 27 мая 2021 года.

Продолжить чтение Решение Реального Варианта ОГЭ 2021 от 27.05 Математика

Источник

Критерии

Оценивание

№ задания	1-19	20-25	Всего
Баллы	1	2	31

Экзаменационная работа состоит из двух частей, включающих в себя 25 заданий. Часть 1 содержит 19 заданий, часть 2 содержит 6 заданий с развёрнутым ответом.

На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

Ответы к заданиям 7 и 13 запишите в бланк ответов № 1 в виде одной цифры, которая соответствует номеру правильного ответа.

Для остальных заданий части 1 ответом является число или последовательность цифр. Ответ запишите в поле ответа в тексте работы, а затем перенесите в бланк ответов №1. Если в ответе получена обыкновенная дробь, обратите её в десятичную.

При выполнении работы Вы можете воспользоваться справочными материалами, содержащими основные формулы курса математики, выдаваемыми вместе с работой.
Разрешается использовать линейку, угольник, иные шаблоны для построения геометрических фигур (циркуль). Запрещается использовать инструменты с нанесёнными на них справочными материалами. Калькуляторы на экзамене не используются.

Для прохождения аттестационного порога необходимо набрать не менее 8 баллов, из которых не менее 2 баллов должны быть получены за решение заданий по геометрии (задания 15–19, 23–25). Однако, невыполнение данного критерия по геометрии лишь снижает оценку на один итоговый балл («5» на «4», «4» на «3» или «3» на «2»), поэтому можно сдать экзамен без верного решения заданий по геометрии.

На экзамене при себе надо иметь документ удостоверяющий личность (паспорт), пропуск и капиллярную или гелевую ручку с черными чернилами! Разрешают брать с собой воду (в прозрачной бутылке) и еду (фрукты, шоколадку, булочки, бутерброды), но могут попросить оставить в коридоре.

№ задания	1-19	20-25	Всего
Баллы	1	2	31

На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут).

Шкалирование

Балл за ОГЭ / Оценка	0-7 / «2»	8-14 / «3»	15-21 / «4»	22-31 / «5»
АЛГЕБРА / ГЕОМЕТРИЯ	0-4 / 0-2	5-10 / 3-4	11-15 / 5-7	16-20 / 8-11

Источник

ОГЭ

Освоение образовательных программ основного общего образования завершается обязательной государственной итоговой аттестацией (далее – ГИА 9) по русскому языку и математике.

Нормативно-правовые документы

Приказы и методические документы

Демоверсии, спецификации, кодификаторы

В данном разделе представлены документы, определяющие структуру и содержание контрольных измерительных материалов основного государственного экзамена.

Для предметных комиссий субъектов РФ

Открытый банк заданий ОГЭ

Новая версия открытого банка заданий

Источник