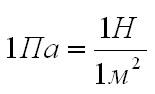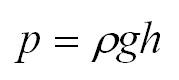Как найти вектор давления

Как найти вектор давления

Гидравлика делится на два раздела: гидростатика и гидродинамика. Гидродинамика является более обширным разделом и будет рассмотрена в последующих лекциях. В этой лекции будет рассмотрена гидростатика.

Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение.

В покоящейся жидкости всегда присутствует сила давления, которая называется гидростатическим давлением. Жидкость оказывает силовое воздействие на дно и стенки сосуда. Частицы жидкости, расположенные в верхних слоях водоема, испытывают меньшие силы сжатия, чем частицы жидкости, находящиеся у дна.

Рассмотрим резервуар с плоскими вертикальными стенками, наполненный жидкостью (рис.2.1, а). На дно резервуара действует сила P равная весу налитой жидкости G = γ V, т.е. P = G.

Если эту силу P разделить на площадь дна S_abcd, то мы получим среднее гидростатическое давление, действующее на дно резервуара.

Гидростатическое давление обладает свойствами.

Свойство 1. В любой точке жидкости гидростатическое давление перпендикулярно площадке касательной к выделенному объему и действует внутрь рассматриваемого объема жидкости.

Для доказательства этого утверждения вернемся к рис.2.1, а. Выделим на боковой стенке резервуара площадку S_бок (заштриховано). Гидростатическое давление действует на эту площадку в виде распределенной силы, которую можно заменить одной равнодействующей, которую обозначим P. Предположим, что равнодействующая гидростатического давления P, действующая на эту площадку, приложена в точке А и направлена к ней под углом φ (на рис. 2.1 обозначена штриховым отрезком со стрелкой). Тогда сила реакции стенки R на жидкость будет иметь ту же самую величину, но противоположное направление (сплошной отрезок со стрелкой). Указанный вектор R можно разложить на два составляющих вектора: нормальный R_n (перпендикулярный к заштрихованной площадке) и касательный R_τ к стенке.

Сила нормального давления R_n вызывает в жидкости напряжения сжатия. Этим напряжениям жидкость легко противостоит. Сила R_τ действующая на жидкость вдоль стенки, должна была бы вызвать в жидкости касательные напряжения вдоль стенки и частицы должны были бы перемещаться вниз. Но так как жидкость в резервуаре находится в состоянии покоя, то составляющая R_τ отсутствует. Отсюда можно сделать вывод первого свойства гидростатического давления.

Свойство 2. Гидростатическое давление неизменно во всех направлениях.

В жидкости, заполняющей какой-то резервуар, выделим элементарный кубик с очень малыми сторонами Δx, Δy, Δz (рис.2.1, б). На каждую из боковых поверхностей будет давить сила гидростатического давления, равная произведению соответствующего давления P_x, P_y , P_z на элементарные площади. Обозначим вектора давлений, действующие в положительном направлении (согласно указанным координатам) как P’_x, P’_y, P’_z, а вектора давлений, действующие в обратном направлении соответственно P»_x, P»_y, P»_z. Поскольку кубик находится в равновесии, то можно записать равенства

где γ — удельный вес жидкости;
Δx, Δy, Δz — объем кубика.

Сократив полученные равенства, найдем, что

Членом третьего уравнения γΔz, как бесконечно малым по сравнению с P’_z и P»_z, можно пренебречь и тогда окончательно

Вследствие того, что кубик не деформируется (не вытягивается вдоль одной из осей), надо полагать, что давления по различным осям одинаковы, т.е.

Это доказывает второй свойство гидростатического давления.

Свойство 3. Гидростатическое давление в точке зависит от ее координат в пространстве.

Это положение не требует специального доказательства, так как ясно, что по мере увеличения погружения точки давление в ней будет возрастать, а по мере уменьшения погружения уменьшаться. Третье свойство гидростатического давления может быть записано в виде

Рассмотрим распространенный случай равновесия жидкости, когда на нее действует только одна массовая сила — сила тяжести, и получим уравнение, позволяющее находить гидростатическое давление в любой точке рассматриваемого объема жидкости. Это уравнение называется основным уравнением гидростатики.

Пусть жидкость содержится в сосуде (рис.2.2) и на ее свободную поверхность действует давление P₀ . Найдем гидростатическое давление P в произвольно взятой точке М, расположенной на глубине h. Выделим около точки М элементарную горизонтальную площадку dS и построим на ней вертикальный цилиндрический объем жидкости высотой h. Рассмотрим условие равновесия указанного объема жидкости, выделенного из общей массы жидкости. Давление жидкости на нижнее основание цилиндра теперь будет внешним и направлено по нормали внутрь объема, т.е. вверх.

Запишем сумму сил, действующих на рассматриваемый объем в проекции на вертикальную ось:

Последний член уравнения представляет собой вес жидкости, заключенный в рассматриваемом вертикальном цилиндре объемом hdS. Силы давления по боковой поверхности цилиндра в уравнение не входят, т.к. они перпендикулярны к этой поверхности и их проекции на вертикальную ось равны нулю. Сократив выражение на dS и перегруппировав члены, найдем

Полученное уравнение называют основным уравнением гидростатики. По нему можно посчитать давление в любой точке покоящейся жидкости. Это давление, как видно из уравнения, складывается из двух величин: давления P₀ на внешней поверхности жидкости и давления, обусловленного весом вышележащих слоев жидкости.

Из основного уравнения гидростатики видно, что какую бы точку в объеме всего сосуда мы не взяли, на нее всегда будет действовать давление, приложенное к внешней поверхности P₀. Другими словами давление, приложенное к внешней поверхности жидкости, передается всем точкам этой жидкости по всем направлениям одинаково. Это положение известно под названием закона Паскаля.

Поверхность, во всех точках которой давление одинаково, называется поверхностью уровня (подробно рассмотрим в п.2.6). В обычных условиях поверхности уровня представляют собой горизонтальные плоскости.

Пусть мы имеем резервуар с наклонной правой стенкой, заполненный жидкостью с удельным весом γ. Ширина стенки в направлении, перпендикулярном плоскости чертежа (от читателя), равна b (рис.2.3). Стенка условно показана развернутой относительно оси АВ и заштрихована на рисунке. Построим график изменения избыточного гидростатического давления на стенку АВ.

Так как избыточное гидростатическое давление изменяется по линейному закон P=γgh, то для построения графика, называемого эпюрой давления, достаточно найти давление в двух точках, например А и B.

Избыточное гидростатическое давление в точке А будет равно

Соответственно давление в точке В:

где H — глубина жидкости в резервуаре.

Согласно первому свойству гидростатического давления, оно всегда направлено по нормали к ограждающей поверхности. Следовательно, гидростатическое давление в точке В, величина которого равна γH, надо направлять перпендикулярно к стенке АВ. Соединив точку А с концом отрезка γH, получим треугольную эпюру распределения давления АВС с прямым углом в точке В. Среднее значение давления будет равно

Если площадь наклонной стенки S=bL, то равнодействующая гидростатического давления равна

где hc = Н/2 — глубина погружения центра тяжести плоской поверхности под уровень жидкости.

Однако точка приложения равнодействующей гидростатического давления ц.д. не всегда будет совпадать с центром тяжести плоской поверхности. Эта точка находится на расстоянии l от центра тяжести и равна отношению момента инерции площадки относительно центральной оси к статическому моменту этой же площадки.

где J_Аx — момент инерции площади S относительно центральной оси, параллельной Аx.

В частном случае, когда стенка имеет форму прямоугольника размерами bL и одна из его сторон лежит на свободной поверхности с атмосферным давлением, центр давления ц.д. находится на расстоянии b/3 от нижней стороны.

Пусть жидкость заполняет резервуар, правая стенка которого представляет собой цилиндрическую криволинейную поверхность АВС (рис.2.4), простирающуюся в направлении читателя на ширину b. Восстановим из точки А перпендикуляр АО к свободной поверхности жидкости. Объем жидкости в отсеке АОСВ находится в равновесии. Это значит, что силы, действующие на поверхности выделенного объема V, и силы веса взаимно уравновешиваются.

Представим, что выделенный объем V представляет собой твердое тело того же удельного веса, что и жидкость (этот объем на рис.2.4 заштрихован). Левая поверхность этого объема (на чертеже вертикальная стенка АО) имеет площадь Sx = bH, являющуюся проекцией криволинейной поверхности АВС на плоскость yOz.

С правой стороны на отсек будет действовать реакция R цилиндрической поверхности. Пусть точка приложения и направление этой реакции будут таковы, как показано на рис.2.4. Реакцию R разложим на две составляющие R_x и R_z.

Из действующих поверхностных сил осталось учесть только давление на свободной поверхности Р₀. Если резервуар открыт, то естественно, что давление Р₀ одинаково со всех сторон и поэтому взаимно уравновешивается.

На отсек АВСО будет действовать сила собственного веса G = γV, направленная вниз.

Спроецируем все силы на ось Ох:

Теперь спроецируем все силы на ось Оz:

Составляющая силы гидростатического давления по оси O_y обращается в нуль, значит R_y = F_y = 0.

Таким образом, реакция цилиндрической поверхности в общем случае равна

а поскольку реакция цилиндрической поверхности равна равнодействующей гидростатического давления R=F, то делаем вывод, что

Тело, погруженное (полностью или частично) в жидкость, испытывает со стороны жидкости суммарное давление, направленное снизу вверх и равное весу жидкости в объеме погруженной части тела.

Для однородного тела плавающего на поверхности справедливо соотношение

где: V — объем плавающего тела;
ρ_m — плотность тела.

Существующая теория плавающего тела довольно обширна, поэтому мы ограничимся рассмотрением лишь гидравлической сущности этой теории.

Способность плавающего тела, выведенного из состояния равновесия, вновь возвращаться в это состояние называется устойчивостью. Вес жидкости, взятой в объеме погруженной части судна называют водоизмещением, а точку приложения равнодействующей давления (т.е. центр давления) — центром водоизмещения. При нормальном положении судна центр тяжести С и центр водоизмещения d лежат на одной вертикальной прямой O’-O», представляющей ось симметрии судна и называемой осью плавания (рис.2.5).

Пусть под влиянием внешних сил судно наклонилось на некоторый угол α, часть судна KLM вышла из жидкости, а часть K’L’M’, наоборот, погрузилось в нее. При этом получили новое положении центра водоизмещения d’. Приложим к точке d’ подъемную силу R и линию ее действия продолжим до пересечения с осью симметрии O’-O». Полученная точка m называется метацентром, а отрезок mC = h называется метацентрической высотой. Будем считать h положительным, если точка m лежит выше точки C, и отрицательным — в противном случае.

Теперь рассмотрим условия равновесия судна:

1) если h > 0, то судно возвращается в первоначальное положение;
2) если h = 0, то это случай безразличного равновесия;
3) если h<0, то это случай неостойчивого равновесия, при котором продолжается дальнейшее опрокидывание судна.

Следовательно, чем ниже расположен центр тяжести и, чем больше метацентрическая высота, тем больше будет остойчивость судна.

Как уже отмечалось выше, поверхность, во всех точках которой давление одинаково, называется поверхностью уровня или поверхностью равного давления. При неравномерном или непрямолинейном движении на частицы жидкости кроме силы тяжести действуют еще и силы инерции, причем если они постоянны по времени, то жидкость принимает новое положение равновесия. Такое равновесие жидкости называется относительным покоем.

Рассмотрим два примера такого относительного покоя.

В первом примере определим поверхности уровня в жидкости, находящейся в цистерне, в то время как цистерна движется по горизонтальному пути с постоянным ускорением a (рис.2.6).

К каждой частице жидкости массы m должны быть в этом случае приложены ее вес G = mg и сила инерции P_u, равная по величине ma. Равнодействующая этих сил направлена к вертикали под углом α, тангенс которого равен

Так как свободная поверхность, как поверхность равного давления, должна быть нормальна к указанной равнодействующей, то она в данном случае представит собой уже не горизонтальную плоскость, а наклонную, составляющую угол α с горизонтом. Учитывая, что величина этого угла зависит только от ускорений, приходим к выводу, что положение свободной поверхности не будет зависеть от рода находящейся в цистерне жидкости. Любая другая поверхность уровня в жидкости также будет плоскостью, наклоненной к горизонту под углом α. Если бы движение цистерны было не равноускоренным, а равнозамедленным, направление ускорения изменилось бы на обратное, и наклон свободной поверхности обратился бы в другую сторону (см. рис.2.6, пунктир).

В качестве второго примера рассмотрим часто встречающийся в практике случай относительного покоя жидкости во вращающихся сосудах (например, в сепараторах и центрифугах, применяемых для разделения жидкостей). В этом случае (рис.2.7) на любую частицу жидкости при ее относительном равновесии действуют массовые силы: сила тяжести G = mg и центробежная сила P_u = mω 2 r, где r — расстояние частицы от оси вращения, а ω — угловая скорость вращения сосуда.

Поверхность жидкости также должна быть нормальна в каждой точке к равнодействующей этих сил R и представит собой параболоид вращения. Из чертежа находим

С другой стороны:

где z — координата рассматриваемой точки. Таким образом, получаем:

Главный вектор и главный момент сил давления

Эти характеристики применяются при интегральной оценке действия сил давления, в частности при рассмотрении взаимодействия жидкости с ограничивающими ее поверхностями и погруженными в нее телами.

Выделим в жидкой среде произвольную незамкнутую поверхность S, площадь которой равна s (рис.3.4). Выделим на этой поверхности бесконечно малый элемент площадью ds, единичный вектор внешней нормали которого *. Пусть на элемент действует нормальное напряжение p, cоздаваемое жидкостью (т.е. не учитывающее давление на ее свободной поверхности и называемое давлением жидкости), вектор которого, следовательно, равен

(3.28)

Знак минус в правой части (3.28) взят по той причине, что, как указывалось в п. 3.2, вектор ` всегда направлен по внутренней нормали к поверхности, т.е. противоположен по направлению вектору . Сила, действующая на элемент ds, очевидно, будет

(3.29)

Главный вектор сил давления `Р представляет собой сумму элементарных сил взятую по всей поверхности . С учетом (3.29) это будет

Закон Архимеда

Самостоятельно

Равновесие погруженного тела

На рис. 3.5. изображено погруженное в жидкость тело объемом V и плотностью ; плотность жидкости пусть будет . Выталкивающая сила, действующая на тело, согласно (3.41), будет

(3.42)

(3.43)

а их равнодействующая

(3.44)

или в проекции на ось Оz (3.45)

Из (3.44) видно, что вес тела, погруженного в жидкость, уменьшается на величину Р. Из формул (3.44), (3.45) также следуют условия, определяющие поведение тела в жидкости (положительным принято направление силы вниз по вертикали):

— тело погружается в жидкость

(3.46)

— тело находится в равновесии

(3.47)

(3.48)

3.10. Давление жидкости на стенку сосуда

Рассмотрим вначале давление жидкости, находящейся в равновесии на боковую стенку сосуда, заключающего эту жидкость. На рис. 3.6 изображена такая стенка М. Выделим около нее плоское сечение S, на

котором построим цилиндр с осью, перпендикулярной плоскости S. Пусть также давление жидкости на уровне центра тяжести плоскости будет р. Тогда сила давления жидкости на плоскость S будет F=pS; она будет направлена по внутренней нормали к плоскости S, т.е. внутрь цилиндра. Из условия равновесия следует, что сила давления на правое основание цилиндра находящееся на стенке сосуда, будет равно силе , действующей на левое основание цилиндра, но противоположна ей по направлению: Согласно третьему закону Ньютона, сила давления жидкости на часть стенки равна силе давления стенки на жидкость, но противоположна ей по направлению: Согласно третьему закону Ньютона, сила давления жидкости на часть стенки равна силе давления стенки на жидкость, но противоположна по направлению: . Из сказанного следует, что сила давления жидкости на стенку Но поскольку давление жидкости р не зависит от формы боковой стенка (для тяжелой несжимаемой жидкости оно зависит лишь от расстояния центра тяжести площадки S до свободной поверхности жидкости и ее плотности – см. (3.31), п. 3.7), не зависит от формы и давление, оказываемое жидкостью на стенку.

Рассмотрим теперь давление на дно сосуда, содержащего жидкость. Возьмем несколько сосудов разной формы с одинаковой площадью дна S, заполненных одинаковой жидкостью на одинаковую высоту h (рис. 3.7).

Сила давления жидкости в каждом из сосудов рис.3.7. будет одна и та же и, согласно (3.35), равна где — плотность жидкости. В то же время очевидно, что объем жидкости, а следовательно, и ее вес в каждом сосуде будет разный.

Обобщая сказанное о давлении на боковую стенку сосуда и на его дно, можем заключить, что давление жидкости на стенки сосуда не зависит от формы сосуда, содержащего жидкость. Этот закон получил название гидростатического парадокса.

Естественная тяга

Равновесие шахтной атмосферы.Рассмотрим два вертикальных или наклонных шахтных ствола 1-2 и 3-4, соединенных между собою горизонтальной выработкой 2-4 (рис.3.8).

Примем в качестве свободной поверхности воздуха, заполняющего шахту, поверхность z=0, давление на которой пусть будет . Пусть также

вертикальная глубина стволов будет Н, плотность воздуха в стволе 1-2 пусть будет r₁, в стволе 3-4 — r₂. Определим давление воздуха в нижних концах стволов (т.т 2 и 4 соответственно). Рассматривая воздух в стволах как тяжелую несжимаемую жидкость, эти давления можно определить по выражению (3.31), в которое вместо z следует подставить Н, а вместоrзначение плотности воздуха в соответствующем стволе. Тогда для т.2 имеем

(3.49)

(3.50)

Выделим теперь на участке 2-4 некоторый объем так, чтобы его грани и были перпендикулярны оси выработки 2-4 и чтобы площадь каждой грани была равна площади поперечного сечения выработки S. Тогда сила давления, действующая на объем слева, будет справа Силы F₁ и F₂, как силы давления, направлены по внутренним нормалям к граням и , т.е. противоположны друг другу по направлениям. Поэтому с учетом (3.49), (3.50) абсолютное значение их равнодействующей будет равно

(3.51)

Если воздух, заполняющий шахту, т.е. заполняющий выработки 1-2-4-3, будет в равновесии, объем также будет находиться в равновесии, т.е. будет неподвижен. Следовательно, условием равновесия (неподвижности) воздуха в шахте будет условие равновесия объема . Очевидно, таким условием будет равенство абсолютных значений сил , или, что то же, равенство нулю их равнодействующей :

(3.52)

Поскольку, согласно (3.51),

(3.53)

то условие равновесия шахтной атмосферы можно записать в виде

(3.54)

Здесь очевидно, давления, создаваемые столбами воздуха 1-2 и 3-4.

Таким образом, можно сформулировать следующее условие равновесия шахтной атмосферы: воздух в шахте (шахтная атмосфера) будет находиться в равновесии, если давления, создаваемые вертикальными или наклонными столбами воздуха, расположенными между поверхностью и выработками шахты, равны.

Если такого равенства нет, т.е. , объем abcdне будет находиться в равновесии, т.е. придет в движение, равно как весь воздух в шахте. Отличная от нуля разность давлений , создаваемая естественными причинами, называется депрессией естественной тяги, а движение воздуха, происходящее под действием этой разности давлений – естественной тягой. Из (3.54) видно, что основной причиной естественной тяги является разность плотностей воздуха в вертикальных или наклонных столбах 1-2 и 3-4*). Естественным путем (т.е. без специального вмешательства человека) эта разность может возникать вследствие разного состава воздуха в столбах 1-2 и 3-4 или разной его температуры.

Равновесие атмосферы карьеров.Равновесие атмосферы карьера, подобно равновесию шахтной атмосферы и вообще равновесию погруженного в жидкость тела, определяется разностью плотностей соприкасающихся сред. Применительно к атмосфе­ре в карьерах это различие вызывается преимущественно термодинамиче­скими условиями, проявляющимися в почти неограниченном воздушном пространстве.

В карьере в соответствии с законами гидростатики слои воздуха, расположенные на большей глубине от земной поверхности, оказываются под большим давлением. Это в соответствии с уравнением состояния приводит к повышению температуры более глубоких слоев воздуха по сравнению с вышерасположенными слоями. В итоге температура воздуха в карьере с глубиной, как правило, увеличивается. Однако на эту общую закономер­ность могут влиять различные теплообменные процессы между атмосферой карьера и окружающей средой (бортами и дном карьера, воздухом над земной поверхностью). Они приводят к тому, что температура воздуха в карьере с глубиной может расти быстрее, чем она растет вследствие только увеличения давления (сжатия), медленнее или даже уменьшаться. Из всех возможных таким образом термодинамических состоя­ний выделяют четыре характерные: адиабатическое (нет теплообмена между атмосферой карьера и окружающей средой, температура воздуха в карьере с глубиной увеличивается только вследствие сжатия воздуха из-за повышения давления), сверхадиабатическое (имеется внешний подвод те­пла к воздуху в карьере, температура с глубиной растет быстрее, чем при адиабатическом состоянии), изотермическое (имеется внешнее охлажде­ние воздуха в карьере, компенсирующее тепловыделение от сжатия возду­ха; температура воздуха с глубиной не меняется) и инверсионное (имеется глубокое внешнее охлаждение воздуха, превышающее его нагрев из-за сжатия; температура воздуха с глубиной уменьшается).

КИНЕМАТИКА ЖИДКОСТИ

Кинематикой жидкости называется раздел гидромеханики, изучающий движение жидкости без учета взаимодействий, определяющих это движение, или, что то же, без привлечения понятия силы. Кинематика изучает траектории движения отдельных частиц жидкости и их скорости, то есть как бы внешнее проявление процессов, происходящих в жидкости при ее движении. Кинематика рассматривает жидкость как сплошную среду, что означает непрерывность распределения в пространстве кинематических характеристик движения, а именно: непрерывность изменения координат частиц жидкости и непрерывность изменения их скоростей.

Векторная величина в физике: определение, обозначение, примеры

В математике вектор — это направленный отрезок определенной длины. В физике под векторной величиной понимают полную характеристику некоторой физической величины, которая обладает модулем и направлением действия. Рассмотрим основные свойства векторов, а также примеры физических величин, которые являются векторными.

Скаляры и вектора

Скалярные величины в физике являются параметрами, которые могут быть измерены и представлены одним числом. Например, температура, масса и объем являются скалярами, поскольку они измеряются числом градусов, килограмм и кубических метров соответственно.

В большинстве же случаев оказывается, что число, определяющее скалярную величину, не несет исчерпывающей информации. Например, рассматривая такую физическую характеристику, как ускорение, будет недостаточно сказать, что оно равно 5 м/с 2 , поскольку нужно знать, куда оно направлено, против скорости движения тела, под некоторым углом к этой скорости или иначе. Помимо ускорения, примером векторной величины в физике является скорость. Также в эту категорию входят сила, напряженность электрического поля и многое другие.

Согласно определению векторной величины как направленного в пространстве отрезка, она может быть представлена в виде набора чисел (компонент вектора), если ее рассматривать в определенной системе координат. Чаще всего в физике и математике возникают задачи, которые для описания вектора требуют знания его двух (задачи на плоскости) или трех (задачи в пространстве) компонентов.

Определение вектора в n-мерном пространстве

В n-мерном пространстве, где n — целое число, вектор будет однозначно определен, если известны его n компонент. Каждая компонента представляет собой координату конца вектора вдоль соответствующей оси координат при условии, что начало вектора находится в начале системы координат n-мерного пространства. В итоге вектор может быть представлен так: v = 1, a₂, a₃, . a_n>, где a₁ — скалярное значение 1-й компоненты вектора v. Соответственно, в 3-х мерном пространстве вектор запишется как v = 1, a₂, a₃>, а в 2-х мерном — v = 1, a₂>.

Как обозначается векторная величина? Любой вектор в 1-мерном, 2-мерном и 3-мерном пространствах можно представить как направленный отрезок, лежащий между точками A и B. В этом случае он обозначается как AB → , где стрелка показывает, что речь идет о векторной величине. Последовательность букв принято указывать от начала вектора к его концу. Это означает, что если координаты точек A и B, например, в 3-мерном пространстве, равны 1, y₁, z₁> и 2, y₂, z₂> соответственно, тогда компоненты вектора AB → будут равны 2-x₁, y₂-y₁, z₂-z₁>.

Графическое представление вектора

На рисунках принято изображать векторную величину в виде отрезка, на его конце имеется стрелочка, указывающая направление действия физической величины, представлением которой она является. Этот отрезок обычно подписывают, например, v → или F → , чтобы было понятно, о какой характеристике идет речь.

Графическое представление вектора помогает понять, куда приложена и в каком направлении действует физическая величина. Кроме того, многие математические операции над векторами удобно совершать, используя их изображения.

Математические операции над векторами

Векторные величины, так же как и обычные числа, можно складывать, вычитать и умножать как друг с другом, так и с другими числами.

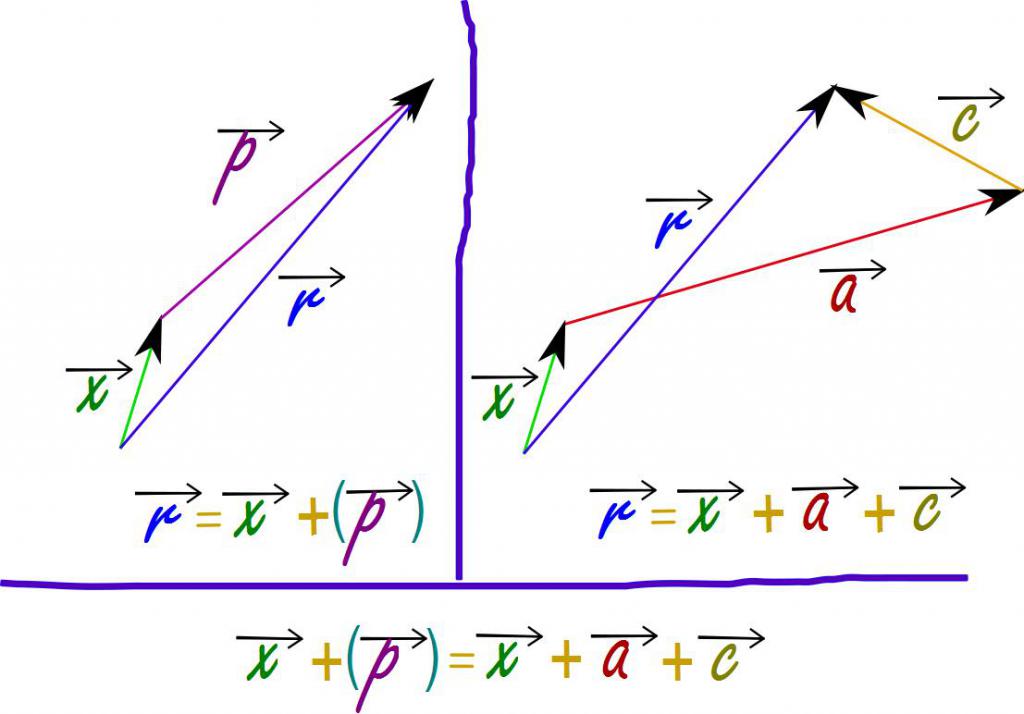
Под суммой двух векторов понимают третий вектор, который получается, если суммируемые параметры расположить так, чтобы конец первого совпадал с началом второго вектора, а затем, соединить начало первого и конец второго. Для выполнения этого математического действия разработаны три основных метода:

1. Метод параллелограмма, заключающийся в построении геометрической фигуры на двух векторах, которые выходят из одной и той же точки пространства. Диагональ этого параллелограмма, которая выходит из общей точки начала векторов, будет являться их суммой.
2. Метод многоугольника, суть которого состоит в том, что начало каждого последующего вектора следует располагать в конце предыдущего, тогда суммарный вектор будет соединять начало первого и конец последнего.
3. Аналитический метод, который состоит в попарном сложении соответствующих компонент известных векторов.

Что касается разницы векторных величин, то ее можно заменить сложением первого параметра с тем, который противоположен по направлению второму.

Умножение вектора на некоторое число A выполняется по простому правилу: на это число следует умножить каждую компоненту вектора. В результате получается также вектор, модуль которого в A раз больше исходного, а направление либо совпадает, либо противоположно исходному, все зависит от знака числа A.

Делить вектор или число на него нельзя, а вот деление вектора на число A аналогично умножению на число 1/A.

Скалярное и векторное произведения

Умножение векторов можно выполнять двумя различными способами: скалярно и векторно.

Скалярным произведением векторных величин называется такой способ их умножения, результатом которого является одно число, то есть скаляр. В матричном виде скалярное произведение записывается как строки компонента 1-го вектора на столбец компонент 2-го. В итоге в n-мерном пространстве получается формула: (A → *B → ) = a₁*b₁+a₂*b₂+. +a_n*b_n.

В 3-мерном пространстве можно определить скалярное произведение иначе. Для этого нужно умножить модули соответствующих векторов на косинус угла между ними, то есть (A → *B → ) = |A → |*|B → |*cos(θ_AB). Из этой формулы следует, что если вектора направлены в одном направлении, то скалярное произведение равно умножению их модулей, а если вектора перпендикулярны друг другу, тогда оно оказывается равным нулю. Отметим, что модуль вектора в прямоугольной системе координат определяется как квадратный корень от суммы квадратов компонент этого вектора.

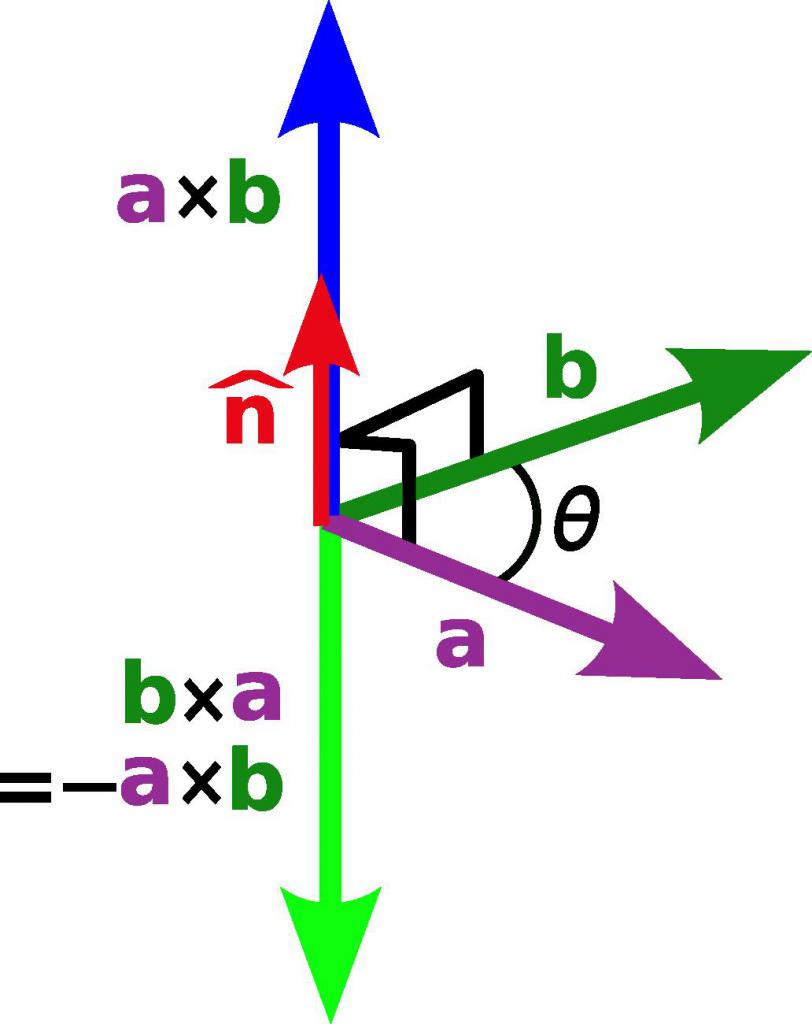
Под векторным произведением понимают такое умножение вектора на вектор, результатом которого также является вектор. Его направление оказывается перпендикулярно каждому из умножаемых параметров, а длина равна произведению модулей векторов на синус угла между ними, то есть A → x B → = |A → |*|B → |*sin(θ_AB), где значок «x» обозначает векторное произведение. В матричном виде этот вид произведения представляется как определитель, строками которого являются элементарные вектора данной системы координат и компоненты каждого вектора.

Как скалярное, так и векторное произведения используют в математике и физике для определения многих величин, например, площади и объема фигур.

Далее в статье приводятся примеры векторных величин в физике.

Скорость и ускорение

Под скоростью в физике понимают быстроту изменения местоположения данной материальной точки. Измеряется скорость в системе СИ в метрах в секунду (м/с), а обозначается символом v → . Под ускорением понимают быстроту изменения скорости. Ускорение измеряется в метрах в квадратную секунду (м/с 2 ), а обозначается обычно символом a → . Значение 1 м/с 2 говорит о том, что за каждую секунду тело увеличивает свою скорость на 1 м/с.

Скорость и ускорение — это векторные величины, которые участвуют в формулах второго закона Ньютона и перемещения тела как материальной точки. Скорость всегда направлена вдоль направления движения, ускорение же может быть направлено произвольным образом относительно движущегося тела.

Физическая величина сила

Сила — векторная физическая величина, которая отражает интенсивность взаимодействия между телами. Обозначается она символом F → , измеряется в ньютонах (Н). По определению, 1 Н — это сила, способная за каждую секунду времени изменять скорость тела, имеющего массу 1 кг, на 1 м/с.

Эта физическая величина широко применяется в физике, поскольку с ней связаны энергетические характеристики процессов взаимодействия. Природа силы может быть самой разной, например, гравитационные силы планет, сила, которая заставляет двигаться автомобиль, упругие силы твердых сред, электрические силы, описывающие поведение электрических зарядов, магнитные, ядерные силы, которые обуславливают стабильность атомных ядер, и так далее.

Векторная величина давление

С понятием силы тесно связана другая величина — давление. Под ним в физике понимают нормальную проекцию силы на площадку, на которую она действует. Поскольку сила является вектором, то, согласно правилу умножения числа на вектор, давление также будет векторной величиной: P → = F → /S, где S — площадь. Давление измеряется в паскалях (Па), 1 Па — это параметр, при котором перпендикулярная сила в 1 Н действует на поверхность площадью 1 м 2 . Исходя из определения, вектор давления направлен в том же направлении, что и вектор силы.

В физике понятие давления часто используется при изучении явлений в жидкостях и газах (например, закон Паскаля или уравнение состояния идеального газа). Давление тесно связано с температурой тела, поскольку кинетическая энергия атомов и молекул, представлением которой является температура, объясняет природу существования самого давления.

Напряженность электрического поля

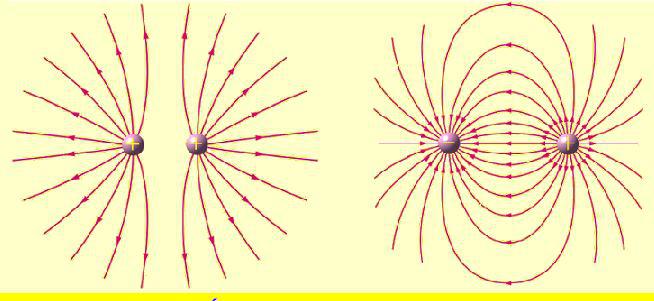
Вокруг любого заряженного тела существует электрическое поле, силовой характеристикой которого является его напряженность. Определяется эта напряженность как сила, действующая в данной точке электрического поля на единичный заряд, помещенный в эту точку. Обозначается напряженность электрического поля буквой E → и измеряется в ньютонах на кулон (Н/Кл). Вектор напряженности направлен вдоль силовой линии электрического поля в ее направлении, если заряд положительный, и против нее, если заряд отрицательный.

Напряженность электрического поля, создаваемого точечным зарядом, можно определить в любой точке, используя закон Кулона.

Магнитная индукция

Магнитное поле, как показали в XIX веке ученые Максвелл и Фарадей, тесно связано с электрическим полем. Так, изменяющееся электрическое поле порождает магнитное, и наоборот. Поэтому оба вида полей описываются в рамках электромагнитных физических явлений.

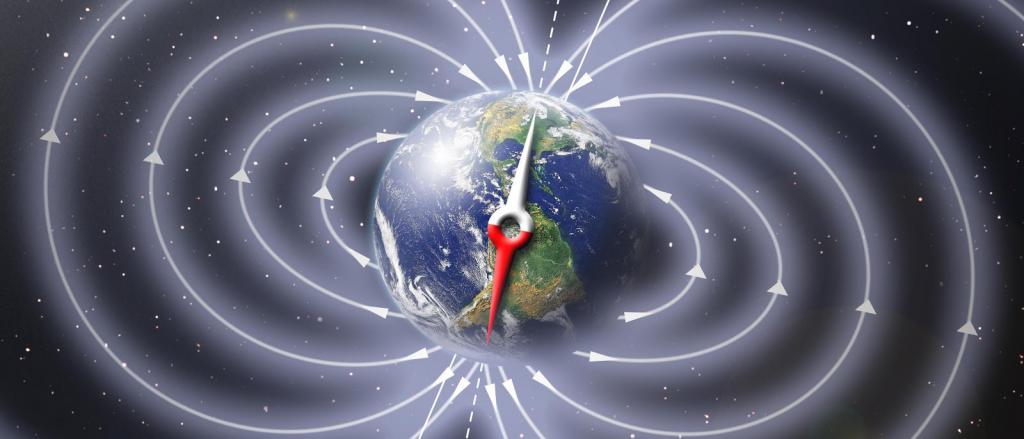
Магнитная индукция описывает силовые свойства магнитного поля. Магнитная индукция — величина скалярная или векторная? Понять это можно, зная, что она определяется через силу F → , действующую на заряд q, который пролетает со скоростью v → в магнитном поле, согласно следующей формуле: F → = q*|v → x B → |, где B → — магнитная индукция. Таким образом, отвечая на вопрос, величина скалярная или векторная — магнитная индукция, можно сказать, что это вектор, который направлен от северного магнитного полюса к южному. Измеряется B → в теслах (Тл).

Физическая величина кандела

Еще одним примером векторной величины является кандела, которая вводится в физику через световой поток, измеряемый в люменах, проходящий через поверхность, ограниченную углом в 1 стерадиан. Кандела отражает яркость света, поскольку показывает плотность светового потока.

Давление

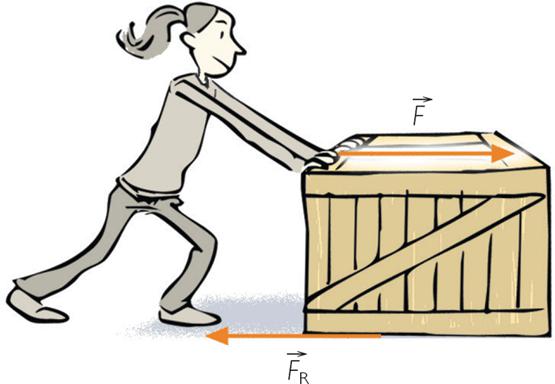
Известно, что человеку удобнее ходить по глубокому снегу на лыжах, так как при этом он меньше проваливается под снег. А разрезать предметы удобнее остро отточенным ножом. Причина этого – давление. В первом случае мы стремимся уменьшить давление на снег, а во втором случае, мы стараемся максимально увеличить давление.

Формула давления твердого тела

Рассмотрим твердое тело, например, кирпич. Пусть он лежит на горизонтальной поверхности и давит на нее своим весом (рис. 1).

Рис. 1. Твердое тело опирается на поверхность площадью S и давит на нее своим весом mg

На рисунке символом S обозначена нижнее основание тела – это площадь, на которую тело опирается (давит). Сила, с которой тело давит на поверхность – это сила тяжести mg.

Давление, которое твердое тело оказывает на поверхность, можно рассчитать так:

[ large boxed{ P = frac{F_{perp}}{S} }]

Примечание: Эта формула подходит для расчета давления твердых тел. Существует еще одна формула, с помощью которой рассчитывают давление жидкостей.

​( P left( text{Па}right) )​ – давление;

( F_{perp} left(H right) )  – сила, которая давит (сила давления). Эта сила располагается под прямым углом к поверхности;

( S left( text{м}^{2}right) ) – площадь, на которую давит сила.

Иногда в условии задачи указывают площадь в квадратных сантиметрах, или других единицах, отличающихся от основных единиц, принятых в СИ. Чтобы правильно рассчитать давление, нужно уметь переводить площадь в квадратные метры.

В системе СИ давление измеряется в Паскалях.

[ large 1 text{Па} = frac{1 H}{1 text{м}^{2}} ]

Поэтому, перед решением задач, нужно давление переводить в Паскали, если в условии встретятся другие единицы измерения давления.

В некоторых школьных задачах просят найти не давление, а силу давления. Нужно уметь их различать.

Сила давления, как и любая сила, измеряется в Ньютонах. Именно она давит на поверхность.

А давление — это дробь, в числителе расположена сила, которая давит, а в знаменателе — площадь поверхности, на которую давят. Давление измеряют в Паскалях.

Примечание: Давление – это сила, деленная на площадь. Сила должна располагаться перпендикулярно поверхности (рис. 2а).

Когда сила не перпендикулярна поверхности

Силу раскладываем на проекции, если она направлена к поверхности не под прямым углом (рис. 2б). Выберем часть силы, расположенную перпендикулярно поверхности. Именно эту часть силы и нужно подставлять в формулу для расчета давления.

Рис. 2. Если сила, которая давит на поверхность, направлена не под прямым углом к поверхности, раскладываем силу на проекции и выбираем часть, которая располагается к поверхности перпендикулярно

Оценка статьи:

Загрузка…

Вектор силы давления жидкости на криволинейную стенку

В отличие от плоской
стенки гидростатическое давление в
разных точках криволинейной стенки
различается не только по величине, но
и по направлению. Поэтому силу
гидростатического давления, действующую
на криволинейную стенку, непосредственно
определить нельзя: ее находят через
составляющие этого вектора.

Рис. 15. К определению
силы давления на криволинейную стенку

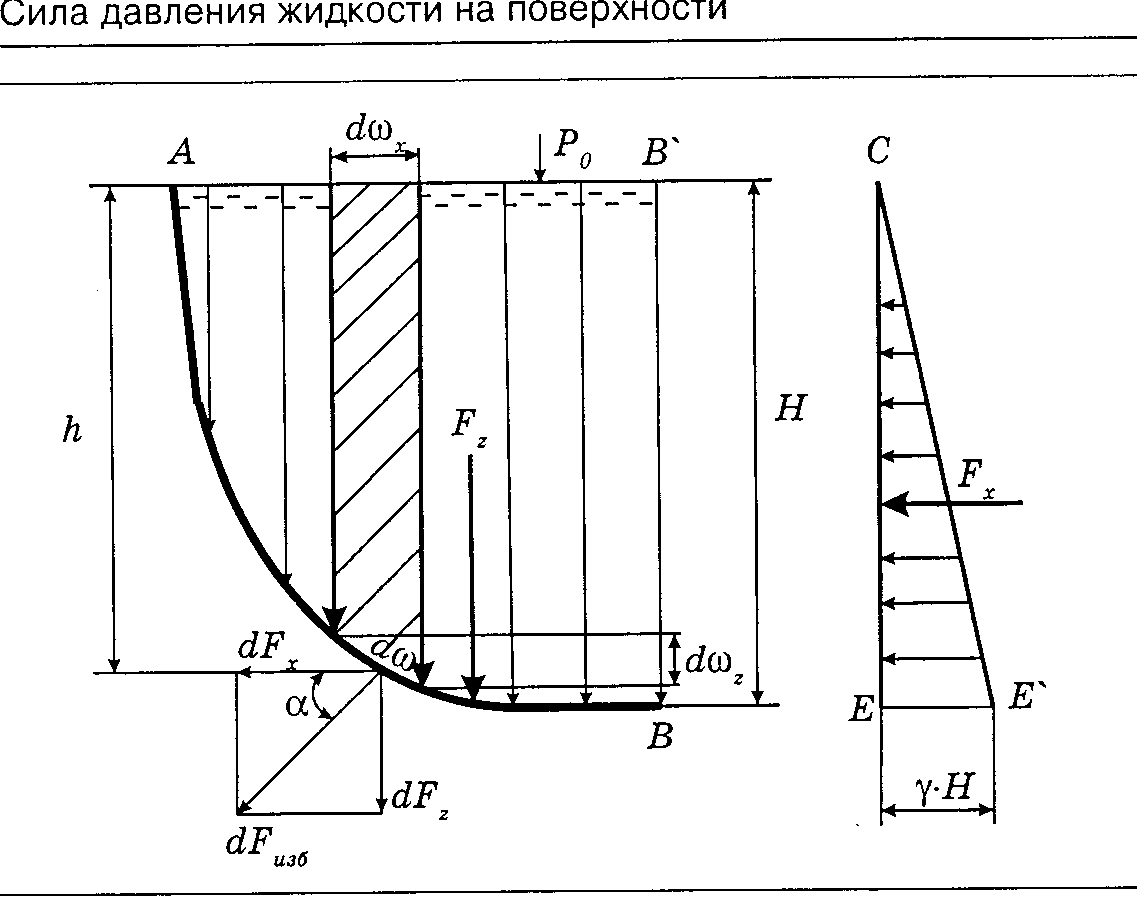
Рассмотрим
криволинейную поверхность АВ,
подверженную действию избыточного
гидростатического
давления (жидкость справа) (рис. 15).

Выделим площадку
,
цент тяжести которой погружен в жидкость
на глубину.На площадку
будет действовать элементарная сила
избыточного давлениянормально ней:

,Н
(38)

Разложим
на составляющие:

— горизонтальная
составляющая

,Н
(39)

— вертикальная
составляющая силы

,Н .
(40)

где
— угол составляющей между элементарной
площадкойи горизонтальной плоскостью,град.

Рассмотрим каждую
в отдельности составляющую силы
избыточного давления, действующего на
криволинейную поверхность АВ.

Элементарная
горизонтальная составляющая силы
избыточного давления равна

.

В то же время

.

Следовательно

.

Из рис. 15 видно,
что

,

где
— площадь проекции элементарной площадкина вертикальную плоскость,.

Откуда

.

Горизонтальная
составляющая силы избыточного давления
после интегрирования равна

(41)

где
—
статический момент инерции всей площади
проекцииотносительно
свободной поверхности жидкости, ;

т.е. статический
момент инерции равен произведениюплощади вертикальной проекциина глубину погружения центра ее тяжести.

Откуда находим

(42)

Элементарная
вертикальная составляющая силы
избыточного гидростатического давления
равна:

,
или (43)

Величина
является площадью проекциина горизонтальную плоскость.
Следовательно

.

Заметим, что
представляет собой бесконечно малый
объембесконечно малой призмы, отмеченной на
рис. 15 штриховкой.

Произведение
является силой тяжести в этом бесконечно
малом объеме:

.

Отсюда вертикальная
составляющая силы избыточного
гидростатического давления будет равна

.

После интегрирования
находим:

;

;

.
(44)

где
— объем тела давления,.

Тело давления
– это объем, ограниченный криволинейной
поверхностью АВ,
ее проекцией на уровень свободной
поверхности АВ
и вертикальными плоскостями проецирования.

Полная сила
гидростатического давления определяется
из выражения

(45)

где		— горизонтальная составляющая силы избыточного гидростатического давления, ;
		— вертикальная составляющая силы избыточного гидростатического давления, .

Направление полной
силы
определяется углом(рис. 15):

.

Полная сила
избыточного гидростатического давления
приложена в центре давления.

Вектор полной силы
давления
должен проходить через точку пересечения
ее горизонтальной и вертикальной
составляющих, т.е.ипод углом.

Таким образом,
цент давления для криволинейных
поверхностей находится графо-аналитическим
путем.

Если криволинейная
поверхность цилиндрическая, то сила
будет проходить через центр радиуса
кривизны этой поверхности.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Поле давления  — двухкомпонентное векторное силовое поле, ковариантным образом описывающее динамическое давление отдельных частиц и давление, возникающее в системах с множеством тесно взаимодействующих частиц. Поле давления является компонентой общего поля, представленной в лагранжиане и в гамильтониане произвольной физической системы членом с энергией частиц в поле давления, и членом с энергией поля.^{[1] [2]}
В уравнение движения поле давления входит через тензор поля давления, а в уравнение для метрики — через тензор энергии-импульса поля давления. Любые силы, действующие на частицы вещества и приводящие к изменению их взаимодействия друг с другом, делают вклад в поле давления, в его энергию и импульс. Поле давления обычно рассматривается как макроскопическое поле, описывающее усреднённое взаимодействие частиц в произвольном малом объёме системы. Причиной возникновения поля давления на микроуровне являются различные взаимодействия. Например, электромагнитные силы и сильная гравитация удерживают вместе электроны и нуклоны в атомах. Под действием внешних сил происходит сдавливание вещества и изменение объёма, занимаемого атомами и электронами в атомах вещества. Это приводит к изменению энергии системы, что может быть представлено как изменение энергии поля давления.

Скалярное поле давления[править | править код]

В равновесных состояниях вещества и в отсутствие массовых сил атомы и молекулы движутся как правило хаотично и их общим направленным движением можно пренебречь. В таких условиях характеристикой внутреннего движения становится средняя скорость частиц

 

v
¯

~ bar {v}

. В молекулярно-кинетической теории для давления

 
p

~ p

имеется формула:

p
=

1
3

m
0

n

v
¯

2

,

p= frac{1}{3}m_0 n bar {v}^2 ,

где

 

m
0

~ m_0

 — средняя масса одной частицы термодинамической системы,

 
n

~ n

 — концентрация частиц.

Будучи термодинамической макроскопической переменной, давление входит в уравнение состояния, связывающее между собой различные термодинамические переменные. В частности давление входит как физическая переменная в уравнение состояния идеального газа:

p
⋅
V
=

m
M

R
⋅
T
,

pcdot V= frac{m}{M}Rcdot T,

 
p
=
n
k
T
,

~p= n k T,

где

 
V

~ V

 — объём газа,

 
m

~ m

 — масса газа,

 
M

~ M

 — молярная масса,

 
R

~R

 — универсальная газовая постоянная,

 
T

~ T

 — температура,

k
=

R

N
A

k = frac{R}{N_A}

 — постоянная Больцмана,

 

N
A

~ N_A

 — число Авогадро.

Давление входит в закон Бернулли для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости, являющийся следствием закона сохранения энергии:

ρ

v
2

2

+
ρ
g
h
+
p
=

const

tfrac{rho v^2}{2} + rho g h + p = mathrm{const}

где

 
ρ

~rho

 — плотность жидкости,

 
v

~v

 — скорость потока,

 
h

~h

 — высота, на которой находится рассматриваемый элемент жидкости,

 
p

~p

 — давление в точке пространства, где расположен центр массы рассматриваемого элемента жидкости,

 
g

~g

 — ускорение свободного падения. Первый член равенства есть динамическое давление, второй член даёт давление от массовых сил (в данном случае от гравитации), третий член представляет собой статическое давление, а константа в правой части называется полным давлением.

Скалярное давление характеризует состояние сплошной среды и в случае состояния равновесия в жидкости становится гидростатическим давлением. При этом давление является диагональной компонентой симметричного трёхмерного тензора напряжений Коши:

 

σ

i
j

=
−
p

δ

i
j

,

~sigma_{ij} = -p delta_{ij} ,

где

 

δ

i
j

~delta_{ij}

есть символ Кронекера.

В общей теории относительности для идеальной жидкости используется тензор энергии-импульса давления, являющийся обобщением формул классической механики:^[3]

 

P

μ
ν

=

p

c
2

u
μ

u
ν

−

g

μ
ν

p
,

~ P^{mu nu } = frac {p}{c^2}u^mu u^nu — g^{mu nu } p,

где

 

g

μ
ν

~ g^{mu nu }

есть метрический тензор,

 

u
μ

~u^mu

 — 4-скорость,

 
c

~ c

 — скорость света.

В концепции скалярного поля под энергией поля давления подразумевается работа, совершаемая давлением по изменению объёма системы от начального состояния с нулевым давлением до текущего состояния, с учётом вклада кинетической энергии частиц от изменения массы-энергии за счёт поля давления.

Векторное поле давления[править | править код]

Недостатком скалярной концепции поля давления является неточный учёт энергии и импульса поля давления в ускоренных системах отсчёта с множеством источников поля, где проявляются эффекты самодействия поля, сложения отдельных волн давления при ограниченной скорости распространения поля. В векторных полях появляется дополнительная степень свободы в виде векторного потенциала. В результате энергия одной компоненты поля может переходить в энергию другой компоненты, напряжённость поля становится функцией скалярного и векторного потенциалов, а сила определяется напряжённостью поля, скоростью движения и соленоидальным вектором. Примерами самодействия поля являются электромагнитная индукция и гравитационная индукция.
Давление как двухкомпонентное векторное поле было представлено Сергеем Федосиным в рамках метрической теории относительности и  ковариантной теории гравитации, а уравнения этого поля появились как следствие принципа наименьшего действия.^{[4] [5]}

Математическое описание[править | править код]

4-потенциал поля давления выражается через скалярный

 
℘

~wp

и векторный

 
Π

~ boldsymbol {Pi }

потенциалы:

 

π
μ

=

(

℘
c

,
−
Π
)

.

~pi_mu = left(frac {wp }{c},- boldsymbol {Pi } right) .

Антисимметричный тензор поля давления вычисляется через 4-ротор от 4-потенциала:

f

μ
ν

=

∇
μ

π
ν

−

∇
ν

π
μ

=

∂

π
ν

∂

x
μ

−

∂

π
μ

∂

x
ν

.

f_{mu nu} = nabla_mu pi_nu — nabla_nu pi_mu = frac{partial pi_nu}{partial x^mu} — frac{partial pi_mu}{partial x^nu}.

Компонентами тензора поля давления являются компоненты вектора напряжённости поля давления

 

C

~mathbf {C}

и соленоидальный вектор давления

 

I

~mathbf { I }

:

 

f

μ
ν

=

|

0

C
x

c

C
y

c

C
z

c

−

C
x

c

0

−

I

z

I

y

−

C
y

c

I

z

0

−

I

x

−

C
z

c

−

I

y

I

x

0

|

.

~ f_{mu nu}= begin{vmatrix} 0 & frac { C_x}{ c} & frac { C_y}{ c} & frac { C_z}{ c} \ -frac { C_x}{ c} & 0 & — I_{z} & I_{y} \ -frac { C_y}{ c} & I_{z} & 0 & — I_{x} \ -frac { C_z}{ c}& — I_{y} & I_{x} & 0 end{vmatrix}.

При этом получается следующее:

(1)

 

C

=
−
∇
℘
−

∂

Π

∂
t

,

I

=
∇
×

Π

.

~mathbf{C}= -nabla wp — frac{partial mathbf{Pi }} {partial t}, qquadqquad mathbf{I }= nabla times mathbf{Pi }. label 1 tag 1

Действие, Лагранжиан и энергия[править | править код]

В ковариантной теории гравитации 4-потенциал

 

π
μ

~ pi_mu

поля давления является частью 4-потенциала общего поля

 

s
μ

~ s_mu

, который является суммой 4-потенциалов таких частных полей, как электромагнитное и гравитационное поля, поле ускорений, поле давления, поле диссипации, поле сильного взаимодействия, поле слабого взаимодействия, других векторных полей, действующих на вещество и его частицы. Все эти поля так или иначе представлены в веществе, так что 4-потенциал

 

s
μ

~ s_mu

не может состоять только из одного 4-потенциала

 

π
μ

~ pi_mu

.
Плотность энергии взаимодействия общего поля с веществом задаётся произведением 4-потенциала общего поля на массовый 4-ток:

 

s
μ

J
μ

~ s_mu J^mu

. Из 4-потенциала общего поля путём применения 4-ротора получается тензор общего поля:

 

s

μ
ν

=

∇
μ

s
ν

−

∇
ν

s
μ

.

~ s_{mu nu} =nabla_mu s_nu — nabla_nu s_mu.

Тензорный инвариант, в виде

 

s

μ
ν

s

μ
ν

~ s_{mu nu} s^{mu nu}

, с точностью до постоянного коэффициента пропорционален плотности энергии общего поля. В результате функция действия, содержащая скалярную кривизну

 
R

~R

и космологическую постоянную

 
Λ

~ Lambda

, определяется выражением:^[1]

 
S
=
∫

L
d
t

=
∫
(
k
R
−
2
k
Λ
−

1
c

s
μ

J
μ

−

c

16
π
ϖ

s

μ
ν

s

μ
ν

)

−
g

d
Σ
,

~S =int {L dt}=int (kR-2k Lambda — frac {1}{c}s_mu J^mu — frac {c}{16 pi varpi} s_{munu}s^{munu} ) sqrt {-g}dSigma,

где

 
L

~L

 — функция Лагранжа или лагранжиан,

 
d
t

~dt

 — дифференциал времени координатной системы отсчёта,

 
k

~k

и 

 
ϖ

~ varpi

 — постоянные, подлежащие определению,

 
c

~c

 — скорость света, как мера скорости распространения электромагнитного и гравитационного взаимодействий,

 

−
g

d
Σ
=

−
g

c
d
t
d

x
1

d

x
2

d

x
3

~sqrt {-g}dSigma= sqrt {-g} c dt dx^1 dx^2 dx^3

 — инвариантный 4-объём, выражаемый через дифференциал временной координаты

 
d

x
0

=
c
d
t

~ dx^0=cdt

, через произведение

 
d

x
1

d

x
2

d

x
3

~ dx^1 dx^2 dx^3

дифференциалов пространственных координат, и через квадратный корень

 

−
g

~sqrt {-g}

из детерминанта

 
g

~g

метрического тензора, взятого с отрицательным знаком.

Варьирование функции действия даёт уравнения общего поля, четырёхмерное уравнение движения и уравнение для определения метрики. Так как поле давления является компонентой общего поля, то из уравнений общего поля вытекают соответствующие уравнения поля давления.

При выполнении условия калибровки космологической постоянной в виде

 
c
k
Λ
=
−

s
μ

J
μ

,

~ c k Lambda = — s_mu J^mu ,

энергия системы не зависит от члена со скалярной кривизной и становится однозначно определённой:^[5]

 
E
=
∫

(

s
0

J
0

+

c
2

16
π
ϖ

s

μ
ν

s

μ
ν

)

−
g

d

x
1

d

x
2

d

x
3

,

~E = int {( s_0 J^0 + frac {c^2 }{16 pi varpi } s_{ munu} s^{ munu} ) sqrt {-g} dx^1 dx^2 dx^3},

где

 

s
0

~ s_0

и 

 

J
0

~ J^0

обозначают временные компоненты 4-векторов

 

s

μ

~ s_{mu }

и 

 

J

μ

~ J^{mu }

.

4-импульс системы определяется формулой:

 

p
μ

=

(

E
c

,

p

)

=

(

E
c

,

E

c
2

v

)

,

~p^mu = left( frac {E}{c}{,} mathbf {p}right) = left( frac {E}{c}{,} frac {E}{c^2}mathbf {v} right) ,

где

 

p

~ mathbf {p}

и 

 

v

~ mathbf {v}

обозначают импульс системы и скорость движения центра масс системы.

Уравнения[править | править код]

Четырёхмерные уравнения поля давления по своей форме оказываются подобными уравнениям Максвелла и имеют следующий вид:

∇
σ

f

μ
ν

+

∇
μ

f

ν
σ

+

∇
ν

f

σ
μ

=

∂

f

μ
ν

∂

x
σ

+

∂

f

ν
σ

∂

x
μ

+

∂

f

σ
μ

∂

x
ν

=
0.

nabla_sigma f_{mu nu}+nabla_mu f_{nu sigma}+nabla_nu f_{sigma mu}=frac{partial f_{mu nu}}{partial x^sigma} + frac{partial f_{nu sigma}}{partial x^mu} + frac{partial f_{sigma mu}}{partial x^nu} = 0.

 

∇
ν

f

μ
ν

=
−

4
π
σ

c
2

J
μ

,

~ nabla_nu f^{mu nu} = — frac{4 pi sigma }{c^2} J^mu,

где

 

J
μ

=

ρ

0

u
μ

~J^mu = rho_{0} u^mu

есть массовый 4-ток,

 

ρ

0

~rho_{0}

 — плотность массы в сопутствующей системе отсчёта,

 

u
μ

~u^mu

 — 4-скорость движения элемента вещества,

 
σ

~ sigma

 — постоянная, определяемая в каждой задаче, и предполагается, что имеется равновесие между всеми полями в рассматриваемой физической системе.

Условие калибровки 4-потенциала поля давления:

 

∇
μ

π
μ

=
0
.

~ nabla^mu pi_mu = 0 .

В пространстве Минковского специальной теории относительности вид уравнений поля давления упрощается и их можно выразить через напряжённость поля

 

C

~mathbf {C}

и соленоидальный вектор

 

I

~mathbf { I }

:

 
∇
⋅

C

=
4
π
σ
γ

ρ
0

,

∇
×

I

=

1

c
2

(
4
π
σ

J

+

∂

C

∂
t

)

,

~ nabla cdot mathbf{C} = 4 pi sigma gamma rho_0, qquadqquad nabla times mathbf{ I } = frac{1}{c^2} left( 4 pi sigma mathbf{J} + frac{partial mathbf{C}} {partial t} right),

 
∇
×

C

=
−

∂

I

∂
t

,

∇
⋅

I

=
0
.

~ nabla times mathbf{C} = — frac{partial mathbf{ I } } {partial t} , qquadqquad nabla cdot mathbf{ I } = 0 .

где

 
γ
=

1

1
−

v
2

c
2

~ gamma = frac {1}{sqrt{1 — {v^2 over c^2}}}

есть фактор Лоренца,

 

J

=
γ

ρ
0

v

~ mathbf{J}= gamma rho_0 mathbf{v }

 — плотность тока массы,

 

v

~ mathbf{v }

 — скорость элемента вещества.

Используя ещё условие калибровки в виде

 

∂
μ

π
μ

=

1

c
2

∂
℘

∂
t

+
∇
⋅
Π
=
0

~ partial^mu pi_mu = frac {1}{c^2} frac{partial wp }{partial t}+nabla cdot boldsymbol {Pi }=0

и соотношения

(1)

eqref {1}

, из уравнений поля можно получить волновые уравнения для потенциалов поля давления:

(2)

 

1

c
2

∂
2

℘

∂

t
2

−
Δ
℘
=
4
π
σ
γ

ρ
0

,

~ frac {1}{c^2}frac{partial^2 wp }{partial t^2 } -Delta wp = 4 pi sigma gamma rho_0, label 2 tag 2

 

1

c
2

∂
2

Π

∂

t
2

−
Δ
Π
=

4
π
σ

c
2

J

.

~ frac {1}{c^2}frac{partial^2 boldsymbol {Pi } }{partial t^2 } -Delta boldsymbol {Pi }= frac {4 pi sigma}{c^2} mathbf{J}.

Уравнение движения элемента вещества в общем поле описывается формулой:

 

s

μ
ν

J
ν

=
0
.

~ s_{mu nu} J^nu =0 .

Так как

 

J
ν

=

ρ
0

u
ν

~ J^nu = rho_0 u^nu

, а тензор общего поля выражается через тензоры частных полей, то уравнение движения можно представить через эти тензоры:^[6]

(3)

 
−

u

μ
ν

J
ν

=

F

μ
ν

j
ν

+

Φ

μ
ν

J
ν

+

f

μ
ν

J
ν

+

h

μ
ν

J
ν

+

γ

μ
ν

J
ν

+

w

μ
ν

J
ν

.

~ — u_{mu nu} J^nu = F_{mu nu} j^nu + Phi_{mu nu} J^nu + f_{mu nu} J^nu + h_{mu nu} J^nu + gamma_{mu nu} J^nu + w_{mu nu} J^nu . label 3 tag 3

Здесь

 

u

μ
ν

~ u_{mu nu}

 — тензор ускорений,

 

F

μ
ν

~ F_{mu nu}

 — тензор электромагнитного поля,

 

j
ν

~ j^nu

 — зарядовый 4-ток,

 

Φ

μ
ν

~ Phi_{mu nu}

 — тензор гравитационного поля,

 

h

μ
ν

~ h_{mu nu}

 — тензор поля диссипации,

 

γ

μ
ν

~ gamma_{mu nu}

 — тензор поля сильного взаимодействия,

 

w

μ
ν

~ w_{mu nu}

 — тензор поля слабого взаимодействия.

Тензор энергии-импульса[править | править код]

Тензор энергии-импульса поля давления вычисляется с помощью тензора давления:

 

P

i
k

=

c
2

4
π
σ

(
−

g

i
m

f

n
m

f

n
k

+

1
4

g

i
k

f

m
r

f

m
r

)

.

~ P^{ik} = frac{c^2} {4 pi sigma }left( -g^{im} f_{n m} f^{n k}+ frac{1} {4} g^{ik} f_{m r} f^{m r}right) .

В составе тензора

 

P

i
k

~ P^{ik}

находится 3-вектор потока энергии-импульса

 

F

~mathbf {F}

, подобный по смыслу вектору Пойнтинга и вектору Хевисайда. Вектор

 

F

~mathbf {F}

можно представить через векторное произведение вектора напряжённости поля

 

C

~ mathbf {C}

и соленоидального вектора

 

I

~ mathbf { I }

:

 

F

=
c

P

0
i

=

c
2

4
π
σ

[

C

×

I

]
,

~ mathbf {F}=c P^{0i} = frac {c^2}{4 pi sigma }[mathbf {C}times mathbf { I }],

здесь индекс

 
i
=
1
,
2
,
3.

~ i=1,2,3.

Ковариантная производная от тензора энергии-импульса поля давления задаёт плотность 4-силы давления:

(4)

 

f
α

=
−

∇
β

P

α
β

=

f
α

k

J
k

.

~ f^alpha = — nabla_beta P^{alpha beta} = {f^alpha}_{k} J^k . label 4 tag 4

Тензор энергии-импульса поля давления входит в состав тензора энергии-импульса общего поля

 

T

i
k

~ T^{ik}

, однако в общем случае тензор

 

T

i
k

~ T^{ik}

содержит в себе ещё перекрёстные члены с произведениями напряжённостей и соленоидальных векторов частных полей:

 

T

i
k

=

k
1

W

i
k

+

k
2

U

i
k

+

k
3

B

i
k

+

k
4

P

i
k

+

k
5

Q

i
k

+

k
6

L

i
k

+

k
7

A

i
k

+
c
r
o
s
s

t
e
r
m
s
,

~ T^{ik}= k_1W^{ik}+ k_2U^{ik}+ k_3B^{ik}+ k_4P^{ik} + k_5Q^{ik}+ k_6 L^{ik}+ k_7A^{ik}+ cross quad terms,

где

 

k
1

,

k
2

,

k
3

,

k
4

,

k
5

,

k
6

,

k
7

~ k_1{,} k_2{,} k_3{,} k_4{,} k_5{,} k_6{,} k_7

 — некоторые коэффициенты,

 

W

i
k

~ W^{ik}

 — тензор энергии-импульса электромагнитного поля,

 

U

i
k

~ U^{ik}

 — тензор энергии-импульса гравитационного поля,

 

B

i
k

~ B^{ik}

 — тензор энергии-импульса поля ускорений,

 

Q

i
k

~ Q^{ik}

 — тензор энергии-импульса поля диссипации,

 

L

i
k

~ L^{ik}

 — тензор энергии-импульса поля сильного взаимодействия,

 

A

i
k

~ A^{ik}

 — тензор энергии-импульса поля слабого взаимодействия.

Через тензор

 

T

i
k

~ T^{ik}

тензор энергии-импульса поля давления входит в уравнение для метрики:

 

R

i
k

−

1
4

g

i
k

R
=

8
π
G
β

c
4

T

i
k

,

~ R^{ik} — frac{1} {4 }g^{ik}R = frac{8 pi G beta }{ c^4} T^{ik},

где

 

R

i
k

~ R^{ik}

 — тензор Риччи,

 
G

~ G

 — гравитационная постоянная,

 
β

~ beta

 — некоторая постоянная, и использовано условие калибровки космологической постоянной.

Применение в некоторых задачах[править | править код]

В случае, когда собственный векторный потенциал некоторого векторного поля частицы равен нулю в системе покоя частицы, 4-потенциал этого векторного поля в произвольной системе отсчёта может быть представлен так:^[4]

 

L
μ

=

k
f

ε
p

ρ
0

c
2

u
μ

,

~ L_mu = frac {k_f varepsilon_p }{rho_0 c^2} u_mu ,

где

 

k
f

=

ρ
0

ρ

0
q

~ k_f = frac {rho_0}{rho_{0q}}

для электромагнитного поля и 

 

k
f

=
1

~ k_f = 1

для остальных полей,

 

ρ

0

~ rho_{0}

и 

 

ρ

0
q

~rho_{0q}

 — плотность массы и соответственно плотность заряда в сопутствующей системе отсчёта,

 

ε
p

~ varepsilon_p

 — плотность энергии частицы в данном поле,

 

u
μ

~ u_mu

 — ковариантная 4-скорость.

Для поля давления

 

ε
p

=

p
0

~ varepsilon_p = p_0

,

 

k
f

=
1

~ k_f = 1

, и согласно определения, для 4-потенциала поля давления одной частицы имеем:

 

π
μ

=

(

℘
c

,
−
Π
)

=

p
0

ρ
0

c
2

u
μ

,

~pi_mu = left(frac {wp }{c},- boldsymbol {Pi } right) = frac {p_0 }{rho_0 c^2} u_mu ,

где

 

p
0

~ p_0

есть скалярное давление. Для произвольной частицы компоненты 4-потенциала в рамках специальной теории относительности (СТО) имеют вид:

 
℘
=

γ

p
0

ρ
0

,

~ wp = frac { gamma p_0 }{rho_0 },

 
Π
=

γ

p
0

ρ
0

c
2

v

,

~ boldsymbol {Pi }= frac { gamma p_0 }{rho_0 c^2}mathbf{v},

и следовательно, векторный потенциал направлен вдоль скорости частицы. Если компоненты векторного потенциала являются функциями от времени и прямо не зависят от пространственных координат, то для такого движения согласно

(1)

eqref {1}

соленоидальный вектор

 

I

~ mathbf { I }

обращается в нуль.

Благодаря взаимодействию множества частиц друг с другом посредством различных полей, в том числе на расстоянии без непосредственного контакта, поле давления в веществе изменяется и отличается от поля давления одной частицы в точке наблюдения. Поле давления в системе частиц задаётся через напряжённость и соленоидальный вектор, характеризующие типичные усреднённые характеристики движения вещества. Например, в гравитационно-связанной системе возникает радиальный градиент вектора

 

C

,

~ mathbf { C },

а если часть частиц движется синхронно или вращается, то возникает вектор

 

I

.

~ mathbf { I }.

Из 

(3)

eqref {3}

и 

(4)

eqref {4}

следует общее выражение для плотности 4-силы с ковариантным индексом, возникающей от поля давления:

 
(

f
μ

)
p

=

f

μ
ν

J
ν

=

ρ
0

c
d
t

d
s

(

1
c

C

⋅

v

,

−

C

−
[

v

×

I

]
)

,

~ (f_mu)_p = f_{mu nu} J^nu = rho_0 frac {cdt}{ds}left(frac {1}{c} mathbf{C} cdot mathbf{v}{,} qquad -mathbf{C}-[mathbf{v} times mathbf{ I }] right),

где

 
d
s

~ ds

обозначает четырёхмерный пространственно-временной интервал.

Для стационарного случая, когда потенциалы поля давления не зависят от времени, волновое уравнение

(2)

eqref {2}

для скалярного потенциала в СТО преобразуется в уравнение:

 
Δ
℘
=
−
4
π
σ
γ

ρ
0

.

~ Delta wp = — 4 pi sigma gamma rho_0.

Решение этого уравнения для неподвижной сферы с хаотически движущимися в ней частицами имеет вид:^[7]

 
℘
=

℘
c

−

σ

γ
c

c
2

η

+

σ

γ
c

c
3

r
η

4
π
η

ρ
0

sin
 Синус 

(

r
c

4
π
η

ρ
0

)

≈

℘
c

−

2
π
σ

ρ
0

r
2

γ
c

3

.

~ wp = wp_c — frac {sigma gamma_c c^2 }{eta } + frac {sigma gamma_c c^3 }{r eta sqrt {4 pi eta rho_0} } sin left(frac {r}{c}sqrt {4 pi eta rho_0} right) approx wp_c — frac {2 pi sigma rho_0 r^2 gamma_c }{3}.

 

p
0

≈

p

0
c

−

2
π
σ

ρ
0
2

r
2

γ
c

3

.

~ p_0 approx p_{0c} — frac {2 pi sigma rho^2_0 r^2 gamma_c }{3}.

 

p

0
c

≈

3
σ

M
2

8
π

R
4

.

~ p_{0c} approx frac {3 sigma M^2 }{8 pi R^4}.

Здесь

 
η

~ eta

есть постоянная поля ускорений,

 

℘
c

~ wp_c

представляет собой скалярный потенциал поля давления в центре сферы,

 

γ
c

=

1

1
−

v
c
2

c
2

~ gamma_c = frac {1}{sqrt{1 — {v^2_c over c^2}}}

есть фактор Лоренца для скоростей

 

v
c

~ v_c

частиц в центре сферы, и ввиду малости аргумента синус разложен до членов второго порядка. Из формулы следует, что потенциал давления и скалярное давление максимальны в центре и уменьшаются при приближении к поверхности сферы радиуса

 
R

~ R

и общей массы

 
M

~ M

.

Найденная зависимость для давления в центре

 

p

0
c

~ p_{0c}

хорошо выполняется для самых разных космических объектов, включая газовые облака и глобулы Бока, Землю, нейтронные звёзды. В центре звёзд главной последовательности, включая Солнце, основной вклад в общее давление вместо гравитации вносят термоядерные реакции. Этот вклад был учтён в статье,^[1] где для давления в центре ядра Солнца получилось соотношение:

 

p

0
s

≈

3
ℵ

M
c
2

8
π

R
c
4

,

~ p_{0s} approx frac {3 aleph M^2_c }{8 pi R^4_c},

где

 

R
c

~ R_c

и 

 

M
c

~ M_c

обозначают радиус и массу ядра Солнца,

 
ℵ

~ aleph

есть постоянная в тензоре энергии-импульса поля сильного взаимодействия, причём

 
ℵ
≈
σ

~ aleph approx sigma

.

В рассмотренной системе скалярный потенциал

 
℘

~ wp

становится функцией радиуса, а векторный потенциал

 
Π

~ boldsymbol {Pi }

и соленоидальный вектор

 

I

~ mathbf { I }

равны нулю. Напряжённость поля давления

 

C

~mathbf {C}

находится с помощью

(1)

eqref {1}

. Далее могут быть вычислены все функции поля давления, включая 4-ускорение от поля давления, энергию частиц в этом поле и энергию самого поля давления.^[8] Для космических тел без дополнительных источников энергии основной вклад в 4-ускорение в веществе вносит гравитационная сила тяжести и поле давления.
При этом автоматически выводится релятивистская энергия покоя системы, с учётом движения частиц внутри сферы. Для системы частиц с полем ускорения, полем давления, гравитационным и электромагнитным полями указанный подход позволил решить проблему 4/3 и показал, где и в какой форме содержится энергия системы. Для постоянной поля давления в этой задаче было найдено соотношение:

 
σ
=
3
G
−

3

q
2

4
π

ε
0

m
2

,

~sigma = 3G- frac {3q^2}{4 pi varepsilon_0 m^2 },

где

 

ε
0

~ varepsilon_0

 — электрическая постоянная,

 
q

~q

и 

 
m

~m

 — полный заряд и масса системы.

В статьях ^{[9] [10]} соотношение для коэффициентов полей было уточнено следующим образом:

 
η
+
σ
=
G
−

ρ

0
q

2

4
π

ε
0

ρ

0

2

.

~eta + sigma = G — frac {rho^2_{0q}}{4 pi varepsilon_0 rho^2_{0}}.

Если ввести параметр

 
μ

~ mu

как количество нуклонов на одну частицу ионизированного газа, то постоянная поля давления выразится так:

 
σ
=

2
G

2
+
3

γ
c

μ

.

~ sigma = frac {2 G}{2+ 3 gamma_c mu }.

Для давления внутри космических тел в модели гравитационного равновесия находится зависимость от текущего радиуса:

 

p
0

=

p

0
c

−

2
π
σ

ρ
0

ρ

0
c

γ
c

r
2

3

+

π
σ
A

ρ
0

γ
c

r
3

3

+

π
σ
B

ρ
0

γ
c

r
4

5

,

~ p_0 = p_{0c} — frac {2 pi sigma rho_0 rho_{0c}gamma_c r^2}{3}+ frac { pi sigma Arho_0 gamma_c r^3}{3} + frac {pi sigma B rho_0 gamma_c r^4}{5} ,

где коэффициенты

 
A

~ A

и 

 
B

~ B

входят в зависимость плотности массы от радиуса в соотношении

 

ρ
0

=

ρ

0
c

−
A
r
−
B

r
2

.

~ rho_0 = rho_{0c}- Ar — Br^2.

В предположении, что типичные частицы системы имеют массу

 

m

−

=
μ

m
u

~stackrel{-}{m } = mu m_u

, где

 

m
u

~ m_u

есть масса одной частицы газа, в качестве которой берётся атомная единица массы, и именно типичные частицы задают температуру и давление, для постоянной поля давления получается следующее:^[11]

 
σ
=

2
5

(
G
−

ρ

0
q

2

4
π

ε
0

ρ
0
2

)

.

~ sigma = frac {2}{5} left( G- frac {rho^2_{0q}}{ 4 pi varepsilon_0 rho^2_0 } right) .

При этом скалярный потенциал в центре сферы приблизительно равен:^[12]

 

℘
c

≈

3
σ
m

10
a

(
1
+

9

2

14

)

.

~ wp_c approx frac {3 sigma m}{10 a} left( 1+frac {9}{2sqrt {14}} right) .

Релятивистское уравнение движения вязкого сжимаемого вещества, с учётом 4-потенциала поля давления, тензора поля давления и тензора энергии-импульса поля давления, в пределе малой кривизны пространства-времени было представлено в виде уравнения Навье-Стокса в гидродинамике в рамках СТО.^[13]

В рамках релятивистской однородной системы учёт векторного поля давления позволил уточнить теорему вириала, которая в релятивистской форме записывается так:^[14]

 
⟨

W
k

⟩
≈
−
0
,
6

∑

k
=
1

N

⟨

F

k

⋅

r

k

⟩
,

~ langle W_k rangle approx — 0,6 sum_{k=1}^Nlanglemathbf{F}_kcdotmathbf{r}_krangle ,

причём величина

 

W
k

≈

γ
c

T

~ W_k approx gamma_c T

превышает кинетическую энергию частиц

 
T

~ T

на множитель, равный фактору Лоренца

 

γ
c

~ gamma_c

частиц в центре системы. В обычных условиях можно считать, что

 

γ
c

≈
1

~ gamma_c approx 1

, и тогда видно, что в теореме вириала кинетическая энергия связана с потенциальной энергией не коэффициентом 0,5, а скорее коэффициентом, близким к 0,6. Отличие от классического случая возникает за счёт учёта поля давления и поля ускорений частиц внутри системы, при этом производная от вириальной скалярной функции

 

G
v

~ G_v

не равна нулю и должна рассматриваться как производная Лагранжа.

Анализ интегральной теоремы обобщённого вириала позволяет найти на основе теории поля формулу для среднеквадратичной скорости типичных частиц системы, не используя понятия температуры:^[15]

v

rms

=
c

1
−

4
π
η

ρ
0

r
2

c
2

γ
c
2

sin
 Синус 

2

(

r
c

4
π
η

ρ
0

)

.

v_mathrm{rms} = c sqrt{1- frac {4 pi eta rho_0 r^2}{c^2 gamma^2_c sin^2 {left( frac {r}{c} sqrt {4 pi eta rho_0} right) } } } .

Интегральная теорема энергии поля для поля давления в искривлённом пространстве-времени выглядит следующим образом:^[16]

 
−
∫

(

8
π
σ

c
2

π
α

J
α

+

f

α
β

f

α
β

)

−
g

d

x
1

d

x
2

d

x
3

=

2
c

d

d
t

(
∫

π
α

f
α

 
0

−
g

d

x
1

d

x
2

d

x
3

)

+
2

∬
S

π
α

f
α

 
k

n
k

−
g

d
S

.

~ — int { left( frac {8 pi sigma }{c^2} pi_alpha J^alpha + f_{alpha beta} f^{alpha beta} right) sqrt {-g} dx^1 dx^2 dx^3 } = frac {2}{c} frac {d}{dt} left( int { pi^alpha f_alpha ^{ 0} sqrt {-g} dx^1 dx^2 dx^3} right) + 2 iint limits_S {pi^alpha f_alpha ^{ k} n_k sqrt {-g} dS} .

В релятивистской однородной системе скалярный потенциал

 
℘

~wp

поля давления связан со скалярным потенциалом

 
ϑ

~vartheta

поля ускорений соотношением: ^[17]

 
℘
=

σ
(
ϑ
−

c
2

)

η

=

2
(
ϑ
−

c
2

)

3

.

~ wp = frac {sigma (vartheta -c^2)}{ eta } = frac {2 (vartheta -c^2)}{ 3 }.

Релятивистское выражение для давления имеет следующий вид:

p
=

2
ρ

c
2

(
γ
−
1
)

3

=

2
ρ

c
2

3

(

1

1
−

v
2

/

c
2

−
1
)

≈

ρ

v
2

3

,

p = frac{2rho c^2 (gamma — 1) }{3}= frac {2 rho c^2 }{3} left( frac {1}{sqrt {1- v^2/ c^2 }}-1 right) approx frac {rho v^2}{3},

где

ρ

rho

— плотность движущегося вещества,

c

c

— скорость света,

γ
=

1

1
−

v
2

/

c
2

gamma =frac {1}{sqrt {1- v^2/ c^2 }}

— Лоренц-фактор.
В пределе малых скоростей это соотношение переходит в стандартную формулу молекулярно-кинетической теории.

См. также[править | править код]

• Общее поле
• Поле ускорений
• Поле диссипации
• Ковариантная теория гравитации
• Метрическая теория относительности
• Тензор поля давления
• Тензор энергии-импульса поля давления
• 4-сила
• Уравнение векторного поля

Ссылки[править | править код]

Внешние ссылки[править | править код]

• Pressure field

Никому не нравится быть под давлением. И не важно, под каким. Об этом спела еще группа Queen вместе с Дэвидом Боуи в своем знаменитом сингле «Under pressure». Что такое давление? Как понять давление? В чем оно измеряется, какими приборами и методами, куда направлено и на что давит. Ответы на эти и другие вопросы – в нашей статье про давление в физике и не только.

Давление в физике

Если преподаватель давит на вас, задавая каверзные задачки, мы сделаем так, чтобы вы смогли верно на них ответить. Ведь понимание самой сути вещей – ключ к успеху! Итак, что такое давление в физике?

По определению:

Давление – скалярная физическая величина, равная силе, действующей на единицу площади поверхности.

В международной системе СИ измеряется в Паскалях и обозначается буквой p. Единица измерения давления – 1 Паскаль. Русское обозначение – Па, международное – Pa.

Согласно определению, чтобы найти давление, нужно силу разделить на площадь.

Любая жидкость или газ, помещенный в сосуд, оказывает на стенки сосуда давление. Например, борщ в кастрюле действует на ее дно и стены с некоторым давлением. Формула определения давления жидкости:

где g – ускорение свободного падения в гравитационном поле земли, h – высота столба борща в кастрюле, греческая буква «ро» – плотность борща.

Одно из важнейших свойств жидкостей — изотропность. Это значит, что по закону Паскаля во всех направлениях жидкости производимое ею давление передается одинаково. Кстати, подробнее о жидкостях, их свойствах и движении читайте в нашем материале про уравнение Бернулли.

Наиболее распространенный в быту прибор для определения давления – барометр. Но в чем измеряют давление? Кроме паскаля существуют и другие внесистемные единицы измерения:

• атмосфера;
• миллиметр ртутного столба;
• миллиметр водяного столба;
• метр водяного столба;
• килограмм-сила.

В зависимости от контекста применяются разные внесистемные единицы.

Например, когда вы слушаете или читаете прогноз погоды, там и речи не идет о паскалях.  Говорят о миллиметрах ртутного столба. Один миллиметр ртутного столба – это 133 Паскаля. Если вы ездите за рулем, то наверное знаете, что нормальное давление в колесах легкового автомобиля — около двух атмосфер.

Атмосферное давление

Атмосфера – это газ, точнее, смесь газов, которая удерживается у Земли благодаря гравитации. Атмосфера переходит в межпланетное пространство постепенно, а ее высота – примерно 100 километров.

Как понимать выражение «атмосферное давление»? Над каждым квадратным метром земной поверхности находится стокилометровый столб газа.  Конечно, воздух прозрачен и приятен, но у него есть масса, которая давит на поверхность земли. Это и есть атмосферное давление.

Нормальное атмосферное давление принято считать равным 101325 Па. Это давление на уровне мирового океана при температуре 0 градусов Цельсия. Такое же давление при этой же температуре оказывает на свое основание столб ртути высотой 766 миллиметров.

Чем больше высота над уровнем моря, тем ниже атмосферное давление. Например, на вершине горы Джомолунгма оно составляет всего одну четвертую от нормального атмосферного давления.

Артериальное давление

Еще один пример, где мы сталкиваемся с давлением в повседневной жизни – это измерение кровяного давления.

Артериальное давление – это кровяное давление, т.е. давление, которое кровь оказывает на стенки сосудов, в данном случае – артерий.

Если вы измерили артериальное давление и оно у вас 120 на 80, то все хорошо. Если 90 на 50 или 240 на 180, то вам уже точно будет неинтересно разбираться, в чем это давление измеряется и что это вообще значит.

Тем не менее, возникает вопрос:  120 на 80 чего именно? Паскалей, миллиметров ртутного столба, атмосфер или еще каких-то единиц измерения?

Артериальное давление измеряется в миллиметрах ртутного столба. Оно определяет превышение давления жидкости в кровеносной системе над атмосферным давлением.

Кровь оказывает давление на сосуды и тем самым компенсирует действие атмосферного давления. Будь иначе, нас бы просто раздавило огромной массой воздуха над нами.

Но почему в измерении артериального давления две цифры?

Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Дело в том, что кровь движется в сосудах не равномерно, а толчками. Первая цифра (120) называется систолическим давлением. Это давление на стенки сосудов в момент сокращения сердечной мышцы, его величина – наибольшая. Вторая цифра (80) определяет наименьшее значение и называется диастолическим давлением.

При измерении фиксируются значения систолического и диастолического давлений. Например, для здорового человека типичное значение артериального давления составляет 120 на 80 миллиметров ртутного столба. Это означает, что систолическое давление равно 120 мм. рт. ст., а диастолическое – 80 мм рт. ст. Разница между систолическим и диастолическим давлениями называется пульсовым давлением.

Физический вакуум

Вакуум – это отсутствие давления. Точнее, практически полное его отсутствие. Абсолютный вакуум является приближением, как идеальный газ в термодинамике и материальная точка в механике.

В зависимости от концентрации вещества различают низкий, средний и высокий вакуум.  Наилучшее приближение к физическому вакууму – космическое пространство, в котором концентрация молекул и давление минимальны.

Давление – основной термодинамический параметр состояния системы. Определить давление воздуха или другого газа можно не только по приборам, но и пользуясь уравнениями, формулами и законами термодинамики. А если у вас нет времени разбираться, студенческий сервис поможет решить любую задачу на определение давления.