Как найти вектор диагональ в параллелепипеде

Вектор, лежащий на диагонали параллелепипеда

Скачать
презентацию

B1 >>

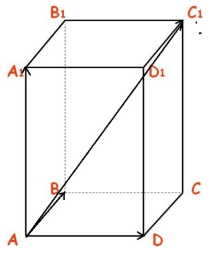
Вектор, лежащий на диагонали параллелепипеда, Равен сумме векторов, лежащих на трех его ребрах, исходящих из одной вершины. Доказательство. B1. C1. A1. D1. B. C. A. D.

Слайд 63 из презентации «Определение вектора в пространстве». Размер архива с презентацией 777 КБ.

Геометрия 11 класс

«Координаты вектора в пространстве» — Величина и направление вектора. Произведение вектора. Решение. Векторы в пространстве. Сумма векторов. Разность векторов. Абсолютная величина. Длина отрезка. Общее начало. Плоскости. Учебник. Доказательство. Скалярное произведение векторов. Рисунок. Действия над векторами в пространстве. Координата.

«Формула объема многогранника» — Прямая призма. Элементы многогранника. Призма. Четырёхугольная пирамида. Пирамида. Невыпуклая пирамида. Многогранники. Грань. Треугольная пирамида. Выпуклые и невыпуклые многоугольники. Пирамиды. Объёмные тела и многогранники. Площадь поверхности призмы. Историческая справка. Объёмные тела. Правильная четырёхугольная пирамида. Правильная пирамида. Пятиугольная пирамида. Параллелепипед и куб.

«Понятие цилиндра» — Сечения цилиндра. Здание. Не правда ли захватывает дух. Объем цилиндра. Что такое цилиндр. Чудо. Цилиндры вокруг нас. Площадь поверхности цилиндра. Два милых кружочка. Откуда и как появился цилиндр. Ножницы. Школьник. Цилиндр стал мужским головным убором. Прямоугольник. В честь шляпы. Цилиндр. Тело вращения. Кружочки. Тетрадь. Цилиндры в архитектуре. Дружба переросла в любовь. Как появился цилиндр.

«В мире многогранников» — Выпуклые многогранники. Многогранники в искусстве. Тетраэдр. Эйлерова характеристика. Тело Ашкинузе. Многогранники. Вершина куба. Геометрия. Правильные многогранники. Пять выпуклых правильных многогранников. Развёртки некоторых многогранников. Тела Кеплера — Пуансо. Огонь. Фаросский маяк. Звездчатый додекаэдр. Александрийский маяк. Царская гробница. Математика. Теорема Эйлера. Магнус Веннинджер. Мир многогранников.

«Геометрические задачи в ЕГЭ» — Основной справочный материал. Осевое сечение конуса. ЕГЭ по математике. Площадь круга. Объем многогранника. Площадь поверхности. Прилежащий катет. Типичные ошибки. Найдите площадь трапеции. Решение задач типа В9. Найдите сумму координат вектора. Уметь выполнять действия с геометрическими фигурами. Диаметры. Основы геометрии. Прямоугольный параллелепипед. Найти длину ребра. Площадь части круга. В создании презентации принимали участие.

«Векторы в пространстве» — Решение. Действие с векторами. Разности. Векторы в пространстве. Умножение двух векторов. Соноправленные векторы. Векторы являются некомпланарными. Разность двух векторов. Координаты вектора. Умение выполнять действия. Единственный вектор. Правило многоугольника. Действия с векторами. Определение вектора.

Всего в теме «Геометрия 11 класс» 45 презентаций

Как находить векторы в параллелепипеде

Правило параллелепипеда. Разложение вектора

Вы будете перенаправлены на Автор24

Правило параллелепипеда

Для правила сложения трех векторов рассмотрим следующую задачу.

Дан прямоугольный параллелепипед $ABCDA_1B_1C_1D_1$. Доказать, что $overrightarrow+overrightarrow+overrightarrow=overrightarrow$

Доказательство.

Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow =overrightarrow$, получим:

Разложение вектора по двум неколлинеарным векторам

Вспомним сначала, какие векторы называются компланарными.

Два вектора, которые параллельны одной плоскости называются компланарными.

Произвольный вектор $overrightarrow

Математически это можно записать следующим образом

Доказательство.

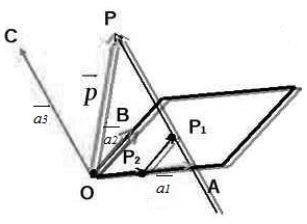
Рассмотрим следующий рисунок:

Произведем следующие дополнительные построения. Проведем через точку $P$ прямую, которая будет параллельна вектору $overrightarrow $. Пусть эта прямая пересекает плоскость $OAB$ в точке $P_1$. Далее, проведем через точку $P_1$ прямую, которая будет параллельна вектору $overrightarrow $. Пусть эта прямая пересекает прямую $OA$ в точке $P_2$ (смотри рисунок выше).

Воспользуемся свойством правила треугольника сложения двух векторов $overrightarrow+overrightarrow =overrightarrow$, получим:

Так как векторы $overrightarrow $ и $overrightarrow $ коллинеарны, то

Так как векторы $overrightarrow

$ и $overrightarrow $ коллинеарны, то

Так как векторы $overrightarrow

$ и $overrightarrow $ коллинеарны, то

Тогда, получаем, что

Существование разложения доказано.

Единственность: Предположим противное. Пусть существует еще одно разложение вектора $overrightarrow

Вычтем эти разложения друг из друга

Из этого получаем

Теорема доказана.

Как находить векторы в параллелепипеде

4.6. Задачи с решениями

1. В параллелепипеде обозначим . Выразить через векторы a, b, с диагонали параллелепипеда и диагонали граней.

Решение. Сделаем чертёж. Пользуясь правилом сложения векторов, получаем:

AC = AB + AD = b + с, AC1 = AA1 + AC = a + b + с .

Из того же треугольника AA1C получаем: A1C = AC — AA1 = b + с — a.

Чтобы найти B1C, заметим, что B1C = A1D, так как у этих векторов совпадают и длины, и направления. Поэтому B1C = A1D = AD — AA1 = с — a.

Аналогично: DC1 = AB1 = AA1 + AB = a + b .

2. Найти длину и направляющие косинусы вектора AB, если его начало и конец находятся в точках A(7, 6), B(2 — 6).

Решение. Так как каждая точка задана двумя координатами, то рассматривается вектор на плоскости. Находим его координаты, вычитая из координат точки B (конца вектора) координаты точки A (начала вектора): AB = (2 — 7, —6 — 6) = (—5, —12). Находим длину: |AB | = 13, направляющие косинусы: .

3. Найти координату z вектора a = (1, —3, z), если известно, что она отрицательна, а модуль |a| = . Где окажется конец вектора a, если его отложить из точки M(5, —2, 1)?

Решение. По условию, . поэтому ZN = —8.

4. Найти расстояние между точками A(5, —2, 4) и B( —1, 0, 6).

Решение. Расстояние равно длине вектора AB. Найдём:

5. При каких p, q векторы a = (2,p, — 1), b = qi + 9j + 3k будут коллинеарными?

Сумма нескольких векторов

Сумма нескольких векторов а ₁, а ₂, а ₃, … , а _n, это вектор, получающийся после ряда последовательных сложений: к вектору а ₁ прибавляется вектор а ₂, к полученному вектору прибавляется вектор а ₃ и т.д.

Из определения вытекает такое построение

Правило многоугольника или правило цепи

Из произвольного начала О строим вектор ОА ₁ = а ₁, из точки А ₁, как из начала, строим вектор А ₁ А ₂ = а ₂, из точки А ₂ строим вектор А ₂ А ₃ = а ₃ и т.д. Вектор ОА _n (на рисунке n = 6) есть сумма векторов а ₁, а ₂, … , а _n.

Свойство сочетательности

Слагаемые векторы можно группировать как угодно.

Так, если найти сначала сумму векторов

и к ней прибавить вектор а ₁ ( ОА ₁), то получим то же вектор:

Правило параллелепипеда

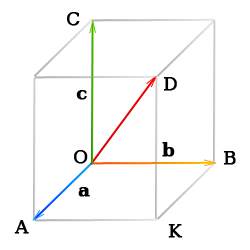
Если три вектора а , b , с после приведения к общему началу не лежат в одной плоскости, то сумму а + b + c можно найти таким построением:

Из любого начала О строим векторы ОА = а , ОВ = b , ОС = с , на отрезках ОА , ОВ , ОС , как на ребрах, строим параллелепипед. Вектор диагонали OD есть сумма векторов a , b , и c (так как ОА = а , АК = ОВ = b , KD = OC = c и OD = OA + AK + KD ).

К векторам, которые (после приведения к общему началу) лежат в одной плоскости, это построение неприменимо.

Прямоугольный параллелепипед. Что это такое?

О чем эта статья:

10 класс, ЕГЭ/ОГЭ

Определение параллелепипеда

Начнем с того, что узнаем, что такое параллелепипед.

Параллелепипедом называется призма, основаниями которой являются параллелограммы. Другими словами, параллелепипед — это многогранник с шестью гранями. Каждая грань — параллелограмм.

На рисунке два параллелограмма АВСD и A₁B₁C₁D₁. Основания параллелепипеда, расположены параллельно друг другу в плоскостях. А боковые ребра АA₁, ВB₁, CC₁, DD₁ параллельны друг другу. Образовавшаяся фигура — параллелепипед.

Внимательно рассмотрите, как выглядит параллелепипед и каковы его составляющие.

Когда пересекаются три пары параллельных плоскостей, образовывается параллелепипед.

Основанием параллелепипеда является, в зависимости от его типа: параллелограмм, прямоугольник, квадрат.

Параллелепипед — это:

Свойства параллелепипеда

Быть параллелепипедом ー значит неотступно следовать законам геометрии. Иначе можно скатиться до простого параллелограмма.

Вот 4 свойства параллелепипеда, которые необходимо запомнить:

1. Противолежащие грани параллелепипеда равны и параллельны друг другу.
2. Все 4 диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
3. Параллелепипед симметричен относительно середины его диагонали.
4. Квадрат длины диагонали прямоугольного параллелепипеда равен сумме квадратов трёх его измерений.

Подготовка к ЕГЭ по математике онлайн в школе Skysmart — отличный способ освежить знания и снять стресс перед экзаменом.

Прямой параллелепипед

Прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию.

Основание прямого параллелепипеда — параллелограмм. В прямом параллелепипеде боковые грани — прямоугольники.

Свойства прямого параллелепипеда:

1. Основания прямого параллелепипеда — одинаковые параллелограммы, лежащие в параллельных плоскостях.
2. Боковые ребра прямого параллелепипеда равны, параллельны и перпендикулярны плоскостям оснований.
3. Высота прямого параллелепипеда равна длине бокового ребра.
4. Противолежащие боковые грани прямого параллелепипеда — равные прямоугольники.
5. Диагонали прямого параллелепипеда точкой пересечения делятся пополам.

На слух все достаточно занудно и сложно, но на деле все свойства просто описывают фигуру. Внимательно прочтите вслух каждое свойство, разглядывая рисунок параллелепипеда после каждого пункта. Все сразу встанет на места.

Формулы прямого параллелепипеда:

• Площадь боковой поверхности прямого параллелепипеда
  Sб = Ро*h
  Ро — периметр основания
  h — высота
• Площадь полной поверхности прямого параллелепипеда
  Sп = Sб+2Sо
  Sо — площадь основания
• Объем прямого параллелепипеда
  V = Sо*h

Прямоугольный параллелепипед

Определение прямоугольного параллелепипеда:

Прямоугольным параллелепипедом называется параллелепипед, у которого основание — прямоугольник, а боковые ребра перпендикулярны основанию.

Внимательно рассмотрите, как выглядит прямоугольный параллелепипед. Отметьте разницу с прямым параллелепипедом.

Свойства прямоугольного параллелепипеда

Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда.

1. Прямоугольный параллелепипед содержит 6 граней. Все грани прямоугольного параллелепипеда — прямоугольники.
2. Противолежащие грани параллелепипеда попарно параллельны и равны.
3. Все углы прямоугольного параллелепипеда, состоящие из двух граней — 90°.
4. Диагонали прямоугольного параллелепипеда равны.
5. В прямоугольный параллелепипеде четыре диагонали, которые пересекаются в одной точке и делятся этой точкой пополам.
6. Любая грань прямоугольного параллелепипеда может быть принята за основание.
7. Если все ребра прямоугольного параллелепипеда равны, то такой параллелепипед является кубом.
8. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений (длины, ширины, высоты).

Формулы прямоугольного параллелепипеда:

• Объем прямоугольного параллелепипеда
  V = a · b · h
  a — длина, b — ширина, h — высота
• Площадь боковой поверхности
  Sбок = Pосн·c=2(a+b)·c
  Pосн — периметр основания, с — боковое ребро
• Площадь поверхности
  Sп.п = 2(ab+bc+ac)

Диагонали прямоугольного параллелепипеда: теорема

Не достаточно просто знать свойства прямоугольного параллелепипеда, нужно уметь их доказывать.

Если есть теорема, нужно ее доказать. (с) Пифагор

Теорема: Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.

В данном случае, три измерения — это длина, ширина, высота. Длина, ширина и высота — это длины трех ребер, исходящих из одной вершины прямоугольного параллелепипеда.

Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁. Доказать теорему.

Доказательство теоремы:

Чтобы найти диагональ прямоугольного параллелепипеда, помните, что диагональ — это отрезок, соединяющий противоположные вершины.

Все грани прямоугольного параллелепипеда — прямоугольники.

ΔABD: ∠BAD = 90°, по теореме Пифагора

ΔB₁BD: ∠B₁BD = 90°, по теореме Пифагора

d² = d₁² + c² = a² + b² + c²

d² = a² + b² + c²

Доказанная теорема — пространственная теорема Пифагора.

Куб: определение, свойства и формулы

Кубом называется прямоугольный параллелепипед, все три измерения которого равны.

Каждая грань куба — это квадрат.

Свойства куба:

1. В кубе 6 граней, каждая грань куба — квадрат.
2. Противолежащие грани параллельны друг другу.
3. Все углы куба, образованные двумя гранями, равны 90°.
4. У куба четыре диагонали, которые пересекаются в центре куба и делятся пополам.
5. Диагонали куба равны.
6. Диагональ куба в √3 раз больше его ребра.
7. Диагональ грани куба в √2 раза больше длины ребра.

Помимо основных свойств, куб характеризуется умением вписывать в себя тетраэдр и правильный шестиугольник.

Формулы куба:

• Объем куба через длину ребра a
  V = a3
• Площадь поверхности куба
  S = 6a2
• Периметр куба
  P = 12a

Решение задач

Чтобы считать тему прямоугольного параллелепипеда раскрытой, стоит потренироваться в решении задач. 10 класс — время настоящей геометрии для взрослых. Поэтому, чем больше практики, тем лучше. Разберем несколько примеров.

Задачка 1. Дан прямоугольный параллелепипед. Нужно найти сумму длин всех ребер параллелепипеда и площадь его поверхности.

Для наглядного решения обозначим измерения прямоугольного параллелепипеда: a — длина, b — ширина, c — высота. Тогда a = 10, b = 5, c = 8.

Так как в прямоугольном параллелепипеде всего по 4 — высота, ширина и длина, и все измерения равны между собой, то:
1) 4 * 10 = 40 (см) — сумма длин параллелепипеда;
2) 4 * 5 = 20 (см) — суммарное значение ширины параллелепипеда;
3) 4 * 8 = 32 (см) — сумма высот параллелепипеда;
4) 40 + 20 + 32 = 92 (см) — сумма длин всех ребер прямоугольного параллелепипеда.

Отсюда можно вывести формулу по нахождению суммы длин всех сторон ПП:
X = 4a + 4b + 4c (где X — сумма длин ребер).

Формула нахождения площади поверхности параллелепипеда Sп.п = 2(ab+bc+ac).
Тогда: S = (5*8 + 8*10 + 5*10) * 2 = 340 см2.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Нужно найти длину ребра A₁B₁.

В фокусе внимания треугольник BDD1.
Угол D = 90°.

По теореме Пифагора:
BD₁ 2 = DD₁ 2 + BD 2
BD 2 = BD₁ 2 – DD₁ 2
BD 2 = 26 – 9 = 17
BD = √17
В треугольнике ADB угол А = 90°.
BD 2 = AD 2 + AB 2
AB 2 = BD 2 — AD 2 = (√17)2 — 4 2 = 1
A₁B₁ = AB = 1.

Задачка 3. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

AB = 4
AD = 6
AA₁= 5
Нужно найти отрезок BD₁.

В треугольнике ADB угол A = 90°.

По теореме Пифагора:
BD 2 = AB 2 +AD 2
BD 2 = 4 2 + 6 2 = 16 + 36 = 52
В треугольнике BDD₁ угол D = 90°.
BD₁ 2 = 52 + 25 = 77
BD₁ = √77.

Самопроверка

Теперь потренируйтесь самостоятельно — мы верим, что все получится!

Задачка 1. Дан прямоугольный параллелепипед. Измерения (длина, ширина, высота) = 8, 10, 20. Найдите диагональ параллелепипеда.

Подсказка: если нужно выяснить, чему равна диагональ прямоугольного параллелепипеда, вспоминайте теорему.

Задачка 2. Дан прямоугольный параллелепипед АВСDA₁B₁C₁D₁.

Вычислите длину ребра AA₁.

Как видите, самое страшное в параллелепипеде — 14 букв в названии. Чтобы не перепутать прямой параллелепипед с прямоугольным, а ребро параллелепипеда с длиной диагонали параллелепипеда, вот список основных понятий:

• прямой параллелепипед — это параллелепипед, у которого боковые ребра перпендикулярны основанию;
• параллелепипед называется прямоугольным, когда его боковые ребра перпендикулярны к основанию;
• основание прямоугольного параллелепипеда — прямоугольник;
• три измерения прямоугольного параллелепипеда: длина, ширина, высота;
• диагональ параллелепипеда равна сумме квадратов его измерений.

Найти длину диагонали параллелепипеда, построенного на векторах

24.09.2019, 04:12. Показов 8281. Ответов 3

---

0

Как найти длину диагонали прямоугольного параллелепипеда ? По какой формуле найти диагональ параллелепипеда ? Диагональ прямоугольного параллелепипеда — это отрезок, соединяющий его противоположные вершины . Итак, у нас есть прямоугольный параллелепипед с диагональю d и со сторонами a, b, c . Одно из свойств параллелепипеда гласит, что квадрат длины диагонали d равен сумме квадратов трёх его измерений a, b, c. Отсюда вывод, что длина диагонали может быть легко рассчитана по следующей формуле : Также : Как найти высоту параллелепипеда? модератор выбрал этот ответ лучшим Nonse­nse [63.5K] 7 лет назад  Прямоугольным параллелепипедом (ПП) является ни что иное, как призма, основанием у которой прямоугольник. У ПП все диагонали равны, значит любая его диагональ рассчитывается по формуле: где а, в — стороны основания ПП; с — его высота. Можно дать и другое определение, рассматривая декартову прямоугольную систему координат: Диагональ ПП это радиус-вектор любой точки пространства, заданной координатами x, y и z в декартовой системе координат. Этот радиус вектор к точке проводится из начала координат. А координатами точки будут проекции радиус-вектора (диагонали ПП) на координатные оси. Проекции совпадают с вершинами данного параллелепипеда. Zolot­ynka [551K] 8 лет назад  Если у прямоугольного параллелепипеда известны длина, высота и ширина (a,b,c) то формула для расчета диагонали будет выглядеть таким образом: Обычно учителя не предлагают своим ученикам «голую» формулу, а прилагают усилия, чтобы те могли самостоятельно ее вывести, задавая наводящие вопросы: что нужно узнать, какими данными мы располагаем? какие свойства имеет прямоугольный параллелепипед? применима ли здесь Теорема Пифагора? Как? достаточное ли данных для применения теоремы Пифагора, или нужны еще какие-то расчеты? Обычно после ответа на поставленные вопросы, ученики без труда самостоятельно выводят данную формулу. Лолоч­ка611 [15.4K] 8 лет назад  Прямоугольный параллелепипед это один из так званных многогранников, который состоит из 6 граней, каждая из которых является прямоугольником. А диагональ — это отрезок, который соединяет противоположные вершины параллелограмма. Если длину, ширину и высоту прямоугольного параллелепипеда принять за a, b, c соответственно, то формула его диагонали ( D ) будет выглядеть следующим образом: D^2=a^2+b^2+c^2. дольф­аника [379K] 8 лет назад  Нашлась в интернете неплохая схема-таблица с полным перечислением всего, что есть в параллепипеде. Есть формула, чтобы найти диагональ, которая обозначается d. Есть изображение грани, вершины и других важных для параллепипеде вещей. Багир­а999 [4.8K] 8 лет назад  Прямоугольный параллелепипед — это разновидность многогранника, состоящая из 6 граней, в основании которого — прямоугольник. Диагональ — это отрезок, который соединяет противоположные вершины параллелограмма. Формула нахождения длины диагонали — квадрат диагонали равен сумме квадратов трех измерений параллелограмма. Koluc­hiy [12.3K] 8 лет назад  Диагонали прямоугольного параллелепипеда равны. Также как и диагонали его противоположных граней. Длину диагонали можно вычислить, зная длину рёбер параллелограмма, исходящих из одной вершины. Эта длина равна корню квадратному из суммы квадратов длин его рёбер. ДРЕСС­ИРОВЩ­ИК [56.5K] 9 лет назад  Квадрат диагонали, квадратного параллилепипеда (смотрите свойства квадратного параллепипеда) равна сумме квадратов трёх его разных сторон (ширине, высоте, толщине), а соответственно диагонали квадратного параллепипеда равна корню из этой суммы. haler­on [8.8K] 8 лет назад  Насколько мне известно еще со школьной программы, класс 9 если не ошибаюсь, и если не изменяет память , то диагональ прямоугольного параллелепипеда ровна корню квадратному суммы квадратов его всех трех сторон. [поль­зоват­ель забло­киров­ан] [-93] 8 лет назад  квадрат диагонали равен, сумме квадратов ширины , высоты и длинны , исходя с этой формулы получаем ответ , диагональ равно корню квадратному с суммы его трех разных измерений , буквами они позначаюnсz abc Космо­с111 [6.8K] 7 лет назад  Вспоминаю школьную программу по геометрии, можно сказать так: диагональ параллелепипеда равняется корню квадратному полученному из суммы его всех трех сторон (обозначаются они маленькими буквами a, b, c). Никол­ай Л [10K] 10 лет назад  Длина диагонали прямоугольного параллепипеда равна корню квадратному из суммы квадратов его сторон. Знаете ответ?

Все вышеупомянутые случаи легко рассмотреть, если разместить векторы на рёбрах параллелепипеда.

Если три вектора некомпланарны, то для их сложения в пространстве применяется закон параллелепипеда.

1. Векторы приводят к общему началу (A).

2. На этих трёх рёбрах строится параллелепипед.

 

Векторы и координаты в пространстве. Геометрический подход

Мы с вами уже знаем про такие математические инструменты, как векторы и координаты; подробно говорили о том, почему в них возникает необходимость и где мы их используем. Кто не помнит – пересмотрите урок по геометрии-9.

В планиметрии мы рассматривали векторные величины на плоскости (или, по-другому, в двумерном пространстве). Для того чтобы задать вектор, нам было достаточно двух координат. В стереометрии мы решаем задаче в привычном нам трехмерном пространстве, и теперь двух координат для задания вектора нам будет недостаточно.

Действительно, представьте себе лягушку, которая собирается поймать комара. Если она будет знать только то, что он в 3 см впереди и на 2 см правее ее, то шансы на удачную охоту будут невысокими. Другой пример: два самолета могут одновременно лететь 30 км южнее и 40 км восточнее Москвы, если будут находиться на разной высоте (на разных эшелонах). 

Чтобы задать вектор в трехмерном пространстве, нам понадобятся три координаты. Повлияет ли это на уже полученные нами свойства векторов? Мы расширяем математические инструменты таким образом, чтобы все уже известные нам свойства и характеристики сохранялись. Такая же ситуация и с векторами и координатами в пространстве – принципиально нового будет немного.

В планиметрии мы параллельно рассматривали два подхода к описанию вектора:

• Геометрический: вектор – направленный отрезок.
• Алгебраический: вектор – это упорядоченная пара чисел – координат вектора.

Используем их для определения вектора в пространстве.

C геометрической точки зрения вектором называется направленный отрезок, т. е. отрезок в пространстве, для которого указаны начало и конец (см. рис. 1).

Рис. 1. Вектор

Обозначается вектор двумя большими или одной малой буквами со стрелкой или черточкой наверху: . Направление вектора считается от начала вектора к концу. Длина отрезка называется длиной или модулем вектора: . Отдельную точку пространства можно считать вектором нулевой длины. Направление такого вектора не определено. Обозначается он как ноль со стрелочкой: .

Векторы могут образовывать разные углы, но есть особые случаи: векторы, которые действуют строго в одном направлении или в прямо противоположных. Например, во втором законе Ньютона результирующая внешних сил и ускорение – векторы, направленные в одну сторону, а в третьем законе Ньютона силы направлены в противоположных направлениях. Формальные понятия сонаправленности и противоположной направленности, а также их общего случая – коллинеарности в пространстве остаются без изменений.

Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или параллельных прямых. Проще говоря, параллельные векторы мы называем коллинеарными.

Рис. 2. Коллинеарные векторы

Два коллинеарных вектора, направленные в одну сторону, называются сонаправленными:

Если они направлены в разные стороны, то их называют противоположно направленными (см. рис. 3):

Рис. 3. Противоположно направленные векторы

Нулевой вектор считается сонаправленным с любым другим вектором. Для обозначения коллинеарности, сонаправленности и противоположно направленности мы используем знак параллельности, сонаправленные или противоположные стрелки.

В параллелепипеде (см. рис. 4):

 и  не являются коллинеарными.

Рис. 4. Рассматриваемый параллелепипед

Равными векторами, как и прежде, будем называть сонаправленные векторы равной длины. Т. к. векторы  и  сонаправлены и имеют равную длину, то:

 и  не являются коллинеарными, следовательно:

 и  сонаправлены, но имеют разную длину, следовательно:

 и  имеют равную длину, но противоположно направлены, следовательно:

Векторы и координаты в пространстве. Алгебраический подход

Рассмотрим теперь алгебраический подход к определению вектора. Для этого расширим понятие декартовой системы координат с плоской до пространственной.

Проведем три взаимно перпендикулярные прямые через одну точку. Выберем направление на каждой прямой и назовем их координатными осями. Общую точку назовем началом координат и обозначим буквой . Выберем масштаб, для этого на каждой оси отметим единицу (см. рис. 5).

Рис. 5. Пространственная система координат

Стандартное обозначение для осей . Стандартное расположение осей –  и  в горизонтальной плоскости,  направлена в нашу сторону,  – вправо. Ось  направлена вертикально вверх. Как и раньше, ось  называется осью абсцисс, а  – осью ординат. Ось  называется осью аппликат.

Чтобы выяснить координаты произвольной точки, необходимо, как и в плоском случае, опустить перпендикуляры из точки на каждую координатную ось.

При изображении важным является то обстоятельство, что если изобразить оси и точку, то еще непонятно, где она находится. Кажется, что точки  и  находятся в одном и том же месте (см. рис. 6). На самом деле, мы этого еще не знаем. Для определения позиции точек обычно строят их проекции на плоскость .

Рис. 6. Расположение точек  и

У точек и их проекций координаты  и  совпадают. Чтобы найти координату , проекцию точки соединяют с началом координат, а потом из точки проводят параллельный отрезок до пересечения с осью аппликат. Полученные координаты называются, соответственно, абсциссой, ординатой и аппликатой точки (см. рис. 7). Записываются координаты точки в виде упорядоченной тройки чисел: абсцисса, ордината, аппликата.

Рис. 7. Полученные координаты точек  и

Теперь перейдем к векторам и их координатам. Вспомним, как на плоскости мы задавали координаты вектора. Если на векторе как на гипотенузе построить прямоугольный треугольник с катетами, параллельными осям, то длины катетов и принимаются за координаты вектора. При таком определении равные векторы получают равные координаты. Координаты вектора с началом в точке  совпадают с координатами конца вектора (см. рис. 8).

Рис. 8. Векторы

При этом если вектор смотрит влево, т. е. его проекция на ось  отрицательна, то координата  вектора считается отрицательной. Аналогично для координаты . Если вектор смотрит вниз, то его координата у отрицательна.

Вектор  смотрит вправо и вниз – у него положительная координата  и отрицательная .

Вектор  смотрит влево и вверх, координата  отрицательная,  положительная.

Вектор  смотрит влево и вниз, обе координаты отрицательны (см. рис. 9).

Рис. 9. Векторы

Чтобы найти координаты, очевидно, нужно из координат конца вектора вычесть координаты начала. Длину вектора можно было выразить, используя теорему Пифагора:

Используем описанный для плоскости подход в пространстве. А именно – у равных векторов должны быть равные координаты (чтобы геометрический и алгебраический подход описывал один и тот же инструмент).

На векторе, как на диагонали, строим прямоугольный параллелепипед с ребрами, параллельными координатным осям.

Рис. 10. Построенный параллелепипед

Очевидно, на равных векторах будут построены равные параллелепипеды (см. рис. 11).

Рис. 11. На равных векторах построены равные параллелепипеды

Три измерения параллелепипеда назовем координатами вектора. У равных двух векторов на рисунке выше равны координаты: . Вычислить их можно как разности соответствующих координат конца и начала вектора:

При этом учитывается направление. Если вектор смотрит в отрицательную сторону вдоль какой-то из осей, то координата отрицательна.

Т. к. длина вектора – это длина диагонали параллелепипеда, то ее можно вычислить по теореме Пифагора:

Пример 1. Найти координаты и длину вектора с началом в точке  и концом в точке  (см. рис. 12).

Рис. 12. Иллюстрация к примеру 1

Решение

Найдем координаты вектора. Для этого вычтем из координат конца координаты начала:

Отрицательные первая и третья координаты означают тот факт, что вдоль осей  и  вектор смотрит в отрицательном направлении.

Вычислим его длину:

Ответ: ; .

С алгебраической точки зрения вектором называется любая упорядоченная тройка чисел. Равные тройки называются равными векторами. Небольшое противоречие состоит в том, что с геометрической точки зрения два несовпадающих, но равных направленных отрезка – это два вектора, равных друг другу. А с алгебраической, т. к. они имеют одинаковый набор координат – это просто один вектор.

Разрешается это противоречие следующим образом. Все равные геометрические векторы считают одним вектором, а конкретные направленные отрезки – различными представлениями этого вектора. Так что в дальнейшем для нас не будет особой разницы сказать «векторы равны» или «это один и тот же вектор».

Рассмотрим коллинеарность векторов с алгебраической точки зрения. Мы знаем, что на плоскости коллинеарность векторов означает пропорциональность их координат. В самом деле, два коллинеарных вектора можно заменить на равные им радиус-векторы. Они будут лежать на одной прямой. Из подобия прямоугольных треугольников следует пропорциональность их координат (см. рис. 13). Во сколько раз длиннее вектор, во столько раз больше модули его координат.

Рис. 13. Коллинеарные векторы

Векторы  и  коллинеарны, и их координаты пропорциональны:

Абсолютно аналогичная ситуация в трехмерном случае. Пусть  и  – коллинеарные векторы. Соответствующие им радиус-векторы лежат на одной прямой. Тогда из подобия двух параллелепипедов следует пропорциональность их координат (см. рис. 14). Таким образом, чтобы выяснить коллинеарность двух векторов, нужно попарно поделить их координаты друг на друга.

Рис. 14. Коллинеарные векторы

Пример 2. Выяснить, коллинеарны ли пары векторов:

1.    и ;

2.    и ;

3.    и .

Решение

1.  и :

Координаты пропорциональны, значит, векторы коллинеарны. Отношение координат – положительное число . Значит, вектор  в  раза длиннее и сонаправлен вектору .

2.  и :

Координаты пропорциональны, значит, векторы коллинеарны. Отношение – отрицательное число . Значит, вектор  в  раза длиннее и противоположно направлен вектору .

3.  и :

Координаты не пропорциональны, значит, векторы не коллинеарны.

Ответ: да, да, нет.

Сложение и вычитание векторов. Умножение вектора на число

Рассмотрим два произвольных вектора в пространстве. Совместим конец вектора  и начало вектора  (см. рис. 15).

Рис. 15. Конец вектора  совместили с началом вектора

Если у двух векторов есть общая точка, то они лежат в одной плоскости. Тогда, чтобы расширенная модель не противоречила исходной, для сложения векторов нужно использовать правило треугольника.

Суммой будет вектор , начало которого совпадает с началом вектора , а конец – с концом вектора  (см. рис. 16):

Рис. 16. Вектор

Иллюстрирует это правило нагляднее всего перемещение: переместиться из точки  на вектор  в точку , а затем из точки  на вектор  в точку  эквивалентно перемещению из точки  в точку  (см. рис. 17).

Рис. 17. Иллюстрация правила сложения векторов

Точно так же сохраняется и правило параллелограмма. Если совместить два вектора,  и  не последовательно, а так, чтобы совпали их начала, то одна диагональ  построенного на них параллелограмма будет суммой, а вторая диагональ  – разностью данных векторов (см. рис. 18):

Рис. 18. Векторы  и

Проверяем себя, куда направить векторы разности, как и раньше:

Два вектора называются противоположными, если они в сумме дают нулевой вектор.

Понятно, что это должны быть противоположно направленные равные по модулю векторы:

Как и в плоском случае, последовательное применение несколько раз правила треугольника для сложения нескольких векторов дает правило многоугольника. Единственная разница будет в том, что многоугольник уже может не быть плоским.

Чтобы сложить несколько векторов, нужно совместить последовательно их концы и начала, и результатом будет вектор, начало которого совпадает с началом первого, а конец – с концом второго:

Например, чтобы сложить векторы  (см. рис. 19), рассмотрим сумму:

Рис. 19. Векторы

С алгебраической точки зрения тоже никаких изменений с определением сложения не произошло. Складывая два вектора  и  в декартовой системе координат, расположим начало вектора  в начале координат, с его концом совместим начало вектора . По правилу треугольника построим их сумму (см. рис. 20).

Рис. 20. Вектор

Очевидно, как и в плоском случае, координаты суммы – это сумма координат исходных векторов:

Как обратную операцию получаем разность векторов. Чтобы найти разность векторов, нужно из координат первого вектора вычесть координаты второго вектора:

Противоположным данному называется вектор с противоположными координатами:

Умножение вектора на число также не претерпевает изменений по сравнению с плоским случаем. С геометрической точки зрения умножить вектор на положительное число означает изменить его длину в это количество раз, а направление оставить прежним, например (см. рис. 21):

Рис. 21. Векторы  и

Если умножить на отрицательное число, то длина вектора меняется пропорционально модулю множителя, а направление меняется на противоположное, например (см. рис. 22):

Рис. 21. Векторы  и

Т. е. умножение на число, по модулю большее единицы, удлиняет вектор, а на число, по модулю меньшее единицы, укорачивает.

Важно понимать, что результатом умножения вектора на число всегда является вектор, поэтому при умножении вектора на ноль получаем нулевой вектор, а не число ноль.

Понятно, что, если умножить вектор на , получим вектор той же длины, но направленный в другую сторону – это соответствует нашему определению противоположного вектора:

Рассмотрим теперь вектор  в декартовой системе координат. Построенный на нем как на диагонали прямоугольный параллелепипед задает координаты вектора. Умножим вектор на число  в геометрическом смысле, т. е. удлиним его в  раз. Новый параллелепипед будет подобен прежнему с коэффициентом подобия  (см. рис. 22). Значит, его измерения будут отличаться в  раз от исходных. Но его измерения и есть координаты нового вектора. Следовательно, изменение длины вектора в  раз означает умножение его координат на . Изменение направления вектора означает изменение знака его координат на противоложный.

Рис. 22. Параллелепипеды подобны с коэффициентом

Таким образом, чтобы умножить вектор на число, надо умножить все его координаты на это число:

Абсолютно без изменения остаются основные свойства умножения вектора на число – сочетательный и два распределительных закона. Сочетательный закон утверждает, что можно перемножить два числа, а потом умножить результат на вектор либо поочередно умножать вектор на эти числа. Результат будет одинаков:

Распределительные законы утверждают, что можно раскрывать скобки при умножении суммы чисел на вектор и умножении числа на сумму векторов:

Убедиться в истинности этих законов не составит никакого труда, если использовать координатную форму записи векторов. Попробуйте сделать это самостоятельно.

Компланарные векторы

Пока ничего нового по сравнению с плоским случаем мы про векторы не рассказали.

Но вот следующее понятие имеет смысл только в трехмерном случае. Если несколько векторов имеют общее начало, то они могут лежать в одной плоскости или нет.

Если они лежат в одной плоскости, то их называют компланарными.

Векторы  компланарны (см. рис. 23).

Рис. 23. Компланарные векторы

Мы не различаем равные векторы, поэтому в этом примере вектор  можем заменить на равный ему вектор . Таким образом, векторы  компланарны. Иными словами, векторы компланарны, если они все параллельны одной плоскости, в данном случае плоскости нижнего основания.

Векторы  некомпланарны (см. рис. 24).

Рис. 24. Некомпланарные векторы

Понятно, что два вектора всегда компланарны. Разберемся, каковы условия компланарности векторов. Вспомним из курса планиметрии еще одно понятие – разложение вектора. Если верно равенство , то говорят, что вектор  разложен по векторам  и .

Но из курса планиметрии мы также знаем, что такой вектор  будет лежать в одной плоскости с векторами  и . В самом деле, векторы  лежат в плоскости одного и того же параллелограмма, как следует из правил умножения векторов на число и сложения векторов. Таким образом, если один из трех векторов раскладывается по двум другим, то такие три вектора компланарны.

Верно и обратное. Если три вектора компланарны, то любой из них можно разложить по двум оставшимся при условии, что эти два вектора не коллинеарны. Это легко доказать, перейдя в плоскость, в которой лежит эта тройка векторов, и воспользоваться соответствующим утверждением из планиметрии, а именно, что любой вектор можно разложить по двум неколлинеарным векторам.

Что касается алгебраического представления векторов, то здесь проверка компланарности трех векторов сводится к решению соответствующего уравнения c переменными  и .

Пример 3. Проверить, являются векторы  компланарными.

Решение

Запишем уравнение:

Умножим в правой части векторы на числа и сложим их:

Два вектора равны, если попарно равны все их координаты. Получаем систему трех простых уравнений:

Ее решение:

Таким образом:

Ответ: векторы компланарны.

Рассмотрим три некомпланарных вектора и найдем их сумму. В алгебраическом подходе нет никакой разницы, складывать ли компланарные или некомпланарные векторы – нужно сложить все соответствующие координаты.

Для геометрического подхода можно сформулировать простое правило параллелепипеда.

Совместим три вектора в общее начало. Построим на них, как на ребрах, параллелепипед (см. рис. 25).

Рис. 25. Построенный параллелепипед

Сложим сначала векторы  и :

Теперь сложим  и вектор :

Таким образом, сумма трех некомпланарных векторов равна диагонали параллелепипеда, построенного на этих векторах.

Теорема о разложении вектора по трем некомпланарным

Мы уже знаем, что любой вектор на плоскости можно разложить по двум неколлинеарным векторам. Аналогичное утверждение сформулируем для векторов в пространстве.

Теорема. Любой вектор в трехмерном пространстве можно разложить единственным образом по любым трем некомпланарным векторам.

Понятно, почему речь идет о некомпланарных векторах. Если мы возьмем компланарные векторы, будем их умножать на разные и числа и складывать друг с другом, мы не выйдем за пределы плоскости, в которой они лежат. Итак, докажем утверждение.

Доказательство

Пусть  – данные некомпланарные векторы (см. рис. 26).

Рис. 26. Иллюстрация к доказательству

Докажем для начала, что любой вектор  можно разложить по этим трем векторам, а потом докажем единственность такого разложения.

Совместим все четыре вектора в общее начало . Обозначим концы векторов такими же буквами, как векторы, только заглавными (см. рис. 27).

Рис. 27. Иллюстрация к доказательству

Через точку  проведем прямую, параллельную вектору . Она пересечет плоскость  в некоторой точке . Через  проведем прямую, параллельную . Она пересечет прямую  в некой точке  (см. рис. 28).

Рис. 28. Иллюстрация к доказательству

Легко увидеть, что:

Но каждый из векторов в правой части равенства коллинеарен одному из исходных трех векторов, т. е. получается из них умножением на некое число. Тогда:

Таким образом, мы разложили вектор  по векторам .

Докажем единственность такого разложения. Предположим, что существует два разложения вектора :

Вычтем из первого второе уравнение:

Т. к. ни один из векторов  не является нулевым (ответьте, почему), то это означает, что все разности в скобках равны нулю. В самом деле, если, например, , то:

Но это означает, что векторы  компланарны, что противоречит условию. А раз все разности в скобках равны нулю, то рассматриваемые разложения совпадают – получили противоречие. Значит, такое разложение будет единственным.

Доказано.

Рассмотрим три единичных вектора, т. е. три вектора с длиной , направленных вдоль осей координат. Стандартное обозначение для них  (см. рис. 29). Т. к. эти векторы некомпланарны, то по ним можно разложить любой другой вектор.

Рис. 29. Векторы

Разложим вектор  по этим трем векторам (см. рис. 30).

Рис. 30. Вектор

Для этого умножим вектор  на число . Очевидно, получим вектор . Аналогично умножим вектор  на , а вектор  – на . Сумма полученных векторов по правилу параллелепипеда равна вектору  (см. рис. 31).

Рис. 31. Построенный параллелепипед

Т. е., чтобы разложить вектор по этим трем, нужно в качестве коэффициентов использовать его координаты:

В связи с этим векторы  называют координатными.

Правило разложения по координатным векторам можно увидеть и из других соображений.

Выпишем координаты самих координатных векторов:

Тогда, очевидно, разложение вектора  имеет вид:

Таким образом, координаты вектора и коэффициенты при его разложении по координатным векторам – это одно и то же. Впрочем, мы уже сталкивались с идентичной ситуацией в планиметрии. Только координатных векторов было всего два.

Список литературы

1. Атанасян Л.С., Бутузов В.Ф., Кадомцев С.Б. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11класс. Учебник. – АО «Издательство “Просвещение”».
2. Мордкович А.Г., Смирнова И.М. Математика. Базовый уровень. 11 класс. Учебник. – ООО «ИОЦ МНЕМОЗИНА».
3. Погорелов А.В. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10-11 класс. Базовый и углубленный уровни. Учебник. – АО «Издательство “Просвещение”».

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-портал yaklass.ru
2. Интернет-портал mathprofi.ru
3. Интернет-портал ru.onlinemschool.com

Домашнее задание

1. Найти координаты и длину вектора , если  и .
2. Даны векторы  и . Найти координаты вектора .
3.  – тетраэдр,  – середины его ребер . Компланарны ли векторы ?