Как найти вектор если даны две точки - Исправление недочетов и поиск решений вместе с Examum.ru

Простейшие задачи Как найти вектор по двум точкам?

Если
даны две точки плоскости
и
,
то вектор
имеет
следующие координаты:

Если
даны две точки пространства
и
,
то вектор
имеет
следующие координаты:

То
есть, из
координат конца вектора нужно
вычесть соответствующие координаты начала
вектора.

Пример

Даны
две точки плоскости
и
.
Найти координаты вектора

Решение: по
соответствующей формуле:

Как
вариант, можно было использовать
следующую запись:

Можно
и так:

Обязательно
нужно понимать различие
между координатами точек и координатами
векторов:

Координаты
точек –
это обычные координаты в прямоугольной
системе координат. Каждая точка обладает
строгим местом на плоскости, и перемещать
их куда-либо нельзя.

Координаты
же вектора –
это его разложение по базису
,
в данном случае
.
Любой вектор является свободным, поэтому
при необходимости мы легко можем отложить
его от какой-нибудь другой точки
плоскости. Интересно, что для векторов
можно вообще не строить оси, прямоугольную
систему координат, нужен лишь базис, в
данном случае ортонормированный базис
плоскости
.

Записи
координат точек и координат векторов
вроде бы схожи:
,
а смысл
координат абсолютно разный,
и следует хорошо понимать эту разницу.

Пример

Даны
точки
.
Найти векторы
.

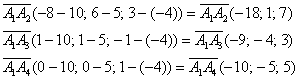
Как найти длину отрезка?

Если
даны две точки плоскости
и
,
то длину отрезка
можно
вычислить по формуле

Если
даны две точки пространства
и
,
то длину отрезка
можно
вычислить по формуле

Примечание: Формулы
останутся корректными, если переставить
местами соответствующие координаты:
и
,
но более стандартен первый вариант

Пример

Даны
точки
и
.
Найти длину отрезка
.

Ответ:

Если
дан вектор плоскости
,
то его длина вычисляется по формуле
.

Если
дан вектор пространства
,
то его длина вычисляется по формуле
.

Пример

Даны
точки
и
.
Найти длину вектора
.

Решение: Сначала
найдём вектор
:

По
формуле
вычислим
длину вектора:

Ответ:

Пример

а)
Даны точки
и
.
Найти длину вектора
.

б)
Даны векторы
,
,
и
.
Найти их длины.

а) Решение: найдём
вектор
:

Вычислим
длину вектора:

Ответ:

б) Решение:

Вычислим
длины векторов:

Действия с векторами в координатах

1) Правило
сложения векторов.
Рассмотрим два вектора плоскости
и
.
Для того, чтобы сложить векторы,
необходимо сложить
их соответствующие координаты:
.

Частный
случай – формула разности векторов:
.

Аналогичное
правило справедливо для суммы любого
количества векторов, например, найдём
сумму трёх векторов:

Если
речь идёт о векторах в пространстве, то
всё точно так же, только добавится
дополнительная координата. Если даны
векторы
,
то их суммой является вектор
.

2) Правило
умножения вектора на число.
Для того чтобы вектор
умножить
на число
,
необходимо каждую координату данного
вектора умножить на число
:

Для
пространственного вектора
правило
такое же:

Пример

Даны
векторы
и
.
Найти
и

Решение: Для
действий с векторами справедлив обычный
алгебраический приоритет: сначала
умножаем, потом складываем:

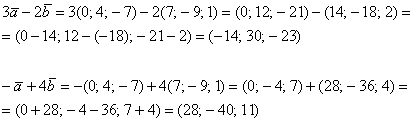
Ответ:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Содержание:

Формула
Примеры нахождения координат вектора по точкам

Формула

Чтобы найти координаты вектора $overline{A B}$ на плоскости, если он задан координатами своих начала $Aleft(x_{1} ; y_{1}right)$ и конца $Bleft(x_{2} ; y_{2}right)$, необходимо от координат конца отнять соответствующие координаты начала, то есть

$$overline{A B}=left(x_{2}-x_{1} ; y_{2}-y_{1}right)$$

Чтобы найти координаты вектора $overline{A B}$, заданного в пространстве координатами $Aleft(x_{1} ; y_{1} ; z_{1}right)$ и $Bleft(x_{2} ; y_{2} ; z_{2}right)$, необходимо, по аналогии с плоским случаем, из координат конца вычесть координаты начала:

$$overline{A B}=left(x_{2}-x_{1} ; y_{2}-y_{1} ; z_{2}-z_{1}right)$$

Примеры нахождения координат вектора по точкам

Пример

Задание. Даны точки
$A(4;-1)$ и $B(2;1)$. Найти координаты векторов $overline{A B}$ и
$overline{B A}$

Решение. Для вектора $overline{A B}$ точка $A$ является началом, а точка $B$ — концом. Тогда координаты вектора $overline{A B}$ равны

$$overline{A B}=(2-4 ; 1-(-1))=(-2 ; 2)$$

Для вектора точка
$B$ является началом, а точка
$A$ — концом. Тогда координаты вектора $overline{B A}$ равны

$$overline{B A}=(4-2 ;-1-1)=(2 ;-2)$$

Ответ. $overline{A B}=(-2 ; 2), overline{B A}=(2 ;-2)$

Пример

Задание. Даны три точки в пространстве точки $A(1;-2;0,5)$, $B(3;2;1,5)$ и $C(0;-1;1)$. Найти координаты векторов
$overline{A B}$,
$overline{A C}$,
$overline{B C}$

Решение. Для искомого вектора
$overline{A B}$ точка
$A$ является началом, а точка
$B$ — концом. Тогда координаты вектора
$overline{A B}$ соответственно равны:

$$overline{A B}=(3-1 ; 2-(-2) ; 1,5-0,5)=(2 ; 4 ; 1)$$

Для вектора $overline{A C}$ точка
$A$ является началом, а точка
$C$ — концом. Тогда его координаты соответственно равны

$$overline{A C}=(0-1 ;-1-(-2) ; 1-0,5)=(-1 ; 1 ; 0,5)$$

Для вектора $overline{B C}$ точка
$B$ является началом, а точка
$C$ — концом. Его координаты равны

$$overline{B C}=(0-3 ;-1-2 ; 1-1,5)=(-3 ;-3 ;-0,5)$$

Ответ. $overline{A B}=(2 ; 4 ; 1), overline{A C}=(-1 ; 1 ; 0,5), overline{B C}=(-3 ;-3 ;-0,5)$

Читать дальше: как найти сумму векторов.

Как найти сумму векторов
Как найти скалярное произведение векторов
Как найти векторное произведение векторов
Как найти смешанное произведение векторов
Как найти вектор коллинеарный вектору
Как найти вектор перпендикулярный вектору
Как найти орт вектора
Как найти разность векторов
Как найти проекцию вектора
Как найти длину вектора
Как найти модуль вектора
Как найти координаты вектора
Как найти направляющие косинусы вектора
Как найти угол между векторами
Как найти косинус угла между векторами

Источник

Нахождение координат вектора через координаты точек

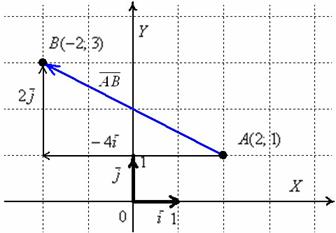
Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i → должно совпадать с осью O x , а направление вектора j → с осью O y .

Векторы i → и j → называют координатными векторами.

Координатные векторы неколлинеарны. Поэтому любой вектор p → можно разложить по векторам p → = x i → + y j → . Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p → по координатным векторам называются координатами вектора p → в данной системе координат.

Координаты вектора записываются в фигурных скобках p → x ; y . На рисунке вектор O A → имеет координаты 2 ; 1 , а вектор b → имеет координаты 3 ; — 2 . Нулевой вектор представляется в виде 0 → 0 ; 0 .

Если векторы a → и b → равны, то и y 1 = y 2 . Запишем это так: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j → , значит x 1 = x 2 , y 1 = y 2 .

Таким образом, координаты равных векторов соответственно равны.

Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на O x y заданы координаты точек начала и конца A B → : A x a , y a , B x b , y b . Найти координаты заданного вектора.

Изобразим координатную ось.

Из формулы сложения векторов имеем O A → + A B → = O B → , где O – начало координат. Отсюда следует, что A B → = O B → — O A → .

O A → и O B → – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения O A → = x a , y a , O B → = x b , y b .

По правилу операций над векторами найдем A B → = O B → — O A → = x b — x a , y b — y a .

Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.

Для нахождения координат вектора, необходимо найти разность его точек конца и начала.

Найти координаты O A → и A B → при значении координат точек A ( 2 , — 3 ) , B ( — 4 , — 1 ) .

Для начала определяется радиус-вектор точки A . O A → = ( 2 , — 3 ) . Чтобы найти A B → , нужно вычесть значение координат точек начала из координат точек конца.

Получаем: A B → = ( — 4 — 2 , — 1 — ( — 3 ) ) = ( — 6 , 2 ) .

Ответ: O A → = ( 2 , — 3 ) , A B → = ( — 6 , — 2 ) .

Задано трехмерное пространство с точкой A = ( 3 , 5 , 7 ) , A B → = ( 2 , 0 , — 2 ) . Найти координаты конца A B → .

Подставляем координаты точки A : A B → = ( x b — 3 , y b — 5 , z b — 7 ) .

По условию известно, что A B → = ( 2 , 0 , — 2 ) .

Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: x b — 3 = 2 y b — 5 = 0 z b — 7 = — 2

Отсюда следует, что координаты точки B A B → равны: x b = 5 y b = 5 z b = 5

Ответ: B ( 5 , 5 , 5 ) .

источники:

Источник

Заказать задачи по любым предметам можно здесь от 10 минут

Координаты вектора по двум точкам

Чтобы найти координаты вектора по двум точкам нужно найти разность между координатами конца и начала вектора. Пусть даны две точки $ A(x_1;y_1) $ и $ B(x_2;y_2) $Вектор $ overline{AB} $ для плоской задачи можно найти по формуле: $$ overline{AB} = (x_2-x_1; y_2-y_1) $$

В случае, если точки расположены в пространстве $ A(x_1;y_1;z_1) $ и $ B(x_2;y_2;z_2) $, то координаты вектора $ overline{AB} $ расчитываются по формуле: $$ overline{AB} = (x_2-x_1; y_2-y_1; z_2-z_1) $$

Следует обратить внимание, что координаты вычисляются именно с помощью вычитания начальной точки из конечной, но не наоборот. То есть векторы $ overline{AB} $ и $ overline{BA} $ имеют разные координаты: $$ overline{AB} neq overline{BA} $$

Пример 1

Даны точки $ A(2;1;-3) $ и $ B(1;0;2) $. Найти координаты векторов $ overline{AB} $ и $ overline{BA} $

Решение

Как найти координаты вектора по двум точкам? Согласну правилу нужно из конечной точки вычесть начальную. Так как вектор $ overline{AB} $ имеет начало в точке $ A $, а конец в $ B $, то получаем:

$$ overline{AB} = (1-2;0-1;2-(-3)) = (-1; -1; 5) $$

Теперь посмотрим на вектор $ overline{BA} $, в котором начало в точке $ B $, а конец в $ A $. Поэтому имеем:

$$ overline{BA} = (2-1;1-0;-3-2)=(1;1;-5) $$

Как видим, векторые разные, и координаты их тоже отличаются.

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ overline{AB} = (-1;-1;5) $$ $$ overline{BA} = (1;1;-5) $$

Источник

В данной публикации мы рассмотрим формулы, с помощью которых можно найти координаты вектора, заданного координатами его начальной и конечной точек, а также разберем примеры решения задач по этой теме.

Нахождение координат вектора
Примеры задач

Нахождение координат вектора

Для того, чтобы найти координаты вектора AB, нужно из координат его конечной точки (B) вычесть соответствующие координаты начальной точки (A).

Формулы для определения координат вектора


Для плоских задач	AB = {B_x — A_x; B_y — A_y}
Для трехмерных задач	AB = {B_x — A_x; B_y — A_y; B_z — A_z}
Для n-мерных векторов	AB = {B₁ — A₁; B₂ — A₂; … B_n — A_n}

Примеры задач

Задание 1
Найдем координаты вектора AB, если у его точек следующие координаты: A = (2; 8), B = (5; 12).

Решение:
AB = {5 – 2; 12 – 8} = {3; 4}.

Задание 2
Определим координаты точки B вектора AB = {6; 14}, если координаты точки A = (2; 5).

Решение:
Координаты точки B можно вывести из формулы для расчета координат вектора:
B_x = AB_x + A_x = 6 + 2 = 8.
B_y = AB_y + A_y = 14 + 5 = 19.

Таким образом, B = (8; 19).

Источник