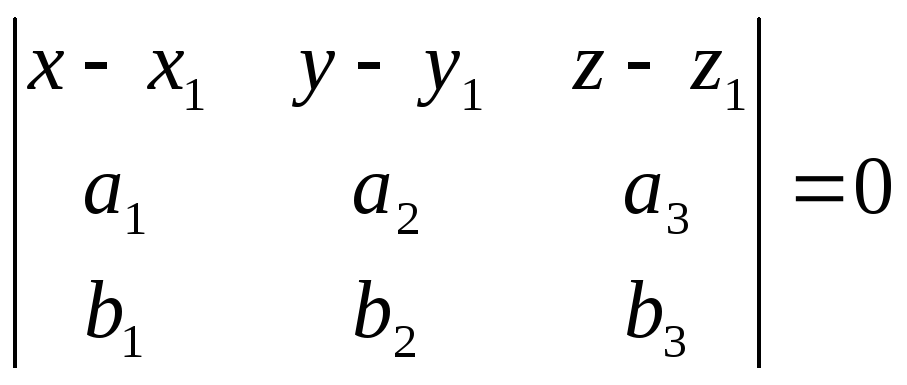Как найти вектор нормали по двум векторам - Исправление недочетов и поиск решений вместе с Examum.ru

Нормальный вектор плоскости, координаты нормального вектора плоскости

Существует ряд заданий, которым для решения необходимо нормальный вектор на плоскости, чем саму плоскость. Поэтому в этой статье получим ответ на вопрос определения нормального вектора с примерами и наглядными рисунками. Определим векторы трехмерного пространства и плоскости по уравнениям.

Нормальный вектор плоскости – определение, примеры, иллюстрации

Чтобы материал легко усваивался, необходимо предварительно изучить теорию о прямой в пространстве и представление ее на плоскости и векторы.

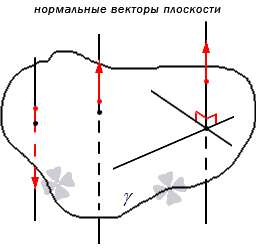
Нормальным вектором плоскости считается любой ненулевой вектор, который лежит на перпендикулярной к данной плоскости прямой.

Отсюда следует, что имеет место существование большого количества нормальных векторов в данной плоскости. Рассмотрим на рисунке, приведенном ниже.

Нормальные векторы располагаются на параллельных прямых, поэтому они все коллинеарны. То есть, при нормальном векторе n → , расположенном в плоскости γ , вектор t · n → , имея ненулевое значение параметра t , также нормальный вектор плоскости γ . Любой вектор может быть рассмотрен как направляющий вектор прямой, которая перпендикулярна этой плоскости.

Имеются случаи совпадения нормальных векторов плоскостей из-за перпендикулярности одной из параллельных плоскостей, так как прямая перпендикулярна и второй плоскости. Отсюда следует, что нормальные векторы перпендикулярных плоскостей должны быть перпендикулярными.

Рассмотрим на примере нормального вектора на плоскости.

Задана прямоугольная система координат О х у z в трехмерном пространстве. Координатные векторы i → , j → , k → считаются нормальными векторами плоскостей O y z , O x z и O x y . Это суждение верно, так как i → , j → , k → ненулевые и расположены на координатных прямых O x , O y и O z . Эти прямые перпендикулярны координатным плоскостям O y z , O x z и O x y .

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости

Статья предназначена для того, чтобы научить находить координаты нормального вектора плоскости при известном уравнении плоскости прямоугольной системы координат О х у z . Для определения нормального вектора n → = ( A , B , C ) в плоскости необходимо наличие общего уравнения плоскости, имеющее вид A x + B y + C z + D = 0 . То есть достаточно иметь уравнение плоскости, тогда появится возможность для нахождения координат нормального вектора.

Найти координаты нормального вектора, принадлежащего плоскости 2 x — 3 y + 7 z — 11 = 0 .

По условию имеем уравнение плоскости. Необходимо обратить внимание на коэффициенты, так как они и являются координатами нормального вектора заданной плоскости. Отсюда получаем, что n → = ( 2 , — 3 , 7 ) — это нормальный вектор плоскости. Все векторы плоскости задаются при помощи формулы t · n → = 2 · t , — 3 · t , 7 · t , t является любым действительным числом не равным нулю.

Ответ: n → = ( 2 , — 3 , 7 ) .

Определить координаты направляющих векторов заданной плоскости x + 2 z — 7 = 0 .

По условию имеем, что дано неполное уравнение плоскости. Чтобы увидеть координаты, необходимо преобразовать уравнение x + 2 z — 7 = 0 к виду 1 · x + 0 · y + 2 z — 7 = 0 . Отсюда получим, что координаты нормального вектора данной плоскости равны ( 1 , 0 , 2 ) . Тогда множество векторов будет иметь такую форму записи ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

Ответ: ( t , 0 , 2 · t ) , t ∈ R , t ≠ 0 .

При помощи уравнения плоскости в отрезках, имеющего вид x a + y b + z c = 1 , и общего уравнения плоскости возможна запись нормального вектора этой плоскости, где координаты равны 1 a , 1 b , 1 c .

Знания о нормальном векторе позволяют с легкостью решать задачи. Часто встречающимися задачами являются задания с доказательствами параллельности или перпендикулярности плоскостей. Заметно упрощается решение задач на составление уравнений заданной плоскости. Если имеется вопрос о нахождении угла между плоскостями или между прямой и плоскостью, то формулы нормального вектора и нахождения его координат помогут в этом.

Вектор нормали: расчет и пример

Содержание:

В нормальный вектор Он определяет направление, перпендикулярное рассматриваемому геометрическому объекту, который может быть, например, кривой, плоскостью или поверхностью.

Это очень полезная концепция для позиционирования движущейся частицы или какой-либо поверхности в пространстве. На следующем графике можно увидеть, как вектор нормали к произвольной кривой C:

Рассмотрим точку P на кривой C. Точка может представлять движущуюся частицу, которая движется по траектории C. Касательная линия к кривой в точке P нарисована красным.

Обратите внимание, что вектор Т касается C в каждой точке, а вектор N перпендикулярно Т y указывает на центр воображаемого круга, дуга которого является сегментом C. Векторы выделены жирным шрифтом в печатном тексте, чтобы отличать их от других не векторных величин.

Вектор Т он всегда указывает, куда движется частица, следовательно, указывает ее скорость. Вместо вектора N всегда указывает в том направлении, в котором вращается частица, отмечая, таким образом, вогнутость кривой C.

Как получить вектор нормали к плоскости?

Вектор нормали не обязательно является единичным вектором, то есть вектором с модулем 1, но если это так, он называется нормальный единичный вектор.

Во многих приложениях необходимо знать вектор нормали к плоскости вместо кривой. Этот вектор показывает ориентацию указанной плоскости в пространстве. Например, рассмотрим самолет п (желтый) рисунка:

К этой плоскости есть два нормальных вектора: п₁ Y п₂. Использование того или другого будет зависеть от контекста, в котором находится упомянутый самолет. Получить вектор нормали к плоскости очень просто, если вы знаете его уравнение:

ах + по + cz + d = 0, с участием к, б, c Y d вещественные числа.

Ну, нормальный вектор к указанной плоскости задается следующим образом:

N = а я + b j + c k

Здесь вектор N Он выражается через единичные векторы и перпендикулярно друг другу. я, j Y k, направленных по трем направлениям, определяющим пространство X и Zсм. рисунок 2 справа.

Вектор нормали из векторного произведения

Очень простая процедура нахождения вектора нормали использует свойства векторного произведения между двумя векторами.

Как известно, три разные точки, не лежащие на одной прямой, определяют плоскость Р. Теперь можно получить два вектора или Y v которые принадлежат упомянутой плоскости, имеющей эти три точки.

Когда у вас есть векторы, векторный продуктили Икс v — операция, результатом которой, в свою очередь, является вектор, который имеет свойство быть перпендикулярным плоскости, определяемой или Y v.

Известный этот вектор, он обозначается как N, и из него можно будет определить уравнение плоскости благодаря уравнению, указанному в предыдущем разделе:

N = или Икс v

На следующем рисунке показана описанная процедура:

пример

Найти уравнение плоскости, определяемой точками A (2,1,3); В (0,1,1); С (4.2.1).

Решение

Это упражнение иллюстрирует описанную выше процедуру. Имея 3 точки, одна из них выбирается как общее начало двух векторов, которые принадлежат плоскости, определенной этими точками. Например, точка A устанавливается в качестве начала координат и строятся векторы AB Y AC.

Вектор AB — вектор, начало которого — точка A, а конец — точка B. Координаты вектора AB определяются соответственно вычитанием координат B из координат A:

AB = (0-2) я + (1-1) j + (1-3) k = -2я + 0j -2 k

Таким же образом поступаем и находим вектор AC:

AC = (4-2) я + (2-1) j + (1-3) k = 2я + j -2 k

Расчет векторного произведения AB x AC

Существует несколько процедур для нахождения векторного произведения между двумя векторами. В этом примере используется мнемоническая процедура, которая использует следующий рисунок для поиска векторных произведений между единичными векторами. я, j Y k:

Для начала следует помнить, что векторные произведения между параллельными векторами равны нулю, поэтому:

я Икс я = 0; j Икс j = 0; k Икс k = 0

А поскольку векторное произведение — это еще один вектор, перпендикулярный участвующим векторам, двигаясь в направлении красной стрелки, мы имеем:

я Икс j = k ; j Икс k = я; k Икс я = j

Если вам нужно двигаться в направлении, противоположном стрелке, добавьте знак (-):

j Икс я = – k; k Икс j = –я; я Икс k = –j

Всего можно составить 9 векторных произведений с единичными векторами. я, j Y k, из которых 3 будут нулевыми.

AB Икс AC = (-2я + 0j -2 k) х (2я + j -2 k)= -4(я Икс я) -2(я Икс j)+4 (я Икс k)+0 (j Икс я) + 0 (j Икс j) – 0 (j Икс k) – 4 (k Икс я)-2 (k Икс j) + 4 (k Икс k) = -2k-4j-4j+2я = 2я -8j-2k

Уравнение плоскости

Вектор N был определен с помощью предварительно рассчитанного векторного произведения:

N = 2я -8j-2k

Следовательно, a = 2, b = -8, c = -2, искомая плоскость:

ах + по + cz + d = 0 → 2x-8y-2z + d = 0

Значение d. Это легко сделать, если значения любой из имеющихся точек A, B или C подставить в уравнение плоскости. Выбор C, например:

2,4 — 8,2 — 2,1 + d = 0

Вкратце, искомая карта:

Пытливый читатель может задаться вопросом, был бы такой же результат, если бы вместо выполнения AB Икс AC они бы предпочли произвести AC Икс AB. Ответ: да, плоскость, определяемая этими тремя точками, уникальна и имеет два вектора нормали, как показано на рисунке 2.

Что касается точки, выбранной в качестве исходной точки векторов, нет проблем с выбором любого из двух других.

Ссылки

Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 1. Кинематика. Отредактировал Дуглас Фигероа (USB). 31-62.
Нахождение нормали к плоскости. Получено с: web.ma.utexas.edu.
Ларсон, Р. (1986). Исчисление и аналитическая геометрия. Мак Гроу Хилл. 616-647.
Линии и плоскости в R 3. Получено с: math.harvard.edu.
Нормальный вектор. Получено с сайта mathworld.wolfram.com.

Гидравлическая механика: история, что изучает, основы

Нормальный вектор прямой

Вы будете перенаправлены на Автор24

В аналитической геометрии часто требуется составить общее уравнение прямой по принадлежащей ей точке и вектору нормали к прямой.

Нормаль – синоним для слова перпендикуляр.

Общее уравнение прямой на плоскости выглядит как $Ax + By + C = 0$. Подставляя в него различные значениях $A$, $B$ и $C$, в том числе нулевые, можно определить любые прямые.

Можно выразить уравнение прямой и другим способом:

Это уравнение прямой с угловым коэффициентом. В нем геометрический смысл коэффициента $k$ заключается в угле наклона прямой по отношению к оси абсцисс, а независимого члена $b$ — в расстоянии, на которое прямая отстоит от центра координатной плоскости, т.е. точки $O(0; 0)$.

Рисунок 1. Варианты расположения прямых на координатной плоскости. Автор24 — интернет-биржа студенческих работ

Нормальное уравнение прямой можно выразить и в тригонометрическом виде:

$x cdot cos <alpha>+ y cdot sin <alpha>- p = 0$

где $alpha$ — угол между прямой и осью абсцисс, а $p$ — расстояние от начала координат до рассматриваемой прямой.

Возможны четыре варианта зависимости наклона прямой от величины углового коэффициента:

когда угловой коэффициент положителен, направляющий вектор прямой идёт снизу вверх;
когда угловой коэффициент отрицателен, направляющий вектор прямой идёт сверху вниз;
когда угловой коэффициент равен нулю, описываемая им прямая параллельна оси абсцисс;
для прямых, параллельных оси ординат, углового коэффициента не существует, поскольку тангенс 90 градусов является неопределенной (бесконечной) величиной.

Готовые работы на аналогичную тему

Чем больше абсолютное значение углового коэффициента, тем круче наклонен график прямой.

Зная угловой коэффициент, легко составить уравнение графика прямой, если дополнительно известна точка, принадлежащая искомой прямой:

$y — y_0 = k cdot (x — x_0)$

Таким образом, геометрически прямую на координатной всегда можно выразить с помощью угла и расстояния от начала координат. В этом и заключается смысл нормального вектора к прямой — самого компактного способа записи ее положения, если известны координаты хотя бы одной точки, принадлежащей этой прямой.

Вектором нормали к прямой, иначе говоря, нормальным вектором прямой, принято называть ненулевой вектор, перпендикулярный рассматриваемой прямой.

Для каждой прямой можно найти бесконечное множество нормальных векторов, равно как и направляющих векторов, т.е. таких, которые параллельны этой прямой. При этом все нормальные векторы к ней будут коллинеарными, хотя и не обязательно сонаправлены.

Обозначив нормальный вектор прямой как $vec(n_1; n_2)$, а координаты точки как $x_0$ и $y_0$, можно представить общее уравнение прямой на плоскости по точке и вектору нормали к прямой как

$n_1 cdot (x — x_n) + n_2 cdot (y — y_0) = 0$

Таким образом, координаты вектора нормали к прямой пропорциональны числам $A$ и $B$, присутствующим в общем уравнении прямой на плоскости. Следовательно, если известно общее уравнение прямой на плоскости, то можно легко вывести и вектор нормали к прямой. Если прямая, задана уравнением в прямоугольной системе координат

то нормальный вектор описывается формулой:

При этом говорят, что координаты нормального вектора «снимаются» с уравнения прямой.

Нормальный к прямой вектор и ее направляющий вектор всегда ортогональны по отношению друг к другу, т.е. их скалярные произведения равны нулю, в чем легко убедиться, вспомнив формулу направляющего вектора $bar

(-B; A)$, а также общее уравнение прямой по направляющему вектору $bar

(p_1; p_2)$ и точке $M_0(x_0; y_0)$:

В том, что вектор нормали к прямой всегда ортогонален направляющему вектору к ней можно убедиться с помощью скалярного произведения:

$bar

cdot bar = -B cdot A + A cdot B = 0 implies bar

perp bar$

Всегда можно составить уравнение прямой, зная координаты принадлежащей ей точки и нормального вектора, поскольку направление прямой следует из его направления. Описав точку как $M(x_0; y_0)$, а вектор как $bar(A; B)$, можно выразить уравнение прямой в следующем виде:

$A(x — x_0) + B(y — y_0) = 0$

Составить уравнение прямой по точке $M(-1; -3)$ и нормальному вектору $bar(3; -1)$. Вывести уравнение направляющего вектора.

Для решения задействуем формулу $A cdot (x — x_0) + B cdot (y — y_0) = 0$

Подставив значения, получаем:

$3 cdot (x — (-1)) — (-1) cdot (y — (-3)) = 0$ $3 cdot (x + 1) — (y + 3) = 0$ $3x + 3 — y — 3 = 0$ $3x — y = 0$

Проверить правильность общего уравнения прямой можно «сняв» из него координаты для нормального вектора:

$3x — y = 0 implies A = 3; B = -1 implies bar(A; B) = bar(3; -1),$

Что соответствует числам исходных данных.

Подставив реальные значения, проверим, удовлетворяет ли точка $M(-1; -3)$ уравнению $3x — y = 0$:

Равенство верно. Осталось лишь найти формулу направляющего вектора:

$bar

(-B; A) implies bar

(1; 3)$

Ответ: $3x — y = 0; bar

(1; 3).$

Получи деньги за свои студенческие работы

Курсовые, рефераты или другие работы

Автор этой статьи Дата последнего обновления статьи: 04 03 2021

источники:

http://ru1.warbletoncouncil.org/vector-normal-6378

http://spravochnick.ru/matematika/normalnyy_vektor_pryamoy/

Источник

Как найти нормаль плоскости

Нормаль плоскости n (вектор нормали к плоскости) – это любой направленный перпендикуляр к ней (ортогональный вектор). Дальнейшие выкладки по определении нормали зависят от способа задания плоскости.

Инструкция

Если задано общее уравнение плоскости — AX+BY+CZ+D=0 или его форма A(x-x0)+B(y-y0)+C(z-z0)=0, то можно сразу записать ответ — n(А, В, С). Дело в том, что это уравнение было получено, как задача определения уравнения плоскости по нормали и точке.

Для получения общего ответа, вам понадобится векторное произведение векторов из-за того, что последнее всегда перпендикулярно исходным векторам. Итак, векторным произведением векторов, является некоторый вектор, модуль которого равен произведению модуля первого (а) на модуль второго (b) и на синус угла между ними. При этом этот вектор (обозначьте его через n) ортогонален a и b – это главное. Тройка этих векторов правая, то есть из конца n кратчайший поворот от a к b совершается против часовой стрелки.
[a,b] — одно из общепринятых обозначений векторного произведения. Для вычисления векторного произведения в координатной форме, используется вектор-определитель (см. рис.1)

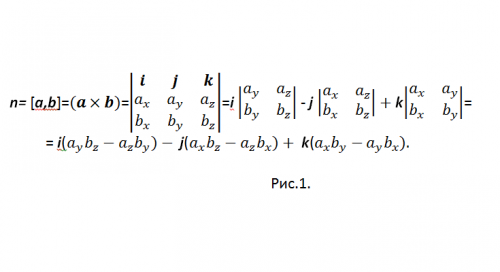
Для того чтобы не путаться со знаком «-», перепишите результат в виде: n={nx, ny, nz}=i(aybz-azby)+j(azbx-axbz)+k(axby-aybx), и в координатах: {nx, ny, nz}={(aybz-azby), (azbx-axbz), (axby-aybx)}.
Более того, дабы не путаться с численными примерами выпишете все полученные значения по отдельности: nx=aybz-azby, ny=azbx-axbz, nz=axby-aybx.

Вернитесь к решению поставленной задачи. Плоскость можно задать различными способами. Пусть нормаль к плоскости определяется двумя неколлинеарными векторами, причем сразу численно.
Пусть даны векторы a(2, 4, 5) и b(3, 2, 6). Нормаль к плоскости совпадает с их векторным произведением и, как только что было выяснено будет равна n(nx, ny, nz),
nx=aybz-azby, ny=azbx-axbz, nz=axby-aybx. В данном случае ax=2, ay=4, az=5, bx=3, by=2, bz=6. Таким образом,
nx=24-10=14, ny=12-15=-3, nz=4-8=-4. Нормаль найдена — n(14, -3, -4). При этом она является нормалью к целому семейству плоскостей.

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Векторы в пространстве и метод координат

Существует два способа решения задач по стереометрии

Первый — классический — требует отличного знания аксиом и теорем стереометрии, логики, умения построить чертеж и свести объемную задачу к планиметрической. Способ хорош тем, что развивает мозги и пространственное воображение.

Другой метод — применение векторов и координат. Это простые формулы, алгоритмы и правила. Он очень удобен, особенно когда времени до экзамена мало, а решить задачу хочется.

Если вы освоили векторы на плоскости и действия с ними — то и с векторами в пространстве разберетесь. Многие понятия окажутся знакомыми.

Система координат в пространстве

Выберем начало координат. Проведем три взаимно перпендикулярные оси X, Y и Z. Зададим удобный масштаб.

Получилась система координат в трехмерном пространстве. Теперь каждая его точка характеризуется тремя числами — координатами по X, Y и Z. Например, запись M(−1; 3; 2) означает, что координата точки M по X (абсцисса) равна −1, координата по Y (ордината) равна 3, а координата по Z (аппликата) равна 2.

Векторы в пространстве определяются так же, как и на плоскости. Это направленные отрезки, имеющие начало и конец. Только в пространстве вектор задается тремя координатами x, y и z:

$vec{a}(x_{a};: y_{a};: z_{a})$

Как найти координаты вектора? Как и на плоскости — из координаты конца вычитаем координату начала.

$vec{a}=vec{AB}(x_{B}-x_{A};: y_{B}-y_{A};: z_{B}-z_{A})$

Длина вектора vec{AB} в пространстве – это расстояние между точками A и B. Находится как корень квадратный из суммы квадратов координат вектора:

$|vec{a}|=sqrt{x^{2}_{a}+y^{2}_{a}+z^{2}_{a}}=sqrt{(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}+(z_{B}-z_{A})^{2}}$ Пусть точка M – середина отрезка AB. Ее координаты находятся по формуле:

$x_{M}=frac{x_{A}+x_{B}}{2};: : y_{M}=frac{y_{A}+y_{B}}{2};: : z_{M}=frac{z_{A}+z_{B}}{2}$

Для сложения векторов применяем уже знакомые правило треугольника и правило параллелограмма

Сумма векторов, их разность, произведение вектора на число и скалярное произведение векторов определяются так же, как и на плоскости. Только координат не две, а три. Возьмем векторы и .

Сумма векторов:

$vec{a}+vec{b}=vec{c}(x_{a}+x_{b};: y_{a}+y_{b};: z_{a}+z_{b})$

Разность векторов:

$vec{a}-vec{b}=vec{d}(x_{a}-x_{b};: y_{a}-y_{b};: z_{a}-z_{b})$

Произведение вектора на число:

$lambda cdot vec{a}=vec{p}(lambda x_{a};: lambda y_{a};:lambda z_{a} )$

Скалярное произведение векторов:

$vec{a}cdot vec{b}=|vec{a}|cdot |vec{b}|cdot cosvarphi =x_{a}cdot x_{b}+y_{a}cdot y_{b}+z_{a}cdot z_{b}$

Косинус угла между векторами:

$cosvarphi =frac{vec{a}cdot vec{b}}{|vec{a}|cdot vec{|b|}}=frac{x_{a}cdot x_{b}+y_{a}cdot y_{b}+z_{a}cdot z_{b}}{sqrt{x^{2}_{a}+y^{2}_{a}+z^{2}_{a}}cdot sqrt{x^{2}_{b}+y^{2}_{b}+z^{2}_{b}}}$

Последняя формула удобна для нахождения угла между прямыми в пространстве. Особенно если эти прямые – скрещиваются. Напомним, что так называются прямые, которые не параллельны и не пересекаются. Они лежат в параллельных плоскостях.

1. В кубе ABCDA₁B₁C₁D₁ точки E и K — середины ребер соответственно A₁B₁ и B₁C₁. Найдите косинус угла между прямыми AE и BK.

Если вам достался куб — значит, повезло. Он отлично вписывается в прямоугольную систему координат. Строим чертеж:

Длина ребра куба не дана. Какой бы она ни была, угол между AE и BK от нее не зависит. Поэтому возьмем единичный куб, все ребра которого равны 1.

Прямые AE и BK — скрещиваются. Найдем угол между векторами vec{AE} и vec{BK} . Для этого нужны их координаты.

$, \ A(0;0;0)\ B(1;0;0)\ E(frac{1}{2};0;1)\ K(1;frac{1}{2};1)$

Запишем координаты векторов:

$vec{AE}left (frac{1}{2};0;1 right )$

$vec{BK}left (0;frac{1}{2};1 right )$

и найдем косинус угла между векторами vec{AE} и vec{BK} :

2. В правильной четырехугольной пирамиде SABCD, все ребра которой равны 1, точки E, K — середины ребер SB и SC соответственно. Найдите косинус угла между прямыми AE и BK.

Лучше всего выбрать начало координат в центре основания пирамиды, а оси X и Y сделать параллельными сторонам основания.

Координаты точек A, B и C найти легко:

$Aleft ( frac{1}{2};-frac{1}{2};0 right )$

$Bleft ( frac{1}{2};frac{1}{2};0 right )$

$Cleft ( -frac{1}{2};frac{1}{2};0 right )$

Из прямоугольного треугольника AOS найдем $OS=frac{sqrt{2}}{2}.$

Координаты вершины пирамиды: $Sleft ( 0;0;frac{sqrt{2}}{2} right ).$

Точка E — середина SB, а K — середина SC. Воспользуемся формулой для координат середины отрезка и найдем координаты точек E и K.

$Eleft ( frac{1}{4};frac{1}{4};frac{sqrt{2}}{4} right )$

$Kleft ( -frac{1}{4};frac{1}{4};frac{sqrt{2}}{4} right )$

Найдем координаты векторов и :

$overrightarrow{AE}left ( -frac{1}{4};frac{3}{4};frac{sqrt{2}}{4} right )$

$overrightarrow{BK}left ( -frac{3}{4};frac{1}{4};frac{sqrt{2}}{4} right )$

и угол между ними:

$cosvarphi =frac{overrightarrow{AE}cdot overrightarrow{BK}}{left |overrightarrow{AE} right |cdot left |overrightarrow{BK} right |}=frac{1}{6}$

Покажем теперь, как вписать систему координат в треугольную призму.

3. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, точка D — середина ребра A₁B₁. Найдите косинус угла между прямыми AD и BC₁

Пусть точка A — начало координат. Возьмем ось X параллельно стороне BC, а ось Y перпендикулярно ей. Другими словами, на оси Y будет лежать отрезок AH, являющийся высотой треугольника ABC. Нарисуем отдельно нижнее основание призмы.

Запишем координаты точек:

$A_{1}(0;0;1)$

$B(frac{1}{2};frac{sqrt{3}}{2};0)$

$B_{1}(frac{1}{2};frac{sqrt{3}}{2};1)$

$C_{1}(-frac{1}{2};frac{sqrt{3}}{2};1)$

Точка D — середина A₁B₁. Значит, пользуемся формулами для координат середины
отрезка.

$D(frac{1}{4};frac{sqrt{3}}{4};1)$

Найдем координаты векторов и $overrightarrow{BC}_{1}$ , а затем угол между ними:

$overrightarrow{AD}(frac{1}{4};frac{sqrt{3}}{4};1)$

$overrightarrow{BC_{1}}(-1;0;1)$

$cosvarphi =frac{overrightarrow{AD}cdot overrightarrow{BC_{1}}}{left |overrightarrow{AD} right |cdot left |overrightarrow{BC_{1}} right |}=frac{3}{2sqrt{10}}$

Смотрите, как легко с помощью векторов и координат найти угол между прямыми. А если требуется найти угол между плоскостями или между прямой и плоскостью? Для решения подобных задач нам понадобится уравнение плоскости в пространстве.

Плоскость в пространстве задается уравнением:

Здесь числа A, B и C — координаты вектора, перпендикулярного этой плоскости. Его называют нормалью к плоскости.

Вместо x, y и z можно подставить в уравнение координаты любой точки, принадлежащей данной плоскости. Получится верное равенство.

Плоскость в пространстве можно провести через любые три точки, не лежащие на одной прямой. Поэтому для того, чтобы написать уравнение плоскости, берем координаты трех принадлежащих ей точек. Подставляем их по очереди в уравнение плоскости. Решаем полученную систему.

Покажем, как это делается.

Напишем уравнение плоскости, проходящей через точки M (1; 0; 1), N (2; −2; 0) и K (4; 1; 2).

Уравнение плоскости выглядит так:

Подставим в него по очереди координаты точек M, N и K.

Для точки M:

То есть A + C + D = 0.

Для точки N:

Аналогично для точки K:

Получили систему из трех уравнений:

$left{begin{matrix} A+C+D=0\ 2A-2B+D=0\ 4A+B+2C+D=0 end{matrix}right.$ .

В ней четыре неизвестных: A, B, C и D. Поэтому одну из них мы выберем сами, а другие выразим через нее. Правило простое — вместо одной из переменных можно взять любое число, не равное нулю.

Пусть, например, D = −2. Тогда:

$left{begin{matrix} A+C-2=0\ 2A-2B-2=0\ 4A+B+2C-2=0 end{matrix}right.$ ;

$left{begin{matrix} A+C=2\ A-B=1\ 4A+B+2C=2 end{matrix}right.$ .

Выразим C и B через A и подставим в третье уравнение:

$left{begin{matrix} C=2-A\ B=A-1\ 4A+A-1+4-2A=2 end{matrix}right.$ .

Решив систему, получим:

$, \ A=-frac{1}{3}\ , \ B=-frac{4}{3}\ , \ C=frac{7}{3}$

Уравнение плоскости MNK имеет вид:

$-frac{1}{3}x-frac{4}{3}y+frac{7}{3}z-2=0.$

Умножим обе части уравнения на −3. Тогда коэффициенты станут целыми:

Вектор — это нормаль к плоскости MNK.

Уравнение плоскости, проходящей через заданную точку $M(x_{0}, y_{0}, z_{0}),$ имеет вид:

$A(x-x_{0})+B(y-y_{0})+C(z-z_{0})=0.$

Угол между плоскостями равен углу между нормалями к этим плоскостям:

$cosvarphi =frac{left |vec{n}_{1}cdot vec{n}_{2} right |}{|vec{n}_{1}|cdot |vec{n}_{2}|}$

Не правда ли, знакомая формула? Скалярное произведение нормалей поделили на произведение их длин.

Заметим, что при пересечении двух плоскостей вообще-то образуется четыре угла.

Мы берем меньший из них. Поэтому в формуле стоит модуль скалярного произведения — чтобы косинус угла был неотрицателен.

4. В кубе ABCDA₁B₁C₁D₁ точки E и F — середины ребер соответственно A₁B₁ и A₁D₁. Найдите тангенс угла между плоскостями AEF и BDD₁.

Строим чертеж. Видно, что плоскости AEF и BDD₁ пересекаются где-то вне куба. В классическом решении пришлось бы строить линию их пересечения. Но векторно-координатный метод значительно всё упрощает. Не будем ломать голову над тем, по какой прямой пересекаются плоскости. Просто отметим координаты нужных нам точек и найдем угол между нормалями к плоскостям AEF и BDD₁.

Сначала — нормаль к плоскости BDD₁. Конечно, мы можем подставить координаты точек B, D и D₁ в уравнение плоскости и найти коэффициенты, которые и будут координатами вектора нормали. А можем сделать хитрее — увидеть нужную нормаль прямо на чертеже. Ведь плоскость BDD₁ — это диагональное сечение куба. Вектор перпендикулярен этой плоскости.

Итак, первый вектор нормали у нас уже есть: $vec{n}_{1}=overrightarrow{AC}(1;1;0).$

Напишем уравнение плоскости AEF.

$, \ A(0;0;0)\ E(frac{1}{2};0;1)\ , \ F(0;frac{1}{2};1)$

Берем уравнение плоскости и по очереди подставляем в него, вместо x, y и z, соответствующие координаты точек A, E и F.

$left.begin{matrix} A\ , \ E\ , \ F end{matrix}right|$ $, \ 0cdot A+0cdot B+0cdot C+D=0\ , \ frac{1}{2}cdot A+0cdot B+1cdot C+D=0\ , \ 0cdot A+frac{1}{2}cdot B+1cdot C+D=0$

Упростим систему:

$left{begin{matrix} D=0\ frac{1}{2}A+C=0\ , \ frac{1}{2}B+C=0 end{matrix}right.$ .

Пусть С = -1. Тогда A = B = 2.

Уравнение плоскости AEF:

Нормаль к плоскости AEF:

Найдем угол между плоскостями:

$cosvarphi =frac{|2+2|}{sqrt{2}cdot sqrt{9}}=frac{4}{sqrt{2}cdot 3}=frac{4}{sqrt{2}cdot 3}=frac{2sqrt{2}}{3}$

5. Основание прямой четырехугольной призмы BCDA₁B₁C₁D₁ — прямоугольник ABCD, в котором AB = 5, AD = √33. Найдите тангенс угла между плоскостью грани AA₁D₁D и плоскостью, проходящей через середину ребра CD перпендикулярно прямой B₁D, если расстояние между прямыми A₁C₁ и BD равно √3.

Эта задача наглядно показывает, насколько векторный метод проще классического. Попробуйте, для разнообразия, построить необходимые сечения и провести все доказательства — как это делается в «классике»

Строим чертеж. Прямую четырехугольную призму можно по-другому назвать «параллелепипед».

Замечаем, что длина и ширина параллелепипеда у нас есть, а вот высота — вроде не дана. Как же ее найти?

«Расстояние между прямыми A₁C₁ и BD равно √3». Прямые A₁C₁ и BD скрещиваются. Одна из них — диагональ верхнего основания, другая — диагональ нижнего. Вспомним, что расстояние между скрещивающимися прямыми равно длине их общего перпендикуляра. Общий перпендикуляр к A₁C₁ и BD — это, очевидно, OO₁, где O — точка пересечения диагоналей нижнего основания, O₁ — точка пересечения диагоналей верхнего. А отрезок OO₁ и равен высоте параллелепипеда.

Итак, AA₁ = √3

Плоскость AA₁ D₁ D — это задняя грань призмы на нашем чертеже. Нормаль к ней — это любой вектор, перпендикулярный задней грани, например, вектор или, еще проще, вектор $vec{n_{1}}(1;0;0)$ .

Осталась еще «плоскость, проходящая через середину ребра CD перпендикулярно прямой B₁D». Но позвольте, если плоскость перпендикулярна прямой B₁D — значит, B₁D и есть нормаль к этой плоскости! Координаты точек B₁ и D известны:

$B_{1}left ( 5;, 0;, sqrt{3} right )$

Координаты вектора $overrightarrow{B_{1}D}$ — тоже:

$overrightarrow{B_{1}D}left ( -5;, sqrt{33};, -sqrt{3} right )=overrightarrow{n}_{2}$

Находим угол между плоскостями, равный углу между нормалями к ним:

$cos, varphi =frac{5}{sqrt{25+33+3}}=frac{5}{sqrt{61}}$

Зная косинус угла, находим его тангенс по формуле

$1+tg^{2}varphi =frac{1}{cos^{2}varphi }$

Получим:
$tg, varphi =frac{6}{5}.$

Ответ: $frac{6}{5}.$

Угол между прямой m и плоскостью α тоже вычисляется с помощью скалярного произведения векторов.

Пусть — вектор, лежащий на прямой m (или параллельный ей), — нормаль к плоскости α.

Находим синус угла между прямой m и плоскостью α по формуле:

$sin, varphi =frac{left | overrightarrow{n}cdotoverrightarrow{a} right |}{left | overrightarrow{n} right |cdot |overrightarrow{a}|}$

6. В кубе ABCDA₁B₁C₁D₁ точка E — середина ребра A₁B₁. Найдите синус угла между прямой AE и плоскостью BDD₁.

Как всегда, рисуем чертеж и выбираем систему координат

$Eleft ( 1;, frac{1}{2};, 1 right )$

Находим координаты вектора $overrightarrow{AE}left ( 0;, frac{1}{2};, 1 right )$ .

Нужно ли нам уравнение плоскости BDD₁? В общем-то, без него можно обойтись. Ведь эта плоскость является диагональным сечением куба, а значит, нормалью к ней будет любой вектор, ей перпендикулярный. Например, вектор .

Найдем угол между прямой и плоскостью:

$sin, varphi =frac{left | overrightarrow{AC}cdot overrightarrow{AE} right |}{|overrightarrow{AC}|cdot|overrightarrow{AE}|}=frac{2}{2cdot sqrt{2}cdot sqrt{5}}=frac{1}{sqrt{10}}$

Ответ: $frac{1}{sqrt{10}}.$

Расстояние от точки M с координатами x₀, y₀ и z₀ до плоскости α, заданной уравнением Ax + By + Cz + D = 0, можно найти по формуле:

$h=frac{|Ax_{0}+By_{0}+Cz_{0}+D|}{sqrt{A^{2}+B^{2}+C^{2}}}$

7. В основании прямоугольного параллелепипеда BCDA₁B₁C₁D₁ лежит прямоугольник ABCD со сторонами AB = , AD = . Высота параллелепипеда AA₁ = $frac{6}{sqrt{5}}$ . Найдите расстояние от точки A до плоскости A₁DB.

Построим чертеж и выпишем координаты точек:

$A_{1}left ( 0, ;0;, frac{6}{sqrt{5}} right )$

Запишем уравнение плоскости A₁DB. Вы помните, как это делается — по очереди подставляем координаты точек A₁, D и B в уравнение A_x + B_e + C_z + D

$left.begin{matrix} A_{1}\ B\ D end{matrix}right|$ $begin{matrix} frac{6}{sqrt{5}}C+D=0\ sqrt{10}A+D=0\ 3sqrt{10}B+D=0 end{matrix}$

Решим эту систему. Выберем

Тогда

Уравнение плоскости A₁DB имеет вид:

Дальше все просто. Находим расстояние от точки A до плоскости A₁DB:

$h=frac{|Ax_{0}+By_{0}+Cz_{0}+D|}{sqrt{A^{2}+B^{2}+C^{2}}}=frac{6sqrt{10}}{sqrt{50+36+4}}=frac{6sqrt{10}}{sqrt{90}}=2.$

В некоторых задачах по стереометрии требуется найти расстояние от прямой до параллельной ей плоскости. В этом случае можно выбрать любую точку, принадлежащую данной прямой.

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Векторы в пространстве и метод координат» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
08.05.2023

Источник

ЛЕКЦИЯ

по
учебной дисциплине

МАТЕМАТИКА

Тема
№ 2. Основы аналитической геометрии

Занятие
.Плоскость в пространстве

Введение

В лекции рассмотрим
различные виды уравнения плоскости в
пространстве, докажем, что уравнение
первой степени определяет в пространстве
плоскость, по уравнениям плоскостей
научимся определять их взаимное
расположение в пространстве.

1.
Основные понятия

Определение.
Пусть задана прямоугольная система
координат, любая поверхность S
и уравнение

F(x,
y,
z)
= 0
(1)

Будем
говорить, что уравнение является (1)
является уравнением поверхности S
в заданной системе координат, если ему
удовлетворяют координаты каждой точки
этой поверхности и не удовлетворяют
координаты никакой точки, которая не
принадлежит этой поверхности. С точки
зрения данного определения поверхность
есть множество точек пространства R³.

Пример.
Уравнение

x²+ y²+ z²= 5²

поверхность,
которая является сферой радиуса 5, с
центром в точке 0(0,0,0).

2.
Уравнения плоскости в пространстве

2.1. Общее уравнение
плоскости

Определение.
Плоскостью
называется
поверхность, вес точки которой
удовлетворяют общему уравнению:

Ax
+ By
+ Cz
+ D
= 0,

где
А, В, С – координаты вектора
–
вектор нормали
к плоскости.

Возможны
следующие частные случаи:

А
= 0 – плоскость параллельна оси Ох

В
= 0 – плоскость параллельна оси Оу

С
= 0 – плоскость параллельна оси Оz

D
= 0 – плоскость проходит через начало
координат

А
= В = 0 – плоскость параллельна плоскости
хОу

А
= С = 0 – плоскость параллельна плоскости
хОz

В
= С = 0 – плоскость параллельна плоскости
yOz

А
= D
= 0 – плоскость проходит через ось Ох

В
= D
= 0 – плоскость проходит через ось Оу

С
= D
= 0 – плоскость проходит через ось Oz

А
= В = D
= 0 – плоскость совпадает с плоскостью
хОу

А
= С = D
= 0 – плоскость совпадает с плоскостью
xOz

В
= С = D
= 0 – плоскость совпадает с плоскостью
yOz

2.2. Уравнение
плоскости, проходящей через три точки

Для
того, чтобы через три какие- либо точки
пространства можно было провести
единственную плоскость, необходимо,
чтобы эти точки не лежали на одной
прямой.

Рассмотрим
точки М₁(x₁,
y₁,
z₁),
M₂(x₂,
y₂,
z₂),
M₃(x₃,
y₃,
z₃)
в общей декартовой системе координат.

Для
того, чтобы произвольная точка М(x,
y,
z)
лежала в одной плоскости с точками М₁,
М₂,
М₃
необходимо, чтобы векторы

были компланарны.

()
= 0

Таким
образом,

Уравнение
плоскости, проходящей через три точки:

2.3.Уравнение
плоскости по двум точкам и вектору,
коллинеарному плоскости.

Пусть
заданы точки М₁(x₁,
y₁,
z₁),
M₂(x₂,
y₂,
z₂)
и вектор
.

Составим
уравнение плоскости, проходящей через
данные точки М₁
и М₂
и произвольную точку М(х, у, z)
параллельно вектору
.

Векторы
и
вектор

должны быть компланарны, т.е.

()
= 0

Уравнение
плоскости:

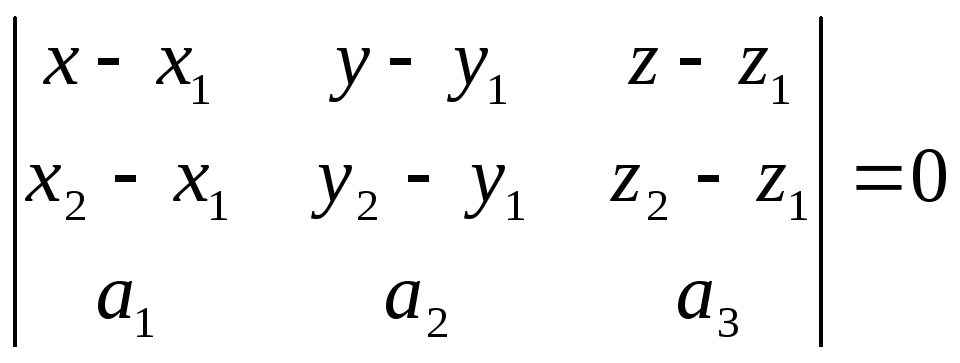
2.4.Уравнение
плоскости по одной точке и двум векторам,

коллинеарным
плоскости.

Пусть
заданы два вектора

и
,
коллинеарные плоскости. Тогда для
произвольной точки М(х,
у, z),
принадлежащей плоскости, векторы

должны быть компланарны.

Уравнение
плоскости:

2.5.Уравнение
плоскости по точке и вектору нормали.

Теорема.
Если в пространстве задана точка М₀(х₀,
у₀,
z₀),
то уравнение плоскости, проходящей
через точку М₀
перпендикулярно вектору нормали
(A,
B,
C)
имеет вид:

A(x
– x₀)
+ B(y
– y₀)
+ C(z
– z₀)
= 0.

Доказательство.
Для произвольной точки М(х, у, z),
принадлежащей плоскости, составим
вектор
.
Т.к. вектор

— вектор нормали, то он перпендикулярен
плоскости, а, следовательно, перпендикулярен
и вектору
.
Тогда
скалярное
произведение

=
0.

Таким
образом, получаем уравнение плоскости

Теорема
доказана.

2.6.Уравнение
плоскости в отрезках.

Если
в общем уравнении Ах
+ Ву + Сz
+ D
= 0 поделить
обе части на –D

заменив
,
получим уравнение плоскости в отрезках:

Числа
a,
b,
c
являются точками пересечения плоскости
соответственно с осями х,
у, z.

2.7.Расстояние от
точки до плоскости.

Расстояние
от произвольной точки М₀(х₀,
у₀,
z₀)
до плоскости Ах+Ву+Сz+D=0
равно:

Пример.
Найти уравнение плоскости, зная, что
точка Р(4; –3; 12) – основание перпендикуляра,
опущенного из начала координат на эту
плоскость.

Таким
образом, A
= 4/13; B
= –3/13; C
= 12/13, воспользуемся формулой:

A(x
– x₀)
+ B(y – y₀)
+ C(z – z₀)
= 0.

Пример.
Найти уравнение плоскости, проходящей
через две точки P(2;
0; –1) и Q(1;
–1; 3) перпендикулярно плоскости 3х + 2у
– z
+ 5 = 0.

Вектор
нормали к плоскости 3х + 2у – z
+ 5 = 0
параллелен
искомой плоскости.

Получаем:

Пример.
Найти уравнение плоскости, проходящей
через точки А(2, –1, 4) и В(3, 2, –1)
перпендикулярно плоскости х
+ у
+ 2z
– 3 = 0.

Искомое
уравнение плоскости имеет вид: Ax
+ By
+ Cz
+ D
= 0, вектор нормали к этой плоскости
(A,
B,
C).
Вектор
(1,
3, –5) принадлежит плоскости. Заданная
нам плоскость, перпендикулярная искомой
имеет вектор нормали
(1,
1, 2). Т.к. точки А и В принадлежат обеим
плоскостям, а плоскости взаимно
перпендикулярны, то

Таким
образом, вектор нормали
(11,
–7, –2). Т.к. точка А принадлежит искомой
плоскости, то ее координаты должны
удовлетворять уравнению этой плоскости,
т.е. 112
+ 71
– 24
+ D
= 0; D
= –21.

Итого,
получаем уравнение плоскости: 11x
– 7y
– 2z
– 21 = 0.

Пример.
Найти уравнение плоскости, зная, что
точка Р(4, -3, 12) – основание перпендикуляра,
опущенного из начала координат на эту
плоскость.

Находим
координаты вектора нормали
=
(4, -3, 12). Искомое уравнение плоскости
имеет вид: 4x
– 3y
+ 12z
+ D
= 0. Для нахождения коэффициента D
подставим в уравнение координаты точки
Р:

16
+ 9 + 144 + D
= 0.

D
= –169.

Итого,
получаем искомое уравнение: 4x
– 3y
+ 12z
– 169 = 0

Пример.
Даны координаты вершин пирамиды А₁(1;
0; 3), A₂(2;
–1; 3), A₃(2;
1; 1), A₄(1;
2; 5).

Найти
длину ребра А₁А₂.

Найти
угол между ребрами А₁А₂
и А₁А₄.

Найти
угол между ребром А₁А₄
и гранью А₁А₂А₃.

Сначала
найдем вектор нормали к грани А₁А₂А₃

как векторное произведение векторов
и.

=
(2–1;
1–0;
1–3)
= (1; 1; –2);

Найдем
угол между вектором нормали и вектором
.

–4
– 4 = –8.

Искомый
угол 
между вектором и плоскостью будет равен

= 90⁰
– .

Найти
площадь грани А₁А₂А₃.

Найти
объем пирамиды.

(ед³).

Найти
уравнение плоскости А₁А₂А₃.

Воспользуемся
формулой уравнения плоскости, проходящей
через три точки.

2x
+ 2y
+ 2z
– 8 = 0

x
+ y
+ z
– 4 = 0;

3.
Взаимное расположение плоскостей

Пусть
заданы две плоскости

3.1.
Угол между плоскостями

₁


0

Рис.
3

Угол
между двумя плоскостями в пространстве

связан с углом между нормалями к этим
плоскостям ₁
соотношением: 
= ₁
или 
= 180⁰
– ₁,
т.е.

cos
= cos₁.

Определим
угол ₁.
Известно, что плоскости могут быть
заданы соотношениями:

где

(A₁,
B₁,
C₁),

(A₂,
B₂,
C₂).

Угол
между векторами нормали найдем из их
скалярного произведения:

Таким
образом, угол между плоскостями находится
по формуле:

Выбор
знака косинуса зависит от того, какой
угол между плоскостями следует найти
– острый, или смежный с ним тупой.

3.2. Условия
параллельности и перпендикулярности
плоскостей.

На
основе полученной выше формулы для
нахождения угла между плоскостями можно
найти условия параллельности и
перпендикулярности плоскостей.

Для
того, чтобы плоскости были перпендикулярны
необходимо и достаточно, чтобы косинус
угла между плоскостями равнялся нулю.
Это условие выполняется, если:

Плоскости
параллельны, векторы нормалей коллинеарны:

.Это
условие выполняется, если:
.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Уравнения плоскости, компланарной двум неколлинеарным векторам

Напомним, что три или более векторов называются компланарными, если существует плоскость, которой они параллельны. Эту плоскость будем называть компланарной заданным векторам.

Направляющими векторами плоскости называются два неколлинеарных вектора, компланарных этой плоскости, т.е. принадлежащих плоскости или параллельных ей.

Пусть в координатном пространстве Oxyz заданы:

а) точка $M_{0}(x_{0},y_{0},z_{0})$ ;

Направляющие векторы плоскости

б) два неколлинеарных вектора $vec{p}_{1}=a_{1}vec{i}+b_{1}vec{j}+c_{1}vec{k},~vec{p}_{2}=a_{2}vec{i}+b_{2}vec{j}+c_{2}vec{k}$ (рис.4.15).

Требуется составить уравнение плоскости, компланарной векторам $vec{p}_{1},,vec{p}_{2}$ и проходящей через точку $M_{0}(x_{0},y_{0},z_{0}).$

Выберем на плоскости произвольную точку M(x,y,z) . Обозначим vec{r}=overrightarrow{OM}, $vec{r}_{0}=overrightarrow{OM_{0}},$ — радиус-векторы точек и $M_{0}(x_{0},y_{0},z_{0})$ (рис.4.16).

Условие компланарности векторов $overrightarrow{M_{0}M},,vec{p}_{1},,vec{p}_{2}$ (рис.4.16) можно записать, используя свойства смешанного произведения $langleoverrightarrow{M_{0}M},vec{p}_{1},vec{p}_{2}rangle=0.$ Применяя формулу (1.17), получаем уравнение плоскости, проходящей через заданную точку и компланарной двум неколлинеарным векторам:

$begin{vmatrix}x-x_{0}&y-y_{0}&z-z_{0}\a_{1}&b_{1}&c_{1}\a_{2}&b_{2}&c_{2}end{vmatrix}=0,.$

(4.18)

Параметрическое уравнение плоскости

Пусть в координатном пространстве Oxyz заданы:

а) точка $M_{0}(x_{0},y_{0},z_{0})$ ;

б) два неколлинеарных вектора $vec{p}_{1}=a_{1}vec{i}+b_{1}vec{j}+c_{1}vec{k},~vec{p}_{2}=a_{2}vec{i}+b_{2}vec{j}+c_{2}vec{k}$ (рис.4.15).

Требуется составить параметрическое уравнение вида (4.10) плоскости, компланарной векторам $vec{p}_{1},,vec{p}_{2}$ и проходящей через точку $M_{0}(x_{0},y_{0},z_{0}).$

Выберем на плоскости произвольную точку M(x,y,z) . Обозначим vec{r}=overrightarrow{OM}, $vec{r}_{0}=overrightarrow{OM_{0}}$ -радиус-векторы точек и $M_{0}(x_{0},y_{0},z_{0})$ (рис.4.16).

Точка принадлежит заданной плоскости тогда и только тогда, когда векторы $overrightarrow{M_{0}M},$ $vec{p}_{1}$ и $vec{p}_{2}$ компланарны (см. разд. 1.3.2). Запишем условие компланарности: $overrightarrow{M_{0}M}=t_{1}vec{p}_{1}+t_{2}vec{p}_{2},$ где $t_{1},,t_{2}$ — некоторые действительные числа (параметры). Учитывая, что $overrightarrow{M_{0}M}=vec{r}-vec{r}_{0},$ получим векторное параметрическое уравнение плоскости:

$vec{r}=vec{r}_{0}+t_{1}cdotvec{p}_{1}+t_{2}vec{p}_{2}, quad t_{1},t_{2}inmathbb{R},,$

(4.19)

где $vec{p}_{1},,vec{p}_{2}$ — направляющие векторы плоскости, а $vec{r}_{0}$ — радиус-вектор точки, принадлежащей плоскости.

Координатная форма записи уравнения (4.19) называется параметрическим уравнением плоскости:

$begin{cases} x= x_{0}+a_{1}cdot t_{1}+a_{2}cdot t_{2},\ y= y_{0}+b_{1}cdot t_{1}+b_{2}cdot t_{2},\ z= z_{0}+c_{1}cdot t_{1}+c_{2}cdot t_{2}, end{cases}t_{1},t_{2}inmathbb{R},,$

(4.20)

где $a_{1},b_{1},c_{1}$ и $a_{2},b_{2},c_{2}$ — координаты направляющих векторов $vec{p}_{1}$ и $vec{p}_{2}$ соответственно. Параметры $t_{1},,t_{2}$ в уравнениях (4.19),(4.20) имеют следующий геометрический смысл: величины $t_{1},,t_{2}$ пропорциональны расстоянию от заданной точки $M_{0}(x_{0},y_{0},z_{0})$ до точки M(x,y,z), принадлежащей плоскости. При $t_{1}=t_{2}=0$ точка совпадает с заданной точкой $M_{0}$ . При возрастании $t_{1}$ (или $t_{2}$ ) точка перемещается в направлении вектора $vec{p}_{1}$ (или $vec{p}_{2}$ ), а при убывании $t_{1}$ (или $t_{2}$ ) — в противоположном направлении.

Замечания 4.4.

1. Поскольку направляющие векторы плоскости неколлинеарны, то они ненулевые.

2. Любой вектор vec{p}=avec{i}+bvec{j}+cvec{k} , коллинеарный плоскости, ортогонален нормальному вектору vec{n}=Avec{i}+Bvec{j}+Cvec{k} для этой плоскости. Поэтому их скалярное произведение равно нулю:

langlevec{p},vec{n}rangle=acdot A+bcdot B+ccdot C=0.

Следовательно, координаты $a_{1},b_{1},c_{1}$ и $a_{2},b_{2},c_{2}$ направляющих векторов $vec{p}_{1}$ и $vec{p}_{2}$ плоскости и ее нормали связаны однородными уравнениями:

$a_{1}cdot A+b_{1}cdot B+c_{1}cdot C=0, quad a_{2}cdot A+b_{2}cdot B+c_{2}cdot C=0.$

3. Направляющие векторы плоскости определяются неоднозначно.

4. Для перехода от общего уравнения плоскости (4.15) Acdot x+Bcdot y+Ccdot z+D=0 к параметрическому (4.20) нужно выполнить следующие действия:

1) найти любое решение $(x_{0},y_{0},z_{0})$ уравнения Ax+By+Cz+D=0, определяя тем самым координаты точки $M_{0}(x_{0},y_{0},z_{0}),$ принадлежащей плоскости;

2) найти любые два линейно независимых решения $(a_{1},b_{1},c_{1}),$ $(a_{2},b_{2},c_{2})$ однородного уравнения Acdot a+Bcdot b+Ccdot c=0 определяя тем самым координаты решения $(a_{1},b_{1},c_{1})$ и $(a_{2},b_{2},c_{2})$ направляющих векторов $vec{p}_{1}$ и $vec{p}_{2}$ плоскости;

3) записать параметрическое уравнение (4.20).

5. Чтобы перейти от параметрического уравнения плоскости к общему, достаточно либо записать уравнение (4.18) и раскрыть определитель, либо найти нормаль как результат векторного произведения направляющих векторов:

$vec{n}= Bigl[vec{p}_{1},vec{p}_{2}Bigr]= begin{vmatrix} vec{i}&vec{j}&vec{k}\a_{1}&b_{1}&c_{1}\a_{2}&b_{2}&c_{2} end{vmatrix}= underbrace{begin{vmatrix}b_{1}&c_{1}\b_{2}&c_{2}end{vmatrix}}_{A}cdot vec{i}- underbrace{begin{vmatrix}a_{1}&c_{1}\a_{2}&c_{2}end{vmatrix}}_{B}cdot vec{j}+ underbrace{begin{vmatrix}a_{1}&b_{1}\a_{2}&b_{2}end{vmatrix}}_{C}cdot vec{k},,$

и записать общее уравнение плоскости в форме (4.14):

$Acdot(x-x_{0})+Bcdot(y-y_{0})+Ccdot(z-z_{0})=0,.$

6. Векторное параметрическое уравнение плоскости (4.19), полученное в прямоугольной системе координат, имеет тот же вид в любой другой аффинной системе координат. Геометрический смысл коэффициентов в уравнении остается прежним.

Пример 4.8. В координатном пространстве Oxyz (в прямоугольной системе координат) заданы точки K(1;2;3) и L(5;0;1) (см. рис.4.11). Требуется:

а) составить параметрическое уравнение плоскости, перпендикулярной отрезку и проходящей через его середину;

б) составить общее уравнение плоскости, проходящей через середину отрезка и компланарной радиус-векторам overrightarrow{OK} и overrightarrow{OL}.

Решение. а) Общее уравнение искомой плоскости было получено в примере 4.5: 2x-y-z-3=0. Составим параметрическое уравнение:

1) находим любое решение уравнения 2x-y-z-3=0 , например, $x_{0}=y_{0}=0,$ $z_{0}=-3,$ следовательно, точка $M_{0}(0;0;-3)$ принадлежит плоскости;

2) находим два линейно независимых (непропорциональных) решения однородного уравнения 2x-y-z=0 например (1;1;1) и (0;1;-1), следовательно, векторы $vec{p}_{1}=vec{i}+vec{j}+vec{k},$ $vec{p}_{2}=vec{j}-vec{k},$ являются направляющими для плоскости;

3) записываем параметрическое уравнение плоскости (4.20):

$begin{cases}x=0+1cdot t_{1}+0cdot t_{2},\ y=0+1cdot t_{1}+1cdot t_{2},\ z=-3+1cdot t_{1}+(-1)cdot t_{2}, end{cases}Leftrightarrow quad! begin{cases}x=t_{1},\ y=t_{1}+t_{2},\ z=-3+t_{1}-t_{2},end{cases} t_{1},t_{2}inmathbb{R},.$

б) Координаты середины M(3;1;2) отрезка были найдены в примере 4.5. Нормаль к искомой плоскости получим как векторное произведение ее направляющих векторов overrightarrow{OK}=vec{i}+2vec{j}+3vec{k}, и overrightarrow{OL}=5vec{i}+vec{k},:

$vec{n}= begin{bmatrix}overrightarrow{OK},overrightarrow{OL}end{bmatrix}= begin{vmatrix}vec{i}&vec{j}&vec{k}\ 1&2&3\ 5&0&1end{vmatrix} = 2cdotvec{i}+14cdotvec{j}-10cdotvec{k},.$

Составляем уравнение (4.14):

2cdot(x-3)+14cdot(y-1)-10cdot(z-2)=0 quad Leftrightarrow quad 2cdot x+14cdot y-10cdot z=0.

Тот же результат можно получить, записывая уравнение (4.18):

$begin{vmatrix}x-3&y-1&z-2\ 1&2&3\ 5&0&1end{vmatrix}=0 quad Leftrightarrow quad 2cdot x+14cdot y-10cdot z=0.$

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Кнопка "Поделиться"

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Источник

Нормальный вектор плоскости, координаты нормального вектора плоскости

Нормальный вектор плоскости – определение, примеры, иллюстрации

Координаты нормального вектора плоскости – нахождение координат нормального вектора плоскости из уравнения плоскости

Вектор нормали: расчет и пример

Содержание:

Как получить вектор нормали к плоскости?

Вектор нормали из векторного произведения

пример

Решение

Расчет векторного произведения AB x AC

Уравнение плоскости

Ссылки

Нормальный вектор прямой

Готовые работы на аналогичную тему

Как найти нормаль плоскости

Векторы в пространстве и метод координат

Система координат в пространстве

Плоскость в пространстве задается уравнением:

Для того, чтобы через три какие- либо точки пространства можно было провести единственную плоскость, необходимо, чтобы эти точки не лежали на одной прямой.

3.2. Условия параллельности и перпендикулярности плоскостей.

Уравнения плоскости, компланарной двум неколлинеарным векторам

Параметрическое уравнение плоскости

Для
того, чтобы через три какие- либо точки
пространства можно было провести
единственную плоскость, необходимо,
чтобы эти точки не лежали на одной
прямой.

3.2. Условия
параллельности и перпендикулярности
плоскостей.