Вычисление векторов
Описанная в предыдущей главе модель отражения света никак не связана с видом проецирования (параллельным или перспективным). Она является общей, т. е. может применяться как к плоским, так и к криволинейным поверхностям, причем расстояние между поверхностью и наблюдателем не учитывается. Большая часть вычислений в процессе закрашивания изображений пространственной сцены приходится на определение компонентов векторов, используемых в модели Фонга, и их скалярных произведений. В процессе выполнения этих вычислений часто используются разнообразные упрощения, учитывающие специфику конкретной ситуации. Например, если анализируемая поверхность — плоский многоугольник, то для всех ее точек вектор нормали будет одним и тем же. Если источник света достаточно далеко удален от поверхности, то для всех точек этой поверхности вектор, характеризующий направление падения лучей от этого источника, будет одним и тем же.
В этой главе рассматриваются методы вычисления компонентов векторов для общего случая.
Вектор нормали к поверхности
Вектор нормали на гладкой поверхности существует в каждой ее точке и определяет локальную ориентацию участка поверхности в окрестности этой точки. Метод вычисления компонентов вектора нормали зависит от способа математического описания поверхности. Продемонстрируем, как вычислить нормаль для плоскости и сферы.
Плоскость описывается уравнением
Уравнение плоскости можно записать в виде произведения вектора нормали п в точке Р0 и любого вектора, принадлежащего этой плоскости,
где Р — любая точка (х, у, z) на рассматриваемой плоскости.
Плоскость может быть однозначно задана совокупностью трех точек плоскости не лежащих на одной прямой (неколлинеарных). Для определения нормали можно использовать их векторное произведение
Для любой поверхности в системе компьютерной графики различают внешнюю и внутреннюю стороны. От порядка сомножителей в векторном произведении зависит направление вектора нормали, а следовательно, определение внешней стороны поверхности. Некоторые графические системы автоматически вычисляют вектор нормали, используя первые три вершины в определении многоугольника, полагая его плоским. В библиотеки OpenGL этого не предусмотрено, но существует возможность самостоятельно организовать в программе определение нормали, что позволяет прикладному программисту гибко управлять свойствами модели освещения.
Способ вычисления компонентов вектора нормали к криволинейной поверхности существенно зависит от принятого способа описания поверхности. Покажем несколько способов определения нормали к сферической поверхности единичного радиуса, центр которой совпадает с началом координат. Обычно такая сфера описывается уравнением в неявной форме
или в векторной форме
Нормаль определяется вектором градиента (gradient vector), который представляется в виде матрицы-столбца
Сфера может быть описана и уравнением в параметрической форме. При этом координаты х, у и z любой точки на сферической поверхности представляют собой независимые уравнения от двух параметров и и v
В системах компьютерной графики предпочтение следует отдать параметрической форме, особенно при описании кривых и поверхностей. Один из вариантов описания сферы имеет вид
Изменяя и и v в диапазоне -я/2 дР дР
ститочки/*. Прямые, параллельные векторам — и —, проходятче-
рез точку Р и лежат в касательной плоскости. Векторы — и —
определяются следующим образом:
Вектор нормали формируется как векторное произведение
Подставляя в это уравнение параметрические функции сферической поверхности, получим
Поскольку нас интересует только направление вектора нормали, то для сферы единичного радиуса получим n = Р.
В графической системе основным типом примитива, с которым выполняются все вычисления, являются вершины. Таким образом, и вектор нормали следует формировать достаточно близко к той точке, нормаль в которой нас интересует. В рамках конвейерной архитектуры графических систем организовать такое вычисление довольно сложно, поскольку по «конвейеру» точки следуют одна за другой. Поэтому в большинстве графических систем программисту приходится самостоятельно организовывать вычисление векторов нормалей в прикладной программе.
Вектор нормали: расчет и пример
Содержание:
В нормальный вектор Он определяет направление, перпендикулярное рассматриваемому геометрическому объекту, который может быть, например, кривой, плоскостью или поверхностью.
Это очень полезная концепция для позиционирования движущейся частицы или какой-либо поверхности в пространстве. На следующем графике можно увидеть, как вектор нормали к произвольной кривой C:
Рассмотрим точку P на кривой C. Точка может представлять движущуюся частицу, которая движется по траектории C. Касательная линия к кривой в точке P нарисована красным.
Обратите внимание, что вектор Т касается C в каждой точке, а вектор N перпендикулярно Т y указывает на центр воображаемого круга, дуга которого является сегментом C. Векторы выделены жирным шрифтом в печатном тексте, чтобы отличать их от других не векторных величин.
Вектор Т он всегда указывает, куда движется частица, следовательно, указывает ее скорость. Вместо вектора N всегда указывает в том направлении, в котором вращается частица, отмечая, таким образом, вогнутость кривой C.
Как получить вектор нормали к плоскости?
Вектор нормали не обязательно является единичным вектором, то есть вектором с модулем 1, но если это так, он называется нормальный единичный вектор.
Во многих приложениях необходимо знать вектор нормали к плоскости вместо кривой. Этот вектор показывает ориентацию указанной плоскости в пространстве. Например, рассмотрим самолет п (желтый) рисунка:
К этой плоскости есть два нормальных вектора: п1 Y п2. Использование того или другого будет зависеть от контекста, в котором находится упомянутый самолет. Получить вектор нормали к плоскости очень просто, если вы знаете его уравнение:
ах + по + cz + d = 0, с участием к, б, c Y d вещественные числа.
Ну, нормальный вектор к указанной плоскости задается следующим образом:
N = а я + b j + c k
Здесь вектор N Он выражается через единичные векторы и перпендикулярно друг другу. я, j Y k, направленных по трем направлениям, определяющим пространство X и Zсм. рисунок 2 справа.
Вектор нормали из векторного произведения
Очень простая процедура нахождения вектора нормали использует свойства векторного произведения между двумя векторами.
Как известно, три разные точки, не лежащие на одной прямой, определяют плоскость Р. Теперь можно получить два вектора или Y v которые принадлежат упомянутой плоскости, имеющей эти три точки.
Когда у вас есть векторы, векторный продуктили Икс v — операция, результатом которой, в свою очередь, является вектор, который имеет свойство быть перпендикулярным плоскости, определяемой или Y v.
Известный этот вектор, он обозначается как N, и из него можно будет определить уравнение плоскости благодаря уравнению, указанному в предыдущем разделе:
N = или Икс v
На следующем рисунке показана описанная процедура:
пример
Найти уравнение плоскости, определяемой точками A (2,1,3); В (0,1,1); С (4.2.1).
Решение
Это упражнение иллюстрирует описанную выше процедуру. Имея 3 точки, одна из них выбирается как общее начало двух векторов, которые принадлежат плоскости, определенной этими точками. Например, точка A устанавливается в качестве начала координат и строятся векторы AB Y AC.
Вектор AB — вектор, начало которого — точка A, а конец — точка B. Координаты вектора AB определяются соответственно вычитанием координат B из координат A:
AB = (0-2) я + (1-1) j + (1-3) k = -2я + 0j -2 k
Таким же образом поступаем и находим вектор AC:
AC = (4-2) я + (2-1) j + (1-3) k = 2я + j -2 k
Расчет векторного произведения AB x AC
Существует несколько процедур для нахождения векторного произведения между двумя векторами. В этом примере используется мнемоническая процедура, которая использует следующий рисунок для поиска векторных произведений между единичными векторами. я, j Y k:
Для начала следует помнить, что векторные произведения между параллельными векторами равны нулю, поэтому:
я Икс я = 0; j Икс j = 0; k Икс k = 0
А поскольку векторное произведение — это еще один вектор, перпендикулярный участвующим векторам, двигаясь в направлении красной стрелки, мы имеем:
я Икс j = k ; j Икс k = я; k Икс я = j
Если вам нужно двигаться в направлении, противоположном стрелке, добавьте знак (-):
j Икс я = – k; k Икс j = –я; я Икс k = –j
Всего можно составить 9 векторных произведений с единичными векторами. я, j Y k, из которых 3 будут нулевыми.
AB Икс AC = (-2я + 0j -2 k) х (2я + j -2 k)= -4(я Икс я) -2(я Икс j)+4 (я Икс k)+0 (j Икс я) + 0 (j Икс j) – 0 (j Икс k) – 4 (k Икс я)-2 (k Икс j) + 4 (k Икс k) = -2k-4j-4j+2я = 2я -8j-2k
Уравнение плоскости
Вектор N был определен с помощью предварительно рассчитанного векторного произведения:
N = 2я -8j-2k
Следовательно, a = 2, b = -8, c = -2, искомая плоскость:
ах + по + cz + d = 0 → 2x-8y-2z + d = 0
Значение d. Это легко сделать, если значения любой из имеющихся точек A, B или C подставить в уравнение плоскости. Выбор C, например:
2,4 — 8,2 — 2,1 + d = 0
Вкратце, искомая карта:
Пытливый читатель может задаться вопросом, был бы такой же результат, если бы вместо выполнения AB Икс AC они бы предпочли произвести AC Икс AB. Ответ: да, плоскость, определяемая этими тремя точками, уникальна и имеет два вектора нормали, как показано на рисунке 2.
Что касается точки, выбранной в качестве исходной точки векторов, нет проблем с выбором любого из двух других.
Ссылки
- Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 1. Кинематика. Отредактировал Дуглас Фигероа (USB). 31-62.
- Нахождение нормали к плоскости. Получено с: web.ma.utexas.edu.
- Ларсон, Р. (1986). Исчисление и аналитическая геометрия. Мак Гроу Хилл. 616-647.
- Линии и плоскости в R 3. Получено с: math.harvard.edu.
- Нормальный вектор. Получено с сайта mathworld.wolfram.com.
Конструктивная апраксия: симптомы, причины и лечение
Страх перед женщинами: виды, причины и способы его преодоления
http://ru1.warbletoncouncil.org/vector-normal-6378
Этот проект относится к учебнику《Ray Tracing in One Weekend》, После прохождения всех примеров, я добавил свое собственное понимание написания заметок, проект использует многопоточность ЦП для ускорения и добавляет отображение прогресса графического интерфейса.
Ссылка на проект:https://github.com/maijiaquan/ray-tracing-with-imgui
оглавление:
«Изучение трассировки лучей за два дня» 1. Введение в проект и вывод изображения ppm
«Изучение трассировки лучей за два дня» 2. Луч, простая камера и фоновый вывод
«Изучение трассировки лучей за два дня» 3. Нормальный вектор сферы и поверхности
«Обучение трассировке лучей за два дня» 4. Распределение по категориям
«Изучение трассировки лучей за два дня» 5. Сглаживание
«Изучение трассировки лучей за два дня» 6. Рассеянный материал.
«Изучение трассировки лучей за два дня» 7. Векторы отражения и металлические материалы
«Изучение трассировки лучей за два дня» 8. Вектор преломления и диэлектрик
«Обучение трассировке лучей за два дня» 9. Камеру можно разместить
«Обучение трассировке лучей за два дня» 10. Размытие в расфокусировке
Обзор последнего раздела
В предыдущем разделе мы использовали начало координат (0,0,0) камеры в качестве отправной точки и испускали луч на каждый пиксель экрана, а также реализовали эффект возврата цвета неба, когда свет не попадает на объект. Но если он попадает в объект, что делать?
Цель этого раздела
Определите, попадает ли луч в сферу, и визуализируйте вектор нормали к поверхности сферы. Эффект такой:
Код этого раздела:main3.cpp
Определите, попадает ли луч в сферу
Все объекты в этом проекте являются сферами, потому что метод расчета попадания луча в сферу очень прост и груб.
Для координат центра сферы
C
=
(
C
x
,
C
y
,
C
z
)
C = (C_x,C_y,C_z)
Радиусом
R
R
Уравнение сферы выглядит следующим образом:
(
x
−
C
x
)
2
+
(
y
−
C
y
)
2
+
(
z
−
C
z
)
2
=
R
2
(x-C_x)^2 + (y-C_y)^2 + (z-C_z)^2 = R^2
Установить точку
P
=
(
x
,
y
,
z
)
P = (x,y,z)
, Тогда вектор из центра сферы в точку P равен
(
p
−
C
)
(p — C)
。
, потому что
(
x
−
C
x
)
2
+
(
y
−
C
y
)
2
+
(
z
−
C
z
)
2
=
(
p
−
C
)
⋅
(
p
−
C
)
(x-C_x)^2 + (y-C_y)^2 + (z-C_z)^2 = (p-C) cdot (p-C)
Таким образом, уравнение мяча можно записать как
(
p
−
C
)
⋅
(
p
−
C
)
=
R
2
(1)
(p-C) cdot (p-C) = R^2 tag 1
Для лучей:
p
(
t
)
=
A
+
t
B
p(t) = A + tB
, Предполагая
t
t
Когда принимается определенное значение, луч может попасть в эту сферу.
Переведите уравнение света в (1), там
(
A
+
t
B
−
C
)
⋅
(
A
+
t
B
−
C
)
=
R
2
(A + tB-C) cdot (A + tB-C) = R^2
Развернуть
t
2
B
⋅
B
+
2
t
B
⋅
(
A
−
C
)
+
(
A
−
C
)
⋅
(
A
−
C
)
−
R
2
=
0
t^2 Bcdot B + 2t B cdot (A-C) + (A-C)cdot(A-C) — R^2 = 0
Деформированный
(
B
⋅
B
)
t
2
+
2
B
⋅
(
A
−
C
)
t
+
(
A
−
C
)
⋅
(
A
−
C
)
−
R
2
=
0
(Bcdot B) t^2 + 2 B cdot (A-C)t + (A-C)cdot(A-C) — R^2 = 0
Это о
t
t
Квадратное уравнение с одним неизвестным.
Предполагать
a
=
(
B
⋅
B
)
a=(Bcdot B)
b
=
2
B
⋅
(
A
−
C
)
b = 2 B cdot (A-C)
c
=
(
A
−
C
)
⋅
(
A
−
C
)
−
R
2
c=(A-C)cdot(A-C) — R^2
то есть дискриминант
Δ
=
b
2
−
4
a
c
=
4
(
B
⋅
(
A
−
C
)
)
2
−
4
(
B
⋅
B
)
(
(
A
−
C
)
⋅
(
A
−
C
)
−
R
2
)
begin{aligned} Delta &=b^2-4ac\ &=4(B cdot (A-C))^2 — 4(Bcdot B)((A-C)cdot(A-C) — R^2) end{aligned}
①. Когда
Δ
>
0
Delta > 0
Когда уравнение имеет два неравных действительных корня, то есть луч проходит через
②. Когда
Δ
=
0
Delta = 0
Когда уравнение имеет два равных действительных корня, то есть луч касается сферы
③. Когда
Δ
<
0
Delta < 0
Когда уравнение не имеет реальных корней, то есть луч не попадает в сферу
Решение уравнения
t
=
−
b
±
Δ
2
a
t = frac{-bpm sqrt{Delta}}{2a}
Если есть положительные корни, возьмите меньший действительный корень
t
=
−
b
−
Δ
2
a
t = frac{-b- sqrt{Delta}}{2a}
В это время координаты конечной точки луча
p
(
t
)
=
A
+
t
B
p(t) = A + tB
, Которое оказывается направлением луча, в котором он попадает в сферу.
Напишите код следующим образом:
// Вводим шар (координаты центра и радиус), луч
// Если луч попадает в мяч, возвращаем меньшее действительное число корня, иначе возвращаем -1
float hit_sphere(const vec3 ¢er, float radius, const ray &r)
{
vec3 oc = r.origin() - center;
float a = dot(r.direction(), r.direction());
float b = 2.0 * dot(oc, r.direction());
float c = dot(oc, oc) - radius * radius;
float discriminant = b * b - 4 * a * c;
if (discriminant < 0) // Нет настоящего корня
{
return -1.0;
}
else
{
return (-b - sqrt(discriminant)) / (2.0 * a); // Возвращаем меньший корень действительного числа
}
}
Вектор нормали к поверхности
В графике векторы нормали к поверхности могут использоваться для достижения зеркального отражения при освещении.
Вектор нормали к поверхности сферы — это начальная точка в точке касания и перпендикулярна касательной плоскости.единичный вектор。
Предположим, луч находится в точке
P
=
(
x
,
y
,
z
)
P = (x,y,z)
Ударьте по сфере, координаты центра сферы равны
C
=
(
C
x
,
C
y
,
C
z
)
C = (C_x,C_y,C_z)
, Тогда вектор нормали к поверхности в это время равен
(
p
−
C
)
(p — C)
。
Затем мы визуализируем вектор нормали к поверхности. Предположим, что есть шар, координаты центра которого (0,0, -1) и радиус 0,5. Мы по-прежнему будем выполнять выборку светового преследования в позиции предыдущего раздела. Если мяч пропущен, вернитесь в небо в соответствии с методом обработки предыдущего раздела. s цвет. Если вы ударили по мячу, вычислите вектор нормали поверхности точки попадания и преобразуйте значение y вектора нормали к поверхности в канал G RGB и используйте зеленый цвет для визуализации.
код показан ниже:
// Испускаем луч и, наконец, выводим образец значения цвета луча на экран
vec3 color(const ray &r)
{
vec3 center = vec3(0,0,-1);
float radius = 0.5;
float t = hit_sphere(center, radius, r);
if (t > 0.0) // Если есть положительные действительные корни
{
vec3 p = r.point_at_parameter(t);
vec3 N = unit_vector(p - center);
vec3 res = 0.5 * vec3(0, (N.y() + 1), 0);
return res;
}
vec3 unit_direction = unit_vector(r.direction());
t = 0.5 * (unit_direction.y() + 1.0);
return (1.0 - t) * vec3(1.0, 1.0, 1.0) + t * vec3(0.5, 0.7, 1.0);
}
Эффект такой:
Объяснение: после получения вектора нормали к поверхности сферы, на которую попадает луч, вектор нормали около «северного полюса» шара составляет приблизительно (0,1,0), а вектор нормали около «южного полюса» Вектор приблизительно равен (0, -1,0). После добавления единицы и уменьшения вдвое он будет масштабирован до (0,1,0) и (0,0,0), которые являются зелеными и черными, как показано на следующем рисунке:
Предполагая, что значения x, y и z вектора нормали к поверхности соответственно преобразованы в соответствующий RGB, вам нужно только изменить код в строке 11 выше, чтобы:
vec3 res = 0.5 * vec3((N.x() + 1), (N.y() + 1), (N.z() + 1));
Эффект такой:
Справочные материалы:《Ray Tracing in One Weekend》
Федеральное агентство по образованию
Государственное
образовательное учреждение
высшего
профессионального образования
ПЕРМСКИЙ
ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Теория поля
Индивидуальные
задания
-
Пособие
разработано ассистентом Оглезневой
А. Н..Одобрено методической комиссией
кафедры «Высшая математика»©
2007, каф. «Высшая математика» ПГТУ
Пермь 2007
Образец решения варианта.
Пример 1: Найти производную скалярного
поляв точке
по направлению
-
вектора
-
нормали к поверхности
:
,
образующей острый угол с положительным
направлением оси -
перпендикулярному к поверхности уровня
функции
,
проходящей через точку.
Решение:
Производную по направлению ищем по
формуле:
,
,
,
-
Найдем вектор
,
т.е.,
Т.к.
,
тогда получаем.
Таким образом
.
-
Найдем вектор
,
т.е.,
где‑ вектор нормали к поверхности
.
Тогда
,
Получаем
,
,
.
Заметим, что
,
то найденный вектор образует острый
угол с осью,
следовательно, требование задачи
выполнено.
Таким образом
.
-
Найдем поверхность уровня функции
,
проходящей через точку:
.
Получаем поверхность
:
.
Аналогично предыдущему пункту находим
вектор
,
где‑ вектор перпендикулярный поверхности
уровня
,
,
,
,
Таким образом
.
Пример 2:Найти градиент скалярного
поля
-
-
.
Построить поверхности уровня для
заданных значений.
Решение
-
По определению градиента скалярного
поля
.
Находим частные производные функции
:
,
,
Таким образом
.
-
Аналогично пункту а), получим:
,
,
Таким образом
.
Построим поверхности уровня:
Тогда
,
‑ конус с вершиной в начале координат.
Если
,
то:
Однополостный Двуполостный
гиперболоид вращения гиперболоид
вращения
вокруг оси
вокруг оси
Пример 3:Найти векторные линии
векторного поля:
Решение:
-
Согласно определению, векторных линий:
,
или.
Решая систему, получаем
.
Таким образом, векторные линии данного
поля представляют собой окружности с
центрами на оси,
лежащие в плоскостях, перпендикулярных
этой оси.
-
Аналогично предыдущему пункту, составляем
систему
.
Решим ее методом составления интегрируемых
комбинаций:
Равенство
образует первую интегрируемую комбинацию.
Получаем.
Для получения еще одной интегрируемой
комбинации используем свойство пропорции:.
Тогда, в нашем случае
.
Интегрируя данное равенство, получаем.
Таким образом, векторные линии задаются
системой:
Т.е. векторные линии данного поля являются
линиями пересечения гиперболических
цилиндров
с плоскостями
.
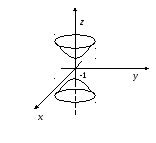
Пример 4.Вычислить поток векторного
полячерез внешнюю сторону боковой поверхности
цилиндра,
ограниченного плоскостями.
Решение:
Вычислим поток векторного поля по
формуле:
,
где‑ нормальный единичный вектор к
поверхности.
Найдем вектор.
Запишем уравнение поверхностив неявном виде:
.
Тогда
.
Т.к.(по условию задачи), то
образует острый угол с осью
:
Следовательно,
.
Поток векторного поля
.
Спроектируем поверхность:
на плоскость
,
получим область,
ограниченную линиями:.
=
Таким образом,

подстановку,
получаем) =.
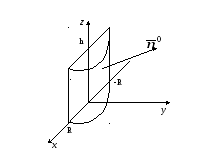
Пример 5.Вычислить поток векторного
поля
через внешнюю сторону части поверхности
,
расположенной над плоскостью.
Решение:
Замкнем данную поверхность куском
плоскости
,
который ограничен окружностью.
Тогда можем применить формулу
Гаусса-Остроградского.
Пусть
‑
объем полученного тела, ограниченного
замкнутой кусочно-гладкой поверхностью,
состоящей из частипараболоида вращения
и части
плоскости
.
Поток данного векторного поля через
поверхность
по теореме Гаусса-Остроградского равен:
,
где.
.
Следовательно, поток
.
В силу аддитивности потока будем иметь
Отсюда искомый поток
Найдем
.
Так как на плоскости,
имеем
,
и тогда
Таким образом, поток
через круг
будет равен площади круга
:
.
Искомый поток .
Пример 6.Вычислить работу векторного
полявдоль линии
,
являющейся пересечением параболического
цилиндрас плоскостью
от точки
до точки
.
Решение:
Зададим линию
параметрически: положив
,
получим,
а.
Тогда,
,
.
Точкесоответствует значение параметра
,
а точке‑
значение.
Таким образом:
.
Пример 7. Вычислить циркуляцию
векторного поля
вдоль периметра треугольника с вершинами
.
Решение:
По определению циркуляции
,
получаем
.
На отрезке
,
следовательно
.
На отрезке
,
следовательно
.
На отрезке
,
следовательно
.
Следовательно,
Пример 8. Найти циркуляцию векторапо контуру

Решение:
Iспособ.
Контур
— окружность радиуса
,
лежащая в плоскости.
Выберем ориентацию как показано на
рисунке, т.е. против часовой стрелки.
Параметрические уравнения окружности
имеют вид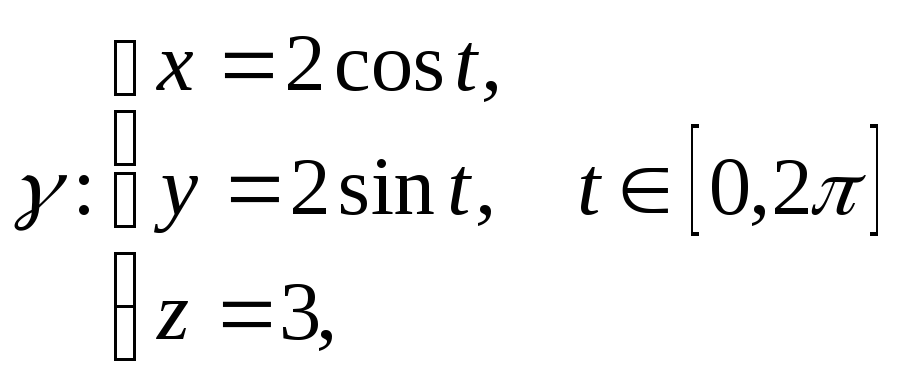
так что
IIспособ.
Для вычисления циркуляции по теореме
Стокса выберем какую-нибудь поверхность
,
натянутую на контур.
Естественно в качествевзять круг, имеющий контур
своей границей. Уравнение поверхности
имеет вид:

Согласно выбранной ориентации контура
нормаль к поверхности необходимо взять
равной.
Далее

В силу теоремы Стокса
Пример 9. Доказать, что векторное
полеявляется потенциальным. Найти его
потенциал.
Решение:
Необходимым и достаточным условием
потенциальности поля является равенство
нулю вихря поля. В нашем случае

Таким образом, поле является потенциальным.
Обозначим
— искомый потенциал. По определению
потенциального поля, поле градиента
искомой функциидолжно совпадать с векторным полем
.
Поэтому
.
Отсюда,
где— некоторая функция аргументов
и
.
Из условия,
можно сделать вывод, что.
Таким образом,.
Неопределенную функциюнайдем из условия
.
Решением последнего уравнения является
функция.
В итоге потенциал имеет вид
.
Пример 10. Пусть— произвольные векторные поля. Показать,
что
обозначено скалярное произведение
векторов).
Решение:
Пусть
и
— произвольные векторные поля. Найдем
векторное произведение.
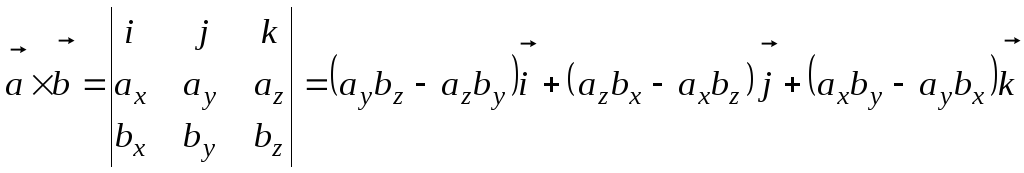
Соседние файлы в папке Индивидуальные_задания
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #