Как найти вектор перемещения точки

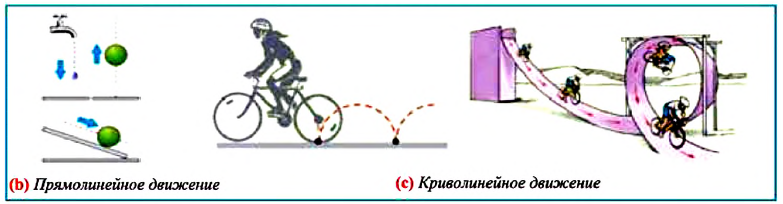
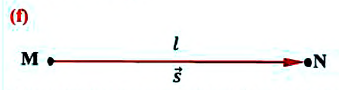
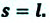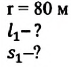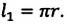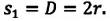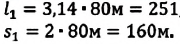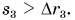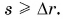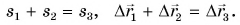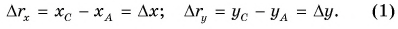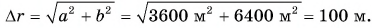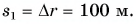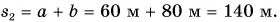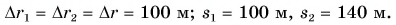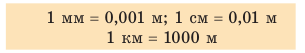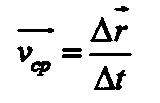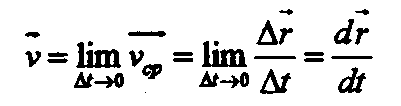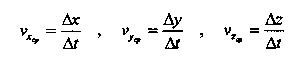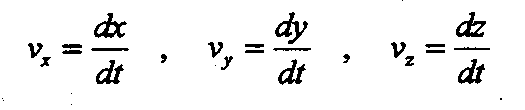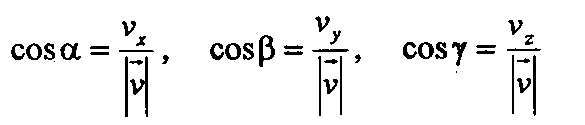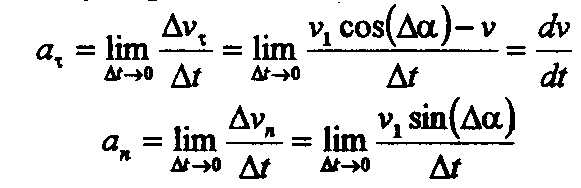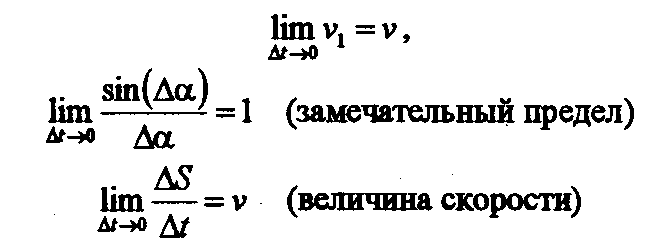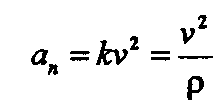Траектория (от позднелатинского trajectories – относящийся к перемещению) – это линия, по которой движется тело (материальная точка). Траектория движения может быть прямой (тело перемещается в одном направлении) и криволинейной, то есть механическое движение может быть прямолинейным и криволинейным.

Траектория прямолинейного движения в данной системе координат – это прямая линия. Например, можно считать, что траектория движения автомобиля по ровной дороге без поворотов является прямолинейной.

Криволинейное движение – это движение тел по окружности, эллипсу, параболе или гиперболе. Пример криволинейного движения – движение точки на колесе движущегося автомобиля или движение автомобиля в повороте.

Движение может быть сложным. Например, траектория движения тела в начале пути может быть прямолинейной, затем криволинейной. Например, автомобиль в начале пути движется по прямой дороге, а затем дорога начинает «петлять» и автомобиль начинает криволинейное движение.

Путь

Путь – это длина траектории. Путь является скалярной величиной и в международной системе единиц СИ измеряется в метрах (м). Расчёт пути выполняется во многих задачах по физике. Некоторые примеры будут рассмотрены далее в этом учебнике.

Вектор перемещения

Вектор перемещения (или просто перемещение) – это направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением (рис. 1.1). Перемещение – величина векторная. Вектор перемещения направлен от начальной точки движения к конечной.

Модуль вектора перемещения (то есть длина отрезка, который соединяет начальную и конечную точки движения) может быть равен пройденному пути или быть меньше пройденного пути. Но никогда модуль вектора перемещения не может быть больше пройденного пути.

Модуль вектора перемещения равен пройденному пути, когда путь совпадает с траекторией (см. разделы Траектория и Путь), например, если из точки А в точку Б автомобиль перемещается по прямой дороге. Модуль вектора перемещения меньше пройденного пути, когда материальная точка движется по криволинейной траектории (рис. 1.1).

Рис. 1.1. Вектор перемещения и пройденный путь.

На рис. 1.1:

Ещё пример. Если автомобиль проедет по кругу один раз, то получится, что точка начала движения совпадёт с точкой конца движения и тогда вектор перемещения будет равен нулю, а пройденный путь будет равен длине окружности. Таким образом, путь и перемещение – это два разных понятия.

Правило сложения векторов

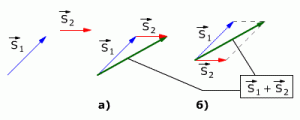
Векторы перемещений складываются геометрически по правилу сложения векторов (правило треугольника или правило параллелограмма, см. рис. 1.2).

Рис. 1.2. Сложение векторов перемещений.

На рис 1.2 показаны правила сложения векторов S1 и S2:

а) Сложение по правилу треугольника
б) Сложение по правилу параллелограмма

Проекции вектора перемещения

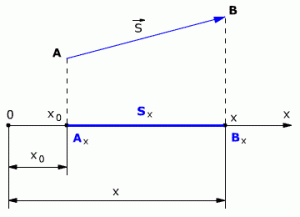
При решении задач по физике часто используют проекции вектора перемещения на координатные оси. Проекции вектора перемещения на координатные оси могут быть выражены через разности координат его конца и начала. Например, если материальная точка переместилась из точки А в точку В, то при этом вектор перемещения  (см.рис. 1.3).

Выберем ось ОХ так, чтобы вектор лежал с этой осью в одной плоскости. Опустим перпендикуляры из точек А и В (из начальной и конечной точек вектора перемещения) до пересечения с осью ОХ. Таким образом мы получим проекции точек А и В на ось Х. Обозначим проекции точек А и В соответственно А_x и В_x. Длина отрезка А_xВ_x на оси ОХ – это и есть проекция вектора перемещения на ось ОХ, то есть

Sx = AxBx

ВАЖНО!
Напоминаю для тех, кто не очень хорошо знает математику: не путайте вектор с проекцией вектора на какую-либо ось (например, S_x). Вектор всегда обозначается буквой или несколькими буквами, над которыми находится стрелка. В некоторых электронных документах стрелку не ставят, так как это может вызвать затруднения при создании электронного документа. В таких случаях ориентируйтесь на содержание статьи, где рядом с буквой может быть написано слово «вектор» или каким-либо другим способом вам указывают на то, что это именно вектор, а не просто отрезок.

Рис. 1.3. Проекция вектора перемещения.

Проекция вектора перемещения на ось ОХ равна разности координат конца и начала вектора, то есть

Sx = x – x0

Аналогично определяются и записываются проекции вектора перемещения на оси OY и OZ:

Sy = y – y0
Sz = z – z0

Здесь x₀, y₀, z₀ — начальные координаты, или координаты начального положения тела (материальной точки); x, y, z — конечные координаты, или координаты последующего положения тела (материальной точки).

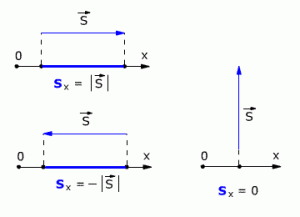
Проекция вектора перемещения считается положительной, если направление вектора и направление координатной оси совпадают (как на рис 1.3). Если направление вектора и направление координатной оси не совпадают (противоположны), то проекция вектора отрицательна (рис. 1.4).

Если вектор перемещения параллелен оси, то модуль его проекции равен модулю самого Вектора. Если вектор перемещения перпендикулярен оси, то модуль его проекции равен нулю (рис. 1.4).

Рис. 1.4. Модули проекции вектора перемещения.

Разность между последующим и начальным значениями какой-нибудь величины называется изменением этой величины. То есть проекция вектора перемещения на координатную ось равна изменению соответствующей координаты. Например, для случая, когда тело перемещается перпендикулярно оси Х (рис. 1.4) получается, что относительно оси Х тело НЕ ПЕРЕМЕЩАЕТСЯ. То есть перемещение тела по оси Х равно нулю.

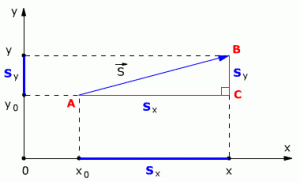
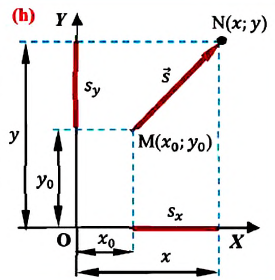
Рассмотрим пример движения тела на плоскости. Начальное положение тела – точка А с координатами х₀ и у₀, то есть А(х₀, у₀). Конечное положение тела – точка В с координатами х и у, то есть В(х, у). Найдём модуль перемещения тела.

Из точек А и В опустим перпендикуляры на оси координат ОХ и OY (рис. 1.5).

Рис. 1.5. Движение тела на плоскости.

Определим проекции вектора перемещения на осях ОХ и OY:

Sx = x – x0
Sy = y – y0

На рис. 1.5 видно, что треугольник АВС – прямоугольный. Из этого следует, что при решении задачи может использоваться теорема Пифагора, с помощью которой можно найти модуль вектора перемещения, так как

АС = sx
CB = sy

По теореме Пифагора

S2 = Sx2 + Sy2

Откуда можно найти модуль вектора перемещения, то есть длину пути тела из точки А в точку В:

Ну и напоследок предлагаю вам закрепить полученные знания и рассчитать несколько примеров на ваше усмотрение. Для этого введите какие-либо цифры в поля координат и нажмите кнопку РАССЧИТАТЬ. Ваш браузер должен поддерживать выполнение сценариев (скриптов) JavaScript и выполнение сценариев должно быть разрешено в настройках вашего браузера, иначе расчет не будет выполнен. В вещественных числах целая и дробная части должны разделяться точкой, например, 10.5.

Траектория, длина пути, вектор перемещения

Траектория движения тела – это линия, которая была описана материальной точкой при перемещении из одной точки в другую с течением времени.

Виды движений тела

Существуют несколько видов движений и траекторий твердого тела:

• поступательное;
• вращательное, то есть движение по окружности;
• плоское, то есть перемещение по плоскости;
• сферическое, характеризующее движение по поверхности сферы;
• свободное, иначе говоря, произвольное.

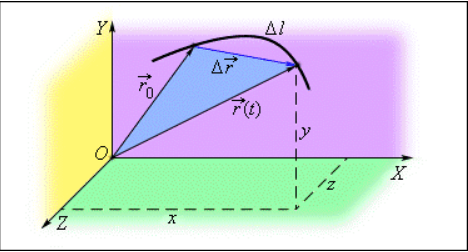
Рисунок 1 . Определение точки при помощи координат x = x ( t ) , y = y ( t ) , z = z ( t ) и радиус-вектора r → ( t ) , r 0 → является радиус-вектором точки в начальный момент времени

Положение материальной точки в пространстве в любой момент времени может быть задано при помощи закона движения, определенный координатным способом, через зависимость координат от времени x = x ( t ) , y = y ( t ) , z = z ( t ) или от времени радиус-вектора r → = r → ( t ) , проведенного из начала координат к заданной точке. Это показано на рисунке 1 .

Перемещение тела

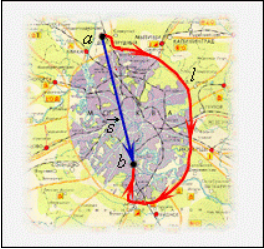
Перемещение тела s → = ∆ r 12 → = r 2 → — r 1 → – направленный отрезок прямой, соединяющий начальную с конечной точкой траектории тела. Значение пройденного пути l равняется длине траектории, пройденной телом за определенный промежуток времени t .

Рисунок 2 . Пройденный путь l и вектор перемещения s → при криволинейном движении тела, a и b – начальная и конечная точки пути, принятые в физике

По рисунку 2 видно, что при движении тела по криволинейной траектории модуль вектора перемещения всегда меньше пройденного пути.

Перемещение принято считать векторной величиной. Этот отрезок имеет направление.

Путь – скалярная величина. Считается числом.

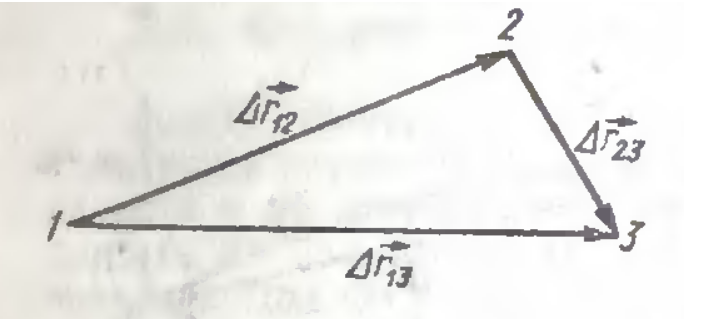
Сумма двух последовательных перемещений из точки 1 в точку 2 и из токи 2 в точку 3 является перемещением из точки 1 в точку 3 , как показано на рисунке 3 .

Рисунок 3 . Сумма двух последовательных перемещений ∆ r → 13 = ∆ r → 12 + ∆ r → 23 = r → 2 — r → 1 + r → 3 — r → 2 = r → 3 — r → 1

Когда радиус-вектор материальной точки в определенный момент времени t является r → ( t ) , в момент t + ∆ t есть r → ( t + ∆ t ) , тогда ее перемещение ∆ r → за время ∆ t равняется ∆ r → = r → ( t + ∆ t ) — r → ( t ) .

Перемещение ∆ r → считается функцией времени t : ∆ r → = ∆ r → ( t ) .

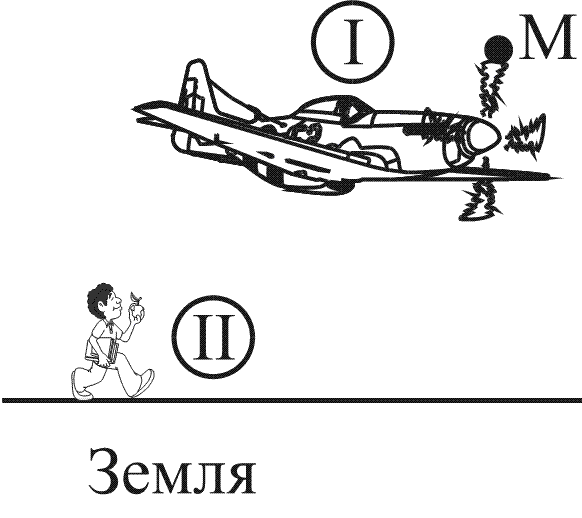
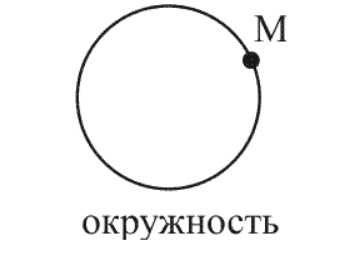
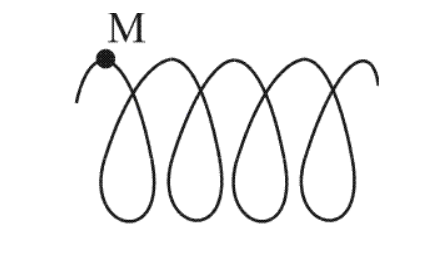
По условию дан движущийся самолет, представленный на рисунке 4 . Определить вид траектории точки М .

Необходимо рассмотреть систему отсчета I , называемую «Самолет» с траекторией движения точки М виде окружности.

Будет задана система отсчета II «Земля» с траекторией движения имеющейся точки М по спирали.

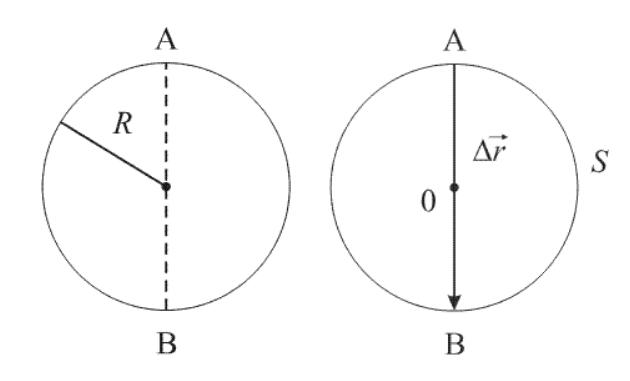
Дана материальная точка, которая совершает движение из А в В . Значение радиуса окружности R = 1 м . Произвести нахождение S , ∆ r → .

Во время движения из А в В точка проходит путь, который равен половине окружности, записываемой формулой:

Подставляем числовые значения и получаем:

S = 3 , 14 · 1 м = 3 , 14 м .

Перемещением ∆ r → в физике считается вектор, соединяющий начальное положение материальной точки с конечным, то есть А с В .

Вектор скорости и ускорения материальной точки и их модули. Пример решения задач.

В очередной раз меня попросили решить пару задачек по физике, и я вдруг обнаружил, что не могу решить их с ходу. Немного погуглив, я обнаружил, что сайты в топе выдачи содержат сканы одного и того же учебника и не описывают конкретных примеров решений задачи о том, как найти вектор скорости и ускорения материальной точки. По-этому я решил поделиться с миром примером своего решения.

Траектория движения материальной точки через радиус-вектор

Подзабыв этот раздел математики, в моей памяти уравнения движения материальной точки всегда представлялись при помощи знакомой всем нам зависимости y(x) , и взглянув на текст задачи, я немного опешил когда увидел векторы. Оказалось, что существует представление траектории материальной точки при помощи радиус-вектора – вектора, задающего положение точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Формула траектория движения материальной точки помимо радиус-вектора описывается так же ортами – единичными векторами i, j , k в нашем случае совпадающими с осями системы координат. И, наконец, рассмотрим пример уравнения траектории материальной точки (в двумерном пространстве):

Что интересного в данном примере? Траектория движения точки задается синусами и косинусами, как вы думаете, как будет выглядеть график в всем нам знакомом представлении y(x) ? “Наверное какой-то жуткий”, подумали вы, но все не так сложно как кажется! Попробуем построить траекторию движения материальной точки y(x), если она движется по представленному выше закону:

Здесь я заметил квадрат косинуса, если вы в каком-нибудь примере видите квадрат синуса или косинуса, это значит что нужно применять основное тригонометрическое тождество, что я и сделал (вторая формула) и преобразовал формулу координаты y, чтобы вместо синуса подставить в нее формулу изменения x:

В итоге жуткий закон движения точки оказался обычной параболой, ветви которой направлены вниз. Надеюсь, вы поняли примерный алгоритм построения зависимости y(x) из представления движения через радиус-вектор. Теперь перейдем к нашему главному вопросу: как же найти вектор скорости и ускорения материальной точки, а так же их модули.

Вектор скорости материальной точки

Всем известно, что скорость материальной точки – это величина пройденного пути точкой за единицу времени, то есть производная от формулы закона движения. Чтобы найти вектор скорости нужно взять производную по времени. Давайте рассмотрим конкретный пример нахождения вектора скорости.

Пример нахождения вектора скорости

Имеем закон перемещения материальной точки:

Теперь нужно взять производную от этого многочлена, если вы забыли как это делается, то вот вам таблица производных различных функций. В итоге вектор скорости будет иметь следующий вид:

Все оказалось проще, чем вы думали, теперь найдем вектор ускорения материальной точки по тому же самому закону, представленному выше.

Как найти вектор ускорения материальной точки

Вектор ускорения точки это векторная величина, характеризующая изменение с течением времени модуля и направления скорости точки. Чтобы найти вектор ускорения материальной точки в нашем примере, нужно взять производную, но уже от формулы вектора скорости, представленной чуть выше:

Модуль вектора скорости точки

Теперь найдем модуль вектора скорости материальной точки. Как вы знаете из 9-го класса, модуль вектора – это его длина, в прямоугольных декартовых координатах равна квадратному корню из суммы квадратов его координат. И откуда же из полученного нами выше вектора скорости взять его координаты спросите вы? Все очень просто:

Теперь достаточно только подставить время, указанное в задаче и получить конкретное числовое значение.

Модуль вектора ускорения

Как вы поняли из написанного выше (и из 9-го класса), нахождение модуля вектора ускорения происходит тем же образом, что и модуля вектора скорости: извлекаем корень квадратный из суммы квадратов координат вектора, все просто! Ну и вот вам, конечно же, пример:

Как вы видите, ускорение материальной точки по заданному выше закону не зависит от времени и имеет постоянную величину и направление.

Еще примеры решений задачи нахождения вектора скорости и ускорения

А вот тут вы можете найти примеры решения и других задач по физике на тему “механика твердых тел”. А для тех, кто не совсем понял как найти вектор скорости и ускорения, вот вам еще парочка примеров из сети без всяких лишних объяснений, надеюсь, они вам помогут.

Если у вас возникли какие-нибудь вопросы, вы можете задать их в комментариях.

Способы описания движения. Векторный способ. Координатный способ

По этой ссылке вы найдёте полный курс лекций по математике:

кинематике существуют три способа аналитического описания движения материальной точки в пространстве. Рассмотрим их, ограничившись случаем движения материальной точки на плоскости, что позволит нам при выборе системы отсчёта задавать лишь две координатные оси. Рис. 1 Рис. 2 1.

Векторный способ. В этом способе положение материальной точки А задаётся с помощью так называемого радиус-вектора г, который представляет совой вектор, проведённый из точки О, соответствующей началу отсчёта выбранной системы координат, в интересующую нас точку А (рис. 1). В процессе движения материальной точки её радиус-вектор может изменяться как по модулю, так и по направлению, являясь функцией времени г = r(t).

Геометрическое место концов радиус-вектора г (t) называют траекторией точки А. В известном смысле траектория движения представляет собой след (явный или воображаемый), который «оставляет за собой» точка А после прохождения той или иной области пространства. Понятно, что геометрическая форма траектории зависит от выбора системы отсчёта, относительно которой ведётся наблюдение за движением точки.

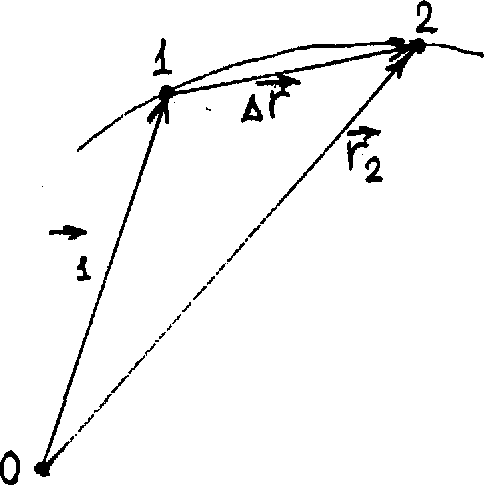
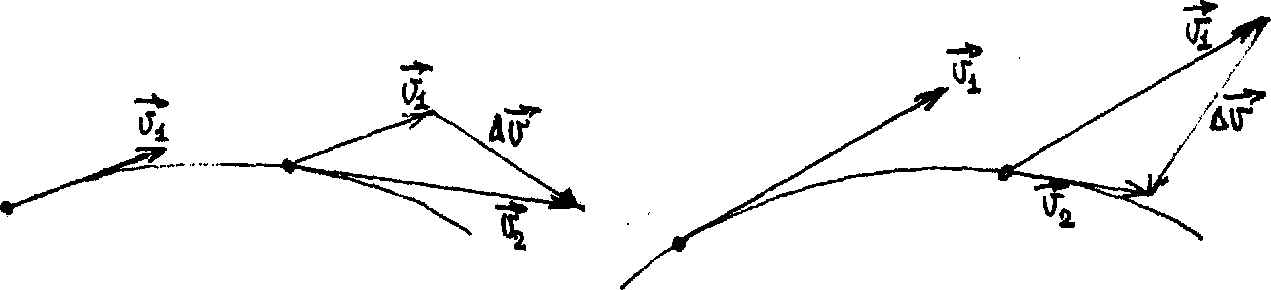
Пусть в процессе движения по некоторой траектории в выбранной системе отсчёта за промежуток времени At тело (точка А) переместилось из начального положения 1 с радиус-вектором Т в конечное положение 2 с радиус-вектором Т (рис. 2). Приращение А г радиус-вектора тела в таком случае равно: Вектор Аг, соединяющий начальное и конечное положения тела, называют перемещением тела. Отношение Аг/At называют средней скоростью (средним вектором скорости) vcp тела за время At: Способы описания движения.

Векторный способ. Координатный способ. Естественный (или траекторный) способ Вектор vcp колли неарен и сонаправлен с вектором Аг, так как отличается от последнего лишь скалярным неотрицательным множителем 1 / Аг. Предложенное определение средней скорости справедливо для любых значений At, кроме Д/ = 0. Однако ничто не мешает брать промежуток времени At сколь угодно малым, но отличным от нуля.

Для точного описания движения вводят понятие мгновенной скорости, то есть скорости в конкретный момент времени t или в конкретной точке траектории. С этой целью промежуток времени At устремляют к нулю. Вместе с ним будет стремиться к нулю и перемещение Аг. При этом отношение А/ / At стремится к определённому значению, не зависящему от At. Величина, к которой стремится отношение Аг / At при стремлении At к нулю, называется мгновенной скоростью v: Теперь заметим, что чем меньше At, тем ближе направление Аг к направлению касательной к траектории в данной точке.

Следовательно, вектор мгновенной скорости направлен по касательной к траектории в данной точке в сторону движения тела. В дальнейшем там, где это не повлечёт недоразумений, мы будем опускать прилагательное «мгновенная» и говорить просто о скорости v тела (материальной точки). Движение тела принято характеризовать также ускорением, по которому судят об изменении скорости в процессе движения.

Его определяют через отношение приращения вектора скорости Av тела к промежутку времени А/, в течение которого это приращение произошло.

Ускорением а тела называется величина, к которой стремится отношение Av / At при стремлении к нулю знаменателя At: При уменьшении At ориентация вектора Av будет приближаться к определённому направлению, которое принимается за направление вектора ускорения а . Заметим, что ускорение направлено в сторону малого приращения скорости, а не в сторону самой скорости! Способы описания движения. Векторный способ. Координатный способ.

Возможно вам будут полезны данные страницы:

Естественный (или траекторный) способ Таким образом, зная зависимость г(/), можно найти скорость v и ускорение а тела в каждый момент времени. В этой связи возникает и обратная задача о нахождении скорости v(t) и радиус-вектора r(t) по известной зависимости от времени ускорения а . Для однозначного решения этой задачи необходимо знать начальные условия, т. е. скорость v0 и радиус-вектор г0 тела в начальный момент времени / = 0.

Напомним, что в системе СИ единицами длины, скорости и ускорения являются соответственно метр (м), метр в секунду (м/с) и метр на секунду в квадрате (м/с2 2. Координатный способ. В этом способе положение материальной точки А на плоскости в произвольный момент времени t определяется двумя координатами хну, которые представляют собой проекции радиус-вектора г тела на оси Ох и Оу соответственно (рис. 3). При движении тела его координаты изменяются со временем, т. е. являются функциями V= y(t).

Если эти функции известны

то они определяют положение тела на плоскости в любой момент времени. В свою очередь, вектор скорости v можно спроецировать на оси координат и определить таким образом скорости i и v.. изменения координат тела (рис. 4). В самом деле, vx и vy будут равны значениям, к которым стремятся соответственно отношения Ах/А t и Ay/At при стремлении к нулю промежутка времени At. Аналогично с помощью проецирования вектора а определяются ускорения ах и ах тела по направлениям координатных осей.

Таким образом, зная зависимости л(/) и >>(/), можно найти не только положение тела, но и проекции его скорости и ускорения, а следовательно, модуль и направление векторов v и а в любой момент времени. Например, модуль вектора скорости будет равен v=yjvx2+vv2 , а его направление может быть задано углом между этим вектором и любой осью координат. Так, угол а между вектором v и осью Ох определяется отношением tga = vy!vx. Аналогичными формулами определяются модуль и направление вектора а .

Обратная задача — нахождение скорости и зависимостей x(t) и y(t) по заданному ускорению — будет иметь однозначное решение, если кроме ускорения заданы ещё и начальные условия: проекции скорости и координаты точки в начальный момент времени t = 0. 3. Естественный (или траекторный) сносов. Этот способ применяют тогда, когда траектория материальной точки известна заранее.

На заданной траектории LM (рис. 5) выбирают начало отсчёта — неподвижную точку О, а положение движущейся материальной точки А определяют при помощи так называемой дуговой координаты /, которая представляет собой расстояние вдоль траектории от выбранного начала отсчёта О до точки А. При этом положительное направление отсчёта координаты / выбирают произвольно, по соображениям удобства, например так, как рис ^ показано стрелкой на рисунке 5.

Движение тела определено, если известны его траектория, начало отсчёта О, положительное направление отсчёта дуговой координаты I и зависимость l(t). Следующие два важных механических понятия — это пройденный путь и средняя путевая скорость. По определению, путь AS — это длина участка траектории, пройденного телом за промежуток времени At. Ясно, что пройденный путь — величина скалярная и неотрицательная, а потому его нельзя сравнивать с перемещением А г, представляющем собой вектор.

Сравнивать можно только путь AS и модуль перемещения Аг . Очевидно, что AS > |Аг|. Средней путевой скоростью г>ср тела называют отношение пути AS к промежутку времени At, в течение которого этот путь был пройден: Определённая ранее средняя скорость vc? (см. формулу (1)) и средняя путевая скорость отличаются друг от друга так же, как Аг отличается от AS, но при этом важно понимать, что обе средние скорости имеют смысл только тогда, когда указан промежуток времени усреднения At.

Само слово «средняя» означает усреднение по времени. Пример 1. Городской троллейбус утром вышел на маршрут, а через 8 часов, проехав в общей сложности 72 км, возвратился в парк и занял своё обычное место на стоянке. Какова средняя скорость vcp и средняя путевая скорость г>ср троллейбуса? Способы описания движения.

Векторный способ. Координатный способ. Естественный (или траекторный) способ Решение. Поскольку начальное и конечное положения троллейбуса совпадают, то его перемещение А г равно нулю Аг = 0, следовательно, = 0 . Но средняя путевая скорость троллейбуса не vcp=Ar/At = 0 и рср равна нулю.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Содержание:

Путь и перемещение:

Вы знаете, что любой вид движения совершается по определенной траектории.

Траектория — это линия, которую описывает материальная точка при своем движении в данной системе отсчета. Эта линия может быть и невидима, например, траектория движения рыбы в воде, самолета в небе, пчелы в воздухе и др., которые можно только вообразить. По форме траектории механическое движение делится на прямолинейное и криволинейное.

Движение, траектория которого представляет собой прямую линию относительно данной системы отсчета, называется прямолинейным движением (b), а движение, траектория которого кривая линия, — криволинейным (с).

Длина траектории движения материальной точки, называется пройденным путем. Пройденный путь является положительной скалярной величиной, обозначается буквой

Для полного описания движения материальной точки необходимо определить изменение его положения в пространстве с течением времени, т.е. определить изменение координат материальной точки, или же изменение его радиус-вектора.

Изменение любой физической величины равно разности его конечного и начального значений и обозначается знаком (буква греч. алфавита) перед этой величиной.

Изменение координат материальной точки во время движения

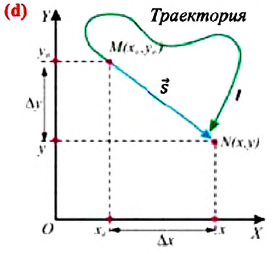
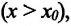
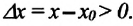
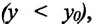
Изменение координат материальной точки во время движения может быть, как положительным, так и отрицательным. Например, предположим, что муравей, двигаясь по показанной на рисунке траектории, попадает из точки М в точку N (d). Так как координата муравья по оси X увеличивается то изменение координаты по этой оси будет положительным: Координата же муравья по оси У уменьшается поэтому изменение его координаты по этой оси будет отрицательным:

Изменение радиус-вектора материальной точки во время движения

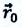
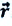
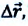
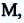
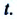
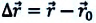
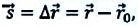
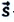
На следующем рисунке представлены радиус-векторы и  начального и конечного положения, материальной точки (муравья) соответственно (е). Вектор соединяющий концы этих радиус-векторов называют перемещением данной материальной точки за промежуток времени Согласно правилу сложения векторов: Из последнего выражения получается, или  где  — перемещение материальной точки.

Перемещение — это направленный отрезок прямой, соединяющий начальное положение движущейся материальной точки с ее конечным положением. Перемещение — векторная величина.

Векторная величина — это величина, определяемая, кроме числового значения (модуля), также и направлением.

К вектору перемещения, как векторной величине, можно применить известные действия над векторами — сложение и вычитание векторов, определение результирующего вектора методом треугольника и параллелограмма.

Единицей измерения перемещения, как и пути, в СИ является метр, однако, перемещение имеет отличающийся физический смысл: перемещение показывает, на какое расстояние и в каком направлении изменилось начальное положение материальной точки за данный промежуток времени.

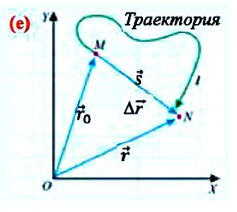
Внимание! Только при прямолинейном движении без изменения направлении, модуль перемещения равен пройденному пути, во всех остальных случаях (при изменении направления прямолинейного движения, криволинейном движении) пройденный путь больше модуля перемещения (е).

Материальная точка прошла расстояние 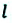от точки М до точки N по прямой линии. В этом случае пройденный путь равен модулю перемещения:

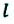
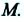
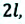
Материальная точка прошла расстояние от точки М до точки N по прямой линии, а затем по этой же линии вернулась назад в точку В этом случае материальная точка прошла путь, равный а модуль перемещения равен нулю:

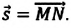
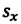
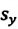
Если при движении материальной точки на плоскости известны его начальные координаты и вектор перемещения, то можно определить координаты конечного положения точки. Например, предположим, что материальная точка совершила перемещение  Опуская перпендикуляры на оси ОХ и OY из начала и конца этого вектора, получаем проекции перемещения  и  (h). Как видно из рисунка, эти проекции равны разности начальных и конечных координат материальной точки: 

Одинаковы ли путь и перемещение

Задача:

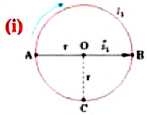
Велосипедист движется по круговому велотреку радиусом 80 м. Он стартует из точки А. Определите путь и перемещение велосипедиста при первом прохождении точки В (i).

Дано:

Решение:

Пройденный путь 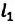 равен длине дуги:

Модуль перемещения же равен диаметру окружности: 

Вычисление:

Что такое путь и перемещение

Автобус отправился из Москвы в 9 часов утра. Можно ли определить, где находился автобус в 11 часов, если известно, что он проделал путь

Конечно, нет. Ясно лишь, что в 11 часов он находился в месте, удаленном от Минска не более чем на 100 км (т. е. внутри окружности, изображенной на рисунке 37). Не исключено, что к 11 часам автобус вернулся в Москву.

Значит, для определения конечного положения тела недостаточно знать его начальное положение и пройденный им путь.

Мы нашли бы местонахождение автобуса в 11 часов, если бы знали траекторию его движения (зеленая линия на рисунке 38). Отсчитав 100 км от начальной точки маршрута вдоль траектории, найдем, что в 11 часов автобус прибыл в Борисов.

А можно поступить иначе. Конечное положение автобуса можно определить, зная его начальное положение и всего одну векторную величину, называемую перемещением.

Перемещение — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).

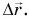
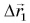
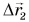
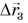
Обозначим перемещение символом На рисунке 38 вектор — это перемещение автобуса из Минска в Мытищи, вектор — из Мытищь в Балашиху, а вектор — из Минска в Борисов.

Теперь, даже не зная траектории, по начальной точке и перемещению мы можем найти конечную точку для каждого из участков движения автобуса и для всего маршрута в целом.

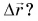
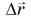
Можно ли сравнивать путь S, пройденный телом, с его перемещением Нельзя, поскольку путь S — скаляр, а перемещение — вектор.

Сравнивать путь S можно с модулем перемещения 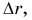который является скалярной величиной. Равен ли путь модулю перемещения?

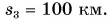
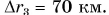
В рассматриваемом примере путь, пройденный автобусом за два часа, Он равен длине траектории движения автобуса от Москвы через Мытищи до Балашихи (см. рис. 38). А модуль перемещения автобуса за это время равен расстоянию от Минска до Борисова: Путь автобуса больше модуля его перемещения:

Пройденный путь был бы равен модулю перемещения, если бы автобус все время двигался по прямой, не изменяя направления движения.

Следовательно, путь всегда не меньше модуля перемещения:

Как складывают между собой пути и как — перемещения? Из рисунка 38 находим:

Пройденные пути складывают арифметически, а перемещения — по правилам сложения векторов.

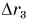
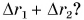
Равен ли при этом модуль сумме модулей Ответьте самостоятельно.

Мы выяснили, что путь и траектория относительны. Покажите на примерах, что перемещение тоже относительно, т. е. зависит от выбора системы отсчета.

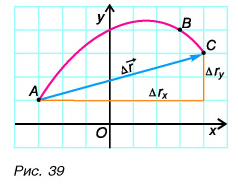
При решении задач важно уметь находить проекции перемещения. Построим вектор перемещения куска мела по школьной доске из точки А в точку С (рис. 39). Из рисунка видно, что проекции вектора 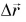на координатные оси Ох и Оу равны разности координат конца и начала этого вектора:

Главные выводы:

1. Путь — это длина участка траектории, пройденного телом за данный промежуток времени. Путь — положительная скалярная величина.
2. Перемещение тела — это вектор, соединяющий начальное положение тела с его конечным положением (для данного промежутка времени).
3. Путь не меньше модуля перемещения тела за то же время.
4. Пройденные пути складываются арифметически, а перемещения — по правилам сложения векторов.

Пример:

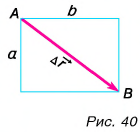
Конькобежец пересек прямоугольную ледовую площадку по диагонали АВ, а пешеход прошел из точки А в точку В по краю площадки (рис. 40). Размеры площадки 60 х 80 м. Определите модули перемещения конькобежца и пешехода и пути, пройденные ими.

Решение

Из рисунка 40 видно, что перемещения пешехода и конькобежца одинаковы. Модуль перемещения:

Путь конькобежца:

Путь пешехода: 

Ответ:

• Заказать решение задач по физике

Траектория движения

Возьмите лист бумаги и карандаш. Поставьте на листе точки А и В и соедините их кривой линией (рис. 7.1). Эта линия совпадает с траекторией движения кончика карандаша, то есть линией, в каждой точке которой последовательно побывал кончик карандаша во время своего движения.

Траектория движения — это воображаемая линия, которую описывает в пространстве движущаяся точка. Обычно мы не видим траектории движения тел, но иногда бывают исключения.

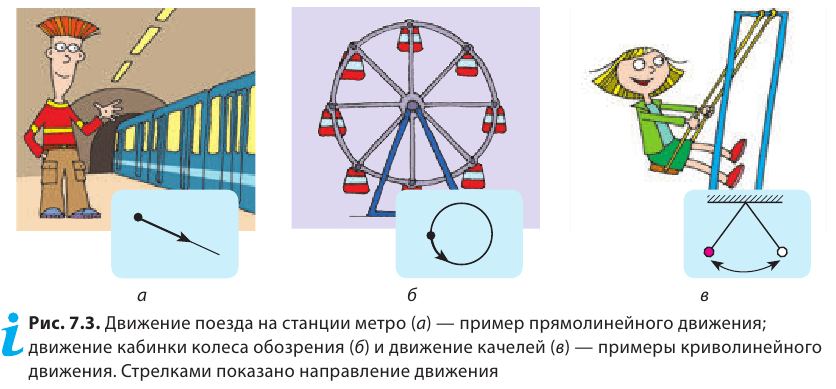
Так, в без­облачную погоду высоко в небе можно увидеть белый след, который во время своего движения оставляет самолет*. По этому следу можно определить траекторию движения самолета. Траектории движения каких тел можно восстановить по следам, изображенным на рис. 7.2? В каких случаях траекторию движения «заготавливают» заранее? Форма траектории может быть разной: прямая, окружность, дуга, ломаная и т. д. В зависимости от формы траектории разли­чают прямолинейное и криволинейное движе­ния тел (рис. 7.3).

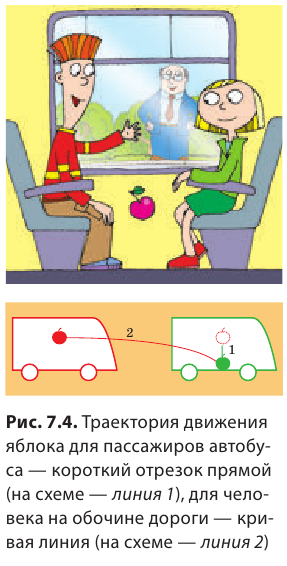
Форма траектории движения тела зависит от того, относительно какой системы отсчета рассматривают движение. Приведем пример. У мальчика, едущего в автобусе, упало из рук яблоко (рис. 7.4). Для девочки, сидящей напротив, траектория движения яблока — короткий отрезок прямой. В этом случае система отсчета, относительно которой рассматривается движение яблока, связана с салоном автобуса. Но все время, пока яблоко падало, оно «ехало» вместе с автобусом, поэтому для человека, стоящего на обочине дороги, траектория движения яблока абсолютно другая. Система отсчета в таком случае связана с дорогой.

Чем путь отличается от перемещения

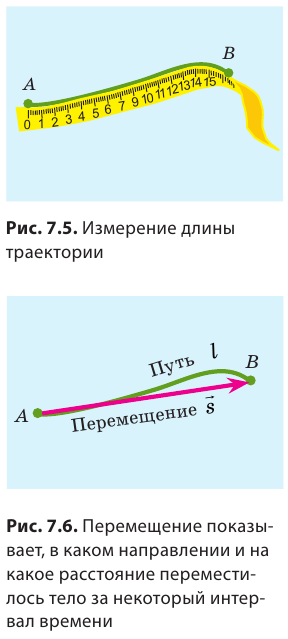
Вернемся к началу (см. рис. 7.1). Чтобы найти путь, который прошел конец карандаша, рисуя кривую линию, необходимо измерить длину этой линии, то есть найти длину траектории (рис. 7.5). Путь — это физическая величина, равная длине траектории. Путь обозначают символом l. Единица пути в СИ — метр: [l]= м. Используют также дольные и кратные единицы пути, например миллиметр (мм), сантиметр (см), километр (км):

Путь, пройденный телом, будет разным относительно разных систем отсчета. Вспомним яблоко в автобусе (см. рис. 7.4): для пассажиров яблоко прошло путь около полуметра, а для человека на обочине дороги — несколько метров. Вернемся к рис. 7.1. Соединив точки А и В отрезком прямой со стрелкой, получим направленный отрезок, который покажет, в каком направлении и на какое расстояние переместился конец карандаша (рис. 7.6).

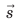
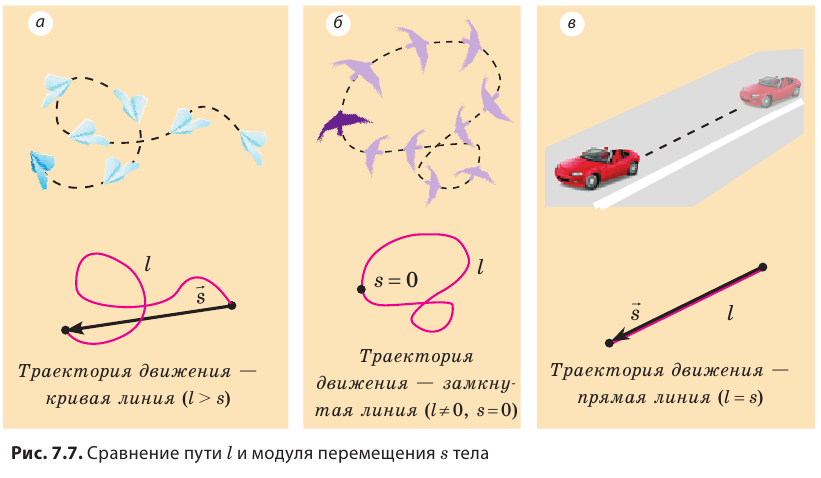
Направленный отрезок прямой, соединяющий начальное и конечное положения тела, называют перемещением. Перемещение обозначают символом . Стрелка над символом показывает, что перемещение — это векторная физическая величина*. Чтобы правильно задать перемещение, необходимо указать не только его значение (модуль), но и направление.

Модуль перемещения, то есть расстояние, на которое переместилось тело в определенном направлении, также обозначают символом s, но без стрелки. Единица перемещения в СИ такая же, как и единица пути, — метр: [s]= м. В общем случае перемещение не совпадает с траекторией движения тела (рис. 7.7, а, б), поэтому путь, пройденный телом, обычно больше модуля перемещения. Путь и модуль перемещения равны только в том случае, когда тело движется вдоль прямой в неизменном направлении (рис. 7.7, в).

Итоги:

Воображаемая линия, которую описывает в пространстве движущаяся точка, называется траекторией. В зависимости от формы траектории различают прямолинейное и криволинейное движения тел. Путь l — это физическая величина, равная длине траектории. Перемещение 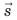— это направленный отрезок прямой, соединяющий начальное и конечное положения тела. Единица пути и перемещения в СИ — метр (м).

Физические величины, имеющие значение и направление, называется векторными а имеющие только значение — скалярными.

Рис.
2

Для определения
перемещения точки в пространстве вводят
вектор перемещения.

Например,
за промежуток времени t
точка перемещается из положения 1 в
положение 2 (рис. 2), определяемые векторным
способом указанием радиус-векторов

и
; вектором
перемещения называют вектор, проведенный
из начального положения 1 в конечное 2
перемещаемого тела. Из векторного
треугольника видно, что вектор перемещения
равен приращению

радиус-вектора
точки.

Наряду с изменением
радиус-вектора точки происходит изменение
ее координат, т.е. перемещение точки
вдоль отдельных координатных направлений.
Из рис.3 видно, что

Вектор
перемещения за конечный промежуток
времени в общем случае не совпадает с
направлением движения (направлением
касательной к траектории движения).
Очевидно, что эти направления будут
совпадать в общем случае движения только
для бесконечно малых перемещений точки
.

1.2. Вектор скорости.

Вектором скорости
называют вектор, определяющий быстроту
и направление движения.

В
ектором
средней скорости называют отношение
вектора перемещения к промежутку
времени, за который это перемещение
происходит:

Так как
в произвольном случае движения вектор
перемещения за конечный промежуток
времени не определяет точно направление
движения, это не может сделать и вектор
средней скорости. Следо­вательно,
необходимо рассматривать перемещения
за бесконечно ма­лые промежутки
времени.

Вектором
истинной (мгновенной) скорости называют
предел, к которому стремится значение
вектора средней скорости при бесконечном
убывании промежутка времени:

Так как
при движении тела в общем случае
изменяются все три его координаты, часто
бывает удобным рассматривать скорость
дви­жения точки вдоль отдельных
координатных направлений (компоненты
или составляющие вектора скорости).
Компоненты средней скорости равны:

Компоненты же
мгновенной скорости определяются как

Вектор
скорости с его компонентами связан
такими же по виду соотношениями, как
радиус-вектор с

координатами
точек:

1.3.Вектор ускорения.

Вектором
ускорения называют вектор, определяющий
быстроту и направление изменения вектора

скорости.
Аналогично определени­ям для вектора
скорости вводятся понятия среднего и
мгновенного

ускорения:

При
движении точки по произвольной траектории
вектор изме­нения скорости Δ
и, следовательно, вектор ускорения
направлены в сторону вогнутости
траектории независимо от того,
увели­чивается или уменьшается
величина скорости (рис. 4, 5):

Рис.
4. Ускоренное движение Рис. 5. Замедленное
движение

Как
видно из рисунков, в обоих случаях вектор
d
направлен в сторону вогнутости
траектории. При ускоренном движении он
отклоняется в сторону движения, при
замедленном — в противоположную

Для
определения мгновенного ускорения надо
рассматривать бесконечно малые
перемещения, т.е. векторы скорости ₁
и ₂
в соседних
точках траектории. Поэтому вектор
ускорения лежит в плоскости, содержащей
касательную к траектории в данной точке
и прямую, параллельную касательной в
соседней точке траектории. Такая
плоскость называется соприкасающейся.
Поэтому наряду с представлением вектора
ускорения компонентами

можно
рассматривать составляющие вектора в
соприкасающейся плос­кости (т.е. только
две компоненты). Для определения этих
составляющих в любой точке траектории
проводят соприкасавшуюся плос­кость
и в ней две оси — нормальную O_n.
в сторону вогнутости тра­ектории и
касательную O_t
по касательной к траектории. Изменение
скорости и, соответственно, ускорение
можно рассматривать в про­екциях на
эти оси (рис. 6).

Двигаясь
вдоль траектории, за промежуток времени
t
точка про­ходит путь S
скорость ее изменяется от 
до ₁,
при этом ₁
составляет
угол 
(альфа) с осью O_t.
По определению мгновенного ускорения:

Рис.
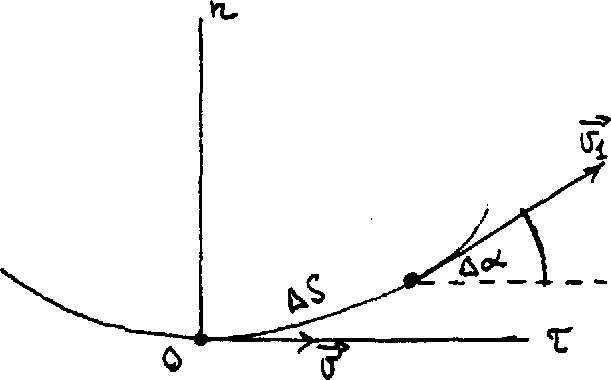
6

П
реобразуем
выражение предела, умножив и разделив
его на 
и S:

О
тметим,
что при t=0
бесконечно убывает и пройденный путь,
и угол (S=0,
a=0).
При этом условии значения пределов
равны:

Предел
же называется
кривизной траектории К. Кривизна
траектории обратно

пропорциональна
радиусу кривизны траектории:

С
учетом этих замечаний выражение для
нормальной составляющей вектора
ускорения принимает вид

Для
выяснения физического смысла ускорения
рассмотрим два частных случая движения.

Р
авномерное
криволинейное движение (V=const, k<>0). В
этом случае, как видно из (14) и (16),

Н
еравномерное
прямолинейное движение (V<>соnst , K=0).
При таком движении

Следовательно,
касательная составляющая ускорения
определяет изменение вектора скорости
по величине, а нормальная — по направлению.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Как найти модуль вектора перемещения

В кинематике для нахождения различных величин используются математические методы. В частности, чтобы найти модуль вектора перемещения, нужно применить формулу из векторной алгебры. В ней фигурируют координаты точек начала и конца вектора, т.е. первоначального и итогового положения тела.

Инструкция

Во время движения материальное тело меняет свое положение в пространстве. Его траектория может быть прямой линией или произвольной, ее длина составляет путь тела, но не расстояние, на которое оно переместилось. Эти две величины совпадают только в случае прямолинейного движения.

Итак, пусть тело совершило некоторое перемещение из точки А (х0, у0) в точку В (х, у). Чтобы найти модуль вектора перемещения, нужно вычислить длину вектора АВ. Начертите координатные оси и нанесите на них известные точки начального и конечного положения тела А и В.

Проведите отрезок из точки А в точку В, укажите направление. Опустите проекции его концов на оси и нанесите на графике параллельные и равные им отрезки, проходящие через рассматриваемые точки. Вы увидите, что на рисунке обозначился прямоугольный треугольник с катетами-проекциями и гипотенузой-перемещением.

По теореме Пифагора найдите длину гипотенузы. Этот метод широко применяется в векторной алгебре и носит название правила треугольника. Для начала запишите длины катетов, они равны разностям между соответствующими абсциссами и ординатами точек А и В:
ABx = x – x0 – проекция вектора на ось Ох;
ABy = y – y0 – его проекция на ось Оу.

Определите перемещение |AB|:
|AB| = √(ABx² + ABy²) = ((x – x0)² + (y – y0)²).

Для трехмерного пространства добавьте в формулу третью координату – аппликату z:
|AB| = √(ABx² + ABy² + ABz²) = ((x – x0)² + (y – y0)² + (z – z0)²).

Полученную формулу можно применять для любой траектории и типа движения. При этом величина перемещения обладает важным свойством. Она всегда меньше либо равна длине пути, в общем случае ее линия не совпадает с кривой траектории. Проекции – величины математические, могут быть как больше, так и меньше нуля. Однако это не имеет значения, поскольку в расчете они участвуют в четной степени.

Источники:

• модуль перемещения

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?