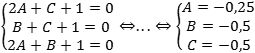Как найти вектор перпендикулярный данной плоскости - Исправление недочетов и поиск решений вместе с Examum.ru

Метод координат в пространстве

30 мая 2011

Для того, чтобы использовать метод координат, надо хорошо знать формулы. Их три:

Главная формула — косинус угла φ между векторами a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂):
Уравнение плоскости в трехмерном пространстве: Ax + By + Cz + D = 0, где A, B, C и D — действительные числа, причем, если плоскость проходит через начало координат, D = 0. А если не проходит, то D = 1.
Вектор, перпендикулярный к плоскости Ax + By + Cz + D = 0, имеет координаты: n = (A; B; C).

На первый взгляд, выглядит угрожающе, но достаточно немного практики — и все будет работать великолепно.

Задача. Найти косинус угла между векторами a = (4; 3; 0) и b = (0; 12; 5).

Решение. Поскольку координаты векторов нам даны, подставляем их в первую формулу:

Задача. Составить уравнение плоскости, проходящей через точки M = (2; 0; 1), N = (0; 1; 1) и K = (2; 1; 0), если известно, что она не проходит через начало координат.

Решение. Общее уравнение плоскости: Ax + By + Cz + D = 0, но, поскольку искомая плоскость не проходит через начало координат — точку (0; 0; 0) — то положим D = 1. Поскольку эта плоскость проходит через точки M, N и K, то координаты этих точек должны обращать уравнение в верное числовое равенство.

Подставим вместо x, y и z координаты точки M = (2; 0; 1). Имеем:
A · 2 + B · 0 + C · 1 + 1 = 0 ⇒ 2A + C + 1 = 0;

Аналогично, для точек N = (0; 1; 1) и K = (2; 1; 0) получим уравнения:
A · 0 + B · 1 + C · 1 + 1 = 0 ⇒ B + C + 1 = 0;
A · 2 + B · 1 + C · 0 + 1 = 0 ⇒ 2A + B + 1 = 0;

Итак, у нас есть три уравнения и три неизвестных. Составим и решим систему уравнений:

Получили, что уравнение плоскости имеет вид: − 0,25x − 0,5y − 0,5z + 1 = 0.

Задача. Плоскость задана уравнением 7x − 2y + 4z + 1 = 0. Найти координаты вектора, перпендикулярного данной плоскости.

Решение. Используя третью формулу, получаем n = (7; − 2; 4) — вот и все!

Вычисление координат векторов

А что, если в задаче нет векторов — есть только точки, лежащие на прямых, и требуется вычислить угол между этими прямыми? Все просто: зная координаты точек — начала и конца вектора — можно вычислить координаты самого вектора.

Чтобы найти координаты вектора, надо из координат его конца вычесть координаты начала.

Эта теорема одинаково работает и на плоскости, и в пространстве. Выражение «вычесть координаты» означает, что из координаты x одной точки вычитается координата x другой, затем то же самое надо сделать с координатами y и z. Вот несколько примеров:

Задача. В пространстве расположены три точки, заданные своими координатами: A = (1; 6; 3), B = (3; − 1; 7) и C = (− 4; 3; − 2). Найти координаты векторов AB, AC и BC.

Рассмотрим вектор AB: его начало находится в точке A, а конец — в точке B. Следовательно, чтобы найти его координаты, надо из координат точки B вычесть координаты точки A:
AB = (3 − 1; − 1 − 6; 7 − 3) = (2; − 7; 4).

Аналогично, начало вектора AC — все та же точка A, зато конец — точка C. Поэтому имеем:
AC = (− 4 − 1; 3 − 6; − 2 − 3) = (− 5; − 3; − 5).

Наконец, чтобы найти координаты вектора BC, надо из координат точки C вычесть координаты точки B:
BC = (− 4 − 3; 3 − (− 1); − 2 − 7) = (− 7; 4; − 9).

Ответ: AB = (2; − 7; 4); AC = (− 5; − 3; − 5); BC = (− 7; 4; − 9)

Обратите внимание на вычисление координат последнего вектора BC: очень многие ошибаются, когда работают с отрицательными числами. Это касается переменной y: у точки B координата y = − 1, а у точки C y = 3. Получаем именно 3 − (− 1) = 4, а не 3 − 1, как многие считают. Не допускайте таких глупых ошибок!

Вычисление направляющих векторов для прямых

Если вы внимательно прочитаете задачу C2, то с удивлением обнаружите, что никаких векторов там нет. Там только прямые да плоскости.

Для начала разберемся с прямыми. Здесь все просто: на любой прямой найдутся хотя бы две различные точки и, наоборот, любые две различные точки задают единственную прямую…

Кто-нибудь понял, что написано в предыдущем абзаце? Я и сам не понял, поэтому объясню проще: в задаче C2 прямые всегда задаются парой точек. Если ввести систему координат и рассмотреть вектор с началом и концом в этих точках, получим так называемый направляющий вектор для прямой:

Зачем нужен этот вектор? Дело в том, что угол между двумя прямыми — это угол между их направляющими векторами. Таким образом, мы переходим от непонятных прямых к конкретным векторам, координаты которых легко считаются. Насколько легко? Взгляните на примеры:

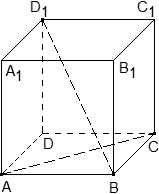
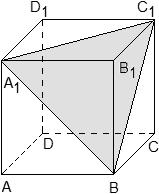
Задача. В кубе ABCDA₁B₁C₁D₁ проведены прямые AC и BD₁. Найдите координаты направляющих векторов этих прямых.

Поскольку длина ребер куба в условии не указана, положим AB = 1. Введем систему координат с началом в точке A и осями x, y, z, направленными вдоль прямых AB, AD и AA₁ соответственно. Единичный отрезок равен AB = 1.

Теперь найдем координаты направляющего вектора для прямой AC. Нам потребуются две точки: A = (0; 0; 0) и C = (1; 1; 0). Отсюда получаем координаты вектора AC = (1 − 0; 1 − 0; 0 − 0) = (1; 1; 0) — это и есть направляющий вектор.

Теперь разберемся с прямой BD₁. На ней также есть две точки: B = (1; 0; 0) и D₁ = (0; 1; 1). Получаем направляющий вектор BD₁ = (0 − 1; 1 − 0; 1 − 0) = (− 1; 1; 1).

Ответ: AC = (1; 1; 0); BD₁ = (− 1; 1; 1)

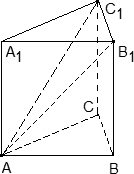
Задача. В правильной треугольной призме ABCA₁B₁C₁, все ребра которой равны 1, проведены прямые AB₁ и AC₁. Найдите координаты направляющих векторов этих прямых.

Введем систему координат: начало в точке A, ось x совпадает с AB, ось z совпадает с AA₁, ось y образует с осью x плоскость OXY, которая совпадает с плоскостью ABC.

Для начала разберемся с прямой AB₁. Тут все просто: у нас есть точки A = (0; 0; 0) и B₁ = (1; 0; 1). Получаем направляющий вектор AB₁ = (1 − 0; 0 − 0; 1 − 0) = (1; 0; 1).

Теперь найдем направляющий вектор для AC₁. Все то же самое — единственное отличие в том, что у точки C₁ иррациональные координаты. Итак, A = (0; 0; 0), поэтому имеем:

Ответ: AB₁ = (1; 0; 1);

Небольшое, но очень важное замечание насчет последнего примера. Если начало вектора совпадает с началом координат, вычисления резко упрощаются: координаты вектора просто равны координатам конца. К сожалению, это верно лишь для векторов. Например, при работе с плоскостями присутствие на них начала координат только усложняет выкладки.

Вычисление нормальных векторов для плоскостей

Нормальные векторы — это не те векторы, у которых все в порядке, или которые чувствуют себя хорошо. По определению, нормальный вектор (нормаль) к плоскости — это вектор, перпендикулярный данной плоскости.

Другими словами, нормаль — это вектор, перпендикулярный любому вектору в данной плоскости. Наверняка вы встречали такое определение — правда, вместо векторов речь шла о прямых. Однако чуть выше было показано, что в задаче C2 можно оперировать любым удобным объектом — хоть прямой, хоть вектором.

Еще раз напомню, что всякая плоскость задается в пространстве уравнением Ax + By + Cz + D = 0, где A, B, C и D — некоторые коэффициенты. Не умаляя общности решения, можно полагать D = 1, если плоскость не проходит через начало координат, или D = 0, если все-таки проходит. В любом случае, координаты нормального вектора к этой плоскости равны n = (A; B; C).

Итак, плоскость тоже можно успешно заменить вектором — той самой нормалью. Всякая плоскость задается в пространстве тремя точками. Как найти уравнение плоскости (а следовательно — и нормали), мы уже обсуждали в самом начале статьи. Однако этот процесс у многих вызывает проблемы, поэтому приведу еще парочку примеров:

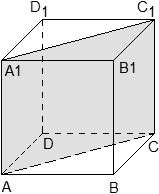
Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение A₁BC₁. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

Поскольку плоскость не проходит через начало координат, ее уравнение выглядит так: Ax + By + Cz + 1 = 0, т.е. коэффициент D = 1. Поскольку эта плоскость проходит через точки A₁, B и C₁, то координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 + 1 = 0 ⇒ C + 1 = 0 ⇒ C = − 1;

Аналогично, для точек B = (1; 0; 0) и C₁ = (1; 1; 1) получим уравнения:
A · 1 + B · 0 + C · 0 + 1 = 0 ⇒ A + 1 = 0 ⇒ A = − 1;
A · 1 + B · 1 + C · 1 + 1 = 0 ⇒ A + B + C + 1 = 0;

Но коэффициенты A = − 1 и C = − 1 нам уже известны, поэтому остается найти коэффициент B:
B = − 1 − A − C = − 1 + 1 + 1 = 1.

Получаем уравнение плоскости: − A + B − C + 1 = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; − 1).

Задача. В кубе ABCDA₁B₁C₁D₁ проведено сечение AA₁C₁C. Найти нормальный вектор для плоскости этого сечения, если начало координат находится в точке A, а оси x, y и z совпадают с ребрами AB, AD и AA₁ соответственно.

В данном случае плоскость проходит через начало координат, поэтому коэффициент D = 0, а уравнение плоскости выглядит так: Ax + By + Cz = 0. Поскольку плоскость проходит через точки A₁ и C, координаты этих точек обращают уравнение плоскости в верное числовое равенство.

Подставим вместо x, y и z координаты точки A₁ = (0; 0; 1). Имеем:
A · 0 + B · 0 + C · 1 = 0 ⇒ C = 0;

Аналогично, для точки C = (1; 1; 0) получим уравнение:
A · 1 + B · 1 + C · 0 = 0 ⇒ A + B = 0 ⇒ A = − B;

Положим B = 1. Тогда A = − B = − 1, и уравнение всей плоскости имеет вид: − A + B = 0, Следовательно, координаты нормального вектора равны n = (− 1; 1; 0).

Вообще говоря, в приведенных задачах надо составлять систему уравнений и решать ее. Получится три уравнения и три переменных, но во втором случае одна из них будет свободной, т.е. принимать произвольные значения. Именно поэтому мы вправе положить B = 1 — без ущерба для общности решения и правильности ответа.

Координаты середины отрезка

Очень часто в задаче C2 требуется работать с точками, которые делят отрезок пополам. Координаты таких точек легко считаются, если известны координаты концов отрезка.

Итак, пусть отрезок задан своими концами — точками A = (x_a; y_a; z_a) и B = (x_b; y_b; z_b). Тогда координаты середины отрезка — обозначим ее точкой H — можно найти по формуле:

Другими словами, координаты середины отрезка — это среднее арифметическое координат его концов.

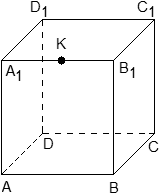
Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Точка K — середина ребра A₁B₁. Найдите координаты этой точки.

Поскольку точка K — середина отрезка A₁B₁, ее координаты равных среднему арифметическому координат концов. Запишем координаты концов: A₁ = (0; 0; 1) и B₁ = (1; 0; 1). Теперь найдем координаты точки K:

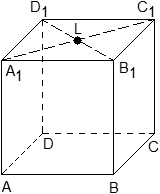
Задача. Единичный куб ABCDA₁B₁C₁D₁ помещен в систему координат так, что оси x, y и z направлены вдоль ребер AB, AD и AA₁ соответственно, а начало координат совпадает с точкой A. Найдите координаты точки L, в которой пересекаются диагонали квадрата A₁B₁C₁D₁.

Из курса планиметрии известно, что точка пересечения диагоналей квадрата равноудалена от всех его вершин. В частности, A₁L = C₁L, т.е. точка L — это середина отрезка A₁C₁. Но A₁ = (0; 0; 1), C₁ = (1; 1; 1), поэтому имеем:

Ответ: L = (0,5; 0,5; 1)

Смотрите также:

Введение системы координат
Четырехугольная пирамида в задаче C2
В 2012 году ЕГЭ по математике станет двухуровневым?
Сводный тест по задачам B12 (1 вариант)
Симметрия корней и оптимизация ответов в тригонометрии
ЕГЭ 2022, задание 6. Касательная и уравнение с параметром

Источник

Перпендикулярность векторов

Мы можем выяснить, будут ли два каких-либо вектора взаимно перпендикулярными. Для этого нужно воспользоваться координатами векторов и некоторыми приемами, описанными в данной статье. Информация о перпендикулярности будет полезной для решения некоторых задач физики и математики.

Координаты вектора на плоскости, равного по модулю и перпендикулярного данному

Пусть на плоскости заданы координаты какого-либо вектора. Из этих координат получим координаты двух дополнительных векторов, перпендикулярных первоначальному вектору. Все три вектора будут иметь равные длины и располагаться в плоскости xOy.

Алгоритм получения координат перпендикулярных векторов

Вектор на плоскости xOy, перпендикулярный данному вектору получают так:

Поменять местами координатные числа «x» и «y».
Заменить знак у одной из координат на противоположный.

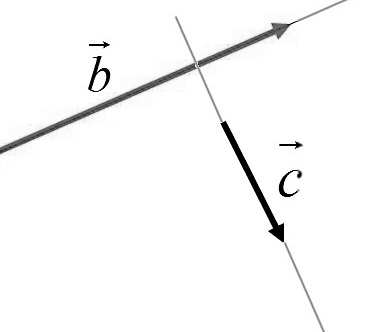
Графический пример

Рассмотрим небольшой графический пример (рис. 1).

Рис. 1. На рисунке векторы, обозначенные черным цветом, перпендикулярны вектору, обозначенному красным цветом

На плоскости проведены три вектора: один красный и два черных и, отмечены их координаты. Рассмотрим подробнее координаты двух векторов: (vec{a}) и (vec{b}).

[ vec{a} = left{ 4 ; 3 right} ]

[ vec{b} = left{ -3 ; 4 right} ]

Из рисунка видно, что векторы (vec{a}) и (vec{b}) перпендикулярны: ( vec{a} perp vec{b} ).

Вектор ( -vec{b} = left{ 3 ; -4 right} ), также будет перпендикулярным вектору ( vec{a} ): ( vec{a} perp vec{(-b)} )

Векторы, изображенные черным цветом, перпендикулярны красному вектору.

Длины векторов ( vec{a} ), ( vec{b} ) и ( vec{(-b)} ) равны.

Условие перпендикулярности векторов

Взаимную перпендикулярность двух векторов можно проверить, вычислив их скалярное произведение. Этот способ проверки можно применять для векторов, расположенных как на плоскости, так и в трехмерном пространстве.

Векторы будут перпендикулярными, когда их скалярное произведение равно нулю.

Пусть, известны координаты двух векторов и пусть каждый вектор имеет ненулевую длину.

[ large boxed { begin{cases} vec{a} = left{ a_{x} ; a_{y} ; a_{z} right} \ vec{b} = left{ b_{x} ; b_{y} ; b_{z} right} \ |vec{a}| ne 0 \ |vec{b}| ne 0 end{cases}}]

Запишем условие перпендикулярности векторов.

Для двумерного случая:

[ large boxed { a_{x} cdot b_{x} + a_{y} cdot b_{y} = 0 }]

Для трехмерного случая:

[ large boxed { a_{x} cdot b_{x} + a_{y} cdot b_{y} + a_{z} cdot b_{z} = 0 }]

Пользуясь любой из этих формул, можно определить одну неизвестную координату вектора.

При этом, должны быть известными остальные координаты этого вектора и все координаты второго вектора.

Примечание:

Есть такое правило: Количество неизвестных должно равняться количеству уравнений.

Чтобы однозначно определить значение неизвестной, в уравнение должна входить только одна неизвестная. Остальные величины должны быть известными.

Перпендикулярные векторы в физике

В физике перпендикулярность некоторых векторов достаточно важна.

Вот несколько примеров:

Если угол между вектором скорости тела и вектором силы, действующей на тело, будет прямым, то такая сила работу по перемещению тела совершать не будет.
На проводник с током магнитное поле действует максимальной силой, когда вектор магнитной индукции и вектор тока в проводнике перпендикулярны.
Когда угол между вращающей силой и, расстоянием между точкой приложения силы и осью вращения, будет прямым, вращательный момент будет максимальным.
Между линейной скоростью точки колеса и расстоянием от этой точки до оси вращения, угол прямой (радиус и касательная перпендикулярны).
На вращающееся тело действует центростремительная сила. Угол прямой между этой силой и линейной скоростью точки тела (радиус и касательная перпендикулярны).

Оценка статьи:

Загрузка…

Источник

Анна Кирпиченкова

Эксперт по предмету «Геометрия»

Задать вопрос автору статьи

Понятие вектора и перпендикулярности векторов

Вначале надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.

Определение 1

Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.

Определение 2

Концами отрезка будем называть точки, которые его ограничивают.

Для введения определения вектора один из концов отрезка назовем его началом.

Определение 3

Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Обозначение: $overline{AB}$ — вектор $AB$, имеющий начало в точке $A$, а конец в точке $B$.

Иначе одной маленькой буквой: $overline{a}$ (рис. 1).

Определение 4

Нулевым вектором будем называть любую точку, которая принадлежит плоскости.

Обозначение: $overline{0}$.

Введем теперь, непосредственно, определение коллинеарных векторов.

Определение 5

Два ненулевых вектора будем называть перпендикулярными (ортогональными), если они лежат на каких-либо перпендикулярных прямых (рис.2).

«Как найти вектор, перпендикулярный вектору» 👇

Также введем определение скалярного произведения, которое будет нам необходимо далее.

Определение 6

Скалярным произведением двух данных векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.

Математически это может выглядеть следующим образом:

$overline{α}overline{β}=|overline{α}||overline{β}|cos⁡∠(overline{α},overline{β})$

Скалярное произведение также можно найти с помощью координат векторов следующим образом

$overline{α}overline{β}=α_1 β_1+α_2 β_2+α_3 β_3$

Признак перпендикулярности через пропорциональность

Теорема 1

Чтобы ненулевые векторы были перпендикулярны между собой, необходимо и достаточно, чтобы их скалярное произведение этих векторов равнялось нулю.

Доказательство.

Необходимость: Пусть нам даны векторы $overline{α}$ и $overline{β}$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они перпендикулярны друг другу. Тогда нам нужно доказать следующее равенство

$overline{α}cdot overline{β}=0$

Так как векторы $overline{α}$ и $overline{β}$ перпендикулярны, то угол между ними равняется $90^0$. Найдем скалярное произведение данных векторов по формуле из определения 6.

$overline{α}cdot overline{β}=|overline{α}||overline{β}|cos⁡90^circ =|overline{α}||overline{β}|cdot 0=0$

Достаточность: Пусть верно равенство $overline{α}cdot overline{β}=0$. Докажем, что векторы $overline{α}$ и $overline{β}$ будут перпендикулярны друг другу.

По определению 6, будет верно равенство

$|overline{α}||overline{β}|cos⁡∠(overline{α},overline{β})=0$

$cos⁡∠(overline{α},overline{β})=0$

$∠(overline{α},overline{β})=90^circ$

Следовательно, векторы $overline{α}$ и $overline{β}$ будут перпендикулярны друг другу.

Теорема доказана.

Пример 1

Доказать, что векторы с координатами $(1,-5,2)$ и $(2,1,3/2)$ перпендикулярны.

Доказательство.

Найдем скалярное произведение для этих векторов через формулу, данную выше

$overline{α}cdot overline{β}=1cdot 2+(-5)cdot 1+2cdot frac{3}{2}=2cdot 5+3=0$

Значит, по теореме 1, эти вектор перпендикулярны.

Нахождение перпендикулярного вектора к двум данным векторам через векторное произведение

Введем вначале понятие векторного произведения.

Определение 7

Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.

Обозначение: $overline{α}хoverline{β}$.

Чтобы найти векторное произведение, будем пользоваться формулой

$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}$

Так как вектор векторного произведения двух векторов перпендикулярен обоим этим векторам, то он и будет иском вектором. То есть, для того, чтоб найти перпендикулярный для двух векторов вектор, нужно просто найти их векторное произведение.

Пример 2

Найти вектор, перпендикулярный к векторам с координатами $overline{α}=(1,2,3)$ и $overline{β}=(-1,0,3)$

Решение.

Найдем векторное произведение данных векторов.

$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\1&2&3\-1&0&3end{vmatrix}=(6-0)overline{i}-(3+3)overline{j}+(0+2)overline{k}=6overline{i}-6overline{j}+2overline{k}=(6,6,2)$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Как найти вектор, перпендикулярный данному

В геометрии вектор определяется как упорядоченная пара точек, одну из которых считают его началом, другую — концом. В начертательной геометрии построить вектор, перпендикулярный заданному, можно с помощью транспортира отмерив нужный угол и начертив соответствующий отрезок. В аналитической геометрии для вычисления координат такого направленного отрезка придется задействовать правила скалярных операций с векторами.

Инструкция

Если исходный вектор изображен на чертеже в прямоугольной двухмерной системе координат и перпендикулярный ему нужно построить там же, исходите из определения перпендикулярности векторов на плоскости. Оно гласит, что угол между такой парой направленных отрезков должен быть равен 90°. Таких векторов можно построить бесконечное множество. Поэтому начертите в любом удобном месте плоскости перпендикуляр к исходному вектору, отложите на нем отрезок, равный длине заданной упорядоченной пары точек и назначьте один из его концов началом перпендикулярного вектора. Сделайте это с помощью транспортира и линейки.

Если же исходный вектор задан двухмерными координатами ā = (X₁;Y₁), исходите из того, что скалярное произведение пары перпендикулярных векторов должно быть равно нулю. Это значит, что вам надо подобрать для искомого вектора ō = (X₂,Y₂) такие координаты, при которых будет выполняться равенство (ā,ō) = X₁*X₂ + Y₁*Y₂ = 0. Это можно сделать так: выберите любое ненулевое значение для координаты X₂, а координату Y₂ рассчитайте по формуле Y₂ = -(X₁*X₂)/Y₁. Например, для вектора ā = (15;5) перпендикулярным будет вектор ō, с абсциссой, равной единице, и ординатой, равной -(15*1)/5 = -3, т.е. ō = (1;-3).

Для трехмерной и любой другой ортогональной системы координат верно то же самое необходимое и достаточное условие перпендикулярности векторов — их скалярное произведение должно быть равно нулю. Поэтому, если исходный направленный отрезок задан координатами ā = (X₁,Y₁,Z₁), подберите для перпендикулярной ему упорядоченной пары точек ō = (X₂,Y₂,Z₂) такие координаты, при которых выполняется условие (ā,ō) = X₁*X₂ + Y₁*Y₂ + Z₁*Z₂ = 0. Проще всего присвоить координатам X₂ и Y₂ единичные значения, а Z₂ рассчитать из упростившегося равенства Z₂ = -1*(X₁*1 + Y₁*1)/Z₁ = -(X₁+Y₁)/Z₁. Например, для вектора ā = (3,5,4) эта формула приобретет такой вид: (ā,ō) = 3*X₂ + 5*Y₂ + 4*Z₂ = 0. Тогда абсциссу и ординату перпендикулярного вектора примите за единицу, а аппликата в этом случае будет равна -(3+5)/4 = -2.

Источники:

найти вектор если он перпендикулярный

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Прежде чем приступить к понятию того, как найти перпендикулярные векторы, сначала нам нужно узнать о векторах. Физические величины, имеющие как величину, так и направление, называются векторами.

Чтобы проиллюстрировать концепцию вектора, сначала нам нужно принять во внимание векторную величину. Например, сила является вектором. Предположим, что вес тела равен 5 Н, это означает, что величина веса равна 5 Н и он действует в направлении вниз. Если говорить о двух векторах, то при выполнении условия, что их скалярное произведение равно нулю, можно сказать, что они перпендикулярны друг другу.

Например, если мы рассмотрим скалярное произведение векторов A и B, то

AB= AB cos х

Здесь x определяется как угол между двумя векторами A и B. Если мы возьмем x = 90 градусов, то значение скалярного произведения A и B равно ABcos90=0 (поскольку cos90=0). И наоборот, если скалярное произведение двух векторов равно 0, то можно сказать, что они перпендикулярны друг другу.

АВ=0

АВ, потому что х=0

потому что х=0

потому что х = потому что 90

х = 90

Концепция перпендикулярных векторов может быть проиллюстрирована некоторыми численными задачами, написанными ниже:

Пример

Значения двух векторов A и B равны (5i+3j-8k) и (i+j+k) соответственно. Эти два вектора перпендикулярны или нет?

=(5i+3j-8k).(i+j+k)

=5i.i+3j.j-8k.k [при ii=1,jj=1 и kk=1]

=5+3-8

= 8-8

Согласно полученному ранее правилу, когда скалярное произведение двух векторов равно нулю, говорят, что они перпендикулярны друг другу. Следовательно, векторы А и В перпендикулярны друг другу.

Два вектора (3i+7j+7k) и (-7i-aj+7k) перпендикулярны друг другу. Найдите значение а.

Сначала нам нужно вычислить скалярное произведение этих двух векторов.

(3i+7j+7k).(-7i-aj+7k)

=(-21-7а+49)

Как мы знаем, в случае перпендикулярных векторов скалярное произведение двух векторов должно быть равно 0. Итак —

(-21-7а+49)=0

Или -7а+28=0

Или 7а=28

Или а=28/7

Или а=4

Подобная концепция не используется ни в какой рабочей силе. Безработная сила – это сила, действующая перпендикулярно направлению перемещения тела.

Вт=ФС

= FScosx

Здесь W = выполненная работа

F= сила

S = смещение

х=90 градусов

W= ФС cos90

Здесь совершенная работа равна 0, что означает, что сила не совершает никакой работы. Следовательно, это называется отсутствием рабочей силы.

Пример

Человек идет по горизонтальной поверхности с грузом на голове. Здесь совершенная работа равна 0, так как сила тяжести и его перемещение на земле перпендикулярны друг другу.

Как найти вектор, перпендикулярный двум векторам?

Здесь применяется условие, что оба вектора, на которых перпендикулярен третий вектор, должны быть непараллельными векторами. Вычислив векторное произведение двух непараллельных векторов, мы сможем получить вектор, перпендикулярный обоим из них по отдельности. Например, A и B — два непараллельных вектора, где A= (a1i+a2j+a3k) и B= (b1i+b2j+b3k), тогда их перпендикулярный вектор будет = перекрестное произведение A и B

векторное произведение двух векторов из википедия

p = (a1i+a2j+a3k)*(b1i+b2j+b3k)

Or, p = (a1b2k-a1b3j-a2b1k+a2b3i+a3b1j-a3b2i)

[Поскольку i*i=0,i*j=k,i*k=-j,j*j=0,j*k=i,j*i=-k,k*k=0,k*i= j,k*j=-i]

Or, p= i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)

Таким образом, искомый перпендикулярный вектор равен i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)

Теперь, если мы хотим перепроверить, перпендикулярен вектор или нет, нам нужно рассмотреть отдельные скалярные произведения pA и pB.

Now, p.A= { i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)}.(a1i+a2j+a3k)

= a1a2b3-a1b2a3+b1a2a3-a1a2b3+a1b2a3-b1a2a3

= 0

And p.B= {i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)}. (b1i+b2j+b3k)

= b1a2b3-b1b2a3+b1b2a3-a1b2b3+a1b2b3-b1a2b3

= 0

Таким образом, из приведенных выше вычислений видно, что перпендикулярный вектор p перпендикулярен обоим векторам A и B по отдельности. Отсюда доказано, что перекрестное произведение двух непараллельных векторов дает перпендикулярный к ним вектор.

Как найти блок вектор перпендикуляр в два векторы?

Возьмем два вектора X и Y.

Компания перекрестное произведение X и Y = X * Y

Величина X и Y равна = |X*Y|

Таким образом, требуемый единичный вектор, перпендикулярный и X, и Y, равен =( X*Y)/ |X*Y|

Пример

A и B — два вектора, где A= (5i+5j+7k) и B= (i+j+k). Найдите единичный вектор, который перпендикулярен и А, и В.

А*В=(5i+5j+7k)*(i+j+k)

= 5k-5j-5k+5i+7j-7i

=-2i+2j

=2(-i+j)

|А*В|=[(-2)^2+(2)^2]^(½)

=2.(2)^(½)

Следовательно, единичный вектор, перпендикулярный A и B = 2(-i+j)/2.(2)^(½)

=(-i+j)/(2)^(½)

Как определить, перпендикулярны ли два вектора?

Чтобы определить, перпендикулярны ли два вектора друг другу или нет, мы должны сначала вычислить их скалярное произведение. По результату мы сможем сделать вывод, перпендикулярны векторы или нет. Значение 0 скалярного произведения означает, что векторы перпендикулярны друг другу, тогда как ненулевое значение означает, что векторы не перпендикулярны друг другу.

Пример

Вес автомобиля F=3i+3j+3k действует вниз. Его перемещение в горизонтальной плоскости равно D=-3i+3j. Что можно сказать о проделанной работе по машине?

Проделанная работа = ФД

=(3i+3j+3k).(-3i+3j+0k)

= -9 + 9

= 0

Здесь в приведенной выше задаче скалярное произведение равно 0. Таким образом, можно сделать вывод, что F и D перпендикулярны друг другу.

Как найти равнодействующую двух перпендикулярных векторов?

результирующий векторная диаграмма из википедия

А+В=Р

Пусть есть два вектора А и В, между которыми есть угол С. Если их результирующая равна R, то величина R будет равна

R = (A ^ 2 + B ^ 2-2ABcosC) ^ (½)

Пример

На тело действуют две силы F1 и F2, причем величина F1 равна 8 Н, а величина F2 равна 6 Н, и они взаимно перпендикулярны. Чему будет равна результирующая сила?

F1=8 Н

F2=6 Н

С= 90 градусов

R= (F1^2+F2^2-2F1F2cosC)^(½)

={(8)^2+(6)^2-2.8.6.cos 90}^(½)

={64+36-0}^(½)

=100^(½)

= 10 Н

Как найти вектор, перпендикулярный трем векторам?

Возьмем три различные точки, лежащие в одной плоскости, но не на одной прямой. Эти точки имеют три разных вектора положения, равные x, y, z соответственно. Пусть r будет вектором положения другой точки на той же плоскости, где лежат остальные три точки. Таким образом, векторы (rx), (yx) и (z-x) компланарны.. Используя формулу для компланарных векторов, можно сказать, что

(рх). (ух)* (zх)=0

Или (rx).(x*y+y*z+z*x)=0

Следовательно, (x*y+y*z+z*x) перпендикулярно (rx) и, следовательно, перпендикулярно плоскости трех различных точек.

Как найти перпендикулярное расстояние между двумя векторами?

Перпендикулярное расстояние — это кратчайшее расстояние между двумя векторами. Формула кратчайшего расстояния между двумя векторами:

Shortest distance=|(b1*b2).(a1-a2)|/|b1*b2|

Пример

r1=(i+j+k)+k1(ijk)

r2=(2i+2j+2k)+k2(2i-2j-2k)

а1=я+j+к

a2=2i+2j+2k

b1=ijk

b2=2i-2j-2k

a2-a1=(2i+2j+2k)-(i+j+k)

=2i+2j+2k-ijk

=я+у+к

b1*b2=(i-j-k)*(2i-2j-2k)

=-2k+2j+2k+2i+2j-2i

= 4j

Shortest distance=|(b1*b2).(a1-a2)|/|b1*b2|

=|4j.(i+j+k)/4|

=|1|

=1 единица

Как найти параллельные и перпендикулярные векторы?

Мы можем использовать следующую формулу, чтобы найти параллельные векторы:

ка=б

Здесь k — константа, а a и b — два вектора.

Пример

Есть два вектора a и b, значения которых равны (3i+6j) и (4i+8j) соответственно. Эти два вектора параллельны друг другу или нет?

По формуле, написанной выше ka=b

к.(3 6)=(4

3к=4 6к=8

Or, k=4/3 or,k=8/6=4/3

Поскольку значения k одинаковы в обоих случаях, векторы a и b параллельны друг другу.

Точно так же мы можем определить, перпендикулярны ли какие-либо два вектора, вычислив их наклоны. Если значение произведения этих наклонов равно -1, то можно сказать, что векторы являются перпендикулярными или ортогональными векторами.

Есть два вектора (3i-5j) и (5i+3j). Определите, перпендикулярны они или нет?

Пусть а=(3i-5j)

и b=(5i+3j)

Следовательно, наклон a=ma=- 5/3 и наклон b=mb= ⅗

Здесь ma.mb=(-5/3)*(⅗)

= -1

Итак, векторы а и b перпендикулярны.

Как найти перпендикулярные векторы в 3D?

Давайте возьмем пример, чтобы получить ответ.

p=(1 2 -2) и q=(-2 2 1). Эти два трехмерных вектора перпендикулярны или нет?

pq= (-2+4-2)

Следовательно, p и q — два перпендикулярных трехмерных вектора.

Прежде чем начать понятие перпендикулярных векторов, сначала нам нужно узнать о векторах. Физические величины, имеющие как величину, так и направление, называются векторами.

AB= AB cos х

АВ=0

АВ, потому что х=0

потому что х=0

потому что х = потому что 90

х = 90

Пример

Значения двух векторов A и B равны (5i+3j-8k) и (i+j+k) соответственно. Эти два вектора перпендикулярны или нет?

=(5i+3j-8k).(i+j+k)

=5i.i+3j.j-8k.k [при ii=1,jj=1 и kk=1]

=5+3-8

= 8-8

2) Два вектора (3i+7j+7k) и (-7i-aj+7k) перпендикулярны друг другу. Найдите значение а.

Сначала нам нужно вычислить скалярное произведение этих двух векторов.

(3i+7j+7k).(-7i-aj+7k)

=(-21-7а+49)

(-21-7а+49)=0

Или -7а+28=0

Или 7а=28

Или а=28/7

Или а=4

Вт=ФС

= FScosx

Здесь W = выполненная работа

F= сила

S = смещение

х=90 градусов

W= ФС cos90

Пример

Как найти вектор, перпендикулярный двум векторам?

Например, A и B — два непараллельных вектора, где A= (a1i+a2j+a3k) и B= (b1i+b2j+b3k), тогда их перпендикулярный вектор будет = перекрестное произведение A и B

p = (a1i+a2j+a3k)*(b1i+b2j+b3k)

Or, p = (a1b2k-a1b3j-a2b1k+a2b3i+a3b1j-a3b2i)

[Поскольку i*i=0,i*j=k,i*k=-j,j*j=0,j*k=i,j*i=-k,k*k=0,k*i= j,k*j=-i]

Or, p= i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)

Таким образом, искомый перпендикулярный вектор равен i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)

Now, p.A= { i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)}.(a1i+a2j+a3k)

= a1a2b3-a1b2a3+b1a2a3-a1a2b3+a1b2a3-b1a2a3

= 0

And p.B= {i(a2b3-a3b2)+j(a3b1-a1b3)+k(a1b2-a2b1)}. (b1i+b2j+b3k)

= b1a2b3-b1b2a3+b1b2a3-a1b2b3+a1b2b3-b1a2b3

= 0

Как найти единичный вектор, перпендикулярный двум векторам?

Возьмем два вектора X и Y.

Перекрестное произведение X и Y равно X*Y

Величина X и Y равна = |X*Y|

Таким образом, требуемый единичный вектор, перпендикулярный и X, и Y, равен =( X*Y)/ |X*Y|

Пример

A и B — два вектора, где A= (5i+5j+7k) и B= (i+j+k). Найдите единичный вектор, который перпендикулярен и А, и В.

А*В=(5i+5j+7k)*(i+j+k)

= 5k-5j-5k+5i+7j-7i

=-2i+2j

=2(-i+j)

|А*В|=[(-2)^2+(2)^2]^(½)

=2.(2)^(½)

Следовательно, единичный вектор, перпендикулярный A и B = 2(-i+j)/2.(2)^(½)

=(-i+j)/(2)^(½)

Как определить, перпендикулярны ли два вектора?

Пример

Проделанная работа = ФД

=(3i+3j+3k).(-3i+3j+0k)

= -9 + 9

= 0

Как найти равнодействующую двух перпендикулярных векторов?

R = (A ^ 2 + B ^ 2-2ABcosC) ^ (½)

Пример

F1=8 Н

F2=6 Н

С= 90 градусов

R= (F1^2+F2^2-2F1F2cosC)^(½)

={(8)^2+(6)^2-2.8.6.cos 90}^(½)

={64+36-0}^(½)

=100^(½)

= 10 Н

Как найти вектор, перпендикулярный трем векторам?

Таким образом, векторы (rx), (yx) и (z-x) компланарны. Используя формулу для компланарных векторов, можно сказать, что

(рх). (ух)* (zх)=0

Или (rx).(x*y+y*z+z*x)=0

Следовательно, (x*y+y*z+z*x) перпендикулярно (rx) и, следовательно, перпендикулярно плоскости трех различных точек.

Как найти перпендикулярное расстояние между двумя векторами?

Shortest distance=|(b1*b2).(a1-a2)|/|b1*b2|

Пример

r1=(i+j+k)+k1(ijk)

r2=(2i+2j+2k)+k2(2i-2j-2k)

а1=я+j+к

a2=2i+2j+2k

b1=ijk

b2=2i-2j-2k

a2-a1=(2i+2j+2k)-(i+j+k)

=2i+2j+2k-ijk

=я+у+к

b1*b2=(i-j-k)*(2i-2j-2k)

=-2k+2j+2k+2i+2j-2i

= 4j

Shortest distance=|(b1*b2).(a1-a2)|/|b1*b2|

=|4j.(i+j+k)/4|

=|1|

=1 единица

Как найти параллельные и перпендикулярные векторы?

Мы можем использовать следующую формулу, чтобы найти параллельные векторы:

ка=б

Здесь k — константа, а a и b — два вектора.

Пример

По формуле, написанной выше ka=b

к.(3 6)=(4

3к=4 6к=8

Or, k=4/3 or,k=8/6=4/3

Поскольку значения k одинаковы в обоих случаях, векторы a и b параллельны друг другу.

Пример

Есть два вектора (3i-5j) и (5i+3j). Определите, перпендикулярны они или нет?

Пусть а=(3i-5j)

и b=(5i+3j)

Следовательно, наклон a=ma=- 5/3 и наклон b=mb= ⅗

Здесь ma.mb=(-5/3)*(⅗)

= -1

Итак, векторы а и b перпендикулярны.

Как найти перпендикулярные векторы в 3D?

Давайте возьмем пример, чтобы получить ответ.

p=(1 2 -2) и q=(-2 2 1). Эти два трехмерных вектора перпендикулярны или нет??

pq= (-2+4-2)

Следовательно, p и q — два перпендикулярных трехмерных вектора.

Источник