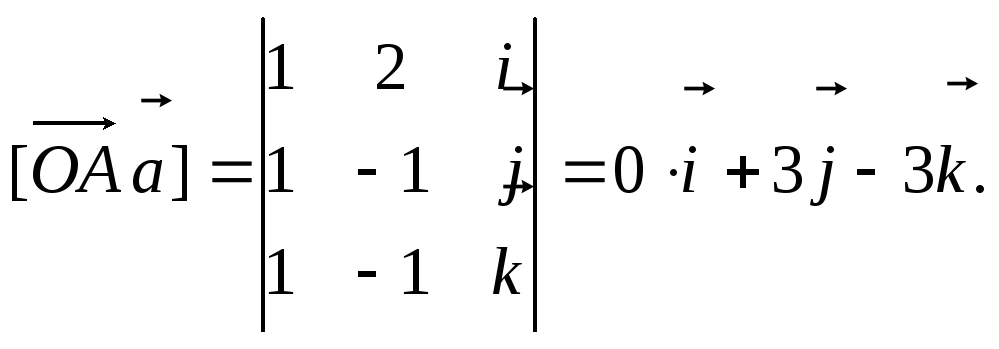Как найти вектор перпендикулярный оси - Исправление недочетов и поиск решений вместе с Examum.ru

векторная-алгебра — Единичный вектор

2 ответа

Пусть $%vec{e}{x;y;z}$% искомый единичный вектор, а $%vec{i}{1;0;0}$% единичный вектор направлнный по оси $%Ox$%. Тогда скалярные поизведения $%vec{e}cdotvec{a}=vec{e}cdotvec{i}=0$% и $%|vec{e}|=1$%. Получаем систему $% begin{cases}x^2+y^2+z^2=1\ 3x+6y+8z=0\ x=0 end{cases}.$% Решив систему найдем $%vec{e}{0;frac{4}{5};-frac{3}{5}}$% или $%vec{e}{0;-frac{4}{5};frac{3}{5}}.$%

Вообще-то, таких векторов два $%frac{[vec{a}times vec{i}]}{|[vec{a}timesvec{i}]|}$% и $%-frac{[vec{a}times vec{i}]}{|[vec{a}timesvec{i}]|}$%.

Здравствуйте

Математика — это совместно редактируемый форум вопросов и ответов для начинающих и опытных математиков, с особенным акцентом на компьютерные науки.

Присоединяйтесь!

отмечен:

векторная-алгебра
×93

задан
23 Ноя ’12 20:50

показан
8040 раз

обновлен
24 Ноя ’12 19:01

Связанные исследования

Связанные вопросы

Отслеживать вопрос

по почте:

Зарегистрировавшись, вы сможете подписаться на любые обновления

по RSS:

Ответы

Ответы и Комментарии

Источник

Анна Кирпиченкова

Эксперт по предмету «Геометрия»

Задать вопрос автору статьи

Понятие вектора и перпендикулярности векторов

Вначале надо разобраться, что является геометрическим вектором. Для этого сначала введем понятие отрезка.

Определение 1

Отрезком будем называть такую часть прямой, которая ограничена точками с двух сторон.

Определение 2

Концами отрезка будем называть точки, которые его ограничивают.

Для введения определения вектора один из концов отрезка назовем его началом.

Определение 3

Вектором (направленным отрезком) будем называть такой отрезок, у которого обозначено, какая граничная точка его начало, а какая является его концом.

Обозначение: $overline{AB}$ — вектор $AB$, имеющий начало в точке $A$, а конец в точке $B$.

Иначе одной маленькой буквой: $overline{a}$ (рис. 1).

Определение 4

Нулевым вектором будем называть любую точку, которая принадлежит плоскости.

Обозначение: $overline{0}$.

Введем теперь, непосредственно, определение коллинеарных векторов.

Определение 5

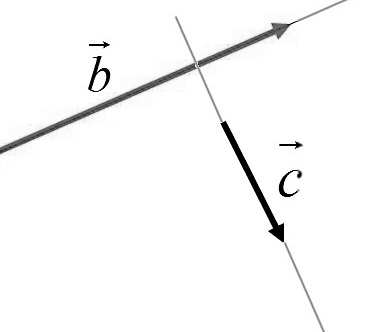
Два ненулевых вектора будем называть перпендикулярными (ортогональными), если они лежат на каких-либо перпендикулярных прямых (рис.2).

«Как найти вектор, перпендикулярный вектору» 👇

Также введем определение скалярного произведения, которое будет нам необходимо далее.

Определение 6

Скалярным произведением двух данных векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.

Математически это может выглядеть следующим образом:

$overline{α}overline{β}=|overline{α}||overline{β}|cos⁡∠(overline{α},overline{β})$

Скалярное произведение также можно найти с помощью координат векторов следующим образом

$overline{α}overline{β}=α_1 β_1+α_2 β_2+α_3 β_3$

Признак перпендикулярности через пропорциональность

Теорема 1

Чтобы ненулевые векторы были перпендикулярны между собой, необходимо и достаточно, чтобы их скалярное произведение этих векторов равнялось нулю.

Доказательство.

Необходимость: Пусть нам даны векторы $overline{α}$ и $overline{β}$, которые имеют координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно, причем они перпендикулярны друг другу. Тогда нам нужно доказать следующее равенство

$overline{α}cdot overline{β}=0$

Так как векторы $overline{α}$ и $overline{β}$ перпендикулярны, то угол между ними равняется $90^0$. Найдем скалярное произведение данных векторов по формуле из определения 6.

$overline{α}cdot overline{β}=|overline{α}||overline{β}|cos⁡90^circ =|overline{α}||overline{β}|cdot 0=0$

Достаточность: Пусть верно равенство $overline{α}cdot overline{β}=0$. Докажем, что векторы $overline{α}$ и $overline{β}$ будут перпендикулярны друг другу.

По определению 6, будет верно равенство

$|overline{α}||overline{β}|cos⁡∠(overline{α},overline{β})=0$

$cos⁡∠(overline{α},overline{β})=0$

$∠(overline{α},overline{β})=90^circ$

Следовательно, векторы $overline{α}$ и $overline{β}$ будут перпендикулярны друг другу.

Теорема доказана.

Пример 1

Доказать, что векторы с координатами $(1,-5,2)$ и $(2,1,3/2)$ перпендикулярны.

Доказательство.

Найдем скалярное произведение для этих векторов через формулу, данную выше

$overline{α}cdot overline{β}=1cdot 2+(-5)cdot 1+2cdot frac{3}{2}=2cdot 5+3=0$

Значит, по теореме 1, эти вектор перпендикулярны.

Нахождение перпендикулярного вектора к двум данным векторам через векторное произведение

Введем вначале понятие векторного произведения.

Определение 7

Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.

Обозначение: $overline{α}хoverline{β}$.

Чтобы найти векторное произведение, будем пользоваться формулой

$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}$

Так как вектор векторного произведения двух векторов перпендикулярен обоим этим векторам, то он и будет иском вектором. То есть, для того, чтоб найти перпендикулярный для двух векторов вектор, нужно просто найти их векторное произведение.

Пример 2

Найти вектор, перпендикулярный к векторам с координатами $overline{α}=(1,2,3)$ и $overline{β}=(-1,0,3)$

Решение.

Найдем векторное произведение данных векторов.

$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\1&2&3\-1&0&3end{vmatrix}=(6-0)overline{i}-(3+3)overline{j}+(0+2)overline{k}=6overline{i}-6overline{j}+2overline{k}=(6,6,2)$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Перпендикулярность векторов

Мы можем выяснить, будут ли два каких-либо вектора взаимно перпендикулярными. Для этого нужно воспользоваться координатами векторов и некоторыми приемами, описанными в данной статье. Информация о перпендикулярности будет полезной для решения некоторых задач физики и математики.

Координаты вектора на плоскости, равного по модулю и перпендикулярного данному

Пусть на плоскости заданы координаты какого-либо вектора. Из этих координат получим координаты двух дополнительных векторов, перпендикулярных первоначальному вектору. Все три вектора будут иметь равные длины и располагаться в плоскости xOy.

Алгоритм получения координат перпендикулярных векторов

Вектор на плоскости xOy, перпендикулярный данному вектору получают так:

Поменять местами координатные числа «x» и «y».
Заменить знак у одной из координат на противоположный.

Графический пример

Рассмотрим небольшой графический пример (рис. 1).

Рис. 1. На рисунке векторы, обозначенные черным цветом, перпендикулярны вектору, обозначенному красным цветом

На плоскости проведены три вектора: один красный и два черных и, отмечены их координаты. Рассмотрим подробнее координаты двух векторов: (vec{a}) и (vec{b}).

[ vec{a} = left{ 4 ; 3 right} ]

[ vec{b} = left{ -3 ; 4 right} ]

Из рисунка видно, что векторы (vec{a}) и (vec{b}) перпендикулярны: ( vec{a} perp vec{b} ).

Вектор ( -vec{b} = left{ 3 ; -4 right} ), также будет перпендикулярным вектору ( vec{a} ): ( vec{a} perp vec{(-b)} )

Векторы, изображенные черным цветом, перпендикулярны красному вектору.

Длины векторов ( vec{a} ), ( vec{b} ) и ( vec{(-b)} ) равны.

Условие перпендикулярности векторов

Взаимную перпендикулярность двух векторов можно проверить, вычислив их скалярное произведение. Этот способ проверки можно применять для векторов, расположенных как на плоскости, так и в трехмерном пространстве.

Векторы будут перпендикулярными, когда их скалярное произведение равно нулю.

Пусть, известны координаты двух векторов и пусть каждый вектор имеет ненулевую длину.

[ large boxed { begin{cases} vec{a} = left{ a_{x} ; a_{y} ; a_{z} right} \ vec{b} = left{ b_{x} ; b_{y} ; b_{z} right} \ |vec{a}| ne 0 \ |vec{b}| ne 0 end{cases}}]

Запишем условие перпендикулярности векторов.

Для двумерного случая:

[ large boxed { a_{x} cdot b_{x} + a_{y} cdot b_{y} = 0 }]

Для трехмерного случая:

[ large boxed { a_{x} cdot b_{x} + a_{y} cdot b_{y} + a_{z} cdot b_{z} = 0 }]

Пользуясь любой из этих формул, можно определить одну неизвестную координату вектора.

При этом, должны быть известными остальные координаты этого вектора и все координаты второго вектора.

Примечание:

Есть такое правило: Количество неизвестных должно равняться количеству уравнений.

Чтобы однозначно определить значение неизвестной, в уравнение должна входить только одна неизвестная. Остальные величины должны быть известными.

Перпендикулярные векторы в физике

В физике перпендикулярность некоторых векторов достаточно важна.

Вот несколько примеров:

Если угол между вектором скорости тела и вектором силы, действующей на тело, будет прямым, то такая сила работу по перемещению тела совершать не будет.
На проводник с током магнитное поле действует максимальной силой, когда вектор магнитной индукции и вектор тока в проводнике перпендикулярны.
Когда угол между вращающей силой и, расстоянием между точкой приложения силы и осью вращения, будет прямым, вращательный момент будет максимальным.
Между линейной скоростью точки колеса и расстоянием от этой точки до оси вращения, угол прямой (радиус и касательная перпендикулярны).
На вращающееся тело действует центростремительная сила. Угол прямой между этой силой и линейной скоростью точки тела (радиус и касательная перпендикулярны).

Оценка статьи:

Загрузка…

Источник

Литература:
[1], гл. 9, § 4, стр. 225–230; [3], гл.1, § 4, стр.
29–30; [27], гл.6, §56, стр.200-204.

Основные
определения, теоремы и формулы

Векторным
произведениемнеколлинеарных векторовииз ориентированного векторного
пространства называется вектор,
обозначаемыйи удовлетворяющий следующим условиям:

1)
где–
направленный угол между векторамии,

2)
вектор
перпендикулярен как вектору,
так и вектору,

3)
– правая тройка векторов.

Из
2) и 3) видно, что вектор
направлен
по правилу “правого винта” при
вращении векторак вектору.

Векторное
произведениеколлинеарных векторов
считается равным нуль-вектору.

Теорема
1. Если векторыив
правом ортонормированном базисе имеют
координатыто вектор

Теорема
2. Векторное произведение двух векторовиравно
нуль-вектору тогда и только тогда, когда
векторыиколлинеарны.

Теорема
3. Модуль векторного произведения
двух векторов равен площади параллелограмма,
построенного на векторах, как на сторонах.

Вопросы
для самоконтроля

Сформулировать
основные свойства векторного произведения
векторов.
Как
найти площадь треугольника ABC, если
в прямоугольной декартовой системе
координат вершины треугольника имеют
координаты:А (а₁, а₂,
а₃), В (b₁, b₂,
b₃), С (с₁, с₂,
с₃)?
Векторы
иперпендикулярны векторуЧто можно сказать о векторе [[]]?
Можно
ли из условия []
= [],
где,
заключить, что=?
Верно
ли утверждение о том, что векторы
иколлинеарны тогда и только тогда, когда
[]
=?
Если да, то почему?
Дан
правильный ортонормированный базис
.
Найти векторные произведения:

а)
[[[[]]]],
б) [(–)(+)],

в)
[[(–)(+ )][(+ )](– )]].

При
каких значениях
справедливо равенство:

[–+ 2,
-3+ 3+]
=?

Что
такое момент силы относительно точки?
Как
определяется направление вектора
магнитной индукциив точке магнитного поля проводника с
током?
Как
определяется направление силы Ампера?
Как
вычислить линейную скорость вращения
точки вокруг неподвижной оси, зная
угловую скорость?

Пример
1. Найти площадьтреугольника, построенного на векторахи.

Решение.
Найдем вектор:

Так
как векторное произведение коллинеарных
векторов равно нулевому вектору, то
Теперь,
зная координатыи, учитывая, что длина вектораравна площади параллелограмма,
построенного на векторахи,
найдем

Тогда

Пример
2. Зная вершинуквадрата,
его центри
векторперпендикулярный
плоскости квадрата, найти остальные
его вершины.

Решение.Так как векторперпендикулярен как вектору,
так и вектору,
токоллинеарен векторуКроме того,и так как векторыиперпендикулярны, тоСледовательно,Зная координаты вектораопределим векторное произведение

Так
как
тоПоэтому вершиныиквадрата соответственно имеют координатыТак как точкасимметрична точкеотносительно начала координат,
то

Задачи

1. Выразить
векторы [2+,+ 3]
и [+,–]
через [].
Найти их длины, если

2.
Вычислить площадь параллелограмма,
построенного на векторах
игдеи–
единичные векторы, величина угла между
которыми равна 60⁰.

3.
Найти площадь треугольника
,
в котором

4.
Найти единичный вектор
перпендикулярный: а) каждому из векторовиб)
векторуи
оси абсцисс.

5.
Вектор
перпендикулярный оси аппликат и векторуобразует острый угол с осью абсцисс.
Зная, чтонайти его координаты.

6.
Сила
приложена к точкеОпределить величину и направление
момента этой силы относительно начала
координат.

7.
Найти векторы
иесли

8. Доказать
тождество: []²+ ()
=²².

9.
Прямая а проходит через точкуА
параллельно вектору.
Доказать, что расстояние от любой точкиВдо прямойвычисляются по формуле:

10.
Даны точки
Доказать, что–
квадрат. Найти вершины куба, для которого
квадратслужит гранью.

11.
Найти вектор, являющийся ортогональной
проекцией вектора
на
плоскость, параллельную векторам

Домашнее
задание

1.
Доказать, что если
то векторы–
компланарны. Верно ли обратное утверждение?

2.
Найти расстояние от точки С(3,2,–2)
до прямой , проходящей через точкиА(1,2,–3),В(5,2,0). Система координат
– прямоугольная декартова.

3.
Ребро куба ABCDA₁B₁C₁D₁равно 1. Найти расстояние между диагональю
куба и скрещивающейся с ней диагональю
грани.

4.
Дан тетраэдр, построенный на векторах
(2,0,0),(3,4,0),(3,4,2)
(базис ортонормированный).

Найти:
а) площади его граней, б) косинус угла
между гранями АВСиADC.

5.
Доказать, что
.

Задачи
повышенной трудности

1. Пусть
– площади граней тетраэдра,– соответствующие этим граням орты
внешних нормалей. Доказать, что

2.
Доказать теорему Мебиуса: В выпуклом
пятиугольнике
площади треугольниковравныПусть– площадь пятиугольника. Доказать, что

3.
Докажите, что параллелепипед является
прямоугольным тогда и только тогда,
когда все его диагонали равны между
собой.

4. Докажите,
что прямоугольный параллелепипед
является кубом тогда и только тогда,
когда его диагональперпендикулярна плоскости.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Как найти перпендикулярный вектор

Перпендикулярными называются вектора, угол между которыми составляет 90º. Перпендикулярные вектора строятся при помощи чертежных инструментов. Если известны их координаты, то проверить или найти перпендикулярность векторов можно аналитическими методами.

Вам понадобится

— транспортир;
— циркуль;
— линейка.

Инструкция

Постройте вектор перпендикулярный данному. Для этого в точке, которая является началом вектора, восстановите к нему перпендикуляр. Это можно сделать при помощи транспортира, отложив угол 90º. Если транспортира нет, сделайте это циркулем.

Установите его в точку начала вектора. Проведите окружность произвольным радиусом. Затем постройте две окружности с центрами в точках, где первая окружность пересекла прямую, на которой лежит вектор. Радиусы этих окружностей должны быть равны между собой и больше радиуса первой построенной окружности. На точках пересечения окружностей постройте прямую, которая будет перпендикулярна исходному вектору в точке его начала, и отложите на ней вектор, перпендикулярный данному.

Определите перпендикулярность двух произвольных векторов. Для этого с помощью параллельного переноса постройте их так, чтобы они исходили из одной точки. Измерьте угол между ними, при помощи транспортира. Если он равен 90º, то вектора перпендикулярны.

Найдите вектор, перпендикулярный тому, координаты которого известны и равны (x;y). Для этого найдите такую пару чисел (x1;y1), которая удовлетворяла бы равенству x•x1+y•y1=0. В этом случае вектор с координатами (x1;y1) будет перпендикулярен вектору с координатами (x;y).

ПримерНайдите вектор, перпендикулярный вектору с координатами (3;4). Используйте свойство перпендикулярных векторов. Подставив в него координаты вектора, получите выражение 3•x1+4•y1=0. Подберите пары чисел, которые делают это тождество верным. Например, пара чисел x1=-4; y1=3 делает тождество верным. Значит, вектор с координатами (-4;3) будет перпендикулярен данному. Таких пар чисел можно подобрать бесконечное множество, а потому и векторов тоже бесконечно много.

Проверяйте перпендикулярность векторов при помощи тождества x•x1+y•y1=0, где (x;y) и (x1;y1) координаты двух векторов. Например, вектора с координатами (3;1) и (-3;9) перпендикулярны, так как 3•(-3)+1•9=0.

Источники:

перпендикулярные векторы

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник