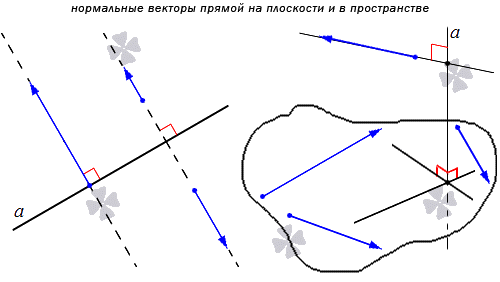
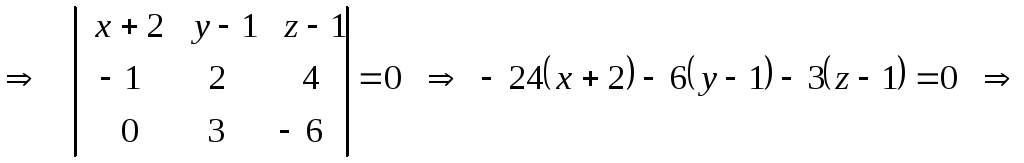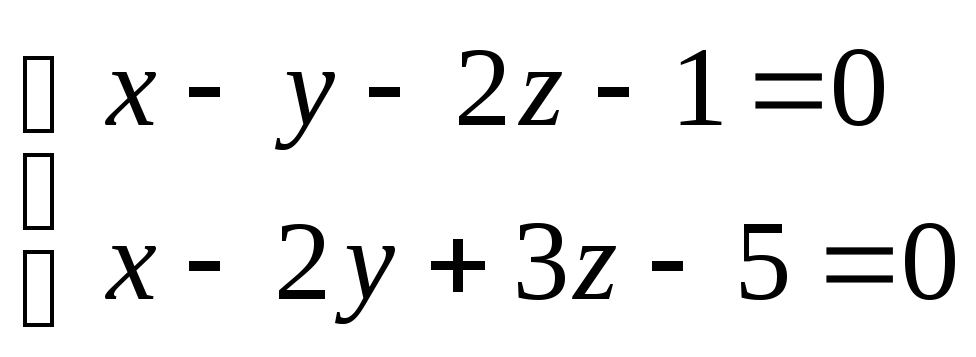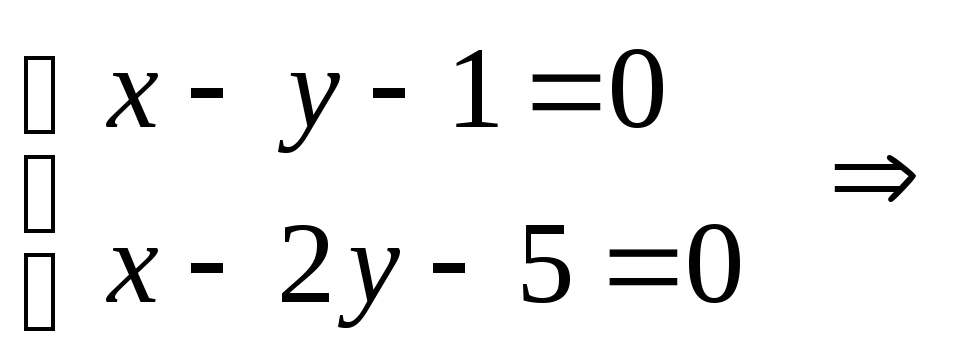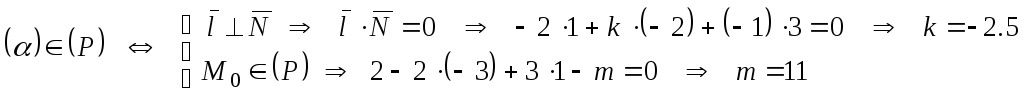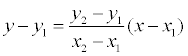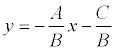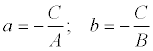Нормальный вектор прямой, координаты нормального вектора прямой
Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.
Нормальный вектор прямой – определение, примеры, иллюстрации
Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.
Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.
Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.
Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а 1 параллельные, а n → считается нормальным вектором прямой a , также считается нормальным вектором для прямой a 1 . Когда прямая а имеет прямой вектор, тогда вектор t · n → является ненулевым при любом значении параметра t , причем также является нормальным для прямой a .
Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.
Если задана плоскость О х у , то множеством векторов для О х является координатный вектор j → . Он считается ненулевым и принадлежащим координатной оси О у , перпендикулярной О х . Все множество нормальных векторов относительно О х можно записать, как t · j → , t ∈ R , t ≠ 0 .
Прямоугольная система O x y z имеет нормальный вектор i → , относящийся к прямой О z . Вектор j → также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный О z , считается нормальным для O z .
Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой
При рассмотрении прямоугольной системы координат О х у выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.
Задана прямая вида 2 x + 7 y — 4 = 0 _, найти координаты нормального вектора.
По условию имеем, что прямая была задана общим уравнением, значит необходимо выписать коэффициенты , которые и являются координатами нормального вектора. Значит, координаты вектора имеют значение 2 , 7 .
Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.
Указать нормальный вектор для заданной прямой y — 3 = 0 .
По условию нам дано общее уравнение прямой, значит запишем его таким образом 0 · x + 1 · y — 3 = 0 . Теперь отчетливо видим коэффициенты, которые и являются координатами нормального вектора. Значит, получаем, что координаты нормального вектора равны 0 , 1 .
Если дано уравнение в отрезках вида x a + y b = 1 или уравнение с угловым коэффициентом y = k · x + b , тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.
Найти координаты нормального вектора, если дано уравнение прямой x 1 3 — y = 1 .
Для начала необходимо перейти от уравнения в отрезках x 1 3 — y = 1 к уравнению общего вида. Тогда получим, что x 1 3 — y = 1 ⇔ 3 · x — 1 · y — 1 = 0 .
Отсюда видно, что координаты нормального вектора имеют значение 3 , — 1 .
Ответ: 3 , — 1 .
Если прямая определена каноническим уравнением прямой на плоскости x — x 1 a x = y — y 1 a y или параметрическим x = x 1 + a x · λ y = y 1 + a y · λ , тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут a → = ( a x , a y ) . Возможность нахождения координат нормального вектора n → возможно, благодаря условию перпендикулярности векторов n → и a → .
Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 = 0
Для решения можно выбирать любой удобный способ.
Найти нормальный вектор заданной прямой x — 2 7 = y + 3 — 2 .
Из прямой x — 2 7 = y + 3 — 2 понятно, что направляющий вектор будет иметь координаты a → = ( 7 , — 2 ) . Нормальный вектор n → = ( n x , n y ) заданной прямой является перпендикулярным a → = ( 7 , — 2 ) .
Выясним, чему равно скалярное произведение. Для нахождения скалярного произведения векторов a → = ( 7 , — 2 ) и n → = ( n x , n y ) запишем a → , n → = 7 · n x — 2 · n y = 0 .
Значение n x – произвольное , следует найти n y . Если n x = 1 , отсюда получаем, что 7 · 1 — 2 · n y = 0 ⇔ n y = 7 2 .
Значит, нормальный вектор имеет координаты 1 , 7 2 .
Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем
x — 2 7 = y + 3 — 2 ⇔ 7 · ( y + 3 ) = — 2 · ( x — 2 ) ⇔ 2 x + 7 y — 4 + 7 3 = 0
Полученный результат координат нормального вектора равен 2 , 7 .
Ответ: 2 , 7 или 1 , 7 2 .
Указать координаты нормального вектора прямой x = 1 y = 2 — 3 · λ .
Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:
x = 1 y = 2 — 3 · λ ⇔ x = 1 + 0 · λ y = 2 — 3 · λ ⇔ λ = x — 1 0 λ = y — 2 — 3 ⇔ x — 1 0 = y — 2 — 3 ⇔ ⇔ — 3 · ( x — 1 ) = 0 · ( y — 2 ) ⇔ — 3 · x + 0 · y + 3 = 0
Отсюда видно, что координаты нормального вектора равны — 3 , 0 .
Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат О х у z .
Когда прямая задается при помощи уравнений пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда нормальный вектор плоскости относится к A 2 x + B 2 y + C 2 z + D 2 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда получаем запись векторов в виде n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .
Когда прямая определена при помощи канонического уравнения пространства, имеющего вид x — x 1 a x = y — y 1 a y = z — z 1 a z или параметрического, имеющего вид x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , отсюда a x , a y и a z считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору a → = ( a x , a y , a z ) . Отсюда следует, что нахождение координат нормального с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору a → = ( a x , a y , a z ) .
2.2.5. Нормальный вектор прямой
Или вектор нормали.
Что такое нормаль? Простыми словами, нормаль – это перпендикуляр. То есть, вектор нормали прямой перпендикулярен данной прямой. Очевидно, что у любой прямой их бесконечно много (так же, как и направляющих векторов), но нам хватит одного:
Если прямая задана общим уравнением 

Обратите внимание, что это утверждение справедливо лишь для «школьной» системы координат; все предыдущие выкладки п. 2.2 работают и в общем аффинном случае.
Вектор нормали всегда ортогонален направляющему вектору прямой. Убедимся в ортогональности данных векторов с помощью скалярного произведения:
И тут всё ещё проще: если координаты направляющего вектора 

Приведу примеры с теми же уравнениями, что и для направляющего вектора:
Можно ли составить уравнение прямой, зная одну точку и вектор нормали? Нутром чувствуется, можно. Ведь вектор нормали ортогонален направляющему вектору и образует с ним «жесткую конструкцию».
Вектор нормали: расчет и пример
Содержание:
В нормальный вектор Он определяет направление, перпендикулярное рассматриваемому геометрическому объекту, который может быть, например, кривой, плоскостью или поверхностью.
Это очень полезная концепция для позиционирования движущейся частицы или какой-либо поверхности в пространстве. На следующем графике можно увидеть, как вектор нормали к произвольной кривой C:
Рассмотрим точку P на кривой C. Точка может представлять движущуюся частицу, которая движется по траектории C. Касательная линия к кривой в точке P нарисована красным.
Обратите внимание, что вектор Т касается C в каждой точке, а вектор N перпендикулярно Т y указывает на центр воображаемого круга, дуга которого является сегментом C. Векторы выделены жирным шрифтом в печатном тексте, чтобы отличать их от других не векторных величин.
Вектор Т он всегда указывает, куда движется частица, следовательно, указывает ее скорость. Вместо вектора N всегда указывает в том направлении, в котором вращается частица, отмечая, таким образом, вогнутость кривой C.
Как получить вектор нормали к плоскости?
Вектор нормали не обязательно является единичным вектором, то есть вектором с модулем 1, но если это так, он называется нормальный единичный вектор.
Во многих приложениях необходимо знать вектор нормали к плоскости вместо кривой. Этот вектор показывает ориентацию указанной плоскости в пространстве. Например, рассмотрим самолет п (желтый) рисунка:
К этой плоскости есть два нормальных вектора: п1 Y п2. Использование того или другого будет зависеть от контекста, в котором находится упомянутый самолет. Получить вектор нормали к плоскости очень просто, если вы знаете его уравнение:
ах + по + cz + d = 0, с участием к, б, c Y d вещественные числа.
Ну, нормальный вектор к указанной плоскости задается следующим образом:
N = а я + b j + c k
Здесь вектор N Он выражается через единичные векторы и перпендикулярно друг другу. я, j Y k, направленных по трем направлениям, определяющим пространство X и Zсм. рисунок 2 справа.
Вектор нормали из векторного произведения
Очень простая процедура нахождения вектора нормали использует свойства векторного произведения между двумя векторами.
Как известно, три разные точки, не лежащие на одной прямой, определяют плоскость Р. Теперь можно получить два вектора или Y v которые принадлежат упомянутой плоскости, имеющей эти три точки.
Когда у вас есть векторы, векторный продуктили Икс v — операция, результатом которой, в свою очередь, является вектор, который имеет свойство быть перпендикулярным плоскости, определяемой или Y v.
Известный этот вектор, он обозначается как N, и из него можно будет определить уравнение плоскости благодаря уравнению, указанному в предыдущем разделе:
N = или Икс v
На следующем рисунке показана описанная процедура:
пример
Найти уравнение плоскости, определяемой точками A (2,1,3); В (0,1,1); С (4.2.1).
Решение
Это упражнение иллюстрирует описанную выше процедуру. Имея 3 точки, одна из них выбирается как общее начало двух векторов, которые принадлежат плоскости, определенной этими точками. Например, точка A устанавливается в качестве начала координат и строятся векторы AB Y AC.
Вектор AB — вектор, начало которого — точка A, а конец — точка B. Координаты вектора AB определяются соответственно вычитанием координат B из координат A:
AB = (0-2) я + (1-1) j + (1-3) k = -2я + 0j -2 k
Таким же образом поступаем и находим вектор AC:
AC = (4-2) я + (2-1) j + (1-3) k = 2я + j -2 k
Расчет векторного произведения AB x AC
Существует несколько процедур для нахождения векторного произведения между двумя векторами. В этом примере используется мнемоническая процедура, которая использует следующий рисунок для поиска векторных произведений между единичными векторами. я, j Y k:
Для начала следует помнить, что векторные произведения между параллельными векторами равны нулю, поэтому:
я Икс я = 0; j Икс j = 0; k Икс k = 0
А поскольку векторное произведение — это еще один вектор, перпендикулярный участвующим векторам, двигаясь в направлении красной стрелки, мы имеем:
я Икс j = k ; j Икс k = я; k Икс я = j
Если вам нужно двигаться в направлении, противоположном стрелке, добавьте знак (-):
j Икс я = – k; k Икс j = –я; я Икс k = –j
Всего можно составить 9 векторных произведений с единичными векторами. я, j Y k, из которых 3 будут нулевыми.
AB Икс AC = (-2я + 0j -2 k) х (2я + j -2 k)= -4(я Икс я) -2(я Икс j)+4 (я Икс k)+0 (j Икс я) + 0 (j Икс j) – 0 (j Икс k) – 4 (k Икс я)-2 (k Икс j) + 4 (k Икс k) = -2k-4j-4j+2я = 2я -8j-2k
Уравнение плоскости
Вектор N был определен с помощью предварительно рассчитанного векторного произведения:
N = 2я -8j-2k
Следовательно, a = 2, b = -8, c = -2, искомая плоскость:
ах + по + cz + d = 0 → 2x-8y-2z + d = 0
Значение d. Это легко сделать, если значения любой из имеющихся точек A, B или C подставить в уравнение плоскости. Выбор C, например:
2,4 — 8,2 — 2,1 + d = 0
Вкратце, искомая карта:
Пытливый читатель может задаться вопросом, был бы такой же результат, если бы вместо выполнения AB Икс AC они бы предпочли произвести AC Икс AB. Ответ: да, плоскость, определяемая этими тремя точками, уникальна и имеет два вектора нормали, как показано на рисунке 2.
Что касается точки, выбранной в качестве исходной точки векторов, нет проблем с выбором любого из двух других.
Ссылки
- Фигероа, Д. (2005). Серия: Физика для науки и техники. Том 1. Кинематика. Отредактировал Дуглас Фигероа (USB). 31-62.
- Нахождение нормали к плоскости. Получено с: web.ma.utexas.edu.
- Ларсон, Р. (1986). Исчисление и аналитическая геометрия. Мак Гроу Хилл. 616-647.
- Линии и плоскости в R 3. Получено с: math.harvard.edu.
- Нормальный вектор. Получено с сайта mathworld.wolfram.com.
Выбор темы исследования: как это делается, важность, примеры
http://mathter.pro/angem/2_2_5_normalnyi_vektor_pryamoy.html
http://ru1.warbletoncouncil.org/vector-normal-6378
8
Занятие 9.
Плоскость
и прямая в пространстве.
9.1. Общее уравнение плоскости. Нормальный
вектор.
9.2. Прямая в пространстве: канонические,
параметрические уравнения.
9.3. Расстояние от точки до плоскости.
Взаимное расположение двух плоскостей,
прямой и плоскости двух прямых в
пространстве.
9.1. Общее уравнение плоскости. Нормальный
вектор.
Общее уравнение плоскости в пространстве
имеет вид
,
где
— числовые коэффициенты,
— координаты произвольной точки плоскости.
Это уравнение получается при решении
следующей задачи.
Задача 1. Найти уравнение плоскости,
проходящей через заданную точку
перпендикулярно вектору
.
Решение. Обозначим искомую плоскость
через
.
Используем далее такую цепочку выводов:
,
где
.
Отметим полную аналогию между общим
уравнением прямой на плоскости
и общим уравнением плоскости в
пространстве.
Из решения задачи видно, что из общего
уравнения плоскости сразу же можно
найти вектор
перпендикулярный плоскости. Этот
вектор называется нормалью (или
нормальным вектором) к плоскости.
Например, из общего уравнения плоскости
( в этом уравнении
)
получаем такой нормальный вектор
.
Коэффициент
не имеет особой смысловой нагрузки,
относительно него можно только сказать,
что при
плоскость проходит через начало координат
,
а при
не проходит через начало координат.
Следует также отметить, что уравнение
задает в пространстве
плоскость с нормалью
,
которая показывает, что данная плоскость
проходит параллельно оси
.
Это же уравнение
на плоскости
определяет прямую.
Аналогично, уравнение
в пространстве
представляет общее уравнение координатной
плоскости
.
Нормалью к этой плоскости служит орт
— единичный вектор положительного
направления оси
.
При нахождении уравнений плоскостей
часто используются условие ортогональности
двух векторов (как это делается в задаче
1) и условие компланарности трех векторов.
Пример 1. Найти уравнение плоскости,
проходящей через три точки
.
Решение. Сначала убедимся, что данные
три точки не лежат на одной прямой (если
эти точки лежат на одной прямой, то
существует бесконечно много плоскостей,
содержащих данные точки). Найдем векторы
.
Их координаты не пропорциональны.
Значит, точки
не лежат на одной прямой и через них
проходит только одна плоскость. Найдем
эту плоскость, которую обозначим
,
двумя способами.
1)
— компланарны
смешанное
произведение векторов
равно нулю
— общее уравнение плоскости
.
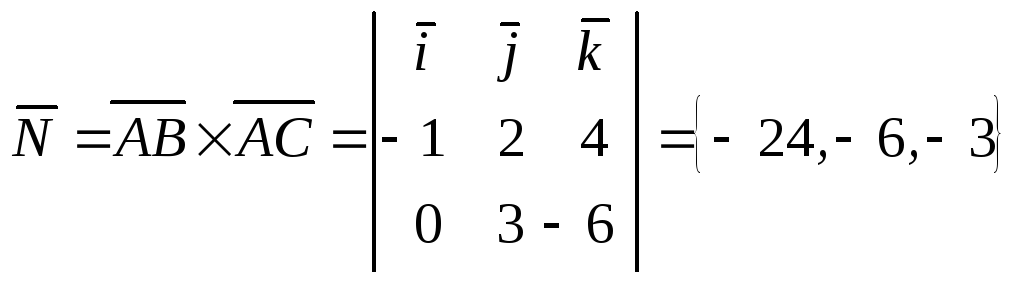
2)
— вектор нормали к плоскости
,
т.к. по определению векторного произведения
перпендикулярен векторам
,
параллельным
.
Дальнейшие рассуждения повторяют
решение задачи 1.
— общее уравнение плоскости
.
Пример 2. Найти уравнение плоскости
,
проходящей через точку
параллельно плоскости
:
.
Решение.
:
— вектор нормали к плоскости
.
Этот же вектор служит вектором нормали
к плоскости
.
Остается повторить решение задачи 1.
— общее уравнение плоскости
.
Пример 3.Найти двугранный угол, под
которым пересекаются плоскостии
.
:
,
:
.
Решение. Двугранный угол
(тупой или острый) между плоскостями
равен углу между их нормалями.
:
,
:
.
—
тупой угол,
. Острый двугранный угол между
и
равен
.
9.2. Прямая в пространстве
:
канонические, параметрические уравнения.
1). Прямую в пространстве
можно определить как линию пересечения
двух плоскостей. Следовательно, система
из двух уравнений плоскостей
,
(1)
задает прямую в пространстве
при обязательном условии, что нормали
,
к этим плоскостям не параллельны.
Если
и
параллельны, то плоскости
,
либо параллельны, либо совпадают. И в
том и другом случае система (1) уже не
будет давать прямую.
Замечание. Задание прямой системой (1)
не совсем удобно, т.к. из него не видно
ни направления прямой, ни одной из точек
на этой прямой. Эту информацию можно
добыть из системы (1) лишь посредством
дополнительных вычислений.
Более предпочтительными в плане
сделанного замечания являются канонические
и параметрические уравнения прямой в
.
2). Канонические уравнения прямой в
пространстве
имеют
вид
.
(2)
Здесь
— заданные числа, они имеют следующий
геометрический смысл:
— координаты фиксированной точки
на прямой;
— координаты направляющего вектора
прямой.
— координаты произвольной точки прямой.
Параметрические уравнения прямой в
имеют вид
(3)
Геометрический смысл величин
и величин
тот же, что и выше.
Уравнения (2),(3) получаются при решении
пространственного варианта задачи 2
из занятия 8.
Замечание. У прямой на плоскости
есть нормаль, которая также как и
направляющий вектор прямой, позволяет
установить направление этой прямой.
Для прямой в пространстве вектор
нормали не имеет смысла, т.к. существует
бесконечно много перпендикулярных к
пространственной прямой векторов с
разным направлением, и один заданный
перпендикулярный к этой прямой вектор
не дает однозначного ответа о ее
направлении.
Пример 4. Найти канонические уравнения
прямой
,
заданной как пересечение двух плоскостей
:
и
:
.
Решение.
Система уравнений
задает прямую
в пространстве, т.к. нормальные векторы
к плоскостям
и
,
а это векторы
и
не параллельны. Найдем две фиксированные
точки
на прямой
.
1. Подставим в систему значение
,
получим
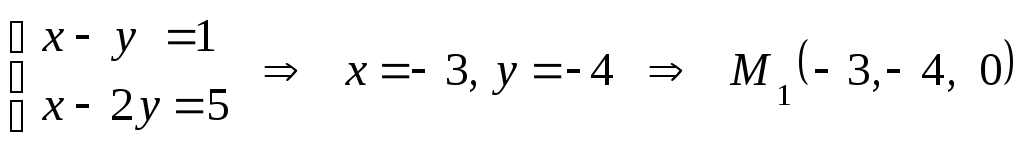
Геометрический смысл точки
:
это — точка пересечения прямой
с плоскостью
.
2. Подставим в систему значение
,
получим

Точка
,
это точка пересечения прямой
с плоскостью
.
3.
— направляющий вектор прямой
.
4.
координаты
векторов
пропорциональны
.
Это и есть каноническое уравнение
прямой
.
5. Замечание. Направляющий вектор прямой
можно было найти по векторам
и
.
Для этого надо вычислить векторное
произведение
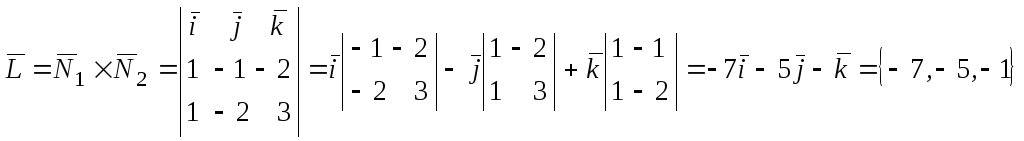
Вектор
перпендикулярен векторам
и
одновременно. Следовательно,
параллелен прямой
и служит другим (по сравнению с вектором
)
направляющим вектором этой прямой.
Кстати:
,
что тоже указывает на параллельность
вектора
прямой
.
При таком подходе канонические уравнения
прямой
получаются после выполнения пунктов
1., 4. и 5. изложенного решения. Только
ответ уже получится в виде
.
Пример 5. Найти параметрические
уравнения прямой
,
проходящей через точку
перпендикулярно плоскости
:
.
Решение.
— вектор нормали к плоскости
.
Этот вектор параллелен прямой
и, значит, является ее направляющим
вектором. Следовательно,
— ответ.
Пример 6. Найти канонические и
параметрические уравнения прямой
,
проходящей через точку
параллельно прямой
:
.
Решение.
— направляющий вектор прямой
.
Этот же вектор является направляющим
вектором искомой прямой
.
Следовательно,
координаты
векторов
пропорциональны
— канонические уравнения прямой
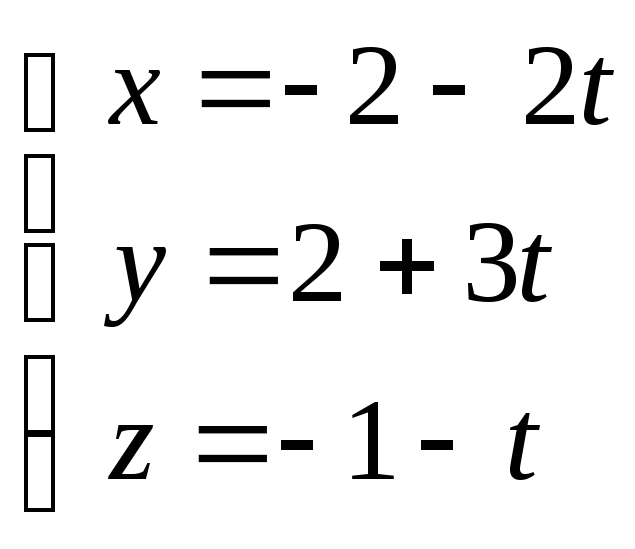
параметрические уравнения прямой
.
9.3. Расстояние от точки до плоскости.
Взаимное расположение двух плоскостей,
прямой и плоскости, двух прямых в
пространстве.
Расстояние
от точки
до плоскости
находится по формуле
.
Наиболее полезную информацию о взаимном
расположении двух плоскостей, прямой
и плоскости, двух прямых в пространстве
можно извлечь из направляющих векторов
прямых и нормалей к плоскостям.
Пример 8. Найти расстояние
от точки
до плоскости
.
Решение.
.
Пример 9. При каком значении параметра
плоскость
:
параллельна плоскости
:
?
Решение. Плоскости параллельны тогда
и только тогда, когда коллинеарны их
нормальные векторы
и
,
т.е. должно быть
.
Это двойное равенство не выполняется
ни при каком
,
т.к.
.
Следовательно, плоскости
и
не параллельны при всех значениях
параметра
.
Пример 10. При каких значениях
параметров
прямая
:
лежит в плоскости
:
?
Решение.
По каноническим уравнениям прямой
запишем ее параметрические уравнения

все точки прямой
удовлетворяют уравнению плоскости

ответ:
.
Можно эту задачу решить по другому.
— направляющий вектор прямой
и
— фиксированная точка этой прямой.
— вектор нормали к плоскости
.
Далее строим такую цепочку рассуждений.
.
Пример 11. Выяснить взаимное
расположение двух прямых
:
и
:
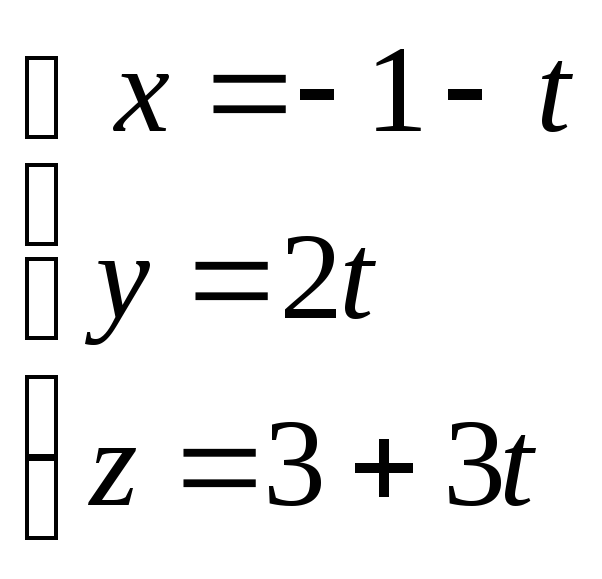
Решение. Прямые в пространстве могут
скрещиваться, могут пересекаться в
одной точке, могут быть параллельны,
могут совпадать. Выясним, какой из
указанных четырех случаев реализуется
в этом примере.
Из уравнения
выводим:
и
.
Из уравнения
выводим:
и
.
.
Если прямые
и
пересекаются или параллельны, или
совпадают, то тройка векторов
— компланарна. А если прямые
и
скрещиваются, то тройка векторов
-некомпланарна. Найдем смешанное
произведение этих трех векторов.
тройка
-некомпланарна
прямые
и
скрещиваются.
Приведенные в занятиях 8, 9 примеры
наглядно демонстрируют мощь векторных
методов и исключительную роль условий:
коллинеарности двух векторов;
ортогональности двух векторов;
компланарности трех векторов при
нахождении уравнений прямых и плоскостей.
Домашнее задание.
1. Найти общее
уравнение плоскости, проходящей через
три точки
.
2. Найти канонические и параметрические
уравнения прямой, являющейся пересечением
плоскостей
.
3. Найти точку
пересечения прямой, проходящей через
точку
перпендикулярно плоскости
,
с этой плоскостью.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
5.2.3. Вектор нормали плоскости (нормальный вектор)
Вектор нормали плоскости – это вектор, который перпендикулярен данной плоскости. Очевидно, что у любой плоскости бесконечно много нормальных векторов.
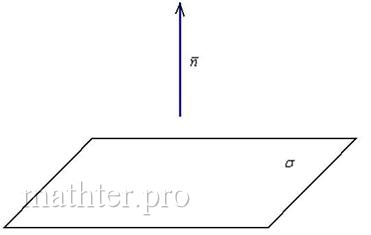
Но для решения задач нам будет хватать и одного: если плоскость задана общим уравнением в прямоугольной (!) системе координат, то вектор
является нормальным вектором данной плоскости.
Просто до безобразия! – всё, что нужно сделать – это «снять» коэффициенты из уравнения плоскости. И чтобы хоть как-то усложнить практику рассмотрим тоже простую, но очень важную задачу, которая часто встречается, причём, не только в геометрии:
Задача 134
Найти единичный нормальный вектор плоскости .
Решение: принципиально ситуация выглядит так:
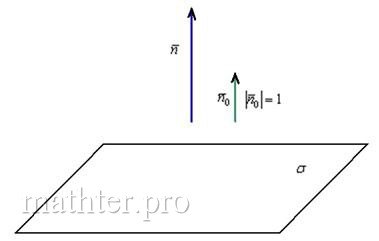
Сначала из уравнения плоскости «снимем» вектор нормали: .
И эту задачку мы уже решали: для того чтобы найти единичный вектор , нужно каждую координату вектора
разделить на длину вектора
.
Вычислим длину вектора нормали:
Таким образом:
Контроль: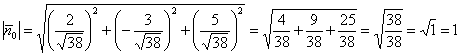
Ответ:
Вспоминаем, что координаты этого вектора – есть в точности направляющие косинусы вектора :
.
И, как говорится, обещанного три страницы ждут 
и двум векторам
, и в результате решения мы получили уравнение
.
Проверяем:
Во-первых, подставим координаты точки в полученное уравнение:
– получено верное равенство, значит, точка
лежит в данной плоскости.
На втором шаге из уравнения плоскости «снимаем» вектор нормали: . Поскольку векторы
параллельны плоскости, а вектор
ей перпендикулярен, то должны иметь место следующие факты:
. Ортогональность векторов элементарно проверяется с помощью скалярного произведения:
Вывод: уравнение плоскости найдено правильно.
В ходе проверки я фактически процитировал следующее утверждение теории: вектор параллелен плоскости
в том и только том случае, когда
.
Итак, с «выуживанием» нормального вектора разобрались, теперь ответим на противоположный вопрос:


| Оглавление |
Автор: Aлeксaндр Eмeлин
Как найти вектор нормали к прямой
Содержание
- Уравнение прямой, проходящей через две точки
- Уравнение прямой по точке и угловому коэффициенту
- Уравнение прямой по точке и направляющему вектору
- Уравнение прямой в отрезках
- Нормальное уравнение прямой
- Нормальный вектор прямой – определение, примеры, иллюстрации
- Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой
Определение. В декартовой прямоугольной системе координат вектор с компонентами (А, В) перпендикулярен прямой , заданной уравнением Ах + Ву + С = 0.
Пример. Найти уравнение прямой, проходящей через точку А(1, 2) перпендикулярно вектору 
Решение. Составим при А = 3 и В = -1 уравнение прямой: 3х – у + С = 0. Для нахождения коэффициента С подставим в полученное выражение координаты заданной точки А. Получаем: 3 – 2 + C = 0, следовательно С = -1. Итого: искомое уравнение: 3х – у – 1 = 0.
Уравнение прямой, проходящей через две точки
Пусть в пространстве заданы две точки M 1 ( x 1 , y 1 , z 1 ) и M2 ( x 2, y 2 , z 2 ), тогда уравнение прямой, проходящей через эти точки:
Если какой- либо из знаменателей равен нулю, следует приравнять нулю соответствующий числитель.На плоскости записанное выше уравнение прямой упрощается:
Дробь 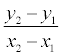
Пример. Найти уравнение прямой, проходящей через точки А(1, 2) и В(3, 4).
Решение. Применяя записанную выше формулу, получаем:
Уравнение прямой по точке и угловому коэффициенту
Если общее уравнение прямой Ах + Ву + С = 0 привести к виду:
и обозначить 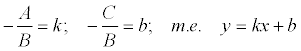
Уравнение прямой по точке и направляющему вектору
По аналогии с пунктом, рассматривающим уравнение прямой через вектор нормали можно ввести задание прямой через точку и направляющий вектор прямой.
Определение. Каждый ненулевой вектор 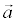
Пример. Найти уравнение прямой с направляющим вектором 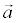
Решение. Уравнение искомой прямой будем искать в виде: Ax + By + C = 0. В соответствии с определением, коэффициенты должны удовлетворять условиям:
1 * A + (-1) * B = 0, т.е. А = В.
Тогда уравнение прямой имеет вид: Ax + Ay + C = 0, или x + y + C / A = 0. при х = 1, у = 2 получаем С/ A = -3, т.е. искомое уравнение:
Уравнение прямой в отрезках
Если в общем уравнении прямой Ах + Ву + С = 0 С≠0, то, разделив на –С, получим: 
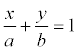
Геометрический смысл коэффициентов в том, что коэффициент а является координатой точки пересечения прямой с осью Ох, а b – координатой точки пересечения прямой с осью Оу.
Пример. Задано общее уравнение прямой х – у + 1 = 0. Найти уравнение этой прямой в отрезках.
С = 1, 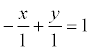
Нормальное уравнение прямой
Если обе части уравнения Ах + Ву + С = 0 разделить на число 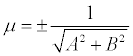
xcosφ + ysinφ — p = 0 –
нормальное уравнение прямой. Знак ± нормирующего множителя надо выбирать так, чтобы μ * С 2 .
Решение. Уравнение прямой имеет вид: 
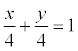
Пример. Составить уравнение прямой, проходящей через точку А(-2, -3) и начало координат.
Решение. Уравнение прямой имеет вид: 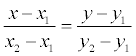
Для изучения уравнений прямой линии необходимо хорошо разбираться в алгебре векторов. Важно нахождение направляющего вектора и нормального вектора прямой. В данной статье будут рассмотрены нормальный вектор прямой с примерами и рисунками, нахождение его координат, если известны уравнения прямых. Будет рассмотрено подробное решение.
Нормальный вектор прямой – определение, примеры, иллюстрации
Чтобы материал легче усваивался, нужно разбираться в понятиях линия, плоскость и определениями, которые связаны с векторами. Для начала ознакомимся с понятием вектора прямой.
Нормальным вектором прямой называют любой ненулевой вектор, который лежит на любой прямой, перпендикулярной данной.
Понятно, что имеется бесконечное множество нормальных векторов, расположенных на данной прямой. Рассмотрим на рисунке, приведенном ниже.
Получаем, что прямая является перпендикулярной одной из двух заданных параллельных прямых, тогда ее перпендикулярность распространяется и на вторую параллельную прямую. Отсюда получаем, что множества нормальных векторов этих параллельных прямых совпадают. Когда прямые a и а 1 параллельные, а n → считается нормальным вектором прямой a , также считается нормальным вектором для прямой a 1 . Когда прямая а имеет прямой вектор, тогда вектор t · n → является ненулевым при любом значении параметра t , причем также является нормальным для прямой a .
Используя определение нормального и направляющего векторов, можно прийти к выводу, что нормальный вектор перпендикулярен направляющему. Рассмотрим пример.
Если задана плоскость О х у , то множеством векторов для О х является координатный вектор j → . Он считается ненулевым и принадлежащим координатной оси О у , перпендикулярной О х . Все множество нормальных векторов относительно О х можно записать, как t · j → , t ∈ R , t ≠ 0 .
Прямоугольная система O x y z имеет нормальный вектор i → , относящийся к прямой О z . Вектор j → также считается нормальным. Отсюда видно, что любой ненулевой вектор, расположенный в любой плоскости и перпендикулярный О z , считается нормальным для O z .
Координаты нормального вектора прямой – нахождение координат нормального вектора прямой по известным уравнениям прямой
При рассмотрении прямоугольной системы координат О х у выявим, что уравнение прямой на плоскости соответствует ей, а определение нормальных векторов производится по координатам. Если известно уравнение прямой, а необходимо найти координаты нормального вектора, тогда необходимо из уравнения A x + B y + C = 0 выявить коэффициенты, которые и соответствуют координатам нормального вектора заданной прямой.
Задана прямая вида 2 x + 7 y — 4 = 0 _, найти координаты нормального вектора.
По условию имеем, что прямая была задана общим уравнением, значит необходимо выписать коэффициенты , которые и являются координатами нормального вектора. Значит, координаты вектора имеют значение 2 , 7 .
Бывают случаи, когда A или В из уравнения равняется нулю. Рассмотрим решение такого задания на примере.
Указать нормальный вектор для заданной прямой y — 3 = 0 .
По условию нам дано общее уравнение прямой, значит запишем его таким образом 0 · x + 1 · y — 3 = 0 . Теперь отчетливо видим коэффициенты, которые и являются координатами нормального вектора. Значит, получаем, что координаты нормального вектора равны 0 , 1 .
Если дано уравнение в отрезках вида x a + y b = 1 или уравнение с угловым коэффициентом y = k · x + b , тогда необходимо приводить к общему уравнению прямой, где можно найти координаты нормального вектора данной прямой.
Найти координаты нормального вектора, если дано уравнение прямой x 1 3 — y = 1 .
Для начала необходимо перейти от уравнения в отрезках x 1 3 — y = 1 к уравнению общего вида. Тогда получим, что x 1 3 — y = 1 ⇔ 3 · x — 1 · y — 1 = 0 .
Отсюда видно, что координаты нормального вектора имеют значение 3 , — 1 .
Ответ: 3 , — 1 .
Если прямая определена каноническим уравнением прямой на плоскости x — x 1 a x = y — y 1 a y или параметрическим x = x 1 + a x · λ y = y 1 + a y · λ , тогда получение координат усложняется. По данным уравнениям видно, что координаты направляющего вектора будут a → = ( a x , a y ) . Возможность нахождения координат нормального вектора n → возможно, благодаря условию перпендикулярности векторов n → и a → .
Имеется возможность получения координат нормального вектора при помощи приведения канонического или параметрического уравнений прямой к общему. Тогда получим:
x — x 1 a x = y — y 1 a y ⇔ a y · ( x — x 1 ) = a x · ( y — y 1 ) ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x — x 1 a x = y — y 1 a y ⇔ a y · x — a x · y + a x · y 1 — a y · x 1 = 0
Для решения можно выбирать любой удобный способ.
Найти нормальный вектор заданной прямой x — 2 7 = y + 3 — 2 .
Из прямой x — 2 7 = y + 3 — 2 понятно, что направляющий вектор будет иметь координаты a → = ( 7 , — 2 ) . Нормальный вектор n → = ( n x , n y ) заданной прямой является перпендикулярным a → = ( 7 , — 2 ) .
Выясним, чему равно скалярное произведение. Для нахождения скалярного произведения векторов a → = ( 7 , — 2 ) и n → = ( n x , n y ) запишем a → , n → = 7 · n x — 2 · n y = 0 .
Значение n x – произвольное , следует найти n y . Если n x = 1 , отсюда получаем, что 7 · 1 — 2 · n y = 0 ⇔ n y = 7 2 .
Значит, нормальный вектор имеет координаты 1 , 7 2 .
Второй способ решения сводится к тому, что необходимо прийти к общему виду уравнения из канонического. Для этого преобразуем
x — 2 7 = y + 3 — 2 ⇔ 7 · ( y + 3 ) = — 2 · ( x — 2 ) ⇔ 2 x + 7 y — 4 + 7 3 = 0
Полученный результат координат нормального вектора равен 2 , 7 .
Ответ: 2 , 7 или 1 , 7 2 .
Указать координаты нормального вектора прямой x = 1 y = 2 — 3 · λ .
Для начала необходимо выполнить преобразование для перехода в общему виду прямой. Выполним:
x = 1 y = 2 — 3 · λ ⇔ x = 1 + 0 · λ y = 2 — 3 · λ ⇔ λ = x — 1 0 λ = y — 2 — 3 ⇔ x — 1 0 = y — 2 — 3 ⇔ ⇔ — 3 · ( x — 1 ) = 0 · ( y — 2 ) ⇔ — 3 · x + 0 · y + 3 = 0
Отсюда видно, что координаты нормального вектора равны — 3 , 0 .
Рассмотрим способы для нахождения координат нормального вектора при уравнении прямой в пространстве, заданной прямоугольной системой координат О х у z .
Когда прямая задается при помощи уравнений пересекающихся плоскостей A 1 x + B 1 y + C 1 z + D 1 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда нормальный вектор плоскости относится к A 2 x + B 2 y + C 2 z + D 2 = 0 и A 2 x + B 2 y + C 2 z + D 2 = 0 , тогда получаем запись векторов в виде n 1 → = ( A 1 , B 1 , C 1 ) и n 2 → = ( A 2 , B 2 , C 2 ) .
Когда прямая определена при помощи канонического уравнения пространства, имеющего вид x — x 1 a x = y — y 1 a y = z — z 1 a z или параметрического, имеющего вид x = x 1 + a x · λ y = y 1 + a y · λ z = z 1 + a z · λ , отсюда a x , a y и a z считаются координатами направляющего вектора заданной прямой. Любой ненулевой вектор может быть нормальным для данной прямой, причем являться перпендикулярным вектору a → = ( a x , a y , a z ) . Отсюда следует, что нахождение координат нормального с параметрическими и каноническими уравнениями производится при помощи координат вектора, который перпендикулярен заданному вектору a → = ( a x , a y , a z ) .
В аналитической геометрии часто требуется составить общее уравнение прямой по принадлежащей ей точке и вектору нормали к прямой.
Нормаль – синоним для слова перпендикуляр.
Общее уравнение прямой на плоскости выглядит как $Ax + By + C = 0$. Подставляя в него различные значениях $A$, $B$ и $C$, в том числе нулевые, можно определить любые прямые.
Можно выразить уравнение прямой и другим способом:
Это уравнение прямой с угловым коэффициентом. В нем геометрический смысл коэффициента $k$ заключается в угле наклона прямой по отношению к оси абсцисс, а независимого члена $b$ — в расстоянии, на которое прямая отстоит от центра координатной плоскости, т.е. точки $O(0; 0)$.
Рисунок 1. Варианты расположения прямых на координатной плоскости. Автор24 — интернет-биржа студенческих работ
Нормальное уравнение прямой можно выразить и в тригонометрическом виде:
$x cdot cos <alpha>+ y cdot sin <alpha>- p = 0$
где $alpha$ — угол между прямой и осью абсцисс, а $p$ — расстояние от начала координат до рассматриваемой прямой.
Попробуй обратиться за помощью к преподавателям
Возможны четыре варианта зависимости наклона прямой от величины углового коэффициента:
- когда угловой коэффициент положителен, направляющий вектор прямой идёт снизу вверх;
- когда угловой коэффициент отрицателен, направляющий вектор прямой идёт сверху вниз;
- когда угловой коэффициент равен нулю, описываемая им прямая параллельна оси абсцисс;
- для прямых, параллельных оси ординат, углового коэффициента не существует, поскольку тангенс 90 градусов является неопределенной (бесконечной) величиной.
Чем больше абсолютное значение углового коэффициента, тем круче наклонен график прямой.
Зная угловой коэффициент, легко составить уравнение графика прямой, если дополнительно известна точка, принадлежащая искомой прямой:
$y — y_0 = k cdot (x — x_0)$
Таким образом, геометрически прямую на координатной всегда можно выразить с помощью угла и расстояния от начала координат. В этом и заключается смысл нормального вектора к прямой — самого компактного способа записи ее положения, если известны координаты хотя бы одной точки, принадлежащей этой прямой.
Задай вопрос специалистам и получи
ответ уже через 15 минут!
Вектором нормали к прямой, иначе говоря, нормальным вектором прямой, принято называть ненулевой вектор, перпендикулярный рассматриваемой прямой.
Для каждой прямой можно найти бесконечное множество нормальных векторов, равно как и направляющих векторов, т.е. таких, которые параллельны этой прямой. При этом все нормальные векторы к ней будут коллинеарными, хотя и не обязательно сонаправлены.
Обозначив нормальный вектор прямой как $vec(n_1; n_2)$, а координаты точки как $x_0$ и $y_0$, можно представить общее уравнение прямой на плоскости по точке и вектору нормали к прямой как
$n_1 cdot (x — x_n) + n_2 cdot (y — y_0) = 0$
Таким образом, координаты вектора нормали к прямой пропорциональны числам $A$ и $B$, присутствующим в общем уравнении прямой на плоскости. Следовательно, если известно общее уравнение прямой на плоскости, то можно легко вывести и вектор нормали к прямой. Если прямая, задана уравнением в прямоугольной системе координат
то нормальный вектор описывается формулой:
При этом говорят, что координаты нормального вектора «снимаются» с уравнения прямой.
Нормальный к прямой вектор и ее направляющий вектор всегда ортогональны по отношению друг к другу, т.е. их скалярные произведения равны нулю, в чем легко убедиться, вспомнив формулу направляющего вектора $ar
(-B; A)$, а также общее уравнение прямой по направляющему вектору $ar
(p_1; p_2)$ и точке $M_0(x_0; y_0)$:
В том, что вектор нормали к прямой всегда ортогонален направляющему вектору к ней можно убедиться с помощью скалярного произведения:
$ar
cdot ar = -B cdot A + A cdot B = 0 implies ar
perp ar$
Всегда можно составить уравнение прямой, зная координаты принадлежащей ей точки и нормального вектора, поскольку направление прямой следует из его направления. Описав точку как $M(x_0; y_0)$, а вектор как $ar(A; B)$, можно выразить уравнение прямой в следующем виде:
$A(x — x_0) + B(y — y_0) = 0$
Составить уравнение прямой по точке $M(-1; -3)$ и нормальному вектору $ar(3; -1)$. Вывести уравнение направляющего вектора.
Для решения задействуем формулу $A cdot (x — x_0) + B cdot (y — y_0) = 0$
Подставив значения, получаем:
$3 cdot (x — (-1)) — (-1) cdot (y — (-3)) = 0$ $3 cdot (x + 1) — (y + 3) = 0$ $3x + 3 — y — 3 = 0$ $3x — y = 0$
Проверить правильность общего уравнения прямой можно «сняв» из него координаты для нормального вектора:
$3x — y = 0 implies A = 3; B = -1 implies ar(A; B) = ar(3; -1),$
Что соответствует числам исходных данных.
Подставив реальные значения, проверим, удовлетворяет ли точка $M(-1; -3)$ уравнению $3x — y = 0$:
Равенство верно. Осталось лишь найти формулу направляющего вектора:
$ar
(-B; A) implies ar
(1; 3)$
Ответ: $3x — y = 0; ar
(1; 3).$
Так и не нашли ответ
на свой вопрос?
Просто напиши с чем тебе
нужна помощь
Наталья Игоревна Восковская
Эксперт по предмету «Математика»
Задать вопрос автору статьи
В аналитической геометрии часто требуется составить общее уравнение прямой по принадлежащей ей точке и вектору нормали к прямой.
Замечание 1
Нормаль – синоним для слова перпендикуляр.
Общее уравнение прямой на плоскости выглядит как $Ax + By + C = 0$. Подставляя в него различные значениях $A$, $B$ и $C$, в том числе нулевые, можно определить любые прямые.
Можно выразить уравнение прямой и другим способом:
$y = kx + b$.
Это уравнение прямой с угловым коэффициентом. В нем геометрический смысл коэффициента $k$ заключается в угле наклона прямой по отношению к оси абсцисс, а независимого члена $b$ — в расстоянии, на которое прямая отстоит от центра координатной плоскости, т.е. точки $O(0; 0)$.
Рисунок 1. Варианты расположения прямых на координатной плоскости. Автор24 — интернет-биржа студенческих работ
Нормальное уравнение прямой можно выразить и в тригонометрическом виде:
$x cdot cos{alpha} + y cdot sin{alpha} — p = 0$
где $alpha$ — угол между прямой и осью абсцисс, а $p$ — расстояние от начала координат до рассматриваемой прямой.
Возможны четыре варианта зависимости наклона прямой от величины углового коэффициента:
- когда угловой коэффициент положителен, направляющий вектор прямой идёт снизу вверх;
- когда угловой коэффициент отрицателен, направляющий вектор прямой идёт сверху вниз;
- когда угловой коэффициент равен нулю, описываемая им прямая параллельна оси абсцисс;
- для прямых, параллельных оси ординат, углового коэффициента не существует, поскольку тангенс 90 градусов является неопределенной (бесконечной) величиной.
«Нормальный вектор прямой» 👇
Чем больше абсолютное значение углового коэффициента, тем круче наклонен график прямой.
Зная угловой коэффициент, легко составить уравнение графика прямой, если дополнительно известна точка, принадлежащая искомой прямой:
$y — y_0 = k cdot (x — x_0)$
Таким образом, геометрически прямую на координатной всегда можно выразить с помощью угла и расстояния от начала координат. В этом и заключается смысл нормального вектора к прямой — самого компактного способа записи ее положения, если известны координаты хотя бы одной точки, принадлежащей этой прямой.
Определение 1
Вектором нормали к прямой, иначе говоря, нормальным вектором прямой, принято называть ненулевой вектор, перпендикулярный рассматриваемой прямой.
Для каждой прямой можно найти бесконечное множество нормальных векторов, равно как и направляющих векторов, т.е. таких, которые параллельны этой прямой. При этом все нормальные векторы к ней будут коллинеарными, хотя и не обязательно сонаправлены.
Обозначив нормальный вектор прямой как $vec{n}(n_1; n_2)$, а координаты точки как $x_0$ и $y_0$, можно представить общее уравнение прямой на плоскости по точке и вектору нормали к прямой как
$n_1 cdot (x — x_n) + n_2 cdot (y — y_0) = 0$
Таким образом, координаты вектора нормали к прямой пропорциональны числам $A$ и $B$, присутствующим в общем уравнении прямой на плоскости. Следовательно, если известно общее уравнение прямой на плоскости, то можно легко вывести и вектор нормали к прямой. Если прямая, задана уравнением в прямоугольной системе координат
$Ax + By + C = 0$,
то нормальный вектор описывается формулой:
$bar{n}(A; B)$.
При этом говорят, что координаты нормального вектора «снимаются» с уравнения прямой.
Нормальный к прямой вектор и ее направляющий вектор всегда ортогональны по отношению друг к другу, т.е. их скалярные произведения равны нулю, в чем легко убедиться, вспомнив формулу направляющего вектора $bar{p}(-B; A)$, а также общее уравнение прямой по направляющему вектору $bar{p}(p_1; p_2)$ и точке $M_0(x_0; y_0)$:
$frac{x — x_0}{p_1} = frac{y — y_0}{p_2}$
В том, что вектор нормали к прямой всегда ортогонален направляющему вектору к ней можно убедиться с помощью скалярного произведения:
$bar{p} cdot bar{n} = -B cdot A + A cdot B = 0 implies bar{p} perp bar{n}$
Всегда можно составить уравнение прямой, зная координаты принадлежащей ей точки и нормального вектора, поскольку направление прямой следует из его направления. Описав точку как $M(x_0; y_0)$, а вектор как $bar{n}(A; B)$, можно выразить уравнение прямой в следующем виде:
$A(x — x_0) + B(y — y_0) = 0$
Пример 1
Составить уравнение прямой по точке $M(-1; -3)$ и нормальному вектору $bar(3; -1)$. Вывести уравнение направляющего вектора.
Для решения задействуем формулу $A cdot (x — x_0) + B cdot (y — y_0) = 0$
Подставив значения, получаем:
$3 cdot (x — (-1)) — (-1) cdot (y — (-3)) = 0$
$3 cdot (x + 1) — (y + 3) = 0$
$3x + 3 — y — 3 = 0$
$3x — y = 0$
Проверить правильность общего уравнения прямой можно «сняв» из него координаты для нормального вектора:
$3x — y = 0 implies A = 3; B = -1 implies bar{n}(A; B) = bar{n}(3; -1),$
Что соответствует числам исходных данных.
Подставив реальные значения, проверим, удовлетворяет ли точка $M(-1; -3)$ уравнению $3x — y = 0$:
$3 cdot (-1) — (-3) = 0$
Равенство верно. Осталось лишь найти формулу направляющего вектора:
$bar{p}(-B; A) implies bar{p}(1; 3)$
Ответ: $3x — y = 0; bar{p}(1; 3).$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме