Как найти вектор равнодействующей двух сил

Кикоин А.К. Когда к телу приложены параллельные силы //Квант. — 1985. — № 2. — С. 23-25.

По специальной договоренности с редколлегией и редакцией журнала «Квант»

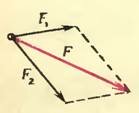
Хорошо известно, как найти равнодействующую двух сил, приложенных к материальной точке (рис. 1). На векторах, изображающих эти силы, как на сторонах строят параллелограмм; диагональ со стрелкой на конце, проведенная из точки, к которой приложены силы, и есть вектор равнодействующей.

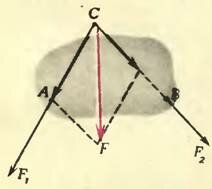
Когда две силы приложены не к материальной точке, а к телу, но так, как показано на рисунке 2, то равнодействующая определяется таким же образом. Пользуясь тем, что точку приложения силы можно переносить вдоль линии ее действия («Физика 8», § 46), находят точку С, в которой пересекаются линии действия обеих сил.

Полагая, что силы (~vec F_1) и (~vec F_2) приложены именно к этой точке, строят параллелограмм и проводят диагональ. Правда, точка С может оказаться и вне тела, но тогда точку приложения равнодействующей можно выбрать в любом месте на линии ее действия. Действительно, какую бы точку мы не выбрали, равнодействующая сила (~vec F) сообщит телу такое же ускорение или вызовет такой же вращающий момент, как и силы (~vec F_1) и (~vec F_2), вместе взятые.

Если силы параллельны и направлены в одну сторону

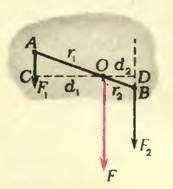
Пусть к телу приложены две параллельные сонаправленные силы (рис. 3). Линии действия таких сил нигде не пересекаются, и параллелограмм на них построить нельзя. Тем не менее сложить эти силы и найти их равнодействующую можно.

Нетрудно понять, что равнодействующая направлена параллельно обеим силам и ее модуль равен арифметической сумме модулей складываемых сил. А в какой точке она приложена? Или, другими словами, к какой точке тела надо приложить силу, равную по модулю, но противоположную по направлению равнодействующей, чтобы тело находилось в равновесии?

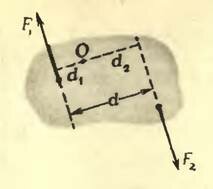
Чтобы найти точку приложения равнодействующей двух параллельных и одинаково направленных сил, можно воспользоваться правилом моментов («Физика 8», § 48). Проведем прямую, соединяющую точки А и В (см. рис. 3). Где-то на этой прямой должна, очевидно, находиться и точка приложения равнодействующей. Пусть это будет точка О. Допустим, что через эту точку проходит закрепленная ось, перпендикулярная плоскости, содержащей обе складываемые силы (то есть перпендикулярная плоскости рисунка). Если О действительно есть точка приложения равнодействующей, то тело будет находиться в равновесии — равнодействующая уравновешивается силой реакции со стороны оси. С другой стороны, если тело с закрепленной осью находится в равновесии, то алгебраическая сумма моментов сил относительно этой оси должна быть равна нулю. Из рисунка 3 видно, что сила (~vec F_2), будь она единственной, поворачивала бы тело вокруг О по часовой стрелке, то есть ее момент F₂d₂ положительный, а сила (~vec F_1) если бы она была единственной, поворачивала бы тело против часовой стрелки — ее моменту F₁d₁ надо приписать отрицательный знак (здесь d₁ и d₂ — плечи сил (~vec F_1) и (~vec F_2)).

Следовательно,

(~F_2 d_2 — F_1 d_1 = 0), или (~frac{F_1}{F_2} = frac{d_2}{d_1}) .

Из подобия треугольников АОС и BOD находим, что (~frac{d_1}{d_2} = frac{r_1}{r_2}) . Поэтому окончательно получаем

(~frac{F_1}{F_2} = frac{r_2}{r_1}) .

Это значит, что равнодействующая двух параллельных, одинаково направленных сил приложена к точке, делящей отрезок, соединяющий точки приложения складываемых сил, в отношении, обратном отношению модулей сил. Ясно, что эта точка лежит ближе к большей из сил.

Если направления параллельных сил противоположны

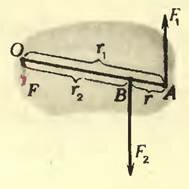
Приложенные к телу параллельные силы могут быть направлены и в противоположные стороны (рис. 4). Теперь точка приложения равнодействующей (~vec F) не может находиться где-то между точками приложения сил (~vec F_1) и (~vec F_2). Ведь вокруг любой точки, лежащей между ними, каждая сила поворачивает тело против часовой стрелки, знаки моментов этих сил одинаковы, и их сумма не может быть равна нулю, как это требуется для равновесия.

Легко догадаться, что точка приложения равнодействующей лежит за точкой приложения большей силы, как это и показано на рисунке 4. Модуль же равнодействующей равен модулю разности модулей сил (~vec F_1) и (~vec F_2). В какой же именно точке приложена равнодействующая? На каком расстоянии r₂ от точки приложения большей силы? Воспользуемся опять правилом моментов:

(~frac{F_1}{F_2} = frac{r_2}{r_1}), или (~F_2 = F_1 frac{r_1}{r_2}) .

Вычтем из правой и левой частей последнего равенства величину F₁:

(~F_2 — F_1 = F_1 frac{r_1}{r_2} — F_1 = F_1 left( frac{r_1}{r_2} — 1 right) = F_1 frac{r_1 — r_2}{r_2}) ,

откуда

(~r_2 = frac{F_1(r_1 — r_2)}{F_2 — F_1} = frac{F_1 r}{F_2 — F_1}) . (*)

Таким образом, точка приложения равнодействующей двух противоположно направленных параллельных сил расположена тем дальше от точки приложения большей из них, чем меньше разность модулей этих сил.

Пара сил

Мы видели, что если к телу приложены параллельные силы, одинаково или противоположно направленные, то всегда можно найти модуль и направление равнодействующей этих сил и определить точку ее приложения. Если к этой точке приложить силу, равную равнодействующей по модулю, но противоположную ей по направлению, то тело будет находиться в равновесии — оно не будет двигаться поступательно и не будет вращаться.

Но, оказывается, есть один случай, когда равнодействующую найти нельзя. Так бывает, если к телу приложены две параллельные, противоположно направленные силы, по модулю равные друг другу. Про такие силы говорят, что они образуют пару сил. Модуль их равнодействующей равен, конечно, нулю, а из формулы (*) видно, что при F₂ — F₁ =0 расстояние r₂ до точки приложения равнодействующей равно бесконечности, то есть что такой точки попросту не существует. И в самом деле, какая же может быть точка приложения равнодействующей, которой нет?

Достаточно, однако, взглянуть на рисунок 5, чтобы понять, что под действием пары сил тело не будет находиться в равновесии — оно будет вращаться. Значит, у пары сил есть некоторый вращающий момент. Но относительно какой оси?

Нетрудно показать, что суммарный момент сил, составляющих пару, одинаков для любой оси, перпендикулярной плоскости, в которой лежат обе эти силы (перпендикулярной плоскости рисунка). Действительно, возьмем любую точку О и проведем через нее ось вращения. Момент M₁ силы (~vec F_1) относительно этой оси равен F₁d₁, момент M₂ силы (~vec F_2) относительно этой же оси равен F₂d₂. Суммарный момент М обеих сил равен M₁ + M₂ :

(~M = F_1 d_1 + F_2 d_2) .

Так как F₁ = F₂ = F, то

(~M = F (d_1 + d_2) = Fd) ,

где d — расстояние между линиями действия сил, составляющих пару, называемое плечом пары сил. Значит, момент пары сил равен произведению модуля одной из сил на плечо пары. Так и говорят — момент пары сил — и не указывают относительно какой оси.

Как же все-таки «ведет» себя тело, к которому приложена пара сил? Чтобы ответить на этот вопрос, вспомним, что центр масс тела (о нем говорится в § 44 «Физики 8») движется так, как будто в нем сосредоточена вся масса тела и к нему приложены все действующие на тело силы (это утверждение называется в физике теоремой о движении центра масс). Но если сумма сил равна нулю, то центр масс не может тронуться с места (если, конечно, он покоился до приложения сил). Когда на тело действует пара сил, сумма сил как раз и равна нулю, и она не может привести в движение центр масс. Тело, однако, вращается. Значит, вращается оно вокруг оси, проходящей через центр масс (ведь все точки на оси вращения находятся в покое). Оси вращения, проходящие через центры масс тел, тем и замечательны, что на них не действуют никакие силы.

Сила реакции опоры (сила, направленная вверх) короче силы тяжести, так как шарик движется по окружности, центростремительное ускорение направлено вниз. Вектор силы тяжести, направленный вниз, длиннее.

Нахождение равнодействующей силы

Для того, чтобы найти равнодействующую силу, необходимо: во-первых, верно обозначить все силы, действующие на тело; затем изобразить координатные оси, выбрать их направления; на третьем шаге необходимо определить проекции векторов на оси; записать уравнения. Кратко: 1) обозначить силы; 2) выбрать оси, их направления; 3) найти проекции сил на оси; 4) записать уравнения.

Как записать уравнения? Если в некотором направлении тело двигается равномерно или покоится, то алгебраическая сумма (с учетом знаков) проекций сил равна нулю. Если в некотором направлении тело движется равноускоренно, то алгебраическая сумма проекций сил равна произведению массы на ускорение, согласно второму закону Ньютона.

Примеры

На движущееся равномерно по горизонтальной поверхности тело, действуют сила тяжести, сила реакции опоры, сила трения и сила, под действием которой тело движется.

Обозначим силы, выберем координатные оси

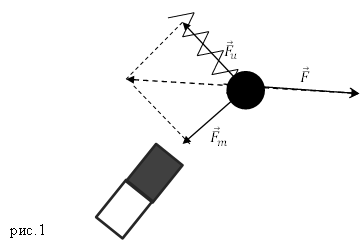
Тело, которое прижимают к вертикальной стенке, равноускоренно движется вниз. На тело действуют сила тяжести, сила трения, реакция опоры и сила, с которой прижимают тело. Вектор ускорения направлен вертикально вниз. Равнодействующая сила направлена вертикально вниз.

Тело равноускоренно движется по клину, наклон которого альфа. На тело действуют сила тяжести, сила реакции опоры, сила трения.

Главное запомнить

1) Если тело покоится или движется равномерно, то равнодействующая сила равна нулю и ускорение равно нулю;
2) Если тело движется равноускоренно, значит равнодействующая сила не нулевая;
3) Направление вектора равнодействующей силы всегда совпадает с направлением ускорения;
4) Уметь записывать уравнения проекций действующих на тело сил

Системы и блоки*

Блок — механическое устройство, колесо, вращающееся вокруг своей оси. Блоки могут быть подвижными и неподвижными.

Неподвижный блок используется лишь для изменения направления силы.

Тела, связанные нерастяжимой нитью, имеют одинаковые по величине ускорения.

Подвижный блок предназначен для изменения величины прилагаемых усилий. Если концы веревки, обхватывающей блок, составляют с горизонтом равные между собой углы, то для подъёма груза потребуется сила вдвое меньше, чем вес груза. Действующая на груз сила относится к его весу, как радиус блока к хорде дуги, обхваченной канатом.

Ускорение тела А в два раза меньше ускорения тела В.

Фактически, любой блок представляет собой рычаг, в случае неподвижного блока — равноплечий, в случае подвижного — с соотношением плеч 1 к 2. Как и для всякого другого рычага, для блока справедливо правило: во сколько раз выигрываем в усилии, во столько же раз проигрываем в расстоянии

Также используется система, состоящая из комбинации нескольких подвижных и неподвижных блоков. Такая система называется полиспаст.

Законы сложения сил в механике

При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.

Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:

R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .

Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.

Правило параллелограмма и правило многоугольника

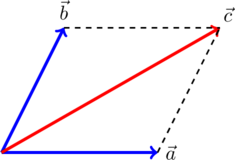
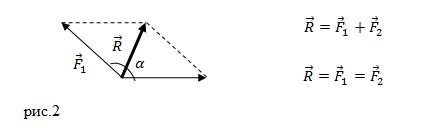
Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).

Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма

Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:

R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α

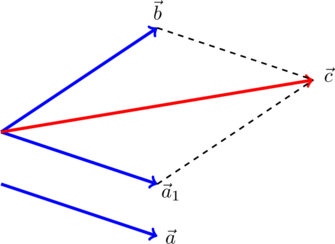
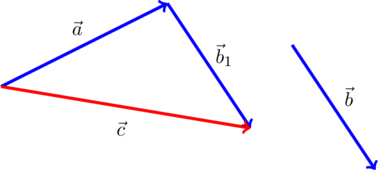
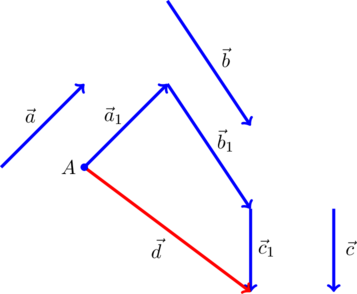
При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.

Рисунок 2 . Сложение сил правилом многоугольника

Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.

Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.

Линией действия силы называют прямую, проходящую через вектор силы.

Рисунок 3 . Сложение сил, приложенных к различным точкам тела

Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.

Разложение вектора силы по направлениям

Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.

Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:

• направления 2 -х составляющих сил;
• модуль и направление одной из составляющих сил;
• модули 2 -х составляющих сил.

Пример 1

Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.

Рисунок 4 . Разложение вектора силы по направлениям

Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).

Рисунок 5 . Нахождение проекции вектора силы по заданным векторам

Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .

Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .

Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.

Решение

Рисунок 6 . Нахождение равнодействующей силы по заданным векторам

Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .

Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .

Модуль равнодействующей определим с помощью теоремы Пифагора:

F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .

Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):

t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .

Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.

Решение

Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна

Дано:

F = 1 к Н = 1000 Н

Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что

F 1 → = F t g β ≈ 577 Н ;

F 2 → = F cos β ≈ 1155 Н .

Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .

Формула равнодействующей всех сил

Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline$ — это векторная величина, то есть она обладает модулем (величиной) и направлением.

Определение и формула равнодействующей всех сил

В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:

На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:

Формула (2) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.

Основной закон динамики поступательного движения при наличии нескольких сил

Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:

$overline=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.

При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.

Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.

Примеры задач на равнодействующую сил

Задание. На материальную точку действуют две силы, направленные под углом $alpha =60<>^circ $ друг к другу. Чему равна равнодействующая этих сил, если $F_1=20 $Н; $F_2=10 $Н?

Решение. Сделаем рисунок.

Силы на рис. 1 складываем по правилу параллелограмма. Длину равнодействующей силы $overline$ можно найти, используя теорему косинусов:

Вычислим модуль равнодействующей силы:

[F=sqrt<<20>^2+<10>^2+2cdot 20cdot 10<cos (60<>^circ ) >>approx 26,5 left(Нright).]

Ответ. $F=26,5$ Н

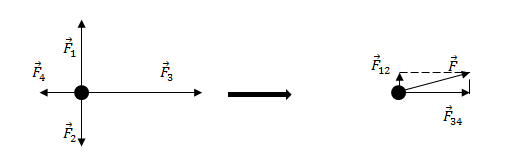
Задание. На материальную точку действуют силы (рис.2). Какова равнодействующая этих сил?

Решение. Равнодействующая сил, приложенных к точке (рис.2) равна:

Найдем равнодействующую сил $<overline>_1$ и $<overline>_2$. Эти силы направлены вдоль одной прямой, но в противоположные стороны, следовательно:

Так как $F_1>F_2$, то сила $<overline>_<12>$ направлена в туже сторону, что и сила $<overline>_1$.

Найдем равнодействующую сил $<overline>_3$ и $<overline>_4$. Данные силы направлены вдоль одной вертикальной прямой (рис.1), значит:

Направление силы $<overline>_<34>$ совпадает с направлением вектора $<overline>_3$, так как $<overline>_3><overline>_4$.

Равнодействующую, которая действует на материальную точку, найдем как:

Силы $<overline>_<12>$ и $<overline>_<34>$ взаимно перпендикулярны. Найдем длину вектора $overline$ по теореме Пифагора:

Модуль равнодействующей силы

Четверг, 24 декабря, 2015

В данной статье рассказано о том, как найти модуль равнодействующей сил, действующих на тело. Репетитор по математике и физике объяснит вам, как найти суммарный вектор равнодействующей сил по правилу параллелограмма, треугольника и многоугольника. Материал разобран на примере решения задачи из ЕГЭ по физике.

Как найти модуль равнодействующей силы

Сила, которая оказывает на материальную точку такое же действие, как и несколько других сил, называется равнодействующей этих сил. Для нахождения вектора равнодействующей силы необходимо геометрически (векторно) сложить все силы, которые действуют на материальную точку.

Напомним, что сложить векторы геометрически можно с помощью одного из трех правил: правила параллелограмма, правила треугольника или правила многоугольника. Разберём каждое из этих правил в отдельности.

1. Правило параллелограмма. На рисунке по правилу параллелограмма складываются векторы и . Суммарный вектор есть вектор :

Если векторы и не отложены от одной точки, нужно заменить один из векторов равным и отложить его от начала второго вектора, после чего воспользоваться правилом параллелограмма. Например, на рисунке вектор заменен на равный ему вектор , и :

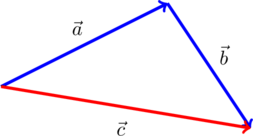
2. Правило треугольника. На рисунке по правилу треугольника складываются векторы и . В сумме получается вектор :

Если вектор отложен не от конца вектора , нужно заменить его равным и отложенным от конца вектора , после чего воспользоваться правилом треугольника. Например, на рисунке вектор заменен равным ему вектором , и :

3. Правило многоугольника. Для того, чтобы сложить несколько векторов по правилу параллелограмма, необходимо от произвольной точки отложить вектор, равный первому складываемому вектору, от его конца отложить вектор, равный второму складываемому вектору, и так далее. Суммарным будет вектор, проведенный из точки в конец последнего отложенного вектора. На рисунке :

Задача на нахождение модуля равнодействующей силы

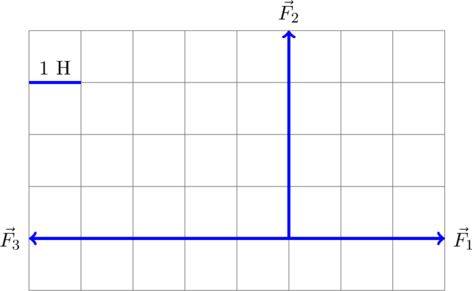
Разберем задачу на нахождение равнодействующей сил на конкретном примере из демонстрационного варианта ЕГЭ по физике 2016 года.

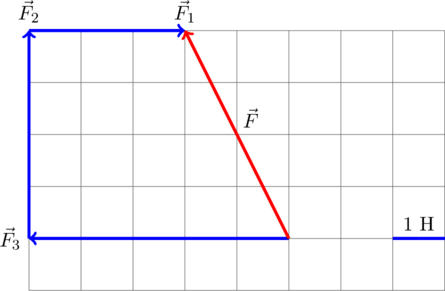
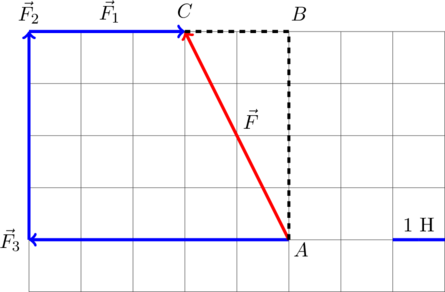
Для нахождения вектора равнодействующей сил найдём геометрическую (векторную) сумму всех изображенных сил, используя правило многоугольника. Упрощенно говоря (не вполне корректно с математической точки зрения), каждый последующий вектор нужно отложить от конца предыдущего. Тогда суммарный вектор будет исходить из точки, из который отложен первоначальный вектор, и приходить в точку, где заканчивается последний вектор:

Требуется найти модуль равнодействующей сил, то есть длину получившегося вектора. Для этого рассмотрим вспомогательный прямоугольный треугольник :

Требуется найти гипотенузу этого треугольника. «По клеточкам» находим длину катетов: Н, Н. Тогда по теореме Пифагора для этого треугольника получаем: Н. То есть искомый модуль равнодействующей сил равен Н.

Итак, сегодня мы разобрали, как находить модуль равнодействующей силы. Задачи на нахождение модуля равнодействующей силы встречаются в вариантах ЕГЭ по физике. Для решения этих задач необходимо знать определение равнодействующей сил, а также уметь складывать векторы по правилу параллелограмма, треугольника или многоугольника. Стоит немного потренироваться, и вы научитесь решать эти задачи легко и быстро. Удачи вам в подготовке к ЕГЭ по физике!

Репетитор по физике на Юго-Западной
Сергей Валерьевич

Формула равнодействующей всех сил в физике

Формула равнодействующей всех сил

Первый закон Ньютона говорит нам о том, что в инерциальных системах отсчета тела могут изменять скорость только, если на них оказывают воздействие другие тела. При помощи силы ($overline{F}$) выражают взаимное действие тел друг на друга. Сила способна изменить величину и направление скорости тела. $overline{F}$ — это векторная величина, то есть она обладает модулем (величиной) и направлением.

Определение и формула равнодействующей всех сил

В классической динамике основным законом, с помощью которого находят направление и модуль равнодействующей силы является второй закон Ньютона:

[overline{F}=moverline{a} left(1right),]

где $m$ — масса тела, на которое действует сила $overline{F}$; $overline{a}$ — ускорение, которое сила $overline{F}$ сообщает рассматриваемому телу. Смысл второго закона Ньютона заключается в том, что силы, которые действуют на тело, определяют изменение скорости тела, а не просто его скорость. Следует знать, что второй закон Ньютона выполняется для инерциальных систем отсчета.

На тело могут действовать не одна, а некоторая совокупность сил. Суммарное действие этих сил характеризуют, используя понятие равнодействующей силы. Пусть на тело оказывают действие в один и тот же момент времени несколько сил. Ускорение тела при этом равно сумме векторов ускорений, которые возникли бы при наличии каждой силы отдельно. Силы, которые оказывают действие на тело, следует суммировать в соответствии с правилом сложения векторов. Равнодействующей силой ($overline{F}$) называют векторную сумму всех сил, которые оказывают действие на тело в рассматриваемый момент времени:

[overline{F}={overline{F}}_1+{overline{F}}_2+dots +{overline{F}}_N=sumlimits^N_{i=1}{{overline{F}}_i} left(2right).]

Формула (2) — это формула равнодействующей всех сил, приложенных к телу. Равнодействующая сила является искусственной величиной, которую вводят для удобства проведения вычислений. Равнодействующая сила направлена как вектор ускорения тела.

Основной закон динамики поступательного движения при наличии нескольких сил

Если на тело действуют несколько сил, тогда второй закон Ньютона записывают как:

[sumlimits^N_{i=1}{{overline{F}}_i}=moverline{a}left(3right).]

$overline{F}=0$, если силы, приложенные к телу, взаимно компенсируют друг друга. Тогда в инерциальной системе отсчета скорость движения тела постоянна.

При изображении сил, действующих на тело, на рисунке, в случае равноускоренного движения, равнодействующую силу, изображают длиннее, чем сумму сил, которые противоположно ей направлены. Если тело перемещается с постоянной скоростью или покоится, длины векторов сил (равнодействующей и сумме остальных сил), одинаковы и направлены они в противоположные стороны.

Когда находят равнодействующую сил, на рисунке изображают все учитываемые в задаче силы. Суммируют эти силы в соответствии с правилами сложения векторов.

Примеры задач на равнодействующую сил

Читать дальше: формула равнодействующей силы.