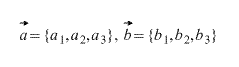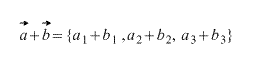Как найти вектор равный сумме трех векторов - Исправление недочетов и поиск решений вместе с Examum.ru

Сложение векторов: длина суммы векторов и теорема косинусов

Определения скалярного произведения векторов через угол между ними

Сложение векторов по правилу треугольника (суммой векторов и называется вектор , начало которого совпадает с началом вектора , а конец — с концом вектора , при условии, что начало вектора приложено к концу вектора ) даёт возможность упрощать выражение перед вычислением произведений векторов.

Сложение векторов, заданных координатами (при сложении одноимённые координаты складываются) даёт возможность узнать, как расположен относительно начала координат вектор, являющийся суммой слагаемых векторов. Подробно эти две операции разбирались на уроке «Векторы и операции над векторами».

Теперь же нам предстоит узнать, как найти длину вектора, являющегося результатом сложения векторов. Для этого потребуется использовать теорему косинусов. Такую задачу приходится решать, например, когда дорога из пункта A в пункт С — не прямая, а отклоняется от прямой, чтобы пройти ещё через какой-то пункт B, а нужно узнать длину предполагаемой прямой дороги. Кстати, геодезия — одна из тех сфер деятельности, где тригонометрические функции применяются во всех их полноте.

При сложении векторов для нахождения длины суммы векторов используется теорема косинусов. Пусть и — векторы, — угол между ними, а — сумма векторов как результат сложения векторов по правилу треугольника. Тогда верно следующее соотношение:

где — угол, смежный с углом . У смежных углов одна сторона общая, а другие стороны лежат на одной прямой (см. рисунок выше).

Поэтому для сложения векторов и определения длины суммы векторов нужно извлечь квадратный корень из каждой части равенства, тогда получится формула длины:

В случае вычитания векторов () происходит сложение вектора с вектором , противоположным вектору , то есть имеющим ту же длину, но противоположным по направлению. Углы между и и и между и являются смежными углами, у них, как уже было отмечено, одна сторона общая, а другие стороны лежат на одной прямой. В случае вычитания векторов для нахождения длины разности векторов нужно знать следующее свойство косинусов смежных углов:

косинусы смежных углов равны по абсолютной величине (величине по модулю), но имеют противоположные знаки.

Перейдём к примерам.

Сложение векторов — решение примеров

Пример 1. Векторы и образуют угол . Их длины: и . Выполнить сложение векторов и найти их сумму . Выполнить вычитание векторов и найти их разность .

Решение. Из элементарной тригонометрии известно, что .

Шаг 1. Выполняем сложение векторов. Находим длину суммы векторов, поставляя в формулу длины косинус угла, смежного с углом между векторами:

Шаг 2. Выполняем вычитание векторов. Находим длину разности векторов, подставляя в формулу косинус «изначального» угла:

Выполнить сложение и вычитание векторов самостоятельно, а затем посмотреть решение

Пример 2. Векторы и образуют угол . Их длины: и . Выполнить сложение векторов и найти их сумму . Выполнить вычитание векторов и найти их разность .

Пример 3. Даны длины векторов и длина их суммы . Найти длину их разности .

Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус угла, смежного с углом между векторами и находим его:

Не забываем, что косинус смежного угла получился со знаком минус. Это значит, что косинус «изначального» угла будет со знаком плюс.

Пример 4. Даны длины векторов и длина их разности . Найти длину их суммы .

Шаг 1. По теореме косинусов составляем уравнение, чтобы найти косинус «изначального» угла (задача обратная по отношению к примеру 1) и находим его:

Шаг 2. Меняем знак косинуса и получаем косинус смежного угла между и :

Шаг 3. Выполняем сложение векторов. Находим длину суммы векторов, подставляя в формулу косинус смежного угла:

Пример 5. Векторы и взаимно перпендикулярны, а их длины . Найти длину их суммы и и длину их разности .

Два смежных угла, как нетрудно догадаться из приведённого в начале урока определения, в сумме составляют 180 градусов. Следовательно, смежный с прямым углом (90 градусов) угол — тоже прямой (тоже 90 градусов). Косинус такого угла равен нулю, то же самое относится и к косинусу смежного угла. Поэтому, подставляя это значение в выражения под корнем в формуле длины суммы и разности векторов, получаем нули как последние выражения — произведения под знаком корня. То есть длины суммы и разности данных векторов равны, вычисляем их:

Пример 6. Какому условию должны удовлетворять векторы и , чтобы имели место слелующие соотношения:

1) длина суммы векторов равна длине разности векторов, т. е. ,

2) длина суммы векторов больше длины разности векторов, т. е. ,

3) длина суммы векторов меньше длины разности векторов, т. е. ?

Находим условие для первого соотношения. Для этого решаем следующее уравнение:

То есть, для того, чтобы длина суммы векторов была равна длине их разности, необходимы, чтобы косинус угла между ними и косинус смежного ему угла были равны. Это условие выполняется, когда углы образуют прямой угол.

Находим условие для второго соотношения. Решаем уравнение:

Найденное условие выполняется, когда косинус угла между векторами меньше косинуса смежных углов. То есть, чтобы длина суммы векторов была больше длины разности векторов, необходимо, чтобы углы образовали острый угол (пример 1).

Находим условие для третьего соотношения. Решаем уравнение:

Найденное условие выполняется, когда косинус угла между векторами больше косинуса смежных углов. То есть, чтобы длина суммы векторов была меньше длины разности векторов, необходимо, чтобы углы образовали тупой угол.

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор.

Сложение векторов. Векторная сумма. Правила сложения векторов. Геометрическая сумма. Он-лайн калькулятор

В механике существуют два типа величин:

скалярные величины, задающие некоторое числовое значение — время, температура, масса и т.д.
векторные величины, которые вместе с некоторым числовым значением задают направление — скорость, сила и т.д..

Рассмотрим сначала алгебраический подход к сложению векторов.

Покоординатное сложение векторов.

Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:

В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.

Теперь перейдем к геометрическому смыслу сложения двух векторов:

При сложении векторов нужно учитывать и их числовые значения, и направления. Есть несколько широко используемых методов сложения:

правило параллелограмма
правило треугольника
тригонометрический способ

Правило параллелограмма. Сложение векторов по правилу параллелограмма.

Процедура сложения векторов по правилу параллелограмма заключается в следующем:

нарисовать первый вектор, учитывая его величину и направление
от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление
дополнить рисунок до параллелограмма, считая, что два нарисованных вектора — это его стороны
результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.

Правило треугольника. Сложение векторов по правилу треугольника.

Сложение векторов по правилу треугольника заключается в следующем:

нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении
от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление
результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом второго.

Тригонометрический способ. Сложение векторов тригонометрическим способом.

Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов:

F_рез. = [ F₁ 2 + F₂ 2 -2 F₁ F₂ cos(180 о -α) ] 1/2 (1)
- где
  - F = числовое значение вектора
  - α = угол между векторами 1 и 2

Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов:

β = arcsin[ F₂ *sin(180 o -α) / F_R ] (2)
- где
  - α = угол между исходными векторами

Пример — сложение векторов.

Сила 1 равна 5кН и воздействует на тело в направлении, на 80 o отличающемся от направления действия второй силы, равной 8 кН.

Результирующая сила вычисляется следующим образом:

F_рез = [ (5 кН) 2 + (8 кН) 2 — 2 (5 кН)(8 kН) cos(180 o — (80 o )) ] 1/2

Угол между результирующей силой и первой силой равен:

А угол между второй и результирующей силой можно посчитать следующим образом: as

α = arcsin [ (5 кН) sin(180 o — (80 o )) / (10,2 кН) ]

Он-лайн калькулятор сложения векторов.

Калькулятор ниже может быть использован для любвых векторных величин ( силы, скорости и т.д.) Точка начала вектора совпадает с началами обоих исходных векторов.

Консультации и техническая
поддержка сайта: Zavarka Team

Сумма и разность векторов

В данной публикации мы рассмотрим, как найти сумму и разность векторов, приведем геометрическую интерпретацию, а также формулы, свойства и примеры этих действий.

Сумма векторов

Сложение векторов выполняется по правилу треугольника.

Геометрическая интерпретация:

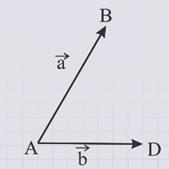
Суммой a и b является вектор c , начало которого совпадает с началом a , а конец – с концом b . При этом конец вектора a должен совпадать с началом вектора b .

Для сложения векторов также используется правило параллелограмма.

Два неколлинеарных вектора a и b можно привести к общему началу, и в этом случае их суммой является вектор c , совпадающий с диагональю параллелограмма и берущий начало в той же точке, что и исходные векторы.

Формула сложения векторов

Элементы вектора c равняются попарной сумме соответствующих элементов a и b .

» data-lang=»default» data-override=»<«emptyTable»:»»,»info»:»»,»infoEmpty»:»»,»infoFiltered»:»»,»lengthMenu»:»»,»search»:»»,»zeroRecords»:»»,»exportLabel»:»»,»file»:»default»>» data-merged=»[]» data-responsive-mode=»2″ data-from-history=»0″>

Для плоских задач	a + b = x + b_x; a_y + b_y>
Для трехмерных задач	a + b = x + b_x; a_y + b_y; a_z + b_z>
Для n-мерных векторов	a + b = 1 + b₁; a₂ + b₂; . a_n + b_n>

Свойства сложения векторов

1. Коммутативность: a + b = b + a

2. Ассоциативность: ( a + b ) + c = a + ( b + c )

3. Прибавление к нулю: a + 0 = a

4. Сумма противоположных векторов: a + (- a ) = 0

Примечание: Вектор – a коллинеарен и равен по длине a , но имеет противоположное направление, из-за чего называется противоположным.

Разность векторов

Для вычитания векторов также применяется правило треугольника.

Если из вектора a вычесть b , то получится c , причем должно соблюдаться условие:

Формула вычитания векторов

Элементы вектора c равны попарной разности соответствующих элементов a и b .

Для плоских задач	a — b = x — b_x; a_y — b_y>
Для трехмерных задач	a — b = x — b_x; a_y — b_y; a_z — b_z>
Для n-мерных векторов	a — b = 1 — b₁; a₂ — b₂; . a_n — b_n>

Примеры задач

Задание 1
Вычислим сумму векторов и .

Задание 2
Найдем разность векторов и .

источники:

http://dpva.ru/Guide/GuideMathematics/linearAlgebra/vectorsaddition/

Сумма и разность векторов

Источник

Сумма нескольких векторов

Сумма нескольких векторов а₁, а₂, а₃, … , а_n, это вектор, получающийся после ряда последовательных сложений:
к вектору а₁ прибавляется вектор а₂, к полученному вектору прибавляется вектор а₃ и т.д.

Из определения вытекает такое построение

Сумма нескольких векторов

Правило многоугольника или правило цепи

Из произвольного начала О строим вектор ОА₁ = а₁,
из точки А₁, как из начала, строим вектор А₁А₂ = а₂,
из точки А₂ строим вектор А₂А₃ = а₃ и т.д.
Вектор ОА_n (на рисунке n = 6) есть сумма векторов а₁, а₂, … , а_n.

Сумма векторов а₁, а₂, а₃, а₄, а₅, а₆ обозначается

[ vector{a_1}+vector{a_2}+vector{a_3}+vector{a_4}+vector{a_5}+vector{a_6} ]

Свойство сочетательности

Слагаемые векторы можно группировать как угодно.

Так, если найти сначала сумму векторов

[ vector{a_2}+vector{a_3}+vector{a_4}+vector{a_5}+vector{a_6} = vector{A_1 A_6} ]

и к ней прибавить вектор а₁ (ОА₁), то получим то же вектор:

[ vector{a_1}+(vector{a_2}+vector{a_3}+vector{a_4}+vector{a_5}+vector{a_6}) = \ = vector{a_1}+vector{a_2}+vector{a_3}+vector{a_4}+vector{a_5}+vector{a_6} ]

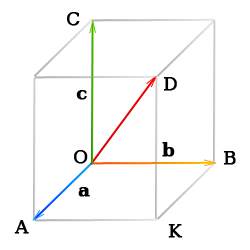
Правило параллелепипеда

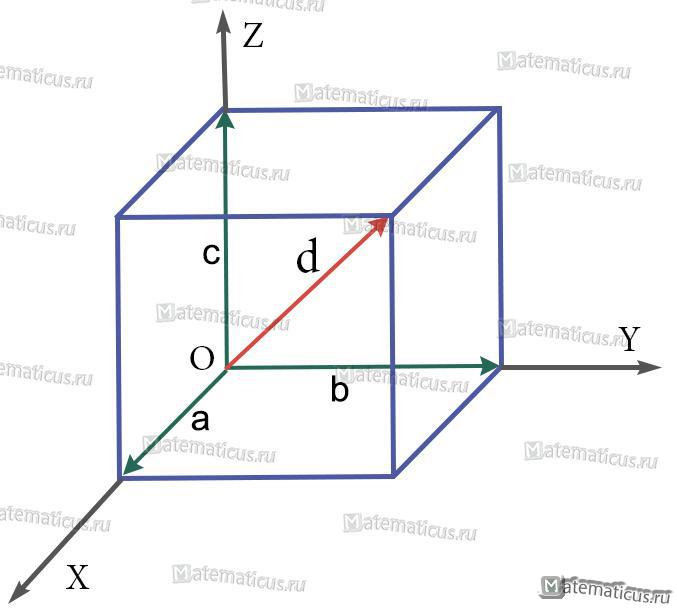
Если три вектора а, b, с после приведения к общему началу не лежат в одной плоскости, то сумму а+b+c можно найти таким построением:

Правило параллелепипеда — Сумма нескольких векторов

Из любого начала О строим векторы ОА = а, ОВ = b, ОС = с,
на отрезках ОА, ОВ, ОС, как на ребрах, строим параллелепипед.
Вектор диагонали OD есть сумма векторов a, b, и c
(так как ОА = а, АК = ОВ = b, KD = OC = c и OD = OA + AK + KD).

Сумма нескольких векторов	стр. 172

Источник

Содержание:

§ 1 Переместительный закон сложения векторов
§ 2 Сочетательный закон сложения векторов
§ 3 Сложение нескольких векторов
§ 4 Краткие итоги урока

§ 1 Переместительный закон сложения векторов

В алгебре часто при упрощении выражений и различных вычислениях используются переместительный и сочетательный законы.

Эти законы также справедливы для векторов.

Вспомним правило сложения векторов – правило треугольника.

Пусть нам даны два вектора а и b.

От произвольно выбранной точки А отложим вектор АВ, равный вектору а.

Затем от точки В отложим вектор ВС, равный вектору b.

Вектор АС называется суммой векторов а и b.

Воспользуемся этим правилом треугольника для доказательства следующей теоремы.

Теорема:

Для любых векторов а , b и с справедливы равенства:

сумма векторов а и b равна сумме векторов b и а (переместительный закон);

сумма векторов а плюс b и с равна сумме векторов а и b плюс с (сочетательный закон).

Для доказательства переместительного закона рассмотрим случай, когда векторы а и b не коллинеарны, т.е. ненулевые и не лежат на одной или параллельных прямых (случай коллинеарных векторов рассмотрите самостоятельно).

От произвольной точки А отложим вектор АВ, равный вектору а, и вектор АD, равный вектору b.

Основываясь на построенных векторах, достроим параллелограмм АВСD так, что вектор АВ равен вектору DС, а вектор АD равен вектору ВС.

По правилу треугольника сумма векторов АВ и ВС равна вектору АС, т.е. равна сумме векторов а и b.

С другой стороны, сумма векторов AD и DC также равна вектору АС, т.е. сумме векторов b и а.

Таким образом, сумма векторов а и b равна сумме векторов b и а.

Переместительный закон доказан.

§ 2 Сочетательный закон сложения векторов

Для доказательства сочетательного закона отложим от произвольной точки А вектор АВ, равный вектору а, от точки В вектор ВС, равный вектору b, и от точки С вектор CD, равный вектору с.

Рассмотрим сумму векторов а плюс b и вектора с с точки зрения правила треугольника: сумма векторов а и b равна вектору АС, в свою очередь, сумма вектора АС и вектора с равна вектору АD.

Теперь рассмотрим сумму векторов а и b плюс с: сумма векторов b и с, согласно рисунку, равна вектору ВD, в свою очередь, сумма векторов а и ВD равна вектору АD.

Исходя из этого, сумма векторов а плюс b и с равна сумме векторов а и b плюс с.

Что доказывает сочетательный закон.

Теорема доказана.

Важно отметить, что при доказательстве переместительного закона было обосновано правило параллелограмма сложения неколлинеарных векторов: чтобы сложить неколлинеарные векторы а и b, необходимо от произвольной точки А отложить вектор АВ, равный вектору а, и вектор AD, равный вектору b, затем достроить параллелограмм АВСD, тогда вектор АС равен сумме векторов а и b.

§ 3 Сложение нескольких векторов

Правило треугольника и правило параллелограмма находят сумму двух векторов, но как сложить несколько векторов?

Чтобы сложить несколько векторов, необходимо сложить первый вектор со вторым, затем сложить их сумму с третьим вектором и так далее.

Из законов сложения векторов следует, что сумма нескольких векторов не зависит от того, в каком порядке происходит сложение.

Рассмотрим рисунок, отражающий сумму векторов а, b и с:

от произвольной точки А отложен вектор АВ, равный вектору а, затем от точки В отложен вектор ВС, равный вектору b, и, наконец, от точки С отложен вектор CD, равный вектору с.

В результате получается вектор АD, равный сумме векторов а, b и с.

Если продолжить процесс откладывания векторов, можно построить сумму четырех, пяти, любого количества векторов.

Правило построения суммы нескольких векторов называется правилом многоугольника: если А1, А2, …,Аn – произвольные точки плоскости, то сумма векторов А1А2, А2А3, …, Аn –1An равна вектору А1Аn.

Это равенство справедливо для всех точек А1, А2, …, Аn, в частности, когда некоторые из них совпадают.

Важно заметить, что если начало первого вектора совпадает с концом последнего вектора, то сумма данных векторов равна нулевому вектору.

§ 4 Краткие итоги урока

Итак, подведем итоги:

– Для любых векторов а, b и с справедливы равенства:

сумма векторов а и b равна сумме векторов b и а;

сумма векторов а плюс b и с равна сумме векторов а и b плюс с.

– Чтобы сложить неколлинеарные векторы а и b, необходимо от точки А отложить вектор АВ, равный вектору а, и вектор AD, равный вектору b, затем достроить параллелограмм АВСD, тогда вектор АС равен сумме векторов а и b (правило параллелограмма).

– Если А1, А2 … An – произвольные точки плоскости, то сумма векторов

А1А2, А2А3,.., Аn–1An равна вектору А1Аn (правило многоугольника).

Список использованной литературы:

Атанасян Л.С. Учебник: Геометрия. 7-9 классы: учеб. для общеобразоват. организаций / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. – М.: Просвещение, 2013. –383 с.
Геометрия. Ч.I. Планиметрия: учебное пособие/ И.Б. Барский, Г.Н. Тимофеев. – Йошкар-Ола: изд-во Марийского гос. ун-та, 2006 и 2008. – 636с.

Источник

В механике существуют два типа величин:

скалярные величины, задающие некоторое числовое значение — время, температура, масса и т.д.
векторные величины, которые вместе с некоторым числовым значением задают направление — скорость, сила и т.д..

Рассмотрим сначала алгебраический подход к сложению векторов.

Покоординатное сложение векторов.

Пусть даны два вектора, заданные покоординатно ( чтобы вычислить координаты вектора, нужно вычесть из соответствующих координат его конца соответствующие координаты его начала, т.е. из первой координаты — первую, из второй — вторую и т.д.):

Тогда координаты вектора, получившегося при сложении этих двух векторов вычисляются по формуле:

В двумерном случае все абсолютно анологично, просто отбрасываем третью координату.

Теперь перейдем к геометрическому смыслу сложения двух векторов:

правило параллелограмма
правило треугольника
тригонометрический способ

Правило параллелограмма. Сложение векторов по правилу параллелограмма.

Процедура сложения векторов по правилу параллелограмма заключается в следующем:

нарисовать первый вектор, учитывая его величину и направление
от начала первого вектора нарисовать второй вектор, также используя и его величину, и его направление
дополнить рисунок до параллелограмма, считая, что два нарисованных вектора — это его стороны
результирующим вектором будет диагональ параллелограмма, причем его начало будет совпадать с началом первого (а, значит, и второго) вектора.

Правило треугольника. Сложение векторов по правилу треугольника.

Сложение векторов по правилу треугольника заключается в следующем:

нарисовать первый вектор, используя данные о его длине ( числовой величине) и направлении
от конца первого вектора нарисовать второй вектор, также учитывая и его размер, и его направление
результирующим вектором будет вектор, начало которого совпадает с началом первого вектора, а конец — с концом второго.

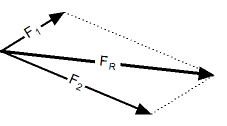
Тригонометрический способ. Сложение векторов тригонометрическим способом.

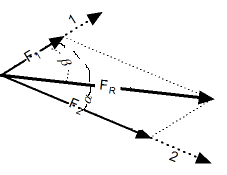Результирующий вектор сложения двух компланарных векторов может быть вычислен с помощью теоремы косинусов:

F_рез. = [ F₁² + F₂² -2 F₁ F₂ cos(180^о-α) ]^1/2 (1)
- где
  - F = числовое значение вектора
  - α = угол между векторами 1 и 2

Угол между результирующим вектором и одним из исходных векторов может быть вычислен по теореме синусов:

β = arcsin[ F₂*sin(180^o-α) / F_R] (2)
- где
  - α = угол между исходными векторами

Пример — сложение векторов.

Сила 1 равна 5кН и воздействует на тело в направлении, на 80^o отличающемся от направления действия второй силы, равной 8 кН.

Результирующая сила вычисляется следующим образом:

F_рез = [ (5 кН)² + (8 кН)² — 2 (5 кН)(8 kН) cos(180^o — (80^o)) ]^1/2

= 10,14кН

Угол между результирующей силой и первой силой равен:

β= arcsin[ (8кН) sin(180^o — (80^o)) / (10,14кН)]

= 51^o

А угол между второй и результирующей силой можно посчитать следующим образом: as

α = arcsin [ (5 кН) sin(180^o — (80^o)) / (10,2 кН)]

= 29^o

Он-лайн калькулятор сложения векторов.

Источник

Сложение векторов

Сложение векторов по правилу параллелограмма

Правило параллелограмма

Если слагаемые a и b не коллинеарны, то

c=a+b

Сложение векторов по правилу треугольника

Правило треугольника

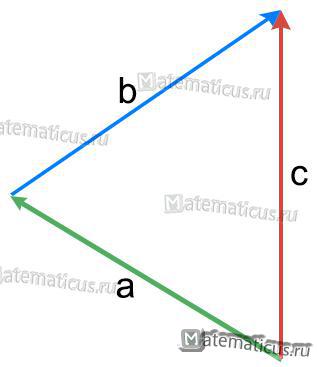
Суммой векторов a (на рисунке зелёный вектор) и b (на рисунке синий вектор) называется третий вектор c (на рисунке красный вектор) , получаемый следующее построение:

Примечание

Нельзя смешивать понятие «сумма отрезков» с понятием «сумма векторов».

Правило параллелепипеда

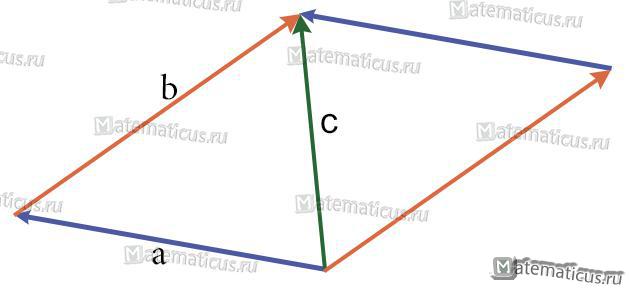
Если три вектора a, b, c после приведения к общему началу не лежат в одной плоскости , то их сумма равна диагонали параллелепипеда

d=a+b+c

Правило параллелепипеда применяется для сложения трех некомпланарных векторов.

Сложение противоположных векторов

Сумма противоположных векторов равна нуль-вектору, т.е.

a+(-a)=0

Свойство переместительности (переместительный закон)

От перестановки слагаемых сумма векторов не меняется.

с=a+b= b+a

Сочетательное свойство (сочетательный закон)

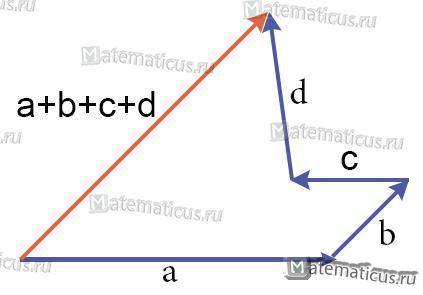
Слагаемые векторы можно группировать как угодно.

a+(b+c+d) = a+b+c+d

Вычитание векторов

Вычесть вектор а (вычитаемое) из вектора b (уменьшаемое) значит найти новый вектор x (разность), который в сумме с вектором а даёт вектор b.
Разность векторов обозначается: a-b
Вычитание есть действие обратное сложению (сложение векторов).
Вычитание векторов показаны на рисунках ниже:

Примечание
Модуль разности может быть меньше модуля «уменьшаемого», но может быть и больше или равен ему. Эти случаи показаны на рисунке выше.

5702

Источник