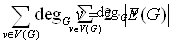Как найти вектор степеней графа

3.02.1. Основные числовые характеристики и матрицы графа. Степени вершин графа

Степенью вершины V графа G называется число инцидентных ей рёбер, т. е. число рёбер, выходящих из данной вершины. (В случае псевдографов каждая петля добавляет 2 в степень вершины). Обозначается степень вершины V графа G: degGv или просто deg V, если ясно, о каком графе G идет речь.

Вершина степени 0 называется Изолированной. Вершина степени 1 называется Концевой (или Висячей). Ребро, инцидентное концевой вершине также

Называется Концевым.

Вершина V Графа G, смежная со всеми другими вершинами G, называется Доминирующей. Её степень degGv очевидно равна |G| —1.

Граф G называется Регулярным (или, по-другому, Однородным), если степени всех его вершин равны. Эта общая степень всех вершин регулярного графа G называется степенью регулярного графа G и обозначается deg G.

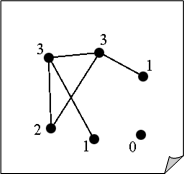
Последовательность степеней вершин графа G, записанная в каком либо порядке называется степенной последовательностью графа G. Например, граф на рисунке справа имеет степенную последовательность (3, 3, 1, 0, 1, 2).

Понятно, что изоморфные графы имеют одинаковые (с точностью до порядка следования элементов) степенные последовательности. Однако, из этого совпадения степенных последовательностей двух графов ещё не следует их изоморфность. На следующих двух рисунках изображены два неизоморфных регулярных графа степени 2.

Таким образом, степенная последовательность не определяет граф полностью и не может

служить способом его задания.

Степенная последовательность не может быть произвольным набором чисел, а обладает определёнными свойствами.

Лемма 1 («о рукопожатиях»). Сумма степеней всех вершин графа G есть число чётное, ровно в два раза большее числа рёбер графа G, т. е.

Доказательство: Действительно, подсчитаем количество рёбер графа G, просматривая поочередно все вершины графа G и считая рёбра выходящие из этих вершин. Так как из каждой вершины V выходит degGV рёбер, то мы получим сумму:

Но при этом каждое ребро будет учтено 2 раза: один раз, когда рассматривался один его конец, другой раз, когда — второй. Таким образом, лемма верна.

Из леммы 1 вытекает

Следствие. В любом графе число вершин нечётной степени является чётным.

Доказательство. В самом деле, иначе, если бы сумма целых чисел содержала нечётное число нечетных слагаемых, то она, очевидно, была бы нечётной, что противоречит лемме о рукопожатиях.

В ориентированных графах для каждой вершины V дополнительно рассматривается также полустепень исхода и полустепень захода. Полустепенью исхода вершины V называется число дуг графа G, для которых V Является началом, а Полустепенью захода – число дуг, для которых V является концом. Обозначаются полустепени захода и исхода графа G соответственно deg-V и deg+V. При этом полная степень degV = deg-V+ deg+V. Поскольку каждая дуга имеет ровно одно начало и один конец, то справедлива

Вектор степеней второго порядка

Вектор, компонентами, которого являются окружения всех вершин графа, называют вектором степеней второго порядка.

У графа Г на рисунке вектор степеней второго порядка равен ((3), (2, 3), (2, 3), (2, 2), (2, 2), (2, 2, 1)).

Чтобы различать эти два вектора, простой вектор степеней иногда называют вектором степеней первого порядка.

Из сохранения отношения смежности при изоморфизме следует, что векторы степеней изоморфных графов совпадают.

Рис. 82. Неизоморфные графы Г1 и Г2 имеют одинаковые векторы степеней

Иначе говоря, для изоморфизма графов необходимо равенство векторов степеней.

Обратное утверждение неверно.

Равенства векторов степеней недостаточно для изоморфизма графов.

Конечно, в некоторых случаях, изоморфизм графов все-таки следует из равенства векторов степеней. Например, два графа с одинаковым числом вершин изоморфны, если оба пусты, или оба полные, или каждый содержит в точности по одному ребру.

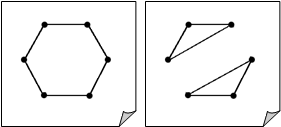
Графический вектор может задавать неизоморфные графы.

Например, вектор (2, 2, 2, 2, 2, 2) — графический, он является вектором степеней графа, причем даже не одного, а двух — неизоморфных графов.

Мало того, что графы Гі и Гг неизоморфны. Первый граф распадается на два, несоединенных между собой «куска». Такой граф называется несвязным, а два «куска» графа — это две компоненты связности.

Пример графов Гі и Гг показывает, что по вектору степеней, вообще говоря, нельзя даже определить, связный граф или не связный. Если граф не связный, то с помощью этого вектора не удастся вычислить точное число компонент связности графа.

Не спасает положения и вектор степеней второй ступени: и эти векторы у графов Г і и Гг одинаковые.

Однако в следующем примере (графы Гз и Гд) вектор степеней второго порядка поможет справиться с ситуацией.

Рис. 83. Векторы степеней у Гз и Гд совпадают

Вектор степеней графа Гз равен вектору степеней графа Гд и равен (2, 2, 2, 3, 3).

Вектор степеней второго порядка графа Г з равен ((3, 3), (3, 2), (3, 2), (3, 2, 1), (3, 2, 2, 1)).

Вектор степеней второго порядка для графа Гд другой: ((3, 3), (3, 3), (3, 3), (2, 2, 2), (2, 2, 2)).

Эти векторы различны, и, следовательно, графы Гз и Гдне изоморфны.

То, что эти графы не изоморфны, видно, впрочем, и из других соображений. Например, в графе Гз есть только один цикл, состоящий из трех ребер, а в графе Гд таких циклов два.

Рис. 84. Помеченные графы R и Ге— равные

Построение графов на основе их характеристик

Отметим, что в задачах на построение решение необходимо искать среди простых неориентированных графов (т.е. графов без кратных ребер и без петель). К сожалению, не существует универсальной методики, позволяющей точно определить, может ли быть построен граф с заданными характеристиками.

Важно помнить, что в любом графе сумма степеней всех его вершин — число четное, равное удвоенному числу ребер графа, так как каждое ребро участвует в этой сумме ровно два раза. Этот результат, известный еще 200 лет назад Эйлеру, часто называют леммой о рукопожатиях. Из нее следует, что если несколько человек обменялись рукопожатиями, то общее число пожатых рук обязательно четно, ибо в каждом рукопожатии участвуют две руки (при этом каждая рука считается столько раз, сколько она участвовала в рукопожатиях). Отсюда следует, что:

• • число вершин с нечетной степенью у любого графа четно;
• • во всяком графе с п вершинами, где п > 2, всегда найдутся по меньшей мере две вершины с одинаковыми степенями;
• • если в графе с вершинами п > 2 в точности две вершины имеют одинаковую степень, то в этом графе всегда найдется либо в точности одна вершина степени 0, либо в точности одна вершина степени (п — 1).

При решении задач необходимо очень внимательно читать условие, так как многие прилагательные, описывающие свойства графа, имеют численные эквиваленты. Приведем таблицу таких соответствий, чаще всего встречающихся в формулировке задач (табл. 2.9).

После того как получены все необходимые числительные, нужно попробовать рассчитать недостающие характеристики графа. Иногда в условии приводятся степени всех или нескольких вершин. В этом случае на основе того факта, что каждое ребро графа добавляет к его суммарной степени вершин ровно два, можно воспользоваться формулой

где т — количество вершин, а суммирование ведется по всем вершинам от 1 до п.

Задача 2.42. Построить граф на восьми вершинах, имеющий следующее распределение степеней вершин: две вершины степени 4; три вершины степени 3; две вершины степени 2; одна вершина степени 1.

Суммарная степень всех вершин равна 2-4 + 3- 3 + 2- 2+1 • 1=22, отсюда следует, что всего 11 ребер. Строить графы на основании вектора степеней проще, начиная с вершин больших степеней. Вер-

Соответствие между описанием графа и его свойствами

1. Дискретная математика

Локальные степени
вершин графа

2. Локальные степени вершин н-графа

Пусть G =(V, E) – н-граф.
Локальной степенью
вершины v V называется
число ρ v равное числу ребер,
инцидентных вершине v. При
этом вклад петли в степень
вершины равен 2.

3. Локальные степени вершин н-графа

Вектор степеней н-графа
G =(V, E) – вектор размерности
n, составленный из степеней
вершин графа, расположенных
по убыванию.

4. Локальные степени вершин н-графа

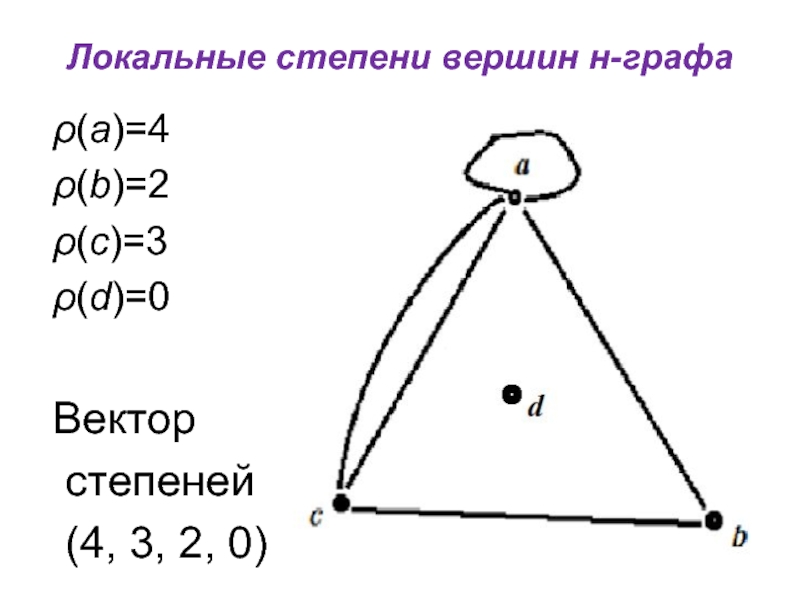
ρ(a)=4
ρ(b)=2
ρ(c)=3
ρ(d)=0
Вектор
степеней
(4, 3, 2, 0)

5. Локальные степени вершин н-графа

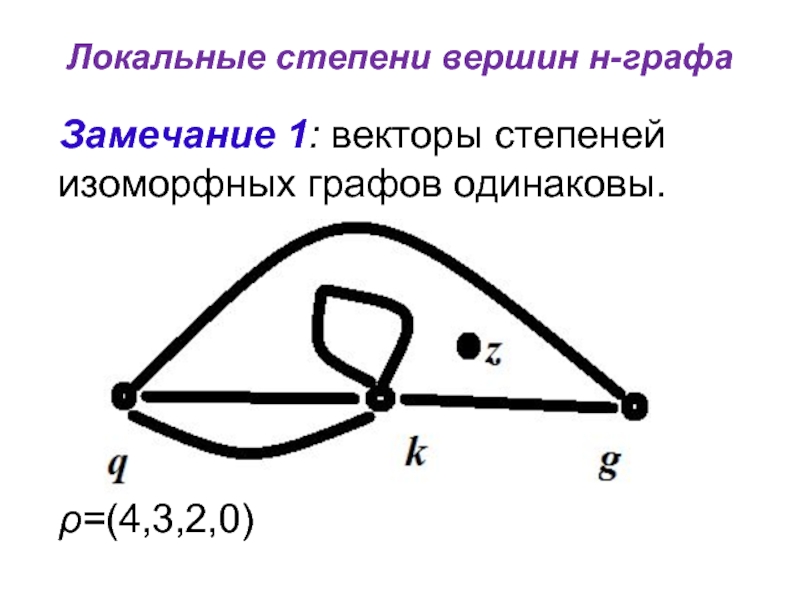
Замечание 1: векторы степеней
изоморфных графов одинаковы.
ρ=(4,3,2,0)

6. Локальные степени вершин н-графа

Замечание 2: Сумма всех
локальных степеней вершин
н-графа равна удвоенному
количеству ребер.
n
vi 2 e
i 1
e — число ребер н-графа.

7. Локальные степени вершин н-графа

Теорема (о числе вершин
нечетной степени):
Число вершин нечетной
степени – четно.

8. Локальные степени вершин н-графа

Доказательство:
vi 2 e
Сумма в левой части равенства – четна.
Если убрать все четные слагаемые,
сумма останется четной.
Сумма нечетных слагаемых четна, если
их четное число.

9. Локальные степени вершин н-графа

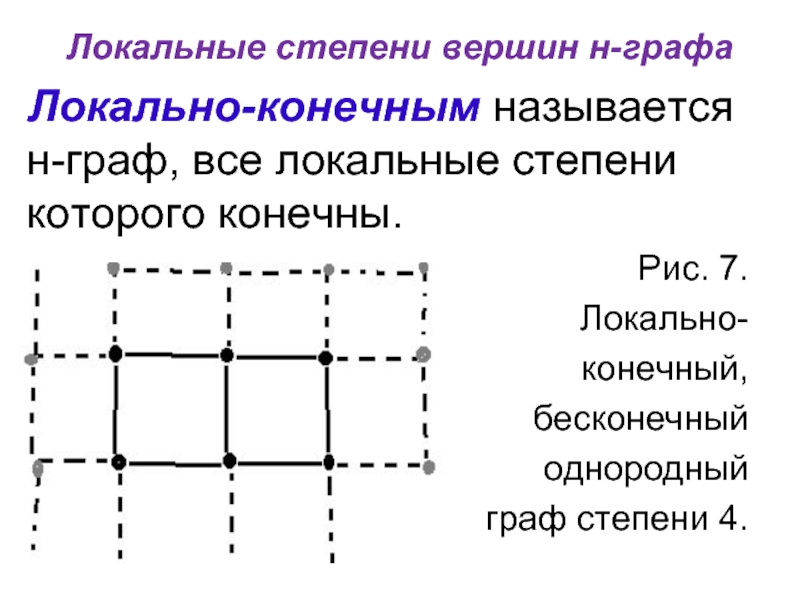
Локально-конечным называется
н-граф, все локальные степени
которого конечны.
Рис. 7.
Локальноконечный,
бесконечный
однородный
граф степени 4.

10. Локальные степени вершин н-графа

Однородным степени k
называется н-граф, локальные
степени которого одинаковы и
равны k.
Для однородного графа степени k:
vi k v 2 e ,
k
e v , v число вершин
2

11. Локальные степени вершин ор-графа

Пусть G = (V, E) – ор-граф.
Локальной степенью исхода
вершины v V называется
число ρ v , равное числу
—
ребер, выходящих из вершины v.

12. Локальные степени вершин ор-графа

Локальной степенью захода
вершины v V называется
число ρ v , равное числу
ребер, выходящих из вершины v.

13. Локальные степени вершин ор-графа

Вектор степеней исхода
ор-графа G =(V, E) – вектор
размерности n, составленный из
степеней исхода вершин графа,
расположенных по убыванию.

14. Локальные степени вершин ор-графа

Вектор степеней захода
ор-графа – вектор размерности
n, составленный из степеней
захода вершин графа,
расположенных по убыванию.

15. Локальные степени вершин ор-графа

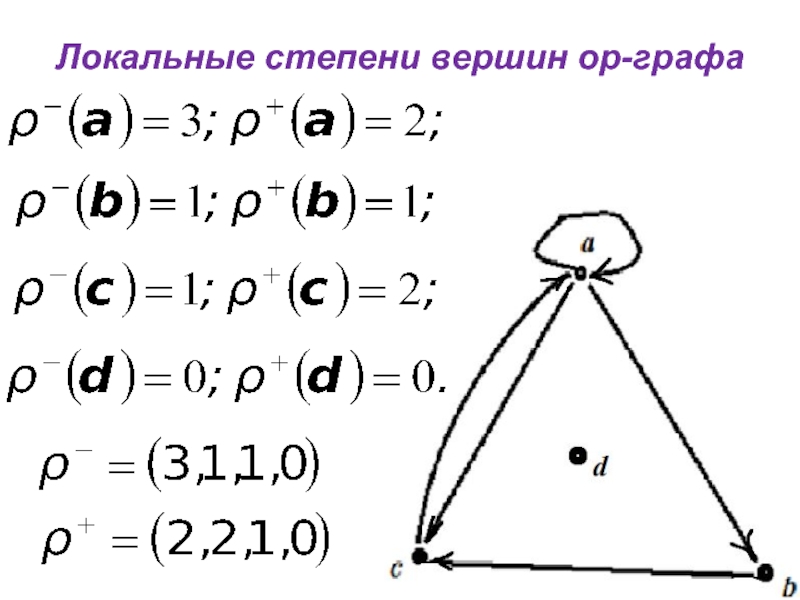
ρ a 3; ρ a 2;
ρ b 1; ρ b 1;
ρ c 1; ρ c 2;
ρ d 0; ρ d 0.
ρ 3,1,1, 0
ρ 2, 2,1, 0

16. Локальные степени вершин ор-графа

Замечание 3: векторы
степеней исхода и степеней
захода изоморфных графов
одинаковы.

17.

ρ 3,1,1, 0 ρ 2, 2,1, 0

18. Локальные степени вершин н-графа

Замечание 4: Сумма всех
локальных степеней исхода
вершин и сумма всех локальных
степеней захода ор-графа равна
количеству ребер.
n
n
vi vi e
i 1
i 1

19. Локальные степени вершин ор-графа

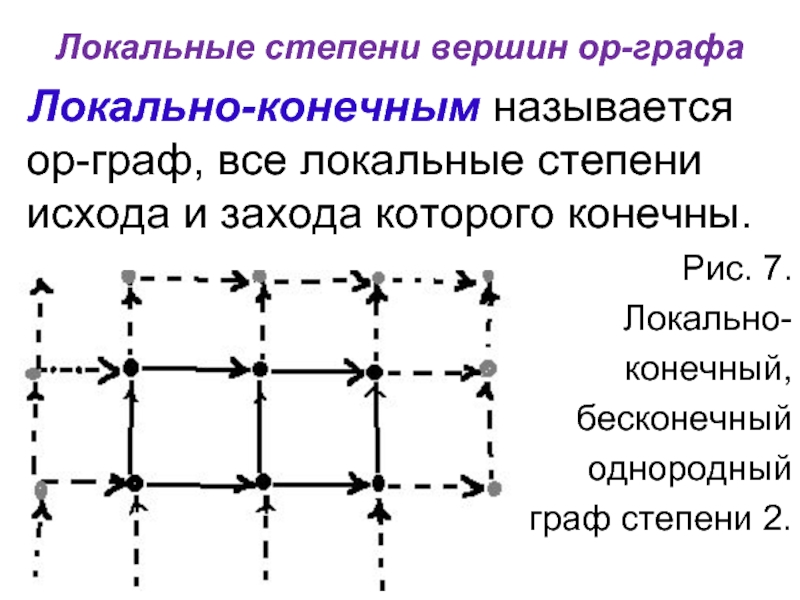
Локально-конечным называется
ор-граф, все локальные степени
исхода и захода которого конечны.
Рис. 7.
Локальноконечный,
бесконечный
однородный
граф степени 2.

20. Локальные степени вершин ор-графа

Однородным степени k
называется ор-граф, локальные
степени исхода и степени захода
которого одинаковы и равны k.
Для однородного графа степени k:
vi vi k v e ,
e k v .