Как найти вектора обратной решетки

Обратная решетка и ее свойства

Обратная решетка. Понятия «обратная решетка» и «обратное пространство» занимают особое место в физике дифракции, в кристаллографин и вообще в физике конденсированного состояния. Эти понятия в физике были введены американским физиком и математиком Джо- зайей Уиллардом Гиббсом*. Рассмотрим вначале определение обратной решетки.

Выберем три базисных вектора а, Ь, с, определяющие элементарную ячейку решетки в обычном пространстве кристалла (в прямом пространстве). Тогда вектор трансляции будет иметь вид (1.2)

Здесь т, п, р — целые числа.

Введем новое пространство, в котором определим также три базисных вектора а*, Ь*, с* и вектор трансляции, размножающий решетку:

Здесь h, к, I пока просто целые числа.

Если введенные в (1.4) векторы удовлетворяют тождествам

то векторы а, Ь, с называются векторами прямой решетки, а векторы а*, Ь*, с* — векторами обратной решетки в обратном пространстве. Тогда целые числа h, k, I являются индексами Миллера плоскостей в прямой решетке.

Свойства обратной решетки. Векторы обратной решетки имеют два важных свойства (рис. 1.8).

• 1. Вектор обратной решетки Н_швсегда перпендикулярен плоскости прямой решетки с индексами (hkl).
• 2. Модуль вектора обратной решетки Н_ш всегда равен обратной величине межплоскостного расстояния для плоскостей в прямой решетке с индексами (hkl), т. е.

Первое свойство обратной решетки доказывается так. Если две любые прямые линии, лежащие в плоскости, перпендикулярны какому- либо вектору, не лежащему в этой плоскости, то этот вектор обязательно перпендикулярен выбранной плоскости.

Выберем три вектора АВ, СВ, СА, лежащих в плоскости АВС, и определим их величины:

Рис. 1.8. Два свойства обратной решетки:

а — вектор обратной решетки с индексами hkl перпендикулярен плоскостям прямой решетки с индексами Миллера (hkl); б — расстояния между плоскостями прямой решетки с индексами Миллера (.hkl) равны модулю вектора обратной

Из векторной алгебры известно, что два вектора перпендикулярны друг другу, если их скалярное произведение равно нулю. Воспользовавшись определением векторов обратной решетки, можно записать

Отсюда следует, что вектор Н перпендикулярен плоскости прямой решетки с индексами (hkl). Рассмотренные свойства векторов обратной решетки делают понятным построение стереографической проекции, когда плоскости заменяются нормалями к плоскостям, т. е. векторами обратной решетки.

Второе свойство обратной решетки также легко доказывается. Выберем в пространстве кристалла любую плоскость АВС с индексами Миллера (hkl) (см. рис. 1.9) Пусть вектор п — единичный вектор нормали к этой плоскости, а вектор R — текущий радиус-вектор точки, лежащей на плоскости АВС. Пусть также а — кратчайшее расстояние от начала координат до плоскости ЛВС.

Тогда уравнение такой плоскости можно записать в виде

Здесь n — единичный вектор нормали к плоскости;

о — кратчайшее расстояние от начала координат до плоскости;

где 5 — целое число (например, для плоскости, проходящей через начало координат, 5 = 0); d — межплоскостное расстояние для этой системы плоскостей.

Рис. 1.9. К выводу второго свойства вектора обратной решетки Н:

А, В, С — точки пересечения плоскости с осями координат; R — текущий радиус-вектор любой точки на плоскости; а — расстояние от начала координат

С учетом сделанных пояснений уравнение плоскости (1.6) представимо как

Запишем текущий радиус-вектор любой точки плоскости АВС:

Тогда уравнение плоскости (1.7) можно переписать в виде

В уравнении плоскости (1.8) выражение есть уравнение плоскости АВС. Следовательно,

что и требовалось доказать.

Для кубической сингонии величина межплоскостного расстояния определяется соотношением

где а — параметр решетки.

Для других сингоний формулы для межплоскостных расстояний приведены в прил. 9 (табл. П.9.10).

Обратное пространство является более общим понятием (в физике конденсированного состояния используются эквивалентные термины: «векторное пространство», «/с-пространство», «пространство дисперсии»). В обратном пространстве разыгрываются все дифракционные явления. Математическим аппаратом, описывающим связь прямого и обратного пространства, является преобразование Фурье (рис. 1.10) — гармонический ряд или интегралы Фурье (более подробно об этом см. в главе 3):

Puc. 1.10. Схематическое изображение связи прямого и обратного пространства

Понятие обратной решетки, введенное выше, — это частный случай обратного пространства. При первом знакомстве эта модель кажется очень абстрактной и сильно усложненным понятием. Однако это не просто удобный способ описания дифракционных явлений: именно в узлах обратной решетки располагаются дифракционные максимумы. Без такого понятия многие дифракционные явления довольно сложно описать. Понятия «обратная решетка», «обратное пространство» проходят красной нитью через всю физику твердого тела (зонная структура вещества, зоны Бриллюэна, Фурье-образ, ^-пространство, дисперсионные зависимости и др.).

Обратная решетка

В физике твердого тела при анализе многих явлений (дифракция, движение электронов в потенциальном поле, рассеяние фотонов), связанных с периодическим расположением частиц, важную и полезную роль играет обратная решетка.

Обратная решетка представляет собой удобную абстракцию, позволяющую математически просто описать условия протекания того или иного явления в твердом кристаллическом теле.

Между векторами элементарных трансляций и периодами обратной решетки существует вполне определенная связь.

Пусть в кристаллической решетке элементарная ячейка определяется тремя элементарными трансляциями

с (рис. 1.14) [75]. Простейшими плоскими сетками являются сами координатные плоскости. Семейство плоскостей, параллельных векторам Ъ и

с (или, другими словами, плоскости семейства (100)), можно изобразить точкой на конце некоторого вектора а*, перпендикулярного к этим плоскостям. За длину этого вектора примем величину, обратную соответствующему межплоскостному расстоянию d _0Q = |Оа 11. Здесь Оп — проекция вектора а на нормаль к плоскости (100). Длину вектора а* можно определить из условия

Рис. 1.14. К выводу связи между параметрами прямой и обратной решеток

Кроме того, вектор а* откладывается вдоль нормали к плоскости так, чтобы для наблюдателя, смотрящего вдоль направления а*, вращение от b к

F совершалось по часовой стрелке. В векторном виде эти условия записываются тремя скалярными произведениями:

Два других вектора Ь* и с* определяют, исходя из сеток на других координатных плоскостях:

Проведем три вектора а*, Ь* и с* из какой-либо произвольной точки, кото рую назовем началом координат обратного пространства. Точечная решетка, построенная на этих векторах, является обратной решеткой для исходной (прямой) решетки кристалла.

Пусть объем элементарной ячейки прямой решетки У_яч, тогда

откуда в соответствии с соотношениями (1.1)—(1.3)

Углы между каждой парой векторов а*, 6*, с* обозначим о*, /3*, 7*. Они равны по величине двугранным углам триэдра, построенного на векторах 7Г, 6 , с, и могут быть вычислены из углов Q, /3, 7 между векторами прямой решетки по формулам:

Если в кристаллической решетке все углы прямые, то векторы элементарных трансляций а*, Ь*, с* обратной решетки параллельны векторам а , b ,

с прямой решетки и обратны им по величине. К этому результату можно прийти из формулы (1.5). Действительно, в этом случае объем элементарной ячейки У_яч = аЬс, а векторное произведение [6 с ] = be. Поэтому а* = 1/а.

Объем элементарной ячейки обратной решетки равен:

откуда

Таким образом, объем элементарной ячейки обратной решетки V* есть величина, обратная объему элементарной ячейки кристалла. Это соотношение является общим и применимо ко всем кристаллическим решеткам, в том числе и к непрямоугольным.

Любой вектор обратной решетки г* hkl = На* + Kb* + Lc* перпендикулярен плоскости (HKL) прямой кристаллической решетки, а длина его является величиной, обратной межплоскостному расстоянию:

Итак, прямая и обратная ячейки взаимно сопряжены. Если для описания кристаллической решетки вместо принятой вначале выбрать другую элементарную ячейку, то для элементарной ячейки обратной решетки получится также другая группа из трех векторов, но в целом решетка, построенная таким образом, будет идентична первой. Это следует из прямой связи между любым вектором одной решетки с одним только семейством плоскостей другой вне зависимости от координатных осей. Соответствие между двумя решетками, их взаимосвязь не зависят от выбора элементарной ячейки.

Решетка, обратная обратной решетке, является исходной (прямой) решеткой.

Каждый узел [[HKL]]* обратной решетки соответствуют семейству параллельных плоскостей (HKL) прямой решетки.

Обратная решетка сама является (по отношению к конкретной решетке Бравэ) решеткой Бравэ. Так, для примитивной кубической ячейки Бравэ со стороной а обратной является примитивная кубическая ячейка Бравэ со стороной 1 /а. Обратная к гранецентрированной есть объемноцентрированная решетка, а прямой объемноцентрированной соответствуют обратная гранецентрированная. Это утверждение будет доказано в одной из задач, приведенных в конце этой главы.

Как найти вектор обратной решетки

Зонные структуры Si и Ge, изображенные на рис. 31, вычерчены в обратном пространстве кристалла. Кое-что о k-пространстве было сказано, но этого явно недостаточно для отчетливого понимания закона дисперсии E(k). Существует несколько десятков пространственных конфигураций атомов: как выглядят их решетки, как найти обратные им, как применить теорию групп для их расчета, как учесть структурный фактор в гамильтониане? Ведь мы не касались вопросов составления ЛКАО-матрицы и не знаем, почему, собственно, ряд матричных элементов в ней равны нулю; есть параметры E_xx и E_xy, но почему-то отсутствуют E_zz, E_yy, E_xz и E_yz. Видимо, это как-то связано с симметрией электронных оболочек и устройством кристаллической решетки, но как?

Не все мы сможем рассказать, поскольку наша цель состоит не в том, чтобы всесторонне осветить задачи физики полупроводников, а в том, чтобы в выгодном свете представить теорию групп, обслуживающую эту самую физику полупроводников. Конечно, мы постараемся приложить максимум усилий для того, чтобы физическая сторона рассматриваемых явлений была понятна читателю, однако главная задача состоит в том, чтобы убедительно продемонстрировать эффективность конструктивной математики, к которой, в частности, принадлежит и теория групп. Будущие специалисты по материалам полупроводниковой техники для уяснения каких-то непонятных им вопросов материаловедения должны будут, очевидно, обратиться все же к литературе, ограниченный список которой приведен и в конце нашего учебника. Итак, обратное пространство кристалла, что это такое и как его найти.

Если узлы прямой решетки определить равенством

то узлы обратной решетки определятся равенством

причем базисные векторы обоих пространств ортогональны и нормированы. Последнее означает, что выполняется условие:

Из последних равенств немедленно вытекает связь между базисными векторами прямого и обратного пространства:

, , .

На рис. 32 показаны 14 пространственных решеток Браве; кубические — простая (P), объемоцентрированная (I) и гранецентрированная (F) для специалистов по материалам полупроводниковой техники являются особенно важными. Прямыми вычислениями можно убедиться, что обратная решетка для простой кубической (ПК) есть также ПК решетка; объемоцентрированной кубической решетке (ОЦК) отвечает гранецентрированная решетка (ГЦК), и наоборот; наконец, для гексагональной плотноупакованной решетки (ГПУ) обратной является опять же ГПУ.

К примеру, ГЦК — решетка определяется следующими тремя векторами:

Найдем по предыдущим формулам вектора обратной решетки, для чего сначала определим произведения векторов, стоящие в числителе и знаменателе дробей:

,

;

, ,

— три вектора определяют узлы ОЦК ячейки.

Процедуру вычисления векторов обратной решетки можно упростить, если прибегнуть к матрицам. Пусть координаты прямой ГЦК решетки a_i будут записаны элементами матрицы A, тогда обратная матрица A –1 = B укажет на координаты обратной ОЦК решетки b_i:

, .

К понятию обратной решетки можно прийти и другим путем. Если рассмотреть разложение какой-либо одномерной периодической функции f (r) = f (r + R), где R — пространственный период прямого пространства, в ряд Фурье:

то здесь появляется структурный фактор S(K), для которого K есть радиус-вектор, пробегающий узлы обратной решетки. Так как exp (iKR) = 1, структурный фактор найдется через интеграл:

,

где Ω — объем элементарной ячейки прямой решетки, по которой и производится интегрирование. Поскольку обратная решетка определяется через коэффициенты преобразования Фурье, то k-пространство часто называют Фурье-пространством. Если в элементарной ячейке содержится N атомов с координатами ai, то распределение атомов в ней можно описать через δ-функцию:

В пределах элементарной ячейки R = 0, следовательно, суммирование производится только по атомам с координатами a_i, а структурный фактор сводится не к интегралу, а к простой сумме:

.

Для ГЦК с координатами

структурный фактор приобретает следующий конкретный вид:

=

Наиболее важные полупроводники, кремний и германий, имеют решетку алмаза, в которой присутствуют еще четыре атома с координатами:

Если начало координат выбрано не на атоме, а посередине между двумя атомами, то можно показать, что структурный фактор алмаза связан со структурным фактором ГЦК решетки по формуле:

Большая группа полупроводников, составленных из атомов III и V группы, II и VI группы Периодической таблицы Менделеева, например: GaAs, GaP, GaSb, InAs, InP и т.д., имеют решетку цинковой обманки (ZnS). Пространственная решетка ZnS, куда входят уже два рода атомов, теряет центр симметрии и структурный фактор становится антисимметричным:

На рис. 33 показаны элементарные ячейки: а) Cu, б) W, в) Mg, г) алмаза, д) NaCl, е) CsCl, ж) ZnS, з) ZnO, и) NiAs, к) CaF, л) CuAu, м) Cu3Au. Для каждой из них, в соответствии со структурным фактором, можно построить элементарные ячейки обратной решетки. Важно уметь строить одну-единственную элементарную ячейку, поскольку закон дисперсии E_n(k) приводится только для нее одной, и здесь на первый план выдвигается понятие зоны Бриллюэна (ЗБ). Первую ЗБ определяют как область в обратном пространстве, окружающую один из узлов обратной решетки и ограниченную набором плоскостей, проходящих через середины векторов, соединяющих в обратной решетке данную точку с ее ближайшими соседями.

На рис. 34 показана первая ЗБ для двумерной косоугольной решетки; на рис. 35 вычерчены уже десять ЗБ для двумерной квадратной решетки. Точно таким же половинным делением расстояния между двумя узлами определяется ЗБ в трехмерном пространстве. На рис. 36а приведены базисные векторы ОЦК решетки, а на рис. 36б — первая ЗБ, имеющая форму правильного ромбододекаэдра. На рис. 37 приведены первых четыре ЗБ для ГЦК решетки. На рис. 38 указаны симметричные точки (Г, L, Λ, Δ, …) первой ЗБ для ГЦК решетки, представляющая собой полуправильный многогранник Архимеда — усеченный октаэдр. Симметричные точки можно видеть на энергетических зонах, рассчитанных ЛКАО-методом (рис. 31а).

На рис. 39 вычерчены ЗБ для всех 14 решеток Браве, показанные в прямом пространстве на рис. 32. Соответствия между ЗБ и решетками Браве следующие: а) триклинная, б) моноклинная Р, в) моноклинная С, г) ромбическая Р, д) ромбическая С, е) ромбическая I, ж) ромбическая F, з) тетрагональная Р’, и) тетрагональная I, к) тригональная R, л) гексагональная Р, м) кубическая Р, н) кубическая F, о) кубическая I. Поскольку выбор ячеек может быть осуществлен несколькими способами, то существует и несколько вариантов ЗБ; поэтому для 14 решеток Браве вычерчено 22 ЗБ.

In physics, the reciprocal lattice represents the Fourier transform of another lattice. The direct lattice or real lattice is a periodic function in physical space, such as a crystal system (usually a Bravais lattice). The reciprocal lattice exists in the mathematical space of spatial frequencies, known as reciprocal space or k space, where refers to the wavevector.

In quantum physics, reciprocal space is closely related to momentum space according to the proportionality , where is the momentum vector and is the reduced Planck constant. The reciprocal lattice of a reciprocal lattice is equivalent to the original direct lattice, because the defining equations are symmetrical with respect to the vectors in real and reciprocal space. Mathematically, direct and reciprocal lattice vectors represent covariant and contravariant vectors, respectively.

The reciprocal lattice is the set of all vectors , that are wavevectors of plane waves in the Fourier series of a spatial function whose periodicity is the same as that of a direct lattice . Each plane wave in this Fourier series has the same phase or phases that are differed by multiples of at each direct lattice point (so essentially same phase at all the direct lattice points).

The reciprocal lattice plays a fundamental role in most analytic studies of periodic structures, particularly in the theory of diffraction. In neutron, helium and X-ray diffraction, due to the Laue conditions, the momentum difference between incoming and diffracted X-rays of a crystal is a reciprocal lattice vector. The diffraction pattern of a crystal can be used to determine the reciprocal vectors of the lattice. Using this process, one can infer the atomic arrangement of a crystal.

The Brillouin zone is a Wigner-Seitz cell of the reciprocal lattice.

Wave-based description[edit]

Reciprocal space[edit]

Reciprocal space (also called k-space) provides a way to visualize the results of the Fourier transform of a spatial function. It is similar in role to the frequency domain arising from the Fourier transform of a time dependent function; reciprocal space is a space over which the Fourier transform of a spatial function is represented at spatial frequencies or wavevectors of plane waves of the Fourier transform. The domain of the spatial function itself is often referred to as real space. In physical applications, such as crystallography, both real and reciprocal space will often each be two or three dimensional. Whereas the number of spatial dimensions of these two associated spaces will be the same, the spaces will differ in their quantity dimension, so that when the real space has the dimension length (L), its reciprocal space will of inverse length, so L⁻¹ (the reciprocal of length).

Reciprocal space comes into play regarding waves, both classical and quantum mechanical. Because a sinusoidal plane wave with unit amplitude can be written as an oscillatory term , with initial phase , angular wavenumber and angular frequency , it can be regarded as a function of both and (and the time-varying part as a function of both and ). This complementary role of and leads to their visualization within complementary spaces (the real space and the reciprocal space). The spatial periodicity of this wave is defined by its wavelength , where ; hence the corresponding wavenumber in reciprocal space will be .

In three dimensions, the corresponding plane wave term becomes , which simplifies to at a fixed time , where is the position vector of a point in real space and now is the wavevector in the three dimensional reciprocal space. (The magnitude of a wavevector is called wavenumber.) The constant is the phase of the wavefront (a plane of a constant phase) through the origin at time , and is a unit vector perpendicular to this wavefront. The wavefronts with phases , where represents any integer, comprise a set of parallel planes, equally spaced by the wavelength .

Reciprocal lattice[edit]

In general, a geometric lattice is an infinite, regular array of vertices (points) in space, which can be modelled vectorially as a Bravais lattice. Some lattices may be skew, which means that their primary lines may not necessarily be at right angles. In reciprocal space, a reciprocal lattice is defined as the set of wavevectors of plane waves in the Fourier series of any function whose periodicity is compatible with that of an initial direct lattice in real space. Equivalently, a wavevector is a vertex of the reciprocal lattice if it corresponds to a plane wave in real space whose phase at any given time is the same (actually differs by with an integer ) at every direct lattice vertex.

One heuristic approach to constructing the reciprocal lattice in three dimensions is to write the position vector of a vertex of the direct lattice as , where the are integers defining the vertex and the are linearly independent primitive translation vectors (or shortly called primitive vectors) that are characteristic of the lattice. There is then a unique plane wave (up to a factor of negative one), whose wavefront through the origin contains the direct lattice points at and , and with its adjacent wavefront (whose phase differs by or from the former wavefront passing the origin) passing through . Its angular wavevector takes the form , where is the unit vector perpendicular to these two adjacent wavefronts and the wavelength must satisfy , means that is equal to the distance between the two wavefronts. Hence by construction and .

Cycling through the indices in turn, the same method yields three wavevectors with , where the Kronecker delta equals one when and is zero otherwise. The comprise a set of three primitive wavevectors or three primitive translation vectors for the reciprocal lattice, each of whose vertices takes the form , where the are integers. The reciprocal lattice is also a Bravais lattice as it is formed by integer combinations of the primitive vectors, that are , , and in this case. Simple algebra then shows that, for any plane wave with a wavevector on the reciprocal lattice, the total phase shift between the origin and any point on the direct lattice is a multiple of (that can be possibly zero if the multiplier is zero), so the phase of the plane wave with will essentially be equal for every direct lattice vertex, in conformity with the reciprocal lattice definition above. (Although any wavevector on the reciprocal lattice does always take this form, this derivation is motivational, rather than rigorous, because it has omitted the proof that no other possibilities exist.)

The Brillouin zone is a primitive cell (more specifically a Wigner-Seitz cell) of the reciprocal lattice, which plays an important role in solid state physics due to Bloch’s theorem. In pure mathematics, the dual space of linear forms and the dual lattice provide more abstract generalizations of reciprocal space and the reciprocal lattice.

Mathematical description[edit]

Assuming a three-dimensional Bravais lattice and labelling each lattice vector (a vector indicating a lattice point) by the subscript as 3-tuple of integers,

where

where is the set of integers and is a primitive translation vector or shortly primitive vector. Taking a function where is a position vector from the origin to any position, if follows the periodicity of this lattice, e.g. the function describing the electronic density in an atomic crystal, it is useful to write as a multi-dimensional Fourier series

where now the subscript , so this is a triple sum.

As follows the periodicity of the lattice, translating by any lattice vector we get the same value, hence

Expressing the above instead in terms of their Fourier series we have

Because equality of two Fourier series implies equality of their coefficients, , which only holds when

where

Mathematically, the reciprocal lattice is the set of all vectors , that are wavevectors of plane waves in the Fourier series of a spatial function whose periodicity is the same as that of a direct lattice as the set of all direct lattice point position vectors , and satisfy this equality for all . Each plane wave in the Fourier series has the same phase (actually can be differed by a multiple of ) at all the lattice point .

As shown in the section multi-dimensional Fourier series, can be chosen in the form of where . With this form, the reciprocal lattice as the set of all wavevectors for the Fourier series of a spatial function which periodicity follows , is itself a Bravais lattice as it is formed by integer combinations of its own primitive translation vectors , and the reciprocal of the reciprocal lattice is the original lattice, which reveals the Pontryagin duality of their respective vector spaces. (There may be other form of . Any valid form of results in the same reciprocal lattice.)

Two dimensions[edit]

For an infinite two-dimensional lattice, defined by its primitive vectors , its reciprocal lattice can be determined by generating its two reciprocal primitive vectors, through the following formulae,

where is an integer and

Here represents a 90 degree rotation matrix, i.e. a quarter turn. The anti-clockwise rotation and the clockwise rotation can both be used to determine the reciprocal lattice: If is the anti-clockwise rotation and is the clockwise rotation, for all vectors . Thus, using the permutation

we obtain

Notably, in a 3D space this 2D reciprocal lattice is an infinitely extended set of Bragg rods—described by Sung et al.^[1]

Three dimensions[edit]

For an infinite three-dimensional lattice , defined by its primitive vectors and the subscript of integers , its reciprocal lattice with the integer subscript can be determined by generating its three reciprocal primitive vectors

where

is the scalar triple product. The choice of these is to satisfy as the known condition (There may be other condition.) of primitive translation vectors for the reciprocal lattice derived in the heuristic approach above and the section multi-dimensional Fourier series. This choice also satisfies the requirement of the reciprocal lattice mathematically derived above. Using column vector representation of (reciprocal) primitive vectors, the formulae above can be rewritten using matrix inversion:

This method appeals to the definition, and allows generalization to arbitrary dimensions. The cross product formula dominates introductory materials on crystallography.

The above definition is called the «physics» definition, as the factor of comes naturally from the study of periodic structures. An essentially equivalent definition, the «crystallographer’s» definition, comes from defining the reciprocal lattice . which changes the reciprocal primitive vectors to be

and so on for the other primitive vectors. The crystallographer’s definition has the advantage that the definition of is just the reciprocal magnitude of in the direction of , dropping the factor of . This can simplify certain mathematical manipulations, and expresses reciprocal lattice dimensions in units of spatial frequency. It is a matter of taste which definition of the lattice is used, as long as the two are not mixed.

is conventionally written as or , called Miller indices; is replaced with , replaced with , and replaced with . Each lattice point in the reciprocal lattice corresponds to a set of lattice planes in the real space lattice. (A lattice plane is a plane crossing lattice points.) The direction of the reciprocal lattice vector corresponds to the normal to the real space planes. The magnitude of the reciprocal lattice vector is given in reciprocal length and is equal to the reciprocal of the interplanar spacing of the real space planes.

Higher dimensions[edit]

The formula for dimensions can be derived assuming an -dimensional real vector space with a basis and an inner product . The reciprocal lattice vectors are uniquely determined by the formula . Using the permutation

they can be determined with the following formula:

Here, is the volume form, is the inverse of the vector space isomorphism defined by and denotes the inner multiplication.

One can verify that this formula is equivalent to the known formulas for the two- and three-dimensional case by using the following facts: In three dimensions, and in two dimensions, , where is the rotation by 90 degrees (just like the volume form, the angle assigned to a rotation depends on the choice of orientation^[2]).

Reciprocal lattices of various crystals[edit]

Reciprocal lattices for the cubic crystal system are as follows.

Simple cubic lattice[edit]

The simple cubic Bravais lattice, with cubic primitive cell of side , has for its reciprocal a simple cubic lattice with a cubic primitive cell of side (or in the crystallographer’s definition). The cubic lattice is therefore said to be self-dual, having the same symmetry in reciprocal space as in real space.

Face-centered cubic (FCC) lattice[edit]

The reciprocal lattice to an FCC lattice is the body-centered cubic (BCC) lattice, with a cube side of .

Consider an FCC compound unit cell. Locate a primitive unit cell of the FCC; i.e., a unit cell with one lattice point. Now take one of the vertices of the primitive unit cell as the origin. Give the basis vectors of the real lattice. Then from the known formulae, you can calculate the basis vectors of the reciprocal lattice. These reciprocal lattice vectors of the FCC represent the basis vectors of a BCC real lattice. Note that the basis vectors of a real BCC lattice and the reciprocal lattice of an FCC resemble each other in direction but not in magnitude.

Body-centered cubic (BCC) lattice[edit]

The reciprocal lattice to a BCC lattice is the FCC lattice, with a cube side of .

It can be proven that only the Bravais lattices which have 90 degrees between (cubic, tetragonal, orthorhombic) have primitive translation vectors for the reciprocal lattice, , parallel to their real-space vectors.

Simple hexagonal lattice[edit]

The reciprocal to a simple hexagonal Bravais lattice with lattice constants and is another simple hexagonal lattice with lattice constants and rotated through 90° about the c axis with respect to the direct lattice. The simple hexagonal lattice is therefore said to be self-dual, having the same symmetry in reciprocal space as in real space. Primitive translation vectors for this simple hexagonal Bravais lattice vectors are , , and .^[3]

Arbitrary collection of atoms[edit]

One path to the reciprocal lattice of an arbitrary collection of atoms comes from the idea of scattered waves in the Fraunhofer (long-distance or lens back-focal-plane) limit as a Huygens-style sum of amplitudes from all points of scattering (in this case from each individual atom).^[4] This sum is denoted by the complex amplitude in the equation below, because it is also the Fourier transform (as a function of spatial frequency or reciprocal distance) of an effective scattering potential in direct space:

Here g = q/(2π) is the scattering vector q in crystallographer units, N is the number of atoms, f_j[g] is the atomic scattering factor for atom j and scattering vector g, while r_j is the vector position of atom j. Note that the Fourier phase depends on one’s choice of coordinate origin.

For the special case of an infinite periodic crystal, the scattered amplitude F = M F_hkl from M unit cells (as in the cases above) turns out to be non-zero only for integer values of , where

when there are j=1,m atoms inside the unit cell whose fractional lattice indices are respectively {u_j, v_j, w_j}. To consider effects due to finite crystal size, of course, a shape convolution for each point or the equation above for a finite lattice must be used instead.

Whether the array of atoms is finite or infinite, one can also imagine an «intensity reciprocal lattice» I[g], which relates to the amplitude lattice F via the usual relation I = F^*F where F^* is the complex conjugate of F. Since Fourier transformation is reversible, of course, this act of conversion to intensity tosses out «all except 2nd moment» (i.e. the phase) information. For the case of an arbitrary collection of atoms, the intensity reciprocal lattice is therefore:

Here r_jk is the vector separation between atom j and atom k. One can also use this to predict the effect of nano-crystallite shape, and subtle changes in beam orientation, on detected diffraction peaks even if in some directions the cluster is only one atom thick. On the down side, scattering calculations using the reciprocal lattice basically consider an incident plane wave. Thus after a first look at reciprocal lattice (kinematic scattering) effects, beam broadening and multiple scattering (i.e. dynamical) effects may be important to consider as well.

Generalization of a dual lattice[edit]

There are actually two versions in mathematics of the abstract dual lattice concept, for a given lattice L in a real vector space V, of finite dimension.

The first, which generalises directly the reciprocal lattice construction, uses Fourier analysis. It may be stated simply in terms of Pontryagin duality. The dual group V^ to V is again a real vector space, and its closed subgroup L^ dual to L turns out to be a lattice in V^. Therefore, L^ is the natural candidate for dual lattice, in a different vector space (of the same dimension).

The other aspect is seen in the presence of a quadratic form Q on V; if it is non-degenerate it allows an identification of the dual space V^* of V with V. The relation of V^* to V is not intrinsic; it depends on a choice of Haar measure (volume element) on V. But given an identification of the two, which is in any case well-defined up to a scalar, the presence of Q allows one to speak to the dual lattice to L while staying within V.

In mathematics, the dual lattice of a given lattice L in an abelian locally compact topological group G is the subgroup L^∗ of the dual group of G consisting of all continuous characters that are equal to one at each point of L.

In discrete mathematics, a lattice is a locally discrete set of points described by all integral linear combinations of dim = n linearly independent vectors in Rⁿ. The dual lattice is then defined by all points in the linear span of the original lattice (typically all of Rⁿ) with the property that an integer results from the inner product with all elements of the original lattice. It follows that the dual of the dual lattice is the original lattice.

Furthermore, if we allow the matrix B to have columns as the linearly independent vectors that describe the lattice, then the matrix has columns of vectors that describe the dual lattice.

See also[edit]

• Brillouin zone
• Crystallography
• Dual basis
• Ewald’s sphere
• Kikuchi line
• Miller index
• Powder diffraction
• Zone axis

References[edit]

External links[edit]

• http://newton.umsl.edu/run//nano/known.html — Jmol-based electron diffraction simulator lets you explore the intersection between reciprocal lattice and Ewald sphere during tilt.
• DoITPoMS Teaching and Learning Package on Reciprocal Space and the Reciprocal Lattice
• Learn easily crystallography and how the reciprocal lattice explains the diffraction phenomenon, as shown in chapters 4 and 5

Каждой кристаллической
структуре соответствуют две решетки ‑
прямая кристаллическая решетка и
обратная
решетка, которая
строится следующим образом:

1) если обычная
прямая решетка построена на векторах
трансляций

, 
, 
,
то оси обратной к ней решетки

, 
, 

определяются как векторные произведения:

; (4.1)

2)
осевые
параметры обратной решетки

, 
, 

равны обратным величинам межплоскостных
расстояний плоских сеток прямой решетки,
нормальных к этой оси.

Каждой плоскости
(hkl)
прямой
решетки отвечает в обратной решетке
узел [[hkl]]*.
Бесконечному семейству параллельных
плоскостей {hkl}
в пространстве
прямой решетки соответствует в
пространстве обратной решетки бесконечное
семейство точек [[hkl]]*
вдоль направления, нормального к этим
плоскостям. Расстояния этих точек от
точки, принятой за начало координат в
обратном пространстве, равны 1/d,
2/d,
3/d,…,
где d
= d_hkl
‑ расстояние
между плоскостями {hkl}
в прямой
решетке (рис. 11).

Рис. 11. Прямая
(а) и
обратная (б)
решетки

Зоне плоскостей
прямой решетки отвечает сетка из точек
(узлов) обратной решетки, причем ось
зоны прямой решетки нормальна к плоскости
сетки обратной решетки. Наконец, прямой
пространственной решетке из плоскостей
{hkl}
отвечает обратная трехмерная решетка
из точек [[hkl]]*.
Основные векторы

, 
, 

обратной решетки определяются векторными
произведениями (4.1) или скалярными
произведениями:

а*а =b*b
= с*с = 1, а*b
= а*с = b*с
= b*а
= с*b
= с*а = 0. (4.2)

Из равенств (4.1)
видно, что вектор

нормален к плоскости векторов

и

и
т.д. Тройка векторов

, 
, 

выбирается так, чтобы они, как и векторы

, 
, 
,
составляли правую тройку.

Векторы

, 
, 

представляют собой площадки элементарных
параллелограммов в координатных
плоскостях прямой решетки, а по абсолютному
значению они обратно пропорциональны
межплоскостным расстояниям прямой
решетки:

(4.3)

(в знаменателе ‑
смешанное произведение векторов).

Прямая и обратная
решетки сопряжены взаимно, т.е.
решетка,
построенная
на осях

, 
, 
,
является обратной по отношению к решетке

, 
, 
,
а решетка, построенная на векторах

, 
, 
,
‑ обратной по отношению к решетке

, 
, 
.

Основные
свойства обратной решетки

1. Вектор

обратной решетки перпендикулярен
плоскости (hkl)
прямой
решетки, а длина этого вектора равна
обратной величине расстояния d
между
плоскостями {hк1}
прямой
решетки, т.е.

. (4.4)

2. Объем V*
элементарной
ячейки обратной решетки равен обратной
величине объема V
элементарной
ячейки прямой решетки (и обратно):

;
. (4.5)

Можно
показать, что кубической
объемно-центрированной решетке
соответствует обратная кубическая
гранецентрированная.

Миллеровские
индексы системы параллельных
плоскостей прямой решетки
являются координатами ряда обратной
решетки.

Физический
смысл обратной решетки

Понятие об обратной
решетке вводится
в основном для описания периодического
распределения отражающей
способности кристалла по отношению
к рентгеновским лучам.

Отражение
рентгеновских лучей от плоскостей
структуры кристалла описывается формулой
Вульфа — Брэгга (см. вывод формулы
Вульфа-Брэгга, стр. 9)

,

где
λ
‑ длина волны рентгеновского излучения,
θ
‑ угол, дополнительный до
90° к углу падения (или к углу отражения),
d
‑
межплоскостное расстояние для семейства
параллельных отражающих
плоскостей, п
‑ порядок
дифракционного спектра.

Из условия Вульфа
‑ Брэгга следует, что при постоянной
λ,
большому d
отвечает
малый угол θ,
т. е. чем больше межплоскостное расстояние,
тем ближе направления отраженных лучей
к направлению падающего пучка. Отражения
рентгеновских лучей от бесконечно
протяженных идеальных кристаллов должны
быть точечными.

Каждый узел обратной
решетки соответствует возможному
отражению от плоскостей прямой решетки
кристалла. Направление вектора обратной
решетки H^*_hkl
совпадает
с направлением отражения от плоскостей
{hkl},
а n-й
узел обратной
решетки в этом ряду отвечает отражению
n-го
порядка от этих плоскостей.

На основании
представления об обратной решетке
Эвальдом дано построение, позволяющее
наглядно геометрически истолковать
пространственное распределение отражений
рентгеновских лучей от кристалла.
Построение Эвальда дает возможность
решать основную задачу рентгеноструктурного
анализа: определять, возникнут ли
дифрагированные лучи и в каких
направлениях, если на кристалл падает
пучок рентгеновских лучей с длиной
волны λ.

П

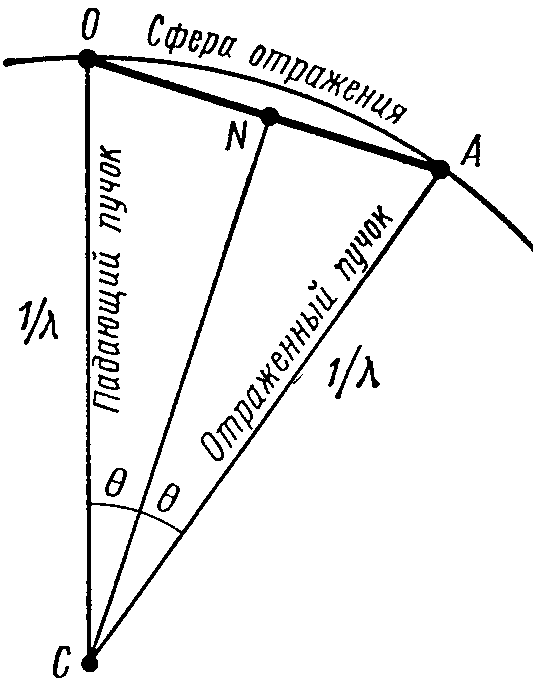
Рис. 12. Построение
Эвальда

усть рентгеновский пучок
падает на кристалл в направлении CO
(рис. 12), CN ‑ направление
r^*_hkl,
т. е. нормаль к плоскостям
{hkl}.

Примем точку О
за начало
координат обратной решетки и проведем
из точки С
сферу радиусом
1/λ
‑ так
называемую сферу отражения, или сферу
Эвальда. Если сфера Эвальда пройдет
через другой узел А
обратной
решетки, то направление СА
есть возможное
направление дифрагированного луча
данной падающей волны. В самом деле,

ОС = АС= 1/λ, ОN
= АО/2 =
п/(2d),
,

отсюда получаем
уже известную нам формулу

Таким образом,
закон Вульфа ‑ Брэгга удовлетворяется
для любого узла обратной решетки,
находящегося на сфере Эвальда.

Вывод формулы
Вульфа-Брегга

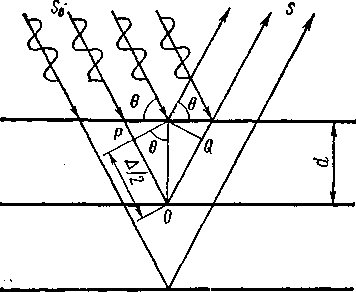
Рис. 13. К выводу
условия Вульфа – Брэгга

Грани кристаллического
многогранника соответствуют определенным
сеткам структуры, поэтому углы между
гранями отвечают углам между плоскими
сетками в структуре кристалла. Теперь
эти углы измеряют с помощью рентгенограмм,
для чего не обязательно иметь большой
кристалл с правильной внешней огранкой,
а достаточно крупинки кристаллического
вещества. Поскольку длины волны
рентгеновского излучения соизмеримы
с межатомными расстояниями в кристаллических
структурах, кристаллы являются природными
дифракционными решетками. Именно с
помощью дифракции рентгеновских лучей
было доказано решетчатое строение
кристаллов (М. Лауэ, 1912). Схема, поясняющая
дифракцию, дана на рис. 3: S₀
‑ пучок монохроматических рентгеновских
лучей, падающих под углом θ
на семейство параллельных атомных
плоскостей, S ‑ пучок
дифрагированных лучей. Дифрагированные
лучи усиливают друг друга, если согласно
условию интерференции разность хода Δ
между ними равна целому числу длин волн,
т.е.

Δ=nλ (n = 1,2,3,
…)

Из чертежа видно,
что разность хода между падающим и
дифрагированным лучами равна

Δ=
РО +
OQ
= 2РО
= 2dsinθ.

Чтобы волны,
рассеянные двумя соседними плоскими
сетками (а значит, и всем семейством
параллельных плоских сеток), дали
максимум интенсивности, необходимо
выполнение основного закона дифракции
рентгеновских лучей в кристаллах:

2dsinθ
= пλ (n = 1, 2, 3,
…) (*)

Это равенство
выражает условие
Вульфа —
Брэгга.

Иначе говоря, если
луч с длиной волны λ,
падает на совокупность параллельных
атомных плоскостей, отстоящих друг от
друга на расстояний d,
то он порождает
дифрагированный луч, идущий так, как
шел бы луч, отраженный под углом θ.
Таким образом, при определенных углах
падения плоские сетки в структуре
кристалла могут «отражать» рентгеновские
лучи. Эти отражения (точнее, максимумы
интенсивности дифрагированных лучей)
можно зарегистрировать на фотографической
пластинке с помощью ионизационного
спектрометра. Симметричный, закономерный
узор на рентгенограмме, например рис.
4, отображает симметрию и закономерность
структуры кристалла и дает возможность
измерять расстояния между атомными
плоскостями и углы между ними, которые
на многогранных формах кристаллов
являются углами между гранями. По
рентгенограммам на основании условия
(*) можно изучать структуры кристаллов,
находить межплоскостные расстояния d,
диагностировать
кристаллические вещества.

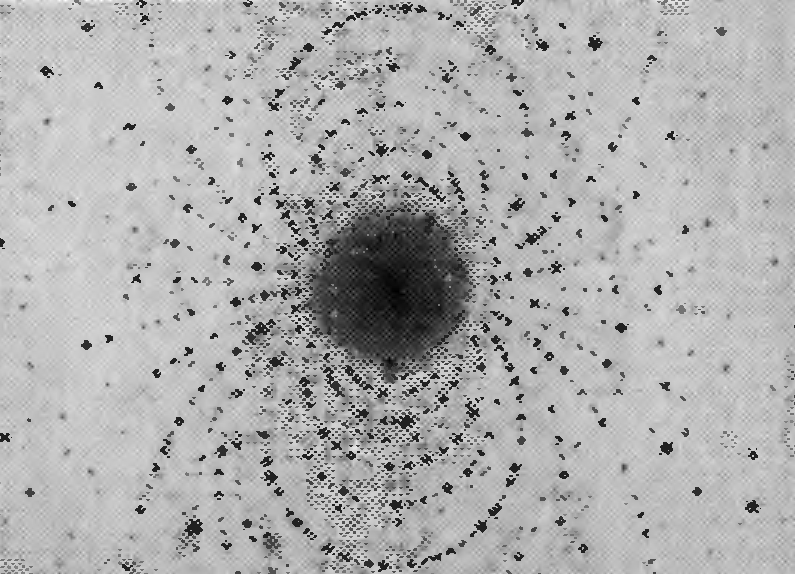
Рис.14. Рентгенограмма
кристалла.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Обра́тная решетка, точечная трехмерная решетка в абстрактном обратном пространстве, где расстояния имеют размерность обратной длины.

Введение понятия обратной решетки и обратного пространства, сопряженных с прямой решеткой и прямым пространством, полезно при решении дифракционных задач физики твердого тела, оптики, структурного анализа, электронной микроскопии.

Обратная решетка, соответствующая любой прямой решетке, описывающей реальную структуру кристалла, строится следующим образом:

1.Если обычная прямая решетка построена на векторах трансляций a, b, c, то оси обратной к ней решетки a*, b*, c* определяются как векторные произведения:

a* = bc, b* = ca, c* = ab

2.Осевые параметры обратной решетки a*, b*, c* равны обратным величинам межплоскостных расстояний плоских сеток прямой решетки, нормальных к этой оси.

Т. е. вектор обратной решетки H*_hkl нормален к каждой плоскости прямой решетки (hkl), а его длина определяется как величина, обратная межплоскостному расстоянию dhkl.

Решетка с вектором H*hkl, построенная на базисных векторах a*, b*, c* называется обратной решеткой, векторы a*, b*, c* — координатными векторами обратной решетки.

Каждой плоскости (hkl) прямой решетки отвечает в обратной решетке узел [[hkl]]*. Бесконечному семейству параллельных плоскостей hkl в пространстве прямой решетки соответствует в пространстве обратной решетки бесконечное семейство точек [[hkl]]* вдоль направления, нормального к этим плоскостям. Расстояния от этих точек от точки, принятой за начало координат в обратном пространстве, равны 1/d, 2/d, 3/d, …, где d=dhkl – расстояние между плоскостями hkl в прямой решетке. Обратная решетка определена в трехмерном обратном пространстве с размерностью «обратных длин».

Зоне плоскостей прямой решетки отвечает сетка из точек (узлов) обратной решетки, причем ось зоны прямой решетки нормальна к плоскости сетки обратной решетки. Прямой пространственной решетке из плоскостей hkl отвечает обратная трехмерная решетка из точек [[hkl]]*.

Основные векторы a*, b*, c* обратной решетки определяются также скалярными произведениями:

aa* = bb* = cc* = 1;

a*b = a*c = b*c = b*a = c*b = c*a = 0

Прямая и обратная решетка сопряжены взаимно, т. е. решетка, построенная на осях a, b, c, является обратной по отношению к решетке a*, b*, c*, а решетка, построенная на векторах a*, b*, c*, — обратной по отношению к решетке a*, b*, c*.

Обратная решетка является важным математическим образом, находящим многочисленные применения в геометрической кристаллографии, в теории дифракции и структурном анализе кристаллов, в физике твердого тела.

Например, понятие обратной решетки используется для описания периодического распределения отражающей способности кристалла по отношению к рентгеновским лучам. Отражение рентгеновских лучей от плоскостей структуры кристалла описывается формулой Вульфа-Брэгга (Брэгга-Вульфа условие), из которого следует, что при постоянной длине волны рентгеновского излучения λ большому межплоскостному расстоянию для семейства параллельных отражающих плоскостей d отвечает малый угол падения θ, т. е., чем больше межплоскостное расстояние, тем ближе направления отраженных лучей к направлению падающего пучка. Отражения рентгеновских лучей от бесконечно протяженных идеальных кристаллов должны быть точечными.

Каждый узел обратной решетки соответствует возможному отражению от плоскостей прямой решетки кристалла. Направление вектора обратной решетки H*_hkl совпадает с направлением отражения от плоскостей hkl в прямой решетке, а n-ый узел обратной решетки в этом ряду отвечает отражению n-го порядка от этих плоскостей.