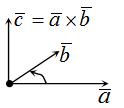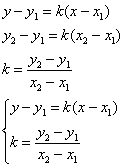Как найти векторное произведение векторов по точками

Заказать задачи по любым предметам можно здесь от 10 минут

Векторное произведение векторов

Определение

Определение

Векторным произведением векторов $ overline{a} $ и $ overline{b} $ является вектор $ overline{c} $, который расположен перпендикулярно к плоскости, образуемой векторами $ overline{a} $ и $ overline{b} $. Само произведение обозначается как $ [overline{a},overline{b}] $, либо $ overline{a} times overline{b} $.

Векторное произведение векторов, формула которого зависит от исходных данных задачи, можно найти двумя способами.

Формула

Формула 1

Если известен синус угла между векторами $ overline{a} $ и $ overline{b} $, то найти векторное произведение векторов можно по формуле: $$ [overline{a},overline{b}] = |overline{a}| cdot |overline{b}| cdot sin (overline{a},overline{b}) $$

Формула 2

В случае когда векторы $ overline{a} $ и $ overline{b} $ заданы в координатной форме, то их произведение определяется по формуле: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} $$ где векторы $ overline{i},overline{j},overline{k} $ называются единичными векторами соответствующих осей $ Ox, Oy, Oz $.

Определитель во второй формуле можно раскрыть по первой строке:

$$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ a_1 & a_2 & a_3 \ b_1 & b_2 & b_3 end{vmatrix} = overline{i} (a_2 b_3 — a_3 b_2) — overline{j} (a_1 b_3 — a_3 b_1) + overline{k} (a_1 b_2 — a_2 b_1) $$

Итого вторая формула приобретает окончательный короткий вид:

$$ overline{a} times overline{b} = (a_2 b_3 — a_3 b_2; a_3 b_1 — a_1 b_3; a_1 b_2 — a_2 b_1) $$

Свойства

1. При изменении порядка множителей меняется знак на противоположный: $$ [overline{a},overline{b}] = -[overline{b},overline{a}] $$
2. Вынос константы за знак произведения: $$ lambda [overline{a},overline{b}] = [lambda overline{a}, overline{b}] = [overline{a}, lambda overline{b}] $$
3. $$ [overline{a}+overline{b}, overline{c}] = [overline{a},overline{c}] + [overline{b}, overline{c}] $$

Примеры решений

Пример 1

Найти векторное произведение векторов, заданных координатами $$ overline{a} = (2,1,-3) $$ $$ overline{b} = (1,2,-1) $$

Решение

Составляем определитель, первая строка которого состоит из единичных векторов, а вторая и третья из координат векторов $ overline{a} $ и $ overline{b} $: $$ overline{a} times overline{b} = begin{vmatrix} overline{i} & overline{j} & overline{k} \ 2&1&-3\1&2&-1 end{vmatrix} = overline{i} (-1+6) — overline{j}(-2+3) + overline{k}(4-1) = 5overline{i} — overline{j} + 3overline{k} $$ Полученный ответ можно записать в удобном виде: $$ overline{a} times overline{b} = (5, -1, 3) $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ overline{a} times overline{b} = (5, -1, 3) $$

Геометрический смысл

• Модуль векторного произведения векторов $ overline{a} $ и $ overline{b} $ в геометрическом смысле равен площади параллелограмма, построенного на этих векторах: $$ S_{parall} = |overline{a} times overline{b}| $$
• Половина этого модуля это площадь треугольника: $$ S_Delta = frac{1}{2} |overline{a} times overline{b} | $$
• Если векторное произведение равно нулю $ overline{a} times overline{b} = 0 $, то векторы коллинеарны.

 

Пример 2

Найти площадь треугольника по заданным векторам $$ overline{a} = (2,1,3) $$ $$ overline{b} = (-1,2,1) $$

Решение

Используя геометрический смысл, в частности вторую формулу находим половину модуля векторного произведения векторов. Находим определитель: $$ begin{vmatrix} overline{i}&overline{j}&overline{k}\2&1&3\-1&2&1 end{vmatrix} = overline{i}(1-6) — overline{j}(2+3) + overline{k}(4+1) = -5overline{i} — 5overline{j} + 5overline{k} $$ Вычисляем модуль полученного вектора как корень квадратный из суммы квадратов координат этого вектора: $$ |overline{a} times overline{b}| = sqrt{(-5)^2 + (-5)^2 + 5^2} = sqrt{25 + 25 + 25} = sqrt{75} $$ По формуле нахождения площади треугольника имеем: $$ S_Delta = frac{1}{2} |overline{a} times overline{b}| = frac{1}{2} sqrt{75} = 4.33 $$

Ответ

$$ S_Delta = 4.33 $$

Содержание:

• Формула
• Примеры вычисления векторного произведения векторов

Формула

Для того чтобы найти векторное произведение
$[bar{a}, bar{b}]$ двух векторов, заданных своими координатами
$bar{a}=left(a_{x} ; a_{y} ; a_{z}right)$ и
$bar{b}=left(b_{x} ; b_{y} ; b_{z}right)$ соответственно, необходимо
вычислить следующий определитель

Обычно такой определитель вычисляют разложением по первой строке. Отметим также, что результатом векторного произведения является вектор.

Примеры вычисления векторного произведения векторов

Читать дальше: как найти смешанное произведение векторов.

Угол между векторами

Для того чтобы мы могли ввести понятие векторного произведения двух векторов, нужно сначала разобраться с таким понятие, как угол между этими векторами.

Пусть нам даны два вектора $overline{α}$ и $overline{β}$. Возьмем в пространстве какую-либо точку $O$ и отложим от нее векторы $overline{α}=overline{OA}$ и $overline{β}=overline{OB}$, тогда угол $AOB$ будет называться углом между этими векторами (рис. 1).

Причем мы будем считать, что если векторы $overline{α}$ и $overline{β}$ будут сонаправленными, или один или оба из них нулевой, то угол между этими векторами будет равен $0^circ$.

Обозначение: $∠(overline{α},overline{β})$

Понятие векторного произведения векторов и формула нахождения

Обозначение: $overline{α}хoverline{β}$.

Математически это выглядит следующим образом:

1. $|overline{α}хoverline{β}|=|overline{α}||overline{β}|sin⁡∠(overline{α},overline{β})$
2. $overline{α}хoverline{β}⊥overline{α}$, $overline{α}хoverline{β}⊥overline{β}$
3. $(overline{α}хoverline{β},overline{α},overline{β})$ и $(overline{i},overline{j},overline{k})$ одинаково ориентированы (рис. 2)

«Как найти векторное произведение векторов» 👇

Очевидно, что внешнее произведение векторов будет равняться нулевому вектору в двух случаях:

1. Если длина одного или обоих векторов равняется нулю.
2. Если угол между этими векторами будет равняться $180^circ$ или $0^circ$ (так как в этом случае синус равняется нулю).

Чтобы наглядно увидеть, как находится векторное произведение векторов, рассмотрим следующие примеры решения.

Вычисление векторного произведения по координатам векторов

Из определения 1 сразу же вытекает и способ нахождения векторного произведения для двух векторов. Поскольку вектор кроме значения имеет еще и направление, находить его только при помощи скалярной величины невозможно. Но помимо него существует еще способ нахождения с помощью координат данных нам векторов.

Пусть нам даны векторы $overline{α}$ и $overline{β}$, которые будут иметь координаты $(α_1,α_2,α_3)$ и $(β_1,β_2,β_3)$, соответственно. Тогда вектор векторного произведения (а именно его координаты) можно найти по следующей формуле:

$overline{α}хoverline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}$

Иначе, раскрывая определитель, получим следующие координаты

$overline{α}хoverline{β}=(α_2 β_3-α_3 β_2,α_3 β_1-α_1 β_3,α_1 β_2-α_2 β_1)$

Свойства векторного произведения векторов

Для произвольных смешанных трех векторов $overline{α}$, $overline{β}$ и $overline{γ}$, а также $r∈R$ справедливы следующие свойства:

1. $overline{α}хoverline{β}=-(overline{β}хoverline{α})$

   Верность этого свойства будет следовать из третьего пункта определения 1.

2. $(roverline{α})хoverline{β}=r(overline{α}хoverline{β})$ и $overline{α}х(roverline{β})=r(overline{α}хoverline{β})$

   Из формулы для нахождения векторного произведения будем получать:

   $(roverline{α})overline{β}=begin{vmatrix}overline{i}&overline{j}&overline{k}\rα_1&rα_2&rα_3\β_1&β_2&β_3end{vmatrix}=rbegin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}=r(overline{α}хoverline{β})$

   $overline{α}х(roverline{β})=begin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\rβ_1&rβ_2&rβ_3end{vmatrix}=rbegin{vmatrix}overline{i}&overline{j}&overline{k}\α_1&α_2&α_3\β_1&β_2&β_3end{vmatrix}=r(overline{α}хoverline{β})$

3. $overline{α}х(overline{β}+overline{γ})=overline{α}overline{β}+overline{α}overline{γ}$ и $(overline{α}+overline{β})overline{γ}=overline{α}overline{γ}+overline{β}overline{γ}$.

   Данное свойство векторного произведения векторов также можно проверить с помощью формулы.

   Следующее свойство называют геометрическим смыслом векторного произведения:

4. Длина вектора векторного произведения равняется площади параллелограмма, который нужно было построить между ними (рис. 4)

   

   Рисунок 4. Длина вектора векторного произведения. Автор24 — интернет-биржа студенческих работ

Векторным
произведением

вектора

на вектор

называется вектор (обозначим его

),
удовлетворяющий следующим условиям.

1.

,
где

.

2.

и

.

3.
Направление вектора

выбрано так, что со стороны вектора

поворот от

к

происходит против часовой стрелки.

Свойства
векторного произведения.

1.

2.

,

— вещественное число

3.

Пример

Найти площадь
параллелограмма и угол

между его диагоналями, если длина сторон
параллелограмма

и угол между ними

.

Решение.

Пусть

и

— векторы, построенные на сторонах
параллелограмма. Площадь параллелограмма

.

Заметим, что

.
Диагонали параллелограмма – это векторы

и

.

Пусть

— угол между диагоналями. Тогда

Ответ:

;

.

Векторное
произведение векторов.

Определение:
Векторным произведением упорядоченной
пары векторов a
и b
называется вектор [a,b],
такой что

1. |
   [a,b]
   |=S_a,b,
   где S_a,b
   – площадь параллелограмма, построенного
   на векторах a
   и b.
   (Если a
   || b,
   то S_a,b=0.)

2. a
   
   
   [a,b]
   

   b.

3. a,
   b,
   [a,b]
   – правая тройка.

Свойства
векторного произведения:

1. [a,b]
   = -[b,a]

2. [a,b]
   = θ
   ó a
   || b
   

3. [a₁+a₂,b]
   = [a₁,b]+[a₂,b]

4. λ·[a,b]
   = [λ·a,b]
   = [a,λ·b]

   
   λ

   
   R.

Утверждение
2:
В декартовой системе координат (базис
i,
j,
k),
a={x₁,
y₁,
z₁},
b={x₂,
y₂,
z₂}

=>
[a,b]
=

=

12.
Смешанное произведение
векторов.

Определение
:
Смешанным
произведением
упорядоченной тройки векторов a,
b
и
c называется
число <a,
b,
c>,
т.ч. <a,b,c>=([a,b],c).

Утверждение
:
<a,b,c>=V_a,b,c,
если a,b,c
– правая
тройка, или <a,b,c>=
-V_a,b,c,
если a,b,c
– левая
тройка. Здесь V_a,b,c
–
объём параллелепипеда, построенного
на векторах a,
b
и
c.
(Если a,
b
и
c компланарны,
то V_a,b,c=0.)

Утверждение
:
В декартовой системе координат, если
a={x₁,
y₁,
z₁},
b={x₂,
y₂,
z₂},

с={x₃,
y₃,
z₃},
=> <a,b,c>=
.

13. Прямая на плоскости. Виды уравнений прямой.

Понятие «уравнение
линии» — есть основное понятие
аналитической геометрии. Из него
вытекают две основные задачи аналитической
геометрии на плоскости:

А) Дана линия,
рассматриваемая как множество точек.
Составить алгебраическое уравнение
этой линии.

Б) Дано уравнение
некоторой линии. Изучить по этому
уравнению её геометрические свойства:
форму и расположение.

Линия называется
линией n-го
порядка
(n=1, 2, 3, …), если она определяется
уравнением n-ой
степени относительно текущих прямоугольных
координат.

Ax+By+C=0 — кривые
первого порядка;

Ax²+2Bxy+Cy²+2Dx+2Ey+F=0
— кривые второго порядка

.Кривая первого
порядка — есть прямая линия.

Уравнение
с угловым коэффициентом.

k=
tg α – угловой коэффициент.

Если
b=0 то прямая проходит через начало
координат. Уравнение примет вид

Если
α=0, то k = tg α = 0. То прямая пройдет
параллельно оси ох.

Если
α=π/2, то уравнение теряет смысл. В этом
случае уравнение примет

вид



и пройдет

параллельно
оси оу.

Общее
уравнение прямой.

A,
B, C – произвольные числа, причем А и В
не равны нулю одновременно.

·
Если В=0, то уравнение имеет вид

или


.
Это уравнение

прямой,
параллельной оси оу. и проходящей через
точку

·
Если В≠0, то получаем уравнение с угловым
коэффициентом

.

·
Если А=0, то уравнение имеет вид

.
Это уравнение прямой, параллельной оси
ох.

·
Если С=0, то уравнение проходит через
т. О (0;0).

Уравнение
прямой, проходящей через точку, в данном
направлении.

т
М (х₀;у₀).

Уравнение
прямой записывается в виде

.

Подставим
в это уравнение точку М

Решим
систему:

Уравнение
прямой, проходящей через 2 точки.

К
(х₁;у₁)
М (х₂;у₂)

Уравнение
прямой в отрезках.

К
(а;0); М (0;b)

Подставим
точки в уравнение прямой:

Уравнение
прямой, проходящей через данную точку,
перпендикулярно данному

вектору.

М₀
(х₀;у₀).

Возьмем
произвольную точку М (х;у).

Т.к.


,
то

Нормальное
уравнение прямой.

Уравнение
прямой можно записать в виде:

Т.к.


;
,
то:

Угол
между прямыми.

Дано:
прямые L₁
и L₂
с угловыми коэффициентами

Требуется
найти угол между прямыми:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Система координат — способ определить положение и перемещение точки или тела с помощью чисел или других символов.

Координаты — это совокупность чисел, которые определяют положение какого-либо объекта на прямой, плоскости, поверхности или в пространстве.

Векторное Произведение Векторов. Свойства, определение

Скаляр — это величина, которая полностью определяется в любой координатной системе одним числом или функцией.

Вектор — направленный отрезок прямой, для которого указано, какая точка является началом, а какая — концом.

Вектор с началом в точке A и концом в точке B принято обозначать как →AB. Векторы также можно обозначать малыми латинскими буквами со стрелкой или черточкой над ними, вот так: →a.

Коллинеарность — отношение параллельности векторов. Два ненулевых вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.

Проще говоря это «параллельные» векторы. Коллинеарные векторы могут быть одинаково направлены или противоположно направлены. Основное обозначение — →a || →b. Сонаправленные коллинеарные векторы обозначаются так →a ↑↑ →b, противоположно направленные — →a ↑↓ →b.

Прежде чем дать определение векторного произведения, разберемся с ориентацией упорядоченной тройки векторов →a, →b, →c в трехмерном пространстве.

Отложим векторы →a, →b, →c от одной точки. В зависимости от направления вектора →c тройка →a, →b, →c может быть правой или левой.

Посмотрим с конца вектора →c на то, как происходит кратчайший поворот от вектора →a к →b. Если кратчайший поворот происходит против часовой стрелки, то тройка векторов →a, →b, →c называется правой, по часовой стрелке — левой.

Теперь возьмем два неколлинеарных вектора →a и →b. Отложим от точки А векторы →AB = →a и →AC = →b. Построим некоторый вектор →AD = →c, перпендикулярный одновременно и →AB и →AC.

Очевидно, что при построении вектора →AD = →c мы можем поступить по-разному, если зададим ему либо одно направление, либо противоположное.

В зависимости от направления вектора →AD = →c упорядоченная тройка векторов →a, →b, →c может быть правой или левой.

И сейчас мы подошли к определению векторного произведения. Оно дается для двух векторов, которые заданы в прямоугольной системе координат трехмерного пространства.

Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что:

Векторным произведением вектора →a на вектор →b называется вектор →c, длина которого численно равна площади параллелограмма построенного на векторах →a и →b, перпендикулярный к плоскости этих векторов и направленный так, чтобы наименьшее вращение от →a к →b вокруг вектора c осуществлялось против часовой стрелки, если смотреть с конца вектора →c.

Векторное произведение двух векторов a = {ax; ay; az} и b = {bx; by; bz} в декартовой системе координат — это вектор, значение которого можно вычислить, используя формулы вычисления векторного произведения векторов:

Векторное произведение векторов →a и →b обозначается как [→a • →b].

Другое определение связано с правой рукой человека, откуда и есть название. На рисунке тройка векторов →a, →b, [→a • →b] является правой.

Еще есть аналитический способ определения правой и левой тройки векторов — он требует задания в рассматриваемом пространстве правой или левой системы координат, причём не обязательно прямоугольной и ортонормированной.

Нужно составить матрицу, первой строкой которой будут координаты вектора →a, второй — вектора →b, третьей — вектора →c. Затем, в зависимости от знака определителя этой матрицы, можно сделать следующие выводы:

• Если определитель положителен, то тройка векторов имеет ту же ориентацию, что и система координат.
• Если определитель отрицателен, то тройка векторов имеет ориентацию, противоположную ориентации системы координат.
• Если определитель равен нулю, то векторы компланарны (линейно зависимы).

Координаты векторного произведения

• Рассмотрим векторное произведение векторов в координатах.
• Сформулируем второе определение векторного произведения, которое позволяет находить его координаты по координатам заданных векторов.
• В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор

1. , где
2. →i, →j, →k — координатные векторы.
3. Это определение показывает нам векторное произведение в координатной форме.
4. Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат:
5. Если разложим этот определитель по элементам первой строки, то получим равенство из определения векторного произведения в координатах:

Важно отметить, что координатная форма векторного произведения согласуется с определением,которое мы дали в первом пункте этой статьи. Более того, эти два определения векторного произведения эквивалентны.

Свойства векторного произведения

Векторное произведение в координатах представляется в виде определителя матрицы:

На основании свойств определителя можно легко обосновать свойства векторного произведения векторов:

1. Антикоммутативность
2. Свойство дистрибутивностиили
3. Сочетательное свойствоили, где λ произвольное действительное число.

• Для большей ясности докажем свойство антикоммутативности векторного произведения.
• По определению
• и
• Нам известно, что значение определителя матрицы изменяется на противоположное, если переставить местами две строки, поэтому
• что доказывает свойство антикоммутативности векторного произведения.
• Чтобы найти модуль векторного произведения векторов u и v нужно найти площадь параллелограмма, который построен на данных векторах: S = | u × v | = | u | * | v | * sinθ, где θ — угол между векторами.
• Векторное произведение векторов u и v равно нулевому вектору, если u и v параллельны (коллинеарны): u × v = 0, если u ∥ v (θ = 0).

Геометрический смысл векторного произведения

По определению длина векторного произведения векторов равна. А из курса геометрии средней школы мы знаем, что площадь треугольника равна половине произведения длин двух сторон треугольника на синус угла между ними.

Поэтому длина векторного произведения равна удвоенной площади треугольника, имеющего сторонами векторы →a и →b, если их отложить от одной точки. Проще говоря, длина векторного произведения векторов →a и →b равна площади параллелограмма со сторонами |→a| и |→b| и углом между ними, равным (→a, →b). В этом состоит геометрический смысл векторного произведения.

Физический смысл векторного произведения

В механике — одном из разделов физики — благодаря векторному произведению можно определить момент силы относительно точки пространства. Поэтому сформулируем еще одно важное определение.

Под моментом силы →F, приложенной к точке B, относительно точки A понимается следующее векторное произведение [→A B × →F]. Вектор линейной скорости →V точки M колеса равен векторному произведению вектора угловой скорости →W и радиус-вектора точки колеса, то есть →V = →W`→rM.

Чтобы ребенок еще лучше учился в школе, запишите его на уроки математики в Skysmart. Наши преподаватели понятно объяснят что угодно — от дробей до векторов — и ответят на вопросы, которые бывает неловко задать перед всем классом. А еще помогут догнать сверстников и справиться со сложной контрольной.

Вместо скучных параграфов ребенка ждут интерактивные упражнения с мгновенной автоматической проверкой и онлайн-доска, где можно рисовать и чертить вместе с преподавателем. Приходите на бесплатный вводный урок и попробуйте сами!

Смешанное произведение векторов: свойства примеры и решения, геометрический смысл смешанного произведения векторов

Для того, чтобы подробно рассмотреть такую тему, нужно охватить еще несколько разделов. Тема напрямую связана с такими терминами, как скалярное и векторное произведение.

В этой статье мы постарались дать точное определение, указать формулу, которая поможет определить произведение, используя координаты векторов. Помимо этого, статья включает в себя разделы с перечислением свойств произведения и представлены подробный разбор типовых равенств и задач.

Термин

Для того, чтобы определить, в чем заключается данный термин, нужно взять три вектора.

Определение 1

Смешанным произведением a→, b→ и d→ является та величина, которая равняется скалярному произведению a→×b→ и d→ , где a→×b→ — умножение a→ и b→ . Операцию умножения a→, b→ и d→ зачастую обозначают a→·b→·d→ . Можно преобразовать формулу так:a→·b→·d→=(a→×b→,d→) .

Умножение в системе координат

• Мы можем умножить вектора, если они указаны на координатной плоскости.
• Возьмем i→, j→, k→
• Произведение векторов в данном конкретном случае будет иметь следующий вид:a→×b→=(ay·bz-az·by)·i→+(az·bx+ax·bz)·j→+(ax·by+ay·bx)·k→=ayazbybz·i→-axazbxbz·j→+axaybxby·k→

Для выполнения скалярного произведения в системе координат необходимо сложить результаты, полученный во время умножения координат.

1. Из этого следует:
2. a→×b→=(ay·bz-az·by)·i→+(az·bx+ax·bz)·j→+(ax·by+ay·bx)·k→=ayazbybz·i→-axazbxbz·j→+axaybxby·k→
3. Мы также можем определить смешанное произведение векторов, если в заданной системе координат указаны координаты векторов, которые умножаются.
4. a→×b→=( ayazbybz·i→-axazbxbz·j→+axaybxby·k→, dx·i→+dy·j→+dz·k→)==ayazbybz·dx-axazbxbz·dy+axaybxby·dz=axayazbxbybzdxdydz
5. Таким образом, можно сделать вывод, что:
6. a→·b→·d=a→×b→, d→=axayazbxbybzdxdydz

Определение 3

Смешанное произведение можно приравнять к определителю матрицы, в качестве строк которой использованы векторные координаты. Наглядно это выглядит так: a→·b→·d=a→×b→, d→=axayazbxbybzdxdydz .

Свойства операции над векторами Из особенностей, которые выделяются в скалярном или векторном произведении, можно вывести особенности, которые характеризуют смешанное произведение. Ниже мы приведем основные свойства.

1. (λ·a→)·b→·d→=a→·(λ·b→)·d→=a→·b→·(λ·d→)=λ·a→·b→·d→    λ∈R ;
2. a→·b→·d→=d→·a→·b→=b→·d→·a→;   a→·d→·b→=b→·a→·d→=d→·b→·a→ ;
3. (a(1)→+a(2)→)·b→·d→=a(1)→·b→·d→+a(2)→·b→·d→a→·(b(1)→+b(2)→)·d→=a→·b(1)→·d→+a→·b(2)→·d→a→·b→·(d(1)→+d(2)→)=a→·b→·d(2)→+a→·b→·d(2)→

Помимо приведенных свойств, следует уточнить, что если множитель нулевой, то результатом умножения также станет нуль. Результатом умножения также будет нуль в том случае, если два или больше множителей равны.

Действительно, если a→=b→ , то, следуя определению векторного произведения [a→×b→]=a→·b→·sin 0 =0 , следовательно, смешанное произведение равно нулю, так как ([a→×b→], d→)=(0→, d→)=0 .

Если же a→=b→ или b→=d→ , то угол между векторами [a→×b→] и d→ равен π2 . По определению скалярного произведения векторов ([a→×b→], d→)=[a→×b→]·d→·cosπ2=0 .

Свойства операции умножения чаще всего требуются во время решения задач. Для того, чтобы подробно разобрать данную тему, возьмем несколько примеров и подробно их распишем.

Пример 1

Докажите равенство ([a→×b→], d→+λ·a→+b→)=([a→×b→], d→) , где λ — некоторое действительное число.

Для того, чтобы найти решение этого равенства, следует преобразовать его левую часть. Для этого необходимо воспользоваться третьим свойством смешанного произведения, которое гласит:

• ([a→×b→], d→+λ·a→+b→)=([a→×b→], d→)+([a→×b→], λ·a→)+([a→×b→], b→) Мы разобрали, что (([a→×b→], b→)=0. Из этого следует, что ([a→×b→], d→+λ·a→+b→)=([a→×b→], d→)+([a→×b→], λ·a→)+([a→×b→], b→)==([a→×b→], d→)+([a→×b→], λ·a→)+0=([a→×b→], d→)+([a→×b→], λ·a→)

Согласно первому свойству ([a⇀×b⇀], λ·a→)=λ·([a⇀×b⇀],a→) , а ([a⇀×b⇀], a→)=0 . Таким образом, ([a⇀×b⇀], λ·a→) . Поэтому,
([a⇀×b⇀], d→+λ·a→+b→)=([a⇀×b⇀], d→)+([a⇀×b⇀], λ·a→)==([a⇀×b⇀], d→)+0=([a⇀×b⇀], d→)

Равенство доказано.

Пример 2

Необходимо доказать, что модуль смешанного произведения трех векторов не больше, чем произведения их длин.

Решение

Исходя из условия, можно представить пример в виде неравенства a→×b→, d→≤a→·b→·d→ .

По определению, преобразуем неравенство a→×b→, d→=a→×b→·d→·cos(a→×b→^, d→)==a→·b→·sin(a→, b→^)·d→·cos([a→×b→^], d)

Используя элементарные функции, можно сделать вывод, что 0≤sin(a→, b→^)≤1,  0≤cos([a→×b→^], d→)≤1 .

Из этого можно сделать вывод, что
(a→×b→, d→)=a→·b→·sin(a→, b→)^·d→·cos(a→×b→^, d→)≤≤a→·b→·1·d→·1=a→·b→·d→

Неравенство доказано.

Разбор типовых задач

Для того, чтобы определить, чему равно произведение векторов, следует знать координаты умножаемых векторов. Для операции можно использовать такую формулу a→·b→·d→=(a→×b→, d→)=axayazbxbybzdxdydz .

Пример 3

В прямоугольной системе координат представлены 3 вектора с такими координатами: a→=(1, -2, 3),  b→(-2, 2, 1),  d→=(3,-2, 5) . Необходимо определить, чему равно произведение указанных векторов a→·b→·d→ .

Исходя из теории, представленной выше, мы можем воспользоваться правилом, которое гласит, что смешанное произведение может быть вычислено через определитель матрицы. Это будет выглядеть так: a→·b→·d→=(a→×b→, d→)=axayazbxbybzdxdydz=1-23-2213-25==1·2·5+(-1)·1·3+3·(-2)·(-2)-3·2·3-(-1)·(-2)·5-1·1·(-2)=-7

Пример 4

Необходимо найти произведение векторовi→+j→, i→+j→-k→, i→+j→+2·k→ , где i→,j→, k→ — орты прямоугольной декартовой системы координат.

Исходя из условия, которое гласит, что вектора расположены в данной системе координат, можно вывести их координаты: i→+j→=(1, 1, 0)i→+j→-k→=(1, 1, -1)i→+j→+2·k→=(1, 1, 2)

Используем формулу, которая использовалась выше
i→+j→×(i→+j→-k→, (i→+j→+2·k→)=11011-1112=0i→+j→×(i→+j→-k→, (i→+j→+2·k→)=0

Смешанное произведение также возможно определить с помощью длины вектора, которая уже известна, и угла между ними. Разберем этот тезис в примере.

Пример 5

В прямоугольной системе координат расположены три вектора a→,b→ и d→ , которые перпендикулярны между собой. Они представляют собой правую тройку, их длины составляют 4, 2 и 3. Необходимо умножить вектора.

Обозначим c→=a→×b→ .

Согласно правилу, результатом умножения скалярных векторов является число, которое равно результату умножения длин используемых векторов на косинус угла между ними. Делаем вывод, что a→·b→·d→=([a→×b→], d→)=c→,d→=c→·d→·cos(c→, d→^) .

Используем длину вектора d→ , указанную в условии примера: a→·b→·d→=c→·d→·cos(c→, d→^)=3·c→·cos(c→, d→^) . Необходимо определить с→и с→, d→^ . По условию a→,b→^=π2, a→=4, b→=2 .

Вектор c→ найдем с помощью формулы: c→=[a→×b→]=a→·b→·sina→, b→^=4·2·sinπ2=8 Можно сделать вывод, что c→ перпендикулярен a→ и b→ . Вектора a→, b→, c→ будут являться правой тройкой, так использована декартовая система координат.

Векторы c→ и d→ будут однонаправленными, то есть, c→,d→^=0 . Используя выведенные результаты, решаем пример a→·b→·d→=3·c→·cos(c→, d→^)=3·8·cos 0=24 .

a→·b→·d→=24 .

Геометрический смысл

Используем множители a→, b→ и d→ .

Вектора a→, b→ и d→ исходят от одной точки. Используем их как стороны для построения фигуры.

Обозначим, что c→=[a→×b→]. Для данного случая можно определить произведение векторов как a→·b→·d→=c→·d→·cos(c→, d→^)=c→·npc→d→ , где npc→d→ — числовая проекция вектора d→ на направление вектора c→=[a→×b→] .

Абсолютная величина npc→d→ равняется числу, которое также является равно высоте фигуры, для которого использованы вектора a→, b→ и d→ в качестве сторон. Исходя из этого, следует уточнить, что c→=[a→×b→] перпендикулярен a→ и вектору и вектору согласно определению умножения векторов. Величина c→=a→xb→ равняется площади параллелепипеда, построенного на векторах a→ и b→ .

Делаем вывод, что модуль произведения a→·b→·d→=c→·npc→d→ равен результату умножения площади основания на высоту фигуры, которая построена на векторах a→, b→ и d→ .

Определение 4

Абсолютная величина векторного произведения является объемом параллелепипеда: Vпараллелепипида=a→·b→·d→ .

Данная формула и является геометрическим смыслом.

Определение 5

Объем тетраэдра, который построен на a→,b→ и d→ , равняется 1/6 объема параллелепипеда Получаем, Vтэтраэда=16·Vпараллелепипида=16·a→·b→·d→ .