В данной публикации мы рассмотрим, как можно найти смешанное произведение трех векторов через вычисление определителя соответствующей матрицы, перечислим свойства этой операции, а также разберем пример решения задачи.
- Нахождение смешанного произведения векторов
- Свойства смешанного произведения векторов
- Пример задачи
Нахождение смешанного произведения векторов
Смешанное произведение векторов равняется определителю матрицы, которая составлена из координат этих векторов.
Алгоритм действий следующей:
Допустим, у нас есть три вектора: a = {ax; ay; az}, b = {bx; by; bz} и с = {сx; сy; сz}. Чтобы найти их смешанное произведение (в декартовой системе) мы составляем матрицу с элементами, как показано ниже, и затем просто вычисляем ее определитель.
Свойства смешанного произведения векторов
1. Модуль смешанного произведения трех векторов равняется объему параллелепипеда, который образован этими векторами.
Vпаралл. = |a · [b × c]|
2. Объем пирамиды, которая образована тремя векторами, равняется 1/6 от модуля смешанного произведения данных векторов.
Vпаралл. = 1/6 · |a · [b × c]|
3. Смешанное произведение трех ненулевых компланарных векторов равняется нулю.
4. a · [b × c] = b · (a · c) – c · (a · b)
5. a · [b × c] = b · [c × a] = c · [a × b] = –a · [c ×b] = –b · [a ×c] = –c · [b ×a]
6. a · [b × c] + b · [c × a] + c · [a × b] = 0 (тождество Якоби)
Пример задачи
Найдем смешанное произведение векторов a = {3; 8; 4}, b = {1; -10; 12} и с = {11; 5; 9}.
Решение:
a · [b × c] = 3 · (-10) · 9 + 11 · 8 · 12 + 1 · 5 · 4 – 11 · (-10) · 4 – 3 · 5 · 12 – 1 · 8 · 9 = -270 + 1056 + 20 + 440 – 180 – 72 = 994
Марина Николаевна Ковальчук
Эксперт по предмету «Геометрия»
Задать вопрос автору статьи
Предварительные сведения
Для того чтобы мы могли ввести понятие смешанного произведения векторов, нужно сначала вспомнить понятия скалярного и векторного произведений этих векторов.
Определение 1
Скалярным произведением двух векторов будем называть такой скаляр (или число), который равняется произведению длин двух этих векторов с косинусом угла между данными векторами.
Математически это может выглядеть следующим образом:
$overline{α}overline{β}=|overline{α}||overline{β}|cos∠(overline{α},overline{β})$
Также, помимо того, как из самого определения 1, для нахождения скалярного произведения можно пользоваться следующей теоремой.
Теорема 1
Скалярное произведение двух данных векторов $overline{α}$ и $overline{β}$ равняется сумме произведений их соответствующих координат.
Математически выглядит следующим образом
$overline{α}overline{β}=α_1 α_2+β_1 β_2$
Обозначение: $overline{α}cdot overline{β}$.
Определение 2
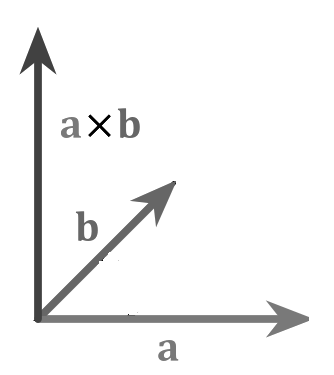
Векторным произведением двух векторов будем называть такой вектор, который будет перпендикулярен обоим данным векторам, и его длина будет равняться произведению длин этих векторов с синусом угла между данными векторами, а также этот вектор с двумя начальными имеют туже ориентацию, как и декартова система координат.
Обозначение: $overline{α}хoverline{β}$.
Математически это выглядит следующим образом:
- $|overline{α}хoverline{β}|=|overline{α}||overline{β}|sin∠(overline{α},overline{β})$
- $overline{α}хoverline{β}⊥overline{α}$, $overline{α}хoverline{β}⊥overline{β}$
- $(overline{α}хoverline{β},overline{α},overline{β})$ и $(overline{i},overline{j},overline{k})$ одинаково ориентированы (рис. 1)
«Как найти смешанное произведение векторов» 👇
Понятие смешанного произведения векторов
Определение 3
Смешанным произведением векторов $overline{α}$, $overline{β}$ и $overline{γ}$ будем называть такой скаляр (или число), которое будет равняться скалярному произведению первого вектора $overline{α}$ на вектор векторного произведения $overline{β}хoverline{γ}$ двух других векторов.
Обозначение: $(overline{α},overline{β},overline{γ})$.
Математически это выглядит следующим образом:
$(overline{α},overline{β},overline{γ})=overline{α}cdot (overline{β}хoverline{γ})$
Очевидно, что смешанное произведение будет равняться нулю в двух случаях:
- Если длина одного или нескольких векторов равняется нулю.
- Если эти векторы будут являться компланарными.
Пример 1
Найти значение смешанного произведения векторов $overline{α}$, $overline{β}$ и $overline{γ}$, которые имеют координаты $(0,0,5)$, $(0,4,0)$ и $(3,0,0)$, соответственно.
Решение.
Из определений 1, и 3 будем получать
$(overline{α},overline{β},overline{γ})=overline{α}cdot (overline{β}хoverline{γ})=|overline{a}||overline{β}хoverline{γ}|cos∠(overline{α},overline{β}хoverline{γ})$
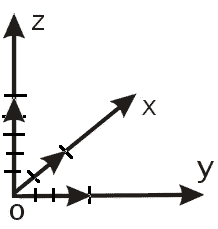
Изобразим эти векторы в декартовом координатном пространстве (рис. 2):
Найдем вначале длину вектора векторного произведения векторов $overline{β}$ и $overline{γ}$
Видим, что эти векторы лежат на осях $Ox$ и $Oy$, соответственно. Следовательно, угол между ними будет равняться $90^0$. Найдем длины этих векторов:
$|overline{β}|=sqrt{0+16+0}=4$
$|overline{γ}|=sqrt{9+0+0}=3$
Тогда, по определению 2, получим
$|overline{β}хoverline{γ}|=|overline{α}||overline{β}|sin90^circ=4cdot 3cdot 1=12$
Из 3 части определения 2 очевидно, что вектор $overline{β}хoverline{γ}$ принадлежит оси $Oz$ и направлен в туже сторону, что и сама ось, следовательно, угол между векторами $overline{α}$ и $overline{β}хoverline{γ}$ равняется $0^circ$.
Длина вектора $overline{α}$
$|overline{α}|=sqrt{0+0+25}=5$
Получим
$(overline{α},overline{β},overline{γ})=|overline{a}||overline{β}хoverline{γ}|cos∠(overline{α},overline{β}хoverline{γ})=5cdot 12cdot cos0^circ=60$
Ответ: $60$.
Вычисление смешанного произведения по координатам векторов
Из определения 1 сразу же вытекает и способ нахождения смешанного произведения для трех данных векторов. Но существует еще способ нахождения с помощью координат данных нам векторов.
Пусть нам даны векторы $overline{α}$, $overline{β}$ и $overline{γ}$, которые будут иметь координаты $(α_1,α_2,α_3)$, $(β_1,β_2,β_3)$ и $(γ_1,γ_2,γ_3)$, соответственно. Тогда значение смешанного произведения можно найти по следующей формуле:
$(overline{α},overline{β},overline{γ})=begin{vmatrix}α_1&α_2&α_3\β_1&β_2&β_3\γ_1&γ_2&γ_3end{vmatrix}$
Иначе, получим
$overline{α}хoverline{β}=α_1 β_2 γ_3+α_3 β_1 γ_2+α_2 β_3 γ_1-α_3 β_2 γ_1-α_2 β_1 γ_3-α_1 β_3 γ_2$
Пример 2
Найти значение смешанного произведения векторов $overline{α}$, $overline{β}$ и $overline{γ}$ с координатами $(1,1,0)$, $(0,3,3)$ и $(-1,2,6)$.
Решение.
Воспользуемся формулой, приведенной выше. Получим
$(overline{α},overline{β},overline{γ})=begin{vmatrix}1&1&0\0&3&3\-1&2&6end{vmatrix}=18+(-3)+0-0-6-0=18-9=9$
Ответ: $9$.
Свойства смешанного произведения векторов
Для произвольных четырех векторов $overline{α}, $overline{β}$, $overline{γ}$ и $overline{δ}$, а также $r∈R$ справедливы следующие свойства: справедливы следующие свойства:
1) При перестановке местами знаков произведений в смешанном произведении можно менять между собой
$(overline{α},overline{δ},overline{γ})=overline{α}cdot (overline{δ}хoverline{γ})=(overline{α}хoverline{δ})cdot overline{γ}$
2) Векторы в смешанном произведении можно менять только циклически
$(overline{α},overline{δ},overline{γ})=(overline{δ},overline{γ},overline{α})=(overline{γ},overline{α},overline{δ})$
3) Перемещение только одного вектора на другое место меняет знак
$(overline{α},overline{δ},overline{γ})=-(overline{β},overline{α},overline{γ})=-(overline{γ},overline{δ},overline{α})=-(overline{α},overline{γ},overline{δ})$
4) Из формулы выше, очевидны следующие равенства:
$(roverline{α},overline{δ},overline{γ})=r(overline{α},overline{δ},overline{γ})$
$(overline{α},roverline{δ},overline{γ})=r(overline{α},overline{δ},overline{γ})$
$(overlie{α},overline{δ},roverline{γ})=r(overline{α},overline{δ},overline{γ})$
5) Справедливы равенства:
$(overline{α}+overline{β},overline{δ},overline{γ})=(overline{α},overline{δ},overline{γ})+(overline{β},overline{δ},overline{γ})$
$(overline{α},overline{δ}+overline{β},overline{γ})=(overline{α},overline{δ},overline{γ})+(overline{α},overline{β},overline{γ})$
$(overline{α},overline{δ},overline{γ}+overline{β})=(overline{α},overline{δ},overline{γ})+(overline{α},overline{δ},overline{β})$
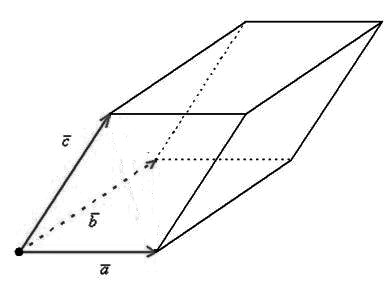
6) Геометрический смысл – площадь параллелепипеда (рис. 3):
$S=|(overline{α},overline{β},overline{c})|$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Смешанное произведение векторов.
Определение. Смешанное произведение векторов — скалярное произведение вектора a на векторное произведение векторов b и c.
Формулы вычисления смешанного произведения векторов
Смешанное произведение векторов равно определителю матрицы, составленной из этих векторов.
Смешанное произведение векторов a = {ax; ay; az}, b = {bx; by; bz} и c = {cx; cy; cz} в декартовой системе координат можно вычислить, используя следующую формулу:
| a · [b × c] = | ax | ay | az |
| bx | by | bz | |
| cx | cy | cz |
Свойства смешанного произведения векторов
-
Геометрический смысл смешанного произведения.
Модуль смешанного произведения трех векторов a, b и с равен объёму параллелепипеда, образованного этими векторами:
Vпарал = |a · [b × c]|
-
Геометрический смысл смешанного произведения.
Объем пирамиды образованной тремя векторами a, b и с равен одной шестой части от модуля смешанного произведения этих векторов:
-
Если смешанного произведения трех не нулевых векторов равно нулю, то эти вектора компланарные.
-
a · [b × c] =
b · (a · c) —
c · (a · b) -
a · [b × c] =
b · [c × a] =
c · [a × b] =
—a · [c × b] =
—b · [a × c] =
—c · [b × a] -
a · [b × c] + b · [c × a] + c · [a × b] = 0 — тождество Якоби.
Примеры задач на вычисления смешанного произведения векторов
Пример 1. Найти смешанное произведение векторов a = {1; 2; 3}, b = {1; 1; 1}, c = {1; 2; 1}.
Решение:
| a · [b × с] = | 1 | 2 | 3 | = |
| 1 | 1 | 1 | ||
| 1 | 2 | 1 |
= 1·1·1 + 1·1·2 + 1·2·3 — 1·1·3 — 1·1·2 — 1·1·2 = 1 + 2 + 6 — 3 — 2 — 2 = 2
Пример 2.
Найти объем пирамиды построенной на векторах a = {1; 2; 3}, b = {1; -1; 1}, c = {2; 0; -1}.
Решение: Найдем смешанное произведение этих векторов:
| a · [b × с] = | 1 | 2 | 3 | = |
| 1 | -1 | 1 | ||
| 2 | 0 | -1 |
= 1·(-1)·(-1) + 2·1·2 + 3·1·0 — 3·(-1)·2 — 2·1·(-1) — 1·1·0 =
= 1 + 4 + 0 + 6 + 2 — 0 = 13
Найдем объем пирамиды воспользовавшись свойствами:
| Vпир = | 1 | |a · [b × c]| = | 13 | = 2 | 1 |
| 6 | 6 | 6 |
Содержание:
- Геометрический смысл смешанного произведения
- Свойства смешанного произведения:
Определение
Смешанным произведением трех векторов $overline{a}$,
$overline{b}$, $overline{c}$
называется число, равное скалярному произведению вектора $overline{a} times overline{b}$
на вектор $overline{c}$: $(overline{a}, overline{b}, overline{c})=([overline{a}, overline{b}], overline{c})$
Геометрический смысл смешанного произведения
Геометрический смысл смешанного произведения: если
тройка векторов ${overline{a}, overline{b}, overline{c}}$ правая,
то их смешанное произведение равно объему параллелепипеда построенного на этих векторах: $(overline{a}, overline{b}, overline{c})=V$.
В случае левой тройки ${overline{a}, overline{b}, overline{c}}$ смешанное произведение указанных векторов равно объему
параллелепипеда со знаком минус: $(overline{a}, overline{b}, overline{c})=-V$. Если $overline{a}$,
$overline{b}$ и $overline{c}$
компланарны, то их смешанное произведение равно нулю.
Итак, из выше сказанного можно сделать вывод, что объем параллелепипеда, построенного на векторах $overline{a}$,
$overline{b}$ и $overline{c}$ равен модулю смешанного произведения этих векторов:
$$V_{text {парал }}=|(bar{a}, bar{b}, bar{c})|$$
Объем пирамиды, построенной на этой тройке векторов равен
$$V_{text {пир }}=frac{1}{6}|(bar{a}, bar{b}, bar{c})|$$
Свойства смешанного произведения:
1 $(overline{a}, overline{b}, overline{c})=(overline{a},[overline{b}, overline{c}])$
2 $(overline{a}, overline{b}, overline{c})=(overline{b}, overline{c}, overline{a})=(overline{c}, overline{a}, overline{b})=-(overline{b}, overline{a}, overline{c})=-(overline{c}, overline{b}, overline{a})=-(overline{a}, overline{c}, overline{b})$
3 Три вектора компланарны тогда и только тогда, когда $(overline{a}, overline{b}, overline{c})=0$
4 Тройка векторов является правой тогда и только тогда, когда $(overline{a}, overline{b}, overline{c})>0$.
Если же $(overline{a}, overline{b}, overline{c})<0$, то векторы $overline{a}$, $overline{b}$ и $overline{c}$ образуют левую тройку векторов.
5 $(lambda overline{a}, overline{b}, overline{c})=(overline{a}, lambda overline{b}, overline{c})=(overline{a}, overline{b}, lambda overline{c})=lambda(overline{a}, overline{b}, overline{c})$
6 $left(overline{a}_{1}+overline{a}_{2}, overline{b}, overline{c}right)=left(overline{a}_{1}, overline{b}, overline{c}right)+left(overline{a}_{2}, overline{b}, overline{c}right)$
7 $left(overline{a}, overline{b}_{1}+overline{b}_{2}, overline{c}right)=left(overline{a}, overline{b}_{1}, overline{c}right)+left(overline{a}, overline{b}_{2}, overline{c}right)$
8 $left(overline{a}, overline{b}, overline{c}_{1}+overline{c}_{2}right)=left(overline{a}, overline{b}, overline{c}_{1}right)+left(overline{a}, overline{b}, overline{c}_{2}right)$
9 $([overline{a}, overline{b}], overline{c})=overline{b}(overline{a}, overline{c})-overline{a}(overline{b}, overline{c}) ;(overline{a},[overline{b}, overline{c}])=overline{b}(overline{a}, overline{c})-overline{c}(overline{a}, overline{b})$
10 Тождество Якоби: $(overline{a},[overline{b}, overline{c}])+(overline{b},[overline{c}, overline{a}])+(overline{c},[overline{a}, overline{b}])=0$
Если векторы $overline{a}=left(a_{1} ; a_{2} ; a_{3}right)$,
$overline{b}=left(b_{1} ; b_{2} ; b_{3}right)$ и $overline{c}=left(c_{1}, c_{2}, c_{3}right)$
заданы своими координатами, то их смешанное произведение вычисляется по формуле
$(overline{a}, overline{b}, overline{c})=left| begin{array}{lll}{a_{1}} & {a_{2}} & {a_{3}} \ {b_{1}} & {b_{2}} & {b_{3}} \ {c_{1}} & {c_{2}} & {c_{3}}end{array}right|$
Пример
Задание. Вычислить
объем пирамиды, построенной на векторах $overline{a}=(2 ; 3 ; 5)$,
$overline{b}=(1 ; 4 ; 4)$,
$overline{c}=(3 ; 5 ; 7)$
Решение. Найдем смешанное произведение заданных векторов, для это составим определитель,
по строкам которого запишем координаты векторов $overline{a}$,
$overline{b}$ и $overline{c}$:
$(overline{a}, overline{b}, overline{c})=left| begin{array}{lll}{2} & {3} & {5} \ {1} & {4} & {4} \ {3} & {5} & {7}end{array}right|=2 cdot 4 cdot 7+1 cdot 5 cdot 5+3 cdot 4 cdot 3-$
$-3 cdot 4 cdot 5-5 cdot 4 cdot 2-1 cdot 3 cdot 7=-4$
$$V_{text {пир }}=frac{1}{6}|(bar{a}, bar{b}, bar{c})|=frac{1}{6} cdot 4=frac{2}{3}(text { куб. ед. })$$
Читать дальше: свойства векторов.

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!