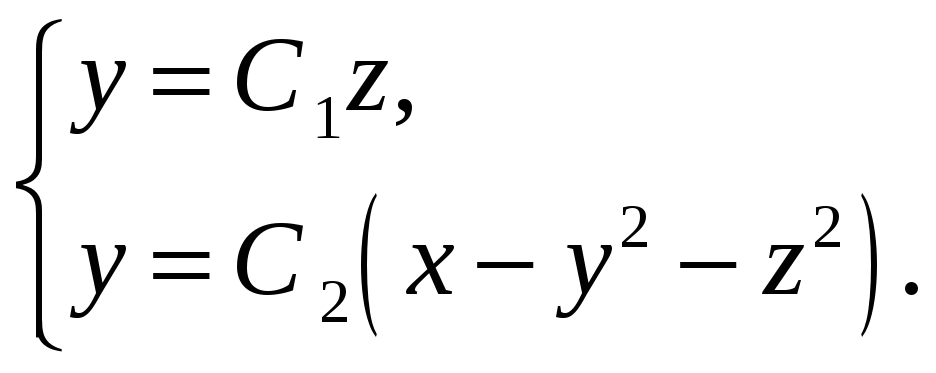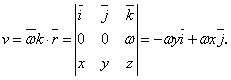Как найти векторные линии поля онлайн

Множество точек поля, в которых функция
поля

принимает постоянное значение
,
образует поверхность с уравнением
,
называемую поверхностью уровня поля.
Если скалярное поле плоское и находится,
например, в плоскости
,
то его функция поля

зависит от двух переменных

и
,
а множество точек,
в которых
,
образуют линию уровня.

Производную поля

по направлению вектора

можно вычислить по формуле

,
где

─ градиент скалярного
поля
,

─ единичный вектор направления
.

Замечания:

1. Скалярное поле
   
   в точке
   
   быстрее всего возрастает в направлении
   вектора
   
   со скоростью, равной
   .

2. Скалярное поле
   
   в точке
   
   быстрее всего убывает в направлении,
   противоположном вектору
   ,
   со скоростью, равной
   .

3. Вектор
   
   направлен по нормали к поверхности
   уровня поля
   ,
   проходящей через точку
   .

Пример 1. Построить линии уровня
поля
.
Найти производную поля в точке

в направлении касательной и нормали к
линии уровня поля, проходящей через
точку
.

Решение. Линией уровня называют
множество точек, в которых скалярная
функция имеет одно и то же значение; в
нашем примере
.
Придадим постоянной различные значения:

а)
;
получаем две прямые

и
;

б)

или

– это уравнение эллипса с центром в
начале координат; в частном случае при

получаем уравнение окружности
.
Точка

принадлежит этой окружности.

в)

или

– уравнение сопряженной гиперболы
(рис. 1).

Для вычисления производной поля по
направлению касательной к линии

в точке

найдем направляющий вектор касательной
.
Запишем уравнение окружности в
векторно-параметрическом виде:
.
Точке

соответствует значение параметра
.
Вектор

коллинеарен направляющему вектору
касательной
:
,
;
единичный вектор, направленный вдоль
касательной
.
Запишем
,
.

По формуле

имеем
,
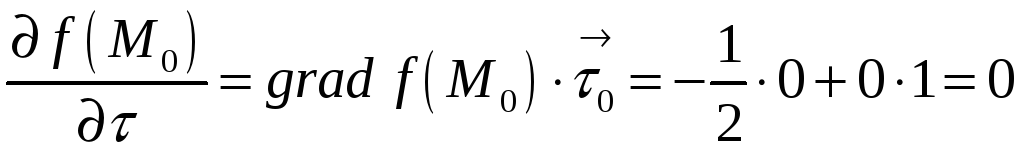
то есть поле по направлению касательной
к линии

в точке

не изменяется.

Направляющий вектор

нормали к линии

равен
,
,
единичный вектор
.
Тогда
,
поле по направлению нормали к линии

в точке

убывает.

Пример 2. Найти точки, в которых поле

по направлению

не изменяется.

Решение. Поле

в точке

не изменяется по направлению
,
если
.

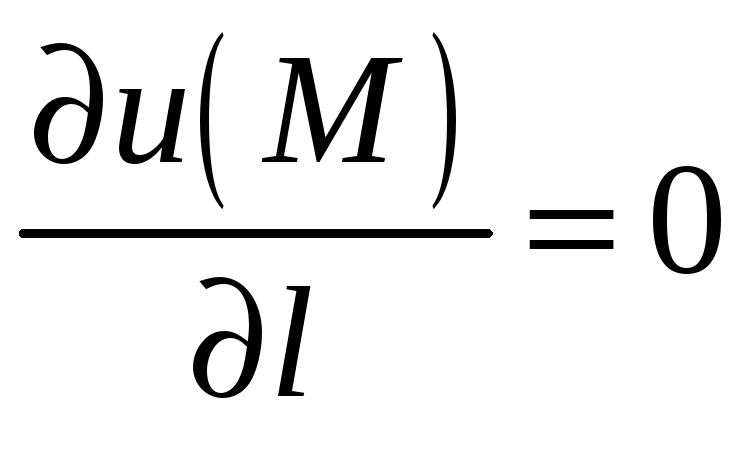
Вычислим
:

,
,
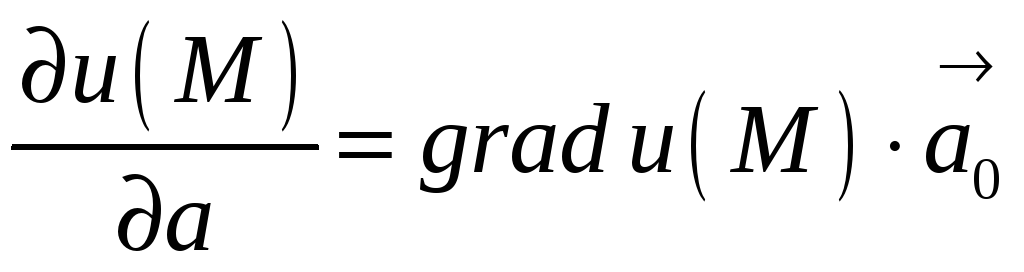
тогда

или
.

Итак, в точках плоскости

поле

по направлению

не изменяется.

Пример 3. Найти производную поля

в точке

в направлении радиус-вектора этой точки.
В каком случае эта производная будет
равна
?

Решение. Вычислим

и
.

Применив формулу
,
имеем:

.

Итак,
.

Рассмотрим случай, когда
.

Найдем

и, приравняв его
,
получаем
.

Равенство возможно, если
:
.

Пример 4. Найти
,
где

– постоянный вектор,

– радиус-вектор точки
.

Решение. В соответствии с формулой
для вычисления скалярного произведения
двух векторов
,
тогда

и

.
Отсюда следует, что

сохраняет во всех точках поля одинаковое
направление, совпадающее с направлением
вектора
,
поэтому поверхностями уровня поля

являются плоскости с нормальным
вектором
.

Это утверждение можно получить и
непосредственно из определения
поверхности уровня
.

Пример 5. Показать, что линии уровня
полей

и

ортогональны.

Решение. Угол между линиями измеряется
углом между касательными к этим линиям
в точке пересечения. Угол между
касательными совпадает с углом между
нормалями (как углы с соответственно
перпендикулярными сторонами). Так как

направлен по нормали к линии уровня, то
угол между линиями уровня полей
,

есть угол между

и
,
где

– точка пересечения линий уровня.

Вычислим скалярное произведение
градиентов:

,
следовательно,
.
Так как

– произвольная точка, то линии уровня
полей
,

ортогональны.

Векторные линии
векторного поля

Определение. Векторной линией
векторного поля называется линия, в
каждой точке которой касательный вектор
коллинеарен вектору поля.

Для вектора поля

система дифференциальных уравнений
для отыскания векторных линий имеет
вид:

.

Пример 6. Найти векторные линии поля
вектора
.

Решение. Запишем дифференциальные
уравнения векторных линий поля
,
используя формулу (6.1):

.

При решении задач подобного типа будем
пользоваться свойством пропорций:

если
,
то
. Учитывая
свойство (6.2), домножим числитель и
знаменатель первой дроби на
,
второй – на
,
третьей – на

и, сложив почленно, получим

.

Отсюда
,

или

(сферы с центром в начале координат
радиуса
,
).

Теперь запишем систему дифференциальных
уравнений в виде

или
.
Домножив равенство на
,
получим:

или

(плоскости с нормальным вектором
).

Таким образом, векторные линии данного
поля есть линии пересечения сфер с
плоскостями:

Пример 7. Найти векторные линии поля
градиентов функции

.

Решение. Найдем градиент скалярного
поля функции
:

.

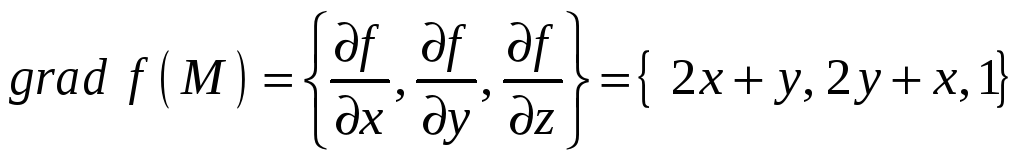
Запишем дифференциальные уравнения
векторных линий:
.

Используя свойство (6.2) пропорций, имеем

и
.

Проинтегрируем оба равенства:

,

.

Таким образом, векторные линии – линии
пересечения поверхностей

Пример 8. Найти векторную линию поля
,
проходящую через точку
.

Решение. Запишем систему дифференциальных
уравнений для отыскания

векторных линий:
.
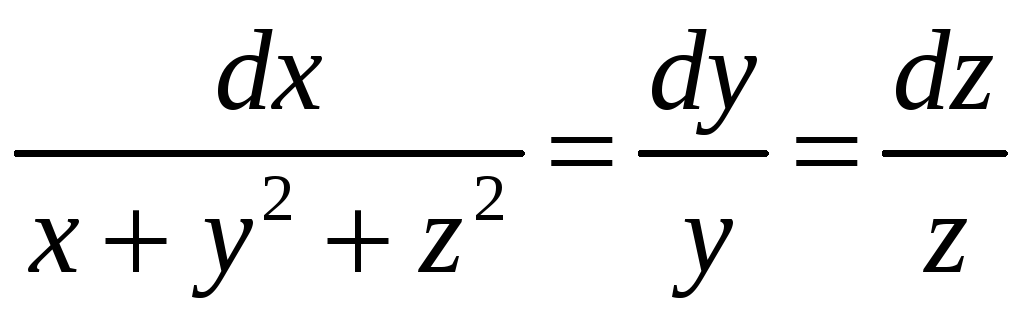
Проинтегрировав дифференциальное
уравнение
,
получим

или
.

Применив свойство (6.2), запишем систему
в виде:

или
.

Проинтегрировав полученное равенство,
имеем

или
.

Тогда векторные линии данного поля есть
линии пересечения поверхностей

Выделим векторную линию, проходящую
через точку
.
Для этого подставим координаты точки
в полученные уравнения поверхностей:

Итак, уравнение искомой векторной линии

Оглавление

15.
Практическое занятие. Скалярное поле. 1

Векторные линии
векторного поля 6

Оглавление 10

Давайте сначала поймем задачу (потом я дам формальное решение). Ваша функция (я перегруппирую члены, в вычислени производной Вы ошиблись, меня тоже проверьте):
[math]u = x^2-2x+y^2+2y+z^2-z=(x-1)^2+(y+1)^2+(z-frac{ 1 }{ 2 })^2- frac{ 1 }{ 4 }[/math]
т.е. речь идет о сферически-симметричном поле с центром в точке [math](1,-1,frac12)[/math]. Силовые линии этого поля — лучи, исходящие из этой точки во все стороны.

Теперь более формально. Градиент поля имеет компоненты [math](2(x-1),2(y+1),2(z-0.5))[/math], а уравнение силовых линий (двойку я отбросил, чтобы не мешалась)
[math]frac{dx}{x-1}=frac{dy}{y+1}=frac{dz}{z-0.5}=ds[/math]
где [math]s[/math] — параметр вдоль линии.
Отсюда уравнение силовых линий (это прямые, лучи, исходящие из указанной точки)
[math]x=1+ae^s, qquad y=-1+be^s, qquad z = 0.5 + c e^s[/math]
Здесь [math]a, b, c[/math] — постоянные интегрирования. Их набор (набор их значений) определяет различные лучи.
Можно перейти к другому параметру [math]t=e^s[/math], но он должен принимать только положительные значения.

Удачи!

Определение. Векторной линией поля  называется векторная функция  точки М вместе с областью её определения [5].

Задание векторного поля  равносильно заданию трёх скалярных функций , , , являющихся проекциями  на координатные оси:

.

Определение. Векторной линией поля  называется такая линия L, в каждой точке которой касательная совпадает с направлением вектора  (рис. 1.36).

Векторная линия обычно называется линией тока при ламинарном течении жидкости (газа) и др. для поля скоростей, силовой линией – для силового поля и др.

Совокупность всех векторных линий, проходящих через точки куска поверхности вращения S, называются векторной трубкой.

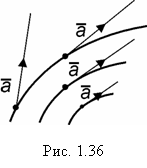
Из определения векторной линии следует, что вектор  параллельный . Из условия коллинеарности векторов  и  следует:

                                     (1.95)

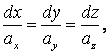
где       a_x, a_y, a_z – заданные функции от x, y, z; и (1.95) является системой дифференциальных уравнений векторных линий.

Таким образом, задача нахождения векторных линий поля  равносильна задаче нахождения интегральных кривых системы (1.95).

Пример 1

Найти векторные линии поля .

Решение. Составим систему (1.95):

Интегрируем систему. Получим:

семейство параболических цилиндров

;

семейство параболических цилиндров

.

Семейством векторных линий являются линии пересечения названных цилиндров.

Пример 2

Найти векторные линии магнитного поля (вектор напряженности магнитного поля), образованного постоянным электрическим током I, текущим по бесконечно длинному проводу, совпадающему с осью Оz (рис.

1.37).

Решение. Как известно вектор напряженности магнитного поля равен:

.

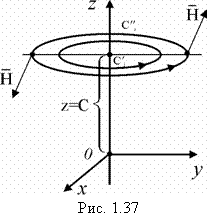
Проекции  на оси:

Дифференциальное уравнение векторных линий имеет вид:

.

Последнее отношение имеет смысл когда z = c – постоянная величина. Оставшееся уравнение запишем так:  Интегрируя, получим:

.

Следовательно, векторные линии поля  определяются уравнениями: , z = c. Они являются окружностями с центрами на оси Оz, лежащие в плоскостях, перпендикулярных к этой оси (т.е. линии пересечения цилиндров и плоскостей) (рис. 1.37).

Пример 3

Вектор  линейных скоростей частиц жидкости, вращающейся вокруг оси Оz с постоянной угловой скоростью , может быть представлен в виде , где  – вектор угловой скорости, направленной по оси Оz;  . точки M(x, y, z).

Найти векторные линии поля.

Решение. Найдем сначала вектор .Он будет найден как векторное произведение векторов  и :

Видно, что задачу свели к предыдущей (вектор ).

Рекомендуется в качестве упражнения проделать шаги до конца.

По этой ссылке вы найдёте полный курс лекций по математике:

Определение. Если в каждой точке M(x,y,z) пространства или части пространства определена векторная величина то говорят, что там задано векторное поле а. Задание векторного поля равносильно заданию ipex скалярных функций от трех переменных , Примерами векторных полей могут служить: силовое поле — поле некоторой силы F, поле скоростей v течения некоторой жидкости и др.

Для геометрической характеристики векторного поля служат векторные линии. Векторной линией векторного поля а называется кривая, касательная к которой в любой точке М имеет то же направление, что и вектор поля а в этой точке (рис. 7). В силовом поле векторные линии называются силовыми линиями’, в поле скоростей дви-женияжидкости векторные линии называются линиями тока. Рис. 7 3.1.

Дифференциальные уравнения векторных линий Пусть векторное поле определяется вектор-функцией ) — непрерывные функции переменных x, у, z, имеющие ограниченные частные производные первого порядка. Пусть — есть радиус-вектор текущей точки векторной линии векторного поля a (t — параметр). Из определения векторной линии следует, что вектор и вектор касательной к этой кривой должны быть коллинеарны в каждой точке векторной линии. Условием коллинеарности векторов является пропорциональность их координат:

Векторное поле Векторные линии и их дифференциальные уравнения Дифференциальные уравнения векторных линий Поток вектора через поверхность и его свойства Свойства потока вектора через поверхность Понятие ориентации поверхности Таким образом, мы получили для векторных линий систему дифференциальных уравнений в симметричной форме. Допустим, что нам удалось найти два независимых интеграла системы (2): . Система уравнений (3) определяет векторную линию как линию пересечения двух поверхностей. Произвольно меняя параметры с, и Сг, мы получаем семейство векторных линий как семейство с двумя степенями свободы.

Пример 1. Найти векторные линии векторного поля 4 Выписываем дифференциальные уравнения векторных линий, или Интегрируя эту систему, получим два уравнения — произвольные постоянные. Пересечение плоскостей у — Сх с параболическими цилиндрами дает двух параметрическое семейство векторных линий поля (рис.8). Олредрм*т . Векторное поле называется плоским, если все векторы а параллельны одной и той же плоскости и в каждой плоскости, параллельной указан ной, векторное поле одно и то же.

Посмотрим, как плоское векторное поле описывается в координатах.

Если указанную в определении плоскость (или любую ей параллельную) принять за плоскость хОу, то векторы плоского поля не будут содержать компоненты по оси Oz и координаты векторов не будут зависеть от z: Дифференциальные уравнения векторныхл иний плоского поля можно записать в следующем виде Отсюда видно, что векторные линии плоского поля являются плоскими кривыми, лежащими в плоскостях, параллельных плоскости хОу.

Возможно вам будут полезны данные страницы:

Пример 2. Найти векторные линии магнитного поля бесконечно длинного прямого провода. ^ Предположим, что проводник направлен вдоль оси Oz и по нему течет ток силы J, т.е. вектор тока Тогда вектор напряженности Н магнитного поля определяется по формуле — радиус-вектор точхи М, р — расстояние от оси провода до точки М. Раскрывая векторное произведение (6), получим Дифференциальные уравнения векторных линий: Отсюда х = const, = или . Окончательно имеем т.е. векторные линии являются офужносгями с центрами на оси О г (рис.9). Пример 3.

Найти векторные линии поля сил тяготения, образованного притягивающей материальной то*«ой массы ш, расположенной в начале координат. Дифференциальные уравнения векторных линий: стсуда, умножая каждую из дробей на , получим Чтобы получить уравнения векторных линий в параметрической форме, приравняем каждую из дробей величине у. Имеем Это — полупрямые, выходящие из начала координат. Чтобы из семейства векторных линий выделить одну, надо задать точку ), через которую эта векторная линия должна проходить, и по координатам заданной точки определить величины.

Пусть, например, точка А/о имеет координаты . Уравнение векторной линии, проходящей через точку, можно записать так: . Сама точка Л/о получается при значении параметра § 4. Поток вектора через поверхность и его свойства Рассмотрим сначала частный случай поля скоростей v течения жидкости. Выделим в поле некоторую поверхность Потоком жидкости через поверхность Е называется количество жидкости, протекающее через поверхность Е за единицу времени.

Этот поток легко вычислить

если скорость течения постоянна (v = const), а поверхность £ —плоская. В этом случае поток жидкости равен объему цилиндрического тела с параллельными основаниями и образующими длины |v|, так как за единицу времени кажд ая частица перемещается на величину v (рис. 10), где S — площадь основания, — высота цилиндра и n — нормаль к его основанию, Итак, при постоянной скорости v поток жидкости через плоскую поверхность Е равен Если скорость v изменяется непрерывно, а поверхность Е — гладкая, то можно разбить поверхность Е на столь малые части , чтобы каждую часть Е* можно было приближенно считать плоской и вектор v на ней постоянным.

Так как поток жидкости через поверхность Е равен сумме потоков жидкости через все ее части Е*, то мы получаем для вычисления потока приближенную формулу Векторное поле Векторные линии и их дифференциальные уравнения Дифференциальные уравнения векторных линий Поток вектора через поверхность и его свойства Свойства потока вектора через поверхность Понятие ориентации поверхности где п — общее число частей Efc, на которые разбита поверхность Е, Рк — точка, лежащая на fc-ой части, Аак — площадь части Е* поверхности, означает скалярное произведение векторов в точке *(рис. 11).

Назовем потоком жидкости через поверхность Е предел суммы (2) при стремлении к нулю наибольшего из . диаметров площадок Е*, где d — наибольший из диаметров частей . Интеграл (3), определяющий поток жидкости, берется от скалярной функции (v, п°) по площади поверхности Е. Понятие потока произвольного вектора а через поверхность Е вводится по аналогии с введенным выше понятием потока жидкости через поверхность. Определение.

Потоком вектора {векторного поля) а через поверхность Е называется интеграл по поверхности Е от проекции вектора а на нормаль к поверхности ( = n da). Ясно, что интеграл (4) существует, если вектор непрерывен,т. е. непрерывны его координаты ), и поверхность Е — гладкая, т. е. имеетнепрерывно меняющуюся касательную плоскость. Пример 1. Поле создается точечным зарядом (электрическое поле) или точечной маосой (поле тяготения), помещенными в начале координат.

Тогда вектор напряженности поля в любой точке Р будет равен где ч — величина заряда (массы), г ОР — радиус-вектор точки Р. Требуется найти поток вектора напряженности Е через Sn — сферу радиуса R с центром в начале координат. Так как направление нормали к сфере совпадает с направлением радиус-вектора г, и поэтому На сфере 5д радиуса R имеем . Поэтому поток вектора чероз Sn равен 4.1. Свойства потока вектора через поверхность 1. Линейность. где А и ц — постоянные числа. 2. Аддитивность. Если поверхность Е разбита кусочно-гладкой кривой на две части , то поток через поверхность Е равен сумме потоков через поверхности Ei и Е2, Это свойство позволяет распространить понятие потока на кусочно-гладкие поверхности Е.

Понятие ориентации поверхности Взяв, к примеру, цилиндрическую поверхность, замечаем, что если в некоторой ее точке М выбрать определенный (один из двух) единичный вектор нормали и непрерывно перемещаться затем по поверхности вместе с соответствующим вектором нормали по любому пути, не переходящему через край поверхности, то при возвращении в точку М единичный вектор нормали совпадает с исходным (рис. 12). Вместе с тем, существуют поверхности, для которых это не так.

Примером такой поверхности может служить лист Мёбиуса (рис. 13). Существует путь (отмеченная на рисунке пунктиром средняя линия листа), перемещаясь по которому, мы возвратимся в начальную точку с единичным вектором нормали, противоположным исходному. Описанное свойство разбивает все поверхности на два класса — двусторонние, или ориентируемые (плоскость, сфера, поверхность куба и т. п.), и односторонние, или неориентируемые (лист Мёбиуса). 3. Зависимость потока от ориентации поверхности (от ориентации вектора нормали к поверхности). Понятие потока вводится только для двусторонних поверхностей.

Будем считать, что если в одной точке такой поверхности направление вектора нормали уже выбрано, то Рис. 13 в любой другой ее точке берется тот вектор нормали, который получается из выбранного при непрерывном перемещении точки по поверхности (без перехода через границу). В частности, на замкнутой поверхности во всех точках берется либо внешняя нормаль, либо внутренняя (внутренняя нормаль направлена внутрьтела, ограниченного замкнутой поверхностью).

Обозначим через ту сторону поверхности £, на которой выбран вектор нормали п+ = п, а через Е~ — сторону поверхности Е, на которой берется вектор нормали (п_ = -п). Тогда получим (7) где . Таким образом, при изменении ориентации поверхности (при изменении направления вектора нормали п° к поверхности Е) поток вектора меняет знак на противоположный.

Пример 2. Вычислить поток радиус-вектора через поверхность прямого кругового цилиндра высоты Н с радиусом основания R и осью Ог. Поверхность состоит из трех частей: боковой поверхности £j, верхнего основания £2 и нижнего основания £3 цилиндра. Искомый поток П в силу свойства аддитивности равен — потоки данного поля через и соответственно. На боковой поверхности цилиндра вектор внешней нормали п? параллелен плоскости хОу, и поэтому (см. рис. 14).

Следовательно, Векторное поле Векторные линии и их дифференциальные уравнения Дифференциальные уравнения векторных линий Поток вектора через поверхность и его свойства Свойства потока вектора через поверхность Понятие ориентации поверхности На верхнем основании £2 вектор нормали параллелен оси Oz, и поэтому можно положить п§ = к-Тогда имеем так что На нижнем основании вектор г перпендикулярен к вектору нормали п» = -к. Поэтому Здесь символ означает двойной интеграл по замкнутой поверхности,