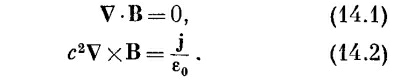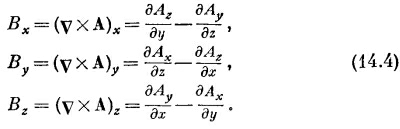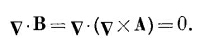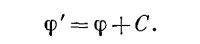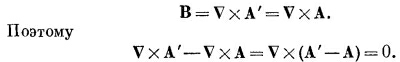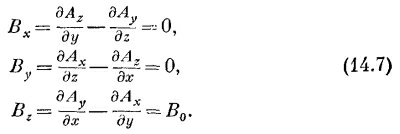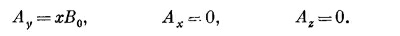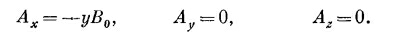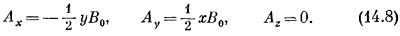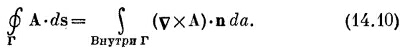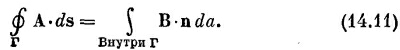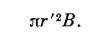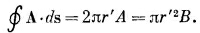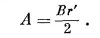Как найти векторный потенциал магнитного поля - Исправление недочетов и поиск решений вместе с Examum.ru

В связи с тем, что введенный ранее
скалярный магнитный потенциал U_m
позволяет описывать магнитные поля
только в областях, не занятых электрическими
токами, желательно ввести в рассмотрение
какую либо другую вспомогательную
величину, с помощью которой можно
было бы анализировать магнитные поля
постоянных токов, как вне проводников
с токами, так и внутри этих проводников.
Это позволит анализировать поле в
областях, где оно имеет либо потенциальный,
либо вихревой характер.

Кроме того, желательно, чтобы эта новая
вспомогательная величина была пригодна
и для исследования переменных
электромагнитных полей, т. е. для случая,
когда плотность тока изменяется во
времени (J(t)
≠ const).

Рассматривая уравнения магнитного
поля:

;
;
;

мы видим, что второе уравнение будет
выполняться всегда, если представить
вектор магнитной индукции, как ротор
некоторого вспомогательного вектора:

; [
];
; [
].

Новый вектор

называют векторным потенциалом магнитного
поля. Он является функцией координат,
так как зависит от распределения индукции
в пространстве, которая в свою очередь
зависит от распределения электрических
токов.

Наложим
на векторный потенциал такие условия,
чтобы при подстановке его в уравнения
магнитного поля эти уравнения выполнялись
бы во всех точках поля – как при

,
так и при

.
В этом случае векторным магнитным
потенциалом можно будет пользоваться
для анализа магнитных полей в любых
средах.

Принцип непрерывности магнитного потока

выполняется всегда, так как именно на
этом основании мы ввели векторный
потенциал.

Подставляя векторный потенциал в закон
полного тока

,
и принимая, что магнитная проницаемость
среды не зависит от координат ( (x,y,z)
= const), умножив обе части
уравнения на ,
получим:

,
что приводит к уравнению:

Рассмотрим
последнее уравнение, используя векторный
оператор Гамильтона (в декартовой
системе координат). Преобразуем левую
часть уравнения, применяя формулу для
двойного векторного произведения:

(*)

В полученном векторном уравнении скрыто
три уравнения для проекций векторов на
координатные оси. Вводя векторный
потенциал, мы задали только одно уравнение
для описания ротора этого вектора:

.
Для полного описания вектора необходимо
задать также его дивергенцию. При
рассмотрении магнитного поля постоянных
токов примем, что дивергенция векторного
магнитного потенциала равна нулю:

.
В интегральной форме это уравнение
записывается в виде:

Э
то
означает, что во всех точках магнитного
поля постоянного тока выполняется
принцип непрерывности линий векторного
магнитного потенциала, т. е. эти линии
не имеют ни начала, ни конца и являются
замкнутыми на себя кривыми. При
рассмотрении граничных условий в
различных средах на основании такого
типа интегралов мы утверждали, что на
границе раздела сред остаются неизменными
нормальные по отношению к границе
составляющие соответствующего вектора.
В данном случае для векторного магнитного
потенциала, можем записать:

A₁_n= A₂_n
.

П
ринятое
ограничение для дивергенции векторного
магнитного потенциала не сужает
возможностей применения уравнений
магнитного поля, так как вектор магнитной
индукции B
определяется лишь ротором векторного
потенциала и не зависит от его дивергенции.
Тогда из уравнения (*) получаем:

или

Так
как в левой части уравнения стоит
Лапласиан векторного потенциала, а
правая часть уравнения не равна нулю,
то полученное уравнение является
уравнением Пуассона для векторного
потенциала. В этом векторном уравнении
содержится три уравнения для проекций
векторов на оси координат, в частности
для декартовой системы можем записать:

;
;
.

Сопоставляя
эти уравнения с уравнением Пуассона
для скалярного электрического потенциала:

можем заметить, что одно уравнение
переходит в другое при замене:

Решение
уравнения Пуассона для скалярного
электрического потенциала известно:

поэтому по аналогии можно записать
решение уравнения Пуассона для проекций
векторного потенциала:

;
;
.

Просуммировав
умноженные на орты проекции векторного
потенциала, получим решение уравнения
Пуассона для векторного потенциала
магнитного поля (под интегралом
геометрическое суммирование):

Интегрирование проводится по всей
области (объему), где плотность тока не
равна нулю. Наиболее часто электрические
токи, создающие магнитное поле, протекают
по проводам, поэтому представляет
интерес вычисление векторного магнитного
потенциала для этого случая.

Соседние файлы в папке Лекции

Источник

From Wikipedia, the free encyclopedia

In classical electromagnetism, magnetic vector potential (often called A) is the vector quantity defined so that its curl is equal to the magnetic field: . Together with the electric potential φ, the magnetic vector potential can be used to specify the electric field E as well. Therefore, many equations of electromagnetism can be written either in terms of the fields E and B, or equivalently in terms of the potentials φ and A. In more advanced theories such as quantum mechanics, most equations use potentials rather than fields.

Magnetic vector potential was first introduced by Franz Ernst Neumann and Wilhelm Eduard Weber in 1845 and in 1846, respectively. Lord Kelvin also introduced vector potential in 1847, along with the formula relating it to the magnetic field.^[1]^[2]

Magnetic vector potential[edit]

The magnetic vector potential A is a vector field, defined along with the electric potential ϕ (a scalar field) by the equations:^[3]

${displaystyle mathbf {B} =nabla times mathbf {A} ,,quad mathbf {E} =-nabla phi -{frac {partial mathbf {A} }{partial t}},,}$

where B is the magnetic field and E is the electric field. In magnetostatics where there is no time-varying charge distribution, only the first equation is needed. (In the context of electrodynamics, the terms vector potential and scalar potential are used for magnetic vector potential and electric potential, respectively. In mathematics, vector potential and scalar potential can be generalized to higher dimensions.)

If electric and magnetic fields are defined as above from potentials, they automatically satisfy two of Maxwell’s equations: Gauss’s law for magnetism and Faraday’s law. For example, if A is continuous and well-defined everywhere, then it is guaranteed not to result in magnetic monopoles. (In the mathematical theory of magnetic monopoles, A is allowed to be either undefined or multiple-valued in some places; see magnetic monopole for details).

Starting with the above definitions and remembering that the divergence of the curl is zero and the curl of the gradient is the zero vector:

${displaystyle {begin{aligned}nabla cdot mathbf {B} &=nabla cdot left(nabla times mathbf {A} right)=0\nabla times mathbf {E} &=nabla times left(-nabla phi -{frac {partial mathbf {A} }{partial t}}right)=-{frac {partial }{partial t}}left(nabla times mathbf {A} right)=-{frac {partial mathbf {B} }{partial t}}.end{aligned}}}$

Alternatively, the existence of A and ϕ is guaranteed from these two laws using Helmholtz’s theorem. For example, since the magnetic field is divergence-free (Gauss’s law for magnetism; i.e., ∇ ⋅ B = 0), A always exists that satisfies the above definition.

The vector potential A is used when studying the Lagrangian in classical mechanics and in quantum mechanics (see Schrödinger equation for charged particles, Dirac equation, Aharonov–Bohm effect).

In the SI system, the units of A are V·s·m⁻¹ and are the same as that of momentum per unit charge, or force per unit current. In minimal coupling, qA is called the potential momentum, and is part of the canonical momentum.

The line integral of A over a closed loop, Γ, is equal to the magnetic flux, Φ_B, through a surface, S, that it encloses:

${displaystyle oint _{Gamma }mathbf {A} ,cdot ,d{mathbf {Gamma } }=iint _{S}nabla times mathbf {A} ,cdot ,dmathbf {S} =Phi _{mathbf {B} }.}$

Therefore, the units of A are also equivalent to Weber per metre. The above equation is useful in the flux quantization of superconducting loops.

Although the magnetic field B is a pseudovector (also called axial vector), the vector potential A is a polar vector.^[4] This means that if the right-hand rule for cross products were replaced with a left-hand rule, but without changing any other equations or definitions, then B would switch signs, but A would not change. This is an example of a general theorem: The curl of a polar vector is a pseudovector, and vice versa.^[4]

Gauge choices[edit]

The above definition does not define the magnetic vector potential uniquely because, by definition, we can arbitrarily add curl-free components to the magnetic potential without changing the observed magnetic field. Thus, there is a degree of freedom available when choosing A. This condition is known as gauge invariance.

Maxwell’s equations in terms of vector potential[edit]

Using the above definition of the potentials and applying it to the other two Maxwell’s equations (the ones that are not automatically satisfied) results in a complicated differential equation that can be simplified using the Lorenz gauge where A is chosen to satisfy:^[3]

${displaystyle nabla cdot mathbf {A} +{frac {1}{c}}{frac {partial phi }{partial t}}=0}$

Using the Lorenz gauge, Maxwell’s equations can be written compactly in terms of the magnetic vector potential A and the electric scalar potential ϕ:^[3]

${displaystyle {begin{aligned}nabla ^{2}phi -{frac {1}{c^{2}}}{frac {partial ^{2}phi }{partial t^{2}}}&=-{frac {rho }{epsilon _{0}}}\nabla ^{2}mathbf {A} -{frac {1}{c^{2}}}{frac {partial ^{2}mathbf {A} }{partial t^{2}}}&=-mu _{0}mathbf {J} end{aligned}}}$

In other gauges, the equations are different. A different notation to write these same equations (using four-vectors) is shown below.

Calculation of potentials from source distributions[edit]

The solutions of Maxwell’s equations in the Lorenz gauge (see Feynman^[3] and Jackson^[5]) with the boundary condition that both potentials go to zero sufficiently fast as they approach infinity are called the retarded potentials, which are the magnetic vector potential A(r, t) and the electric scalar potential ϕ(r, t) due to a current distribution of current density J(r′, t′), charge density ρ(r′, t′), and volume Ω, within which ρ and J are non-zero at least sometimes and some places):

${displaystyle {begin{aligned}mathbf {A} left(mathbf {r} ,tright)&={frac {mu _{0}}{4pi }}int _{Omega }{frac {mathbf {J} left(mathbf {r} ',t'right)}{left|mathbf {r} -mathbf {r} 'right|}},mathrm {d} ^{3}mathbf {r} '\phi left(mathbf {r} ,tright)&={frac {1}{4pi epsilon _{0}}}int _{Omega }{frac {rho left(mathbf {r} ',t'right)}{left|mathbf {r} -mathbf {r} 'right|}},mathrm {d} ^{3}mathbf {r} 'end{aligned}}}$

where the fields at position vector r and time t are calculated from sources at distant position r′ at an earlier time t′. The location r′ is a source point in the charge or current distribution (also the integration variable, within volume Ω). The earlier time t′ is called the retarded time, and calculated as

${displaystyle t'=t-{frac {left|mathbf {r} -mathbf {r} 'right|}{c}}.}$

There are a few notable things about A and ϕ calculated in this way:

The Lorenz gauge condition: ${textstyle nabla cdot mathbf {A} +{frac {1}{c^{2}}}{frac {partial phi }{partial t}}=0}$ is satisfied.
The position of r, the point at which values for ϕ and A are found, only enters the equation as part of the scalar distance from r′ to r. The direction from r′ to r does not enter into the equation. The only thing that matters about a source point is how far away it is.
The integrand uses retarded time, t′. This simply reflects the fact that changes in the sources propagate at the speed of light. Hence the charge and current densities affecting the electric and magnetic potential at r and t, from remote location r′ must also be at some prior time t′.
The equation for A is a vector equation. In Cartesian coordinates, the equation separates into three scalar equations:^[6]

${displaystyle {begin{aligned}A_{x}left(mathbf {r} ,tright)&={frac {mu _{0}}{4pi }}int _{Omega }{frac {J_{x}left(mathbf {r} ',t'right)}{left|mathbf {r} -mathbf {r} 'right|}},mathrm {d} ^{3}mathbf {r} '\A_{y}left(mathbf {r} ,tright)&={frac {mu _{0}}{4pi }}int _{Omega }{frac {J_{y}left(mathbf {r} ',t'right)}{left|mathbf {r} -mathbf {r} 'right|}},mathrm {d} ^{3}mathbf {r} '\A_{z}left(mathbf {r} ,tright)&={frac {mu _{0}}{4pi }}int _{Omega }{frac {J_{z}left(mathbf {r} ',t'right)}{left|mathbf {r} -mathbf {r} 'right|}},mathrm {d} ^{3}mathbf {r} 'end{aligned}}}$

In this form it is easy to see that the component of A in a given direction depends only on the components of J that are in the same direction. If the current is carried in a long straight wire, A points in the same direction as the wire.

In other gauges, the formula for A and ϕ is different; for example, see Coulomb gauge for another possibility.

Depiction of the A-field[edit]

Representing the Coulomb gauge magnetic vector potential A, magnetic flux density B, and current density J fields around a toroidal inductor of circular cross section. Thicker lines indicate field lines of higher average intensity. Circles in the cross section of the core represent the B-field coming out of the picture, plus signs represent B-field going into the picture. ∇ ⋅ A = 0 has been assumed.

See Feynman^[7] for the depiction of the A field around a long thin solenoid.

Since

${displaystyle nabla times mathbf {B} =mu _{0}mathbf {J} }$

assuming quasi-static conditions, i.e.

${displaystyle {frac {partial E}{partial t}}to 0,quad nabla times mathbf {A} =mathbf {B} ,,}$

the lines and contours of A relate to B like the lines and contours of B relate to J. Thus, a depiction of the A field around a loop of B flux (as would be produced in a toroidal inductor) is qualitatively the same as the B field around a loop of current.

The figure to the right is an artist’s depiction of the A field. The thicker lines indicate paths of higher average intensity (shorter paths have higher intensity so that the path integral is the same). The lines are drawn to (aesthetically) impart the general look of the A-field.

The drawing tacitly assumes ∇ ⋅ A = 0, true under one of the following assumptions:

the Coulomb gauge is assumed
the Lorenz gauge is assumed and there is no distribution of charge, ρ = 0
the Lorenz gauge is assumed and zero frequency is assumed
the Lorenz gauge is assumed and a non-zero but sufficiently low frequency to neglect ${textstyle {frac {1}{c}}{frac {partial phi }{partial t}}}$ is assumed

Electromagnetic four-potential[edit]

In the context of special relativity, it is natural to join the magnetic vector potential together with the (scalar) electric potential into the electromagnetic potential, also called four-potential.

One motivation for doing so is that the four-potential is a mathematical four-vector. Thus, using standard four-vector transformation rules, if the electric and magnetic potentials are known in one inertial reference frame, they can be simply calculated in any other inertial reference frame.

Another, related motivation is that the content of classical electromagnetism can be written in a concise and convenient form using the electromagnetic four potential, especially when the Lorenz gauge is used. In particular, in abstract index notation, the set of Maxwell’s equations (in the Lorenz gauge) may be written (in Gaussian units) as follows:

${displaystyle {begin{aligned}partial ^{mu }A_{mu }&=0\Box A_{mu }&={frac {4pi }{c}}J_{mu }end{aligned}}}$

where □ is the d’Alembertian and J is the four-current. The first equation is the Lorenz gauge condition while the second contains Maxwell’s equations. The four-potential also plays a very important role in quantum electrodynamics.

Notes[edit]

^ Neumann, Franz Ernst (January 1, 1846). «Allgemeine Gesetze Der Inducirten Elektrischen Ströme (General laws of induced electrical currents)». Annalen der Physik. 143 (11): 31–34. doi:10.1002/andp.18461430103.
^ Yang, ChenNing (2014). «The conceptual origins of Maxwell’s equations and gauge theory». Physics Today. 67 (11): 45–51. Bibcode:2014PhT….67k..45Y. doi:10.1063/PT.3.2585.
^ ^a ^b ^c ^d Feynman (1964, p. 15)
^ ^a ^b Tensors and pseudo-tensors, lecture notes by Richard Fitzpatrick
^ Jackson (1999, p. 246)
^ Kraus (1984, p. 189)
^ Feynman (1964, p. 11, cpt 15)

References[edit]

Duffin, W.J. (1990). Electricity and Magnetism, Fourth Edition. McGraw-Hill.
Feynman, Richard P; Leighton, Robert B; Sands, Matthew (1964). The Feynman Lectures on Physics Volume 2. Addison-Wesley. ISBN 0-201-02117-X.
Jackson, John David (1999), Classical Electrodynamics (3rd ed.), John Wiley & Sons, ISBN 0-471-30932-X
Kraus, John D. (1984), Electromagnetics (3rd ed.), McGraw-Hill, ISBN 0-07-035423-5

External links[edit]

Media related to Magnetic vector potential at Wikimedia Commons

Источник

Виталий Викторович Карабут

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Определение векторного потенциала

Одно из основных уравнений магнитостатики имеет вид:

Решение этого уравнения может быть определено как:

где вектор $overrightarrow{A }$ называют векторным потенциалом магнитного поля. Из векторного анализа хорошо известно тождество:

Многозначность векторного потенциала

Поле, в котором известен вектор индукции ($overrightarrow{B}$) может быть описано несколькими векторными потенциалами. Покажем, что если потенциал $overrightarrow{A }$описывает поле с индукцией $overrightarrow{B}$, то и другой потенциал $overrightarrow{A’}$, в виде:

при любом $varkappa$, описывает то же самое поле. Проведем операцию rot уравнения (4), получим:

так как $rotleft(gradvarkappa right)equiv 0.$

Многозначность векторного потенциала магнитного поля эквивалентна неоднозначности скалярного потенциала электростатического поля. Разница состоит в том, что потенциал в электростатике определяется с точностью до произвольной постоянной, тогда как векторный потенциал магнитостатического поля, определятся с точностью до произвольной функции определённого класса. Произвольность в выборе векторного потенциала показывает, что векторный потенциал имеет вспомогательное значение. Он не может быть измерен в эксперименте.

Калибровка векторного потенциала

В магнитостатике в качестве калибровочного условия для векторного потенциала используют уравнение:

Уравнение (6) называют условием калибровки потенциала.

Уравнение для векторного потенциала

Запишем теорему о циркуляции вектора $overrightarrow{B}$ в дифференциальной форме:

где $overrightarrow{j}$ — вектор плотности тока, ${mu }_0$ — магнитная постоянная. Подставим (2) в уравнение циркуляции (7), получим:

Преобразуем выражение $rotrotoverrightarrow{A}$ согласно известному из векторного анализа соотношению:

$graddivoverrightarrow{A}=0 (из условия калибровки (6) ),$ следовательно, уравнение (8) приобретет вид:

В координатном представлении уравнение (10) запишется в форме:

В системе уравнений (11) мы получили, что каждая компонента векторного потенциала подчиняется уравнению Пуассона. Следовательно, можно предположить, что решение уравнений (11) можно записать в виде:

где $r$ — радиус вектор, который проведен из элемента тока в точку наблюдения. В векторной форме (12) запишем как:

«Векторный потенциал и его связь с вектором индукции магнитного поля» 👇

Для тока в прямолинейном проводнике (линейного тока), можно записать, что векторный потенциал равен:

где $L_i$- контуры токов, $I_i$- силы токов в контурах.

Если найден векторный потенциал, то используя его определение можно отыскать соответствующую ему индукцию магнитного поля. Введение векторного потенциала существенно облегчает изучение магнитного поля постоянных токов.

Пример 1

Задание: Найдите вектор-потенциал магнитного поля, которое создается прямолинейным током проводника длинны L. Сила тока в проводнике I.

Решение:

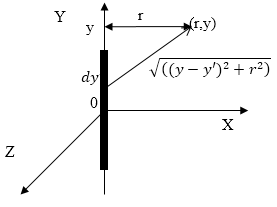
Пусть начало координат находится в середине, рассматриваемого участка с током (рис.1).

Рис. 1

Магнитное поле прямолинейного проводника с током обладает цилиндрической симметрией, следовательно. Координаты точки в данной плоскости характеризуются расстоянием r от оси Y и координатой y. В качестве основы для решения задачи используем выражение:

[overrightarrow{A}=frac{{mu }_0}{4pi }intlimits_L{frac{I}{r}}doverrightarrow{l}=frac{{mu }_0}{4pi }sumlimits_i{I_i}intlimits_{L_i}{frac{doverrightarrow{l}}{r}}left(1.1right).]

Из (1.1) следует, что не равна нулю только компонента $A_yne 0$. ($A_x=0{,A}_z=0$) так как ток течет только по оси Y. В таком случае запишем:

[{A=A}_y=frac{mu_0I}{4 pi}intlimits^{frac{L}{2}}_{-frac{L}{2}}{frac{dy’}{sqrt{{left(y-y’right)}^2+r^2}}}=frac{mu_0I}{4 pi}lnleft(frac{-y+frac{L}{2}+sqrt{{left(y-frac{L}{2}right)}^2+r^2}}{-left(y+frac{L}{2}right)+sqrt{{left(y+frac{L}{2}right)}^2+r^2}}right)(1.2).]

Для бесконечно длинного проводника векторный магнитный потенциал равен:

[Lto infty ;А=frac{{mu }_0I}{4pi }lnr+const.]

Ответ: A=$frac{{mu }_0I}{4pi }lnleft(frac{-y+frac{L}{2}+sqrt{{left(y-frac{L}{2}right)}^2+r^2}}{-left(y+frac{L}{2}right)+sqrt{{left(y+frac{L}{2}right)}^2+r^2}}right).$

Пример 2

Задание: Используя результат решения задачи «Пример 1». Найдите индукцию магнитного поля, которое создается прямолинейным током проводника длинны L. Сила тока в проводнике I. (рис.1).

Решение:

Из симметрии магнитного поля данного проводника с током индукцию достаточно вычислить в точках плоскости XY. Будем вычислять ее по формуле:

[overrightarrow{B}=rotoverrightarrow{A }left(2.1right),]

где из предыдущей задачи имеем:

[A_y=frac{mu_0I}{4 pi}lnleft(frac{-y+frac{L}{2}+sqrt{{left(y-frac{L}{2}right)}^2+r^2}}{-left(y+frac{L}{2}right)+sqrt{{left(y+frac{L}{2}right)}^2+r^2}}right)(2.2).]

Удобнее индукцию, опять таки из соображений симметрии поля, записать в цилиндрических координатах. При этом будем иметь, что не равна нулю только проекция $B_{varphi }$, где $varphi $ — угол цилиндрической системы координат. При этом можно записать, что:

[B_{varphi }=-frac{partial A_y}{partial r}left(2.3right).]

На рис. 1 на плоскости XY $компонента B_{varphi }$ направлена перпендикулярно плоскости в против оси Z. Подставим (2.2) в (2.3), получим:

[B_{varphi }=frac{{mu }_0I}{4pi }left{frac{-y+frac{L}{2}}{sqrt{{left(y-frac{L}{2}right)}^2+r^2}}+frac{y+frac{L}{2}}{sqrt{{left(y+frac{L}{2}right)}^2+r^2}}right}.]

Для бесконечного прямолинейного проводника имеем:

[Lto infty ; B_{varphi }=frac{{mu }_0I}{2pi r}.]

Ответ: B=$B_{varphi }=frac{{mu }_0I}{4pi }left{frac{-y+frac{L}{2}}{sqrt{{left(y-frac{L}{2}right)}^2+r^2}}+frac{y+frac{L}{2}}{sqrt{{left(y+frac{L}{2}right)}^2+r^2}}right}.$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Главная >> Фейнмановские лекции по физике >> Том 5 >> Глава 14. Магнитное поле в разных случаях

Векторный потенциал

В этой главе мы продолжим разговор о магнитостатике, т. е. о постоянных магнитных полях и постоянных токах. Магнитное поле и электрические токи связаны нашими основными уравнениями:

На этот раз нам нужно решить эти уравнения математически самым общим образом, а не ссылаться на какую-нибудь особую симметрию или на интуицию. В электростатике мы нашли прямой способ вычисления поля, когда известны положения всех электрических зарядов: скалярный потенциал φ дается просто интегралом по зарядам, как в уравнении (4.25) на стр. 77. Если затем нужно знать электрическое поле, то его получают дифференцированием φ. Мы покажем сейчас, что для нахождения поля В существует аналогичная процедура, если известна плотность тока j всех движущихся зарядов.

В электростатике, как мы видели (из-за того, что rot от Е везде равен нулю), всегда можно представить Е в виде градиента от скалярного поля φ. А вот rot от В не везде равен нулю, поэтому представить его в виде градиента, вообще говоря, невозможно. Однако дивергенция В везде равна нулю, а это значит, что мы можем представить В в виде ротора от другого векторного поля. Ибо, как мы видели в гл. 2, § 8, дивергенция ротора всегда равна нулю. Следовательно, мы всегда можем выразить В через поле, которое мы обозначим А:

Или, расписывая компоненты:

Запись В=vхА гарантирует выполнение (14.1), потому что обязательно

Поле А называется векторным потенциалом.

Вспомним, что скалярный потенциал φ оказывается не полностью определенным. Если мы нашли для некоторой задачи потенциал φ, то всегда можно найти столь же хороший другой потенциал φ′, добавив постоянную:

Новый потенциал φ′ дает те же электрические поля, потому что градиент vС есть нуль; φ′ и φ отвечают одной и той же картине.

Точно так же у нас может быть несколько векторных потенциалов А, приводящих к одним и тем же магнитным полям. Опять-таки, поскольку В получается из А дифференцированием, то прибавление к А константы не меняет физики дела. Но для А свобода больше. Мы можем добавить к А любое поле, которое есть градиент от некоторого скалярного поля, не меняя при этом физики. Это можно показать следующим образом. Пусть у нас есть А, которое в какой-то реальной задаче дает правильное поле В. Спрашивается, при каких условиях другой векторный потенциал А′, будучи подставлен в (14.3), дает то же самое поле В. Значит, А и А′ имеют одинаковый ротор

Но если ротор вектора есть нуль, то вектор должен быть градиентом некоторого скалярного поля, скажем ψ, так что А′—A=vψ. Это означает, что если А есть векторный потенциал, отвечающий данной задаче, то при любом ψ

также будет векторным потенциалом, в одинаковой степени удовлетворяющим данной задаче и приводящим к тому же полю В.

Обычно бывает удобно уменьшить «свободу» А, накладывая на него произвольно некоторое другое условие (почти таким же образом мы считали удобным — довольно часто — выбирать потенциал φ равным нулю на больших расстояниях). Мы можем, например, ограничить А, наложив на него такое условие, чтобы дивергенция А чему-нибудь равнялась. Мы всегда можем это сделать, не задевая В. Так получается потому, что, хотя А′ и А имеют одинаковый ротор и дают одно и то же В, они вовсе не обязаны иметь одинаковую дивергенцию. В самом деле, v·A` = v·A+ v²ψ, и, подбирая соответствующее ψ, можно придать v·A′ любое значение.

Чему следует приравнять v·А? Выбор должен обеспечить наибольшее математическое удобство и зависит от нашей задачи. Для магнитостатики мы сделаем простой выбор

(Потом, когда мы перейдем к электродинамике, мы изменим наш выбор.) Итак, наше полное определение А в данный момент есть vхА = В и v·А = 0.

Чтобы привыкнуть к векторному потенциалу, посмотрим сначала, чему он равен для однородного магнитного поля В₀. Выбирая ось z в направлении В₀, мы должны иметь

Рассматривая эти уравнения, мы видим, что одно из возможных решений есть

Или с тем же успехом можно взять

Еще одно решение есть комбинация первых двух

Ясно, что для каждого поля В векторный потенциал А не единственный; существует много возможностей.

Третье решение [уравнение (14.8)] обладает рядом интересных свойств. Поскольку х-компонента пропорциональна –у, а y-компонента пропорциональна +х, то вектор А должен быть перпендикулярен вектору, проведенному от оси z, который мы обозначим r′ (штрих означает, что это не вектор расстояния от начала). Кроме того, величина А пропорциональна √x²+ y² и, следовательно, пропорциональна r`. Поэтому А (для однородного поля) может быть записано просто

Векторный потенциал А равен по величине Вr′/2 и вращается вокруг оси z, как показано на фиг. 14.1. Если, например, поле В есть поле внутри соленоида вдоль его оси, то векторный потенциал циркулирует точно таким же образом, как и токи в соленоиде.

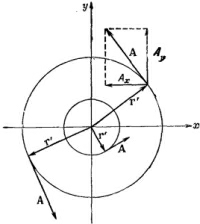
Векторный потенциал однородного поля может быть получен и другим способом. Циркуляция А вдоль любой замкнутой петли Г может быть выражена через поверхностный интеграл от vХА с помощью теоремы Стокса [уравнение (3.38), стр. 63]

Но интеграл справа равен потоку В сквозь петлю, поэтому

Итак, циркуляция А вдоль всякой петли равна потоку В сквозь петлю. Если мы возьмем круглую петлю радиуса r′ в плоскости, перпендикулярной однородному полю В, то поток будет в точности равен

Если выбрать начало отсчета в центре петли, так что А можно считать направленным по касательной и функцией только от r′, то циркуляция будет равна

Как и раньше, получаем

В только что разобранном примере мы вычисляем векторный потенциал из магнитного поля, обычно поступают наоборот. В сложных задачах всегда проще найти векторный потенциал, а затем уже из него найти магнитное поле. Сейчас мы покажем, как это можно сделать.

СМОТРИТЕ ТАКЖЕ:

Социальные комментарии Cackle

Источник

Magnetic vector potential[edit]

Gauge choices[edit]

Maxwell’s equations in terms of vector potential[edit]

Calculation of potentials from source distributions[edit]

Depiction of the A-field[edit]

Electromagnetic four-potential[edit]

See also[edit]

Notes[edit]

References[edit]

External links[edit]

Определение векторного потенциала

Многозначность векторного потенциала

Калибровка векторного потенциала

Уравнение для векторного потенциала

Векторный потенциал

СМОТРИТЕ ТАКЖЕ: