Как найти векторы в треугольнике по координатам

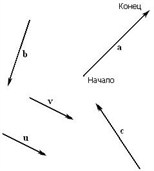
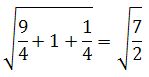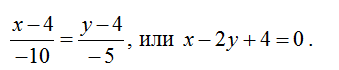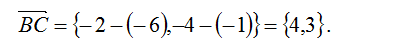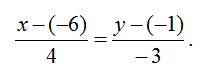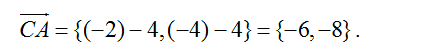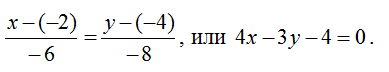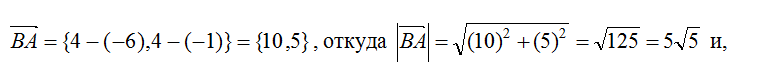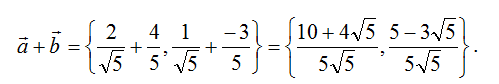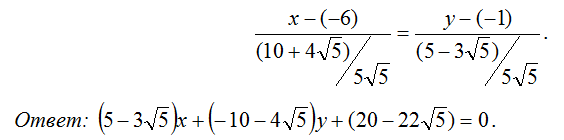Нахождение координат вектора через координаты точек

Отложим от начала координат единичные векторы, то есть векторы, длины которых равны единице. Направление вектора i → должно совпадать с осью O x , а направление вектора j → с осью O y .

Векторы i → и j → называют координатными векторами.

Координатные векторы неколлинеарны. Поэтому любой вектор p → можно разложить по векторам p → = x i → + y j → . Коэффициенты x и y определяются единственным образом. Коэффициенты разложения вектора p → по координатным векторам называются координатами вектора p → в данной системе координат.

Координаты вектора записываются в фигурных скобках p → x ; y . На рисунке вектор O A → имеет координаты 2 ; 1 , а вектор b → имеет координаты 3 ; — 2 . Нулевой вектор представляется в виде 0 → 0 ; 0 .

Если векторы a → и b → равны, то и y 1 = y 2 . Запишем это так: a → = x 1 i → + y 1 j → = b → = x 2 i → + y 2 j → , значит x 1 = x 2 , y 1 = y 2 .

Таким образом, координаты равных векторов соответственно равны.

Если точка координат не совпадает с его началом системы координат, тогда рассмотрим задачу. Пусть в декартовой системе координат на O x y заданы координаты точек начала и конца A B → : A x a , y a , B x b , y b . Найти координаты заданного вектора.

Изобразим координатную ось.

Из формулы сложения векторов имеем O A → + A B → = O B → , где O – начало координат. Отсюда следует, что A B → = O B → — O A → .

O A → и O B → – это радиус-векторы заданных точек А и В, значит координаты точек имеют значения O A → = x a , y a , O B → = x b , y b .

По правилу операций над векторами найдем A B → = O B → — O A → = x b — x a , y b — y a .

Нахождение в трехмерном пространстве проходит по такому же принципу, только для трех точек.

Для нахождения координат вектора, необходимо найти разность его точек конца и начала.

Найти координаты O A → и A B → при значении координат точек A ( 2 , — 3 ) , B ( — 4 , — 1 ) .

Для начала определяется радиус-вектор точки A . O A → = ( 2 , — 3 ) . Чтобы найти A B → , нужно вычесть значение координат точек начала из координат точек конца.

Получаем: A B → = ( — 4 — 2 , — 1 — ( — 3 ) ) = ( — 6 , 2 ) .

Ответ: O A → = ( 2 , — 3 ) , A B → = ( — 6 , — 2 ) .

Задано трехмерное пространство с точкой A = ( 3 , 5 , 7 ) , A B → = ( 2 , 0 , — 2 ) . Найти координаты конца A B → .

Подставляем координаты точки A : A B → = ( x b — 3 , y b — 5 , z b — 7 ) .

По условию известно, что A B → = ( 2 , 0 , — 2 ) .

Известно, что равенство векторов справедливо тогда, когда координаты равны соответственно. Составим систему уравнений: x b — 3 = 2 y b — 5 = 0 z b — 7 = — 2

Отсюда следует, что координаты точки B A B → равны: x b = 5 y b = 5 z b = 5

Ответ: B ( 5 , 5 , 5 ) .

Решить треугольник Онлайн по координатам

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

A ( ; ), B ( ; ), C ( ; )

Примечание: дробные числа записывайте через точку, а не запятую. Округлять до -го знака после запятой. Как найти вектор по точкам Формула Чтобы найти координаты вектора $overline$ на плоскости, если он задан координатами своих начала $Aleft(x_ <1>; y_<1>right)$ и конца $Bleft(x_ <2>; y_<2>right)$, необходимо от координат конца отнять соответствующие координаты начала, то есть Чтобы найти координаты вектора $overline$, заданного в пространстве координатами $Aleft(x_ <1>; y_ <1>; z_<1>right)$ и $Bleft(x_ <2>; y_ <2>; z_<2>right)$, необходимо, по аналогии с плоским случаем, из координат конца вычесть координаты начала: Примеры нахождения координат вектора по точкам Задание. Даны точки $A(4;-1)$ и $B(2;1)$. Найти координаты векторов $overline$ и $overline$ Решение. Для вектора $overline$ точка $A$ является началом, а точка $B$ — концом. Тогда координаты вектора $overline$ равны Для вектора точка $B$ является началом, а точка $A$ — концом. Тогда координаты вектора $overline$ равны Ответ. $overline=(-2 ; 2), overline=(2 ;-2)$ Задание. Даны три точки в пространстве точки $A(1;-2;0,5)$, $B(3;2;1,5)$ и $C(0;-1;1)$. Найти координаты векторов $overline$, $overline$, $overline$ Решение. Для искомого вектора $overline$ точка $A$ является началом, а точка $B$ — концом. Тогда координаты вектора $overline$ соответственно равны: $$overline=(3-1 ; 2-(-2) ; 1,5-0,5)=(2 ; 4 ; 1)$$ Для вектора $overline$ точка $A$ является началом, а точка $C$ — концом. Тогда его координаты соответственно равны Для вектора $overline$ точка $B$ является началом, а точка $C$ — концом. Его координаты равны Ответ. $overline=(2 ; 4 ; 1), overline=(-1 ; 1 ; 0,5), overline=(-3 ;-3 ;-0,5)$ источники: http://mathhelpplanet.com/static.php?p=onlain-reshit-treugolnik http://www.webmath.ru/poleznoe/formules_13_0.php

Решить треугольник Онлайн по координатам

Данный онлайн-сервис вычисляет (показываются промежуточные расчёты) следующие параметры треугольника:

1) длины и уравнения сторон, медиан, средних линий, высот, серединных перпендикуляров, биссектрис;

2) система линейных неравенств, определяющих треугольник;

2) уравнения прямых, проходящих через вершины параллельно противолежащим сторонам;

3) внутренние углы по теореме косинусов;

4) площадь треугольника;

5) точка пересечения медиан (центроид) и точки пересечения медиан со сторонами;

10) параметры вписанной и описанной окружностей и их уравнения.

Внимание! Этот сервис не работает в браузере IE (Internet Explorer).

Запишите координаты вершин треугольника и нажмите кнопку.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Вспомним для начала основные понятия и формулы.

Пусть даны две точки: А(x1; x2) и B(y1; y2). Рассмотрим отрезок AB.

Длина отрезка АВ – это расстояние между точками A и B, его величина вычисляется по следующей формуле:

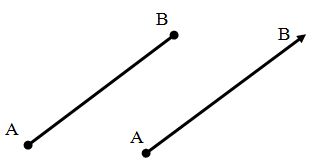
Рассмотрим теперь вектор AB. Напомню, что вектор – это направленный отрезок, то есть для него указано, какая из двух точек A и B является началом, а какая – концом. На рисунке ниже слева изображен отрезок AB, а справа – вектор AB с началом в точке A и концом в точке B.

Координаты вектора AB вычисляются следующим образом: из соответствующих координат конца вектора вычитаются соответствующие координаты начала вектора. Например, для нашего вектора AB это будет выглядеть так: AB(x2 – x1; y2 – y1).

Замечу, что модулем вектора AB называется длина отрезка AB.

Вспомним как найти координаты середины отрезка AB. Для этого есть простая формула:

x = (x1 + x2)/2, y = (y1 + y2)/2.

До этого момента мы рассматривали координаты на плоскости, а что, если речь пойдет о пространстве? Тут, оказывается, тоже все просто.

Пусть даны две точки A(x1; x2; x3) и B(y1; y2; y3).

Формула для вычисления длины отрезка AB, расположенного в пространстве будет выглядеть так:

А координаты середины отрезка AB найдем по формуле

x = (x1 + x2)/2, y = (y1 + y2)/2, z = (z1 + z2)/2.

И еще одна полезная формула: если вектор задан своими координатами, например,  MN(x1; x2; x3), то его модуль вычисляется по формуле:

Чтобы сложить два или более векторов, нужно сложить их соответствующие координаты, например,

(x1; x2; x3) + (y1; y2; y3) = (x1 + y1; x2 + y2; x3 + y3).

Чтобы умножить вектор на число, нужно умножить каждую его координату на это число, например,

5 · (x1; x2; x3) = (5 · x1; 5 · x2; 5 · x3).

Скалярным произведением двух векторов а и b называется число

a · b = |a»b| · сos (a, b),

Чтобы вычислить скалярное произведение векторов, заданных координатами, например, MN(x1; x2; x3) и PK(y1; y2; y3), можно воспользоваться следующей формулой:

MN · PK = x1 · y1 + x2 · y2 + x3 · y3.

Два вектора называются коллинеарными, если они лежат на параллельных прямых или на одной прямой.

На практике коллинеарность векторов (x1; x2) и (y1; y2) проще всего проверить, используя следующее свойство: коллинеарные векторы имеют пропорциональные координаты, то есть существует число p, такое, что (x1; x2) = p · (y1; y2).

Существуют также такие понятия, как сонаправленные векторы и противоположно направленные векторы. Сонаправленные векторы – это коллинеарные векторы, которые направлены в одну сторону, соответственно, противоположно направленные векторы – это коллинеарные векторы, которые направлены в разные стороны.

Теперь давайте рассмотрим несколько задач на эту тему.

Задача 1.

Доказать, что треугольник с вершинами A(6; -4; 2), B(3; 2; 3) и C(3; -5; -1) прямоугольный.

Решение.

Вполне очевидно, что для доказательства этой задачи достаточно показать, что один из углов треугольника ABC равен 90 градусов. Вспомним формулу для вычисления скалярного произведения через модули соответствующих векторов и косинус угла между ними, преобразуем ее и воспользуемся для нахождения угла.

сos (a, b) = a · b/|a»b|.

Для начала нам понадобятся координаты всех векторов, задающих стороны треугольника, их модули и всевозможные скалярные произведения. Вычисляем их.

Координаты векторов:

AB(3 – 6; 2 – (-4); 3 – 2) = AB(-3; 6; 1);

BC(3 – 3; -5 – 2; -1 – 3) = BC(0; -7; -4);

CA(6 – 3; -4 – (-5); 2 – (-1)) = CA(3; 1; 3).

Модули:

|AB| =

|BC| =

|CA| =

Скалярные произведения:

AB · BC = (-3) · 0 + 6 · (-7) + 1 · (-4) = 0 – 42 – 4 = -46;

BC · CA = 0 · 3 + (-7) · 1 + (-4) · 3 = 0 – 7 – 12 = -19;

AB · CA = (-3) · 3 + 6 · 1 + 1 · 3 = -9 + 6 + 3 = 0.

Теперь легко заметить, что угол между векторами AB и CA равен 90 градусов, так как

сos (AB, CA) = AB · CA / |AB»CA| = 0.

А, значит, угол А треугольника ABC равен 90 градусов, то есть треугольник ABC – прямоугольный, что и требовалось доказать.

Задача 2.

Даны точки А(0; 1; 2), B(1; 2; 4), C(-1; -1; 3) и D(1; 0; 0). Точки M и N – середины отрезков AC и BD. Найдите вектор MN и его модуль.

Решение.

Для начала найдем координаты точек M и N.

M((0 – 1)/2; (1 – 1)/2; (2 + 3)/2) = M(-1/2; 0; 5/2);

N((1 + 1)/2; (2 + 0)/2; (4 + 0)/2) = N(1; 1; 2).

Теперь найдем координаты вектора MN:

MN(1 – (-1/2); 1 – 0; 2 – 5/2) = MN(3/2; 1; -1/2).

Осталось найти модуль вектора MN.

|MN| =

Задача 3.

При каких значениях x векторы (x³ – 1)a и 2xa сонаправлены, где a – вектор, не равный нулевому вектору?

Решение.

Для того чтобы данные векторы были сонаправлены, необходимо, чтобы коэффициенты (x³ – 1) и 2x имели одинаковый знак, а значит, чтобы выполнялось следующее неравенство: (x³ – 1) · 2x > 0. Решим его методом интервалов и найдем соответствующие x.

Получим x € (-∞; 0) U (1; +∞).

Если бы в задаче требовалось узнать, при каких x данные векторы будут противоположно направлены, мы бы потребовали, чтобы у коэффициентов (x³ – 1) и 2x были различные знаки.

Задача 4.

Даны координаты вершин четырехугольника: A(2; -2), B(-3; 1), C(7; 7) и D(7; 1). Доказать, что ABCD – трапеция.

Решение.

Так как трапеция – это четырехугольник, у которого одна пара противолежащих сторон параллельна, то для доказательства нам достаточно показать, что векторы BC и AD – коллинеарны, то есть лежат на параллельных прямых. Найдем для начала их координаты.

BC(7 – (-3); 7 – 1) = BC(10; 6);

AD(7 – 2; 1 – (-2)) = AD(5; 3).

Заметим, что координаты векторов пропорциональны: (10; 6) = 2 · (5; 3). Это и указывает на то, что данные векторы коллинеарны, а, значит, ABCD – трапеция.

Остались вопросы? Не знаете, как выполнять действия над векторами?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.

По известным координатам вершин треугольника  А(4;4), В(-6;-1), С(-2;-4) записать для его сторон уравнения в общем виде и уравнение в общем виде биссектрисы угла АВС. 

Решение

Так как нам известны координаты вершин, то проще всего получить уравнение стороны в канонической форме – формула, от которого легко перейти к уравнению в общей форме. Для канонического уравнения нам нужны координаты точки, принадлежащей стороне и координаты направляющего вектора (параллельного рассматриваемому).

1. Найдем уравнение стороны АВ. В качестве точки прямой можно взять точку А с заданными координатами, а в качестве направляющего вектора – вектор АВ. Найдем координаты вектора АВ:

2. Тогда каноническое уравнение стороны АВ запишется:

3. Аналогично можно получить уравнения остальных сторон треугольника: для стороны ВС: координаты вектора 

4. Откуда каноническое уравнение:

Следовательно, общее уравнение: 3x+4y+22=0.

5. Для стороны CА: координаты направляющего вектора

6. Каноническое уравнение: 

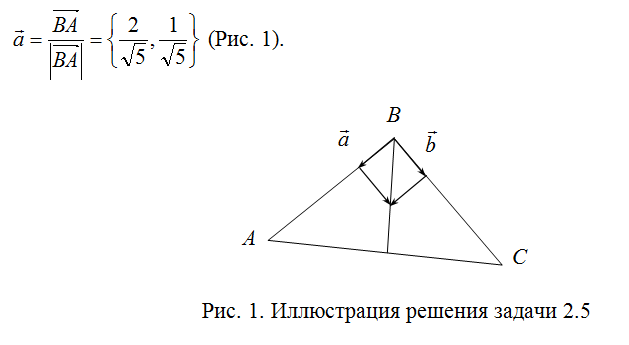
7. Выведем общее уравнение для биссектрисы. Известно, что биссектриса делит угол пополам. Если на сторонах АВ и ВС треугольника отложить орты (соответственно a и b) и построить на них ромб, то диагональ ромба также поделит угол пополам (по своему свойству) и, значит, ее можно будет взять направляющей биссектрисы. Вектор, построенный на диагонали ромба, равен сумме векторов a и b).

8. Для нахождения орта a необходимо знать координаты вектора BA:

соответственно a определится как:

9. Аналогично определим орт b:

Теперь определим их сумму:

10. Тогда каноническое уравнение биссектрисы: