Как найти большую дугу окружности
Задача 10 (ОГЭ — 2015)
На окружности с центром O отмечены точки A и B так, что ∠ AOB = 18°. Длина меньшей дуги AB равна 5. Найдите длину большей дуги окружности.
∠ AOB = 18°. Вся окружность составляет 360°. Поэтому ∠ AOB составляет 18/360 = 1/20 окружности.
Значит, и меньшая дуга AB составляет 1/20 всей окружности, поэтому большая дуга — это остальная часть, т.е. 19/20 окружности.
1/20 окружности соответствует длине дуги, равной 5. Тогда длина большей дуги равна 5*19 = 95.
Задача 10 (ОГЭ — 2015)
На окружности с центром O отмечены точки A и B так, что ∠ AOB = 40°. Длина меньшей дуги AB равна 50. Найдите длину большей дуги окружности.
∠ AOB = 40°. Вся окружность составляет 360°. Поэтому ∠ AOB составляет 40/360 = 1/9 окружности.
Значит, и меньшая дуга AB составляет 1/9 всей окружности, поэтому большая дуга — это остальная часть, т.е. 8/9 окружности.
1/9 окружности соответствует длине дуги, равной 50. Тогда длина большей дуги равна 50*8 = 400.
Задача 10 (ГИА — 2014)
Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
По теореме Пифагора из прямоугольного треугольника AOB получим:
AO 2 = OB 2 +AB 2 ,
AO 2 = 27 2 +36 2 = 729+1296 = 2025,
Тогда диаметр равен 2R = 2*45 = 90.
Задача 10 (ГИА — 2014)
Точка O — центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC = 134° и ∠OAB = 75°. Найдите угол BCO. Ответ дайте в градусах.
∠ABC — вписанный, а значит равен половине дуги, на которую опирается. Поэтому большая дуга AC = 2*134 = 268°.
Тогда дуга ABC = 360° — 268° =92°.
∠AOC = 92°,так как он является центральным углом и опирается на дугу ABC.
Сумма углов в выпуклом четырехугольнике равна 360°, откуда получаем:
Площадь круга и его частей. Длина окружности и ее дуг
| Основные определения и свойства. Число π |
| Формулы для площади круга и его частей |
| Формулы для длины окружности и ее дуг |
| Площадь круга |
| Длина окружности |
| Длина дуги |
| Площадь сектора |
| Площадь сегмента |
Основные определения и свойства
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Часть окружности, расположенная между двумя точками окружности
Конечная часть плоскости, ограниченная окружностью
Часть круга, ограниченная двумя радиусами
Часть круга, ограниченная хордой
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
| Фигура | Рисунок | Определения и свойства |
| Окружность | ||
| Дуга | ||
| Круг | ||
| Сектор | ||
| Сегмент | ||
| Правильный многоугольник | ||
Множество точек плоскости, находящихся на одном и том же расстоянии от одной точки — центра окружности
Дуга
Часть окружности, расположенная между двумя точками окружности
Круг
Конечная часть плоскости, ограниченная окружностью
Сектор
Часть круга, ограниченная двумя радиусами
Сегмент
Часть круга, ограниченная хордой
Правильный многоугольник
Выпуклый многоугольник, у которого все стороны равны и все углы равны
Около любого правильного многоугольника можно описать окружность
Определение 1 . Площадью круга называют предел, к которому стремятся площади правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Определение 2 . Длиной окружности называют предел, к которому стремятся периметры правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон.
Замечание 1 . Доказательство того, что пределы площадей и периметров правильных многоугольников, вписанных в круг, при неограниченном возрастании числа сторон действительно существуют, выходит за рамки школьной математики и в нашем справочнике не приводится.
Определение 3 . Числом π (пи) называют число, равное площади круга радиуса 1.
Замечание 2 . Число π является иррациональным числом, т.е. числом, которое выражается бесконечной непериодической десятичной дробью:
Число π является трансцендентным числом, то есть числом, которое не может быть корнем алгебраического уравнения с целочисленными коэффициентами.
Формулы для площади круга и его частей
,
где R – радиус круга, D – диаметр круга
,
если величина угла α выражена в радианах
,
если величина угла α выражена в градусах
,
если величина угла α выражена в радианах
,
если величина угла α выражена в градусах
| Числовая характеристика | Рисунок | Формула |
| Площадь круга | ||
| Площадь сектора | ||
| Площадь сегмента |
,
где R – радиус круга, D – диаметр круга
Площадь сектора
,
если величина угла α выражена в радианах
,
если величина угла α выражена в градусах
Площадь сегмента
,
если величина угла α выражена в радианах
,
если величина угла α выражена в градусах
Формулы для длины окружности и её дуг
где R – радиус круга, D – диаметр круга
если величина угла α выражена в радианах
,
если величина угла α выражена в градусах
| Числовая характеристика | Рисунок | Формула |
| Длина окружности | ||
| Длина дуги |
где R – радиус круга, D – диаметр круга
Длина дуги
если величина угла α выражена в радианах
,
если величина угла α выражена в градусах
Площадь круга
Рассмотрим две окружности с общим центром ( концентрические окружности ) и радиусами радиусами 1 и R , в каждую из которых вписан правильный n – угольник (рис. 1).
Обозначим через O общий центр этих окружностей. Пусть внутренняя окружность имеет радиус 1 .
Поскольку при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса 1 , стремится к π , то при увеличении n площадь правильного n – угольника, вписанного в окружность радиуса R , стремится к числу πR 2 .
Таким образом, площадь круга радиуса R , обозначаемая S , равна
Длина окружности
то, обозначая длину окружности радиуса R буквой C , мы, в соответствии с определением 2, при увеличении n получаем равенство:
откуда вытекает формула для длины окружности радиуса R :
Следствие . Длина окружности радиуса 1 равна 2π.
Длина дуги
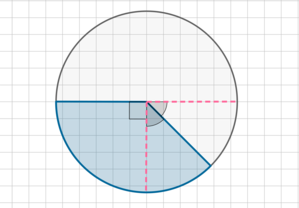
Рассмотрим дугу окружности, изображённую на рисунке 3, и обозначим её длину символом L(α), где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сектора
Рассмотрим круговой сектор, изображённый на рисунке 4, и обозначим его площадь символом S (α) , где буквой α обозначена величина соответствующего центрального угла.
В случае, когда величина α выражена в градусах, справедлива пропорция
из которой вытекает равенство:
В случае, когда величина α выражена в радианах, справедлива пропорция
из которой вытекает равенство:
Площадь сегмента
Рассмотрим круговой сегмент, изображённый на рисунке 5, и обозначим его площадь символом S (α), где буквой α обозначена величина соответствующего центрального угла.
Поскольку площадь сегмента равна разности площадей кругового сектора MON и треугольника MON (рис.5), то в случае, когда величина α выражена в градусах, получаем
В случае, когда величина α выражена в в радианах, получаем
Геометрия. Урок 5. Окружность
Смотрите бесплатные видео-уроки на канале Ёжику Понятно.
Видео-уроки на канале Ёжику Понятно. Подпишись!
Содержание страницы:
- Определение окружности
- Отрезки в окружности
Определение окружности
Окружность – геометрическое место точек, равноудаленных от данной точки.
Эта точка называется центром окружности .
Отрезки в окружности
Радиус окружности R – отрезок, соединяющий центр окружности с точкой на окружности.
Хорда a – отрезок, соединяющий две точки на окружности.
Диаметр d – хорда, проходящая через центр окружности, он равен двум радиусам окружности ( d = 2 R ).
O A – радиус, D E – хорда, B C – диаметр.
Теорема 1:
Радиус, перпендикулярный хорде, делит пополам эту хорду и дугу, которую она стягивает.
Касательная к окружности – прямая, имеющая с окружностью одну общую точку.
Из одной точки, лежащей вне окружности, можно провести две касательные к данной окружности.
Теорема 2:
Отрезки касательных, проведенных из одной точки, равны ( A C = B C ).
Теорема 3:
Касательная перпендикулярна радиусу, проведенному к точке касания.
Дуга в окружности
Часть окружности, заключенная между двумя точками, называется дугой окружности .
Например, хорда A B стягивает две дуги: ∪ A M B и ∪ A L B .
Теорема 4:
Равные хорды стягивают равные дуги.
Если A B = C D , то ∪ A B = ∪ C D
Углы в окружности
В окружности существует два типа углов: центральные и вписанные.
Центральный угол – угол, вершина которого лежит в центре окружности.
∠ A O B – центральный.
Центральный угол равен градусной мере дуги, на которую он опирается . ∪ A B = ∠ A O B = α
Если провести диаметр, то он разобьёт окружность на две полуокружности. Градусная мера каждой полуокружности будет равна градусной мере развернутого угла, который на неё опирается.
Градусная мара всей окружности равна 360 ° .
Вписанный угол – угол, вершина которого лежит на окружности, а стороны пересекают окружность.
∠ A C B – вписанный.
Вписанный угол равен половине градусной меры дуги, на которую он опирается . ∠ A C B = ∪ A B 2 = α 2 ∪ A B = 2 ⋅ ∠ A C B = α
Теорема 5:
Вписанные углы, опирающиеся на одну и ту же дугу, равны .
∠ M A N = ∠ M B N = ∠ M C N = ∪ M N 2 = α 2
Теорема 6:
Вписанный угол, опирающийся на полуокружность (на диаметр), равен 90 ° .
∠ M A N = ∠ M B N = ∪ M N 2 = 180 ° 2 = 90 °
Длина окружности, длина дуги
Мы узнали, как измеряется градусная мера дуги окружности (она равна градусной мере центрального угла, который на нее опирается) и всей окружности целиком (градусная мера окружности равна 360 ° ). Теперь поговорим о том, что же такое длина дуги в окружности. Длина дуги – это значение, которое мы бы получили, если бы мерили дугу швейным сантиметром. Рассмотрим две окружности с разными радиусами, в каждой из которых построен центральный угол равный α .
Градусная мера дуги ∪ A B равна градусной мере дуги ∪ C D и равна α .
Но невооуруженным глазом видно, что длины дуг разные. Если градусная мера дуги окружности зависит только от величины центрального угла, который на неё опирается, то длина дуги окружности зависит ещё и от радиуса самой окружноси.
Длина окружности находится по формуле:
Длина дуги окружности , на которую опирается центральный угол α равна:
l α = π R 180 ∘ ⋅ α
Площадь круга и его частей
Теперь поговорим про площадь круга, площадь сектора и площадь сегмента.
Круг – часть пространства, которая находится внутри окружности.
Иными словами, окружность – это граница, а круг – это то, что внутри.
Примеры окружности в реальной жизни: велосипедное колесо, обруч, кольцо.
Примеры круга в реальной жизни: пицца, крышка от канализационного люка, плоская тарелка.
Площадь круга находится по формуле: S = π R 2
Сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Примеры сектора в реальной жизни: кусок пиццы, веер.
Площадь кругового сектора, ограниченного центральным углом α находится по формуле: S α = π R 2 360 ° ⋅ α
Сегмент – это часть круга, ограниченная дугой и хордой, стягивающей эту дугу.
Примеры сегмента в реальной жизни: мармелад “лимонная долька”, лук для стрельбы.
Чтобы найти площадь сегмента, нужно сперва вычислить площадь кругового сектора, который данный сегмент содержит, а потом вычесть площадь треугольника, который образован центральным углом и хордой.
S = π R 2 360 ° ⋅ α − 1 2 R 2 sin α
Теорема синусов
Если вокруг произвольного треугольника описана окружность, то её радиус можно найти при помощи теоремы синусов:
a sin ∠ A = b sin ∠ B = c sin ∠ C = 2 R Достаточно знать одну из сторон треугольника и синус угла, который напротив неё лежит. Из этих данных можно найти радиус описанной окружности.
Примеры решений заданий из ОГЭ
Модуль геометрия: задания, связанные с окружностями.
http://www.resolventa.ru/demo/diaggia6.htm
Задания
Версия для печати и копирования в MS Word
Тип 16 № 349689
i
На окружности с центром O отмечены точки A и B так, что
Длина меньшей дуги AB равна 67. Найдите длину большей дуги.
Спрятать решение
Решение.
Пусть длина большей дуги AB равна Длина дуги прямо пропорциональна её градусной мере, поэтому имеет место отношение:
Ответ: 134.
Аналоги к заданию № 333117: 339904 348493 348698 … Все
Раздел кодификатора ФИПИ: 5.1 Планиметрия. Нахождение геометрических величин.
Спрятать решение
·
Прототип задания
·
Помощь
Из условия задачи известно, на окружности, с центром О, отмечены точка А и В так, что угол АОВ равен 28 градусов. Длина меньшей дуги равна 63. Прежде, чем вычислять длину большей дуги, необходимо вычислить градусную меру большей дуги.
Вычисляем градусную меру большей дуги.
1) 360 — 28 = 332 (градуса) — градусная мера большей дуги.
Теперь, с помощью пропорции вычислим длину большей дуги.
63 — 28 градусов;
х — 332 градуса.
2) (63 * 332) : 28 = 747 — длина большей дуги.
Ответ: длина большей дуги равна 747.
№12. Четырехугольник A B C D вписан в окружность. Угол ∠ A B C равен 70 ° , угол ∠ C A D равен 49 ° . Найдите угол ∠ A B D .
Решение:
Оба вписанных угла ∠ D A C и ∠ D B C опираются на одну дугу ∪ D C .
Вписанные углы, опирающиеся на одну и ту же дугу, равны.
∠ D A C = ∠ D B C = 49 °
Рассмотрим △ A B C :
∠ A B D + ∠ D B C = ∠ A B C
∠ A B D + 49 ° = 70 °
∠ A B D = 70 ° − 49 °
∠ A B D = 21 °
Ответ: 21
№13. Окружность с центром в точке O описана около равнобедренного треугольника △ A B C , в котором A B = B C и ∠ A B C = 177 ° . Найдите величину угла ∠ B O C .
Решение:
∠ A B C – вписанный, опирается на дугу ∪ A C .
Вписанный угол равен половине градусной меры дуги, на которую он опирается.
∪ A C = 2 ⋅ ∠ A B C = 2 ⋅ 177 ° = 354 °
∪ A B C = 360 ° − 354 ° = 6 °
Дуги ∪ A B и ∪ B C равны, так как их стягивают равные хорды.
∪ A B = ∪ B C = ∪ A B C 2 = 6 ° 2 = 3 °
∠ B O C – центральный.
Центральный угол равен градусной мере дуги, на которую он опирается.
∠ B O C = ∪ B C = 3 °
Ответ: 3
№14. Боковая сторона равнобедренного треугольника равна 14. Угол при вершине, противолежащий основанию, равен 120 ° . Найдите диаметр окружности, описанной около этого треугольника.
Решение:
В равнобедренном треугольнике углы при основании равны.
∠ A = ∠ C = α
Сумма углов в треугольнике равна 180 ° .
α + α + 120 ° = 180 °
2 α = 180 ° − 120 °
2 α = 60 °
α = 30 °
Применим расширенную теорему синусов для стороны B C и угла ∠ B A C :
B C sin ∠ B A C = 2 R
14 0,5 = 2 R
2 R = 28
Поскольку диаметр окружности равен двум радиусам,
D = 2 R = 28
Ответ: 28
№15. В окружность вписан равносторонний восьмиугольник. Найдите величину угла ∠ A B C .
Решение:
Равные хорды стягивают равные дуги. Правильный восьмиугольник разбивает окружность на восемь равных дуг. Градусная мера одной дуги равна
360 ° 8 = 45 °
∠ A B C – вписанный, он равен половине градусной меры дуги, на которую он опирается.
∠ A B C = 45 ° + 45 ° + 45 ° + 45 ° 2 = 90 °
Ответ: 90
№16. Точки A, B, C и D лежат на одной окружности так, что хорды A B и C D взаимно перпендикулярны, а ∠ B D C = 25 ° . Найдите величину угла ∠ A B D .
Решение:
∠ B A O = ∠ B D C = 25 ° , так как они опираются на одну и ту же дугу d.
Рассмотрим треугольник △ A B O , он прямоугольный, поэтому:
∠ A B O + 25 ° + 90 ° = 180 °
∠ A B O = 180 ° − 90 ° − 25 ° = 65 °
Ответ: 65
№17. На окружности по разные стороны от диаметра A B взяты точки M и N. Известно, что ∠ N B A = 38 ° . Найдите угол ∠ N M B .
Решение:
∠ N M B = ∠ N A B , так как они опираются на одну и ту же дугу.
∠ N A B найдем из треугольника △ A N B .
Так как по условию задачи A B – диаметр, ∠ A N B = 90 ° , то есть △ A N B прямоугольный.
∠ N A B + 38 ° + 90 ° = 180 °
∠ N A B = 180 ° − 90 ° − 38 °
∠ N A B = 52 ° = ∠ N M B
Ответ: 52
№18. Треугольник △ A B C вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника △ A B C , если ∠ A O B = 115 ° .
Решение:
∠ A O B – центральный.
Градусная мера центрального угла равна градусной мере дуги, на которую он опирается.
Значит ∪ A B = 115 ° .
∠ A C B – вписанный, опирается на дугу ∪ A B
Вписанный угол равен половине градусной меры дуги, на которую он опирается.
∠ A C B = ∪ A B 2 = 115 ° 2 = 57,5 °
Ответ: 57,5
№19. На окружности с центром O отмечены точки A и B так, что ∠ A O B = 120 ° . Длина меньшей дуги ∪ A B равна 67. Найдите длину большей дуги.
Решение:
1 способ:
Обозначим большую дугу за l.
Длина дуги окружности, на которую опирается центральный угол α равна:
l α = π R 180 ∘ ⋅ α
∪ A B = π R 180 ° 3 ⋅ 120 ° 2 = 67
2 π R 3 = 67 ⇒ π R = 3 ⋅ 67 2
Центральный угол, который опирается на большую дугу l равен 360 ° − 120 ° = 240 ° .
Найдем длину дуги l по формуле:
l = π R 180 ° ⋅ 240 ° = 3 ⋅ 67 2 ⋅ 240 ° 4 180 ° 3 = 3 ⋅ 67 2 ⋅ 4 2 3 = 67 ⋅ 2 = 134
2 способ:
На большую дугу опирается угол в 240 ° , он в два раза больше, чем угол, который опирается на меньшую дугу. Значит длина большей дуги будет в два раза больше, чем длина меньшей дуги.
l = 2 ⋅ 67 = 134
Ответ: 134
№20. A C и B D – диаметры окружности с центром O. ∠ A C B = 78 ° . Найдите угол ∠ A O D .
Решение:
∠ A O D = ∠ B O C , так как они вертикальные.
Рассмотрим треугольник △ B O C . Он равнобедренный, O B = O C , так как они являются радиусами окружности.
Раз △ B O C равнобедренный, справедливо равенство: ∠ C B O = ∠ B C O = 78 ° .
∠ B O C + 78 ° + 78 ° = 180 °
∠ B O C = 180 ° − 78 ° − 78 °
∠ B O C = 24 °
Ответ: 24
№21. Центр окружности, описанной около треугольника △ A B C , лежит на стороне A B . Найдите угол ∠ A B C , если ∠ B A C = 24 ° .
Решение:
Центр окружности лежит на стороне A B , значит A B – диаметр окружности, тогда ∠ A C B = 90 ° , так как является вписанным углом, опирающимся на дугу в 180 ° .
∠ A B C + 24 ° + 90 ° = 180 °
∠ A B C = 180 ° − 90 ° − 24 °
∠ A B C = 66 °
Ответ: 66
№22. В угол ∠ C = 71 ° вписана окружность, которая касается сторон угла в точках A и B, точка O – центр окружности. Найдите угол ∠ A O B .
Решение:
O A и O B – радиусы окружности, которые проведены к точкам касания A и B соответственно.
Радиус, проведенный к точке касания, образует с касательной прямой угол.
Рассмотрим четырехугольник A B C D .
Сумма углов в четырехугольнике равна 360 ° .
∠ A O B + 71 ° + 90 ° + 90 ° = 360 °
∠ A O B = 360 ° − 90 ° − 90 ° − 71 °
∠ A O B = 109 °
Ответ: 109
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Нахождение длины окружности и площади круга
(blacktriangleright) Длина окружности равна (large{C=2pi R}), а в градусной мере составляет (360^circ).
(blacktriangleright) Длина дуги окружности равна (large{C_{alpha}=dfrac{2pi R}{360}cdot alpha}), где (alpha) – угол в градусах, задающий данную дугу (центральный угол, опирающийся на дугу).
(blacktriangleright) Площадь круга равна (large{S=pi R^2}).
(blacktriangleright) Площадь сектора круга равна (large{S_{alpha}=dfrac{pi R^2}{360}cdot alpha}), где (alpha) – угол в градусах, задающий данный сектор.
Задание
1
#2953
Уровень задания: Равен ЕГЭ
На клетчатой бумаге нарисован круг площадью (2,8). Найдите площадь закрашенного сектора.
Заметим, что закрашенная фигура состоит из двух непересекающихся частей, равных (frac14) и (frac12) от (frac14) круга:
Таким образом, ее площадь равна [dfrac14S+dfrac12cdot left(dfrac14Sright)=dfrac38S=dfrac38cdot 2,8=1,05.]
Ответ: 1,05
Задание
2
#302
Уровень задания: Равен ЕГЭ
Длина окружности с центром в точке (O) равна 12. (angle AOB = 120^{circ}), точки (A) и (B) лежат на окружности и разбивают её на две дуги. Во сколько раз длина большей из получившихся дуг превосходит длину меньшей?
Длины дуг относятся так же, как их градусные меры. Так как (O) – центр окружности, то (angle AOB) – центральный.
Градусная мера дуги, меньшей, чем полуокружность, есть градусная мера центрального угла, который на неё опирается. Тогда градусная мера меньшей из дуг равна (120^{circ}), а большей из дуг (240^{circ}).
Градусная мера большей дуги в (240 : 120 = 2) раза больше, чем градусная мера меньшей дуги.
Ответ: 2
Задание
3
#1735
Уровень задания: Равен ЕГЭ
Найдите (angle AOB).
Длина всей окружности складывается из длин составляющих ее дуг (С = 1 + 2 + 5 + 10 = 18). Тогда (frac{C_{angle AOB}}{C} = frac{angle AOB}{360^circ}) (Rightarrow) (frac{5}{18} = frac{angle AOB}{360^circ}) (Rightarrow) (angle AOB = 100^circ).
Ответ: 100
Задание
4
#1791
Уровень задания: Равен ЕГЭ
Длина окружности с центром в точке (O) равна 18 см. Площадь сектора (AOB) равна (dfrac{18}{pi})см(^2). Найдите длину дуги (AB) этого сектора. Ответ дайте в сантиметрах.
Длина окружности равна (2pi R), где (R) – радиус этой окружности. Для данной окружности (2pi R = 18) см, тогда (R = dfrac{9}{pi}) см.
Площадь сектора, градусная мера дуги которого есть (alpha) равна (pi R^2 cdot dfrac{alpha}{360}).
Длина дуги с градусной мерой (alpha) равна (2pi Rcdot dfrac{alpha}{360}).
Из этих формул видно, что длина дуги с градусной мерой (alpha) получится из площади сектора, градусная мера дуги которого есть (alpha), при помощи умножения этой площади на (dfrac{2}{R}).
Длина дуги (AB) данного сектора равна (dfrac{18}{pi} cdot
dfrac{2pi}{9} = 4) см.
Ответ: 4
Задание
5
#304
Уровень задания: Равен ЕГЭ
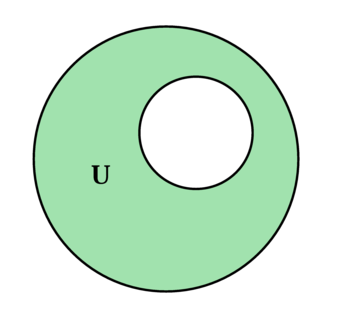
Внутри большой окружности расположена маленькая, радиус которой в 2,5 раза меньше, чем радиус большой окружности. Найдите отношение площади зеленой области (U) к площади круга, ограниченного большой окружностью.
Обозначим радиус меньшей из окружностей за (r), тогда радиус большей окружности (2,5cdot r).
Площадь круга, ограниченного окружностью радиуса (R), равна (pi R^2).
Площадь меньшего круга равна (pi r^2), а площадь большего равна (pi cdot (2,5r)^2 = 6,25pi r^2).
Площадь области (U) равна разности площадей большего и меньшего кругов и равна (6,25pi r^2 — pi r^2 = 5,25pi r^2).
Искомое отношение площадей есть (dfrac{5,25pi r^2}{6,25pi r^2} = 0,84).
Ответ: 0,84
Задание
6
#1733
Уровень задания: Равен ЕГЭ
Две окружности касаются внутренним образом так, что один из радиусов большей окружности совпадает с диаметром меньшей окружности (смотри рисунок). Найдите радиус большей окружности, если площадь зеленой области равна (48pi).
Обозначим за (R) – радиус большей окружности и одновременно диаметр меньшей. Тогда площадь зеленой области (S) можно выразить через площади кругов следующим образом: (S = pi R^2 — frac{pi R^2}{4} = frac{3}{4}pi R^2). Т.к. (S = 48pi) (Rightarrow) (frac{3}{4}pi R^2 = 48pi) (Rightarrow) (R^2 = 64) (Rightarrow) (R = 
Ответ: 8
Задание
7
#1732
Уровень задания: Сложнее ЕГЭ
На рисунке изображены две окружности с общим центром (O), где радиусы (OB = 3) и (OA = 1), а угол (angle BOD = 90^circ). Найдите площадь фигуры (ABCDEFA) деленную на (pi).
Площадь сектора с углом (90^circ) в большой окружности равна (S_{big} = frac{picdot3^2}{360^circ}cdot90^circ = frac{9pi}{4}), а в маленькой (S_{small} = frac{picdot1^2}{360^circ}cdot90^circ = frac{pi}{4}). Тогда (frac{S_{ABCDEFA}}{pi} = frac{S_{big} — S_{small}}{pi} = 2).
Ответ: 2
Задачи на нахождение площади круга — обязательная часть ЕГЭ по математике. Как правило, этой теме отводится сразу несколько заданий в аттестационном испытании. Понимать алгоритм нахождения длины окружности и площади круга должны все старшеклассники, независимо от уровня их подготовки.
Если подобные планиметрические задачи вызывают у вас затруднения, рекомендуем обратиться к образовательному порталу «Школково». С нами вы сможете восполнить пробелы в знаниях.
В соответствующем разделе сайта представлена большая подборка задач на нахождение длины окружности и площади круга, подобных тем, которые включены в ЕГЭ. Научившись их правильно выполнять, выпускник сможет успешно справиться с экзаменом.
Основные моменты
Задачи, в которых требуется применить формулы площади, могут быть прямыми и обратными. В первом случае известны параметры элементов фигуры. При этом искомой величиной является площадь. Во втором случае, наоборот, площадь известна, а найти необходимо какой-либо элемент фигуры. Алгоритм вычисления правильного ответа в подобных заданиях различается только порядком применения базовых формул. Именно поэтому, приступая к решению таких задач, необходимо повторить теоретический материал.
На образовательном портале «Школково» представлена вся базовая информация по теме «Нахождение длины окружности или дуги и площади круга», а также по другим темам, например, «Центральный угол окружности». Ее наши специалисты подготовили и изложили в максимально доступной форме.
Вспомнив основные формулы, учащиеся могут приступить к выполнению задач на нахождение площади круга, подобных тем, которые включены в ЕГЭ, в режиме онлайн. Для каждого упражнения на сайте представлено подробное решение и дан правильный ответ. При необходимости любое задание можно сохранить в разделе «Избранное», чтобы в дальнейшем вернуться к нему и обсудить с преподавателем.

УСТАЛ? Просто отдохни