Задача 11797 В равностороннем треугольнике АВС…
Условие
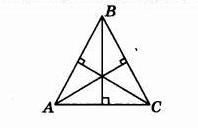
В равностороннем треугольнике АВС найдите величину острого угла между его высотами.
математика 8-9 класс
20205
Решение
Тогда угол между высотами будет равен 90 — 60 :2 = 90 — 30 = 60 (градусов).
Ответ: 60
Все решения

Точка пересечения высот треугольника является вершиной шести равных углов, сумма которых равна 360*. Отсюда искомый угол равен 360*:6=60*
Ответ: 60*
Написать комментарий
Углы равностороннего треугольника
Чему равны углы равностороннего треугольника?
(свойство углов равностороннего треугольника)
Все углы равностороннего треугольника равны по 60º.
Аналогично, так как AC=BC, ∠A=∠B.
Отсюда следует, что в равностороннем треугольнике все углы равны между собой: ∠A=∠B=∠C
Так как сумма углов треугольника равна 180º, то ∠A=∠B=∠C=180º:3=60º, то есть каждый угол равностороннего треугольника равен 60º.
Что и требовалось доказать .
Тот факт, что все углы равностороннего треугольника равны между собой, можно рассмотреть также как следствие из теоремы о соотношении между сторонами и углами треугольника. В треугольнике напротив большей стороны лежит больший угол, напротив меньшей стороны — меньший угол. Так как все три стороны правильного треугольника равны, то и все углы тоже равны.
Свойства равностороннего треугольника: теория и пример задачи
В данной статье мы рассмотрим определение и свойства равностороннего (правильного) треугольника. Также разберем пример решения задачи для закрепления теоретического материала.
Определение равностороннего треугольника
Равносторонним (или правильным) называется треугольник, в котором все стороны имеют одинаковую длину. Т.е. AB = BC = AC.
Примечание: правильный многоугольник – это выпуклый многоугольник, имеющий равные стороны и углы между ними.
Свойства равностороннего треугольника
Свойство 1
В равностороннем треугольнике все углы равны 60°. Т.е. α = β = γ = 60°.
Свойство 2
В равностороннем треугольнике высота, проведенная к любой из сторон, одновременно является биссектрисой угла, из которого она проведена, а также медианой и серединным перпендикуляром.
CD – медиана, высота и серединный перпендикуляр к стороне AB, а также биссектриса угла ACB.
Свойство 3
В равностороннем треугольнике биссектрисы, медианы, высоты и серединные перпендикуляры, проведенные ко всем сторонам, пересекаются в одной точке.
Свойство 4
Центры вписанной и описанной вокруг равностороннего треугольника окружностей совпадают и находятся на пересечении медиан, высот, биссектрис и серединных перпендикуляров.
Свойство 5
Радиус описанной вокруг равностороннего треугольника окружности в 2 раза больше радиуса вписанной окружности.
- R – радиус описанной окружности;
- r – радиус вписанной окружности;
- R = 2r.
Свойство 6
В равностороннем треугольнике, зная длину стороны (условно примем ее за “a”), можно вычислить:
1. Высоту/медиану/биссектрису:
2. Радиус вписанной окружности:
3. Радиус описанной окружности:
4. Периметр:
5. Площадь:
Пример задачи
Дан равносторонний треугольник, сторона которого равна 7 см. Найдите радиус описанной вокруг и вписанной окружности, а также, высоту фигуры.
Решение
Применим формулы, приведеные выше, для нахождения неизвестных величин:
Решение треугольников онлайн
С помощю этого онлайн калькулятора можно решить треугольники, т.е. найти неизвестные элементы (стороны, углы) треугольника. Теоретическую часть и численные примеры смотрите ниже.
Решение треугольников − это нахождение всех его элементов (трех сторон и трех углов) по трем известным элементам (сторонам и углам). В статье Треугольники. Признаки равенства треугольников рассматриваются условия, при которых два треугольника оказываются равными друг друга. Как следует из статьи, треугольник однозначно определяется тремя элементами. Это:
- Три стороны треугольника.
- Две стороны треугольника и угол между ними.
- Две стороны и угол противостоящий к одному из этих сторон треугольника.
- Одна сторона и любые два угла.
Заметим, что если у треугольника известны два угла, то легко найти третий угол, т.к. сумма всех углов треугольника равна 180°.
Решение треугольника по трем сторонам
Пусть известны три стороны треугольника a, b, c (Рис.1). Найдем 
 |
(1) |
 |
(2) |
Из (1) и (2) находим cosA, cosB и углы A и B (используя калькулятор). Далее, угол C находим из выражения

Пример 1. Известны стороны треугольника ABC: 

Решение. Из формул (1) и (2) находим:
И, наконец, находим угол C:
Решение треугольника по двум сторонам и углу между ними
Пусть известны стороны треугольника a и b и угол между ними C (Рис.2). Найдем сторону c и углы A и B.
Найдем сторону c используя теорему косинусов:


Далее, из формулы

 . . |
(3) |
Далее из (3) с помощью калькулятора находим угол A.
Поскольку уже нам известны два угла то находим третий:

Пример 2. Известны две стороны треугольника ABC: 

Решение. Иcпользуя теорму косинусов найдем сторону c:

Из формулы (3) найдем cosA:

Поскольку уже нам известны два угла то находим третий:
Решение треугольника по стороне и любым двум углам
Пусть известна сторона треугольника a и углы A и B (Рис.4). Найдем стороны b и c и угол C.
Так как, уже известны два угла, то можно найти третий:

Далее, для находждения сторон b и c воспользуемся тероемой синусов:
Пример 3. Известна одна сторона треугольника ABC: 

Решение. Поскольку известны два угла, то легко можно найти третий угол С:
Найдем сторону b. Из теоремы синусов имеем:
Найдем сторону с. Из теоремы синусов имеем:
Свойства равностороннего треугольника: теория и пример задачи
http://matworld.ru/geometry/reshenie-treugolnikov.php
Информация по назначению калькулятора
Треугольник — это одна из основных геометрических фигур: многоугольник с тремя углами (или вершинами) и тремя сторонами (или ребрами), которые являются прямыми отрезками.
В евклидовой геометрии любые три неколлинеарные точки определяют треугольник и единственную плоскость, то есть двумерное декартово пространство.
Сумма длин любых двух сторон треугольника всегда превышает длину третьей стороны. Это и есть неравенство треугольника.
Треугольники могут быть классифицированы в соответствии с относительной длиной их сторон:
⇒ В равностороннем треугольнике все стороны имеют одинаковую длину. Равносторонний треугольник также является равноугольным многоугольником, т.е. все его внутренние углы равны, а именно 60° — это правильный многоугольник.
⇒ В равнобедренном треугольнике две стороны имеют одинаковую длину. Равнобедренный треугольник также имеет два совпадающих угла (а именно, углы, противоположные совпадающим сторонам). Равносторонний треугольник — это равнобедренный треугольник, но не все равнобедренные треугольники являются равносторонними треугольниками.
⇒ В скалярном треугольнике все стороны имеют разную длину. Внутренние углы в скалярном треугольнике все разные.
Треугольники также могут быть классифицированы в соответствии с их внутренними углами:
⇒ Прямоугольный треугольник имеет один внутренний угол 90° (прямой угол). Сторона, противоположная прямому углу, является гипотенузой; это самая длинная сторона в прямоугольном треугольнике. Две другие стороны — катеты треугольника.
⇒ Тупой треугольник имеет один внутренний угол, больший 90° (тупой угол).
⇒ Острый треугольник имеет внутренние углы, которые все меньше 90° (три острых угла). Равносторонний треугольник — это острый треугольник, но не все острые треугольники являются равносторонними треугольниками.
⇒ Наклонный треугольник имеет только углы, которые меньше или больше 90°. Следовательно, это любой треугольник, который не является прямоугольным треугольником.
Онлайн калькулятор поможет найти параметры треугольника, такие как:
- Длины сторон
- Углы
- Высота
- Периметр
- Площадь
- Медианы
- Биссектрисы
- Радиус Вписанной и Описанной окружностей
- Диаметр Вписанной и Описанной окружностей
- Длина Вписанной и Описанной окружностей
- Площадь Вписанной и Описанной окружностей
— равны в равностороннем треугольнике
— также равны в равностороннем треугольнике
— это прямая линия, проходящая через вершину и перпендикулярная противоположной стороне (т. е. образующая прямой угол с ней)
— равен сумме всех 3х сторон (P=AB+BC+AC)
— равна половине произведения высоты и стороны к которой построена высота (S=1/2 * H * AC)
Ответ: 120° — угол между высотами
Пошаговое объяснение:
Рисунок к задаче в приложении.
1. У равностороннего треугольника АВС все углы по 60°.
2. Точка пересечения высот — О. Получили треугольник ΔAOB.
3. Высота в таком треугольнике является и биссектрисой.
∠DAB = ∠ABF = 30°
4. Сумма углов в треугольнике равна 180 градусов.
Угол между высотами
∠АОВ = 180° — 2*30° = 180° — 60° = 120° — ответ
Чему равны углы равностороннего треугольника?
Теорема
(свойство углов равностороннего треугольника)
Все углы равностороннего треугольника равны по 60º.

AB=BC=AC
Доказать: ∠A=∠B=∠C=60º.
Доказательство:
Так как AB=BC, ∠A=∠C (как углы при основании равнобедренного треугольника).
Аналогично, так как AC=BC, ∠A=∠B.
Отсюда следует, что в равностороннем треугольнике все углы равны между собой: ∠A=∠B=∠C
Так как сумма углов треугольника равна 180º, то ∠A=∠B=∠C=180º:3=60º, то есть каждый угол равностороннего треугольника равен 60º.
Что и требовалось доказать.
Замечание.
Тот факт, что все углы равностороннего треугольника равны между собой, можно рассмотреть также как следствие из теоремы о соотношении между сторонами и углами треугольника. В треугольнике напротив большей стороны лежит больший угол, напротив меньшей стороны — меньший угол. Так как все три стороны правильного треугольника равны, то и все углы тоже равны.


















