Угловой коэффициент прямой. В этой статье мы с вами рассмотрим задачи связанные с координатной плоскостью включённые в ЕГЭ по математике. Это задания на:
— определение углового коэффициента прямой, когда известны две точки через которые она проходит;
— определение абсциссы или ординаты точки пересечения двух прямых на плоскости.
Что такое абсцисса и ордината точки было описано в данной рубрики. В ней мы уже рассмотрели несколько задач связанных с координатной плоскостью. Что необходимо понимать для рассматриваемого типа задач? Немного теории.
Уравнение прямой на координатной плоскости имеет вид:
где
k
–
это и есть угловой коэффициент прямой.
Следующий момент! Угловой коэффициент прямой равен тангенсу угла наклона прямой. Это угол между данной прямой и осью
ох.
Он лежит в пределах от 0 до 180 градусов.
То есть, если мы приведём уравнение прямой к виду y
=
kx
+
b
, то далее всегда сможем определить коэффициент k (угловой коэффициент).
Так же, если мы исходя из условия сможем определить тангенс угла наклона прямой, то тем самым найдём её угловой коэффициент.
Следующий теоретический момент!
Уравнение прямой походящей через две данные точки.
Формула имеет вид:
Рассмотрим задачи (аналогичные задачам из открытого банка заданий):
Найдите угловой коэффициент прямой, проходящей через точки с координатами (–6;0) и (0;6).
В данной задаче самый рациональный путь решения это найти тангенс угла между осью ох и данной прямой. Известно, что он равен угловому коэффициенту. Рассмотрим прямоугольный треугольник образованный прямой и осями ох и оу:
Тангенсом угла в прямоугольном треугольнике является отношение противолежащего катета к прилежащему:

Конечно, данную задачу можно решить используя формулу нахождения уравнения прямой проходящей через две данные точки. Но это будет более длительный путь решения.
Ответ: 1
Найдите угловой коэффициент прямой, проходящей через точки с координатами (5;0) и (0;5).
Наши точки имеют координаты (5;0) и (0;5). Значит,
Приведём формулу к виду y
=
kx
+
b
Получили, что угловой коэффициент k
= – 1.
Ответ: –1
Прямая a
проходит через точки с координатами (0;6) и (8;0). Прямая b
проходит через точку с координатами (0;10) и параллельна прямой a
b
с осью оx.
В данной задаче можно найти уравнение прямой a
, определить угловой коэффициент для неё. У прямой b
угловой коэффициент будет такой же, так как они параллельны. Далее можно найти уравнение прямой b
. А затем, подставив в него значение y = 0, найти абсциссу. НО!
В данном случае, проще использовать свойство подобия треугольников.
Прямоугольные треугольники, образованные данными (параллельными) прямыми о осями координат подобны, а это значит, что отношения их соответствующих сторон равны.
Искомая абсцисса равна 40/3.
Ответ: 40/3
Прямая a
проходит через точки с координатами (0;8) и (–12;0). Прямая b
проходит через точку с координатами (0; –12) и параллельна прямой a
. Найдите абсциссу точки пересечения прямой b
с осью оx
.
Для данной задачи самый рациональный путь решения — это применение свойства подобия треугольников. Но мы решим её другим путём.
Нам известны точки, через которые проходит прямая а
. Можем составить уравнение прямой. Формула уравнения прямой походящей через две данные точки имеет вид:
По условию точки имеют координаты (0;8) и (–12;0). Значит,
Приведём к виду y
=
kx
+
b
:
Получили, что угловой k
= 2/3.
*Угловой коэффициент можно было найти через тангенс угла в прямоугольном треугольнике с катетами 8 и 12.
Известно, у параллельных прямых угловые коэффициенты равны. Значит уравнение прямой проходящей через точку (0;-12) имеет вид:
Найти величину b
мы можем подставив абсциссу и ординату в уравнение:
Таким образом, прямая имеет вид:
Теперь чтобы найти искомую абсциссу точки пересечения прямой с осью ох, необходимо подставить у = 0:
Ответ: 18
Найдите ординату точки пересечения оси оy
и прямой, проходящей через точку В(10;12) и параллельной прямой, проходящей через начало координат и точку А(10;24).
Найдём уравнение прямой проходящей через точки с координатами (0;0) и (10;24).
Формула уравнения прямой походящей через две данные точки имеет вид:
Наши точки имеют координаты (0;0) и (10;24). Значит,
Приведём к виду y
=
kx
+
b
Угловые коэффициенты параллельных прямых равны. Значит, уравнение прямой, проходящей через точку В(10;12) имеет вид:
Значение b
найдём подставив в это уравнение координаты точки В(10;12):
Получили уравнение прямой:
Чтобы найти ординату точки пересечения этой прямой с осью оу
нужно подставить в найденное уравнение х
= 0:
*Самый простой способ решения. При помощи параллельного переноса сдвигаем данную прямую вниз вдоль оси оу
до точки (10;12). Сдвиг происходит на 12 единиц, то есть точка А(10;24) «перешла» в точку В(10;12), а точка О(0;0) «перешла» в точку (0;–12). Значит, полученная прямая будет пересекать ось оу
в точке (0;–12).
Искомая ордината равна –12.
Ответ: –12
Найдите ординату точки пересечения прямой, заданной уравнением
3х
+
2у = 6
, с осью
Oy
.
Координата точки пересечения заданной прямой с осью оу
имеет вид (0;у
). Подставим в уравнение абсциссу х
= 0, и найдём ординату:
Ордината точки пересечения прямой с осью оу
равна 3.
*Решается система:
Ответ: 3
Найдите ординату точки пересечения прямых, заданных уравнениями
3х + 2у = 6
и
у = – х
.
Когда заданны две прямые, и стоит вопрос о нахождении координат точки пересечения этих прямых, решается система из данных уравнений:
В первом уравнении подставляем – х
вместо у
:
Ордината равна минус шести.
Ответ: –
6
Найдите угловой коэффициент прямой, проходящей через точки с координатами (–2;0) и (0;2).
Найдите угловой коэффициент прямой, проходящей через точки с координатами (2;0) и (0;2).
Прямая a проходит через точки с координатами (0;4) и (6;0). Прямая b проходит через точку с координатами (0;8) и параллельна прямой a. Найдите абсциссу точки пересечения прямой b с осью Ox.

1. Необходимо чётко усвоить, что угловой коэффициент прямой равен тангенсу угла наклона прямой. Это поможет вам при решении многих задач данного типа.
2. Формулу нахождения прямой проходящей через две данные точки нужно понимать обязательно. С её помощью всегда найдёте уравнение прямой, если даны координаты двух её точек.
3. Помните о том, что угловые коэффициенты параллельных прямых равны.
4. Как вы поняли, в некоторых задачах удобно использовать признак подобия треугольников. Задачи решаются практически устно.
5. Задачи в которых даны две прямые и требуется найти абсциссу или ординату точки их пересечения можно решить графическим способом. То есть, построить их на координатной плоскости (на листе в клетку) и определить точку пересечения визуально. *Но этот способ применим не всегда.
6. И последнее. Если дана прямая и координаты точек её пересечения с осями координат, то в таких задачах удобно находить угловой коэффициент через нахождение тангенса угла в образованном прямоугольном треугольнике. Как «увидеть» этот треугольник при различных расположениях прямых на плоскости схематично показано ниже:
>> Угол наклона прямой от 0 до 90 градусов <<
>> Угол наклона прямой от 90 до 180 градусов <<
На этом всё. Успеха Вам!
С уважением, Александр.
P.S: Буду благодарен Вам, если расскажете о сайте в социальных сетях.
Теме «Угловой коэффициент касательной как тангенс угла наклона» в аттестационном экзамене отводится сразу несколько заданий. В зависимости от их условия, от выпускника может требоваться как полный ответ, так и краткий. При подготовке к сдаче ЕГЭ по математике ученику обязательно стоит повторить задачи, в которых требуется вычислить угловой коэффициент касательной.
Сделать это вам поможет образовательный портал «Школково». Наши специалисты подготовили и представили теоретический и практический материал максимально доступно. Ознакомившись с ним, выпускники с любым уровнем подготовки смогут успешно решать задачи, связанные с производными, в которых требуется найти тангенс угла наклона касательной.
Основные моменты
Для нахождения правильного и рационального решения подобных заданий в ЕГЭ необходимо вспомнить базовое определение: производная представляет собой скорость изменения функции; она равна тангенсу угла наклона касательной, проведенной к графику функции в определенной точке. Не менее важно выполнить чертеж. Он позволит найти правильное решение задач ЕГЭ на производную, в которых требуется вычислить тангенс угла наклона касательной. Для наглядности лучше всего выполнить построение графика на плоскости ОХY.
Если вы уже ознакомились с базовым материалом на тему производной и готовы приступить к решению задач на вычисление тангенса угла наклона касательной, подобных заданиям ЕГЭ, сделать это можно в режиме онлайн. Для каждого задания, например, задач на тему «Связь производной со скоростью и ускорением тела» , мы прописали правильный ответ и алгоритм решения. При этом учащиеся могут попрактиковаться в выполнении задач различного уровня сложности. В случае необходимости упражнение можно сохранить в разделе «Избранное», чтобы потом обсудить решение с преподавателем.
Прямая y=f(x) будет касательной к изображенному на рисунке графику в точке х0 в том случае, если она проходит через точку с координатами (х0; f(x0)) и обладает угловым коэффициентом f»(x0). Найти такой коэффициент, зная особенности касательной, несложно.
Вам понадобится
- — математический справочник;
- — простой карандаш;
- — тетрадь;
- — транспортир;
- — циркуль;
- — ручка.
Инструкция
Если значения f‘(x0) не существует, то либо касательной нет, либо она проходит вертикально. Ввиду этого, наличие производной функции в точке х0 обусловлено существованием невертикальной касательной, соприкасающейся с графиком функции в точке (х0, f(х0)). В этом случае угловой коэффициент касательной равен будет f»(х0). Таким образом, становится ясен геометрический смысл производной – расчет углового коэффициента касательной.
Изобразите на дополнительные касательные, которые бы соприкасались с графиком функции в точках x1, х2 и х3, а также отметьте углы, образуемые этими касательными с осью абсцисс (такой угол отсчитывают в положительном направлении от оси до касательной прямой). К примеру, угол, то есть, α1, будет острым, второй (α2) – тупой, а третий (α3) равен нулю, поскольку касательная прямая параллельна оси ОХ. В таком случае тангенс тупого угла – отрицательное , тангенс острого угла – положительное, а при tg0 результат равен нулю.
Обратите внимание
Правильно определите угол, образуемый касательной. Для этого используйте транспортир.
Полезный совет
Две наклонные прямые будут параллельными в том случае, если их угловые коэффициенты равны между собой; перпендикулярными, если произведение угловых коэффициентов этих касательных равно -1.
Источники:
- Касательная к графику функции
Косинус, как и синус, относят к «прямым» тригонометрическим функциям. Тангенс (вместе с котангенсом) причисляют к другой паре, называемой «производными». Существует несколько определений этих функций, которые делают возможным нахождение тангенса заданного по известному значению косинуса от этой же величины.
Инструкция
Вычтите частное от единицы на возведенное в значение косинуса заданного угла, а из результата извлеките квадратный корень — это и будет значение тангенса от угла, выраженное его косинус: tg(α)=√(1-1/(cos(α))²). При этом обратите внимание на то, что в формуле косинус стоит в знаменателе дроби. Невозможность деления на ноль исключает использование этого выражения для углов, равных 90°, а также отличающихся от этой величины на числа, кратные 180° (270°, 450°, -90° и т.д.).
Существует и альтернативный способ вычисления тангенса по известному значению косинуса. Его можно применять, если не установлено ограничение на использование других . Для реализации этого способа сначала определите величину угла по известному значению косинуса — это можно сделать с помощью функции арккосинус. Затем просто рассчитайте тангенс для угла полученной величины. В общем виде этот алгоритм можно записать так: tg(α)=tg(arccos(cos(α))).
Есть и еще экзотический вариант с использованием определения косинуса и тангенса через острые углы прямоугольного треугольника. Косинусу в таком определении соответствует отношение длины прилежащего к рассматриваемому углу катета к длине гипотенузы. Зная значение косинуса можно подобрать соответствующие ему длины этих двух сторон. Например, если cos(α)=0,5, то прилежащий можно принять равным 10см, а гипотенузу — 20см. Конкретные числа здесь значения не имеют — одинаковое и правильное вы получите с любыми значениями, имеющими же . Затем по теореме Пифагора определите длину недостающей стороны — противолежащего катета. Она будет равна квадратному корню из разницы между длинами возведенных в квадрат гипотенузы и известного катета: √(20²-10²)=√300. Тангенсу по определению соответствует отношение длин противолежащего и прилежащего катетов (√300/10) — рассчитайте его и получите значение тангенса, найденное с использованием классического определения косинуса.
Источники:
- косинус через тангенс формула
Одна из тригонометрических функций, чаще всего обозначаемая буквами tg, хотя встречаются и обозначения tan. Проще всего представить тангенс как отношение синуса угла
к его косинусу. Это нечетная периодическая и не непрерывная функция, каждый цикл которой равен числу Пи, а точка разрыва соответствует отметке в половину этого числа.
В предыдущей главе было показано, что, выбрав определенную систему координат на плоскости, мы можем геометрическое свойства, характеризующее точки рассматриваемой линии, выразить аналитически уравнением между текущими координатами. Таким образом, мы получим уравнение линии. В этой главе будут рассматриваться уравнения прямых линий.
Чтобы составить уравнение прямой в декартовых координатах, нужно каким-то образом задать условия, определяющие положение ее относительно координатных осей.
Предварительно мы введем понятие об угловом коэффициенте прямой, который является одной из величин, характеризующих положение прямой на плоскости.
Назовем углом наклона прямой к оси Ох тот угол, на который нужно повернуть ось Ох, чтобы она совпала с данной прямой (или оказалась параллельной ей). Как обычно, угол будем рассматривать с учетом знака (знак определяется направлением поворота: против или по часовой стрелке). Так как добавочный поворот оси Ох на угол в 180° снова совместит ее с прямой, то угол наклона прямой к оси может быть выбран не однозначно (с точностью до слагаемого, кратного ).
Тангенс этого угла определяется однозначно (так как изменение угла на не меняет его тангенса).
Тангенс угла наклона прямой к оси Ох называется угловым коэффициентом прямой.
Угловой коэффициент характеризует направление прямой (мы здесь не различаем двух взаимно противоположных направлений прямой). Если угловой коэффициент прямой равен нулю, то прямая параллельна оси абсцисс. При положительном угловом коэффициенте угол наклона прямой к оси Ох будет острым (мы рассматриваем здесь наименьшее положительное значение угла наклона) (рис. 39); при этом чем больше угловой коэффициент, тем больше угол ее наклона к оси Ох. Если угловой коэффициент отрицателен, то угол наклона прямой к оси Ох будет тупым (рис. 40). Заметим, что прямая, перпендикулярная к оси Ох, не имеет углового коэффициента (тангенс угла не существует).
Производная функции — одна из сложных тем в школьной программе. Не каждый выпускник ответит на вопрос, что такое производная.
В этой статье просто и понятно рассказано о том, что такое производная и для чего она нужна
. Мы не будем сейчас стремиться к математической строгости изложения. Самое главное — понять смысл.
Запомним определение:
Производная — это скорость изменения функции.
На рисунке — графики трех функций. Как вы думаете, какая из них быстрее растет?
Ответ очевиден — третья. У нее самая большая скорость изменения, то есть самая большая производная.
Вот другой пример.
Костя, Гриша и Матвей одновременно устроились на работу. Посмотрим, как менялся их доход в течение года:
На графике сразу все видно, не правда ли? Доход Кости за полгода вырос больше чем в два раза. И у Гриши доход тоже вырос, но совсем чуть-чуть. А доход Матвея уменьшился до нуля. Стартовые условия одинаковые, а скорость изменения функции, то есть производная
, — разная. Что касается Матвея — у его дохода производная вообще отрицательна.
Интуитивно мы без труда оцениваем скорость изменения функции. Но как же это делаем?
На самом деле мы смотрим, насколько круто идет вверх (или вниз) график функции. Другими словами — насколько быстро меняется у с изменением х. Очевидно, что одна и та же функция в разных точках может иметь разное значение производной — то есть может меняться быстрее или медленнее.
Производная функции обозначается .
Покажем, как найти с помощью графика.
Нарисован график некоторой функции . Возьмем на нем точку с абсциссой . Проведём в этой точке касательную к графику функции. Мы хотим оценить, насколько круто вверх идет график функции. Удобная величина для этого — тангенс угла наклона касательной
.
Производная функции в точке равна тангенсу угла наклона касательной, проведённой к графику функции в этой точке.
Обратите внимание — в качестве угла наклона касательной мы берем угол между касательной и положительным направлением оси .
Иногда учащиеся спрашивают, что такое касательная к графику функции. Это прямая, имеющая на данном участке единственную общую точку с графиком, причем так, как показано на нашем рисунке. Похоже на касательную к окружности.
Найдем . Мы помним, что тангенс острого угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему. Из треугольника :
Мы нашли производную с помощью графика, даже не зная формулу функции. Такие задачи часто встречаются в ЕГЭ по математике под номером .
Есть и другое важное соотношение. Вспомним, что прямая задается уравнением
Величина в этом уравнении называется угловым коэффициентом прямой
. Она равна тангенсу угла наклона прямой к оси .
.
Мы получаем, что
Запомним эту формулу. Она выражает геометрический смысл производной.
Производная функции в точке равна угловому коэффициенту касательной, проведенной к графику функции в этой точке.
Другими словами, производная равна тангенсу угла наклона касательной.
Мы уже сказали, что у одной и той же функции в разных точках может быть разная производная. Посмотрим, как же связана производная с поведением функции.
Нарисуем график некоторой функции . Пусть на одних участках эта функция возрастает, на других — убывает, причем с разной скоростью. И пусть у этой функции будут точки максимума и минимума.
В точке функция возрастает. Касательная к графику, проведенная в точке , образует острый угол ; с положительным направлением оси . Значит, в точке производная положительна.
В точке наша функция убывает. Касательная в этой точке образует тупой угол ; с положительным направлением оси . Поскольку тангенс тупого угла отрицателен, в точке производная отрицательна.
Вот что получается:
Если функция возрастает, ее производная положительна.
Если убывает, ее производная отрицательна.
А что же будет в точках максимума и минимума? Мы видим, что в точках (точка максимума) и (точка минимума) касательная горизонтальна. Следовательно, тангенс угла наклона касательной в этих точках равен нулю, и производная тоже равна нулю.
Точка — точка максимума. В этой точке возрастание функции сменяется убыванием. Следовательно, знак производной меняется в точке с «плюса» на «минус».
В точке — точке минимума — производная тоже равна нулю, но ее знак меняется с «минуса» на «плюс».
Вывод: с помощью производной можно узнать о поведении функции всё, что нас интересует.
Если производная положительна, то функция возрастает.
Если производная отрицательная, то функция убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
Запишем эти выводы в виде таблицы:
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| + | 0 | — | 0 | + |
Сделаем два небольших уточнения. Одно из них понадобится вам при решении задачи . Другое — на первом курсе, при более серьезном изучении функций и производных.
Возможен случай, когда производная функции в какой-либо точке равна нулю, но ни максимума, ни минимума у функции в этой точке нет. Это так называемая :
В точке касательная к графику горизонтальна, и производная равна нулю. Однако до точки функция возрастала — и после точки продолжает возрастать. Знак производной не меняется — она как была положительной, так и осталась.
Бывает и так, что в точке максимума или минимума производная не существует. На графике это соответствует резкому излому, когда касательную в данной точке провести невозможно.
А как найти производную, если функция задана не графиком, а формулой? В этом случае применяется
Загрузить PDF
Загрузить PDF
Угловой коэффициент характеризует угол наклона прямой к оси абсцисс (угловой коэффициент численно равен тангенсу этого угла). Угловой коэффициент присутствует в уравнении прямой и используется в математическом анализе кривых, где всегда равен производной функции. Для облегчения понимания углового коэффициента представьте, что он влияет на скорость изменения функции, то есть чем больше значение углового коэффициента, тем больше значение функции (при одном и том же значении независимой переменной).
-
1
Используйте угловой коэффициент для нахождения угла наклона прямой к оси абсцисс и направления этой прямой. Вычислить угловой коэффициент довольно легко, если вам дано уравнение прямой. Запомните, что в любом уравнении прямой:
-
2
Для нахождения углового коэффициента необходимо найти значение k (коэффициент при «х»). Если данное вам уравнение имеет вид
, то для нахождения углового коэффициента вам нужно просто посмотреть на число, стоящее перед «х». Обратите внимание, что k (угловой коэффициент) всегда находится при независимой переменной (в данном случае «х»). Если вы запутались, просмотрите следующие примеры:
-
3
Если данное вам уравнение имеет вид, отличный от
, обособьте зависимую переменную. В большинстве случаев зависимая переменная обозначается как «у», а для ее обособления можно выполнять операции сложения, вычитания, умножения и другие. Помните, что любая математическая операция должна быть выполнена на обеих сторонах уравнения (чтобы не менять его исходного значения). Вам необходимо привести любое данное вам уравнение к виду
. Рассмотрим пример:
Реклама
-
1
Для вычисления углового коэффициента воспользуйтесь графиком и двумя точками. Если вам дан просто график функции (без уравнения), вы все еще можете найти угловой коэффициент. Для этого вам понадобятся координаты любых двух точек, лежащих на этом графике; координаты подставляются в формулу:
. Чтобы избежать ошибок при вычислении углового коэффициента, запомните следующее:
- Если график возрастает, то угловой коэффициент имеет положительное значение.
- Если график убывает, то угловой коэффициент имеет отрицательное значение.
- Чем больше значение углового коэффициента, тем круче график (и наоборот).
- Угловой коэффициент прямой, параллельной оси абсцисс, равен 0.
- Угловой коэффициент прямой, параллельной оси ординат, не существует (он бесконечен).[4]
-
2
Найдите координаты двух точек. На графике отметьте любые две точки и найдите их координаты (х,у). Например, на графике лежат точки А(2,4) и В(6,6).[5]
- В паре координат первое число соответствует «х», а второе – «у».
- Каждому значению «х» соответствует определенное значение «у».
-
3
Приравняйте x1, y1, x2, y2 к соответствующим значениям. В нашем примере с точками А(2,4) и В(6,6):
- x1: 2
- y1: 4
- x2: 6
-
y2: 6[6]
-
4
Подставьте найденные значения в формулу для вычисления углового коэффициента. Чтобы найти угловой коэффициент, используются координаты двух точек и следующая формула:
. Подставьте в нее координаты двух точек.
-
5
Объяснение сути формулы. Угловой коэффициент равен отношению изменения координаты «у» (двух точек) к изменению координаты «х» (двух точек). Изменение координаты – это разность между значениями соответствующей координаты первой и второй точек.
-
6
Другой вид формулы для вычисления углового коэффициента. Стандартная формула для вычисления углового коэффициента: k =
. Но она может иметь следующий вид: k = Δy/Δx, где Δ – это греческая буква «дельта», обозначающая в математике разность. То есть, Δx = x_2 — x_1, а Δy = y_2 — y_1.[8]
Реклама
-
1
Научитесь брать производные от функций. Производная характеризует скорость изменения функции в определенной точке, лежащей на графике этой функции. В данном случае графиком может быть как прямая, так и кривая линия. То есть производная характеризует скорость изменения функции в конкретный момент времени. Вспомните общие правила, по которым берутся производные, и только потом переходите к следующему шагу.
- Прочитайте статью Как брать производную.
- Как брать простейшие производные, например, производную показательного уравнения, описано этой статье. Вычисления, представленные в следующих шагах, будут основаны на описанных в ней методах.
-
2
Научитесь различать задачи, в которых угловой коэффициент требуется вычислить через производную функции. В задачах не всегда предлагается найти угловой коэффициент или производную функции. Например, вас могут попросить найти скорость изменения функции в точке А(х,у). Также вас могут попросить найти угловой коэффициент касательной в точке А(х,у). В обоих случаях необходимо брать производную функции.
-
3
Возьмите производную данной вам функции. Здесь строить график не нужно – вам понадобится только уравнение функции. В нашем примере возьмите производную функции
. Берите производную согласно методам, изложенным в упомянутой выше статье:
- Производная:
- Производная:
-
4
В найденную производную подставьте координаты данной вам точки, чтобы вычислить угловой коэффициент. Производная функции равна угловому коэффициенту в определенной точке. Другими словами, f'(х) – это угловой коэффициент функции в любой точке (x,f(x)). В нашем примере:
-
5
Если возможно, проверьте полученный ответ на графике. Помните, что угловой коэффициент можно вычислить не в каждой точке. Дифференциальное исчисление рассматривает сложные функции и сложные графики, где угловой коэффициент можно вычислить не в каждой точке, а в некоторых случаях точки вообще не лежат на графиках. Если возможно, используйте графический калькулятор, чтобы проверить правильность вычисления углового коэффициента данной вам функции. В противном случае проведите касательную к графику в данной вам точке и подумайте, соответствует ли найденное вами значение углового коэффициента тому, что вы видите на графике.
- Касательная будет иметь тот же угловой коэффициент, что и график функции в определенной точке. Для того, чтобы провести касательную в данной точке, двигайтесь вправо/влево по оси Х (в нашем примере на 22 значения вправо), а затем вверх на единицу по оси Y. Отметьте точку, а затем соедините ее с данной вам точкой. В нашем примере соедините точки с координатами (4,2) и (26,3).
Реклама
Об этой статье
Эту страницу просматривали 144 343 раза.
Была ли эта статья полезной?
В декартовых координатах каждая прямая
определяется уравнением первой степени
и, обратно, каждое уравнение первой
степени определяет прямую.
Уравнение
вида
(1)
называется
общим уравнением прямой.
Угол ,
определяемый, как показано на рис.,
называется углом наклона прямой к оси
Ох. Тангенс угла наклона прямой к оси
Ох называется угловым коэффициентом
прямой; его обычно обозначают буквой
k:
Уравнение называется
уравнением прямой с угловым коэффициентом;
k — угловой коэффициент, b — величина
отрезка, который отсекает прямая на оси
Оу, считая от начала координат.
Если
прямая задана общим уравнением
,
то
ее угловой коэффициент определяется
по формуле
.
Уравнение является
уравнением прямой, которая проходит
через точку (
,
)
и имеет угловой коэффициент k.
Если
прямая проходит через точки (
,
),
(
,
),
то ее угловой коэффициент определяется
по формуле
.
Уравнение
является
уравнением прямой, проходящей через
две точки (
,

и 
,
).
Если
известны угловые коэффициенты и
двух
прямых, то один из углов между
этими прямыми определяется по формуле
.
Признаком
параллельности двух прямых является
равенство их угловых коэффициентов:.
Признаком
перпендикулярности двух прямых является
соотношение
,
или .
Иначе говоря, угловые коэффициенты
перпендикулярных прямых обратны по
абсолютной величине и противоположны
по знаку.
4.Общее уравнение прямой
Уравнение
Ах+Ву+С=0
(где А, В, Смогут иметь любые
значения, лишь бы коэффициентыА,
Вне были нулями оба сразу)
представляетпрямую
линию. Всякую прямую можно
представить уравнением этого вида.
Поэтому его называютобщим уравнением
прямой.
Если А=0, то есть уравнение не
содержитх, то оно представляет
прямую,параллельную
оси ОХ.
Если В=0, то есть уравнение не
содержиту, то оно представляет
прямую,параллельную
оси ОY.
Когла Вне равно нулю, то общее
уравнение прямой можноразрешить
относительно ординаты у,
тогда оно преобразуется к виду
y=ax+b
(где a=-A/B; b=-C/B).
Аналогично, при Аотличным от
нуля общее уравнение прямой можно
разрешить относительнох.
Если С=0, то есть общее уравнение
прямой не содержит свободного члена,
то оно представляет прямую, проходящую
через начало координат
5. Уравнение прямой, проходящей через данную точку с данным угловым коэффициентом
Уравнение прямой, проходящей
через данную точку A(x1, y1)
в данном направлении, определяемом
угловым коэффициентом k,
y — y1 = k(x — x1). (1)
Это уравнение определяет
пучок прямых, проходящих через
точку A(x1, y1),
которая называется центром пучка.
6. уравнение прямой,
проходящей через две данные точки.
. Уравнение
прямой, проходящей через две точки: A(x1, y1)
и B(x2, y2),
записывается так:
(2)
Угловой коэффициент прямой, проходящей
через две данные точки, определяется
по формуле
(3)
7.
Уравнение прямой в отрезках
Если в общем уравнении
прямой ,
то разделив (1) на ,
получаем уравнение прямой в отрезках

где 
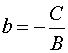
Прямая пересекает ось в
точке ,
ось в
точке .
8.
Формула: Угол между прямыми на плоскости
У
двумя прямыми, заданными
уравнениями: y=k1x+b1 (первая
прямая) и y=k2x+b2 (вторая
прямая), может быть вычислен по формуле
(угол отсчитывается от 1й прямой
ко 2й против
часовой стрелки):
|
tg(α)=(k2-k1)/(1+k1k2) |
9. Взаимное
расположение двух прямых на плоскости.
Пусть сейчас
оба уравнения прямых
записаны в общем виде.
Теорема. Пусть
и
– общие уравнения двух
прямых на координатной плоскости
Оху. Тогда
1) если ,
то прямые и
совпадают;
2) если ,
то прямые и
параллельные;
3) если ,
то прямые пересекаются.
Доказательство.
Условие равносильно
коллинеарности нормальных векторов данных
прямых:
.
Поэтому, если ,
то и прямыепересекаются.
Если же ,
то ,
,
иуравнение прямой
принимает
вид:
или
,
т.е. прямые совпадают.
Заметим, что коэффициент пропорциональности ,
иначе все коэффициенты общего уравнения были
бы равны нулю, что невозможно.
Если же прямые не
совпадают и не пересекаются, то остается
случай ,
т.е. прямые параллельны.
Теорема доказана.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Задачи на нахождение производной касательной включены в ЕГЭ по математике и встречаются там ежегодно. При этом статистика последних лет показывает, что подобные задания вызывают у выпускников определенные затруднения. Поэтому, если учащийся рассчитывает получить достойные баллы по итогам прохождения ЕГЭ, то ему непременно стоит научиться справляться с задачами из раздела «Угловой коэффициент касательной как значение производной в точке касания», подготовленными специалистами образовательного портала «Школково». Разобравшись с алгоритмом их решения, ученик сможет успешно преодолеть аттестационное испытание.
Основные моменты
Приступая к решению задач ЕГЭ по данной теме, необходимо вспомнить основное определение: производная функции в точке равна угловому коэффициенту касательной к графику функции в этой точке. В этом и состоит геометрический смысл производной.
Необходимо освежить в памяти и другое важное определение. Оно звучит следующим образом: угловой коэффициент равняется тангенсу угла наклона касательной к оси абсцисс.
Какие еще важные моменты стоит отметить в этой теме? При решении задач на нахождение производной в ЕГЭ необходимо помнить, что угол, который образует касательная, может быть меньше, больше 90 градусов или равняться нулю.
Как подготовиться к экзамену?
Для того, чтобы задания в ЕГЭ на тему «Угловой коэффициент касательной как значение производной в точке касания» давались вам достаточно легко, воспользуйтесь при подготовке к выпускному испытанию информацией по этому разделу на образовательном портале «Школково». Здесь вы найдете необходимый теоретический материал, собранный и понятно изложенный нашими специалистами, а также сможете попрактиковаться в выполнении упражнений.
Для каждого задания, например, задач на тему «Угловой коэффициент касательной как тангенс угла наклона», мы прописали правильный ответ и алгоритм решения. При этом учащиеся могут выполнять упражнения различного уровня сложности в режиме онлайн. В случае необходимости задачу можно сохранить в разделе «Избранное», чтобы потом обсудить ее решение с преподавателем.
Калькулятор углового коэффициента прямой может не только рассчитать коэффициент, но и найдет точки пересечения прямой с осями абсцисс и ординат (x и y), а также покажет решение и построит график прямой.
Содержание:
- калькулятор углового коэффициента прямой
- определение углового коэффициента прямой
- формула углового коэффициента прямой
- геометрический смысл углового коэффициента
- k>0
- k<0
- k=0
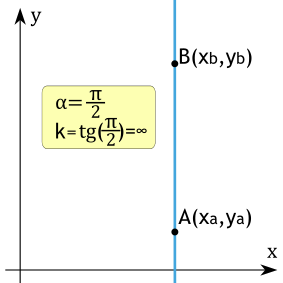
- k не определен (k=∞)
- угловой коэффициент параллельных прямых
- угловой коэффициент перпендикулярных прямых
- примеры расчета углового коэффициента прямой по заданным координатам точек
Определение углового коэффициента прямой
Угловой коэффициент прямой — это число, которое определяет наклон прямой относительно положительного направления оси OX. Численно он равен тангенсу угла (отсчитываемого против часовой стрелки) между положительным направлением оси OX и прямой.
Угловой коэффициент прямой обозначается буковой k.
Угловой коэффициент показывает, как быстро прямая меняет свое положение по оси OX при изменении координаты y и является ключевым понятием в геометрии и физике, используемым для описания многих физических явлений, например, движения тела в пространстве или распространение света.
В геометрии, угловой коэффициент прямой используется для определения угла наклона прямой относительно оси абсцисс и для вычисления ее точек пересечения с осями координат. Также угловой коэффициент прямой используется для записи уравнения прямой в общем виде. Знание углового коэффициента прямой является необходимым при решении многих задач геометрии, таких как построение перпендикуляров и параллельных линий, определение углов между прямыми и плоскостями, а также решение задач на поиск расстояний между прямыми и плоскостями.
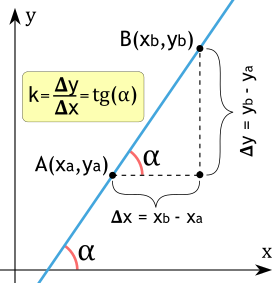
Формула углового коэффициента прямой
Формула вычисления углового коэффициента прямой определяется как отношение изменения координаты y к изменению координаты x между любыми двумя точками на прямой. Математически это можно записать следующим образом:
{k=dfrac{y_b — y_a}{x_b — x_a} = tg(alpha)}
k — угловой коэффициент прямой,
xa, ya — координаты точки A,
xb, yb — координаты точки B
α — угол между осью OX и прямой (против часовой стрелки).
Если прямая задана уравнением в общем виде y = kx + b, то угловой коэффициент прямой равен коэффициенту при x, то есть k.
Геометрический смысл углового коэффициента прямой
Рассмотрим возможные значения углового коэффициента и какой геометрический смысл он несет.
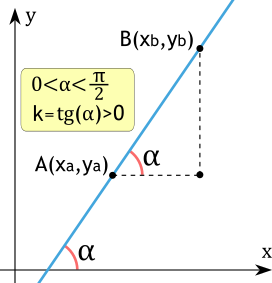
Угловой коэффициент прямой больше нуля
Если угловой коэффициент прямой больше нуля (k>0), то угол между осью OX и прямой является острым, а график прямой возрастающий. Обратное утверждение также справедливо — если график прямой возрастает, то ее угловой коэффициент больше нуля.
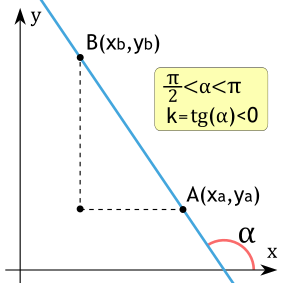
Угловой коэффициент прямой меньше нуля
Если угловой коэффициент прямой меньше нуля (k<0), то угол между осью OX и прямой является тупым, а график прямой убывающий. И наоборот — если график прямой убывает, то ее угловой коэффициент меньше нуля.
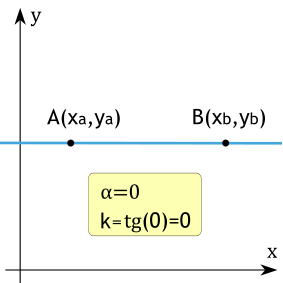
Угловой коэффициент равен нулю
Если угловой коэффициент прямой равен нулю (k=0), то это значит, что прямая параллельна оси x.
Угловой коэффициент не определен (равен бесконечности)
Если угловой коэффициент прямой не определен (или можно сказать обращается в бесконечность) (k=∞), то это значит, что прямая параллельна оси y.
Угловой коэффициент параллельных прямых
Если прямые параллельны, то их угловые коэффициенты равны и наоборот — если у прямых равные угловые коэффициенты, то они параллельны друг другу.
Угловой коэффициент перпендикулярных прямых
Если прямые перпендикулярны, то их угловые коэффициенты обратно пропорциональны и имеют противоположный знак.
Для примера рассмотрим две прямые, заданные угловыми коэффициентами:
y = k_{m} x + b_m
y = k_{n} x + b_n
Прямые будет перпендикулярны, если k_{m} = — dfrac{1}{k_{n}}
Как рассчитать угловой коэффициент прямой по заданным координатам точек
Чтобы закрепить материал, рассмотрим решение задачи.
Задача 1
Найдите угловой коэффициент прямой, проходящей через точки A(5, -2) и B(-3, 1).
Решение
Воспользуемся формулой углового коэффициента прямой. Для начала найдем разницу между соответствующими координатами двух точек:
{Delta x = x_b — x_a = -3 -5 -= -8}
{Delta y = y_b — y_a = 1 — -(2) = 3}
Осталось применить формулу и поделить Delta y на Delta x:
k = dfrac{Delta y}{Delta x} = dfrac{3}{-8} = — dfrac{3}{8} approx -0.375
Это и есть угловой коэффициент прямой AB.
А если вы внимательно читали статью, то, учитывая, что полученный угловой коэффициент отрицательный, можно сказать, что прямая AB убывающая.
Ответ: k = — dfrac{3}{8} approx -0.375
Проверить ответ нам поможет калькулятор .