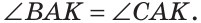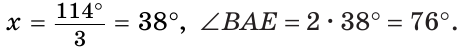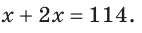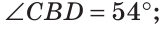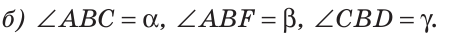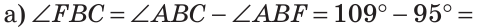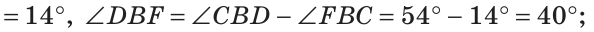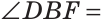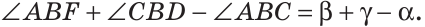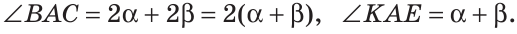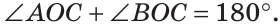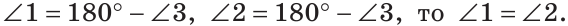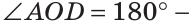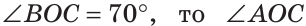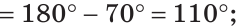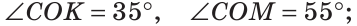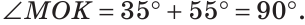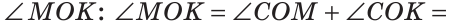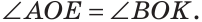Что такое развёрнутый угол — понятие и обозначение
Определение
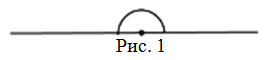
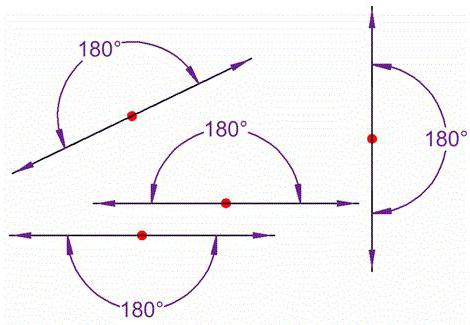
Развернутым называют угол со сторонами, лежащей на одной прямой.
Стороны развернутого угла взаимно дополняют друг друга. В результате получается прямая линия. Таким образом, стороны данной геометрической фигуры представляют собой дополнительные лучи. К примеру, на рисунке изображен ∠CDK, который является развернутым. Точка D служит его вершиной, лучи, обозначенные, как DK и DC – сторонами ∠CDK.
Решить задачу, в которой требуется начертить развернутый угол достаточно просто. Необходимо нарисовать прямую линию и поставить на ней отметку в виде точки, которая будет являться вершиной. Существует другой способ. В начале на плоскости отмечают произвольную точку. Данная отметка будет принята за вершину угла. Если через нее прочертить прямую линию, то получится развернутый угол. Схематично оба способа представлены на рисунке.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Определить, является ли угол развернутым, тупым или острым можно с помощью ряда признаков.
Основные свойства развернутого угла:
- Стороны геометрической фигуры являются антипараллельными и складываются в прямую линию.
- Развернутый угол в любом случае, независимо от способа начертания, будет составлять 180 градусов.
- Если соединить вместе пару смежных углов, то полученная фигура будет выглядеть, как развернутый угол.
- В случае, когда соединяют пару развернутых углов, в результате получают полный угол в 360 градусов, который равен сумме этих углов.
- Прямой угол является половиной развернутого угла.
Геометрические фигуры с развернутыми углами
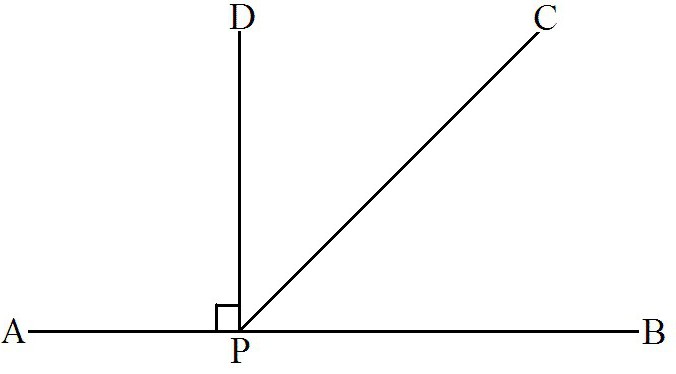
В геометрии производя некоторые манипуляции с развернутыми углами, можно получить новые фигуры. К примеру, если такую геометрическую фигуру разделить лучом на два угла, то полученные углы называют смежными. Такие элементы изображены на рисунке.
∠ABD в данном случае является развернутым углом, а ВС представляет собой луч. Таким образом, углы ∠ABС и ∠CBD — смежные углы.
С помощью биссектрисы можно разделить представленную фигуру на два прямых угла. Наглядно данный метод получения геометрических фигур продемонстрирован на рисунке.
Так, согласно изображению, KF является биссектрисой развернутого ∠MKP. Полученные углы, ∠MKF и ∠FKP представляют собой прямые углы.
Какова градусная мера развернутого угла (сколько радиан)
Как и любой другой, развернутый угол можно измерить. Градусная величина геометрической фигуры будет составлять (180^{0}). Известно, что в данной единице меры укладывается 3,1415926… радиан. Так как длинные числа не всегда удобно использовать в расчетах, как правило, это число обозначают буквой π. Таким образом, можно записать следующее справедливое обозначение:
(180^{0}approx 3,14) радиан.
Точное отношение будет иметь следующий вид:
(180^{0}=pi) радиан.
Примеры решения задач с развернутыми углами
Задача №1
Развернутый угол разделили с помощью луча на две части, которые являются аналогичными геометрическими фигурами. Градусные меры этих элементов относятся, как 1:4. Требуется найти полученные углы.
Решение
Следует обозначить искомые фигуры, как α и β. Предположим, что х является коэффициентом пропорциональности, тогда справедливы равенства:
α = х
β = 4х
Зная, что развернутый угол равен 180 градусам, что является суммой градусных мер углов, на которые он разбит с помощью луча, проходящего между его сторонами. Данное утверждение вытекает из свойств этой геометрической фигуры. Можно записать следующую формулу:
(x+4x=180^{0}Rightarrow 5x=180^{0})
Исходя из этого, можно определить углы:
(x=alpha =36^{0})
(beta =4x=4*36^{0}=144^{0})
Ответ: после разделения развернутого угла на две части один угол будет равен (36^{0}) второй ставит (144^{0})
Задача 2
С помощью луча ОС развернутый угол, обозначенный, как АОВ, делят на два угла АОС и ВОС таким образом, что градусная мера угла АОС больше на 30 градусов, чем градусная мера угла ВОС. Требуется найти углы АОС и ВОС.
Решение
Условия задачи следует представить на рисунке:
Допустим, что ∠BOC = x, тогда, согласно условию задачи, получим следующее равенство:
∠AOC=(x+30)
Известно, что образованные углы являются смежными. Таким образом, в сумме эти углы будут составлять (180^{0})
∠AOC+∠BOC=180
В результате уравнение приобретает следующий вид:
(x+x+30=180Rightarrow 2x=150Rightarrow x^{0}=75^{0})
∠BOC=75, откуда следует:
∠AOC=(x+30)=105
Ответ: угол (BOC=75^{0}) угол (AOC=105^{0})
Содержание:
- Определение развернутого угла
- Примеры решения задач с развернутыми углами
Определение развернутого угла
Определение
Развернутый угол — это угол,
стороны которого составляют прямую (рис. 1).
Градусная мера развернутого угла равна $180^{circ}$.
Любой луч, проведенный из вершины развернутого угла, делит его на два угла. Полученные в результате углы имеют
одну общую сторону, а две другие составляют прямую. Такие углы называются смежными.
Биссектриса развернутого угла делит его на два
прямых угла.
Если произвольный луч, проведенный из вершины развернутого угла, не является биссектрисой,
то он делит развернутый угол на два, один из которых острый (меньше прямого), а другой — тупой (больше прямого)
Примеры решения задач с развернутыми углами
Пример
Задание. Развернутый угол разделен лучом на два угла,
градусные меры которых относятся как 1:4.
Найдите полученные углы.
Решение. Обозначим искомые углы как
$alpha$ и
$beta$ . Пусть
$x$ — коэффициент пропорциональности, тогда
$alpha = x$, а соответственно
$beta = 4x$ . Так как градусная мера развернутого угла равна
$180^{circ}$ и согласно свойствам угла, что градусная мера
угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами, то делаем вывод, что
$$x+4 x=180^{circ} Rightarrow 5 x=180^{circ}$$
Отсюда находим:
$x=alpha=36^{circ}$ и $beta=4 x=4 cdot 36^{circ}=144^{circ}$
Ответ. $36^{circ}$ и $144^{circ}$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Луч
$OC$ делит развернутый угол
$AOB$ на два угла
$AOC$ и
$BOC$ так, что угол
$AOC$ на
$30^{circ}$ больше угла
$BOC$ . Найти углы
$AOC$ и
$BOC$ .
Решение. Изобразим заданный развернутый угол и проведем луч
$OC$ (рис. 2).
Пусть $angle B O C=x^{circ}$, тогда из условия получаем, что
$angle A O C=(x+30)^{circ}$. Так как эти углы являются
смежными, то их сумма равна
$180^{circ}$, то есть
$$angle A O C+angle B O C=180^{circ}$$
а тогда
$$x+x+30=180 Rightarrow 2 x=150 Rightarrow x^{circ}=angle B O C=75^{circ}$$
Отсюда
$$angle A O C=(x+30)^{circ}=105^{circ}$$
Ответ. $angle A O C=105^{circ}, angle B O C=75^{circ}$
Читать дальше: что такое вертикальные углы.
Содержание:
Определение: Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, и частью плоскости, которую они ограничивают.
Два угла называются равными, если их можно совместить наложением.
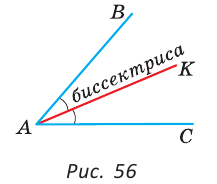
Биссектрисой угла называется луч, который выходит из вершины угла и делит его на два равных угла.
Определение. Развернутым углом называется угол, стороны которого являются дополнительными лучами.
На рисунке 56 луч АК — биссектриса угла ВАС и 
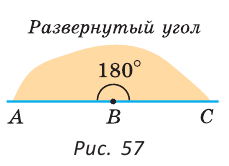
На рисунке 57 угол ABC — развернутый, лучи ВА и ВС — дополнительные. Другая (незакрашенная) полуплоскость относительно прямой АС также задает развернутый угол ABC.
Углы измеряются в градусах, минутах, секундах.
Развернутый угол равен 180°;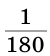 
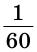
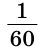
часть развернутого угла называется градусом и обозначается 1°; 
часть одного градуса называется минутой и обозначается 1′; 
часть минуты называется секундой и обозначается 1″.
Угол, равный 5 градусов 20 минут и 35 секунд, записывается так: 5°20’35».
Вместо «градусная мера угла равна 20°» часто говорят «угол равен 20°», вместо найти «градусную меру угла» говорят «найти угол».
Определения
Определение: Угол — это геометрическая фигура, образованная двумя лучами, выходящими из одной точки, и частью плоскости, которую они ограничивают.
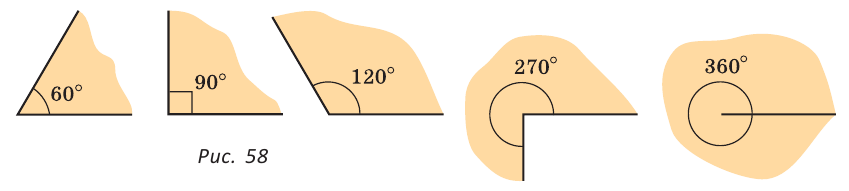
Определение: Угол, равный 90°, называется прямым; угол, меньший 90°, — острым; угол, больший 90°, но меньший 180°, — тупым; угол, равный 360°, называется полным (его стороны совпадают).
На рисунке 58 последовательно изображены: острый угол, равный 60°; прямой угол, равный 90°; тупой угол, равный 120°; угол, равный 270°; и полный угол, равный 360°.
Градусная мера угла является его важной характеристикой. Свойства градусной меры угла: любой угол имеет градусную меру, выраженную некоторым положительным числом; равным углам соответствуют равные градусные меры, а большему углу — большая градусная мера. И наоборот.
Аксиомы
Аксиома измерения углов. Если внутри угла из его вершины провести луч, то он разобьет данный угол на два угла, сумма градусных мер которых равна градусной мере данного угла.
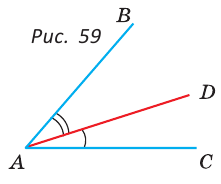
Аксиома откладывания углов. От любого луча в данную полуплоскость можно отложить угол данной градусной меры, и притом только один.
На рисунке 59 луч AD проходит внутри угла ВАС. По аксиоме измерения углов 
Например, если из вершины развернутого угла АОВ (рис. 60) провести ЛУЧ ОС, который составит со стороной ОВ угол 50°, то со стороной OA луч ОС составит 180° — 50° = 130°.
Два луча с общим началом задают на плоскости два угла. В дальнейшем будем рассматривать меньший из этих двух углов (если они неразвернутые). Такой угол меньше 180°.
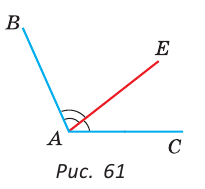
Пример №1
Внутри угла ВАС, равного 114°, из его вершины проведен луч АЕ. Угол ВАЕ в 2 раза больше угла ЕАС. Найти величину угла ВАЕ.
Решение:
Пусть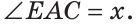 
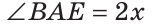
Тогда 
(рис. 61).
По аксиоме измерения углов 
Тогда 
Ответ: 76о
Замечания. 1. Возможен другой способ записи решения, когда рядом с буквой 
пишут знак градуса: 
Тогда в уравнении знак градуса писать не нужно: 
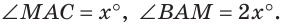
2. В дальнейшем при решении задач не будем ссылаться на аксиому измерения углов.
Пример №2
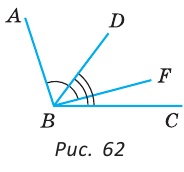
Внутри угла проведены лучи BD и BF (рис. 62).
Найти величину угла DBF, если:
Решение:
Если сложить углы ABF и CBD, то получим угол ABC плюс угол DBF.
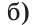
Отсюда 
Ответ: 
Пример №3
Луч AD делит угол ВАС на два угла BAD и CAD. Доказать, что угол между биссектрисами АК и АЕ углов BAD и CAD равен половине угла ВАС (рис. 63).
Доказательство:
Так как АК иАЕ — биссектрисы, то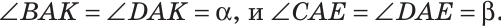 
Тогда 
Следовательно,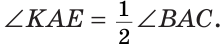 
Что и требовалось доказать.
Замечание. В данной задаче мы доказали свойство: «Если внутри угла из его вершины провести луч, то угол между биссектрисами полученных углов равен половине данного угла».
Геометрия 3D
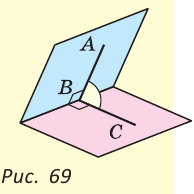
В пространстве при пересечении двух плоскостей образуются двугранные углы. Две полуплоскости с общей границей являются гранями такого двугранного угла, а их граница — его ребром. Измеряется двугранный угол величиной линейного угла, образованного двумя лучами, проведенными в каждой из полуплоскостей из точки на ребре двугранного угла перпендикулярно этому ребру. На рисунке 69 ZABC — линейный угол изображенного двугранного угла.
Геометрия 3D
В пространстве при пересечении двух плоскостей образуются двугранные углы. Две полуплоскости с общей границей являются гранями такого двугранного угла, а их граница — его ребром. Измеряется двугранный угол величиной линейного угла, образованного двумя лучами, проведенными в каждой из полуплоскостей из точки на ребре двугранного угла перпендикулярно этому ребру. На рисунке 69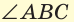 
— линейный угол изображенного двугранного угла.
Смежные углы. Вертикальные углы
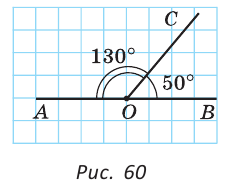
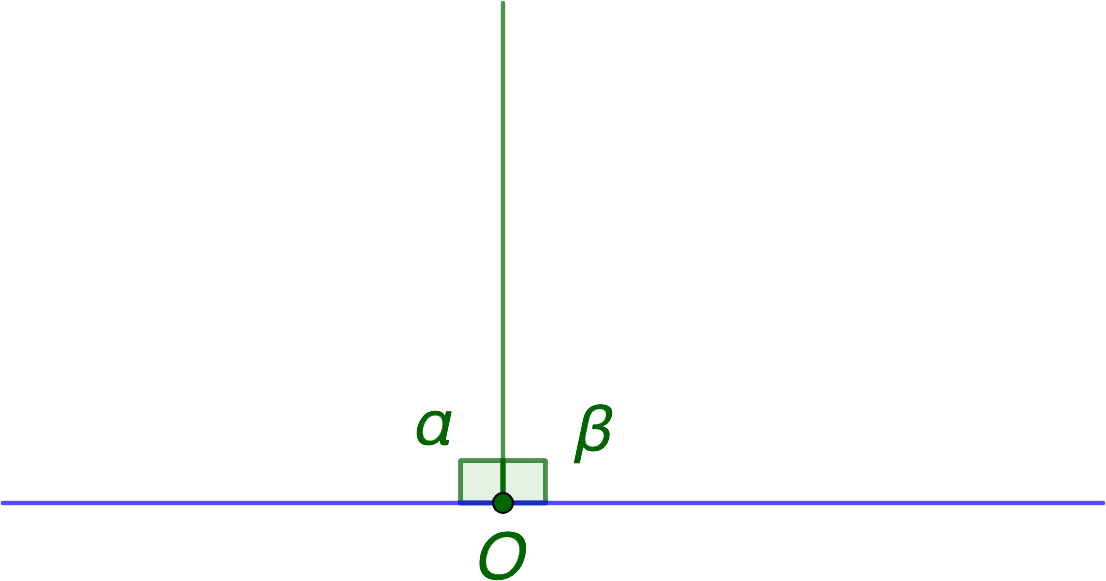
Определение. Два угла называются смежными, если у них одна сторона общая, а две другие являются дополнительными лучами.
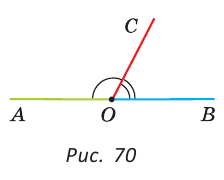
Если на рисунке 70 лучи OA и ОВ дополнительные, то углы АОС и ВОС — смежные.
Теорема (свойство смежных углов). Сумма смежных углов равна 180°.
Дано: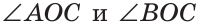 
— смежные.
Доказать: 
Доказательство:
Из определения смежных углов следует, что лучи OA и ОВ являются дополнительными и поэтому образуют развернутый угол АОВ, равный 180°. Луч ОС проходит между сторонами этого угла, и по аксиоме измерения углов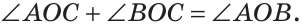 
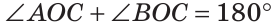
Поэтому 
. Теорема доказана.
Следствия.
- Если смежные углы равны, то каждый из них прямой.
- Если два угла равны, то равны и смежные с ними углы.
Замечание. Все теоремы курса геометрии 7—9 классов описывают свойства фигур на плоскости.
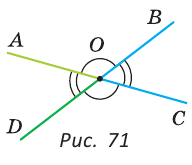
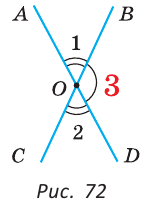
Определение. Два угла называются вертикальными, если стороны одного угла являются дополнительными лучами к сторонам другого.
При пересечении двух прямых АС и DB в точке О (рис. 71) получим, что лучи OA и ОС, О В и OD — дополнительные. Поэтому углы AOD и BОС — вертикальные. Углы АОВ и DOC также вертикальные.
Теорема (свойство вертикальных углов). Вертикальные углы равны.
Дано: 
— вертикальные (рис. 72).
Доказать: 
Доказательство:
Углы 1 и 3 смежные, так как лучи OA и OD — дополнительные по определению вертикальных углов. По свойству смежных углов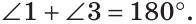 
Углы 2 и 3 также смежные, 
Так как 
Теорема доказана.
Углом между двумя пересекающимися прямыми называется меньший из образованных ими углов. Если при пересечении прямых АВ и CD (рис. 73)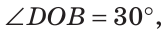 
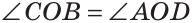
то 
как вертикальные. Угол между прямыми АВ и CD равен 30°. Говорят, что прямые пересекаются под углом 30°.
При пересечении двух прямых образуются четыре угла (не считая развернутых). Если один из них 90°, то и остальные по 90° (докажите самостоятельно). Говорят, что прямые пересекаются под прямым углом.
Угол между параллельными прямыми считается равным 0°.
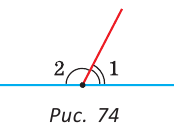
Пример №4
Смежные углы относятся как 2:3. а) Найти величину каждого из углов, б) Определить, сколько процентов развернутого угла составляет меньший угол.
Решение:
а) Пусть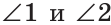 
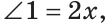
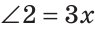
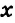
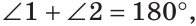
— данные смежные углы (рис. 74). Согласно условию 
(градусную меру одной части принимаем за 
). По свойству смежных углов
то есть 
б) Меньшим является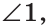 
а 72° от 180° составляют 
Ответ: 72°, 108°; 40 %.
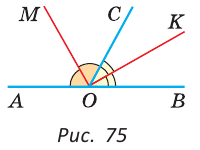
Пример №5
а) Найти угол между биссектрисами ОК и ОМ смежных углов ВОС и АОС (рис. 75), если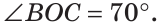 
б) Доказать, что биссектрисы смежных углов образуют прямой угол.
Решение:
а) Если 
б) Так как ОМ и ОК — биссектрисы, то
Найдем градусную меру 
По свойству смежных углов 
Тогда 
. Что и требовалось доказать.
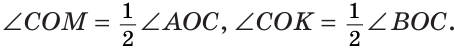
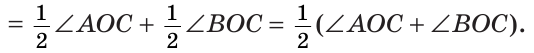
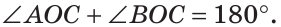
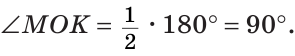
Замечание. Можно было сослаться на ключевую задачу 3* к § 5.
Пример №6
Доказать, что биссектрисы вертикальных углов образуют развернутый угол.
Решение:
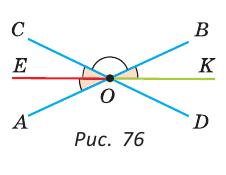
а) Пусть ОЕ и ОК — биссектрисы вертикальных углов АОС и BOD (рис. 76). Докажем, что 
— развернутый. Известно, что биссектриса делит угол пополам. Так как вертикальные углы равны, то равны и их половины. Поэтому 
б) 
так как лучи OA и ОВ дополнительные, и поэтому 
— развернутый. Заменив в последнем равенстве 
на равный ему 
получим 
Отсюда следует, что — развернутый.
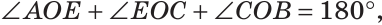
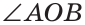
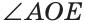
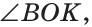
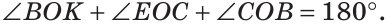
Замечание. Из решения задачи следует свойство: если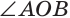 
— развернутый и 
— вертикальные.
- Перпендикулярные прямые в геометрии
- Признаки равенства треугольников
- Признаки равенства прямоугольных треугольников
- Соотношения в прямоугольном треугольнике
- Свойства прямоугольного треугольника
- Расстояние между параллельными прямыми
- Задачи на построение циркулем и линейкой
- Задачи на построение по геометрии
Развернутый угол в геометрии
В этой статье будет рассматриваться одна из основных геометрических фигур – угол. После общего введения в это понятие мы уделим основное внимание отдельному виду такой фигуры. Развернутый угол – важное понятие геометрии, которое и будет основной темой этой статьи.
Введение в понятие геометрического угла
В геометрии существует ряд объектов, которые составляют основу всей науки. Угол как раз относиться к ним и определяется с помощью понятия луча, поэтому начнем именно с него.
Также перед тем, как приступать к определению самого угла, нужно вспомнить о нескольких не менее важных объектах в геометрии – это точка, прямая на плоскости и собственно сама плоскость. Прямой называют самую простую геометрическую фигуру, у которой нет ни начала, ни конца. Плоскостью – поверхность, которая имеет два измерения. Ну и луч (или же полупрямая) в геометрии – это часть прямой, у которой есть начало, но нет конца.
Используя данные понятия, можем составить утверждение, что углом является геометрическая фигура, которая полностью лежит в некоторой плоскости и состоит из двух несовпадающих лучей с общим началом. Такие лучи называются сторонами угла, а общее начало сторон – это его вершина.
Виды углов и геометрии
Мы знаем о том, что углы могут быть совсем разными. А потому немного ниже будет приведена небольшая классификация, которая поможет лучше разобраться в видах углов и их главных особенностях. Итак, существует несколько видов углов в геометрии:
- Прямой угол. Он характеризируется величиной в 90 градусов, а значит, его стороны всегда перпендикулярны между собой.
- Острый угол. К таким углам относятся все их представители, имеющие размер меньше 90 градусов.
- Тупой угол. Здесь же могут быть все углы с величиной от 90 до 180 градусов.
- Развернутый угол. Имеет размер строго 180 градусов и внешне его стороны составляют одну прямую.
Понятие развернутого угла
Теперь давайте рассмотрим развернутый угол более подробно. Это тот случай, когда обе стороны лежат на одной прямой, что можно четко увидеть на рисунке немного ниже. Значит, мы можем с уверенностью сказать, что у развернутого угла одна из его сторон по сути есть продолжением другой.
Стоит запомнить тот факт, что такой угол всегда можно разделить с помощью луча, который выходит из его вершины. В результате мы получим два угла, которые в геометрии называются смежными.
Также развернутый угол имеет несколько особенностей. Для того, чтобы рассказать о первой из них, нужно вспомнить понятие «биссектриса угла». Напомним, что это луч, который делит любой угол строго пополам. Что касается развернутого угла, то его биссектриса разделяет его таким образом, что образуется два прямых угла по 90 градусов. Это очень легко просчитать математически: 180˚ (градус развернутого угла) : 2 = 90˚.
Если же разделять развернутый угол совсем произвольным лучом, то в результате мы всегда получаем два угла, один из которых будет острым, а другой – тупым.
Свойства развернутых углов
Будет удобно рассматривать этот угол, собрав воедино все его главные свойства, что мы и сделали в данном списке:
- Стороны развернутого угла антипараллельны и составляют прямую.
- Величина развернутого угла всегда составляет 180˚.
- Два смежных угла вместе всегда составляют развернутый угол.
- Полный угол, который составляет 360˚, состоит из двух развернутых и равен их суме.
- Половина развернутого угла – это прямой угол.
Итак, зная все эти характеристики данного вида углов, мы можем использовать их для решения ряда геометрических задач.
Задачи с развернутыми углами
Для того, чтобы понять, усвоили ли вы понятие развернутого угла, попытайтесь ответить на несколько следующих вопросов.
- Чему равен развернутый угол, если его стороны составляют вертикальную прямую?
- Будут ли два угла смежными, если величина первого 72˚, а другого — 118˚?
- Если полный угол состоит из двух развернутых, то сколько в нем прямых углов?
- Развернутый угол разделили лучом на два таких угла, что их градусные меры относятся как 1:4. Вычислите полученные углы.
Решения и ответы:
- Как бы ни был расположен развернутый угол, он всегда по определению равен 180˚.
- Смежные углы имеют одну общую сторону. Поэтому, чтобы вычислить размер угла, который они составляю вместе, нужно просто прибавить значение их градусных мер. Значит, 72 +118 = 190. Но по определению развернутый угол составляет 180˚, а значит, два данных угла не могут быть смежными.
- Развернутый угол вмещает два прямых угла. А так как в полном имеется два развернутых, значит, прямых в нем будет 4.
- Если мы назовем искомые углы а и b, то пусть х — это коэффициент пропорциональности для них, а это значит, что а=х, и соответственно b=4х . Развернутый угол в градусах равен 180˚. И согласно своим свойствам, что градусная мера угла всегда равна сумме градусных мер тех углов, на которые он разбивается любым произвольным лучом, что проходит между его сторонами, можем сделать вывод, что х + 4х = 180˚, а значит, 5х = 180˚. Отсюда находим: х=а=36˚ и b = 4х = 144˚. Ответ: 36˚ и 144˚.
Если у вас получилось ответить на все эти вопросы без подсказок и не подглядывая в ответы, значит вы готовы переходить к следующему уроку по геометрии.
Что такое развернутый угол
В данной публикации мы рассмотрим, что такое развернутый угол, перечислим его основные свойства, а также разберем пример задачи по этой теме.
Определение развернутого угла
Угол является развернутым, если его градусная мера равняется 180 градусам.
Т.е. стороны угла образуют прямую.
Свойства развернутого угла
1. Луч, берущий начало в вершине развернутого угла, делит его на два угла, которые называются смежными.
2. Биссектриса развернутого угла делит его на два угла по 90° (т.е. прямых).
3. Если луч, который делит развернутый угол, не является его биссектрисой, то один из образованных углов меньше 90° (острый), а другой находится в промежутке от 90° до 180° (тупой).
Пример задачи
Дан развернутый угол, поделенный лучом на два угла, один из которых в три раза больше другого. Найдем градусные меры этих углов.
Решение
Пусть меньший угол будет “x” , тогда больший равен “3x” . Сумма этих углов равняется 180 градусам. Составим соответствующее уравнение и решим его:
Таким образом, первый угол равен 45°, а второй – 135° (45° умножаем на 3).
Проверка: 45° + 135° = 180° (верно).
Развернутый угол
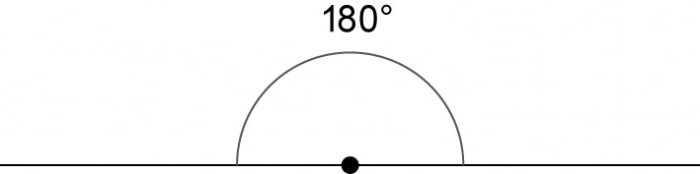
Развернутый угол — это угол, стороны которого лежат на одной прямой.
Градусная мера развёрнутого угла равна 180º.
Каждая сторона развернутого угла дополняет другую сторону до прямой, то есть стороны развёрнутого угла являются дополнительными лучами.
Например, ∠CDK — развёрнутый. Точка D — вершина, лучи DK и DC — стороны угла CDK.
Чтобы нарисовать развернутый угол, достаточно провести прямую и отметить на ней точку — вершину угла.
Можно поступить иначе — сначала отметить точку — вершину угла, затем через неё провести прямую:
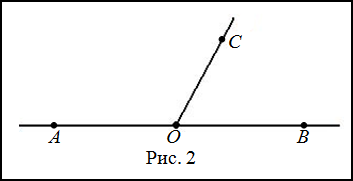
∠AOB — развернутый угол
Если луч делит развернутый угол на два угла, то эти углы — смежные:
Например, ∠ABD — развернутый, BC — луч,
Биссектриса развернутого угла делит его на два прямых угла.
Например, KF — биссектриса развернутого угла MKP,
Загрузить PDF
Загрузить PDF
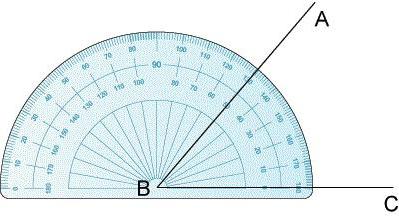
В геометрии угол — это фигура, которая образована двумя лучами, которые выходят из одной точки (она называется вершиной угла). В большинстве случаев единицей измерения угла является градус (°) — помните, что полный угол или один оборот равен 360°. Найти значение угла многоугольника можно по его типу и значениям других углов, а если дан прямоугольный треугольник, угол можно вычислить по двум сторонам. Более того, угол можно измерить с помощью транспортира или вычислить с помощью графического калькулятора.
-
1
Сосчитайте число сторон многоугольника. Чтобы вычислить внутренние углы многоугольника, сначала нужно определить, сколько у многоугольника сторон. Обратите внимание, что число сторон многоугольника равно числу его углов.[1]
- Например, у треугольника 3 стороны и 3 внутренних углов, а у квадрата 4 стороны и 4 внутренних углов.
-
2
Вычислите сумму всех внутренних углов многоугольника. Для этого воспользуйтесь следующей формулой: (n — 2) x 180. В этой формуле n — это количество сторон многоугольника. Далее приведены суммы углов часто встречающихся многоугольников:[2]
- Сумма углов треугольника (многоугольника с 3-мя сторонами) равна 180°.
- Сумма углов четырехугольника (многоугольника с 4-мя сторонами) равна 360°.
- Сумма углов пятиугольника (многоугольника с 5-ю сторонами) равна 540°.
- Сумма углов шестиугольника (многоугольника с 6-ю сторонами) равна 720°.
- Сумма углов восьмиугольника (многоугольника с 8-ю сторонами) равна 1080°.
-
3
Разделите сумму всех углов правильного многоугольника на число углов. Правильный многоугольник это многоугольник с равными сторонами и равными углами. Например, каждый угол равностороннего треугольника вычисляется так: 180 ÷ 3 = 60°, а каждый угол квадрата находится так: 360 ÷ 4 = 90°.[3]
- Равносторонний треугольник и квадрат — это правильные многоугольники. А у здания Пентагона (Вашингтон, США) и дорожного знака «Стоп» форма правильного восьмиугольника.
-
4
Вычтите сумму всех известных углов из общей суммы углов неправильного многоугольника. Если стороны многоугольника не равны друг другу, и его углы также не равны друг другу, сначала сложите известные углы многоугольника. Теперь полученное значение вычтите из суммы всех углов многоугольника — так вы найдете неизвестный угол.[4]
- Например, если дано, что 4 угла пятиугольника равны 80°, 100°, 120° и 140°, сложите эти числа: 80 + 100 + 120 + 140 = 440. Теперь вычтите это значение из суммы всех углов пятиугольника; эта сумма равна 540°: 540 — 440 = 100°. Таким образом, неизвестный угол равен 100°.
Совет: неизвестный угол некоторых многоугольников можно вычислить, если знать свойства фигуры. К примеру, в равнобедренном треугольнике две стороны равны и два угла равны; в параллелограмме (это четырехугольник) противоположные стороны равны и противоположные углы равны.
Реклама
-
1
Помните, что в любом прямоугольном треугольнике один угол всегда равен 90°. Это так, даже если прямой угол никак не отмечен или его значение не указано. Таким образом, один угол прямоугольного треугольника всегда известен, а другие углы можно вычислить с помощью тригонометрии.[5]
-
2
Измерьте длину двух сторон треугольника. Самая длинная сторона прямоугольного треугольника называется гипотенузой. Прилежащая сторона это сторона, которая находится возле неизвестного угла. Противолежащая сторона — это сторона, которая находится напротив неизвестного угла. Измерьте две стороны, чтобы вычислить неизвестные углы треугольника.[6]
Совет: воспользуйтесь графическим калькулятором, чтобы решить уравнения, или найдите онлайн-таблицу со значениями синусов, косинусов и тангенсов.
-
3
Вычислите синус угла, если вам известны противолежащая сторона и гипотенуза. Для этого подставьте значения в уравнение: sin(x) = противолежащая сторона ÷ гипотенуза. Например, противолежащая сторона равна 5 см, а гипотенуза равна 10 см. Разделите 5/10 = 0,5. Таким образом, sin(x) = 0,5, то есть x = sin-1 (0,5).[7]
- Если у вас есть графический калькулятор, введите 0,5 и нажмите клавишу sin-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 30°.
-
4
Вычислите косинус угла, если вам известны прилежащая сторона и гипотенуза. Для этого подставьте значения в уравнение: cos(x) = прилежащая сторона ÷ гипотенуза. Например, прилежащая сторона равна 1,67 см, а гипотенуза равна 2 см. Разделите 1,67/2 = 0,83. Таким образом, cos(x) = 0,83, то есть x = cos-1 (0,83).[8]
- Если у вас есть графический калькулятор, введите 0,83 и нажмите клавишу cos-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 33,6°.
-
5
Вычислите тангенс угла, если вам известны противолежащая и прилежащая стороны. Для этого подставьте значения в уравнение: tg(x) = противолежащая сторона ÷ прилежащая сторона. Например, противолежащая сторона равна 75 см, а прилежащая сторона равна 75 см. Разделите 75/100 = 0,75. Таким образом, tg(x) = 0,75, то есть x = tg-1 (0,75).[9]
- Если у вас есть графический калькулятор, введите 0,75 и нажмите клавишу tg-1. Если у вас нет такого калькулятора, используйте онлайн-таблицу, чтобы найти значение угла. В нашем примере угол равен 36,9°.
Реклама
Советы
- Названия углов соответствуют их значениям. Угол в 90° — это прямой угол. Угол в 180° — это развернутый угол. Угол, который лежит между 0° и 90° — это острый угол. Угол, который лежит между 90° и 180° — это тупой угол. Угол, который лежит между 180° и 360° — это невыпуклый угол.
- Если сумма двух углов равна 90°, они называются дополнительными. Запомните: два острых угла прямоугольного треугольника всегда являются дополнительными. Если же сумма двух углов равна 180°, они называются смежными.
Реклама
Об этой статье
Эту страницу просматривали 238 090 раз.