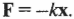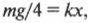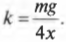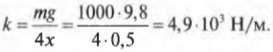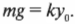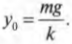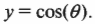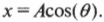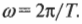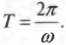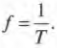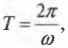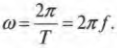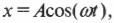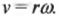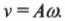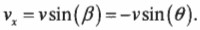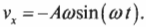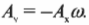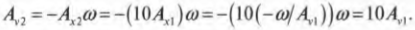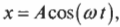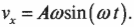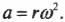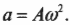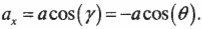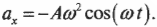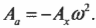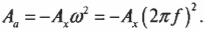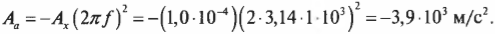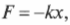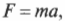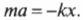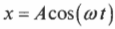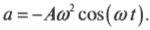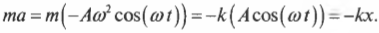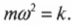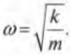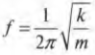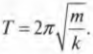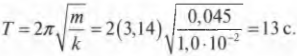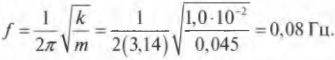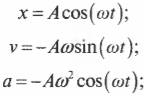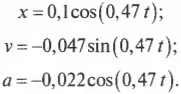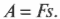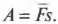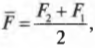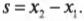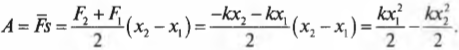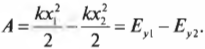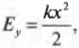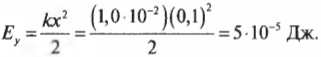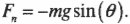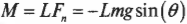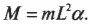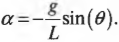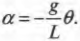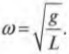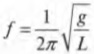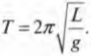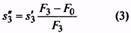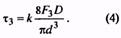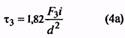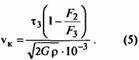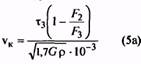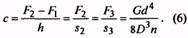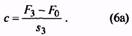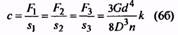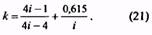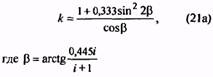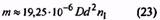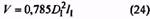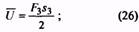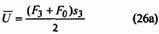Как найти величину сжатия пружины

0 Пользователей и 1 Гость просматривают эту тему.

---

---

В этой главе …

• Изучаем закон Гука
• Осваиваем основы простого гармонического движения
• Изучаем особенности простого гармонического движения
• Измеряем энергию простого гармонического движения
• Вычисляем период колебаний маятника

Эта глава посвящена описанию еще одного типа движения, а именно: описанию периодического движения. Примерами такого движения являются колебания грузика на пружинке, качания маятника и даже прыжки с высоты с помощью эластичной веревки. В этой главе рассматриваются закономерности и особенности таких повторяющихся, т.е. периодических движений. Здесь мы научимся вычислять характеристики периодического движения: период колебаний пружинки и маятника, упругую энергию сжатой пружины и т.д.

Постигаем закон Гука

Все объекты природы могут деформироваться, т.е. менять свою форму или объем, под действием приложенной силы. Если такие деформации (т.е. изменения) исчезают после прекращения действия приложенной силы, то они называются упругими. Упругость играет важную роль в технике. Упругие пружины используются для гашения удара при посадке космического корабля на поверхность планеты. Свернутые в спираль упругие пластины применяются в заводных механизмах часов. Даже в мышеловке используется упругая деформация пружины.

Еще в XVII-M веке английский физик Роберт Гук, изучая упругие свойства разных материалов, вывел закон, названный его именем. Согласно закону Гука, для упругого деформирования материала требуется приложить силу, величина которой прямо пропорциональна его деформации. Например, чтобы растянуть пружину на величину ​( x )​, потребуется приложить внешнюю силу ​( F_{вн} )​, которая равна:

где ​( k )​ — это коэффициент пропорциональности.

Точнее говоря, вектор деформации ​( mathbf{x} )​ всегда направлен противоположно силе сопротивления пружины (или силе упругости) ( mathbf{F} ), а потому в векторную формулировку закона Гука обычно входит знак “минус”:

Растягиваем и сжимаем пружины

Следует помнить, что закон Гука относится только к упруго деформируемым материалам.

В реальном мире, помимо упругих деформаций, имеются еще и пластические деформации. Так называют деформации, которые остаются в объекте, хотя бы частично, даже после прекращения действия внешних сил. Если сила не превосходит некоторой известной величины, которая называется пределом упругости, то возникающая деформация будет пластической. Предел упругости имеет разные значения для разных материалов. Если деформируемый объект, например пружина, испытывает только упругие деформации, то его называют идеально упругим, например, идеально упругой пружиной. Коэффициент пропорциональности ​( k )​ в законе Гука ​( F=kx )​ называется коэффициентом упругости объекта, который зависит от материала объекта, его размеров и измеряется в Н/м.

Допустим, вам нужно спроектировать подвеску автомобиля массой 1000 кг, состоящую из 4 пружин, которые могут идеально упруго деформироваться на расстояние 0,5 м. Каким коэффициентом упругости должна обладать пружина, чтобы выдержать вес автомобиля?

Вес автомобиля равен ​( mg )​, где ​( g )​ — это ускорение свободного падения под действием силы гравитационного притяжения. Это значит, что на каждую пружину приходится вчетверо меньшая нагрузка ​( mg/4 )​.

Определим упругую деформацию пружины под действием этой нагрузки по формуле закона Гука:

т.е. коэффициент упругости равен:

Подставляя значения, получим:

Итак, чтобы выдержать вес автомобиля, потребуется пружина с коэффициентом упругости равным 4,9·10³ Н/м. Не забудьте, что каждый элемент подвески автомобиля должен обладать определенным запасом прочности, чтобы выдерживать непредсказуемые превышения нагрузки, например на ухабах. Однако эта задача выходит за рамки данного курса.

Изучаем особенности закона Гука

Как уже упоминалось выше, в векторную формулировку закона Гука обычно входит знак “минус”:

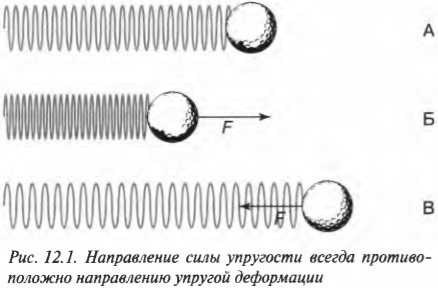
Таким образом, знак “минус” выражает следующую особенность упругой деформации: сила упругости всегда противоположна деформации. На рис. 12.1 схематически показаны направления силы упругости и деформации при сжатии и растяжении пружины.

Как видите, при отсутствии растяжении или сжатия нет и деформации (см. схему А на рис. 12.1). Если пружина сжимается влево, то сила упругости направлена вправо (см. схему Б на рис. 12.1), а если пружина растягивается вправо, то сила упругости направлена влево (см. схему В на рис. 12.1).

Сила упругости пружины не зря называется силой сопротивления, ведь она стремится установить равновесие.

Движется дальше: простое гармоническое движение

Простым гармоническим движением называется такое движение, при котором сила сопротивления движению пропорциональна перемещению. При этом сила трения не учитывается, и никакие другие внешние силы не оказывают никакого влияния на движение. Такое движение будет выполняться периодически и бесконечно долго. Конечно же, в реальной ситуации так не бывает, но здесь имеется в виду именно идеализированная ситуация.

Изучаем простое гармоническое движение по горизонтали и по вертикали

На рис. 12.1 показан пример движения мячика, прикрепленного к пружине. При сжатии пружины внешней силой справа налево в пружине возникает сила упругости, которая стремится вернуть мячик в исходное положение. После возврата мячика в исходное положение он останавливается не сразу, а спустя какое-то время. Оно необходимо для торможения ускорившегося мячика с помощью силы упругости, возникающей при растягивании вправо. Дело в том, что мячик обладает некоторой массой, и инерция (см. главу 11) не позволяет ему остановиться мгновенно. В результате имеем следующую последовательность событий (см. рис. 12.1).

• Схема А. Мячик находится в состоянии равновесия. Никакие силы не действуют на него. Пружина находится в нерастянутом и в несжатом состоянии.
• Схема Б. Внешняя сила сжала пружину справа налево. В пружине возникла упругая сила сопротивления ​( F )​.
• Схема В. Внешняя сила отпускает пружину (и далее не участвует в процессе движения). Упругая сила сопротивления пружины ​( F )​ стремится распрямить пружину, т.е. вернуть мячик в исходное состояние. Мячик начинает ускоренное движение.

Когда мячик проходит точку исходного положения, его скорость становится очень большой (фактически максимальной) и он продолжает движение вправо. При этом возникает деформация растяжения и соответственно направленная противоположно упругая сила сопротивления пружины. Именно так и происходит при повторяющихся движениях мячика слева направо и, наоборот, справа налево. После первоначального толчка из неподвижного состояния мячик начинает совершать периодические колебания из самого крайнего левого положения в самое крайнее правое положение.

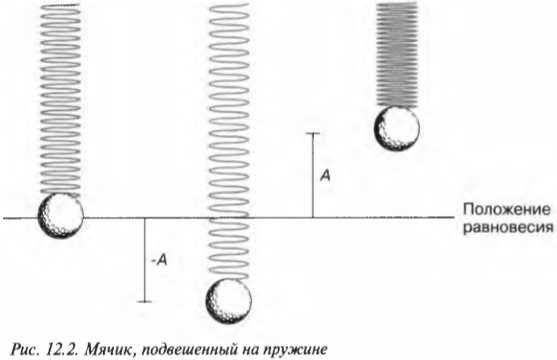
В примере на рис. 12.1 предполагается, что силы трения нет. А что будет, если пружинку с мячиком подвесить вертикально, как показано на рис. 12.2?

В подвешенном состоянии изменится положение равновесия, но после воздействия внешней силы мячик будет совершать аналогичные периодические движения, но теперь уже вверх-вниз.

Это новое равновесное положение определяется равенством веса мячика ​( mg )​ и силы упругости ​( ky_0 )​ растянутой пружины под действием этого веса:

Итак, новое положение исходного равновесия будет определяться формулой:

Теперь если потянуть мячик вниз с помощью внешней силы и отпустить мячик, то он начнет совершать периодическое движение, как и в прежнем примере (см. рис. 12.1), но теперь уже относительно нового положения равновесия.

Периодическое движение подобного рода называется периодическим колебанием, а крайние положения мячика при таком периодическом движении мячика называются амплитудами периодических колебаний. Амплитуда является важным элементом математического описания простого гармонического движения.

Изучаем свойства простого гармонического движения

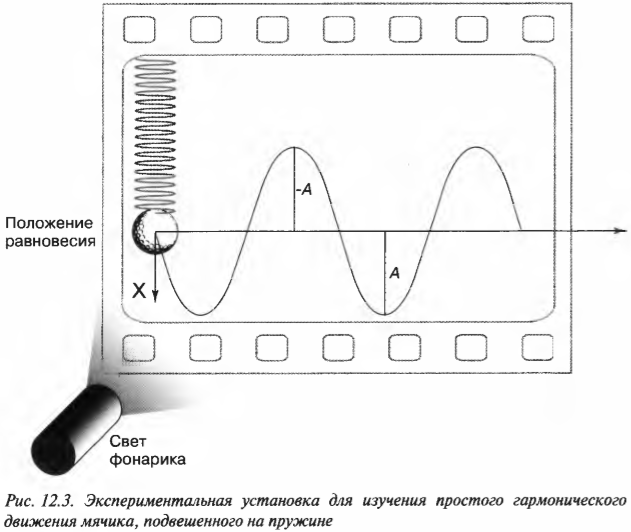
Представьте себе, что для изучения простого гармонического движения ученые решили освещенный фонариком мячик из предыдущего примера заснять на движущуюся по горизонтали фотопленку.

После проявки фотопленки на ней оказался четкий волнообразный след, который показан на рис. 12.3.

Оказывается, мячик действительно совершает периодические движения вверх-вниз относительно исходного равновесного положения с амплитудой А. Вблизи точки равновесия скорость мячика максимальна, а в точках амплитуды минимальна.

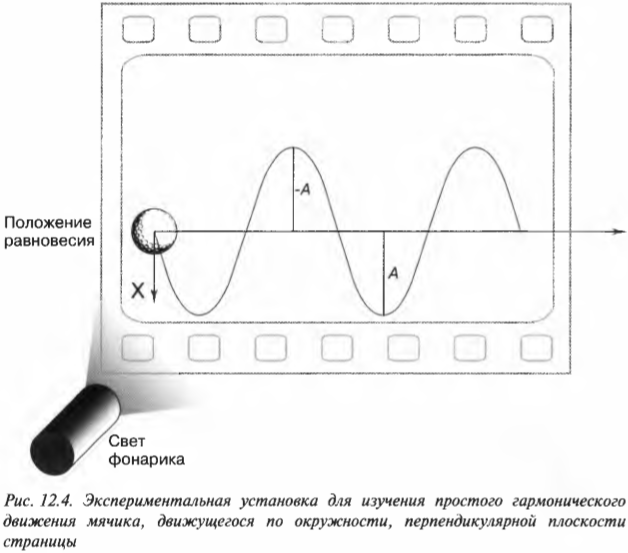
Траектория мячика очень похожа на синусоидальную кривую, т.е. след мячика на движущейся фотопленке описывается графиком функции ​( sin )​ (“синус”) либо ​( cos )​ (“косинус”) со сдвигом от начала координат. Действительно, решением уравнения простого гармонического движения является функция ​( sin )​ или ​( cos )​.

Изучаем траекторию простого гармонического движения

Построим и рассмотрим внимательно кривую функции:

Наверняка эта функция и ее графическое представление в виде синусоидальной кривой уже знакомо многим читателям этой книги из курса математики. Ее часто можно встретить на экранах разных приборов в реальной жизни или даже в виртуальном мире кино и компьютерных игр.

Пусть освещенный фонариком мячик движется по окружности перпендикулярной плоскости страницы и снимается на движущуюся по горизонтали фотопленку. Тогда после проявки фотопленки на ней снова появится синусоидальная кривая, как показано на рис. 12.4.

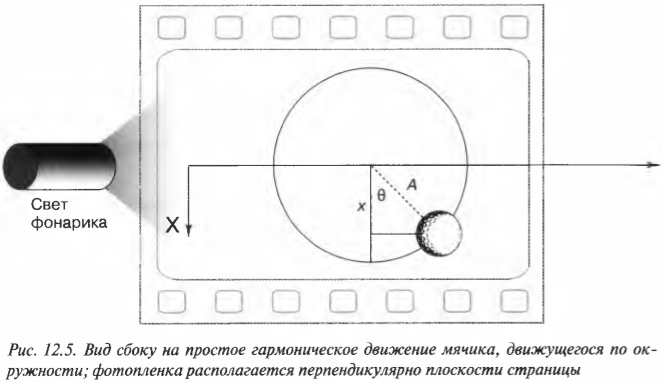
Если расположить окружность так, чтобы она была параллельна плоскости страницы (рис. 12.5), то можно легко заметить, что положение мячика определяется формулой:

где ​( x )​ — это текущее смещение мячика по оси X от положения равновесия, ​( theta )​ — это угол поворота мячика при вращении по окружности, а ​( A )​ — это амплитуда периодического движения.

Если мячик вращается по окружности с постоянной угловой скоростью, то ​( theta=omega t )​ и ​( x=Acos(omega t) )​.

Определяем период простого гармонического движения

Прохождение мячиком пути, равного длине окружности, называется циклом, а время его прохождения — периодом. Период обозначается символом ​( T )​ и измеряется в секундах.

На рис. 12.4 и 12.5 полный цикл соответствует движению мячика от исходного положения с амплитудой ​( A )​, затем к положению с амплитудой ​( -A )​, а потом снова к положению с амплитудой ( A ).

Как связан период с уже знакомыми нам параметрами движения? За один цикл мячик проходит угол величиной ​( 2pi )​ за период ​( T )​, т.е. его угловая скорость равна:

Откуда получаем выражение для периода:

Для характеристики периодического движения часто используют понятие частота, которое равно количеству циклов за единицу времени. Например, если мячик на рис. 12.4 совершает 1000 полных оборотов в секунду, то его частота равна 1000 с^-1. В системе СИ частоту измеряют в герцах (или сокращенно Гц), т.е. 1 с^-1 = 1 Гц. Таким образом, частота вращения мячика по окружности равна 1000 Гц.

Частота ​( f )​ и период ​( T )​ связаны очень простым соотношением:

Поскольку:

то теперь можно легко найти связь между частотой и угловой скоростью:

При описании периодических движений угловую скорость ​( omega )​ часто называют циклической частотой.

Определяем скорость в простом гармоническом движении

На рис. 12.5 мячик совершает движение по окружности, а координата перемещения по оси X определяется формулой:

где ​( x )​ — это текущее смещение мячика по оси X от положения равновесия, ​( omega )​ — это угловая скорость мячика при вращении по окружности, а ​( A )​ — это амплитуда периодического движения.

В любой точке с координатой х мячик обладает некоторой скоростью, которая зависит от времени. Как выразить ее с помощью математической формулы?

Очень просто, ведь для этого достаточно вспомнить о связи между угловой ​( omega )​ и тангенциальной ​( v )​ скоростью (см. главу 10):

Поскольку в данном случае ​( r=A )​, то в итоге получим для тангенциальной скорости:

Теперь для определения скорости периодических колебаний следа мячика по оси X на фотопленке нужно вычислить проекцию тангенциальной скорости на ось X:

(Здесь знак “минус” возникает, поскольку фотопленка движется вниз и ось Y направлена вниз, а потому угол ​( beta )​ между вектором скорости и осью X равен ​( 180^circ+theta )​, a ​( sin(beta)=sin(180^circ+theta )=-sin(theta) )​. — Примеч. ред.)

После подстановки выражений для ​( theta=omega t )​ и для ​( v=Aomega )​ получим:

Обратите внимание, что скорость меняется от исходного положения с амплитудой перемещения ​( A )​ и амплитудой скорости ​( 0 )​, затем к положению с амплитудой перемещения ​( 0 )​ и амплитудой скорости ​( -Aomega )​, потом к положению с амплитудой перемещения ​( -A )​ и амплитудой скорости ​( 0 )​, затем к положению с амплитудой перемещения ​( 0 )​ и амплитудой скорости ​( Aomega )​, а потом снова к положению с амплитудой перемещения ​( A )​ и амплитудой скорости ​( 0 )​.

Как видите, в простом гармоническом движении амплитуда скорости ​( A_v=Aomega )​ связана с амплитудой перемещения ​( A_х=A )​ формулой:

Рассмотрим следующий простой пример. Представьте себе, что несколько отчаянных парней и девушек прыгают с высоты с помощью эластичной веревки. Известно, что при прыжке с некоторой высоты относительно точки равновесия максимальная скорость в точке равновесия одного из смельчаков достигает величины 4 м/с. Он решает в 10 раз увеличить высоту прыжка. Какой будет его максимальная скорость в точке равновесия?

Итак, амплитуда скорости в первом прыжке ​( A_{v1}=-A_{х1}omega )​ равна 4 м/с. Амплитуда перемещения во втором прыжке (с новой высоты) в 10 раз больше амплитуды перемещения в начале, т.е. ​( A_{х2}=10A_{х1} )​. Вопрос: чему равна амплитуда скорости ( A_{v2}=-A_{х2}omega ) во втором прыжке? Подставляя выражение для ( A_{х2}=-omega/A_{v1} ) в формулу ( A_{х2}=10A_{х1} ), а затем в формулу ( A_{v2}=-A_{х2}omega ), получим:

Итак, при увеличении амплитуды прыжка в 10 раз амплитуда скорости возрастает тоже в 10 раз, т.е. становится равной 40 м/с.

Определяем ускорение в простом гармоническом движении

Вернемся к примеру на рис. 12.5, где мячик совершает движение по окружности. Его координата перемещения по оси X определяется формулой:

где ​( x )​ — это текущее смещение мячика по оси X от положения равновесия, ​( omega )​ — это угловая скорость мячика при вращении по окружности, а ​( A )​ — это амплитуда периодического движения.

Как мы уже выяснили в предыдущем разделе, его скорость перемещения по оси X определяется формулой:

Однако вращательное движение мячика также характеризуется центростремительным ускорением. Как выразить ее с помощью математической формулы?

Как известно (см. главу 10), угловая скорость ​( omega )​ центростремительное ускорение ​( a )​ связаны следующей формулой:

Поскольку в данном случае ​( r=A )​, то в итоге получим для центростремительного ускорения:

Теперь для определения ускорения периодических колебаний следа мячика по оси X на фотопленке нужно вычислить проекцию центростремительного ускорения на ось X:

(Здесь знак “минус” возникает, поскольку фотопленка движется вниз и ось Y направлена вниз, а потому угол ​( gamma )​ между вектором центростремительного ускорения и осью X равен ​( 180^circ + theta )​, a ​( cos(gamma)=cos(180^circ + theta)=-cos(theta) )​. — Примеч. ред.)

После подстановки выражений для ​( theta=omega t )​ и для ​( a=Aomega^2 )​ получим:

Как видите, в простом гармоническом движении амплитуда ускорения ​( A_а=Aomega^2 )​ связана с амплитудой перемещения ​( A_х=A )​ формулой:

Рассмотрим еще один простой пример. Пусть диафрагма (тоненькая пластинка) в трубке домашнего телефона совершает простое гармоническое движение с частотой ​( theta=omega t )​ величиной 1 кГц (т.е. 1000 Гц) и амплитудой перемещения ( A_х=A ) величиной 1,0·10^-4 м. Чему равна амплитуда ускорения мембраны ​( A_а )​?

Поскольку ​( omega=2pi!f )​, то после подстановки этого выражения в предыдущую формулу ( A_а=-A_хomega^2 ) получим:

Подставляя численные значения, получим:

Как видите, мембрана обычного телефона испытывает очень большое ускорение, которое почти в 400 раз больше ускорения свободного падения ​( g )​ = 9,8 м/с² под действием гравитационного притяжения Земли.

Определяем частоту колебаний груза на пружине

С математической точки зрения колебания груза на пружине и движение мячика по окружности (см. предыдущие разделы этой главы) принципиально не отличаются. Дело в том, что оба эти движения являются простыми гармоничными. Поэтому их основные характеристики (например, скорость, ускорение, частота и период колебаний) должны описываться аналогичными математическими формулами. Остановимся и подробно проследим за этой аналогией.

Как известно, согласно закону Гука (см. выше в этой главе), при растяжении пружины на величину ​( x )​ возникает упругая сила ​( F )​, которая равна:

где ​( k )​ — это коэффициент пропорциональности.

Согласно закону Ньютона (см. главу 5), сила и вызванное ею ускорение ​( a )​ связаны следующим соотношением:

откуда получаем:

Из предыдущего раздела нам уже известно, что в простом гармоническом движении перемещение и ускорение выражаются следующими формулами:

и

Подставляя эти выражения в предыдущую формулу, полученную на основе законов Гука и Ньютона, получим:

Сокращая некоторые переменные, получим:

Откуда легко можно выразить циклическую частоту:

Поскольку ​( omega=2pi!f )​ и ( omega=2pi/T )​, то после подстановки предыдущего выражения в эти формулы получим:

и

Пусть пружина на рис. 12.1 обладает коэффициентом упругости ​( k )​, равным 1,0·10^-2 Н/м, а к ней прикреплен груз массой 4 г. Чему будет равен период колебаний груза на пружине? Подставляя значения в предыдущую формулу для периода, получим:

А какова частота этих колебаний? Снова подставляя значения в предыдущую формулу для частоты, получим:

Используя формулы перемещения, скорости и ускорения для простого гармонического движения (см. ранее в этой главе):

можно вычислить координату, скорость и ускорение груза на пружине в произвольный момент времени. Как будут выглядеть эти формулы для задачи с грузиком на пружине?

Сначала вычислим циклическую частоту:

Если амплитуда ​( A )​ равна 10 см, то получим:

Вычисляем энергию простого гармонического движения

В простом гармоническом движении периодически происходит увеличение и уменьшение кинетической энергии, например груза на пружине. Ясно, что кинетическая энергия груза не пропадает, а преобразуется в энергию сжатой или растянутой пружины. Эта энергия называется упругой потенциальной энергией пружины. Сколько энергии запасено в сжатой или растянутой пружине?

Попробуем вычислить ее с помощью простых соображений. Как известно, работа ​( A )​ силы ​( F )​ при перемещении на расстояние ​( s )​ равна:

При сжатии или растяжении пружины сила ​( F )​ меняется линейно с расстоянием, поэтому работу этой силы по сжатию или растяжению пружины на расстояние ( s ) можно представить как произведение средней силы ​( overline{F} )​ на перемещение ( s ):

Средняя ( overline{F} ) сила определяется как:

где ​( F_1=-kx_1 )​ — это сила упругости в точке с координатой ​( x_1 )​, a ( F_2=-kx_2 ) — сила упругости в точке с координатой ( x_2 )​. При этом перемещение ​( s )​ будет равно:

Подставляя выражения для ( s ) и ( overline{F} ) в формулу работы, получим:

Члены ​( frac{kx^2_1}{2} )​ и ( frac{kx^2_2}{2} ) выражают упругую потенциальную энергию пружины ​( E_{у1} )​ и ( E_{у2} ) в точках с координатами ​( x_1 )​ и ( x_2 ), соответственно. Таким образом, работа силы упругости равна изменению упругой потенциальной энергии пружины:

Рассмотрим простой пример. Насколько возрастет упругая потенциальная энергия пружины с коэффициентом упругости 1,0·10^-2 Н/м при сжатии ее на 10 см? Подставляя значения в формулу

получим:

Учтите, что при изменении упругой потенциальной пружины с грузом (при отсутствии внешних сил) изменяется кинетическая энергия груза. Причем эти изменения происходят так, что неизменной остается полная энергия системы, состоящей из пружины и груза. Например, при достижении точки равновесия пружина полностью разжимается, и ее упругая потенциальная энергия становится равной нулю, а кинетическая энергия груза при этом становится максимальной. И наоборот, при максимальном сжатии или растяжении пружины ее упругая потенциальная энергия становится максимальной, а кинетическая энергия груза при этом становится равной нулю.

Качаемся вместе с маятником

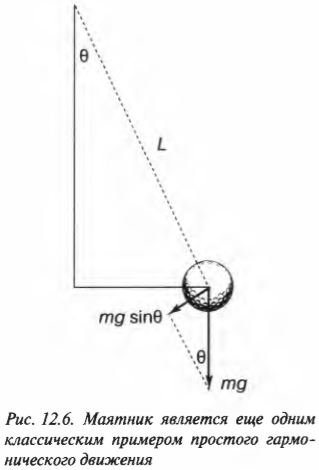
Еще одним типичным примером простого гармонического движения (кроме груза на пружине) является простой маятник, который показан на рис. 12.6.

Можно ли движение маятника описать математическими формулами простого гармонического движения, которые (выше в этой главе) использовались для описания движения груза на пружине? Да, и вот почему.

Дело в том, что на маятник, подвешенный на нити длиной ​( L )​ и отклоненный на угол ​( theta )​, действует сила гравитационного притяжения ​( mathbf{F}=mmathbf{g} )​. Перпендикулярная нити компонента силы создает сопротивление движению:

Момент этой компоненты силы

определяет угловое ускорение маятника ​( alpha )​:

Отсюда получаем формулу математического маятника:

(Математическим маятником называется идеализированная система, состоящая из невесомой и нерастяжимой нити, на которой подвешен груз с массой, сосредоточенной в одной точке. — Примеч. ред.)

При малых колебаниях, т.е. при малых значениях угла ​( theta )​; можно считать, что ​( sin(theta)approxtheta )​, и тогда прежняя формула приобретает следующий вид:

Эта формула связи ускорения и перемещения объекта очень похожа на прежние формулы простого гармонического движения груза на пружине и мячика по окружности (см. ранее в этой главе). Но прежде в эту формулу входило линейное перемещение, а теперь — угловое.

По аналогии с прежними формулами связи ускорения и перемещения объекта, совершающего простое гармоническое движение, коэффициент пропорциональности между ускорением и перемещением ​( g/L )​ равен квадрату циклической частоты ​( omega^2 )​. Отсюда получаем, что:

Далее, поскольку ​( omega=2pi!f )​ и ( omega=2pi/T ), то после подстановки предыдущего выражения в эти формулы получим:

и

Обратите внимание, что период качаний математического маятника не зависит от его массы!

Пружина
сжатия — это винтовая пружина с
фиксированным зазором между рабочими
витками способными выдержать работу
внешних сил противодействия, которые
рождаются в оси пружины.

Размеры

d	диаметр проволоки [мм, д]
D	средний диаметр пружины [мм, д]
D1	наружный диаметр пружины [мм, д]
D2	внутренний диаметр пружины [мм, д]
H	рабочая деформация [мм, д]
t	шаг активных витков в ненагруженном состоянии [мм, д]
a	расстояние между активными витками в свободном состоянии [мм, дюйм]
sx	деформация пружины [мм, д]
Lx	длина пружины [мм, д]
Fx	рабочая сила, действующая на пружину [Н, фунт]
W8	энергия деформации [Дж, фут фунт]
x	индекс, обозначающий состояние пружины

Навивка

1. Вправо
   (стандарт)

2. Влево
   (должна отображаться соответствующая
   надпись)

Состояния

1. Свободное:
   пружина не нагружена (индекс 0)

2. Предварительная
   нагрузка: пружина с минимальной рабочей
   нагрузкой (индекс 1)

3. Полная
   нагрузка: пружина с максимальной рабочей
   нагрузкой (индекс

4. Предел:
   пружина вдавлена до касания витков
   (индекс 9).

Расчетные
формулы для метрических единиц

Общие
формулы расчета

Коэффициент использования материала uS

Этот
коэффициент является отношением
напряжения при кручении полностью
нагруженной пружины к допустимому
напряжению при кручении, например
u_S₈ / _A.
Чем больше величина коэффициента, тем
меньше материала уходит на изготовление
пружины и тем меньшими получаются ее
размеры и требуемое посадочное место;
однако, при этом становится хуже
эксплуатационная стабильность пружины.
Следовательно, коэффициент использования
материала обратно пропорционален
коэффициенту долговечности. Рекомендуемый
диапазон значений коэффициента
использования материала для обычных
рабочих условий: u_S = 0,75 … 0,95.
Для пружин, применяемых в условиях
агрессивной среды, высоких температур
или ударной нагрузки, можно использовать
меньшие значения.

Запас прочности при пределе усталости kf

Этот
коэффициент используется при расчете
пружин с динамической нагрузкой (с
циклической усталостной нагрузкой при
сроке службы N > 10⁵ рабочих
циклов). Он определяется отношением
предела выносливости пружины к напряжению
при кручении материала полностью
нагруженной пружины: k_f_e / ₈.
Рекомендуемый диапазон значений запаса
прочности при предельной усталости
k_f для стандартных рабочих
условий — от 1,1 до 1,5. Более высокие
значения kf обычно используются для
пружин, применяемых в условиях сильной
коррозии, высоких температур или ударной
нагрузки. Агрессивная среда оказывает
серьезное влияние на усталостную
прочность пружины, так как в результате
этого влияния допустимая нагрузка
пружины может снизиться до одной пятой,
в зависимости от материала и типа
агрессивной среды.

Наружный
диаметр пружины

D₁ =
D + d [мм]

Где:

	D	средний диаметр пружины [мм]
	d	диаметр проволоки [мм]

Внутренний
диаметр пружины

D₂ =
D — d [мм]

Где:

	D	средний диаметр пружины [мм]
	d	диаметр проволоки [мм]

Рабочая
деформация

H
= L₁ —
L₈ =
s₈ —
s₁ [мм]

Где:

	L8	длина полностью нагруженной пружины [мм]
	L1	длина предварительно нагруженной пружины [мм]
	s8	деформация полностью нагруженной пружины [мм]
	s1	деформация предварительно нагруженной пружины [мм]

Индекс
пружины

c
= D/d [-]

Где:

	D	средний диаметр пружины [мм]
	d	диаметр проволоки [мм]

Поправочный
коэффициент Валя

Где:

	c	индекс пружины [-]
	d	диаметр проволоки [мм]

Общая
сила, действующая в пружине

Где:

	d	диаметр проволоки [мм]
		обобщенное напряжение материала пружины при кручении [МПа]
	D	средний диаметр пружины [мм]
	Kw	поправочный коэффициент Валя [-]
	G	модуль упругости материала пружины [МПа]
	s	обобщенная деформация пружины [мм]
	n	количество активных витков [-]
	F0	начальное растяжение пружины [Н]

Жесткость
пружины

Где:

	d	диаметр проволоки [мм]
	F8	рабочее усилие в полностью нагруженной пружине [МПа]
	D	средний диаметр пружины [мм]
	H	рабочая деформация [мм]
	G	модуль упругости материала пружины [МПа]
	n	количество активных витков [-]
	F1	рабочее усилие в минимально нагруженной пружине [МПа]

Средний
диаметр пружины

Где:

	d	диаметр проволоки [мм]
	k	жесткость пружины [Н/дюйм]
	G	модуль упругости материала пружины [МПа]
	n	количество активных витков [-]

Отклонение
пружины в большинстве случаев

s
= F / k [мм]

Где:

	F	Общая сила, действующая в пружине [Н]
	k	жесткость пружины [Н/дюйм]

Длина
пружины в свободном состоянии

L₀ =
L₁ +
s₁ =
L₈ +
s₈ [мм]

Где:

	L8	длина полностью нагруженной пружины [мм]
	L1	длина предварительно нагруженной пружины [мм]
	s8	деформация полностью нагруженной пружины [мм]
	s1	деформация предварительно нагруженной пружины [мм]

Расчет
конструкции пружины

При
проектировании пружины подбирается
диаметр проволоки, количество витков
и длина свободной пружины L0 для указанной
нагрузки, материала и сборочных размеров
или диаметра пружины. Шаг резьбы пружины
в свободном состоянии с рекомендуемыми
диаметрами проволоки должен лежать в
диапазоне 0,3 D ≤ t ≤ 0,6 D [мм].

Конструкция
пружины определяется с учетом условия
прочности ₈≤ u_s
_A и
рекомендуемых диапазонов некоторых
геометрических параметров пружины:

L₈ ≤ L_minF и
D ≤ L₀≤ 10
D и L₀≤ 31,5
д. и 4 ≤ D/d ≤ 16 и n≤ 2 и 12
d ≤ t < D

Где:

	D	средний диаметр пружины [мм]
	d	диаметр проволоки [мм]
	шаг активных витков в ненагруженном состоянии	шаг активных витков в ненагруженном состоянии [мм]
	8	напряжение при кручении материала пружины полностью нагруженной пружины [МПа]
	A	допустимое напряжение материала пружины при кручении [МПа]
	us	коэффициент использования материала [-]
	L8	длина полностью нагруженной пружины [мм]
	LminF	предельная длина пружины при испытании [мм]
	n	количество активных витков [-]

Если
в спецификации указаны условия
безопасности при изгибе и условия
проверки для усталостной нагрузки, они
учитываются при проектировании пружины.

В
следующем списке приведены процедуры
различных типов проектирования пружины.

Процедуры
разработки

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

10. Формулы и способы расчета пружин из стали круглого сечения по ГОСТ 13765-86 в ред. 1990г.

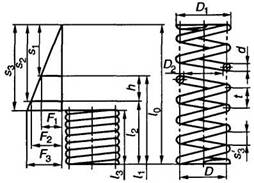
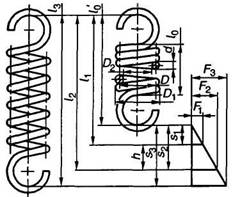
Пружина сжатия

Пружина растяжения

Продолжение табл. 10

Продолжение табл. 10

Методика определения разме­ров пружин по ГОСТ 13765-86.

1. Исходными величинами для определения размеров пружин являются силы F₁ и F₂, ра­бочий ход h, наибольшая скорость перемеще­ния подвижного конца пружины при нагружении или при разгрузке v_mах, выносливость N_F и наружный диаметр пружины D₁ (пред­варительный).

Если задана только одна сила F₂, то вместо рабочего хода h для подсчета берут величину рабочей деформации s₂, соответствующую заданной силе.

2. По величине заданной выносливости N_F предварительно определяют принадлежность пружины к соответствующему классу по табл. 1.

3. По заданной силе F₂ и крайним значени­ям инерционного зазора δ вычисляют по фор­муле (2) значение силы F₃.

4. По значению F₃, пользуясь табл. 2, пред­варительно определяют разряд пружины.

5. По табл. 11-17 находят строку, в кото­рой наружный диаметр витка пружины наибо­лее близок к предварительно заданному значе­нию D₁. В этой же строке находят соответствующие значения силы F₃ и диаметра прово­локи d.

6. Для пружин из закаливаемых марок ста­лей максимальное касательное напряжение τ₃ находят по табл. 2, для пружин из холоднотя­нутой и термообработанной τ₃ вычисляют с

учетом значений временного сопротивления R_m. Для холоднотянутой проволоки R_m опре­деляют из ГОСТ 9389-75, для термообрабо­танной — из ГОСТ 1071-81.

7. По полученным значениям F₃ и τ₃, aтакже по заданному значению F₂ по формулам (5) и (5а) вычисляют критическую скорость v_K и отношение v_max/v_K, подтверждающее или

отрицающее принадлежность пружины к предварительно установленному классу.

При несоблюдении условий v_max/v_K<1 пружины I и II классов относят к последую­щему классу или повторяют расчеты, изменив исходные условия. Если невозможно измене­ние исходных условий, работоспособность обеспечивается комплектом запасных пружин.

8. По окончательно установленному классу и разряду в соответствующей таблице на па­раметры витков пружин, помимо ранее най­денных величин F₃, D₁, и d, находят величины c₁ и s₃, после чего остальные размеры пружины и габариты узла вычисляют по формулам (6)… (25).

matios — 15 октября, 2009 — 19:49

• версия для печати