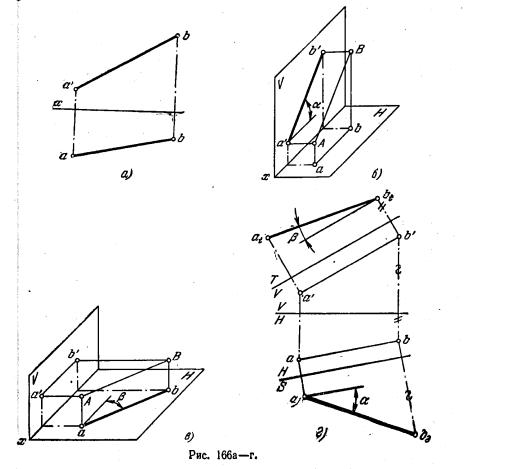
171*. Определить углы наклона прямой АВ к пл. V и пл. Н фис. 166, а).
Решение. Если прямая параллельна пл. V (рис. 166, б), то угол между этой прямой и пл. H (угол α) изображается без искажения на фронт. проекции. Если же прямая параллельна пл. H (рис. 166, в), то образуемый зтой прямой угол с пл. V (угол β) изображается без искажения на горизонт. проекции. Поэтому, поставив заданную прямую общего положения сначала параллельно пл. V, а затем параллельно пл. H, можно определить соответственно углы α и β.
На рис. 166, г показано применение способа перемены пл. проекций для определения углов α и β. Так, для определения угла α введена дополнительная пл. S, перпендикулярная к пл. H и параллельная АВ, а для определения угла β — дополнительная плоскость Т ⊥ V и в то же время || АВ.
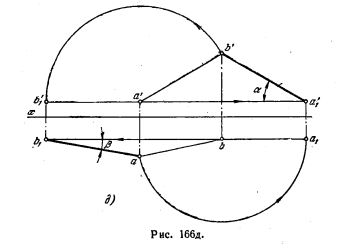
На рис. 166, д прямая как бы повернута: а) вокруг оси, проходящей через точку В и перпендикулярной к пл. H, до параллельности пл. V (положение а’1b’ , а1b) —
определен угол α; б) вокруг оси, проходящей через точку А перпендикулярно и пл. V, до параллельности пл. H (положение a’b’1, ab1) — определен угол β.
Конечно, можно изобразить эти оси на чертеже; но, как видно, построение возможно и без этого.
172. Дана пирамида SABCD (см. рис. 154). Определить углы наклона ребер пирамиды к пл. V и пл. Н.
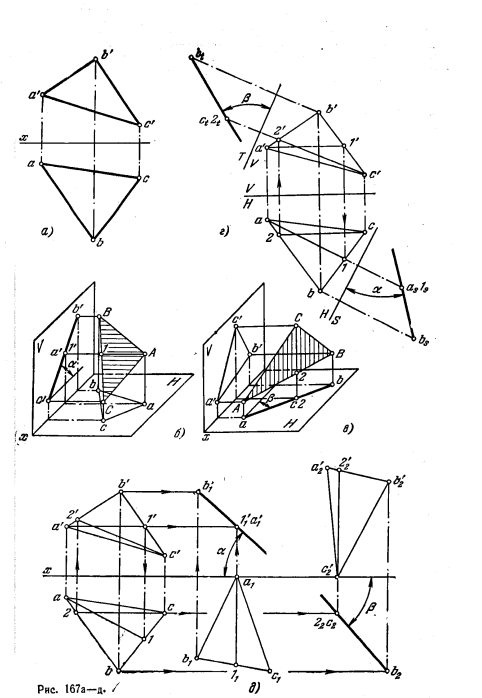
173*. Определить углы наклона плоскости, заданной треугольникам ABC (рис. 167, а), к пл. Н и пл. V.
Решение. Как известно, угол наклона (α) плоскости к пл. H проецируется без искажения на пл. V, если плоскость перпендикулярна к пл. V (рис. 167, 6), а угол наклона (β) плоскости к пл. V проецируется без искажения на пл. H, если плоскость перпендикулярна к пл. H (рис. 167, в).
На рис. 167, г для определения углаос переходим к системе S, H, где пл. S перпендикулярна к пл. H и к заданной плоскости (ось S/Н перпендикулярна к горизонт. проекции а—1 горизонтали).
Определение угла β произведено путем перехода от системы V, Н к системе Т, V, где пл. Т перпендикулярна к пл. V и к данной плоскости треугольника (ось T/V перпендикулярна к фронт. проекции с’2′ фронтали).
На рис. 167,д та же задача решена способом параллельного перемещения. Сначала все вершины заданного треугольника ABC перемещены в плоскостях, параллельных H, так, чтобы плоскость треугольника оказалась перпендикулярной к пл. V. Это
достигнуто с помощью горизонтали А—1, перемещенной так, что она расположилась перпендикулярно к пл. V (горизонт. проекция а111 перпендикулярна к оси х). Получаем угол α наклона плоскости треугольника к пл. H без искажения.
Для определения величины угла β наклона плоскости треугольника ABC к пл. V треугольник повернут так, чтобы он расположился перпендикулярно к пл. H. Это сделано при помощи фронтали С—2: она поставлена перпендикулярно к пл. H (положение C222, фронт. проекция с’22′2 ⊥ х) и, следовательно, проходящая через эту фронтвль плоскость также перпендикулярна к пл. H.
174. Дана пирамида SABC (см. рис. 161). Определить углы наклона граней SAB, SAC и ABC к пл. H и пл. V.
175. Дан параллелепипед (см. рис. 165). Определить углы наклона основания ABCD и грани CDHG к пл. V и грани ADEH к пл. Н.
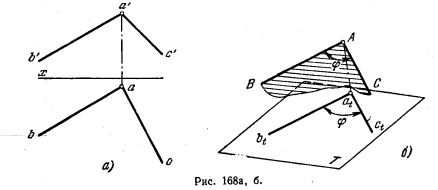
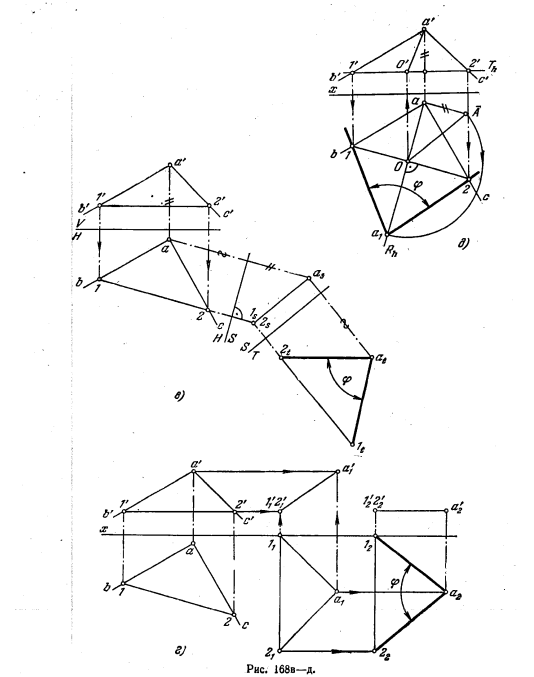
176*. Определить величину угла ВАС (рис. 168, а).
Решение. Если плоскость угла параллельна какой-либо пл. проекций, то данный угол проецируется на нее без искажения (рис. 168, б).
На рис. 168, в задача решена при помощи способа перемены пл. проекций. Так как плоскость угла ВАС является плоскостью общего положения (ее горизонталь не перпендикулярна ни к одной из плоскостей V, Н, W), то приходится сначала дополнить систему V, H пл. S, взяв ее перпендикулярно к пл. H и к плоскости угла ВАС. В результате этого преобразования проекция угла на плоскости S получится в виде отрезка as ls. Теперь можно ввести еще одну дополнительную пл. проекций (T), проведя ее перпендикулярно к пл. S и в то же время параллельно плоскости угла ВAС. Угол ltat2t представит собою натуральную величину угла ВАС.
На рис. 168, а искомый угол ср определен способом параллельного перемещения.
Сначала плоскость угла перемещена так, чтобы она стала перпендикулярной к пл. V (для этого располагаем горизонт. проекцию горизонтали перпендикулярно к оси х). Затем располагаем плоскость угла параллельно пл. H, для чего перемещаем проекцию 1′1a’1 в положение 1′2a’2 (т. е. || оси х). Еще одно построение показано на рис. 168,6. Здсь для определения величины угла применен поворот вокруг горизонтали: плоскость угла расположится параллельно пл. H (положение Т).
Построения выполнены в следующем порядке:
1. Проведена плоскость вращения точки А — горизонтально-проецирующая пл. R, перпендикулярная к горизонтали (т. е. к оси вращения).
2. Отмечен центр вращения точки АВ пересечении горизонтали с пл. R (точка О, О’) и указаны проекции радиусАВращения (Оа и О’а’).
3. Определена натуральная величина радиуса вращения (ее выражает гипотенуза ОА треугольника ОаА).
4. Проведена дуга окружности радиуса ОА я на Rh, найдена точка a1— горизонт. проекция вершины угла после его поворота вокруг горизонтали до совмещения с пл. Т — и построен угол 1а12, равный искомому.
Для решения задач типа 176 наиболее рациональным является применение вращения вокруг горизонтали (или фронтали), как это показано на рис. 168, д.
177. Дана пирамида SABC (см. рис. 156). Вращением вокруг горизонтали определить угол между ребрами и SB, SB и SC, SC и SA.
178. Дан параллелепипед (см. рис. 165). Определить углы между ребрами DH и CD, CG и CD, АВ и ВС.
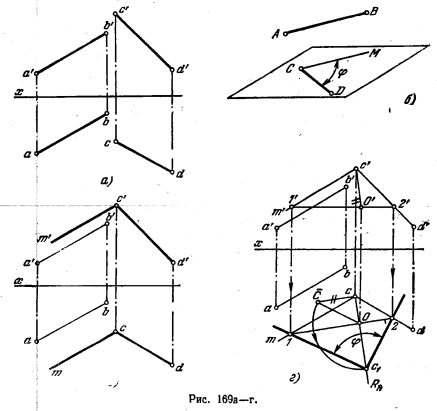
179*. Определить величину угла между скрещивающимися прямыми АВ и CD (рис. 169, а).
Решение. Угол между двумя скрещивающимися прямыми определяется углом, доставленным пересекающимися прямыми, соответственно параллельными данным скрещивающимся. Для определения величины угла надо начать с его изображения нр чертеже. Это сделано на рис. 169,6, причем использована одна из заданных прямых — CD, через точку С которой проведена прямая СМ, параллельная другой заданнай прямой—АВ. Величина угла MCD (рнс.169, в) выражает угол между прямыми АВ и CD. Это сделано при помощи поворота вокруг горизонтали 1—2 (рис. 169, а), взятой в пл. угла MCD.
180. Дана пирамида SABC (см. рис. 160). Определить величину угла между ее ребрами: a) SB и АС, б) SA и ВС.
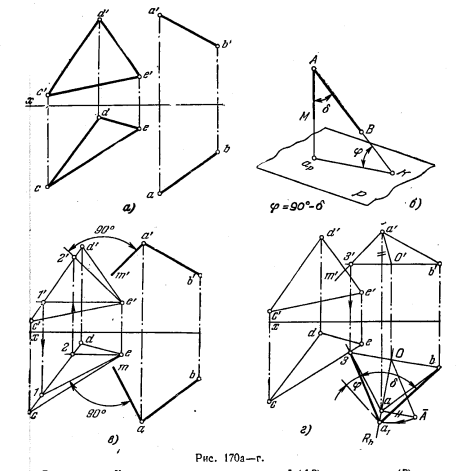
181*. Определить величину угла φ наклона прямой АВ к плоскости, заданной треугольником CDE (рис. 170, а).
Решение. Как известно, углом между прямой (АВ) и плоскостью (Р) называется острый угол (φ) между прямой и ее проекцией (аpК) на этой плоскости. Для построения (рис. 170, б) этого угла надо найти точки пересечения с пл. Р прямой АВ и перпендикуляра, проведенного из какой-либо точки прямой АВ на пл. Р. Но если, как в данной задаче, требуется лишь определить величину угла наклона прямой к плоскости, то проще определить величину угла δ, дополнительного к углу φ: найдя угол δ, можно определить величину угла φ из соотношения φ = 90° — δ. На рис. 170, в показано построение проекций am и а’m’ перпендикуляра к плоскости треугольника CDE, для чего взяты горизонталь цфронталь этой плоскости: am ⊥ e — 1, а’m’ ⊥ е’2′.
Теперь можно определить (рис. 170,г) натуральную величину угла δ с вершиной А,- что сделано поворотом вокруг горизонтали b’З’, b—3. Искомый угол φ = 90°—δ.
182. Дана пирамида SABC (см. рис. 1611. Определить углы наклона ребер SA, SB и SC к грани AВС
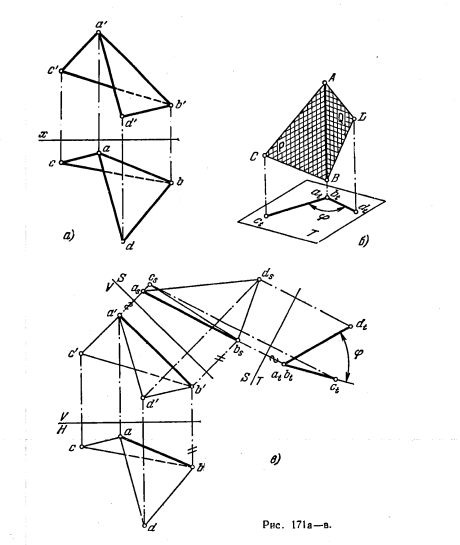
183*. Определить угол между гранями АBС и ABD (рис. 171, а).
Решение. Двугранный угол измеряется линейным углом, полученным в пересечении граней двугранного угла плоскостью, перпендикулярной к обеим граням двугранного,а следовательно, и к линии их пересечения, т. е. ребру двугранного угла. Если это ребро АВ окажется перпендикулярным к какой-либо пл. Т (рис. 171,6), то полученная на пл. Т проекция двугранного угла выражает его линейный угол.
Для решения задачи (рис. 171, в) применен способ перемены пл. проекций. Oт системы V, H совершен переход к системе S, V, где S ⊥ V и S || АВ, а затем от этой системы S, V переход к системе Т, S, где T ⊥ S и Т ⊥ AB.
Треугольники проецируются на пл.Т в виде отрезков аtct и аtdt. Угол между ними равен искомому углу φ.
На рис. 171, г показано решение той же задачи при помощи способа параллельного перемещения: ребро АВ поставлено перпендикулярно к пл. Н.
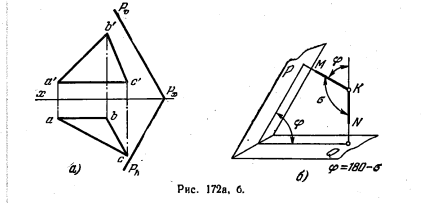
184*. Определить величину угла, образованного плоскостью Р и плоскостью треугольника ABC (рис. 172, а).
Решение. Если, решая данную задачу, придерживаться схемы решения предыдущей, то необходимо построить прямую пересечения заданных плоскостей. Но можно поступить и иначе, без построения этой прямой, т. е. не определяя ребра искомого двугранного угла. Можно поступить следующим образом: определить не непосредственно угол φ, а угол σ (рис. 172, б) между перпендикулярами КМ и KN, проведенными из какой-либо точки К на заданные плоскости. Найдя угол σ, получаем φ = 180° — σ.
Такое решение отличается в своей сущности от решений по рис. 171, в и 171, а. Взяв некоторую точку К (рис. 172, в), проведем из нее перпендикуляры КN и КМ соответственно к плоскости треугольника ABC н к пл. Р: из точки k’ проводим k’n’ ⊥ a’b’ и k’m’ ⊥ Pϑ, а из точки k — kn ⊥ ac и km ⊥ Ph. Таким образом получается угол с проекциями mkn и n’k’n’ (угол σ) .Натуральная величина этого угла получена поворотом вркруг фронтали 1—2 (рис. 172, г). Так как получен острый угол, то можно
считать, что он определяет искомый угол между заданными плоскостями, так как из смежных углов, полученных при взаимном пересечении двух плоскостей, углом между плоскостями считается острый.
185. Дана пирамида SABCD (см. рис. 154). Определить способом перемены плоскостей проекций углы между гранями SAB и SBC, SBC и SCD, SAD и SAB.
186. Дан параллелепипед (рис. 165). Определить углы между гранями CDHG и EFGH, BCGF и CDHG.
Определение натуральной величины угла
Чтобы определить натуральную величину угла, нужно перевести его в положение, в котором его стороны будут параллельны плоскости проекции. Наиболее рациональный путь решения данной задачи – использовать способ вращения вокруг линии уровня. Более трудоемкими вариантами являются метод замены плоскостей проекций и параллельное перемещение.
Задача
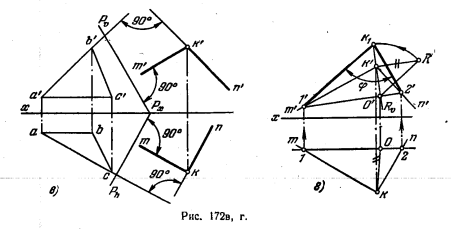
Приведенный ниже пример иллюстрирует нахождение угла между пересекающимися прямыми m и n способом вращения вокруг фронтали.
Последовательность построений:
- В произвольном месте чертежа проводим фронталь f. Она пересекает прямые m и n в точках 1 и 2. Определяем их недостающие проекции.
- Через точку K» проводим перпендикуляр к f». На пересечении этого перпендикуляра с фронталью находится проекция центра вращения O». По линии связи определяем положение т. O’.
- Находим величину радиуса R поворота точки K. Для этого перпендикулярно O»K» откладываем отрезок K»K0 = yk – yo. Таким образом, R равен O»K0 – гипотенузе прямоугольного треугольника O»K»K0.
- Проводим дугу радиусом R до её пересечения с перпендикуляром O»K» в точке K»1. Соединяем K»1 c точками 1» и 2». Натуральная величина угла между прямыми m и n равна углу ϕ при вершине K»1.
Более подробную информацию о методе вращения вокруг линии уровня, который мы здесь использовали, вы можете найти на следующей странице.
Определение угла между скрещивающимися прямыми
Углом между скрещивающимися прямыми называют плоский угол, стороны которого параллельны данным прямым. На изображении, приведенном ниже, прямые e и d скрещивающиеся и друг с другом не пересекаются. Чтобы найти угол между ними, выполним ряд графических построений:
Описание решения
- На любом свободном месте чертежа отмечаем точку S. Располагаем её произвольно (проекции S» и S’ показаны на рисунке).
- Через точку S проводим прямые a и b так, чтобы они были параллельны e и d. В нашем случае a||e, b||d соответственно.
- Строим горизонталь h, которая будет играть роль оси вращения. Перпендикулярно h’ из точки S’ проводим прямую. Она пересекает h’ в т. O’ – горизонтальной проекции центра вращения.
- Определяем радиус поворота R как гипотенузу треугольника O’S’S0. При этом катет S’S0 равен разности удаления точек S» и O» от горизонтальной плоскости.
- Находим т. S’1 на пересечении дуги радиуса R с прямой S’O’. Соединяем S’1 c точками 1′ и 2′, которые своего положения не меняют. Угол ϕ при вершине S’1 искомый. Задача решена.
Похожие задачи:
- Построение угла между прямой и плоскостью
- Построение угла между двумя плоскостями
Определение угла между плоскостями
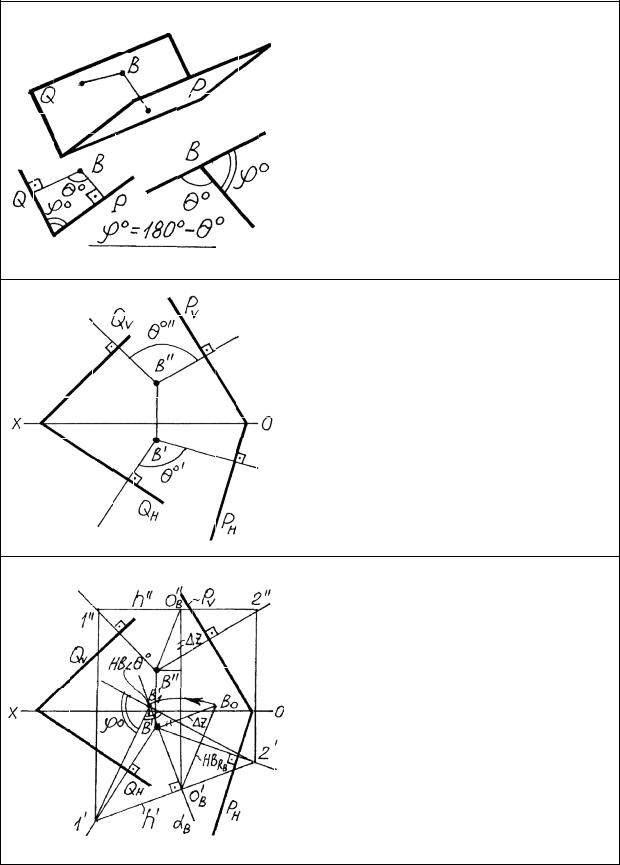
Наиболее эффективным методом определения угла между двумя плоскостями является метод дополнительного угла. Дополнительным углом называется угол между двумя перпендикулярами, опущенными из любой точки на обе плоскости. Искомый и дополнительный углы связаны формулой, которая реализуется графически.
Требуется определить угол между двумя плоскостями. Из любой точки между плоскостями, например В, опустим перпендикуляры на заданные плоскости. Проекции перпендикуляров проводим согласно алгоритму перпендикулярности. Между проекциями перпендикуляров образуются проекции дополнительного угла.
Определим натуральную величину дополнительного угла методом вращения вокруг горизонтали. Объектом вращения будет вершина В угла. Проводим через В/ плоскость вращения, находим центр вращенияО, определяем натуральную величину радиуса вращения Rв и откладываем его вдоль плоскости вращения. Графически находим искомый угол.
45
Методы построения сечений многогранников
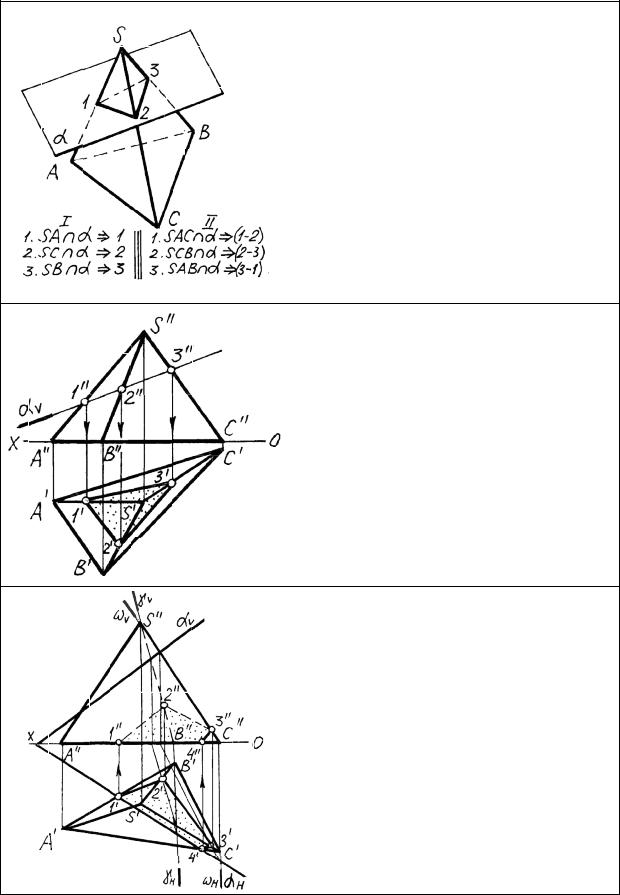
Разработано два метода построения сечений многогранников – метод ребер и метод граней. В методе ребер находят точки пересечения ребер многогранника с секущей плоскостью, т.е. несколько раз решают типовую задачу о пересечении прямой с плоскостью. В методе граней находят линии пересечения граней многогранника с плоскостью, т.е. решают типовую задачу о -пере сечении плоскостей.
Рассмотрим пересечение пирамиды фронтально-проецирующей плоскостью. Решаем задачу методом ребер. Так как секущая плоскость фрон- тально-проецирующая, то на фронтальной проекции точки пересечения определяются без построений. По линиям связи находим горизонтальные проекции точек, соединив которые получим сечение.
Если секущая плоскость является плоскостью общего положения,то задача усложняется. При построении точек сечения проводим через ребра вспомогательные плоскости частного положения, находим линии пересечения заданной и вспомогательной плоскостей и на пересечении ребер с линиями пересечения находим искомые точки.
46
Построение разверток многогранников
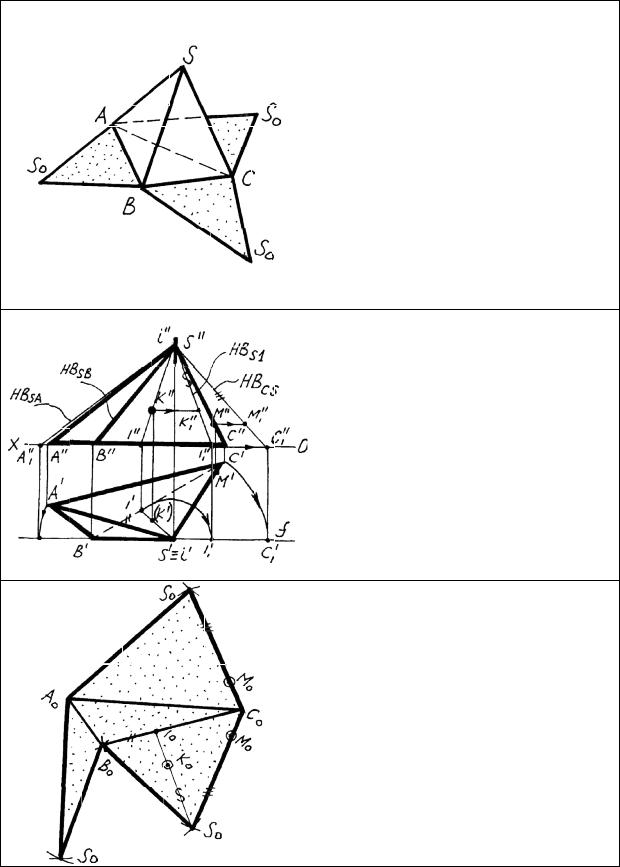
При построении разверток многогранников используют два метода: метод раскатки и метод нормального сечения. Наиболее распространен первый метод. Метод раскатки заключается в том, что многогранник условно разрезают по ребрам и «раскатывают» грани в одну плоскость.
Рассмотрим построение развертки пирамиды.
Требуется построить развертку и указать на ней точкиК и М, лежащие на поверхности пирамиды. Сначала определяем натуральную величину ребер методом вращения вокруг оси i. Проекции точки К находим с помощью вспомогательной прямой.
Далее на свободном поле чертежа строим основание пирамиды. К основанию пристраиваем боковые грани пирамиды. Точку К на развертке строим с помощью вспомогательной прямой. Все построения проводятся с помощью циркуля.
47
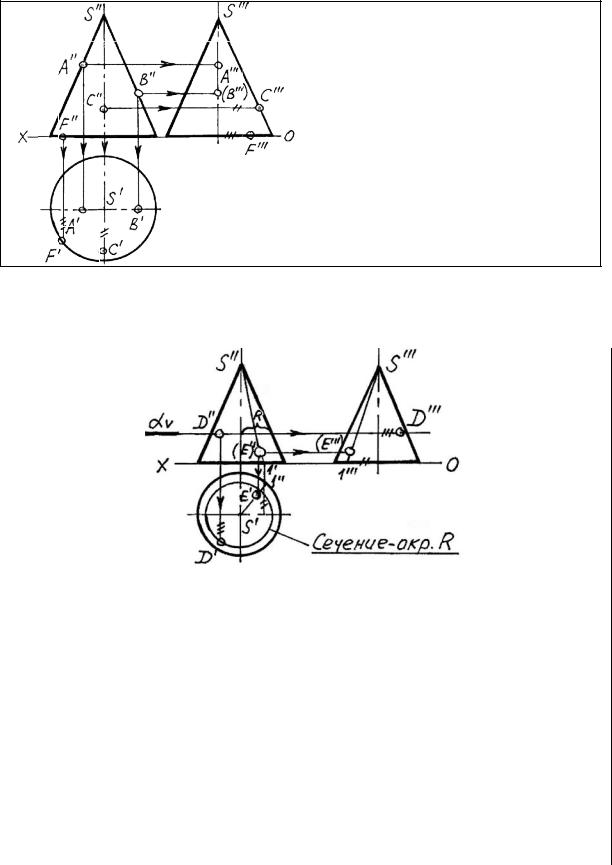
Построение проекций особых точек на поверхности
Особые (характерные) точки – это точки, лежащие на образующих поверхности, основаниях, и точки, совпадающие с осями. При построении проекций характерных точек исполь-
зуется одно из свойств эпюра Монжа : АХА/ = AZA///.
Построение промежуточных точек на поверхности
|
Промежуточные |
точки |
занимают |
общее |
положение |
на |
|
|
поверхности. Их построение связано с определенными трудностями. |
||||||
|
Имеется два способа построения проекций промежуточных точек: |
||||||
|
способ образующих и метод секущих вспомогательных плоскостей. |
||||||
|
Первый метод заключается в том, что через проекцию точки проводят |
||||||
|
образующую линию (прямую), строят ее проекции и на них находят |
||||||
|
проекции точки. |
||||||
|
По второму способу через точку проводят вспомогательную |
||||||
|
плоскость, строят сечение поверхности вспомогательной плоскостью |
||||||
|
и на контуре сечения находят проекцию промежуточной точки. |
||||||
|
Третью проекцию строят с помощью упомянутого свойства эпюра |
||||||
|
Монжа. В качестве вспомогательных плоскостей применяют плос- |
||||||
|
кости, которые образуют простые сечения поверхностей. |
48
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
На этой странице вы узнаете
- Как мы сталкиваемся с двугранными углами, когда читаем книгу?
- Где в комнате можно найти перпендикулярные плоскости?
- Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Стереометрия — это не просто раздел математики, который нужно долго и нудно учить. На самом деле стереометрия описывает всю нашу жизнь. Стало интересно? Давайте разбираться.
Углы между плоскостями
Мы точно знаем, что угол между стеной и полом равен 90°. Также, как и угол между стеной и потолком, или полом и любым предметом мебели.
Но чему равен угол между двумя открытыми страницами тетради? Или угол между стеной и полуоткрытой дверью? Угол между перилами и плоскостью пола? Все эти углы достаточно легко найти. И ответы на все эти вопросы нам дает именно стереометрия.
Начнем разбирать в углах между плоскостями с того, что введем понятие двугранного угла.
Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу.
Если мы откроем книгу не полностью и посмотрим на пространство между двумя страницами, это пространство и будет двугранным углом.

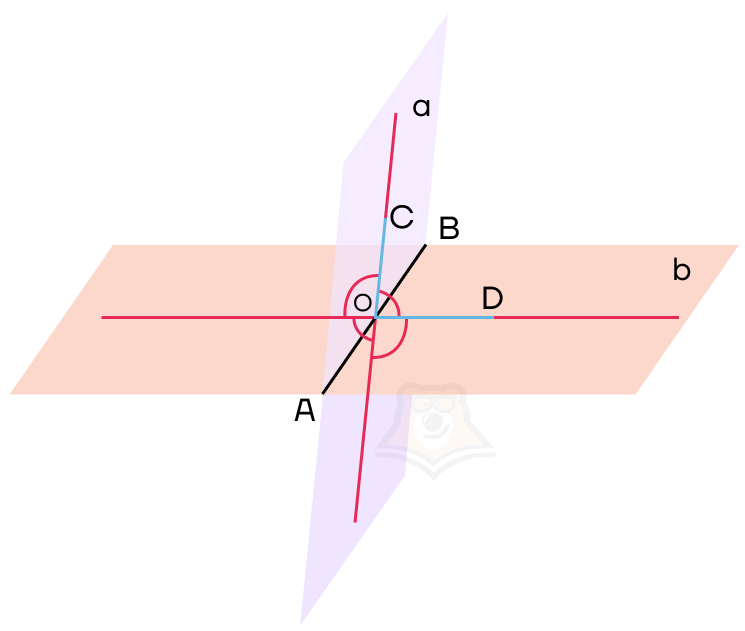
На рисунке:
АВ — общая прямая для плоскостей, ее называют ребром двугранного угла;
a, b — плоскости, которые образуют двугранный угол, они называются гранями двугранного угла.
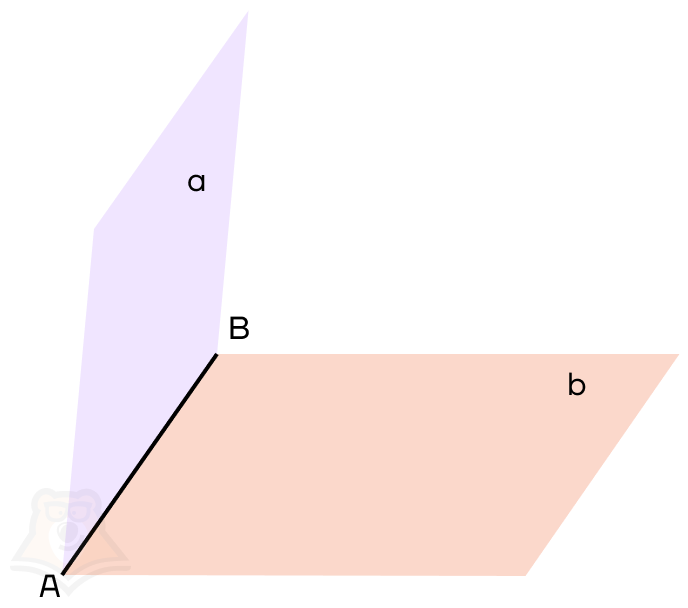
Если раскрыть книгу не полностью, то ее страницы будут образовывать двугранный угол, то есть часть пространства, заключенную между двумя страницами.
Заметим, что при пересечении двух плоскостей обычно образуется четыре двугранных угла. Нас интересует меньший из них.
Настало время ввести понятие угла между двумя плоскостями. Но для этого нам нужно провести перпендикуляры к ребру двугранного угла в каждой плоскости. Важно, чтобы перпендикуляры пересекались в одной точке.
Проведенные перпендикуляры образовали четыре угла. Меньший из них и будет называться углом между плоскостями.
Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях.
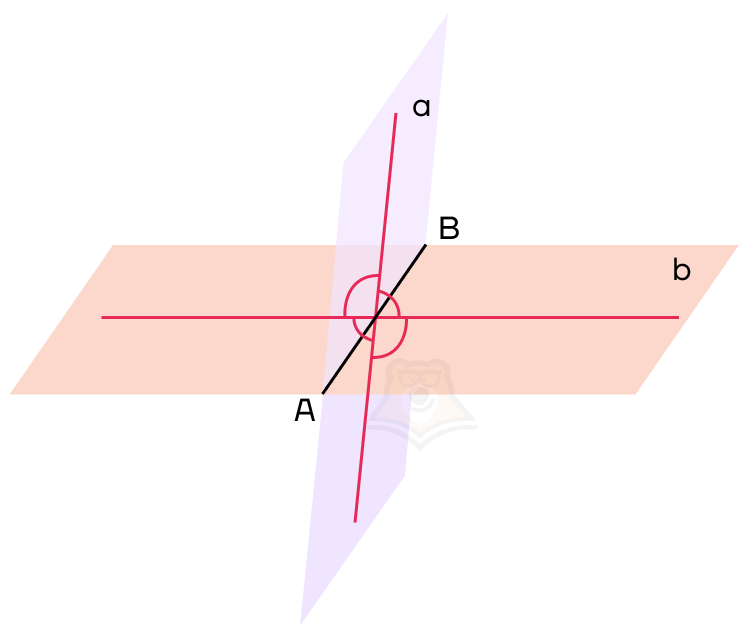
Обозначим нужный нам угол на рисунке как угол COD. Он и будет являться углом между данными плоскостями.
Угол COD также будет называться линейным углом двугранного угла.
Линейный угол двугранного угла показывает градусную меру двугранного угла. Поскольку двугранный угол — это часть пространства, то в этом пространстве можно провести множество линейных углов, которые будут равны между собой.
Как и обычные углы, углы между плоскостями бывают трех видов:
- Острые, то есть меньше 900
- Прямые, равные 900
- Тупые, которые больше 90и меньше 1800
Как уже было сказано выше, за угол между плоскостями всегда принимается острый угол, образованный этими плоскостями.
А что будет, если между плоскостями получится прямой угол?
Такие плоскости называются перпендикулярными.
Достаточно посмотреть на стены и пол, или стены и потолок. А еще на углы потолка — в них будет три перпендикулярные плоскости.
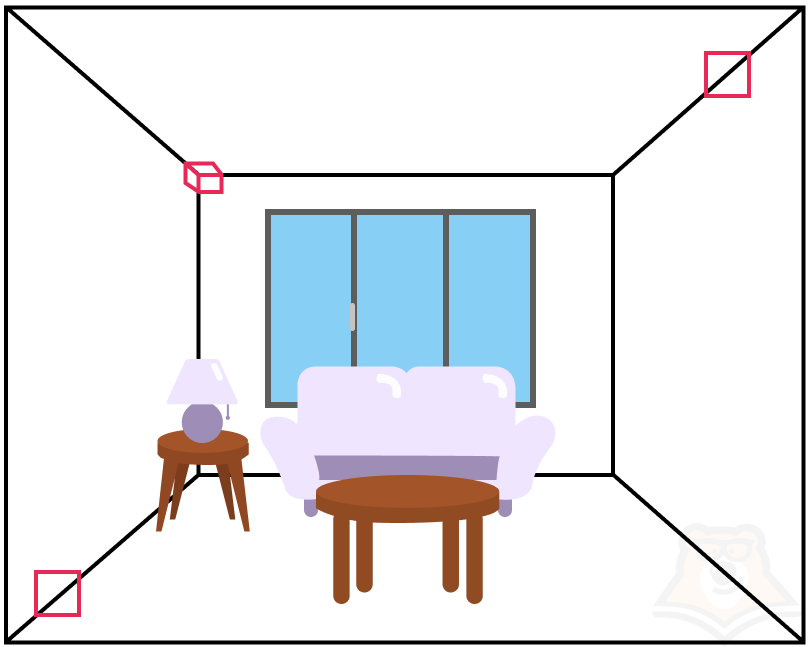
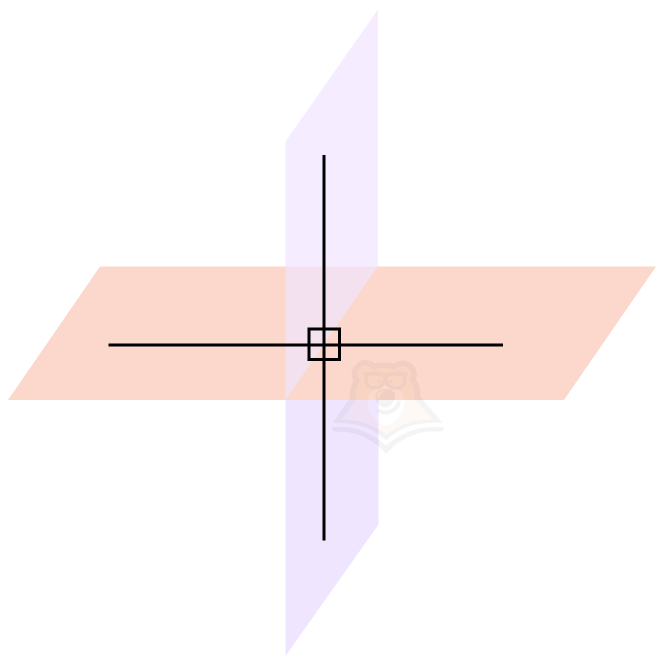
У перпендикулярных плоскостей есть одна очень интересная особенность: все углы, образованные ими, равны между собой и равняются 90° градусам.
Чтобы найти угол между плоскостями, необходимо следовать следующему алгоритму.
1 шаг. Найти линию пересечения плоскостей.
2 шаг. Достроить к этой линии перпендикуляр в каждой плоскости.
3 шаг. Найти острый угол между построенными перпендикулярами.
Углы между прямой и плоскостью
Если нарисовать две прямые на листе бумаги, мы с легкостью можем измерить угол между ними с помощью транспортира. А если провести прямую к плоскости, как точно измерить угол между ними?
И в этом вопросе к нам снова на помощь приходит стереометрия. Но для начала рассмотрим, что такое угол между прямой и плоскостью.
Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость.
Что такое проекция? Предположим, мы проткнем лист бумаги (плоскость) очень длинной иглой.
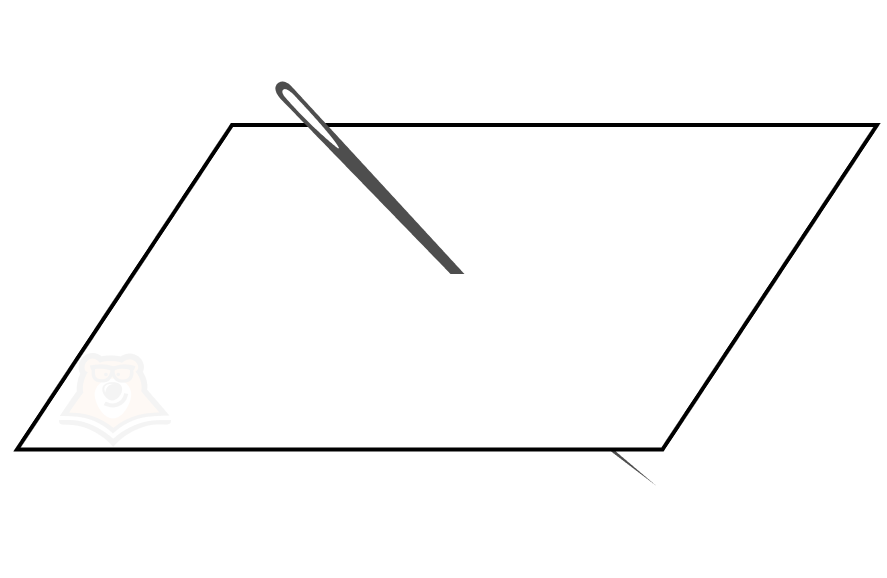
А теперь сделаем этот рисунок ближе к чертежу. Пусть плоскость а пересекает прямая а в точке О.
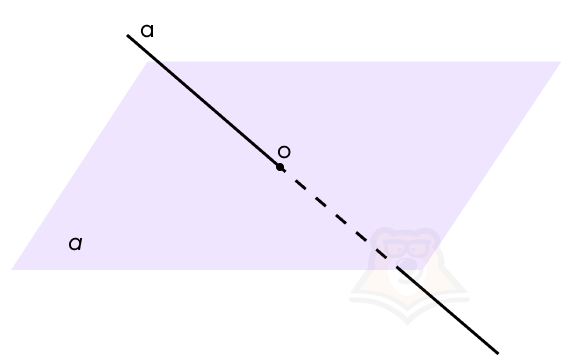
Начнем строить проекцию. Прежде чем разобраться, что такое проекция прямой на плоскость, найдем проекцию точки на плоскость.
Возьмем на нашей прямой а точку А и опустим из нее перпендикуляр к плоскости а. Точка, в которой перпендикуляр пересечет плоскость, будет называться проекцией точки на плоскость. На рисунке обозначим ее как А1.
Проекция точки на плоскость — это основание перпендикуляра, опущенного из этой точки на плоскость.
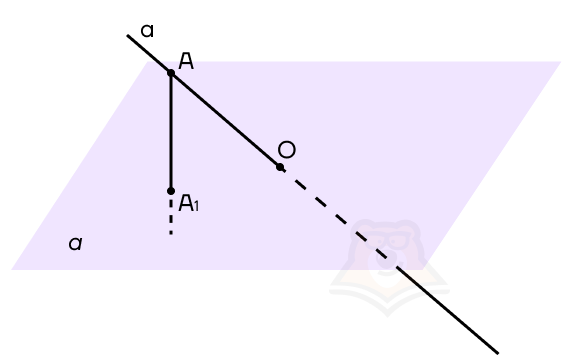
Теперь, если мы будем брать каждую точку на прямой и проектировать ее на плоскость а, то получим проекцию этой прямой на плоскость. Но поскольку на прямой бесконечное множество точек, достаточно соединить точки А1 и О, получаем, что А1О — проекция прямой а на плоскость а.
Заметим, что если мы проведем из любой точки прямой проекцию к плоскости, то попадем на прямую А1О.
Проекция прямой а на плоскость — это прямая а1, образованная проекциями всех точек прямой а на плоскость.
Таким образом можно построить проекции не только прямой, но и любой фигуры.
Мы построили угол из определения. Тогда углом между прямой а и плоскость а будет угол А1ОА.
В этом случае мы также берем острый угол, образованный прямой и плоскостью.
Шаг 1. Построить проекцию прямой на плоскость.
Шаг 2. Найти угол между прямой и построенной проекцией.
Если прямая параллельна плоскости угол будет равен 0.
Проекция прямой на плоскость будет этой же прямой, просто лежащей в плоскости.
Когда прямая перпендикулярна плоскости, проекцией прямой на плоскость будет точка пересечения прямой и плоскости. Угол между прямой и плоскостью будет равен 90°.
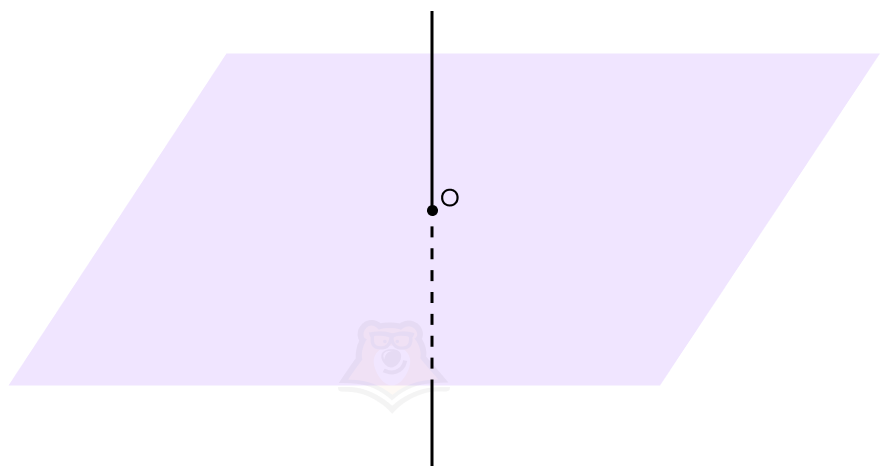
Чуть подробнее остановимся на случае, когда прямая перпендикулярна плоскости.
Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости.
А что делать, если прямая будет перпендикулярна только одной прямой из плоскости? По определению обязательно, чтобы она была перпендикулярна всем прямым из плоскости. Как тогда проверить перпендикулярность?
Для этого существует признак перпендикулярности прямой и плоскости:
- Если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.
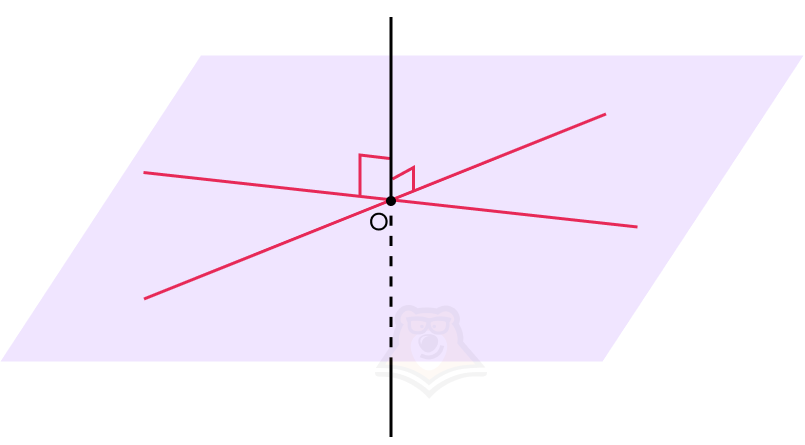
Следовательно, если необходимо в задаче доказать перпендикулярность прямой и плоскости, достаточно доказать, что прямая будет перпендикулярна всего двум пересекающимся прямым в этой плоскости, а не всему множеству прямых, лежащий в данной плоскости.
Рассмотрим несколько интересных свойств, связанных с прямой, перпендикулярной к плоскости.
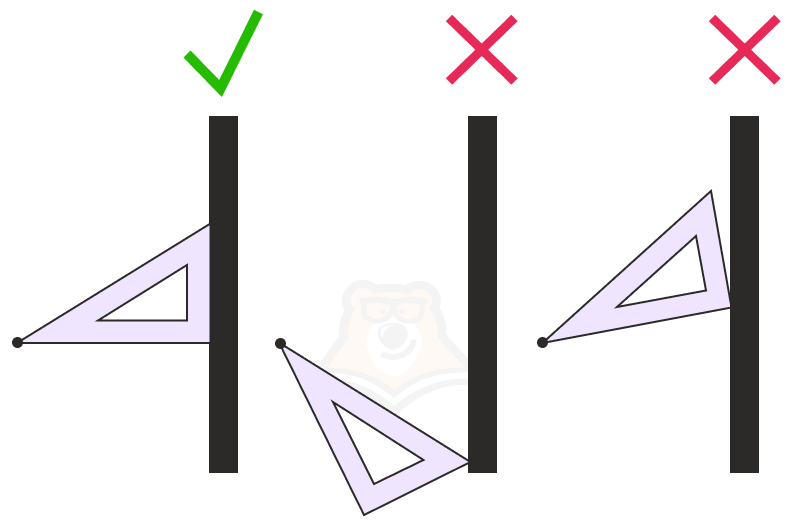
Свойство 1. Через любую точку пространства можно провести единственную прямую, перпендикулярную плоскости.
Попробуйте подставить уголок к стене из любой точки. Получится ли у вас сделать так, что из одной и той же точки уголок встанет перпендикулярно стене несколько раз? Нет.
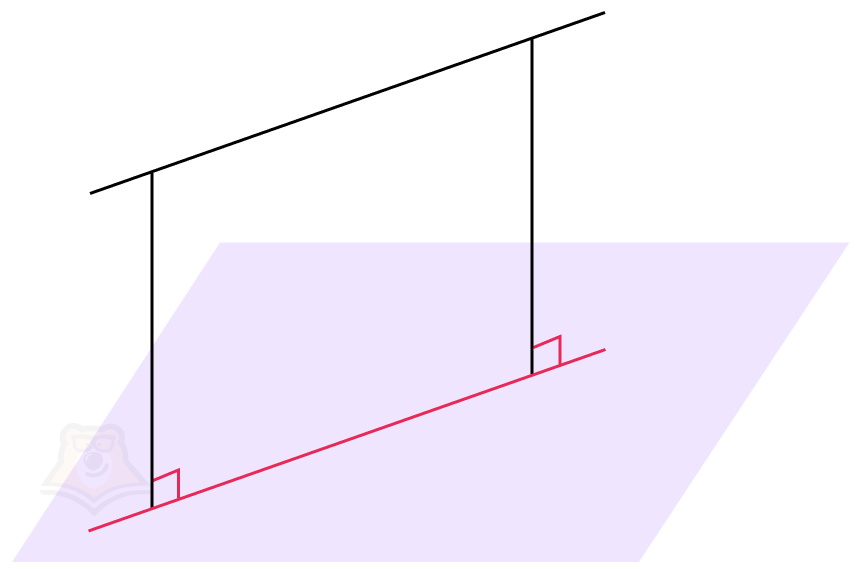
Свойство 2. Если две прямые перпендикулярны одной и той же плоскости, то такие прямые параллельны.
Здесь тоже просто все доказать. Достаточно построить в плоскости прямую, которая пересечет две данные прямые и посмотреть на рисунок “сбоку”. Заметим, что соответственные углы равны, а значит, прямые параллельны.
Подробнее про соответственные углы и параллельные прямые можно прочитать в статье “Основы планиметрии”.

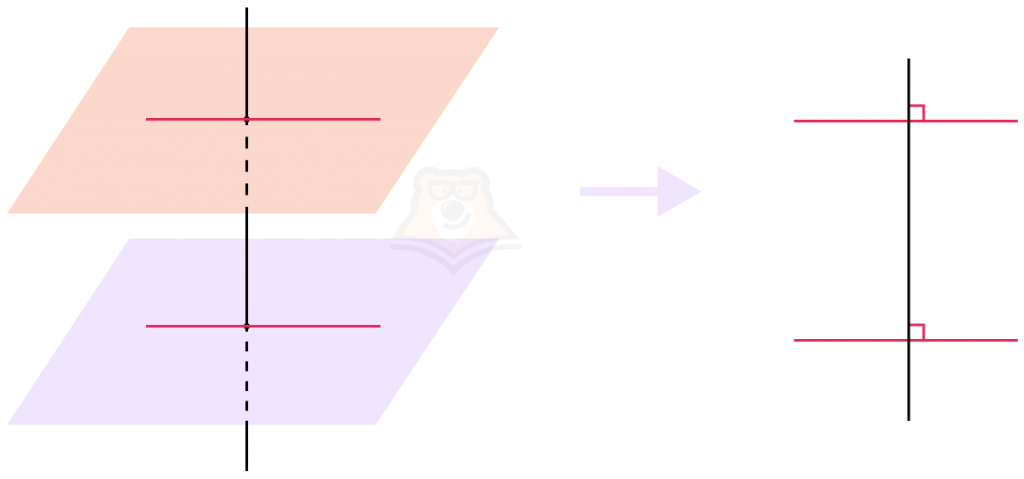
Свойство 3. Если к одной прямой перпендикулярны две плоскости, то такие плоскости параллельны.
Тут такие же рассуждения, как и в предыдущем свойстве: достаточно построить прямые, принадлежащие плоскостям, и посмотреть на них “сбоку”.
Свойство 4. Если через перпендикулярную к плоскости прямую проходит плоскость, то данные плоскости будут перпендикулярны.
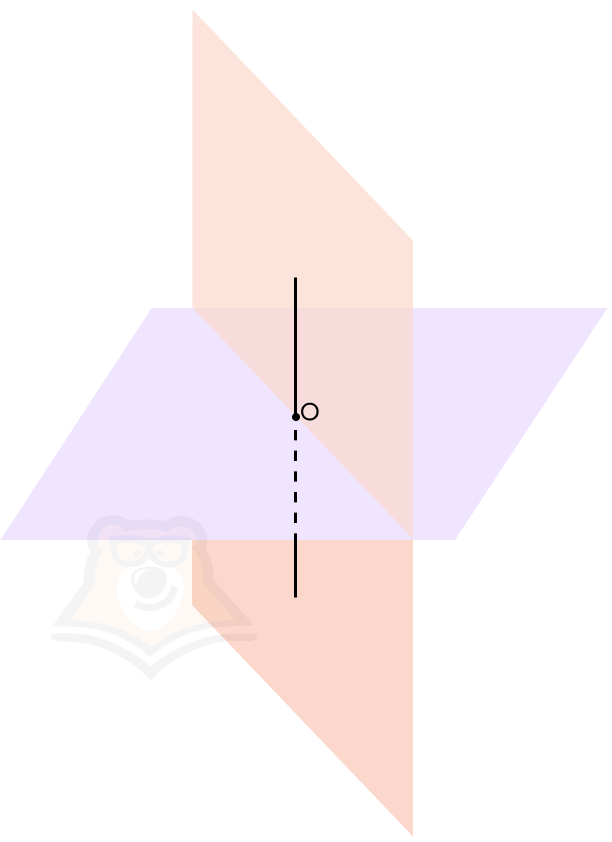
Это легко проверить, если найти любой двугранный угол между построенными плоскостями.
Теорема о трех перпендикулярах
Разберем еще одну очень интересную теорему, связанную с проекциями прямой на плоскость. А именно мы рассмотрим теорему о трех перпендикулярах.
Для начала попробуем понять ее на реальных предметах.
Как с помощью линейки и листа воспроизвести в жизни теорему о трех перпендикулярах?
Возьмем уголок и зафиксируем его строго вертикально на листе. Для удобства назовем уголок АВС, где С — прямой угол.
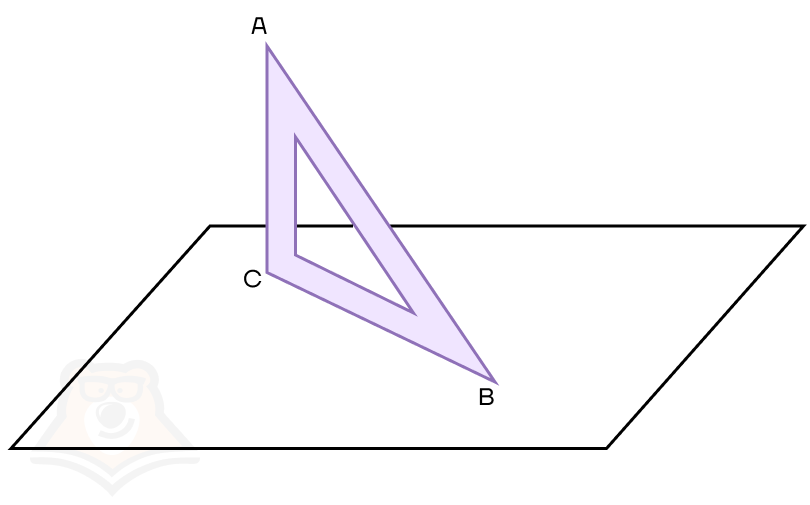
Сразу заметим, что прямая АС будет перпендикулярна плоскости листа (поскольку уголок стоит строго вертикально, а лист лежит строго горизонтально).
Дальше заметим, что прямые АС и ВС также перпендикулярны, поскольку в уголке угол С равен 90°.
Посмотрим чуть-чуть внимательнее и обратим внимание, что прямая ВС при этом будет проекцией на плоскость листа прямой АВ.
Немного достроим наш рисунок и через точку В проведем прямую, перпендикулярную ВС. Назовем эту прямую КМ.
Сразу отмечаем, что прямая КМ перпендикулярна ВС по построению, а также перпендикулярна прямой АС (поскольку АС — перпендикуляр к плоскости листа).
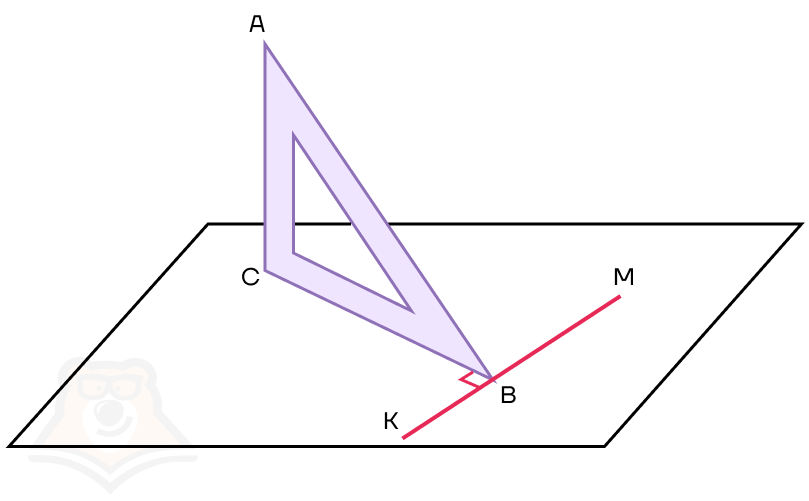
Можем ли мы что-то еще сказать про нашу ситуацию? Оказывается, прямая АВ также будет перпендикулярна прямой КМ.
Возникнет вопрос, почему?
1. Вспомним признак перпендикулярности прямой и плоскости: если прямая перпендикулярна к двум пересекающимся прямым в этой плоскости, то она будет перпендикулярна этой плоскости.
Теперь узнаем, как этот признак выполняется в данной ситуации.
2. Посмотрим на ситуацию немного под другим углом и в этот раз возьмем за плоскость не лист, а нашу линейку.
3. Тогда две пересекающиеся прямые в плоскости линейки будут перпендикулярны прямой КМ: BCKM по построению, а ACKM как прямая, перпендикулярная к плоскости листа, а значит, и перпендикулярная всем прямым в этой плоскости.
4. Получается, что прямая КМ перпендикулярна плоскости АВС, следовательно, перпендикулярна и всем прямым в этой плоскости, в том числе прямой АВ.
Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции.
Мы рассмотрели теорему о трех перпендикулярах. Осталось ее только сформулировать математическим языком.
Теорема о трех перпендикулярах
Если наклонная прямая АВ к плоскости а перпендикулярна прямой КМ в этой плоскости, то и проекция прямой АВ на плоскость а перпендикулярна к прямой КМ.
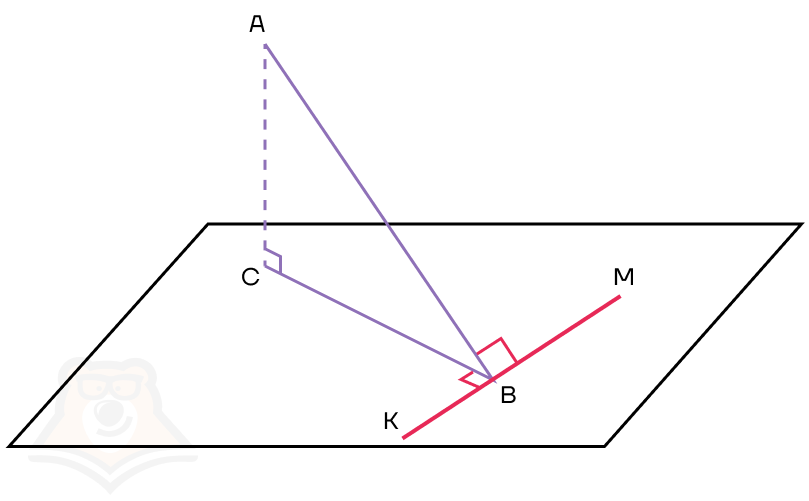
Для построения чертежа заменим линейку на несколько отрезков. Тогда АВ — наклонная, ВС — проекция, КМ — прямая в плоскости.
Для этого нужно взять лист бумаги и треугольную линейку. На листе бумаги построить произвольную прямую, а после поставить линейку строго вертикально так, чтобы основание линейки на листе было перпендикулярно начерченной прямой.
Таким образом, длинная сторона линейки будет наклонной прямой, основание — ее проекцией, а начерченная линия — перпендикуляром к проекции.
Вот и все, ничего сложного. А называется теорема так потому, что в построении действительно присутствуют три перпендикуляра, которые отлично видно на рисунке.
Теорему о трех перпендикулярах можно активно использовать для доказательства и решении задач.
Фактчек
- Двугранный угол — это часть пространства, заключенная между двумя полуплоскостями, имеющими общую границу. Градусной мерой двугранного угла будет линейный угол двугранного угла или, другими словами, угол между плоскостями.
- Угол между плоскостями — это угол между перпендикулярами, проведенными к линии пересечения плоскостей. Перпендикуляры должны лежать в данных плоскостях. За угол между плоскостями принимают острый угол, образованный этими плоскостями. Если угол между плоскостями равен 90°, то такие плоскости перпендикулярны.
- Угол между прямой и плоскостью — это угол между прямой и ее проекцией на эту плоскость. Чтобы найти угол между прямой и плоскостью, необходимо построить проекцию прямой на плоскость и найти угол между прямой и ее проекцией. Если прямая параллельна плоскости, то угол между ними будет равен 0°. Если прямая перпендикулярна плоскости, то угол между ними будет равен 90°.
- Прямая, перпендикулярная плоскости — прямая, которая перпендикулярна к каждой прямой, лежащей в этой плоскости. Чтобы доказать, что прямая перпендикулярна плоскости, достаточно доказать, что эта прямая перпендикулярна двум пересекающимся в плоскости прямым.
- Теорема о трех перпендикулярах гласит, что если наклонная прямая а к плоскости а перпендикулярна прямой b в этой плоскости, то и проекция прямой а на плоскость а перпендикулярна к прямой b.
Проверь себя
Задание 1.
Выберите верное утверждение.
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом все линейные углы двугранного угла равны между собой;
- Градусной мерой двугранного угла будет линейный угол двугранного угла. При этом линейные углы двугранного угла не равны между собой;
- Грань двугранного угла — это общая прямая плоскостей, которые его образуют;
- Ребра двугранного угла — это плоскости, которые его образуют.
Задание 2.
Угол между плоскостями — это…
- Тупой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между перпендикулярами, проведенными к линии пересечения плоскостей;
- Тупой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей;
- Острый или прямой угол между двумя произвольными линиями, проведенными к линии пересечения плоскостей.
Задание 3.
Что такое проекция прямой на плоскость?
- Это любая прямая, проведенная из точки пересечения прямой и плоскости;
- Это перпендикуляр, опущенный из любой точки на плоскость;
- Это всегда точка пересечения прямой и плоскости;
- Это прямая, образованная проекциями всех точек прямой на плоскость.
Задание 4.
Какой будет проекция прямой, перпендикулярной к плоскости, на эту плоскость?
- Проекция будет равна этой прямой и параллельна ей;
- Проекция будет меньше прямой и образовывать с ней угол;
- Проекция будет точкой пересечения прямой и плоскости;
- Проекция будет больше прямой и образовывать с ней угол.
Задание 5.
Как доказать, что прямая перпендикулярна плоскости?
- Достаточно доказать, что прямая перпендикулярна одной любой прямой в плоскости;
- Достаточно доказать, что прямая перпендикулярна двум параллельным прямым в плоскости;
- Достаточно доказать, что угол между прямой и любой прямой в плоскости равен 90°;
- Достаточно доказать, что прямая перпендикулярна к двум пересекающимся прямым в этой плоскости.
Ответы: 1. — 1 2. — 2 3. — 4 4. — 3 5. — 4
Бонусы: вебинары из нашего курса по подготовке к ЕГЭ по математике
ЕГЭ 14. Стереометрия. Расстояние между точками и от точки до прямой
Расстояние между точками и от точки до прямой — это первое видео раздела «Стереометрия», входящее в полный курс подготовки к ЕГЭ (о нем ниже).
В этом видео мы научимся «видеть» 3-мерное пространство и изображать 3-мерные объекты на бумаге (то есть на плоской поверхности).
Затем мы научимся двум основным вещам — находить расстояние между точками на таких рисунках, а также расстояние от точки до прямой.
На этих умениях строится всё дальнейшее изучение стереометрии. В общем это очень важное, базовое видео, с которого нужно начинать изучение стереометрии.
Не перескакивайте, не пропускайте его! Даже если вы знаете стереометрию, вы найдете для себя очень много полезного и нового в этом видео.
ЕГЭ №14. Стереометрия. Разбор варианта профильного ЕГЭ
Нужно великолепно знать основные теоремы планиметрии, уметь рассчитывать расстояния, площади и объемы плоских и объемных фигур.
Но самое сложное, нужно научиться строить доказательства с помощью этих теорем и правильно их записывать.
Об этом в нашем вебинаре в задаче о шестиугольной призме.
ЕГЭ 14 Стереометрия. Разбора задачи статграда, февраль 2021
Что проще: призма или пирамида? Хоть в призме и больше рёбер и граней, но с пирамидами справляться сложнее, причём прямо начиная с рисунка: все линии налезают друг на друга, ничего нигде не параллельно, в общем, лучше бы призму дали.
Но как только научились рисовать пирамиду, сразу всё стало проще: кругом одни треугольники, а как известно, фигур проще треугольника в геометрии найти не так-то просто 
А если где прямые углы найдём, то вообще сказка.
Из этого видео вы узнаете, как правильно рисовать пирамиду и научитесь решать задачу №14 из февральского СтатГрада