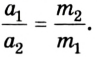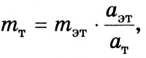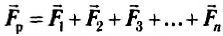Как найти величину вектора силы

Вектор силы (Определение, Пример)

ЧТО ТАКОЕ ВЕКТОР СИЛЫ

Это то, что тянет и толкает; силы мы чувствуем, когда они на нас действуют; силы растягивают пружины, заставляют тело двигаться быстрее. Мы будем измерять силы при помощи пружинных весов. Поскольку эти приборы обычно градуируют в килограммах силы мы будем пока выражать силу тоже в килограммах силы.

При сооружении и проектировании мостов, зданий, кранов, машин инженеров очень заботит сложение сил или же разность сил для определения силы, необходимой для достижения равновесия. Можно показать, что силы — это векторы, т. е. они подчиняются правилу геометрического сложения.

Векторному сложению и разложению уравновешенных сил посвящен раздел физики, называемый «статикой». Это большой, но скучный раздел физики, и большинство учебников уделяет ему много места, излагая приемы решения задач инженерной статики. Мы ограничимся лишь несколькими примерами, и даже их, пожалуй, лучше было бы опустить, чтобы уделить больше времени изучению силы и движения.

Прежде всего мы должны удостовериться в том, что силы — это векторы. Сказать, что они должны быть векторами, поскольку они характеризуются величиной и направлением, недостаточно. Это не убеждает нас в том, что силы складываются геометрически.

Хотя это утверждение кажется вполне правдоподобным, особенно тем, кто имеет дело с канатами и веревками на кораблях или кому приходится заниматься разбивкой палаток, мы же должны проворить его непосредственно.

Опыт по определению вектора силы

Часто прибегают еще к одному способу проверки. Этот способ проще, но его косвенный характер порой (не совсем добросовестно) игнорируют. К узлу прикладывают две тянущие силы F_А и F_В (применяют гири и блоки или пружинные весы), а третья сила F_С удерживает узел в покое. Затем при помощи построения определяется сумма сил F_А и F_В .

Она равна и проти воположна силе F_С. Это требует дополнительного доказательства, поскольку F_С не равнодействующая (сумма) двух других сил, а «равновесная» сила, необходимая, чтобы им противостоять.

Рис. Косвенная проверка векторного сложения сил.

Равновесие сил

Если на какую-нибудь деталь крана или моста действует несколько сил сразу, а инженеру нужно, чтобы она была и оставалась в состоянии покоя, то для этого сумма всех действующих сил должна быть равна нулю. Тогда в соответствии с представлением Галилея эта деталь должна либо постоянно двигаться, либо постоянно оставаться в состоянии покоя.

В этом случае мы говорим, что силы находятся «в равновесии». Если сумма нескольких сил равна нулю, то это должно быть видно на диаграмме векторного сложения; длина линии, соединяющей исходную точку диаграммы с конечной, должна быть равна нулю. Это означает, что векторная диаграмма должна представлять собой замкнутую фигуру.

Таким образом, если сумма сил равна нулю, то конец векторного многоугольника должен прийти обратно к началу. Это иллюстрирует рис. 3. Условие равенства нулю равнодействующей для постоянного равновесия сил должно выполняться для всей конструкции, например для всего крана или моста, но оно должно также выполняться для каждой отдельной детали конструкции, находящейся в состоянии равновесия.

Применяя это условие к какой-нибудь определенной детали, например к стреле крана, к одной опоре моста, к заклепке, связывающей воедино несколько различных деталей моста, или к грузу маятника, нужно быть внимательным и учитывать все силы, действующие на данную деталь. Тогда мы сможем утверждать, что имеем полный набор сил, образующих замкнутую векторную диаграмму, если, конечно, деталь находится в равновесии.

При решении задач не следует включать в рассмотрение силы, приложенные к другим деталям. Сначала выберите и пометьте выбранную деталь, которая, как вы считаете, находится в равновесии.

Равновесие трех сил, треугольник сил

Если три силы находятся в равновесии, то их векторная диаграмма должна представлять собой замкнутый треугольник (рис. 4). Если известны две силы, то можно вычислить величину и направление третьей.

а — три силы в равновесии) б — три силы не находятся в равновесии.

Этим пользуются при решении инженерных задач. Во многих конструкциях на каждую деталь, играющую важную роль, действуют как раз три силы. Чтобы конструкция была устойчивей, каждая деталь должна оставаться в состоянии покоя; сумма всех действующих на нее сил должна быть равна нулю. Таким образом, если к любой детали приложены три силы, мы строим для них замкнутый треугольник.

Похожие страницы:

Понравилась статья поделись ей

Законы сложения сил в механике

При воздействии на одно тело нескольких сил одновременно тело начинает двигаться с ускорением, являющимся векторной суммой ускорений, которые бы возникли под воздействием каждой силы по отдельности. К действующим на тело силам, приложенным к одной точке, применяется правило сложения векторов.

Векторная сумма всех сил, одновременно воздействующих на тело, это сила равнодействующая, которая определяется по правилу векторного сложения сил:

R → = F 1 → + F 2 → + F 3 → + . . . + F n → = ∑ i = 1 n F i → .

Равнодействующая сила действует на тело также, как и сумма всех действующих на него сил.

Правило параллелограмма и правило многоугольника

Для сложения 2 -х сил используют правило параллелограмма (рисунок 1 ).

Рисунок 1 . Сложение 2 -х сил по правилу параллелограмма

Выведем формулу модуля равнодействующей силы с помощью теоремы косинусов:

R → = F 1 → 2 + F 2 → 2 + 2 F 1 → 2 F 2 → 2 cos α

При необходимости сложения более 2 -х сил используют правило многоугольника: от конца
1 -й силы необходимо провести вектор, равный и параллельный 2 -й силе; от конца 2 -й силы необходимо провести вектор, равный и параллельный 3 -й силе и т.д.

Рисунок 2 . Сложение сил правилом многоугольника

Конечный вектор, проведенный от точки приложения сил в конец последней силы, по величине и направлению равняется равнодействующей силе. Рисунок 2 наглядно иллюстрирует пример нахождения равнодействующей сил из 4 -х сил: F 1 → , F 2 → , F 3 → , F 4 → . Причем суммируемые векторы совсем необязательно должны быть в одной плоскости.

Результат действия силы на материальную точку будет зависеть только от ее модуля и направления. У твердого тела есть определенные размеры. Потому силы с одинаковыми модулями и направлениями вызывают разные движения твердого тела в зависимости от точки приложения.

Линией действия силы называют прямую, проходящую через вектор силы.

Рисунок 3 . Сложение сил, приложенных к различным точкам тела

Если силы приложены к различным точкам тела и действуют не параллельно по отношению друг к другу, тогда равнодействующая приложена к точке пересечения линий действия сил (рисунок 3 ). Точка будет находиться в равновесии, если векторная сумма всех сил, действующих на нее, равняется 0 : ∑ i = 1 n F i → = 0 → . В данном случае равняется 0 и сумма проекций данных сил на любую координатную ось.

Разложение вектора силы по направлениям

Разложение сил на две составляющие – это замена одной силы 2 -мя, приложенными в той же точке и производящими на тело такое же действие, как и эта одна сила. Разложение сил осуществляется, как и сложение, правилом параллелограмма.

Задача разложения одной силы (модуль и направление которой заданы) на 2 , приложенные в одной точке и действующие под углом друг к другу, имеет однозначное решение в следующих случаях, когда известны:

• направления 2 -х составляющих сил;
• модуль и направление одной из составляющих сил;
• модули 2 -х составляющих сил.

Пример 1

Необходимо разложить силу F на 2 составляющие, находящиеся в одной плоскости с F и направленные вдоль прямых a и b (рисунок 4 ). Тогда достаточно от конца вектора F провести 2 прямые, параллельные прямым a и b . Отрезок F A и отрезок F B изображают искомые силы.

Рисунок 4 . Разложение вектора силы по направлениям

Второй вариант данной задачи – найти одну из проекций вектора силы по заданным векторам силы и 2 -й проекции (рисунок 5 а ).

Рисунок 5 . Нахождение проекции вектора силы по заданным векторам

Во втором варианте задачи необходимо построить параллелограмм по диагонали и одной из сторон, как в планиметрии. На рисунке 5 б изображен такой параллелограмм и обозначена искомая составляющая F 2 → силы F → .

Итак, 2 -й способ решения: прибавим к силе силу, равную — F 1 → (рисунок 5 в ). В итоге получаем искомую силу F → .

Три силы F 1 → = 1 Н ; F 2 → = 2 Н ; F 3 → = 3 Н приложены к одной точке, находятся в одной плоскости (рисунок 6 а ) и составляют углы с горизонталью α = 0 ° ; β = 60 ° ; γ = 30 ° соответственно. Необходимо найти равнодействующую силу.

Решение

Рисунок 6 . Нахождение равнодействующей силы по заданным векторам

Нарисуем взаимно перпендикулярные оси О Х и O Y таким образом, чтобы ось О Х совпадала с горизонталью, вдоль которой направлена сила F 1 → . Сделаем проекцию данных сил на координатные оси (рисунок 6 б ). Проекции F 2 y и F 2 x отрицательны. Сумма проекций сил на координатную ось О Х равняется проекции на данную ось равнодействующей: F 1 + F 2 cos β — F 3 cos γ = F x = 4 — 3 3 2 ≈ — 0 , 6 Н .

Точно также для проекций на ось O Y : — F 2 sin β + F 3 sin γ = F y = 3 — 2 3 2 ≈ — 0 , 2 Н .

Модуль равнодействующей определим с помощью теоремы Пифагора:

F = F x 2 + F y 2 = 0 , 36 + 0 , 04 ≈ 0 , 64 Н .

Направление равнодействующей найдем при помощи угла между равнодействующей и осью (рисунок 6 в ):

t g φ = F y F x = 3 — 2 3 4 — 3 3 ≈ 0 , 4 .

Сила F = 1 к Н приложена в точке В кронштейна и направлена вертикально вниз (рисунок 7 а ). Необходимо найти составляющие данной силы по направлениям стержней кронштейна. Все необходимые данные отображены на рисунке.

Решение

Рисунок 7 . Нахождение составляющих силы F по направлениям стержней кронштейна

Дано:

F = 1 к Н = 1000 Н

Пускай стержни прикручены к стене в точках А и С . На рисунке 7 б изображено разложение силы F → на составляющие вдоль направлений А В и В С . Отсюда понятно, что

F 1 → = F t g β ≈ 577 Н ;

F 2 → = F cos β ≈ 1155 Н .

Ответ: F 1 → = 557 Н ; F 2 → = 1155 Н .

Сила в физике — виды, формулы и определения с примерами

Содержание:

Сила:

При изучения природных явлений используют разные физические величины. Для того чтобы описать качественно и количественно взаимодействие тел, вводят физическую величину, которую называют силой.

Определение силы

Сила — это физическая величина, которая служит мерой взаимодействия тел и является причиной изменения скоростей тел или их частей.

Наблюдение. Если мы рассматриваем, например, взаимодействие руки с волейбольным мячом, то мы говорим: «Мяч действует с силой на руку или рука действует с силой на мяч».

Опыт. Подвесим на пружину яблоко (рис. 66).

Пружина удлинится. Если на неё подвесить два яблока, то она удлинится больше. Итак, два яблока действуют на пружину с большей силой, чем одно.

Результат действия одного тела на другое зависит от значения приложенной силы.

Чем плотнее закрыта дверь, тем с большей силой мы должны её толкать или тянуть на себя, чтобы отворить.

Для того чтобы легче открывать дверь, её ручку прикрепляют как можно дальше от петель. Попробуйте открыть дверь, толкая её в точке, размещённой вблизи петель. Вы убедитесь, что это сделать намного труднее, чем с помощью ручки. Результат действия одного тела на другое зависит от точки приложения силы.

Для достижения определённого результата действия, например, растяжения или сжатия пружины, закрытия или открытия двери, нужно прикладывать силы в разных направлениях.

Действие одного тела на другое зависит от направления действия силы.

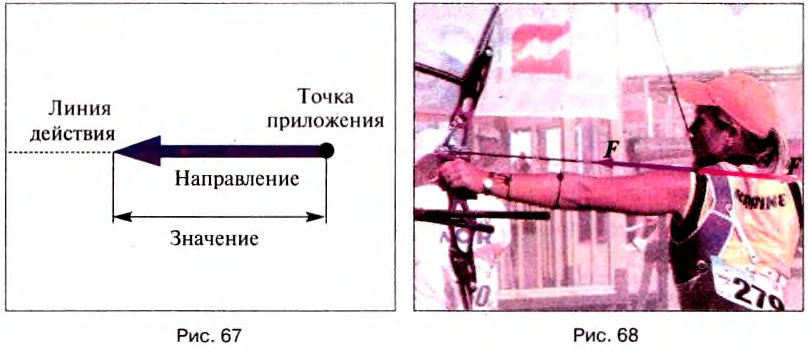
Графически силу изображают в виде отрезка прямой со стрелкой на конце (рис. 67).

Начало отрезка совмещают с точкой приложения силы. Длина отрезка в определённом масштабе равна значению силы. Стрелка показывает направление силы. Величины, характеризующиеся кроме числового значения еще и направлением в пространстве, называют векторными, или векторами (от латинского слова вектор — ведущий, несущий).

Почему тела изменяют свое состояние в пространстве

Любые изменения в природе происходят в результате взаимодействия между телами. Чтобы изменить положение вагона на рельсах, железнодорожники направляют к нему локомотив, который смещает вагон с места и приводит его в состояние движения (рис. 32).

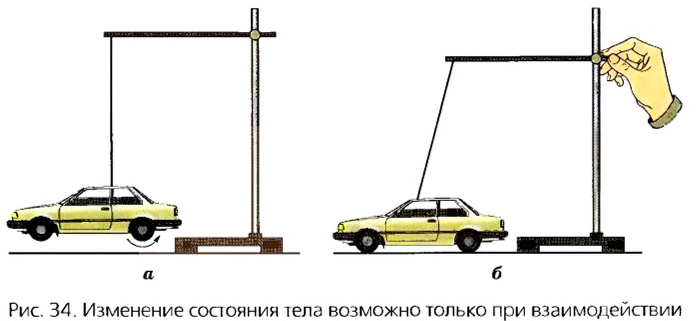
Парусник может длительное время стоять возле берега до тех пор, пока не подует попутный ветер и подействует на его паруса (рис. 33). Колеса игрушечного автомобиля могут вращаться с любой скоростью, но игрушка не изменит своего положения, если под игрушку не положить дощечку или линейку (рис.34). Форму или размер пружины можно изменить, лишь подвесив к ней груз или потянув рукой за один из его концов.

Все тела в природе так или иначе связаны между собой и действуют друг на друга или непосредственно, или через физические поля. Такое действие всегда является взаимным. Если тепловоз действует на вагон и изменяет его скорость, то скорость тепловоза при этом также изменяется благодаря обратному действию вагона. Солнце действует на все тела на Земле и на саму Землю, удерживая ее на орбите. Но и Земля притягивает Солнце и, в свою очередь, изменяет его траекторию. Таким образом, во всех случаях можно говорить только о взаимном действии тел — взаимодействии.

При взаимодействии могут изменяться скорости тел или их частей.

Однако, взаимодействуя с различными телами, данное тело будет изменять свою скорость по-разному. Так, парусник может приобрести скорость вследствие действия на него ветра. Но такой же результат можно получить, включив двигатель, который находится на паруснике. Парусник может сдвинуть с места и катер, действуя на него через трос. Чтобы каждый раз не называть все взаимодействующие тела, все эти действия объединяют одним понятием силы.

Что такое сила

Сила как физическое понятие может быть большей или меньшей, как и вызванные ею изменения в состоянии тела или его частей.

Сила — это физическое понятие, которое обобщает все взаимодействия, вследствие чего тело или его части изменяют свое состояние.

Действие тепловоза на вагон будет значительно интенсивнее, чем действие нескольких грузчиков. Под действием тепловоза вагон быстрее сдвинется с места и начнет двигаться с большей скоростью, чем тогда, когда вагон будут толкать грузчики, которые еле сдвинут его на небольшое расстояние или совсем его не сдвинут.

Сила как физическая величина количественно характеризует действие одного тела на другое.

Для того чтобы можно было производить математические расчеты, силу обозначают определенной буквой. Как правило, это латинская буква F.

Как и все другие физические величины, сила имеет единицы измерения. Современная наука пользуется единицей, которая называется ньютоном (Н). Единица получила такое название в честь английского ученого Исаака Ньютона, который внес значительную лепту в развитие физической и математической наук.

Исаак Ньютон (1643-1727) — выдающийся английский ученый, основоположник классической физики. Научные труды касаются механики, оптики, астрономии и математики. Сформулировал основные законы классической механики, открыл закон всемирного тяготения, дисперсию света, развил корпускулярную теорию света, разработал дифференциальное и интегральное исчисление.

Силы могут иметь различные значения. Так, на стакан с водой действует сила со стороны Земли, которая равна примерно 2 Н. А трактор, когда тянет плуг, действует на него с силой в несколько тысяч ньютонов.

Чем измеряют силу

Для измерения силы используют специальные приборы, называющиеся динамометрами (dina — сила; metro — меряю). Как правило, каждый такой прибор имеет измерительный элемент в виде пружины определенной формы (рис. 35).

Сила характеризуется направлением.

Указать числовое значение силы не всегда достаточно для определения результата ее действия. Важно знать точку ее приложения и направление действия.

Если высокий брусок, стоящий на столе, толкать в нижней части, то он будет скользить по поверхности стола. Если же к бруску приложить силу в верхней его части, то он просто перевернется (рис. 36).

Понятно, что направление падения бруска зависит от того, в каком направлении будем его толкать. Следовательно, сила имеет направление. От направления силы зависит изменение скорости тела, на которое эта сила действует.

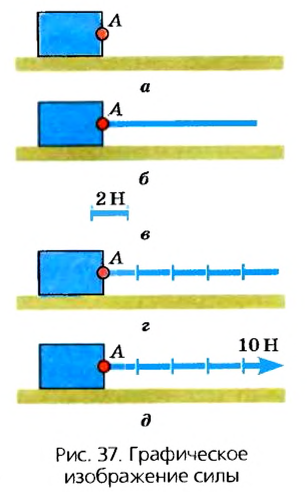
Учитывая, что сила имеет направление и числовое значение, ее изображают в виде стрелки определенной длины и направления (вектора). Такая стрелка начинается в точке на теле, которая называется точкой приложения силы. На рисунке 37 изображена сила, значение которой равно 10 Н, направлена она слева направо и приложена в точке А.

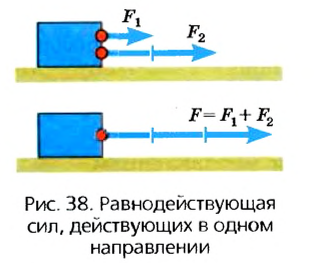
Пользуясь графическим методом, можно производить различные математические операции с силами. Так, если к одной точке на теле приложены силы 2 Н и 3 Н, которые действуют в одном направлении, то их можно заменить одной силой, которая будет приложена в той же точке и действовать в том же направлении, а ее значение будет равно сумме значений каждой из сил (рис. 38). Вектор этой силы будет иметь длину, равную сумме длин двух векторов.

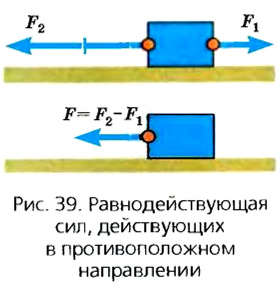
Возможен и другой случай, когда силы, приложенные в одной точке тела, действуют в противоположных направлениях. Тогда их можно заменить одной силой, направленной в направлении большей силы, а ее значение будет равняться разности значений каждой силы (рис. 39). Длина вектора этой силы будет равна разности длин векторов приложенных сил.

Сила, которой можно заменить действие нескольких сил, приложенных в определенной точке тела, называется равнодействующей.

Равнодействующая — это сила, действие которой равнозначно действию нескольких сил, приложенных к телу в определенной его точке.

Силу обозначают большой латинской буквой .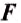

На рис. 68 спортсменка приготовилась стрелять из лука. В этом случае её рука действует на тетиву с силой направленной вправо, а тетива действует на руку с такой же по значению силой, направленной влево. Итак, значения сил одинаковы, но их направления противоположны.

Сложение сил

Главная задача динамики — по действующей силе определить движение тела или по характеру движения тела установить, какая сила на него действует. Понятие о силе является основным в механике. И. Ньютон утверждал то, что мы называем силой, есть действие одного тела на другое, или их взаимодействие.

Действие одних тел на другие сообщает ускорение их движению. Полученное телом ускорение является внешним проявлением того, что оно взаимодействовало с другим телом. Когда мы говорим «сила», то подразумеваем, что на данное тело действуют другие тела.

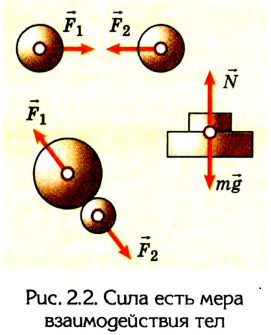
Сила, являющаяся причиной изменения состояния движения тел или их деформации, характеризует взаимодействие тел, которое происходит при их непосредственном контакте (например столкновении) или через поля (рис. 2.2).

Сила — векторная величина, характеризующая действие, которое является причиной изменения состояния движения или покоя.

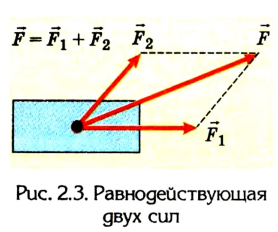
Действие на тело нескольких сил может быть заменено их равнодействующей (рис. 2.3), которую определяют геометрическим сложением этих сил как векторов: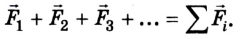

Не скорость тела, а ее изменение есть следствием действия силы (действия других тел).

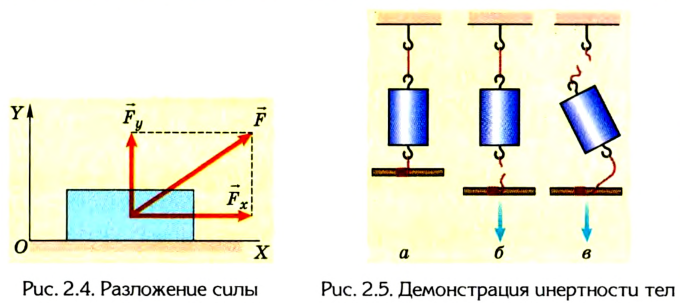
Помимо значения и направления сила характеризуется еще и точкой приложения, которую можно перемещать вдоль линии действия силы, если тело абсолютно твердое (не деформируется). Поскольку действия сил независимы, то сила может быть разложена на составляющие 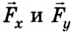(рис. 2.4) как проекции на оси координат.

Для того чтобы выявить инертность тел и увидеть, как на нее влияет время их взаимодействия, проведем такой опыт. На тонкой нитке подвесим груз (рис. 2.5, а). Снизу к грузу прикрепим точно такую же нитку. Если резко дернуть за нижнюю нитку, то она оборвется, а груз останется висеть на верхней нитке (рис. 2.5, б). Если нижнюю нитку натягивать медленно, то оборвется верхняя нитка (рис. 2.5, в).

Когда мы резко дергаем за нижнюю нитку, взаимодействие руки и нитки кратковременно, груз не успевает изменить свою скорость — верхняя нитка не обрывается, т. к. груз имеет значительную инертность.

Если же за нижнюю нитку тянуть медленно (рука действует на груз продолжительное время), то груз набирает такую скорость, что его перемещение достаточно для разрыва и без того натянутой верхней нитки.

Как вы уже знаете, инертность тел определяется их массой, т. е. масса тела характеризует его инертность.

Во время тщательных исследований взаимодействия двух тел, например столкновения двух абсолютно упругих шаров, установлено, что отношение модулей ускорений взаимодействующих тел равно обратному отношению их масс:

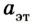
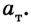
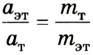
Следствием этого соотношения является один из методов измерения массы тел. Сначала выбирают тело, массу которого условно берут за единицу, — эталон массы. Между эталоном массы и телом, массу которого нужно измерить, можно поместить сжатую при помощи нитки пружину. Потом нитку поджечь и определить ускорение эталона и исследуемого тела Из соотношения находим массу исследуемого тела:

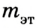
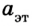
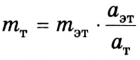
где и — масса и ускорение эталона (1 единица массы). Отсюда единиц массы.

По международному соглашению за единицу массы принята масса эталона килограмма (рис. 2.6).

Килограмм (кг) — основная единица массы в Международной системе единиц (СИ). Килограмм равен массе международного прототипа килограмма — гире из платино-иридиевого сплава (90 % Pt, 10 % lr) в виде цилиндра диаметром и высотой 39 мм, хранящейся в Международном бюро мер и весов (г. Севр, предместье Парижа).

С достаточной точностью можно сказать, что массу 1 кг имеет 1 чистой воды при 15 °C.
Для измерения массы тела часто используют способ сравнения масс тел с помощью весов. При этом учитывают способность тел взаимодействовать с Землей. Как подтверждают опыты, тела, имеющие одинаковую массу, одинаково притягиваются к Земле в данном месте.

Равнодействующая сила

При изучении физики в 7-м классе вы познакомились с понятием «сила», которое используется для описания взаимодействия тел.

Чтобы вспомнить основные характеристики силы, проведем опыт, например, с куском поролона, покоящимся на неподвижном столе, так как притяжение Земли уравновешено воздействием стола.

Используя пинцет, можно действовать на поролон в различных точках и видеть его поступательное, вращательное или более сложное движение в зависимости от направления, места и величины воздействия.

При этом легко наблюдать не только изменение скорости поролона, но и его деформацию (изменение формы и размеров) (рис. 34) в местах контакта поролона с пинцетом.

Рис. 34

Изменение скорости и деформация тел проявляются в любых опытах при самых разнообразных взаимодействиях, и поэтому принято следующее определение силы:

• сила — физическая векторная величина, являющаяся количественной мерой действия одного тела на другое, в результате которого изменяется скорость тела и происходит его деформация.

Опыт показывает, что результат воздействия силы определяется не только ее направлением и модулем, но и точкой приложения.

Единицей измерения силы в СИ является 1 ньютон (сокращенно 1 Н).

Вспомним исторически сложившиеся названия сил и их обозначения.

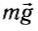
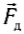
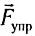
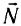
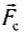
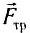
Силой тяжести называется сила, с которой тело притягивается к Земле. Силой давления называется сила, с которой тело действует на опору или жидкость и газ действуют на стенки сосуда. Силой упругости называется сила, возникающая при деформации тела. Силой реакции называется сила, действующая на тело со стороны опоры или подвеса. Силой сопротивления и силой трения называются силы, препятствующие механическому движению тела.

Силы могут действовать на поверхность тела (например, сила давления воздуха) (рис. 35) или быть приложены в некоторой условной точке (например, сила упругости нити в точке ее крепления к телу) (рис. 36).

Для упрощения математического описания механического движения тело рассматривается как материальная точка, если не указаны его размеры и форма. На рисунке тело чаще всего изображают прямоугольником.

Можно изображать силы, действующие на тело, приложенными в центре прямоугольника. Но обычно в центре прямоугольника изображают приложенной силу тяжести, а силу трения и силу реакции опоры рисуют приложенными в точке на нижней грани тела под его центром (рис. 37). Если на тело действуют другие тела, то необходимо учесть одновременно действие нескольких сил.

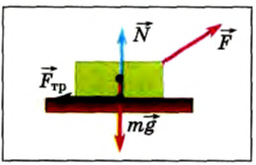
Рис. 37

При изучении физики в 7-м классе вы познакомились со сложением сил и научились складывать силы, действующие на тело вдоль одной прямой.

В этом случае действие, например, двух сил можно заменить одной силой. Модуль равнодействующей силы равен сумме или разности модулей двух слагаемых сил в зависимости от того, совпадают их направления (рис. 38, а, б) или противоположны (рис. 39. а, б). Направление равнодействующей двух сил совпадает с направлением большей силы.

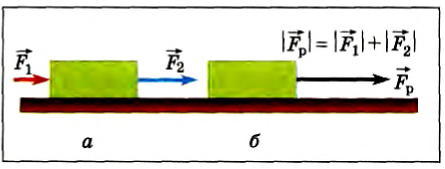
Рис. 38

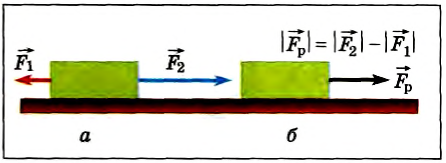
Рис. 39

А как складываются силы, если они направлены под некоторым углом друг к другу? Покажем на опыте, что они складываются также векторно. Подвесим груз массой 0,2 кг на динамометре, закрепленном на неподвижном штативе. Если груз покоится, то сила упругости пружины динамометра уравновешивает силу тяжести груза (рис. 40), а показания прибора равны: F_упр = mg = 2H ()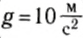

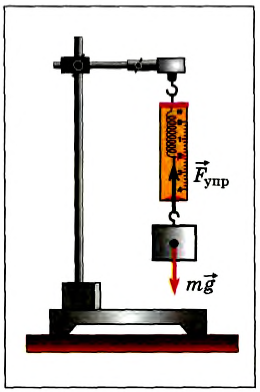
Рис. 40

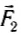
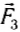
Теперь подвесим этот же груз с помощью двух одинаковых динамометров (рис. 41, а), закрепленных на одной высоте. Меняя положения динамометров, а следовательно, угол между силами и , действующими на груз со стороны динамометров, можно убедиться, что их показания зависят от этого угла и лишь при угле, равном нулю, в сумме равны 2 Н.

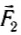
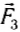
Следовательно, совместное действие сил и уравновешивает действие силы тяжести груза, но сумма модулей этих сил не равна 2 Н, т. е. силы нельзя складывать как скалярные величины.

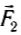
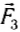
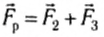
Когда угол между силами и равен 120° (рис. 41,6), то сумма показаний динамометров — 4 Н, а сила тяжести груза все та же — 2 H. Но если найти в этом случае векторную сумму по правилу сложения векторов, то она по модулю равна F_p= 2 Н.

Следовательно, силы нужно складывать по правилам сложения векторов.

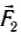
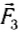
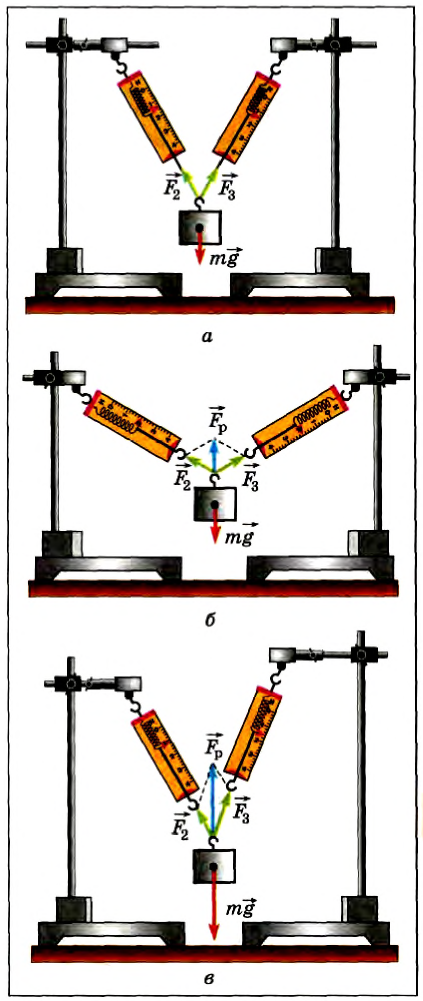
Модуль векторной суммы сил и равен 2 H при любом значении угла между направлениями этих сил, а также и во всех случаях, когда модули сил не равны друг другу (рис. 41, в).

Рис. 41

Какие бы более сложные опыты не проводились (и при действии на тело нескольких сил), всегда результаты измерений показывают, что действие нескольких сил можно заменить их векторной суммой, т. е. силы складываются, как векторы, — геометрически.

Векторная сумма сил, действующих на тело, называется равнодействующей и определяется по формуле:

Если размерами тела нельзя пренебречь и силы приложены в разных его точках, то векторы сил можно перенести в одну точку, сохраняя модуль и направление, и векторно сложить (рис. 42).

Необходимо понимать, что равнодействующая сила заменяет действие нескольких сил только по отношению к движению тела в целом, но не заменяет действие каждой слагаемой силы в других отношениях.

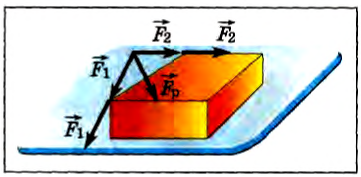
Рис. 42

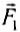
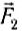
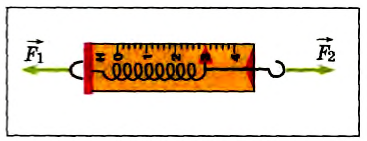
Например, растянутая двумя руками пружина покоится (рис. 43), а значит, равнодействующая сил и равна нулю, но каждая из этих сил деформирует соответственно подвес динамометра и пружину.

Рис. 43

Если тело движется с постоянной скоростью, то согласно первому закону Ньютона все воздействия на тело скомпенсированы, т. е. равнодействующая всех сил также должна быть равна нулю.

Главные выводы:

1. Сила — физическая векторная величина, являющаяся количественной мерой действия одного тела на другое, в результате которого изменяется скорость тела и происходит его деформация.
2. Сила характеризуется модулем, направлением, а также точкой приложения.
3. Заменить действие нескольких сил можно равнодействующей силой, которая определяется как векторная сумма этих сил.
4. При движении тела с постоянной скоростью (или в состоянии покоя) равнодействующая всех сил, действующих на него, равна нулю.

Что означает понятие «Сила» в физике

Вам хорошо известно слово «сила». Обычно смысл слова «сила» и образованных от него слов «силач», «сильный» и т. д. связан с возможностями человека, животного, механизма, с интенсивностью проявления природных явлений. Мы говорим «самый сильный человек», «сила воли», «сильные чувства», «сильный мороз», «сильный двигатель». А какое содержание вкладывают в слово «сила» физики?

Мы уже говорили о том, что причина изменения скорости движения тела — его взаимодействие с другими телами.

Чтобы теннисный мяч вернулся на сторону соперника, вы бьете по мячу ракеткой, но и мяч «бьет» по ракетке. Чтобы остановить велосипед, вы нажимаете на ручки тормоза и в то же время ощущаете, как они давят на ваши ладони. Обратите внимание: в любом случае результат зависит от того, насколько «сильным» будет взаимодействие: сильнее ударите по мячу — мяч наберет большую скорость (рис. 18.1); сильнее нажмете на тормоз — быстрее остановится велосипед. Мерой действия одного тела на другое служит физическая величина сила.

Сила — это физическая величина, которая является мерой действия одного тела на другое (мерой взаимодействия тел).

Силу обычно обозначают символом F. Единица силы в СИ — ньютон (названа в честь Исаака Ньютона): [F]=Н. 1 Н — это сила, которая, действуя на тело массой 1 кг в течение 1 с, изменяет скорость его движения на 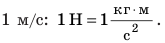Чем больше сила и чем дольше она действует на тело, тем заметнее изменяется скорость движения тела (см. рис. 18.1). Чтобы тела разной массы за одинаковое время изменяли скорости своего движения одинаково, на них должны действовать разные силы (рис. 18.2).

Графическое изображение сил

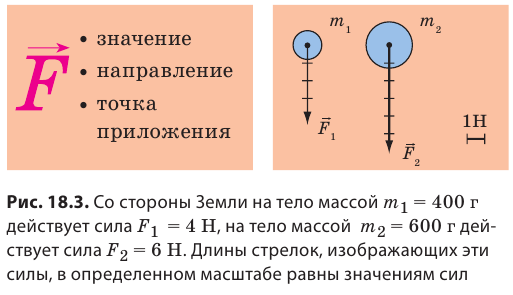
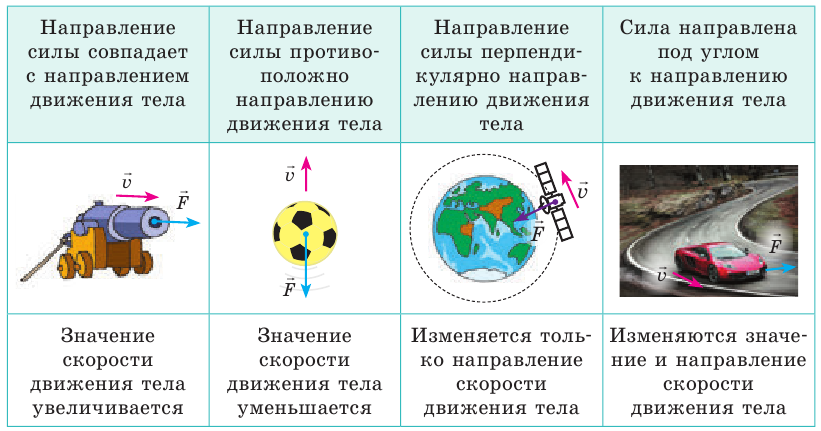
Сила, действуя на тело, может изменить скорость его движения как по значению, так и по направлению, поэтому сила определяется и значением, и направлением. Уже говорилось о том, что физические величины, имеющие значение и направление, называют векторными. Итак, сила — векторная величина. На рисунках вектор силы начинают в точке, к которой приложена сила (эту точку так и называют — точка приложения силы), и направляют в сторону действия силы. Длину стрелки иногда выбирают так, чтобы она в определенном масштабе соответствовала значению силы (рис. 18.3). Изменение скорости движения тела (по значению, по направлению) зависит от направления силы (см. таблицу на с. 123).

Сложение сил, действующие вдоль одной прямой

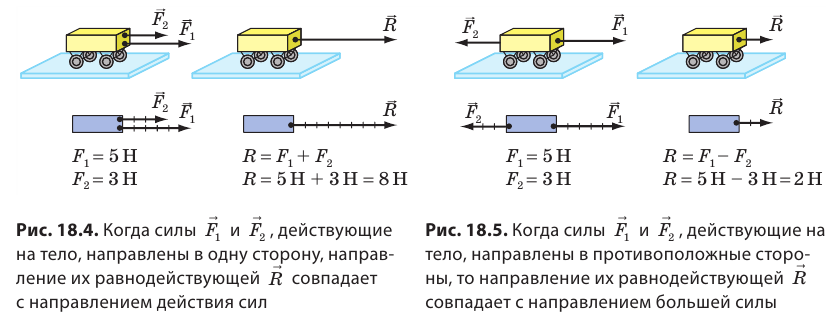
Обычно на тело действует не одна сила, а две, три или больше. Проведем опыт. Поставим на стол тележку и привяжем к ней две нити. Потянем за одну нить с силой 5 Н, а за другую — в том же направлении — с силой 3 Н (рис. 18.4). Тележка придет в движение, увеличивая свою скорость так, как если бы на нее действовала одна сила 8 Н. Силу 8 Н, которой в данном случае можно заменить две силы 5 и 3 Н, называют равнодействующей двух сил и обозначают символом R (или F). Силу, которая производит на тело такое же действие, как несколько одновременно действующих сил, называют равнодействующей этих сил. Если тележку одновременно тянуть за две нити в противоположные стороны (рис. 18.5), то силы не будут «помогать» друг другу разгонять тележку, а наоборот — будут «мешать». В этом случае тележка будет двигаться так, будто на нее действует одна сила 2 Н в направлении, в котором действует сила 5 Н, то есть равнодействующей сил 5 и 3 Н будет сила 2 Н.

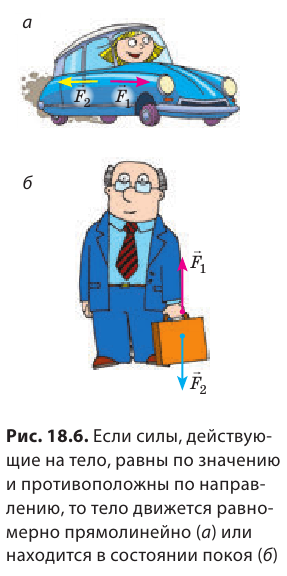
Как вы считаете, какой будет равнодействующая, если нити, привязанные к тележке с противоположных сторон, потянуть с силами, одинаковыми по значению, например 5 Н? Изменится ли в этом случае скорость движения тележки? 4 Выясняем, когда силы компенсируют друг друга Надеемся, вы правильно ответили на вопрос в п. 3 и самостоятельно пришли к выводу: если две силы равны по значению, противоположны по направлению и приложены к одному телу, то равнодействующая этих сил равна нулю. Силы уравновешивают (компенсируют) друг друга, поэтому причины для изменения скорости движения тела нет. Так, по горизонтальному прямолинейному отрезку шоссе автомобиль движется равномерно (рис. 18.6, а), если сила тяги его двигателя компенсирует силу сопротивления движению (сила сопротивления движению достаточно быстро остановит автомобиль, если двигатель не будет работать). Портфель в руке находится в состоянии покоя, если сила притяжения Земли, действующая на портфель, компенсируется силой, которую прикладывает к портфелю человек (рис. 18.6, б).

Итоги:

Сила F — физическая величина, являющаяся мерой действия одного тела на другое (мерой взаимодействия тел). Сила — причина изменения скорости движения тела. Единица силы в СИ — ньютон (Н). 1 Н равен силе, которая, действуя на тело массой 1 кг в течение 1 с, изменяет скорость его движения на 1 м/с.

Сила — векторная величина. Чтобы охарактеризовать силу, необходимо указать значение, направление и точку приложения силы. Если на тело действуют несколько сил, то их общее действие всегда можно заменить действием одной силы — равнодействующей. Равнодействующей сил, которые действуют на тело в одном направлении, является сила, значение которой равно сумме значений сил, а направление совпадает с направлением этих сил. Если две силы, действующие на тело, направлены в противоположные стороны, то направление равнодействующей совпадает с направлением большей силы, а для нахождения значения равнодействующей нужно из значения большей силы вычесть значение меньшей. Две силы компенсируют (уравновешивают) друг друга, если они равны по значению, противоположны по направлению и приложены к одному телу.

Рекомендую подробно изучить предметы:

Физика Атомная физика Ядерная физика Квантовая физика Молекулярная физика

Ещё лекции с примерами решения и объяснением:

• Силы в механике
• Сила тяжести в физике
• Сила упругости в физике и закон Гука
• Деформация в физике
• Звук в физике и его характеристики
• Звуковые и ультразвуковые колебания
• Инерция в физике
• Масса тела в физике

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Расчет величин для сил является важной частью физики. Когда вы работаете в одном измерении, величина силы не должна учитываться. Вычисление величины является более сложной задачей в двух или более измерениях, потому что сила будет иметь «компоненты» вдоль осей x и y и, возможно, оси z, если это трехмерная сила. Научиться делать это с одной силой и с результирующей силой двух или более отдельных сил — важный навык для любого начинающего физика или любого, кто работает над проблемами классической физики в школе.

TL; DR (слишком долго; не читал)

Найти результирующую силу от двух компонент вектора, используя теорему Пифагора. Используя координаты x и y для компонентов, это дает F = √ ( x ² + y ²) для величины силы.

Найдите результирующую силу от двух векторов, сначала добавив x -компоненты и y -компоненты, чтобы найти результирующий вектор, а затем используйте ту же формулу для его величины.

Основы: что такое вектор?

Первый шаг к пониманию того, что значит вычислять величину силы в физике, — это узнать, что такое вектор. «Скаляр» — это простая величина, которая просто имеет значение, например температуру или скорость. Когда вы читаете температуру 50 градусов по Фаренгейту, она говорит вам все, что вам нужно знать о температуре объекта. Если вы читаете, что что-то движется со скоростью 10 миль в час, эта скорость говорит вам все, что вам нужно знать о том, как быстро оно движется.

Вектор отличается, потому что у него есть направление и величина. Если вы посмотрите прогноз погоды, вы узнаете, насколько быстро ветер движется и в каком направлении. Это вектор, потому что он дает вам дополнительную информацию. Скорость — это векторный эквивалент скорости, где вы узнаете направление движения и скорость его движения. Таким образом, если что-то движется со скоростью 10 миль в час к северо-востоку, скорость (10 миль в час) — это величина, северо-восток — это направление, и обе части вместе составляют векторную скорость.

Во многих случаях векторы делятся на «компоненты». Скорость может быть задана как комбинация скорости в северном направлении и скорости в восточном направлении, чтобы результирующее движение было к северо-востоку, но вам нужны оба бита информации для понять, как быстро он движется и куда идет. В задачах физики восток и север обычно заменяются координатами x и y соответственно.

Величина одного вектора силы

Чтобы вычислить величину векторов силы, вы используете компоненты вместе с теоремой Пифагора. Думайте о координате x силы как о основе треугольника, о компоненте y как о высоте треугольника, а о гипотенузе как о результирующей силе обоих компонентов. Расширяя связь, угол, который делает гипотенуза с основанием, является направлением силы.

Если сила толкает 4 Ньютона (N) в направлении x и 3 N в направлении y, теорема Пифагора и объяснение треугольника показывают, что вам нужно сделать при расчете величины. Используя x для x -координаты, y для y -координаты и F для величины силы, это можно выразить как:

Здесь θ обозначает угол между вектором и осью x . Это означает, что вы можете использовать компоненты силы, чтобы решить это. Вы можете использовать величину и определение cos или sin, если хотите. Направление определяется:

Используя тот же пример, что и выше:

???? = загар ^{— 1} (3/4)

= 36, 9 градусов

Итак, вектор составляет около 37 градусов с осью X.

Результирующая сила и величина двух или более векторов

Если у вас есть две или более силы, определите величину результирующей силы, сначала найдя результирующий вектор, а затем применив тот же подход, что и выше. Единственный дополнительный навык, который вам нужен, — это найти результирующий вектор, и это довольно просто. Хитрость в том, что вы добавляете соответствующие компоненты x и y вместе. Использование примера должно прояснить это.

Представьте себе парусник на воде, движущийся вместе с силой ветра и течением воды. Вода придает силу 4 Н в направлении x и 1 Н в направлении y, а ветер добавляет силу 5 Н в направлении x и 3 Н в направлении y. Результирующий вектор представляет собой компоненты x, сложенные вместе (4 + 5 = 9 N), и компоненты y, сложенные вместе (3 + 1 = 4 N). Таким образом, вы получите 9 N в направлении x и 4 N в направлении y. Найдите величину результирующей силы, используя тот же подход, что и выше:

F = √ ( x ² + y ²)

= √ (9 ² + 4 ²) N

= √97 N = 9, 85 N

Сила как мера взаимодействия тел. Равнодействующая сил

Содержание:

Сила:

При изучения природных явлений используют разные физические величины. Для того чтобы описать качественно и количественно взаимодействие тел, вводят физическую величину, которую называют силой.

Определение силы

Сила — это физическая величина, которая служит мерой взаимодействия тел и является причиной изменения скоростей тел или их частей.

Наблюдение. Если мы рассматриваем, например, взаимодействие руки с волейбольным мячом, то мы говорим: «Мяч действует с силой на руку или рука действует с силой на мяч».

Опыт. Подвесим на пружину яблоко (рис. 66).

Пружина удлинится. Если на неё подвесить два яблока, то она удлинится больше. Итак, два яблока действуют на пружину с большей силой, чем одно.

Результат действия одного тела на другое зависит от значения приложенной силы.

Чем плотнее закрыта дверь, тем с большей силой мы должны её толкать или тянуть на себя, чтобы отворить.

Для того чтобы легче открывать дверь, её ручку прикрепляют как можно дальше от петель. Попробуйте открыть дверь, толкая её в точке, размещённой вблизи петель. Вы убедитесь, что это сделать намного труднее, чем с помощью ручки. Результат действия одного тела на другое зависит от точки приложения силы.

Для достижения определённого результата действия, например, растяжения или сжатия пружины, закрытия или открытия двери, нужно прикладывать силы в разных направлениях.

Действие одного тела на другое зависит от направления действия силы.

Графически силу изображают в виде отрезка прямой со стрелкой на конце (рис. 67).

Начало отрезка совмещают с точкой приложения силы. Длина отрезка в определённом масштабе равна значению силы. Стрелка показывает направление силы. Величины, характеризующиеся кроме числового значения еще и направлением в пространстве, называют векторными, или векторами (от латинского слова вектор — ведущий, несущий).

Почему тела изменяют свое состояние в пространстве

Любые изменения в природе происходят в результате взаимодействия между телами. Чтобы изменить положение вагона на рельсах, железнодорожники направляют к нему локомотив, который смещает вагон с места и приводит его в состояние движения (рис. 32).

Парусник может длительное время стоять возле берега до тех пор, пока не подует попутный ветер и подействует на его паруса (рис. 33). Колеса игрушечного автомобиля могут вращаться с любой скоростью, но игрушка не изменит своего положения, если под игрушку не положить дощечку или линейку (рис.34). Форму или размер пружины можно изменить, лишь подвесив к ней груз или потянув рукой за один из его концов.

Все тела в природе так или иначе связаны между собой и действуют друг на друга или непосредственно, или через физические поля. Такое действие всегда является взаимным. Если тепловоз действует на вагон и изменяет его скорость, то скорость тепловоза при этом также изменяется благодаря обратному действию вагона. Солнце действует на все тела на Земле и на саму Землю, удерживая ее на орбите. Но и Земля притягивает Солнце и, в свою очередь, изменяет его траекторию. Таким образом, во всех случаях можно говорить только о взаимном действии тел — взаимодействии.

При взаимодействии могут изменяться скорости тел или их частей.

Однако, взаимодействуя с различными телами, данное тело будет изменять свою скорость по-разному. Так, парусник может приобрести скорость вследствие действия на него ветра. Но такой же результат можно получить, включив двигатель, который находится на паруснике. Парусник может сдвинуть с места и катер, действуя на него через трос. Чтобы каждый раз не называть все взаимодействующие тела, все эти действия объединяют одним понятием силы.

Что такое сила

Сила как физическое понятие может быть большей или меньшей, как и вызванные ею изменения в состоянии тела или его частей.

Сила — это физическое понятие, которое обобщает все взаимодействия, вследствие чего тело или его части изменяют свое состояние.

Действие тепловоза на вагон будет значительно интенсивнее, чем действие нескольких грузчиков. Под действием тепловоза вагон быстрее сдвинется с места и начнет двигаться с большей скоростью, чем тогда, когда вагон будут толкать грузчики, которые еле сдвинут его на небольшое расстояние или совсем его не сдвинут.

Сила как физическая величина количественно характеризует действие одного тела на другое.

Для того чтобы можно было производить математические расчеты, силу обозначают определенной буквой. Как правило, это латинская буква F.

Как и все другие физические величины, сила имеет единицы измерения. Современная наука пользуется единицей, которая называется ньютоном (Н). Единица получила такое название в честь английского ученого Исаака Ньютона, который внес значительную лепту в развитие физической и математической наук.

Исаак Ньютон (1643-1727) — выдающийся английский ученый, основоположник классической физики. Научные труды касаются механики, оптики, астрономии и математики. Сформулировал основные законы классической механики, открыл закон всемирного тяготения, дисперсию света, развил корпускулярную теорию света, разработал дифференциальное и интегральное исчисление.

Силы могут иметь различные значения. Так, на стакан с водой действует сила со стороны Земли, которая равна примерно 2 Н. А трактор, когда тянет плуг, действует на него с силой в несколько тысяч ньютонов.

Чем измеряют силу

Для измерения силы используют специальные приборы, называющиеся динамометрами (dina — сила; metro — меряю). Как правило, каждый такой прибор имеет измерительный элемент в виде пружины определенной формы (рис. 35).

Сила характеризуется направлением.

Указать числовое значение силы не всегда достаточно для определения результата ее действия. Важно знать точку ее приложения и направление действия.

Если высокий брусок, стоящий на столе, толкать в нижней части, то он будет скользить по поверхности стола. Если же к бруску приложить силу в верхней его части, то он просто перевернется (рис. 36).

Понятно, что направление падения бруска зависит от того, в каком направлении будем его толкать. Следовательно, сила имеет направление. От направления силы зависит изменение скорости тела, на которое эта сила действует.

Учитывая, что сила имеет направление и числовое значение, ее изображают в виде стрелки определенной длины и направления (вектора). Такая стрелка начинается в точке на теле, которая называется точкой приложения силы. На рисунке 37 изображена сила, значение которой равно 10 Н, направлена она слева направо и приложена в точке А.

Пользуясь графическим методом, можно производить различные математические операции с силами. Так, если к одной точке на теле приложены силы 2 Н и 3 Н, которые действуют в одном направлении, то их можно заменить одной силой, которая будет приложена в той же точке и действовать в том же направлении, а ее значение будет равно сумме значений каждой из сил (рис. 38). Вектор этой силы будет иметь длину, равную сумме длин двух векторов.

Возможен и другой случай, когда силы, приложенные в одной точке тела, действуют в противоположных направлениях. Тогда их можно заменить одной силой, направленной в направлении большей силы, а ее значение будет равняться разности значений каждой силы (рис. 39). Длина вектора этой силы будет равна разности длин векторов приложенных сил.

Сила, которой можно заменить действие нескольких сил, приложенных в определенной точке тела, называется равнодействующей.

Равнодействующая — это сила, действие которой равнозначно действию нескольких сил, приложенных к телу в определенной его точке.

Силу обозначают большой латинской буквой .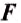

На рис. 68 спортсменка приготовилась стрелять из лука. В этом случае её рука действует на тетиву с силой направленной вправо, а тетива действует на руку с такой же по значению силой, направленной влево. Итак, значения сил одинаковы, но их направления противоположны.

• Заказать решение задач по физике

Сложение сил

Главная задача динамики — по действующей силе определить движение тела или по характеру движения тела установить, какая сила на него действует. Понятие о силе является основным в механике. И. Ньютон утверждал то, что мы называем силой, есть действие одного тела на другое, или их взаимодействие.

Действие одних тел на другие сообщает ускорение их движению. Полученное телом ускорение является внешним проявлением того, что оно взаимодействовало с другим телом. Когда мы говорим «сила», то подразумеваем, что на данное тело действуют другие тела.

Сила, являющаяся причиной изменения состояния движения тел или их деформации, характеризует взаимодействие тел, которое происходит при их непосредственном контакте (например столкновении) или через поля (рис. 2.2).

Сила — векторная величина, характеризующая действие, которое является причиной изменения состояния движения или покоя.

Действие на тело нескольких сил может быть заменено их равнодействующей (рис. 2.3), которую определяют геометрическим сложением этих сил как векторов:

 

Не скорость тела, а ее изменение есть следствием действия силы (действия других тел).

Помимо значения и направления сила характеризуется еще и точкой приложения, которую можно перемещать вдоль линии действия силы, если тело абсолютно твердое (не деформируется). Поскольку действия сил независимы, то сила может быть разложена на составляющие 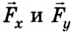(рис. 2.4) как проекции на оси координат.

Для того чтобы выявить инертность тел и увидеть, как на нее влияет время их взаимодействия, проведем такой опыт. На тонкой нитке подвесим груз (рис. 2.5, а). Снизу к грузу прикрепим точно такую же нитку. Если резко дернуть за нижнюю нитку, то она оборвется, а груз останется висеть на верхней нитке (рис. 2.5, б). Если нижнюю нитку натягивать медленно, то оборвется верхняя нитка (рис. 2.5, в).

Когда мы резко дергаем за нижнюю нитку, взаимодействие руки и нитки кратковременно, груз не успевает изменить свою скорость — верхняя нитка не обрывается, т. к. груз имеет значительную инертность.

Если же за нижнюю нитку тянуть медленно (рука действует на груз продолжительное время), то груз набирает такую скорость, что его перемещение достаточно для разрыва и без того натянутой верхней нитки.

Как вы уже знаете, инертность тел определяется их массой, т. е. масса тела характеризует его инертность.

Во время тщательных исследований взаимодействия двух тел, например столкновения двух абсолютно упругих шаров, установлено, что отношение модулей ускорений взаимодействующих тел равно обратному отношению их масс:

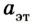
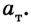
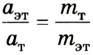
Следствием этого соотношения является один из методов измерения массы тел. Сначала выбирают тело, массу которого условно берут за единицу, — эталон массы. Между эталоном массы и телом, массу которого нужно измерить, можно поместить сжатую при помощи нитки пружину. Потом нитку поджечь и определить ускорение эталона и исследуемого тела Из соотношения находим массу исследуемого тела:

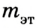
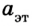
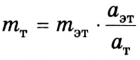
где и — масса и ускорение эталона (1 единица массы). Отсюда  единиц массы. 

По международному соглашению за единицу массы принята масса эталона килограмма (рис. 2.6).

 

Килограмм (кг) — основная единица массы в Международной системе единиц (СИ). Килограмм равен массе международного прототипа килограмма — гире из платино-иридиевого сплава (90 % Pt, 10 % lr) в виде цилиндра диаметром и высотой 39 мм, хранящейся в Международном бюро мер и весов (г. Севр, предместье Парижа).

С достаточной точностью можно сказать, что массу 1 кг имеет 1 чистой воды при 15 °C.
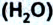
Для измерения массы тела часто используют способ сравнения масс тел с помощью весов. При этом учитывают способность тел взаимодействовать с Землей. Как подтверждают опыты, тела, имеющие одинаковую массу, одинаково притягиваются к Земле в данном месте.

Равнодействующая сила

При изучении физики в 7-м классе вы познакомились с понятием «сила», которое используется для описания взаимодействия тел.

Чтобы вспомнить основные характеристики силы, проведем опыт, например, с куском поролона, покоящимся на неподвижном столе, так как притяжение Земли уравновешено воздействием стола.

Используя пинцет, можно действовать на поролон в различных точках и видеть его поступательное, вращательное или более сложное движение в зависимости от направления, места и величины воздействия.

При этом легко наблюдать не только изменение скорости поролона, но и его деформацию (изменение формы и размеров) (рис. 34) в местах контакта поролона с пинцетом.

Рис. 34

Изменение скорости и деформация тел проявляются в любых опытах при самых разнообразных взаимодействиях, и поэтому принято следующее определение силы:

• сила — физическая векторная величина, являющаяся количественной мерой действия одного тела на другое, в результате которого изменяется скорость тела и происходит его деформация. 

Опыт показывает, что результат воздействия силы определяется не только ее направлением и модулем, но и точкой приложения.

Единицей измерения силы в СИ является 1 ньютон (сокращенно 1 Н).

Вспомним исторически сложившиеся названия сил и их обозначения.

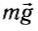
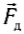
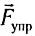
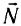
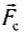
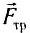
Силой тяжести называется сила, с которой тело притягивается к Земле. Силой давления называется сила, с которой тело действует на опору или жидкость и газ действуют на стенки сосуда. Силой упругости называется сила, возникающая при деформации тела. Силой реакции  называется сила, действующая на тело со стороны опоры или подвеса. Силой сопротивления и силой трения  называются силы, препятствующие механическому движению тела.

Силы могут действовать на поверхность тела (например, сила давления воздуха) (рис. 35) или быть приложены в некоторой условной точке (например, сила упругости нити в точке ее крепления к телу) (рис. 36).

Для упрощения математического описания механического движения тело рассматривается как материальная точка, если не указаны его размеры и форма. На рисунке тело чаще всего изображают прямоугольником.

Можно изображать силы, действующие на тело, приложенными в центре прямоугольника. Но обычно в центре прямоугольника изображают приложенной силу тяжести, а силу трения и силу реакции опоры рисуют приложенными в точке на нижней грани тела под его центром (рис. 37). Если на тело действуют другие тела, то необходимо учесть одновременно действие нескольких сил.

Рис. 37

При изучении физики в 7-м классе вы познакомились со сложением сил и научились складывать силы, действующие на тело вдоль одной прямой.

В этом случае действие, например, двух сил можно заменить одной силой. Модуль равнодействующей силы равен сумме или разности модулей двух слагаемых сил в зависимости от того, совпадают их направления (рис. 38, а, б) или противоположны (рис. 39. а, б). Направление равнодействующей двух сил совпадает с направлением большей силы.

Рис. 38

Рис. 39

А как складываются силы, если они направлены под некоторым углом друг к другу? Покажем на опыте, что они складываются также векторно. Подвесим груз массой 0,2 кг на динамометре, закрепленном на неподвижном штативе. Если груз покоится, то сила упругости пружины динамометра уравновешивает силу тяжести груза (рис. 40), а показания прибора равны: F_упр = mg = 2H ()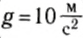

Рис. 40

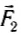
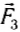
Теперь подвесим этот же груз с помощью двух одинаковых динамометров (рис. 41, а), закрепленных на одной высоте. Меняя положения динамометров, а следовательно, угол между силами  и , действующими на груз со стороны динамометров, можно убедиться, что их показания зависят от этого угла и лишь при угле, равном нулю, в сумме равны 2 Н.

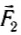
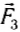
Следовательно, совместное действие сил и уравновешивает действие силы тяжести груза, но сумма модулей этих сил не равна 2 Н, т. е. силы нельзя складывать как скалярные величины.

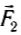
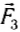
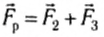
Когда угол между силами и равен 120° (рис. 41,6), то сумма показаний динамометров — 4 Н, а сила тяжести груза все та же — 2 H. Но если найти в этом случае векторную сумму по правилу сложения векторов, то она по модулю равна F_p= 2 Н.

Следовательно, силы нужно складывать по правилам сложения векторов.

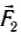
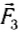
Модуль векторной суммы сил и равен 2 H при любом значении угла между направлениями этих сил, а также и во всех случаях, когда модули сил не равны друг другу (рис. 41, в).

Рис. 41

Какие бы более сложные опыты не проводились (и при действии на тело нескольких сил), всегда результаты измерений показывают, что действие нескольких сил можно заменить их векторной суммой, т. е. силы складываются, как векторы, — геометрически.

Векторная сумма сил, действующих на тело, называется равнодействующей и определяется по формуле:

Если размерами тела нельзя пренебречь и силы приложены в разных его точках, то векторы сил можно перенести в одну точку, сохраняя модуль и направление, и векторно сложить (рис. 42).

Необходимо понимать, что равнодействующая сила заменяет действие нескольких сил только по отношению к движению тела в целом, но не заменяет действие каждой слагаемой силы в других отношениях.

Рис. 42

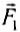
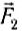
Например, растянутая двумя руками пружина покоится (рис. 43), а значит, равнодействующая сил и равна нулю, но каждая из этих сил деформирует соответственно подвес динамометра и пружину.

Рис. 43

Если тело движется с постоянной скоростью, то согласно первому закону Ньютона все воздействия на тело скомпенсированы, т. е. равнодействующая всех сил также должна быть равна нулю.

Главные выводы:

1. Сила — физическая векторная величина, являющаяся количественной мерой действия одного тела на другое, в результате которого изменяется скорость тела и происходит его деформация.
2. Сила характеризуется модулем, направлением, а также точкой приложения.
3. Заменить действие нескольких сил можно равнодействующей силой, которая определяется как векторная сумма этих сил.
4. При движении тела с постоянной скоростью (или в состоянии покоя) равнодействующая всех сил, действующих на него, равна нулю.

Что означает понятие «Сила» в физике

Вам хорошо известно слово «сила». Обычно смысл слова «сила» и образованных от него слов «силач», «сильный» и т. д. связан с возможностями человека, животного, механизма, с интенсивностью проявления природных явлений. Мы говорим «самый сильный человек», «сила воли», «сильные чувства», «сильный мороз», «сильный двигатель». А какое содержание вкладывают в слово «сила» физики?

Мы уже говорили о том, что причина изменения скорости движения тела — его взаимодействие с другими телами.

Чтобы теннисный мяч вернулся на сторону соперника, вы бьете по мячу ракеткой, но и мяч «бьет» по ракетке. Чтобы остановить велосипед, вы нажимаете на ручки тормоза и в то же время ощущаете, как они давят на ваши ладони. Обратите внимание: в любом случае результат зависит от того, насколько «сильным» будет взаимодействие: сильнее ударите по мячу — мяч наберет большую скорость (рис. 18.1); сильнее нажмете на тормоз — быстрее остановится велосипед. Мерой действия одного тела на другое служит физическая величина сила.

Сила — это физическая величина, которая является мерой действия одного тела на другое (мерой взаимодействия тел).

Силу обычно обозначают символом F. Единица силы в СИ — ньютон (названа в честь Исаака Ньютона): [F]=Н. 1 Н — это сила, которая, действуя на тело массой 1 кг в течение 1 с, изменяет скорость его движения на 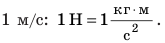Чем больше сила и чем дольше она действует на тело, тем заметнее изменяется скорость движения тела (см. рис. 18.1). Чтобы тела разной массы за одинаковое время изменяли скорости своего движения одинаково, на них должны действовать разные силы (рис. 18.2).

Графическое изображение сил

Сила, действуя на тело, может изменить скорость его движения как по значению, так и по направлению, поэтому сила определяется и значением, и направлением. Уже говорилось о том, что физические величины, имеющие значение и направление, называют векторными. Итак, сила — векторная величина. На рисунках вектор силы начинают в точке, к которой приложена сила (эту точку так и называют — точка приложения силы), и направляют в сторону действия силы. Длину стрелки иногда выбирают так, чтобы она в определенном масштабе соответствовала значению силы (рис. 18.3). Изменение скорости движения тела (по значению, по направлению) зависит от направления силы (см. таблицу на с. 123).

Сложение сил, действующие вдоль одной прямой

Обычно на тело действует не одна сила, а две, три или больше. Проведем опыт. Поставим на стол тележку и привяжем к ней две нити. Потянем за одну нить с силой 5 Н, а за другую — в том же направлении — с силой 3 Н (рис. 18.4). Тележка придет в движение, увеличивая свою скорость так, как если бы на нее действовала одна сила 8 Н. Силу 8 Н, которой в данном случае можно заменить две силы 5 и 3 Н, называют равнодействующей двух сил и обозначают символом R (или F). Силу, которая производит на тело такое же действие, как несколько одновременно действующих сил, называют равнодействующей этих сил. Если тележку одновременно тянуть за две нити в противоположные стороны (рис. 18.5), то силы не будут «помогать» друг другу разгонять тележку, а наоборот — будут «мешать». В этом случае тележка будет двигаться так, будто на нее действует одна сила 2 Н в направлении, в котором действует сила 5 Н, то есть равнодействующей сил 5 и 3 Н будет сила 2 Н.

Как вы считаете, какой будет равнодействующая, если нити, привязанные к тележке с противоположных сторон, потянуть с силами, одинаковыми по значению, например 5 Н? Изменится ли в этом случае скорость движения тележки? 4 Выясняем, когда силы компенсируют друг друга Надеемся, вы правильно ответили на вопрос в п. 3 и самостоятельно пришли к выводу: если две силы равны по значению, противоположны по направлению и приложены к одному телу, то равнодействующая этих сил равна нулю. Силы уравновешивают (компенсируют) друг друга, поэтому причины для изменения скорости движения тела нет. Так, по горизонтальному прямолинейному отрезку шоссе автомобиль движется равномерно (рис. 18.6, а), если сила тяги его двигателя компенсирует силу сопротивления движению (сила сопротивления движению достаточно быстро остановит автомобиль, если двигатель не будет работать). Портфель в руке находится в состоянии покоя, если сила притяжения Земли, действующая на портфель, компенсируется силой, которую прикладывает к портфелю человек (рис. 18.6, б).

Итоги:

Сила F — физическая величина, являющаяся мерой действия одного тела на другое (мерой взаимодействия тел). Сила — причина изменения скорости движения тела. Единица силы в СИ — ньютон (Н). 1 Н равен силе, которая, действуя на тело массой 1 кг в течение 1 с, изменяет скорость его движения на 1 м/с.

Сила — векторная величина. Чтобы охарактеризовать силу, необходимо указать значение, направление и точку приложения силы. Если на тело действуют несколько сил, то их общее действие всегда можно заменить действием одной силы — равнодействующей. Равнодействующей сил, которые действуют на тело в одном направлении, является сила, значение которой равно сумме значений сил, а направление совпадает с направлением этих сил. Если две силы, действующие на тело, направлены в противоположные стороны, то направление равнодействующей совпадает с направлением большей силы, а для нахождения значения равнодействующей нужно из значения большей силы вычесть значение меньшей. Две силы компенсируют (уравновешивают) друг друга, если они равны по значению, противоположны по направлению и приложены к одному телу.

Проекция силы на координатную плоскость это скалярная величина или векторная?

Проеция силы на плоскость характеризуется не только величиной, но и положением (направлением) в этой плоскости, поэтому проекцию силы на плоскость нельзя считать скалярной величиной. Это величина векторная.

На плоскости сила  может быть представлена как векторная сумма двух взаимно перпендикулярных сил  и , которые по модулю равны абсолютным значениям соответствующих проекций

Здесь имеем случай разложения силы на две состав­ляющие по координатным осям. Отличие проекции силы от ее составляющей заключается в том, что проекция силы на ось — величина скалярная, а составляющая — величина векторная.

При рассмотрении силы в пространстве приходится проектировать ее на три координатные оси. Установим, как определяются в пространстве проекции и составляющие произвольной силы , приложенной в точке А.

Первоначально сила  проектируется на координатные плоскости, например, на плоскость хОу и на плоскость yOz. Эти проекции будем снабжать двумя индексами: проекцию на плоскость хОу обозначим , а проекцию на плоскость yOz обозначим .

Проекции сил на координатные плоскости представ­ляют собой векторные величины. Каждую из проекций на координатные плоскости и  легко спроекти­ровать на две координатные оси, в плоскости которых она лежит. При этом получим три проекции силы ,  и .

Сила  может быть представлена диагональю прямо­угольного параллелепипеда, построенного на составляющих ,  и   (см.рис. выше), которые по модулю равны соответствующим проек­циям. Следовательно, мо­дуль и направление силы в пространстве определят­ся по формулам:

Таким образом, в пространстве силу можно разложить на три составляющие по координатным осям

Определите величину и направление вектора силы, если известно, что   Р_x= 30 Н, Р_y  = 40 Н.

Решение. Сначала определим величину силы по формуле

. Значение силы при подстановке значений Р = 50 Н.

Направление определим по формуле

 

Вычислите проекции силы Р на оси координат, если модуль силы Р = 100 Н; cos (Р, х) = 0,575; cos (Р, у) = 0,820.

Ответ: Р_x = 57,5 H ; P_y = 82 H.

Укажите, при каком направ­лении оси проекция век­тора Р будет положительной.

Проекция вектора положительна, если ось будет направлена слева направо.

Часто геометрическое сложение векторов сил требует сложных и громоздких построений. В таких случаях прибегают к другому методу, где геометрическое построе­ние заменено вычислениями скалярных величин. Дости­гается это проектированием заданных сил на оси прямо­угольной системы координат.

Как известнее из математики, осью называют неограни­ченную прямую линию, которой приписано определенное направление. Проекция вектора на ось является скаляр­ной величиной, которая определяется отрезком оси, отсе­каемым перпендикулярами, опущенными из начала и конца вектора на ось.

Проекция вектора считается положительной (+), если направление от начала проекции к ее концу совпадает с положительным направлением оси. Проекция вектора считается отрицательной (—), если направление от на­чала проекции к ее концу противоположно положитель­ному направлению оси.

Рассмотрим ряд случаев проектирования сил на ось.

1. Дана сила Р (рис.а), она лежит в одной пло­скости с осью х. Вектор силы составляет с положительным направлением оси острый угол α.

Чтобы найти величину проекции, из начала и конца вектора силы опускаем перпендикуляры на ось х, полу­чаем

Р_х = ab = Р cos α.

Проекция вектора в данном случае положительна.

2. Дана сила Q (рис. б), которая лежит в одной плоскости с осью х, но ее вектор составляет с положи­тельным направлением оси тупой угол α.

Проекция силы Q на ось х

Q_х = ab = Q cos α,

но

cos a = — cos β.

Так как α > 90°, то cos cos α — отрицательная величина. Выразив cos α через cos β  (β — острый угол), оконча­тельно получим

Q_х = — Q cos β

В этом случае проекция силы отрицательна.

Итак, проекция силы на ось координат равна произве­дению модуля силы на косинус угла между вектором силы и положительным направлением оси.

При определении проекции вектора силы на ось поль­зуются обычно косинусом острого угла, независимо от того, с каким направлением оси — положительным или отрицательным — он образо­ван. Знак проекции легче устанавливать непосредствен­но по чертежу.

Силу, расположенную на плоскости хОу, можно спроек­тировать на две координатные оси Ох и Оу. Рассмотрим рисунок.

На нем изображена сила Р и ее проекции Р_х и Р_у. Ввиду того что проекции образуют между собой прямой угол, из прямоугольного треугольника ABC следует:

Этими формулами можно пользоваться для определения величины и направления силы, когда из­вестны ее проекции на координатные оси. Эти же формулы могут применяться для определения величины и направ­ления любого вектора через его проекции.

Какой многоугольник сил соответствует уравновешенной си­стеме сходящихся сил  — а или б?

Многоугольник сил на рисунке б замкнут вектором ОА. Система сил приводится к равнодействующей R = ОА ≠ 0, а в таком случае система сил не уравновешена.

Система сходящихся сил уравновешена на рисунке а.  R  =  0.

Укажите, какой вектор силового многоугольника является равнодействующей силой:

Равнодействующая сила в силовом многоугольнике всегда направлена от начала первого слагаемого вектора к концу последнего. Так как векторы ОА, АВ, ВС,СD направлены последовательно один за другим, то ни один из них не может быть равнодействующей силой.

Равнодействующей силой является вектор ОD.

На рис. а показана система сходящихся сил, приложенных в точке А. Определить, уравновешена ли данная система сил.

Решение. Построение силового многоугольника выполним в последовательности (см. — здесь).

Из произвольной точки О отложим вектор первой силы P₁. Из конца первого вектора силы отложим вектор второй силы Р₂. Аналогично откладываем остальные векторы сил P₃, P₄, P₅ и P₆. Конец век­тора P₆ совпал с началом вектора P₁.

Равнодействующая равна нулю (R = 0); следовательно, система сил уравновешена.