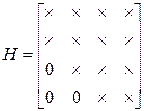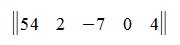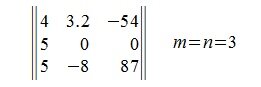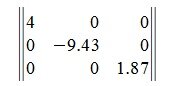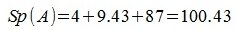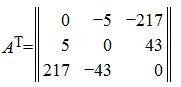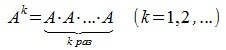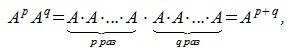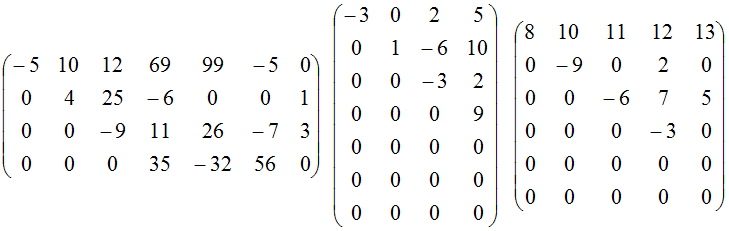A matrix is defined as a rectangular array of numbers that are arranged in rows and columns. The size of a matrix can be determined by the number of rows and columns in it. A matrix is said to be an “m by n” matrix when it has “m” rows and “n” columns and is written as an “m × n” matrix. For example, a matrix of order “5 × 6” has five rows and six columns. We have different types of matrices, such as rectangular, square, triangular, symmetric, singular, etc.
What is a Triangular Matrix?
A triangular matrix is a special case of a square matrix, where all elements above or below the principal diagonal are zeros. An upper triangular matrix is a square matrix, whose all elements below the principal diagonal are zeros. A lower triangular matrix is a square matrix, whose all elements above the principal diagonal are zeros. The matrices in the image given below are upper triangular and lower triangular matrices of order “4 × 4.”
Types of Triangular Matrices
There are different types of matrices which are discussed below in this article:
- Upper Triangular Matrix: An upper triangular matrix is a square matrix, whose all elements below the principal diagonal are zeros.
- Lower Triangular Matrix: A lower triangular matrix is a square matrix, whose all elements above the principal diagonal are zeros.
- Strictly Triangular Matrix: A triangular matrix is referred to as a strictly triangular matrix if all the elements of the principal diagonal are zero.
- Strictly Lower Triangular Matrix: A lower triangular matrix is referred to as a strictly lower triangular matrix if all the elements of the principal diagonal are zero.
- Strictly Upper Triangular Matrix: An upper triangular matrix is referred to as a strictly upper triangular matrix if all the elements of the principal diagonal are zero.
- Unit Triangular Matrix: A triangular matrix is referred to as a unit triangular matrix if all the elements of the principal diagonal are one.
- Unit Lower Triangular Matrix: A lower triangular matrix is referred to as a unit lower triangular matrix if all the elements of the principal diagonal are one.
- Unit Upper Triangular Matrix: An upper triangular matrix is referred to as a unit upper triangular matrix if all the elements of the principal diagonal are one.
Upper Triangular Matrix
An upper triangular matrix is a square matrix, whose all elements below the principal diagonal are zeros. A square matrix “A = [aij]” is said to be an upper triangular matrix when aij = 0 for all i > j.
If Un,n is a square matrix of order “n × n” and uij represents an element in the ith row and jth column of the given matrix, then
Examples of Upper Triangular Matrix
The matrix given below is an upper triangular matrix of order “2 × 2.” We can see that the elements below the principal diagonal are zeros.
The matrix given below is an upper triangular matrix of order “3 × 3.”
Lower Triangular Matrix
A lower triangular matrix is a square matrix whose all elements above the principal diagonal are zeros. A square matrix “A = [aij]” is said to be a lower triangular matrix when aij = 0 for all i < j.
If L is a square matrix of order “n × n” and lij represents an element in the ith row and jth column of the given matrix, then the condition for the given matrix to be a lower triangular matrix is given as follows:
If L is a square matrix of order “n × n” and lij represents an element in the ith row and jth column of the given matrix, then the condition for the given matrix to be a lower triangular matrix is given as follows:
Examples of Lower Triangular Matrix
The matrix given below is a lower triangular matrix of order “2 × 2.”
The matrix given below is a lower triangular matrix of order “3 × 3.” We can see that the elements above the principal diagonal are zeros.
Properties of a Triangular Matrix
Various properties of the Triangular Matrix are discussed below in this article:
- The transpose of an upper triangular matrix is a lower triangular matrix, i.e., UT = L, and the transpose of a lower triangular matrix is an upper triangular matrix, i.e., LT = U.
- The determinant of a triangular matrix of any order is equal to the product of the principal diagonal elements.
- The inverse of a triangular matrix will also be a triangular matrix.
- A triangular matrix is invertible if and only if all elements of the principal diagonal are non-zero.
- When two triangular matrices are multiplied, the resultant matrix is also triangular.
- When two upper (lower) triangular matrices are multiplied, the resultant matrix is also an upper (lower) triangular matrix.
- When two upper (lower) triangular matrices are added, the resultant matrix is also an upper (lower) triangular matrix.
Also, Check
- Minors and Cofactors of Determinants
- Determinant of the Square Matrix
- Adjoint of the Square Matrix
Solved Examples on Triangular Matrix
Example 1: Calculate the determinant of the matrix given below.
Solution:
We can notice that the given matrix is an upper triangular matrix.
We know that the determinant of an upper triangular matrix of any order is equal to the product of the principal diagonal elements.
So, |A| = 1 × 7 × 8 = 56
Hence, the determinant of the given matrix is 56.
Example 2: Prove the inverse of the inverse of a lower triangular matrix will also be a lower triangular matrix.
Solution:
Let us consider a lower triangular matrix of order “2 × 2,” to prove the inverse of the inverse of a lower triangular matrix will also be a lower triangular matrix.
L-1 = Adj L/ |L|
|L| = 5 × 8
= 40
We can see the inverse matrix is also a lower triangular matrix.
Hence, proved.
Example 3: Prove that the transpose of an upper triangular matrix is a lower triangular matrix.
Solution:
To prove that the transpose of an upper triangular matrix is a lower triangular matrix, let us consider an upper triangular matrix.
Now,
We can notice that the resultant matrix is a lower triangular matrix.
Hence proved.
Example 4: Find the values of “a” and “b” in the given matrix P, if P is a unit lower triangular matrix.
Solution:
We know that a lower triangular matrix is referred to as a unit lower triangular matrix if all the elements of the principal diagonal are one.
So, 2a + 5 = 1
2a = 1 − 5 = −4
a = −4/2 = −2
3b − 2 = 1
3b = 1 + 2 = 3
b = 3/3
= 1Hence, the values of “a” and “b” are −2 and 1 respectively.
FAQs on Triangular Matrix
Question 1: What is meant by a triangular matrix?
Answer:
A triangular matrix is a special case of a square matrix where all elements above or below the principal diagonal are zeros.
Question 2: What is an upper triangular matrix?
Answer:
An upper triangular matrix is a square matrix, whose all elements below the principal diagonal are zeros. A square matrix “A = [aij]” is said to be an upper triangular matrix when aij = 0 for all i > j.
Question 3: What is the determinant of an upper triangular matrix?
Answer:
The determinant of an upper triangular matrix of any order is equal to the product of the principal diagonal elements.
Question 4: What is meant by a lower triangular matrix?
Answer:
A lower triangular matrix is a square matrix, whose all elements above the principal diagonal are zeros.
Question 5: What is the transpose of a unit upper triangular matrix?
Answer:
An upper triangular matrix is referred to as a unit upper triangular matrix if all the elements of the principal diagonal are one.
Last Updated :
09 Jan, 2023
Like Article
Save Article
Треугольные матрицы и характеристическое уравнение
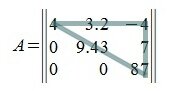
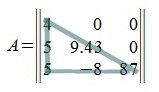
Квадратная матрица, у которой все элементы, расположенные ниже или выше главной диагонали, равны нулю, называется треугольной. Треугольная матрица может быть верхнего и нижнего строения. Верхняя и нижняя формы имеют соответственно вид:
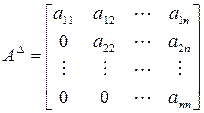
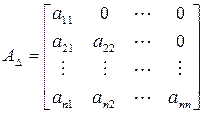
Треугольные матрицы обладают рядом важных в практическом отношении свойств:
1) Определитель треугольной матрицы равен произведению ее диагональных элементов:
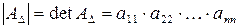
Следовательно, треугольная матрица является неособенной только тогда, когда все элементы ее главной диагонали отличны от нуля.
2) Сумма и произведение треугольных матриц одинакового строения есть также треугольная матрица того же строения.
3) Неособенная треугольная матрица легко обращается, и ее обратная матрица снова имеет треугольную структуру того же строения.
4) Всякая неособенная матрица при помощи элементарных преобразований только над строками или только над столбцами может быть приведена к треугольной матрице. В качестве примера рассмотрим известную в теории устойчивости матрицу Гурвица
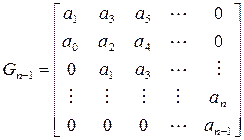
Для перехода к верхнему треугольному виду проделаем следующие элементарные преобразования. Из каждого элемента второй строки вычтем стоящий над ним элемент первой строки, предварительно умноженный на 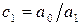
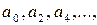
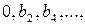
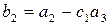
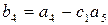
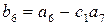
Выполним аналогичные операции в остальных нижележащих строках. Затем вычтем из каждого элемента третьей строки преобразованной матрицы стоящие над ней элементы строки, умноженные на 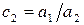
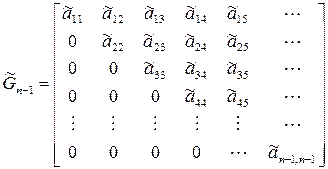
Такие преобразования по существу эквивалентны умножению матрицы справа (или слева) на некоторую другую вспомогательную матрицу.
Определитель матрицы Гурвица
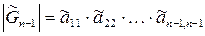
Существует теорема о разложении любой квадратной матрицы в произведение двух треугольных. Согласно этой теореме, всякая квадратная матрица может быть представлена в виде произведения нижней и верхней треугольных матриц:
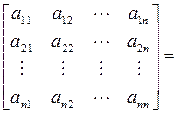
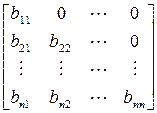
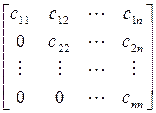
при условии, что ее диагональные миноры отличны от нуля:
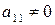
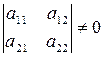
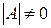
Это разложение является единственным, если зафиксировать диагональные элементы одной из треугольных матриц (например, положить их равными единице). Разложение любой квадратной матрицы в произведение двух треугольных с предписанными диагональными элементами широко используется в вычислительных методах при решении задач с помощью ЭВМ.
Однозначное представление матрицы в виде произведения двух треугольных может быть обобщено на клеточные матрицы. В таких матрицах сами элементы являются матрицами. При этом матрица может быть разложена в произведение нижней и верхней квазитреугольных матриц.
Определитель квазитреугольной матрицы равен произведению ее диагональных клеток.
В отличие от диагональных матриц операция умножения треугольных матриц в общем случае не коммутативна.
В вычислительных методах теории управления существенную роль играют не только треугольные, но и так называемые почти треугольные матрицы. Многие методы используют разложение матрицы в виде произведения двух матриц, одна из которых имеет треугольное строение. Матрица А называется правой (левой) почти треугольной или матрицей Хессенберга, если для ее элементов аij выполняются соотношения:
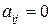
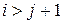
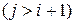
Например, матрица Хессенберга правой почти треугольной формы размерности (4×4) имеет вид
Отметим полезные особенности рассматриваемых матриц, которые используются в вычислительных методах:
а) сумма почти треугольных матриц одинакового строения будет треугольной матрицей того же строения, а произведение — нет;
б) построение характеристического полинома почти треугольных матриц экономично, так как требует гораздо меньшего объема вычислений, чем при произвольной форме матрицы. Число операций умножений составляет 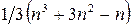
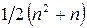
в) почти треугольная матрица может быть разложена в произведение двух треугольных, причем в разложении одна из матриц будет иметь более простую структуру, а именно, будет двухдиагональной.
В современных инженерных методах, заложенных в системы автоматизированного проектирования, широко используется мультипликативное представление матриц, например, QR-представление. Его сущность состоит в том, что любую квадратную матрицу А можно представить в виде произведения ортогональной и почти треугольной форм
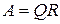
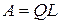
где Q — ортогональная матрица; R — правая (верхняя) треугольная форма; L — левая (нижняя) треугольная форма матрицы.
Представление (4.4) называется QR-разложением (в случае нижней треугольной матрицы QL-разложением) и для матрицы А является единственным.
QR- и QL-алгоритмы принципиально мало различаются. Их использование зависит от того, как расположены элементы матрицы. Если они сосредоточены в нижнем правом углу, эффективнее использовать QL-алгоритм. Если элементы матрицы сосредоточены в левой верхней части, то целесообразнее использовать QR-алгоритм. При правильной реализации на ЭВМ ошибки округления во многих случаях не оказывают большого влияния на точность вычисления.
Дата добавления: 2014-12-27 ; просмотров: 6286 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Введение в матричные типы в линейной алгебре для машинного обучения
Дата публикации 2018-02-09
Много линейной алгебры связано с операциями над векторами и матрицами, и есть много различных типов матриц.
Есть несколько типов матриц, с которыми вы можете столкнуться снова и снова, когда начинаете изучать линейную алгебру, в частности части линейной алгебры, относящиеся к машинному обучению.
В этом уроке вы обнаружите набор различных типов матриц из области линейной алгебры, с которыми вы можете столкнуться при машинном обучении.
После завершения этого урока вы узнаете:
- Квадратные, симметричные, треугольные и диагональные матрицы, которые соответствуют их названиям.
- Все матрицы идентичности имеют нулевые значения, кроме главной диагонали, где значения равны 1.
- Ортогональные матрицы, которые обобщают идею перпендикулярных векторов и имеют полезные вычислительные свойства.
- Обновление февраль / 2018: Исправлена небольшая опечатка в уравнении эквивалентности для ортогональной матрицы.
Обзор учебника
Этот урок разделен на 6 частей, чтобы охватить основные типы матриц; они есть:
- Квадратная матрица
- Симметричная матрица
- Треугольная матрица
- Диагональная матрица
- Единичная матрица
- Ортогональная матрица
Квадратная матрица
Квадратная матрица — это матрица, в которой количество строк (n) равно количеству столбцов (m).
Квадратная матрица контрастирует с прямоугольной матрицей, где количество строк и столбцов не равно.
Учитывая, что количество строк и столбцов совпадают, размеры обычно обозначаются как n, например, п х н. Размер матрицы называется порядком, поэтому квадратная матрица порядка 4 имеет размер 4 x 4.
Вектор значений по диагонали матрицы от левого верхнего до правого нижнего угла называется главной диагональю.
Ниже приведен пример квадратной матрицы порядка 3.
Квадратные матрицы легко складываются и умножаются вместе и являются основой многих простых линейных преобразований, таких как вращения (как в поворотах изображений).
Симметричная матрица
Симметричная матрица — это тип квадратной матрицы, в которой верхний правый треугольник совпадает с нижним левым треугольником.
Не будет преувеличением сказать, что симметричные матрицы S являются наиболее важными матрицами, которые мир когда-либо увидит — в теории линейной алгебры, а также в приложениях.
Чтобы быть симметричным, ось симметрии всегда является главной диагональю матрицы, слева направо и снизу справа.
Ниже приведен пример симметричной матрицы 5 × 5.
Симметричная матрица всегда квадратная и равна ее собственной транспонировании.
Треугольная матрица
Треугольная матрица — это тип квадратной матрицы, в которой все значения находятся в верхнем правом или нижнем левом углу матрицы, а остальные элементы заполнены нулевыми значениями.
Треугольная матрица со значениями только выше главной диагонали называется верхней треугольной матрицей. Принимая во внимание, что треугольная матрица со значениями только ниже основной диагонали называется нижней треугольной матрицей.
Ниже приведен пример верхней треугольной матрицы 3 × 3.
Ниже приведен пример нижней треугольной матрицы 3 × 3.
Разложение LU разрешает данную матрицу в верхнюю и нижнюю треугольные матрицы.
NumPy предоставляет функции для вычисления треугольной матрицы из существующей квадратной матрицы. Функция tril () для вычисления нижней треугольной матрицы по заданной матрице и функция triu () для вычисления верхней треугольной матрицы по заданной матрице
Пример ниже определяет квадратную матрицу 3 × 3 и вычисляет нижнюю и верхнюю треугольную матрицу из нее.
При выполнении примера печатается определенная матрица, за которой следуют нижняя и верхняя треугольные матрицы.
Диагональная матрица
Диагональная матрица — это матрица, в которой значения вне главной диагонали имеют нулевое значение, а главная диагональ берется из верхнего левого угла матрицы в правый нижний угол.
Диагональная матрица часто обозначается переменной D и может быть представлена в виде полной матрицы или вектора значений на главной диагонали.
Диагональные матрицы состоят в основном из нулей и имеют ненулевые элементы только вдоль главной диагонали.
Ниже приведен пример квадратной диагональной матрицы 3 × 3.
Как вектор, он будет представлен как:
Или с указанными скалярными значениями:
Диагональная матрица не обязательно должна быть квадратной. В случае прямоугольной матрицы диагональ будет охватывать кратчайшее измерение; например:
NumPy предоставляет функцию diag (), которая может создать диагональную матрицу из существующей матрицы или преобразовать вектор в диагональную матрицу.
В приведенном ниже примере определяется квадратная матрица 3 × 3, извлекается главная диагональ в виде вектора, а затем создается диагональная матрица из извлеченного вектора.
При выполнении примера сначала печатается определенная матрица, за которой следует вектор главной диагонали и диагональная матрица, построенная из вектора.
Единичная матрица
Тождественная матрица — это квадратная матрица, которая не меняет вектор при умножении.
Значения единичной матрицы известны. Все скалярные значения вдоль главной диагонали (сверху-слева-внизу-справа) имеют значение один, а все остальные значения равны нулю.
Тождественная матрица — это матрица, которая не меняет вектор, когда мы умножаем этот вектор на эту матрицу.
Тождественная матрица часто представляется с использованием обозначения «I» или с размерностью «In», где n — индекс, который указывает размерность квадратной единичной матрицы. В некоторых обозначениях тождество может упоминаться как единичная матрица или «U», чтобы соответствовать одному значению, которое оно содержит (это отличается от унитарной матрицы).
Например, единичная матрица размером 3 или I3 будет выглядеть следующим образом:
В NumPy матрица идентичности может быть создана с определенным размером, используя функцию identity ().
В приведенном ниже примере создается единичная матрица I3.
При выполнении примера печатается созданная единичная матрица.
В одиночку единичная матрица не так интересна, хотя она является компонентом других операций импорта матрицы, таких как инверсия матрицы.
Ортогональная матрица
Два вектора ортогональны, когда их скалярное произведение равно нулю, и называется ортонормированным.
Это интуитивно понятно, если учесть, что одна линия ортогональна другой, если она перпендикулярна ей.
Ортогональная матрица — это тип квадратной матрицы, столбцы и строки которой представляют собой ортонормированные единичные векторы, например, перпендикулярно и имеет длину или величину 1.
Ортогональная матрица — это квадратная матрица, строки которой взаимно ортонормированы, а столбцы взаимно ортонормированы
Ортогональная матрица часто обозначается заглавной буквой «Q».
Умножение на ортогональную матрицу сохраняет длины.
Ортогональная матрица формально определяется следующим образом:
Где Q — ортогональная матрица, Q ^ T обозначает транспонирование Q, а I — единичная матрица.
Матрица ортогональна, если ее транспонирование равно обратному.
Другая эквивалентность для ортогональной матрицы состоит в том, если скалярное произведение матрицы само по себе равно единичной матрице.
Ортогональные матрицы часто используются для линейных преобразований, таких как отражения и перестановки.
Ниже приведена простая ортогональная матрица 2 × 2, которая является примером матрицы отражения или координатного отражения.
Пример ниже создает эту ортогональную матрицу и проверяет вышеуказанные эквивалентности.
Выполнение примера сначала печатает ортогональную матрицу, инверсию ортогональной матрицы и транспонирование ортогональной матрицы затем печатают и показывают, что они эквивалентны. Наконец, печатается единичная матрица, которая вычисляется из точечного произведения ортогональной матрицы с ее транспонированием.
Ортогональные матрицы являются полезными инструментами, поскольку они дешевы в вычислительном отношении и стабильны, чтобы вычислять их обратные значения как просто их транспонирование.
расширения
В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.
- Модифицируйте каждый пример, используя свои собственные маленькие надуманные данные.
- Напишите свои собственные функции для реализации каждой операции.
- Исследуйте один пример, где каждая операция использовалась в машинном обучении.
Если вы исследуете какое-либо из этих расширений, я хотел бы знать.
Дальнейшее чтение
Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться.
книги
- Раздел 6.2. Специальные типы матриц.Руководство по линейной алгебре, 2017
- Введение в линейную алгебру, 2016
- Раздел 2.3. Идентичность и обратные матрицы,Глубокое обучение, 2016
- Раздел 2.6. Специальные виды матриц и векторов,Глубокое обучение, 2016
статьи
Резюме
В этом уроке вы обнаружили набор различных типов матриц из области линейной алгебры, с которыми вы можете столкнуться при машинном обучении.
В частности, вы узнали:
- Квадратные, симметричные, треугольные и диагональные матрицы, которые соответствуют их названию.
- Матрицы идентичности, которые являются нулевыми значениями, кроме главной диагонали, где значения равны 1
- Ортогональные матрицы, которые обобщают идею перпендикулярных векторов и имеют полезные вычислительные свойства.
У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.
Матрицы. Виды матриц
Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.
Матрица порядка m × n записывается в форме:
или (i=1,2. m; j=1,2. n).
Числа aij входящие в состав данной матрицы называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j— номер столбца.
Матрица строка
Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:
Матрица столбец
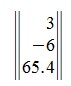
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например
Нулевая матрица
Если все элементы матрицы равны нулю,то матрица называется нулевой матрицей . Например
Квадратная матрица
Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:
Главная диагональ матрицы
Элементы расположенные на местах a 11, a 22 . ann образуют главную диагональ матрицы. Например:
В случае m×n -матриц элементы aii ( i= 1,2. min(m,n)) также образуют главную диагональ. Например:
Элементы расположенные на главной диагонали называются главными диагональными элементами или просто диагональными элементами .
Побочная диагональ матрицы
Элементы расположенные на местах a 1n, a 2n-1 . a n1 образуют побочную диагональ матрицы. Например:
Диагональная матрица
Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:
Единичная матрица
Квадратную матрицу n-го порядка, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю, называется единичной матрицей и обозначается через E или E n , где n — порядок матрицы. Единичная матрица порядка 3 имеет следующий вид:
След матрицы
Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:
Верхняя треугольная матрица
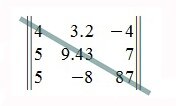
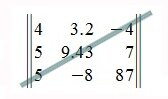
Квадратная матрица порядка n×n называется верхней треугольной матрицей, если равны нулю все элементы матрицы, расположенные под главной диагональю, т.е. aij=0, при всех i>j . Например:
Нижняя треугольная матрица
Квадратная матрица порядка n×n называется нижней треугольной матрицей, если равны нулю все элементы матрицы, расположенные над главной диагональю, т.е. aij=0, при всех i T ).
Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).
Ядро или нуль пространство матрицы
Множесто всех решений уравнения Ax=0, где A- mxn-матрица, x— вектор длины n — образует нуль пространство или ядро матрицы A и обозначается через Ker(A) или N(A).
Противоположная матрица
Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.
Кососимметричная (Кососимметрическая) матрица
Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:
В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.
Пример кососимметрической матрицы:
Разность матриц
Разностью C двух матриц A и B одинакового размера определяется равенством
Для обозначения разности двух матриц используется запись:
Степень матрицы
Пусть квадратная матрица размера n×n. Тогда степень матрицы определяется следующим образом:
где E-единичная матрица.
Из сочетательного свойства умножения следует:
где p,q— произвольные целые неотрицательные числа.
Симметричная (Симметрическая) матрица
Матрица, удовлетворяющая условию A=A T называется симметричной матрицей.
Для симметричных матриц имеет место равенство:
http://www.machinelearningmastery.ru/introduction-to-types-of-matrices-in-linear-algebra/
http://matworld.ru/matrix/matrix.php
Матрицы. Виды матриц
Матрицей называется прямоугольная таблица из чисел с некоторым количеством m строк и с некоторым количеством n столбцов. Числа m и n называются порядками или размерами матрицы.
Матрица порядка m × n записывается в форме:
или 
Числа aij входящие в состав данной матрицы называются ее элементами. В записи aij первый индекс i означает номер строки, а второй индекс j— номер столбца.
Матрица строка
Матрица размером 1×n, т.е. состоящая из одной строки, называется матрицей-строкой. Например:
Матрица столбец
Матрица размером m×1, т.е. состоящая из одного столбца, называется матрицей-столбцом. Например
Нулевая матрица
Если все элементы матрицы равны нулю,то матрица называется нулевой матрицей . Например
Квадратная матрица
Матрица A порядка m×n называется квадратной матрицей, если количество строк и столбцов совпадают: m=n. Число m=n называется порядком квадратной матрицы. Например:
Главная диагональ матрицы
Элементы расположенные на местах a11, a22 ,…, ann образуют главную диагональ матрицы. Например:
В случае m×n -матриц элементы aii ( i=1,2,…,min(m,n)) также образуют главную диагональ. Например:
Элементы расположенные на главной диагонали называются главными диагональными элементами или просто диагональными элементами .
Побочная диагональ матрицы
Элементы расположенные на местах a1n, a2n-1 ,…, an1 образуют побочную диагональ матрицы. Например:
Диагональная матрица
Квадратная матрица называется диагональной, если элементы, расположенные вне главной диагонали равны нулю. Пример диагональной матрицы:
Единичная матрица
Квадратную матрицу n-го порядка, у которой на главной диагонали стоят единицы, а все остальные элементы равны нулю, называется единичной матрицей и обозначается через E или E n, где n — порядок матрицы. Единичная матрица порядка 3 имеет следующий вид:
След матрицы
Сумма главных диагональных элементов матрицы A называется следом матрицы и обозначается Sp A или Tr A. Например:
|
|
Верхняя треугольная матрица
Квадратная матрица 
Нижняя треугольная матрица
Квадратная матрица 
Cтроки матрицы A образуют пространство строк матрицы и обозначаются через R(AT).
Cтолбцы матрицы A образуют пространство столбцов матрицы и обозначаются через R(A).
Ядро или нуль пространство матрицы
Множесто всех решений уравнения Ax=0, где A- mxn-матрица, x— вектор длины n — образует нуль пространство или ядро матрицы A и обозначается через Ker(A) или N(A).
Противоположная матрица
Для любой матрицы A сущеcтвует противоположная матрица -A такая, что A+(-A)=0. Очевидно, что в качестве матрицы -A следует взять матрицу (-1)A, элементы которой отличаются от элементов A знаком.
Кососимметричная (Кососимметрическая) матрица
Кососимметричной называется квадратная матрица, которая отличается от своей транспонированной матрицы множителем −1:
AT=−A.
В кососимметричной матрице любые два элемента, расположенные симметрично относительно главной диагонали отличаются друг от друга множителем −1, а диагональные элементы равны нулю.
Пример кососимметрической матрицы:
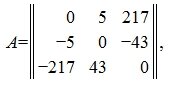
Разность матриц
Разностью C двух матриц A и B одинакового размера определяется равенством
C=A+(-1)B.
Для обозначения разности двух матриц используется запись:
C=A-B.
Степень матрицы
Пусть 
A0=E,
где E-единичная матрица.
Из сочетательного свойства умножения следует:
где p,q— произвольные целые неотрицательные числа.
Симметричная (Симметрическая) матрица
Матрица, удовлетворяющая условию A=AT называется симметричной матрицей.
Для симметричных матриц 
aij=aji ; i=1,2,…n, j=1,2,…n
Методы вычисления определителей
При вычислении определителей высокого порядка (больше 3-го) определение, как правило, не используется, так как это приводит к громоздким выражениям и требует большого количества арифметических операций. Гораздо эффективнее использовать свойства определителей. Наиболее важными для вычисления определителей являются свойства 3, 6, 9. Эти свойства можно назвать элементарными преобразованиями определителя, что соответствует элементарным преобразованиям матрицы.
I. Перестановка двух столбцов (строк) определителя приводит к изменению его знака на противоположный.
II. Умножение всех элементов одного столбца (строки) определителя на одно и то же число, отличное от нуля, приводит к умножению определителя на это число.
III. Прибавление к элементам одного столбца (строки) определителя соответствующих элементов другого столбца, умноженных на одно и то же число, не изменяет определитель.
При помощи элементарных преобразований можно упростить определитель, т.е. привести его к виду, удобному для вычислений.
Метод приведения определителя к треугольному виду
При помощи элементарных преобразований любую матрицу можно привести к верхнему (или нижнему) треугольному виду (метод Гаусса). Отсюда следует, что любой определитель, используя перечисленные выше элементарные преобразования, можно привести к треугольному виду, а затем вычислить согласно п.3 замечаний 2.2.
Итак, метод состоит из двух шагов.
1. При помощи элементарных преобразований привести определитель к треугольному виду.
2. Вычислить определитель треугольного вида, перемножая его элементы, стоящие на главной диагонали.
Пример 2.12. Вычислить определитель четвёртого порядка
приводя его к треугольному виду.
Решение. 1. При помощи элементарных преобразований приведем матрицу к треугольному виду. Взяв элемент первой строки в качестве ведущего, все остальные элементы первого столбца сделаем равными нулю. Для этого ко второй строке прибавим первую, умноженную на (-2), к третьей строке прибавим первую, умноженную на (-3), а к четвертой строке прибавим первую, умноженную на (-4):
Заметим, что при использовании этих элементарных преобразований III типа определитель не изменяется.
Умножим элементы второй строки на (-1), а элементы третьей строки — на 0,5, при этом, чтобы не нарушить равенство, надо полученный определитель разделить на , т.е. умножить на (-2):
В полученной матрице нужно сделать равными нулю элементы и
второго столбца, стоящие ниже главной диагонали. Для этого берем в качестве ведущего элемента
и прибавляем к третьей и четвертой строкам вторую строку, умноженную на 1 и на 7 соответственно:
Осталось сделать равным нулю элемент . К четвертой строке прибавим третью, умноженную на 2 (определитель при этом не изменится):
Получили определитель треугольного вида.
2. Вычислим определитель верхней треугольной матрицы, перемножая элементы, стоящие на главной диагонали:
Метод понижения порядка определителя
Этот метод также основан на элементарных преобразованиях определителя.
1. При помощи элементарного преобразования III типа нужно в одном столбце (или одной строке) сделать равными нулю все элементы, за исключением одного.
2. Разложить определитель по этому столбцу (строке) и получить определитель меньшего порядка, чем исходный. Если его порядок больше 1, то следует перейти к п. 1, иначе вычисления закончить.
Пример 2.13. Вычислить определитель четвёртого порядка методом понижения порядка.
Решение. 1. В качестве ведущего элемента возьмем , а все остальные элементы второй строки при помощи элементарных преобразований сделаем равными нулю. Для этого ко второму столбцу прибавим четвертый, умноженный на (-3):
2. Разложим определитель по второй строке
Получили определитель третьего порядка.
Вынесем за знак определителя множитель (2) из второго столбца (точнее все элементы второго столбца умножим на 0,5 , а получившийся определитель умножим на 2):
Прибавим ко второму столбцу первый
Полученный определитель разложим по второму столбцу
Получили определитель 2-го порядка.
Прибавим ко второй строке первую, умноженную на (-2)
Разложим определитель по второй строке и заменим определитель первого порядка единственным его элементом
Результат совпадает с полученным в примере 2.7.
Метод изменения всех элементов определителя
При вычислении определителей бывает полезно изменить все его элементы, умножив их на одно и то же число, не равное нулю, либо прибавить к каждому элементу одно и то же число. Найдем формулы изменения определителя при этих преобразованиях.
Пусть дана квадратная матрица n-го порядка. Из свойства 6 следует, что при умножении всех элементов определителя n-го порядка на число
определитель умножается на число
.
Рассмотрим теперь определитель матрицы , элементы которой
получены из соответствующих элементов матрицы
прибавлением числа
Применяя свойство 7 к первому столбцу этого определителя, получаем сумму определителей
То же свойство применяем к каждому определителю («раскладывая» второй столбец) и т.д. В итоге получим сумму определителей n-го порядка, причем определители, имеющие по два и более столбцов из элементов, равных
, равны нулю (по свойству 4). Поэтому в сумме остаются только
слагаемых: определитель матрицы
и
определителей вида
отличающихся от определителя матрицы только j-м столбцом. Раскладывая этот определитель по j-му столбцу, получаем сумму алгебраических дополнений элементов этого столбца, умноженную на
Следовательно, сумма всех таких определителей равна сумме алгебраических дополнений всех элементов матрицы
, умноженной на
Окончательно получаем, что при увеличении всех элементов определителя на число , определитель увеличивается на сумму всех алгебраических дополнений, умноженную на число
Пример 2.14. Вычислить определитель n-го порядка
Решение. Рассмотрим определитель диагональной матрицы
Искомый определитель получается прибавлением к каждому элементу определителя матрицы
числа
. Поэтому
Определитель диагональной матрицы равен произведению диагональных элементов:
Осталось вычислить сумму алгебраических дополнений всех элементов матрицы . Заметим, что алгебраическое дополнение недиагонального элемента равно нулю (
при
, так как дополнительный минор содержит нулевой столбец). Дополнительный минор диагонального элемента — это определитель диагональной матрицы, т.е.
Поэтому
Вычисление определителей с помощью рекуррентных уравнений
Этот метод заключается в том, что исходный определитель n-го порядка выражается через определители
того же вида, но меньшего порядка. Получается рекуррентное уравнение
Решая это уравнение, находим формулу, выражающую определитель через определители
и порядок
В последнюю формулу подставляем определители невысокого
порядка, которые нетрудно вычислить каким-либо другим способом.
Замечание 2.6. Рекуррентным уравнением называется равенство вида , выражающее n-й член
искомой числовой последовательности
через
её предыдущих членов
. Методы решения таких уравнений рассматриваются в разд.
Пример 2.15. Вычислить определитель n-го порядка
Решение. Разложим определитель по первой строке
Первый из полученных определителей (n-l)-ro порядка обозначим , так как он имеет такой же вид, что и
. Разложив последний определитель по первому столбцу, получим определитель того же вида, что и
, но (n-2)-го порядка
Следовательно, искомый определитель удовлетворяет рекуррентному уравнению
Решение этого уравнения будем искать в виде , где
и
— неизвестные коэффициенты. Заметим, что эта формула дает решение рекуррентного уравнения при любых коэффициентах
и
. В самом деле, подставляя
в уравнение, получаем тождество
Подберем теперь коэффициенты и
в формуле
так, чтобы при
и
она давала правильные результаты, т.е.
Решая систему уравнений получаем
. Следовательно, искомый определитель равен
Пример 2.16. Вычислить определитель Вандермонда
где
— действительные числа.
Решение. Рассмотрим определитель
который отличается от определителя Вандермонда последним столбцом, но совпадает с ним при . Раскладывая определитель
по последнему столбцу, получаем многочлен (n-1)-й степени действительной переменной
где старший коэффициент равен алгебраическому дополнению элемента
т.е. определителю — определителю Вандермонда (n-l)-ro порядка. Заметим, что при
определитель
равен нулю, так как он имеет два одинаковых столбца (свойство 4). Следовательно,
— корень многочлена
. То же самое можно сказать про числа
. Все они являются корнями многочлена
. Следовательно, этот многочлен имеет вид:
Подставляя в это равенство и учитывая, что
, получаем рекуррентное уравнение
Записывая аналогичным образом и учитывая, что
, получаем
Таким образом, определитель Вандермонда равен произведению всех разностей при
.
Математический форум (помощь с решением задач, обсуждение вопросов по математике).
Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.
-
Сформулируйте определение треугольной матрицы
Треугольная
матрица
—
это квадратная
матрица, у которой все элементы, стоящие
ниже (или выше) главной
диагонали,
равны
нулю.
Подразделяется
на верхнюю
и нижнюю
треугольные матрицы.
Верхняя
треугольная матрица — квадратная
матрица, у которой равны нулю все элементы
матрицы, расположенные под
главной диагональю, т.е. aij=0,
при всех i>j .
Например:
Нижняя
треугольная матрица – это
квадратная
матрица,
у
которой равны нулю все элементы,
расположенные над
главной диагональю, т.е. aij=0, при
всех i<j.
Например:
Диагональная
матрица — квадратная матрица,
все элементы которой, стоящие вне главной
диагонали, равны нулю.
Пример:
Диагональная
матрица является
одновременно и верхней
треугольной,
и нижней
треугольной.
Единичная
– частный случай диагональной.
Как
и нулевая.
!
Заметьте,
что в определении треугольной матрицы
ничего не сказано про значения элементов,
расположенных над главной диагональю
или на главной диагонали. Они могут быть
нулевыми или нет, – это несущественно.
Это тоже треугольные матрицы:
-
Сформулируйте определение трапециевидной матрицы
Матрицу Am×n называют трапециевидной,
если у нее:
— Все
элементы, лежащие на главной диагонали,
не
равны нулю,
а
— Все
элементы, расположенные ниже
главной диагонали, равны
нулю.
В случае,
если матрица не
квадратная, то она будет иметь нулевые
строки, если строк больше чем столбцов
и не будет иметь нулевых строк, если
столбцов больше чем строк.
То есть
она может и не содержать нулевых строк,
но уж если они есть, то располагаются
внизу матрицы. Примеры трапециевидных
матриц:
-
Сформулируйте определение ступенчатой матрицы
Матрица
называется ступенчатой,
если
в каждой ее
строке
первый
НЕнулевой
элемент
стоит правее,
чем в предыдущей (т. е. получаются
ступеньки и высота
каждой ступеньки должна быть равна
единице).
Если
эта матрица содержит нулевую
строку (т.е.
строку, все элементы которой равны
нулю), то все строки, расположенные под
нею, также нулевые.
Примеры ступенчатых
матриц:
То есть,
если нарисовать ступеньки, увидим, что
матрица ступенчатая.
Примеры НЕ
ступенчатых матриц(т.к. высота ступеньки
больше
1строки):
-
Сформулируйте определение единичной матрицы
Единичная
матрица
— квадратная
матрица n-го
порядка, у которой на главной диагонали
стоят единицы,
а все остальные элементы равны нулю.
Обозначают E или En,
где n –
порядок матрицы. Например единичная
матрица порядка 3
:
Единичная
матрица также является треугольной,
диагональной
и скалярной.
-
Какие матрицы называют равными
Матрицы
называются равными,
если у них одинаковое число строк и
столбцов и все соответствующие элементы
совпадают. То
есть ВСЁ
одинаковое!
!
не путать с
эквивалентными
матрицами
(см. вопрос 12)
-
Как выполняется сложение матриц?
Складывать
и вычитать можно матрицы только
одного размера в результате получается
матрица того
же
размера.
Суммой
двух матриц A и B порядка
m×n
называется матрица C=A+B того же
порядка, элементы которой равны
cij=aij+bij (i=1,2,…,m;
j=1,2,…n).
Аналогично
вычитание
(разность) матриц A — B есть
операция вычисления матрицы C,
все элементы которой равны попарной
разности всех соответствующих элементов
матриц A и B, то есть каждый
элемент матрицы C равен: cij=aij
— bij
Свойства
сложения матриц
Из
определения сложения
матриц
непосредственно следует, что эта операция
обладает свойствами:
переместительным
(коммутативным) A+B = B+A.
и
сочетательным (ассоциативным) (A+B)+C =
A+(B+C).
А
также A + Θ = Θ + A = A, где Θ — нулевая
матрица
A
— A = Θ
!
Складывать матрицу с числом нельзя!
Матрицу
можно умножить
на число. Но сложить матрицу можно
только с
другой матрицей,
причём точно такого же размера.
Соседние файлы в папке экз 1 сем
- #
- #


![Rendered by QuickLaTeX.com U = left[begin{array}{ccc} a & b & c\ 0 & d & e\ 0 & 0 & f end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1f57401892f74026b58593d2dfe3441a_l3.png)
![Rendered by QuickLaTeX.com L = left[begin{array}{ccc} 1 & 0 & 0\ 2 & 3 & 0\ 4 & 5 & 6 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-056f46d28db4a56ddf93871e4fea1ab0_l3.png)
![Rendered by QuickLaTeX.com A = left[begin{array}{ccc} 0 & 0 & 0\ p & 0 & 0\ q & r & 0 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e3ee2c530db96915b81e0829695d54d4_l3.png)
![Rendered by QuickLaTeX.com B = left[begin{array}{ccc} 0 & 12 & -7\ 0 & 0 & 9\ 0 & 0 & 0 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-debebebf8143fa1e944f2fe904cb55c0_l3.png)
![Rendered by QuickLaTeX.com P = left[begin{array}{ccc} 1 & 0 & 0\ 2 & 1 & 0\ 5 & 6 & 1 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-773f6bf5929c35225595f0378001cb90_l3.png)
![Rendered by QuickLaTeX.com Q = left[begin{array}{ccc} 1 & 21 & 19\ 0 & 1 & 17\ 0 & 0 & 1 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b90d279a11e4ec492757a56eb6f41638_l3.png)
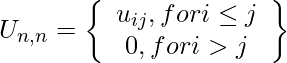
![Rendered by QuickLaTeX.com U_{2,2} = left[begin{array}{cc} 13 & 9\ 0 & 7 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4df88646c7887d0b19b67a7e576cc8c9_l3.png)
![Rendered by QuickLaTeX.com U_{3,3} = left[begin{array}{ccc} 3 & -8 & 6\ 0 & 5 & 11\ 0 & 0 & 4 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2d11cb1a22b5a6f32dc0abe43730b9db_l3.png)

![Rendered by QuickLaTeX.com L = left[begin{array}{cc} 1 & 0\ 3 & 5 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a2ffe4102972378ff972938f189d41c6_l3.png)
![Rendered by QuickLaTeX.com L_{3,3} = left[begin{array}{ccc} 4 & 0 & 0\ 7 & 9 & 0\ -5 & 3 & 11 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a09f5929ef88e26ad0d969f5b268e6bd_l3.png)
![Rendered by QuickLaTeX.com A = left[begin{array}{ccc} 1 & 3 & -4\ 0 & 7 & 0\ 0 & 0 & 8 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-54632ab91e02b4b8982d54d2a2f08361_l3.png)
![Rendered by QuickLaTeX.com L = left[begin{array}{cc} 5 & 0\ -7 & 8 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-488c092b3c44415879eca56956f93d43_l3.png)
![Rendered by QuickLaTeX.com Adj L = left[begin{array}{cc} 8 & 0\ 7 & 5 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-32116ad33d66c9897e724c9e927ae91c_l3.png)
![Rendered by QuickLaTeX.com L^{-1} = frac{1}{40} left[begin{array}{cc} 8 & 0\ 7 & 5 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3313a79008fabd1f9eec243acc95aeca_l3.png)
![Rendered by QuickLaTeX.com U^{T} = left[begin{array}{ccc} a & 0 & 0\ b & d & 0\ c & e & f end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3b011707a6685e3099e47af9bbe990a8_l3.png)
![Rendered by QuickLaTeX.com P = left[begin{array}{cc} 2a+5 & 0\ 5 & 3b-2 end{array}right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5a7e427df431b4afa33e25f11255b8d5_l3.png)