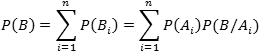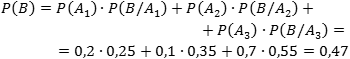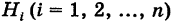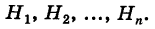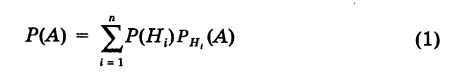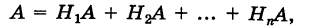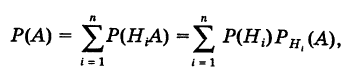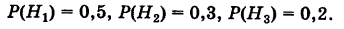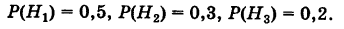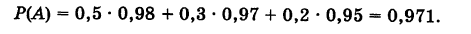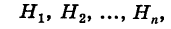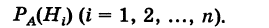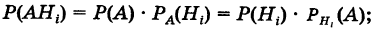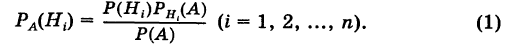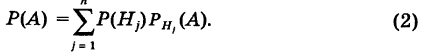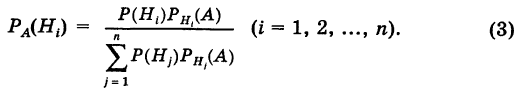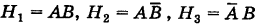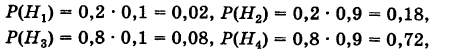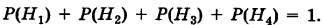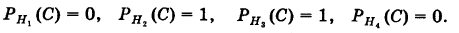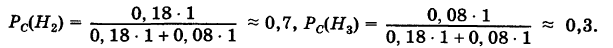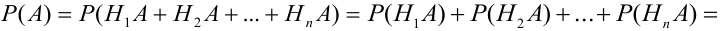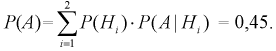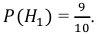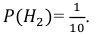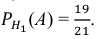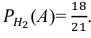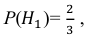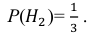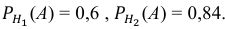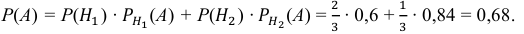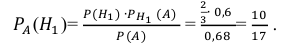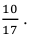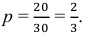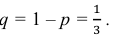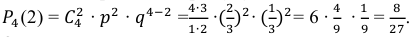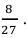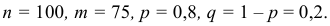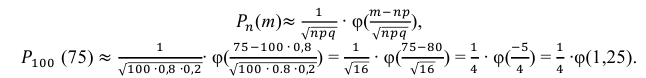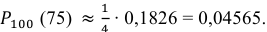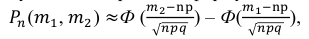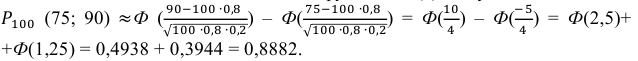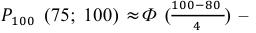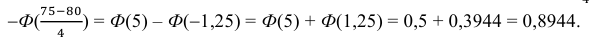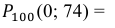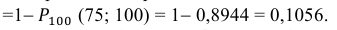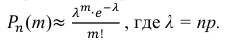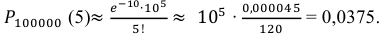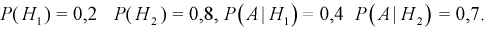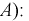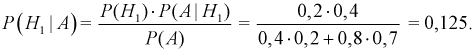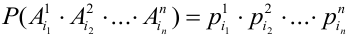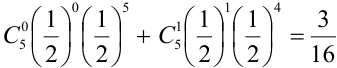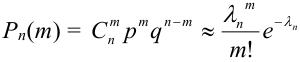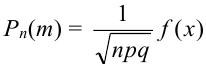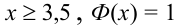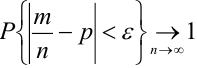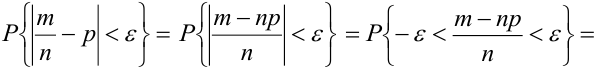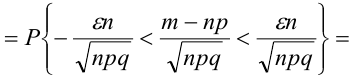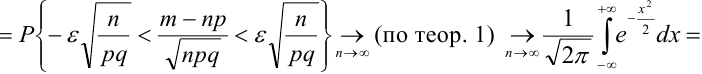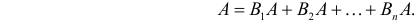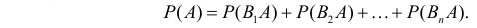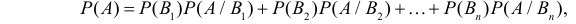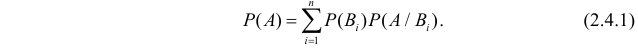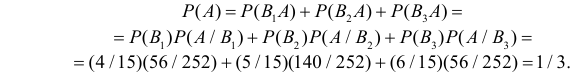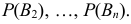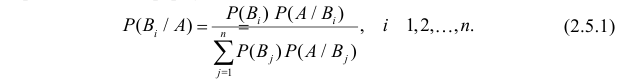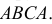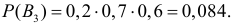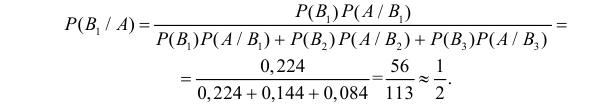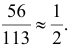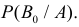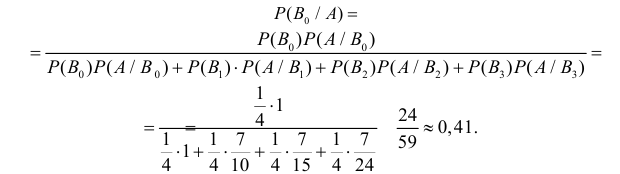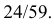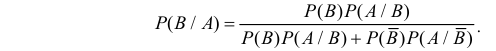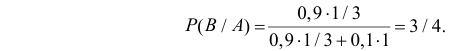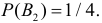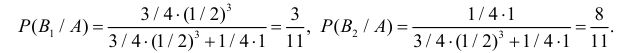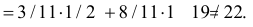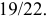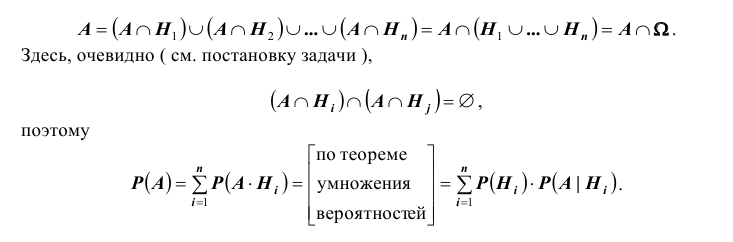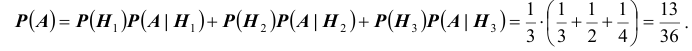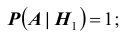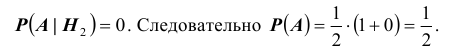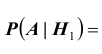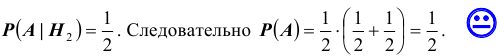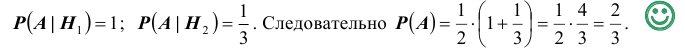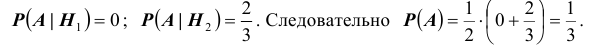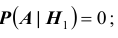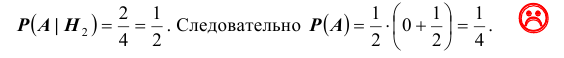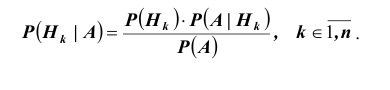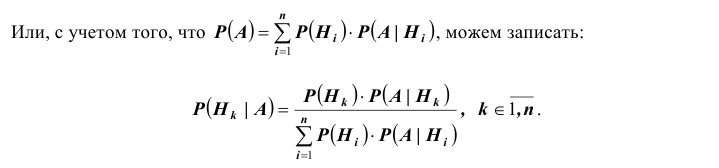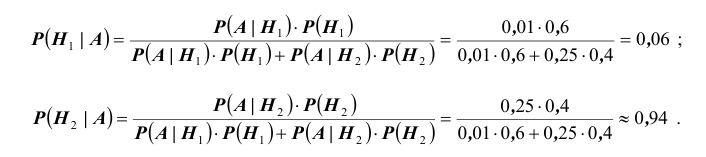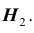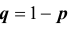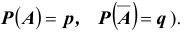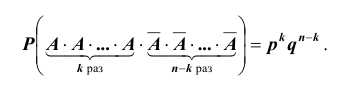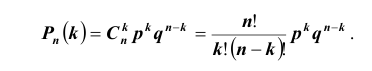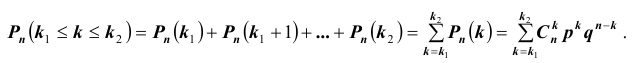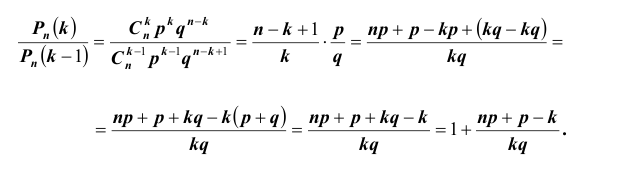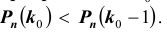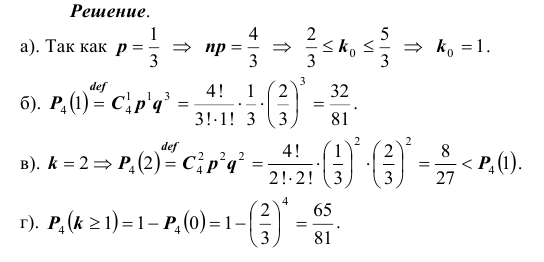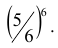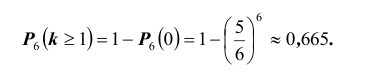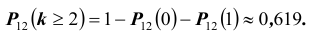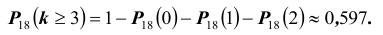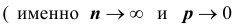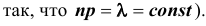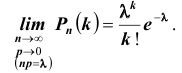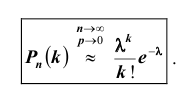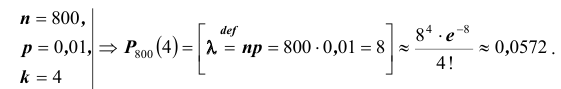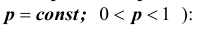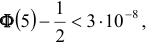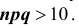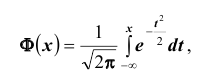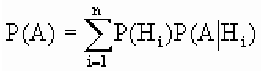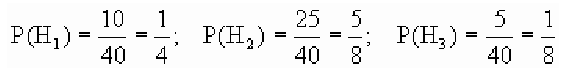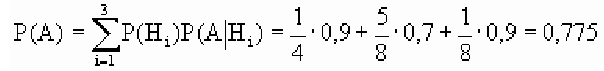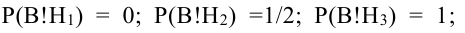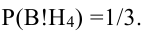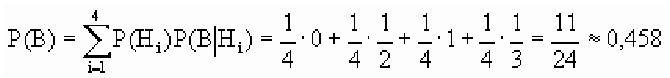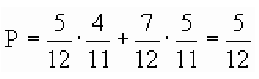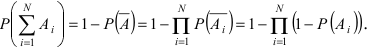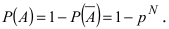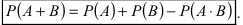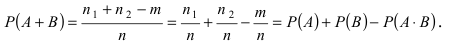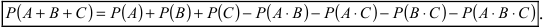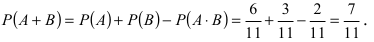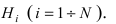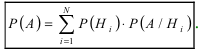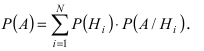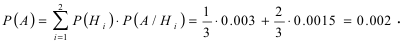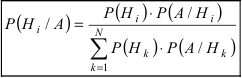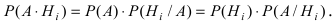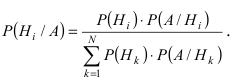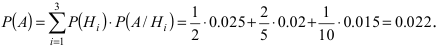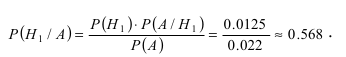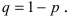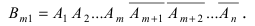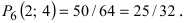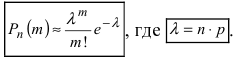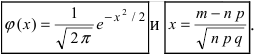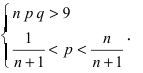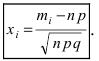Формула полной вероятности
4 июля 2011
Предположим, что событие B может произойти только с одним из несовместных событий A1, A2, …, An. Например, на склад поступает оборудование от нескольких производителей, причем от каждого из них может поступить разное количество оборудования. Также может различаться и вероятность брака у каждого производителя.
Из совокупной партии оборудования случайным образом выбирается один образец. Как определить вероятность того, что этот образец окажется бракованным?
Пусть в совокупной партии встречается только оборудование производителей A1, A2, …, An. Тогда вероятность события Bk (получить бракованный образец) для k-го производителя считается по формуле условной вероятности:
Важно понимать, что P(Ak) — это вероятность наткнуться на образец от k-го производителя во всей партии, P(B/Ak) — это вероятность брака именно в партии от k-го производителя. Поскольку оборудование не может принадлежать сразу двум производителям, события A1, A2, …, An несовместны. По теореме сложения вероятностей получаем:
Это и есть формула полной вероятности. Она работает только если события A1, A2, …, An покрывают все возможные исходы опыта, и позволяет найти вероятность нового события через его условные вероятности при условиях A1, A2, …, An.
Вообще говоря, теория вероятностей сегодня активно изучается не только в университетах, но и в школах. Как следствие, этот вопрос относится не только к компетенции репетиторов по высшей математике в Москве, но и к обычным школьным учителям. Поэтому задача, которую мы рассмотрим далее, будет одинаково полезна и школьникам, и студентам.
Задача. На склад поступает оборудование от трех разных производителей. От первого поступило 20 образцов, от второго — 10, а от третьего — 70. Вероятность брака у этих производителей соответственно равна 0,25; 0,35 и 0,55. Найти вероятность получить бракованный образец при выборе наугад.
Всего у нас 20 + 10 + 70 = 100 образцов. Поэтому вероятность события A1, что образец получен именно от первого производителя (от него поступило 20 образцов), равна P(A1) = 20/100 = 0,2.
Аналогично, P(A2) = 10/100 = 0,1; P(A3) = 70/100 = 0,7. События A1, A2 и A3 попарно несовместны и в сумме покрывают пространство всех возможных событий. Применяем формулу полной вероятности:
Смотрите также:
- Схема Бернулли. Примеры решения задач
- Геометрическая вероятность
- Сложение и вычитание десятичных дробей
- Четырехугольная пирамида в задаче C2
- Процент: налоги и зарплата. Считаем с помощью коэффициентов
- Задача B14: сложные проценты
Пример 1
На фабрике
станки 1,2 и 3 производят соответственно 20%, 35% и 45% всех деталей. В их
продукции брак составляет соответственно 6%, 4%, 2%. Какова вероятность того,
что случайно выбранное изделие оказалось дефектным? Какова вероятность того,
что оно было произведено: а) станком 1; б) станком 2; в) станком 3?
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Обозначим через
событие, состоящее в том,
что стандартное изделие оказалось дефектным.
Событие
может произойти только
при условии наступления одного из трех событий:
-изделие произведено на
станке 1;
— изделие произведено на
станке 2;
— изделие произведено на
станке 3;
Запишем условные вероятности:
По формуле полной вероятности
находим вероятность события
:
Вероятность того, что дефектное изделие
изготовлено на станке 1 найдем по формуле Бейеса:
Вероятность того, что дефектное изделие
изготовлено на станке 2:
Вероятность того, что дефектное изделие
изготовлено на станке 3:
Ответ: а)
; б)
; в)
.
Задача 1
На
отборочное предприятие поступили однотипные комплектующие с трех заводов в
количестве: 20 с первого завода; 50 со второго завода; 30 с третьего. Вероятность качественного
изготовления изделий на первом заводе 0,8, на втором 0,9
, на третьем 0,9. 1) Какова вероятность
того, что взятое случайным образом изделие будет качественным? 2) Взятое наугад
изделие оказалось качественным. Какова вероятность того, что это изделие завода
с номером N=1.
Задача 2
В
пирамиде 15 винтовок, 12 из которых снабжены оптическим прицелом. Вероятность
того, что стрелом поразит мишень при выстреле из винтовки с оптическим прицелом
равна 12/25; для винтовки без оптического прицела эта вероятность равна 2/25.
Найти вероятность того, что мишень будет поражена, если стрелок произведет один
выстрел из наудачу взятой винтовки.
Задача 3
На
предприятии работают две бригады рабочих: первая производит в среднем 3/4
продукции с процентом брака 4%, вторая – 1/4 продукции с процентом брака 6%.
Найти вероятность того, что взятое наугад изделие:
а)
окажется бракованным;
б)
изготовлено второй бригадой при условии, что изделие оказалось бракованным.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
В одном
сосуде находятся 7 белых и 6
черных шаров. Во втором – 5
белых и 9
черных. Бросают два кубика. Если сумма очков,
выпавших на верхних гранях, меньше 10, берут шар из первого сосуда, если больше
или равна 10 – из второго. Вынут белый шар. Какова вероятность того, что сумма
очков была не меньше 10?
Задача 5
Вероятность
того, что во время работы цифровой электронной машины произойдет сбой в
арифметическом устройстве, в оперативной памяти, в остальных устройствах,
относятся как 3:2:5. Вероятность обнаружения сбоя в арифметическом устройстве,
в оперативной памяти и в остальных устройствах соответственно равна 0,8; 0,9;
0,9. Найти вероятность того, что возникший в машине сбой будет обнаружен.
Задача 6
Имеется
пять урн. В первой, второй и третьей урнах находится по 2 белых и 3 черных
шара, в четвертой и пятой урнах — по 1 белому и 1 черному шару. Случайно
выбирается урна и из нее извлекается шар. Какова условная вероятность того, что
выбрана четвертая или пятая урна, если извлеченный шар оказался белым?
Задача 7
В двух
пакетах находятся конфеты. В первом пакете 16 штук сорта «Белочка» и 8 штук
сорта «Жар-птица», во втором 15 сорта «Белочка» и 5 сорта «Жар-птица». Из
первого пакета во второй переложили две конфеты, взятые случайным образом,
содержимое второго пакета перемешали и вытащили оттуда одну конфету, которая
оказалась «Жар-птицей».
Какова
вероятность, что из первого пакета во второй переложили одну «Белочку» и одну
«Жар-птицу»?
Задача 8
В городе N – 600
гостиничных номеров. Из них 100 номеров – в первой гостинице, 200 – во второй,
остальные – в третьей. В турфирме известно, что наличие свободного номера
нужного класса составляет вероятность 0,7; 0,5 и 0,8 соответственно в первой,
второй и третьей гостиницах. Определить вероятность того, что клиентов поселили
во вторую гостиницу.
Задача 9
Имеются
три партии радиоламп, насчитывающих соответственно 20,30 и 50 шт. Вероятности
того, что радиолампа проработает заданное время, равны 0,7; 0,8; 0,9. Какова
вероятность того, что наудачу выбранная лампа из 100 данных проработает
заданное время?
Задача 10
В первом
ящике 2 карандаша и 4 ручки, во втором — 3 карандаша и 1 ручка. Случайным
образом выбрали ящик и из него достали один предмет. Найти вероятность того,
что им оказался карандаш.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 11
Для
участия в студенческих отборочных соревнованиях выделено из первой группы курса
4 студента, 6 из второй и 5 студентов из третьей. Вероятности того, что
отобранный студент из первой, второй, третьей группы попадает в сборную
института, соответственно равны 0.5, 0.4 и 0.2. Наудачу выбранный участник
соревнований попал в сборную. К какой из указанных групп он вероятнее всего
принадлежит?
Задача 12
Из 10
лотерейных билетов 3 выигрышных. При подготовке вечера 2 билета потеряли, и
было решено добавить один выигрышный. Какой стала вероятность того, что
случайно выбранным билет будет выигрышным?
Задача 13
В урне
находятся 5 шаров белого цвета и 4 шара
черного цвета. Три шара последовательно извлекаются из урны (без возвращения их
в урну). Найти вероятность того, что третий извлеченный шар будет белым.
Задача 14
Родион
Раскольников покупает себе топор. У первых трех торговцев по 15 топоров с
сосновыми топорищами и по 10 топоров с дубовыми. Имеются еще два торговца, у каждого из
которых по 5 топоров с сосновыми топорищами и по 5 топоров с дубовыми. Раскольников
покупает первый попавшийся топор у наугад выбранного торговца. Какова
вероятность покупки топора с дубовым топорищем?
Задача 15
На базу
поступили одинаковые по объему партии холодильников с двух разных заводов.
Вероятность того, что холодильник проработает без поломок в течение гарантийного
срока, равна 0,85, если холодильник собран на 1-ом заводе, и 0,95, если на
втором. Найти вероятность того, что наугад взятый холодильник не сломается в
течение гарантийного срока.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 16
Банки
закатывают два автомата с одинаковой производительностью. Доля банок с дефектом
укупорки для первого автомата составляет 1%, а для второго — 0,5%. Какова
вероятность того, что взятая наугад банка будет иметь дефект укупорки?
Задание 17
У рыбака
есть три излюбленных места рыбалки. Эти места он посещает с одинаковой
вероятностью. Вероятность того, что рыба клюнет в 1-м месте – 1/3, во втором –
1/2, в 3-м – 1/4. Известно, что рыбак забросил удочку 3 раза, а вытащил только
одну рыбу. Какова вероятность того, что рыбак рыбачил в первом месте?
Задача 18
В группе
из 20 пациентов имеются 4 человека с заболеванием A
, 10 — с заболеванием B
и 6 с заболеванием C
. Вероятность аллергической
реакции при приеме витаминов для первой группы больных — 0,9, для второй — 0,7,
для третьей — 0,5. Найдите вероятность того, что: а) у наудачу выбранного
больного возникнет аллергическая реакция; б) у 2 наудачу выбранных больных
возникнет аллергическая реакция.
Задача 19
В
результате исследований, проведенных в хирургическом отделении одного лечебного
учреждения, установлено, что первая группа крови встречается у 40% больных,
вторая — у 30%, третья — у 20% , четвертая — у 10%. Во время операций
переливание крови требуется пациентам с первой группой — 2%, второй — 1%,
третьей -0,5% и четвертой -0,2%. Найдите вероятность того, что во время
операции пациенту не потребуется переливание крови.
Задача 20
Покупатель
пробует шестизарядный револьвер. Найти вероятность того, что при нажатии
покупателем на курок раздастся выстрел, если равновозможны все предположения о
количестве заряженных в револьвер патронов.
Содержание:
Формула полной вероятности:
Пусть событие А может произойти в результате появления одного и только одного события
События этой группы обычно называются гипотезами.
Теорема: Вероятность события А равна сумме парных произведений вероятностей всех гипотез, образующих полную группу, на соответствующие условные вероятности данного события А, т. е.
(формула полной вероятности), причем здесь
Доказательство. Так как
причем, ввиду несовместности событий 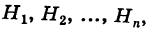
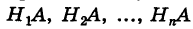
что и требовалось доказать.
Пример:
В магазин для продажи поступает продукция трех фабрик, относительные доли которых есть: I — 50%, II — 30%, III — 20%. Для продукции фабрик брак соответственно составляет: I — 2%, II — 3%, III — 5%. Какова вероятность того, что изделие этой продукции, случайно приобретенное в магазине, окажется доброкачественным (событие А)?
Решение:
Здесь возможны следующие три гипотезы: 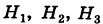
Соответствующие условные вероятности события А равны
По формуле полной вероятности имеем
Формула Бейеса:
Пример:
Имеется полная группа несовместных гипотез
вероятности которых 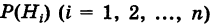
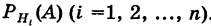
Например, очевидно, следует отбросить гипотезы, отрицающие появление события А. Вообще, проблема состоит в том, что, имея новую информацию, мы должны переоценить вероятности наших гипотез.
Иными словами, нам нужно определить условные вероятности
На основании теоремы умножения вероятностей имеем
отсюда
Для нахождения вероятности Р(А) можно использовать формулу полной вероятности
Отсюда имеем формулу вероятностей гипотез после опыта (<формулу Бейеса)
Пример:
Вероятность поражения самолета при одиночном выстреле для 1-го ракетного расчета (событие А) равна 0,2, а для 2-го (событие В) — 0,1. Каждое из орудий производит по одному выстрелу, причем зарегистрировано одно попадание в самолет (событие С). Какова вероятность, что удачный выстрел принадлежит первому расчету?
Решение:
До опыта возможны четыре гипотезы: 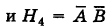
Вероятности их, при независимом действии расчетов, соответственно равны
причем
Условные вероятности для наблюдаемого события С при данных гипотезах будут
Следовательно, гипотезы 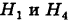
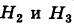
Таким образом, с вероятностью приблизительно 0,7 можно утверждать, что удачный выстрел принадлежит 1-му расчету,
Формула полной вероятности
Пусть событие А еще не произошло, но вскоре должно произойти. Событие А может протекать в различных условиях, относительно характера которых сделано 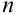
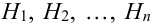
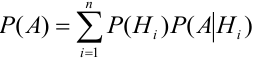
Доказательство.
По условию теоремы гипотезы 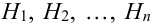
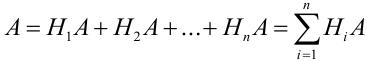
Т.к. гипотезы несовместны, то и комбинации 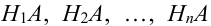
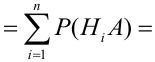
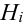
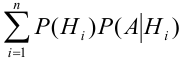
Пример:
Имеется пять урн:
2 урны состава 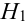
1 урна состава 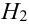
2 урны состава 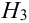
Наудачу выбирается урна, и из нее наудачу выбирается шар. Чему равна вероятность события А = {будет вынут белый шар}?
Решение.
Событие А еще не произошло. Шар может быть вынут из урн разных составов, следовательно, в алгебре событий событие А запишется в виде: 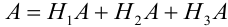
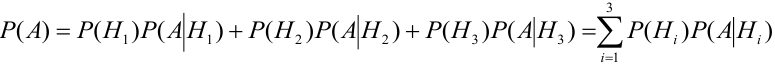
Найдем отдельно вероятности событий:
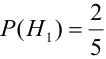
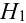
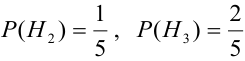
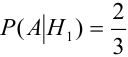
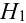
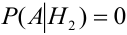
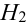
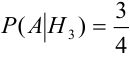
Подставим найденные вероятности в формулу (*): 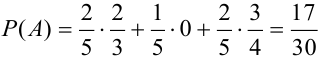
Формула полной вероятности и решение задач
Пример:
В двух одинаковых коробках имеется по 100 резисторов. В 1-й — 60 резисторов по 100 КОм, во 2-й 30 — резисторов по 100 КОм. Определить вероятность того, что взятый наугад из какой-либо коробки резистор будет 100 КОм.
Решение:
Пусть событие 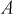
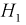
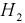
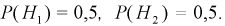
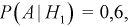
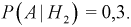
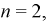
Пример №1
В первой коробке находится 20 деталей, из них 18 стандартных, во второй коробке – 10 деталей, из них 9 стандартных. Из второй коробки наудачу взята одна деталь и переложена в первую коробку.
Какова вероятность того, что деталь, наудачу извлечённая после этого из первой коробки, окажется стандартной?
Решение. Обозначим события:
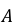
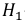
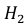
Событие А может наступить при условии наступления одного из событий 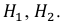
Вероятность того, что из второй коробки извлечена нестандартная деталь
Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была переложена стандартная деталь,
Условная вероятность того, что из первой коробки извлечена стандартная деталь, при условии, что из второй коробки в первую была переложена нестандартная деталь,
Искомая вероятность того, что из первой коробки будет извлечена стандартная деталь, по формуле полной вероятности равна:
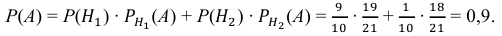
Ответ: 0,9.
Пример №2
Два станка производят одинаковые детали, которые поступают на общий конвейер. Производительность первого станка в два раза больше производительности второго станка. Первый производит 60 % деталей высшего сорта, а второй – 84 %. Наудачу взятая с конвейера деталь оказалась высшего сорта. Какова вероятность того, что эта деталь произведена на первом станке?
Решение. Обозначим события:
А – деталь, взятая с конвейера, оказалась высшего сорта.
Это событие наступит с одним из двух событий (гипотез):
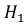
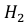
Поскольку производительность первого станка в два раза больше производительности второго станка, вероятности гипотез равны:
Условные вероятности события А даны:
По формуле полной вероятности находим:
По формуле Байеса найдём условную вероятность того, что взятая наудачу деталь высшего сорта произведена на первом станке:
Ответ:
Пример №3
В ящике 20 белых и 10 чёрных шаров. Поочерёдно извлекают 4 шара, причём каждый извлечённый шар возвращают в ящик перед извлечением следующего. Какова вероятность того, что среди четырёх извлечённых шаров окажется два белых?
Решение. Вероятность извлечения белого шара одна и та же во всех четырёх испытаниях, так как каждый извлечённый шар возвращается в ящик:
Тогда вероятность извлечения чёрного шара во всех четырёх испытаниях равна
Используя формулу Бернулли, находим вероятность того, что из четырёх извлечённых шаров два шара будут белыми:
Ответ:
Пример №4
Вероятность поражения мишени при одном выстреле равна 0,8. Какова вероятность того, что при 100 выстрелах мишень будет поражена 75 раз?
Решение. По условию задачи
Так как n – достаточно большое число, воспользуемся локальной формулой Лапласа:
В таблице значений функции 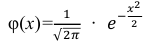
0,1826.
Следовательно,
Ответ: 0,04565.
Пример №5
Вероятность поражения мишени при одном выстреле равна 0,8. Какова вероятность того, что при 100 выстрелах мишень будет поражена
а) не менее 75 раз и не более 90 раз?
б) не менее 75 раз?
в) не более 74 раз?
Решение.
Воспользуемся интегральной формулой Лапласа:
где 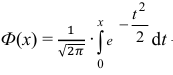
а) По условию задачи 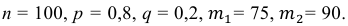
б) Требование того, чтобы событие наступило не менее 75 раз, означает следующее: число появлений события может быть равно либо 75, либо 76, … , либо 100.
Тогда следует принять 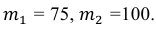
в) Событие «мишень поражена не более 74 раз» и событие «мишень поражена не менее 75 раз» являются противоположными. Поэтому сумма их вероятностей равна 1. Следовательно, искомая вероятность
Ответ: а) 0,8882; б) 0,8944; в) 0,1056.
Пример №6
Учебник издан тиражом 100000 экземпляров.
Вероятность того, что один учебник сброшюрован неправильно, равна 0,0001. Какова вероятность того, что тираж содержит 5 бракованных книг?
Решение. По условию задачи n = 100000, p = 0,0001.
События «из n книг ровно m книг сброшюрованы неправильно», где m = 0,1,2, … ,100000, являются независимыми. Так как число n велико, а вероятность p мала, вероятность 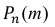
В рассматриваемой задаче 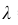
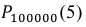
Ответ: 0,0375.
Формула Байеса (Бейеса)
Пусть событие А произошло, причем А могло протекать в различных условиях, относительно характера которых было сделано 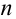
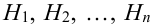
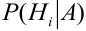
Решение:
По условию теоремы гипотезы 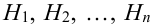
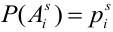
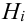
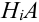
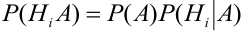
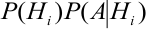
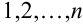
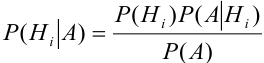
Выразим Р(А) с помощью формулы полной вероятности:
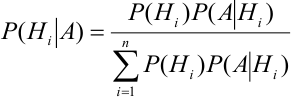
Пример №7
Имеется пять урн:
2 урны состава 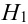
2 урны состава 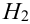
1 урна состава 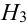
Из одной наудачу выбранной урны взят шар. Он оказался белым (событие А). Чему равна после опыта вероятность события, что шар вынут из урны третьего состава.
Решение.
Событие А произошло. Шар мог быть вынут из урн разных составов, следовательно, в алгебре событий событие А запишется в виде: 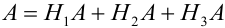
Найдем вероятности событий:
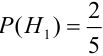
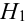
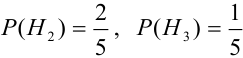
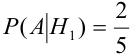
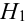
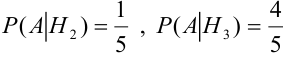
По формуле Байеса найдем условную вероятность 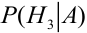
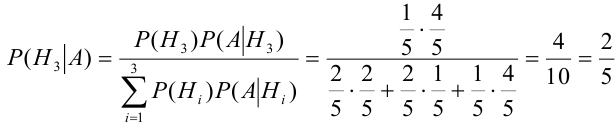
Пример №8
Вероятность дождливого дня в городе равна 0,2. Известно, что вероятность выиграть футбольный матч команде этого города в дождливый день равна 0,4, а в сухой — 0,7. Известно, что команда выиграла матч. Определить, что в этот день шел дождь.
Решение:
Событие 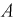
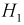
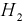
Чтобы ответить на вопрос, пересмотрим вероятность 1-й гипотезы с учетом результата опыта-появилось событие 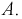
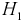
Из полученного результата видим, что с учетом события 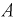
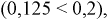
Независимые испытания
Под испытанием станем понимать осуществление определенного комплекса условий, в результате которого может произойти то или иное элементарное событие пространства 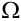
Определение 26. Если производятся испытания, при которых вероятность появления события А в каждом испытании не зависит от исходов других испытаний, то такие испытания называются независимыми относительно события А.
В каждом испытании вероятность появления события А одинакова.
Ряд задач связан с экспериментом, в котором проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.
Рассматривается последовательность п независимых испытаний, под которой будем понимать дискретное новое пространство 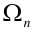
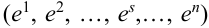
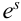

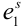
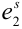
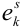
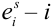



Пример №9
Пусть испытание состоит в подбрасывании игральной кости. Пространство элементарных событий 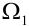
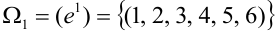
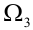
Обычно исходы обозначали большими заглавными буквами. Переобозначим! Пусть происходит 



Обозначим событие 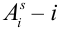



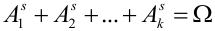
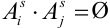
Обозначим вероятность 
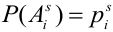
Пусть при первом испытании произошло событие под номером 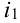
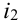

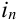

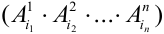
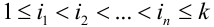
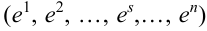
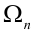
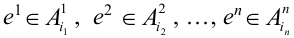
Испытания — независимые, следовательно, по теореме 4, имеет место равенство:
В случае, когда вероятности событий 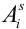
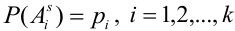
В силу несовместности и единственной возможности исходов, очевидно, что 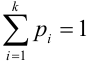
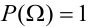
Теорема. Если данные 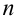
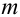
Теорема. Для того, чтобы 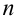
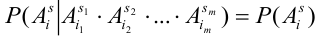
для любой группы чисел 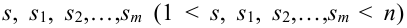
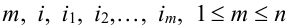
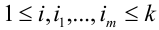
Формулы Бернулли
Пусть проводятся последовательные независимые испытания, и наблюдается результат совместного осуществления тех или иных исходов каждого испытания.
Схема независимых испытаний является математической моделью серии испытаний, повторяющихся при неизменных условиях. Такая схема называется полиномиальной.
Простейшим классом повторяющихся независимых испытаний является последовательность независимых испытаний с двумя исходами (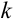
Определение 27. Независимые испытания при двух исходах называются испытаниями Бернулли.
Пример №10
Определить вероятность того, что в результате проведения 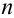

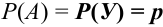
Решение.
Искомую вероятность обозначим 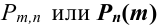
Событие А в данных испытаниях может появиться ровно 
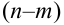
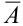
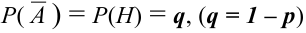
Сначала найдем вероятность того, что события У наступают при определенных 

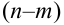
По условию данные события — независимые, следовательно, по теореме 4 для произведения независимых событий можем записать, что
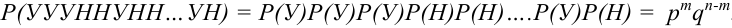
Число успехов и неудач задано. Можно менять только их расположения в цепочках, которое однозначно определяется выбором из 

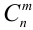
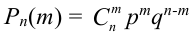
В данной задаче мы доказали теорему Бернулли.
Теорема Бернулли. Если 


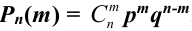
Следствие. 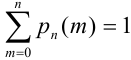

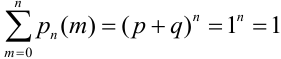
Пример №11
Пусть монета брошена 5 раз. Требуется найти вероятность того, что выпало ровно 3 орла.
Решение.
В каждом из 5 независимых испытаниях (
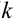
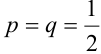

По формуле Бернулли 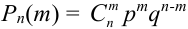
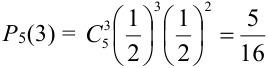
Замечания.
Замечание 1. Вероятность 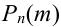
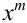
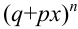
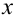
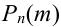
Замечание 2. Рассмотрим схему испытаний с произвольным количеством исходов. Пусть каждое из 
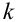
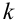
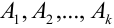
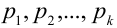

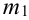
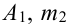
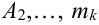
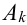

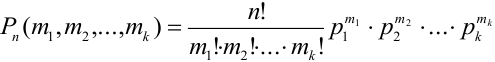
Эта совокупность вероятностей является коэффициентом при 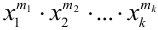
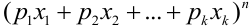
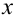
Например. При 

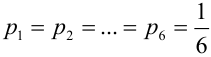
Если различать только «6» и «не 6», то получим схему Бернулли с двумя исходами (
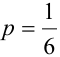
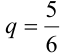
Замечание 3. При вычислении вероятности события, состоящего в том, что число успехов m лежит, например, между а и b, приходится находить числовые значения сумм вероятностей вида: 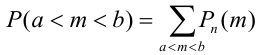
Например, вероятность того, что событие наступит а) менее 



a) 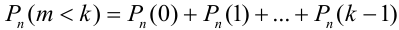
b) 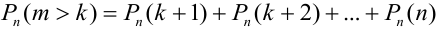
c) 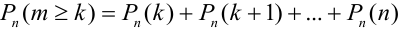
d) 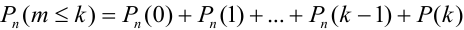
В некоторых случаях удобнее перейти к противоположному событию, например, 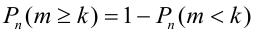
Пример №12
Пусть монета брошена 5 раз. Требуется найти вероятность того, что 1) менее двух раз выпал орел, 2) не менее двух раз выпал орел.
Решение.
Два исхода (
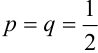
1) Орел выпал менее двух раз, значит, не выпал или выпал раз.
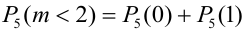
2) Орел выпал не менее двух раз, т.е. выпал два раза или три или четыре или пять:
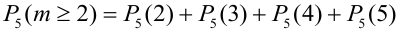
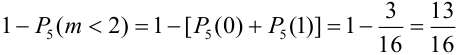
Замечание 4. В примере на формулу Бернулли вычисления проводятся очень легко, однако часто приходится вычислять вероятности при очень больших значениях n и m, например, при n = 1000, m = 500. Также затруднения при вычислении возникают при малых значениях р или q.
В этих случаях удается заменить формулу Бернулли какой-нибудь приближенной асимптотической формулой. Существуют три предельные теоремы, содержащие такие формулы.
Предельные теоремы в схеме Бернулли
Теорема Пуассона (асимптотическая формула для случая малых значений р)
Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна р, причем 

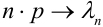
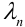
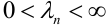
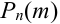

Замечания.
1. Часто формула Пуассона записывается в виде равенства, но надо помнить при этом, что оно верно при 
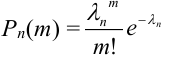
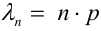
2. Формулой пользуются при больших n и малых р. Например, при n > 100, 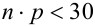
3. Теорема имеет место и в том случае, когда вероятность события А в каждом испытании равна нулю. В этом случае 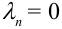
4. Существуют таблицы значений данной вероятности (стр. 410, 411 в задачнике Ефимова -Демидовича).
Пример №13
Вероятность попадания в цель при каждом выстреле равна 0,001. Найти вероятность попадания в цель двумя и более пулями, если число выстрелов равно 5000.
Решение.
Считаем каждый выстрел за испытание и попадание в цель за событие. Количество испытаний n = 5000 (велико), р = 0,001 (мало). По формуле Бернулли считать сложно. Поэтому применим формулу Пуассона.
Найдем среднее число попаданий: 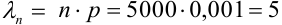
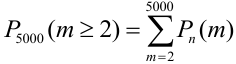
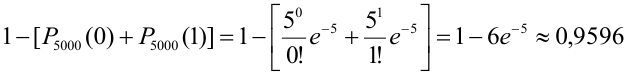
По точной формуле (формуле Бернулли) 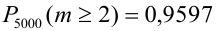
Локальная предельная теорема Муавра — Лапласа (асимптотическая формула для случая больших значений n и m)
Если вероятность наступления некоторого события А в n независимых испытаниях постоянна и равна р, (0 < р < 1), то вероятность 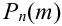

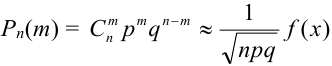
где 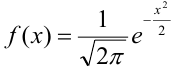
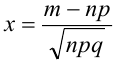
Замечания.
1. Часто формула Пуассона записывается в виде равенства, но надо помнить при этом, что оно верно при 
2. Формулой пользуются при больших n и m. Например, при п > 100, 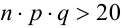
3. Из того, что 
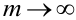
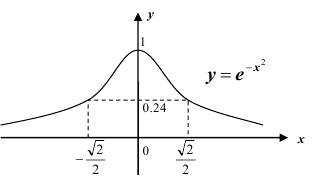
4. Существуют таблицы значений функции 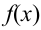
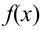
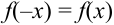
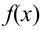
Пример №14
Найти вероятность того, что событие А наступит ровно 70 раз в 243 испытаниях, если вероятность появления этого события в каждом испытании равна 0,25.
Решение.
Количество испытаний n = 243, количество успехов m = 70, вероятность успеха р = 0,25, вероятность неудачи q = 1 — 0,25 = 0,75.
По формуле Бернулли считать сложно. Так как n и m велики, поэтому применим формулу Муавра — Лапласа.
Найдем сначала х и 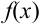
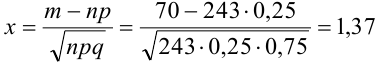
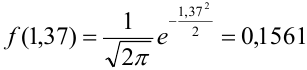
Можно было не считать значение 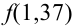
Подставим найденное значение 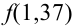
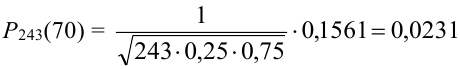
Предельная интегральная теорема Муавра — Лапласа (асимптотическая формула для случая, когда число успехов m лежит в некоторых пределах)
Теорема 1. Если m — число наступлений события А в n независимых испытаниях, в каждом из которых вероятность этого события равна р (0 < р < 1), то равномерно относительно а и b 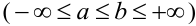
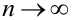
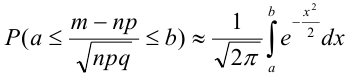
В некоторых источниках 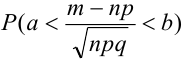
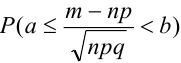
Ранее вывели, что 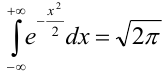
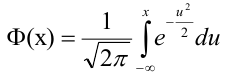
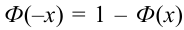
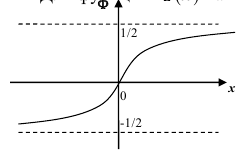
Либо, функция Лапласа может быть в виде: 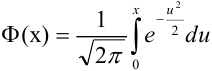
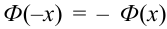
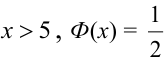
Теорема 2. (Теорема Муавра-Лапласа) Вероятность того, что в n независимых испытаниях, в каждом из которых вероятность появления события равна р (0 < р < 1), событие А наступит не менее 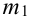
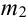
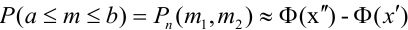
где Ф(х) — функция Лапласа, значения 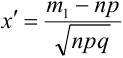
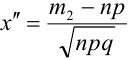
Теорема 3. (Закон больших чисел или теорема Бернулли).
При неограниченном увеличении числа однородных независимых опытов частота события будет сколь угодно мало отличаться от вероятности события в отдельном опыте.
Иначе, вероятность того, что отклонение относительной частоты наступления события 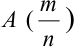
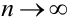
Доказательство.
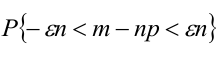
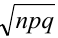
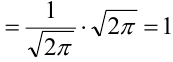
Пример №15
Вероятность появления события А в каждом из 100 независимых испытаний постоянна и равна 0,8. Найти вероятность того, что событие появиться не менее 75 раз и не более 90 раз.
Решение.
Количество испытаний n = 100, вероятность успеха р = 0,8, вероятность неудачи q = 1 — 0,8 = 0,2 , 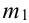
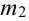
Найдем 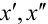
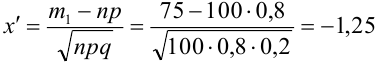
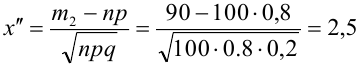
По теореме 2:
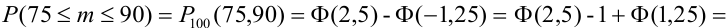
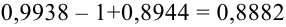
Наивероятнейшее число появления события в независимых испытаниях
Определение 28. Число 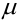
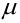
Наивероятнейшее число 
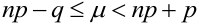
причем 1) если (np — q) -дробное, то существует одно 

Пример №16
Испытывается каждый из 15 элементов некоторого устройства. Вероятность того, что элемент выдержит испытание, равна 0,9. Найти наивероятнейшее число элементов, которые выдержат испытание и вероятность этого числа.
Решение.
Количество испытаний n = 15, вероятность успеха р = 0,9, вероятность неудачи q = 0,1.
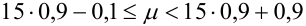
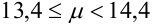
Т.к. 

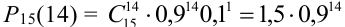
Всё о формуле полной вероятности
Пусть событие 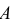
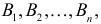
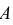
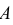
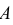
В силу несовместимости событий можно записать
Используя теорему умножения вероятностей, получаем формулу
которая и называется формулой полной вероятности.
Обычно ее записывают кратко:
Пример №17
Имеется две коробки деталей, в каждой из которых по 10 деталей. В первой коробке среди деталей две низкого сорта, а во второй четыре низкосортных детали. Из первой коробки для нужд производства взяли наугад половину деталей, а оставшиеся высыпали во вторую коробку. Через некоторое время из второй коробки взяли наугад деталь. Какова вероятность того, что это деталь низкого сорта?
Решение. Обозначим через A событие, состоящее в выборе из второй коробки детали низкого сорта. Возможность этого выбора зависит от того, какие именно детали были добавлены во вторую коробку. На этот счет можно выдвинуть следующие предположения: B1 – во вторую коробку добавили пять годных деталей; B2 – добавили одну деталь низкого сорта и четыре доброкачественные; B3 – добавили две детали низкого сорта и три доброкачественные. Пять деталей во вторую коробку можно переложить 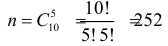
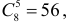
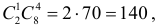
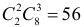
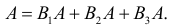

Ответ. 1/ 3.
Всё о Формуле Байеса
Пусть событие A может наступить только при появлении одного из несовместных событий 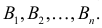

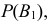
Проделан опыт, в результате которого событие A произошло. Тогда вероятности событий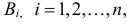
Формулы Байеса позволяют переоценивать вероятности гипотез (событий 
Пример №18
По каналу связи передается одна из последовательностей букв 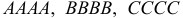
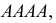
Решение. Для краткости записи формулы обозначим 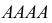
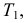
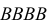
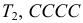
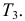
Ответ. 8/9.
Пример №19
Три стрелка производят по одному выстрелу в одну и ту же мишень. Вероятности попадания в мишень при одном выстреле для этих стрелков соответственно равны 0,8; 0,7; 0,6. Какова вероятность того, что третий стрелок промахнулся, если в мишени оказалось две пробоины?
Решение. Обозначим через А событие, состоящее в появлении двух пробоин в мишени. В отношении двух пробоин могут быть три предположения: В1 – попали первый и второй стрелки, а третий не попал, вероятность чего равна 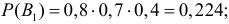
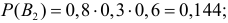
Заметим, что 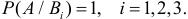
Ответ.
Пример №20
В партии из 10 изделий с равными шансами может оказаться от нуля до трех бракованных. Наугад взяли и проверили три изделия. Они оказались годными. Какова вероятность того, что остальные изделия в партии тоже годные?
Решение. Насчет содержания в партии бракованных изделий по условиям задачи может быть четыре предположения 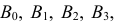
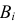
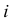
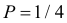
Заметим, что 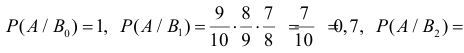
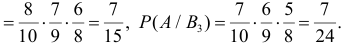
Ответ.
Пример №21
Вероятность того, событие B произойдет в течение часа, равна 0,9. Оказалось, что в течение первых 40 мин. событие B не произошло. Какова вероятность того, что это событие появится в оставшиеся 20 мин. времени?
Решение. В отношении события 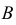
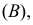
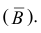
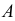
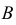
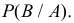
В задаче по умолчанию предполагается, что событие 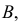
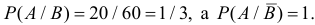
Ответ. 3/4.
Пример №22
В кошельке лежат четыре монеты. Три монеты обычных, а у четвертой на той и другой стороне изображен герб. Наугад взяли монету и подбросили три раза. Все три раза выпал герб. Какова вероятность того, что и при четвертом подбрасывании выпадет герб?
Решение. Обозначим через B1 – выбор монеты с одним гербом, через B2 – выбор монеты с двумя гербами. Априорные вероятности этих событий равны: 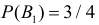
Обозначим через A – выпадение трех гербов подряд. Апостериорные вероятности по формулам Байеса равны:
Тогда по формуле полной вероятности (2.4.1):
P(выпадения герба в четвертый раз)
Ответ.
Подробное объяснение формулы полной вероятности
Постановка задачи: Пусть 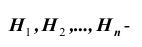
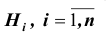


Требуется найти вероятность события A.
Выведем формулу решения этой задачи. Имеем
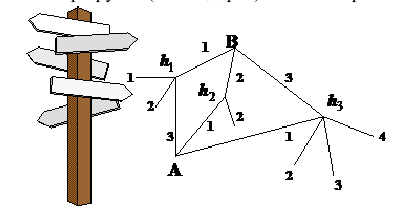
маршрутов (схема дорог). Какова вероятность того, что он попадет в пункт А ?
Решение. Как видим из схемы дорог, путь туриста обязательно проходит через один из пунктов 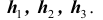
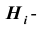
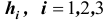
Заметим, что события (гипотезы)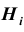
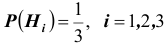
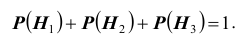
видеть (см. схему), что 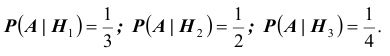
Пример №23 (о мудреце и властелине).
Властелин, разгневавшись на мудреца, приказал отрубить ему голову. Но затем, смягчившись, дал мудрецу возможность попытаться спастись. Итак, властелин взял 2 белых и 2 черных шара и предложил мудрецу распределить их по своему усмотрению по двум одинаковым урнам. После чего, палач сначала наугад выберет одну из урн, а затем также наугад, не глядя, вытащит из неё один шар. Мудрец будет помилован, если вытянутый шар оказался белым. Какую стратегию распределения шаров по урнам должен
выбрать мудрец, чтобы быть помилованным? Какова максимальная вероятность спастись мудрецу? Какая стратегия наименее выгодна для него?
Решение. Выдвинем гипотезы (предположения) 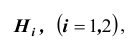
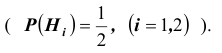
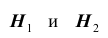
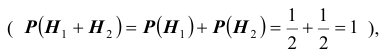
палачом вытянут белый шар. Далее, рассмотрим следующие варианты распределения мудрецом шаров по
урнам:
1). В первой урне 2 белых, а во второй 2 черных шара. Тогда
2 Хотим заметить, что далеко не всегда властелины были глупыми людьми, не знающими математики. Так, например, Наполеон был немного математиком, интересовался, в частности, геометрией. Он вёл дискуссии с Лагранжем и Лапласом, когда ещё не был правителем Франции.
Как-то в одной из таких дискуссий Лаплас резко оборвал Бонапарта: «Менее всего мы хотим от Вас, генерал, урока геометрии». В дальнейшем Лаплас стал его главным военным инженером. Наполеону приписывают теорему: «Если на сторонах произвольного треугольника во внешнюю сторону построены равносторонние треугольники, то их центры образуют равносторонний треугольник» — это так называемый вешний треугольник Наполеона.Так же ему приписывают один из знаменитых палиндромов (читается в обе стороны одинаково): «ABLE WAS I ERE I SAW ELBA» — я был силён, пока не увидел Эльбу.
2). В первой и во второй урнах по 1 белому и 1 черному шару. Тогда
3). В первой урне 1 белый, а во второй 1 белый и 2 черных шара. Тогда
4). В первой урне 1 черный, а во второй 2 белых и 1 черный шары. Тогда
5). Первая урна оказалась пустой, т.е. все шары во второй урне. Тогда
Как видим, наиболее предпочтительной является 3-я стратегия, ей соответствует вероятность быть помилованным равная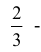
Вероятность гипотез. Формула Байеса
Постановка задачи: Пусть 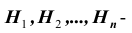
и пусть событие A может произойти лишь совместно с каким — либо одним из этих событий (гипотез) — ситуация аналогичная той, которая была ранее. И пусть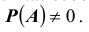
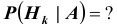
По теореме об умножении вероятностей
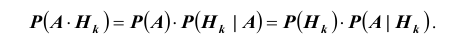
Полученная формула называется формулой Байеса (Бейеса) для переоценки гипотез. Другими словами: вероятность 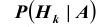
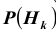
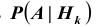
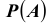
Пример №24
При обследовании больного имеется подозрение (т.е. делаются предположения или, что то же самое, выдвигаются гипотезы)
на одно из двух заболеваний 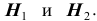
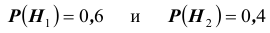
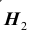
Решение. Во — первых, очевидно, что события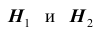
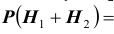
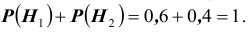
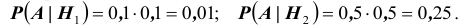
Как видим, при данных результатах обследования следует предполагать болезнь
Повторение испытаний
Формула Бернулли (схема повторения опытов)
Опыты называются независимыми , если вероятность того или иного исхода каждого опыта не зависит от того, какие исходы имели другие опыты. Независимые опыты могут проводиться как в одинаковых условиях, так и в различных. В первом случае вероятность появления какого — либо события A во всех опытах одна и та же, во втором случае — она меняется от опыта к опыту. Ниже мы воспользуемся понятием сложного события, понимая под ним совмещение нескольких отдельных событий, которые называют простыми. Итак, пусть производится n независимых опытов в одинаковых условиях, в каждом из которых некоторое событие A может произойти с одной и той же вероятностью 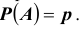
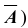
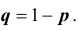
Итак, еще раз: схемой Бернулли называется последовательность n независимых испытаний, проводимых при одних и тех же условиях, в каждом из которых событие A либо происходит с постоянной вероятностью p , не зависящей от номера испытания, либо не происходит с вероятностью
Ставятся задачи:
Задача №1. Найти вероятность 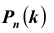
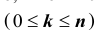
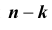
Задача № 2. Найти вероятность 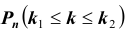
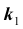
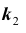
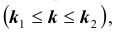
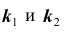
Задача № 3. Найти наивероятнейшее число 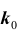
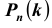
Решение №1.
Вероятность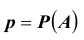
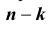
Таких несовместных событий столько, сколько сочетаний из n элементов по k элементов в каждом. Поэтому по теореме о вероятности суммы несовместных событий получим формулу, называемую формулой Бернулли:
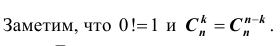
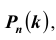
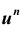
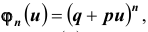
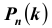
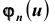
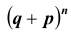
которую называют биномиальным законом распределения вероятностей события A в n испытаниях схемы Бернулли.
Заметим, что вероятность хотя бы одного появления события A в n испытаниях схемы Бернулли равна: 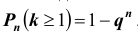
следующим вопросом: честное ли пари вам предлагают, если вы выиграете в том случае, когда при 24-х кратном бросании двух игральных костей хотя бы один раз одновременно появятся две шестёрки? Ответ дайте в конце пары.
(РЕШЕНИЕ. Вероятность одновременного выпадения двух шестерок при одном подбрасывании равна 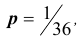
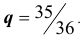
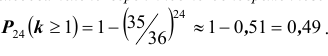
Другие примеры на применение формулы Бернулли, рассмотрим немного позднее, а именно после того, как решим задачи № 2 и № 3
Решение № 2.
Нетрудно показать, что вероятность 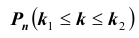
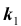
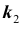
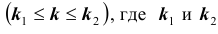
Решение № 3
Важной является задача № 3 о наивероятнейшем числе 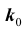
Рассмотрим отношение:
Из полученного следует, что:
1) если 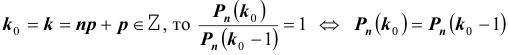
два максимума;
2) если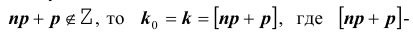
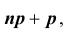
Пример №25
При некоторых условиях стрельбы вероятность p попадания в цель при одном выстреле равна
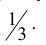
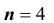
- а). Каково наивероятнейшее число попаданий в цель?
- б). Какова его вероятность?
- в). Какова вероятность двух попаданий?
- г). Какова вероятность хотя бы одного попадания?
Пример №26
Некто Сэмюэль Пепайс обратился к Исааку Ньютону с вопросом: какое из событий наиболее вероятно —
- появление по крайней мере одной «шестерки» при подбрасывании 6-ти игральных костей;
- хотя бы двух «шестерок» при подбрасывании 12-ти;
- хотя бы трех «шестерок» при подбрасывании 18-ти?
Решение.
Вероятность q непоявления «шестерки» при одном подбрасывании, как известно, равна 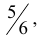
5 . Таким образом, вероятность появления по крайней мере одной «шестерки» при подбрасывании 6-ти игральных костей может быть найдена по формуле:
Событие «хотя бы две» противоположно событию «либо ни разу, либо один раз», т.е.
Событие «хотя бы три» противоположно событию «либо ни разу, либо один раз, либо два раза», т.е.
Таким образом, как видим, предпочтительнее первая стратегия – таким и был ответ Ньютона.
Замечу, что при больших значениях числа n испытаний в схеме Бернулли формула для подсчета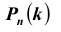
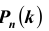
ТЕОРЕМА Пуассона 3. Пусть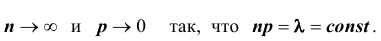
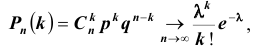
Доказательство
Что и требовалось доказать.
При доказательстве можно воспользоваться приближенной формулой Стирлинга.
Следствие: при указанных выше условиях, т.е. при 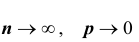
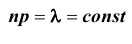
Пример №27
Телефонная станция обслуживает 800 абонентов. Для каждого абонента вероятность того, что в течении часа он позвонит на станцию равна p =0,01. Найти вероятность того, что четыре абонента позвонят на станцию в течении часа.
Решение
Теорема Муавра — Лапласа (локальная)
Остановлюсь еще на двух предельных теоремах в схеме Бернулли — локальной теореме Муавра — Лапласа (её доказательство получим как частный случай закона больших чисел — предельной теоремы Ляпунова, доказательство которой нам ещё предстоит провести) и интегральной теореме Муавра — Лапласа. Итак:
причем, во-первых, погрешность этой формулы есть величина порядка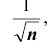
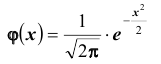
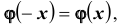
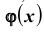
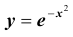
интегральная приближенная формула Лапласа ( при больших
Для функции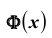
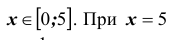
равносильно условию 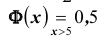
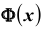
Замечание: если функция Лапласа записана в виде 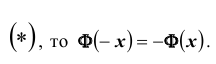
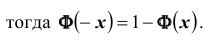
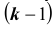
Формула полной вероятности и сложные задачи
В данном разделе мы рассмотрим более сложные задачи, имеющие большое практическое значение. Эти задачи встречается на практике в случае, если имеются несколько возможных сценариев развития событий (несколько вероятных гипотез). Известны как величины вероятности реализации каждого из сценариев, так и вероятность наступления интересующего нас события для любого из этих сценариев, а нас интересует, какова полная (совокупная) вероятность наступления интересующего нас события.
Предположим, что в результате опыта может произойти одно из n несовместных событий (гипотез) 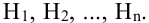
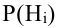
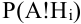
Пример №28
Из 40 деталей 10 изготовлены в первом цехе, 25 — во втором, а остальные — в третьем. Первый и третий цехи дают продукцию отличного качества с вероятностью 0,9, второй цех — с вероятностью 0,7. Какова вероятность того, что взятая наудачу деталь будет отличного качества?
Решение:
Обозначим событие А = {выбрана деталь отличного качества}, Hi= {выбранная деталь изготовлена в i цехе}, i = 1, 2, 3. Тогда
По условию задачи 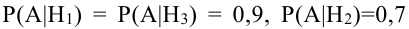
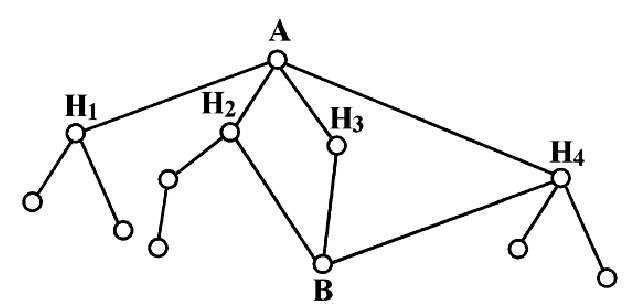
Пример №29
На рисунке изображена схема дорог. Найти вероятность того, что турист, вышедший из пункта А, попадет в пункт В, если на развилке он наугад выбирает любую дорогу (кроме обратной).
Решение:
Обозначим Нi = {приход туриста в пункт Hi}, i = 1, 2, 3, 4. Поскольку, выйдя из пункта А, он выбирает любую дорогу наугад, то 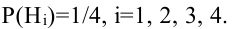
Исходя из схемы дорог, определяем, что
Таким образом, по формуле полной вероятности
Пример №30
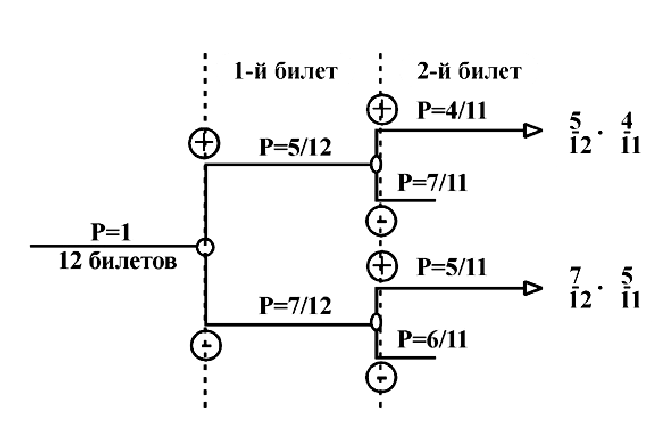
Из двенадцати лотерейных билетов пять выигрышных. Билеты вытягиваются по одному без возвращения. Какова вероятность того, что во второй раз вытянут выигрышный билет?
Решение:
Как обычно, вдоль каждой ветви «дерева вероятностей» значения вероятностей перемножаются, а затем значения на концах нужных веток между собой складываются. В результате получаем ответ:
Случайные события независимые в совокупности
Следует различать попарно независимые случайные события и случайные события независимые в совокупности.
Определение: События называются попарно независимыми событиями, если любые два из них независимы.
Определение: События 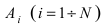
Замечание: Из определений видно, что из попарной независимости еще не следует, что эти события независимы в совокупности. Это означает, что условие независимости в совокупности является более сильным, чем условие попарной независимости случайных событий.
Теорема: Вероятность наступления хотя бы одного из событий 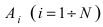
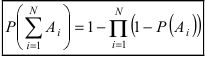
Доказательство: Обозначим через А событие, состоящее в том, что наступит хотя бы одно из событий 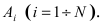
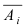
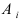
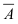
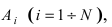
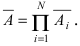
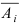
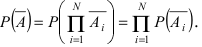
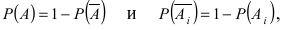
Пример №31
Пусть прибор содержит N последовательно соединенных блоков. Определить вероятность того, что цепь будет разорвана, если вероятность работы каждого блока равна р и она не зависит от работы других блоков.
Решение:
Пусть А — событие, которое состоит в том, что данная цепь разорвана. Это событие происходит, если выходит из строя хотя бы один из блоков, так как блоки включены последовательно. Противоположное событие состоит в том, что все блоки работают, т.е. 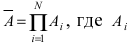
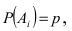
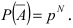
Теорема сложения вероятностей для совместных событий
Если случайные события одновременно появляются в условиях опыта, то имеет место следующая теорема.
Теорема: Вероятность суммы двух совместных событий равна сумме вероятностей этих событий минус вероятность их произведения:
Доказательство: Пусть в результате опыта возможно n равно возможных, несовместных, элементарных исходов. При этом в 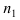
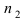
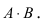
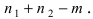
Замечание: Методом математической индукции вышеприведенная теорема может быть обобщена на любое число совместных событий, например, в случае 3 совместных событий А, В и С теорема принимает вид:
Пример №32
Найти вероятность того, что взятое наугад число из чисел от 10 до 20 делится или на 2, или на 3.
Решение:
Всего равновозможных, элементарных исходов 11 (числа от 10 включительно до 20 включительно). В 6 случаях (10, 12, 14, 16, 18, 20) число кратно 2; в 3 случаях (12, 15, 18) число кратно 3; в 2 случаях (12, 18) число кратно и 2, и 3. Пусть событие А состоит в том, что наугад взятое число кратно 2, а событие В состоит в том, что наугад взятое число кратно 3. Сложное событие С состоит в том, что наугад взятое число делится или на 2, или на 3, т.е. С = А + В. Следовательно, вероятность этого события равна:
Все вышерассмотренные теоремы объединяются в теории вероятностей общим названием “основные теоремы теории вероятностей”.
Формула полной вероятности и события
Формула полной вероятности является следствием основных теорем теории вероятностей: теорем сложения и умножения вероятностей событий.
Пусть некоторое случайное событие А наступает с одним и только с одним из несовместных событий
Определение: События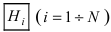
Теорема: Формула полной вероятности определяет вероятность случайного
события л, как сумму произведений вероятности каждой гипотезы 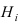
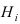
Доказательство: Событие А наступает с одним и только с одним из несовместных событий 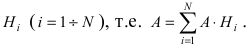
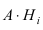
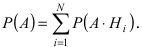
Пример №33
Пусть на сборку поступают детали с двух автоматических станков. Первый станок дает в среднем 0.3 % брака, а второй — 0.15 % брака. Производительность второго станка в два раза выше, чем первого станка. Найти вероятность того, что наугад взятая деталь окажется бракованной.
Решение:
Пусть событие А состоит в том, что наугад взятая деталь окажется бракованной. Тогда гипотеза 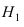
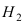
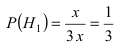
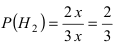
Вероятности события А при условии реализации первой и второй гипотез равны: 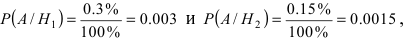
Формула вероятностей гипотез (формула Байеса)
Ниже будет получена формула, которая является следствием основных теорем теории вероятностей и формулы полной вероятности. Эта формула применяется для решения задач следующего типа. Пусть проводится эксперимент, в результате которого может появиться или не появиться событие л, которое наступает с одним и только с одним из несовместных событий 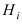
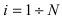
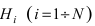
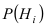
Теорема: Вероятность гипотезы 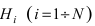
Доказательство: Событие А наступает с одним и только с одним из несовместных событий 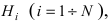
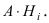
Следовательно, 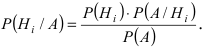
Пример №34
Однотипные пластмассовые детали изготавливаются на 3 прессах. Первый пресс выпускает 50 % всех деталей, второй — 40 %, третий — 10 % . При этом с первого пресса сходит в среднем 0.025 нестандартных деталей, со второго — 0.02 и с третьего — 0.015. Все детали поступают на сборку. Взятая наудачу деталь оказалась нестандартной. Какова вероятность того, что она изготовлена на первом прессе.
Решение:
Событие А состоит в том, что наудачу взятая деталь изготовлена на первом прессе. Гипотеза 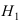
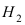
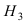
По условию задачи 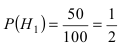
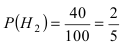
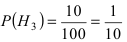
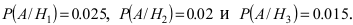
Используя формулу Байеса, получим
Независимые испытания и формула Бернулли
Пусть испытания повторяются n раз, причем событие А появляется в каждом опыте с одной и той же вероятностью р или не появляется с одной и той же вероятностью
Определение: Испытания называются независимыми, если вероятность события А не зависит от того, какие события появились в предыдущих опытах, или появятся в последующих экспериментах.
Пример:
Независимы ли следующие испытания: а) многократное бросание кубика; б) извлечение карты из колоды без ее возвращения в колоду (выяснить самостоятельно).
Формула Бернулли
Теорема: Пусть проводится серия из n независимых испытаний, в каждом из которых событие А появляется с постоянной вероятностью 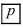
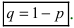
Доказательство: Пусть 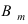
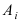
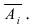
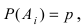
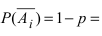
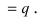
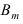
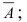
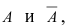
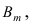
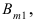
Воспользуемся теоремой умножения вероятностей для независимых событий, получим: 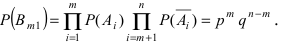
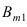
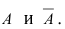
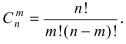
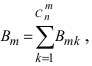
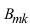
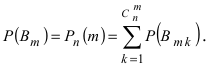
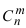
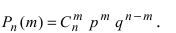

Пример №35
Монета подбрасывается 6 раз. Определить вероятность того, что герб выпадет а) 5 раз; б) от 2 до 4 раз.
Решение:
Вероятность выпадения герба не изменяется от опыта к опыту и равна 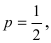
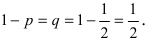
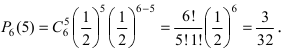
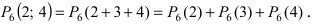
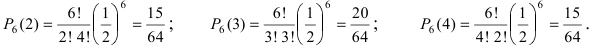
При больших значениях чисел m и n применение формулы Бернулли затруднительно, так как вычисление коэффициентов 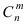
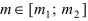
Формула Пуассона
Если при проведении серии испытаний по схеме Бернулли вероятность появления события А мала (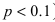
Формулы Муавра-Лапласа
Если при проведении серии испытаний по схеме Бернулли вероятность появления события А р>0.1, то при больших значениях чисел m и n применяют дифференциальную формулу Муавра-Лапласа: 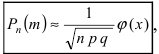
Замечание: В общем случае дифференциальная формула Муавра-Лапласа применяется при выполнении неравенств
Если при проведении серии испытаний по схеме Бернулли числа m и n принимают большие значения, причем число m принимает значения от 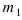
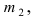
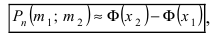
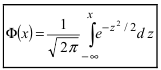
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин
- Комбинаторика — правила, формулы и примеры
- Классическое определение вероятности
- Геометрические вероятности
- Теоремы сложения и умножения вероятностей
Федеральное
агентство по образованию
Государственное
образовательное учреждение
высшего
профессионального образования
«Сибирский
государственный индустриальный
университет»
Ю. Г. Сильвестров,
А.В. Феоктистов
ПРИМЕНЕНИЕ
СТАТИСТИЧЕСКИХ МЕТОДОВ
В УПРАВЛЕНИИ
КАЧЕСТВОМ
Рекомендовано
Сибирским региональным учебно-методическим
центром
высшего
профессионального образования
для межвузовского
использования
в качестве учебного
пособия для студентов специальности
220501 «Управление качеством»
УДК 658.562.012.7
С368
Рецензенты:
кафедра управления
качеством и механики
Иркутского
государственного технического
университета
(заведующий, доктор
технических наук П.А. Лонцих);
начальник центральной
комплексной лаборатории комбината
ОАО «НКМК», к.т.н.
В.П. Дементьев
Сильвестров
Ю.Г.
С368 Статистические
методы в управлении качеством:
учебное пособие
/ Ю.Г. Сильвестров, А.В. Феоктистов; СибГИУ.
Новокузнецк, 2007.
208 с.
Рассмотрены
современные статистические инструменты
качества, предназначенные для сбора,
обработки и оценки данных о процессах,
параметрах качества и т.п. Дано
теоретическое обоснование этих методов
и изложены особенности их практического
применения.
Предназначено для
студентов, обучающихся по специальности
220501
Управление
качеством. Может быть также использовано
менеджерами в их практической работе
по управлению качеством продукции и
услуг.
УДК 658.562.012.7
© Сибирский
государственный
индустриальный
университет, 2007
ISBN
978-5-7806-0257-6 © Сильвестров Ю.Г., Феоктистов
А.В., 2007
|
СОДЕРЖАНИЕ |
|
|
Предисловие |
8 |
|
Введение |
9 |
|
12 |
|
19 19 21 22 23 23 24 |
|
29 29 30 32 33 34 |
|
39 39 42 44 |
|
52 52 52 53 54 54 |
|
59 59 61 62 68 71 |
|
83 83 83 87 94 96 99 101 102 |
|
110 110 111 114 |
|
116 116 117 117 118 122 123 124 |
|
132 132 134 136 147 |
|
158 158 159 160 174 175 178 |
|
Заключение…………………………………………………………… |
189 |
|
Библиографический |
190 |
|
Приложения…………………………………………………………… |
192 |
ПРЕДИСЛОВИЕ
Качество продукции
или услуги, их соответствие требованиям
потребителей являются основным условием
успешного функционирования и
совершенствования любой организации
в современном мире. Для обеспечения
качества за последние десятилетия
разработано, опробовано в действие и
успешно применяется ряд методов
организации и управления деятельностью
предприятия, такие как: TQM,
системы менеджмента качества на основе
стандартов ИСО 9000, шесть сигм, бережливое
производство и ряд других.
Любой из этих
организационных подходов для управления
качеством использует методы принятия
решения, основанные на фактах. Для этого
организуется сбор информации о параметрах
качества продукции или услуги, параметрах
процессов. Эта информация систематизируется,
анализируется, оценивается и уже на
основе результатов этой оценки
используется для принятия управленческих
решений. Так как собираемая информация
характеризуется разбросом и имеет,
поэтому статистический характер, большое
значение для сбора, анализа и оценки
данных приобрели статистические методы.
Учитывая важность
для профессионалов в области управления
качеством знания статистических методов
и умения практически владеть ими,
государственным образовательным
стандартом высшего профессионального
образования Российской Федерации для
специальности 220501
Управление качеством введена дисциплина
«Статистические методы в управлении
качеством».
Следует отметить,
что в настоящее время имеется острый
дефицит учебной литературы по этой
дисциплине. Предлагаемое учебное пособие
призвано, в некоторой степени, восполнить
этот пробел. Большое внимание при этом
уделено теоретическим основам
разработанных и широко используемых в
мировой практике статистических методов.
В то же время практическое применение
некоторых простых инструментов качества,
таких как гистограммы, диаграммы
рассеивания, вынесено за рамки этого
пособия. При этом учитывалось, что
подробная информация об этих инструментах
рассматривается в других дисциплинах,
предусмотренных государственным
образовательном стандартом, таких как:
«Основы обеспечения качества» и «Средства
и методы управления качеством». В конце
каждой главы учебного пособия для
закрепления изучаемого материала
предлагаются контрольные вопросы и
задания для самостоятельного решения.
ВВЕДЕНИЕ
Продукция, которую
мы приобретаем в магазине, с нашей точки
зрения – ее потребителей, должна быть
качественной. В то же время практически
всегда остается вероятность, что она
будет содержать дефекты, т.е. окажется
некачественной.
В чем причина
появления дефектов? Почему нельзя со
сто процентной гарантией обойтись без
них? Почему производитель с налаженными
и отрегулированными процессами выпускает
тысячу качественных изделий, а в тысяче
первом вкрадывается дефект. Причина
кроется в изменчивости факторов,
параметров, формирующих качество. Обычно
этих факторов очень много. Некоторые
из них связаны с материалами, другие с
оборудованием, третьи с технологией,
четвертые с персоналом и т.п. Если бы
поставщику удалось обеспечить их
абсолютное постоянство, то вся его
продукция была бы качественной. Но
выполнить это требование практически
невозможно. Окружающий нас мир, его
законы настолько сложны и многообразны,
что все факторы, формирующие качество,
обладают изменчивостью и имеют
вероятностный характер и их практически
невозможно сохранить неизменными.
Поступающие материалы имеют от партии
к партии, и даже внутри партии, чуть
разные свойства, двигающиеся части
оборудования имеют люфты, и детали
поэтому имеют чуть разные размеры,
оператор получил плохое известие и
начал делать ошибки и т.п. Изменчивость
факторов формирующих качество, их
вероятностный характер
– вот в чем причина того, что продукция
получается чуть разной и может оказаться
даже дефектной.
Классическим
способом оберегания потребителя от
дефектной продукции являлся и является
контроль качества. Контроль качества,
как самостоятельный вид профессиональной
деятельности берет свое начало от эпохи
Ф. Тейлора. Каждое предприятие, выпускающее
продукцию, имеет службу контроля
качества. Контролю подвергаются материалы
и комплектующие, поступающие от
поставщиков, процессы, оборудование,
приборы и инструменты, полуфабрикаты
после операций производственного
процесса, готовая продукция.
Контролю может
подвергаться вся продукция, либо часть
ее в виде выборки, взятой по определенным
правилам. При сплошном контроле
потребителю будет отправлена только
качественная продукция (хотя и в этом
случае возможны ошибки). При выборочном
контроле о качестве всей партии продукции,
из которой была взята выборка, судить
будут по результатам контроля выборки,
используя оговоренные с заказчиком
правила, записанные, например, в
стандартных планах контроля.
Однако постепенно
мир пришел к пониманию, что контроля
качества вовсе недостаточно для полной
защиты потребителя от некачественной
продукции. Контроль качества в роли
только надзорного процесса не улучшает
качество продукции и поэтому его
возможности крайне ограничены. Качеством
надо управлять. Надо предвосхищать
события, предупреждать причины появления
дефектов. Родилась и окрепла концепция
управления качеством.
Для управления
качеством разработаны и успешно
применяются различные модели, методы
менеджмента, такие как: всеобщее
управление качеством, модели международных
стандартов ИСО 9000, шесть сигм, кайдзен
и т.п.
Однако в любом из
этих подходов нужны методы и средства
обработки и анализа фактических данных
о процессах, их параметрах, параметрах
качества, которые могут дать нужную
информацию к управлению. Учитывая
многообразие факторов, формирующих
качество, их изменчивость и вероятностный
характер особое место среди них заняли
статистические методы [1].
Начало их успешного
применения для управления качеством
принадлежит Уолтеру Шухарту, предложившему
и разработавшему свои контрольные
карты. Но по настоящему широкое применение
статистические методы получили в
послевоенной Японии. Усилиями К. Исикавы
и других японских ученых и практиков
были разработаны и приняты к массовому
использованию многие статистические
методы, в том числе и семь простых
инструментов качества [5, 6].
Многие годы
статистические методы широко и успешно
применяются в промышленно развитых
странах, особенно в Японии, США, Германии,
Англии и др. Ведущие компании этих стран
добились с помощью статистических
методов управления процессами столь
малого разброса, что на миллион операций
(возможностей) возможно появление всего
лишь несколько несоответствий.
С переходом на
новые формы управления лед тронулся и
на Российских предприятиях. Так на
предприятиях компании «РУСАЛ» началось
широкое внедрение контрольных карт для
управления основными технологическими
процессами. Расширяют применение
статистических методов изготовители
автомобильной продукции. В отделах
менеджмента качества многих отечественных
предприятий в обиход вошли такие методы
как диаграммы Парето, Исикавы и др.
Однако для массового
применения статистических методов
необходимо знакомство с ними широкого
круга производственников:
инженерно-технических работников и
рабочих. Этому должны способствовать
профессионалы в области управления
качеством. Особое место здесь отводится
инженерам-менеджерам − выпускникам
высших учебных заведений по специальности
«Управление качеством».
Статистические
методы в управлении качеством включают
в себя достаточно обширный набор
инструментов. Среди них есть и классические
методы теории вероятности и математической
статистики, такие как методы определения
вероятности наступления случайных
событий, методы проверки гипотез, методы
корреляционного анализа и т.п. [2, 4, 7, 8]
В то же время
разработано и большое количество
специальных статистических методов
управления качеством. Часть из них
группируют обычно в семь, так называемых,
«старых инструментов качества», другие
в семь «новых инструментов». Некоторые
методы основаны на закономерностях
теории вероятности и математической
статистики и предназначены, как правило,
для анализа количественных данных. Сюда
следует отнести, например, контрольные
карты, гистограммы, диаграммы рассеивания,
методы выборочного контроля на основе
планов контроля [5]. Другие методы никак
не связаны с классической математикой.
Так многие инструменты разработаны для
вербальной информации и определения
характера и силы связи между отдельными
факторами, параметрами из определенного
набора, определения их причинно-следственных
взаимоотношений. Можно назвать, для
примера, такие инструменты как
причинно-следственная диаграмма,
диаграмма сродства, матричные диаграммы
и т.п.
В данном учебном
пособии будут рассмотрены методы,
основанные на принципах теории вероятности
и математической статистики. При
рассмотрении каждого метода будут даны
теоретические предпосылки, основные
особенности применения для конкретных
задач управления качеством, представлены
практические примеры.
Учебное пособие
предназначено для студентов, изучающих
дисциплину «Статистические методы в
управлении качеством». Может быть
полезно также всем, кто, по роду своей
деятельности, связан с проблемами
контроля и управления качеством.
-
ИСТОРИЯ РАЗВИТИЯ
СТАТИСТИЧЕСКИХ МЕТОДОВ
Разработка и
применение статистических методов для
управления качеством берет начало от
работ Уолтера Шухарта, основателя
концепции управляемой и неуправляемой
изменчивости, статистического контроля
процессов и связанного с ними инженерного
метода контрольных карт.
Перед
молодым физиком У. Шухартом (1891
1967),
принятым в 1923 г. на работу в знаменитую
Ве11
Laboratories
(лаборатория
того самого А.
Белла, что изобрел телефон), была
поставлена практическая
задача борьбы с
дефектами продукции.
Задача эта была
связана с одной трудностью, возникшей
в ходе
телефонизации Америки. При технологии
прокладки телефонных сетей, используемой
в те годы, приходилось примерно
через каждые 500 м вставлять в линию связи
усилительную подстанцию размером с
письменный
стол,
закапывая ее в землю. Лампы
в
этих усилителях перегорали не по графику,
а когда
им вздумается. Из-за этого у бригад
ремонтников
возникали большие трудности. Не удавалось
заранее
определить требуемое число ремонтных
бригад,
их потребности в транспорте и запасах
ламп
для замены. Проблема заключалась в
большом
разбросе времени наработки на отказ
усилительных
ламп. Хотя завод-изготовитель определял
нормативный
срок непрерывной работы, лампы почему-то
отказывали, как попало. Естественно,
возникало много вопросов. Например,
почему разброс
так велик и нерегулярен? И что можно
сделать, чтобы ввести его в приемлемые
рамки?
Традиционный
взгляд на контроль качества был
обращен в то время на обнаружение и
изъятие негодных изделий из партии
продукции. У. Шухарт увидел
возможность увеличения выхода годных
изделий
непосредственно в процессе производства.
Профилактика,
направленная на предотвращение брака
или
несоответствий, несомненно, важнее и
полезнее, чем отбраковка, ибо отбраковка
сама по себе не приводит
к улучшению изделий: она лишь разделяет
их на
две группы
принимаемых и бракуемых. Качество, как
данной партии, так и будущих партий при
отбраковке не меняется. В то же время
профилактика, т.е. система мер, направленных
на предотвращение появления
некачественных изделий, ведет к улучшению
будущих партий продукции.
Работая
над поставленной проблемой, анализируя
результаты отказов и их причины
У. Шухарт в 1924 г. заложил основы того,
что сейчас принято называть теорией
вариабельности. Основные положения
этой теории можно кратко сформулировать
следующим образом: все виды продукции
и
услуг, а также все процессы, в которых
они создаются и/или преобразуются,
подвержены отклонениям от заданных
значений, называемых вариациями.
Своим
происхождением вариации обязаны двум
принципиально
разным источникам, которые принято
называть общими
(соттоп) и
специальными
(аssignable)
причинами вариаций.
Общими
причинами вариаций называют
причины, являющиеся
неотъемлемой частью данного процесса
и
внутренне ему присущие. Они связаны с
неабсолютной
точностью поддержания параметров и
условий
осуществления процесса, с неабсолютной
идентичностью
условий на его входах и выходах и т.д.
Другими
словами, это
результат совместного воздействия
большого числа случайных факторов,
каждый
из которых вносит весьма малый вклад в
результирующую
вариацию и влияние которых мы, по тем
или
иным соображениям, не можем или не хотим
отделить
друг от друга.
Специальные
причины вариаций
те
причины, которые
возникают из-за внешних по отношению к
процессу воздействий на него и не
являются его неотъемлемой
частью. Они связаны с приложением к
процессу незапланированных воздействий,
не предусмотренных
его нормальным ходом. Другими словами,
это
результат конкретных случайных
воздействий
на процесс, причем тот факт, что именно
данная конкретная причина вызывает
данное конкретное отклонение параметров
(характеристик) процесса от заданных
значений часто (но далеко не всегда) и
приводит к тому, что эту причину можно
обнаружить без приложения каких-то
исключительных усилий или затрат.
Разделение
причин вариаций на два указанных вида
принципиально потому, что борьба с
вариабельностью
процесса в этих двух случаях требует
различного
подхода. Специальные
причины вариаций требуют
локального
вмешательства в
процесс, тогда как общие
причины вариаций требуют
вмешательства
в
систему.
Локальное
вмешательство:
-
обычно
осуществляется людьми, занятыми в
процессе
и близкими к нему (т.е. это линейный
персонал,
линейные руководители и т.д.); -
обычно
нужно примерно для 15 % всех возникающих
в
процессе проблем (это выяснилось после
многих лет
применения данного подхода на практике,
откуда и вытекает известное правило
Дж. Джурана 85:15, и все следствия из
этого правила); -
неэффективно
или ухудшает ситуацию, если в процессе
отсутствуют специальные причины
вариаций, и,
напротив, эффективно, если они
присутствуют.
Вмешательство
в систему:
-
почти
всегда требует действий со стороны
высшего менеджмента; -
обычно
нужно примерно для 85 % всех возникающих
в процессе проблем; -
неэффективно
или ухудшает ситуацию, если в процессе
присутствуют специальные причины
вариаций,
и, напротив, эффективно, если они
отсутствуют.
Как
же разделить
причины вариаций на два указанных вида.
В
1924 г. У. Шухарт предложил свое решение.
16 мая 1924 г. доктор У. Шухарт подготовил
небольшую
памятную записку руководителю своего
департамента Р. Джонсу размером всего
в одну страницу.
Около трети ее занимала простая диаграмма,
которая сегодня известна всем нам сейчас
как контрольная карта. Та диаграмма и
текст к ней заключали в себе все
существенные принципы и выводы,
составляющие то, что известно нам теперь
как управление
процессом.
Контрольные
карты и стали, по мысли У. Шухарта,
диагностическим инструментом,
предназначенным
для различения процессов с общими и
специальными причинами вариаций. В
знаменитой книге
У. Шухарта, опубликованной в 1931 г.
«Экономический контроль качества
производственных изделий» (Economic
Control
of
Quality
of
Manufacture
Product)
[17] была описана теория контрольных
карт.
В
1939 г. Э. Деминг убедил У. Шухарта прочесть
серию лекций, которые были опубликованы
под общим названием «Статистический
метод с точки зрения контроля качества».
Э. Деминг высоко ценил работы Шухарта,
о чем свидетельствуют
следующие его слова: «Полстолетия прошло
с тех пор, как великая книга доктора
Шухарта увидела свет в 1931 г., и почти
полстолетия – после того как появилась
его вторая книга в 1939 г. Еще полстолетия
пройдет, прежде чем в промышленности и
науке по заслугам оценят содержание
этих великих работ. Можно сказать, что
содержание моих семинаров и книг в
большой степени основано на моем
понимании учения доктора Шухарта. Даже
если только 10 % слушателей воспримут
часть его учения, они со временем смогут
вызвать изменение в стиле западного
менеджмента».
В то время как
Шухарт концентрировался в основном на
производственных процессах, Деминг
осознал, что его идеи применимы также
и для других типов систем и приложений,
например в администрировании, обслуживании,
финансах, прогнозировании и т.п. И
действительно, одно из наиболее
плодотворных приложений его подхода
относится к управленческой деятельности.
В 1939 г. Деминг начал
работать в Национальном бюро переписей
и почти сразу же стал прилагать концепции
Шухарта к выполняемым служащими рутинным
операциям, таким как кодирование данных
при подготовке переписи населения 1940
г. Путем приведения этих процессов в
статистически управляемое состояние,
а также дальнейшего улучшения самих
процессов была колоссально снижена
потребность в перепроверках, инспекциях
и т.п. Как результат было зафиксировано
шестикратное увеличение производительности
некоторых из этих процессов. Экономия
составила несколько сотен тысяч долларов
(невероятная сумма, учитывая ценность
денег в то время), и результаты переписи
были опубликованы гораздо раньше, чем
обычно.
Другим разработанным
примерно в то же время статистическим
методом управления качеством стал
выборочный контроль продукции с
применением статистических методов
обработки и интерпретации результатов
контроля. Переход от сплошного контроля
к выборочному был обусловлен
неэкономичностью сплошного контроля,
особенно в условиях массового производства.
Фактически выборочный контроль берет
свое начало от эпохи домануфактурного
производства, когда, например, для оценки
качества поставляемой партии зерна или
хлопка покупатель прокалывал отдельные
мешки с продукцией, чтобы взять пробу.
Идея выборочного
контроля продукции заключается в том,
что о генеральных характеристиках
испытуемой партии изделий судят по
выборочным характеристикам, определяемым
по малой выборке из партии. Эта идея
была высказана впервые еще в 1846 г.
академиком М.В. Остроградским. Научное
обоснование современных методов
выборочного контроля связано с именами
таких известных статистиков и специалистов
в области менеджмента качества как Х.
Додж и Х. Роминг. Первые таблицы
выборочного контроля качества они
разработали во время работы одновременно
с У. Шухартом в той же Ве11
Laboratories.
Благодаря их усилиям, а также работам
Э. Пирсона, А. Вальда, Э. Деминга и других
ученых и практиков стала возможной
стандартизация методов выборочного
контроля, что сделало эти методы
доступными для широкого круга
производственников. Стандартные планы
выборочного контроля нашли огромное
распространение в США, Германии, России
и других развитых промышленных странах.
Безусловным лидером
в разработке и применении статистических
методов управления качеством стала
послевоенная Япония. Причем особенность
японского подхода состоит в широком
массовом использовании специально
подобранных, несложных для понимания
и применения, не требующих специальной
математической подготовки, широко в
настоящее время известных семи простых
инструмента качества.
Знаменитый японский
специалист в области менеджмента
качества К. Исикава в своей книге
«Японские методы управления качеством»
[6] говорит, что только в 1949 г. Япония
стала активно применять статистические
методы анализа. Именно в этом году
Японский союз ученых и инженеров создал
исследовательскую группу по контролю
качества, которая стала заниматься
анализом применения статистических
методов в промышленности.
К. Исикава разделяет
статистические методы, используемые
японцами по степени их трудности на
следующие три категории.
1. Элементарные
статистические методы, включающие в
себя семь, так называемых простых
инструмента качества:
-
диаграмма Парето;
-
причинно-следственный
анализ; -
группировка данных
по общим признакам; -
контрольный
листок; -
гистограмма;
-
диаграмма разброса
(анализ корреляции); -
график и контрольная
карта (контрольная карта Шухарта).
Все вышеизложенные
методы применяются всеми без исключения
– от главы фирмы до простого рабочего.
Ими пользуются не только в производственном
отделе, но и в таких отделах, как отделы
планирования, маркетинга,
материально-технического снабжения и
технологии. Основываясь на опыте своей
деятельности, К. Исикава утверждает,
что 95 % проблем фирмы могут быть решены
с помощью этих семи инструментов. Они
просты, однако без них невозможно
овладеть более сложными методами.
Применение этих
методов в Японии имеет большое значение.
Ими пользуются без всякого труда даже
выпускники средних школ.
Параллельно с
применением этих методов рабочие должны
понимать концепцию качества, основывающуюся
на том, что следующий производственный
процесс является потребителем твоей
продукции. Рабочие должны участвовать
в кружках качества, действовать по схеме
цикла Шухарта – Деминга и знать принципы
управления качеством. Рабочие должны
мыслить статистическими категориями,
знать о разбросе данных и применять эти
знания при статистической оценке,
принимать решения о проведении необходимых
мероприятий и определять действенные
статистические критерии.
2. Промежуточные
статистические методы включают:
-
теорию выборочных
исследований; -
статистический
выборочный контроль; -
различные методы
проведения статистических оценок
определения критериев; -
метод применения
сенсорных проверок; -
метод планирования
эксперимента.
В Японии эти методы,
рассчитанные на инженеров и специалистов
в области управления качеством,
используется весьма эффективно.
3. Передовые
статистические методы с использованием
ЭВМ:
-
передовые методы
расчета экспериментов; -
многофакторный
анализ; -
различные методы
исследования операций.
Этим методам
обучается ограниченное количество
инженеров и техников, поскольку они
применяются при проведении очень сложных
анализов процесса и качества. Эти методы
положены в основу создания высоких
технологий.
Считается, что
применение статистических методов во
многом способствовало достижению
Японией огромных успехов в экономическом
развитии.
-
Контрольные
вопросы
-
Что вы знаете об
У. Шухарте? -
Охарактеризуйте
общие причины
вариаций? -
Охарактеризуйте
специальные
причины
вариаций? -
Какого характера
вмешательство в процесс необходимо
для уменьшения вариаций в случае, если
они обусловлены только общими
причинами? -
Какого характера
вмешательство в процесс необходимо
для уменьшения вариаций в случае, если
они обусловлены специальными
причинами? -
Какой метод
предложил У. Шухарт для управления
процессами? -
Что вы знаете об
Э. Деминге и его деятельности по
применению статистических методов
управления качеством? -
В чем состоит идея
выборочного контроля? -
Кто явился
основоположником научных разработок
в области выборочного контроля? -
Что вы можете
сказать о К. Исикава.? -
Как подразделяет
К. Исикава статистические методы,
используемые японцами? -
Назовите семь
простых инструмента качества?
-
Задания для
самостоятельной работы
-
Опишите вклад У.
Шухарта в развитие статистических
методов управления качеством. -
Проанализируйте
вклад Э. Деминга в развитие статистических
методов управления качеством. -
Опишите вклад К.
Исикавы в развитие статистических
методов управления качеством. -
Проанализируйте
японский вклад в развитие статистических
методов управления качеством. -
Выполните
исторический обзор развития статистических
методов управления качеством.
-
ОСНОВЫ ТЕОРИИ
ВЕРОЯТНОСТИ
-
Случайные
события, случайные величины, вероятность
Теория вероятности
и основанная на ней математическая
статистика имеют дело с рядом специфических
понятий. Основными из них являются
следующие:
-
испытание
(наблюдение); -
событие;
-
случайная величина;
-
вероятность;
-
частота;
-
частость
(относительная частота).
Опытной основой
контроля качества является наблюдение.
Наблюдение (
испытание)
− это практическое осуществление
какого-либо комплекса условий.
Событие −
это явление, происходящее в результате
испытания (соблюдения определенного
комплекса условий). Событие может быть
достоверным,
невозможным
либо случайным.
Достоверным
называют событие, которое неизбежно
происходит при каждом испытании.
Невозможным
называют событие, которое в условиях
данного испытания заведомо не может
произойти.
Случайным называют
такое событие, которое при испытании
может либо наступить, либо не наступить.
Пример 1.
В ящике находится 100 деталей (гаек),
среди которых одна бракованная (сорвана
резьба). Вы вытаскиваете наугад две
детали.
Достоверным
событием в этом случае будет то, что обе
детали являются гайками. Невозможным
событием
то, что обе они бракованные. Случайным
событием
то, что обе они качественные.
Случайная величина
переменная величина , которая в результате
испытаний может принять то, или иное
значение в границах определенного
интервала.
Пример 2.
Содержание кремния (Si)
в стали марки Ст3сп по ГОСТ 380 составляет
от 0.05 до 0.15 %. В этом диапазоне содержание
Si
является случайной величиной.
Пример 3. Диаметр
вала, задается конструктором на чертеже
с полем допуска. Действительный размер
вала, выточенного на токарном станке,
является случайной величиной. Главное,
чтоб он попал в поле допуска.
Любое случайное
событие обладает той или иной объективной
возможностью или необходимостью своего
проявления. Для количественной оценки
возможности осуществления случайного
события вводят понятие вероятность.
Вероятность
какого – либо события А
обозначают символом Р(А)
или «р» (от probabilitas)
и представляет собой численную меру
объективной возможности этого события.
Рассмотрим
классическое определение вероятности.
Вероятностью
случайного события А
называют отношение числа благоприятных
для данного события случаев m
к числу единственно возможных,
равновозможных и несовместимых случаев
n
числу всех возможных случаев (по Лапласу):
.
(2.1)
Поясним некоторые
термины из этого определения:
Единственно
возможные
случаи в заданном определении означают,
что они образуют полную группу, т.е. хотя
бы один из них обязательно произойдет.
Несовместные
события не могут появиться вместе,
одновременно.
Примеры несовместных
событий:
1. Выпадение герба
и цифры при бросании монеты.
2. Ровно один отказ,
ровно два отказа станка за три часа
работы.
Равновозможные
события – это такие несколько событий
в данном испытании, каждое из которых
по условиям симметрии не является
объективно более возможным, чем другое.
Примеры равновозможных
событий:
1. Выпадение герба
и выпадение цифры при бросании монеты.
2. Вынимание карты,
какой либо масти из колоды.
Примеры вычисления вероятности.
1. Определить
вероятность выпадения герба при бросании
монеты.
Список единственно
возможных, равновозможных и несовместимых
случаев будет: надпись, герб, т.е. n
= 2; из них благоприятен случай герба: m
= 1. Подставляя численные значения в
формулу (2.1) получаем:
2. Определить
вероятность того, что при бросании двух
монет герб выпадет оба раза. Запишем
возможные варианты развития событий:
-
Монета №1
надпись
надпись
герб
герб
Монета №2
надпись
герб
герб
надпись
Из этих данных
видно, что m
= 1, n
= 4, следовательно: p
= 0,25.
3. В партии из 90
изделий 5 бракованных. Какова вероятность
оказаться бракованным наудачу взятому
изделию:
-
Статистическая
устойчивость и вероятность
Пользуясь
классическим определением можно
вычислить вероятность случайного
события теоретически, не прибегая к
опыту. Однако, это не всегда выполнимо,
т.к. не всегда выполняются условия
равновозможности, независимости и т.п.
Вероятность случайной величины также
обычно нельзя вычислить теоретически.
В таких случаях прибегают к статистическому
определению вероятности. Суть его
состоит в следующем. Пусть какое либо
испытание при постоянных условиях
производится N
раз. При этом случайное событие А
(или случайная величина) появилось f
раз. Число f
называют частотой появления события
А,
а отношение
– частостью события (относительной
частотой). При увеличении числа испытанийN
относительная частота будет изменяться.
Но чем больше N,
тем меньше изменение
,
тем более она приближается к некоторому
числу.
Стремление
относительной частоты события к
некоторому предельному значению –
числу называют статистической
устойчивостью.
Это закон природы. Предельное же
значение, к которому стремится
относительная частота называют
вероятностью.
Для примера в
таблице 2.1 представлены результаты
контроля деталей, обработанных на
станке.
Таблица 2.1 –
Результаты контроля партий деталей
|
N |
10 |
20 |
100 |
200 |
300 |
500 |
1000 |
|
f число |
0 |
1 |
7 |
18 |
23 |
41 |
79 |
|
|
0,000 |
0,050 |
0,070 |
0,090 |
0,077 |
0,082 |
0.079 |
Определялось
количество бракованных деталей f
в партии количеством N
и относительная частота
.
Видим, что относительная частота
появления брака с увеличением объема
партии изменяется, приближаясь к числу
0,08. Это и есть вероятность появления
брака при обработке на данном станке.
-
Основные свойства
вероятностей
Из классического
определения вероятности (формула 2.1)
вытекают следующие свойства:
-
Вероятность
достоверного события
равна 1:
.
Действительно, в этом случае число
случаевm,
благоприятных событию, равно числу
всех возможных случаев n
(m
= n)
и, следовательно:
.
-
Вероятность
невозможного события
равна 0:
.
Действительно, в этом случае число
случаевm,
благоприятных событию, равно нулю: m
= 0,
.
-
Вероятность
случайного события
:
,
т. к. в этом случае 0 <m
< n. -
Вероятность любого
события
:
.
-
Правило сложения
вероятностей
Вероятность того,
что произойдет одно из двух несовместных
событий С
или Д
(безразлично какое) равняется сумме
вероятностей этих событий:
.
(2.2)
Пример.
Изготовлена партия из 100 деталей по
чертежу, на котором обозначен размер
мм. Из этих деталей 6 штук имеют размер
ниже нижнего предельного отклонения,
а 4 выше, чем верхнее предельное отклонение.
Определить вероятность извлечения
наугад бракованной детали.
Пусть С
событие извлечения детали с завышенным
размером, а Д
– событие
извлечения детали с заниженным размером.
Тогда:
,
.
Из правила сложения
вероятностей вытекают два очень полезных
при решении задач следствия:
Следствие 1.
Пусть р
– вероятность того, что событие А
произойдет, а q
– вероятность противоположного события
В,
т.е., что событие А
не произойдет. Т.к. два эти результата
несовместимы, а вместе они образуют
достоверное событие, то:
,
т.е.:
.
Следствие 2.
Вытекает из следствия 1:
.
(2.3)
Последнее следствие
часто бывает полезным в задачах по
вычислению вероятностей.
-
Правило умножения
вероятностей
Согласно правилу
умножения вероятность совмещения двух
взаимно независимых событий С
и Д
(Р(С и Д))
равна произведению вероятностей этих
событий:
.
(2.4)
События С
и Д
называют независимыми, если вероятность
появления одного из них не зависит от
того, произошло второе или нет.
Пример.
Какова вероятность того, что при трех
бросках игральной кости трижды выпадает
цифра 6.
Пусть событие А1
выпадение цифры 6 при первом бросании,
А2
при втором и А3
при третьем бросании. Тогда искомая
вероятность запишется следующим образом:
.
Если же вероятность
появления одного из возможных событий
изменяется от появления или не появления
других событий, то такие события называют
зависимыми. Например, если в партии
деталей имеется несколько штук
бракованных, то извлечение бракованных
деталей будет независимым событием при
условии, что после каждого извлечения
деталь будет возвращаться обратно. Если
же после извлечения деталь обратно не
возвращается, то извлечение второй раз
бракованной детали будет зависимым
событием, т.к. вероятность при этом
зависит от того, вынута первая деталь
бракованной или годной.
Если события А
и В
зависимы, то вероятность появления
события В,
вычисленная в предположении, что событие
А
наступило, называется условной
вероятностью события В
и обозначается Р(В/А).
Для зависимых
событий правило умножения вероятностей
формулируется следующим образом:
вероятность появления нескольких
зависимых событий А,
В
и С
одновременно равна произведению их
вероятностей, вычисленных для каждого
из них в предположении, что предшествующее
ему событие имело место:
.
(2.5)
-
Примеры вычисления
вероятностей
-
В урне находится
3 белых и 4 черных шара. Наугад вынимается
один шар. Найти вероятность того, что
этот шар будет белым.
Решение.
Обозначим через А
событие, состоящее в появлении белого
шара. Число случаев благоприятных
событию А
равно трем: m = 3.
Общее число случаев n = .
Все они равновозможны,
несовместимы
и независимы.
Используя выражение (2.1) имеем:
.
-
По условию
предыдущего примера определить
вероятность извлечения двух белых
шаров одновременно.
Решение.
Обозначим через В
событие, состоящее в появлении двух
белых шаров. Подсчитаем число благоприятных
этому событию случаев m.
Это число равно количеству вариантов
извлечения двух белых шаров из семи:
,
где
– число сочетаний двух элементов из
трех.
Из комбинаторики
известно, что
.
Поэтому:
.
Подсчитаем общее
число возможных случаев n.
Это число равно количеству вариантов
извлечения двух шаров из семи, находящихся
в ящике.
.
Подсчитаем из
выражения (2.1) вероятность события В:
-
По условию
предыдущего примера определить
вероятность извлечения подряд трех
белых шаров без их возвращения в
корзину. Используйте правило умножения
вероятностей.
Решение.
Пусть А
– событие извлечения первого белого
шара. Вероятность наступления этого
события запишется следующим образом:
.
После этого в урне
осталось 6 шаров и из них только 2 белых.
Пусть В
– событие извлечения второго белого
шара. Оно зависимо
от события А:
.
Пусть С
– событие извлечения третьего белого
шара. Оно зависимо от наступления событий
А
и В:
.
И окончательно из
формулы (2.5):
Этот же ответ можно
получить, используя формулу (2.1):
-
По условию
предыдущего примера, но с возвращением
шаров в урну, определить вероятность
извлечения подряд трех белых шаров.
Т.к. в этом случае
шары возвращаются в урну, события
извлечения являются независимыми. При
этом:
.
-
Установка состоит
из трех узлов А, В и С, соединенных
последовательно. Вероятность выхода
элементов из строя следующая:
,
,
.
Какова вероятность выхода из строя
всей установки.
Установка выходит
из строя при отказе хотя бы одного узла.
При решении задачи целесообразно
использовать правило умножения
вероятностей, и следствие № 2 из правила
сложения вероятностей.
Найдем вероятность
того, что установка не выйдет из строя
:
.
Это событие
заключается в одновременном выполнении
трех независимых событий: все узлы не
выходят из строя:
,
,
.
Используя правило
умножения вероятностей, получим:
.
Тогда:
.
-
Контрольные
вопросы
-
Что такое достоверное
событие и какова его вероятность? -
Что такое невозможное
событие и какова его вероятность? -
Что такое случайное
событие и какова его вероятность? -
Что такое случайная
величина. Приведите примеры? -
Дайте классическое
определение вероятности? -
Что такое
статистическая устойчивость? -
В чем состоит суть
статистического определения вероятности? -
В чем заключается
правило сложения вероятностей? -
В чем заключается
правило умножения вероятностей? -
Назовите два
следствия из правила сложения
вероятностей? -
Чему равна
вероятность совмещения двух независимых
событий? -
Чему равна
вероятность совмещения двух зависимых
событий?
-
Задачи для
самостоятельной работы
-
Бросают
игральный кубик. Какова вероятность
того, что при единственном бросании
выпадет цифра «1» или цифра «3»? -
Бросают
игральный кубик три раза. Какова
вероятность того, что три раза подряд
выпадет цифра «2»? -
Какова
вероятность того, что в примере 2
цифра «2» выпадет, по крайней мере,
1 раз? -
Установка
состоит из узлов x,
y,
z,
выполненных параллельно. Вероятность
выхода из строя этих узлов следующая:
Рx=0,02,
Py=0,2,
Pz=0,02.
Для того, чтобы установка вышла из
строя должны отказать одновременно
все узлы. Подсчитать вероятность
отказа всей установки Ру. -
Установка
состоит из трех узлов: А,
В,
С,
расположенных последовательно.
Узел В,
в свою очередь состоит из 2-х узлов
В1
и В2
включенных параллельно. Вероятность
отказа Р(А)=0,02,
Р(В1)=0,2,
Р(В2)=0,2,
Р(С)=0,02.
Найти вероятность отказа всей
установки. -
В партии из 30
изделий 6 бракованных. Из партии
наугад выбирается 5 изделий. Определить
вероятность того, что среди этих
пяти одно окажется бракованным. -
В партии из 10
изделий, 2 бракованных. Из партии
наугад выбирается 3 изделия, определить
вероятность того, что одно из них
окажется бракованным. -
Прибор,
работающий в течение времени t,
состоит из трех узлов, каждый из
которых, независимо от других, может
в течение времени t
отказать (выйти из строя). Отказ хотя
бы одного узла приводит к отказу
прибора в целом. За время
t
надежность (вероятность безотказной
работы) первого узла равна Р1=0,8;
второго Р2=0,9;
третьего Р3=0,7.
Найти надежность прибора в целом. -
При изготовлении
детали на станке выполняются три
технологические операции. Вероятность
появления дефекта при выполнении
1, 2 и 3 операции равны соответственно
Р1=0,1;
Р2=0,05;
Р3=0,08.
Найти вероятность того, что при
изготовлении детали в ней будет
обнаружен ровно один дефект. -
По условию
предыдущего примера найти вероятность
того, что деталь после снятия со
станка будет бракованной.
-
РАСПРЕДЕЛЕНИЕ
СЛУЧАЙНЫХ ВЕЛИЧИН
-
Общие определения
О качестве продукции
или услуги судят по каким-либо признакам
качества. В качестве таких признаков
могут выступать размер детали, ее вес,
наличие или отсутствие внутренних или
поверхностных дефектов и т.п. Официальным
синонимом слова «признак» является
термин «показатель
качества
продукции».
Различают
количественные
признаки качества и качественные
признаки (альтернативные).
Количественный
признак качества может быть измерен
каким-либо инструментом и оценен числом,
например 157,15 мм; 20,46 г; 320 МПа и т.п.
Качественные
признаки – это такие признаки качества
продукции, которые исследуют и оценивают
органами чувств – визуально, на слух,
осязанием – с целью проверки, удовлетворяют
ли они требованиям стандарта. В качестве
примера можно назвать визуальное
фиксирование поверхностных дефектов
продукта. К признакам, исследуемым
визуально, относятся также оценки,
сделанные с помощью предельных калибров
«проходных» и «непроходных».
В дальнейшем,
говоря о случайной
величине,
будем иметь ввиду какой-либо количественный
признак качества, либо количество
альтернативных признаков.
Случайные величины
разделяют на дискретные
и непрерывные.
Дискретная
– это такая случайная величина, которая
в результате испытания может принимать
только отдельные, конкретные, большей
частью, изолированные значения.
Пример.
Количество бракованных деталей в партии
может быть только положительным целым
числом: 0, 1, 2… и т.п., но не может быть
равным 1,5; 2,4.
Непрерывная
– это такая случайная величина, которая
в результате испытания может принимать
любое численное значение из непрерывного
ряда их возможных значений в границах
определенного интервала.
Пример. Вес
булки хлеба, диаметр вала, вытачиваемого
на токарном станке и т.п.
Распределение
случайной величины – совокупность ее
значений, расположенная в возрастающем
порядке с указанием ее вероятности (или
частости).
Различают
теоретические и эмпирические распределения
случайных величин. Вероятность используют
для теоретических распределений, а
частности – для эмпирических, полученных
в результате опыта или испытаний.
Рассмотрим способы
представления распределения случайной
величины.
-
Табличный и
графический способы
представления
распределения случайных величин
Способы представления
распределения несколько отличаются
для дискретных и непрерывных величин.
Распределение дискретной случайной
величины можно представить либо в
табличном виде, либо графически. Пример
эмпирического распределения показан
в таблице 3.1, а теоретического распределения
величины дискретного типа в таблице
3.2.
Таблица 3.1 −
Распределение частоты количества пятен
на яблоках в партии из 100 шт.
|
Количество пятен: |
0 |
1 |
2 |
3 |
4 |
5 |
>5 |
|
|
|
|
|
|
|
|
0 |
Таблица 3.2 −
Распределение вероятностей количества
бракованных деталей в выборе объема
50шт. из партии с 1 % брака.
|
Количество |
0 |
1 |
2 |
3 |
4 |
|
|
Вероятность |
0,607 |
0,303 |
0,075 |
0,012 |
0,001 |
0,02 |
Такую таблицу
распределения случайной дискретной
величины, называют рядом распределения.
Пример графического
представления данных из таблицы 3.1
представлен на рисунке 3.1.
Рисунок
3.1 − Распределение относительных частот
количества пятен на яблоках.
Такая фигура
называется многоугольником распределения.
Таким образом, и ряд распределения и
многоугольник распределения полностью
характеризует случайную дискретную
величину и являются разными формами
представления ее распределения.
Распределение
непрерывной случайной величины достаточно
сложно представить в виде ряда
распределения. Действительно, непрерывная
случайная величина может иметь
бесчисленное множество возможных
значений, сплошь заполняющих некоторый
промежуток. Составить таблицу, в которой
были бы перечислены все ее значения при
большом числе измерений, не всегда
представляется возможным. Кроме того,
вероятность появления конкретного
значения случайной величины равна нулю.
При практическом
наблюдении случайной величины поступают
следующим образом. Весь наблюдаемый
диапазон изменения случайной величины
разбивают на определенные интервалы
(разряды). Частоты подсчитывают не по
действительным значениям случайной
величины, а по разрядам. При этом имеют
дело не с частотами наблюденных значений
случайной величины непрерывного типа,
а с частотами их значений, лежащих в
границах установленного разряда (таблица
3.3).
Таблица 3 –
Интервальный ряд распределения диаметра
вала.
|
Интервал значений |
20,00-20,05 |
20,05-20,10 |
20,10-20,15 |
20,15-20,20 |
20,20-20,25 |
20,25-20,30 |
20,30-20,35 |
|
Частота |
2 |
10 |
24 |
30 |
22 |
10 |
2 |
|
Частость fi/N |
0,02 |
0,10 |
0,24 |
0,30 |
0,22 |
0,10 |
0,02 |
Графическое
представление распределения случайной
величины выполняют в данном случае
обычно в виде гистограммы (рисунок 3.2).
Рисунок 3.2 −
Гистограмма результатов измерения
диаметра вала
При теоретическом
описании непрерывной случайной величины
разбивка ее на разряды представляет
значительные трудности. Поэтому вводится
понятие функции распределения.
-
Функция
распределения
Пусть Х
случайная величина, а х
– какое-либо действительное число.
Пусть
.
Этому событию соответствует вероятность
.
Эта вероятность зависит от x,
т.е. есть некоторая функция от x.
Эту функцию и называют функцией
распределения случайной величины и
обозначают F(x):
.
(3.1)
Иногда функцию
распределения называют интегральной
функцией распределения.
Таким образом,
интегральная функция распределения
определяет вероятность того, что
случайная величина Х
примет значение меньше произвольно
изменяемого действительного числа х
.
Случайная величина считается заданной,
если известна ее функция распределения.
Сформируем некоторые
общие свойства функции распределения:
-
Функция распределения
есть неубывающая функция своего
аргумента, т.е. при
.
-
На минус бесконечности
функция распределения равна нулю:
.
-
На плюс бесконечности
функция распределения равна единице:.
-
Для
непрерывной случайной величины функция
распределения представляет собой
непрерывную, монотонно возрастающую
функцию (рисунок 3.3).
Рисунок 3.3 − График
интегральной функции распределения.
-
В
-∞ероятность попадания случайной
величины
на заданный
участок
При решении
практических задач, связанных со
случайными величинами, часто бывает
необходимым вычислить вероятность
того, что случайная величина примет
значение, заключенное в некоторых
пределах, например от x1
до x2.
Условимся для
определенности, левый конец x1
включать
в участок (x1,
x2),
а правый x2
– не включать. Тогда попадание случайной
величины X
на участок (x1,
x2),
равносильно выполнению неравенства:
Выразим вероятность
этого события через
.
Рассмотрим для этого три события:
-
событие А,
состоящее в том, что
.
-
событие В,
состоящее в том, что
.
-
событие С,
состоящее в том, что
.
Учитывая, что А=В+С
(В
или С), по теореме сложения вероятностей
имеем:
,
или:
,
откуда:
.
(3.2)
Таким образом,
вероятность попадания случайной величины
на заданный участок равна приращению
функции распределения на этом участке.
-
Плотность
распределения
Вычислим вероятность
попаданий случайной величины Х
на участок от х
до
:
.
Рассмотрим отношение
этой вероятности к длине участка, т.е.
среднюю вероятность на этом участке и
будем приближать ∆х
к 0. В пределе получим производную от
функции распределения.
.
Введем обозначение:
.
(3.3)
Функция
− производная функции распределения
характеризует как бы плотность, с которой
распределяется значение случайной
величины в данной точке. Ее называют
плотностью распределения непрерывной
случайной величиных.
Другие названия
:
дифференциальная функция распределения,
плотность вероятности.
Кривая, изображающая
зависимость
отх,
называется кривой распределения (рисунок
3.4).
Рисунок 3.4 − Кривая
плотности распределения
Отметим основные
свойства плотности распределения:
-
Плотность
распределения есть неотрицательная
величина при всех значениях аргумента.
Это следует из того, что
есть производная нигде не убывающей
функции
.
-
Вероятность
попадания случайной величины на
элементарный участок
примерно равна
:
.
(3.4)
Геометрически это
площадь элементарного прямоугольника,
опирающегося на кривой распределения
на отрезок
(рисунок 3.4).
-
Вероятность
попадания величины Х
на отрезок от х1
до х2
выраженная через плотность распределения
запишется следующим образом:

(3.5)
Это следует из
того, что
является первообразной функцией по
отношению к
.
Поэтому:
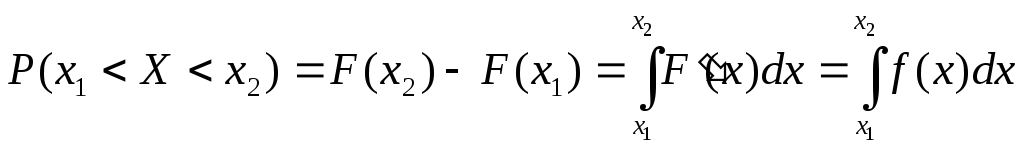
Графически
это выразится площадью криволинейной
трапеции (рисунок 3.5).
Рисунок 3.5
– Графическое представление вероятности
-
Если задаться
обратной задачей – выразить
через
,
то получим следующее. По определению:
.
Отсюда с учетом
формулы (3.5) имеем:
.
(3.6)
Геометрически
есть площадь под кривой распределения,
лежащей левее точки х.
-
Интеграл в
бесконечных пределах от
равен единице:
.
(3.7)
Это следует из
предыдущей формулы и из того, что
.
Пример.
Функция распределения непрерывной
случайной величины задана выражением:
Найти:
а) плотность
распределения;
б) вероятность
попадания х
на участок от 0,1 до 0,3.
Решение:
а)
б)
-
Контрольные
вопросы
-
Что вы понимаете
под количественными показателями
качества. Приведите примеры? -
Что вы понимаете
под альтернативными показателями
качества. Приведите примеры? -
Что вы понимаете
под дискретной случайной величиной.
Приведите примеры? -
Что вы понимаете
под непрерывной случайной величиной.
Приведите примеры? -
Что такое
распределение случайной величины? -
Какие способы
представления случайных величин вы
знаете? -
Что такое ряд
распределения случайной величины? -
Что такое
упорядоченный ряд распределения? -
Что такое
интервальный ряд распределения? -
Какие способы
графического описания случайной
величины вы знаете? -
Что такое
гистограмма? -
Что такое функция
распределения? -
Чему равно значение
функции распределения на минус
бесконечности? -
Чему равно значение
функции распределения на плюс
бесконечности? -
Опишите характер
изменения значений функции распределения
от минус бесконечности до плюс
бесконечности? -
Чему равна
вероятность попадания случайной
величины на участок
через значения функции распределения? -
Что такое плотность
распределения? -
Чему равна
вероятность попадания случайной
величины на участок
через значения плотности распределения? -
Выразите значение
функции распределения через плотность
распределения? -
Чему равно значение
интеграла плотности распределения
случайной величины от минус бесконечности
до плюс бесконечности?
-
Числовые
характеристики случайных величин
Выше мы рассмотрели
способы описания случайных величин и
их распределения в табличном, графическом
виде, функцией распределения и плотностью
распределения. Каждый из этих способов
полностью описывает случайную величину
с вероятностной точки зрения.
Однако на практике,
в большинстве случаев, нет необходимости
характеризовать случайную величину
полностью, исчерпывающим образом. Чаще
всего достаточно указать отдельные
числовые параметры, которые характеризуют
существенные черты распределения
случайной величины.
В качестве таких
черт распределения можно отметить
следующие:
-
среднее
значение, вокруг которого группируются
возможные значения случайной величины; -
степень
разброса случайных величин; -
асимметричность
распределения и т. п.
Характеристики,
назначение которых – выразить в сжатой
форме наиболее существенные особенности
распределения, называются числовыми
характеристиками
случайной величины. В статистических
методах управления качеством используются
обычно две группы таких характеристик:
характеристики положения и характеристики
рассеивания.
-
Характеристики
положения
Среди числовых
характеристик случайных величин нужно,
в первую очередь, отметить те, которые
характеризуют положение случайной
величины на числовой оси, т.е. указывают
некоторое среднее, ориентировочное
значение, около которого группируются
все её возможные значения. Среднее
значение случайной величины есть
некоторое число, являющееся как бы её
«представителем» и заменяющее её при
ориентировочных расчетах. В качестве
характеристик положения используют
обычно математическое ожидание, среднее
арифметическое и медиану.
Математическое
ожидание
используют для теоретических значений
случайной величины. Для дискретной
случайной величины математическое
ожидание находят следующим образом:
Пусть случайная
величина х
имеет возможные значения х1,
х2,
…, хn
с вероятностями p1,
p2,
…, pn.
Для того, чтобы охарактеризовать
положение значений случайной величин
на оси х
каким-либо числом, возьмем среднее
взвешенное значение. Каждое хi
при осреднении учитывается со своим
весом – вероятностью pi:

С
учетом того, что
получаем:
.
(4.1)
Это среднее
взвешенное значение случайной величины
и называют её математическим ожиданием.
В некоторых источниках его обозначают
символом μ. Итак, математическим ожиданием
случайной величины называется сумма
произведений всех её возможных значений
на вероятности этих значений.
Для непрерывной
случайной величины математическое
ожидание выражается уже не суммой, а
интегралом:
,
(4.2)
где
– плотность распределения случайной
величиных.
Формула (4.2)
получается из (4.1), если в ней заменить
отдельные значения хi
непрерывно
изменяющимся параметром х
, соответствующие вероятности pi
на
,
а сумму на интеграл.
Среднее
арифметическое
используют для эмпирических (опытных)
распределений случайных величин. Средним
арифметическим значением в этом случае
называют отношение суммы всех измеренных
значений случайной величины на их
количество n:
.
(4.3)
Для рядов с
повторяющимися значениями величин
используют следующее выражение:
,
(4.4)
где hi
– частота появления значений хi.;
n
– общее число наблюденных значений хi:
;
m
– число отдельных значений хi.
Для непрерывных
случайных величин, представляемых в
виде интервального ряда, в выражении
(4.4) в качестве хi,
принимают обычно середину интервалов.
Медианой
случайной величины (Ме)
называют такое её значение, для которого
функция распределения равна 1/2. Это
означает, что вероятность случайной
величины х
принять значение меньше медианы, в
точности равно вероятности этой величины
принять значение больше медианы.
Для непрерывной
случайной величины это можно выразить
следующим образом:
,
(4.5)
или графически на
рисунке 4.1, где площади под кривой
плотности вероятности левее и правее
значения х,
равного Ме,
соответственно S1
и S2
равны.
Рисунок 4.1 –
Графическое определение положения
медианы
Для дискретной
случайной величины в качестве Ме
принимают такое значение хm-1
и хm
, чтобы удовлетворялось условие:
.
(4.6)
Таким же образом,
только через относительные частоты
определяется медиана для эмпирического
ряда.
-
Характеристики
рассеивания случайной величины
Для достаточно
полной характеристики случайной величины
недостаточно знать положение среднего
значения, вокруг которого она группируется.
Необходимо ещё знать, как ложатся
отдельные величины относительно этого
центра, сильно разбросаны, или, напротив,
тесно сгруппированы. Для этого вводят
характеристики рассеивания случайной
величины: дисперсию,
стандартное отклонение и размах.
Дисперсия.
Дисперсией
теоретической случайной величины
называют математическое ожидание
квадрата отклонения её значений от её
математического ожидания.
Для дискретной
случайной величины хi
дисперсия – это сумма произведений
квадратов отклонений хi
от её математического ожидания
,
умноженных на соответствующие вероятности:
.
(4.7)
Для непрерывной
случайной величины:
.
(4.8)
Для эмпирического
распределения дисперсию обозначают
обычно через σ2
и определяют её как сумму произведений
квадратов отклонений измеренных значений
случайной величины от её среднего
арифметического значения на соответствующие
частоты (hi).
Выражение для
дисперсии зависит от числа данных в
ряду – n,
что доказывается в соответствующих
разделах математической статистики.
При небольшом
числе n
(n<30)
величина дисперсии для ряда с повторяющимися
значениями хi
запишется следующим образом:
,
(4.9)
а для короткого
статистического ряда, в котором значения
хi
не повторяются:
.
(4.10)
Если же число n
достаточно велико (n>30),
то в выражениях для σ2
в знаменателе значение (n-1)
должно быть заменено на n:
,
(4.11)
или
.
(4.12)
Стандартнее
отклонение.
Дисперсия
имеет размерность, представляющую собой
квадрат размерности самой случайной
величины. Это обычно неудобно на практике.
Поэтому в управлении качеством чаще
используют не дисперсию, а корень
квадратный из дисперсии со знаком плюс.
Эту величину называют стандартным
отклонением и обозначают символом σ.
,
(4.13)
.
(4.14)
Размерность σ
совпадает с размерностью самой случайной
величины.
Размах.
Размахом распределения случайной
величины называют разность между
наибольшим и наименьшим измеренными
значениями случайной величины:
.
(4.15)
-
Вычисления для
рядов с большим числом наблюдений
-
Подготовительные
работы
В статистическом
ряду с небольшим количеством наблюдений
легко проследить общие закономерности
ряда и организовать вычисления
,
,
,
.
При увеличении количества членов в ряду
задача осложняется. Так в ряду наблюдений,
представленном в условии задачи для
самостоятельной работы № 2 (таблица
4.6) приведены данные измерений длины
160 блоков. Сказать что-то определенное
о характере изменений величины ряда и
организовать вычисление его числовых
характеристик представляется
затруднительным. Вычислительная работа
с такими рядами организуется следующим
образом.
Значения, приведенные
в таблице, располагаются в порядке их
возрастания и подсчитываются частоты
отдельных наблюдений, получая, так
называемый, упорядоченный ряд наблюдений.
Для нашего ряда в задаче № 2 находим
наибольшее и наименьшее значения
величин:
,
.
Составляем таблицу, в которой располагаем
наблюдения от 159 до 190 в порядке возрастания.
Для облегчения подсчета частоты отмечаем
штрихами встречающиеся значения по
мере просмотра данных. В результате
получаем упорядоченный ряд из 160
наблюдений (таблица 4.1).
Упорядоченный ряд
дает уже более наглядную картину
изменения случайной величины (признака
качества), чем первоначальный список
данных. Блоки с длиной от 170 см до 179 см
встречаются чаще других, а блоки с длиной
до 159 см и больше 190 см вообще не встречаются.
Из таблицы 4.1 видно как распределяются
значения длины измеренных блоков в
пределах от 159 до 190 см.
Однако в этой
таблице еще слишком много данных. Это
затрудняет анализ и дальнейшую
математическую обработку для определения
числовых характеристик ряда. В таких
случаях принято переходить к интервальному
ряду, объединяя несколько соседних
значений признака.
При этом возникает
вопрос, сколько интервалов выбрать и
как установить их границы. Практика
показывает, что количество интервалов
не должно быть меньше шести и больше
двадцати. Оптимальным считается
двенадцать интервалов. При таком выборе
числа интервалов среднюю арифметическую
и дисперсию можно вычислить достаточно
точно, объем вычислений при этом не
слишком велик и, в большинстве случаев,
картина распределения выглядит достаточно
наглядно.
Ширина интервала
для всего ряда должна быть одинаковой.
Каждое отдельное значение должно быть
однозначно отнесено к определенному
интервалу. Если оно попадает на границу
интервалов, что бывает сравнительно
редко, то возникает вопрос, к какому
интервалу отнести это значение. Иногда
рекомендуют причислять данное значение
наполовину к верхнему, наполовину к
нижнему интервалам. Можно рекомендовать
и такой порядок: в каждый интервал
включать те наблюдения, числовые значения
которых больше нижней границы интервала
и меньше или равны верхней.
Таблица 4.1 −
Упорядоченный ряд наблюдений, составленный
по результатам
измерений длины 160 блоков
|
|
|
|
|
||
|
159 |
/ |
1 |
175 |
/// |
9 |
|
160 |
/ |
1 |
176 |
/// |
8 |
|
161 |
/ |
1 |
177 |
///// |
14 |
|
162 |
/ |
1 |
178 |
/// |
10 |
|
163 |
179 |
/// |
10 |
||
|
164 |
// |
2 |
180 |
/ |
1 |
|
165 |
// |
2 |
181 |
/// |
7 |
|
166 |
// |
2 |
182 |
/// |
6 |
|
167 |
/// |
9 |
183 |
/// // |
5 |
|
168 |
/// |
10 |
184 |
/// |
3 |
|
169 |
/// |
3 |
185 |
/// // |
5 |
|
170 |
/// |
7 |
186 |
/ |
1 |
|
171 |
/// |
6 |
187 |
// |
2 |
|
172 |
/// |
6 |
188 |
/ |
1 |
|
173 |
///// |
17 |
189 |
// |
2 |
|
174 |
/// |
6 |
190 |
// |
2 |
|
Сумма |
160 |
Для
нашего ряда объединим по три значения
признака, получив интервал, равный 3 см.
При этом объединение возможно тремя
способами, показанными в таблице 4.2.
Следует отметить,
что во втором и третьем вариантах к
числу 159
подключаются
соответственно
одно и два значения слева. Так как на
самом деле эти значения не наблюдались,
то их частоты равны нулю. То же самое
происходит и в конце упорядоченного
ряда.
Таблица 4.2 −
Варианты объединения значений признака
в интервалы
|
Вариант 1 |
Вариант 2 |
Вариант 3 |
|||
|
середина интервала |
|
Середина Интервала |
|
середина интервала |
|
|
и т.д. |
3 3 |
и т.д. |
2 3 |
и т.д. |
1 3 |
Воспользуемся
третьим вариантом объединения и получим
ряд, который называют интервальным, с
числом интервалов
и границами интервалов равными 156,5;
159,5; 162,5 и т.д. Этот интервальный ряд
представлен в таблице 4.3.
Таблица 4.3 −
Интервальный ряд распределения длин
160-ти бетонных блоков
|
Интервалы |
Середина |
Частота, |
Относительная |
|
156,5 – 159,4 159,5 – 162,4 162,5 – 165,4 165,5 – 168,4 168,5 – 171,4 171,5 – 174,4 174,5 – 177,4 177,5 – 180,4 180,5 – 183,4 183,5 – 186,4 186,5 – 189,4 189,5 |
158 161 164 167 170 173 176 179 182 185 188 191 |
1 3 4 21 16 29 31 21 18 9 5 2 |
0,6 1,9 2,5 13,1 10,0 18,1 19,4 13,1 11,3 5,6 3,1 1,3 |
-
Вычисление
средней арифметической и дисперсии.
При
вычислении средней арифметической
упорядоченного ряда пользуются формулой
(4.4).
Для
упорядоченного ряда в таблице 4.1 число
интервалов равно: k=32.
Подставляя численные значения
соответствующих параметров в выражение
(4.4) получаем:
.
Таким
же образом вычисляют среднюю арифметическую
интервального ряда в таблице 4.3, с той
лишь разницей, что в качестве значения
признака принимают середину интервалов:
.
Как
видно, обе средние немного не совпадают.
Вычисление
дисперсии для упорядоченного ряда
выполняется по формуле (4.9), а для
интервального ряда по следующей формуле:
,
(4.16)
где
середина интервала.
Для
вычисления дисперсии (и средней
арифметической) рекомендуется все
промежуточные вычисления представить
в табличном виде. Пример организации
таких записей для упорядоченного ряда
представлен в таблице 4.4.
Вычисление
дисперсии по формуле (4.16) дало:
.
Итак,
для упорядоченного ряда из таблицы 4.1
рассчитанные величины среднего
арифметического, дисперсии и стандартного
отклонения равны соответственно:
=175,14
см,
см2
и
см.
Для
интервального ряда из таблицы 4.3
аналогичные расчеты представлены в
таблице 4.5.
Таблица 4.4 −
Промежуточные вычисления при определении
для упорядоченного ряда
|
|
|
|
|
|
|
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 |
1 1 1 1 0 2 2 2 9 10 3 7 6 6 17 6 9 8 14 10 10 1 7 6 5 3 5 1 2 1 2 2 |
-16.14 -15.14 -14.14 -13.14 -12.14 -11.14 -10.14 -9.14 -8.14 -7.14 -6.14 -5.14 -4.14 -3.14 -2.14 -1.14 -0.14 0.86 1.86 2.86 3.86 4.86 5.86 6.86 7.86 8.86 9.86 10.86 11.86 12.86 13.86 14.86 |
260.5 229.22 199.94 172.66 147.38 124.1 102.82 83.54 66.26 50.98 37.7 26.42 17.14 9.86 4.58 1.3 0.02 0.74 3.46 8.18 14.9 23.62 34.34 47.06 61.78 78.5 97.22 117.94 140.66 165.38 191.2 220.82 |
260.5 229.22 199.94 172.66 0 248.2 205.64 167.08 596.3 509.8 113.1 184.94 102.84 59.16 77.85 7.8 0.18 5.92 48.43 81.79 149.0 23.62 240.38 282.36 308.9 235.5 486.1 117.94 281.32 165.38 382.4 441.64 |
|
Сумма: |
6387.89 |
Таблица
4.5 − Промежуточные вычисления при
определении
для интервального ряда
|
№ |
Интервал |
|
|
|
|
|
|
|
1 2 3 4 5 6 7 8 9 10 11 12 |
156,5 –159,4 159,5 –162,4 162,5 –165,4 165,5 –168,4 168,5 –171,4 171,5 –174,4 174,5 –177,4 177,5 –180,4 180,5 –183,4 183,5 –186,4 186,5 –189,4 189,5 |
158 161 164 167 170 173 176 179 182 185 188 191 |
1 3 4 21 16 29 31 21 18 9 5 2 |
158 483 656 3507 2720 5017 5456 3759 3276 1665 940 382 |
-17,14 -14,14 -11,14 -8,14 -5,14 -2,14 0,86 3,86 6,86 9,86 12,86 15,86 |
293,91 200,05 124,18 66,32 26,46 4,60 0,73 14,87 47,01 97,15 165,28 251,42 |
293,91 600,14 496,73 1392,73 423,33 133,27 22,73 312,28 846,15 874,31 826,42 502,84 |
|
Сумма |
160 |
28019 |
6724,84 |
На
основании этих данных получены следующие
результаты:
,
и
.
Как видно из
сравнения полученных данных, численные
характеристики, рассчитанные для
упорядоченного и интервального рядов,
несколько отличаются друг от друга. Это
связано с тем, что в формулах для
интервального ряда истинные значения
измеренного параметра заменены на
величину середины интервалов. Однако
полученные различия не велики и не имеют
принципиального характера.
-
Контрольные
вопросы
-
Что такое
математическое ожидание? -
Как находится
математическое ожидание для дискретной
случайной величины? -
Как находится
математическое ожидание для непрерывной
случайной величины? -
Что такое среднее
арифметическое и как оно находится? -
Что такое медиана
и как она находится? -
Какое свойство
распределения случайной величины
характеризует дисперсия? -
Как вычисляется
дисперсия теоретической дискретной
случайной величины? -
Как вычисляется
дисперсия теоретической непрерывной
случайной величины? -
Как вычисляется
дисперсия экспериментального ряда
случайных величин? -
Что такое стандартное
отклонение? -
Что такое размах?
-
Почему отличаются
значения средних арифметических и
дисперсий, подсчитанных для упорядоченного
и интервального рядов?
-
Задачи для
самостоятельной работы
-
Пусть измерения
длины десяти бетонных блоков дали
следующий результат в cм:
177, 174, 178, 176, 175, 175, 173, 171, 167, 177,175. Найти:
,
,
,
.
-
Результаты
измерений длины 160-ти бетонных блоков
представлены в таблице 4.6.
Таблица
4.6 − Результаты измерения длины 160-ти
бетонных блоков.
|
171 179 169 168 168 175 167 181 168 179 165 173 173 173 167 182 |
177 178 176 173 176 159 167 181 177 187 181 186 179 170 168 185 |
175 176 178 167 177 162 171 172 170 168 179 172 181 177 171 176 |
177 167 182 178 176 173 184 173 165 171 185 177 185 178 189 179 |
174 171 175 175 168 181 173 178 164 173 170 172 173 184 178 179 |
174 174 172 167 168 179 176 182 176 190 178 164 173 185 177 182 |
173 175 177 160 171 166 175 173 181 169 178 168 173 174 172 173 |
183 177 177 177 183 170 167 166 189 177 183 182 187 177 170 170 |
183 173 179 182 168 178 167 174 168 170 169 184 179 180 176 173 |
178 172 167 179 175 177 174 188 175 161 173 185 175 183 181 190 |
Найти следующие
числовые характеристики представленного
ряда:
,
,
,
.
-
В таблице 4.7
представлены результаты испытаний 100
стальных образцов на ударную вязкость.
Таблица
4.7 − Результаты испытаний на ударную
вязкость
|
11,4 11,0 12,1 11,4 11,3 10,9 11,4 11,6 11,7 11,6 |
11,7 10,4 11,6 11,8 11,2 10,8 11,6 10,7 11,8 11,5 |
11,7 11,2 11,5 12,0 11,6 11,5 11,4 11,4 11,9 11,3 |
11,5 11,2 11,7 11,5 11,1 12,1 11,5 11,2 11,0 11,5 |
11,3 11,5 11,5 11,6 11,4 11,5 12,2 11,0 11,4 12,5 |
11,8 11,2 10,9 11,7 11,2 11,9 11,7 11,5 10,6 11,4 |
12,2 11,4 11,8 11,6 11,4 11,3 11,6 12,1 11,9 11,7 |
11,5 11,4 11,5 10,8 11,5 11,4 11,6 11,4 11,5 11,3 |
11,3 11,7 11,5 11,4 11,3 11,3 10,8 11,5 11,3 11,4 |
11,2 11,6 11,4 11,3 11,1 11,4 11,2 11,3 11,8 11,5 |
Данные результаты
испытаний представить в виде интервального
ряда и рассчитать значения средней
арифметической и дисперсии.
-
Приведенная ниже
таблица 4.8 является результатом 60
наблюдений за удельным расходом
жидкости.
Таблица
4.8 – Результаты наблюдений
|
0,52 0,53 0,55 0,54 0,52 0,52 0,48 0,58 0,50 0,51 |
0,50 0,55 0,54 0,54 0,52 0,53 0,56 0,52 0,52 0,54 |
0,56 0,53 0,52 0,51 0,56 0,54 0,49 0,54 0,54 0,56 |
0,50 0,51 0,52 0,55 0,52 0,50 0,54 0,54 0,56 0,57 |
0,53 0,54 0,52 0,53 0,52 0,54 0,56 0,54 0,55 0,57 |
0,56 0,60 052 0,54 0,56 0,54 0,58 0,54 0,52 0,51 |
Обработайте
данные, разбив их на интервалы 0,475-0,495;
0,495-0,515 и т.д. Вычислите среднее
арифметическое и стандартное отклонение.
-
Основы выборочного
метода контроля
качества
-
Сплошной и
выборочный контроль
На производстве
контролируют качество сырья, полуфабрикатов,
деталей, узлов и готовой продукции. В
некоторых случаях прибегают к сплошному
контролю качества, т.е. проверяют все
изделия подряд. Такой контроль необходим,
если использование дефектных изделий
представляет потенциальную опасность
больших убытков или угрозы для жизни
потребителя. Сплошному контролю
необходимо, например, подвергать основные
функциональные свойства таких изделий
как парашют, тормозная система автомобиля,
пассажирские лифты и т.п.
В то же время
сплошной контроль в принципе невозможен
для некоторых изделий, если они в процессе
проверки разрушаются. К таким изделиям
следует отнести лампы накаливания,
боеприпасы, фотопленки и т.п.
Применение сплошного
контроля обычно становится экономически
невыгодным при большом объеме контроля.
Сплошной контроль, в то же время, вовсе
не гарантирует безупречной оценки,
особенно если число изделий велико.
Вследствие монотонности процесса
контролер может принять дефектное
изделие за годное и, наоборот, годное
оценить как брак. Поэтому основным
методом контроля и управления качеством
на производстве является выборочный
контроль.
-
Генеральная
совокупность и выборка из нее
Введем некоторые
основные определения:
-
генеральная
совокупность
– статистическая совокупность, из
которой сделана выборка. -
выборка
– часть членов совокупности, отобранных
из нее для получения сведений о всей
совокупности. -
статистическая
совокупность
– группа предметов, объединенных
каким-либо общим признаком или свойством
качественного или количественного
характера.
Пример.
Изготовленная партия рельсов –
статистическая совокупность. Качественный
признак: соответствует рельс показателям
качества, или не соответствует (брак,
не брак). Количественный признак:
твердость головки рельса.
Для того чтобы по
данным выборки можно было достаточно
уверенно судить об интересующем нас
признаке генеральной совокупности,
необходимо, чтобы члены выборки его
правильно представляли. Это требование
формулируют так: выборка должна быть
репрезентативной (представительной).
-
Виды выборок
В зависимости от
особенностей организации извлечения
предметов из генеральной совокупности
можно выделить следующие виды выборок:
-
повторная (с
возвращением).
После извлечения детали из генеральной
совокупности деталь измеряется, затем
возвращается, партия перемешивается
и вновь производится извлечение. При
этом деталь может быть извлечена
повторно. -
бесповторная
(без возвращения).
Деталь не возвращается после ее
извлечения из генеральной совокупности. -
случайная.
Все детали генеральной совокупности
должны иметь равную возможность попасть
в выборку, не зависимо от того годные
они или дефектные.
Эта предпосылка
кажется простой и легко осуществимой.
К сожалению, это не так. Существует
несколько способов осуществления
случайной выборки:
1. Тщательное
перемешивание деталей и отбор из разных
мест. Аналогом можно считать лотерейный
барабан.
2. Если отдельные
детали упорядочены, т.е. пронумерованы,
то можно использовать жребий, таблицу
случайных чисел, либо возможности
компьютерной техники.
Предположим,
требуется наугад произвести выборку
объема n = 10
из партии N
= 90 сложенных друг на друга листов металла
и исследовать их механические свойства.
Чтобы гарантировать случайный выбор,
каждому листу приписывают некоторое
число, например, от 00 до 89. Затем организуют
получение случайных двухзначных чисел,
игнорируя повторные.
-
преднамеренная.
Отбор деталей для выборки производится
с определенной тенденцией, приводящей
к повышению или понижению вероятности
выявления изучаемого признака качества. -
мгновенная
(текущая).
Выборка малого объема из числа деталей,
изготовленных в малый промежуток
времени, в котором не могут проявиться
систематические погрешности. -
общая.
Выборка, состоящая из серии мгновенных
выборок. -
малая.
Выборка объемом 5…10 (до 25) деталей. -
большая.
Выборка объемом более 25 деталей (обычно
50…100).
-
Задачи выборочного
метода
Можно назвать
следующие задачи выборочного контроля
на производстве.
1. Разбраковка
деталей, готовой продукции. Для этого
разрабатываются различные планы
контроля.
2. Оценка статистической
управляемости процесса. С этой целью
применяют контрольные карты.
3. Установление
закона распределения изучаемой случайной
величины.
4. Установление
параметров этого распределения по
данным выборки (оценка параметров).
5. Статистическая
проверка гипотез, выдвигаемых при
производственных исследованиях.
Примеры:
а) проверка гипотезы
случайности выборки;
б) проверка гипотезы
о принадлежности двух выборок к одной
и той же генеральной совокупности.
-
Распределение
выборочных средних арифметических
Если во время
изготовления деталей отбирать выборки,
то статистические характеристики этих
выборок будут колебаться. Для оценки
параметров генеральной совокупности
выборка меньшего объема менее благоприятна,
чем выборка большего объема.
Но все-таки выгодно
вместо одной большой использовать
несколько выборок небольшого объема,
чтобы получить представление о системе
случайных причин, воздействующих на
процесс, т.е. обо всей генеральной
совокупности.
Пусть у нас есть
генеральная совокупность с параметрами
µ и σ2.
Будем делать из нее малые выборки, и
определять их параметр
.
Т.к. значениявыборок будут разные, расположим их в
упорядоченный ряд, затем построим
интервальный ряд, получив, таким образом,
распределение средних арифметических.
Если количество
выборок достаточно велико, то:
-
средняя арифметическая
распределения выборочных средних
совпадает с математическим ожиданием
генеральной совокупности µ; -
дисперсия
распределения выборочных средних
значений
зависит от объема выборкиn
и связаны с дисперсией генеральной
совокупности σ2
соотношением:
,
;
-
если генеральная
совокупность распределена по нормальному
закону, то распределение средних
значений тоже будет нормальным.
Это свойство широко
используют при интерпретации контрольных
карт. А как будет выглядеть распределение
выборочных средних, если генеральная
совокупность имеет закон распределения,
отличный от нормального. Оказывается,
что и в этом случае распределение
выборочных средних приближается к
нормальному, и тем лучше, чем больше
объем выборок.
Этот закон имеет
большую роль в технике составления
контрольных карт для средних значений
.
Он имеет математическое доказательство.
Поясним его на
практическом примере. Представьте себе
генеральную совокупность в виде
определенного количества пронумерованных
деревянных шариков. Номера шариков
соответствуют значениям признака.
Частота появления отдельных значений
признака соответствует количеству
шариков с одинаковым номером. Известны
также математическое ожидание и
стандартное отклонение этой генеральной
совокупности.
Шарики ссыпаны в
лотерейный барабан и хорошо перемешаны.
Затем произвольно вытаскиваем один
шарик, записываем его номер (значение
признака) и кладем его обратно в барабан.
Каждые n
номеров, записанных последовательно
один за другим, образуют выборку объемом
n.
Для каждой выборки вычисляем среднюю
арифметическую и, наконец, составляем
распределение средних значений всех
выборок. Такие опыты были проделаны с
двумя различными генеральными
совокупностями, одна из которых имела
односторонне треугольной распределение,
а другая – нормальное распределение
[4].
В результате
обработки опытных данных получены
следующие результаты:
-
Нормальное
распределение генеральной совокупности,
состоящей из 200 шаров, изображено на
рисунке 5.1. Математическое ожидание
этой совокупности равно µ = 6,0, дисперсия
σ2=4.14,
а стандартное отклонение σ = 2,035. Из этой
совокупности было отобрано 120 выборок
объемом n=5. На рисунке 5.2 в виде гистограммы
представлено распределение средних
арифметических, вычисленных по этим
выборкам.
Рисунок 5.1
Нормальное распределение
Рисунок 5.2 –
Распределение средних значений
-
Одностороннее
треугольное распределение.
На рисунке 5.3 изображено треугольное
распределение.
Рисунок 5.3 Треугольное
распределение
Математическое
ожидание этой совокупности равно µ = 4,
а стандартное отклонение σ = 8,1. Из
совокупности, представляющей это
распределение, было отобрано 80 выборок
объемом n
= 5. Распределение средних значений этих
выборок изображено в виде гистограммы
на рисунке 5.4. На гистограмму наложено
вычисленное теоретическое нормальное
распределение с
и
.
Рисунок 5.4 —
Распределение средних значений
Анализ результатов,
представленных на рисунках 5.1 – 5.4
показывает справедливость описных выше
особенностей распределения выборочных
средних арифметических.
-
Контрольные
вопросы
-
В
каких случаях целесообразно применение
сплошного контроля? -
В
чем вы можете увидеть недостатки
сплошного контроля? -
Почему
основным методом контроля и управления
качеством на производстве является
выборочный контроль? -
Дайте
определение следующим понятиям:
статистическая совокупность, генеральная
совокупность, выборка? -
Какие
вы знаете виды выборок? -
Какие
вы знаете способы осуществления
случайной выборки? -
В
чем могут состоять задачи выборочного
контроля на производстве? -
Какие
особенности распределения выборочных
средних вы знаете? -
Как
найти стандартное отклонение выборочных
средних при известном стандартном
отклонении генеральной совокупности? -
Как
будет выглядеть распределение выборочных
средних, если генеральная совокупность
имеет нормальный закон распределения? -
Как
будет выглядеть распределение выборочных
средних, если генеральная совокупность
имеет закон распределения, отличный
от нормального?
-
ЗАКОНЫ РАСПРЕДЕЛЕНИЯ
СЛУЧАЙНЫХ ВЕЛИЧИН
В теории вероятности
и математической статистике рассматривается
большое количество законов распределения
случайных величин. В статистических
методах управления качеством чаще всего
используют следующие распределения:
гипергеометрическое, биноминальное,
нормальное распределение Лапласа –
Гаусса и распределение Пуассона. Прежде,
чем перейти к изучению этих распределений,
рассмотрим основные положения
комбинаторики.
-
Элементы
комбинаторики
При вычислении
вероятности часто оказывается полезным
знать различные типы соединений.
Соединения
– это группы (множества), составленные
из каких-либо предметов: деталей, шаров,
цифр и т.п. Предметы, из которых составлены
соединения, называются элементами.
Обычная задача статистических методов
управления качеством выглядит следующим
образом. Имеется вся совокупность
деталей, качество которых необходимо
определить. Её называют генеральной
совокупностью.
Исследование же показателей качества
осуществляют на каком-то ограниченном
количестве деталей n,
выбранных из генеральной совокупности
– выборке.
Практический
интерес представляет соединения деталей
(элементов) в выборке. Например, ставится
вопрос: какова вероятность того, что в
выборке из пяти деталей находится одна
бракованная деталь, если известно, что
в генеральной совокупности из ста
деталей имеется две бракованные.
Для таких задач
необходимо рассмотреть три вида
соединений: перестановки, размещения
и сочетания.
Перестановки.
Перестановками из n
элементов называют соединения, из
которых каждое содержит n
элементов и отличается друг от друга
только порядком элементов. Из одного
элемента a
можно составить только одну перестановку
(1); из двух элементов а
и в
– две перестановки
:ав,
ва;
из трех элементов а,
в,
с–шесть
перестановок: авс,
асв,
вас,
вса,
сав,
сва.
Из последнего случая видно, что каждый
из трех элементов может стоять на первом
месте, в то время, как два других
рассматриваются двумя различными
способами. Всего получается
перестановок.
При рассмотрении
четырёх элементов каждый из них может
стоять на первом месте, а три других
могут быть расположены
способами. Следовательно, в этом случае
имеютсявозможности рассмотрения элементов.
Этот ряд можно
продолжить дальше: n
элементов могут быть расположены
(6.1)
способами. Итак,
для n
элементов существует n!
перестановок.
Размещения.
Размещениями из n
элементов по k
называют соединения, в каждое из которых
входит k
элементов, взятых из данных n
элементов, и которые отличаются между
собой элементами (хотя бы одним) или их
порядком.
Если n
элементов распределить по
ячейкам, причем
,
то в первой ячейке можно поместить любой
изn
элементов. Другими словами имеется n
таких возможностей. Для второй ячейки
останутся в рассмотрении только
элементов. Т.о., две ячейки из
имеющихся могут быть заняты
способами. Продолжая рассуждения,
находим, чтоячеек дляn
элементов могут быть заняты
(6.2)
способами. Это и
есть число размещений. Помножив и
разделив полученное выражение на
,
его можно записать в другом виде:
.
(6.3)
Сочетания.
Сочетаниями из n
элементов по k
называют
соединения, в каждое из которых входит
k
элементов, взятых из данных n
элементов, и которые отличаются только
элементами (хотя бы одним).
Число различных
сочетаний из n
элементов по k
обозначают символом
(от латинского combinare
– соединять). Вместо
употребляют также обозначение
.
По определению сочетания отличают от
размещений тем, что не учитывают порядок
распределения элементовn
по ячейкам
.
Поэтому число возможных сочетаний
меньше числа возможных размещений на
число возможных перестановок из(
!).
Выражение для
запишется следующим образом:
.
(6.4)
Числа
являются биноминальными коэффициентами,
т.е. коэффициентами при соответствующих
членах разложения бинома Ньютона
:
-
Гипергеометрическое
распределение
Предположим, что
генеральная совокупность состоит из N
деталей, среди которых S
бракованных и N—S
годных. Делаем выборку объёмом n
из генеральной совокупности. Найдём
вероятность того, что среди n
извлеченных деталей будет ровно x
бракованных. Обозначим искомую вероятность
через P(x).
Общее число
возможных случаев равно числу способов,
которыми можно извлечь n
деталей из генеральной совокупности
объёмом N,
т.е. равно
.
При этом количество возможных способов,
которыми можно отобрать бракованные
детали составляет
,
а годные −
.
Так как каждую из
возможностей для бракованные деталей
можно скомбинировать с
возможностями для хороших, то общее
число благоприятных случаев составляет
произведение
.
Искомая вероятность,
согласно классическому определению,
равна:

(6.5)
При этом должны
соблюдаться условия:
и
.
Если вероятность
для определения x
уже вычислена, то вероятность последующего
события
можно определить с помощью рекурентной
формулы:
.
(6.6)
Совокупность
вероятностей для
образует гипергеометрическое
распределение. Оно описывает особенности
модели выборки без возвращения.
Математическое
ожидание и дисперсия этого распределения
запишутся следующим образом:
,
(6.7)
,
(6.8)
где
– доля брака в генеральной совокупности.
Пример 6.1.
В ящике лежит 12 деталей, три из них
бракованные. Контролируется выборка
из трёх деталей. Найти вероятности того,
что из этих трёх деталей бракованными
являются: 0,1,2,3.
Найдём
,
используя выражение (6.5):




Графическое
представление полученных результатов
показано на рисунке 6.1.
-
Биноминальное
распределение
Рассмотренное
нами гипергеометрическое распределение
соответствует обычному контролю
качества, когда проконтролированная
деталь не возвращается в свою партию
(выборку). Этот процесс называют контроль
без возвращения.
Однако на практике
большее применение нашла модель процесса
контроля с
возвращением,
как более простая для математического
описания. Вносимая погрешность будет
несущественна, если размер выборки n
невелик по сравнению с числом деталей
в генеральной совокупности N.
Рисунок 6.1 –
Распределение количества бракованных
деталей в выборке
Для того чтобы
качественно описать основные особенности
распределения случайных событий для
модели с возвращением, обратимся к
лотерейному барабану с черными и белыми
шарами. При этом черные шары могут
выступать, к примеру, в качестве
бракованных деталей, а белые − хороших
деталей. Пусть р
− вероятность
того, что будет извлечен черный шар.
Вероятность противоположного события
− извлечения белого шара обозначим q
, причем q
= 1 − р.
Каждый раз вынутый шар тотчас возвращается
в барабан, т.е. величина р
не изменяется.
Если извлечь из
барабана два шара, то возможны следующие
варианты сочетаний цветов и их вероятности:
-
черный
− черный (р
и р); -
черный
− белый (р
и q); -
белый
− черный (q
и р); -
белый
− белый (q
и q).
Для нас неважно,
появится ли сначала черный или белый
шар, т.к. при анализе выборки порядок
результатов не имеет значения. На
практике имеет значение только число
бракованных деталей в выборке. Используя
теоремы умножения и сложения вероятностей,
получаем следующие значения вероятностей
различных комбинаций появления шаров:
-
два
черных −
;
-
черный
– белый −
;
-
два
белых −
.
Перечисленные
результаты представляют собой полную
группу событий, т.е. какое-то из них
обязательно произойдет и это является
достоверным событием. Поэтому, можно
записать следующее выражение:
.
(6.9)
Совокупность всех
перечисленных вероятностей составляет
распределение. Выражение
представляет собой бином. Все перечисленные
вероятности являются членами его
разложения. Полученное распределение
назвали поэтому биноминальным.
Продолжая
рассмотрение подобным образом извлечение
из барабана трех и более шаров, приходим
к следующему. Если с возвращением
извлекать из барабана n
шаров, то вероятности различных
результатов их комбинаций получатся
при разложении бинома:
.
(6.10)
Вероятность же
того, что при n
извлечениях появится ровно х
черных шаров, запишется:
.
(6.11)
Можно так
сформулировать закон биномиального
распределения в применении к контролю
качества. Если вероятность появления
брака постоянна при производстве серии
изделий (генеральной совокупности) и
равна р,
то вероятность появления брака х
раз в выборке размером n
изделий запишется выражением (6.11), где
q
– вероятность непоявления брака, равная
q
= 1 — р.
В выражении (6.11)
коэффициент
есть число
сочетаний из n
по х,
т.е. число способов, которыми можно
выбрать х
бракованных изделий из совокупности n
изделий.
(6.12)
Для того, чтобы
построить распределение, необходимо
по формуле (6.11) определить вероятность
для всех х,
начиная с х = 0
и заканчивая х
= n.
Числовые
характеристики биномиального ряда
распределения имеют следующие значения:
математическое
ожидание:
,
(6.13)
дисперсия:
,
(6.14)
среднее квадратичное
отклонение:
,
(6.15)
Пример 6.2.
В партии деталей имеется брак, доля
которого составляет 0,1. Производится
последовательное извлечение 10 деталей
(n=10).
После каждого извлечения и обследования
деталь возвращается в партию (если
партия очень большая, то можно и не
возвращать, ошибка вычисления будет
незаметная). Какова вероятность того,
что среди извлеченных деталей одна
будет бракованная (x
= 1)?
Очевидно, что
вероятность извлечения бракованной
детали составляет р
= 0,1, а вероятность извлечения годной: q
= 1 – p
= 0.9. Используя выражения (6.11) и (6.12)
получаем:
.
Ответ: вероятность
извлечения бракованной детали составляет
0,387.
Пример 6.3.
Для условий примера 6.2 построить
распределение вероятностей извлечения
0, 1, 2, 3, 4, …, 10 бракованных деталей и
подсчитать его математическое ожидание
и стандартное отклонение.
Результаты расчетов
вероятностей для х
= 0, 1, … , 10 представлены в таблице 6.1 и на
рисунке 6.2. Числовые характеристики
распределения равны:
=1,
= 0,95.
Таблица 6.1 −
Результаты расчетов для примера 6.3
|
Х |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0,349 |
0,387 |
0,194 |
0,057 |
0,011 |
0,001 |
0 |
0 |
0 |
0 |
0 |
Рисунок 6.2 −
Биноминальное распределение для n
= 10, p
= 0,1.
Пример 6.4.
Построить биноминальное распределение
для условий примера 6.3 при доле брака,
равной 0,5 и определить его числовые
характеристики.
Полученный
в результате расчетов ряд распределения
представлен в таблице 6.2, а график
распределения на рисунке 6.3.
Таблица 6.2 −
Результаты расчетов для примера 6.4
|
х |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
|
0,001 |
0,01 |
0,044 |
0,117 |
0,213 |
0,246 |
0,213 |
0,117 |
0,044 |
0,01 |
0,001 |
Числовые
характеристики полученного распределения
равны:
,
= 1,58.
Как видно из
представленных расчетных данных,
биноминальное распределение является
симметричным при p
= q
= 0.5, а при других значениях p
и q
– ассиметричным. Чем больше отклонение
от 0,5, тем больше асимметрия.
Рисунок 6.3 −
Биноминальное распределение для n=10,
p=0,5.
В практике
статистических расчетов используют
несколько способов подсчета вероятностей
случайных величин, распределенных по
биноминальному закону.
При небольшом
количестве наблюдений можно использовать
прямой расчет вероятности по формуле
(6.11). При большом количестве наблюдений
простой расчет по формуле становится
достаточно сложным. В таком случае
обычно используют таблицы интегральных
(кумулятивных) биноминальных вероятностей.
Такая таблица (Приложение А) определяет
вероятность получения r
или более успешных результатов при n
независимых испытаниях.
При подсчете
кумулятивных вероятностей используется
следующая формула:
.
(6.16)
Пусть, например,
р
= 0,15, n
= 20. Найти
вероятность того, что в этой выборке
окажется пять или более бракованных
деталей. В таблице из приложения A
находим столбец для вероятности р
= 0,15. Найдя
блок для n
= 20 на
пересечении строки для r
=5 и столбца
для р = 0,15
находим искомое число:
.
Таблица кумулятивных
вероятностей может быть также использована
для вычисления вероятностей следующих
событий: получение менее r
бракованных изделий и получение ровно
r
бракованных изделий.
Для определения
вероятности получения в выборке менее
r
бракованных
изделий используют выражение:
.
(6.17)
Вероятность
получить ровно r
бракованных изделий рассчитывают по
следующей формуле:
.
(6.18)
Пример 6.5.
Пусть вероятность брака в генеральной
совокупности составляет р
= 0,2. Найти вероятность того, что в выборке
объемом n
= 100 окажется ровно 12 бракованных деталей.
По формуле (6.18)
находим:
-
Распределение
Пуассона
Распределение
Пуассона
это самостоятельный функциональный
закон природы. Его применяют, если число
испытаний n
велико, а событие наступает очень редко,
т.е. значение p
мало.
Распределение
Пуассона аппроксимирует биноминальное
распределение следующим образом. Пусть
объем выборки n
очень большой (в пределе стремится к
бесконечности), а доля брака p
очень мала. С увеличением n
величина p
стремится к нулю, но так, чтобы произведение
pn
сохраняло постоянное значение:
(6.19)
В таком случае в
пределе при
вероятность
того, что бракованное изделие появится
ровно х
раз, находится следующим образом. На
основании (6.19) имеем:
.
(6.20)
Записываем на
основании биноминального распределения
вероятность появления х
бракованных деталей в выборке n:
.
(6.21)
Преобразуем
выражение (6.21) с использованием (6.20)
следующим образом:

Но:
,
,
.
Всилу этого:
.
И окончательно:
.
… (6.22)
На практике
распределение Пуассона можно использовать
вместо биноминального распределения
в случаях, если:
.
Для вычисления вероятностей распределения
Пуассона удобно пользоваться рекуррентной
формулой, которую легко можно вывести:
.
(6.23)
Пример 6.6.
В партии деталей имеется 3% брака. Какова
вероятность того, что при взятии из
партии выборки объемом 50 шт., в ней будет
находиться 0, 1, 2, 3, 4, 5, 6, 7 дефектных
деталей?
Здесь p
= 0,03, n
= 50, n∙p
= m
= 1,5.
Используя формулу
(6.22) получаем:
,
,
,
,
.
,
,
.
Графическое
представление полученных результатов
дано на рисунке:
Рисунок 6.4 –
Распределение количества бракованных
деталей
в выборке
Как видно из этого
рисунка распределение Пуассона является
ассиметричным. С возрастанием m
эта асимметричность уменьшается.
Числовые
характеристики распределения Пуассона
записываются следующим образом:
математическое
ожидание −
дисперсия −
.
стандартное
отклонение −
Таким образом,
видно, что для этого распределения
математическое ожидание численно равно
дисперсии. Поэтому когда в распределении
дискретной случайной величины
и
мало отличаются друг от друга, можно
уверенно говорить, что данное распределение
подчиняется закону Пуассона.
Так как распределением
Пуассона пользуются очень часто, особенно
в выборочных планах, то составлены
таблицы вероятностей. В справочной
литературе имеются таблицы двух видов.
Во первых, таблица
отдельных членов распределения
представленная в приложении Б. Каждая
ячейка этой таблицы является пересечением
столбца, которому соответствует
определенная величина m,
и строки для соответствующего значения
x.
В этой ячейке записывается численное
значение вероятности; полученное из
формулы (6.22).
Пример 6.7.
Используйте распределение Пуассона
для оценки вероятности наличия двух
дефектных изделий в выборке, содержащей
100 изделий и взятой из потока продукции,
в котором доля дефектных изделий
составляет 0,03.
Для этой задачи x
= 2, n
= 100, p
= 0,03. Находим
математическое ожидание:
.
Используя таблицу
распределения Пуассона в приложении
Б, находим столбец для m
= 3 и соответствующую этому m
строку для
x = 2.
В ячейке на их пересечении находим
ответ:
.
Во вторых, таблица
кумулятивных Пуассоновских вероятностей,
представленная в приложении В. В ячейках
этой таблицы записывается вероятность
того, что r
или более случайных событий содержится
в выборке, если среднее количество этих
событий в выборке составляет m:
.
(6.24)
Пример 6.8.
Для условий примера 6.7 определите
вероятность наличия в выборке не менее
двух бракованных деталей.
Не менее двух по
условию задачи – это означает два и
более:
.
В таблице кумулятивных Пуассоновских
вероятностей находим столбец m
= 3 и строку x = 2.
В ячейке на их пересечении читаем ответ:
-
Нормальный
закон распределения
В то время как
законы распределения биноминальный и
Пуассона применяются при работе с
дискретными данными, нормальный закон
распределения применяется при работе
с непрерывно изменяющими переменными.
Закон нормального распределения находит
большое применение во многих областях
человеческой деятельности. Этому закону
подчиняются многие непрерывные величины,
например, ошибки измерений, размер
обрабатываемой детали, вес булки хлеба,
рост человека и т.п.
Обоснование такому
широкому применению можно найти в
теореме, доказанной российским математиком
Ляпуновым. Она называется центральной
теоремой теории вероятности и объясняет,
почему многие случайные величины следуют
закону нормального распределения.
Следствие из этой
теоремы заключается в следующем. Если
случайная величина х
представляет собой сумму очень большого
числа взаимно независимых случайных
величин х1,
х2,
х3,
… хn,
влияние каждой из которых на всю сумму
ничтожно мало, то независимо от того,
каким законам распределения подчиняются
слагаемые
х1, х2,
х3,
… хn
сама величина х
будет иметь распределение вероятности
близкое к нормальному, и тем точнее, чем
больше число слагаемых.
В применении к
качеству это означает, что если какой
то показатель качества зависит от
большого числа независимых случайных
факторов, то даже не зная их можно
считать, что показатель качества
подчиняется нормальному закону
распределения. Например, предел прочности
листового проката из стали О9Г2С зависит,
в первую очередь, от химического состава,
структуры и наличия дефектов. В свою
очередь каждый из этих трех факторов
есть сумма ряда случайных независимых
величин. Так для химического состава
значение имеет содержание углерода,
марганца, кремния, серы и фосфора,
структура характеризуется соотношением
ферритной и перлитной фаз, характером
перлитной фазы, размером зерна и т.д.
Перечисляя так дальше, можно выделить
несколько десятков факторов, каждый из
которых имеет случайный характер.
Плотность вероятности
(дифференциальная функция распределения)
случайной величины х
непрерывного типа, подчиняющейся
нормальному закону распределения, имеет
следующий вид:

(6.25)
где
математическое ожидание распределения,
стандартное
отклонение.
Графически плотность
вероятности для нормального распределения
выражается в виде характерной кривой
холмообразного вида (рисунок 6.5).
Рисунок 6.5
Кривая плотности вероятности нормального
вида
Вершина кривой
лежит над абсциссой, соответствующей
математическому ожиданию. Кривая
симметрична, имеет форму колокола и
асимптотически приближается к оси
абсцисс. Имеется две точки перегиба с
координатами
и
.
Из выражения (6.25)
видно, что нормальное распределение
определяется двумя параметрами:
и
.
С изменениемформа кривой не меняется, но изменяется
ее положение относительно начала
координат (рисунок 6.6а). С изменениемположение кривой не меняется, но меняется
ее форма (рисунок 6.6б). С уменьшениемкривая становится более высокой, а ее
ветви сближаются, с увеличением
наоборот.
Функция распределения
нормально распределенной величины
запишется следующим образом:

(6.26)
В задачах качества
при статистических вычислениях удобнее
использовать приведенную нормальную
величину:
.
(6.27)
Для приведенной
нормальной величины математическое
ожидание равно нулю:
=0,
а стандартное отклонение единице:=1.
Плотность
распределения запишется в этом случае
следующим образом:
,
(6.28)
а функция
распределения:
.
(6.29)
а)
б)
Рисунок 6.6
Влияние параметров
и
на кривую нормального распределения.
Функции (6.28) и
(6.29) затабулированы в соответствующих
таблицах. В практических применениях
используется также дополнительная
функция:

(6.30)
Вероятность того,
что случайная величина будет находиться
в интервале между х1
и х2
запишется следующим образом:

(6.31)
где
.
Преобразуем (6.31)
следующим образом:
Интеграл

Лапласа, функции Лапласа или интеграла
вероятности. Величина интегралачисленно равна площади под нормированной
нормальной кривой распределения от 0
доu
(рисунок 6.7). Численные значения функции
приведены в виде таблицы в приложении
Г. Функция распределения нормированной
величиныu
также может
быть определена по этой таблице как:
.
(6.32)
Рисунок 6.7
Геометрический эквивалент функции
Лапласа
Так как кривая
симметрична, то
.
Если необходимо вычислить площадь между
u
и u
необходимо взять величину
.
Рассмотрим некоторые
случаи расположения значений приведенных
величин
относительно математического ожидания.
-
:
(Рисунок 6.8 а).
-
:
(Рисунок 6.8 б).
-
,
:
(Рисунок 6.8 в)
а) б) в)
Рисунок 6.8
Графическая интерпретация определения
вероятности
при различном расположении
относительно математического ожидания
Пример 6.9.
Необходимо
выяснить, как велика площадь, заключенная
между ординатами кривой распределения
х1=124
и х2=138,
если
=128
и=4.
Для решения этой
задачи необходимо, прежде всего, вычислить
нормированные значения величин:
,
.
По
таблице в приложении Г находим:
,
.
В связи с тем, что
лежат по разные стороны от средней
величины=0,
для получения искомой площади оба
полученных значения нужно сложить.
Таким образом, вероятность того, что
случайная величина лежит между значениямих1
и х2
равна:
.
Площадь
же под кривой распределения, заключенная
между этими координатами равна 83,51 %.
Ответ:
83,51 %.
Пример 6.10. Для
предыдущего примера определить, как
велика площадь между ординатами х1=122
и х2=126.
Находим:
,
,
,
,
Так
как здесь обе координаты лежат по одну
сторону от центральной точки, то найденные
значения Ф(u)
необходимо вычитать, а не складывать.
После
вычислений получаем, что значение
искомой площади равно 30,27 %.
Ответ:
30,27 %.
Пример 6.11.
Нормальное
распределение случайной величины имеет
следующие параметры:
=28
и=2.
Найти вероятность того, что случайная
величина принимает значение менее 22.
Для
решения этой задачи находим u:
Согласно
выражению (6.32):
.
Ответ: 0,0446.
Рассмотрим некоторые
цифры характерные для кривой нормального
распределения, которые можно получить
с использованием таблицы функции
.
В практических
задачах представляет интерес какое
количество случайных величин лежит в
диапазонах:
;
и
.
Расчеты, аналогичные проведенным выше
показывают следующее. 68,26 % случайных
величин, т.е. примерно 2/3 значений, лежат
в пределах между границамии
.
Остальная треть, т.е. 31,74 % наблюдений,
лежит за этими границами, а именно: 15,87
% правееи 15,87% левее
.
Границыи
охватывают 95,44 % всех значений, а вне их
находится 4,56 % (по 2,28 % левееи правее
).
Наконец, между трехсигмовыми границами
(и
)
находится 99,73 % всех наблюдений, т.е.
практически все. Только 0,27 %, т.е. 27 из
10000 находится за пределами этих границ.
В статистических
методах контроля качества особое
значение имеют границы
.
Если какое-то значение случайной величины
появляется за пределами этого участка,
то, скорее всего, что-то произошло с
процессом. Т. к. вероятность появления
такого события очень мала, следует
считать, что данное значение оказалось
слишком маленьким или слишком большим
не из-за случайного варьирования, а
из-за существенной помехи в самом
процессе, способной вызвать изменения
в характере распределения.
Участок, лежащий
внутри трехсигмовых границ, называют
областью статистического допуска
соответствующей машины или процесса.
-
Контрольные
вопросы
-
Какие типы
соединений вы знаете? -
Что такое
перестановки и как рассчитывается их
число? -
Что такое размещения
и как рассчитывается их число? -
Что такое сочетания
и как рассчитывается их число? -
Как должен быть
организован выборочный контроль, чтобы
его результаты могли быть описаны
гипергеометрическим распределением? -
Как рассчитывается
вероятность наличия бракованных деталей
в выборке для гипергеометрического
закона? -
Чем отличается
контроль без возвращения от контроля
с возвращением? -
В каких случаях
результаты контроля можно описывать
биномиальным законом распределения? -
Почему биномиальный
закон распределения получил такое
название? -
Как рассчитывается
вероятность наличия бракованных деталей
в выборке для биномиального закона? -
Чему равны числовые
характеристики биномиального
распределения? -
Какой характер
имеет биномиальное распределение
бракованных изделий при доле брака: а)
0,1; б) 0,5? -
Как рассчитывают
вероятность случайных величин,
распределенных по биноминальному
закону при небольшом количестве
наблюдений? -
Как рассчитывают
вероятность случайных величин,
распределенных по биноминальному
закону при большом количестве наблюдений? -
Что такое
кумулятивные биномиальные вероятности? -
Как используют
таблицу кумулятивных биномиальных
вероятностей для расчетов? -
В каких случаях
можно использовать распределение
Пуассона при выборочном контроле? -
Как рассчитывается
вероятность наличия бракованных деталей
в выборке для закона Пуассона? -
Чему равны числовые
характеристики распределения Пуассона? -
Какой характер
имеет распределение бракованных
изделий, подчиняющее закону Пуассона? -
Как рассчитывают
вероятность случайных величин,
распределенных по закону Пуассона, при
использовании таблиц отдельных членов
распределения? -
Как используют
таблицу кумулятивных Пуассоновских
вероятностей для расчетов? -
Чем вызвано широкое
распространение закона нормального
распределения? -
Как записывается
плотность распределения случайной
величины, подчиняющейся нормальному
закону распределения? -
Как записывается
уравнение для функции нормального
распределения случайной величины? -
Как изменяется
кривая плотности нормального распределения
при изменении математического ожидания
и неизменном стандартном отклонении? -
Как изменяется
кривая плотности нормального распределения
при изменении стандартного отклонения
и постоянном математическом ожидании? -
Чему равны
математическое ожидание и стандартное
отклонение для нормального распределения
нормированной случайной величины? -
Как записываются
выражения для функции распределения
и плотности вероятности нормированной
случайной величины? -
Чему равна
вероятность расположения случайной
величины в интервале между х1
и х2,
записанная через функцию Лапласа? -
Как находится
численное значение вероятности
расположения случайной величины в
интервале между х1
и х2
при помощи таблиц? -
Чему равна
вероятность расположения случайной
величины в диапазоне
?
-
Чему равна
вероятность расположения случайной
величины в диапазоне
?
-
Чему равна
вероятность расположения случайной
величины в диапазоне
?
-
Задачи для
самостоятельного решения
Биномиальный
закон распределения.
-
Вычислить
следующие биномиальные коэффициенты:
-
Какова вероятность
того, что дефектные изделия не будут
обнаружены в случайной выборке,
содержащей семь образцов из партии
изделий, в которой имеется 8 % брака? -
Какова вероятность
обнаружения шести бракованных изделий
в партии из пятидесяти штук, если
вероятность брака в генеральной
совокупности составляет 5 %? -
Выборка, состоящая
из двух микросхем, извлечена из партии,
в которой было десять микросхем. Если
три из них дефектные, то какова вероятность
того, что в выборке окажется одна
дефектная микросхема? -
Вычислите числовые
характеристики биноминальных
распределений со следующими параметрами:
а) р
= 0,1, n
= 20; б) р
= 0,05, n
= 500; в) р
= 0,2, n
= 10. -
Какова вероятность
того, что в выборке из 20 изделий окажется
более одного бракованного изделия,
если доля брака составляет 4 %? -
Какова вероятность
того, что в выборке из 50 изделий окажется
ровно три бракованных, если доля брака
в партии составляет 7 %? -
При бросании
монеты 100 раз, какова вероятность
выпадения орла: а) более 50 раз; б) ровно
50 раз. -
Известно, что 3 %
булок хлеба, выпеченных в печи хлебозавода,
имеют брак. Вычислите вероятность того,
что в выборке из 50 штук имеется 0, 1, 2, 3,
4, 5 бракованных булок. Постройте
графическую зависимость.
Закон распределения
Пуассона
-
В
партии деталей имеется 2 % брака. Из
партии взята выборка объемом 100 деталей.
Найти вероятность того, что в выборке
будут находиться 0, 1, 2, 3, 4 дефектных
деталей. Построить график распределения
вероятностей. -
Определите
числовые характеристики Пуассоновского
распределения, если p
= 0,04; n
=
96. -
В
большом объеме деталей, упакованных в
коробке, среднее число бракованных
деталей составляет четыре. Определите
вероятность того, что в коробке
содержится:
а) ни одной
бракованной детали;
б) более пяти
бракованных деталей;
в) по меньшей мере,
три бракованные детали.
-
В
конверторном цехе металлургического
завода в среднем две плавки стали из
100 выходят за пределы допусков марочного
химического состава. Для выполнения
очередного заказа требуется металл
десяти плавок. Определите вероятность
того, что весь металл, взятый для
выполнения этого заказа, имеет марочный
химический состав. -
Полагая
вероятность нарушения паяного соединения
на этапе сборки прибора равной 0,04, и
пользуясь распределением Пуассона,
найдите вероятность того, что из 100
приборов:
а)
по крайней мере, шесть будут иметь
нарушения соединения;
б) по крайней мере,
98 не будут иметь брака.
-
Постройте
распределение вероятностей наличия в
выборке из 100 деталей следующего
количества бракованных: 0, 1, 2, 3, 4, 5, 6 при
условии, что вероятность брака составляет:
а) р
=
0,01; б) р
= 0,02; в) р
= 0,03; г) р
= 0,04.
Нормальный
закон распределения
-
Определить
площадь между ординатами:
а)
и
;
б)
и
;
если
и
.
-
Сроки службы ламп
накаливания распределены нормально,
причем средний срок службы и среднее
квадратичное отклонение срока службы
таких ламп равны соответственно 1050 и
190 часов. Определить процентное содержание
ламп сроком службы менее 750 часов. -
Для условий
предыдущей задачи при
=1620
часов и=62
часа вычислить процент лампочек, которые
скорее всего перегорят:
а) менее, чем через
1500 часов;
б) более, чем через
1750 часов.
-
Какая доля
генеральной совокупности, подчиняющейся
нормальному закону распределения,
лежит между следующими значениями:
а)
и
;
б)
и
;
в)
и
.
-
Изделие должно
иметь показатель качества, лежащий
между 41 и 46. Требуется, чтобы только 2 %
изделий имели показатель качества
менее 41 и только 8 % более 46. Найти
и
распределения.
-
Требуется
расфасовочная машина для наполнения
мешков с пределами отклонений по весу
от 750 г до 760 г. Допускается, что 2 %
мешков будут иметь вес менее 750 г, а
более 6% мешков
более 760 г. Исходя их нормального
закона распределения, определите
и
для машины, удовлетворяющей этим
требованиям. -
Хлебозавод
выпускает сухари в упаковке. Вес пачки
не должен быть меньше 170 г. При расчете
сырья за основу берут вес, равный 180 г.
При статистическом исследовании 500
пачек сухарей оказалось, что
=176
г и=3,3
г. Ответьте на вопросы:
а) как часто вес
пачки будет меньше минимально допустимого;
б) на сколько
граммов надо увеличить расчетный вес,
чтобы вес пачки не оказался меньше
допустимого.
-
Шарики для
подшипников качения делятся на классы
точности. Для шариков третьего класса
точности диаметром 8 мм допустимо
отклонение
0,001
мм. Пусть станок настроен на 8,0 мм, а
среднее квадратичное отклонение
составляет 0,003 мм. После изготовления
партия шариков сортируется по размерам.
Сколько шариков необходимо изготовить,
чтобы выполнить заказ на 1000 шариков
третьего класса точности.
-
СТАТИСТИЧЕКАЯ
ПРОВЕРКА ГИПОТЕЗ
-
Общая постановка
задачи
Статистическая
проверка гипотез применяется для того,
чтобы использовать полученную при
выборочном контроле партии изделий
информацию для выработки суждения об
особенностях генеральной совокупности,
например законе ее распределения, или
параметрах.
На первом этапе,
используя общие представления о
неизвестном распределении и его
параметрах, формируется статистическая
гипотеза. Она называется нулевой
(основной) гипотезой и обозначается
символом
или
.
Примеры записей:
−означает допущение
(гипотезу), что
есть функция распределения генеральной
совокупности.
−означает
допущение, что принятое значение
есть математическое ожидание генеральной
совокупности.
Затем, с помощью
статистических методов или критериев
для проверки гипотезы, устанавливается,
соответствуют ли взятые из выборки
данные выдвинутой гипотезе или нет,
т.е. нужно ли принять выдвинутую гипотезу,
или отвергнуть ее.
-
Некоторые
выборочные характеристики,
применяемые при
проверке гипотез
При статистической
проверке гипотез используют ряд
характеристик и их распределений.
Назовем их без вывода и доказательств.
-
Выборочная
нормированная характеристика
удовлетворяет
нормированному нормальному распределению
со следующими параметрами: математическое
ожидание равно нулю, дисперсия равна
единице.
-
Выборочная
характеристика:
;
где S2
– эмпирическая дисперсия:
.
Таким образом
.
Плотность
распределения
характеристики записывается следующим
образом:
(при
> 0),
где
,
−гамма-функция
(интеграл Эйлера):
,
где m
= n
1 – число степеней свободы. Оно равно
разности между числом наблюдений n
и числом независимых параметров
.
На рисунке 7.1
представлены значения плотности
распределения
дляn
= 7 и n
= 4.
Рисунок 7.1 −
— распределение
Плотность
распределения
ассиметрична, но приn→∞
приближается к плотности нормального
распределения.
Функция
распределения запишется следующим
образом:
Эта функция играет
важную роль в проверке статистических
гипотез.
-
Выборочная
характеристика (функция) t.
Из выборочных
характеристик
иS2
образуется новая вторичная характеристика:
.
Она имеет непрерывную
функцию распределения с плотностью:
для -∞ < x
< ∞,
где m
= n
1;

множитель, зависящий только от числа
степеней свободы m;
−гамма-функция
(интеграл Эйлера).
Эта плотность
вероятности получена У.С. Госсетом и
названа по его псевдониму (Student)
плотностью распределения «Стьюдента»
или t-распределением
с n
− 1 степенями свободы.
Из формулы видно,
что плотность вероятности t-распределения
симметрична относительно нулевой точки
t
= 0. Кривая
тем более полога, чем меньшеm.
При m→∞
(n→∞)
Кривая
переходит в кривую нормального
распределения (рисунок 7.2).
Функция t-распределения
находит широкое применение при
статистической оценке параметров
распределения и при статистической
проверке гипотез.
1
m=1;
2
m=9;
3
кривая нормального распределения
Рисунок 7.2 −
t-распределение
-
F-распределение
Фишера.
Пусть имеются две
независимые выборки объемом n1
и n2,
средние значения которых равны
соответственно
и
.
Для этих выборок определяют оценкиS12
и S22
дисперсий генеральных совокупностей:
,
;
для которых числа
степеней свободы равны соответственно:
m1=n1−1
и m2=n2−1.
Предполагается,
что обе генеральные совокупности, из
которых сделана выборка, распределены
нормально с параметрами:
,
,
,
и что
=
.
Из условия
вводится характеристика (функция):

Эта функция имеет
непрерывную функцию распределения с
плотностью:дляF≥0,
где
зависит только отm1
и m2;

График
представлен на рисунке 7.3.
Рисунок 7.3 − F—
распределение.
F-распределение
находит применение при проверке гипотез
и, в первую очередь, при проверке гипотез
о дисперсиях.
-
Проверка гипотезы
о среднем значении нормально
распределённой генеральной совокупности
при известной дисперсии
Будем исходить из
предпосылки, что функция распределения
генеральной совокупности имеет нормальное
распределение с параметрами
и
.
Для пояснения
постановки задачи рассмотрим пример.
Пример.
В цехе токарных автоматов завода
выпускают поршневые кольца. Из суточной
продукции одного станка случайным
образом отбирают 90 колец и микрометром
измеряют их толщину. Значение среднего
арифметического выборки равно
мм. Дисперсия толщины колец для станка
известна и составляетмм2.
Можно ли на основании этих результатов
сделать вывод о том, что станок постоянно
обеспечивает заданный номинальный
размер 12,000 мм, на который он был
настроен в начале смены.
В нашем случае
вопрос об обеспечении номинального
размера 12,000 мм предполагает проверку
гипотезы о том, что математическое
ожидание генеральной совокупности
составляет
мм.
Итак, выдвигаем нулевую гипотезу:,
гдемм.
По результатам
выборочного контроля толщины имеем
отклонение полученного среднего от
математического ожидания, равное:
мм. Какой вывод можно сделать на основании
данного отклонения. Является ли оно
достаточно малым, чтобы принять гипотезу
и рассматривать
90 выполненных измерений, как выборку
из генеральной совокупности с
мм, или нет? В общем виде, последовательность
рассуждений по проверке этой гипотезы
в нашем случае выглядит следующим
образом.
Известно, что
выборочная характеристика
имеет
нормальное распределение с параметрамии
,
если
генеральная совокупность имеет нормальное
распределение с параметрами
и
.
Таким образомэто случайная величина, которая может
принимать любое значение на осих,
согласно своему закону распределения.
Но при этом, чем дальше
от среднего значения
,
тем это событие менее вероятно.
Из этого ясно, что
любое принятое решение о величине
полученного отклонения должно иметь
вероятностный характер. Примем, в
качестве условия отказа от нулевой
гипотезы, выполнение следующего
неравенства:
,
(7.1)
где
− вероятность события, состоящего в
том, что абсолютная величина отклонения
среднего арифметического выборокот
гипотетического среднего генеральной
совокупностиравна или более значения 0,0075;
−число, принятое
в качестве заданного предела, которое
называют вероятностью
ошибки или
уровнем
значимости.
Выбор вероятности
ошибки
зависит от поставленной задачи. В
математической статистике используют
следующие значения:.
При статистическом контроле качества
чаще всего используют величину.
Эта величина соответствует отклонению
равному плюс – минус.
Вероятность
запишется следующим образом:
(7.2)
Таким образом,
если событию
отвечает
вероятность, меньшая или равная заданному
пределу,
то отклонениеназывается значимым или статистическим
достоверным. Значимое значение ведет
к отклонению гипотезы.
Если же вероятность рассматриваемого
события больше,
то отклонение является случайным или
статистически недостоверным, и гипотеза
принимается.
Однако это еще не
свидетельствует истинности гипотезы
,
а лишь означает, что выборочный результат
не противоречит выдвинутой гипотезе.
Такой метод проверки
нулевой гипотезы
называют критерием значимости, т.к.
помимо гипотезыдругие гипотезы не исследуются.
Из сказанного
ясно, что в математической статистике
абсолютно достоверные утверждения
невозможны, поскольку приходится иметь
дело со случайными величинами, а,
следовательно, с вероятностями. Суждение
о принятии или отклонении выдвинутой
гипотезы может быть высказано всегда
лишь с некоторой вероятностью, с
определенной степенью достоверности.
Это не исключает
возможность ошибки в оценке результатов
измерения. Если задан уровень значимости
,
то вслучаях результат измерений может быть
оценен неверно, а это значит, что будет
отвергнута правильная гипотеза. В этом
случае говорят об ошибке первого рода.
Вероятность того,
что гипотеза не будет отвергнута, хотя
она является ложной (ошибка второго
рода), зависит от истинного значения
параметра
генеральной совокупности и не может
быть указана по критерию значимости.
Вероятность ошибки второго рода
обозначают.
В этом случае нужно было бы противопоставить
нулевой гипотезе альтернативную гипотезу
и исследовать качество теста, которое
определяется вероятностью отклонения
нулевой гипотезы, если она неверна, и
зависит от параметра.
Эти вопросы изучает общая теория тестов.
Пусть в нашем
примере
.
Рассчитаем величину вероятности.
Для этого используем выборочную
характеристику
.
Как уже сказано выше, она имеет нормальное
распределение
с параметрами
= 0 и
= 1. Проводя соответствующие подстановки,
получаем:

где F(Z)
– функция распределения нормированного
нормального распределения.
Так как в нашем
случае
,
тои, следовательно
.
Величину
находим по таблице нормированной функции
распределения (приложение Д):.
После подстановки полученных чисел в
выражение (7.3) получаем:
.
Полученное значение
вероятности меньше выбранной величины
вероятности ошибки:
.
Таким образом,
отклонение 0,075мм для рассматриваемой
задачи является значимым, вследствие
чего гипотеза
мм
отвергается. Это означает, что выборка
из 90 колец взята не из генеральной
совокупности смм. Следовательно, станок не обеспечивает
номинального размера и следует проверить
его наладку.
На практике проверку
гипотезы проводят несколько иначе,
сохраняя изложенный выше метод. Для
этого находят критическое отклонение
,
при котором гипотеза отвергается из
следующего соотношения:
.
(7.4)
После некоторых
преобразований получаем:

откуда:
.
(7.6)
Подставляя в
полученное выражение (7.6) значение
по таблице нормированной функции
распределения (приложение Д) находим
величину критического отклонения для
заданного уровня значимости.
Выражение (7.5) может
быть записано с использованием функции
Лапласа
:
,
(7.7)
и
,
.
(7.8)
В этом случае
значение
находят по таблицам функции Лапласа
(приложение Г).
При выполнении
условия
нулевая гипотеза
отвергается, т.е. расхождение между
выборочным средними гипотетическим средним генеральной
совокупностиявляется значимым. При выполнении
условиягипотеза
принимается.
Для нашего примера
,
а.
Т.о. критическое отклонение больше по
величине назначенного уровня значимостии гипотеза
отвергается.
Область выборочной
характеристики
,
влекущая за собой отклонение гипотезы,
называется критической областью
отклонения гипотезы, или критической
областью гипотезы,
и обозначается символомК.
Она определяется следующим неравенством:
,
(7.9)
или поскольку:
,
,
.
(7.10)
Критическая область
К
изображена на рисунке 7.4. Заштрихованные
участки над К
в сумме дают
всей площади под кривой нормального
распределения. Т.о. критическая область
находится симметрично по обе стороны
от нуля с границамии
.
При этом по обе стороны отсекаетсявсей площади нормального распределения.
В таком случае речь идет о двухстороннем
ограничении.
Рисунок 7.4 −
Критические области гипотезы
В некоторых случаях
интерес представляет одностороннее
ограничение. Критическая область
гипотезы
выбирается по одну сторону кривой
нормального распределения (либо справа
от среднего значения, либо слева).
Например, если малые значениянесущественны, то отклонение гипотезы
вводят при больших положительных
расхождениях междуи
.
Критическая область (обозначим ее через
К΄) определяется при этом неравенством:
,
или
,
(7.11)
где
− критическое отклонение, при котором
гипотеза отвергается.
Его значение
получается из соотношения:
,
откуда:
.
Гипотеза отвергается,
если для рассчитанного по выборке
значения Ζ выполняется неравенство:
.
(7.12)
Резюме.
-
Для проверки
предположения о среднем значении
нормально распределенной совокупности
выдвигается статистическая гипотеза:
.
-
Для проверки
гипотезы из генеральной совокупности
отбирают выборку объемом n. -
Определяют числовые
характеристики этой выборки
и
-
Вычисляют величину
критерия
.
Дисперсия генеральной совокупностипри этом должна быть известна. При
достаточно большомn
можно считать
.
-
Принимается
величина вероятности ошибки
.
-
Принимается
решение о характере ограничения:
одностороннее или двустороннее. -
Находят границы
критической области К
(или К΄):.
-
Формулируется
критерий следующим образом: при
или
гипотеза
отвергается; а при
принимается. В последнем случае
выборочное значениене противоречит гипотезе.
-
Проверка гипотезы
о среднем значении нормально
распределённой
генеральной совокупности
при неизвестной
дисперсии
Для проверки
гипотезы
с использованием характеристики
необходимо знать значение дисперсии
генеральной совокупности. Для этого
надо либо проводить предварительные
исследования, либо заменитьна выборочную дисперсию
по выборке большого объема. При этом
возникает вопрос, когда объем выборкиn
можно считать достаточно большим, чтобы
принять
.
Для выборок малого
объема используют характеристику t:
,
(7.13)
где
,
(7.14)
Эта выборочная
характеристика t
имеет распределение Стьюдента с m
= n-1
степенями свободы.
Критическая
область, т.е. область неприятия гипотезы
,
для двухстороннего ограничения в этом
случае определяется неравенством:
,
(7.15)
где величину
получают из соотношения
.
(7.16)
Преобразуем это
уравнение, с учетом того, что f(t)
– симметричная функция относительно
нуля (рисунок 7.2):
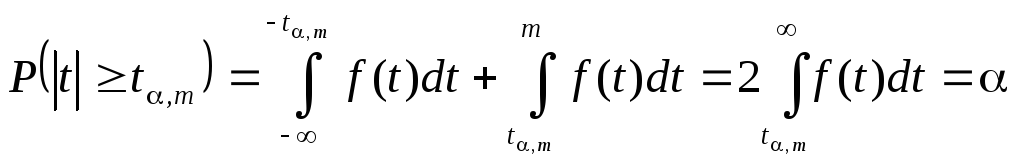
(7.17)
откуда:
.
(7.18)
Эта формула является
определяющей для нахождения
.
В справочной литературе имеются следующие
таблицы:
-
Таблица вероятностей
.
-
Таблица значений
для заданных чиселm
и a,
представленная в приложении Е.
Пример:
а) m
= 10; a
= 0,05; = 2,23;
б) m
= 4; a
= 0,05; = 2,78;
в) m
= 120; a
= 0,05; = 1,98;
г) m
= ;
a
= 0,05; = 1,96;
Считают, что при
m
>
120:
.
(7.19)
При одностороннем
ограничении критическая область
определяется неравенством:
,
или
.
(7.20)
Величины
можно взять из той же таблицы приложения
Е с учетом того, что,
или(см. рисунок 7.5)
Пример. Косозубая
шестерня имеет номинальный диаметр
90,018 мм. Измерялась выборка объемом
10 шестерен. Результаты обработки
полученных данных следующие:
= 90,016 мм,
=30μкм2,
= 5,48μкм.
Необходимо проверить
гипотезу:
= 90,018 дляa
= 0,05.
Рисунок 7.5 −
Критические области распределения
Стьюдента
По таблице приложения
Е для m
= 10 – 1 = 9
находим что
=2,26.
Посчитываем:
,т.е.
Сравнивая
и
,
получаем:.
Таким образом, нулевая гипотеза
принимается, т.е. станок обеспечивает
номинальный размер 90,018 мм.
-
Проверка гипотезы
о значениях двух средних
из нормально
распределенных генеральных совокупностях
-
Случай
зависимых выборок.
На
практике часто возникает необходимость
сравнивать два различных технологических
процесса, два метода обработки и т.п.
Для этого у изделия измеряют один и тот
же признак и рассчитывают статистические
характеристики. Как правило, удобнее
сравнивать средние значения.
Пример.
Необходимо сравнить два микрометра,
относительно их измерительных свойств.
Для этого измеряют
попарно диаметр 25 осей. Получают
результаты:
(i
= 1, 2,…, n)
микрометром №1 и
(i
= 1, 2,…, n)
микрометром №2.
Эти выборки называют
зависимыми или связанными, т.к. диаметр
каждой из n
= 25 осей измерялся как первым, так и
вторым микрометром. Поэтому, индивидуальные
значения результатов измерений попарно
взаимосвязаны.
Пусть
и
− выборки из нормально распределенных
генеральных совокупностей с характеристиками
и
соответственно.
Считаем, что
и
не зависят от i.
Проверяется нулевая
гипотеза : для i
= 1, 2,…, n,
т.е. попарное совпадение средних
генеральных совокупностей. При этом
значения
могут для разных i
различаться.
Чтобы проверить
гипотезу
для каждой пары измерений вычисляют
разность
(i
= 1, 2,…, n).
Полученный ряд разностей считается
выборкой объема n,
для которой определяют числовые
характеристики:
и
Если сформулированная
гипотеза верна, то ряд значений
является выборкой объемаn
из нормально распределенной генеральной
совокупности, со средним значением
и дисперсией ,
которая неизвестна.
Воспользуемся
поэтому выборочной характеристикой которая имеет
распределение Стьюдента с m
= n
− 1 степенями свободы.
Предельное значение
для критической области
находится из таблицы в приложении Е.
Если,
то гипотеза отвергается.
Для нашего примера:
мм,
мм, .
Считая, что a
= 0,01, находим
= 2,8.
Таким образом
и гипотезу отвергаем. Микрометры № 1 и
2 не обеспечивают одинаковую точность
измерений.
-
Случай
независимых выборок.
Пример.
Необходимо сравнить две марки сталей
А и В по пределу текучести .
Испытывается 145 (n1)
образцов стали А и 200 образцов (n2)
стали В. В общем случае n1
≠ n2.
По полученным
значениям средних арифметических
выборок необходимо решить, различаются
ли эти стали по величине предела
текучести.
Предполагаем, что
оба ряда измерений являются выборками
из двух нормально распределенных
генеральных совокупностей с характеристиками
соответственно ,
,
и .
Пусть кроме того выполняется равенство
.
При этом дисперсия может быть
неизвестна.
Допущение о
равенстве дисперсий, проверяется в свою
очередь гипотезой, о чем речь пойдет
дальше. В случае, если ,
описываемый метод проверки не годится.
Выдвигаем гипотезу
.
При проверке этой
гипотезы используют t—распределение
Стьюдента с
степенями свободы:
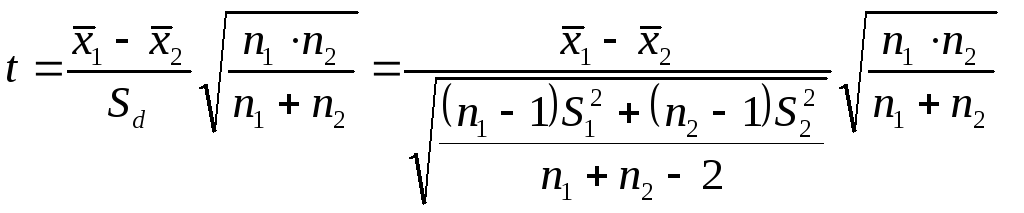
(7.21)
где
− средние арифметические независимых
выборок,
−их выборочные
дисперсии.
Таким образом, по
заданному уровню значимости (вероятности
ошибки) a
при
степенях свободы можно по таблице из
приложения
Е найти значение
.
В этом случае статистический критерий
(сокращенно его называют двойнымt—
критерием) приобретает следующий вид:
при
гипотеза
отвергается, при
– принимается.
Для нашего примера
получены следующие параметры выборок:
Сталь А:.
Сталь В: .
Подставляя в (5.22)
численные значения, получаем:

Для α
= 0,01 и m
= 343 степеней свободы
.
Таким образоми гипотеза
отвергается, т.е. сталь А имеет более
высокий предел текучести, чем сталь В.
Если объем
независимых выборок одинаков, т.е. n1
= n2.,
то формула (5.22) упрощается:

(7.22)