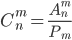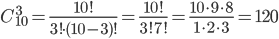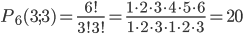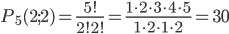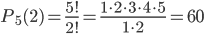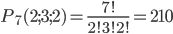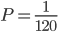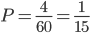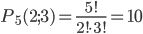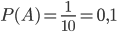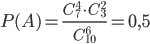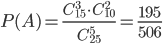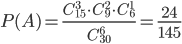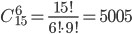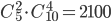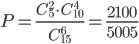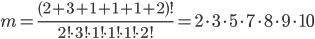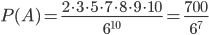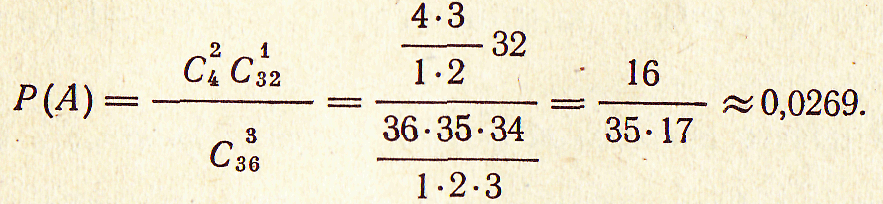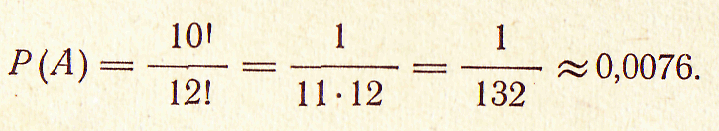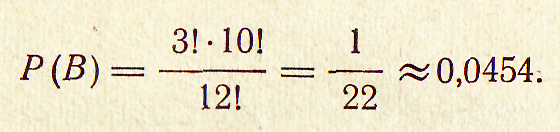Как найти вероятность если буквы одинаковые - Исправление недочетов и поиск решений вместе с Examum.ru

Решение задачи о карточках с буквами

Задача 8. На каждой из пяти одинаковых карточек напечатана одна из следующих букв: «а», «м», «р», «т», «ю». Карточки тщательно перемешаны. Найти вероятность того, что на четырех вынутых по одной карточке можно прочесть слово «юрта».

Решение: Используем классическое определение вероятности: $P=m/n$, где $m$ — число исходов, благоприятствующих осуществлению события, а $n$ — число всех равновозможных элементарных исходов.

$n = 5 cdot 4 cdot 3 cdot 2 = 120$ способов, так как первую карточку (букву) можно вытянуть (выбрать) 5 способами (так как всего карточек пять), вторую — 4 (осталось к этому шагу четыре), третью — 3 и четвертую — 2 способами.

$m = 1$, так как искомая последовательность карточек «ю», потом «р», потом «т», потом «а» только одна.

Получаем вероятность $P = 1/120$.

Ответ: 1/120.

Источник

Комбинаторика и вероятность

Комбинаторика изучает способы подсчета числа элементов в конечных множествах. Формулы комбинаторики, используют при непосредственном вычислении вероятностей.
Множества элементов, состоящие из одних и тех же различных элементов и отличающиеся друг от друга только их порядком, называются перестановками этих элементов. Число всевозможных перестановок из n элементов обозначают через 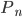P_n , и это число равно n! (читается «эн-факториал»):
(P_n=n) (1.3.1)
где
. (1.3.2)

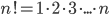
З а м е ч а н и е 1. Для пустого множества принимается соглашение: пустое множество можно упорядочить только одним способом; по определению полагают 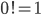0! = 1 .

Размещениями называют множества, составленные из n различных элементов по m элементов, которые отличаются либо составом элементов, либо их порядком. Число всех возможных размещений определяется формулой
. (1.3.3)

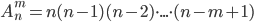
Сочетаниями из n различных элементов по m называются множества, содержащие m элементов из числа n заданных, и которые отличаются хотя бы одним элементом. Число сочетаний из n элементов по m обозначают: 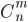C_n^m или (^n_m) . Это число выражается формулой

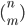
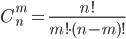
$C_n^m=displaystylefrac{n!}{m!cdot (n-m)!}$ . (1.3.4)

З а м е ч а н и е 2. По определению полагают 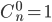C_n^0=1 .

Для числа сочетаний справедливы равенства:
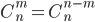
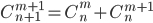
$C_n^m=C_n^{n-m}$ , $C_{n+1}^{m+1}=C_n^m+C_n^{m+1}$ , (1.3.5)
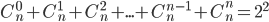
$C_n^{0}+C_n^1+C_n^2+...+C_n^{n-1}+C_n^n=2^2$ . (1.3.6)

Последнее равенство иногда формулируется в виде следующей теоремы о конечных множествах:
Число всех подмножеств множества, состоящего их n элементов, равно 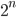2^n .
Отметим, что числа перестановок, размещений и сочетаний связаны равенством

$C_n^m=displaystylefrac{A_n^m}{P_m}$

З а м е ч а н и е 3. Выше предполагалось, что все n элементов различны. Если же некоторые элементы повторяются, то в этом случае множества с повторениями вычисляют по другим формулам.

Например, если среди n элементов есть 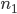n_1 элементов одного вида, n_2 элементов другого вида и т .д., то число перестановок с повторениями определяется формулой
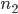
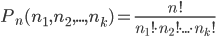
$P_n(n_1,n_2,...,n_k)=displaystylefrac{n!}{n_1!cdot n_2!cdot ... cdot n_k!}$ (1.3.7)
где .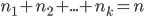

Число размещений по m элементов с повторениями из n элементов равно
n^m , то есть
(A_n^m) _{с повт} =n^m (1.3.8)
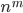
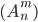
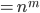
Число сочетаний с повторениями из n элементов по m элементов равно числу сочетаний без повторений из n + m — 1 элементов по m элементов, то есть
(C_n^m) _{с повт} $=?_{n+m-1}^m$ . (1.3.9)

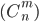
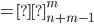
При решении задач комбинаторики используют следующие правила.

Правило суммы. Если некоторый объект А может быть выбран из множества объектов m способами, а другой объект В может быть выбран n способами, то выбрать либо А, либо В можно m + n способами.

Правило произведения. Если объект А можно выбрать из множества объектов m способами и после каждого такого выбора объект В можно выбрать n способами, то пара объектов (А, В) в указанном порядке может быть выбрана 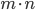mcdot n способами.

Классическая схема подсчета вероятностей пригодна для решения ряда сугубо практических задач. Рассмотрим, например, некоторое множество элементов объема N. Это могут быть изделия, каждое из которых является годным или бракованным, или семена, каждое из которых может быть всхожим или нет. Подобного рода ситуации описываются урновой схемой: в урне имеется N шаров, из них М голубых, (N — M) красных.

Из урны, содержащей N шаров, в которой находится М голубых шаров, извлекается n шаров. Требуется определить вероятность того, что в выборке объема n будет обнаружено m голубых шаров. Обозначим через А событие «в выборке объема n имеется m голубых шаров», тогда
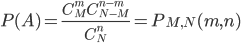
$P(A)=displaystylefrac{C_M^mC_{N-M}^{n-m}}{C_N^n}=P_{M,N}(m,n)$ (1.3.10)

Пример 1. Сколькими различными способами можно выбрать три лица на три различные должности из десяти кандидатов?

Решение. Воспользуемся формулой (1.3.3). При n = 10, m = 3 получаем
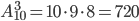
$A_{10}^3=10cdot 9cdot 8=720$ .

Пример 2. Сколькими различными способами могут разместиться на скамейке 5 человек?

Решение. Согласно формуле (1.3.1) при n=5 находим
P₅ =5!=1·2·3·4·5=120.

Пример 3. Сколькими способами можно выбрать три лица на три одинаковые должности из десяти кандидатов?

Решение. В соответствии с формулой (1.3.4) находим
$C_{10}^3=displaystylefrac{10!}{3!cdot(10-3)!}=frac{10!}{3!7!}=frac{10cdot 9cdot 8}{1cdot 2cdot 3}=120$

Пример 4. Сколько различных шестизначных чисел можно записать с помощью цифр 1; 1; 1; 2; 2; 2?

Решение. Здесь нужно найти число перестановок с повторениями, которое определяется формулой (1.3.7). При k =2, n₁ = 3, n₂ = 3, n=6 по этой формуле получаем
$P_6(3;3)=displaystylefrac{6!}{3!3!}=frac{1cdot 2cdot 3cdot 4cdot 5cdot 6}{1cdot 2cdot 3cdot 1cdot 2cdot 3}=20$

Пример 5. Сколько различных перестановок букв можно сделать в словах: замок, ротор, топор, колокол?

Решение. В слове замок все буквы различны, всего их пять. В соответствии с формулой (1.3.1) получаем P₅ = 5! = 1·2·3·4·5 = 120. В слове ротор, состоящем из пяти букв, буквы p и o повторяются дважды. Для подсчета различных перестановок применяем формулу (1.3.7). При n = 5, n₁ = 2, n₂= 2 по этой формуле находим

$P_5(2;2)=displaystylefrac{5!}{2!2!}=frac{1cdot 2cdot 3cdot 4cdot 5}{1cdot 2cdot 1cdot 2}=30$

В слове топор буква о повторяется дважды, поэтому
$P_5(2)=displaystylefrac{5!}{2!}=frac{1cdot 2cdot 3cdot 4cdot 5}{1cdot 2}=60$

В слове колокол, состоящем из семи букв, буква к встречается дважды, буква о — трижды, буква л — дважды. В соответствии с формулой (13.7) при n = 7, n₁= 2, n₂= 3, n_з = 2 получаем
$P_7(2;3;2)=displaystylefrac{7!}{2!3!2!}=210$

Пример 6. На пяти одинаковых карточках написаны буквы И, К, М, Н, С. Карточки перемешиваются и наугад раскладываются в ряд. Какова вероятность того, что получится слово МИНСК?

Решение. Из пяти различных элементов можно составить Р5 перестановок:
. Значит, всего равно возможных исходов будет 120, а благоприятствующих данному событию — только один. Следовательно,
$P=frac{1}{120}$

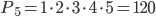
Пример 7. Из букв слова ротор, составленного с помощью разрезной азбуки, наудачу последовательно извлекаются 3 буквы и складываются в ряд. Какова вероятность того, что получится слово тор?

Решение. Чтобы отличить одинаковые буквы друг от друга, снабдим их номерами: p₁, p₂, 0₁, 0₂. Общее число элементарных исходов равно: 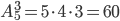. Слово ротор получится в случаях (то₁р₁, то₁р₂, то₂р₁, то₂р₂). Искомая вероятность равна $P=frac{4}{60}=frac{1}{15}$

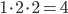
При подсчете числа благоприятных случаев здесь воспользовались правилом произведения: букву m можно выбрать одним способом, букву о — двумя, букву р — двумя способами.

Пример 8. На шести одинаковых по форме и размеру карточках написаны буквы слова талант — по одной букве на каждой карточке. Карточки тщательно перемешаны. их вынимают наудачу и располагают на столе одна за другой. Какова вероятность снова получить слово талант?

Решение. Занумеруем карточки с буквами:

1	2	3	4	5	6
а	а	л	н	т	т

Слово т а л а н т (513246) не изменится, если буквы а переставить местами, но по расположению карточек получится иная комбинация: т а л а н т (523146). Если в каждой из этих двух комбинаций то же проделать с буквой т, то получим еще 2 различные комбинации карточек со словом талант. Значит, появлению слова талант благоприятствуют 4 элементарных исхода. Общее число равно возможных элементарных исходов равна числу перестановок из 6 элементов: n = 6! = 720. Следовательно, искомая вероятность

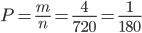
$P=frac{m}{n}=frac{4}{720}=frac{1}{180}$ .

З а м е ч а н и е. Эту вероятность можно найти и с помощью формулы (1.3.7), которая при n = 6, n₁ = 1, n₂ = 1, n_з = 2, n₄ = 2 принимает вид:

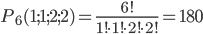
$P_6(1;1;2;2)=displaystylefrac{6!}{1!cdot 1!cdot 2!cdot 2!}=180$ . Таким образом, Р = 1/180.

Пример 9. На пяти одинаковых карточках написаны буквы: на двух карточках л, на остальных трех и. Выкладывают наудачу эти карточки в
ряд. Какова вероятность того, что при этом получится слово лилии?

Решение. Найдем число перестановок из этих пяти букв с повторениями.
По формуле (1.3.7) при n = 5, n₁ = 2, n₂ = 3 получаем
$P_5(2;3)=displaystylefrac{5!}{2!cdot 3!}=10$
Это общее число равновозможных исходов опыта, данному событию А — «появление слова лилии» благоприятствует один. В соответствиис формулой (1.2.1) получаем

$P(A)=frac{1}{10}=0,1$

Пример 10. В партии из 10 деталей 7 стандартных. Найти вероятность
того, что среди 6 взятых наудачу деталей 4 стандартных.

Решение. Общее число возможныIx элементарных исходов испытания равно числу способов, которыми можно извлечь 6 деталей из 10, то есть числу сочетаний из 10 элементов по 6 элементов ( 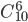$C_{10}^6$ ).

Определяем число исходов, благоприятствующих событию А — «среди 6 взятых деталей 4 стандартных». Четыре стандартные детали из семи стандартных можно взять 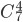C_7^4 способами, при этом остальные 6 — 4 = 2 детали должны быть нестандартными; взять же 2 нестандартные детали из 10 — 7 = 3 нестандартных деталей можно C_3^2 способами. Следовательно, число благоприятных исходов равно .

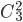
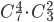
Искомая вероятность равна отношению числа исходов, благоприятствующих событию, к числу всех элементарных исходов:
$P(A)=displaystylefrac{C_7^4cdot C_3^2}{C_{10}^6}=0,5$

З а м е ч а н и е. Последняя формула является частным случаем формулы (1.3.10): N= 10, М= 7, n = 6, m = 4.

Пример 11. Среди 25 студентов группы, в которой 10 девушек, разыгрывается 5 билетов. Найти вероятность того, что среди обладателей билетов окажутся 2 девушки.

Решение. Число всех равновозможных случаев распределения 5 билетов среди 25 студентов равно числу сочетаний из 25 элементов по 5, то есть 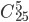$C_{25}^5$ . Число групп по трое юношей из 15, которые могут получить билеты, равно $C_{15}^{3}$ . 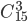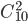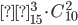Каждая такая тройка может сочетаться с любой парой из десяти девушек, а число таких пар равно $C_{10}^2$ .Следовательно, число групп по 5 студентов, образованных из группы в 25 студентов, в каждую из которых будут входить трое юношей и две девушки, равно произведению $?_{15}^3cdot C_{10}^2$ . Это произведение равно числу благоприятствующих случаев распределения пяти билетов среди студентов группы так, чтобы три билета получили юноши и два билета — девушки. В соответствии с формулой (1.2.1) находим искомую вероятность

$P(A)=displaystylefrac{C_{15}^3cdot C_{10}^2}{C_{25}^5}=frac{195}{506}$

З а м е ч а н и е. Последняя формула является частным случаем формулы (1.3.10): N= 25, М= 15,n = 5, m = 3.

Пример 12. В ящике находятся 15 красных, 9 голубых и 6 зеленых шаров. Наудачу вынимают 6 шаров. Какова вероятность того, что вынуты 1 зеленый, 2 голубых и 3 красных шара (событие А)?

Решение. В ящике всего 30 шаров. При данном испьпании число всех равновозможных элементарных исходов будет 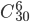$C_{30}^6$ . Подсчитаем число элементарных исходов, благоприятствующих событию А. Три красных шара из 15 можно выбрать $C_{15}^3$ способами, два голубых шара из 9 можно выбрать C_9^2 споcобами, один зеленый из 6 — C_6^1 способами.
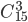
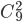
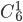
Следовательно (в силу принципа произведения в комбинаторике), число исходов, благоприятствующих событию А, будет 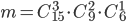$m=C_{15}^3cdot C_9^2cdot C_6^1$ . По формуле (1.2.1) находим искомую вероятность
$P(A)=displaystylefrac{C_{15}^3cdot C_9^2cdot C_6^1}{C_{30}^6}=frac{24}{145}$

Пример 13. В ящике 15 шаров, из которых 5 голубых и 10 красных. Наугад выбирают 6 шаров. Найти вероятность того, что среди вынутых шаров 2 голубых.

Решение. Общее число элементарных исходов данного опыта равно числу сочетаний из 15 по 6, то есть
$C_{15}^6=frac{15!}{6!cdot 9!}=5005$
Число благоприятных исходов равно произведению
$C_5^2cdot C_{10}^4=2100$
Искомая вероятность определяется формулой (1.3.10):
$P=displaystylefrac{C_5^2cdot C_{10}^4}{C_{15}^6}=frac{2100}{5005}$

Пример 14. Игральный кубик подбрасывают 10 раз. Какова вероятность того, что при этом грани 1, 2, 3, 4, 5, 6 выпадут соответственно 2, 3, 1, 1, 1, 2 раза (событие А)?

Решение. Число исходов, благоприятных для события А, подсчитаем по формуле (1.3.7):
$m=displaystylefrac{(2+3+1+1+1+2)!}{2!cdot 3!cdot 1!cdot 1!cdot 1!cdot 2!}=2cdot 3cdot 5cdot 7cdot 8cdot 9cdot 10$
Число всех элементарных исходов в данном опыте n = 6¹⁰, поэтому
$P(A)=displaystylefrac{2cdot 3cdot 5cdot 7cdot 8cdot 9cdot 10}{6^{10}}=frac{700}{6^7}$

Задачи
1. На 5 одинаковых карточках написаны буквы Б, Е, Р, С, Т. Эти карточки наудачу разложены в ряд. Какова вероятность того, что получится слово БРЕСТ?
2. В ящике 4 голубых и 5 красных шаров. Из ящика наугад вынимают 2 шара. Найдите вероятность того, что эти шары разного цвета.
3. В бригаде 4 женщины и 3 мужчины. Среди членов бригады разыгрываются 4 билета в театр. Какова вероятность того, что среди обладателей билетов окажется 2 женщины и 2 мужчины?
4. В ящике 10 шаров, из которых 2 белых, 3 красных и 5 голубых.Наудачу извлечены 3 шара. Найдите вероятность того, что все 3 шара разного цвета.
5. На пяти одинаковых карточках написаны буквы л, м, о, о, т. Какова вероятность того, что извлекая карточки по одной наугад, получим в порядке их выхода слово молот?
6. Из партии, содержащей 10 изделий, среди которых 3 бракованных, наудачу извлекают 3 изделия. Найдите вероятность того, что в полученной выборке одно изделие бракованное.
7. Из десяти билетов выигрышными являются два. Чему равна вероятность того, что среди взятых наудачу пяти билетов один выигрышный?

Ответы
1.1/120. 2. 5/9. 3. 18/35. 4 . 0,25. 5. 1/60. 6. 21/40. 7. 5/9.

Вопросы
1. Что назьrвают перестановками?
2. По какой форме вычисляют число перестановок из n различных элементов?
3. Что называют размещениями?
4. По какой формуле вычисляют число размещений из n различных элементов по m элементов?
5. Что называют сочетаниями?
6. По какой формуле вы исляют число сочетаний из n элементов по m элементов?
7. Каким равенством связаны числа перестановок, размещений и сочетаний?
8. По какой формуле вычисляется число перестановок из n элементов, если некоторые элементы повторяются?
9. Какой формулой определяется число размещений по m элементов с повторениями из n элементов?
10. Какой формулой определяется число сочетаний с повторениями из n элементов по m элементов?

Источник

Тут надо построить конечный автомат, который принимает строки, которые кончаются на заданную строку. Посмотрите эту статью, там в начале расписан этот автомат (секции перфикс функция — атомат КМП).

Только там все вероятности перехода одинаковые, у вас же они заданы для каждой буквы.

Вот построили вы автомат. Теперь задача состоит в том, чтобы найти вероятность, что случайный путь в этом автомате длины n пройдет через конечное состояние ровно один раз. Для этого подсчитайте 2 вероятности: что путь из начала длины k дойдет до конечного состояния один раз, и что путь из конечного состояния длины n-k не вернется в него.

Обе эти вероятности можно подсчитать динамическим программированием:
P1(i, k) — вероятность того, что путь начиная с состояния i (i < n) за k шагов дойдет до состояния n первый раз. Это просто сумма по всем возможным переходам:

P1(i, k) = sum_{c - все символы} P1(next(i, c), k-1) * p(c)

База:

P1(m, 0) = 1
P1(m, k>0) = 0
P1(i < m, 0) = 0

Вторая вероятность: сделать k шаговиз состояния i и ни разу не войти в конечное состояние:

P2(i, k) = sum_{c - все символы, next(i,c) < m} P2(next(i, c), k-1) * p(c)

База:
P1(i, 0) = 1

Ответ к задаче — сумма по всем возможным длинам первой части пути:
sum_{k=m..n} P1(0, k) * P2(m, n-k)

Это решение через динамическое программирование будет O(n*m) по вермени и по памяти.

Замкнутой формулы, как в задаче в моей статье я тут не вижу. Может, если бы вероятности всех символов были бы одинаковы, то что-то можно было бы сократить.

Источник

План урока:

Частота и вероятность

Элементарные события

Противоположные события

Сложение вероятностей

Умножение вероятностей

Условная вероятность

Вероятность и геометрия

Частота и вероятность

В мире происходят события, которые можно предсказать. Например, можно предсказать приезд лифта после того, как человек нажмет кнопку его вызова. Астрономы могут заранее предсказывать солнечные и лунные затмения.

Однако нередко нам приходится иметь дело с событиями, результат которых заранее предсказать невозможно. Не получается заранее сказать, упадет ли монетка при подбрасывании орлом вверх, также как нельзя заранее предсказать поломку прибора. Такие события называются случайными.

1gfdgd

Случайные события обычно могут произойти только в определенной ситуации. Так, событие «выпадение решки» может произойти только при броске монеты. В математике подбрасывание монетки будет называться испытанием или экспериментом.

2gfd

Здесь не следует воспринимать термин «эксперимент» как некое научное исследование. Испытанием может оказаться любая жизненная ситуация. Приведем несколько примеров опытов и соответствующих им случайных событий:

Бросок кубика с 6 гранями – это эксперимент, а выпадение или невыпадение шестерки на нем – это случайное событие.
Полет самолета – испытание, а отказ двигателя в полете – это случайное событие.
Ожидание автобуса на остановке в течение 10 минут – эксперимент, а появление или непоявление автобуса в этот промежуток времени – случайное событие.
Футбольный матч – опыт, а победа в нем команды хозяев или травма одного из игроков – случайное событие.
Выстрел из винтовки – испытание, а попадание в мишень – случайное событие.
Изготовление рабочим детали – эксперимент, а получение бракованной детали – случайное событие.

Здесь важно отметить, что для математики не важно, является ли событие по-настоящему случайным. Возможно, что автобус ходит строго по расписанию, и человек, знающий его, точно может определить, через сколько минут он приедет. Но если рядом стоит другой человек, не знающий этой информации, то для него приезд автобуса будет случайным событием.

Предположим, что есть возможность провести какой-то эксперимент множество раз. Например, кубик можно бросить 500 раз. Обозначим это число, количество экспериментов, как n. В ходе серии этих бросков шестерка выпала, например, 85 раз. Обозначим эту величину, количество произошедших случайных событий, как m. Само событие «выпадение шестерки» обозначим как А. Тогда отношение m/n будет называться частотой случайного события А. В данном случае частота события А равна

85/500 = 0,17

3tyut

Наблюдения показывают, что если условия экспериментов примерно одинаковы, а их число велико, то частота одного и того же события будет примерно одинаковой. Чем больше число испытаний, тем обычно ближе частота события к некоторому постоянному числу. Это число и называют вероятностью случайного события А.

4gdfs

Грубо говоря, частота и вероятность событий – это примерно одно и то же. Частоту определяют на практике, входе эксперимента, а вероятность можно рассчитать аналитически.

Вероятность – это величина, которая характеризует возможность события произойти. Если она близка к единице, то событие, скорее всего, произойдет. Если она близка к нулю, то событие, скорее всего, не случится. Для обозначения вероятности используется буква Р. Если надо указать вероятность конкретного события А, то его записывают как Р(А).

Вероятность – это безразмерная величина, то есть для нее нет никакой единицы измерения. Она может принимать значение от 0 до 1. Иногда на практике ее указывают в процентах. Например, вероятность 0,5 означает 50%. Чтобы перевести вероятность в проценты, ее надо просто умножить на 100.

Элементарные события

Часто одно случайное событие можно представить как результат нескольких случайных событий. Например, событие «выпадение на кубике четного числа» произойдет в том случае, если случится хотя бы одно из следующих событий:

выпадет двойка;
выпадет четверка;
выпадет шестерка.

Если событие нельзя «разбить» на более простые события, то его называют элементарным событием. Считается, что в ходе испытания может произойти только одно элементарное событие. Так, при броске кубика произойдет одно из 6 элементарных событий:

выпадет единица;
выпадет двойка;
выпадет тройка;
выпадет четверка;
выпадет пятерка;
выпадет шестерка.

5gdfg

В большинстве случаев вероятность элементарных событий одинакова. Действительно, нет причин полагать, что при броске кубика шестерка будет выпадать чаще двойки. Если у двух элементарных событий одинаковая вероятность, то их называют равновозможными событиями.

6hfgh

Если в результате эксперимента происходит одно из равновозможных событий, число которых равно n, то вероятность каждого из них принимается равной дроби 1/n.

7gfdg

Например, при броске кубика может произойти 6 равновозможных событий. Значит, вероятность каждого из них равна 1/6. При броске монетки она может выпасть либо орел, либо решка. Этих событий два, и они равновозможны, поэтому их вероятность равна 1/2, то есть 0,5.

Пример. В урне 20 шариков, один из которых окрашен в желтый цвет. Какова вероятность, что человек, вытаскивающий вслепую один из шариков, вынет именно желтый шар?

Решение. Так как шаров 20, то возможны 20 равновозможных событий, одно из которых – вытаскивание желтого шара. Его вероятность равна 1/20 = 0,05

Ответ: 0,05

Пример. Вася составил произвольную последовательность из букв А, Б, В, Г, Д, и записал ее на бумаге. Каждую букву Вася использовал один раз. Аналогично свою последовательность записал и Петя. Какова вероятность, что они оба загадали одну и ту же последовательность.

Решение. Вася записал перестановку 5 букв. Общее количество таких перестановок равно 5! = 1•2•3•4•5 = 120. Все последовательности равновероятны. Значит, вероятность того, что они совпали, равна 1/120.

Ответ: 1/120

Противоположные события

Заметим, что если сложить вероятности всех элементарных событий, которые возможны в ходе эксперимента, то получится единица. Действительно, при броске монеты возможны два события с вероятностью 1/2. Сумма их вероятностей составляет 1/2 + 1/2 = 1.

8gfdg

Это правило действует и в том случае, когда речь идет о не равновозможных событиях. Так, при выстреле по мишени возможны два варианта развития событий – попадание в цель или промах. Пусть вероятность попадания в цель равна 0,3. Это значит, что вероятность промаха составляет 0,7, так как только в этом случае сумма этих вероятностей будет равна единице:

0,7 + 0,3 = 1

Заметим, что при стрельбе стрелок либо попадет в цель, либо промажет. То есть одно из двух этих событий обязательно произойдет, но только оно одно. Подобные события называют противоположными.

9ghdhg

Противоположными являются такие события, как:

падение монеты либо одной стороной вверх (орлом), либо другой (решкой);
выпадение четного или нечетного числа на шестигранном кубике;
изготовление рабочим годной или получение бракованной детали.

Стоит отметить, что победа одной и победа другой команды в футбольном матче – это не противоположные события, так как возможен третий исход – ничья. Однако в ряде спортивных состязаний ничья невозможна, и тогда победы команд – это противоположные события.

Очевидно, что сумма вероятностей противоположных событий равна единице.

10klhl

Пример. Вероятность того, что рабочий изготовит годную деталь, оценивается в 0,97. Чему равна вероятность изготовления бракованной детали?

Решение. Изготовление бракованной детали (обозначим это событие как А) и получение годного изделие (событие Б) – это два противоположных события. Их сумма равна единице

Р(А) + Р(B) = 1

По условию Р(А) = 0,97. Тогда

0,97 + Р(В) = 1

Перенесем в равенстве слагаемое 0,97 в правую часть и получим:

Р(B) = 1 – 0,97

Р(В) = 0,03

Ответ: 0,03

Сложение вероятностей

До этого мы рассматривали элементарные события. Однако значительно чаще нас интересуют более сложные события, которые состоят из элементарных. Как рассчитать их вероятность?

Введем понятие несовместных событий.

11dadfg

Так, при броске кубика не может сразу выпасть пятерка и четное число (потому что 5 – это нечетное число). Хоккейный матч не может одновременно окончиться и ничьей, и победой одной из команд.

Заметим, что любые два элементарных события несовместны, также как и любые два противоположных события.

Для несовместных событий справедлива теорема сложения вероятностей.

Пример. В забеге на 1500 метров участвуют два китайца. Эксперты полагают, что вероятность победы Мао Луня составляет 0,16, а шансы Ван Юнпо оцениваются в 0,14. Если эти оценки справедливы, то каковы шансы того, что чемпионом станет китаец?

Решение. Обозначим победу Мао Луня как событие А, а победу Ван Юнпо – как Б. Очевидно, что события несовместны, так как победитель будет лишь один. По Условию Р(А) = 0,16, а Р(В) = 0,14.

Событие «победа китайца» произойдет, если выиграет хоть один из этих спортсменов, поэтому произведем сложение вероятностей:

Р(А или В) = Р(А) + Р(В) = 0,16 + 0,14 = 0,3

Ответ: 0,3

Заметим, что выполнять сложение вероятностей событий можно и в случае, когда несовместных событий больше двух.

Пример. При стрельбе по мишени стрелок выбьет 10 баллов (максимальный результат) с вероятностью 0,2, 9 баллов с вероятностью 0,25, 8 баллов с вероятностью 0,15. Какова вероятность, что стрелок НЕ наберет даже 8 баллов одним выстрелом?

Решение. Здесь несовместные события – это выбивание 10 (событие А), 9 (В) и 8 (С) баллов. Действительно, в ходе одного выстрела стрелок покажет только один результат. Если одно из этих событий случится, то спортсмен получит не менее 8 баллов. Вероятность этого события равна:

Р(А или В или С) = 0,2 + 0,25 + 0,15 = 0,6

Но нас спрашивают о другом, о вероятности того, что стрелок НЕ наберет 8 очков. Очевидно, что он их либо наберет, либо нет. Значит, это противоположные события, поэтому сумма равняется 1. Мы посчитали, что стрелок наберет 8 баллов с вероятностью 0,6. Значит, он не наберет их с вероятностью

1 – 0,6 = 0,4

Ответ: 0,4

Пример. В урне лежит 500 шариков, из которых 120 являются черными. Человек вслепую вытаскивает из урны один шар. Какова вероятность, что он будет черным.

Решение. Присвоим каждому шару номер от 1 до 500, причем первые 120 номеров получат черные шары. Обозначим вероятность того, что вытащат шар с номером n, как Р(n). Очевидно, что события «выбран шар 1», «выбран шар 2», … «выбран шар 500» – это элементарные и равновозможные события. Их вероятность равна 1/500:

Р(1) = Р(2) = Р(3) =…..=Р(500) = 1/500

Эти события несовместны, как и любые элементарные события. Значит, вероятность того, что вытащат черный шар, равна сумме вероятностей:

Р(выбран черный шар) = Р(1) + Р(2) + … + Р(120)

В этой сумме 120 слагаемых, каждое из которых равно 1/500. Следовательно, вся сумма равна произведению 120 и 500

Р(выбран черный шар) = 120•(1/500) = 120/500 = 0,24

Ответ: 0,24

В этом примере рассматривался особый случай, когда все элементарные события (вытаскивание конкретного шарика) равновозможны, и несколько из них приводили к одному событию (вытаскиванию черного шара). В итоге мы получили, что вероятность этого события равна отношению числа «благоприятных» для него равновозможных событий (120) к общему числу этих событий (500). Такой же результат мы получим при рассмотрении любой схожей задачи.

13fgdsa

В результате мы получили одну из основных формул теории вероятности.

Пример. Компьютер случайным образом генерирует число от 1 до 200. Вероятность появления каждого числа одинакова. Какова вероятность того, что он сгенерирует число от 51 до 75 (включительно)?

Решение. Задача предполагает 200 равновозможных исходов события. Из них 25 (между 51 и 75 находится 25 чисел) являются «благоприятными». Тогда вероятность описанного события равна отношению 25 к 200:

Р = 25/200 = 1/8 = 0,125

Ответ: 0,125

Ещё раз напомним принципиальный момент. Такой метод решения задач может быть применен только в том случае, когда все элементарные события равновероятны!

Пример. Изготовлено 10 велосипедов, но из них 3 – с дефектом. Необходимо выбрать 4 велосипеда. Каков шанс, что они все будут без дефекта?

Решение. Выбирая 4 велосипеда из 10, мы составляем, с точки зрения комбинаторики сочетание из 10 по 4. Подсчитаем количество возможных сочетаний:

14khg

Теперь подсчитаем, сколько можно составить сочетаний, не содержащих дефектный велосипед. Годных велосипедов 10 – 3 = 7, из них надо выбрать 4. Имеем сочетания из 7 по 4:

15fdasa

Вероятность выбора качественных велосипедов равна отношению количества «благоприятных» исходов (их 35) к общему числу возможных исходов:

Р = 35/210 = 1/6

Ответ: 1/6

Пример. В турнире по футболу участвуют команды «Барселона», «Реал», «Атлетико» и «Валенсия». Эксперты полагают, что:

шансы «Атлетико» выиграть чемпионат 1,5 раза выше шансов «Валенсии»;
шансы «Реала» и «Атлетико» равны;
шансы «Барселоны» на победу в 4 раз больше шансов «Реала».

Определите вероятность победы каждой команды в турнире.

Решение.

Обозначим за х вероятность победы «Валенсии». Шансы «Реала» и «Атлетико» в 1,5 раза выше, а потому составляют по 1,5х. Вероятность триумфа «Барселоны» в 4 раза выше, чем у «Реала», а потому составляют 4•1,5х = 6х.

Ясно, что турнир выиграет лишь одна команда, то есть речь идет о несовместных событиях. С другой стороны, какая-то команда обязательно его выиграет, а потому в вероятности побед команд дадут единицу. В результате, используя формулу сложения вероятностей, можно записать уравнение:

х + 1,5х + 1,5х + 6х = 1

10х = 1

х = 0,1

Решив уравнение, мы нашли, что шансы триумфа «Валенсии» составляют всего 0,1. Шансы «Реала» и «Атлетико» равны

1,5х = 1,5•0,1 = 0,15

Вероятность успеха «Барселоны» составляет

6х = 6•0,1 = 0,6

Ответ. «Барселона» – 0,6, «Реал» и «Атлетико» – по 0,15, «Валенсия» – 0,1.

Умножение вероятностей

До этого мы рассматривали сложные события, которые происходили тогда, когда происходило одно из элементарных событий. Например, в забеге, где участвовали два китайца, представитель Поднебесной побеждал, если выигрывал ИЛИ 1-ый китаец, ИЛИ 2-ой. Ключевое слово здесь – ИЛИ.

Однако в некоторых случаях событие происходит лишь тогда, когда происходят одновременно сразу два более простых события. Пусть надо вычислить вероятность того, что при двух подбрасываниях монеты они оба раза упадет на орлом вверх. Возможны 4 случая:

сначала выпадет орел, потом еще раз орел (назовем этот случай ОО);
сначала падает орел, а потом решка (ОР);
первым выпадет решка, а потом орел (РО);
оба раза выпадет решка (РР).

Все 4 исхода удобно представить в виде таблицы. По вертикали запишем результат 1-ого броска монеты, а по горизонтали – второго:

16hgfh

Видно, что лишь в одном из 4 случаев орел выпадет оба раза. Поэтому вероятность будет равна 1/4, или 0,25.

Этот результат можно было получить иначе. Событие ОО случится, только если случатся два события: Орел выпадет при первом броске,и он же выпадет во второй раз. Вероятность каждого из них равна 1/2, или 0,5. Если перемножить эти две вероятности, то снова получим 0,5•0,5.

Рассмотрим более сложный случай с броском двух шестигранных кубиков. Какова вероятность, что в сумме выпадет ровно 12 очков. Снова построим таблицу, по вертикали укажем результат первого броска, по горизонтали – второго, а в ячейках – выпавшую сумму:

17hgfh

Всего получилась табличка с 36 ячейками. Лишь в одной из них стоит число 12. Эта сумма на кубиках будет лишь тогда, когда на обоих кубиках выпадет по шестерке. Так как ячеек 36, а каждая комбинация равновозможна, то вероятность выпадения 12 равна 1/36. Обратите особое внимание, что, например, семерка записана сразу в 6 ячейках (по диагонали, начиная с нижнего левого угла). Значит, вероятность выпадения семерки за 2 броска равна 6/36 = 1/6. И действительно, на практике 7 очков выпадет у игроков в 6 раз чаще, чем 12. Посчитайте с помощью таблицы самостоятельно, какого вероятность выпадения 10 очков.

Как и в случае с монеткой, число вероятность 1/36 можно получив, перемножив вероятность того, что в первой кости выпадет шестерка (1/6), и того, что на второй кости выпадет она же (1/6):

(1/6)•(1/6) = 1/36

Введем одно важное понятие – независимые события.

18kjhu

Так, какое бы число не выпало на 1-ой кости, вероятность выпадения на второй, например, четверки останется равной 1/6. Как бы ни падала монетка при первом броске, при 2-ом шанс выпадения орла останется равным 1/2.

Для наглядности приведем пример зависимых событий. Пусть А – вероятность победы в забеге одного бегуна, и Р(А) = 0,1. В – вероятность победы второго бегуна, и Р(В) = 0,1. Но очевидно, что победить может лишь один спортсмен. Поэтому, если случится событие А, то вероятность события В изменится – она опустится до нуля.

Таблички, которые мы строили для игры в кости, не всегда удобно использовать, поэтому на практике используют теорему умножения вероятностей.

19hjtyu

Ещё раз обратим внимание, что оно действует только для независимых случайных событий.

Пример. Рабочий изготавливает две детали. Вероятность изготовления первой детали с браком составляет 0,05, а второй детали – 0,02. Рабочего оштрафуют, если обе детали будут сделаны с браком. Какова вероятность штрафа для рабочего?

Решение. Штраф выпишут, если одновременно произойдет два независимых события – будет допущен брак при изготовлении И 1-ой, И 2-ой детали. Ключевое слово – И, а не ИЛИ, как в случае со сложением вероятностей. Вероятность такого развития событий найдем, произведя умножение вероятностей:

0,05•0,02 = 0,001

Ответ: 0,001

Умножение вероятностей событий возможно и тогда, когда их больше двух.

Пример. Для победы команды в турнире ей надо выиграть все 4 оставшиеся встречи. Вероятность победы в каждой игре составляет 80%. Какова вероятность победы в турнире?

Решение. Обозначим вероятности победы в отдельных матчах как Р₁, Р₂, Р₃, Р₄. По условию они все равны 0,8. Команда станет чемпионом, только если случатся все события. Вероятность этого можно найти, применив формулу умножения вероятностей:

Р₁ • Р₂ • Р₃ • Р₄ = (0,8)⁴ = 0,4096

Ответ: 0,4096

Пример. В первой партии 4% лампочек бракованы, а во второй – 5%. Из каждой партии берут по лампочке. Какова вероятность того, что обе выбранных лампочки окажутся бракованными? Какова вероятность, что они обе окажутся исправными? Какова вероятность, что ровно одна лампа будет бракованной?

Решение. Обозначим выбор бракованной детали из 1-ой партии как событие «брак-1», а выбор годной детали (годная-1). Эти события противоположны, то есть сумма их вероятностей равна единице.

Р(брак-1) + Р(годная-1) = 1

Р(годная-1) = 1 – Р(брак-1)

По условию Р(брак-1) = 0,04. Следовательно, Р(годная-1) = 1 – 0,04 = 0,96.

Аналогично для второй партии можно записать, что Р(брак-2) = 0,05, Р(годная-2) = 0,95.

Будут выбраны две бракованные детали только в том случае, когда произойдут события Р(брак-1) и Р(брак-2). Вероятность этого, по правилу умножения вероятностей, равна:

0,05•0,04 = 0,002

Две годные детали бут выбраны, если одновременно случатся события Р(годная-1) и Р(годная-2). Это случится с вероятностью

0,95•0,96 = 0,912

Ответ: 0,002; 0,912

Пример. По мишени стреляют из двух орудий. Вероятность попадания из первого орудия составляет 0,3, а из второго – 0,4. С какой вероятностью по мишени попадет ровно одно орудие?

Решение. Пусть событие «попал-1» означает попадание из 1-ого орудия, а «попал-2» – попадание из 2-ого орудия. Казалось бы, нам надо найти вероятность попадания ИЛИ 1-ого, ИЛИ 2-ого орудия. Однако слово ИЛИ здесь не означает, что вероятности можно просто сложить! Вспомним, что закон сложения вероятностей действует только для несовместных событий. Но выстрелы из орудий таковыми не являются, так как возможно одновременное попадание двух снарядов в мишень.

Введем события «промах-1» и «промах-2», означающие промах из 1-ого или второго орудия. Их вероятности составляют

Р(«промах-1») = 1 – Р(«попал-1») = 1 – 0,3 = 0,7

Р(«промах-2») = 1 – Р(«попал-2») = 1 – 0,4 = 0,6

Одно попадание случится в случае, если произойдет одно из двух «сложных» событий:

событие А – первая пушка стреляет точно, а вторая мажет;
событие Б – первая пушка мажет, а вторая попадает в цель.

Вероятность события А можно рассчитать так:

Р(А) = Р(«попал-1») •Р(«промах-2») = 0,3•0,6 = 0,18

Аналогично рассчитаем и вероятность Б:

Р(Б) = Р(«попал-2») •Р(«промах-1») = 0,4•0,7 = 0,28

События А и Б несовместны, а потому их вероятности можно сложить

Р(А) + Р(Б) = 0,18 + 0,28 = 0,46

Ответ: 0,46

Условная вероятность

Иногда можно перемножать вероятности событий, не являющихся в полном смысле слова независимыми. Пусть для того, чтобы произошло событие А, необходимо, чтобы последовательно произошли В и С. В зависимости от того, произошло ли В, вероятность С может отличаться. Например, в урне лежат 4 шарика – 2 красных и 2 желтых. Предположим, что произошло событие В – был вытащен красный шар. Его вероятность равна 0,5. Чему тогда равна вероятность события С – вытаскивания желтого шарика? В урне осталось 3 шара, из них 2 желтых, поэтому Р(С) = 2/3.

С другой стороны, пусть В не произошло, то есть первым был вынут желтый шар. Чему тогда равна вероятность С? В урне снова 3 шарика, но лишь 1 из них желтый. Следовательно, Р(С) = 1/3. Получается, что в зависимости от того, случилось ли В, вероятность Р(С) принимает разные значения. В математике такую вероятность называют условной.

20tre

Обозначается она так:

Р(С|B).

Первая буква в скобках соответствует событию, для которого указываем вероятность, а вторая буква – событию, которое является условием для С.

Если событие А произойдет тогда, когда свершится сначала В, а потом С, то вероятность А также можно найти с помощью умножения

Р(А) = Р(В)•Р(С|B)

Пример. В урне находится 52 шара, из них на 4 написана буква Т. Из урны последовательно вынимаются два шара. Какова вероятность, что на обоих вытащенных шарах будет буква Т?

Решение. Так как в урне 52 шара, и лишь на 4 есть буква Т, то шанс на то, что первым вытащат именно шар с буквой Т, равен 4/52 = 1/13. Если это событие произошло, то в урне остался 51 шар, и лишь на трех будет находиться нужный символ. Тогда вероятность появления шара с буквой Т составит 3/51 = 1/17. Общая же вероятность появления 2 таких шаров подряд найдется как произведение этих вероятностей:

Р = (1/13)•(1/17) = 1/221 ≈ 0,004525

Эту вероятность можно рассчитать и иначе, по аналогии с задачей про бракованные велосипеды, которая приведена выше. Подсчитаем, сколькими способами можно выбрать 2 шара из 52:

21gfdh

Но всего 6 способами можно выбрать 2 шара из 4:

Поделив число благоприятных исходов на их общее количество, получим искомую вероятность:

Р = 6/1326 = 1/221.

Ответ: 1/221

Пример. Известно, что вероятность мужчины дожить до 90 лет составляет 5,126%, а до 95 лет – 1,326%. С какой вероятностью мужчина, которому уже сейчас 90 лет, доживет до 95 лет?

Решение. Пусть А – это дожитие до 95 лет, С – дожитие 90-летнего мужчины до 95 лет, В – дожитие до 90 лет. Чтобы отпраздновать 95-летие, человек сначала должен отметить 90-летний юбилей, а потом ещё прожить 5 лет. Другими словами, чтобы случилось А, сначала должно случиться В, а потом событие С при условии В. То есть можно записать

Р(А) = Р(В)•Р(С|B)

По условию Р(А) = 0,01326, а Р(В) = 0,05126. Зная это, легко найдем Р(С|B):

Р(А) = Р(В)•Р(С|B)

0,01326 = 0,05126•Р(С|B)

Р(С|B) = 0,01326/0,05126 ≈ 0,2587

Это и есть вероятность мужчины, отметившего 90-ый день рождения, дожить до 95 лет.

Ответ: 0,2587

Вероятность и геометрия

Теория вероятности затрагивает и геометрию. Пусть есть отрезок АВ, в середине которого располагается точка С.

Теперь мы ставим на отрезке АВ случайную точку D. С какой вероятностью она попадет наАС, а с какой на ВС? Так как эти отрезки ничем не отличаются, то можно предположить, что события «попадание точки на АС» и «попадание точки на ВС» являются равновероятными событиями. Так и есть. Их вероятность обоих событий составляет 0,5.

Теперь предположим, что точка С выбрана так, что отрезок АС вдвое короче, чем ВС, то есть ВС = 2 АС:

24gfdg

Чему в этом случае равны вероятности попадания случайной точки D на отрезки АС и ВС? Для ответа на этот вопрос раздели ВС надвое с помощью ещё одной точки K:

25hgfty

Получили три одинаковых отрезка АС, СК и КВ. Раз они одинаковы, то и вероятности случайной точки оказаться на каждом из этих отрезков равны:

Р(АС) = Р(СК) = Р(КВ) = 1/3

Отсюда вероятность попадания точки на ВС равна 2/3:

Р(ВС) = Р(СК) + Р(КВ) = 1/3 + 1/3 =2/3

Получили, что вероятность попадания точки на ВС вдвое выше, чем на АС. И при этом ВС вдвое длиннее. И это не случайно. В общем случае верно следующее правило:

26jhgyu

Данное свойство может пригодиться не только в геометрии, но и при решении задач.

Пример. Прохожий пришел на остановку автобуса в случайный момент времени. Он знает, что автобус ходит с интервалом в 40 минут, но не знает, когда отъехал предыдущий автобус. С какой вероятностью автобус придется ждать менее 10 минут?

Решение. Построим схему. На ней время будем откладывать по горизонтальной оси. Отметим точки, соответствующие приезду автобуса (А₁, А₂, А₃, А₄), и точку, соответствующую приходу прохожего (D):

27hgfh

Ясно, что точка D окажется между какими-то двумя точками, которым соответствуют последовательные прибытия поезда.На рисунке это А₂ и А₃. В каком случае время ожидания составить менее 10 минут? В том случае, если точка D окажется на «расстоянии» менее 10 минут от точки А₃, то есть попадет в отрезок ВА₃:

28gfhf

Отрезок ВА₃ вчетверо короче отрезка А₂А₃, поэтому вероятность точку D попасть на него составляет 1/4. Именно такова вероятность, что прохожему придется ждать автобус менее 10 минут.

Ответ: 1/4

В случае, когда точка случайным образом ставится не на отрезке, а на плоской фигуре, то справедливо следующее правило:

29hfgh

Пример. В треугольнике АВС проведена средняя линия NM. С какой вероятностью случайная точка, отмеченная на треугольнике АВС, попадет и на треугольник ANM?

30ghfgh

Решение. Средняя линия NM параллельна стороне ВС (это свойство средней линии), а потому равны углы АNM и АВС (соответственные углы при параллельных прямых). Это значит, что треугольники АВС и ANM подобны по двум равным углам. Коэффициент подобия равен 1/2, так как AN/АВ = 1/2. Известно, что отношение площадей подобных фигур равно квадрату их коэффициента подобия, поэтому площадь АMN в 4 раза меньше площади АВМ. По условию точка гарантированно попадает в АВС, то есть вероятность этого события равна 1. Тогда вероятность попадания точки в АNM будет в 4 раза меньше и составит 1/4 .

Ответ:1/4.

Источник

В этом
параграфе, пользуясь
определением вероятности, будем находить
вероятности событий так же, как это
делалось в примерах 4—6 §
2.

При
непосредственном
вычислении события А
часто для
подсчета благоприятствующих этому
событию случаев и общего
числа равновозможных,
единственно возможных и несовместных
случаев применяются
формулы комбинаторики .

Пример
1. Бросается
монета правильной формы. Какова
вероятность выпадения
герба?

Решение.
Обозначим событие «выпал герб» буквой
А. Число
равновозможных
случаев n=2.
Из этого числа случаев благоприятствует
событию А только
один случай, т=1.
Следовательно,

Пример
2. На пяти одинаковых
карточках написаны буквы л,
м, о, о, т.
Какова вероятность
того, что

а)
извлекая все карточки по
одной наугад, получим
в порядке их
выхода слово «молот»;

б)
извлекая три карточки по
одной наугад, получим
в порядке
выхода слово «том»?

Решение,

а) Занумеруем буквы
в том порядке, в каком они написаны:

Подсчитаем
равновозможные случаи, их будет столько,
сколько можно сделать
перестановок из пяти
элементов, т. е.
.
Из этих
120 случаев два случая
благоприятствуют событию
А —
получение слова
«молот». Действительно,
событие А произойдет,
если карточки будут
взяты только в таком
порядке:

Таким образом,

б)
Число всех равновозможных
случаев равно числу размещений из 5
элементов по три,
т.е.

n=А₅³== 60.

Из
этих 60 равновозможных
случаев два случая
благоприятствуют событию
В—
получению слова «том».
Действительно, событие
В произойдет,
если карточки будут взяты в таком
порядке:

Следовательно,

Пример
3. Из колоды в
36 карт наугад
вынимаются три карты.
Найти вероятность того,
что среди них окажутся
два туза.

Решение.
Обозначим интересующее
нас событие буквой А.
Общее число равновозможных,
единственно возможных
и несовместных случаев
Из этого числа случаев
благоприятствуют событию

случаев.

Следовательно,

Пример
4. Среди 50 деталей 20
первого сорта и
30 второго сорта. Найти
вероятность того, что
из взятых наугад пяти деталей
окажутся 2 первого
сорта и
3 второго.

Решение.
Интересующее нас
событие обозначим буквой
А. Из
условия задачи следует, что

Пример
5. На полке расставлены
наугад 12 книг.
Найти вероятность того, что

а) три
тома одного сочинения окажутся
поставленными вместе в
порядке номеров;

б) три
тома будут поставлены
вместе.

Решение,

а)
событие «три тома поставлены вместе в
порядке номеров»
обозначим буквой А.
Число равновозможных
случаев расставить
12 книг на полке равно n=12!. Найдем число
случаев, благоприятствующих событию
А. Будем
считать «связку» книг 1, 2, 3-го томов,
следующих один
за другим, за один
элемент и еще 9 элементов (9 книг), т.
е. всего 10. Таким образом,
событию А благоприятствует
число случаев m=10! Следовательно,

б)
Событие «три тома поставлены вместе»
обозначим буквой В.
Теперь уже в «связке»
книг порядок следования томов любой и
число возможных перестановок
из этих трех
элементов Р₃=3!
Таким образом, число благоприятствующих
случаев событию В
будет
.
Вероятность

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник