Как найти вероятность обратного события - Исправление недочетов и поиск решений вместе с Examum.ru

Если все исходы опыта одинаково возможны, то вероятность (P(A)) любого события (A) можно вычислить по формуле:

(P(A) =)

количество исходов, благоприятных событию Аколичество всех возможных исходов

Вероятность противоположного события можно вычислить по формуле:

P(A¯)=1−P(A)

Бросается игровой кубик. Событие (A) — выпадет цифра (2). Ранее уже было вычислено, что (P(A) =)

Противоположное событие

A¯

— не выпадет цифра (2) (т. е. выпадет (1), (3), (4), (5) или (6)).

Эту формулу удобно использовать, если у опыта много исходов.

Пример:

в корзине лежат (100) пронумерованных шариков. Какова вероятность, что не вынут шарик под номером (6)?

Событие (A) — вынут мячик (№) (6).

Событие

A¯

— вынутый мячик не будет под номером (6).

P(A¯)=1−P(A)=1−1100=99100

Источник

сложения применима. Искомая вероятность

P(A+B)=P(A)+P(B)=1/3+1/6=1/2.

Противоположными называют два единственно возможных события, образующих полную группу. Если одно из двух противоположных событий обозначено через А, то другое принято

обозначать A .

Пример. Попадание и промах при выстреле по цели —

противоположные события. Если А — попадание, то A — промах.

Пример . Из ящика наудачу взята деталь. События «появилась стандартная деталь» и «появилась нестандартная деталь» — противоположные.

Теорема. Сумма вероятностей противоположных событий равна единице:

Р(А) + Р( A )=1.

Замечание. Если вероятность одного из двух противоположных событий обозначена через р, то вероятность другого события обозначают q . Таким образом, в силу предыдущей теоремы

р+q=1.

Пример 1.15. Вероятность того, что день будет дождливым, р=0,7. Найти вероятность того, что день будет ясным.

Решение. События «день дождливый» и «день ясный» — противоположные, поэтому искомая вероятность

q=1-р=1-0,7 = 0,3.

1.9. Принцип практической невозможности маловероятных событий

При решении многих практических задач приходится иметь дело с событиями, вероятность которых весьма мала,

т. е. близка к нулю. Можно ли считать, что маловероятное событие А в единичном испытании не произойдет? Такого заключения сделать нельзя, так как не исключено, хотя и мало вероятно, что событие А наступит.

Казалось бы, появление или не появление маловероятного события в единичном испытании предсказать невозможно. Однако длительный опыт показывает, что маловероятное событие в единичном испытании в подавляющем большинстве случаев не наступает. На основании этого факта принимают следующий «принцип практической невозможности маловероятных событий»:

если случайное событие имеет очень малую вероятность, то практически можно считать, что в единичном испытании это событие не наступит.

Естественно возникает вопрос: насколько малой должна быть вероятность события, чтобы можно было считать невозможным его появление в одном испытании? На этот вопрос нельзя ответить однозначно. Для задач, различных по существу, ответы разные. Например, если вероятность того, что парашют при прыжке не раскроется, равна 0,01, то было бы недопустимым применять такие парашюты. Если же вероятность того, что поезд дальнего следования прибудет с опозданием, равна 0,01, то можно практически быть уверенным, что поезд прибудет вовремя.

Достаточно малую вероятность, при которой (в данной определенной задаче) событие можно считать практически невозможным, называют уровнем значимости. На практике обычно принимают уровни значимости, заключенные между 0,01 и 0,05. Уровень значимости, равный 0,01 называют однопроцентным; уровень значимости, 0,02, называют двухпроцент-

ным, и т. д.

Подчеркнем, что рассмотренный здесь принцип позволяет делать предсказания не только о событиях, имеющих малую вероятность, но и о событиях, вероятность которых близка к единице. Действительно, если событие А имеет вероятность, близкую к нулю, то вероятность противоположного события А близка к единице. С другой стороны не появление события А означает наступление противоположного события А . Таким образом, из принципа невозможности маловероятных событий вытекает следующее важное для приложений следствие: если случайное событие имеет вероятность, очень близкую к единице, то практически можно считать, что в единичном испытании это событие наступит. Разумеется, и здесь ответ на вопрос о том, какую вероятность считать близкой к единице, зависит от существа задачи.

1.10. Теорема умножения вероятностей. Произведение событий

Произведением двух событий А и В называют событие А

В, состоящее в совместном появлении (совмещении) этих событий. Например, если А—деталь годная, В—деталь окрашенная, то АВ—деталь годна и окрашена. Произведением нескольких событий называют событие, состоящее в совместном появлении всех этих событий. Например, если А, В, С—появление «орла» соответственно в первом, втором и третьем бросаниях монеты, то ABC — выпадение «орла» во всех трех испытаниях.

1.11. Условная вероятность

Во введении случайное событие определено как событие, которое при осуществлении совокупности условий S может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий S, не налагается, то такую вероятность называют безусловной; если

же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события В при дополнительном условии, что произошло событие А. Заметим, что и безусловная вероятность, строго говоря, является условной, поскольку предполагается осуществление условий.

Условной вероятностью РА (В) называют вероятность события В, вычисленную в предположении, что событие А уже наступило.

Условная вероятность события В при условии, что событие A уже наступило, по определению, равна

РА(В) = Р(АВ)/Р(А) (Р( A) 0).

1.12. Теорема умножения вероятностей

Рассмотрим два события: A и В; пусть вероятности Р (А) и РА (В) известны. Как найти вероятность совмещения этих событий, т. е. вероятность того, что появится и событие А и событие В? Ответ на этот вопрос дает теорема умножения.

Теорема. Вероятность совместного появления двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило:

Р(АВ) = Р(А)РА(В).

Замечание. Справедливо равенство

Р(А)РА(В) = Р(В)РВ(А).

Следствие. Вероятность совместного появления нескольких событий равна произведению вероятности одного из них на условные вероятности всех остальных, причем вероятность каждого последующего события вычисляется в предположении,

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

На этой странице вы узнаете

Как кот может быть одновременно жив и мертв?
Можно ли всегда выигрывать спор с монеткой?
Если рандомно ответить на вопрос теста, какой шанс угадать ответ?

Какова вероятность выиграть в лотерею? Исследователи подсчитали: один на восемь миллионов. «Или выиграю, или проиграю», — решаю я, покупая лотерейный билет. Так понятие вероятности преследует нас в обычной жизни. И не только в лотерее. Давайте разберемся подробнее.

Вероятность

Выходя утром из дома, мы задумываемся: брать ли с собой зонт? Проверяем прогноз погоды — вероятность выпадения осадков 2%. Зонтик нам сегодня вряд ли понадобится. В пути нас настигает ливень…

Прогноз погоды — самый яркий пример вероятности. Он не всегда бывает точный, не всегда сбывается. Мы не можем с уверенностью сказать, что будет завтра. Зато можем по совокупности факторов определить, на какую погоду стоит ориентироваться.

Теория вероятности — один из разделов математики, в котором изучаются модели случайных экспериментов.

Случайными экспериментами называются такие, результаты которых неизвестны заранее. Подбрасывая монетку, мы не знаем, что выпадет — орел или решка. Только поймав монетку, мы узнаем результат.

Как кот может быть одновременно жив и мертв?

Ученый по имени Эрвин Шредингер провел мысленный эксперимент. Он поместил кота в закрытый ящик, в котором был расположен механизм, содержащий атомное ядро и ёмкость с ядовитым газом.

По эксперименту с вероятностью 0,5 ядро распадется, емкость с газом откроется и кот умрет. Но при этом с вероятностью 0,5 ядро не распадается и кот останется жив.

Пока ящик закрыт, мы не знаем результат эксперимента — такой эксперимент в математике можно назвать случайным. Тем временем кот находится одновременно в двух состояниях: он и жив, и мертв.

Рассмотрим чуть подробнее пример с монеткой. Есть всего два варианта, какое событие может произойти:

выпадет орел;
выпадет решка.

Эти два события образуют множество элементарных событий.

Множество элементарных событий — множество всех возможных результатов случайного эксперимента.

В случае выше их всего два. А если мы будем подбрасывать игральную кость, то их будет уже 6. Множество элементарных событий будет менять в зависимости от ситуации.

Допустим, мы поспорили с друзьями, что выпадет орел. Для нас это событие будет благоприятным, поскольку мы выиграем спор. Второе событие будет неблагоприятным, потому что спор будет проигран.

Как найти вероятность, что мы выиграем спор? Нужно разделить число благоприятных событий на общее число событий. Таким образом, мы получили классическое определение вероятности.

Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.

Пусть m — количество благоприятных исходов, а n — количество всех событий. Получаем следующую формулу.

(P = frac{m}{n})

Вероятность можно обозначить, как P(x), где х — некоторое событие.

Заметим, что количество благоприятных исходов должно быть либо меньше, либо равно количеству всех исходов. Если благоприятных событий больше, чем всех, значит, мы нашли не все множество элементарных событий.

Когда вероятность равна 1, то такое событие точно наступит. Иначе говоря, мы можем быть уверены на 100% — оно произойдет.

Можно ли всегда выигрывать спор с монеткой?

Можно, если хитро сформулировать условия. Например: «Орел — я выиграл, решка — ты проиграл». Вероятность выигрыша в этом случае будет равна (P = frac{2}{2} = 1), то есть мы точно выиграем спор.

Однако вероятность не так проста, и даже здесь подготовила ловушку.

В редких случаях есть и третий вариант событий — монетка встанет на ребро. Вероятность такого события составляет (frac{1}{6000}). То есть за миллион бросков это может случиться 150 раз или 1 раз в 2 дня, если подкидывать монету каждый день по 8 часов в течение года. Чтобы монета встала на ребро два раза подряд, придется подбрасывать ее в том же темпе около 35 лет.

Вероятность всегда будет меньше или равна 1. Но ее можно выразить и через проценты. Для этого достаточно умножить полученный результат на 100%.

Пример 1. На ресепшене одного из отелей стоит ваза с конфетами. В вазе 56 яблочных конфет, 49 апельсиновых и 35 малиновых. Гость отеля наугад тянет конфету. Какова вероятность, что ему попадется апельсиновая конфета?

Решение. Найдем, сколько всего конфет в вазе: 56 + 49 + 35 = 140. Вероятность вытащить апельсиновую конфету будет равна
(frac{49}{140} = 0,35)

Выразим в процентах:
0,35 * 100% = 35%

Задача решена. Обычно в ответе пишут значение вероятности через дробное число, а не проценты. Поэтому получаем следующий ответ.

Ответ: 0,35

Чтобы выразить вероятность через проценты в одно действие, достаточно воспользоваться следующей формулой.

(P = frac{m}{n} * 100%)

Но что, если нам нужно найти вероятность для более сложных экспериментов? Первым делом нужно определить, какие события перед нами.

Равновозможные и противоположные события

Когда мы бросаем игральную кость, вероятность выпадения любого из чисел равна 16. То есть вероятности выпадения чисел равны между собой. Такие события называются равновозможными.

Равновозможные события — такие события, что по условиям опыта ни одно из них не является более возможным, чем другие.

Вероятности появления событий равны.

Для игрального кубика существует всего шесть событий, которые могут произойти: выпадет число 1, 2, 3, 4, 5 или 6. Все эти события образуют полную группу событий.

Полная группа событий — такая группа событий, если в результате опыта обязательно появится хотя бы одно из них.

В результате подбрасывания монеты выпадет либо орел, либо решка. То есть полная группа событий состоит из двух событий.

Мы подбросили монету и выпал орел. Следовательно, не выпала решка.

А если не выпадет орел? Обязательно выпадет решка. Эти события будут называться противоположными.

Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.

Обозначим событие “выпала решка” как A. Противоположное ему событие “выпал орел” обозначим как (overline{A}).

Заметим, что вероятность события A равняется 12, как и вероятность события (overline{A}). Чему равна их сумма?

)frac{1}{2} + frac{1}{2} = 1)

Так мы вывели связь между противоположными событиями. Поскольку они всегда образуют полную группу событий, то сумма их вероятностей будет равна 1.

(P(A) + P(overline{A}) = 1)

Какие еще примеры противоположных событий можно назвать? Ясная и дождливая погода. Если наступает одно из этих событий, то второе уже не может наступить.

Объединение и пересечение событий

Допустим, у нас есть два события: сегодня пойдет снег и сегодня пойдет дождь. Что будет, если мы их объединим?

Объединение событий — событие, состоящее из всех элементарных исходов, благоприятствующих хотя бы одному из событий.

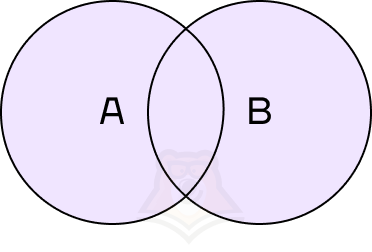
В этом случае мы получим событие, которое будет выполняться при любом из исходов: и если пойдет снег, и если не пойдет снег.

Объединение событий обозначается знаком (cup). Объединение событий А и В можно записать как (A cup B).

Рассмотрим немного другой пример. В первое событие входит, что Илья получит пятерку по физике, а второе событие — Антон получит пятерку по физике. А как можно назвать событие, если оба мальчика получат пятерку по физике?

Пересечение событий — событие, состоящее из всех элементарных исходов, благоприятствующих обоим событиям.

Пересечение событий обозначается знаком (cap). Пересечение событий А и В можно записать как (A cap B).

Несовместные и совместные события

Рассмотрим два события: “чайник исправно работает” и “чайник сломался”. Могут ли эти события существовать одновременно? Нет, поскольку появление одного из них исключает появление другого.

Такие события называются несовместными. Название само говорит, что события не могут существовать одновременно.

Несовместные события — такие события, появление одного из которых исключает появление другого.

Решим небольшую задачу. На экзамене есть несколько билетов. С вероятностью 0,5 попадется билет по планиметрии. С вероятностью 0,3 попадется билет по экономике. При этом не существует билетов, которые включают обе эти темы. С какой вероятностью на контрольной попадется билет по одной из этих тем?

Представим билеты в виде схемы. Заметим, что нам нужно объединить два из трех кругов, то есть сложить их вероятности.

Следовательно, вероятность будет равна 0,5 + 0,3 = 0,8.

Сформулируем определение суммы вероятностей двух несовместных событий.

Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей:

(P(A cup B) = P(A) + P(B))

Если существуют несовместные события, то существуют и совместные.

Совместные события — события, наступление одного из которых не исключает наступления другого.

В магазине работают два консультанта. Один из них занят общением с клиентом. Означает ли это, что второй консультант тоже занят? Нет, поскольку они работают независимо друг от друга. Если занят первый консультант, второй может быть как занят, так и нет.

Подбросим игральный кубик и рассмотрим два вида событий. Пусть событие А — это “выпадет число 2”, событие В — “выпадет четное число”.

Найдем вероятность события А: (frac{1}{6}).

Для события В всего три благоприятных исхода из шести: выпадет число 2, 4 или 6. Тогда вероятность наступления события В равна (frac{3}{6} = frac{1}{2})

Исключают ли события А и В друг друга? Нет, поскольку если произойдет событие А, произойдет и событие В. Когда произойдет событие В, есть вероятность, что произойдет и событие А.

Найдем объединение совместных событий на примере кругов. Если мы наложим их друг на друга, то в середине получится как бы два слоя. Проверить это можно, если наложить друг на друга два листа бумаги.

А нужно получить вот такую картину:

Поэтому для объединения двух кругов нам нужно будет исключить одну из серединок.

Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения:

(P(A cup B) = P(A) + P(B) — P(A cap B))

В каких случаях нужно пользоваться формулой со сложением? Достаточно, чтобы задачу можно было сформулировать с помощью “или”. Например, нужно, чтобы выпали темы по планиметрии или по экономике.

Независимые и зависимые события

Прогуляемся в магазин за булочками. В упаковке две булочки, а сама упаковка непрозрачная, то есть увидеть булочки до вскрытия упаковки мы не можем.

Известно, что на заводе, где изготавливаются булочки, 5 из 100 булочек подгорают. Значит, 95 из 100 булочек не подгорают. По классическому определению вероятности находим, что вероятность каждой булочки не подгореть равна (frac{95}{100} = 0,95).

Какова вероятность, что в упаковке попадутся только не подгорелые булочки? Как найти вероятность сразу для двух булочек?

Ответим на вопрос: зависят ли булочки друг от друга?

Если подгорит одна из булочек в упаковке, не обязательно подгорит другая. Следовательно, булочки не зависят друг от друга. Такие события называются независимыми.

Независимые события — такие события, появление одного из которых не зависит от появления другого события.

Определим вероятность независимых событий.

Пусть вероятность, что подгорела первая булочка, будет равна Р(А) = 0,95, а вероятность для второй булочки будет равна Р(В) = 0,95.

А чтобы найти вероятность независимых событий, нужно воспользоваться следующей формулой:

(P(A cap B) = P(A) * P(B))

Тогда вероятность, что булочки в одной упаковке не подгорят, равняется P = 0,95 * 0,95 = 0,9025.

В каком случае нужно пользоваться этой формулой? Нужно подставить союз “и”.

Мы хотим, чтобы в упаковке первая булочка была не подгорелой и вторая булочка была не подгорелой.

Приведем еще один пример. В здании два автомата с кофе на разных этажах. Даже если сломается один из них, работа второго не будет зависеть от первого.

Но если автоматы стоят рядом и включены в одну розетку, то при поломке одного из них есть вероятность выхода из строя розетки, а значит, и второй автомат тоже сломается. Такие события будут зависимыми: появление одного из них зависит от появления другого.

Предположим, что в мешке лежит семь кубиков: два из них оранжевые, а пять — фиолетовые. Из мешка дважды вытаскивают кубики. Какова вероятность, достать во второй раз именно фиолетовый кубик?

Нужная последовательность может быть в двух случаях:

сначала вытащат фиолетовый кубик и потом снова фиолетовый;
сначала вытащат оранжевый кубик, а потом фиолетовый.

Разберем первый случай. Вероятность в первый раз вытащить фиолетовый кубик равна (frac{5}{7}). После этого в мешке останется шесть кубиков, четыре из которых будут фиолетовые.

Вероятность вытащить во второй раз фиолетовый кубик равна (frac{5}{7} * frac{4}{6} = frac{20}{42} = frac{10}{21}).

Теперь рассмотрим второй случай. Вероятность в первый раз достать оранжевый кубик равна (frac{2}{7}). В мешке останется шесть кубиков, пять из которых будут фиолетовыми.

Вероятность вытащить во второй раз фиолетовый кубик будет уже равна (frac{2}{7} * frac{5}{6} = frac{10}{42} = frac{5}{21}).

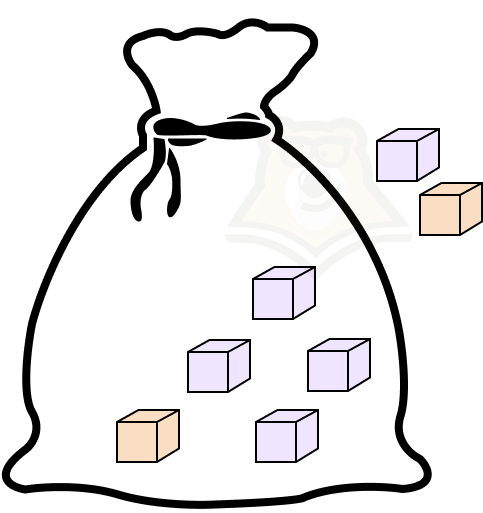
В этом примере очень наглядно видно, что вероятность напрямую зависит от того, какой кубик попался первым. Следовательно, эти события зависимы.

Как отличить зависимые и независимые события? Если после наступления первого события меняется количество благоприятных и всех исходов, то такие события — зависимые. Если количество благоприятных и всех исходов не меняется, то события независимые.

Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.

Условная вероятность обозначается P(B|A). В нашем примере условной вероятностью будет вычисление, что во второй раз попадется именно фиолетовый кубик.

Найдем вероятность двух зависимых событий. Формула похожа на ту, что используется для независимых событий. Но в этот раз нам нужно применить условную вероятность.

Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило:

(P(A cap B) = P(A) * P(B | A))

Формула Бернулли

Рассмотрим случаи, когда испытание повторяется многократно. Для этого еще раз обратимся к игральному кубику. Подбросим кубик 8 раз. Какова вероятность, что цифра 5 выпала ровно три раза?

Пусть p — вероятность, что выпадет цифра 5. Тогда (p = frac{1}{6}).

Теперь возьмем q — противоположное р событие — вероятность, что цифра 5 не выпадет. (q = frac{5}{6}).

Обозначим количество всех бросков за n, а количество выпадения цифры 5 за k.

Чтобы решить задачу, нужно воспользоваться формулой Бернулли.

(P_n(k) = C_n^k * p^k * q^{n — k})

Множитель (C_n^k) — это число сочетаний. Подробнее узнать про сочетания можно в статье «Основы комбинаторики».

Решим задачу, подставив значения в формулу:

(P_8(3) = C_8^3 * (frac{1}{6})^3 * (frac{5}{6})^5 = frac{8!}{5!3!} * frac{1}{6^3} * frac{5^5}{6^5} = frac{6 * 7 * 8}{1 * 2 * 3} * frac{5^5}{6^8} approx 0,1)

Фактчек

Вероятность — отношение количества благоприятных событий к количеству всех возможных событий.
События могут быть противоположными. Противоположные события — такие события, если при не наступлении одного обязательно наступает второе.
События можно разделить на совместные и несовместные. Несовместные события — такие события, появление одного из которых исключает появление другого. Если события А и В несовместны, то вероятность их объединения равна сумме их вероятностей: P(A (cup) B) = P(A) + P(B). Совместные события — события, наступление одного из которых не исключает наступления другого. Если события А и В совместны, то вероятность их объединения равна сумме их вероятностей без вероятности их пересечения: P(A cup B) = P(A) + P(B) — P(A cap B).
События также можно разделить на независимые и зависимые. Независимые события — такие события, появление одного из которых не зависит от появления другого события. Вероятность независимых событий можно найти по формуле P(A cap B) = P(A) * P(B). Зависимые события — это события, появление одного из которых зависит от появления другого. Вероятность появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, при условии, что первое событие уже наступило. P(A cap B) = P(A) * P(B | A).
Условная вероятность — вероятность некоторого события В при условии наступления некоторого события А.

Проверь себя

Задание 1.
Какие события являются несовместными?

Подбрасывание монетки.
Брак батареек в одной упаковке.
“Миша идет” и “Миша стоит”.
Случайное вытаскивание конфет из вазы.

Задание 2.
Алена делает ошибку при решении задач по математике с вероятностью 0,17. С какой вероятностью она не сделает ошибку при решении задачи?

0,17
1
0,83
1,17

Задание 3.
Артем решал задачи на вероятность. Ниже приведены его ответы. В какой из задач он точно совершил ошибку?

1
0,216
0,45
1,5

Задание 4.
В упаковке три шариковые ручки. С вероятностью 0,1 такая ручка не будет писать. Найдите вероятность, что все три ручки в упаковке пишут.

0,3
0,001
2,7
0,729

Задание 5.
Перед Дашей лежит несколько карточек. Она случайно переворачивает одну из них. С вероятностью 0,5 на карточке окажется рисунок природы. С вероятностью 0,27 на карточке окажется мотивационная цитата. Карточек и с рисунком, и с цитатой нет. Найдите вероятность, что Дана перевернет карточку или с рисунком, или с цитатой.

0,77
0,135
0,23
-0,23

Ответы: 1. — 3 2. — 3 3. — 4 4. — 4 5. — 1

Источник

Сложение и умножение вероятностей

Сложение вероятностей несовместных событий
Вероятность противоположного события
Умножение вероятностей независимых событий
Вероятность появления хотя бы одного события
Примеры

п.1. Сложение вероятностей несовместных событий

События называют несовместными, если они не могут произойти одновременно в результате одного опыта.

Например:
1) Нельзя одновременно A = «получить 5» и B = «получить 2» на экзамене. События A и B – несовместны.
2) Нельзя одновременно C = «достать туз» и D = «достать шестерку» из колоды карт. События C и D – несовместны.

Вероятность появления одного из двух несовместных событий A или B равна сумме вероятностей этих событий: $$ mathrm{ P(Avee B)=P(A) + P(B) } $$

Если обобщить на любое количество событий:

Вероятность появления нескольких несовместных событий A₁ или A₂ или …A_k равна сумме вероятностей этих событий: $$ mathrm{ P(A_1vee A_2vee … vee A_k)=P(A_1) + P(A_2) + … + P(A_k) } $$

Например:
Стрелок может попасть в «10» с вероятностью P(10) = 0,3, в «9» – с вероятностью P(9) = 0,2. Значит, попасть в «10 или 9» он может с вероятностью:

P(«10 или 9») = 0,3 + 0,2 = 0,5

п.2. Вероятность противоположного события

Пространство элементарных событий образует полную группу событий.

Сумма вероятностей всех событий, образующих полную группу, равна единице. $$ mathrm{ Omega={A_1, A_2, …, A_k}, P(A_1) + P(A_2) + … + P(A_k) = 1 } $$

Например:
При бросании кубика Ω = {1; 2; … ; 6} – полная группа событий.
Вероятности выпадения каждой грани: (mathrm{p_1=p_2=…=p_6=frac16})
Сумма всех вероятностей: (mathrm{p_1+p_2+…+p_6=6cdot frac16=1})

Два случайных события A и B называют противоположными, если они несовместны и образуют полную группу событий: $$ mathrm{ Omega=left{A;Bright}, B=overline{A}, } $$ Сумма вероятностей противоположных событий равна единице. $$ mathrm{ P(A) + P(B) = P(A) + P(overline{A}) = 1 } $$

Например:
Вероятность попадания стрелка в мишень p = 0,8.
Противоположное событие: стрелок не попадёт в мишень. Его вероятность:
q = 1 – p = 0,2.

п.3. Умножение вероятностей независимых событий

Два случайных события A и B называют независимыми, если наступление одного из них не изменяет вероятность наступления другого.
Вероятность совместного появления двух независимых событий A и B равна произведению вероятностей этих событий: $$ mathrm{ P(A wedge B) = P(A) cdot P(B) } $$

Если обобщить на любое количество событий:

Вероятность совместного появления нескольких независимых событий A₁ и A₂ и … A_k равна произведению вероятностей этих событий: $$ mathrm{ P(A_1wedge A_2wedge …wedge A_k)=P(A_1)cdot P(A_2)cdot … cdot P(A_k) } $$

Например:
Вероятность попадания стрелка в мишень p = 0,8.
Стрелок делает три выстрела подряд.
1) Какова вероятность, что он попал все три раза?
Каждый выстрел является независимым событием, поэтому вероятность трёх удачных выстрелов подряд:

P₃ = P(+, +, +) = p · p · p = 0,8³ = 0,512

2) Какова вероятность, что он не попал ни разу?
Вероятность промаха равна q = 1 – p = 0,2.
Вероятность трёх промахов подряд:

P₀ = P(–, –, –) = q · q · q = 0,2³ = 0,008

3) Какова вероятность, что он попал только один раз?
Стрелок мог попасть при первом выстреле, а затем два раза промахнуться, или при втором выстреле (промахнуться на первом и третьем), или при третьем (промахнувшись два раза поначалу). Сложение и умножение вероятностей даёт итоговую вероятность одного попадания:

P₁ = P(+,–,–) + P(–,+,–) + P(–,–,+) =
p · q · q + q · p · q + q · q · p = 3pq² = 3 · 0,8 · 0,2² = 0,096

4) Какова вероятность, что он промахнулся один раз?
Аналогичные предыдущему пункту рассуждения приводят к такому выражению для вероятности двух попаданий (одного промаха):

P₂ = P(–,+,+) + P(+,–,+) + P(+,+,–) =
q · p · p + p · q · p + p · p · q = 3p²q = 3 · 0,8² · 0,2 = 0,384

Мы получили следующий закон распределения для возможного количества попаданий из трёх выстрелов:

Количество попаданий, X

Вероятность, P_x

0,008

0,096

0,384

0,512

X = {0; 1; 2; 3} образует полную группу событий. Сумма всех вероятностей:

P₀ +P₁ + P₂ + P₃ = 0,008 + 0,096 + 0,384 + 0,512 = 1

п.4. Вероятность появления хотя бы одного события

Вероятность появления хотя бы одного из событий A₁, A₂, …, A_k, независимых в совокупности, равна разности между единицей и произведением вероятностей противоположных событий: $$ mathrm{ P(A)=1-q_1cdot q_2cdot … cdot q_{k}, q_{i}=1-p_{i} } $$

Например:
Студент сдаёт два экзамена.
Вероятность сдать первый экзамен равна p₁ = 0,7 второй – p₂ = 0,6.
Тогда вероятность сдать хотя бы один экзамен: P = 1 – q₁q₂ = 1 – 0,3 · 0,4 = 0,88.

п.5. Примеры

Пример 1. Подбрасывают четыре игральных кубика. Какова вероятность, что на каждом из них выпадет нечётное число очков?

Для кубика Ω = {1; 2; 3; 4; 5; 6} – пространство элементарных событий.
Выпадение нечётного числа A = {1; 3; 5}. Вероятность выпадения нечётного числа для одного кубика: (mathrm{p=frac{k}{n}=frac36=frac12}).
Результаты подбрасывания 4-х кубиков являются независимыми. Вероятность, что на каждом выпадет нечётное число: $$ mathrm{ P=pcdot pcdot pcdot p=p^4=frac{1}{2^4}=frac{1}{16} } $$ Ответ: (frac{1}{16}).

Пример 2. На полигоне испытываются три ракеты.
Вероятность успешного испытания для каждой из ракет: p₁ = 0,8, p₂ = 0,75, p₃ = 0,6.
Какова вероятность, что хотя бы одна ракета пройдёт испытания успешно?

Найдём вероятность того, что ни одна из ракет не пройдёт испытаний:

q₁ = 1 – p₁ = 0,2, q₂ = 1 – p₂ = 0,25, q₃ = 1 – p₃ = 0,4
q₁ · q₂ · q₃ = 0,2 · 0,25 · 0,4 = 0,02

Тогда, искомая вероятность (противоположное событие):

P = 1 – q₁ · q₂ · q₃ = 1 – 0,02 = 0,98

Ответ: 0,98.
Мораль: инвестору нужно показывать сразу несколько сырых проектов.

Пример 3. В системе пожарной сигнализации установлены два независимых датчика. Вероятность срабатывания каждого из датчиков при пожаре: p₁ = 0,6; p₂ = 0,7. Найдите вероятность того, что при пожаре:
1) сработает ровно один датчик;
2) сработает хотя бы один датчик.

Вероятности отказов: q₁ = 1 – p₁ = 0,4; q₂ = 1 – p₂ = 0,3.
1) Событие «сработает ровно один датчик» является суммой двух событий «первый сработал, второй – отказал» или «первый отказал, второй – сработал». Вероятность:

P₁ = p₁q₂ + q₁p₂ = 0,6 · 0,3 + 0,4 · 0,7 = 0,46

2) Найдем вероятность отказа обоих датчиков:

P₀ = q₁q₂ = 0,4 · 0,3 = 0,12

Событие «сработает хотя бы один датчик» является противоположным отказу обоих датчиков. Вероятность:

P_{1 ∨ 2} = 1 – P₀ = 1 – 0,12 = 0,88

Ответ: 1) 0,46; 2) 0,88.

Пример 4. У админа в ящике 11 плат, из которых 3 – бракованные.
Наугад берётся 2 платы. Какова вероятность того, что хотя бы одна из них – рабочая?

Найдём вероятность того, что обе выбранные платы – бракованные.
Выбрать 2 платы из 3 бракованных можно (mathrm{C_3^2=C_3^1=3}) способами.
Выбрать 2 платы из общей совокупности можно (mathrm{C_{11}^2=frac{11cdot 10}{1cdot 2}=55}) способами.
Вероятность взять обе бракованные платы из ящика: (mathrm{P_{2 text{бр}}=frac{C_3^2}{C_2^{11}}=frac{3}{55}})
Значит, вероятность того, что хотя бы одна плата не будет бракованной (противоположное событие):
(mathrm{P=1-P_{2 text{бр}}=1-frac{3}{55}=frac{52}{55}}).
Ответ: (mathrm{frac{52}{55}}).

Пример 5*. Парадокс дней рождения
В классе учится k человек. Исследуйте вероятность того, что хотя бы у двух одноклассников дни рождения совпадают.

Считаем, что в году n = 365 дней.
Пусть день рождения одного из учеников известен (один день в году – «занят»).
Тогда вероятность того, что день рождения второго ученика не совпадает с днём рождения первого: (mathrm{q_2=1-frac{1}{365}}) («заняты» два дня).
Вероятность того, что день рождения третьего ученика не совпадает с днями рождения первых двух: (mathrm{q_3=1-frac{2}{365}}) («заняты» три дня). И т. д.
Для всех k учеников вероятность того, что все дни рождения разные: begin{gather*} mathrm{ widetilde{p}(k)=q_2cdot q_3cdot … cdot q_{k}=left(1-frac{1}{365}right)left(1-frac{2}{365}right)…left(1-frac{k-1}{365}right)= }\ mathrm{ =frac{364cdot 363cdot … cdot(365-k+1)}{365^{k-1}}= frac{365cdot 364cdot 363cdot … cdot(365-k+1)}{365^{k}}= frac{365!}{365^{k}(365-k)!} } end{gather*} Значит, вероятность того, что хотя бы у двух одноклассников дни рождения совпадают: begin{gather*} mathrm{ p(k)=1-widetilde{p}(k)=1-frac{365!}{365^{k}(365-k)!} } end{gather*}

Таким образом, в классе из 30 человек вероятность совпадения дней рождения равна 70,63%. А в группе из 50 человек она достигает 97,04%.

Источник