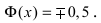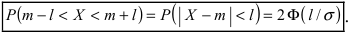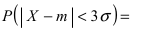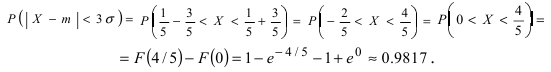Часто
требуется вычислить вероятность того,
что отклонение нормально распределенной
случайной величины
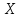
абсолютной величине меньше заданного
положительного числа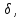
требуется найти вероятность осуществления
неравенства
Перейдем
к двойному неравенству
так
как
то
События,
состоящие в осуществление неравенств
противоположные.
Поэтому,
если вероятность осуществления
неравенства
равна
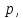
равна
Рассмотрим
пример.
Случайная величина

нормально. Математическое ожидание и
среднее квадратическое отклонение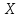
равны 20 и 10. Найти вероятность того, что
отклонение по абсолютной величине будет
меньше трех.
По
условию
Тогда
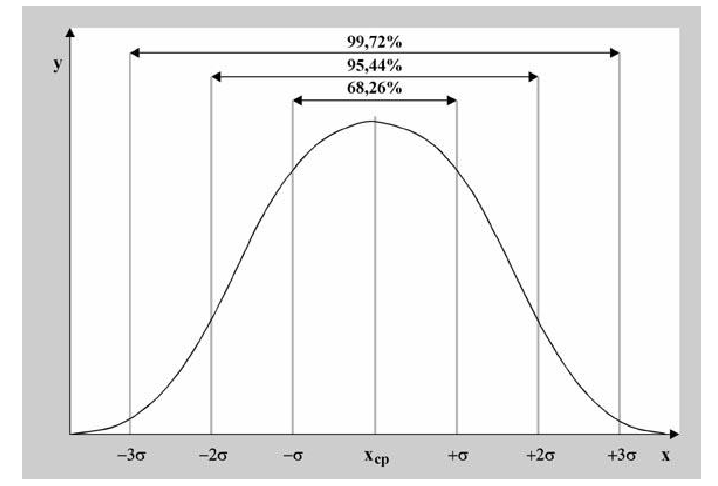
Правило
трех сигм.
Преобразуем
формулу
Пусть
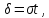
Если
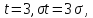
т.е.
вероятность того, что отклонение по
абсолютной величине будет меньше
утроенного среднего квадратического
отклонения, равна 0,9973. Другими
словами, вероятность того, что абсолютная
величина отклонения превысит утроенное
среднее квадратическое отклонение,
очень мала, а именно 0,0027.
В
этом и состоит правило
трех сигм:
если случайная величина распределена
нормально, то абсолютная величина ее
отклонения от математического ожидания
не превосходит утроенного среднего
квадратического отклонения.
На
практике применяют правило трех сигм
в случаях: если распределение изучаемой
случайной величины неизвестно, но
условие, указанное в приведенном правиле,
выполняется, то есть основание
предполагать, что изучаемая случайная
величина распределена нормально; в
противном случае, случайная величина
не распределена нормально.
Контрольные
вопросы
1.
Сформулировать понятие потока событий.
2.
Записать аналитически и изобразить
графически нормальный, равномерный и
показательный законы распределения.
3.
В чем состоит смысл правила трех сигм?
Лекция
№48. Закон больших чисел
48.1.
Закон больших чисел и его практическое
значение.
48.2.
Центральная предельная теорема Ляпунова.
48.3.
Применение закона больших чисел и
центральной предельной теоремы.
48.1. Закон больших чисел и его практическое значение
Нельзя
заранее уверенно предвидеть, какое из
возможных значений примет случайная
величина в итоге испытания; это зависит
от многих случайных причин, учесть
которые невозможно. Вряд ли можно
установить закономерности поведения
и суммы достаточно большого числа
случайных величин. На самом деле это не
так. При некоторых сравнительно широких
условиях суммарное поведение достаточно
большого числа случайных величин почти
утрачивает случайный характер и
становится закономерным.
Для
практики очень важно знание условий,
при выполнении которых совокупное
действие очень многих случайных причин
приводит к результату, почти не зависящему
от случая, так как позволяет предвидеть
ход явлений. Эти условия указываются в
теоремах, носящих название закона
больших чисел (теоремы Чебышева и
Бернулли).
Нормально
распределенные случайные величины
широко распространены на практике. Чем
это объясняется?
Ответ
дал А.М. Ляпунов. Если случайная величина
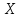
собой сумму очень большого числа взаимно
независимых случайных величин, влияние
каждой из которых на всю сумму ничтожно
мало, то
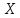
распределение, близкое к нормальному.
В
практической деятельности большое
значение имеют события с вероятностями,
близкими к единице или нулю. Отсюда
становится ясным, что одной из основных
задач теории вероятностей должно быть
установление закономерностей, происходящих
с вероятностями, близкими к единице,
при этом особую роль должны играть
закономерности, возникающие в результате
наложения большого числа независимых
или слабо зависимых случайных факторов.
Закон больших чисел является одним из
таких предложений теории вероятностей.
Под
законом больших
чисел понимают всю
совокупность предложений, утверждающих
с вероятностью, близкой к единице, что
наступит некоторое событие, зависящее
от неограниченного числа случайных
событий, каждое из которых оказывает
на него лишь незначительное влияние.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Нормальным называют распределение вероятностей непрерывной случайной величины
, плотность которого имеет вид:
где
–
математическое ожидание,
–
среднее квадратическое отклонение
.
Вероятность того, что
примет
значение, принадлежащее интервалу
:
где
– функция Лапласа:
Вероятность того, что абсолютная
величина отклонения меньше положительного числа
:
В частности, при
справедливо
равенство:
Асимметрия, эксцесс,
мода и медиана нормального распределения соответственно равны:
, где
Правило трех сигм
Преобразуем формулу:
Положив
. В итоге получим
если
, и, следовательно,
, то
то есть вероятность того, что
отклонение по абсолютной величине будет меньше утроенного среднего квадратического отклонение, равна 0,9973.
Другими словами, вероятность того,
что абсолютная величина отклонения превысит утроенное среднее квадратическое отклонение, очень мала, а именно равна
0,0027. Это означает, что лишь в 0,27% случаев так может произойти. Такие
события исходя из принципа невозможности маловероятных
событий можно считать практически невозможными. В этом и состоит
сущность правила трех сигм: если случайная величина распределена нормально, то
абсолютная величина ее отклонения от математического ожидания не превосходит
утроенного среднего квадратического отклонения.
На практике правило трех сигм
применяют так: если распределение изучаемой случайной величины неизвестно, но
условие, указанное в приведенном правиле, выполняется, то есть основание
предполагать, что изучаемая величина распределена нормально; в противном случае
она не распределена нормально.
Смежные темы решебника:
- Таблица значений функции Лапласа
- Непрерывная случайная величина
- Показательный закон распределения случайной величины
- Равномерный закон распределения случайной величины
Пример 2
Ошибка
высотометра распределена нормально с математическим ожиданием 20 мм и средним
квадратичным отклонением 10 мм.
а) Найти
вероятность того, что отклонение ошибки от среднего ее значения не превзойдет 5
мм по абсолютной величине.
б) Какова
вероятность, что из 4 измерений два попадут в указанный интервал, а 2 – не
превысят 15 мм?
в)
Сформулируйте правило трех сигм для данной случайной величины и изобразите
схематично функции плотности вероятностей и распределения.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
а) Вероятность того, что случайная величина, распределенная по
нормальному закону, отклонится от среднего не более чем на величину
:
В нашем
случае получаем:
б) Найдем
вероятность того, что отклонение ошибки от среднего значения не превзойдет 15
мм:
Пусть событие
– ошибки 2
измерений не превзойдут 5 мм и ошибки 2 измерений не превзойдут 0,8664 мм
– ошибка не
превзошла 5 мм;
– ошибка не
превзошла 15 мм
в)
Для заданной нормальной величины получаем следующее правило трех сигм:
Ошибка высотометра будет лежать в интервале:
Функция плотности вероятностей:
График плотности распределения нормально распределенной случайной величины
Функция распределения:
График функции
распределения нормально распределенной случайной величины
Задача 1
Среднее
количество осадков за июнь 19 см. Среднеквадратическое отклонение количества
осадков 5 см. Предполагая, что количество осадков нормально-распределенная
случайная величина найти вероятность того, что будет не менее 13 см осадков.
Какой уровень превзойдет количество осадков с вероятностью 0,95?
Задача 2
Найти
закон распределения среднего арифметического девяти измерений нормальной
случайной величины с параметрами m=1.0 σ=3.0. Чему равна вероятность того, что
модуль разности между средним арифметическим и математическим ожиданием
превысит 0,5?
Указание:
воспользоваться таблицами нормального распределения (функции Лапласа).
Задача 3
Отклонение
напряжения в сети переменного тока описывается нормальным законом
распределения. Дисперсия составляет 20 В. Какова вероятность при изменении
выйти за пределы требуемых 10% (22 В).
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 4
Автомат
штампует детали. Контролируется длина детали Х, которая распределена нормально
с математическим ожиданием (проектная длинна), равная 50 мм. Фактическая длина
изготовленных деталей не менее 32 и не более 68 мм. Найти вероятность того, что
длина наудачу взятой детали: а) больше 55 мм; б) меньше 40 мм.
Задача 5
Случайная
величина X распределена нормально с математическим ожиданием a=10и средним
квадратическим отклонением σ=5. Найти
интервал, симметричный относительно математического ожидания, в котором с
вероятностью 0,9973 попадает величина Х в результате испытания.
Задача 6
Заданы
математическое ожидание ax=19 и среднее квадратическое отклонение σ=4
нормально распределенной случайной величины X. Найти: 1) вероятность
того, что X примет значение, принадлежащее интервалу (α=15;
β=19); 2) вероятность того, что абсолютная величина отклонения значения
величины от математического ожидания окажется меньше δ=18.
Задача 7
Диаметр
выпускаемой детали – случайная величина, распределенная по нормальному закону с
математическим ожиданием и дисперсией, равными соответственно 10 см и 0,16 см2.
Найти вероятность того, что две взятые наудачу детали имеют отклонение от
математического ожидания по абсолютной величине не более 0,16 см.
Задача 8
Ошибка
прогноза температуры воздуха есть случайная величина с m=0,σ=2℃. Найти вероятность
того, что в течение недели ошибка прогноза трижды превысит по абсолютной
величине 4℃.
Задача 9
Непрерывная
случайная величина X распределена по нормальному
закону: X∈N(a,σ).
а) Написать
плотность распределения вероятностей и функцию распределения.
б) Найти
вероятность того, что в результате испытания случайная величина примет значение
из интервала (α,β).
в) Определить
приближенно минимальное и максимальное значения случайной величины X.
г) Найти
интервал, симметричный относительно математического ожидания a, в котором с
вероятностью 0,98 будут заключены значения X.
a=5; σ=1.3;
α=4; β=6
Задача 10
Производится измерение вала без
систематических ошибок. Случайные ошибки измерения X
подчинены нормальному закону с σx=10. Найти вероятность того, что измерение будет
произведено с ошибкой, превышающей по абсолютной величине 15 мм.
Задача 11
Высота
стебля озимой пшеницы — случайная величина, распределенная по нормальному закону
с параметрами a = 75 см, σ = 1 см. Найти вероятность того, что высота стебля:
а) окажется от 72 до 80 см; б) отклонится от среднего не более чем на 0,5 см.
Задача 12
Деталь,
изготовленная автоматом, считается годной, если отклонение контролируемого
размера от номинала не превышает 10 мм. Точность изготовления деталей
характеризуется средним квадратическим отклонением, при данной технологии
равным 5 мм.
а)
Считая, что отклонение размера детали от номинала есть нормально распределенная
случайная величина, найти долю годных деталей, изготовляемых автоматом.
б) Какой
должна быть точность изготовления, чтобы процент годных деталей повысился до
98?
в)
Написать выражение для функции плотности вероятности и распределения случайной
величины.
Задача 13
Диаметр
детали, изготовленной цехом, является случайной величиной, распределенной по
нормальному закону. Дисперсия ее равна 0,0001 см, а математическое ожидание –
2,5 см. Найдите границы, симметричные относительно математического ожидания, в
которых с вероятностью 0,9973 заключен диаметр наудачу взятой детали. Какова
вероятность того, что в серии из 1000 испытаний размер диаметра двух деталей
выйдет за найденные границы?
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 14
Предприятие
производит детали, размер которых распределен по нормальному закону с
математическим ожиданием 20 см и стандартным отклонением 2 см. Деталь будет
забракована, если ее размер отклонится от среднего (математического ожидания)
более, чем на 2 стандартных отклонения. Наугад выбрали две детали. Какова вероятность
того, что хотя бы одна из них будет забракована?
Задача 15
Диаметры
деталей распределены по нормальному закону. Среднее значение диаметра равно d=14 мм
, среднее квадратическое
отклонение σ=2 мм
. Найти вероятность того,
что диаметр наудачу взятой детали будет больше α=15 мм и не меньше β=19 мм; вероятность того, что диаметр детали
отклонится от стандартной длины не более, чем на Δ=1,5 мм.
Задача 16
В
электропечи установлена термопара, показывающая температуру с некоторой
ошибкой, распределенной по нормальному закону с нулевым математическим
ожиданием и средним квадратическим отклонением σ=10℃. В момент когда термопара
покажет температуру не ниже 600℃, печь автоматически отключается. Найти
вероятность того, что печь отключается при температуре не превышающей 540℃ (то
есть ошибка будет не меньше 30℃).
Задача 17
Длина
детали представляет собой нормальную случайную величину с математическим
ожиданием 40 мм и среднеквадратическим отклонением 3 мм. Найти:
а)
Вероятность того, что длина взятой наугад детали будет больше 34 мм и меньше 43
мм;
б)
Вероятность того, что длина взятой наугад детали отклонится от ее
математического ожидания не более, чем на 1,5 мм.
Задача 18
Случайное
отклонение размера детали от номинала распределены нормально. Математическое
ожидание размера детали равно 200 мм, среднее квадратическое отклонение равно
0,25 мм, стандартами считаются детали, размер которых заключен между 199,5 мм и
200,5 мм. Из-за нарушения технологии точность изготовления деталей уменьшилась
и характеризуется средним квадратическим отклонением 0,4 мм. На сколько
повысился процент бракованных деталей?
Задача 19
Случайная
величина X~N(1,22). Найти P{2
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 20
Заряд пороха для охотничьего ружья
должен составлять 2,3 г. Заряд отвешивается на весах, имеющих ошибку
взвешивания, распределенную по нормальному закону со средним квадратическим
отклонением, равным 0,2 г. Определить вероятность повреждения ружья, если максимально
допустимый вес заряда составляет 2,8 г.
Задача 21
Заряд
охотничьего пороха отвешивается на весах, имеющих среднеквадратическую ошибку
взвешивания 150 мг. Номинальный вес порохового заряда 2,3 г. Определить
вероятность повреждения ружья, если максимально допустимый вес порохового
заряда 2,5 г.
Задача 21
Найти
вероятность попадания снарядов в интервал (α1=10.7; α2=11.2).
Если случайная величина X распределена по
нормальному закону с параметрами m=11;
σ=0.2.
Задача 22
Плотность
вероятности распределения случайной величины имеет вид
Найти
вероятность того, что из 3 независимых случайных величин, распределенных по
данному закону, 3 окажутся на интервале (-∞;5).
Задача 23
Непрерывная
случайная величина имеет нормальное распределение. Её математическое ожидание
равно 12, среднее квадратичное отклонение равно 2. Найти вероятность того, что
в результате испытания случайная величина примет значение в интервале (8,14)
Задача 24
Вероятность
попадания нормально распределенной случайной величины с математическим
ожиданием m=4 в интервал (3;5) равна 0,6. Найти дисперсию данной случайной
величины.
Задача 25
В
нормально распределенной совокупности 17% значений случайной величины X
меньше 13% и 47% значений случайной величины X
больше 19%. Найти параметры этой совокупности.
Задача 26
Студенты
мужского пола образовательного учреждения были обследованы на предмет
физических характеристик и обнаружили, что средний рост составляет 182 см, со
стандартным отклонением 6 см. Предполагая нормальное распределение для роста,
найдите вероятность того, что конкретный студент-мужчина имеет рост более 185
см.
Вычисление вероятности заданного отклонения
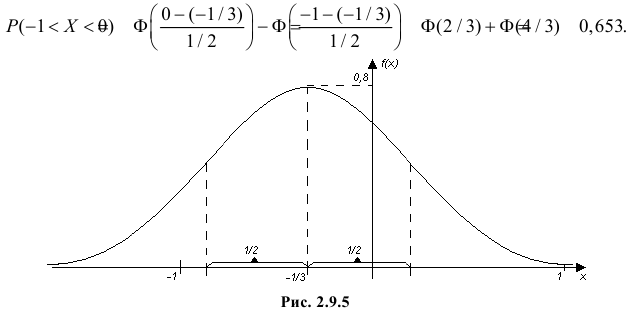
Часто требуется вычислить вероятность того, что отклонение нормально распределенной случайной величины $X$ от ее математического ожидания по абсолютной величине меньше заданного положительного числа $xi $, т.е. требуется найти вероятность осуществления неравенства $left| { X-a }right|prec xi $
Заменим его равносильным $-xi prec X-aprec xi или a-xi prec Xprec xi -a$.
Воспользуемся формулой Лапласа (*) $ P( { alpha prec Xprec beta } )=Phi ( { frac { beta -a } { sigma } } )-Phi ( { frac { alpha -a } { sigma } } ) $ получим
$begin{array} { l } P( { left| { X-a }right|prec xi } )=P( { a-xi prec Xprec xi +a } )=Phi ( { frac { ( { a+xi } )-a } { sigma } } )-Phi ( { frac { a-xi -a } { sigma } } )= \ =Phi ( { frac { xi } { sigma } } )-Phi ( { frac { -xi } { sigma } } )=2Phi ( { frac { xi } { sigma } } ) \ end{array} $
В частности для $a=0$
$P( { left| X right|prec xi } )=2Phi ( { frac { xi } { sigma } } )$
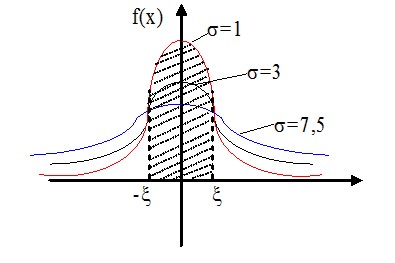
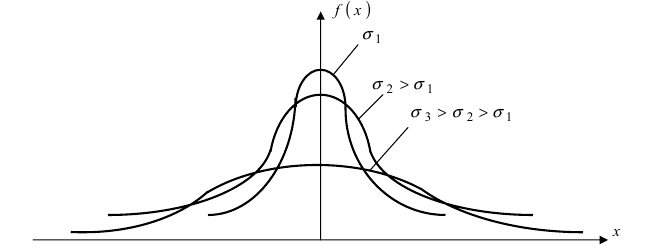
Из рисунка видно, что вероятность того, что случайная величина $X$ примет значения $left| X right|prec xi ( { при,a=0 } )$ больше у той кривой, где $sigma -$ меньше. Этот факт полностью соответствует вероятностному смыслу $sigma , sigma -$ есть среднее квадратическое отклонение, оно характеризует рассеяние случайной величины вокруг ее математического ожидания.
Замечание. Если событие $left| { X-a }right|prec xi $ осуществляется с вероятностью $P$, то противоположное событие $left| { X-a }right|geqslant xi $ с вероятностью $1-P=q$
Пример. Случайная величина $X$ распределена нормально. Математическое ожидание 20 и среднее квадратическое отклонение 10. Найти вероятность того, что отклонение от математического ожидания по абсолютной величине будет меньше 3. $ begin{array} { l } P( { left| { X-a }right|prec xi } )=2Phi ( { frac { xi } { sigma } } ) \ P( { left| { X-20 }right|<3 } )=2Phi ( { frac { 3 } { 10 } } )=2Phi ( { 0,3 } )=2cdot 0,1179=0,2358 \ end{array} $
Тема
«Нормальное распределение»
Нормальным
называют распределение вероятностей непрерывной случайной величины, которое
задается плотностью
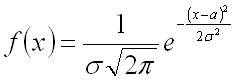
Нормальное распределение задается двумя параметрами:
– математическим ожиданием,
– средним квадратическим отклонением.
График плотности нормального распределения называют нормальной кривой
(кривой Гаусса).
Нормированным называют нормальное распределение с параметрами
.
Плотность нормированного распределения задается формулой
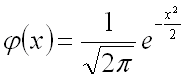
Вероятность
попадания в заданный интервал нормальной случайной величины
Как уже было установлено,
вероятность того, что непрерывная случайная величина
примет значение, принадлежащее интервалу ,
равна определенному интегралу от плотности распределения, взятому в соответствующих
пределах:
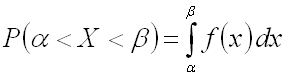
Для нормально распределенной случайной величины соответственно получим:
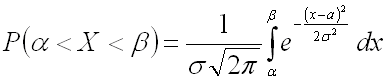
Преобразуем последнее выражение, введя новую переменную 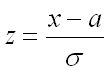
Следовательно, показатель степени выражения, стоящего под интегралом преобразуется
в:
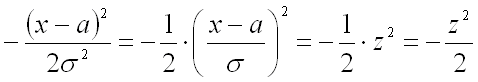
Для замены переменной в определенном интеграле еще необходимо заменить дифференциал
и пределы интегрирования, предварительно выразив переменную из формулы замены:
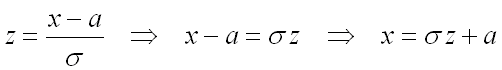
;
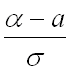
нижний предел интегрирования;
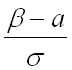
верхний предел интегрирования;
(для нахождения пределов интегрирования по новой переменной
в формулу замены переменной были подставлены
и –
пределы интегрирования по старой переменной ).
Подставим все в последнюю из формул для нахождения вероятности:
где
– функция Лапласа.
Вывод: вероятность того, что нормально распределенная случайная величина
примет значение, принадлежащее интервалу ,
равна:
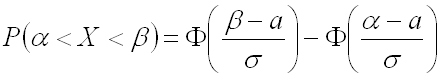
где
– математическое ожидание,
– среднее квадратическое отклонение данной случайной величины.
Примеры
решения задач
Пример 1.
Случайная величина
имеет нормальное распределение с математическим ожиданием
и средним квадратическим отклонением .
Найти вероятность того, что случайная величина
примет значение, принадлежащее интервалу .
Решение.
Известно, что вероятность
того, что нормально распределенная случайная величина
примет значение, принадлежащее интервалу ,
равна:
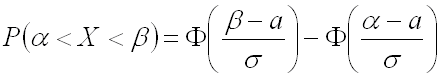
где
– математическое ожидание,
– среднее квадратическое отклонение.
По условию .
Следовательно,
Ответ:
.
Вычисление
вероятности заданного отклонения
Вычислим вероятность того,
что отклонение нормально распределенной случайной величины
от своего математического ожидания по абсолютной величине не превысит ,
то есть вероятность осуществления неравенства .
Заменим неравенство с модулем равносильным ему двойным неравенством:
Теперь мы можем воспользоваться формулой для нахождения вероятности попадания
в заданный интервал нормальной случайной величины, где границами интервала являются
:
(в последних преобразованиях использовано свойство нечетности функции Лапласа:
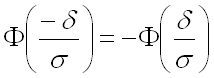
Вывод: вероятность того, что отклонение нормально распределенной случайной величины
от своего математического ожидания по абсолютной величине не превысит ,
равна:
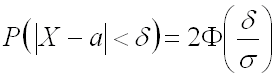
где
– математическое ожидание,
– среднее квадратическое отклонение.
Примеры
решения задач
Пример 1.
Случайная величина
имеет нормальное распределение с математическим ожиданием
и средним квадратическим отклонением .
Найти вероятность того, что случайная величина
отклонится от своего математического ожидания по абсолютной величине не больше,
чем на .
Решение.
Известно, что вероятность
того, что отклонение нормально распределенной случайной величины от
своего математического ожидания по абсолютной величине не превысит ,
равна:
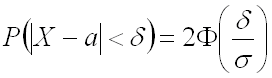
где
– математическое ожидание, –
среднее квадратическое отклонение.
По условию .
Следовательно,
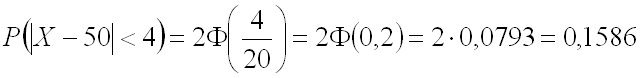
Ответ:
.
Правило
трех сигм
Вычислим вероятность того,
что отклонение нормально распределенной случайной величины
от своего математического ожидания по абсолютной величине не превысит .
Воспользуемся формулой для нахождения вероятности заданного отклонения, в которую
в качестве
подставим :
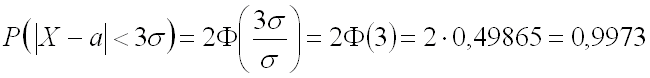
Таким образом, вероятность того, что отклонение случайной величины
по абсолютной величине будет меньше утроенного среднего квадратического отклонения,
равна 0,9973.
Другими словами, вероятность того, что абсолютная величина отклонения превысит
,
составляет всего 0,0027. Такое событие, исходя их принципа невозможности маловероятных
событий, можно считать практически невозможным.
Вывод (правило трех сигм): если случайная величина распределена
нормально, то абсолютная величина ее отклонения от математического ожидания
не превосходит утроенного среднего квадратического отклонения.
Понятие о теореме Ляпунова
Известно, что нормально
распределенные случайные величины широко распределены на практике. Объяснение
этому было дано А.М.Ляпуновым в центральной предельной теореме:
если случайная величина
представляет собой сумму очень большого числа взаимно независимых случайных
величин, влияние каждой из которых на всю сумму ничтожно мало, то
имеет распределение, близкое к нормальному.
Содержание:
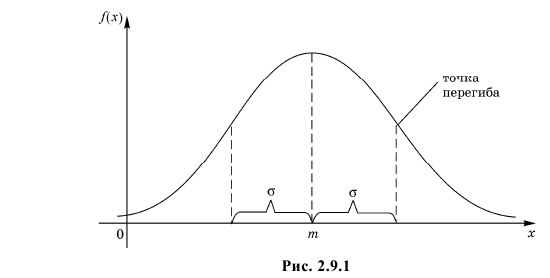
Нормальный закон распределения:
Нормальный закон распределения имеет плотность вероятности
где
График функции плотности вероятности (2.9.1) имеет максимум в точке 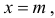

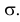
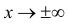
Помимо геометрического смысла, параметры нормального закона распределения имеют и вероятностный смысл. Параметр 
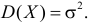
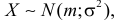

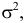
где 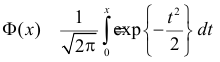
Значения функции 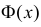
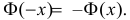
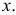
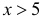
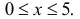
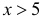
Если 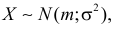
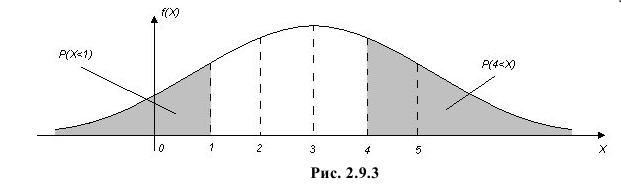
Пример:
Случайная величина X имеет нормальный закон распределения 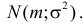
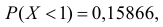
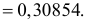
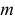
Решение. Воспользуемся формулой (2.9.2):
Так как 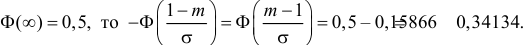
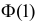
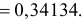
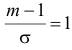
Аналогично 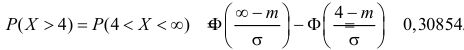
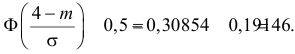
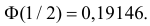
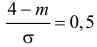
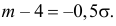
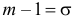
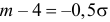
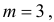
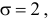
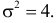
График функции плотности вероятности этого закона распределения изображен на рис. 2.9.3.
Ответ.
Пример:
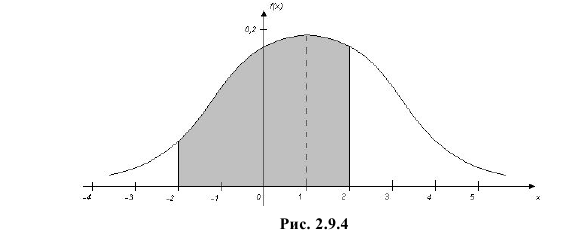
Ошибка измерения X имеет нормальный закон распределения, причем систематическая ошибка равна 1 мк, а дисперсия ошибки равна 4 мк2. Какова вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет по модулю 2 мк?
Решение. По условиям задачи 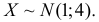
Вычисленная вероятность численно равна заштрихованной площади на рис. 2.9.4.
Каждое измерение можно рассматривать как независимый опыт. Поэтому по формуле Бернулли (2.6.1) вероятность того, что в трех независимых измерениях ошибка ни разу не превзойдет 2 мк, равна
Ответ.
Пример:
Функция плотности вероятности случайной величины X имеет вид
Требуется определить коэффициент 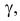
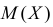
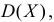
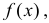
Замечание. Если каждый закон распределения из некоторого семейства законов распределения имеет функцию распределения , 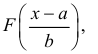
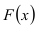
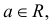
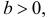
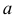
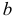
Решение. Так как (2.9.4) функция плотности вероятности, то интеграл от нее по всей числовой оси должен быть равен единице:
Преобразуем выражение в показателе степени, выделяя полный квадрат:
Тогда (2.9.5) можно записать в виде
Сделаем замену переменных так, чтобы 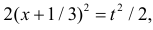
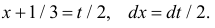
Умножим и разделим левую часть равенства на 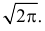
Так как 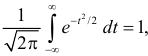
Поэтому
Последняя запись означает, что случайная величина имеет нормальный закон распределения с параметрами 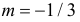
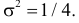
Ответ.
Пример:
Цех на заводе выпускает транзисторы с емкостью коллекторного перехода 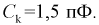
Решение.
Статистическими исследованиями в цеху установлено, что 
Чтобы вычислить количество транзисторов, попадающих в группу 
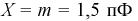
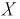
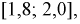
Для расчета этой вероятности надо построить математическую модель. Экспериментальные данные говорят о том, что нормальное распределение можно принять в качестве математической модели. Эмпирическая оценка (установлена статистическими исследованиями в цеху) среднего значения
дает 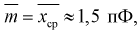
Обозначая 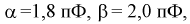
Тогда количество транзисторов 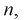
Нормальное распределение и его свойства
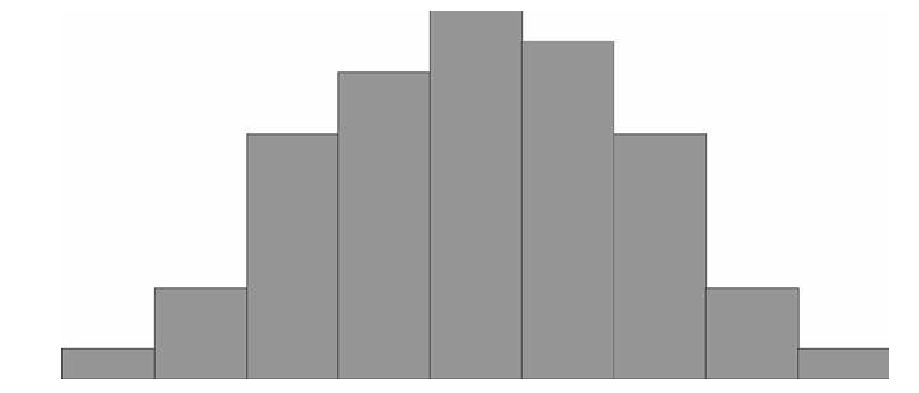
Если выйти на улицу любого города и случайным образом выбранных прохожих спросить о том, какой у них рост, вес, возраст, доход, и т.п., а потом построить график любой из этих величин, например, роста… Но не будем спешить, сначала посмотрим, как можно построить такой график.
Сначала, мы просто запишем результаты своего исследования. Потом, мы отсортируем всех людей по группам, так чтобы каждый попал в свой диапазон роста, например, «от 180 до 181 включительно».
После этого мы должны посчитать количество людей в каждой подгруппе-диапазоне, это будет частота попадания роста жителей города в данный диапазон. Обычно эту часть удобно оформить в виде таблички. Если затем эти частоты построить по оси у, а диапазоны отложить по оси х, можно получить так называемую гистограмму, упорядоченный набор столбиков, ширина которых равна, в данном случае, одному сантиметру, а длина будет равна той частоте, которая соответствует каждому диапазону роста. Если
Вам попалось достаточно много жителей, то Ваша схема будет выглядеть примерно так:
Дальше можно уточнить задачу. Каждый диапазон разбить на десять, жителей рассортировать по росту с точностью до миллиметра. Диаграмма станет глаже, но уменьшится по высоте, «оплывет» вниз, т.к. в каждом маленьком диапазоне количество жителей уменьшается. Чтобы избежать этого, просто увеличим масштаб по вертикальной оси в 10 раз. Если гипотетически повторить эту процедуру несколько раз, будет вырисовываться та знаменитая колоколообразная фигура, которая характерна для нормального (или Гауссова) распределения. В результате, относительная частота встречаемости каждого конкретного диапазона роста может быть посчитана как отношение площади «ломтика» кривой, приходящегося на этот диапазон к площади подо всей кривой. Стандартизированные кривые нормального распределения, значения функций которых приводятся в таблицах книг по статистике, всегда имеют суммарную площадь под кривой равную единице. Это связано с тем, что, как Вы помните из курса теории вероятности, вероятность достоверного события всегда равна 100% (или единице), а для любого человека иметь хоть какое-то значение роста — достоверное событие. А вот вероятность того, что рост произвольного человека попадет в определенный выбранный нами диапазон, будет зависеть от трех факторов.
Во-первых, от величины такого диапазона — чем точнее наши требования, тем меньше вероятности, что нам повезет.
Во-вторых, от того, насколько «популярен» выбранный нами рост. Напомним, что мода — самое часто встречающееся значение роста. Кстати для нормального распределения мода, медиана и среднее значение совпадают. Кривая нормального распределения симметрична относительно среднего значения.
И, в-третьих, вероятность попадания роста в определенный диапазон зависит от характеристики рассеивания случайной величины. Отчасти это связано с единицами измерения (представьте, что мы бы измеряли людей в дюймах, а не в миллиметрах, но сами люди и их рост были бы теми же). Но дело не только в этом. Просто некоторые процессы кучнее группируются возле среднего значения, в то время как другие более разбросаны.
Например, рост собак и рост домашних кошек имеют разный разброс значений, их кривые нормального распределения будут выглядеть по-разному (напомним еще раз, что площадь под обеими кривыми будет единичной).
Так, кривая для роста кошек будет более узкой и высокой, а для роста собак кривая будет ниже и шире. Для характеристики разброса конечного ряда данных в прошлом разделе мы использовали величину среднего квадратического отклонения. Аналогичная величина используется для характеристики кривой нормального распределения. Она обозначается буквой s и называется в этом случае стандартным отклонением. Это очень важная величина для кривой нормального распределения. Кривая нормального распределения полностью задана, если известно среднее значение 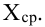
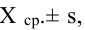
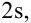
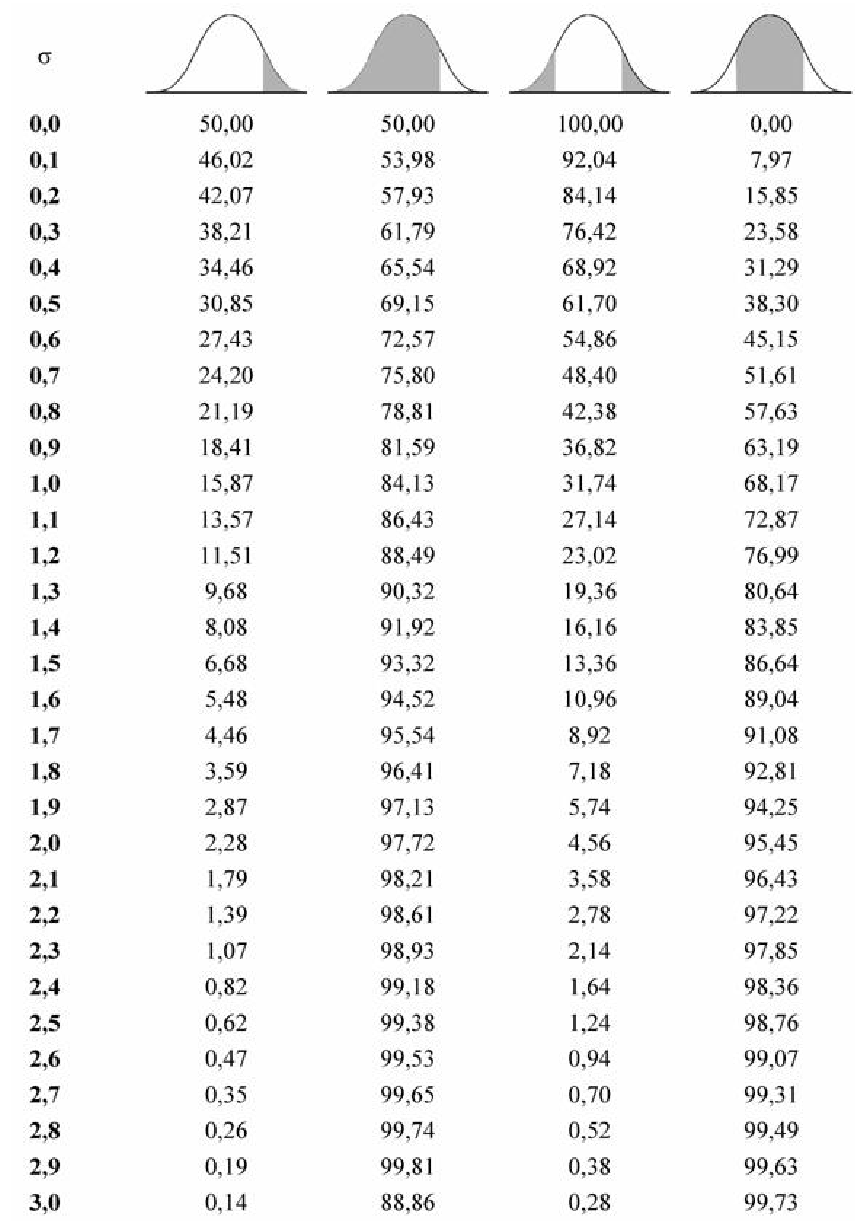
Для вычисления других значений вероятности, которые могут Вам понадобиться, можно воспользоваться приведенной таблицей:
Таблица вероятности попадания случайной величины в отмеченный (заштрихованный) диапазон
Нормальный закон распределения
Нормальный закон распределения случайных величин, который иногда называют законом Гаусса или законом ошибок, занимает особое положение в теории вероятностей, так как 95 % изученных случайных величин подчиняются этому закону. Природа этих случайных величин такова, что их значение в проводимом эксперименте связано с проявлением огромного числа взаимно независимых случайных факторов, действие каждого из которых составляет малую долю их совокупного действия. Например, длина детали, изготавливаемой на станке с программным управлением, зависит от случайных колебаний резца в момент отрезания, от веса и толщины детали, ее формы и температуры, а также от других случайных факторов. По нормальному закону распределения изменяются рост и вес мужчин и женщин, дальность выстрела из орудия, ошибки различных измерений и другие случайные величины.
Определение: Случайная величина X называется нормальной, если она подчиняется нормальному закону распределения, т.е. ее плотность распределения задается формулой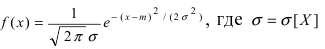
Приведенная дифференциальная функция распределения удовлетворяет всем свойствам плотности вероятности, проверим, например, свойство 4.:
Выясним геометрический смысл параметров 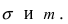
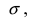
Рис. 8. Изменение графика плотности вероятности в зависимости от изменения математического ожидания при фиксированном значении средне-квадратичного отклонения. Из рисунка видно, кривая 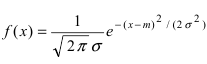
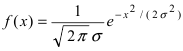
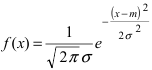
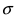
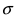
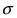
Рис. 9. Изменение графика плотности вероятности в зависимости от изменения средне-квадратичного отклонения при фиксированном значении математического ожидания.
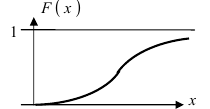
Интегральная функция нормального распределения имеет вид:
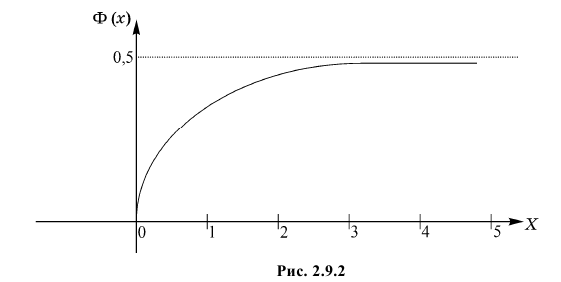
График функции распределения имеет вид (Рис. 10):
Рис. 10. Графика интегральной функции распределения нормальной случайной величины.
Вероятность попадания нормальной случайной величины в заданный интервал
Пусть требуется определить вероятность того, что нормальная случайная величина попадает в интервал 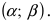
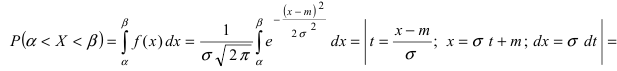
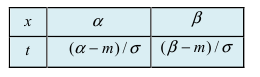
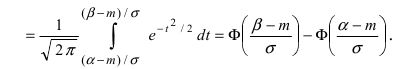
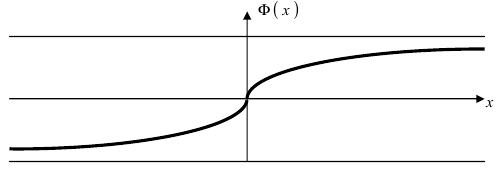
Рассмотрим основные свойства функции Лапласа Ф(х):
- Ф(0) = 0 — график функции Лапласа проходит через начало координат.
- Ф (-х) = — Ф(х) — функция Лапласа является нечетной функцией, поэтому
- таблицы для функции Лапласа приведены только для неотрицательных значений аргумента.
— график функции Лапласа имеет горизонтальные асимптоты
Следовательно, график функции Лапласа имеет вид (Рис. 11):
Рис. 11. График функции Лапласа.
Пример №1
Закон распределения нормальной случайной величины X имеет вид: 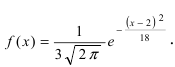
Решение:
Согласно условиям задачи 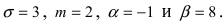
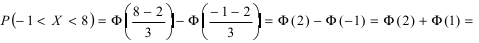
Вычисление вероятности заданного отклонения
Вычисление вероятности заданного отклонения. Правило 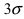
Если интервал, в который попадает нормальная случайная величина X, симметричен относительно математического ожидания 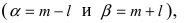
Данная формула показывает, что отклонение случайной величины Х от ее математического ожидания на заданную величину l равна удвоенному значению функции Лапласа от отношения / к среднему квадратичному отклонению. Если положить 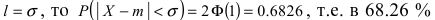
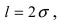
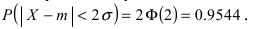
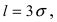
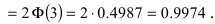
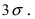
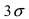
Показательный закон распределения
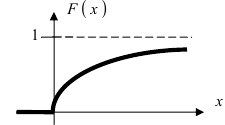
Определение: Закон распределения, определяемый фу нкцией распределения:
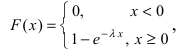
График экспоненциального закона распределения имеет вид (Рис. 12):
Рис. 12. График функции распределения для случая экспоненциального закона.
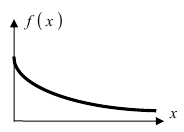
Дифференциальная функция распределения (плотность вероятности) имеет вид: 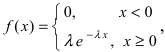
Рис. 13. График плотности вероятности для случая экспоненциального закона.
Пример №2
Случайная величина X подчиняется дифференциальной функции распределения 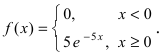
Решение:
Интегральная функция распределения 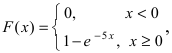
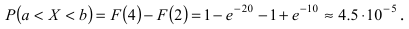
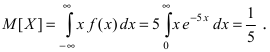
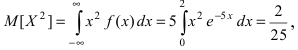
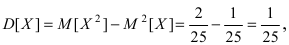
отклонение 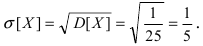
- Основные законы распределения вероятностей
- Асимптотика схемы независимых испытаний
- Функции случайных величин
- Центральная предельная теорема
- Повторные независимые испытания
- Простейший (пуассоновский) поток событий
- Случайные величины
- Числовые характеристики случайных величин

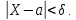
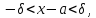
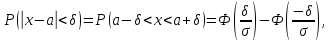
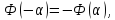
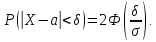
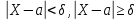

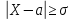
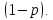
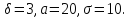
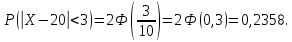
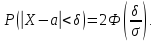
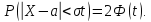
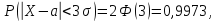
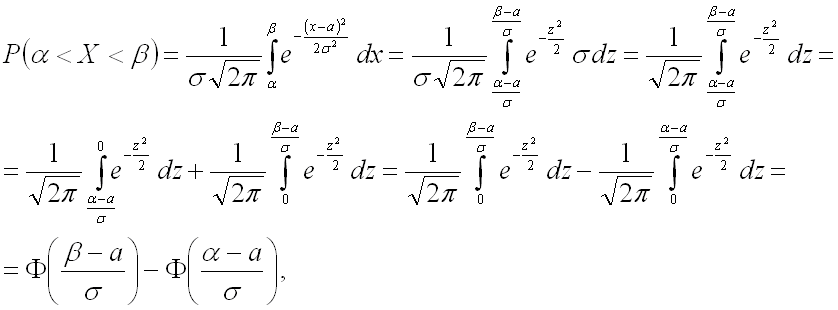
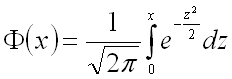
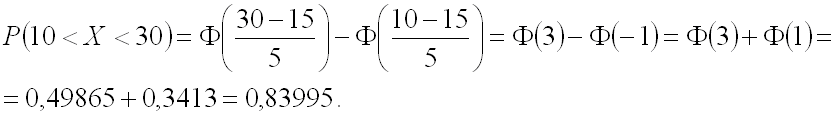
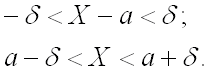
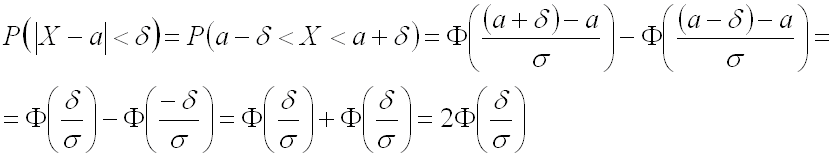
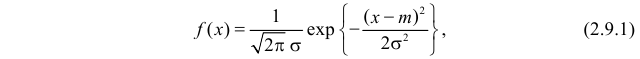
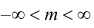
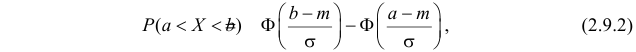
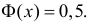
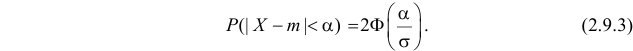
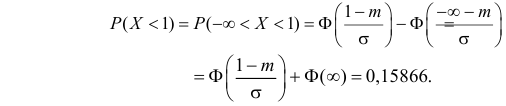
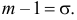
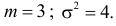
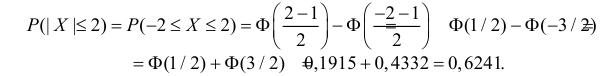
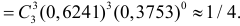
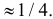
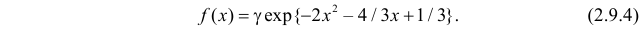
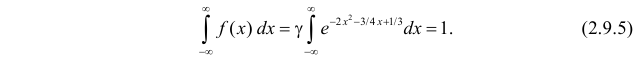
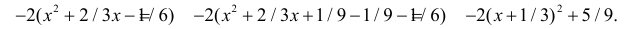
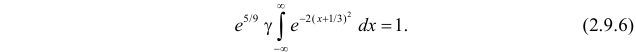

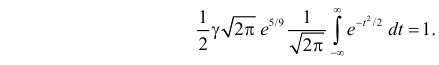

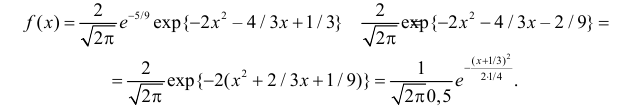
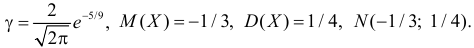
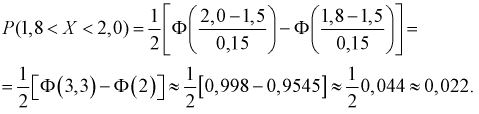
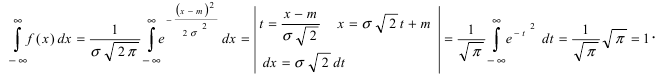
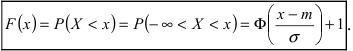
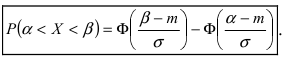
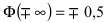 — график функции Лапласа имеет горизонтальные асимптоты
— график функции Лапласа имеет горизонтальные асимптоты