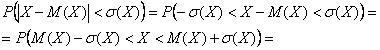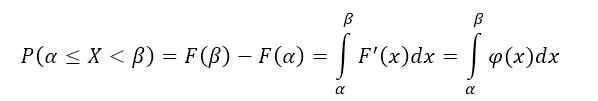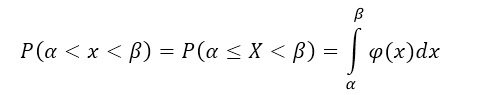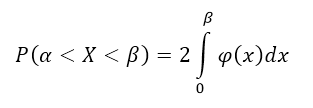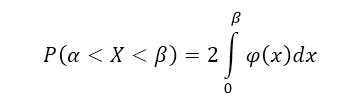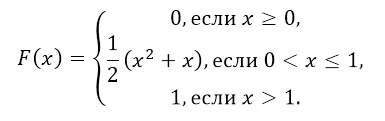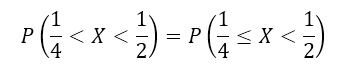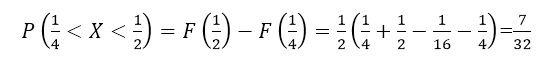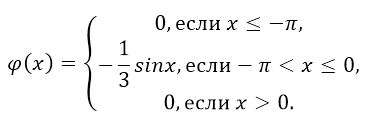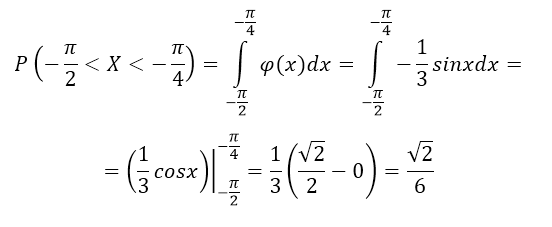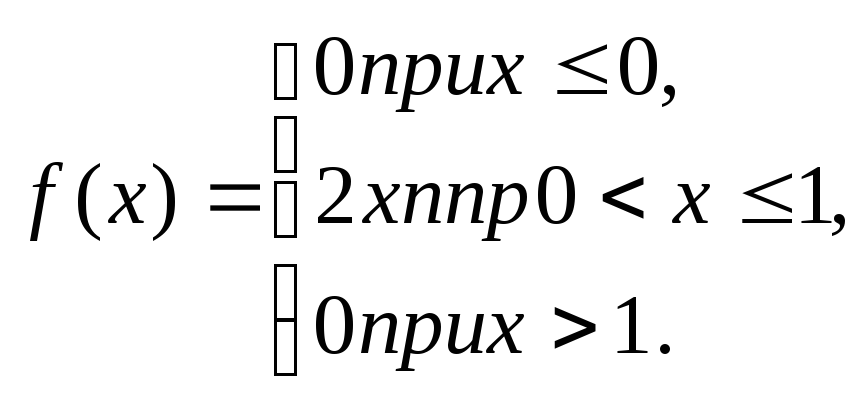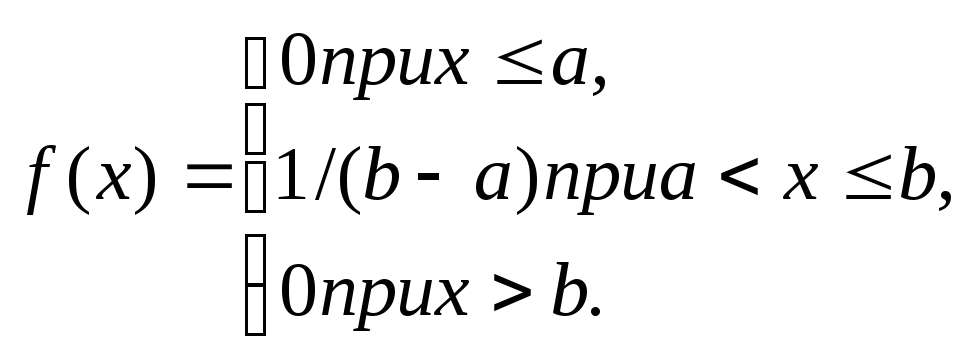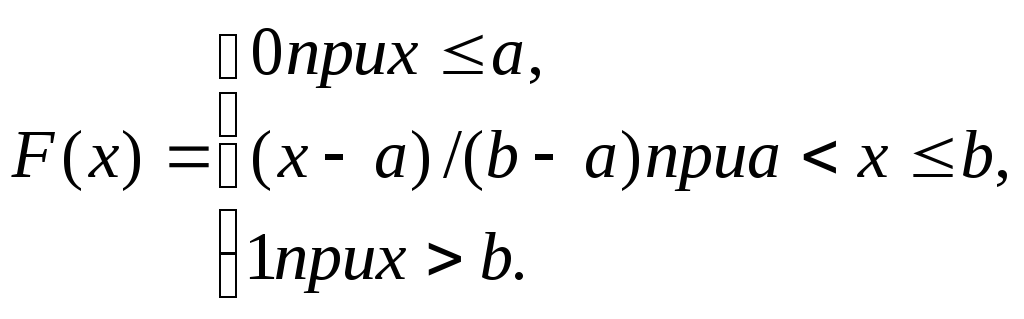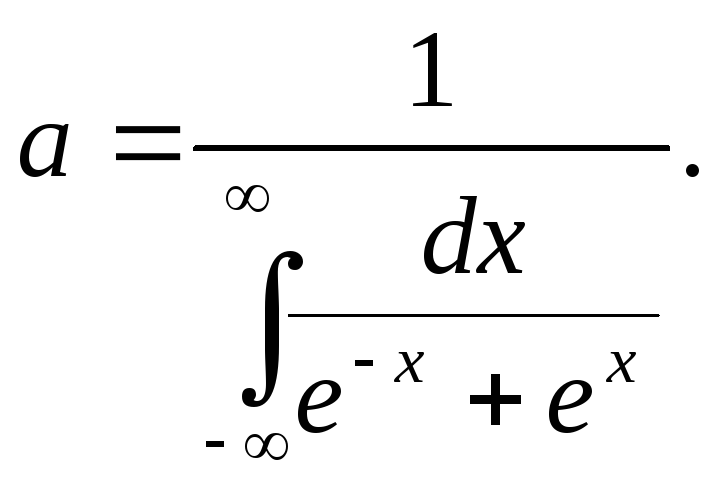Как найти вероятность попадания на промежутке - Исправление недочетов и поиск решений вместе с Examum.ru

2.2.8. Вероятность попадания в промежуток

Найдём – вероятность того,

что случайная величина примет

какое-нибудь значение из интервала .

В данном случае концы интервала (–1 и 5) находятся в области непрерывности функции распределения поэтому: .
И действительно, на данном интервале находятся значения , вероятности появления которых: .
Вычислим вероятность . Оба

конца этого промежутка не «попадают» в точки разрыва, поэтому:
– вероятность того, что

случайная величина примет

значение из данного промежутка. И в самом деле – на нём находится единственное значение , которое может появиться с вероятностью .

Та же самая история с –

единственное, тут левый конец промежутка равен «минус» бесконечности:
– самостоятельно

проанализируйте, какие значения , и с какими вероятностями располагаются на промежутке

Теперь более занятная ситуация, где нужно особо включать голову: если хотя бы один из концов промежутка «попадает» в точку

разрыва функции , то указанную

выше формулу можно использовать лишь в одном случае из четырёх, а именно для неравенства:

Примечание: если , то

левое неравенство становится строгим, но формула тоже применима.

Найдём . Как быть? – под

правило не подходит! Вспоминаем теоремы тервера. По теореме сложения вероятностей несовместных событий:

– вероятность того, что

случайная величина примет

значение из отрезка .
И действительно, этот отрезок включает в себя два значения , которые появляются с вероятностями .

Тут же рассмотрим три других неравенства:
, т.к. на интервале нет значений случайной величины.

Да-да, так и пишем.

– это «штатный» случай

(см. правило).

И для 2-го полуинтервала используем теорему сложения вероятностей несовместных событий:

Едем дальше:

– поскольку там нет

значений случайной величины.

Кстати, случай с нестрогим неравенством – есть «штатный» случай:
, который можно оформить и

так:
– ведь на функции

распределения «свет клином не сошёлся».
И, наконец, типовая вероятность – того, что значение случайной величины отклонится от своего математического ожидания не более чем на одно среднее квадратическое отклонение. И, как вы догадываетесь, эти характеристики нужно

вычислить. Но на самом деле не нужно, поскольку они уже рассчитаны в Задаче 87:

Раскрываем модуль:

подставляем конкретные значения и пользуемся тем фактом, что они не «попадают» в точки разрыва функции

распределения:

– искомая вероятность.

Напоминаю, что в типичном случае на интервале или вблизи него «сконцентрированы» наиболее вероятные значения случайной

величины. Так сказать, «центр событий».

Ответ:

Аналогичное задание для самоконтроля, весь трафарет приведён выше:

Задача 94
Составить функцию распределения случайной величины

Выполнить чертёж. Найти вероятности следующих событий:

Подумайте над рациональным масштабом графика. Если возникают сомнению с нахождением вероятностей, помните – их всегда можно

пересчитать вручную, просто посмотрев на исходную табличку.

Решение и ответ там, где обычно.

И не успел я запостить этот материал на сайте (давно это было J), как от читателей стали поступать просьбы включить

в статью контрольный пример. Я даже прослезился (прямо как тот

профессор), и, конечно же, не смог вам отказать:

2.2.9. Контрольное задание

2.2.7. Функция распределения случайной величины

| Оглавление |

Полную и свежую версию этой книги в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

Евгений Николаевич Беляев

Эксперт по предмету «Математика»

Задать вопрос автору статьи

Пусть нам задана функция плотности распределения непрерывной случайной величины. Тогда с её помощью мы можем найти вероятность того, что случайная величина попадет в интервал $(alpha ,beta )$.

Для начала вспомним несколько свойств функции распределения вероятности $F(x)$, которые понадобятся нам в дальнейшем.

Свойство 1: Для любых $X$ выполняется равенство:

Сформулируем и докажем следующую теорему:

Вероятность того, что непрерывная случайная величина $X$ примет значение из интервала $(alpha ,beta )$ равна значению определенного интеграла от $alpha $ до $beta $ плотности распределения $varphi (x)$.

Доказательство.

Используя свойство 1, имеем:

[Pleft(alpha le XИспользуя формулу Ньютона-Лейбница, получим:

Рисунок 1.

Так как случайная величина $X$ непрерывна, то и функция распределения $F(x)$ также непрерывна. Следовательно, по свойству 2, получим:

Рисунок 2.

ч. т. д.

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

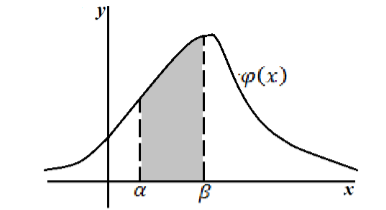
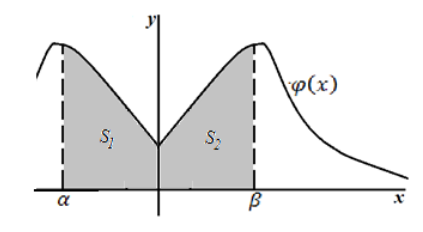
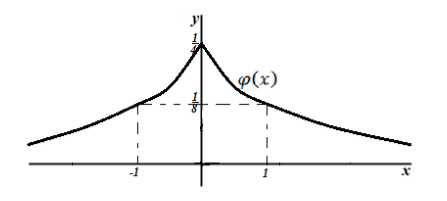
Геометрически данную теорему можно интерпретировать следующим образом: Вероятность попадания случайной непрерывной величины $X$ в интервал $(alpha ,beta )$ равна площади криволинейной трапеции, ограниченной кривыми $y=varphi left(xright), x=alpha ,$ $x=beta $ и $y=0$ (рис. 1).

Рисунок 3. Геометрическое изображение вероятности попадания непрерывной случайной величины в интервал $(alpha ,beta )$.

Следствие 1: Если плотность распределения $varphi (x)$ — четная функция, а значения $alpha и beta $ равны по абсолютной величине (по модулю), причем $alpha ne beta $, то вероятность попадания непрерывной случайной величины в интервал $(alpha ,beta )$ можно найти по формуле:

Рисунок 4.

«Вероятность попадания непрерывной величины в заданный интервал » 👇

Этот факт может быть легко показан геометрически:

Рисунок 5.

Очевидно, что $S_1=S_2$.

Используя геометрический смысл плотности распределения, и получаем, что

Рисунок 6.

Примеры задач на нахождение вероятности попадания непрерывной случайной величины в заданный интервал

Пример 1

Функция распределения имеет вид:

Рисунок 7.

Найти вероятности попадания случайной величины в интервал $(frac{1}{4},frac{1}{2})$.

Решение: Очевидно, что функция $F(x)$ непрерывна на сей области определения (в том числе непрерывна справа на всем интервале $(frac{1}{4},frac{1}{2})$). Значит по свойству 2, получим

Рисунок 8.

Теперь, пользуясь свойством 1, получим:

Рисунок 9.

Ответ: $frac{7}{32}$.

Пример 2

Плотность распределения задана в виде:

Рисунок 10.

Найти вероятности попадания случайной величины в интервал $(-frac{pi }{2},-frac{pi }{4})$.

Решение: Используя теорему 1, получим:

Рисунок 11.

Ответ: $frac{sqrt{2}}{6}$.

Пример 3

Функция плотности распределения имеет вид:

[varphi left(xright)=frac{1}{4x^2+4}]

Построить график плотности распределения и найти вероятность попадания случайной величины в интервал $left(-2,2right).$

Решение: Построим график функции $varphi left(xright)$:

Рисунок 12.

Функция $varphi left(xright)$ четна, концы интервала $left(-2,2right)$ симметричны относительно начала координат, следовательно, по следствию 1, получаем:

[Pleft(-2Ответ: $frac{1}{2}arctg2.$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Зная плотность
распределения, можно вычислить вероятность
того, что непрерывная случайная величина
примет значение, принадлежащее заданному
интервалу. Вычисление основано на
следующей теореме.

Теорема. Вероятность
того, что непрерывная случайная величина
X
примет значение, принадлежащее интервалу
(а,
b),
равна определенному интегралу от
плотности распределения, взятому в
пределах от а до b:

Р(а<Х<b)
=

Доказательство.
Используем соотношение (**) (см. гл. X,
§ 2)

Р(а

Х<b)
= F(b)
— F(a).

По формуле Ньютона
— Лейбница,

F(b)
— F(a)=.

Таким образом,

Р(а

Х<b)
=

Так как Р(а

Х<b)
= Р(а<Х<b),то
окончательно получим

Р(а<Х<b)
=
(*)

Геометрически
полученный результат можно истолковать
так: вероятность того, что непрерывная
случайная величина примет значение,
принадлежащее интервалу (а,b),
равна площади
криволинейной трапеции, ограниченной
осью Ох,
кривой
распределения f
(х)
и прямыми х
=а и х=b.

Замечание. В
частности, если f
(х)
— четная
функция и концы интервала симметричны
относительно начала координат, то

Р(-а<Х<a)
= Р(|Х|<a)
=2

Пример.
Задана плотность вероятности случайной
величины X

Найти вероятность
того, что в результате испытания X
примет
значение, принадлежащее интервалу (0,5;
1).

Решение. Искомая
вероятность

Р (0,5
< X
< 1)=

§ 3. Нахождение функции распределения по известной плотности распределения

Зная плотность
распределения f(х),
можно найти функцию распределения F
(х)
по формуле

F(x)
=

Действительно, мы
обозначили через F
(х)
вероятность
того, что случайная величина примет
значение, меньшее х,
т. е.

F(x)
= P(X<x).

Очевидно, неравенство
X
< х
можно записать
в виде двойного неравенства —<X
< х,
следовательно,

F(х)=Р(—<X
< х)
(*)

Полагая в формуле
(*) (см. § 2) а=—,b
= х, имеем

Р(—<X
< х)
=

Наконец, заменив
Р (—<
X
< х) на F
(х),
в силу (*), окончательно получим

F(x)
=

Таким образом,
зная плотность распределения, можно
найти функцию распределения. Разумеется,
по известной функции распределения
может

быть найдена
плотность распределения, а именно:

f(x)=Г’(x).

Пример.
Найти функцию распределения по данной
плотности распределения:

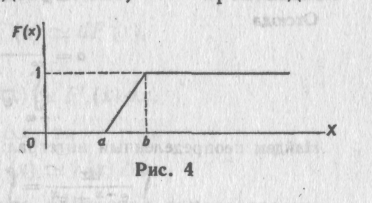
Построить график
найденной функции.

Решение. Воспользуемся
формулой F(x)=

Если x

a,
то f(x)
=0, следовательно, F(x)=0.
Если a<x

b,то
f(x)=1/(b
— а),
следовательно,

Если х
> b,
то

F(x)=

Итак, искомая
функция распределения

График этой функции
изображен на рис. 4.

§ 4. Свойства плотности распределения

Свойство 1. Плотность
распределения—неотрицательная
функция:

f(x)
0.

Доказательство.
Функция распределения — неубывающая
функция, следовательно, ее производная
F‘(х)=f(х)—функция
неотрицательная.

Геометрически
это свойство означает, что точки,
принадлежащие графику плотности
распределения, расположены либо над
осью Ох, либо
на этой оси.

График плотности
распределения называют кривой
распределения.

Свойство 2.
Несобственный
интеграл от плотности распределения в
пределах от —
до

равен единице:

Доказательство.
Несобственный интеграл
выражает
вероятность события, состоящегов
том, что
случайная величина примет значение,
принадлежащее интервалу (—,).
Очевидно, такое событие достоверно,
следовательно, вероятность его равна
единице.

Геометрически это
означает, что вся площадь криволинейной
трапеции, ограниченной осью Ох
и кривом
распределения, равна единице.

В частности, если
все возможные значения случайной
величины принадлежат интервалу (а,
b),
то

Пример. Плотность
распределения случайной величины X
задана:

f
(x)=

Найти постоянный
параметр а.

Решение. Плотность
распределения должна удовлетворять
условию
,
поэтому потребуем, чтобы выполнялось
равенство

Отсюда

Найдем неопределенный
интеграл:

Вычислим несобственный
интеграл:

Таким образом,
искомый параметр

a=.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Равномерное случайное распределение

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Краткая теория

Равномерным называют распределение вероятностей непрерывной случайной величины

, если на интервале

, которому принадлежат все возможные
значения

, плотность сохраняет постоянное значение.

Функция распределения
равномерного закона:

Числовые характеристики равномерного распределения

Математическое ожидание равномерно распределенной случайной величины:

Дисперсия
равномерного случайного
распределения:

Среднее квадратическое отклонение случайной величины, распределенной равномерно:

Для равномерного распределения коэффициент асимметрии:

Коэффициент эксцесса

При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.

Кроме равномерного, основные законы распределения непрерывных случайных величин:

Смежные темы решебника:

Непрерывная случайная величина
Нормальный закон распределения случайной величины
Экспоненциальный (показательный) закон распределения случайной величины

Примеры решения задач

Пример 1

Все
значения равномерно распределенной случайной величины X лежат на отрезке [2;8].
Найти вероятность попадания случайной величины X в промежуток (1;5).

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Плотность вероятности
равномерного распределения на интервале

Искомая вероятность:

Ответ:

Пример 2

Случайная
величина X равномерно распределена на интервале (2;7). Составить f(x), F(x),
построить графики. Найти M(X), D(X).

Решение

Плотность
вероятности случайной величины, распределенной равномерно на интервале

В нашем
случае

Получаем:

Функцию
распределения

найдем из
формулы:

Учитывая
свойства

, сразу можем
отметить, что:

Остается
найти выражение для

, когда х принадлежит интервалу

Получаем:

Построим
графики:

График плотности распределения

График функции распределения

Математическое
ожидание величины, распределенной равномерно:

Дисперсия:

Среднее
квадратическое отклонение:

Пример 3

Минутная
стрелка электрических часов перемещается скачком в конце каждой минуты. Найти
вероятность того, что в данное мгновение часы покажут время, которое отличается
от истинного не более чем на 20 с.

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Решение

Плотность
равномерного распределения:

Вероятность
того, что в данное мгновение часы покажут время, которое отличается от
истинного не более чем на 20 с:

Ответ:

Пример 4

Пассажир
метро в случайный момент времени приходит на платформу. Известно, что среднее
квадратическое отклонение времени ожидания поезда равно 0,8 мин. Найти интервал
времени следования поездов в метро.

Решение

Дисперсия
равномерного распределения:

при
начале интервала

Искомый
интервал времени:

Ответ:

Задачи контрольных и самостоятельных работ

Задача 1

Случайные
величины X₂, X₃, X₄ имеют равномерное,
показательное и нормальное распределения соответственно. Найти вероятности
P(3<X_i<6), если у этих случайных величин
математические ожидания и средние квадратические отклонения равны 3.

Задача 2

Постройте
интегральную и дифференциальную функции распределения случайной величины X.
Найдите M(X), D(X),σ, x_mod, x_med, если известно, что
случайная величина X имеет равномерное распределение с параметрами a=2 и b=4.

Задача 3

Найти: M(X) НСВ X,
распределенной равномерно в интервале (1;9); функцию распределения F(x) и
функцию плотности вероятности f(x); вероятность попадания
НСВ X в интервал (2;7).

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 4

Непрерывная случайная величина X равномерно распределена на сегменте [1; 8.5].

Найти:

1) дифференциальную и интегральную
функцию распределения, а также построить их графики.

2) математическое ожидание и
дисперсию;

2) вероятность того, что X примет какое-нибудь значение из интервала (1;20).

Задача 5

Интервал движения парома 3 часа.
Найти: а) числовые характеристики времени ожидания для случайного пассажира; б)
вероятность времени ожидания менее 40 минут.

Задача 6

Равномерно распределенная случайная
величина

задана
плотностью распределения f(x)=0.125 в интервале (1;9) и f(x)=0 вне его.
Найти M(X), D(X), σ(X).

Задача 7

Случайная
величина X равномерно распределена на отрезке [5;11]. Найдите
математическое ожидание X, дисперсию X,
медиану, P(7<X<15), x_0.2.

Задача 8

Случайная
величина

равномерно распределена на отрезке [-1;9].
Запишите функцию плотности распределения, изобразите ее график. Найдите
вероятность того, что X примет значение в
интервале (-3;2). Найдите математическое ожидание X и медиану. Укажите
найденные значения на графике f(x).

Задача 9

Вычислить
вероятность того, что при 10 испытаниях значение X три раза попадет в
интервал [-1;1], если случайная величина X распределена по
равномерному закону на интервале [0;4].

Задача 10

Трамваи
данного маршрута идут с интервалом в 5 мин. Пассажир подходит к трамвайной
остановке в некоторый момент времени. Какова вероятность появления пассажира не
ранее чем через 1 мин после ухода предыдущего трамвая, но не позднее чем за 2
мин до отхода следующего трамвая?

Задача 11

Найти
функцию распределения, плотность, математическое ожидание и дисперсию случайной
величины, распределенной равномерно на отрезке [2,4].

Задача 12

Цена
деления шкалы прибора равна 0,4. Показания прибора округляют до ближайшего
деления. Найти вероятность того, что при отсчете будет сделана ошибка
округления, большая 0,05.

Задача 13

СВ X
распределена равномерно в промежутке [1∕3,5∕4]. Найти функцию плотности
распределения f(x), функцию распределения F(x),
математическое ожидание M(X), дисперсию D(X) и среднее квадратическое отклонение σ(X). Построить
графики функций f(x) и F(x). Найти вероятность того, что x∈[1,5∕4].

ВКонтакте
WhatsApp
Telegram

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 14

Шкала
рычажных весов, установленных в лаборатории, имеет цену делений 1 г. При
измерении массы химических компонентов смеси отсчет делается с точностью до
целого деления с округлением в ближайшую сторону. Какова вероятность, что
абсолютная ошибка определения массы будет заключена между значениями σ и 2σ.

Задача 15

Автобусы
некоторого маршрута идут строго по расписанию с интервалом 5 мин. Найти
вероятность того, что пассажир, подошедший к остановке будет ждать очередного
автобуса меньше трех минут.

Задача 16

Все
значения равномерно распределенной случайной величины Х принадлежат отрезку
[2,8]. Найти вероятность попадания случайной величины X в отрезок [3,5].

Задача 17

Случайная величина X имеет равномерное распределение на отрезке [1,6].
Найти дисперсию D(X) и вероятность попадания случайной величины X в интервал (2,4).

Задача 18

По маршруту
независимо друг от друга ходит два автобуса: №20 –через 10 и №15 –через 7
минут. Студент приходит на остановку в случайный момент. Какова вероятность
того, что ему придется ждать автобус менее трех минут.

Задача 19

Автобусы идут с интервалом 5 минут.
Считая, что случайная величина X – время
ожидания автобуса на остановке, распределена равномерно на указанном интервале,
найти среднее время ожидания и дисперсию времени ожидания.

Задача 20

Шкала
секундомера имеет цену деления 0,2 с. Какова вероятность сделать по этому
секундомеру отсчет времени с ошибкой менее 0,05 с, если отсчет делается наудачу
с округлением в ближайшую сторону, до целого деления?

Краткая теория
Примеры решения задач
Задачи контрольных и самостоятельных работ

Источник

Содержание:

Непрерывные случайные величины и их характеристики
Функция распределения
Плотность распределения
Математическое ожидание
Дисперсия
Нормальное распределение
Понятие о теореме Ляпунова
Показательное распределение

Непрерывные случайные величины и их характеристики

Как было подчеркнуто в предыдущем разделе, дискретная случайная величина может принимать значения некоторой числовой последовательности — конечной или бесконечной.

Дискретность случайной величины, принимающей эти значения, будет состоять в том, что между любыми значениями xt и Xj будет только конечное число членов этой последовательности, и в случае необходимости мы можем все эти промежуточные значения записать.

Это позволит строить закон распределения дискретной случайной величины в форме таблицы, в которой по порядку перечислены все или сколько угодно много возможных значений этой случайной величины.

В случае непрерывной случайной величины которая принимает все реальные значения некоторого промежутка реальных чисел, между любыми двумя такими значениями х’ и х» имеется бесконечно много реальных чисел, и все эти числа записать не представляется возможным. Как ни пробовать, например, эти числа пронумеровать, между любыми из них опять существует бесконечно много реальных чисел. Так что процесс нумерования окажется бесконечным, а это и обусловливает отсутствие возможности закон распределения непрерывной случайной величины представить в форме, аналогичной той, которая применяется в случае дискретной случайной величины.

Функция распределения

Рассмотрим величину

Поскольку каждому значению х соответствует один и только один промежуток а каждому такому промежутку — одно и только одно событие вероятность которого , то выходит, что каждому значению х соответствует одно и только одно значение .

Значит, между x и существует функциональная зависимость в том смысле, как это изложено в традиционном курсе математики. Логично обозначить привычным для нас символом F (х) и назвать функцией распределения непрерывной случайной величины. Итак:

Определение:

Функцией распределения непрерывной случайной величины называется вероятность того, что примет значение меньше х.

Очевидны следующие свойства F (х):

1. F (х) — неубывающая функция. Действительно, пусть

Событие представляет собой объединение событий Поэтому в силу несовместимости их

Поскольку то

2. F (х) — непрерывная слева функция.

Выберем какую-нибудь возрастающую последовательность сходящуюся к х. Пусть — событие Тогда в силу свойства 1

Событие достоверное, поэтому

(8.1)

Событие невозможное, поэтому

Примечание. Когда известно, что случайная величина может принимать только значения промежутка то достоверным событием является событие а невозможным В таком случае

(8.2)

Когда известна функция распределения F (х), можно найти вероятность попадания случайной величины на заданный интервал. Именно:

Вероятность попадания случайной величины на заданный интервал равна приращению функции распределения на этом интервале, т. е.

(8.3)

Доказать это нетрудно. В результате несовместимости событий

Примеры с решением:

Пример 1. Функция распределения случайной величины (рис. 37) О

Найти вероятность того, что в результате испытания примет значение, заключенное в промежутке [0; 1).

По формуле (8.3)

Пример 2. Функция распределения случайной величины (рис. 38)

Найти вероятность того, что в результате испытания примет значение в промежутке .

По формуле (8.3)

Пример 3. Доказать, что

поэтому

Также поэтому

Равенство вероятностей (8.4) полезно запомнить для изучения следующих разделов книги.

Плотность распределения

У читателя, возможно, мог возникнуть вопрос: каким путем, наблюдая случайные значения построить функцию распределения F (х)? Оказывается, что к этой функции практически проще подходить через другую функцию.

Исходной точкой наших дальнейших рассуждений мы примем понятие производной.

По формуле (8.3)

(8.5)

Из школьного курса математики известна формула

(8.6)

Она и поможет нам дальнейшие рассуждения провести так, чтобы само понятие «плотность» имело смысл, адекватный смыслу плотности вообще.

Действительно,

это доля вероятности соответствующая единице измерения длины отрезка (рис. 39), т. е. плотность этой вероятности на .

Но в силу (8.6)

Тогда плотность этой вероятности в точке будет равна:

Для произвольной точки

p(x)=F'(x). (8.7)

Итак:

Плотностью вероятностей р (х) называется производная функции распределения F (х) непрерывной случайной величины.

Следовательно, функция распределения F (х) представляет собой первообразную от плотности р (х). Поэтому содержание формулы (8.3) может быть расширено:

(8.8)

Из этой формулы следует:

1. Если все возможные значения принадлежат промежутку —достоверное событие, и поэтому

Это значит: площадь, ограниченная кривой плотности и осью Ох при всех значениях, которые может принимать случайная величина , равна единице. Следовательно,

2. (8.9)

так как известно, что

3. (8.10)

так как

В тех случаях, когда имеем дело с определенными интегралами типа где F (х) — первообразная от f (х) то будем их понимать в таком смысле:

(8.11)

Очень важно подчеркнуть, что плотность вероятностей непрерывной случайной величины — это исходная точка для получения всех ее характеристик. А к самой плотности и ее геометрической интерпретации можно подойти от практических наблюдений случайной величины.

Допустим, Разделим этот промежуток на m равных частей длиной

Пусть в результате n наблюдений мы установили, что:

в промежуток попала раз;

в промежуток попала раз. Статистические частоты попадания в соответствующий интервал будут а плотности этих статистических частот

Строим диаграмму распределения этих плотностей частот (рис. 40).

Такая диаграмма называется гистограммой. На ее основании будем подходить к геометрической интерпретации плотности вероятностей р(х), аналитическое выражение которой нам неизвестно.

Можно рассуждать так. Для каждого i = 1, 2, 3, …, m:

1. — площадь i-го прямоугольника гистограммы, представляющая статистическую частоту попадания значений в i-й интервал.

2. С возрастанием n эти статистические частоты сосредоточиваются около вероятности

3. В силу формулы (8.6) эта вероятность приближенно должна быть равна

где р (x) — предполагаемая плотность.

Поскольку это выражение представляет площадь прямоугольника с основанием А, то значение предполагаемой плотности

представляет высоту некоторого прямоугольника, у которого то же самое основание и площадь которого близка к .

Вывод:

Последовательность значений предполагаемого р (х)

представляет высоты прямоугольников, по площади близких к значениям статистических частот

Следовательно, предполагаемая плотность представляет собой некоторую кривую, которая огибает гистограмму статистических частот.

Примеры с решением:

Пример 1. Плотность распределения случайной величины

Найти вероятность попадания на промежуток .

По формуле (8.9)

Пример 2. Плотность распределения случайной величины

Найти вероятность того, что

По формуле (8.9)

Математическое ожидание

Пусть непрерывная случайная величина распределена на интервале с плотностью р (х). Разделим промежуток на n необязательно равных частей

Случайная величина принимает:

значения из промежутка с вероятностью

Тогда по аналогии с формулой (7.1) математическое ожидание случайной величины приближенно равно:

Разумеется, что

при Обозначим

Тогда

В Силу формулы (8.3)

По известной формуле приращения функции

следовательно,

В случаях, когда область распределения не указана,

(8.13)

где интеграл понимается в смысле определений (8.11).

Примеры с решением:

Пример 1. Случайная величина распределена на промежутке [0; 2) с плотностью Найти М (). По формуле (8.12)

Пример 2. Случайная величина распределена с плотностью

Найти М (). По формуле (8.13)

Непосредственно убедимся, что первообразная от f(x) = х sin х есть F (х)= — х cos х + sin х.

Действительно, F’ (х) = ( — х cos х +sin х)’ = х sin х. Поэтому по формуле Ньютона — Лейбница

Дисперсия

Согласно формулам (7.7) и (8.12), когда все возможные значения принадлежат промежутку

(8.14)

В случаях, когда область возможных значений не указана,

где эти интегралы понимаются в смысле понятий (8.11).

Примеры с решением:

Пример 1. Плотность распределения случайной величины

Найти По формуле (8.15)

Пример 2. Случайная величина распределена на промежутке [0; 2) по закону Симпсона:

(рис. 41).

Доказать, что

Для достижения выдвинутой нами цели будем применять неравенство Чебышева. Следовательно, нам необходимо знать

По формуле (8.12)

По формуле (8.14)

По неравенству Чебышева

Нормальное распределение

В формулировках теорем Муавра — Лапласа мы уже ознакомили читателя с функцией

(8.16)

и ее первообразной

(8.17)

Значения этих функций представлены в таблицах 2 и 4. График представлен на рисунке 3. Нам также известно, что вероятность

представляет собой площадь фигуры, образованной кривой у = р(х), прямыми и осью Ох. Когда всевозможные значения принадлежат некоторому промежутку то, разумеется,

Имеет место и обратное: если площадь фигуры, образованной кривой y = f (х), прямыми и осью Ох, равна 1, то f (х) можно считать плотностью вероятностей некоторой непрерывной случайной величины.

Методами, пока для нашего читателя недоступными, Пуассоном доказано, что

Следовательно,

и поэтому представляет плотность распределения некоторой непрерывной случайной величины.

Поскольку функция максимальное значение принимает в точке х = 0, причем в результате четности функции ее график симметричен относительно оси у, то, разумеется,

По формуле (8.15) при условии

(8.18)

Поскольку т. e.

то первообразная от равна первообразной от Следовательно,

Как известно,

Тогда

(8.19)

Подставляя (8.19) в (8.18), получаем .

В результате четности функции ее колоколообраз-ный график будет симметричен. Поэтому точкой максимума является Естественными, т. е. нормальными, особенностями интуитивно нам кажутся такие:

а) равные вероятности одинаковых отклонений в обе стороны от

б) убывание вероятности по мере увеличения отклонения от

Это как бы подводит к мысли сам закон распределения называть нормальным. Поскольку числовые характеристики стандартные: , то данный нормальный закон распределения можно называть стандартным. Итак, будем считать, что случайная величина распределена по стандартному нормальному закону, когда ее плотность распределений вероят-

ностей , и, следовательно,

Попробуем построить плотность распределения случайной величины — случайная величина распределена по стандартному нормальному закону, — некоторые константы, причем

Пусть Ф (х) — первообразная от т. е. функция нормального стандартного распределения.

Поскольку то

(8.20)

Такой функции распределения соответствует плотность распределения

(8.21)

Выясним, что собой представляют константы

Поскольку

Значит, (8.21) представляет собой плотность вероятностей случайной величины, распределенной по нормальному закону, когда ее

Из (8.20) следует, что для такой случайной величины имеет место

(8.22)

Поскольку значения функции у = Ф(х) заданы в таблице 4, то вычисление таких вероятностей не вызывает никаких затруднений.

График плртности такого нормального распределения также представляет собой колоколообразную кривую.

Точкой максимума плотности является высота «колокола» равна Полезно запомнить следующие зависимости:

1. Если при равных дисперсиях то графики плотностей распределения случайных величин х и у по форме и высоте одинаковые, но график плотности распределения у правее (рис. 42).

2. Если при равных математических ожиданиях D(x)<D(y), то графики плотностей максимумов достигают в одной и той же точке, но график плотности распределения одной из них будет и ниже и шире (рис. 43).

Примеры с решением:

Пример 1. Случайная величина распределена по нормальному закону. Найти вероятность того, что примет значение, принадлежащее промежутку [20; 60).

По формуле (3.22)

По таблице 4 Ф (2) = 0,4772. Отсюда искомая вероятность

Пример 2. Случайная величина распределена по нормальному закону. Найти вероятность того, что примет значение, принадлежащее промежутку

По формуле (8.22)

По таблице 4 Ф (3) = 0,49865. Отсюда что равносильно

Нами доказано так называемое правило трех сигм: если случайная величина распределена нормально, то абсолютная величина ее отклонения от математического ожидания не превосходит утроенного среднего стандартного отклонения. Такое событие происходит почти наверняка.

Понятие о теореме Ляпунова

Мы уже упомянули, что нормально распределенные случайные величины широко встречаются на практике. Чем это объяснить? Выдающимся русским математиком А. М. Ляпуновым была доказана центральная предельная теорема теории вероятностей, из которой вытекает следующее следствие: если случайная величина представляет собой сумму очень большого числа взаимно независимых случайных величин, влияние каждой из которых на всю сумму ничтожно мало, то имеет распределение, близкое к нормальному.

Примеры с решением:

Пример 1. Производится измерение некоторой физической величины. Любое измерение дает лишь приближенное значение измеряемой величины, так как на результат измерения оказывают влияние многие независимые между собой факторы (влажность, слой пыли на приборе, температура, вибрация прибора и т. д.). В результате влияния каждого из этих факторов рождается ничтожная случайная ошибка. Поскольку число этих факторов велико, совокупное их действие порождает уже заметную суммарную ошибку. Эту суммарную ошибку мы можем рассматривать как сумму большого числа взаимно независимых ошибок, т. е. суммарную ошибку £ можем рассматривать как случайную величину, которая распределена по закону, близкому к нормальному. Практически это значит, что

Примером практического применения вышеизложенного следствия теоремы Ляпунова может служить такая задача:

Известно, что среднее значение случайной погрешности весов дисперсия

Пример 2. Какова вероятность того, что при очередном взвешивании погрешность показания весов

Пусть — случайная погрешность. Можно считать, что распределена по закону, близкому к нормальному. Поэтому

По таблице 4 Ф (0,25) = 0,0987, а Ф (1,75) = 0,4599. Поэтому

Пусть нам дана случайная величина математическое ожидание которой Рассмотрим соотношение

Это выражение можно изложить словами так: вероятность того, что не выйдет за пределы промежутка равна Принято этот интервал называть доверительным интервалом случайной величины с уровнем достоверности

Пример построения доверительного интервала приводим на основе условия вышеизложенной задачи.

Пример 3. Найти доверительный интервал погрешности этих весов с гарантией 95%.

На второй вопрос ответ находим так:

Поскольку симметричны в отношении 0,03, то а Значит,

Отсюда Такому значению Ф (х) в таблице 4 соответствует х=1,96. Таким образом,

Тогда Значит, с гарантией 95% доверительный интервал случайной погрешности весов [ — 0,0484; 0,1084].

Упомянутое следствие теоремы Ляпунова позволяет также оценить вероятность события по экспериментальным данным.

Пусть исследователь при проведении n независимых испытаний обнаружил, что его интересующий факт А имел место в m случаях. Он фиксирует, что статистическая частота появления факта А равна . Но исследователя интересует сама вероятность появления факта А при одном испытании. Он знает, что . Но какая тут степень приближенности?

Частота есть случайная величина математическое ожидание которой а дисперсия

При достаточно большом распределено по закону, близкому к нормальному, поэтому согласно формуле (8.22)

(8.23)

Последняя формула может быть использована для решения ряда практических задач. Несколько из них представляем читателю.

Пример 4. 15% продукции фабрики представляют изделия второго сорта. Магазин получил 1000 изделий. Какова вероятность того, что в полученной партии продукция второго сорта составит 15% ±2%?

По условию задачи Пусть — ожидаемая доля продукции второго сорта. Находим

Следовательно,

Тогда

По таблице 4 Ф (1,77) = 0,4616, поэтому

Ответ можно сформулировать и так: с гарантией 92% в полученной партии изделия второго сорта составят 15% ±2%.

Пример 5. Исследованиями установлено, что 20% школьников не знают правил уличного движения. В случайной выборке 1600 учеников. Сколько учеников знают правила уличного движения с гарантией 95%?

По условию задачи — доля учащихся этой «выборки», знающих правила уличного движения.

Тогда

поэтому

По таблице 4 значению 0,475 соответствует х = 1,96, т. е. Значит,

или приближенно Но 0,78 от 1600 составляет 1248, а 0,82 от 1600 — 1312. Значит, с гарантией 95% число учеников, знающих правила уличного движения, принадлежит промежутку [1248; 1312].

Пример 2 — это задача на определение доверительного интервала выборочной числовой характеристики случайной величины которая представляет собой долю случайно обследованных объектов, обладающих некоторым признаком.

Пример 6. При массовом производстве обуви брак составляет 4% выпускаемой продукции. Сколько изделий нужно отобрать для проверки качества продукции, чтобы с вероятностью 0,9 можно было бы утверждать, что в случайном наборе обуви доля брака по абсолютной величине отличается от 4% не более чем на 1%?

По условию задачи неизвестно. Пусть — доля брака в случайной партии изделий. Случайная величина распределена по закону, близкому к нормальному, поэтому

Отсюда

Но подстановкой в предыдущее уравнение находим

Показательное распределение

Допустим, в момент времени х = 0 включается мотор сложного механизма. В результате износа его узлов по истечению времени х вероятность исправности механизма следует считать монотонно убывающей. Как известно, для удобной моделыо убывающей плотности вероятностей может служить показательная функция

(8.24)

где — положительные константы, причем

Выясним суть этих констант, используя в данном случае известное свойство плотности

Итак, должны быть такими, чтобы

Нетрудно показать, что представляет собой первообразную от Действительно, Значит,

Из условия следует откуда , где Подставляя полученное значение в формулу (8.24), получаем:

(8.25)

Это есть плотность показательного распределения вероятностей.

Напоминаем, что с возрастанием х плотность р (х) убывает. Это значит, что х можно представить как время, а р(х) — как вероятность безотказной работы какого-нибудь устройства: со временем эта вероятность в результате износа устройства постепенно убывает.

Согласно формуле (8.8) вероятность того, что случайная величина распределенная по показательному закону, примет значение из интервала , равна:

(8.26)

где F (х) — первообразная от функции Покажем, что

(8.27)

Действительно, откуда следует (8.27). Значит,

(8.28)

По этой формуле

(8.29)

означает, что отказ наступит до момента времени Т.

Поскольку

то

Последняя формула означает вероятность того, что отказ до момента Т не наступит, поэтому логично называть функцией надежности. Итак,

(8.30)

Какой смысл константы k ?

Чем k больше, тем надежности меньше. Поэтому k и называется интенсивностью отказов.

Примеры с решением:

Пример 1. Вероятность того, что некий прибор проработает 1 ч, равна 0,9. Какова вероятность того, что прибор безотказно проработает сутки?

Мы сразу могли бы дать ответ по формуле (8.30), если бы знали k. Как определить значение этого параметра? Очень просто!

По условию задачи

Тогда из уравнения получаем:

Опять по формуле (8.30)

Пример 2. 98% топливных насосов дизельных тракторов выходит из строя после 3000 моточасов. Какова вероятность того, что насос выйдет из строя в интервале времени от 2000 до 2500 моточасов?

Пусть — время безотказной работы насоса. По условию задачи

Из этого уравнения находим k = 0,0000067. Значит, плотность распределения равна По формуле (8.28)

По этой ссылке вы найдёте полный курс лекций по теории вероятности:

Возможно вам будут полезны данные страницы:

Лекции:

Дискретные и непрерывные случайные величины
Закон распределении дискретной случайной величины
Математическое ожидание дискретной случайной величины
Дисперсия дискретной случайной величины
Закон распределении и числовые характеристики непрерывной случайной величины
Схема с повторением испытаний (схема Бернулли)
Вероятность случайного события
Операции над вероятностями с примерами решения
Независимые повторные испытания
Дискретные случайные величины и их характеристики

Источник