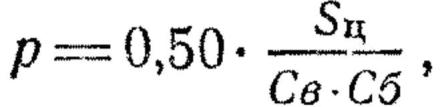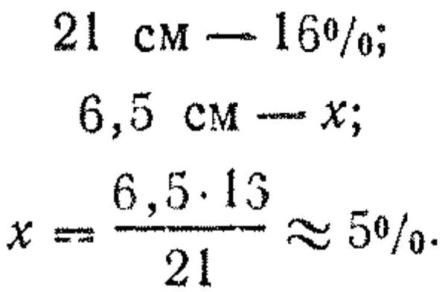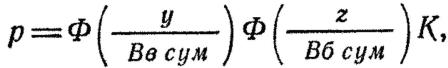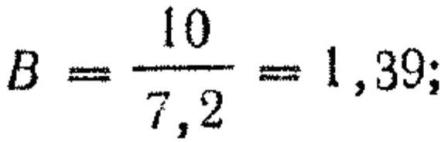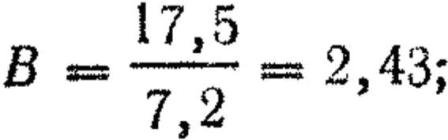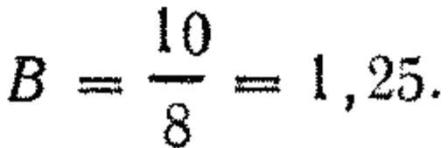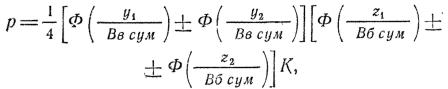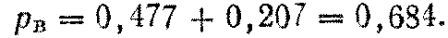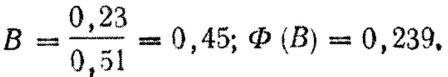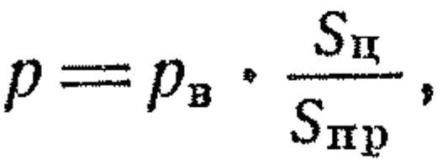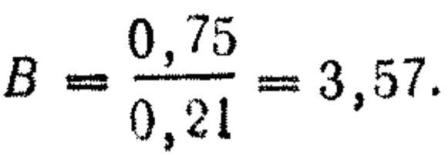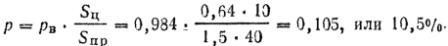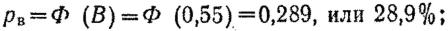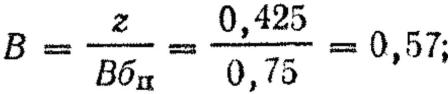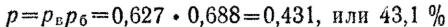Как найти вероятность попадания в цель

Решение задач о выстрелах и попаданиях в цель

В предыдущих статьях мы разобрали популярные учебные задачи по теории вероятностей: задачи про бросание игральных костей и задачи о подбрасывании монет.

Перейдем еще к одному типу задач: про стрелков, которые делают выстрелы по целям (или мишеням), причем вероятности попаданий для каждого стрелка обычно заданы, а нужно найти вероятность ровно одного попадания, или не более двух попаданий, или всех трех и так далее, в зависимости от конкретной задачи.

Основной метод решения подобных задач — использование теорем о сложении и умножении вероятностей, который мы и разберем на примерах ниже. А перед примерами вы найдете онлайн калькулятор, который поможет решить подобные задачи буквально в один клик! Удобно решать самому? Посмотрите видеоурок и скачайте бесплатный шаблон Excel для решения задач о выстрелах.

Онлайн решение задачи про попадание в цель

Выберите количество стрелков и затем введите в поля вероятности $p_i$ их попаданий в цель (десятичный разделитель — точка):

Видеоурок и шаблон Excel

Посмотрите наш ролик о решении задач с выстрелами: как использовать Excel для решения типовых задач с 2, 3 и 4 стрелками (выстрелами).

Расчетный файл Эксель из видео можно бесплатно скачать.

Два стрелка

Начнем традиционно с более простых задач, а именно, с двух стрелков. Пусть первый стрелок попадает в цель с вероятностью $p_1$, а второй — с вероятностью $p_2$ (конкретные числа см. в примерах ниже). Соответственно, сразу можно сделать вывод, что промахиваются они с вероятностями $q_1=1-p_1$ и $q_2=1-p_2$.

Чтобы иметь возможность оперировать с событиями, нужно сначала их (события) ввести. Кстати, сразу заметим, что события эти независимые (то есть вероятность попадания первого стрелка не зависит от того, как стреляет второй и наоборот). Итак, пусть:

Событие $A_1$ = (Первый стрелок попал в цель),

Событие $A_2$ = (Второй стрелок попал в цель).

Соответственно, события $overline{A_1}$, $overline{A_2}$ обозначают промах первого и второго стрелка (не попал в цель).

Сразу можно выписать все, что нам стало известно к этому времени о данных событиях, в терминах теории вероятности (так сказать, формализуем задачу, чтобы легче было ее решать дальше):
$$
P(A_1)=p_1, quad P(A_2)=p_2, quad Pleft(overline{A_1}right)=1-p_1=q_1, quad Pleft(overline{A_2}right)=1-p_2=q_2.
$$

Теперь можно переходить к подсчету вероятностей попаданий. Например, пусть событие $X$ =(При двух выстрелах не было ни одного поражения цели). Вопрос, когда такое случится? Ясно, что когда ни первый стрелок, ни второй не попадут в цель, то есть одновременно произойдут события $overline{A_1}$ и $overline{A_2}$, что можно записать как произведение событий: $X=overline{A_1} cdot overline{A_2}$. Согласно теореме умножения вероятностей независимых событий, вероятность произведения событий равна произведению соответствующих вероятностей, или:
$$
P(X)=Pleft(overline{A_1} cdot overline{A_2}right)= Pleft(overline{A_1}right) cdot Pleft(overline{A_2}right) = q_1 cdot q_2. qquad (1)
$$

Рассмотрим еще одно событие $Y$ =(При двух выстрела ровно один стрелок попадет в цель). Как можно записать это событие через уже известные нам $A_1$ и $A_2$? Подумаем, когда такое событие произойдет:
1. Когда первый стрелок попадет в цель (событие $A_1$) и одновременно с этим второй стрелок промахнется (событие $overline{A_2}$), то есть получили произведение событий $A_1 cdot overline{A_2}$.

2. Когда второй стрелок попадет в цель (событие $A_2$) и одновременно с этим первый стрелок промахнется (событие $overline{A_1}$), то есть получили произведение событий $overline{A_1} cdot A_2$.

Так как других вариантов для получения одного попадания нет, а эти два варианта — несовместные (они не могут произойти одновроменно, или первая ситуация, или вторая), то по теореме сложения вероятностей несовместных событий:
$$
P(Y) = Pleft(A_1 cdot overline{A_2} + overline{A_1} cdot A_2right)= Pleft(A_1 cdot overline{A_2} right)+ Pleft( overline{A_1} cdot A_2right) =
$$
дальше уже по известной теореме умножения вероятностей раскрываем скобки:
$$
= P(A_1) cdot left(overline{A_2} right) + Pleft( overline{A_1} right) cdot P(A_2) = p_1 cdot q_2 + q_1 cdot p_2.
$$
Мы получили формулу, позволяющую найти вероятность в точности одного попадания в цель:
$$
P(Y) = p_1 cdot q_2 + q_1 cdot p_2. qquad (2)
$$

Если вы одолели последние пару абзацев, дальше все будет проще, поверьте:). Просто нужно привыкнуть к формулам, а потом они сами будут подсказывать вам верный ход решения.

Ну и наконец, найдем вероятность события $Z$ = (Оба стрелка попадут в цель), которое, как вы наверное и сами уже поняли, можно выразить так: $Z = A_1 cdot A_2$. Итоговая формула:
$$
P(Z) = P(A_1 cdot A_2) = P(A_1) cdot P(A_2)= p_1 cdot p_2. qquad (3)
$$

Большая теоретическая часть окончена, теперь можно решать примеры как орешки.

Пример 1. Два одновременно стреляют по мишени. Вероятность попадания по мишени у первого стрелка равна 0,6, у второго — 0,7. Какова вероятность того, что в мишени будет только одна пробоина?

Не будем повторять все выкладки выше, для этого мы их и делали подробно. Сразу перейдем к решению. Так как нужно найти вероятность всего одного попадания, используем формулу (2), где по условию $p_1=0,6$, $p_2=0,7$, значит $q_1=1-p_1=0,4$, $q_2=1-p_2=0,3$. Получаем:
$$
P = p_1 cdot q_2 + q_1 cdot p_2 = 0,6 cdot 0,3 + 0,4 cdot 0,7 = 0,46.$$

Пример 2. Два стрелка, для которых вероятности попадания в мишень равны соответственно 0,7 и 0,8, производят по одному выстрелу. Найти вероятность того, что мишень поражена дважды.

Опять же, нужно только применить формулу (3) с данными задачи $p_1=0,7$, $p_2=0,8$ и сразу получим ответ:
$$
P = p_1 cdot p_2=0,7 cdot 0,8 = 0,56.
$$

Пример 3. Производятся два выстрела по цели, вероятности попадания равны 0,3 и 0,4. Найти вероятность того, что хотя бы один выстрел попал в цель.

На этот раз задача будет решена не в одно, а в два действия, но пусть это вас не пугает. Как обычно, в задачах содеражащих фразу «хотя бы один…» мы помимо основного события: $Q$ = (Хотя бы один выстрел попал в цель) вводим сразу противоположное событие $overline{Q}$ = (Ни один выстрел не попал в цель, 0 попаданий). А дальше уже известно, применяем формулу (1), которая выведена выше:
$$
P(overline{Q}) = q_1 cdot q_2= (1-0,3) cdot (1-0,4) =0,7 cdot 0,6 = 0,42.
$$
Вероятность нужного нам события тогда равна:
$$
P(Q) = 1- P(overline{Q}) = 1 — 0,42 = 0,58.
$$

Три стрелка

К двум устрелявшимся стрелкам наконец присоединяется третий, бодрый и полный сил. А мы принимаемся за вывод формул. Напомню общую постановку задачи: три стрелка, вероятности попаданий в цель которых равны $p_1$, $p_2$ и $p_3$, делают по одному выстрелу и подсчитывают число попаданий. Наша задача — вычислить вероятности 1, 2, 3 или ни одного попадания.

Начало одинаковое — формализуем задачу и вводим независимые события:

Событие $A_1$ = (Первый стрелок попал в цель),

Событие $A_2$ = (Второй стрелок попал в цель),

Событие $A_3$ = (Третий стрелок попал в цель).

Известно, что:
$$
P(A_1)=p_1, quad P(A_2)=p_2, quad P(A_3)=p_3, \ Pleft(overline{A_1}right)=1-p_1=q_1, quad Pleft(overline{A_2}right)=1-p_2=q_2, quad Pleft(overline{A_3}right)=1-p_3=q_3.
$$

Вероятность того, что не будет ни одного попадания, вычисляется абсолютно аналогично случаю для двух стрелков, только добавляется третий сомножитель (см. формулу (1)), так как все трое должны промахнуться:
$$
P_0=Pleft(overline{A_1} cdot overline{A_2} cdot overline{A_3}right)= Pleft(overline{A_1}right) cdot Pleft(overline{A_2}right) cdot Pleft(overline{A_3}right)= q_1 cdot q_2 cdot q_3. qquad (4)
$$

Желающие потренироваться в выводе формул могут на этом этапе самостоятельно попытаться выписать вероятности для 2 и 3 попаданий (соответственно, $P_2$ и $P_3$), и сравнить с теми формулами, что я приведу ниже:
$$
P_2 = P(X_2)= \
= P(A_1) cdot P(A_2) cdot Pleft(overline{A_3} right) + P(A_1)cdot Pleft(overline{A_2} right) cdot P(A_3) + Pleft(overline{A_1} right) cdot P(A_2) cdot P(A_3)=\
= p_1 cdot p_2 cdot q_3 + p_1 cdot q_2 cdot p_3 + q_1 cdot p_2 cdot p_3. qquad (6)
$$

$$
P_3 = P(X_3)= P(A_3) cdot P(A_2) cdot P(A_3) = p_1 cdot p_2 cdot p_3. qquad (7)
$$

Теперь, вооружившись формулами до зубов, снова возвращаемся к задачнику и решаем примеры буквально в одну строчку (конечно, если вы оформляете эти работы для сдачи преподавателю, используйте в решении и вывод формул, приведенный выше).

Пример 4. Три стрелка производят по одному выстрелу. Вероятности попадания 1-го, 2-го и 3-го стрелков соответственно равны: 0,2, 0,3 и 0,4. Найти вероятность получения одного попадания?

Так как речь идет об одном попадании, используем формулу (5), куда подставляем значения из условия задачи:
$$
p_1=0,2, quad p_2=0,3, quad p_3=0,4, quad q_1=0,8, quad q_2=0,7, quad q_3=0,6
$$
Получаем:
$$
P_1 = p_1 cdot q_2 cdot q_3 + q_1 cdot p_2 cdot q_3 + q_1 cdot q_2 cdot p_3=\
= 0,2 cdot 0,7cdot 0,6 + 0,8 cdot 0,3 cdot 0,6 + 0,8 cdot 0,7 cdot 0,4 = 0,452.
$$

Пример 5. 3 стрелка делают по одному выстрелу в мишень. Вероятности попадания для каждого стрелка соответственно равны 0,8; 0,7; 0,5. Определите вероятность того, что в мишени окажется ровно 2 пробоины.

Так как речь идет о двух попаданиях, используем формулу (6), куда подставляем значения из условия задачи:
$$
p_1=0,8, quad p_2=0,7, quad p_3=0,5, quad q_1=0,2, quad q_2=0,3, quad q_3=0,5
$$
Получаем:
$$
P_2 = p_1 cdot p_2 cdot q_3 + p_1 cdot q_2 cdot p_3 + q_1 cdot p_2 cdot p_3 = \
= 0,8 cdot 0,7 cdot 0,5 + 0,8 cdot 0,3 cdot 0,5 + 0,2 cdot 0,7 cdot 0,5 = 0,47.
$$

Пример 6. Из трех орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,8; для второго и третьего орудий эти вероятности соответственно равны 0,7 и 0,9. Найти вероятность хотя бы одного попадания при одном залпе из всех орудий.

Надеюсь, вас не смутили орудия вместо стрелков? На самом деле, не суть важно, что происходит: три стрелка вышли на линию, или три пушки готовят залп, или три снайпера целятся в одного террориста. С точки зрения теории вероятностей, все формулы остаются прежними.

Поэтому смело приступаем к решению. Требуется найти вероятность события $A$ = (Будет хотя бы одно попадания при одновременном залпе из всех орудий), поэтому введем для простоты расчетов противоположное событие $overline{A}$ = (Все три орудия дали промашку), вероятность которого найдем по формуле (4), подставляя значения:
$$
p_1=0,8, quad p_2=0,7, quad p_3=0,9, quad q_1=0,2, quad q_2=0,3, quad q_3=0,1
$$
Получаем:
$$
Pleft(overline{A} right) = P_0 = q_1 cdot q_2 cdot q_3 = 0,2 cdot 0,3 cdot 0,1 = 0,006.
$$
Искомая вероятность:
$$
P(A) = 1 — Pleft(overline{A} right) = 1 — 0,006 = 0,994.
$$

Задачи на формулу Бернулли

Когда я писала первый вариант статьи, этого раздела не было. Но ведь задачи, когда выстрелы попадают в цель с одинаковой вероятностью, встречаются весьма и весьма часто и фактически являются частным и более простым случаем разобранных выше. Так что перед вами дополнительный раздел, надеюсь, он окажется полезным:).

Итак, вернемся к нашим стрелкам. Теперь будем считать, что вероятность попадания в цель при каждом выстреле одинакова и равна $p$, число выстрелов равно $n$ и конечно, как и прежде, выстрелы попадают в цель независимо друг от друга. Хм… Что-то знакомое? Конечно! Это схема независимых повторных испытаний, иначе говоря, схема Бернулли.

Ну вот, скажете вы, только научились решать одним способом, и тут на тебе, «схема Бернулли»!

А я отвечу, что в ней как минимум пара преимуществ:

• нужно запомнить всего одну формулу вместо нескольких (см. выше)
• теперь количество стрелков может быть не только 2, 3 или 4 (что уже громоздко), а практически любое — 5, 10, 12…

Пора приступать. Сначала сама формула, а потом разберем несколько примеров для закрепления пройденного:).

Пусть производится $n$ выстрелов, вероятность попадания в цель каждом из которых равна $p$. Вероятность, что окажется в точности $k$ попаданий, можно вычислить по формуле Бернулли:
$$
P_n(k)=C_n^k cdot p^k cdot (1-p)^{n-k} = C_n^k cdot p^k cdot q^{n-k}.
$$

Пример 7. Стрелок производит 4 выстрела, вероятность попадания при каждом из них равна $p=0,8$. Найти вероятность того, что:
1) Стрелок попадёт 3 раза
2) Стрелок попадёт не менее 3-ёх раз.

Вот она, типовая задача на формулу Бернулли. Наши параметры: $n=4$ (число выстрелов), $p=0,8$ (вероятность попадания при одном выстреле), $q=1-p=0,2$ (вероятность промаха).

1) Вероятность того, что стрелок попадёт 3 раза:

$$
P_4(3)=C_4^3 cdot 0,8^3 cdot 0,2^{4-3} = 4 cdot 0,8^3 cdot 0,2 =0,41.
$$

2) Вероятность того, что стрелок попадёт не менее 3-ёх раз из 4 (то есть или 3, или 4 раза — складываем вероятности соответствующих событий):

$$
P_4(k ge 3) =P_4(3) + P_4(4)=0,41+ C_4^4 cdot 0,8^4 cdot 0,2^{0} = 0,41+0,8^4 =0,819.
$$

И это все! Проще некуда, но не забывайте, что задачи разные, где-то формула Бернулли подходит (повторяем: вероятности одинаковые, события независимые и повторные), а где-то — нет (как в разобранных в начале этой статьи задачах).

Пример 8. Вероятность попасть в десятку у данного стрелка при одном выстреле равна 0,2. Определить вероятность выбивания не менее 20 очков при десяти выстрелах.

И опять проверяем выполнение условий схемы Бернулли: вероятности одинаковые (да, $p=0,2$), выстрелы независимые, число выстрелов задано ($n=10$).

Сформулируем вопрос задачи математически: что значит выбито не менее 20 очков? Это значит, что в 10 выстрелах было не менее 2 попаданий в цель (то есть 2, 3, 4,…, 10). Что-то многовато…

В таком случае проще подсчитать сначала вероятность противоположного события: «В 10 выстрелах было менее 2 попаданий в цель» (то есть 0 или 1). Вот тут полегче, давайте посчитаем:

$$
P_{10}(k lt 2) =P_{10}(0) + P_{10}(1)=C_{10}^{0} cdot 0,2^{0} cdot 0,8^{10}+ C_{10}^{1} cdot 0,2^{1} cdot 0,8^{9} =\
=0,8^{10}+ 10 cdot 0,2 cdot 0,8^{9} =0,376.
$$

Тогда искомая вероятность выбить не менее 20 очков будет:

$$
P_{10}(k ge 2) =1-P_{10}(k lt 2)=1-0,376=0,624.
$$

Пригодится: онлайн калькулятор для таких задач

Другие задачи про выстрелы и попадания

Конечно же, не все задачи про выстрелы можно решать по данным формулам (точнее, не все вписываются в эту схему напрямую), это лишь один из популярных классов задач. Для полноты изложения я приведу еще несколько типовых задач с немного отличающимся решением. Задачи из существенно других разделов (например, на формулу Байеса или построение ряда распределения случайной величины) будут разобраны в других статьях.

Пример 9. Вероятность того, что стрелок попадет в цель при одном выстреле, равна 0,7. Производится пять независимых выстрелов. Какова вероятность того, что в мишени окажется хотя бы одна пробоина?

Требуется найти вероятность события $A$ = (В мишени окажется хотя бы одна пробоина), поэтому вводим сначала противоположное событие $overline{A}$ = (Все пять выстрелов не попали в цель). Если обозначить вероятность попадания в цель как $p=0,7$ (она одинакова при каждом выстреле), а вероятность промаха как $q=1-p=0,3$, то вероятность всех пяти промахов будет
$$
Pleft(overline{A} right) = q^5 = 0,3^5.
$$
Искомая вероятность:
$$
P(A) = 1 — Pleft(overline{A} right) = 1 — 0,3^5 = 0,998.
$$

Общий случай: как найти вероятность наступления хотя бы одного события

Пример 10. Два стрелка стреляют по мишени по одному разу. Вероятность того, что оба попали равна 0,42, а вероятность того что оба промахнулись, 0,12. Найти вероятность попадания в мишень каждым стрелком при одном выстреле.

Если обозначить вероятности попадания первым и вторым стрелком соответственно как $p_1$ и $p_2$, то, используя формулы (1) и (3), запишем условие задачи в виде системы уравнений:
$$
P_2 = p_1 cdot p_2 = 0,42;\
P_0 = (1-p_1) cdot (1-p_2) = 0,12.\
$$
Решая эту систему, найдем искомые вероятности попадания для каждого стрелка: $p_1 = 0,6$ и $p_2 = 0,7$ (или наоборот, $p_1 = 0,7$ и $p_2 = 0,6$).

Пример 11. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.

Если обозначить вероятность попадания в цель как $p$ (она одинакова при каждом выстреле), а вероятность промаха как $q=1-p$, то вероятность 4 промахов при четырех выстрелах будет равна $q^4$, а соответственно вероятность хотя бы одного попадания в цель при четырех выстрелах — $1-q^4$. Получаем уравнение:
$$
1-q^4=0,9984;\
q^4=0,0016;\
q=0,2;\
p=1-q=0,8.
$$
Нашли вероятность попадания в цель при одном выстреле, она равна 0,8.

Пример 12. Два стрелка независимо выстрелили по мишени по два раза. Меткость первого стрелка равна 0,8; второго – 0,7. Найти вероятность того, что в мишень попадут все четыре пули.

Все 4 пули попадут в мишень, если первый стрелок попадет оба раза (вероятность попадания при одном выстреле у него $p_1=0,8$), и одновременно второй стрелок попадет оба раза (вероятность попадания при одном выстреле у него $p_2=0,7$). По правилу умножения вероятностей
$$
P = p_1 cdot p_1 cdot p_2 cdot p_2 = 0,8 cdot 0,8 cdot 0,7 cdot 0,7 = 0,3136.
$$

Полезная информация

Онлайн калькуляторы Онлайн учебник Более 200 примеров Решенные контрольные

Формулы и таблицы Сдача тестов Решение на заказ Онлайн помощь

Решебник по вероятности

В решебнике вы найдете более 700 задач о выстрелах и попаданиях с полными решениями (вводите часть текста для поиска своей задачи):

Величину
вероятности попадания можно определить
опытным пу­тем по частоте попаданий
или одним из расчетных способов: по
сердце­вине, по шкале рассеивания, по
таблице вероятностей и по сетке
рассеи­вания.

Знание
закономерности и характеристик
рассеивания дает возмож­ность еще до
стрельбы определять вероятность
попадания в цель.

Общий
принцип определения вероятности
попадания за­ключается в определении
той части площади рассеивания, которая
на­крывает цель. Затем на основании
закона рассеивания подсчитывают процент
попаданий, приходящихся на эту площадь.
Размеры рассеива­ния в каждом конкретном
случае берут из таблиц, которые составлены
на основании большого числа опытных
стрельб.

Определение
вероятности попадания по частоте
попаданий (на ос­новании результатов
опытных стрельб)

Пусть
по некоторой цели стрелок произвел
большое количество выстрелов в одинаковых
условиях. В ходе стрельбы установлено,
что на каждые 100 выстрелов приходится
75 попаданий, т. е. частота попада­ний
в данном случае равна 0,75 или 75%.

Из
главы III
известно, что при большом числе испытаний
частота

стремится к вероятности.
Отсюда мы можем принять, что вероятность
по­падания в данных условиях равна
0,75.

Этот
способ определения вероятности связан
с расходом большого количества
боеприпасов, но он дает при достаточно
большом количестве стрельб конкретное
значение вероятности попадания для
данного стрел­ка из данного образца
оружия. Практически при проведении ряда
стрельб (подготовка к соревнованиям,
подбор упражнений для курса стрельб,
отбор снайперов и отличных стрелков и
т. д.) руководствуются именно этим
способом нахождения вероятности
попадания.

Определение
вероятности попадания по сердцевине
рассеивания

Данный
способ определения вероятности попадания
в одиночные цели применим только в тех
случаях, когда площадь цели меньше
серд­цевины рассеивания и не выходит
за ее пределы.

При
подсчете вероятности попадания
допускается, что в пределах сердцевины
рассеивания пробоины располагаются
равномерно. Тогда оп­ределение
вероятности попадания можно производить
по отношению мер, путем сравнения площади
цели с площадью сердцевины рассеивания
(рис. 54).

Так как сердцевина
рассеивания вмещает в себя лучшую
половину (0,5) всех пробоин, то вероятность
попадания в цель будет меньше 0,5 во
столько раз, во сколько раз площадь цели
меньше площади сердце­вины:

Р_ф
= 0,5

,

где
Р_ф
—
вероятность попадания в цель;

S_ц
— площадь цели;

S
— площадь сердцевины (S=Св·Сб).

Рис. 54.Определение
вероятности попадания по сердцевине.

Пример.
Определить вероятность попадания при
стрельбе из ручно­го пулемета на
дальность 400 м по грудной фигуре (залегший
стрелок).

Решение.
По таблице ТС ГРАУ находим, что на
дальности 400 м Св
= 0,7 м, Сб=0,6
м, площадь грудной фигуры равна 0,18 м².
Определяем вероятность попадания в
фигуру:

;
Р_ф
= 0,21 или 21°/_в.

Полученный результат
следует понимать так. Если произвести
боль­шое число выстрелов, то в среднем
на каждые 100 выстрелов придется 21
попадание и 79 промахов или в среднем на
один выстрел приходится 0,21 попадания.

Определение
вероятности попадания по шкале рассеивания

Если
цель по своим размерам больше сердцевины
рассеивания, то вероятность попадания
определяется по шкале рассеивания.

Сущность
этого способа состоит в том, что на листе
бумаги в одном и том же масштабе изображают
цель и шкалу рассеивания с учетом
по­ложения средней точки попадания.
Затем по шкале подсчитывают веро­ятность
попадания в данном направлении.

Пусть цель накрыта
эллипсом рассеивания так, как это
показано на рис. 55. Для определения
вероятности попадания надо:

—
определить вероятность попадания по
высоте (Рв)
в полосу вы­сотой 2у, равную высоте
цели;

• определить
  вероятность попадания по боковому
  направлению (Рб)
  в полосу шириной 2 z
  , равную ширине цели;

• определить
  вероятность попадания в прямоугольник,
  образуемый пересечением этих полос.

В
ероятность
попадания в прямоугольник равна
веро­ятности попадания по высоте,
умноженной на вероятность по­падания
по боковому направлению: Р
= Рв·Рб.

При
подсчете вероятности попадания в
фигурные цели учитывается еще так
называемый коэффициент фигурности
(К_ф).

где
Sф.
– площадь прямоугольника;

Sпр.
– площадь прямоугольника.

Коэффициентом
фигурности называют отношение площади
фигуры цели к площади описанного около
нее прямоугольника (рис. 56).

S_ф

Коэффициент
фигурности показывает, насколько
вероятность попа­дания в фигуру меньше
вероятности попадания в описанный
прямоуголь­ник. Поэтому для определения
вероятности попадания в фигурную цель
необходимо умножить вероятность
попадания по высоте на вероятность
попадания по боковому направлению и на
К_ф:

Р_ф
= Р_в·Р_б
·
К_ф.

При
пользовании К_ф
следует помнить, что он дает положительные
результаты только в том случае, если
пули располагаются по всей пло­щади
равномерно. Такое явление можно наблюдать,
когда цель очень мала по сравнению с
площадью рассеивания или находится в
сердце­вине рассеивания. Если цель
по своим размерам приближается к
разме­рам полного рассеивания, то
применение К_ф
будет приводить к большим ошибкам.

(В
этих случаях вместо коэффициента
фигурности гораздо удобнее пользоваться
приведенными размерами цели. Этот способ
будет описан ниже).

Пример
1.
Определить вероятность попадания в
ам­бразуру высотой 20 см и шириной 35
см при стрельбе из снайперской винтовки
Драгунова на расстояние 400 м, если средняя
траектория пройдет через центр цели.

Решение.
1. По таблицам находим: Вв=7,2
см,
Вб=7,2
см.

2. Определяем
вероятность попадания в полосу, равную
высоте цели, для чего:

а)
находим отношение половины высоты цели
к сре­динному отклонению по высоте:

В=10:7,2=1,39;

б)
по табл. 1 приложения № 4 в графе В
находим цифру 1,39; стоящая рядом с этой
цифрой в гра­фе Ф
(В)
цифра 0,652 и есть величина вероятности
попадания в данную полосу (р_а).

3. Определяем
вероятность попадания в полосу,
равную ширине цели:

В=17,5:7,2=2,43,

по
таблице находим: р_б
=0,899.

4. Определяем
вероятность попадания в цель:

р
= р_в
·
р_б
= 0,652·0,899 = 0,586,
или 58,6%.

Пример
2. Определить вероятность попадания в
бегу­щую фигуру при стрельбе из
пулемета Калашникова на расстояние
500 м, если средняя траектория пройдет
ниже середины цели на 0,4 м.

Решение.
1. По таблицам находим: Вв
сум=
0,37 м, Вб
сум=0,51
м; из приложения
№ 4 находим
приведенные размеры цели: высота 1,40 м;
ширина 0,46 м.

2. Определяем
вероятность попадания в полосу от оси
рассеивания по высоте до верхнего края
цели:

3. Определяем
вероятность попадания в полосу от этой
же оси рассеивания до нижнего края цели:

4. Определяем
вероятность попадания в полосу,
равную высоте цели:

р_в
= 0,477 + 0,207 = 0,684.

5. Определяем
вероятность попадания в полосу,
равную ширине цели р_в.

1. Определяем
   вероятность попадания в цель:

р=р_в
р_б
= 0,684·0,239 = 0,163, или
16,3%.

Определение
вероятности попадания по таблице
значений вероятностей

Этот
способ применим для целей любых размеров.
Сущность его со­стоит в том, что при
заданном положении СТП относительно
центра це­ли определенному отношению
высоты цели к Вв
или ширины цели к Вб
соответствует вполне определенная
вероятность попадания в данном
на­правлении. Это позволяет составить
специальные таблицы и, вместо кро­потливого
построения в одном масштабе цели и
размеров шкалы рассеи­вания, найдя
«входное число», т. е. во сколько раз
высота или ширина цели больше Вв
или Вб,
по таблице определить вероятность
попадания в данном направлении. После
этого остается по общей формуле: Рф=
Рв
·Рб
·К_ф
определить вероятность попадания в
фигурную цель.

Существует
несколько видов таблиц определения
вероятности попа­дания. Рассмотрим
устройство таблицы, помещенной в
Наставлении по стрелковому делу «Основы
и правила стрельбы» (1986 г.), так называемую
таблицу функций Ф
(В).

Данная
таблица составлена в предположении,
что центр рассеива­ния (СТП) совпадает
с центром цели. Для определения вероятности
по­падания по этой таблице необходимо
разделить половину высоты цели (у)
на Вв
или половину ширины цели (z)
на Вб.
Полученные отношения

и

называются
входными числами по высоте и по боковому
направлению. По найденному входному
числу в таблице определяют вероятность
попадания.

Пример.
Определить вероятность попадания в
головную фигуру при стрельбе из пулемета
ПКМ на дальность 200 м.

Размеры
цели: 2у=0,3 м; 2 z
=0,5 м.

Решение.
1. По таблице ТС № 61 ГРАУ[24] находим на
дальность 200 м Вв=0,06
м и Вб=0,08
м.

2.
Определяем вероятность попадания по
высоте Рв.

а)
Определяем входное число по высоте

.

б)
По таблице вероятностей находим, что
входному числу 2,5 со­ответствует
вероятность попадания 0,908; Рв=0,908.

3.
Определяем вероятность попадания по
боковому направлению.

а)
Определяем входное число по боковому
направлению

.

б)
По таблице вероятностей определяем,
что входному числу 3,125 соответствует
вероятность попадания 0,965; Рб=0,965.

4.
Вероятность попадания в фигуру определяем
по формуле:

Рф = Рв·Рб·Кф;
Рф=0,908·0,965 ·0,6=0,525.

Пример
2.
Определить вероятность попадания в БМП
(мишень № 14) при стрельбе из 30-мм
автоматической пушки 2А42 БТ снарядом
на дальность 1200 м (средняя точка попадания
совмещена с цент­ром цели).

Решение.
1. По таблицам стрельбы [24] находим, что
на дальность 1200 м Вв
= 0,4 м, Вб=0,5
м.

2.
По Курсу стрельб [22] находим, что высота
цели — 2,2 м, ширина цели — 2,96 м. Коэффициент
фигурности цели — 0,9.

3.Определяем
вероятность попадания по высоте Рв.

а)Определяем
входное число по высоте

.

б)По
таблице вероятностей определяем, что
входному числу 2,75

соответствует
вероятность попадания в цель 0,936.

4.
Аналогичным образом определяем
вероятность попаданий в цель по боковому
направлению.

.

По
таблице вероятностей определяем, что
входному числу 2,96

соответствует
вероятность попадания в цель 0,954.

5. Определяем
вероятность попадания в цель с учетом
ее фигурности.

Рф
= Рв · Рб · Кф; Рф=0,936 · 0,954 · 0,9=0,803.

При
несовмещении средней точки попадания
с центром цели, кото­рое может появиться
в результате действия целого ряда
систематиче­ских причин (неучет ветра,
неточный выбор прицела и точки
прицелива­ния и т. п.), вероятность
попадания определяется по той же таблице,
которая была рассмотрена выше. Однако
при этом необходимо произвести некоторые
простые дополнительные построения,
сущность которых рас­смотрим на
конкретном примере.

Пример
3.
Определить вероятность попадания в
грудную мишень при стрельбе из пулемета
ПКМ на 400 м, если наводчик ошибочно
по­ставил целик вправо 1 и ведет огонь
с прицелом 5, прицеливаясь под обрез
мишени.

Решение.
1. Определим отклонение СТП от центра
цели.

а)
На 400 м одна тысячная составляет 40 см.
Принимаем, что СТП

будет отклонена
от центра цели вправо на 40 см.

б)
С прицелом 5 на 400 м превышение средней
траектории равно

0,5 м; т. к. высота
грудной мишени равна 0,5 м, то отклонение
СТП от

центра цели по высоте составит
0,25 м (рис. 56).

1. Определим
   размеры рассеивания при стрельбе на
   400 м. По таб

   лице ТС ГРАУ Вв=0,15
   м; Вб=0,15
   м.

2. Определим
   вероятность попадания по высоте (Рв).

Для
определения входного числа (В)
необходимо взять отношение всей высоты
цели 2у к Вв.
Учитывая, что по найденному значению
таб­лица даст значение вероятности
в обе стороны от оси рассеивания (таблица
составлена в предположении, что СТП
совпадает с центром цели), необходимо
найденную из таблицы вероятность
попадания уменьшить в два раза.

а)
Определим

;

.

б)
Определим вероятность попадания в
полосу, равную высоте цели.

.

4
.
Определим вероятность попадания по
боковому направлению (Рб).

Для
определения вероятности попадания в
полосу, равную ширине цели, необходимо
сначала определить вероятность попадания
в полосу шириной, равной 65 см (50 см ширина
цели плюс 15см — расстояние меж­ду
краем цели и вертикальной осью
рассеивания); затем — в полосу 15 см.

Вычтя
из первой вероятности вторую, получим
нужную нам вероят­ность попадания по
боковому направлению.

Определим
вероятность попадания в полосу шириной
65 см.

а)

;

б)
.

Определим
вероятность попадания в полосу, равную
ширине цели 15 см. а)
;

б)
.

Определим
вероятность попадания в полосу, равную
ширине цели 50 см (Рб)

Рб=Ру₁
–Ру₂=0,487-0,25=0,248.

5.
Определим вероятность попадания в
фигуру по обычной формуле

Рф=Рв
· Рб · Кф;
Рф=0,487
· 0,248 · 0,72 = 0,087.

Практически
может быть бесконечно большое число
вариантов за­дач на несовпадение
средней точки попадания с центром цели.
Все они решаются на основе рассуждений
и построений, аналогичных приведен­ным
выше.

Решение
задач на определение вероятности
попадания по таблице вероятностей
значительно упрощается, если вместо
применения коэффициента фигурности
пользоваться так называемыми приведенными
раз­мерами цели.

Приведенными
размерами фигурной цели
называются ус­ловно взятые значения
высоты и ширины цели, при которых площадь
цели можно представить в виде прямоугольника
такого размера, чтобы вероятность
попадания в него была равна вероятности
попадания в фи­гурную цель.

Тогда
при решении задач для определения
входного числа вместо фактических
размеров цели пользуются приведенными
данными. На рис. 58 изображен реальный
вид всех наиболее распространенных
ми­шеней и штриховкой показаны
прямоугольники по приведенным разме­рам
цели. Данные о приведенных размерах
целей даются в таблицах размеров целей
(Наставление по стрелковому делу «Основы
и правила стрельбы», 1986 г.).

Рис.
58. Приведенные размеры целей.

Пользование
приведенными размерами покажем на
примере.

Пример.
Определить вероятность попадания в
мишень № 10а (пулеметный расчет) при
стрельбе из пулемета РПК74 на 500 м средним
пулемётчиком, СТП совпадает с центром
цели.

Решение.
1. По таблицам ТС ГРАУ определяем значе­ние
Вв
и Вб:
Вв=0,2
м, Вб
= 0,2 м. Определяем приведенные размеры
цели (высоту — 2у¹
и ширину — 2 z¹);
2у¹=0,75
м; 2z¹
=1,0 м.

2.
Определим вероятность попадания по
высоте (Рв)

;
Рв=0,793.

3. Определим
вероятность попадания по боковому
направлению

;
Рб=0,908

Определим
вероятность попадания в цель: Р=Рв
· Рб=0,793 · 0, 908 =0,72.

Понятно,
что здесь уже не требуется учитывать
коэффициент фигурности. Это делает
способ решения задач по приведенным
размерам це­ли более точным и более
простым. Поэтому он и рекомендуется
Настав­лением «Основы и правила
стрельбы», изд. 1986 г.

При
стрельбе из личного оружия на небольшие
дальности, когда рассеивание пуль
приближается к форме круга, вероятность
попадания в круглые мишени удобно
определять по специально рассчитанной
таб­лице, аналогичной таблице Ф(
В).
В ней в качестве входного числа р
берут отношение радиуса цели (R_ц)
к радиусу круга, вмещающего 50% всех
попаданий (R₅₀),
т.е.
.
Такая таблица дается в Наставлении
«Основы и правила стрельбы», изд. 1986 г.

Пример.
Определить вероятность попадания в
круг радиусом 12,5 см при стрельбе из
пистолета Макарова на дальность 50 м.

Решение.
1. Из Наставления по стрелковому делу
«Пистолет Мака­рова (ПМ)»[8] стр. 83
находим значение R₅₀
= 8 см.

2.
Определим входное число:

1. По
   таблице определяем, что вероятность
   попадания в круглую мишень равна 83%
   (см. прилож.№ 6).

Вероятность
попадания в цель любого очертания и при
любом рас­положении средней траектории
может быть определена графическим
спо­собом по сетке рассеивания (рис.
59).

Определение
вероятности попадания по сетке рассеивания

Сетка
рассеивания составляется следующим
образом. Проводятся прямые линии,
параллельные осям рассеивания, через
целые срединные отклонения или доли
их. В результате этого вся площадь
рассеивания разбивается на ряд
прямоугольников. Вероятность попадания
в образо­вавшиеся прямоугольники
подсчитывается умножением вероятности
попадания в полосы, которые образуются
этими прямоугольниками (рис. 59).

Определение
вероятности попадания по сетке рассеивания
произво­дится в той же последовательности,
что и по шкале рассеивания. Для этого
надо начертить в условном масштабе цель
и на нее наложить сетку рассеивания в
том же масштабе так, чтобы центр
рассеивания был в точ­ке согласно
условиям стрельбы. Затем подсчитать
вероятность попада­ния в цель
суммированием вероятностей попадания
в прямоугольники, накрывающие цель;
причем там, где прямоугольники неполностью
вхо­дят в цель, вероятности берутся
примерным сравнением площади, заня­той
целью, с площадью всего прямоугольника.

Пример.
Определить вероятность попадания в
амбразуру ДЗОТа размерами: высотой 0,6
м и шириной 1,2 м, если стрельба ведется
из 30-мм автоматической пушки 2А72
осколочно-фугасным сна­рядом на
дальность 1000 м (средняя траектория
совпадает с центром цели).

Решение.
1. Определим по таблицам стрельбы [25]
сре­динные отклонения по высоте и
боковому направлению на дальность 1000
м – Вв
=0,4
м; Вб
=0,4
м.

1. Вычертим цель в
   масштабе 1 : 20 и в том же масштабе
   наложим

   сетку рассеивания на цель
   (рис. 58).

2. Подсчитаем
   вероятность попадания в цель

Р
=
6,25 + 6,25 + 6,25 + 6,25 + 4,0 + 4,0 + 4,0 + 4,0 + 4,0 + 4,0 + 4,0
4,0+2,56+2,56+2,56+2,56=67,24%.

Р
= 67,24%.

0

	-4Вб	–3Вб	–2Вб	–1Вб	+1Вб	+2Вб	+3Вб	+4Вб
2%	0,04	0,14	0,32	0,5	0,5	0,32	0,14	0,04	+4Вв
7 %	0,14	0,49	1,12	1,75	1,75	1.12	0,49	0,14	+3Вв
16%	0,32	1.12	2,56	4,0	4,0	2,56	1,12	0,32	+2Вв
0 25%	0,5	1,75	4,0	6,25	6,25	4,0	1,75	0,5	+1Вв
25%	0,5	1,75	4,0	6,25	6,25	4,0	1,75	0,5	-1Вв
16%	0,32	1,12	2,56	4,0	4,0	2,56	1,12	0,32	-2Вв
7%	0,14	0,49	1,12	1,75	1,75	1,12	0,49	0,14	-3Вв
2%	0,04	0,14	0,32	0,5	0,5	0,32	0,14	0,04	-4Вв
	2%	7%	16%	25%	25%	16%	7%	2%

Рис.
59. Определение вероятности попадания
по сетке рассеивания.

Определение
вероятности попадания в групповую цель

Для
определения действительности стрельбы
по групповым целям необходимо знать
вероятность попадания в одну из фигур,
составляю­щих данную групповую цель.
Рассмотрим способ определения вероятно­сти
попадания при стрельбе по широкой цели
с искусственным рассеива­нием по
фронту.

Пусть
на фронте АВ
расположено некоторое количество
ростовых фигур (рис. 60).

Рис.
60. Определение вероятности попадания
в групповую цель.

Определение
вероятности попадания в одну из фигур
данной цели производят на основе
следующих допущений.

1. Известно
   положение горизонтальной оси
   искусственного рассеивания по фронту
   (ось х у).

2. Размеры фигур в
   цели и коэффициенты фигурности их
   одинаковы.

3. Рассеивание
   по фронту происходит равномерно и
   все пули не выходят за пределы рассеивания
   по боковому направлению. Таким образом,
   вероятность попадания по боковому
   направлению в полосу, занятую

   фигурами
   (полосу АВМК),
   равна 1 или 100%.

4. Распределение
   пуль по высоте подчиняется нормальному
   закону

   рассеивания.

На
основе сделанных допущений вероятность
попадания в одну из фигур групповой
цели определяется следующим образом:

1.
Определяют вероятность попадания в
прямоугольник АВМК.
Для этого достаточно определить
вероятность попадания по высоте Р
(АВМК)
= Рв,
так как вероятность попадания по боковому
направле­нию (согласно принятому
допущению) равна 100%.

2.
Исходя из равномерного распределения
пробоин, считают, что ве­роятность
попадания в фигуру будет во столько раз
меньше вероятности попадания в
прямоугольник, включающий все фигуры,
во сколько раз площадь фигуры будет
меньше площади прямоугольника.

Таким образом,
вероятность попадания в одну фигуру
групповой цели определится по формуле;

,

где
S
– площадь одной фигуры;

Sпр
– площадь прямоугольника, описанного
около всей групповой цели.

Пример.
Определить вероятность попадания в
одну фигуру залегшей пехоты на фронте
50 метров при стрельбе из пулемета ПКМ
с равномерным рассеиванием по фронту,
если дальность до цели 400 м средним
пулеметчиком (рис. 61). Площадь одной
фигуры равна 0,48 м².
Горизонтальная ось рассеивания проходит
под нижний обрез цели.

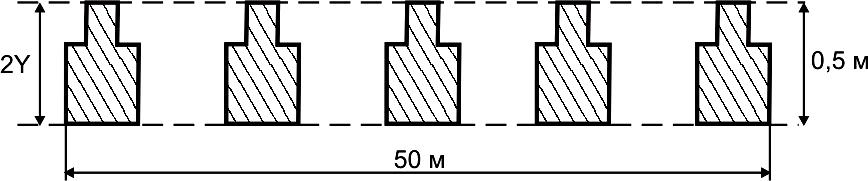
Рис.
61. Определение вероятности попадания
в одну фигуру групповой цели при
стрельбе с равномерным рассеиванием
по фронту.

Решение.
1) По таблице ТС ГРАУ находим, что на
дальности 400 м Вв
= 0,18 м.

Так
как стрельба ведется с рассеиванием по
фронту, рассеивание по высоте увеличится
в 1,5—2 раза по сравнению с табличным
(возьмем в среднем значение 1, 75 Вв).
Тогда Вв
= 0,18· 1,75 = 0,32 м).

2)
Определим вероятность попадания в
прямоугольник, занятый все­ми фигурами
(Рв).

А)
Определим входное число

.

Б)Находим вероятность
попадания по таблице:

.

1. По
   формуле
   
   определим
   вероятность попадания в фигуру:

или
0,55%.

Для определения
вероятности попадания в любую из фигур
цели, не указывая в какую именно,
необходимо найденную вероятность
умножить на число фигур групповой цели.
Однако следует отметить, что все
прак­тические задачи, связанные со
стрельбой по групповым целям, полно­стью
решаются на основе известной вероятности
попадания в одну фигу­ру по приведенной
выше формуле.

Способы определения вероятности попадания

107. Вероятность попадания в цель может быть определена сравнением площади цели с площадью сердцевины рассеивания, по шкале рассеивания, по таблице значений вероятностей и по сетке рассеивания.

При стрельбе автоматическим огнем (очередями) для вычисления вероятности попадания берутся характеристики суммарного рассеивания.

108. Если цель по своим размерам равна сердцевине рассеивания или меньше ее, то вероятность попадания в цель определяется приближенно сравнением площади цели с площадью сердцевины рассеивания. При этом допускается, что рассеивание пуль в пределах сердцевины равномерное.

Вероятность попадания в цель будет во столько раз меньше вероятности попадания в сердцевину, во сколько раз площадь цели меньше площади сердцевины, т. е.

где

р — вероятность попадания в цель;

0,50, или 50% — вероятность попадания в сердцевину;

Св и Сб— сердцевинные полосы соответственно по высоте и боковому направлению;

Sц — площадь цели.

Пример. Определить вероятность попадания в грудную фигуру (залегший стрелок) при стрельбе очередями из ручного пулемета Калашникова на 200 м, если средняя траектория пройдет через середину цели.

Решение. 1. Из таблицы находим: Св=0,50 м, Сб=0,50 м; из приложения 4 (табл. 6) площадь цели 5ц = 0,20 м2.

2. Определяем вероятность попадания в цель:

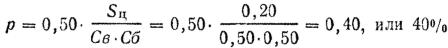
(0,50 — вероятность попадания в сердцевину).

Пример показывает, что если произвести большое число выстрелов в возможно одинаковых условиях, то в среднем на каждые 100 выстрелов придется 40 попаданий и 60 промахов, или в среднем на один выстрел приходится 0,40 попадания.

109. Если в каком-либо направлении цель по своим размерам больше сердцевины рассеивания, то вероятность попадания в нее может быть определена по шкале рассеивания. При этом вероятность попадания в цель определяется как произведение вероятности попадания в полосу, равную высоте (глубине) цели, на вероятность попадания в полосу, равную ширине цели, т. е.

p = pв • рб

где р — вероятность попадания в цель;

рв — вероятность попадания в полосу, равную высоте цели;

рб — вероятность попадания в полосу, равную ширине цели.

Для определения вероятности попадания в полосу, равную высоте (ширине) цели, необходимо вычертить в произвольном масштабе цель и на ней в том же масштабе шкалу рассеивания, например, по высоте; подсчитать по шкале рассеивания процент попаданий, приходящийся в полосу, равную высоте цели; вычертить на цели шкалу рассеивания по боковому направлению и также подсчитать по ней процент попаданий в полосу, равную ширине цели.

При расчетах по шкале рассеивания с масштабом в одно срединное отклонение допускают, что рассеивание равномерно в пределах полосы, равной по ширине одному срединному отклонению.

Если цель не является прямоугольником, а имеет фигурное очертание, то сначала по шкале рассеивания определяется вероятность попадания в прямоугольник, описанный вокруг фигурной цели. Затем полученную вероятность умножают на коэффициент фигурности, равный отношению площади цели к площади описанного вокруг цели прямоугольника, т. е.

р = рв • рб • К

где К — коэффициент фигуриости.

При применении коэффициента фигурности допускают, что рассеивание в пределах описанного вокруг цели прямоугольника равномерно. Это допущение приводит к ошибке, которая тем больше, чем больше размеры цели по отношению к площади рассеивания. При определении вероятности попадания в фигурную цель коэффициент фигурности можно применять только в тех случаях, когда размеры цели меньше размеров полного рассеивания.

Примечание. Для более точных расчетов коэффициент фигурности определяется как отношение вероятности попадания в цель к вероятности попадания в прямоугольник, описанный вокруг цели.

Значения коэффициента фигурности для различных целей даны в приложении 4, табл. 6.

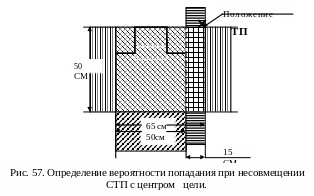
Пример. Определить вероятность попадания в пулемет противника при стрельбе из ручного пулемета Дегтярева из положения стоя из окопа на расстояние 300 м, если средняя траектория пройдет через середину цели.

Решение. 1. По таблицам и приложению 4 находим: Bв сум =0,21 м, Вб п/ж.=0,29 м, высота цели равна 0,55 м, ширина 0,75 м, коэффициент фигурности К=0,75.

2. Определяем вероятность попадания в полосу, равную высоте цели (рв), для чего:

а) вычерчиваем в произвольном масштабе цель и накладываем на нее (вычерчиваем на ней) в том же масштабе шкалу рассеивания по высоте (рис, 46);

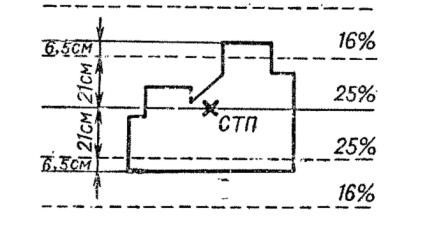
Рис. 46. Определение вероятности попадания по шкале рассеивания в полосу, равную высоте цели

б) подсчитываем по шкале рассеивания процент попадания в ту часть шкалы, которой накрывается цель; по одну сторону центра рассеивания цель накрывается полосой, включающей 25% попаданий, и частью полосы, включающей 16% попаданий.

Для определения процента попаданий в эту часть полосы, равную 6,5 см (27,5 — 21), составляем пропорцию:

Следовательно, часть шкалы рассеивания, накрывающая половину цели, включает в себя

25%+ 5%=30%

Тогда вероятность попадания в полосу, равную высоте цели, будет вдвое больше, т. е.

рв=30%+30%=60%, или 0,60%

3. Определяем вероятность попадания в полосу, равную ширине цели (рб) для чего:

а) накладываем на цель шкалу рассеивания по боковому направлению;

б) подсчитываем по шкале рассеивания процент попаданий, который равен

рб = (25% + 5%) 2 = 60%, или 0,60.

4. Определяем, вероятность попадания в цель:

р = рв•рб•К= 0,60•0,60•0,75 = 0,27, или 27%.

Для удобства определения вероятности попадания иногда фигурную цель заменяют равновеликим прямоугольником, стороны которого соответственно равны произведению ширины (высоты) мишени на корень квадратный из коэффициента фигурности (рис. 47).

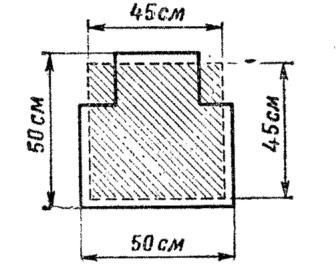
Рис. 47. Приведённые размеры грудной фигуры

Приведенные размеры цели даны в приложении 4, табл. 6. Найденную вероятность попадания в такой прямоугольник принимают за вероятность попадания в фигурную цель.

110. Для более точного определения вероятности попадания в цель пользуются таблицей значений вероятностей (шкалой рассеивания), рассчитанной с учетом неравномерности рассеивания через каждую десятую или сотую и т. д. долю срединного отклонения (приложение 4, табл.1).

При этом допускают, что рассеивание равномерно только в пределах полосы по ширине, равной десятой, сотой и т. д. доле срединного отклонения.

Для определения вероятности попадания по таблице значений вероятностей необходимо:

— подсчитать отношения половины высоты (глубины) или ширины цели к срединному отклонению по высоте (дальности) или боковому направлению; эти отношения в таблипе обозначены через В;

— в графе В найти цифры, соответствующие этим отношениям; стоящие рядом в графе Ф (В) цифры являются вероятностью попадания в полосы, равные высоте (глубине) или ширине цели.

Вероятность попадания в цель прямоугольной формы будет равна произведению вероятности попадания в полосу, равную высоте (глубине) цели, на вероятность по падания в полосу, равную ширине цели.

Если цель по своей форме отличается от прямоугольника, то найденную вероятность попадания необходимо умножить на коэффициент фигурности, Вероятность попадания в такую цель может быть найдена также по приведенным размерам цели без использования коэффициента фигурности

где

р — вероятность попадания в цель;

у — половина высоты цели;

z — половина ширины цели;

Вв сум и Вб сум — суммарные срединные отклонения соответственно по высоте и боковому направлению;

К— коэффициент фигурности.

Пример. Определить вероятность попадания в амбразуру бронеколпака высотой 20 см и шириной 35 см при стрельбе из снайперской винтовки Драгунова на расстояние 400 м, если средняя траектория пройдет через центр цели.

Решение. 1. По таблицам находим: Вв=7,2 см, Вб=7,2 см.

2. Определяем вероятность попадания в полосу, равную высоте цели, для чего:

а) находим отношение половины высоты цели к срединному откло­нению по высоте:

б) по табл. 1 приложения 4 в графе В находим цифру 1,39; стоящая рядом с этой цифрой в графе Ф (В) цифра 0,652 и есть величина вероятности попадания в данную полосу (рв).

3. Определяем вероятность попадания в полосу, равную ширине дели:

по таблице нзходим: рб = 0,899.

4. Определяем вероятность попадания в цель:

Р = Рв • Рб = 0,652 • 0,899 = 0,586, или 58,6%.

111. Для определения вероятности попадания по таблице вероятностей (табл. 2, приложение 4) в круглую мишень при площади рассеивания, близкой по форме к кругу, и при совмещении средней точки попадания с центром мишени необходимо:

— определить отношение радиуса круглой мишени к радиусу круга рассеивания, вмещающего 50% попаданий;

— по таблице в графе В найти это отношение; стоящая рядом в графе Ф (В) цифра будет являться вероятностью попадания в цель.

Пример. Определить вероятность попадания в круглую мишень (круг) радиусом 10 см при стрельбе из пистолета Макарова на рас­стояние 50 м, если средняя траектория пройдет через центр круга.

Решение. 1. В таблице находим: р50 = 8см.

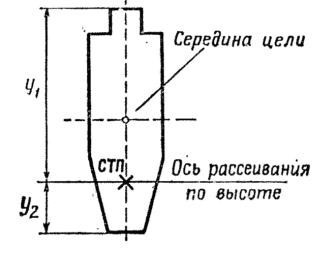
Рис. 48. Определение вероятности попадания в цель при несовпадении средней точки попадания с серидиной цели

2. Определяем отношение радиуса круглой мишени (круга) к р50

3. По табл. 2 приложения 4 находим в графе В цифру 1,25; рядом стоящая цифра в графе Ф {В) дает вероятность попадания в круг равную 66,1%.

112. Когда средняя точка попадания не совпадает с серединой цели, для определения вероятности попадания в цель необходимо (рис. 48):

1. Определить вероятность попадания в полосу, равную высоте (глубине) цели, для чего:

а) определить вероятность попадания в полосу, высота (глубина) которой равна расстоянию от оси рассеивания по высоте (дальности) до верхнего (дальнего) края цели; для этого найти отношение высоты (глубины) этой полосы к срединному отклонению по высоте (дальности), т. е. В, и по таблице вероятностей взять половину (Уз) значения, указанного в графе Ф (В);

б) определить таким же образом вероятность попадания в полосу, высота (глубина) которой равна расстоянию от этой же оси рассеивания до нижнего (ближнего) края цели;

в) определить вероятность попадания в полосу, равную высоте (глубине) цели; она будет равна: если средняя точка попадания расположена в пределах цели, — сумме вероятностей попадания в эти полосы; если средняя точка попадания вне пределов цели, — разности вероятностей попадания в эти полосы.

2. Подобным же образом определить вероятность попадания в полосу, равную ширине цели.

3. Определить вероятность попадания в цель, для чего вероятность попадания в полосу, равную высоте цели, умножить на вероятность попадания в полосу, равную ширине цели. Если цель имеет фигурное очертание, то полученную вероятность умножить на коэффициент фигурности или для определения вероятности попадания взять приведенные размеры цели.

где

у1 и у2 — расстояния от оси рассеивания по высоте соответственно до дальнего и ближнего края цели;

z1 и z2 — расстояния от оси рассеивания по боковому направлению соответственно до дальнего и ближнего края цели;

Bв сум и Вб сум — суммарные срединные отклонения соответственно по высоте и боковому направлению;

К— коэффициент фигурности.

Знак плюс (+) берется, когда ось рассеивания проходит через цель, а знак минус (—), когда ось рассеивания вне цели.

Пример. Определить вероятность попадания в бегущую фигуру при стрельбе из пулемета Калашникова на расстояние 500 м, если средняя траектория пройдет ниже середины цели на 0,4 м.

Решение. 1. По таблицам находим: Be сум=0,37 м, Вб сум= =0,51 м; из приложения 4 (табл. 6) находим приведенные размеры цели: высота равна 1,40 м; ширина 0,46 м.

2. Определяем вероятность попадания в полосу от оси рассеивания по высоте до верхнего края цели:

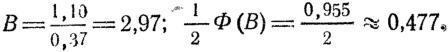
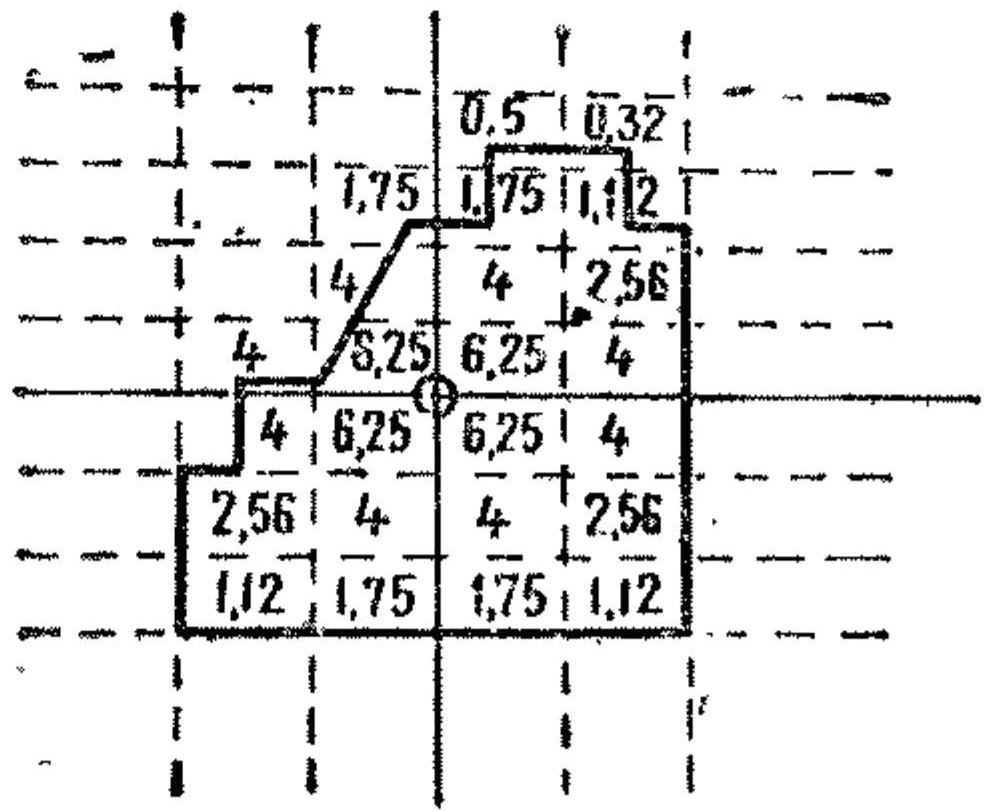
Рис. 49. Определение вероятности попадания по сетке рассеивания

р=0,1+0,05+0,2+1,5+0,8+2+4+2,56+0,2+5,8+6,25+4+2,5+6,25+4+2,56+4+4+2,56+1,12+1,75+1,75+1,12=65,32%

3. Определяем вероятность попадания рассеивания до нижнего края цели:

в полосу от этой же оси рассеивания до нижнего края цели:

4. Определяем вероятность попадания в полосу, равную высоте:

Рв =0,477+0,207 = 0,684

5. Определяем вероятность попадания в полосу равную ширине цели pб:

6. Определяем вероятность попадания в цель:

р = рв • рб = 0,684 • 0,239 = 0,163, или 16,3%.

113. Вероятность попадания в цель любого очертания и при любом расположении средней траектории может быть определена графическим способом по сетке рассеивания (рис. 49).

Сетка рассеивания составляется проведением прямых линий, параллельных осям рассеивания, через целые срединные отклонения или доли их. В результате этого вся площадь рассеизания разбивается на ряд прямоугольников. Вероятности попадания в образовавшиеся прямоугольники подсчитываются умножением вероятностей по-дадания в полосы, которыми образуются эти прямоугольники. Например, вероятность попадания в прямоугольник, отмеченный в табл. 5 приложения 4, равна 0,16 • 0,25 = 0,04, или 4%. Сетка рассеивания в этой таблице дана в масштабе в одно срединное отклонение.

Определение вероятности попадания по сетке рассеивания производится в той же последовательности, что и по шкале рассеивания. Для этого надо начертить в условном масштабе цель и на нее наложить в том же масштабе сетку рассеивания так, чтобы центр рассеивания был в точке согласно условиям стрельбы. Затем подсчитать вероятность попадания в цель суммированием вероятностей попадания в прямоугольники, накрывающие цель; причем там, где прямоугольники не полностью входят в цель, вероятности берутся примерным сравнением площади, занятой целью, с площадью всего прямоугольника.

где

р — вероятность попадания в цель;

р1 р2 и т. д. — вероятности попадания в прямоугольники.

114. Для определения вероятности попадания в одиночную (групповую прерывчатую) цель при стрельбе с искусственным рассеиванием по фронту необходимо найти вероятность попадания в полосу, равную высоте цели, и умножить ее на отношение площади одиночной цели (занятой всеми фигурами) к площади прямоугольника, ширина которого равна ширине фронта искусственного рассеивания, а высота — высоте цели. При этом допускается, (что рассеивание пуль по боковому направлению равномерно и вероятность попадания в полосу, равную фронту цели (рассеивания), равна 100%. Если групповая цель состоит из одинаковых по размерам фигур, то ее площадь определяется умножением площади одной фигуры на число фигур.

где

р — вероятность попадания в цель;

рв — вероятность попадания в полосу, равную высоте цели;

Sц— площадь цели;

Sпр— площадь прямоугольника,

Пример. Определить вероятность попадания в группозую цель, состоящую из 10 бегущих фигур на фронте 40 м на расстоянии 300 м, при стрельбе из пулемета Калашникова (ПКС) с рассеиванием по фронту при условии, что ось рассеивания по высоте пройдет через середину цели.

Решение. 1. По таблицам находим: £ = 0,15 м; при стрельбе с рассеиванием по фронту Бв увеличивается в 1,4 раза; из приложе­ния 4 (табл. 6) высота цели равна 1,5 м, площадь одной фигуры цели 0,64 м2.

2. Определяем срединное отклонение по высоте при стрельбе с рассеиваннем по фронту:

вв=0,15 м. • 1,4 = 0,21 м.

3. Определяем вероятность попадания в полосу, равную высоте цели:

По табл, 1 приложения 4 находим

Рв = Ф (В)-0,984.

4. Определяем вероятность попадания в групповую цель:

115. Вероятность попадания в цель с учетом ошибок в подготовке стрельбы определяется вышеуказанными способами. При этом кроме характеристик рассеивания учитываются ошибки в подготовке стрельбы (ст. 103 и 104) и принимается, что средняя точка попадания проходит через середину цели.

Пример. Определить вероятность попадания в появляющееся реактивное противотанковое ружье при стрельбе из пулемета Калашникова на расстояние 600 м/с учетом возможных ошибок в стрельбе; ветер боковой; расстояние до цели определено глазомерно.

Решение. 1. По таблицам находим: Be сум = 0,44 м, Вб сум = 0,61 м; из приложения 4 (табл. 7 и 6) Ев = 0,63 м, Ен = 0,43м, при­веденные размеры цели: высота 0,85 м, ширина 0,85 м.

2. Определяем суммарные (приведенные) ошибки в подготовке стрельбы:

а) по высоте;

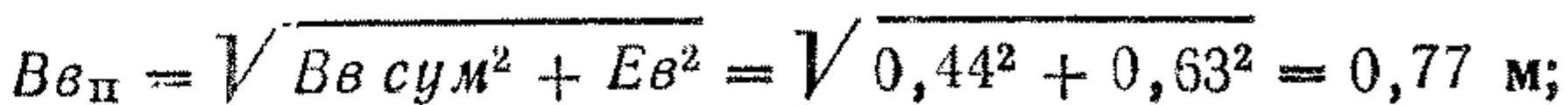
б) по боковому направлению:

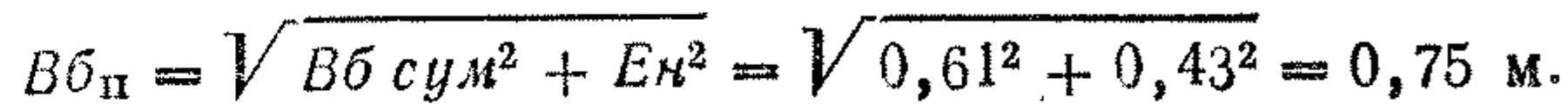
а) в полосу, равную приведенной высоте цели:

б) в полосу, равную приведенной ширине цели:

в) в цель:

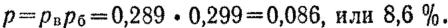
116. Вероятность попадания при стрельбе из автомата, а также из ручного пулемета из положения с колена, стоя, на ходу с короткой остановки определяется вышеуказанными способами отдельно для первых пуль очередей и для последующих пуль очередей.

Пример. Определить вероятность попадания в грудную фигуру при стрельбе из автомата Калашникова (АКМ) из положения лежа с упора на расстояние 400 м при условии, что ошибок в стрельбе нет.

Решение. 1. По таблицам находим: Bв1 = 0,17м, B61=0,l5м (для первых пуль очередей); Ввпос = 0,23 м, Вбпос = 0,36 м (для последующих пуль очередей); из приложения 4 (табл. 6) приведенные размеры грудной фигуры: высота 0,45 м, ширина 0,45 м.

2. Определяем вероятность попадания для первой пули очереди:

а) в полосу, равную приведенной высоте цели:

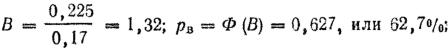
б) в полосу, равную приведенной ширине цели:

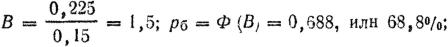
в) в цель:

3. Определяем вероятность попадания для любой последующей пули очереди:

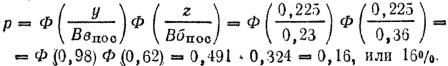
Вероятности попадания для первой пули очереди и для последующей пули очереди и коэффициент зависимости между ними затем учитываются при определении вероят ности поражения цели заданным количеством патронов.

Решение задач о выстрелах и попаданиях в цель

Задачи про стрелков, которые делают выстрелы по целям (или мишеням), причем вероятности попаданий для каждого стрелка обычно заданы, а нужно найти вероятность ровно одного попадания, или не более двух попаданий, или всех трех и так далее, в зависимости от конкретной задачи.

Основной метод решения подобных задач — использование теорем о сложении и умножении вероятностей, который мы и разберем на примерах ниже.

Два стрелка

Пример 1. Два одновременно стреляют по мишени. Вероятность попадания по мишени у первого стрелка равна 0,6, у второго — 0,7. Какова вероятность того, что в мишени будет только одна пробоина?

Не будем повторять все выкладки выше, для этого мы их и делали подробно. Сразу перейдем к решению. Так как нужно найти вероятность всего одного попадания, используем формулу (2), где по условию p1=0,6p1=0,6, p2=0,7p2=0,7, значит q1=1−p1=0,4q1=1−p1=0,4, q2=1−p2=0,3q2=1−p2=0,3. Получаем:

P=p1⋅q2+q1⋅p2=0,6⋅0,3+0,4⋅0,7=0,46.P=p1⋅q2+q1⋅p2=0,6⋅0,3+0,4⋅0,7=0,46.

Пример 2. Два стрелка, для которых вероятности попадания в мишень равны соответственно 0,7 и 0,8, производят по одному выстрелу. Найти вероятность того, что мишень поражена дважды.

Опять же, нужно только применить формулу (3) с данными задачи p1=0,7p1=0,7, p2=0,8p2=0,8 и сразу получим ответ:

P=p1⋅p2=0,7⋅0,8=0,56.P=p1⋅p2=0,7⋅0,8=0,56.

Пример 3. Производятся два выстрела по цели, вероятности попадания равны 0,3 и 0,4. Найти вероятность того, что хотя бы один выстрел попал в цель.

На этот раз задача будет решена не в одно, а в два действия, но пусть это вас не пугает. Как обычно, в задачах содеражащих фразу «хотя бы один…» мы помимо основного события: QQ = (Хотя бы один выстрел попал в цель) вводим сразу противоположное событие Q¯¯¯¯Q¯ = (Ни один выстрел не попал в цель, 0 попаданий). А дальше уже известно, применяем формулу (1), которая выведена выше:

P(Q¯¯¯¯)=q1⋅q2=(1−0,3)⋅(1−0,4)=0,7⋅0,6=0,42.P(Q¯)=q1⋅q2=(1−0,3)⋅(1−0,4)=0,7⋅0,6=0,42.

Вероятность нужного нам события тогда равна:

P(Q)=1−P(Q¯¯¯¯)=1−0,42=0,58.P(Q)=1−P(Q¯)=1−0,42=0,58.

Три стрелка

К двум устрелявшимся стрелкам наконец присоединяется третий, бодрый и полный сил. А мы принимаемся за вывод формул. Напомню общую постановку задачи: три стрелка, вероятности попаданий в цель которых равны p1p1, p2p2 и p3p3, делают по одному выстрелу и подсчитывают число попаданий. Наша задача — вычислить вероятности 1, 2, 3 или ни одного попадания.

Пример 4. Три стрелка производят по одному выстрелу. Вероятности попадания 1-го, 2-го и 3-го стрелков соответственно равны: 0,2, 0,3 и 0,4. Найти вероятность получения одного попадания?

Так как речь идет об одном попадании, используем формулу (5), куда подставляем значения из условия задачи:

p1=0,2,p2=0,3,p3=0,4,q1=0,8,q2=0,7,q3=0,6p1=0,2,p2=0,3,p3=0,4,q1=0,8,q2=0,7,q3=0,6

Получаем:

P1=p1⋅q2⋅q3+q1⋅p2⋅q3+q1⋅q2⋅p3==0,2⋅0,7⋅0,6+0,8⋅0,3⋅0,6+0,8⋅0,7⋅0,4=0,452.P1=p1⋅q2⋅q3+q1⋅p2⋅q3+q1⋅q2⋅p3==0,2⋅0,7⋅0,6+0,8⋅0,3⋅0,6+0,8⋅0,7⋅0,4=0,452.

Пример 5. 3 стрелка делают по одному выстрелу в мишень. Вероятности попадания для каждого стрелка соответственно равны 0,8; 0,7; 0,5. Определите вероятность того, что в мишени окажется ровно 2 пробоины.

Так как речь идет о двух попаданиях, используем формулу (6), куда подставляем значения из условия задачи:

p1=0,8,p2=0,7,p3=0,5,q1=0,2,q2=0,3,q3=0,5p1=0,8,p2=0,7,p3=0,5,q1=0,2,q2=0,3,q3=0,5

Получаем:

P2=p1⋅p2⋅q3+p1⋅q2⋅p3+q1⋅p2⋅p3==0,8⋅0,7⋅0,5+0,8⋅0,3⋅0,5+0,2⋅0,7⋅0,5=0,47.P2=p1⋅p2⋅q3+p1⋅q2⋅p3+q1⋅p2⋅p3==0,8⋅0,7⋅0,5+0,8⋅0,3⋅0,5+0,2⋅0,7⋅0,5=0,47.

Пример 6. Из трех орудий произвели залп по цели. Вероятность попадания в цель при одном выстреле из первого орудия равна 0,8; для второго и третьего орудий эти вероятности соответственно равны 0,7 и 0,9. Найти вероятность хотя бы одного попадания при одном залпе из всех орудий.

Надеюсь, вас не смутили орудия вместо стрелков? На самом деле, не суть важно, что происходит: три стрелка вышли на линию, или три пушки готовят залп, или три снайпера целятся в одного террориста. С точки зрения теории вероятностей, все формулы остаются прежними.

Поэтому смело приступаем к решению. Требуется найти вероятность события AA= (Будет хотя бы одно попадания при одновременном залпе из всех орудий), поэтому введем для простоты расчетов противоположное событие A¯¯¯¯A¯ = (Все три орудия дали промашку), вероятность которого найдем по формуле (4), подставляя значения:

p1=0,8,p2=0,7,p3=0,9,q1=0,2,q2=0,3,q3=0,1p1=0,8,p2=0,7,p3=0,9,q1=0,2,q2=0,3,q3=0,1

Получаем:

P(A¯¯¯¯)=P0=q1⋅q2⋅q3=0,2⋅0,3⋅0,1=0,006.P(A¯)=P0=q1⋅q2⋅q3=0,2⋅0,3⋅0,1=0,006.

Искомая вероятность:

P(A)=1−P(A¯¯¯¯)=1−0,006=0,994.P(A)=1−P(A¯)=1−0,006=0,994.

Другие задачи про выстрелы и попадания

Конечно же, не все задачи про выстрелы можно решать по данным формулам (точнее, не все вписываются в эту схему напрямую), это лишь один из популярных классов задач. Для полноты изложения я приведу еще несколько типовых задач с немного отличающимся решением.

Пример 7. Вероятность того, что стрелок попадет в цель при одном выстреле, равна 0,7. Производится пять независимых выстрелов. Какова вероятность того, что в мишени окажется хотя бы одна пробоина?

Требуется найти вероятность события AA = (В мишени окажется хотя бы одна пробоина), поэтому вводим сначала противоположное событие A¯¯¯¯A¯ = (Все пять выстрелов не попали в цель). Если обозначить вероятность попадания в цель какp=0,7p=0,7 (она одинакова при каждом выстреле), а вероятность промаха как q=1−p=0,3q=1−p=0,3, то вероятность всех пяти промахов будет

P(A¯¯¯¯)=q5=0,35.P(A¯)=q5=0,35.

Искомая вероятность:

P(A)=1−P(A¯¯¯¯)=1−0,35=0,998.P(A)=1−P(A¯)=1−0,35=0,998.

Пример 8. Два стрелка стреляют по мишени по одному разу. Вероятность того, что оба попали равна 0,42, а вероятность того что оба промахнулись, 0,12. Найти вероятность попадания в мишень каждым стрелком при одном выстреле.

Если обозначить вероятности попадания первым и вторым стрелком соответственно как p1p1 и p2p2, то, используя формулы (1) и (3), запишем условие задачи в виде системы уравнений:

P2=p1⋅p2=0,42;P0=(1−p1)⋅(1−p2)=0,12.P2=p1⋅p2=0,42;P0=(1−p1)⋅(1−p2)=0,12.

Решая эту систему, найдем искомые вероятности попадания для каждого стрелка: p1=0,6p1=0,6 и p2=0,7p2=0,7 (или наоборот, p1=0,7p1=0,7 и p2=0,6p2=0,6).

Пример 9. Вероятность хотя бы одного попадания в цель при четырех выстрелах равна 0,9984. Найти вероятность попадания в цель при одном выстреле.

Если обозначить вероятность попадания в цель как pp (она одинакова при каждом выстреле), а вероятность промаха как q=1−pq=1−p, то вероятность 4 промахов при четырех выстрелах будет равна q4q4, а соответственно вероятность хотя бы одного попадания в цель при четырех выстрелах — 1−q41−q4. Получаем уравнение:

1−q4=0,9984;q4=0,0016;q=0,2;p=1−q=0,8.1−q4=0,9984;q4=0,0016;q=0,2;p=1−q=0,8.

Нашли вероятность попадания в цель при одном выстреле, она равна 0,8.

Пример 10. Два стрелка независимо выстрелили по мишени по два раза. Меткость первого стрелка равна 0,8; второго – 0,7. Найти вероятность того, что в мишень попадут все четыре пули.

Все 4 пули попадут в мишень, если первый стрелок попадет оба раза (вероятность попадания при одном выстреле у него p1=0,8p1=0,8), и одновременно второй стрелок попадет оба раза (вероятность попадания при одном выстреле у него p2=0,7p2=0,7). По правилу умножения вероятностей

P=p1⋅p1⋅p2⋅p2=0,8⋅0,8⋅0,7⋅0,7=0,3136.

Теория
вероятностей.

       
Задачи на «Стрельбу».

№ 1. Стрелок  стреляет  по 
мишени  один  раз.  В  случае  промаха 
стрелок  делает второй
выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 
0,8.  Найдите  вероятность  того,  что  мишень 
будет  поражена  (либо  первым  либо вторым
выстрелом).

Решение. Первый способ.

 Пусть A —
со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на стрел­ком с пер­во­го вы­стре­ла, B —
со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на со вто­ро­го вы­стре­ла.
Ве­ро­ят­ность со­бы­тия A равна P(A) = P₁(A)
= 0,8. Со­бы­тие B на­сту­па­ет, если, стре­ляя пер­вый раз,
стре­лок про­мах­нул­ся P₁() =1 –
0,8 = 0,2, а, стре­ляя вто­рой раз, попал P₂(A) = 0,8. Это не­за­ви­си­мые
со­бы­тия, их ве­ро­ят­ность равна про­из­ве­де­нию ве­ро­ят­но­стей этих со­бы­тий: P(B)
= P₁() ∙ P₂(A)
= 0,2·0,8 = 0,16. Со­бы­тия A и B не­сов­мест­ные, ве­ро­ят­ность
их суммы равна сумме ве­ро­ят­но­стей этих со­бы­тий: P (A + B) = P(A) + P(B) = 0,8 + 0,16 =
0,96.

Ответ:
0,96.

Второй способ. Пусть A —
со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на стрел­ком
при одном выстреле, B — со­бы­тие,
со­сто­я­щее в том, что ми­шень по­ра­же­на (либо  первым 
либо вторым выстрелом).

Так как вероятность попасть
в мишень при одном выстреле равна 0,8, то есть P(A) = 0,8, то ве­ро­ят­ность
того, что, стре­ляя пер­вый раз, стре­лок про­мах­нул­ся, равна P₁() = 1 — 0,8 =  0,2. Ве­ро­ят­ность
того, что, стре­ляя второй  раз, стре­лок про­мах­нул­ся, равна P₂() = 1 — 0,8 =  0,2. Ве­ро­ят­ность
того, что, стре­лок про­мах­нул­ся оба раза,  равна P₁() ∙ P₂() = 0,2∙0,2 = 0,04. Ве­ро­ят­ность
противоположного события (хотя бы один раз не промахнется) равна P(B)= 1 – 0,04 = 0,96.

Ответ: 0,96.

№
2. Стрелок  4  раза 
стреляет  по  мишеням. Вероятность  попадания  в 
мишень при одном выстреле равна 0,7. Найдите вероятность того, что стрелок первый раз попал

 в мишень, а последние 3 раза промахнулся.

Решение. Пусть A — со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на
стрел­ком при одном выстреле, B — со­бы­тие, со­сто­я­щее в том, что ми­шень
по­ра­же­на.

Так
как вероятность попасть
в мишень при одном выстреле равна 0,7, то
вероятность попадания при первом выстреле равна P₁(A) = 0,7, тогда ве­ро­ят­ность того, что, стре­ляя
второй раз, стре­лок про­мах­нул­ся, равна P₂() = 1 — 0,7 =  0,3. Ве­ро­ят­ность того,
что, стре­ляя третий  раз, стре­лок про­мах­нул­ся, равна P₃() = 1 — 0,8 =  0,2. Ве­ро­ят­ность того,
что, стре­ляя четвертый раз, стре­лок про­мах­нул­ся, равна P₃() = 1 — 0,8 =  0,2. Все события
независимы. Ве­ро­ят­ность того, что стрелок первый раз попал в мишень, а последние 

3 раза промахнулся.
P(B)= P₁(A)∙ P₂()∙ P₃()∙ P₄() = 0,7∙0,3∙0,3∙0.3 = 0,0189

Ответ: 0,0189.

№ 3.
Вероятность попадания в мишень при одном выстреле для первого стрелка равна 0,7
, а для второго — 0,8. Найти вероятность того, что при одном залпе в мишень
попадает только один из стрелков.

Решение. Пусть A₁ —
со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на первым стрелком, A₂ —
со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на вторым стрелком. С — со­бы­тие, со­сто­я­щее в том, что в ми­шень попал только один из стрелков, то есть (первый попадет и второй промажет) либо (первый промажет и
второй попадет).

Вероятность попадания в мишень первым стрелком р
(А₁)=0,7, вероятность его промаха
р ()=1-р(А₁)=1-
0,7 = 0,3.

 Вероятность попадания в мишень вторым стрелком р
(А₂)=0,8, вероятность его промаха
 р ()=1-р(А₂)=1
— 0,8 = 0,2.
р (С) = р(А₁)∙р () + р(А₂)∙р
() = 0,7∙0,2 +
0,8∙0,3 = 0,38

Ответ.0,38.

№ 4. Каждый
из трех стрелков стреляет в мишень по одному разу, причем вероятность попадания
1 стрелка составляет 80%, второго – 70%, третьего – 60%. Найдите вероятность
того, что двое из трех стрелков попадет в мишень.

Решение.

 Пусть A₁ — со­бы­тие, со­сто­я­щее в том,
что ми­шень по­ра­же­на первым стрелком, A₂ — со­бы­тие, со­сто­я­щее
в том, что ми­шень по­ра­же­на вторым стрелком. A₃ — со­бы­тие,
со­сто­я­щее в том, что ми­шень по­ра­же­на третьим стрелком. С — со­бы­тие, со­сто­я­щее в том, что в ми­шень попали только двое из трех из стрелков,

Вероятность попадания в мишень первым стрелком р
(А₁)=0,8, вероятность его промаха
р ()=1-р(А₁)=1-
0,8 = 0,2.

 Вероятность попадания в мишень вторым стрелком р
(А₂)=0,7, вероятность его промаха
 р ()=1-р(А₂)=1
– 0,7 = 0,3.

Вероятность попадания в мишень третьим стрелком р
(А₃)=0,6, вероятность его промаха
 р ()=1-р(А₂)=1
– 0,6 = 0,4.

Чтобы
вычислить вероятность (двое из трех попали), надо вычислить вероятности, когда:

1. Промахнулся только первый стрелок, а второй и
третий попали.
2. Промахнулся только второй стрелок,  а первый
и третий попали.
3. Промахнулся только третий стрелок, а первый и
второй попали.
Вероятность того, что промахнулся только первый
стрелок, а второй и третий попали: P₁ = р ()∙ р (А₂)∙ р (А₃)=  0,2∙0,7∙0,6 = 0,084.
Вероятность того, что промахнулся только второй
стрелок, а первый и третий попали P₂ = р (А₁) ∙ р () р (А₃)= 0,8∙0,3∙0,6 = 0,144.
Вероятность того, что промахнулся только третий
стрелок, а первый и второй попали P₃ = р (А₁) ∙ р (А₂) ∙ р () = 0,8∙0,7∙0,4
= 0,224.
Отсюда вероятность (2 из 3 попали) р (С) = P₁+ P₂+ P₃ = 0,084+0,144+0,224 = 0,452
Ответ: 0,452

№5. Стрелок
3 раза стреляет по мишеням. Вероятность попадания в мишень при  одном выстреле равна 0,8.
Найдите вероятность того, что стрелок первые 2 раза попал  в мишени, а последний раз
промахнулся.

Решение. Пусть A — со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на
стрел­ком при одном выстреле, B — со­бы­тие, со­сто­я­щее в том, что ми­шень
по­ра­же­на.

Так
как вероятность попасть
в мишень при одном выстреле равна 0,8, то
вероятность попадания при первом выстреле равна P₁(A) = 0,8, вероятность попадания при втором выстреле
равна P₂(A)
= 0,8, ве­ро­ят­ность того, что, стре­ляя третий раз, стре­лок про­мах­нул­ся,
равна P₃() = 1 — 0,8 =  0,2.

Все события независимы. Ве­ро­ят­ность того, что стрелок первые 2 раза попал  в мишени, а последний раз
промахнулся.

P(B)= P₁(A)∙ P₂(А)∙ P₃() = 0,8∙0,8∙0,2 = 0,128

Ответ: 0,128

№ 6. Биатлонист 5 раз стреляет по мишеням.
Вероятность попадания в мишень при одном выстреле 0,8. Какова вероятность,
что он попал в мишень 4 раза и один промахнулся? 

Решение.

Промахнуться он мог первым, вторым, ..пятым выстрелом.
ХОООО; ОХООО; ООХОО; ОООХО; ООООХ.
Вероятность каждого исхода равна 0,8⁴ ∙ 0,2 .
Суммируем вероятности: p = 5∙(0,8⁴ ∙ 0,2) = 0,8⁴ =
0,4096.
Ответ.0,4096.

№ 7.  Три стрелка стреляют
в цель. Вероятность попадания в цель для первого, второго и третьего стрелка
соответственно равна 0,6; 0,7 и 0,75; Определить вероятность хотя бы одного попадания
в цель, если каждый стрелок сделает по одному выстрелу.

Решение.

 Пусть A₁ —
со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на первым стрелком, A₂ —
со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на вторым стрелком. A₃ —
со­бы­тие, со­сто­я­щее в том, что ми­шень по­ра­же­на третьим стрелком. С — со­бы­тие, со­сто­я­щее в том, что в ми­шень попали хотя бы один раз.

Вероятность попадания в мишень первым стрелком р
(А₁)=0,6, вероятность его промаха
р ()=1-р(А₁)=1-
0,6 = 0,4.

 Вероятность попадания в мишень вторым стрелком р
(А₂)=0,7, вероятность его промаха
 р ()=1-р(А₂)=1
– 0,7 = 0,3.

Вероятность попадания в мишень третьим стрелком р
(А₃)=0,75, вероятность его промаха
 р ()=1-р(А₂)=1
– 0,75= 0,25.

Посчитаем вероятность события: никто не попал
(то есть  все промазали):

Р= р ()∙ р ()∙ р ()=
0,4∙0,3∙0,25= 0,03.
Вероятность хотя бы одного попадания в цель,
если каждый стрелок сделает по одному выстрелу р (С) = 1 – Р = 1 – 0,03 = 0,97.

Ответ .0,97.

№ 8. Три стрелка один за
другим стреляют в цель. Вероятность попадания первого — 0,8. Второго — 0,75.
Третьего 0,7.
Какова вероятность того, что попадут все три стрелка?

Решение.

 Пусть A₁ —
со­бы­тие, со­сто­я­щее в том, что цель по­ра­же­на первым стрелком, A₂ —
со­бы­тие, со­сто­я­щее в том, что цель по­ра­же­на вторым стрелком. A₃ —
со­бы­тие, со­сто­я­щее в том, что цель по­ра­же­на третьим стрелком. С — со­бы­тие, со­сто­я­щее в том, что в цель попали все три стрелка.

Вероятность попадания в мишень первым стрелком р
(А₁)=0,8. Вероятность попадания в мишень вторым стрелком р (А₂)=0,75.
Вероятность попадания в мишень третьим стрелком р (А₃)=0,7.

Вероятность того, что в цель попали все три стрелка:

р (С) = р (А₁)∙ р (А₁)∙ р
(А₁)=0,8∙0,75∙0,7= 0,42

Ответ. 0,42.

 № 9. Ковбой Джон попадает в муху на стене с
вероятностью 0,9, если стреляет

 из пристрелянного револьвера.
Если Джон стреляет из не пристрелянного револьвера, то он попадает в муху с
вероятностью 0,2. На столе лежит 10 револьверов,  из них только 4
пристрелянные. Ковбой Джон видит на стене муху, наудачу хватает первый
попавшийся револьвер и стреляет в муху. Найдите вероятность того, что Джон
промахнётся.

Решение.1 способ.

 Пусть A₁ —
со­бы­тие, со­сто­я­щее в том, что ковбой берет пристрелянный револьвер, A₂ —
со­бы­тие, со­сто­я­щее в том, что ковбой берет не пристрелянный револьвер. В₁—
со­бы­тие, со­сто­я­щее в том, что ковбой попадает в муху из пристрелянного
револьвера. В₂— со­бы­тие, со­сто­я­щее в том, что ковбой попадает в
муху из не пристрелянного револьвера. С —
со­бы­тие, со­сто­я­щее в том, что Джон  не промахнётся.

Вероятность того, что ковбой схватит пристрелянный револьвер
р (А₁) = 0,4. Вероятность того, что ковбой попадает в муху из
пристрелянного револьвера р (В₁) = 0,9. Вероятность того, что попадется пристрелянный револьвер и
Джон попадет, равна Р₁= р (А₁)∙
р (В₁)  = 0,4∙0,9 = 0,36.

Вероятность того, что ковбой схватит не  пристрелянный
револьвер р (А₂) = 0,6. Вероятность того, что ковбой попадает в муху
из не пристрелянного револьвера р (В₂) = 0,2. Вероятность того, что попадется не пристрелянный револьвер
и Джон попадет, равна Р₁= р (А₂)∙
р (В₂) = 0,6∙0,2 = 0,12.

Вероятность
того, что Джон  не промахнётся р(С) = Р₁
+ Р₂ = 0,36 +0,12 = 0,48.

Вероятность противоположного
события Джон  промахнётся р()= 1 — р(С) =
1 — 0,48 = 0.52.

Ответ. 0,52.

2 способ.

 Пусть A₁ —
со­бы­тие, со­сто­я­щее в том, что ковбой берет пристрелянный револьвер. A₂ —
со­бы­тие, со­сто­я­щее в том, что ковбой берет не пристрелянный револьвер. В₁—
со­бы­тие, со­сто­я­щее в том, что ковбой попадает в муху из пристрелянного
револьвера. В₂— со­бы­тие, со­сто­я­щее в том, что ковбой попадает в
муху из не пристрелянного револьвера. — со­бы­тие, со­сто­я­щее в
том, что ковбой промахнется из пристрелянного револьвера. — со­бы­тие, со­сто­я­щее в
том, что ковбой промахнется из не пристрелянного револьвера. С — со­бы­тие, со­сто­я­щее в том, что Джон  
промахнётся.

 Вероятность
того, что ковбой схватит пристрелянный револьвер р (А₁) = 0,4.
Вероятность того, что ковбой попадает в муху из пристрелянного револьвера р (В₁)
= 0,9, вероятность промаха Р() =  1 — р (В₁) = 1 — 0,9 = 0,1.Вероятность
того, что попадется пристрелянный револьвер и Джон промахнется, равна Р₁=
р (А₁)∙ р () = 0,4∙0,1 = 0,04.

Вероятность того, что ковбой схватит не  пристрелянный
револьвер р (А₂) = 0,6. Вероятность того, что ковбой попадает в муху
из не пристрелянного револьвера р (В₂) = 0,2, вероятность промаха Р() =  1 — р (В₁) = 1 — 0,2 = 0,8.Вероятность
того, что попадется не пристрелянный револьвер и Джон промахнется, равна Р₂=
р (А₂) ∙ р () = 0,6∙0,8= 0,48.

 Вероятность того, что Джон  промахнётся р(С) =
Р₁ + Р₂ = 0,04 +0,48 = 0,52.

Ответ. 0,52.

№10. При ар­тил­ле­рий­ской стрель­бе ав­то­ма­ти­че­ская си­сте­ма де­ла­ет
вы­стрел по цели. Если цель не уни­что­же­на, то си­сте­ма де­ла­ет по­втор­ный
вы­стрел. Вы­стре­лы по­вто­ря­ют­ся до тех пор, пока цель не будет уни­что­же­на.
Ве­ро­ят­ность уни­что­же­ния не­ко­то­рой цели при пер­вом вы­стре­ле равна
0,4, а при каж­дом по­сле­ду­ю­щем — 0,6. Сколь­ко вы­стре­лов по­тре­бу­ет­ся
для того, чтобы ве­ро­ят­ность уни­что­же­ния цели была не менее 0,98?

Решение. Переформулируем вопрос задачи:

Сколько
выстрелов потребуется для того, чтобы вероятность промаха была бы меньше 1
-0,98 = 0,02?

При
первом  выстреле вероятность промаха  1- 0,4 = 0,6.

При
каждом последующем выстреле вероятность промаха 1 — 0,6 = 0,4.

При
двух выстрелах вероятность промаха  0,6∙0,4 = 0,24  (первый
выстрел – промах и второй выстрел – промах).

При
трех выстрелах вероятность промаха

0,6∙0,4∙0,4
= 0,096

При
четырех выстрелах вероятность промаха

0,6∙0,4∙0,4 ∙0,4=
0,0384

При
пяти выстрелах вероятность промаха

0,6∙0,4∙0,4 ∙0,4∙0,4 = 0,01536

Замечаем,
что  0,015360,2

Итак,
пяти выстрелов достаточно, чтобы ве­ро­ят­ность уни­что­же­ния цели была
не менее 0,98.

Ответ:
5.

№11. При
артиллерийской стрельбе автоматическая система делает выстрел по цели. Если
цель не уничтожена, то система делает повторный выстрел. Выстрелы повторяются
до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой
цели при первом выстреле равна 0,6, а при каждом последующем — 0,8. Сколько
выстрелов потребуется для того, чтобы вероятность уничтожения цели была не
менее 0,95?

Сколько бы не было сделано выстрелов, все эти события (каждый
отдельный выстрел) будут независимыми. При совершении независимых событий (в
данном случае группы выстрелов) одновременно вероятность такого события будет
равна произведению вероятностей этих независимых событий.

Вероятность поразить цель при первом выстреле равна 0,6.

Значит, вероятность промахнуться при первом выстреле равна 0,4.

Вероятность поразить цель при каждом последующем выстреле (втором
ит.д.) равна 0,8.

Значит, вероятность промаха при каждом последующем выстреле равна
0,2.

Необходимо поставить  вопрос: каким образом может быть
поражена
цель?              

Цель может быть поражена либо при первом выстреле, либо вторым
выстрелом, либо третьим, либо четвёртым, либо пятым выстрелом и т.д. …

Все перечисленные события независимые. Найдём их вероятности.

При первом:

Вероятность поражения равна 0,6.

При втором:

Вероятность поражения равна  0,4 ∙ 0,8 = 0,32 (мимо -попал).

То есть, вероятность поражения цели не более, чем двумя выстрелами
равна  0,6 + 0,32 = 0,92 < 0,95

При третьем:

Вероятность поражения равна  0,4 ∙ 0,2 ∙ 0,8 = 0,064 (мимо
–мимо -попал).

То есть, вероятность поражения цели не более, чем тремя выстрелами
равна  0,6 + 0,32 + 0,064 = 0,984 > 0,95

Таким образом, необходимо сделать три выстрела, чтобы мишень была
поражена  с вероятностью не менее  0,95.

Ответ: 3

№
12. Вероятность  попасть  в  мишень  равна  0,6.
 Произведено  три  выстрела.  Какова  вероятность, что
мишень была поражена не менее  двух раз?

Решение: 

Вероятность
того, что все три  выстрела попадут в цель, равна P₁=0,6³=0,216.

Вероятность
того, что мишень будет поражена два раза, равна P₂=3∙(0,4∙0,6∙0,6)=3∙0,144=0,432. 
Здесь умножили на 3, потому что возможны три варианта (попал — не попал 
-попал, попал – попал — не попал и не попал-попал-попал). Тогда искомая
вероятность равна P=P1+P₂=0,216 +0,432 = 0,648.

Ответ
0.648.