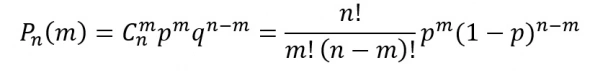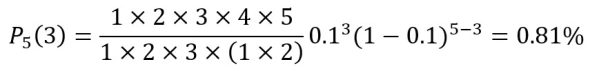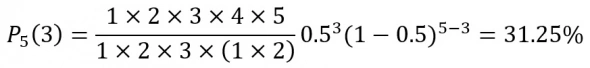Поскольку нормальное распределение вероятностей имеет так много применений, профессионалы в области финансов и инвестиций должны тщательно его изучить.
Роль нормального распределения в статистических выводах и регрессионном анализе значительно расширена благодаря центральной предельной теореме. Центральная предельная теорема (англ. ‘central limit theorem’) утверждает, что сумма (и среднее) большого числа независимых случайных величин приблизительно нормально распределена.
Центральная предельная теорема обсуждается далее в чтении о выборочном методе.
[см.: CFA — Центральная предельная теорема и распределение выборочного среднего]
Французский математик Абрахам Де Муавр (Abraham de Moivre, 1667-1754) ввел понятие нормального распределения в 1733 году при разработке своей версии центральной предельной теоремы.
Как показано на Рисунке 5, нормальное распределение является симметричным и имеет колоколообразную форму.
Диапазоном возможных исходов нормального распределения является вся вещественная ось: все действительные числа, лежащих между (-infty) и (+infty). Хвосты колоколообразной кривой распространяются без ограничений слева и справа.
Определяющими характеристиками нормального распределения являются:
Нормальное распределение полностью описывается двумя параметрами — ее средним значением, ( mu ), и дисперсией, ( sigma^2 ). Обозначим это как ( X sim N (mu, sigma^2) ) (читается «X имеет нормальное распределение со средним (p) и дисперсией (sigma^2)» ).
Мы также можем определить нормальное распределение с точки зрения среднего и стандартного отклонения, ( sigma ) (часто это удобно, так как ( sigma ) измеряется в тех же единицах, что и (X) и (mu)). Как следствие, мы можем ответить на любой вопрос о вероятности нормальной случайной величины, если мы знаем его среднее значение и дисперсию (или стандартное отклонение).
Нормальное распределение имеет асимметрию 0 (симметрично). Нормальное распределение имеет эксцесс (мера крутизны или островершинности распределения) 3; его избыточный эксцесс (эксцесс — 3.0) равен 0.
Если мы имеем выборку размера (n) из нормального распределения, мы хотим знать о возможном изменении в асимметрии и эксцессе выборки. Для нормальной случайной величины, стандартное отклонение ассиметрии выборки равно (6/n), стандартное отклонение эксцесса выборки равно ( 24/n ).
Как следствие симметрии, среднее, медиана и мода равны для нормальной случайной величины.
Линейная комбинация двух или более нормальных случайных величин также распределена нормально.
Перечисленные характеристики касаются только одной переменной величины или одномерного нормального распределения: распределения одной нормальной случайной величины.
Одномерное распределение (англ. ‘univariate distribution’) описывает одну случайную величину.
Многомерное распределение (англ. ‘multivariate distribution’) определяет вероятности для группы связанных случайных величин. Вы столкнетесь с многомерным нормальным распределением (англ. ‘multivariate normal distribution’) в инвестиционной деятельности и должны знать о нем следующее.
Когда мы имеем группу финансовых активов, мы можем моделировать распределение доходности для каждого актива в отдельности, или распределение доходности для активов как для группы. «Как для группы» означает, что мы принимаем во внимание всех статистических взаимосвязей между доходностью активов.
Одна из моделей, которая часто используется для оценки доходности ценных бумаг, является многомерным нормальным распределением. Многомерное нормальное распределение для доходности ценных бумаг полностью определяется этими тремя списками параметров:
- списком средних ставок доходности по отдельным ценным бумагам (всего (n) средних всего);
- списком дисперсий доходности ценных бумаг (всего (n) дисперсий); а также
- списком всех отчетливых попарных корреляций доходности (всего (n (n — 1) / 2) различных корреляций).
Например, распределение для двух акций (двумерное нормальное распределение) имеет 2 средние, 2 дисперсии и 1 корреляцию: ( 2 (2 — 1) / 2).
Распределение для 30 акций имеет 30 средних, 30 дисперсий и 435 различных корреляций: (30(30 — 1)/2 ).
Корреляция доходности акций Dow Chemical с акциями American Express такая же, как корреляция American Express с Dow Chemical, поэтому они считаются одной отчетливой корреляцией.
Необходимость в указании корреляций является отличительной чертой многомерного нормального распределения в отличии от одномерного нормального распределения.
Формулировка «предположим, что ставки доходности нормально распределены» или «предположим, что ставки доходности соответствуют нормальному распределению» иногда используется для обозначения совместного нормального распределения для нескольких ценных бумаг.
Для портфеля из 30 ценных бумаг, например, доходность портфеля представляет собой средневзвешенное значение доходности 30 ценных бумаг. Средневзвешенное значение представляет собой линейную комбинацию. Таким образом, портфель доходности нормально распределен, если доходность отдельных ценных бумаг (совместно) нормально распределена.
Напомним, что для того, чтобы указать нормальное распределение доходности портфеля, нам нужны средние значения, дисперсии, и отчетливые парные корреляции ценных бумаг портфеля.
Имея все это в виду, мы можем вернуться к нормальному распределению для одной случайной величины. Кривые на графике Рисунка 5, являются функцией плотности нормального распределения:
( large dst begin{aligned}
f(x) &= {1over sigma sqrt{2pi}} exp{ left( {-(x-mu)^2 over 2 sigma^2} right)} \
& {для} -infty < x < +infty end{aligned} ) (Формула 3)
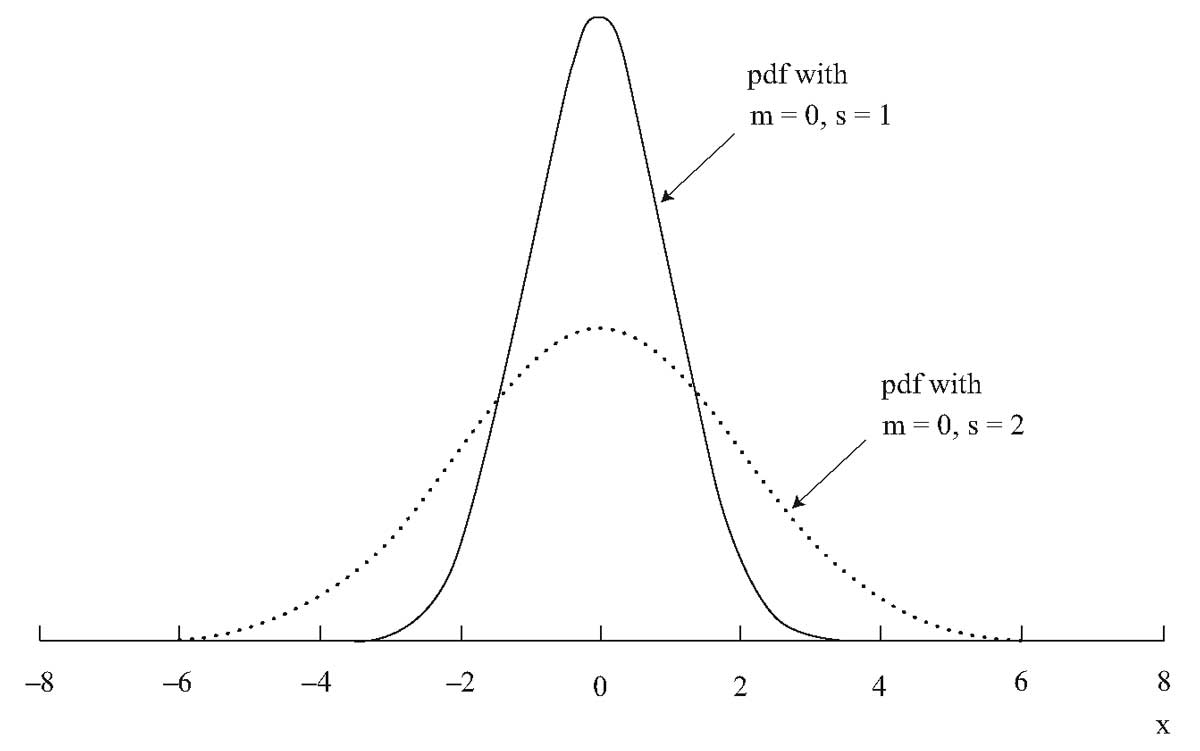
Эти две плотности, графически представленные на Рисунке 5, соответствуют среднему значению ( mu = 0 ) и стандартным отклонениям (sigma = 1) и (sigma = 2). Плотность нормального распределения при (mu = 0) и (sigma = 1), называется стандартным нормальным распределением (англ. ‘standard normal distribution’) или единичным нормальным распределением (англ. ‘unit normal distribution’),
Представленные на одном графике, эти два нормальных распределения с одинаковыми средними и различными стандартными отклонениями помогают нам понять, почему стандартное отклонение является хорошей мерой дисперсии для нормального распределения:
Наблюдения гораздо больше сконцентрированы вокруг среднего значения для нормального распределения (sigma = 1), чем для нормального распределения с (sigma = 2).
Хоть это и не совсем точно, нормальное распределение можно считать приближенной моделью для ставок доходности.
Почти все вероятность нормальной случайной величины находится в пределах трех стандартных отклонений от среднего значения. Для реалистичных значений средней доходности и стандартного отклонения доходности для многих активов, нормальная вероятность результатов ниже -100% очень мала.
Полезно ли такое приближение для данного применения, является эмпирическим вопросом. Например, нормальное распределение лучше подходит для доходности за квартальные и годовые периоды владения диверсифицированным портфелем акций, чем для ежедневной или еженедельной доходности.
Постоянное отклонение от нормальности для доходности большинства долевых ценных бумаг с эксцессом больше 3 — это проблема толстых хвостов распределения. Поэтому, когда мы приближаем распределения доходности долевых инструментов с помощью нормального распределения, мы должны иметь в виду, что нормальное распределение имеет тенденцию недооценивать вероятность экстремальных значений доходности.
Толстые хвосты распределений можно смоделировать с помощью комбинации нормальных случайных величин или с помощью t-распределения Стьюдента с относительно небольшим числом степеней свободы.
Мы обсудим распределение Стьюдента далее, в чтении о выборочном методе и статистической оценке.
Доходность опционов ассиметрична. Поскольку нормальное распределение является симметричным распределением, мы должны быть осторожными в его использовании для моделирования доходности портфелей, содержащих значительные позиции по опционам.
Нормальное распределение, однако, менее подходит в качестве модели для цен на активы, чем в качестве модели для доходности активов. Нормальная случайная величина не имеет нижнего предела. Эта характеристика имеет несколько последствий для применения нормальных распределений в инвестициях. Цена актива может упасть только до 0 и в этот момент финансовый актив становится бесполезным.
В результате, на практике, финансовые аналитики, как правило, не используют нормальное распределение для моделирования распределения цен на активы. Также обратите внимание, что переход от цены актива любого уровня до 0 означает доходность -100%. Поскольку нормальное распределение распространяется ниже 0 без ограничений, оно не может быть полностью точной моделью для доходности активов.
Установив, что нормальное распределение является подходящей моделью для интересующей нас случайной величины, мы можем использовать его, чтобы сделать следующие вероятностные утверждения:
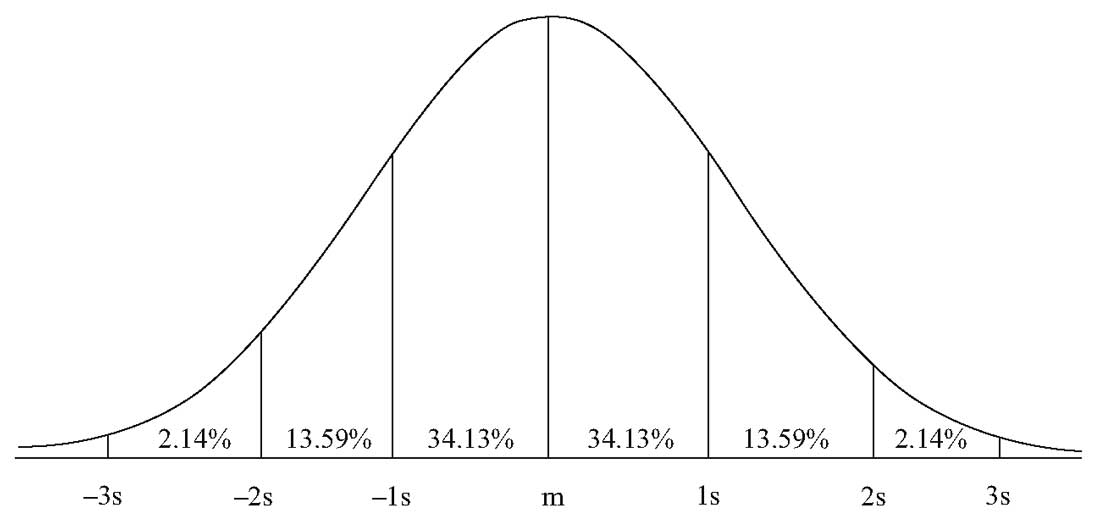
- Приблизительно 50% всех наблюдений попадают в интервал ( mu pm (2/3) sigma ).
- Приблизительно 68% всех наблюдений попадают в интервал ( mu pm sigma ).
- Приблизительно 95% всех наблюдений попадают в интервал ( mu pm 2 sigma ).
- Приблизительно 99% всех наблюдений попадают в интервал ( mu pm 3 sigma ).
Интервалы в один, два и три стандартных отклонения показаны на Рисунке 6. Эти доверительные интервалы легко запомнить, но они лишь приблизительные для указанных вероятностей. Более точные интервалы составляют ( mu pm 1.96sigma ) для 95% наблюдений и ( mu pm 2.58sigma ) для 99% наблюдений.
В целом, мы не наблюдаем среднее или стандартное отклонение генеральной совокупности распределения, поэтому нам нужно оценить их.
Генеральная совокупность — это все элементы указанной группы, и математическое ожидание представляет собой среднее арифметическое, рассчитанное для совокупности.
Выборка представляет собой подмножество генеральной совокупности, и выборочное среднее представляет собой среднее арифметическое для выборки.
Для получения более подробной информации об этих понятиях см. чтение о статистических концепциях и рыночной доходности.
Мы вычисляем среднее совокупности, (mu), используя выборочное среднее, ( overline X ) (иногда обозначаемое как ( hat{mu} ) ) и вычисляем стандартное отклонение, (sigma ), используя стандартное отклонение выборки, ( s ) (иногда обозначаемое как ( hat{sigma} ) ).
Существует столь же много различных нормальных распределений, сколько средних ((mu)) и дисперсий ( (sigma^2 )). Мы можем ответить на все поставленные выше вопросы с точки зрения любого нормального распределения. Электронные таблицы, например, имеют функции для расчета нормальной кумулятивной функции распределения с любыми спецификациями среднего и дисперсии.
Ради эффективности, однако, мы хотели бы свести все вероятностные утверждения к одному нормальному распределению. Стандартное нормальное распределение (нормальное распределение с ( mu = 0 ) и ( sigma = 1 ) ) как раз и выполняет эту роль.
Есть два шага в стандартизации случайной величины ( X ): вычесть среднее ( X ) из ( X ), а затем разделить результат на стандартное отклонение ( X ). Если у нас есть список наблюдений для нормальной случайной величины ( X ), мы вычитаем среднее из каждого наблюдения, чтобы получить список отклонений от среднего значения, а затем разделить каждое отклонение на стандартное отклонение.
Результатом является стандартная нормальная случайная величина, ( Z ) (символ (Z ) используется по соглашению в качестве символа для стандартной нормальной случайной величины).
Если мы имеем выражение ( X sim N(mu, sigma^2) ) (читается «X следует нормальному распределению с параметрами ( mu ) и ( sigma^2 )» ), мы стандартизируем его, используя формулу:
( Large dst Z = (X-mu)/ sigma ) (Формула 4)
Предположим, что мы имеем нормальную случайную величину, ( X ), при ( mu = 5 ) и ( sigma = 1.5 ). Мы стандартизируем X с помощью выражения: ( Z = (Х — 5) /1.5 ). Например, значение ( Х = 9.5 ) соответствует стандартизованному значению 3, рассчитанному как ( Z = (9.5 — 5)/1.5 = 3 ).
Вероятность того, что мы будем наблюдать значение, не превышающее 9.5 для ( X sim N(5,1.5) ) точно такая же, как вероятность того, что мы будем наблюдать значение, не превышающее 3 для ( Z sim N(0.1) ).
Мы можем ответить на все вопросы о вероятности ( X ), используя стандартные значения и вероятностные таблицы для Z. Как правило, мы не знаем среднее и стандартное отклонения генеральной совокупности, поэтому мы часто используем выборочное среднее ( overline X ) для ( mu ) и стандартное отклонение выборки ( s ) для ( sigma ).
Стандартные нормальные вероятности также можно вычислить с помощью электронных таблиц, статистического и эконометрического программного обеспечения и языков программирования.
В Таблице 5 приведены выдержки из таблиц кумулятивной функции распределения для стандартной нормальной случайной величины. По соглашению ( N(x) ) обозначает кумулятивную функцию распределения (cdf) для стандартной нормальной случайной величины.
Другим часто использующимся обозначением cdf стандартной нормальной случайной величины является ( Phi (х) ).
|
x или z |
0 |
0.01 |
0.02 |
0.03 |
0.04 |
0.05 |
0.06 |
0.07 |
0.08 |
0.09 |
|---|---|---|---|---|---|---|---|---|---|---|
|
0.00 |
0.5000 |
0.5040 |
0.5080 |
0.5120 |
0.5160 |
0.5199 |
0.5239 |
0.5279 |
0.5319 |
0.5359 |
|
0.10 |
0.5398 |
0.5438 |
0.5478 |
0.5517 |
0.5557 |
0.5596 |
0.5636 |
0.5675 |
0.5714 |
0.5753 |
|
0.20 |
0.5793 |
0.5832 |
0.5871 |
0.5910 |
0.5948 |
0.5987 |
0.6026 |
0.6064 |
0.6103 |
0.6141 |
|
0.30 |
0.6179 |
0.6217 |
0.6255 |
0.6293 |
0.6331 |
0.6368 |
0.6406 |
0.6443 |
0.6480 |
0.6517 |
|
0.40 |
0.6554 |
0.6591 |
0.6628 |
0.6664 |
0.6700 |
0.6736 |
0.6772 |
0.6808 |
0.6844 |
0.6879 |
|
0.50 |
0.6915 |
0.6950 |
0.6985 |
0.7019 |
0.7054 |
0.7088 |
0.7123 |
0.7157 |
0.7190 |
0.7224 |
Например, для того, чтобы найти вероятность того, что стандартная нормальная величина меньше или равна 0.24, нужно найти строку с заголовком 0.20, а также столбец с заголовком 0.04, и найти на их пересечении значение 0.5948. Таким образом, ( P(Z leq 0.24) = 0.5948 ) или 59.48%.
Ниже приведены некоторые из наиболее часто упоминаемых значений из таблицы стандартного нормального распределения:
Точка 90-го процентиля соответствует 1.282: ( P(Z leq 1.282) = N(1.282) = 0.90 ) или 90%, и 10% значений остаются в правом хвосте.
Точка 95-го процентиля соответствует 1.65: ( P(Z leq 1.65) = N (1.65) = 0.95 ) или 95%, и 5% значений остаются в правом хвосте. Обратите внимание на разницу между использованием точки процентиля при работе с одним хвостом, а не двумя хвостами.
Ранее мы использовали 1.65 стандартных отклонений для 90-процентного доверительного интервала, где 5% значений лежат вне этого интервала на каждой из двух сторон. Здесь мы используем 1.65, потому что мы имеем дело с 5% значений, которые лежат только на одной стороне распределения, в правом хвосте.
Точка 99-го процентиля соответствует 2.327: ( P (Z leq 2.327) = N(2.327) = 0.99), или 99%, и 1% значений остается в правом хвосте.
Таблицы, которые мы даем для нормального распределения включают вероятности для ( x leq 0 ). Многие источники, однако, дают только таблицы для ( geq 0 ).
Как следует использовать такие таблицы, чтобы найти нормальную вероятность?
Благодаря симметрии нормального распределения, можно найти все вероятности, используя таблицы стандартной нормальной случайной величины, ( P(Z leq x) = N(x) ) при ( х geq 0 ).
Приведенные ниже соотношения полезны при использовании таблиц при ( х geq 0 ), а также в других случаях:
Для неотрицательного числа ( x ), используйте ( N(x) ) из таблицы. Обратите внимание, что для вероятности справа от ( x ), мы имеем ( P(Z geq x) = 1.0 — N(x) ).
Для отрицательного числа ( -x ), ( N(-x) = 1.0 — N(x) ): Найдите ( N(x) ) и вычтите его из 1. Вся площадь под кривой нормального распределения слева от (x) равна ( N(x) ). Разница ( 1.0 — N(x) ), является площадью и вероятностью, находящейся справа от ( x ).
В силу симметрии нормального распределения вокруг его среднего значения, площадь и вероятность справа от х равна площади и вероятности слева от ( -x ), ( N(-x)).
Для вероятности справа от ( -x ), ( P(Z geq -x) = N(x) ).
Пример (8) расчета вероятностей для обычного портфеля акций.
Допустим, средняя доходность портфеля составляет 12%, а стандартное отклонение доходности оценивается в 22% в год.
Вы хотите вычислить следующие вероятности, при условии, что нормальное распределение описывает доходность портфеля. (Вы можете использовать приведенную выше выдержку из таблицы нормальных вероятностей, чтобы ответить на эти вопросы.)
- Какова вероятность того, что доходность портфеля будет превышать 20%?
- Какова вероятность того, что доходность портфеля будет между 12 и 20%? Другими словами, какова вероятность того, что P(12% ( leq ) Доходность портфеля ( leq ) 20%)?
- Вы можете купить годовой казначейский вексель, который приносит 5.5%. Эта доходность является эффективной годовой безрисковой процентной ставкой. Какова вероятность того, что доходность вашего портфеля не превысит безрисковую ставку?
Если ( X) является доходностью портфеля, стандартизированной доходностью портфеля будет ( Z = (X — overline X ) / s = (X -12%) / 22% ). Мы используем это выражение в решениях.
Решение для части 1:
Для (X = 20% ), (Z = (20 % — 12 %)/22 % = 0.363636). Вы хотите найти (P (Z> 0.363636)). Сначала заметим, что ( P(Z > x) = P(Z geq x) ), так как нормальное распределение является непрерывным распределением. Напомним, что ( P(Z geq x) = 1.0 — P(Z leq x) ) или ( 1 — N(x) ).
Округлим 0.363636 до 0.36, в соответствии с таблицей, ( N(0.36) = 0.6406 ). Таким образом, 1 — 0.6406 = 0.3594. Вероятность того, что доходность портфеля будет превышать 20%, составляет около 36%, если ваше предположение о нормальности доходности является точным.
Решение для части 2:
P(12% ( leq ) Доходность портфеля ( leq ) 20%) = ( N(Z ), соответствующее ( 20 %) — N(Z,) соответствующее ( 12 % ).)
Для первого члена выражения, ( Z = (20 % — 12 %) / 22 % = 0.36 ) примерно, и ( N(0.36) = 0.6406 ( (как в решении для части 1).
Для того, чтобы сразу получить второй член выражения, обратите внимание, что 12% это среднее, и для нормального распределения 50% вероятности лежат по обе стороны от среднего значения.
Следовательно, ( N(Z,) соответствующее ( 12 %)) должно быть равно 50%. Таким образом, P(12% ( leq ) Доходность портфеля ( leq ) 20%) = 0.6406 — 0.50 = 0.1406 или приблизительно 14%.
Решение для части 3:
Если ( X ) является доходностью портфеля, то мы хотим найти P(Доходность портфеля — 12% ( leq ) 5.5% — 12%). Этот вопрос является более сложным, чем в частях 1 или 2, но когда вы разберетесь в решении, представленном ниже, у вас будет полезный алгоритм для расчета вероятности других недостающих вероятностей.
Необходимо выполнить три шага, включающих стандартизацию доходности портфеля:
- Во-первых, вычесть среднюю доходность портфеля с каждой стороны неравенства: P(Доходность портфеля — 12% ( leq ) 5.5% — 12%).
- Во-вторых, разделить каждую сторону неравенства на стандартное отклонение доходности портфеля: ( P[( )Доходность портфеля (- 12 %)/22 % leq (5.5 % — 12 %) / 22 %] ) ( = P(Z leq -0.295455) = N(-0.295455) ).
- В-третьих, признать, что на левой стороне мы имеем стандартную нормальную величину, обозначаемую как ( Z ). Как отмечалось выше, ( N(-x) = 1 — N(x) ).
Округлив -0.29545 к -0.30 для использования выдержки из таблицы, мы получим ( N(-0.30) = 1 — N(0.30) = 1 — 0.6179 = 0.3821 ) или примерно 38%. Вероятность того, что ваш портфель будет отставать от годовой безрисковой ставки составляет около 38%.
Мы можем получить тот же ответ более быстро, путем вычитания средней доходности портфеля из 5.5%, деления на стандартное отклонение доходности портфеля, и сопоставления результата (-0.295455) с вероятностной таблицей.
Большинство начинающих инвесторов теряют деньги, потому что не диверсифицируют свой портфель. Они покупают акции и/или облигации, потому что их эмитенты у них на слуху, а оценка возможности банкротства/дефолта сводится к эмпирическому: «ну это же Сбербанк, ему не дадут обанкротиться».
Те же кто уже что-то прочел или обжегся хотя бы раз знают, что диверсификация вещь критически важная, но зачастую не знают какой уровень необходим для их портфелей. Иными словами, они пытаются найти ответы на вопрос подобный такому: «10 эмитентов – это нормально или нет? А может стоит брать 50? И на сколько лучше 50, чем 10?»
Ответ на этот вопрос не так прост, как кажется. Большинство апологетов пассивного инвестирования считают, что диверсификация должна быть очень большой и в том числе поэтому рекомендуют покупать индексные фонды на широкий рынок. Даже старик Баффет, выступая перед выпускниками MBA во Флориде в 2007 году говорил, что если человек не является профессиональным инвестором, то он должен следовать именно этой стратегии и скорее всего это будет лучшим вариантом для 99% людей. Но если он разбирается в бизнесе компаний, акции которых приобретает, то ему хватит и 5.
Не надо быть семь пядей во лбу, чтобы эмпирически понять эти идеи и осознать их. Но куда как интересней посмотреть на эти рассуждения с точки зрения теории вероятности.
Сначала небольшой ликбез. Решение задачи размера диверсификации можно сравнить с решением задачи по лотерейным билетам. Задача это звучит примерно так: пусть мы купили n-лотерейных билетов, вероятность выигрыша каждого билета — p. Какова вероятность того, что m билетов из всех купленных нами будут выигрышными?
Такая задача решается при помощи формулы Бернулли:
Например, пусть мы купили 5 билетов, вероятность выигрыша каждого из них составляет 10%, и мы стараемся ответить на вопрос – какова вероятность того, что 3 из этих билетов выигрышные?
Как видно из решения этой простой задачки вероятность выигрыша 3-х билетов составляет 0.81%
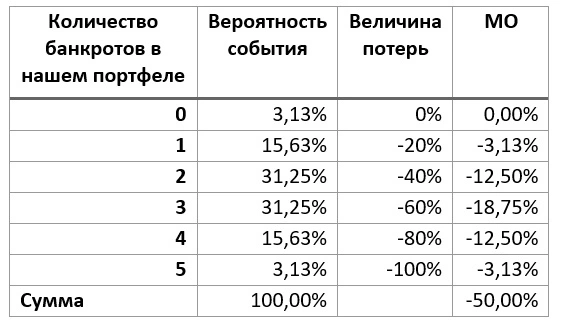
Эту же формулу можно использовать для ответа на вопрос об уровне диверсификации. Сформулируем задачу следующим образом. Мы купили акции 5 различных эмитентов, вероятность банкротства любого из них пусть составляет 50%(может обанкротится, а может нет 😊). Какова вероятность того, что три из них обанкротятся?
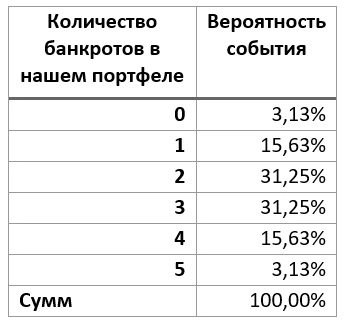
Подставив все данные в формулу Бернулли мы получим, что вероятность такого события составляет 31,25%. А если мы пока не рассматриваем ожидаемые доходности, волатильности наших акций и вложили одинаковое количество денег в каждый актив, то это значит, что потерять 60% капитала мы можем с вероятностью 31,25%. Но чтобы решение было полным, нам нужно посчитать вероятности и других событий, а именно: что не обанкротится ни одна из 5 компаний, 1 из 5, 2 из 5, 4 из 5 и все 5. Тогда мы получим полное поле возможных решений. Сегодня при нынешних вычислительных мощностях и программах такие задачи решаются на раз два, и для любого объема выборки, не то, что для нашего портфеля из 5 бумаг.
Теперь же, когда нам известны все вероятности для всех возможных комбинаций мы можем легко посчитать математическое ожидание. Сделать это просто – достаточно взять каждую из вероятностей и умножить на потенциальный результат. Например, если обанкротятся все 5 компаний, то мы потерям весь вложенный капитал, то есть 100%, если только 4 – то потери составят 80% и т.п.
Как и ожидалось, в нашем случае математическое ожидание (МО) будет равно вероятности банкротства отдельно взятой компании. А как нас учит теория вероятности, что игра стоит свечи только тогда, когда МО больше 0. И чем больше, тем лучше для нас! Если же мы хотели бы посмотреть случай, когда МО равно нулю, то мы должны были требовать от каждой акции входящий в наш портфель доходность в 50% (в идеале, конечно, больше).
Даже на эмпирическом уровне понятно, что это через чур завышенные ожидания. Таким потенциалом роста с фундаментальной точки зрения могут обладать единичные компании, но они вряд ли будут представлены на бирже.
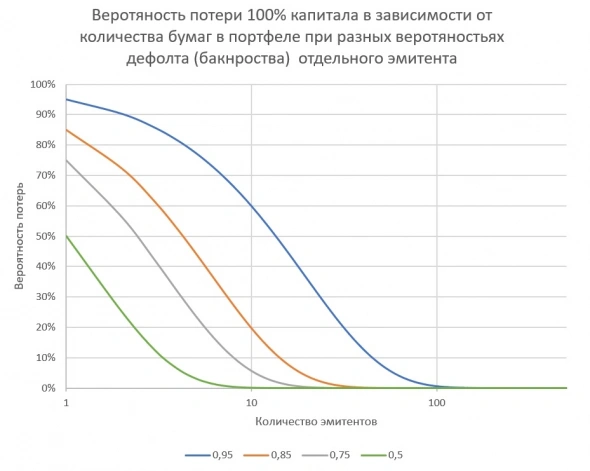
Интересно посмотреть, как выгляди уровень диверсификации в зависимости о вероятности банкротства одной компании, который мы принимаем одинаковым для все акций входящих в портфель.
Так, например, вероятность потерять 100% капитала для случая с вероятностью банкротства каждой в 95%, стремится к нулю при примерно 500 эмитентах. А при вероятности банкротства одного равному 50%, будет вполне достаточно около 15. Но беда в том, что вероятность не потерять совсем убывает с такой же скоростью.
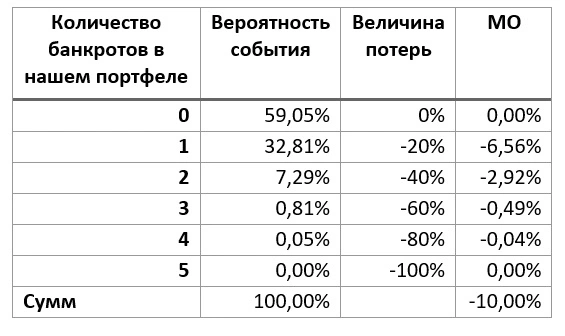
Преимущество в том, что в жизни и на рынке, мы не встречаемся с такими апокалиптическими сценариями. Если усреднить вероятность банкротства по всем компаниям, которые торгуются на бирже, то скорее всего мы столкнемся с показателем что-то на уровне 5%, а как максимум 10%. То есть нам достаточно будет ожидать получение доходности на уровне 5% (10%) на каждый актив, чтобы МО стало равным 0. А это уже вполне разумная цель.
И кажется вот он Грааль. Даже при вероятности банкротства в 10% каждой компании, вероятность ничего не потерять составляет почти 60%. А если мы ожидаемая доходность каждого актива составит 10%, то мы еще и заработаем. И получается старик Баффет был прав?!
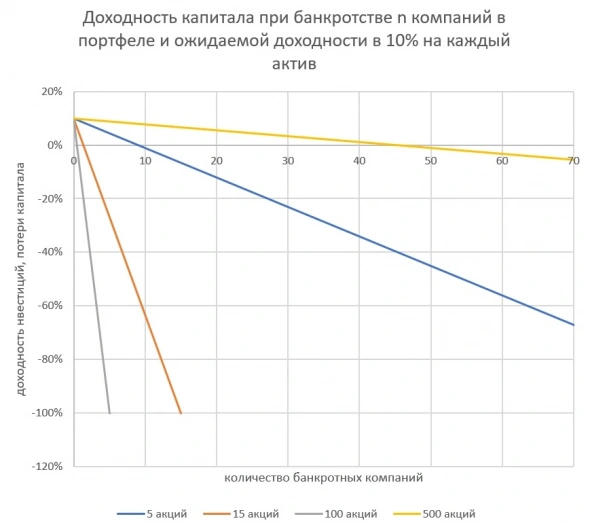
Не всё так радужно! Давайте посмотрим на следующий график.
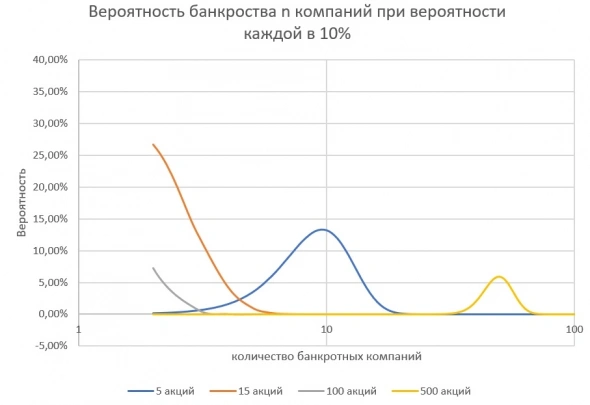
Из графика прекрасно видно, при банкротстве хотя бы одной компании в портфеле из 5 акций, наш портфель отрицательным по доходности, и это несмотря на то, что вероятность «ничего не потерять» составляла 60%. Для портфеля из 15 бумаг — отрицательный результат будет уже при банкротстве 2-х. Существенно лучше ситуация в портфеле из 100 бумаг, там должно быть 10 банкротов, а для 500 мы уйдем в минус только если одновременно обанкротится 48!!!
Поэтому высокая диверсификация в реальности спасает нас от ошибок инвестирования. Конечно, инвестиции гораздо сложнее, и вероятности банкротства для разных компаний разные. Более того, в представленной моделе нет волатильности, как меры риска, которая добавляет существенные корректировки. Но подобное рассмотрение предмета, дает начинающему инвестору прекрасный ответ на вопрос, который был сформулирован в самом начале. А именно — чем Выше будет ваше диверсификация, тем меньше шансов получить негативный результат от инвестиций.
И да! Баффет в реальности был прав, говоря: «если человек не является профессиональным инвестором, то он должен следовать стратегии инвестиций в индексы широкого рынка. Но если он разбирается в бизнесе компаний, акции которых приобретает, то ему хватит и 5». Знания о бизнесе компании и его понимание, существенно понижает риск инвестиций, а активное отслеживание позволяет инвестору предпринять необходимые действия, чтобы избежать потерь. Но большинство людей не являются профессионалами, а значит разумнее идти более диверсифицированным путем – покупать фонд на широкий рынок.
КУРС
ИНВЕСТИЦИОННЫЙ АНАЛИТИК
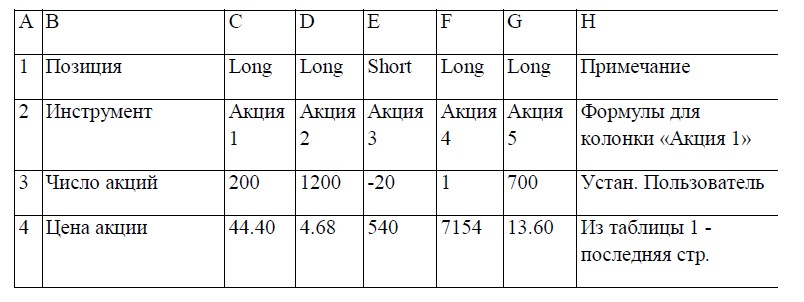
Инвестору чрезвычайно важно знать степень риска, которому подвержены открытые позиции. Определить меру риска VaR (Value-at-Risk) для единичного актива можно по формуле:
95% VaR = 1.65 X Волатильность * Размер позиции * SQRT(Время)
где
(SQRT – корень квардатный) и 95% – это 95%-ный доверительный уровень;
Волатильность – стандартное отклонение изменения цен (выясняется как натуральный логарифм «сегодня/вчера»);
Размер позиции – лицевая стоимость торгуемого контракта;
Время – горизонт оценки.
Полученный результат трактуют так: ценовые изменения в данный промежуток времени не приведут к потерям выше полученного результата в 95% случаев. Иными словами, есть только 5%-ная вероятность потери, превышающей значение 95% VaR.
В банковской практике чаще применяется 99% VaR, отличие которого от представленной формулы в коэффициенте: 2.33 вместо 1.65. Соответственно, 99% VaR говорит нам, что цены с вероятностью 99% не способны измениться настолько, чтобы убытки превысили вычисленное значение.
Пользуясь указанной выше формулой, можно определить риск широкого спектра финансовых активов, попадающих в категорию простых инструментов и линейных производных. К ним относятся: акции, иностранные валюты, облигации обычные и с плавающим купоном (не имеющие высокую дюрацию), процентные и валютные свопы, валютные форвардные контракты, FRA. Тем самым формулировка доступна для применения практически на всех рынках, традиционно вызывающих интерес у отечественных инвесторов, в первую очередь – на рынке акций и FOREX.
Обычно проблемы оценки риска рассматриваются на стадии портфеля, состоящего из двух активов. Для большего числа инструментов предлагаются формулы, труднопонимаемые без специальной математической подготовки. Но данная задача решается просто, если подойти к ней сугубо с практической точки зрения, исключив теоретические аспекты.
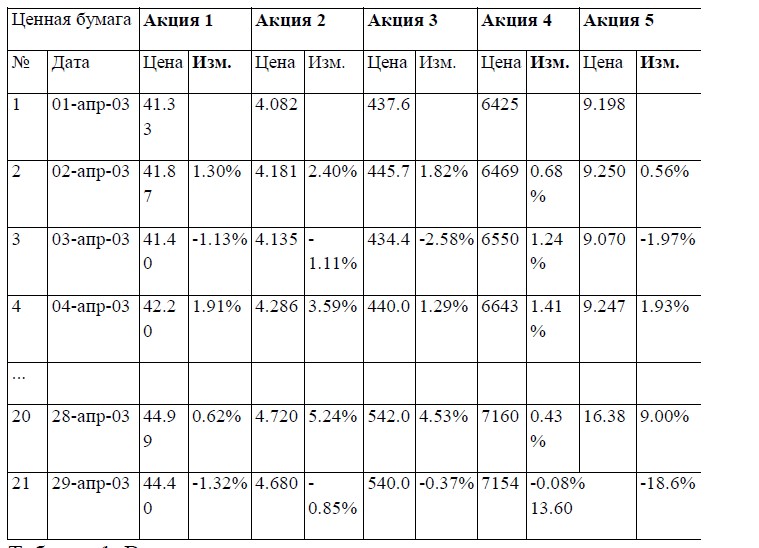
Поэтому здесь дается только то, что необходимо знать, чтобы самостоятельно составить программу в электронных таблицах (Excel), обеспечивающую вычисления VaR портфеля. Для иллюстрации использованы случайно выбранные пять российских акций в произвольно взятый период времени: с 1 по 29 апреля 2003 года.
Шаг 1. Первичная обработка данных
Сначала выясним значение среднего изменения цен и волатильности. Для этого нам потребуется как минимум объем данных, удовлетворяющих выбранному периоду оценки.
Предположим, используется 20-периодный цикл, тогда нужно не менее 21 дня, если анализ выполняется по дневным данным. Для каждого дня необходимо выяснить натуральный логарифм отношения цен «сегодня/вчера» (см. значение «Изм.» в табл. 1).
«Изменение» = ln (сегодня / вчера)
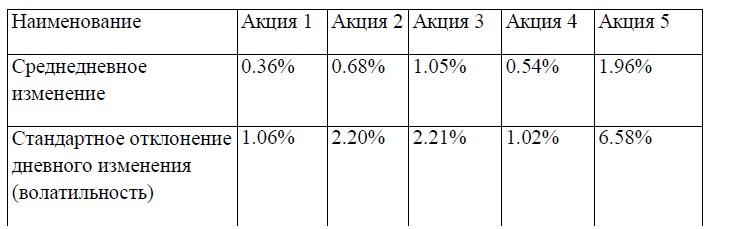
Теперь можно найти среднедневное изменение и величину стандартного отклонения, используя полученный ряд (колонки «Изм.»).
Среднедневное изменение – это среднеарифметическое, которое в Excel записывается «=average()», а стандартное отклонение как «=stdev()», которое и является дневной волатильностью.
При этом калькуляция охватывает область переменных, находящихся на строчках от 2 до 21 в колонке «Изм.» (результат см. в табл. 2).
Следует иметь в виду: предлагаемый алгоритм оценки волатильности основан на методе постоянных, а не экспоненциально взвешенных ковариаций. Но к ним можно перейти, используя полученные ряды изменения цен, для чего необходимо ввести соответствующие поправки, обеспечивающие больший вклад более поздних наблюдений.
Хороший аналог данного метода оценки волатильности – взвешенная скользящая средняя по сравнению с обычной скользящей средней. Характерно, что множитель, практикуемый в методологии J.P. Morgan RiskMetrics, равен 0.98, как и в установках по умолчанию в программах, предназначенных для технического анализа рынка.
Шаг 2. Необходимый минимум теории
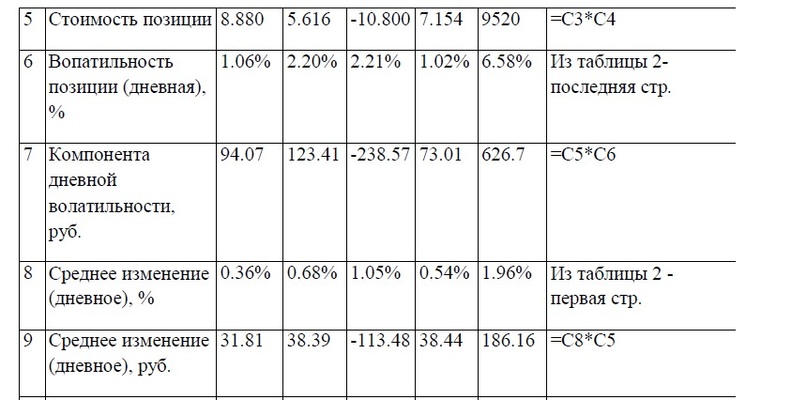
Прежде чем перейти к вычислению VaR портфеля, обратимся к некоторым сведениям, которые дают понимание расчетных алгоритмов. В целом VaR портфеля из многих активов можно определить по следующей формуле:
VaR портфеля = Среднее изменение – К * Волатильность портфеля,
где
Среднее изменение – просто сумма средних изменений всех компонентов портфеля;
К – число стандартных отклонений, требуемых для заданного доверительного уровня, вычисляемое по формуле в Excel «=NORMSINV()», где аргумент – соответствующий доверительный уровень.
Волатильность портфеля калькулируется с использованием формулы, предложенной Г. Марковицем:
Волатильность портфеля = SQRT (Вектор волатильной компоненты *Корреляционная матрица * Транспонированный вектор волатильной компоненты)
Вектор волатильной компоненты можно вычислить, пользуясь формулой:
Компонента волатильности = Стоимость позиции * Волатильность позиции
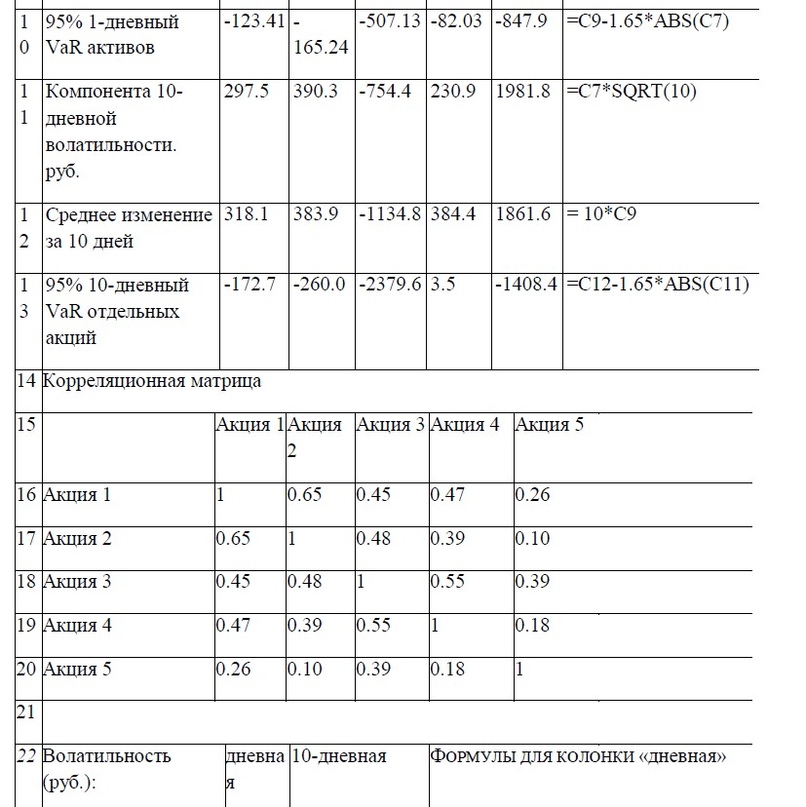
Помимо уже выполненных расчетов для вычисления VaR портфеля потребуется построить корреляционную матрицу, основываясь на данных, обработанных в шаге 1.
Она представляет собой совокупность коэффициентов, отражающих корреляцию между каждым из инструментов, входящих в портфель.
Вычисления в Excel выполняются с помощью соответствующей функции «=correl()», причем построение матрицы лучше выполнить на странице, где будут размещены все прочие расчеты, в том числе и VaR. Это уже будет шаг 3.
КУРС
ИНВЕСТИЦИОННЫЙ АНАЛИТИК
Шаг 3. Вычисление VaR портфеля
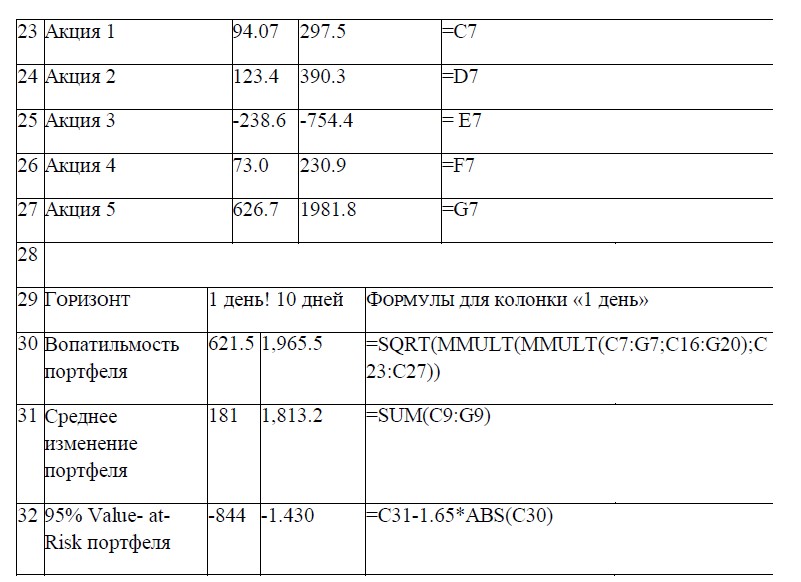
Протокол расчета, позволяющий видеть все промежуточные этапы, представлен в таблице 3. Здесь же даны формулы, с помощью которых производятся вычисления.
Следует иметь в виду: данная таблица есть копия рабочего листа Excel, поэтому при написании программы рекомендуется придерживаться указанного порядка, пользуясь для подсказки формулами, выложенными в крайней колонке «Н» справа. Позже, если возникнет желание, структуру таблицы можно изменить.
Остается сделать ряд важных замечаний
Во-первых, в зависимости от задачи число входящих в портфель активов можно увеличить или уменьшить.
Во-вторых, при оценке по ценам внутри дня при вычислениях надо придерживаться единого масштаба, поэтому VaR будет получаться для задаваемого числа часов в параметре «время». Для перевода в дневной масштаб следует учесть число торговых часов в одном дне.
Для обращающихся на бирже активов обычно это не вызывает трудностей, но в ряде случаев можно столкнуться с проблемами. Как, скажем, на рынке FOREX, где трудно предложить однозначное решение, поскольку приходится учитывать неравномерный характер торговой активности.
В-третьих, следует иметь в виду: портфель может содержать различные активы. Единственное условие – они должны быть выражены в одной валюте.
Например, если бы мы пожелали оценить риск портфеля, состоящего из акций в рублях, валютной позиции по евро/доллар и процентного фьючерса в британских фунтах, нам пришлось бы прежде выбрать счетную валюту.
Если мы выбрали евро, то потребуется пересчитать все ценовые ряды в евро по соответствующему курсу для каждого дня. После этого нам удастся без труда получить результирующую цифру, которая также будет в евро.
Шаг 4. Оптимизация портфеля
Поняв процедуру оценки риска, можно решать такие серьезные задачи, как поиск более эффективных решений. В Excel существует опция «Solver» в разделе «Tools», позволяющая выполнять поиск решений по заданным условиям. О других полезных функциях Excel мы рассказываем на нашем открытом курсе «Аналитика в Excel».
Например, если мы укажем, что нас устраивает иное значение 95% VaR – скажем, -500, а не -844 – и определим при этом возможность изменения числа всех акций, то программа вычислит: «Акция 1» следует иметь 119 акций, «Акция 2» – 1193, «Акция 3» – 11, «Акция 4» – 2 и «Акция 5» – 227 акций. Причем с длинными позициями по всем бумагам.
Легко заметить: подобный подход отличается ограниченностью, поскольку мы никак не определяем имеющийся в нашем распоряжении капитал, а указываем лишь уровень принимаемого риска.
Эта проблема легко разрешима: имеющиеся данные позволяют производить любые вычисления, необходимые для определения стоимости портфеля, а также размера требуемого капитала как при торговле с маржой, так и без нее. После этого определить степень риска в относительных величинах не представляет труда, это будет частное от VaR и рабочего капитала или размера счета – в зависимости от того, что необходимо оценить.
С полученной величиной мы можем обращаться точно так же, как и со значением VaR в денежных единицах. Скажем, если нам для создания портфеля, представленного в таблице 3, потребуется капитал в размере 42 тыс. руб. (исходя из правил брокера), то 1-дневный 95% VaR составит 2.01%, а 10-дневный – 3.41%.
Данные цифры говорят: существует 95%-ная вероятность, что потери портфеля за 1 день не превысят 2.01% от работающего капитала, а за 10 дней – 3.41%. Естественно, если нам нужна более полная картина, следует проводить расчеты также и для всего капитала, с учетом резервов.
Опираясь на эти цифры, можно выполнять оптимизацию, пользуясь алгоритмом, описанным выше. Например, задавая 1-дневные потери в размере 1% от работающего капитала при доверительном уровне в 95%, мы узнаем, что это достигается за счет увеличения короткой позиции в «Акция 3» (с 20 до 23 акций) и покупки 18, а не одной, акций «Акция 4», при неизменности числа прочих бумаг.
Обратите внимание: не введя в данную процедуру ограничений на капитал, мы обнаружим, что эта возможность для нас нереальна или не отвечает нашим намерениям, поскольку для создания портфеля требуется 163 тыс. руб. Поэтому следующий этап усложнения алгоритмов оценки риска – ввод ограничений.
Шаг 5. Ввод ограничений
Ввод ограничений, позволяющих решать проблему оптимизации, требует немного больше знаний об электронных таблицах. Полностью описать то, как можно решить ту или иную задачу, здесь не представляется возможным.
Во-первых, можно найти немало подходящих алгоритмов, позволяющих достичь поставленной цели. Во-вторых, многие из них связаны с уровнем квалификации инвесторов – пользователей среды Windows, а обучение не является нашей задачей. В-третьих, как показывает практика, пользователям лучше всего самостоятельно создавать интерфейс, если работа ведется с Excel.
Поэтому в шаге 5 только указывается путь, ведущий к построению потокового процесса контроля над риском и управления им.
Наиболее простой способ решить задачу – ввести условия, опираясь на соотношение между показателем меры риска и размером имеющегося в нашем распоряжении капитала. Если одновременно мы хотим автоматизировать процесс, нам потребуется ввести дополнительные ограничения, описывающие наши реальные возможности. Обычно это реализуется через совместное использование таких функций, как «=IF(), OR(), AND()».
Дополнительные возможности появляются, если изменениям будет подвергаться не число акций, а их доля в портфеле. Описание связей в таком случае будет легче, так как мы заранее указываем размер капитала, под который формируется портфель. Число акций уже будет не задаваться пользователем, как это предложено в таблице 3, а вычисляться на основе весовой доли в портфеле.
Причем подходы, основанные на оценке веса, могут иметь и другие решения. Вводя граничные условия с целью автоматизации процесса оценки риска, мы неминуемо столкнемся с проблемой управления резервами.
И здесь следует обратить внимание на важную деталь. Дело в том, что непосредственное применение VaR – это определение, какой капитал необходимо резервировать, чтобы иметь достаточное покрытие рыночного риска. В практике рядового инвестора – это решение вопроса, сколько надо иметь свободных средств на счете, чтобы не потерять свыше заданной величины или не получить margin call (при маржевой торговле).
В банковской практике рекомендуемые резервы – 3-кратный 10-дневный 99% VaR (для портфеля из таблицы 3 такие резервы составят 8299 рублей). Поскольку резервы, оцениваемые через VaR, – величина «плавающая» и зависит от волатильности, этот аспект может оказаться для кого-то привлекательным. В таком случае вполне естественно включить данный параметр в алгоритмы, обеспечивающие обсчет риска.
Наконец, следует включить и ожидаемую прибыль. Это дополнение позволяет получать новые оценочные коэффициенты, играющие важную роль в торговой практике. Скажем, мы можем вывести соотношение «прибыль/возможный убыток». Если при этом учтены издержки на транзакции, а также соответствуют горизонты, использованные для оценки потерь и прибыли, то у нас получится формулировка для оценки рисков RAROC по методике Bankers Trust.
Решений автоматизации процедур, связанных с риск-менеджментом, существует много. Окажутся ли они эффективными, в значительной степени зависит от точности поставленной задачи и желания получить действительно простую и понятную процедуру оценки меры риска.
Вершиной здесь является построение потокового процесса управления ценовыми и финансовыми рисками, решающего с максимально возможной эффективностью основную задачу инвестора – как понадежней заработать.
Автор: Михаил Чекулаев
КУРС
ИНВЕСТИЦИОННЫЙ АНАЛИТИК
Продолжаем наш цикл статей про метрики оценки портфеля. В этой статье мы познакомимся с VaR — вероятностным измерением убытков.
Стоимость под риском
VaR — это основанная на вероятности мера потенциального убытка по позиции или портфелю. Обычно она выражается в процентах от стоимости портфеля и используется для измерения убытков из-за изменения биржевых цен, но при должном умении может применяться и для измерения убытков из-за кредитного и других видов рисков.
В течение 1990-х годов вычисление величины VaR (стоимости под риском) стало основой процесса управления рисками в сфере финансовых услуг. Разработанная холдингом JPMorgan, эта оригинальная концепция поначалу использовалась лишь внутри компании, однако спустя некоторое время была опубликована в открытых источниках. С тех пор, пожалуй, никакой другой аспект в области управления рисками не выступал предметом таких жарких обсуждений и споров, как VaR.
Пример VAR
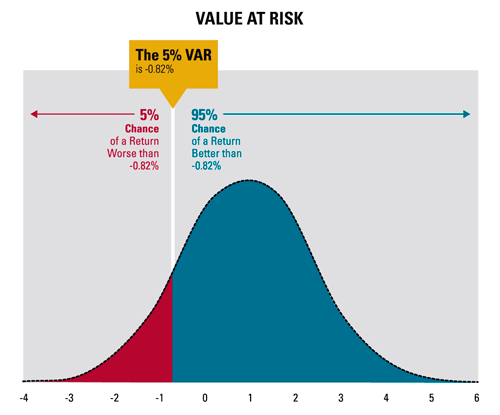
Как мы отметили выше, VaR является вероятностной мерой потенциальных потерь. Более формальное определение звучит так: стоимость под риском (VaR) — это потери (в денежном выражении), которые, как ожидается, будут превышены с заданным уровнем вероятности за определённый период времени.
VaR для портфеля на графике составляет не менее 0.82% убытков (или, что то же самое, не более -0.82% дохода) за один день с вероятностью 5%.
Ещё раз: существует 5-процентная вероятность того, что портфель потеряет как минимум 0.82% своей стоимости за один день. Обратите внимание на тот факт, что речь здесь идёт о минимальных потерях (не менее 0.82%, то есть реальные потери могут составить и 1%, и 10%, и даже 100%!). Можно, конечно, выразить VaR и зеркальным образом: вероятность того, что портфель потеряет не более 0.82% своей стоимости (другими словами, вырастет лучше, чем на -0.82%) за один день, равна 95%. Но мы предпочитаем выражать VaR в форме минимального убытка: этот подход чуть более консервативен, поскольку напоминает нам о том, что потери могут быть намного выше указанных.
Итого:
- VaR является оценкой потерь, которые мы ожидаем превысить. Следовательно, эта величина отражает минимальные потери. Фактические потери могут быть намного хуже, не ставя при этом под сомнение вычисленное значение VaR.
- VaR связана с конкретной вероятностью. Предположим, VaR говорит о доходности -0.82% с вероятностью 5% в течение дня. При прочих равных, если мы снизим вероятность наступления потерь с 5% до 1%, значение VaR изменится и станет значительно больше по модулю. Это соответствует движению по графику распределения влево с целью поиска более страшных событий, влияющих на портфель.
- VaR зависит от выбранного временного интервала. VaR нельзя сравнивать между разными активами, если они не разделяют один и тот же интервал времени. Существует большая разница между потенциальными убытками, которые можно понести ежедневно, еженедельно, ежемесячно, ежеквартально или ежегодно. Потенциальные потери за более длинные периоды должны быть больше, чем за более короткие.
Величина риска VaR — это порог потерь: имея определённый набор активов, вы можете быть уверены, что ваши потери в большинстве случаев не превысят X. Существует также условное значение риска (Conditional Value at Risk, CVaR) — это взвешенное по вероятности среднее значение потерь при нарушении порога VaR. Как VaR, так и CVaR измеряют потенциальные потери в самых худших ситуациях.
Как измерить VAR
Хотя величина VaR стала отраслевым стандартом, она может быть реализована в нескольких видах. Для установления соответствующей формулы VaR необходимо принять ряд решений относительно структуры расчёта. Тремя важными факторами являются:
- выбор уровня вероятности,
- выбор периода времени, то есть VaR за день, за неделю или за год.
- выбор конкретного подхода к моделированию распределения потерь.
Выбранная вероятность обычно равна 0,05 или 0,01 (что соответствует доверительным уровням 95% или 99%). Использование значения 0,01 приводит к более консервативной оценке VaR.
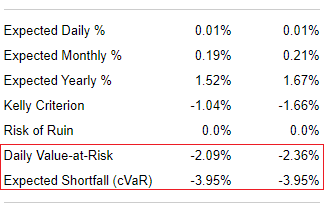
На rusetfs.com значения VaR вычисляются для периода, равного одному дню, вероятности, равной 5%, и на основе стандартного нормального распределения. Для примера проведём анализ рисков для FXUS, который мы изучали в статье про матстат.
- VaR равен -2.09%. Это означает, что в среднем раз в 20 дней мы можем наблюдать по данному активу или портфелю доходность хуже, чем -2.09%.
- CVaR равен -3.95%. Это означает, что каждые 20 дней мы можем наблюдать по данному активу или портфелю красный день со средним ожидаемым убытком -3.95%.
Выводы
Сегодня мы рассказали о новой риск-метрике при инвестициях в фонды. Коэффициенты Шарпа и Сортино, которые мы разобрали в прошлой статье, дают возможность оценить рискованность портфеля в обычных условиях. VaR же позволяет оценить вероятность реальных потерь в экстремальных случаях и быть готовым к ним.
Новая статья, новая акция! Первый, кто напишет на почту info@rusetfs.com письмо с темой «VaR для моего портфеля!», представится уникальная возможность в индивидуальном порядке получить анализ своего портфеля. Анализ будет проведён для любого портфеля (даже если в нём имеются отличные от ETF активы), а результат будет выглядеть как привычный отчёт сравнения портфелей. Это прекрасная возможность узнать и улучшить качество вашего управления собственными инвестициями.
-
отчет
-
портфель
-
математика
KVAAl | Экзамен 5.0 | Глава 12
Риски в деятельности инвестиционных фондах
Негосударственные пенсионные фонды
Инвестиционные риски — это вероятность неполучения прибыли либо потери основного капитала — частичной или полной. Уменьшение стоимости первоначальных вложений может произойти под влиянием различных факторов.
VaR — это показатель риска, который говорит о том:
Вопрос: 12.1.1
- какую максимальную сумму денег может потерять портфель инвестора в течение определенного периода времени с заданной доверительной вероятностью.
Стоимость портфеля инвестора составляет 10 млн. руб., VaR для одного дня равен 100 тыс. руб. с доверительной вероятностью 90%. Как можно интерпретировать данную информацию?
Вопрос: 12.1.2
- вероятность того, что в течение следующих 24 часов потери в стоимости портфеля составят меньше 100 тыс. руб. равна 90%.
- вероятность того, что в течение следующих 24 часов потери в стоимости портфеля превысят 100 тыс. руб. равна 10%.
- инвестор вправе ожидать, что в среднем его потери в течение 90 дней из каждых 100 дней не превысят 100 тыс. руб., или что они окажутся больше 100 тыс. руб. в течение 10 дней из каждых 100 дней.
Стоимость портфеля инвестора составляет 5 млн. руб., VaR для одного дня с доверительной вероятностью 95% равен 60 тыс. руб. В течение какого количества дней из каждых 100 дней инвестор вправе ожидать, что его потери не превысят 60 тыс. руб.
Вопрос: 12.1.3
- в течение 95 дней из каждых 100 дней.
Стоимость портфеля инвестора составляет 1 млн. руб., VaR для одного дня с доверительной вероятностью 95% равен 20 тыс. руб. В течение какого количества дней из каждых 100 дней инвестор вправе ожидать, что его потери составят больше 20 тыс. руб.
Вопрос: 12.1.4
- в течение 5 дней из каждых 100 дней.
Стоимость портфеля инвестора составляет 20 млн. руб., VaR для десяти дней равен 5 млн. руб. с доверительной вероятностью 99%. Какова вероятность того, что потери инвестора в течение следующих десяти дней превысят 5 млн. руб.?
Вопрос: 12.1.5
- 1%.
Какой уровень доверительной вероятности необходимо использовать при расчете VaR?
Вопрос: 12.1.6
- уровень выбирается компанией самостоятельно, исходя из риск-профиля портфеля.
В каком случае значение абсолютного VaR равно значению относительного VaR?
Вопрос: 12.1.7
- если ожидаемая доходность портфеля равна нулю.
Определить однодневный VaR с доверительной вероятностью 90% для портфеля стоимостью 10 млн. руб., в который входят акции только одной компании. Стандартное отклонение доходности акции в расчете на день равно 1,5%. Доходность портфеля распределена нормально.
Вопрос: 12.1.8
- 192 тыс, руб.
Определить однодневный VaR с доверительной вероятностью 95% для портфеля стоимостью 10 млн. руб., в который входят акции только одной компании. Стандартное отклонение доходности акции в расчете на день равно 1,5%. Доходность портфеля распределена нормально.
Вопрос: 12.1.9
- 247,5 тыс, руб.
Определить однодневный VaR с доверительной вероятностью 99% для портфеля стоимостью 10 млн. руб., в который входят акции только одной компании. Стандартное отклонение доходности акции в расчете на день равно 1,5%. Доходность портфеля распределена нормально.
Вопрос: 12.1.10
- 349,5 тыс, руб.
Бесплатный тренажер ФСФР
Закрепим материал
10 вопросов (12.1.1 — 12.1.10)
нажмите на кнопку
VaR — это показатель риска, который говорит о том:
I. какую максимальную сумму денег может потерять портфель инвестора в течение определенного периода времени.
II. какую максимальную сумму денег может потерять портфель инвестора в течение определенного периода времени с заданной доверительной вероятностью.
III. какую максимальную сумму денег может потерять портфель инвестора с заданной доверительной вероятностью.
Стоимость портфеля инвестора составляет 10 млн. руб., VaR для одного дня равен 100 тыс. руб. с доверительной вероятностью 90%. Как можно интерпретировать данную информацию?
I. Вероятность того, что в течение следующих 24 часов потери в стоимости портфеля составят меньше 100 тыс. руб. равна 90%.
II. Вероятность того, что в течение следующих 24 часов потери в стоимости портфеля превысят 100 тыс. руб. равна 10%.
III Инвестор вправе ожидать, что в среднем его потери в течение 90 дней из каждых 100 дней не превысят 100 тыс. руб., или что они окажутся больше 100 тыс. руб. в течение 10 дней из каждых 100 дней.
Стоимость портфеля инвестора составляет 5 млн. руб., VaR для одного дня с доверительной вероятностью 95% равен 60 тыс. руб. В течение какого количества дней из каждых 100 дней инвестор вправе ожидать, что его потери не превысят 60 тыс. руб.
A. В течение 95 дней из каждых 100 дней.
B. В течение 5 дней из каждых 100 дней.
C. Информации для ответа недостаточно.
Стоимость портфеля инвестора составляет 1 млн. руб., VaR для одного дня с доверительной вероятностью 95% равен 20 тыс. руб. В течение какого количества дней из каждых 100 дней инвестор вправе ожидать, что его потери составят больше 20 тыс. руб.
A. В течение 95 дней из каждых 100 дней.
B. В течение 5 дней из каждых 100 дней.
C. Информации для ответа недостаточно.
Стоимость портфеля инвестора составляет 20 млн. руб., VaR для десяти дней равен 5 млн. руб. с доверительной вероятностью 99%. Какова вероятность того, что потери инвестора в течение следующих десяти дней превысят 5 млн. руб.?
D. Информации для ответа недостаточно
Какой уровень доверительной вероятности необходимо использовать при расчете VaR?
C. Уровень выбирается компанией самостоятельно, исходя из риск-профиля портфеля.
В каком случае значение абсолютного VaR равно значению относительного VaR?
A. Их значения никогда не равны.
B. Если относительный VaR рассчитывается для доверительной вероятности 90%, а абсолютный VaR для доверительной вероятности 95%.
C. Если ожидаемая доходность портфеля равна нулю.
Определить однодневный VaR с доверительной вероятностью 90% для портфеля стоимостью 10 млн. руб., в который входят акции только одной компании. Стандартное отклонение доходности акции в расчете на день равно 1,5%. Доходность портфеля распределена нормально.
Определить однодневный VaR с доверительной вероятностью 95% для портфеля стоимостью 10 млн. руб., в который входят акции только одной компании. Стандартное отклонение доходности акции в расчете на день равно 1,5%. Доходность портфеля распределена нормально.
Определить однодневный VaR с доверительной вероятностью 99% для портфеля стоимостью 10 млн. руб., в который входят акции только одной компании. Стандартное отклонение доходности акции в расчете на день равно 1,5%. Доходность портфеля распределена нормально.
Следует закрепить материал
Переходим к сдедующей теме
Нет! Уж лучше я вложусь в свое образование, чем в «ракеты каналы» и мутные справки. Ведь учеба расширит мой кругозор, раскроет ответы на многие термины и вещи, которые могут попадаться при изучении материалов аналитиков. Я сделал свой выбор, буду учиться.