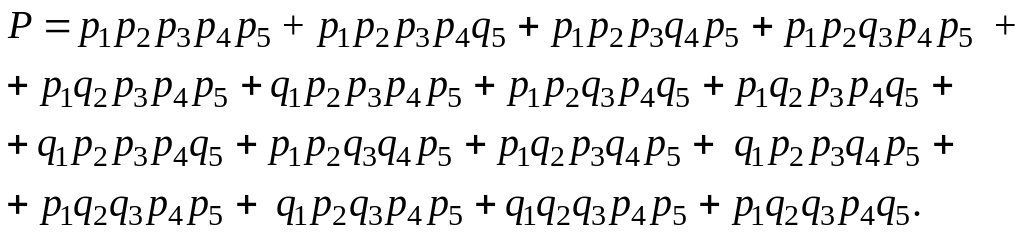Как решать задачи о прохождении тока через электрические схемы
В предыдущих статьях мы разобрали популярные учебные задачи по теории вероятностей: задачи про подбрасывания игральных кубиков и монеток, задачи про стрелков и станки.
В этой статье мы рассмотрим задачи вида
«задана схема электрической цепи с надежностью элементов (или вероятностями выхода из строя), найти вероятность работы цепи (или вероятность разрыва цепи)».
Задачи могут иметь чуть разные формулировки, но принцип решения для них одинаков, и его мы изучим, чтобы суметь решать такие задачи со схемами любой сложности.
Далее:
- Базовые события, обозначения и формулы
- Последовательно или параллельно?
- Усложняем схему цепи
- Примеры решений
- На закуску: схема с мостиком
- Полезные ссылки
- Решебник
Спасибо за ваши закладки и рекомендации
Базовые события, обозначения и формулы
Самое первое, с чего мы начнем — формализация задачи (и решение любой своей задачи рекомендую начинать с этого). А именно, мы введем основные события:
$X$ = (Цепь работает) = (Цепь пропускает ток) и противоположное ему:
$overline{X}$ =(Цепь не пропускает ток) = (Произошел разрыв в цепи).
$A_i$ = (Элемент i работает, пропускает ток) и $overline{A_i}$ =(Элемент i отказал, не пропускает ток), $i=1,2,…,n$.
Обычно в условии задачи известны вероятности работы элементов (надежности): $p(A_i)=p_i$ или вероятности отказа $p(overline{A_i})=q_i=1-p_i$, $i=1,2,…,n$.
Также напомним основные формулы (из темы действий с событиями, формулы сложения и умножения вероятностей), которые пригодятся в решении этого типа задач.
Для независимых в совокупности событий (а отказы/работа элементов цепи — именно такие):
$$
P(A cdot B) = P(A) cdot P(B); quad(1)
$$
$$
P(A+B) = P(A)+P(B)-P(A)cdot P(B); quad(2)
$$
$$
P(A_1+A_2+…+A_n)=1-P(overline{A_1})cdot P(overline{A_2})cdot … cdot P(overline{A_n}). quad(3)
$$
Последовательно или параллельно?
Еще немного времени посвятим теории, вспомним о том, как могут соединяться элементы в цепи.
Последовательное соединение
Элементы цепи «нанизаны» на провод один за другим (следуют один за другим, отсюда и «последовательно»). Если откажет один любой — ток в цепи прервётся. Или, иначе говоря, цепь работает тогда и только тогда, когда ВСЕ элементы работают. В терминах теории вероятностей получаем произведение событий: $X=A_1 cdot A_2 cdot A_3$, а вероятность работы цепи равна
$$
P(X)=P(A_1 cdot A_2 cdot A_3)= P(A_1) cdot P(A_2) cdot P(A_3) =p_1 cdot p_2 cdot p_3.
$$
Если в цепи последовательно соединены не три, а больше независимо работающих элементов, формула легко обобщается и получаем:
$$
P(X) = p_1 cdot p_2 cdot …cdot p_n; qquad P(overline{X})=1-p_1 cdot p_2 cdot …cdot p_n. quad(4)
$$
Параллельное соединение
Тут тоже сама схема дает нам подсказку, когда мы видим, что элементы в схеме расположены как бы на параллельных проводах, речь идет о параллельном соединении.
В этом случае если откажет, скажем, элемент 1, ток может пройти через 2. Если откажут 1 и 2, ток пройдет через 3. И только если ВСЕ элементы откажут, цепь разорвется.
Еще говорят, цепь работает, если работает хотя бы один элемент в ней, в терминах теории вероятностей — это сумма событий: $X=A_1+A_2+A_3$.
Используем формулу (3) чтобы записать вероятность работы такой цепи:
$$
P(A_1+A_2+A_3)=1-P(overline{A_1})cdot P(overline{A_2}) cdot P(overline{A_3})=1-q_1 cdot q_2 cdot q_3.
$$
И обобщим на случай $n$ параллельных элементов в цепи:
$$
P(X) = 1-q_1 cdot q_2 cdot …cdot q_n; qquad P(overline{X})=q_1 cdot q_2 cdot …cdot q_n. quad(5)
$$
Важно запомнить правило
Последовательному соединению соответствует произведение событий,
параллельному соединению — сумма событий.
Усложняем схему цепи
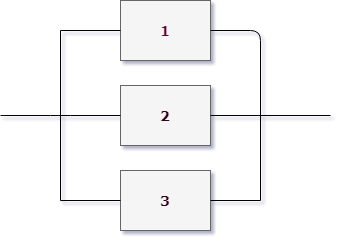
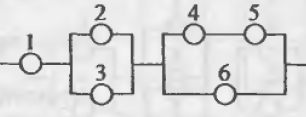
И все это была присказка к настоящему решению задач. Конечно, даже если у вас простая контрольная, схема с «тремя лампочками подряд» вряд ли попадется. Давайте посмотрим на типовые электрические схемы, для которых надо находить надежность в задачах:
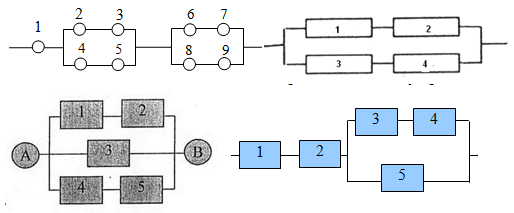
Как для таких схем выписывать вероятности? Нам нужно научиться делать декомпозицию: выделять уровни схемы и определять тип соединения на каждом уровне.
Возьмем для примера левую верхнюю схему:
Работаем с первым уровнем схемы. Нужно мысленно выделить крупные части, которые между собой соединены одинаково (параллельно или последовательно). В данном случае видно три группы элементов, соединенных последовательно. Выделим для наглядности цветом:
То есть тип схемы на первом уровне — последовательный:
Как мы уже знаем, если соединение последовательное, нужно перемножать события, то есть
$$
X=X_1 cdot X_2 cdot X_3,
$$
$X_1$ — работает первая группа элементов,
$X_2$ — работает вторая группа элементов,
$X_3$ — работает третья группа элементов.
Теперь смотрим на каждую группу. В первой группе всего один элемент, то есть она работает, когда работает первый элемент цепи ($X_1=A_1$). Мы дошли до элемента, разбор этой группы закончен.
А вот дальше интереснее. Рассмотрим поближе вторую группу:
В ней сразу выделим цветом подгруппы элементов. Видно, что вторая группа имеет уже параллельную структуру из розовых и фиолетовых элементов (они «висят» на параллельных линиях, это второй уровень вложенности схемы). А вот внутри розовые соединены последовательно (розовая группа работает — $A_4 cdot A_5$), фиолетовые элементы также между собой последовательно (фиолетовая группа работает — $A_2 cdot A_3$). Это уже третий уровень вложенности и он заканчивается отдельными элементами, значит, разбор окончен.
Так как розовая и фиолетовая группа соединены параллельно, речь идет о сумме этих событий, то есть вторая группа работает если:
$$X_2 = A_2 cdot A_3 + A_4 cdot A_5.$$
Абсолютно аналогично разбирается третья подгруппа (она совпадает по структуре со второй):
$$X_3 = A_6 cdot A_7 + A_8 cdot A_9.$$
Сводим все в одну формулу и выпишем искомое событие (Цепь работает исправно):
$$
X=X_1 cdot X_2 cdot X_3 = A_1 cdot left( A_2 cdot A_3 + A_4 cdot A_5 right) cdot left( A_6 cdot A_7 + A_8 cdot A_9right).
$$
Теперь переходим ко второму этапу решения задачи. Не забываем, что мы решаем задачу по теории вероятностей и надо определить вероятность того, что ток проходит в цепи. Будем использовать формулы (1)-(3).
Так как вероятность произведения для независимых событий равна произведению вероятностей, получим:
$$
P(X)= P left( A_1 cdot left( A_2 cdot A_3 + A_4 cdot A_5 right) cdot left( A_6 cdot A_7 + A_8 cdot A_9right) right) =\
= P (A_1) cdot P left ( A_2 cdot A_3 + A_4 cdot A_5 right ) cdot P left( A_6 cdot A_7 + A_8 cdot A_9right) =
$$
Для множителей с суммой событий внутри используем формулу (2):
$$
= P (A_1) cdot left[ P(A_2 cdot A_3) + P(A_4 cdot A_5) — P(A_2 cdot A_3 cdot A_4 cdot A_5) right] cdot left[ P(A_6 cdot A_7) + P(A_8 cdot A_9) — P(A_6 cdot A_7 cdot A_8 cdot A_9)right] =
$$
И снова раскрываем вероятности произведений:
$$
= P (A_1) cdot left[ P(A_2) cdot P(A_3) + P(A_4) cdot P(A_5) — P(A_2) cdot P(A_3) cdot P(A_4) cdot P(A_5) right] cdot left[ P(A_6) cdot P(A_7) + P(A_8) cdot P(A_9) — P(A_6) cdot P(A_7) cdot P(A_8) cdot P(A_9)right].
$$
Перейдем к более компактной записи, положив $p_i=P(A_i)$:
$$
P(X)= p_1 cdot left[ p_2 cdot p_3 + p_4 cdot p_5 — p_2 cdot p_3 cdot p_4 cdot p_5 right] cdot left[ p_6 cdot p_7 + p_8 cdot p_9 — p_6 cdot p_7 cdot p_8 cdot p_9right].
$$
Если заданы надежности отдельных элементов $p_i$, подставляя их в формулу, можно найти вероятность работы схемы.
Алгоритм разбора схемы
- Выделяем в схеме основу: группы элементов, соединенные ТОЛЬКО последовательно или ТОЛЬКО параллельно между собой. Это верхний уровень. Записываем событие $X$ = (Цепь работает) как произведение или сумму соответственно.
- Каждую полученную группу анализируем также: ищем в ней подгруппы, соединенные только последовательно или только параллельно. Записываем событие соответственно типу соединения.
- Продолжаем до тех пор, пока не опустимся на уровень элементов (событий $A_i$).
- Подставляем все выражения в исходную формулу, получаем итоговую запись события $X$.
- Пользуясь формулами (1)-(3) выписываем вероятность события $P=P(X)$.
- Подставляем числовые значения $p_i, q_i$ и находим численное значение надежности схемы $P$.
- Если необходимо, находим вероятность отказа цепи $1-P$.
Примеры решений
Отработаем несколько раз этот алгоритм на примерах, чтобы он закрепился.
Пример 1. Дана схема включения элементов. Вероятность безотказной работы каждого элемента в течение времени Т равна р. Элементы работают независимо и включены в цепь по приведенной схеме. Пусть событие $А_i$ означает безотказную работу за время Т элемента с номером $i$ ($i=1,2,3,…$), а событие $В$ – безотказную работу цепи. Требуется:
1) Написать формулу, выражающую событие $В$ через все события $А_i$.
2) Найти вероятность события $B$.
3) Вычислить $Р(В)$ при $р=0,6$.
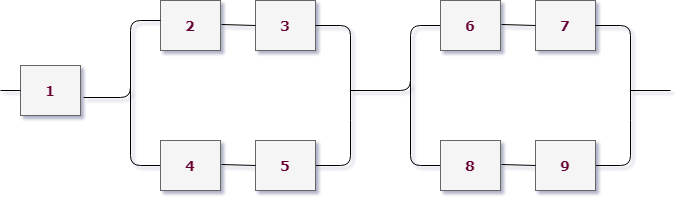
Приступим к разбору схемы. Можно увидеть, что на первом уровне мы имеем три группы, соединенные последовательно: (1), (2,3) и (4,5,6) элементы. Выделим их цветом для наглядности:
Значит, исходное событие можно представить в виде произведения трех событий $B=B_1 cdot B_2 cdot B_3$, где $B_i$ — работает $i$-aя группа элементов.
Первая группа элементов состоит из одного элемента, то есть $B_1=A_1$.
Вторая группа элементов состоит из двух элементов, соединенных параллельно (см. розовые), поэтому $B_2=A_2+A_3$.
Третья группа элементов (см. зеленые) состоит из трех элементов, ее можно представить как параллельное соединение двух подгрупп: (4 и 5, соединены последовательно) и (6), поэтому $B_3=A_4 cdot A_5 + A_6$.
Подставляем все и получаем выражение для события $B$
$$
B=B_1 cdot B_2 cdot B_3 = A_1 cdot (A_2+A_3) cdot (A_4 cdot A_5 + A_6).
$$
Теперь выразим вероятность безотказной работы цепи за время T. Сначала применим формулу (1), чтобы раскрыть произведение:
$$
P(B)=P left( A_1 cdot (A_2+A_3) cdot (A_4 cdot A_5 + A_6) right) = P(A_1) cdot P left( A_2+A_3 right) cdot P left( A_4 cdot A_5 + A_6 right) =
$$
Раскроем вторую вероятность по формуле (3), а третью по формуле (2), получим:
$$= P(A_1) cdot left(1 — P(overline{A_2}) cdot P(overline{A_3}) right) cdot left( P(A_4) cdot P(A_5) + P(A_6) — P(A_4) cdot P(A_5) cdot P(A_6) right).$$
Подставляем $P(A_i)=p$ и получим:
$$
p(B)=pcdot(1-(1-p)cdot(1-p))cdot(pcdot p + p -p cdot p cdot p) = pcdotleft(1-(1-p)^2right)cdot left(p+p^2-p^3right).
$$
Осталось только найти значение при $p=0,6$:
$$
p(B)= 0,6cdotleft(1-(1-0,6)^2right)cdot left(0,6+0,6^2-0,6^3right) approx 0,375.
$$
Пример 2. Найти вероятность обрыва цепи, если вероятность отказа каждого элемента равна 0,2, а отказы элементов – независимые события.
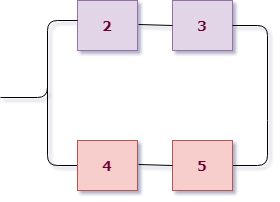
Пронумеруем элементы и сразу раскрасим схему, чтобы выделить ее структуру.
Это опять последовательная схема, но розовая группа состоит из двух элементов, соединенных параллельно, поэтому можем сразу выписать:
$$
X= A_1 cdot (A_2+A_3) cdot A_4 cdot A_5.
$$
Найдем вероятность этого события (работы цепи):
$$
P(X)= P left( A_1 cdot (A_2+A_3) cdot A_4 cdot A_5 right)= P(A_1) cdot P(A_2+A_3) cdot P(A_4) cdot P(A_5)= \
= P(A_1) cdot left( 1- P(overline{A_2}) cdot P(overline{A_3}) right) cdot P(A_4) cdot P(A_5).
$$
Вероятности отказа элементов цепи равна 0,2, вероятность работы элементов — 0,8, поэтому
$$
P(X)= 0,8 cdot left( 1- 0,2 cdot 0,2 right) cdot 0,8 cdot 0,8 = 0,492.
$$
Но в задаче требовалось найти вероятность обрыва цепи, это противоположное событие:
$$
P(overline{X}) = 1- P(X) = 1-0,492 = 0,508.
$$
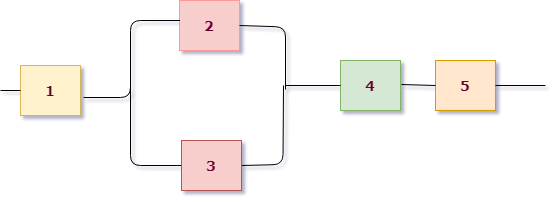
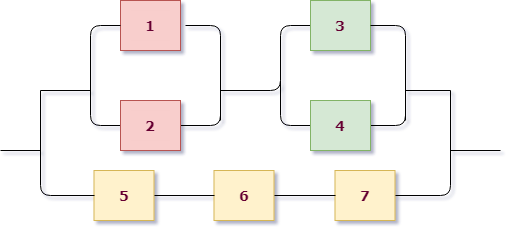
Пример 3. Найти вероятность безотказной работы функциональной цепи, состоящей из независимо работающих элементов, если вероятность надежной работы элементов равна $p_1=p_2=p_3=p_4=0,8$, $p_5=p_6=p_7=0,9$.
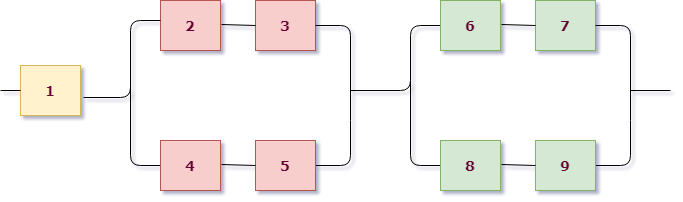
Приступим к решению, сразу раскрасив схему. В этот раз схема на первом уровне имеет параллельное соединение: верхняя розово-зеленая группа и нижняя желтая находятся на параллельных линиях. Поэтому $X=X_1+X_2$, где $X_1$ — работает розово-зеленая линия, $X_2$ — работает желтая.
Для желтой группы, состоящей из трех последовательно расположенных элементов, сразу выписываем $X_2=A_5 cdot A_6 cdot A_7$.
Теперь рассмотрим верхнюю группу. Она состоит из двух подгрупп, связанных последовательно: розовой и зеленой. При этом каждая из них состоит из двух параллельно соединенных элементов. Записываем: розовая группа работает = $A_1+A_2$, зеленая группа работает = $A_3+A_4$, значит ток проходит через розово-зеленую группу $X_1 =(A_1+A_2) cdot (A_3+A_4)$.
Объединяем рассуждения и выписываем событие, соответствующее безотказной работе цепи:
$$
X=X_1+X_2 = (A_1+A_2) cdot (A_3+A_4) + A_5 cdot A_6 cdot A_7.
$$
Следующий шаг: выразить вероятность этого события. Во всех предыдущих примерах схема на первом уровне была последовательной, и событие выражалось как произведение. В этом случае схема на первом уровне параллельна, событие выглядит как сумма других событий, что немного усложняет выкладки. Для суммы событий можно использовать формулу (2) или (3), выбирая наиболее удобную в каждом конкретном случае.
В данном случае слагаемых всего два, поэтому возьмем формулу (2):
$$
P(X)= P left( (A_1+A_2) cdot (A_3+A_4) + A_5 cdot A_6 cdot A_7 right) = \
= P left( (A_1+A_2) cdot (A_3+A_4) right) + P left( A_5 cdot A_6 cdot A_7 right) — P left( (A_1+A_2) cdot (A_3+A_4) cdot A_5 cdot A_6 cdot A_7 right)
$$
Раскрываем все произведения по формуле (1):
$$
= P (A_1+A_2) cdot P(A_3+A_4) + P(A_5) cdot P(A_6) cdot P(A_7) — P (A_1+A_2) cdot P(A_3+A_4) cdot P(A_5) cdot P(A_6) cdot P(A_7) =
$$
По формуле (3) расписываем $P(A_1+A_2)=1-P(overline{A_1}) cdot P(overline{A_2}) = 1-q_1cdot q_2$ и $P(A_3+A_4)=1-P(overline{A_3}) cdot P(overline{A_4})= 1-q_3cdot q_4$.
Итого:
$$
P(X)= (1-q_1cdot q_2) cdot (1-q_3cdot q_4) + p_5 cdot p_6 cdot p_7 — \- (1-q_1cdot q_2) cdot (1-q_3cdot q_4) cdot p_5 cdot p_6 cdot p_7.
$$
Подставляем значения надежности элементов:
$$
P(X)= (1-0,2^2)^2 + 0,9^3 — (1-0,2^2)^2 cdot 0,9^3 approx 0,9788.
$$
Еще: другие уроки о решении задач по вероятности
На закуску: схема с мостиком
Для 99% учебных задач вам хватит той теории и примеров, что приведены выше: подробно изучите их и приступайте к своим примерам по аналогии. Но есть такие схемы, для которых нельзя выделить единую структуру на верхнем уровне — параллельную или последовательную, и весь алгоритм решения рушится.
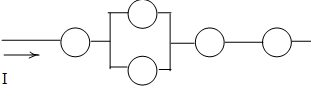
Речь идет о схемах смешанного типа, еще их часто называют схемами с мостиком (мостиковые схемы). Типичная схема имеет такой вид:
Видно, что как ни крути, схему нельзя отнести ни к последовательным, ни к параллельным. Элемент №5 (мостик) «портит» тип схемы. Если его убрать (разорвать этот участок цепи), получим обычную параллельную структуру, а если предположить, что через этот участок всегда идет ток — последовательную (конкретные схемы изобразим ниже).
Поэтому для решения задачи о вычислении надежности подобной электросхемы используют формулу полной вероятности в форме теоремы разложения (см. подробнее тут, стр. 118)
Надежность цепи с избыточностью равна произведению вероятности безотказной работы $i$-го элемента цепи на вероятность безотказной работы оставшейся цепи (места подключения $i$-го элемента замкнуты накоротко) плюс произведение вероятности отказа того же $i$-го элемента на вероятность безотказной работы оставшейся цеии (места подключения $i$-го элемента разомкнуты).
То есть, для выделенного на схеме элемента-мостика рассматриваем две гипотезы:
$H_1$ = (Элемент 5 не пропускает ток), $P(H_1)=1- p_5 = q_5$;
$H_2$ = (Элемент 5 пропускает ток), $P(H_2)=p_5$.
Далее вычисляем надежность схемы при условии верности каждой из гипотез. Для наглядности нарисуем обе схемы:
Рассмотрим левую схему, верную при гипотезе $H_1$, через нее проходит ток, если $X|H_1 = A_1cdot A_3+ A_2cdot A_4$, вероятность
$$
P(X|H_1) = P(A_1cdot A_3+ A_2cdot A_4)= P(A_1cdot A_3)+ P(A_2cdot A_4) — P(A_1cdot A_3 cdot A_2cdot A_4)=\
=p_1 cdot p_3 + p_2 cdot p_4 — p_1 cdot p_2 cdot p_3 cdot p_4.
$$
Рассмотрим правую схему, верную при гипотезе $H_2$, и выпишем для нее аналогично событие и вероятность прохода тока:
$$
X|H_2 = (A_1+A_2)cdot (A_3+A_4),\
P(X|H_2) =P( (A_1+A_2)cdot (A_3+A_4)) = P(A_1+A_2)cdot P(A_3+A_4)=\ = (1-P(overline{A_1}) cdot P(overline{A_2})) cdot (1-P(overline{A_3}) cdot P(overline{A_4})) = (1-q_1cdot q_2) cdot (1-q_3cdot q_4).
$$
Тогда по формуле полной вероятности, надежность схемы равна:
$$
P(X)=P(X|H_1)cdot P(H_1) + P(X|H_2)cdot P(H_2) = \
= q_5 (p_1 cdot p_3 + p_2 cdot p_4 — p_1 cdot p_2 cdot p_3 cdot p_4) + p_5 (1-q_1cdot q_2) cdot (1-q_3cdot q_4).
$$
Аналогичным образом можно разбирать более сложные схемы (в которые более одного мостика), применяя на каждом этапе формулу полной вероятности (как бы вкладывая одну в другую).
Лучшее спасибо — порекомендовать эту страницу
Полезные ссылки по ТВ
|
|
Решебник по вероятности
А здесь вы найдете разные задачи по теории вероятностей с полными решениями (вводите часть текста для поиска своей задачи):
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ АМУРСКОЙ ОБЛАСТИ
государственное
профессиональное образовательное автономное учреждение
«Райчихинский индустриальный
техникум»
Тема: Практическое применение задач по теории
вероятности в электрических схемах
для специальности
Релейная защита и
автоматизация электроэнергетических систем
Преподаватель: Ершова Е. В.
г. Райчихинск
2014г
|
Цели: |
Учебные: · · · Воспитательные: · · Развивающие: · |
|
Формируемые компетенции |
ПК 1.3. Проводить ПК 4.1. Планировать |
Ход урока:
1. Составление опорного
конспекта.
2. Решение задач на определение
вероятности безотказной работы функциональной цепи.
3. Решение задач на определение
вероятности безотказной работы элементов устройства.
4. Решение задач на определение
вероятности безотказной работы сигнализаторов.
5. Практическая работа в парах.
Краткие теоретические сведения
На прошлых уроках вы изучили уроках теоремы сложения и
умножения вероятностей, формулу полной вероятности, научились решать простейшие
задачи с применением теорем.
Сегодня на уроке мы рассмотрим практическое применение задач
по теории вероятностей в электрических схемах.
Надежность каждого элемента системы электроснабжения можно
характеризовать вероятностью рабочего состояния p и вероятностью отказа q. Если не учитывать плановые простои
(ремонты), то можно считать, что элементы в любой момент времени находятся в
одном из этих состояний. Тогда сумма вероятностей этих состояний равна 1: .
Для группы из двух элементов возможны следующие сочетания:
1)
оба
элемента в рабочем состоянии;
2)
первый
элемент в вынужденном простое, второй в рабочем состоянии;
3)
первый
элемент в рабочем состоянии, второй в вынужденном простое;
4)
оба
элемента в вынужденном простое.
Вероятности этих состояний можно найти, воспользовавшись
теоремой умножения вероятностей.
Надежность сложной электрической схемы определяется
надежностью каждого элемента схемы и типом их соединения между собой.
(Перед вами на столах лежат бланки для опорных схем, по
мере объяснения материала вам необходимо заполнить их: зарисовать схему,
записать формулы и их словесное описание (Приложение 1)).
Вид заполненной схемы (Приложение 2).
Так при последовательном соединении двух элементов с
надежностью каждого p1 и p2 надежность всей схемы определяется как
Рис.1
Другими словами схема
работает, если работают оба элемента. При отказе одного (любого) из них схема
работать не будет (ток через цепь не пойдет).
Рис.
2
.
Вероятность отказа для последовательного соединения
(для двух элементов).
, здесь
(для n –элементов).
При
параллельном соединении двух элементов с надежностью каждого р1
и р2 надежность всей схемы определяется как
Пользуясь
формулой для вероятности появления хотя бы одного события, надежность схемы
параллельного соединения записывают в виде
.

Другими словами схема работает, если работают оба элемента, но
также она работает, если выйдет из строя и какой либо один из элементов.
Очевидно, что схема с п параллельно соединенными
элементами будет иметь надежность , здесь
.
Вероятность отказа для параллельного соединения
(для двух элементов).
, здесь
(для n –элементов).
Решение задач совместно преподавателем
Решение задач на определение вероятности безотказной работы
функциональной цепи
Задача 1: Цепь состоит из независимых блоков, соединенных
в систему с одним входом и одним выходом.
рис. 4
Выход из строя за время Т различных элементов цепи — независимые
события, имеющие следующие вероятности: Отказ любого из
элементов приводит к прерыванию сигнала в той ветви цепи, где находится данный
элемент. Найти надежность системы.
Решение: Событие А –
система надежна.
Событие Ai – i-й блок работает
безотказно.
Элементы 1 и 2
соединены параллельно, и элементы 3 и 4 соединены параллельно, а между собой
они соединены последовательно, тогда используя формулы, получим .

рис.5
Элементы А1 и А2 электрической цепи
соединены параллельно, а А3 присоединен к ним
последовательно. Вероятность выхода из строя за данный период времени элементов
А1, А2 и А3 равна соответственно ,
,
.
,
,
.
Предполагается,
что элементы выходят или не выходят из строя независимо друг от друга. Найти
вероятность того, что за рассматриваемый период по цепи будет проходить ток.
Решение: Параллельное соединение элементов А1 и
А2 , работает, если работает хотя бы один из них. Событие А произойдет,
если одновременно с этим работает элемент А3.
Используя формулы, получим .
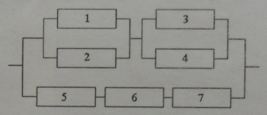
Задача 3. Найти вероятность безотказной работы
функциональной цепи, состоящей из независимо работающих элементов, если
вероятность работы каждого элемента цепи равна p1=0,8, p2= p3=0,7, p4= p5= p6=0,9, p7= p8= p9=0,8
Решение. — надежность работы прибора, т. е. вероятность
того, что ток пройдет через весь прибор.
Событие — сигнал пройдет через участок 1 -2 ,
если будет работать хотя бы один из элементов этого участка, т.е. надежность
этого участка
Событие — сигнал
пройдет через участок 4 -5- 6 , если будет работать хотя бы один из элементов
этого участка, т.е. надежность этого участка
Событие — сигнал пройдет через участок 7 — 8 ,
если будет работать хотя бы один из элементов этого участка, т.е. надежность
этого участка
Событие А состоит
в совмещении событий ,
,
и безотказной работы 3-го и
9-го элементов, т.е. надежность всей системы:
.
Вывод по задаче: Обратите внимание, если элементы цепи
соединены параллельно, то их надежность выше.
Решение задач на определение вероятности безотказной работы элементов
устройства
Задача 4:
Прибор состоит из 3-х узлов, которые за время работы могут
выходить из строя независимо друг от друга. Надежность (вероятность
безотказной работы) i-го узла равна pi, вероятность отказа qi = 1 – pi (i = 1, 2, 3).
p1=0,95; p2=0,98; p3=0,9
Найти вероятности следующих событий: А — все узлы работают
безотказно; В — первый узел отказал, остальные нет; С —
один из узлов отказал, остальные нет; D — отказали два узла из 3-х; E — отказал хотя бы
один узел.
Решение. Пусть Аi -работа i-го узла (i= 1,2,3), — отказ i-го узла.
1) Событие А произойдет, если одновременно произойдут
события . Следовательно,
оно является их произведением:
Применяя к этому равенству событий теорему умножения вероятностей
для независимых событий, получим
.
2) Событие В произойдет, если одновременно произойдут события. Следовательно
Вероятность этого события будет равна
.
3) Событие С может осуществиться, если откажет первый узел,
а остальные два работают или, если откажет второй узел, а работают первый и третий
или, если откажет третий узел, а работают первый и второй. Следовательно, С
— сложное событие, представляющее собой сумму произведений простых
событий:
Применяя к этому равенству сначала теорему сложения вероятностей
для несовместных событий, а затем к каждому слагаемому теорему умножения
вероятностей для независимых событий, получим
4) D — событие, которое может осуществиться тремя различными
способами:
.
Поэтому
5) Для вычисления вероятности события E применим теорему
о вероятности появления хотя бы одного события. Тогда получим
.
Решение
задач на определение вероятности безотказной работы сигнализаторов
Задача 5: Для сигнализации об аварии установлены два независимо работающих
сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна
0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что
при аварии сработает только один сигнализатор.
Решение: A – при аварии сработает только один сигнализатор.
.
.
.
.
Работа в парах
Карточка 1
Задача 1. Найти вероятность безотказной работы функциональной
цепи, состоящей из независимо работающих элементов, если вероятность работы
каждого элемента цепи равна p=0,8.
Задача 2. Устройство состоит из 3 элементов, работающих
независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно
равны: 0,6; 0,7; 0,8. Найти вероятность того, что безотказно будут работать:
а) только один элемент; б) два элемента; в) все три элемента.
Задача 3. Для сигнализации об аварии установлены два независимо
работающих сигнализатора. Вероятность того, что при аварии сигнализатор
сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность
того, что при аварии сработает хотя бы один сигнализатор.
___________________________________________________________________
Карточка 2
Задача 1. Найти вероятность безотказной работы функциональной
цепи, состоящей из независимо работающих элементов, если вероятность работы каждого
элемента цепи равна p=0,9.
Задача 2. Устройство состоит из 3 элементов, работающих
независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно
равны: 0,9; 0,7; 0,8. Найти вероятность того, что безотказно будут работать: а)
только один элемент; б) два элемента; в) все три элемента.
Задача 3. Вероятность того что при аварии сигнализатор
сработает, равна 0,8 для первого сигнализатора и 0,9 для второго. Найти
вероятность того, что при аварии сработает хотя бы один сигнализатор.
Карточка 3
Задача 1. Найти вероятность безотказной работы функциональной
цепи, состоящей из независимо работающих элементов, если вероятность работы
каждого элемента цепи равна p=0,8.
Задача 2: В электрическую цепь последовательно включены 5
элементов, работающих независимо друг от друга. Вероятность отказов первого,
второго, третьего, четвертого, пятого элементов соответственно равны 0,1; 0,2;
0,3; 0,2; 0,1. Найти вероятность того, что тока в цепи не будет.
Задача 3: Для сигнализации об аварии установлены два
независимо работающих сигнализатора. Вероятность того, что при аварии
сработает первый сигнализатор равна 0,7, что сработает второй — равна 0,8.
Найти вероятность того, что сработает только один сигнализатор.
___________________________________________________________________
Карточка 4
Задача 1. Найти вероятность безотказной работы функциональной
цепи, состоящей из независимо работающих элементов, если вероятность работы
каждого элемента цепи равна p=0,8.
Задача 2. Устройство состоит из 3 элементов, работающих
независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно
равны: 0,8; 0,75; 0,8. Найти вероятность того, что безотказно будут работать:
а) только один элемент; б) два элемента; в) все три элемента.
Задача 3: Для сигнализации об аварии установлены два
независимо работающих сигнализатора. Вероятность того, что при аварии
сработает первый сигнализатор равна 0,7, что сработает второй — равна 0,8.
Найти вероятность того, что не сработает ни один сигнализатор.
Карточка 5
Задача 1. Найти вероятность безотказной работы функциональной
цепи, состоящей из независимо работающих элементов, если вероятность работы
каждого элемента цепи равна p=0,9.
Задача 2. Устройство состоит из 3 элементов, работающих
независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно
равны: 0,9; 0,8; 0,85. Найти вероятность того, что безотказно будут работать:
а) только один элемент; б) два элемента; в) все три элемента.
Задача 3: Для сигнализации об аварии установлены два
независимо работающих сигнализатора. Вероятность того, что при аварии
сработает первый сигнализатор равна 0,85, что сработает второй — равна 0,8.
Найти вероятность того, что сработает первый, но не сработает второй.
_________________________________________________________________
Карточка 6
Задача 1. Найти вероятность безотказной работы функциональной
цепи, состоящей из независимо работающих элементов, если вероятность работы
каждого элемента цепи равна p=0,9.
Задача 2. Устройство состоит из 3 элементов, работающих
независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно
равны: 0,95; 0,8; 0,8. Найти вероятность того, что безотказно будут работать:
а) только один элемент; б) два элемента; в) все три элемента.
Задача 3: Для сигнализации об аварии установлены два
независимо работающих сигнализатора. Вероятность того, что при аварии
сработает первый сигнализатор равна 0,85, что сработает второй — равна 0,9.
Найти вероятность того, что сработает хотя бы одни сигнализатор.
Карточка 7
Задача 1. Найти вероятность безотказной работы функциональной
цепи, состоящей из независимо работающих элементов, если вероятность работы
каждого элемента цепи равна p=0,8.
Задача 2. Устройство состоит из 3 элементов, работающих
независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно
равны: 0,85; 0,75; 0,8. Найти вероятность того, что безотказно будут работать:
а) только один элемент; б) два элемента; в) все три элемента.
Задача 3: Для сигнализации об аварии установлены два
независимо работающих сигнализатора. Вероятность того, что при аварии
сработает первый сигнализатор равна 0,95, что сработает второй — равна 0,9.
Найти вероятность того, что сработают оба сигнализатора.
______________________________________________________________________
Карточка 8
Задача 1. Найти вероятность безотказной работы функциональной
цепи, состоящей из независимо работающих элементов, если вероятность работы
каждого элемента цепи равна p=0,8.
Задача 2. Устройство состоит из 3 элементов, работающих
независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно
равны: 0,92; 0,6; 0,8. Найти вероятность того, что безотказно будут работать:
а) только один элемент; б) два элемента; в) все три элемента.
Задача 3: Для информирования про аварию установлены три
независимых между собой сигнализатора. Вероятность того, что во время аварии
сработает первый сигнализатор р1=0,95, второй – р2=0,9,
третий – р3=0,86. Найдите вероятность того, что во время аварии
сработают все три сигнализатора.
Карточка 9
Задача 1. Найти вероятность безотказной работы функциональной
цепи, состоящей из независимо работающих элементов, если вероятность работы
каждого элемента цепи равна p1=0,8,
p2= p3=0,7,
p4= p5= p6=0,9, p7= p8=0,7
Задача 2. Устройство состоит из 3 элементов, работающих
независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно
равны: 0,95; 0,75; 0,8. Найти вероятность того, что безотказно будут работать:
а) только один элемент; б) два элемента; в) все три элемента.
Задача 3: Для сигнализации об аварии установлены два
независимо работающих сигнализатора. Вероятность того, что при аварии
сработает первый сигнализатор равна 0,85, что сработает второй — равна 0,95.
Найти вероятность того, что сработают оба сигнализатора.
_____________________________________________________________
Карточка 10
Задача 1. Найти вероятность безотказной работы функциональной
цепи, состоящей из независимо работающих элементов, если вероятность работы
каждого элемента цепи равна p1=0,9,
p2=p3=0,6,
p4=0,8, p5=p6=0,7,
Задача 2. Устройство состоит из 3 элементов, работающих
независимо. Вероятность безотказной работы 1. 2 и 3-го элемента соответственно
равны: 0,8; 0,9; 0,95. Найти вероятность того, что безотказно будут работать:
а) только один элемент; б) два элемента; в) все три элемента.
Задача 3: Для информирования про аварию установлены три
независимых между собой сигнализатора. Вероятность того, что во время аварии
сработает первый сигнализатор р1=0,95, второй – р2=0,9,
третий – р3=0,86. Найдите вероятность того, что во время аварии
сработает только один сигнализатор.
Дополнительные карточки:
1. Питание
потребителя осуществляется по одной цепи, состоящей из КЛ, трансформатора и
выключателя. Вероятность безотказной работы за время t для этих элементов: . Отказ любого
элемента приводит к перерыву питания, причем отказы взаимно независимы. Найти
вероятность безотказной работы передачи.
2.

Известны
вероятности отказов элементов схемы:
3.
Пусть
вероятность КЗ одной фазы ЛЭП; вероятность КЗ второй фазы
при условии, что одна фаза повреждена, ; вероятность КЗ третьей фазы
при повреждениях первых двух . Требуется определить
вероятность полного выхода ЛЭП из строя.
Домашнее
задание: Выучить
формулы.
Выводы урока: Сегодня на уроке вы научились
решать задачи на нахождение безотказной работы цепи через определение
вероятности ее надежности, расширили и обобщили представление о надежности
электрических цепей. Оценки за работу в парах на следующий урок.
Номер задачи: Tv-47
Решение: бесплатно
В электрическую сеть включены лампочки, соединенный между собой указанным на схеме образом. Вероятность безотказной работы каждой – 0,8. Найти вероятность безотказной работы цепи.
| a) | b) | c) |
 |
 |
 |
|
Посмотреть другие задачи |
Отправить также файл на почту |
|
Заказать / Оценить подобную работу |
Отправить также файл на почту |
1.2.6. Расчет вероятности безотказной работы прибора
Рассмотрим примеры, в которых требуется вычислить вероятностьь безотказной работы и вероятность отказа работы прибора, в состав которого входят несколько элементов и используются различные способы их соединения между собой.
Пример 1.14. Прибор состоит из двух независимо работающих элементов. Вероятность отказа первого элемента равна P1= 0,1, а второго – P2 = 0,2.

Решение: Обозначим через A1 Событие, которое заключается в том, что откажет элемент А1 = , и через A2 —
Тогда данный прибор не будет работать (событие А), если выйдет из строя Хотя бы Один из элементов (или первый, или второй, или оба не будут работать). Такое состояние прибора можно описать, используя Определение суммы событий, т. е. A=A1+A2 . Из теоремы о вероятности суммы двух независимых событий [ формула (***)] получаем
P (A) = p (A1+A2) = p (A1) + p (A2) – p (A1 A2) = p (A1) + p (A2) – p (A1) p (A2) =
= p1+p2 — p1 p2 = 0,1 +0,2 – 0,1*0,2 = 0,28.

Состояние прибора, когда он работает правильно, есть событие А — противоположное событию А, когда прибор откажет.

р (

Решение. Данный прибор откажет в том случае, если Откажут оба элемента Одновременно. Следовательно, отказ прибора в этом случае может быть представлен как Произведение Событий А1 и А2 , т. е. A=A1A2 . Так как элементы перестают работать Независимо друг от друга, то из независимости событий A1 и A2 получаем P(A) = P(A1) P(A2) = P1 P2 = 0,1 * 0,2 = 0,02.
Определение. События A1 A2 ¼ AN называют Взаимно независимыми, если для любой их части 
P(



1<=i1<i2 ¼<im<=n , m=2, ¼,n.

Обозначим вероятность того, что первый элемент оказался бракованным,
Равной P1, второй элемент бракованный — P2, третий элемент бракованный — P3.
Прибор будем считать Бракованным, если хотя бы один из его элементов бракованный. Найти вероятность того, что прибор Стандартный.
Решение: Обозначим события
В данном случае прибор нормально работает в том случае, если все три элемента одновременно работают, т. е. все три элемента, входящие в прибор, стандартные. Тогда работу прибора можно описать как событие А, состоящее из Произведения трех Независимых Событий A=A1*A2*A3 , вероятность которого можно вычислить по формуле вероятности произведения независимых событий
/> />P(A) = P(A1)P(A2)P(A3) =(1 – P1) (1- P2) (1 – P3).

Р ( А) = 1 – Р (А).
Примечание. Рассмотренные примеры 1.13, 1.14 и 1.15 являются аналогом решения контрольной задачи №3 (первого пункта задания) из методических указаний для выполнения контрольных работ.
Рассмотрим некоторые свойства независимых событий.
Свойство7. Если A и B независимы, то 
Свойство 8. Если событие A не зависит от событий B1 и B2, а события B1 и B2 несовместны, тогда события A и B1+ B2 независимы.
Свойство 9. Если события A, A1 и A2 взаимно независимы, тогда события A и A1+ A2 независимы.
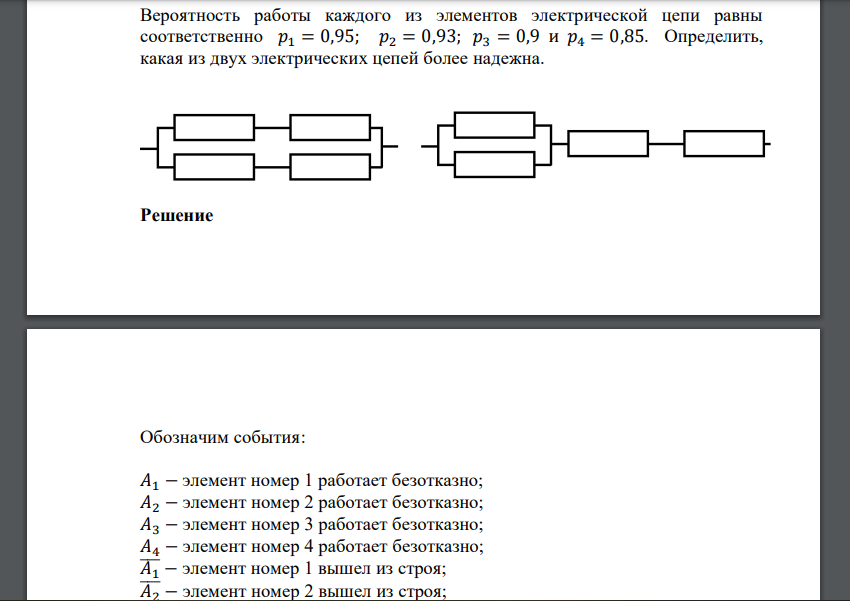
Вероятность работы каждого из элементов электрической цепи равны соответственно 1 = 0,95; 2 = 0,93; 3 = 0,9 и 4 = 0,85. Определить
Обозначим события: 1 − элемент номер 1 работает безотказно; 2 − элемент номер 2 работает безотказно; 3 − элемент номер 3 работает безотказно; 4 − элемент номер 4 работает безотказно; 1 ̅̅̅ − элемент номер 1 вышел из строя; 2 ̅̅̅ − элемент номер 2 вышел из строя; 3 ̅̅̅ − элемент номер 3 вышел из строя; 4 ̅̅̅ − элемент номер 4 вышел из строя. Часть схемы из двух последовательных элементов 1 и 2 исправна только тогда, когда исправны оба этих элемента: Часть схемы из двух параллельных элементов 1 и 2 исправна во всех случаях, кроме одновременной поломки всех элементов: Рассмотрим первую схему. Поскольку не указано, какая из заданных вероятностей к какому из элементов относится, то пронумеруем элементы схемы произвольно.
Похожие готовые решения по математической статистике:
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Telegram и логотип telegram являются товарными знаками корпорации Telegram FZ-LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Как решать задачи о прохождении тока через электрические схемы
В предыдущих статьях мы разобрали популярные учебные задачи по теории вероятностей: задачи про подбрасывания игральных кубиков и монеток, задачи про стрелков и станки.
В этой статье мы рассмотрим задачи вида
«задана схема электрической цепи с надежностью элементов (или вероятностями выхода из строя), найти вероятность работы цепи (или вероятность разрыва цепи)».
Задачи могут иметь чуть разные формулировки, но принцип решения для них одинаков, и его мы изучим, чтобы суметь решать такие задачи со схемами любой сложности.
Базовые события, обозначения и формулы
Самое первое, с чего мы начнем — формализация задачи (и решение любой своей задачи рекомендую начинать с этого). А именно, мы введем основные события:
$X$ = (Цепь работает) = (Цепь пропускает ток) и противоположное ему:
$overline$ =(Цепь не пропускает ток) = (Произошел разрыв в цепи).
$A_i$ = (Элемент i работает, пропускает ток) и $overline$ =(Элемент i отказал, не пропускает ток), $i=1,2. n$.
Обычно в условии задачи известны вероятности работы элементов (надежности): $p(A_i)=p_i$ или вероятности отказа $p(overline)=q_i=1-p_i$, $i=1,2. n$.
Также напомним основные формулы (из темы действий с событиями, формулы сложения и умножения вероятностей), которые пригодятся в решении этого типа задач.
Для независимых в совокупности событий (а отказы/работа элементов цепи — именно такие):
$$ P(A cdot B) = P(A) cdot P(B); quad(1) $$ $$ P(A+B) = P(A)+P(B)-P(A)cdot P(B); quad(2) $$ $$ P(A_1+A_2+. +A_n)=1-P(overline)cdot P(overline)cdot . cdot P(overline). quad(3) $$
Последовательно или параллельно?
Еще немного времени посвятим теории, вспомним о том, как могут соединяться элементы в цепи.
Последовательное соединение
Элементы цепи «нанизаны» на провод один за другим (следуют один за другим, отсюда и «последовательно»). Если откажет один любой — ток в цепи прервётся. Или, иначе говоря, цепь работает тогда и только тогда, когда ВСЕ элементы работают. В терминах теории вероятностей получаем произведение событий: $X=A_1 cdot A_2 cdot A_3$, а вероятность работы цепи равна
$$ P(X)=P(A_1 cdot A_2 cdot A_3)= P(A_1) cdot P(A_2) cdot P(A_3) =p_1 cdot p_2 cdot p_3. $$
Если в цепи последовательно соединены не три, а больше независимо работающих элементов, формула легко обобщается и получаем:
$$ P(X) = p_1 cdot p_2 cdot . cdot p_n; qquad P(overline)=1-p_1 cdot p_2 cdot . cdot p_n. quad(4) $$
Параллельное соединение
Тут тоже сама схема дает нам подсказку, когда мы видим, что элементы в схеме расположены как бы на параллельных проводах, речь идет о параллельном соединении.
В этом случае если откажет, скажем, элемент 1, ток может пройти через 2. Если откажут 1 и 2, ток пройдет через 3. И только если ВСЕ элементы откажут, цепь разорвется.
Еще говорят, цепь работает, если работает хотя бы один элемент в ней, в терминах теории вероятностей — это сумма событий: $X=A_1+A_2+A_3$.
Используем формулу (3) чтобы записать вероятность работы такой цепи:
$$ P(A_1+A_2+A_3)=1-P(overline)cdot P(overline) cdot P(overline)=1-q_1 cdot q_2 cdot q_3. $$
И обобщим на случай $n$ параллельных элементов в цепи:
$$ P(X) = 1-q_1 cdot q_2 cdot . cdot q_n; qquad P(overline)=q_1 cdot q_2 cdot . cdot q_n. quad(5) $$
Важно запомнить правило
Последовательному соединению соответствует произведение событий,
параллельному соединению — сумма событий.
Усложняем схему цепи
И все это была присказка к настоящему решению задач. Конечно, даже если у вас простая контрольная, схема с «тремя лампочками подряд» вряд ли попадется. Давайте посмотрим на типовые электрические схемы, для которых надо находить надежность в задачах:
Как для таких схем выписывать вероятности? Нам нужно научиться делать декомпозицию: выделять уровни схемы и определять тип соединения на каждом уровне.
Возьмем для примера левую верхнюю схему:
Работаем с первым уровнем схемы. Нужно мысленно выделить крупные части, которые между собой соединены одинаково (параллельно или последовательно). В данном случае видно три группы элементов, соединенных последовательно. Выделим для наглядности цветом:
То есть тип схемы на первом уровне — последовательный:
Как мы уже знаем, если соединение последовательное, нужно перемножать события, то есть
$$ X=X_1 cdot X_2 cdot X_3, $$
$X_1$ — работает первая группа элементов,
$X_2$ — работает вторая группа элементов,
$X_3$ — работает третья группа элементов.
Теперь смотрим на каждую группу. В первой группе всего один элемент, то есть она работает, когда работает первый элемент цепи ($X_1=A_1$). Мы дошли до элемента, разбор этой группы закончен.
А вот дальше интереснее. Рассмотрим поближе вторую группу:
В ней сразу выделим цветом подгруппы элементов. Видно, что вторая группа имеет уже параллельную структуру из розовых и фиолетовых элементов (они «висят» на параллельных линиях, это второй уровень вложенности схемы). А вот внутри розовые соединены последовательно (розовая группа работает — $A_4 cdot A_5$), фиолетовые элементы также между собой последовательно (фиолетовая группа работает — $A_2 cdot A_3$). Это уже третий уровень вложенности и он заканчивается отдельными элементами, значит, разбор окончен.
Так как розовая и фиолетовая группа соединены параллельно, речь идет о сумме этих событий, то есть вторая группа работает если:
$$X_2 = A_2 cdot A_3 + A_4 cdot A_5.$$
Абсолютно аналогично разбирается третья подгруппа (она совпадает по структуре со второй):
$$X_3 = A_6 cdot A_7 + A_8 cdot A_9.$$
Сводим все в одну формулу и выпишем искомое событие (Цепь работает исправно):
$$ X=X_1 cdot X_2 cdot X_3 = A_1 cdot left( A_2 cdot A_3 + A_4 cdot A_5 right) cdot left( A_6 cdot A_7 + A_8 cdot A_9right). $$
Теперь переходим ко второму этапу решения задачи. Не забываем, что мы решаем задачу по теории вероятностей и надо определить вероятность того, что ток проходит в цепи. Будем использовать формулы (1)-(3).
Так как вероятность произведения для независимых событий равна произведению вероятностей, получим:
$$ P(X)= P left( A_1 cdot left( A_2 cdot A_3 + A_4 cdot A_5 right) cdot left( A_6 cdot A_7 + A_8 cdot A_9right) right) =\ = P (A_1) cdot P left ( A_2 cdot A_3 + A_4 cdot A_5 right ) cdot P left( A_6 cdot A_7 + A_8 cdot A_9right) = $$
Для множителей с суммой событий внутри используем формулу (2):
$$ = P (A_1) cdot left[ P(A_2 cdot A_3) + P(A_4 cdot A_5) — P(A_2 cdot A_3 cdot A_4 cdot A_5) right] cdot left[ P(A_6 cdot A_7) + P(A_8 cdot A_9) — P(A_6 cdot A_7 cdot A_8 cdot A_9)right] = $$
И снова раскрываем вероятности произведений:
$$ = P (A_1) cdot left[ P(A_2) cdot P(A_3) + P(A_4) cdot P(A_5) — P(A_2) cdot P(A_3) cdot P(A_4) cdot P(A_5) right] cdot left[ P(A_6) cdot P(A_7) + P(A_8) cdot P(A_9) — P(A_6) cdot P(A_7) cdot P(A_8) cdot P(A_9)right]. $$
Перейдем к более компактной записи, положив $p_i=P(A_i)$:
$$ P(X)= p_1 cdot left[ p_2 cdot p_3 + p_4 cdot p_5 — p_2 cdot p_3 cdot p_4 cdot p_5 right] cdot left[ p_6 cdot p_7 + p_8 cdot p_9 — p_6 cdot p_7 cdot p_8 cdot p_9right]. $$
Если заданы надежности отдельных элементов $p_i$, подставляя их в формулу, можно найти вероятность работы схемы.
Алгоритм разбора схемы
- Выделяем в схеме основу: группы элементов, соединенные ТОЛЬКО последовательно или ТОЛЬКО параллельно между собой. Это верхний уровень. Записываем событие $X$ = (Цепь работает) как произведение или сумму соответственно.
- Каждую полученную группу анализируем также: ищем в ней подгруппы, соединенные только последовательно или только параллельно. Записываем событие соответственно типу соединения.
- Продолжаем до тех пор, пока не опустимся на уровень элементов (событий $A_i$).
- Подставляем все выражения в исходную формулу, получаем итоговую запись события $X$.
- Пользуясь формулами (1)-(3) выписываем вероятность события $P=P(X)$.
- Подставляем числовые значения $p_i, q_i$ и находим численное значение надежности схемы $P$.
- Если необходимо, находим вероятность отказа цепи $1-P$.
Примеры решений
Отработаем несколько раз этот алгоритм на примерах, чтобы он закрепился.
Пример 1. Дана схема включения элементов. Вероятность безотказной работы каждого элемента в течение времени Т равна р. Элементы работают независимо и включены в цепь по приведенной схеме. Пусть событие $А_i$ означает безотказную работу за время Т элемента с номером $i$ ($i=1,2,3,…$), а событие $В$ – безотказную работу цепи. Требуется:
1) Написать формулу, выражающую событие $В$ через все события $А_i$.
2) Найти вероятность события $B$.
3) Вычислить $Р(В)$ при $р=0,6$.
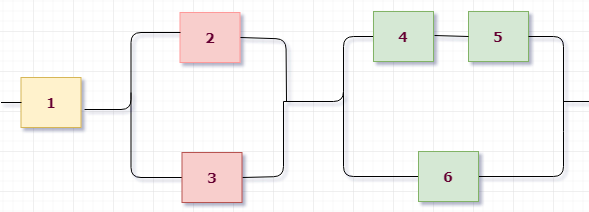
Приступим к разбору схемы. Можно увидеть, что на первом уровне мы имеем три группы, соединенные последовательно: (1), (2,3) и (4,5,6) элементы. Выделим их цветом для наглядности:
Значит, исходное событие можно представить в виде произведения трех событий $B=B_1 cdot B_2 cdot B_3$, где $B_i$ — работает $i$-aя группа элементов.
Первая группа элементов состоит из одного элемента, то есть $B_1=A_1$.
Вторая группа элементов состоит из двух элементов, соединенных параллельно (см. розовые), поэтому $B_2=A_2+A_3$.
Третья группа элементов (см. зеленые) состоит из трех элементов, ее можно представить как параллельное соединение двух подгрупп: (4 и 5, соединены последовательно) и (6), поэтому $B_3=A_4 cdot A_5 + A_6$.
Подставляем все и получаем выражение для события $B$
$$ B=B_1 cdot B_2 cdot B_3 = A_1 cdot (A_2+A_3) cdot (A_4 cdot A_5 + A_6). $$
Теперь выразим вероятность безотказной работы цепи за время T. Сначала применим формулу (1), чтобы раскрыть произведение:
$$ P(B)=P left( A_1 cdot (A_2+A_3) cdot (A_4 cdot A_5 + A_6) right) = P(A_1) cdot P left( A_2+A_3 right) cdot P left( A_4 cdot A_5 + A_6 right) = $$
Раскроем вторую вероятность по формуле (3), а третью по формуле (2), получим:
$$= P(A_1) cdot left(1 — P(overline) cdot P(overline) right) cdot left( P(A_4) cdot P(A_5) + P(A_6) — P(A_4) cdot P(A_5) cdot P(A_6) right).$$
Подставляем $P(A_i)=p$ и получим:
$$ p(B)=pcdot(1-(1-p)cdot(1-p))cdot(pcdot p + p -p cdot p cdot p) = pcdotleft(1-(1-p)^2right)cdot left(p+p^2-p^3right). $$
Осталось только найти значение при $p=0,6$:
$$ p(B)= 0,6cdotleft(1-(1-0,6)^2right)cdot left(0,6+0,6^2-0,6^3right) approx 0,375. $$
Пример 2. Найти вероятность обрыва цепи, если вероятность отказа каждого элемента равна 0,2, а отказы элементов – независимые события.
Пронумеруем элементы и сразу раскрасим схему, чтобы выделить ее структуру.
Это опять последовательная схема, но розовая группа состоит из двух элементов, соединенных параллельно, поэтому можем сразу выписать:
$$ X= A_1 cdot (A_2+A_3) cdot A_4 cdot A_5. $$
Найдем вероятность этого события (работы цепи):
$$ P(X)= P left( A_1 cdot (A_2+A_3) cdot A_4 cdot A_5 right)= P(A_1) cdot P(A_2+A_3) cdot P(A_4) cdot P(A_5)= \ = P(A_1) cdot left( 1- P(overline) cdot P(overline) right) cdot P(A_4) cdot P(A_5). $$
Вероятности отказа элементов цепи равна 0,2, вероятность работы элементов — 0,8, поэтому
$$ P(X)= 0,8 cdot left( 1- 0,2 cdot 0,2 right) cdot 0,8 cdot 0,8 = 0,492. $$
Но в задаче требовалось найти вероятность обрыва цепи, это противоположное событие:
$$ P(overline) = 1- P(X) = 1-0,492 = 0,508. $$
Пример 3. Найти вероятность безотказной работы функциональной цепи, состоящей из независимо работающих элементов, если вероятность надежной работы элементов равна $p_1=p_2=p_3=p_4=0,8$, $p_5=p_6=p_7=0,9$.
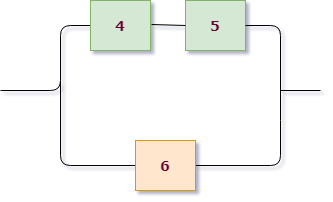
Приступим к решению, сразу раскрасив схему. В этот раз схема на первом уровне имеет параллельное соединение: верхняя розово-зеленая группа и нижняя желтая находятся на параллельных линиях. Поэтому $X=X_1+X_2$, где $X_1$ — работает розово-зеленая линия, $X_2$ — работает желтая.
Для желтой группы, состоящей из трех последовательно расположенных элементов, сразу выписываем $X_2=A_5 cdot A_6 cdot A_7$.
Теперь рассмотрим верхнюю группу. Она состоит из двух подгрупп, связанных последовательно: розовой и зеленой. При этом каждая из них состоит из двух параллельно соединенных элементов. Записываем: розовая группа работает = $A_1+A_2$, зеленая группа работает = $A_3+A_4$, значит ток проходит через розово-зеленую группу $X_1 =(A_1+A_2) cdot (A_3+A_4)$.
Объединяем рассуждения и выписываем событие, соответствующее безотказной работе цепи:
$$ X=X_1+X_2 = (A_1+A_2) cdot (A_3+A_4) + A_5 cdot A_6 cdot A_7. $$
Следующий шаг: выразить вероятность этого события. Во всех предыдущих примерах схема на первом уровне была последовательной, и событие выражалось как произведение. В этом случае схема на первом уровне параллельна, событие выглядит как сумма других событий, что немного усложняет выкладки. Для суммы событий можно использовать формулу (2) или (3), выбирая наиболее удобную в каждом конкретном случае.
В данном случае слагаемых всего два, поэтому возьмем формулу (2):
$$ P(X)= P left( (A_1+A_2) cdot (A_3+A_4) + A_5 cdot A_6 cdot A_7 right) = \ = P left( (A_1+A_2) cdot (A_3+A_4) right) + P left( A_5 cdot A_6 cdot A_7 right) — P left( (A_1+A_2) cdot (A_3+A_4) cdot A_5 cdot A_6 cdot A_7 right) $$
Раскрываем все произведения по формуле (1):
$$ = P (A_1+A_2) cdot P(A_3+A_4) + P(A_5) cdot P(A_6) cdot P(A_7) — P (A_1+A_2) cdot P(A_3+A_4) cdot P(A_5) cdot P(A_6) cdot P(A_7) = $$
По формуле (3) расписываем $P(A_1+A_2)=1-P(overline) cdot P(overline) = 1-q_1cdot q_2$ и $P(A_3+A_4)=1-P(overline) cdot P(overline)= 1-q_3cdot q_4$.
$$ P(X)= (1-q_1cdot q_2) cdot (1-q_3cdot q_4) + p_5 cdot p_6 cdot p_7 — \- (1-q_1cdot q_2) cdot (1-q_3cdot q_4) cdot p_5 cdot p_6 cdot p_7. $$
Подставляем значения надежности элементов:
$$ P(X)= (1-0,2^2)^2 + 0,9^3 — (1-0,2^2)^2 cdot 0,9^3 approx 0,9788. $$
На закуску: схема с мостиком
Для 99% учебных задач вам хватит той теории и примеров, что приведены выше: подробно изучите их и приступайте к своим примерам по аналогии. Но есть такие схемы, для которых нельзя выделить единую структуру на верхнем уровне — параллельную или последовательную, и весь алгоритм решения рушится.
Речь идет о схемах смешанного типа, еще их часто называют схемами с мостиком (мостиковые схемы). Типичная схема имеет такой вид:
Видно, что как ни крути, схему нельзя отнести ни к последовательным, ни к параллельным. Элемент №5 (мостик) «портит» тип схемы. Если его убрать (разорвать этот участок цепи), получим обычную параллельную структуру, а если предположить, что через этот участок всегда идет ток — последовательную (конкретные схемы изобразим ниже).
Поэтому для решения задачи о вычислении надежности подобной электросхемы используют формулу полной вероятности в форме теоремы разложения (см. подробнее тут, стр. 118)
Надежность цепи с избыточностью равна произведению вероятности безотказной работы $i$-го элемента цепи на вероятность безотказной работы оставшейся цепи (места подключения $i$-го элемента замкнуты накоротко) плюс произведение вероятности отказа того же $i$-го элемента на вероятность безотказной работы оставшейся цеии (места подключения $i$-го элемента разомкнуты).
То есть, для выделенного на схеме элемента-мостика рассматриваем две гипотезы:
$H_1$ = (Элемент 5 не пропускает ток), $P(H_1)=1- p_5 = q_5$;
$H_2$ = (Элемент 5 пропускает ток), $P(H_2)=p_5$.
Далее вычисляем надежность схемы при условии верности каждой из гипотез. Для наглядности нарисуем обе схемы:
Рассмотрим левую схему, верную при гипотезе $H_1$, через нее проходит ток, если $X|H_1 = A_1cdot A_3+ A_2cdot A_4$, вероятность
$$ P(X|H_1) = P(A_1cdot A_3+ A_2cdot A_4)= P(A_1cdot A_3)+ P(A_2cdot A_4) — P(A_1cdot A_3 cdot A_2cdot A_4)=\ =p_1 cdot p_3 + p_2 cdot p_4 — p_1 cdot p_2 cdot p_3 cdot p_4. $$
Рассмотрим правую схему, верную при гипотезе $H_2$, и выпишем для нее аналогично событие и вероятность прохода тока:
$$ X|H_2 = (A_1+A_2)cdot (A_3+A_4),\ P(X|H_2) =P( (A_1+A_2)cdot (A_3+A_4)) = P(A_1+A_2)cdot P(A_3+A_4)=\ = (1-P(overline) cdot P(overline)) cdot (1-P(overline) cdot P(overline)) = (1-q_1cdot q_2) cdot (1-q_3cdot q_4). $$
Тогда по формуле полной вероятности, надежность схемы равна:
$$ P(X)=P(X|H_1)cdot P(H_1) + P(X|H_2)cdot P(H_2) = \ = q_5 (p_1 cdot p_3 + p_2 cdot p_4 — p_1 cdot p_2 cdot p_3 cdot p_4) + p_5 (1-q_1cdot q_2) cdot (1-q_3cdot q_4). $$
Аналогичным образом можно разбирать более сложные схемы (в которые более одного мостика), применяя на каждом этапе формулу полной вероятности (как бы вкладывая одну в другую).
Полезные ссылки по ТВ
Решебник по вероятности
А здесь вы найдете разные задачи по теории вероятностей с полными решениями (вводите часть текста для поиска своей задачи):
|
m |
Общее число элементов , n |
||||
|
1 |
2 |
3 |
4 |
5 |
|
|
1 |
|
|
|
|
|
|
2 |
— |
|
|
|
|
|
3 |
— |
— |
|
|
|
|
4 |
— |
— |
— |
|
|
|
5 |
— |
— |
— |
— |
|
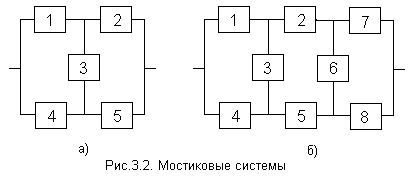
3.4. Мостиковые схемы
Мостиковая структура (рис. 3.2, а, б)
не сводится к параллельному или
последовательному типу соединения
элементов, а представляет собой
параллельное соединение последовательных
цепочек элементов с диагональными
элементами, включенными между узлами
различных параллельных ветвей (элемент
3 на рис. 3.2, а, элементы 3 и 6 на рис. 3.2, б).
Работоспособность такой системы
определяется не только количеством
отказавших элементов, но и их положением
в структурной схеме. Например,
работоспособность ТС, схема которой
приведена на рис. 3.2, а, будет утрачена
при одновременном отказе элементов 1 и
2, или 4 и 5, или 2, 3 и 4 и т.д.. В то же время
отказ элементов 1 и 5, или 2 и 4, или 1, 3 и
4, или 2, 3 и 5 к отказу системы не приводит.
ТТаблица 3.3
Таблица состояний мостиковой
системы
|
сост. |
Состояние элементов |
Состояние системы |
Вероятность состояния |
|||||
|
1 |
2 |
3 |
4 |
5 |
в общем случае |
при равнонадежных элементах |
||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
1 |
+ |
+ |
+ |
+ |
+ |
+ |
|
|
|
2 |
+ |
+ |
+ |
+ |
— |
+ |
|
|
|
3 |
+ |
+ |
+ |
— |
+ |
+ |
|
|
|
4 |
+ |
+ |
— |
+ |
+ |
+ |
|
|
|
5 |
+ |
— |
+ |
+ |
+ |
+ |
|
|
|
6 |
— |
+ |
+ |
+ |
+ |
+ |
|
|
|
7 |
+ |
+ |
+ |
— |
— |
— |
|
|
|
8 |
+ |
+ |
— |
+ |
— |
+ |
|
|
|
9 |
+ |
— |
+ |
+ |
— |
+ |
|
|
|
10 |
— |
+ |
+ |
+ |
— |
+ |
|
|
|
11 |
+ |
+ |
— |
— |
+ |
+ |
|
|
|
12 |
+ |
— |
+ |
— |
+ |
+ |
|
|
|
13 |
— |
+ |
+ |
— |
+ |
+ |
|
|
|
14 |
+ |
— |
— |
+ |
+ |
+ |
|
|
|
15 |
— |
+ |
— |
+ |
+ |
+ |
|
|
|
16 |
— |
— |
+ |
+ |
+ |
— |
|
|
|
17 |
+ |
+ |
— |
— |
— |
— |
|
|
|
18 |
+ |
— |
+ |
— |
— |
— |
|
|
|
19 |
— |
+ |
+ |
— |
— |
— |
|
|
|
Продолжение табл. 3.3 |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
20 |
+ |
— |
— |
— |
+ |
— |
|
|
|
21 |
— |
+ |
— |
— |
+ |
+ |
|
|
|
22 |
— |
— |
— |
+ |
+ |
— |
|
|
|
23 |
+ |
— |
— |
+ |
— |
+ |
||
|
24 |
— |
+ |
— |
+ |
— |
— |
|
|
|
25 |
— |
— |
+ |
— |
+ |
— |
|
|
|
26 |
— |
— |
+ |
+ |
— |
— |
|
|
|
27 |
+ |
— |
— |
— |
— |
— |
|
|
|
28 |
— |
+ |
— |
— |
— |
— |
|
|
|
29 |
— |
— |
+ |
— |
— |
— |
|
|
|
30 |
— |
— |
— |
+ |
— |
— |
|
|
|
31 |
— |
— |
— |
— |
+ |
— |
|
|
|
32 |
— |
— |
— |
— |
— |
— |
|
|
Для расчета надежности мостиковых
систем можно воспользоваться методом
прямого перебора, как это было сделано
для систем “m из n“ (п. 3.3), но при анализе
работоспособности каждого состояния
системы необходимо учитывать не только
число отказавших элементов, но и их
положение в схеме (табл. 3.3). Вероятность
безотказной работы системы определяется
как сумма вероятностей всех работоспособных
состояний:
(3.21)
В случае равнонадёжных элементов
(3.22)
Метод прямого перебора эффективен
только при малом количестве элементов
n, о чем говорилось в начале разд. 3,
поскольку число состояний системы
составляет
.
Например, для схемы на рис. 3.2,б их
количество составит уже 256. Некоторое
упрощение достигается, если в таблицу
состояний включать только сочетания,
отвечающие работоспособному (или только
неработоспособному) состоянию системы
в целом.
Для анализа надежности ТС, структурные
схемы которых не сводятся к параллельному
или последовательному типу, можно
воспользоваться также методом
логических схем с применением алгебры
логики (булевой алгебры). Применение
этого метода сводится к составлению
для ТС формулы алгебры логики, которая
определяет условие работоспособности
системы. При этом для каждого элемента
и системы в целом рассматриваются два
противоположных события — отказ и
сохранение работоспособности.
Для составления логической схемы можно
воспользоваться двумя методами —
минимальных путей и минимальных сечений.
Рассмотрим метод минимальных путей
для расчета вероятности безотказной
работы на примере мостиковой схемы
(рис. 3.2,а).
Минимальным путем называется
последовательный набор работоспо-собных
элементов системы, который обеспечивает
ее работоспособность, а отказ любого
из них приводит к ее отказу.
Минимальных путей в системе может быть
один или несколько. Очевидно, система
с последовательным соединением элементов
(рис. 2.1) имеет только один минимальный
путь, включающий все элементы. В системе
с параллельным соединением (рис. 2.2)
число минимальных путей совпадает с
числом элементов и каждый путь включает
один из них.
Для мостиковой системы из пяти элементов
(рис. 3.2,а) минимальных путей четыре:
(элементы 1 и 4), (2 и 5), (1, 3 и 5), (2, 3 и 5).
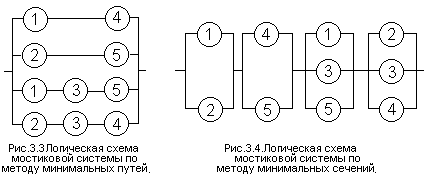
Логическая схема такой системы (рис.
3.3) составляется таким образом, чтобы
все элементы каждого минимального пути
были соединены друг с другом последовательно,
а все минимальные пути параллельно.
Затем для логической схемы составляется
функция алгебры логики А по общим
правилам расчета вероятности безотказной
работы , но вместо символов вероятностей
безотказной работы элементов
и системы Р используются символы
события (сохранения работоспособности
элемента ai и системы А).
Так, “отказ“ логической схемы рис. 3.3
состоит в одновременном отказе всех
четырех параллельных ветвей, а “безотказная
работа” каждой ветви — в одновременной
безотказной работе ее элементов.
Последовательное соединение элементов
логической схемы соответствует
логическому умножению (“И”), параллельное
— логическому сложению (“ИЛИ”).
Следовательно, схема рис. 3.3 соответствует
утверждению: система работоспособна,
если работоспособны элементы 1 и 4, или
2 и 5, или 1,3 и 5, или 2,3 и 4. Функция алгебры
логики запишется:
(3.23)
В выражении (3.23) переменные а
рассматриваются как булевы, т.е. могут
приниматься только два значения: 0 или
1. Тогда при возведении в любую степень
k любая переменная a сохраняет
свое значение:
.
На основе этого свойства функция алгебры
логики (3.23) может быть преобразована к
виду
(3.24)
Заменив в выражении (3.24) символы событий
их вероятностями
,
получим уравнение для определения
вероятности безотказной работы системы
(3.25)
Для системы равнонадёжных элементов
(
)
выражение (3.25) легко преобразуется в
формулу (3.22).
Метод минимальных путей дает точное
значение только для сравнительно простых
систем с небольшим числом элементов.
Для более сложных систем результат
расчета является нижней границей
вероятности безотказной работы.
Для расчета верхней границы вероятности
безотказной работы системы служит метод
минимальных сечений.
Минимальным сечением называется
набор неработоспособных элементов,
отказ которых приводит к отказу системы,
а восстановление работоспособности
любого из них — к восстановлению
работоспособности системы. Как и
минимальных путей, минимальных сечений
может быть несколько. Очевидно, система
с параллельным соединением элементов
имеет только одно минимальное сечение,
включающее все ее элементы (восстановление
любого восстановит работоспособность
системы). В системе с последовательным
соединением элементов число
минимальных путей совпадает с числом
элементов, и каждое сечение включает
один из них .
В мостиковой системе (рис. 3.2, а) минимальных
сечений четыре (элементы 1 и 2), (4 и 5), (1,
3 и 5) , (2, 3 и 4). Логическая схема системы
(рис.3.4) составляется таким образом,
чтобы все элементы каждого мини-мального
сечения были соединены друг с другом
параллельно, а все мини-мальные сечения
— последовательно. Аналогично методу
минимальных путей, составляется функция
алгебры логики. “Безотказная работа”
логической системы рис. 3.4 заключается
в “безотказной работе” всех
последовательных участков, а “отказ”
каждого из них — в одновременном “отказе”
всех парал-лельно включенных элементов.
Как видно, поскольку схема метода
минимальных сечений формулирует условия
отказа системы, в ней последо-вательное
соединение соответствует логическому
“ИЛИ”, а параллельное — логическому
“И”. Схема рис. 3.4 соответствует
формулировке: система отка-жет, если
откажут элементы 1 и 2, или 4 и 5, или 1, 3 и
5, или 2, 3 и 4. Функция алгебры логики
запишется
(3.26)
После преобразований с использованием
свойств булевых переменных (3.26) приобретает
форму (3.24), после замены событий их
вероятностями переходит в выражение
(3.25).
Таким образом, для мостиковой системы
из пяти элементов верхняя и нижняя
границы вероятности безотказной работы,
полученные методами минимальных сечений
и минимальных путей, совпали с точными
значениями (3.22), полученными методом
прямого перебора. Для сложных систем
это может не произойти, поэтому методы
минимальных путей и минимальных сечений
следует применять совместно.
В ряде случаев анализа надежности ТС
удается воспользоваться методом
разложения относительно особого
элемента, основанными на известной
в математической логике теореме о
разложении функции логики по любому
аргументу. Согласно ей, можно
записать:
(3.27)
где
и
— вероятности безотказной работы и
отказа i — го элемента,
и
-вероятности
работоспособного состояния системы
при условии, что i — й элемент абсолютно
надежен и что i — й элемент отказал.
Для мостиковой схемы (рис. 3.2, а) в качестве
особого элемента целесообразно выбрать
диагональный элемент 3. При
мостиковая схема превращается в
параллельно — последовательное соединение
(рис. 3.5, а), а при
—
в последовательно — параллельное (рис.
3.5, б).
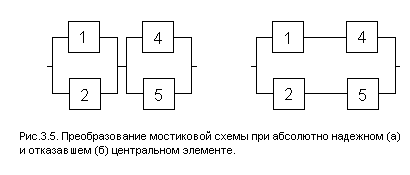
Для преобразованных схем можно записать:
(3.28)
(3.29)
Тогда на основании формулы (3.27) получим:
(3.30)
Легко убедиться, что для равнонадёжных
элементов формула (3.30) об-ращается в
(3.22).
Этим методом можно воспользоваться и
при разложении относительно нескольких
“особых” элементов. Например, для двух
элементов (i, j) выражение (3.27) примет
вид:
(3.31)
Вероятность безотказной работы мостиковой
схемы (рис. 3.2, б) при разложении относительно
диагональных элементов 3 и 6 по (3.31)
определится:
(3.32)
Вероятности
легко ставить, выполнив предварительно
преобразованные схемы, подобно рис.
3.5, а, б.
3.5. Комбинированные системы
Большинство реальных ТС имеет сложную
комбинированную структуру, часть
элементов которой образует последовательное
соединение, другая часть — параллельное,
отдельные ветви элементы или ветви
структуры образуют мостиковые схемы
или типа “m из n”.
Метод прямого перебора для таких
систем оказывается практически не
реализуем. Более целесообразно в этих
случаях предварительно произвести
декомпозицию системы, разбив ее на
простые подсистемы — группы элементов,
методика расчета надежности которых
известна. Затем эти подсистемы в
структурной схеме надежности заменяются
квазиэлементами с вероятностями
безотказной работы, равными вычисленным
вероятностям безотказной работы этих
подсистем. При необходимости такую
процедуру можно выполнить несколько
раз, до тех пор, пока оставшиеся
квазиэлементы не образуют структуру,
методика расчета надежности которой
также известна.
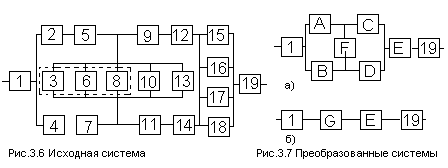
В качестве примера рассмотрим
комбинированную систему, представленную
на рис. 3.6. Здесь элементы 2 и 5, 4 и 7, 9 и
12, 11 и 14 попарно образуют друг с другом
последовательные соединения. Заменим
их соответственно квазиэлементами А,
В, С, Д, для которых расчет надежности
элементарно выполняется по формулам
п. 3.1. Элементы 15, 16, 17 и 18 образуют
параллельное соединение (п. 3.2), а элементы
3, 6, 8, 10 и 13 — систему “3 из 5” (п. 3.2).
Соответствующие квазиэлементы обозначим
E и F. В результате преобразованная схема
примет вид, показанный на рис. 3.7, а. В
ней в свою очередь элементы А, В, С, Д, F
образуют мостиковую схему (п. 3.4), которую
заменяем квазиэлементом 6. Схема,
полученная после таких преобразований
(рис.3.7,б), образует последовательное
соединение элементов 1, G, E, 19, для которых
справедливы соотношения п. 3.1. Отметим,
что метод прямого перебора для исходной
системы потребовал бы рассмотреть
возможных состояний.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #