Как найти вероятность события а при условии

Случайное событие определено как событие, которое при осуществлении совокупности условий эксперимента может произойти или не произойти. Если при вычислении вероятности события никаких других ограничений, кроме условий эксперимента, не налагается, то такую вероятность называют безусловной; если же налагаются и другие дополнительные условия, то вероятность события называют условной. Например, часто вычисляют вероятность события $B$ при дополнительном условии, что произошло событие $А$.

Условной вероятностью $P_A(B)=P(B|A)$ (два обозначения) называют вероятность события $В$, вычисленную в предположении, что событие $А$ уже наступило.

Вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность второго, вычисленную при условии, что первое событие произошло, т.е.

$$P(AB)=P(B)cdot P(A|B) = P(A) cdot P(B|A).$$

В частности, отсюда получаем формулы для условной вероятности:

$$P(A|B)=frac{P(AB)}{P(B)}, quad P(B|A)=frac{P(AB)}{P(A)}.$$

Примеры решений на условную вероятность

Случайное
событие определено как событие, которое
при осуществлении совокупности условий
эксперимента может произойти или не
произойти. Если при вычислении вероятности
события никаких других ограничений,
кроме условий эксперимента, не налагается,
то такую вероятность называют безусловной;
если же налагаются и другие дополнительные
условия, то вероятность события
называют условной.
Например, часто вычисляют вероятность
события В при
дополнительном условии, что произошло
событие А.

Условной
вероятностью (два
обозначения) называют вероятность
события В,
вычисленную в предположении, что
событие А уже
наступило.

Вероятность совместного
появления двух зависимых событий равна
произведению вероятности одного из
них на условную вероятность второго,
вычисленную при условии, что первое
событие произошло, т.е.

.

В
частности, отсюда получаем 
.

Пример. В
урне находятся 3 белых шара и 2 черных.
Из урны вынимается один шар, а затем
второй. Событие В –
появление белого шара при первом
вынимании. Событие А –
появление белого шара при втором
вынимании.

Решение. Очевидно,
что вероятность события А,
если событие В произошло,
будет 
. 
Вероятность
события А при
условии, что событие В не
произошло, будет 
.

Пример. В
урне 3 белых и 3 черных шара. Из урны
дважды вынимают по одному шару, не
возвращая их обратно. Найти вероятность
появления белого шара при втором
испытании (событие В), если при первом
испытании был извлечен черный шар
(событие А).

Решение.
После первого испытания в урне осталось
5 шаров, из них 3 белых. Искомая условная
вероятность .

Этот
же результат можно получить по формуле
.

Действительно,
вероятность появления белого шара при
первом испытании
.

Найдем
вероятность того,
что в первом испытании появится черный
шар, а во втором — белый. Общее число
исходов — совместного появления двух
шаров, безразлично какого цвета, равно
числу размещений .
Из этого числа исходов
событию благоприятствуют исходов.
Следовательно, .

Искомая
условная вероятность 

Результаты
совпали.

Пример. В
трамвайном парке имеются 15 трамваев
маршрута №1 и 10 трамваев маршрута №2.
Какова вероятность того, что вторым по
счету на линию выйдет трамвай маршрута
№1?

Решение.
Пусть А —
событие, состоящее в том, что на линию
вышел трамвай маршрута №1, В —
маршрута №2.

Рассмотрим
все события, которые могут при этом
быть (в условиях нашей задачи): .
Из них нас будут интересовать только
первое и третье, когда вторым выйдет
трамвай маршрута №1.

Так
как все эти события совместны, то:

;

;

отсюда
искомая вероятность

Пример. Какова
вероятность того, что 2 карты, вынутые
из колоды в 36 карт, окажутся одной масти?

Решение.
Сначала подсчитаем вероятность того,
что две карты окажутся одной определенной
масти (например «пики»). Пусть А —
появление первой карты такой масти, В—
появление второй карты той же масти.
Событие В зависит
от события А,
т.к. его вероятность меняется от того,
произошло или нет событие А.
Поэтому придется воспользоваться
теоремой умножения в ее общей форме:

, 
где (после
вынимания первой карты осталось 35 карт,
из них той же масти, что и первая — 8).

Получаем 
.

События,
состоящие в том, что будут вынуты две
карты масти «пики», масти «треф» и т.д.,
несовместны друг с другом. Следовательно,
для нахождения вероятности их объединения
воспользуемся теоремой сложения:
.

Соседние файлы в папке 3 Семестр ИНФ

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

 Условная вероятность. Формула Байеса

Условная вероятность является одним из важнейших понятий теории вероятностей.

Условная вероятность — вероятность наступления события А при условии, что событие В произошло.

Вероятность события А, вычисленная в предположении, что событие В уже произошло, обозначается .

Прежде чем привести формулу, позволяющую вычислить условную вероятность, проиллюстрируем это понятие с помощью кругов Эйлера:

Пусть для некоторого эксперимента красный круг обозначает множество всех возможных исходов. Зеленый круг обозначает множество исходов, благоприятствующих событию , синий круг обозначает множество исходов, благоприятствующих событию , область, лежащая в пересечении этих кругов обозначает множество исходов, благоприятствующих обоим событиям  и , обозначим его .

Как мы знаем, вероятностью события называется отношение числа благоприятных исходов к числу всех возможных исходов.

То есть вероятность события показывает, какую часть благоприятные исходы составляют от всех возможных исходов.

Если мы вычисляем вероятность события в предположении, что событие уже произошло (то есть условную вероятность), то в этом случае для нас множество исходов, благоприятствующих событию событию  окажется множеством всех возможных исходов, а благоприятными исходами будут те исходы, которые при этом еще благоприятствуют событию . То есть нам нужно найти, какую часть число исходов, благоприятствующих событиям  и  составляет от числа исходов, благоприятствующих событию .

Пусть , где — число исходов, благоприятствующих событию , — число всех возможных исходов. ( В нашей иллюстрации  — число элементов множества )

Пусть , где — число исходов, благоприятствующих событию , — число всех возможных исходов. ( В нашей иллюстрации  — число элементов множества )

Пусть , где — число исходов, благоприятствующих событиям  и , — число всех возможных исходов. ( В нашей иллюстрации  — число элементов множества , которое является пересечением множеств и ).

Тогда

Но по определению условной вероятности , следовательно

(1)

Заметим, что аналогично получим формулу для нахождения вероятности наступления события   при условии, что событие  произошло:

(2)

Очевидно, что 

Формулы (1) и (2) для нахождения условной вероятности по сути одна и та же формула, это и есть формула Байеса.

Рассмотрим примеры задач на условную вероятность.

Пример 1. На фабрике керамической посуды 10% произведённых тарелок имеют дефект. При контроле качества продукции выявляется 80% дефектных тарелок. Остальные тарелки поступают в продажу. Найдите вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов. Результат округлите до сотых.

Решение.

В задаче описана следующая ситуация: при производстве посуды часть тарелок имеют дефект. Но контроль качества отбраковывает не все дефектные тарелки, а только 80% из них, остальные (20%) поступают в продажу.

Нам нужно найти вероятность того, что  что случайно выбранная при покупке тарелка не имеет дефектов. То есть нас интересует какая часть из всех тарелок, которые поступили в продажу, не имеют дефекта.

Нарисуем дерево вероятностей:

Красными веточками обозначены тарелки, которые поступили в продажу. Это тарелки без дефектов (они составляют 0,9 от всех тарелок) и тарелки с дефектами, которые пропустила система контроля. Их от всех тарелок.

Таким образом, вероятность того, что тарелка поступила в продажу равна . При этом вероятность того, что тарелка не имеет дефектов равна .

Следовательно, вероятность того, что случайно выбранная при покупке тарелка не имеет дефектов равна

Ответ: 0,98.

Пример 2.

40% пакетов с молоком производят на молочном комбинате в Л., а остальные на молокозаводе в С. Известно, что в среднем 3% пакетов, поступивших в продажу протекают, а среди пакетов, изготовленных в Л. протекают в среднем 5%.

а) Найдите вероятность того, что протекающий пакет изготовлен на заводе в С.

б) Найдите вероятность того, что пакет, изготовленный на заводе в С протекает. 

Решение. Нам нужно найти вероятность того, что протекающий пакет изготовлен на заводе в С. То есть нам нужно найти, какая часть из всех протекающих пакетов изготовлена на заводе в С. По условию задачи всего протекает 3%, то есть 0,03 часть всех пакетов. Пусть среди пакетов, изготовленных на заводе в С. протекает %.

Нарисуем дерево вероятностей:

Красными веточками обозначены пакеты, которые протекают. При этом на заводе в Л. изготовлено всех протекающих пакетов. На заводе в С. изготовлено   от всех протекающих пакетов.

Получаем , отсюда . То есть вероятность того, что пакет, изготовленный на  заводе в С.  протекает, равна . Получим, что на заводе в С. изготовлено от всех протекающих пакетов. Это число мы могли бы получить, если бы из части всех протекающих пакетов (0,03) вычли бы часть протекающих пакетов, изготовленных на заводе в Л. (0,02). (Мы бы так и поступили, если бы нужно было бы ответить только на п. а) задачи)

Тогда вероятность того, что протекающий пакет изготовлен на заводе в С. равна .

Ответ: а)  , б) .

Часть 1, Часть 2, Часть 3, Часть 4, Часть 5

---

Условная вероятность

Условная вероятность — это вероятность наступления некоторого события, при условии, что другое событие уже произошло.

Условная вероятность обозначается через P(A|B), которое читается как «вероятность А при условии В». Она вычисляется по формуле:

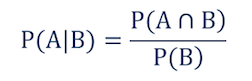
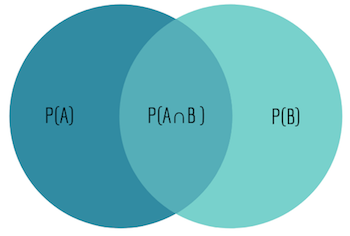
A ∩ B — это пересечение событий А и В на диаграмме Венна. Таким образом, P(A∩B) — это вероятность того, что оба события — А и В — произойдут. 
Следовательно:

Вероятность события А при условии В равно вероятности событий А и В, деленной на вероятность В.

---

Пример:

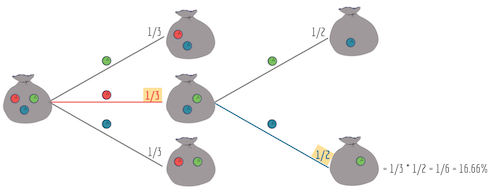
Предположим, из мешка достают три шарика: красный, зеленый и синий.

Какова условная вероятность того, что после красного шарика из мешка достанут синий?

Если событие А — это событие, при котором первым достают красный шарик, а событие В — это событие, при котором достают синий шарик, то нам нужно найти P(A∩B):

• P(A) — это вероятность того, что в первую очередь достанут красный шарик. Так как это один из трех возможных результатов, то далее мы имеем:

P(A) = 1/3 = 33.33%

• P(B|A) — это вероятность того, что вторым достанут синий шарик. Так как у нас останется два шарика, то получается:

P(B) = 1/2 = 50%

• P(A ∩ B) — это вероятность того, что первым достанут красный шарик, а вторым — синий:

P(A ∩ B) = P(A) * P(B|A) = 33.33% * 50% = 16.66%

Для визуализации воспользуемся древовидной диаграммой: у каждой ветки есть условная вероятность

---

Причинно-следственная связь

Причинно-следственная связь описывается в четвертой части. Условная вероятность не указывает на то, что между данными двумя события обязательно существует причинно-следственная связь, а также на то, что два события произойдут одновременно.

Независимые события

Независимыми называются такие события, исход которых не влияет на вероятность исхода другого события. Следовательно:

P(A|B) = P(A)
P(B|A) = P(B)

Взаимоисключающие события

Взаимоисключающими называются такие события, которые не могут произойти одновременно, т.е. если одно событие уже произошло, то другое произойти не может. Следовательно:

P(A|B) = 0
P(B|A) = 0

---

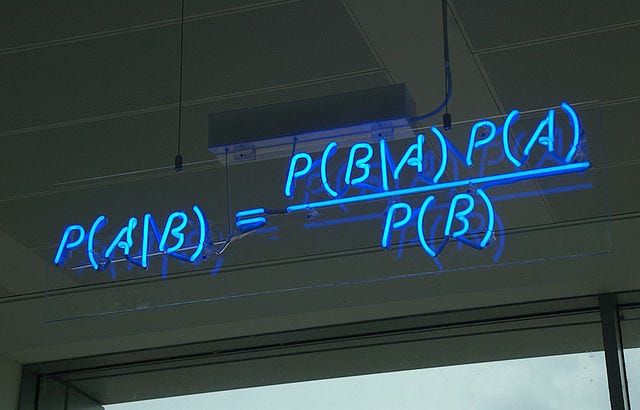
Теорема Байеса

После условной вероятности, давайте рассмотрим теорему Байеса. Она гласит:

Вероятность события А при условии В равна вероятности события В при условии А, умноженной на вероятность события А и деленной на вероятность В.

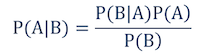
Другими словами, она позволяет удобно найти зависимость P(A|B) и P(B|A) друг от друга.

Теорема Байеса является фундаментом целого направления в статистике («Байесовская статистика»). Она применяется во многих дисциплинах, например, ярким примером служит медицинская и фармакологическая сферы, а также финансовая (для прогноза вероятности успеха каких-либо вложений).

Количество почти так же важно, как и качество, при применении этих условных переменных к теореме Байеса. Например, необходимо просчитать риск кредитования заемщика. Если учесть другие вероятности, такие как возраст заемщика, его кредитоспособность и готовность к принятию риска, то возможность получения кредита для разных лиц может отличаться.

Теорема допускает следующее:

Чем больше переменных учитывается и чем больше в нас уверенности в переменных, тем точнее будет вывод при использовании условных вероятностей.

---

Пример:

Представим, что мы врачи некоторой больницы и мы знаем следующее: — вероятность того, что у пациента заболевание печени, равна 20%; — вероятность того, что пациент болен алкоголизмом — 5%; вероятность того, что среди тех пациентов, у которых диагностировали заболевание печени, есть больные алкоголизмом — 10%. Теперь найдем:

Какова условная вероятность того, что пациент с заболеванием печени — болен алкоголизмом?

• P(A) — вероятность наличия заболевания печени:

P(A) = 20%

• P(B) — вероятность того, что пациент болен алкоголизмом:

P(B) = 5%

• P(B|A) — условная вероятность того, что пациент болен алкоголизмом при условии заболевания печени:

P(B|A) = 10%

• P(A|B) — это условная вероятность того, что у пациента заболевание печени при условии, что он болен алкоголизмом:

P(A|B) = (10% * 20%) / 5% = 40%

---

Взаимоисключающие события

Частным случаем теоремы Байеса является то, когда событие А — это двоичное значение. В таком случае «А-» обозначает то, что событие А произошло, и «А+» — не произошло (т.е. события А- и А+ являются взаимоисключающими) 
 Формула:

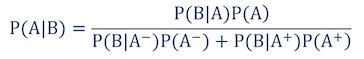
Точность

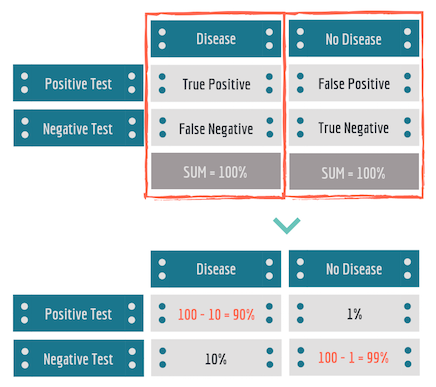
Истинно положительный случай — это результат, при котором модель правильно прогнозирует положительный класс. Так же истинно отрицательный случай — это результат, при котором модель правильно прогнозирует отрицательный класс.

Ложноположительный случай — это результат, при котором модель неправильно прогнозирует положительный класс. Так же ложноотрицательный случай — это результат, при котором модель неправильно прогнозирует отрицательный класс.

Чувствительность показывает вероятность того, что тест правильно спрогнозирует положительный класс → истинно положительные случаи.

Специфичность показывает вероятность того, что тест правильно спрогнозирует отрицательный класс → истинно отрицательные случаи.

Чувствительность = истинно положительные случаи / (истинно положительные + ложнооттрицательные) 
Специфичность = истинно отрицательные случаи / (истинно отрицательные + ложноположительные)

---

Пример:

Предположим, что определенное заболевание имеет коэффициент заболевания 2%. Если ложноотрицательный коэффициент равен 10%, а ложноположительный — 1%, то:

Какова условная вероятность того, что человек с положительным результатом теста на самом деле болен?

Если событие А — это событие, при котором человек болен, а событие В — это событие, при котором результаты теста положительны, то необходимо вычислить P(A|B), т.е. несмотря на положительный результат теста (В), человек окажется болен (А).

• P(A+) или P(A) — это вероятность наличия заболевания:

P(A+) = 2%

• P(A–) — это вероятность отсутствия заболевания, которая высчитывается следующим образом:

P(A-) = 100% - 2% = 98%

• P(B|A–) — это вероятность ложноположительного случая, т.е. человек здоров (А-), но результат теста положительный (В):

P(B|A-) = 1%

• P(B–|A) — это вероятность ложноотрицательного случая, т.е. человек болен (А), но результат теста отрицательный (В-):

P(B-|A) = 10%

• P(B|A+) или P(B|A) — это истинно положительный случай, т.е. человек болен (А) и результат теста положительный (В). Высчитывается это следующим образом:

P(B|A) = 100% - 10% = 90%

• Теперь у нас есть вся необходимая информация, чтобы найти P(A|B):

P(A|B) = [ P(B|A) x P(A) ] / [ P(B|A-) x P(A-) + P(B|A+) x P(A+) ]
       = [ 90% x 2% ] / [ 1% x 98% + 90% x 2% ] =
       = 64.7%

Для визуализации точности теста можно использовать матрицу:

И древовидную диаграмму:

---

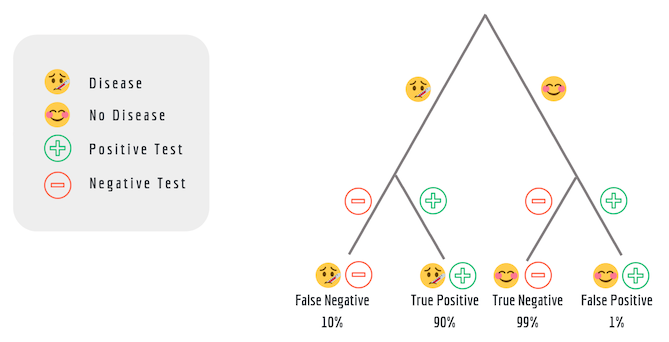
Конец

---

Перевод статьи Semi Koen: Statistics is the Grammar of Data Science — Part 5/5

Алгебра и начала математического анализа, 11 класс

Урок №34. Условная вероятность. Независимость событий.

Перечень вопросов, рассматриваемых в теме:

— Условная вероятность

— Совместные и несовместные события

— Схема решения задач на вычисление условной вероятности события;

— Задачи на определение независимости событий.

Глоссарий по теме

Совместные события – события, одновременное появление которых возможно.

Несовместные события – события, одновременное появление которых невозможно.

События являются независимыми, если вероятность наступления любого из них не зависит от появления остальных событий рассматриваемого множества событий.

Событие В называется зависимым, если вероятность P(B) зависит от появления или непоявления события А. Вероятность события В, вычисленная в предположении того, что событие А уже произошло, называется условной вероятностью наступления события В и обозначается P_A(B).

Условная вероятность – вероятность наступления одного события при условии, что другое событие уже произошло.

Основная литература:

Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014. с. 186-194.

Открытые электронные ресурсы:

Решу ЕГЭ образовательный портал для подготовки к экзаменам https://ege.sdamgia.ru/.

Открытый банк заданий ЕГЭ ФИПИ, Элементы комбинаторики, статистики и теории вероятностей, базовый уровень. Элементы комбинаторики, статистики и теории вероятностей. Базовый уровень. http://ege.fipi.ru/.

Теоретический материал для самостоятельного изучения

Иногда нам требуется выяснить вероятность совместного появления зависимых событий. Самый простой пример – найти вероятность получить выигрышную комбинацию в азартной карточной игре, где вероятность выпадения каждой новой карты зависит от того, какие карты уже лежат на столе.

Рассмотрим примерную задачу:

Из колоды карт извлекают четыре карты. Первые две оказались семёрками. Какова вероятность, что одна или обе оставшиеся карты окажутся семёрками? (колода содержит 36 карт)

1. 1/561

2. 65/561

3. 1/105

4. 17/518

Теоретическая часть

События называются совместными, если появление одного из них не исключает появления другого в одном и том же испытании.

Пример совместных событий: выпадение чётного числа и выпадение числа, кратного трём, при броске игрального кубика. Когда выпадает шесть, реализуются сразу оба события.

События называются несовместными, если появление одного из них исключает появление другого в одном и том же испытании.

Пример несовместных событий: выпадение чётного числа и выпадение нечётного числа при броске игрального кубика.

Теорема о сумме двух событий:

Вероятность суммы любых двух событий А и В равна сумме вероятностей этих событий без вероятности их совместного осуществления: Р(А+В) = Р(А)+Р(В)-Р(АВ)

Рассмотрим пример.

В лотерее выпущено 10 000 билетов, из них: 10 выигрышей по 200 рублей, 100 выигрышей по 100 рублей, 500 выигрышей по 50 рублей и 1000 выигрышей по 10 рублей. Какова вероятность того, что человек, купивший билет, выиграет не менее 50 рублей?

Решение: Введем для удобства обозначение событий А — «человек выиграл 50 рублей», В — «человек выиграл 100 рублей», С — «человек выиграл 200 рублей», D — «человек выиграл не менее 50 рублей». Событие D означает, что выигрыш может составлять 50 и более рублей, то есть 50, 100 или 200 рублей: М=А+В+С. События А, В, С – попарно несовместны.

Воспользуемся теоремой: Р(М)=Р(А)+Р(В)+Р(С)=0,061.

Задача.

Дана вероятность исходного события. Чему равна вероятность противоположного события?

Вероятность исходного события А обозначим Р(А). Вероятность противоположного события Р(Ᾱ).

Решение:

События А и Ᾱ образуют полную группу событий, вероятность которой равна 1.

Тогда вероятность противоположного события находится по формуле:

P(Ᾱ)=1-P(A)

1. События являются независимыми, если вероятность наступления любого из них не зависит от появления остальных событий рассматриваемого множества событий.

Например, монета брошена два раза.

A – выпала «Решка»

B – выпал «Орёл»

Вероятность появления «Орла» во втором испытании не зависит от результата первого испытания.

Теорема умножения вероятностей независимых событий: вероятность совместного появления независимых событий A и B равна произведению вероятностей этих событий:

Р(АВ)=Р(А)·Р(В)

Рассмотрим пример.

Задача.

Подбрасываются две монеты. Найдите вероятность выпадения двух орлов.

Решение:

Введем обозначение событий:

A₁– на 1-й монете выпадет орёл;

A₂– на 2-й монете выпадет орёл.

Событие “выпадение двух орлов” заключается в том, что на 1-й монете появится орёл и на 2-й монете появится орёл, следовательно, это произведение событий A₁A₂. Вероятность выпадения орла на одной монете не зависит от результата броска другой монеты, следовательно, события A₁ и A₂ независимы. По теореме умножения вероятностей независимых событий получим:

P(A₁A₂) = P(A₁)· P(A₂) = 1/2 · 1/2 = 1/4.

1. Событие B называется зависимым, если вероятность P(B) зависит от появления или непоявления события А. Вероятность события B, вычисленная в предположении того, что событие А уже произошло, называется условной вероятностью наступления события В  и обозначается P_A(B).

Отыскать вероятность совместного появления зависимых событий помогает теорема умножения вероятностей зависимых событий: вероятность совместного появления двух зависимых событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже произошло: P(AB) = P(A)·P_A(B).

Связь теории вероятностей с теорией множеств.

В математике принято устанавливать связи между различными разделами. Связь между теорией вероятностей и теорией множеств устанавливается следующим образом: события отождествляются с множествами. В таком случае понятию исход будет эквивалентно понятие элемент множества. При таком подходе выберите из списка, какому понятию из теории множеств соответствует данное понятие из теории вероятностей:

— Невозможное событие (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)

— Сумма событий (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)

— Произведение событий (подмножество, бесконечное множество, пустое множество, пересечение множеств, объединение множеств, разность множеств, декартово произведение множеств)

Примеры и разбор решения заданий тренировочного модуля

1. В урне 6 черных, 5 красных и 4 белых шара. Последовательно извлекают три шара без возврата. Найдите вероятность того, что первый шар окажется черным, второй – красным и третий – белым.

Решение.

А – первый шар окажется черным

В — второй шар красный

С — третий шар белый

. 

Ответ: 4/91.

2. Колю отпускают гулять при условии сделанных уроков с вероятностью 0,8. Папа выдает ему деньги на мороженое с вероятностью 0,6. С какой вероятностью Коля пойдет гулять без мороженого?

Решение.

A – папа выдал Коле денег на мороженое

B – Колю отпустили гулять

Вероятность того, что Коля пойдёт гулять, есть в условии задачи P(B) = 0,8. Вероятность, что папа не выдаст ему деньги на мороженое, равна P(Ᾱ) = 1 – P(A) = 1 – 0,6 = 0,4. Вероятность одновременного осуществления двух независимых событий – произведение их вероятностей P(ᾹB) = P(Ᾱ)·P(B) = 0,8·0,4 = 0,32.

Ответ: 0,32.