Как найти вероятность в математике игральные кости

Решение задач о бросании игральных костей

Еще одна популярная задача теории вероятностей (наравне с задачей о подбрасывании монет) — задача о подбрасывании игральных костей.

Обычно задача звучит так: бросается одна или несколько игральных костей (обычно 2, реже 3). Необходимо найти вероятность того, что число очков равно 4, или сумма очков равна 10, или произведение числа очков делится на 2, или числа очков отличаются на 3 и так далее.

Основной метод решения подобных задач — использование формулы классической вероятности, который мы и разберем на примерах ниже.

Ознакомившись с методами решения, вы сможете скачать супер-полезный Excel-файл для расчета вероятности при бросании 2 игральных костей (с таблицами и примерами).

Одна игральная кость

С одной игральной костью дело обстоит до неприличия просто. Напомню, что вероятность находится по формуле $P=m/n$, где $n$ — число всех равновозможных элементарных исходов эксперимента с подбрасыванием кубика или кости, а $m$ — число тех исходов, которые благоприятствуют событию.

Пример 1. Игральная кость брошена один раз. Какова вероятность, что выпало четное число очков?

Так как игральная кость представляет собой кубик (еще говорят, правильная игральная кость, то есть кубик сбалансированный, так что выпадает на все грани с одинаковой вероятностью), граней у кубика 6 (с числом очков от 1 до 6, обычно обозначаемых точкам), то и общее число исходов в задаче $n=6$. Благоприятствуют событию только такие исходы, когда выпадет грань с 2, 4 или 6 очками (только четные), таких граней $m=3$. Тогда искомая вероятность равна $P=3/6=1/2=0.5$.

Пример 2. Брошен игральный кубик. Найти вероятность выпадения не менее 5 очков.

Рассуждаем также, как и в предыдущем примере. Общее число равновозможных исходов при бросании игрального кубика $n=6$, а условию «выпало не менее 5 очков», то есть «выпало или 5, или 6 очков» удовлетворяют 2 исхода, $m=2$. Нужная вероятность равна $P=2/6=1/3=0.333$.

Даже не вижу смысла приводить еще примеры, переходим к двум игральным костям, где все интереснее и сложнее.

Две игральные кости

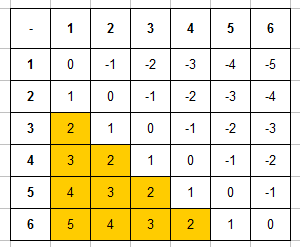
Когда речь идет о задачах с бросанием 2 костей, очень удобно использовать таблицу выпадения очков. По горизонтали отложим число очков, которое выпало на первой кости, по вертикали — число очков, выпавшее на второй кости. Получим такую заготовку (обычно я делаю ее в Excel, файл вы сможете скачать ниже):

А что же в ячейках таблицы, спросите вы? А это зависит от того, какую задачу мы будем решать. Будет задача про сумму очков — запишем туда сумму, про разность — запишем разность и так далее. Приступаем?

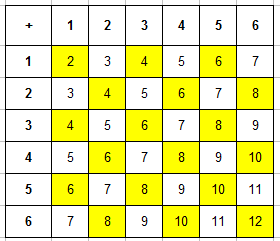
Пример 3. Одновременно бросают 2 игральные кости. Найти вероятность того, что в сумме выпадет менее 5 очков.

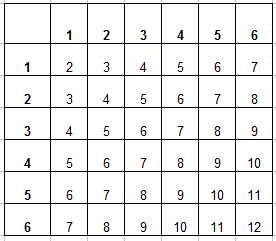
Сначала разберемся с общим числом исходов эксперимента. когда мы бросали одну кость, все было очевидно, 6 граней — 6 исходов. Здесь костей уже две, поэтому исходы можно представлять как упорядоченные пары чисел вида $(x,y)$, где $x$ — сколько очков выпало на первой кости (от 1 до 6), $y$ — сколько очков выпало на второй кости (от 1 до 6). Очевидно, что всего таких пар чисел будет $n=6cdot 6=36$ (и им соответствуют как раз 36 ячеек в таблице исходов).

Вот и пришло время заполнять таблицу. В каждую ячейку занесем сумму числа очков выпавших на первой и второй кости и получим уже вот такую картину:

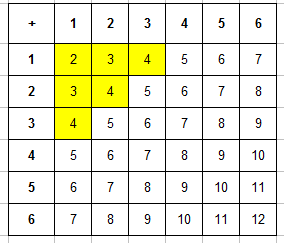
Теперь эта таблица поможем нам найти число благоприятствующих событию «в сумме выпадет менее 5 очков» исходов. Для этого подсчитаем число ячеек, в которых значение суммы будет меньше 5 (то есть 2, 3 или 4). Для наглядности закрасим эти ячейки, их будет $m=6$:

Тогда вероятность равна: $P=6/36=1/6$.

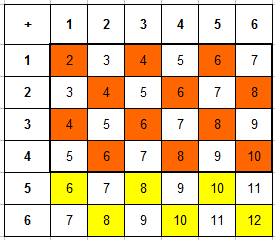
Пример 4. Брошены две игральные кости. Найти вероятность того, что произведение числа очков делится на 3.

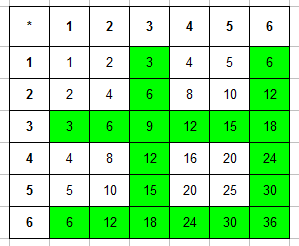
Составляем таблицу произведений очков, выпавших на первой и второй кости. Сразу выделяем в ней те числа, которые кратны 3:

Остается только записать, что общее число исходов $n=36$ (см. предыдущий пример, рассуждения такие же), а число благоприятствующих исходов (число закрашенных ячеек в таблице выше) $m=20$. Тогда вероятность события будет равной $P=20/36=5/9$.

Как видно, и этот тип задач при должной подготовке (разобрать еще пару тройку задач) решается быстро и просто. Сделаем для разнообразия еще одну задачу с другой таблицей (все таблицы можно будет скачать внизу страницы).

Пример 5. Игральную кость бросают дважды. Найти вероятность того, что разность числа очков на первой и второй кости будет от 2 до 5.

Запишем таблицу разностей очков, выделим в ней ячейки, в которых значение разности будет между 2 и 5:

Итак, что общее число равновозможных элементарных исходов $n=36$, а число благоприятствующих исходов (число закрашенных ячеек в таблице выше) $m=10$. Тогда вероятность события будет равной $P=10/36=5/18$.

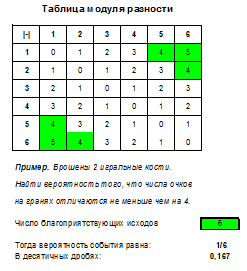
Итак, в случае, когда речь идет о бросании 2 костей и простом событии, нужно построить таблицу, выделить в ней нужные ячейки и поделить их число на 36, это и будет вероятностью. Помимо задач на сумму, произведение и разность числа очков, также встречаются задачи на модуль разности, наименьшее и наибольшее выпавшее число очков (подходящие таблицы вы найдете в файле Excel).

Другие задачи про кости и кубики

Конечно, разобранными выше двумя классами задач про бросание костей дело не ограничивается (просто это наиболее часто встречаемые в задачниках и методичках), существуют и другие. Для разнообразия и понимания примерного способа решения разберем еще три типовых примера: на бросание 3 игральных костей, на условную вероятность и на формулу Бернулли.

Пример 6. Бросают 3 игральные кости. Найдите вероятность того, что в сумме выпало 15 очков.

В случае с 3 игральными костями таблицы составляют уже реже, так как их нужно будет аж 6 штук (а не одна, как выше), обходятся простым перебором нужных комбинаций.

Найдем общее число исходов эксперимента. Исходы можно представлять как упорядоченные тройки чисел вида $(x,y,z)$, где $x$ — сколько очков выпало на первой кости (от 1 до 6), $y$ — сколько очков выпало на второй кости (от 1 до 6), $z$ — сколько очков выпало на третьей кости (от 1 до 6). Очевидно, что всего таких троек чисел будет $n=6cdot 6cdot 6=216$ .

Теперь подберем такие исходы, которые дают в сумме 15 очков.

$$
(3,6,6), (6,3,6), (6,6,3),\
(4,5,6), (4,6,5), (5,4,6), (6,5,4), (5,6,4), (6,4,5),\
(5,5,5).
$$

Получили $m=3+6+1=10$ исходов. Искомая вероятность $P=10/216=0.046$.

Пример 7. Бросают 2 игральные кости. Найти вероятность того, что на первой кости выпало не более 4 очков, при условии, что сумма очков четная.

Наиболее простой способ решения этой задачи — снова воспользоваться таблицей (все будет наглядно), как и ранее. Выписываем таблицу сумм очков и выделяем только ячейки с четными значениями:

Получаем, что согласно условию эксперимента, всего есть не 36, а $n=18$ исходов (когда сумма очков четная).

Теперь из этих ячееек выберем только те, которые соответствуют событию «на первой кости выпало не более 4 очков» — то есть фактически ячейки в первых 4 строках таблицы (выделены оранжевым), их будет $m=12$.

Искомая вероятность $P=12/18=2/3.$

Эту же задачу можно решить по-другому, используя формулу условной вероятности. Введем события:
А = Сумма числа очков четная
В = На первой кости выпало не более 4 очков
АВ = Сумма числа очков четная и на первой кости выпало не более 4 очков
Тогда формула для искомой вероятности имеет вид:
$$
P(B|A)=frac{P(AB)}{P(A)}.
$$
Находим вероятности. Общее число исходов $n=36$, для события А число благоприятствующих исходов (см. таблицы выше) $m(A)=18$, а для события АВ — $m(AB)=12$. Получаем:
$$
P(A)=frac{m(A)}{n}=frac{18}{36}=frac{1}{2}; quad P(AB)=frac{m(AB)}{n}=frac{12}{36}=frac{1}{3};\
P(B|A)=frac{P(AB)}{P(A)}=frac{1/3}{1/2}=frac{2}{3}.
$$
Ответы совпали.

Пример 8. Игральный кубик брошен 4 раза. Найти вероятность того, что четное число очков выпадет ровно 3 раза.

В случае, когда игральный кубик бросается несколько раз, а речь в событии идет не о сумме, произведении и т.п. интегральных характеристиках, а лишь о количестве выпадений определенного типа, можно для вычисления вероятности использовать формулу Бернулли.

Итак, имеем $n=4$ независимых испытания (броски кубика), вероятность выпадения четного числа очков в одном испытании (при одном броске кубика) равна $p=3/6=1/2=0.5$ (см. выше задачи для одной игральной кости).

Тогда по формуле Бернулли $P=P_n(k)=C_n^k cdot p^k cdot (1-p)^{n-k}$, подставляя $k=3$, найдем вероятность того, что четное число очков появится 3 раза:
$$
P_4(3)=C_4^3 cdot left(1/2right)^3 cdot left(1-1/2right)^1=4 cdot left(1/2right)^4=1/4=0,25.
$$

Приведем еще пример, решаемый аналогичным образом.

Пример 9. Игральную кость бросают 8 раз. Найти вероятность того, что шестёрка появится хотя бы один раз.

Подставляем в формулу Бернулли следующие значения: $n=8$ (число бросков), $p=1/6$ (вероятность появления 6 при одном броске), $kge 1$ (хотя бы один раз появится шестерка). Прежде чем вычислять эту вероятность, напомню, что практически все задачи с формулировкой «хотя бы один…» удобно решать, переходя к противоположному событию «ни одного…». В нашем примере сначала стоит найти вероятность события «Шестёрка не появится ни разу», то есть $k=0$:
$$
P_8(0)=C_8^0 cdot left(1/6right)^0 cdot left(1-1/6right)^8=left(5/6right)^8.
$$
Тогда искомая вероятность будет равна
$$
P_8(kge 1)=1-P_8(0)=1-left(5/6right)^8=0.767.
$$

А еще у нас есть онлайн калькулятор для формулы Бернулли

Полезные ссылки

Для наглядного и удобного расчета вероятностей в случае бросания двух игральных костей я сделала
Файл с таблицами для расчета вероятности.

В нем приведены таблицы суммы, произведения, разности, минимума, максимума, модуля разности числа очков.

Вводя число благоприятствующих исходов в специальную ячейку вы получите рассчитанную вероятность (в обычных и десятичных дробях). Файл открывается программой Excel.

Еще по теории вероятностей:

Онлайн калькуляторы Онлайн учебник Более 200 примеров Решенные контрольные

Формулы и таблицы Сдача тестов Решение на заказ Онлайн помощь

В решебнике вы найдете более 400 задач о бросании игральных костей и кубиков с полными решениями (вводите часть текста для поиска своей задачи):

Probability is also known as a possibility, which works in the happening of a likely event. The utility is designated from zero to one. In math, Probability has been obvious to approximate how possible events are to occur. Basically, the probability is the scope to which something is to be expected to take place.

Probability

To understand probability more exactly, let’s understand an example of flipping a coin, the possible outcomes are – head and tail. The possibility of happening any of the likely events is 1/2. As the possibility of occurring any of the likely events is the same so there is an equal possibility of happening any favorable affair, in this case, it is 1/2.

Formula of Probability

P(A) = {Number of affair A} ⁄ {Total number of affair}

DICE

Dice is a small block that has between one and six mark or tint on its boundary and is used in games to give a randomly integer. Dice are small, tossable blocks with a detectable boundary that can stop in respective figures. They are handed down to give stand-up to respective figures, often as part of sideboard games, as well as dice games, board games, role-playing games, and games of chance.

A usual die is a block with each of its six sides detectable with a different integers of figures from one to six. When throwable or rolled, the die comes to pause shows a random number from one to six on its higher side, with the happening of each affair being equally likely. Dice may also have concave or unequal shapes and may have faces noticeable with figures or characters instead of the pit. Filled dice are drawn to favour some results over others for break out or relaxation.

How to calculate Dice Probabilities?

Answer:

• One Dice Rolls

The uncomplicated and easiest case of dice probabilities is the possibility of occurring a specific integer with one dice. In probability, the primary act is that one must compute it by looking at the number of likely events in collation to the desired events.

Dice presents six likely events. Furthermore, the attentiveness of the independent would be only for one affair disregarding of the choice of integer. A dice probability calculator would be totally convenient in this regard.

The formula one may use in this case is,

P(A) = {Number of affair to A} ⁄ {Total number of affair}

Therefore, the odds of getting a specific number, if the number is 6, this gives,

Probability = 1 ÷ 6 = 0.167

Probabilities are accessible as numbers between no possibility and reliability. Furthermore, no possibility resembles 0 and reliability resembles 1. An independent can multiply this by 100 to operate a percentage. As a consequence, the possibility of getting 6 on the dice is 16.7%.

• Two or More Dice

The probabilities definitely get a little more complex to work out when two dice are concerned. The calculation of uncommon probabilities takes place when one wish to know the probability of getting two 6s by throwing two dice. Most remarkable, the result of one dice does not rely upon on the result of the other dice.

Unconventional probabilities have the rule that one must multiply the individual probabilities jointly to attain the outcome. Therefore, the formula for this is,

Probability of both = Probability of result one × Probability of result two

• Total Score from Two or More Dice

If an individual wants to know the likelihood of getting a particular total sore by rolling two or more dice, then one must go back to the simple rule.

This simple rule is probability = number of likely result divided by the number of likely results. Again, the use of a dice probability calculator is critical here. Calculating the number of result one is concerned in requires more work. If an individualistic wish a total score of 4 on two dice, then this is attainable by rolling 1 and 3, 3 and 1, or 2 and 2.

Furthermore, the individual must observe the dice individually, 1 on first dice and 3 on other dice is surely different than a 3 on first dice and 1 on the second dice. For rolling a 4, there are three ways to get the result one wishes. Hence, there are 36 likely result. The work out of this is as follows,

Probability = Number of desired outcomes/Number of possible outcomes = 3 ÷ 36 = 0.0833.

The proportion comes out to be 8.33 percent. Also, 7 is the most favourable  outcome for two dice. In addition, there are six ways to attain it. The probability in this case is 6 ÷ 36 = 0.167 = 16.7%.

Similar Problems

Question 1: Find the probability of retrieving a sum of 8 on throwing two dice?

Answer:

There are 36 total likely results on throwing two dice i.e., 6² = 6 × 6 = 36.

There are 5 total possibility of retrieving a sum of 8 on throwing two dice i.e., (2, 6), (3, 5), (4, 4), (5, 2), (6, 2).

Hence, the probability of retrieve a sum of 8 on throwing two dice is 5/36.

Question 2: Shawn tosses a die 400 times and he documents the score of getting 6 as 30 times. What could be the probability of

a) retrieving a score of 6?

b) retrieving a score under 6?

Solution:

a) P (getting a score of 6)  

= Number of times getting 6/total times

= 30/400

= 3/40

b) P (getting a score under 6)

= number of times getting under 6/total times

= 370/400

= 37/40

a) P (getting 5) = 3/40

b) P (getting under 6) = 37/40

Question 3: What is the probability of retrieving a sum of 6 if two dice are thrown?

Solution:

When two dice are rolled, n(S) = 36. Let, A be the event of getting a sum of 6. Then,

A = {(3, 3), (2, 4), (4, 2), (1, 5), (5, 1)}

n(A) = 5

Hence, the required probability will be,

P(A) = n(A)/n(S) = 5/36.

Question 4: Find the probability of throwing two dice and retrieving a sum of 4.

Solution:

The set of possible outcomes when we roll a die are {1, 2, 3, 4, 5, 6}

So, when two dice are rolled, there are 6 × 6 = 36 chances.

When we roll two dice, the probability of retrieving number 4 is (1, 3), (2, 2), and (3, 1).

So, the number of favorable outcomes = 3

Total number of possibilities = 36

Probability = {Number of likely affair } ⁄ {Total number of affair} = 3 / 36 = 1/12.

Thus, 1/12 is the probability of rolling two dice and retrieving a sum of 4.

Last Updated :
12 May, 2022

Like Article

Save Article

Была ли эта статья полезной?

Для решения посчитаем через полную вероятность событий.

Рассмотрим возможные варианты:

Гипотеза 1

Кость бросили 1 раз.

В этом случае должна выпасть только «4»

Вероятность этого события P₁(4) = 1/6

---

Гипотеза 2

Кость бросили 2 раза.

В этом случае возможно «1+3» — 1/36

«3+1» — 1/36

«2+2» — 1/36

Вероятность такого события P₂(4) = 1/36 + 1/36 + 1/36 = 3/36

---

Гипотеза 3

Кость бросили 3 раза.

В этом случае возможно «1+1+2» — 1/216

«1+2+1» — 1/216

«2+1+1» — 1/216

Вероятность такого события P₃(4) = 1/216 + 1/216 + 1/216 = 3/216

---

Гипотеза 4

Кость бросили 4 раза.

В этом случае возможно «1+1+1+1» — 1/1296

Вероятность такого события P₄(4) = 1/1296

---

Гипотеза 5

Кость бросили более 4 раз.

Вероятность события, что выпадет 4 при этом P₅(4) = 0

---

Полная вероятность события будет равна P(4) = P₁(4) + P₂(4) + P₃(4) + P₄(4) + P₅(4)

P(4) = 1/6 + 3/36 + 3/216 + 1/1296 = (216 + 108 + 18 + 1)/1296 = 343/1296

В задаче же спрашивается вероятность того что бросили не более 3 раз.

То есть произошли гипотезы 1; 2 и 3. А гипотезы 4 и 5 не произошли.

Тогда вероятность P₁₂₃(4) = P₁(4) + P₂(4) + P₃(4) = P(4) — P₄(4) = 342/1296

И вероятность, того что кубик бросали не более 3 раз будет отношение вероятностей

P = P₁₂₃(4) / P(4) = 342/343 = 0,997

Ответ: 0,997

П.С. Это расписанная по полочкам полная формула Байеса.