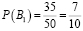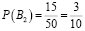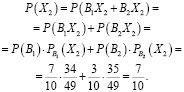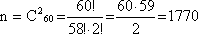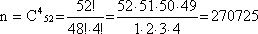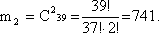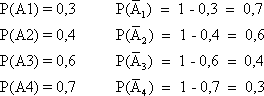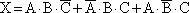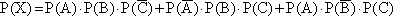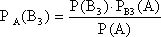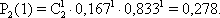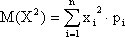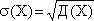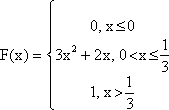Как найти вероятность вытянутого билета - Исправление недочетов и поиск решений вместе с Examum.ru

Авторы
Резюме
Файлы
Ключевые слова
Литература

Ревегук Ю.А.

1

Рудикова Е.С.

1 ФГБОУ ВО «Ставропольский государственный аграрный университет»

Вокруг нас происходит так много вещей и событий, которые, несмотря на уровень развития науки, трудно спрогнозировать. Сложно предугадать с каким номером выпадет бочонок при игре в лото или сколько будет солнечных дней в году. Но при этом, имея дополнительные сведения, возможно прогнозировать и вычислять вероятность таких событий. В данной статье идет речь о теории вероятности, составлен алгоритм решения задач по этой теме, а так же приведены примеры, с помощью которых возможно вычислить вероятность выпадения «счастливого» билета на экзамене. Теория вероятности – это отличный помощник, при предсказании наступления определенного события, в том числе выпадения «счастливого» билета на экзамене. Простые формулы позволяют провести расчеты любому человеку.

теория вероятности

«счастливый» билет

задачи

1. Бондаренко В.А., Цыплакова О.Н. Задачи с экономическим содержанием на занятиях по дифференциальному исчислению // Актуальные вопросы теории и практики бухгалтерского учета, анализа и аудита: ежегодная 75-я научно-практическая конференция / Редколлегия: В.З. Мазлоев, А.В. Ткач, И.С. Санду, И.Ю. Скляров, Е.И. Костюкова, ответственный за выпуск А.Н. Бобрышев, 2011. – С. 124–127.

2. Гулай Т.А., Жукова В.А., Мелешко С.В., Невидомская И.А. Математика: рабочая тетрадь. – Ставрополь, 2015.

3. Литвин Д.Б., Гулай Т.А., Жукова В.А., Мамаев И.И. Модель экономического роста с распределенным запаздыванием в инвестиционной сфере // Вестник АПК Ставрополья. – 2017. – № 2 (26). – С. 225–228.

4. Математика. Теория вероятностей и случайные величины: рабочая тетр.; учеб. пособие для студентов вузов по направлениям: 38.03.04 – «Гос. муницип. упр.», 38.03.05 – «Бизнес-информатика» / Т.А. Гулай, В.А. Жукова, С.В. Мелешко, И.А. Невидомская; СтГАУ. – Ставрополь: Сервисшкола, 2016.

5. Элементы теории вероятностей случайных событий: Рабочая тетрадь / И.А. Невидомская, С.В. Мелешко, Т.А. Гулай. – Ставрополь: Сервисшкола, 2015.

6. Теория вероятностей для экономических специальностей на базе Excel (практикум) / А.Ф. Долгополова, О.В. Морозова, Е.В. Долгих, Р.В. Крон, Н.Н. Тынянко, С.В. Попова, Н.Б. Смирнова // Международный журнал экспериментального образования. – 2009. – № S4. – С. 19.

Каждый человек в той или иной мере применяет теорию вероятности для анализа произошедших в его жизни событий. Люди обращают внимание на вероятность вещей и прогнозируют свое дальнейшие поведение. Но к большому сожалению, не всегда возможны точно определить вероятность того или иного события [1, 3].

Примеров реального использования теории вероятности в жизни огромное множество. Так, практически вся современная экономика базируется на ней. В общем, можно сказать, что теория вероятности будет иметь большое значение в начале практически любой деятельности, а так же в её регулировании. Она дает возможность оценить шансы той или иной неполадки, позволяет нам понять, что нужно проверить и какие усилия необходимо предпринять, исходя из полученных данных [5].

Любую деятельность любой сферы можно проанализировать, используя статистику, рассчитать благодаря теории вероятности и заметно улучшить.

Попробуем составить собственный алгоритм для решения задач по теории вероятности [2, 4]:

1. Необходимо ознакомится с условием задачи и понять какие действия, с какими предметами выполняются.

2. Определить ключевой вопрос задачи и обозначить событие, вероятность которого необходимо вычислить.

3. Чтобы выбрать дальнейшую последовательность действий следует конкретизировать тип задачи и выяснить, какие формулы будут использоваться в дальнейшем для её решения.

4. Исходя из ответов на приведенные вопросы, выбрать формулы и подставить в них данные задачи.

5. Готово, вероятность найдена.

Одно из важных событий в жизни любого студента – это сессия. Это то время, когда нервничают все, включая отличников. Ведь всегда существует вероятность не сдать экзамен. Чтобы этого не произошло необходимо соблюдать десятки различных примет, можно даже обратиться к нумерологии. Но один из простых способов вытянуть счастливый билет – рассчитать вероятность его выпадения.

Составим и решим несколько простыхзадач, на примере которых каждый студент может вычислить вероятность выпадения счастливого билета на экзамене [6].

Задача 1. «На экзамене по математике шесть студентов второго курса факультета агробиологии и земельных ресурсов друг за другом вытягивают билеты. Тридцать билетов включают в себя четыре простых вопроса. Необходимо вычислить вероятность, что хотя бы одному студенту попадется билет с простыми вопросами».

Решение. В первую очередь, определим ключевой вопрос задачи – вычислить вероятность, что хотя бы одному студенту попадется билет с простыми вопросами.

Далее пойдем от обратного, найдем вероятность того, что никому из студентов не попадется простой билет.

Эта вероятность будет равна

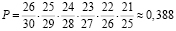
Первая дробь 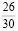показывает вероятность того, что билет со сложным вопросом достался первому студенту.

Вторая дробь 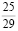показывает вероятность того, что билет со сложным вопросом достался второму студенту. Третья дробь показывает вероятность того, что билет со сложным вопрос достался третьему студенту и так далее до шестого студента. Так как в задаче требуется одновременное выполнение условий, то вероятности следует перемножить.

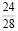
Для того, чтобы найти искомую вероятность, надо вычесть полученную выше вероятность из единицы.

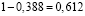
Задача 2. Леша, студент второго курса факультета механизации сельского хозяйства, сдаёт экзамен по теоретической механике, при этом из 50 билетов 35 он знает хорошо, а 15 плохо. Допустим, группа сдаёт экзамен по частям. В первый день 15 человек, включая Алексея. В каком случае Леше достанется с большей вероятностью «счастливый» билет – если он пойдет на экзамен в числе первых, в середине или же будет тянуть билет последним? Когда ему лучше зайти в кабинет?

Для начала рассмотрим случай, при котором Леша сохраняет свои шансы постоянными, то есть он не знает какие билеты вытянули однокурсники и не учит вопросы, которые знает плохо.

Пусть Алексей зайдет в аудиторию первым и вытянет «счастливый» билет, обозначим это событие 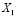. По классическому определению вероятности:

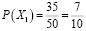
Может ли измениться вероятность извлечения нужного билета, если пропустить вперед отличника Жору? В этом случае станут возможными две несовместимые гипотезы:

– Жора вытянет «счастливый» (для Леши) билет;

– Жора вытянет «несчастливый» билет, таким образом, увеличивая шансы Леши.

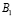
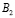
Событие 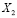, при котором Леша зайдет вторым и вытянет «счастливый» билет становится зависимым.

1) Можно предположить, что Жора с вероятностью

забрал у Леши «удачный» билет. Тогда останется всего 49 билетов, среди которых 34 «Счастливых». По классическому определению вероятности:

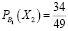
2) Допустим, что Жора с вероятностью

«спас» Лешу от одного сложного билета. В этом случае останется 49 билетов, 35 из которых «счастливые». Тогда по классическому определению вероятности:

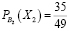
Воспользовавшись теоремами сложения вероятностей несовместных и умножение вероятностей зависимых событий, определим вероятность, что Леша вытянет «счастливый» билет, будучи вторым в очереди:

Вероятность не изменилась.

Рассмотрим следующее событие 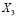, при котором Леша пойдет третьим, пропустив перед собой Жору и Леру, и вытянет «счастливый» билет.

В данном событии гипотез будет больше: однокурсники могут забрать два удачных билета или же два неудачных, так же вытянуть один «счастливый» билет и один «несчастливый» билет. Проведем аналогичные рассуждения, воспользуемся теми же теоремами и получим значение вероятности

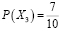
И так далее.

Следовательно, не важно, когда идти – первоначальные вероятности останутся неизменными. Но нужно помнить, что это лишь усредненная теоретическая оценка. Если Леша пойдет последним на экзамен, то это не значит, что ему достанутся на выбор 17 «счастливых» билетов и 19 «несчастливых» билетов в соответствии с его изначальными шансами. Это соотношение может изменяться, как в лучшую, так и в худшую сторону. Однако, маловероятно, что среди билетов останутся одни «счастливые» или же наоборот – «несчастливые».

Математика и «чистый эксперимент» – это хорошо, но чего следует придерживаться в реальных условиях? Нужно принять во внимание субъективные факторы, такие как дополнительный балл для «храбрецов» или же усталость преподавателя в конце экзамена. Часто они могут решающими факторами.

В случае, если вы хорошо подготовились к экзамену, то лучше идти в числе первых, так как есть полный комплект билетов, постулат «мало возможные события не происходят» работает в большей степени.

Если же студент готов к экзамену достаточно хорошо, но пробелы в знаниях всё-таки есть, то будет целесообразно пропустить вперед несколько человек и ожидать подходящего момента вне аудитории. Здесь нужно действовать по ситуации, когда начнет поступать информация о вытянутых билетах, и можно будет учить и повторять оставшиеся билеты, повышая первоначальную вероятность своего успеха.

В случае, если вы готовы неважно или плохо, то лучше идти в последнюю очередь. Существует небольшая вероятность, что останутся «счастливые» для вас билеты, вы можете изучить материал за время экзамена или же (в крайнем случае) сделать «шпаргалку».

Никогда невозможно точно предугадать, что произойдет с нами через день, два. Ведь событий связанных с нами в каждый момент невероятно много. Безусловно, мало кто будет высчитывать по формулам вероятность появления событий, но иногда бывает интересно проверить совпадает ли «эмпирический анализ» с математическим. Теория вероятности позволяет предугадать лишь однотипные события. Именно поэтому её применение связанно с большим количеством условий и ограничений, существуют такие задачи, вычисления в которых можно провести лишь с использованием компьютера.

Библиографическая ссылка

Ревегук Ю.А., Рудикова Е.С. ВЕРОЯТНОСТЬ ВЫПАДЕНИЯ «СЧАСТЛИВОГО» БИЛЕТА НА ЭКЗАМЕНЕ // Международный студенческий научный вестник. – 2018. – № 3-1.
;

URL: https://eduherald.ru/ru/article/view?id=18220 (дата обращения: 30.05.2023).

Предлагаем вашему вниманию журналы, издающиеся в издательстве «Академия Естествознания»

(Высокий импакт-фактор РИНЦ, тематика журналов охватывает все научные направления)

Источник

К экзамену по теории вероятностей студент подготовил только 18 билетов из 25. Как вы думаете, в каком случае у этого студента больше вероятность вытащить билет, который он знает: когда он тянет первым или когда он тянет вторым?

У меня получилось, что без разницы. Неужели без разницы — когда тянуть? Я думал, что вероятность должна уменьшиться.

Если тянет первым

$p_1=dfrac{18}{25}$

Если тянет вторым

$H_1$ — первый студент вытащил тот билет, который знает второй

$H_2$ — первый студент вытащил тот билет , который не знает второй

$A$ — второй студент вытащил билет, который знае

$p_2=p(A)=dfrac{17}{24}cdotdfrac{18}{25}+dfrac{18}{24}cdot dfrac{7}{25}=dfrac{18}{25}$

Источник

Основы теории вероятностей

В этой статье мы расскажем кратко о том, что такое вероятность события. Дадим определение вероятности, введем понятия зависимых и независимых, совместных и несовместных событий. Объясним, что такое сумма событий и произведение событий.

Больше задач – в статье «Задание 2 Профильного ЕГЭ по математике. Теория вероятностей».

БЕСПЛАТНЫЙ МИНИ-КУРС ПО ТЕОРВЕРУ

Случайным называется событие, которое невозможно точно предсказать заранее. Оно может либо произойти, либо нет. Теория вероятностей изучает случайные события и их закономерности, а также случайные величины и действия над ними.

Благоприятным мы называем исход, способствующий наступлению данного события.

Вероятность события равна отношению числа благоприятных исходов к общему числу исходов.

Очевидно, что вероятность – величина положительная и не может быть больше единицы.

Например, перед экзаменом вы выучили 3 билета из 20. Вероятность вытянуть счастливый билет равна $frac{3}{20}.$

Вот две простых задачи из вариантов ЕГЭ, где применяется определение вероятности:

1. На борту самолёта 12 мест рядом с запасными выходами и 18 мест за перегородками, разделяющими салоны. Остальные места неудобны для пассажира высокого роста. Пассажир Иванов высокого роста. Найдите вероятность того, что на регистрации при случайном выборе места пассажиру Иванову достанется удобное место, если всего в самолёте 300 мест.

В самолете 21+18=30 мест, удобных для Иванова. Всего в самолете 400 мест. Поэтому вероятность того, что пассажир Иванов получит удобное место, равна 30 : 300 = 0,1.

Просто применили определение вероятности.

2. В группе туристов 32 человека. Их вертолётом в несколько приёмов забрасывают в труднодоступный район по 4 человека за рейс. Порядок, в котором вертолёт перевозит туристов, случаен. Найдите вероятность того, что турист К. полетит пятым рейсом вертолёта.

Каждый рейс, в том числе и пятый, перевозит 4 человек из 32. Вероятность полететь пятым рейсом:

$p=frac{4}{32}=frac{1}{8}=0,125$

Ответ: 0,125.

События, взаимоисключающие друг друга в рамках данной задачи, называются несовместными. Появление одного из несовместных событий исключает появление других.

Например, вы бросаете монету. «Выпал орел» и «выпала решка» — несовместные события.

Сумма двух событий – термин, означающий, что произошло или первое событие, или второе, или оба сразу.
Вероятность суммы несовместных событий равна сумме их вероятностей.

Вы бросаете игральную кость. Вероятность выпадения «тройки» равна $frac{1}{6}.$ Вероятность выпадения «шестерки» также равна $frac{1}{6}.$
Вероятность выпадения числа, которое делится на 3, $frac{1}{6}+frac{1}{6}=frac{1}{3}.$

Произведение двух событий – термин, означающий, что произошло и одно, и другое событие.

События А и В называют независимыми, если вероятность появления события А не меняет вероятности появления события В.

Для нескольких независимых событий вероятность того, что все они произойдут, равна произведению вероятностей.

3. Говорят, что в старину каждый десятый на Руси был Иван, а каждый двадцатый Петр. Если это верно, то кого было больше: Иванов Петровичей или Петров Ивановичей?

Можно по-разному решать эту задачу, и вероятностный подход здесь тоже применим. Посчитаем вероятности двух событий
Событие А. Случайно выбранного мужчину зовут Иван Петрович
Событие В. Мужчину зовут Петр Иванович.

Вероятность быть Иваном Петровичем для жившего в старину россиянина равна Мы перемножили вероятности того, что наш древнерусский житель – Иван и что его отца зовут Петр.
А вероятность оказаться Петром Ивановичем точно такая же:

4. (ЕГЭ) Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с ве-роятностью 0,5. Если А. играет чёрными, то А. выигрывает у Б. с вероятностью 0,32. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза.

Шахматист А. играет две партии, одну – белыми фигурами, другую – черными. События «выиграть белыми» и «выиграть черными фигурами» независимы. Вероятность того, что шахматист А. выиграет оба раза, равна произведению вероятностей выигрышей в каждой партии: 0,5 · 0,32 = 0,16.

5. (ЕГЭ) В классе 26 человек, среди них два друга — Андрей и Сергей. Класс случайным образом разбивают на 2 группы по 13 человек. Найдите вероятность того, что Андрей и Сергей окажутся в одной группе.

Пусть Андрей первым занял место в группе (неважно, в какой). И, кроме него, осталось еще 25 человек, среди которых его друг Сергей. Сколько у Сергея шансов оказаться в той же группе, что и Андрей? В группе должно быть 13 человек, то есть Андрей и еще 12. Значит, вероятность того, что Сергей окажется в той же группе, что и Андрей, равна $frac{12}{25}$ , то есть 0,48.

Следующую задачу можно решить методами комбинаторики – например, с помощью формулы Бернулли. Однако в обычной школе не изучают комбинаторику, и тем не менее эта задача появилась в сборниках для подготовки к ЕГЭ.

Лень разбираться самому?
Присоединяйся к мини-курсу по теории вероятностей

ПОДРОБНЕЕ

6. Монету бросают 10 раз. Во сколько раз событие «Орел выпадет ровно 8 раз» более вероятно, чем событие «Орел выпадет ровно 9 раз»?

Начнем с числа возможных исходов. Если мы бросаем монету, возможных исходов два – орел или решка.
Бросим монету два раза (или две монеты одновременно, все равно). И вот уже 4 возможных исхода:
ОО
ОР
РО
РР
(буквой О обозначен выпавший «орел», буквой «р» — решка.
Каждый следующий бросок монеты увеличивает число возможных исходов в 2 раза (орел или решка).
Для 10 бросков монеты количество возможных исходов, очевидно, равно $2^{10}.$

По определению, вероятность равна отношению числа благоприятных исходов к общему числу исходов.

Рассмотрим случай, когда орел выпадет ровно 9 раз из 10 бросков монеты. Это значит, что решка выпала ровно 1 раз.

Это могло произойти при первом броске, при втором, при третьем… и, наконец, при десятом, всего 10 благоприятных исходов. Вероятность выпадения решки ровно 1 раз из 10 бросков $P_1=frac{10}{2^{10}}.$

Теперь случай, когда орел выпал ровно 8 раз из 10 бросков монеты. Значит, решка выпала ровно 2 раза.

Пронумеруем броски: 1,2,3…10.

Решка могла выпасть в первый и во второй раз. Обозначим эту комбинацию 12.

Могла также выпасть в первый и третий раз, в первый и четвертый… Эти комбинации обозначаем как 13, 14…

Пронумеруем таким образом все благоприятные исходы.

12, 13, 14, 15, 16, 17, 18, 19, 1 10

23, 24, 25, 26, 27, 28, 29, 2 10

34, 35, 36, 37, 38, 39, 3 10

45, 46, 47, 48, 49, 4 10

56, 57, 58, 59, 5 10

67, 68, 69, 6 10

78, 79, 7 10

89, 8 10

9 10
Количество благоприятных исходов равно 9 + 8 + 7 + 6 + 5 + 4 + 3 + 2 + 1 = 45.

$P_2=frac{45}{2^{10}}.$

Поделив P_2 на P_1 , получим, во сколько раз выпадение решки ровно 8 раз более вероятно, чем выпадение решки ровно 9 раз:

$frac{P_2}{P_1}=frac{45}{2^{10}}:frac{10}{2^{10}}=4,5$

Ответ: 4,5.

Разберем какую-нибудь типовую задачу ЕГЭ по теме «Теория вероятностей». Такую, в которой мы рисуем «дерево» возможных исходов.

7. (ЕГЭ) Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая — 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая — 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным.

Изобразим все возможные исходы.

По условию, купленное в магазине стекло для автомобильной фары оказалось бракованным. Как это могло получиться?

Стекло сделано либо на первой фабрике, либо на второй. Эти события несовместны.

Вероятность того, что стекло с первой фабрики, равна 0,45.

Вероятность того, что стекло сделано на второй фабрике, равна 0,55.

Первая фабрика выпускает 3% бракованных стекол. Значит, с вероятностью 0,03 стекло, произведенное на первой фабрике, бракованное.

Вторая фабрика выпускает 1% бракованных стекол. Значит, с вероятностью 0,01 сделанное на ней стекло бракованное.

Покупатель купил бракованное стекло. Оно могло быть сделано на первой фабрике и оказалось бракованным. Это означает одновременное наступление, или произведение, двух независимых случайных событий – «стекло сделано на первой фабрике» и «стекло бракованное». Вероятность произведения этих двух событий равна

Или другой случай. Стекло могло быть со второй фабрики и также бракованное. Вероятность одновременного наступления этих двух событий равна События «стекло с первой фабрики» и «стекло со второй фабрики» несовместны – они не могут случиться одновременно.
Вероятность суммы несовместных событий равна сумме вероятностей.

Значит, вероятность купить бракованное стекло равна:

Ответ: 0,019.

Следующая задача будет интересна и старшеклассникам, и студентам. В самом деле – как быть, если вы пришли на экзамен, выучив всего 20 билетов из 30? Идти отвечать первым? Или вторым? Или предпоследним? В каком случае вероятность вытянуть билет, который ты выучил, будет наибольшей?

8. Экзамен проходит по следующей схеме: если некоторый билет уже был вытянут, то после ответа экзаменатор откладывает его в сторону. Студент выучил 20 билетов из 30. Когда ему выгоднее идти, первым или вторым, чтобы вероятность вынуть выученный билет была больше?

Назовем билеты, которые студент выучил, «счастливыми».
Если студент пошел отвечать первым, вероятность вытянуть «счастливый» билет равна $frac{20}{30}=frac{2}{3}.$

Если идти отвечать вторым, возможны два случая:

1) Первый билет, который вытянул кто-то другой, был «счастливым», и тогда «счастливых» билетов теперь 19.

2) Первый билет не был «счастливым», и «счастливых» билетов так и осталось 20.

Нарисуем схему возможных исходов, как всегда делаем в подобных задачах:

Вот наш студент идет отвечать вторым. Вероятность вытянуть «счастливый» билет равна $frac{2}{3}cdot frac{19}{29}+frac{1}{3}cdotfrac{20}{29}=frac{2}{3}.$ Удивительный ответ! Та же самая вероятность! Значит, неважно, первым или вторым идти отвечать, если ты выучил 20 билетов из 30.

Конечно, это были самые простые задачи по теории вероятностей. Такие, которые встречаются на ЕГЭ по математике.

Продолжение:
Задание 2 Профильного ЕГЭ по математике. Теория вероятностей
Теория вероятностей. Парадокс Монти Холла

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Теория вероятностей» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.05.2023

Источник

На чтение 11 мин Просмотров 2к. Опубликовано 25.04.2021

ЗАДАЧА № 2

Расписание одного дня содержит 5 уроков. Определить количество таких расписаний при выборе из 11 дисциплин.

Количество различных расписаний можно определить с помощью формулы комбинаторики для размещения по 5 из 11 элементов. Выбор размещения определяется тем, что при построении расписания необходимо учитывать порядок следования уроков.

ОТВЕТ: При данных условиях можно составить 55440 различных расписаний.

ЗАДАЧА № 3

Сколькими способами можно выбрать 3 дежурных из группы в 20 человек?

Так как для данной задачи несущественен порядок выбора, то воспользуемся формулой комбинаторики для сочетания из 20 по 3:

ОТВЕТ: Трех дежурных из группы в 20 человек можно выбрать 1140 способами.

Задача №4

Вычислить вероятность того, что некоторое событие не произойдет, если известно, что при n испытаниях оно в среднем происходит в m случаях.

1) Обозначим событие А = «Событие произошло». Определим вероятность появления данного события. Для этого воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле:

где m – число исходов, при которых появляется событие А,

n – общее число элементарных несовместных равновозможных исходов.

2) Определим вероятность того, что событие А не произойдет, по формуле:

ОТВЕТ: Вероятность того, что событие не произойдет, равна

ЗАДАЧА №5

Из 60 вопросов, входящих в экзаменационные билеты, студент подготовил 50. Какова вероятность того, что взятый наудачу студентом билет, содержащий 2 вопроса, будет состоять из подготовленных им вопросов?

1) Обозначим событие А = «Вытянутый студентом билет состоит из подготовленных им билетов». Для вычисления вероятности появления данного события воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле:

где m – число исходов, при которых появляется событие А,

n – общее число элементарных несовместных равновозможных исходов.

2) Определим n. Общее число билетов определяется сочетанием по 2 из 60:

3) Количество билетов, вопросы которых студент знает, определяется сочетанием по 2 из 50:

4) Определим вероятность события А:

ОТВЕТ: Вероятность того, что взятый наудачу студентом билет, содержащий 2 вопроса, будет состоять из подготовленных им вопросов равна Р(А) = 0,69. То есть, если будет, например, 100 таких студентов, то 69 из них вытянут билеты, к вопросам которых они подготовлены.

ЗАДАЧА № 6

Какова вероятность того, что среди вынутых наудачу 4 карт из полной колоды 52 карт ровно две окажутся принадлежащими пиковой масти?

1) Для вычисления вероятности появления данного события воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле:

где m – число исходов, при которых появляется событие А,

n – общее число элементарных несовместных равновозможных исходов.

2) Определим n. Для этого воспользуемся формулой сочетания по 4 из 52(так как нас не интересует порядок вытянутых карт):

3) Обозначим событие А = «Из 4 вынутых карт 2 принадлежат пиковой масти». Найдем вероятность вытягивания 2 пиковых карт по формуле сочетания по 2 из 13 (так как всего карт пиковой масти 13):

4) Найдем вероятность вытягивания оставшихся двух карт не пиковой масти по формуле сочетания по 2 из 39 (52-13).

5) Полученные значения мы перемножаем: m = m1 ? m2

m = 78 ? 741 = 57798

6) Найдем вероятность того, что среди вынутых наудачу 4 карт из полной колоды 52 карт ровно две окажутся принадлежащими пиковой масти:

ОТВЕТ: Вероятность того, что среди вынутых наудачу 4 карт из полной колоды 52 карт ровно две окажутся принадлежащими пиковой масти, равна 0,21.

Задача № 7

Один из мальчиков родился в марте, а другой в апреле. Какова вероятность того, что оба они родились в первой неделе месяца?

1) Вероятность того, что первый мальчик родился в первой неделе марта равна:

2) Вероятность того, что второй мальчик родился в первой неделе апреля равна:

3) Вероятность того, что оба они родились в первой неделе месяца, равна P(A) ? P(B):

ОТВЕТ: Вероятность того, что оба мальчика родились в первой неделе месяца равна 0,05.

ЗАДАЧА №8

Для разрушения моста достаточно попадания одной бомбы. Найти вероятность того, что мост будет разрушен, если на него будут сброшены 4 бомбы с вероятностями попадания соответственно 0,3; 0,4; 0,6; 0,7.

Для определения вероятности воспользуемся формулой вероятности появления хотя бы одного из n событий:

Обозначим события: А1 = «Первая бомба попала на мост»

А2 = «Вторая бомба попала на мост»

А3 = «Третья бомба попала на мост»

А4 = «Четвертая бомба попала на мост»

Тогда P (A1 + A2 + A3 + A4) = 1 – 0,7 ? 0,6 ? 0,4 ? 0,3 = 0,9496.

ОТВЕТ: Вероятность того, что мост будет разрушен, если на него будут сброшены 4 бомбы с заданными вероятностями попадания, равна 0,9496, то есть это достаточно достоверное событие.

ЗАДАЧА № 9

Чему равна вероятность того, что при одновременном бросании трех игральных костей 2 очка появятся на 2 костях?

Обозначим события: А = «2 очка выпали на первой кости»

В = «2 очка выпали на второй кости»

С = «2 очка выпали на третьей кости»

Искомое событие X описывается следующей комбинацией:

Так как события А, В и С несовместные и независимые, то вероятность события Х определяется по формуле:

P(X) = 0,17 ? 0,17 ? 0,83 + 0,83 ? 0,17 ? 0,17 + 0,17 ? 0,83 ? 0,17 = 0,17 ? 0,17 ? 0,83 ? 3 = 0,07.

ОТВЕТ: Вероятность того, что при одновременном бросании трех игральных костей 2 очка появятся на 2 костях, равна 0,07.

ЗАДАЧА № 10

Некоторое изделие может поступить для обработки в случайном порядке на один из трех станков с вероятностями соответственно равными Р1 = 0,2; Р2 = 0,3; Р3 = 0,5. При обработке на первом станке вероятность брака равна 0,02, на втором – 0,03, на третьем – 0,05. Найти вероятность того, что поступившее в цех изделие после обработки окажется удовлетворяющим техническим условиям.

Обозначим события: А = «Изделие удовлетворяет техническим условиям»

В1 = «Изделие обрабатывалось на первом станке»

В2 = «Изделие обрабатывалось на втором станке»

В3 = «Изделие обрабатывалось на третьем станке»

Для решения поставленной задачи используем формулу полной вероятности:

ОТВЕТ: Вероятность того, что поступившее в цех изделие после обработки окажется удовлетворяющим техническим условиям, равна 0,745.

ЗАДАЧА №11

Пусть в условиях предыдущей задачи поступившее в цех изделие после обработки оказалось удовлетворяющим техническим условиям. Какова вероятность того, что изделие обрабатывалось на третьем станке?

Для решения данной задачи применим формулу Бейеса:

ОТВЕТ: Вероятность того, что изделие обрабатывалось на третьем станке, при том что оно оказалось удовлетворяющим техническим условиям, равна 0,638.

ЗАДАЧА № 12

Вероятность изготовления на автоматическом станке стандартной детали равна 0,9. Определить вероятность того, что из трех наудачу взятых деталей: а) две окажутся стандартными; б) все три окажутся стандартными.

Для решения используем формулу Бернулли:

а) p = 0,9; q = 1 – 0,9 = 0,1

б) p = 0,9; q = 1 – 0,9 = 0,1

ОТВЕТ: Вероятность того, что из трех наудачу взятых деталей две окажутся стандартными, равна 0,243; а того, что все три окажутся стандартными, — 0,729.

ЗАДАЧА №13

Вероятность выхода из строя за некоторое время Т одного конденсатора равна 0,1. Найти вероятность того, что из 100 конденсаторов в течение времени Т из строя выйдут: а) ровно 16 конденсаторов; б) от 4 до 19 конденсаторов.

а) Для решения используем формулу Бернулли:

k = 16, n = 100, p = 0,1; q = 1 – 0,1 = 0,9

б) Для решения используем интегральную теорему Муавра-Лапласа:

По таблице(Приложение 2) определим значение функции при данных значениях х:

Ф(-2) = -Ф(2) = 0,4772; Ф(3) = 0,49865

ОТВЕТ: Вероятность того, что из 100 конденсаторов в течение времени T из строя выйдут ровно 16 конденсаторов, равна 0,019, а от 4 до 19 конденсаторов – 0,02145.

ЗАДАЧА № 14

Игральная кость брошена два раза. Составить закон распределения случайной величины Х – числа появления двойки. Найти математическое ожидание и дисперсию случайной величины.

1) Составим закон распределения случайной величины Х:

2) Найдем вероятность события А = «При бросании кости выпала двойка». Для вычисления вероятности появления данного события воспользуемся классическим определением вероятности события, согласно которому вероятность определяется по формуле:

где m – число исходов, при которых появляется событие А, n – общее число элементарных несовместных равновозможных исходов.

В нашем случае m = 1, а n = 6 (так как на кости шесть граней с числами).

3)Для определения вероятностей того, что двойка выпадет 0, 1 или 2 раза воспользуемся формулой Бернулли:

4) Найдем вероятность того, что двойка на игральной кости не выпадет ни разу (Х=0).

5) Найдем вероятность того, что двойка на игральной кости выпадет один раз (Х=1).

6) Найдем вероятность того, что двойка на игральной кости выпадет два раза (Х=2).

7) Заполним теперь таблицу, выражающую закон распределения случайной величины Х:

P 0,694 0,278 0,028

Определим математическое ожидание данной случайной величины Х (математическое ожидание характеризует среднее значение случайной величины при большом числе испытаний):

М(Х) = 0 ? 0,694 + 1 ? 0,278 + 2 ? 0,028 = 0,334.

9) Определим дисперсию для данной случайной величины по формуле (дисперсия характеризует средний квадрат отклонения случайной величины от среднего):

10) Определим среднеквадратическое отклонение, которое характеризует среднее отклонение случайной величины от среднего, по формуле:

ОТВЕТ: Математическое ожидание случайной величины равно М(Х) = 0,334. Дисперсия случайной величины равна Д(Х) = 0,278.

ЗАДАЧА № 15

Дискретная случайная величина Х задана законом распределения:

X 2 5 8

P 0,4 P2 0,1

Найти: Р2; функцию распределения F(х) и построить ее график; математическое ожидание; дисперсию и среднеквадратическое отклонение случайной величины Х. Найти закон распределения случайной величины Y, где Y = 2X, Y = X2.

1) Определим Р2. Так как сумма всех вероятностей, указанных в таблице, должна быть равна единице (то есть Р1 + Р2 + Р3 = 1), то Р2 найдем из формулы:

Р2 = 1 – 0,4 – 0,1 = 0,5.

2) Построим функцию распределения

а) Рассмотрим первый интервал х 8:

Запишем закон распределения:

3) Построим график функции распределения:

4) Определим математическое ожидание данной случайной величины Х (математическое ожидание характеризует среднее значение случайной величины при большом числе испытаний):

М(Х) = 2 ? 0,4 + 5 ? 0,5 + 8 ? 0,1 = 4,1.

5) Определим дисперсию для данной случайной величины по формуле (дисперсия характеризует средний квадрат отклонения случайной величины от среднего):

М(Х2) = 22 ? 0,4 + 52 ? 0,5 + 82 ? 0,1 = 20,5.

Д(Х) = 20,5 – 4,12 = 3,69.

6) Определим среднеквадратическое отклонение, которое характеризует среднее отклонение случайной величины от среднего, по формуле:

7) Составим закон распределения для функций Y = 2X и Y = X2

Y= 4 25 64

ЗАДАЧА №16

Случайная величина Х задана функцией распределения F(x):

Найти: а) плотность распределения вероятностей, математическое ожидание, дисперсию, СКО, медиану и моду случайной величины Х;

б) вероятность того, что в результате испытания случайная величина примет значение, принадлежащее интервалу (1/6; 1/3);

Задача №13. Из 60 экзаменационных вопросов студент подготовил 50. Найти вероятность того, что вытянутый билет из 2 вопросов будет состоять из подготовленных вопросов.

Задача №14. Из 30 карточек с буквами русского алфавита наудачу выбирают 4 карточки. Чему равна вероятность того, что эти 4 карточки в порядке выхода составят слово «небо»?

Задача №15. На полке расставлено наудачу 10 книг. Определить вероятность того, что 3 определённые книги окажутся рядом.

Пояснение. При вычислении m три указанные книги принимаем за одну.

Задача №16. В лотерее 1000 билетов. Из них 500 выигрывают, 500 проигрывают. Куплено 2 билета. Найти вероятность того, что оба билета выиграют.

Решение. Пусть случайное событие А=<2 билета выигрывают>, тогда:

Задача №17. Наудачу выбирается 5-тизначное число. Какова вероятность события:

Решение. Всего пятизначных чисел:

Задача №18. В коробке 15 одинаковых изделий, 5 из них окрашены. Наугад извлекают 3 изделия. Найти вероятность того, что

a) все 3 изделия окрашены;

b) одно изделие окрашено.

Решение. Рассмотрим события:

Задача №19. Среди 12-ти студентов, 7 из которых девушки, раздают 5 билетов. Найти вероятность того, что среди обладателей билетов будут 3 девушки (событие А).

Задача №20. Из колоды карт (36 штук) наудачу извлекают 3 карты. Найти вероятность того, что среди них окажется туз.

Задача №21. Из 10 изделий, из которых 3 бракованные, наудачу извлекают три изделия для контроля. Найти вероятность того, что:

a)в полученной выборке все изделия бракованные;

b)в полученной выборке 2 изделия бракованные.

Задача №22. Дано пять отрезков, длины которых составляют соответственно 1, 3, 5, 7, 9. Определить вероятность того, что из взятых наудачу 3-х отрезков из данных пяти можно построить треугольник (событие А).

Решение. Всего отобрать 3 отрезка из заданных 5-ти можно

Из 60 вопросов, включенных в экзамен, студент подготовил 50. Какова вероятность того, что студент из предложенных ему вопросов знает два?

Лучший ответ:

60-10=50Ответ: 50 вероятность тому

Другие вопросы:

Набор реальных молекул- это А) N2, He2 Б) O2, H2 В) F2, Mg2 Г) S2, Mn2 ПОМОГИТЕ ПОЖАЛУЙСТА,ОЧЕНЬ НУЖНА ПОМОЩЬ. ЗАРАНЕЕ ОГРОМНОЕ СПАСИБО

Проект про 7 чудес света

Пожалуйста напишите пять предложений в past simple и пять предложений в present perfect

Пожалуйста помогите. Как бы вы ответили на вопросы автора?отчего же на капельку солнца прибавилось в мире ?отчего же на капельку счастья прибавилось в мире ?отчего же на капельку радостней сделалась жизнь ?

Біля води нерідко можна побачити, як літають невеликі комахи з прозорими крильцями-одноденки; їхнє життя вкрай коротке, в окремих видів лише декілька годин. Як за такий короткий час встигають чинники природного добору? Як сформувалися корисні пристосування у тварин, чиє життя таке недовговічне?

Источник

Из 30 билетов не выучил всего три.

Очень добросовестный этот ученик Сережа. Выучить все билеты ему очевидно просто времени не хватило.

Итак, у нас задача по теории вероятности

Вероятностью события, что Сережа вытянет знакомый ему билет, назовем ее A, в данном испытании мы называем отношением:

Если бы Сережа не выучил все 30 билетов, то вероятность вытянуть выученный как достоверного события была бы равна нулю.

И наоборот, если бы Сережа выучил все 30 билетов, то вероятность вытянуть выученный была бы равна единице.

Решаем так: от 30 билетов всего отнимем 3 невыученных. 30 — это число элементарных исходов (n)

30 — 3 = 27.

Число случаев, благоприятствующих появлению билета выученного (А) равно 27 (m).

27/30 = 9/10.

Ответ пишем как десятичную дробь — 0,9.

Источник