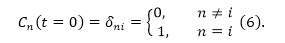Как найти вероятности перехода - Исправление недочетов и поиск решений вместе с Examum.ru

Переходные вероятности. Матрица перехода.

Переходной
вероятностью

называют
условную вероятность того, что из
состояния

в итоге следующего испытания система
перейдет в состояние

.
Таким образом, индекс

относится к предшествующему, а

— к последующему состоянию.

Будем считать, что
число состояний конечно и равно k.

Матрицей
перехода
системы называют матрицу, которая
содержит все переходные вероятности
этой системы:

где

представляют вероятности перехода за
один шаг.

Отметим некоторые
особенности матрицы перехода.

Элементы
каждой строки матрицы представляют
собой вероятности всех возможных
переходов за один шаг из выбранного
состояния, в том числе и вероятность
отсутствия перехода (элемент строки с
равными индексами)
Элементы
столбцов задают вероятности всех
переходов системы за один шаг в заданное
состояние
Так
как в каждой строке матрицы помещены
вероятности событий (т.е. вероятности
перехода из состояния

в любое возможное состояние

),
которые образуют полную группу, то
сумма вероятностей этих событий равна
единице:

По
главной диагонали матрицы перехода
стоят вероятности

того, что система не выйдет из состояния,
а останется в нем.

Равенство Маркова

Обозначим через

вероятность того, что в результате n
шагов (испытаний) система перейдет из
состояния

в состояние

.
Например,

—
вероятность перехода за 10 шагов из
третьего состояния в шестое. Отметим,
что при n
= 1 эта вероятность сводится просто к
переходной вероятности

.

Возникает вопрос,
как, зная переходные вероятности

,
найти вероятности перехода состояния

в состояние

за n
шагов. С этой целью вводится в рассмотрение
промежуточное (между

) состояние r.
Другими словами, полагают, что из
первоначального состояния

за m
шагов система перейдет в промежуточное
состояние r
с вероятностью

,
после чего за оставшиеся n
– m
шагов из промежуточного состояния r
она перейдет в конечное состояние

с вероятностью

.
Используя формулу полной вероятности,
можно показать, что справедлива формула

Эту формулу называют
равенством
Маркова.

Зная все переходные
вероятности

,
т.е. зная матрицу перехода

из состояния в состояние за один шаг,
можно найти вероятности

перехода из состояние в состояние за
два шага, а значит, и саму матрицу перехода

,
далее – по известной матрице

— найти

и т.д.

Действительно,
полагая в равенстве Маркова n
= 2, m
= 1 получим

или

.
В матричном виде это можно записать как

.

Полагая n=3,
m
=2, получим

.
В общем случае справедливо соотношение

Пример.
Пусть матрица перехода

равна

Требуется найти
матрицу перехода

Умножая матрицу

саму на себя, получим

Для
практических применений чрезвычайно
важным является вопрос о расчете
вероятности
нахождения системы
в том или ином состоянии в конкретный
момент времени.
Решение этого вопроса требует знания
начальных условий, т.е. вероятностей
нахождения системы в определенных
состояниях в начальный момент времени.
Начальным распределением вероятностей
марковской цепи называется распределение
вероятностей состояний в начале процесса

Здесь через

обозначена вероятность нахождения
системы в состоянии

в начальный момент времени. В частном
случае, если начальное состояние системы
в точности известно (например

),
то начальная вероятность

,
а все остальные равны нулю.

Если
для однородной цепи Маркова заданы
начальное распределение вероятностей
и матрица перехода, то вероятности
состояний системы на n-м
шаге

вычисляются
по рекуррентной формуле

Для иллюстрации
приведем простой пример. Рассмотрим
процесс функционирования некоторой
системы (например, прибора). Пусть прибор
в течение одних суток может находиться
в одном из двух состояний – исправном
(
)
и неисправном (
).
В результате массовых наблюдений за
работой прибора составлена следующая
матрица перехода

где

— вероятность того, что прибор останется
в исправном состоянии;

—
вероятность перехода прибора из
исправного в неисправное состояние;

—
вероятность перехода прибора из
неисправного в исправное состояние;

—
вероятность того, что прибор останется
в состоянии «неисправен».

Пусть вектор
начальных вероятностей состояний
прибора задан соотношением

,
т.е.

(в начальный момент прибор был
неисправен). Требуется определить
вероятности состояния прибора через
трое суток.

Решение:
Используя матрицу перехода, определим
вероятности состояний после первого
шага (после первых суток):

Вероятности
состояний после второго шага (вторых
суток) равны

Наконец,
вероятности состояний после третьего
шага (третьих суток) равны

Таким образом,
вероятность того, что прибор будет
находиться в исправном состоянии равна
0,819, и того, что в неисправном –
соответственно 0,181.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Сергей Сергеевич Соев

Эксперт по предмету «Физика»

Задать вопрос автору статьи

Вероятность перехода

Общая задача нахождения состояний квантовой системы, например, атома в поле электромагнитной волны в дипольном приближении — это решение нестационарного уравнения Шредингера при использовании дипольного приближения:

где оператор взаимодействия ($hat{W}left(overrightarrow{r},tright)$) определяется как:

Допустим, что система при t=0 (начальный момент времени) пребывает в стационарном состоянии и имеет невозмущенный атомный оператор Гамильтона ${hat{H}}_0$ и:

где $Psi_i$ — функция, которая удовлетворяет стационарному уравнению Шредингера вида:

Система собственных функций ${hat{H}}_0$ является полной, что значит — волновая функция любого состояния $Psileft(overrightarrow{r},tright)$ может быть выражена как линейная комбинация собственных функций невозмущенного оператора Гамильтона:

Сдай на права пока
учишься в ВУЗе

Вся теория в удобном приложении. Выбери инструктора и начни заниматься!

Получить скидку 3 000 ₽

Приняв во внимание выражение (5) можно представить уравнение (3) в виде:

Рисунок 1.

Коэффициенты $C_nleft(tright)$ — это амплитуды вероятности найти систему в момент времени $t$ в стационарном состоянии $n$. В процессе воздействия на квантовую систему со стороны поля электромагнитной волны переходы между состояниями оператора Гамильтона для атома происходят с вероятность равной ${left|C_nleft(tright)right|}^2$. Так, амплитуда вероятности перехода из начального состояния $left|left.irightrangle right.$ в конечное состояние $left|left.srightrangle right.$ за время $t$, если возмущение задано оператором $hat{W}left(overrightarrow{r},tright)$ в первом порядке возмущений будет равна:

«Вероятность перехода. Понятие о правилах отбора. Разрешенные и запрещенные переходы» 👇

где ${omega }_{si}=frac{E_s-E_i}{hbar }$ — частота перехода. Если учесть выражение (2), то уравнение (7) можно преобразовать к виду:

где $d_{si}$ — матричный элемент оператора z —проекции дипольного момента системы. $Eleft(tright)=E_0{cos left(щtright) }$ — электрическое поле волны. Применяем формулу:

получаем:

при этом ${omega }_{si}$ может быть и больше, и меньше нуля.

Выражение для вероятности электромагнитного перехода из состояния $left|left.irightrangle right.$ в конечное состояние $left|left.srightrangle right.$ за время $t$ вблизи от резонанса при переходе с поглощением энергии можно определить как:

где $triangle omega =omega_{si}-omega.$

Разрешенные и запрещенные переходы

Если выполняется равенство вида:

то переход называют разрешенным. В том случае, если:

переход является запрещенным. Так как если $d_{si}=0$, то вероятность перехода оказывается равной нулю даже в электромагнитном поле, которое является сильным (для электрического дипольного приближения в низком порядке теории возмущений). Запрещенный в электрическом дипольном приближении переход может стать разрешенным в высоких порядках разложения по мультиполям. Следует отметить, что если имеем дело в исследуемом случае с запрещенным переходом — это не значит, что он не возможен в принципе. Лучше сказать, что он является маловероятным, в сравнении с разрешенными переходами в электрическом дипольном приближении.

Понятие о правилах отбора

Соотношения между квантовыми числами в начальном и конечном состояниях квантовой системы, при которых электромагнитные переходы становятся возможными, называют правилами отбора.

Можно привести несколько примеров формулировок правил отбора для разных квантовых систем.

Правила отбора для переходов в линейном гармоническом осцилляторе. Так, электромагнитные переходы возможны только между парой соседних состояний гармонического осциллятора. Эффективное взаимодействие осциллятора с внешним полем электромагнитной волны возможно только, если частота осциллятора совпадает с частотой внешнего поля.
Правила отбора для заряженной частицы находящейся в поле с центральной симметрией. По магнитному квантовому числу ($m$) правило отбора запишется как:

то есть в случае электромагнитных переходов магнитное квантовое число изменяется не 1 или не изменяется.

При электрическом дипольном переходе орбитальное квантовое число изменяется не один:

Допустим, что в процесс перехода сопровождается излучением (поглощением) фотона. Спин фотона равен единице. Выражение (14) является представлением закона сохранения момента количества движения в системе атом — электромагнитное поле. Фотон унесет при излучении единичный момент. При этом проекция может изменить значение на единицу или не менять его вовсе. В случае $triangle m=0$ испускаются фотоны, имеющие линейную поляризацию. При $triangle m=pm 1$ испускаются фотоны с круговой поляризацией.

Ограничений на изменение главного квантового числа нет. Правила отбора (13) — (14) выполняются для переходов в поле с центральной симметрией, например, в атоме водорода.

Полные правила отбора учитывают существование спинового механического момента электрона. Оператор взаимодействия с электромагнитным полем в дипольном приближении не зависит от спиновых переменных, можно записать:

Правило отбора для изменения полного механического момента атома ($j$) и его проекции формулируют как:

Для квантового числа $j$ имеем:

Пример 1

Покажите, что в общем случае теорию возмущений при рассмотрении взаимодействия атома с полем электромагнитной волны можно применять, только если воздействие поля на атом ограничено по времени.

Решение:

Запишем выражение для амплитуды вероятности перехода из начального состояния $left|left.irightrangle right.$ в конечное состояние $left|left.srightrangle right.$ за время $t$:

[C^{left(1right)}_sleft(tright)=frac{id_{si}E_0}{2hbar }left(frac{e^{ileft({omega }_{si}-omega right)t}-1}{ileft({omega }_{si}-omega right)}+frac{e^{ileft({omega }_{si}+omega right)t}-1}{ileft({omega }_{si}+omega right)}right)left(1.1right).]

Рассмотрим переход, который происходит около резонансной частоты ($omega approx left|{omega }_{si}right|$) с поглощением энергии внешнего поля. Тогда можно пренебречь $frac{e^{ileft({omega }_{si}+omega right)t}-1}{ileft({omega }_{si}+omega right)}$ в сравнении с $frac{e^{ileft({omega }_{si}-omega right)t}-1}{ileft({omega }_{si}-omega right)}$ в выражении (1.1), имеем:

[C^{left(1right)}_sleft(tright)=frac{id_{si}E_0}{2hbar }left(frac{e^{ileft({omega }_{si}-omega right)t}-1}{ileft({omega }_{si}-omega right)}right)left(1.2right).]

Введем обозначение: $triangle omega ={omega }_{si}-omega $, тогда выражение (1.2) перепишем в виде:

[C^{left(1right)}_sleft(tright)=frac{id_{si}E_0}{2hbar }e^{ifrac{triangle omega t}{2}}frac{{sin left(frac{triangle omega t}{2}right) }}{frac{triangle omega }{2}}left(1.3right).]

При этом вероятность перехода ($P_{si}$) из состояния textit{i} в состояние textit{s} равна:

[P_{si}left(tright)={left|{C_s}^{left(1right)}left(tright)right|}^2=frac{{left|d_{si}right|}^2E^2_0}{4{hbar }^2}frac{{sin}^2left(frac{triangle omega t}{2}right)}{{left(frac{triangle omega }{2}right)}^2}left(1.4right).]

Так как теория возмущений применима только при условии $P_{si}ll 1, $для резонанса (при $triangle omega =0$) из (1.4) получим:

[P_{si}left(tright)=frac{{left|d_{si}right|}^2E^2_0}{4{hbar }^2}frac{{sin}^2left(frac{triangle omega t}{2}right)}{{left(frac{triangle omega}{2}right)}^2}approx t^2(1.5)]

Выражение (1.5) показывает, что условие $P_{si}ll 1$ выполняется на ограниченном интервале времени.

Что и следовало показать.

Пример 2

Чему равна вероятность перехода в единицу времени для $tto infty $, но малых вероятностях перехода ($p_{si}$)?

Решение:

Для решения задачи применим формулу:

[{mathop{lim }_{tto infty } frac{{sin}^2alpha t}{{alpha }^2t} }=pi delta left(alpha right)left(2.1right),]

где $delta left(alpha right)$ —дельта функция. Из выражения, полученного в примере 1 (1.4) получим:

[P_{si}left(tright)=frac{{left|d_{si}right|}^2E^2_0}{4{hbar }^2}2pi delta left({omega }_{si}-omega right)tleft(2.2right).]

Выражение (2.2) показывает, что при $tto infty $ вероятность перехода увеличивается прямо пропорционально времени. Величину $p_{si}=frac{P_{si}}{t}$ называют вероятностью перехода в единицу времени, она будет равна:

[p_{si}=frac{{left|d_{si}right|}^2E^2_0}{4{hbar }^2}2pi deltaleft(omega_{si}-omegaright)=frac{{left|d_{si}right|}^2E^2_0}{4{hbar }^2}2pi delta left(E_s-E_i-hbar omega right).]

Ответ: $p_{si}=frac{{left|d_{si}right|}^2E^2_0}{4{hbar }^2}2omega deltaleft(E_s-E_i-hbar omegaright).$

Находи статьи и создавай свой список литературы по ГОСТу

Поиск по теме

Источник

Марковская цепь

Способы математических описаний марковских случайных процессов в системе с дискретными состояниями (ДС) зависят от того, в какие моменты времени (заранее известные или случайные) могут происходить переходы системы из состояния в состояние.

Если переход системы из состояния в состояние возможен в заранее фиксированные моменты времени, имеем дело со случайным марковским процессом с дискретным временем. Если переход возможен в любой случайный момент времени, то имеем дело со случайным марковским процессом с непрерывным временем.

Пусть имеется физическая система S, которая может находиться в n состояниях S₁, S₂, …, S_n. Переходы из состояния в состояние возможны только в моменты времени t₁, t₂, …, t_k, назовём эти моменты времени шагами. Будем рассматривать СП в системе S как функцию целочисленного аргумента 1, 2, …, k, где аргументом является номер шага.

Пример: S₁ → S₂ → S₃ → S₂.

Условимся обозначать S_i⁽^k⁾ – событие, состоящее в том, что после k шагов система находится в состоянии S_i.

При любом k события S₁⁽^k⁾ , S₂⁽^k⁾ ,…, S_n⁽^k⁾образуют полную группу событий и являются несовместными.

Процесс в системе можно представить как цепочку событий.

Пример:S₁⁽⁰⁾, S₂⁽¹⁾, S₃⁽²⁾, S₅⁽³⁾,….

Такая последовательность называется марковской цепью, если для каждого шага вероятность перехода из любого состояния S_iв любое состояние S_jне зависит от того, когда и как система пришла в состояние S_i.

Пусть в любой момент времени после любого k-го шага система S может находиться в одном из состояний S₁, S₂, …, S_n, т. е. может произойти одно событие из полной группы событий: S₁⁽^k⁾, S₂⁽^k⁾, …, S_n⁽^k⁾. Обозначим вероятности этих событий:

P₁(1) = P(S₁⁽¹⁾); P₂(1) = P(S₂⁽¹⁾); …; P_n(1) = P(S_n⁽^k⁾);

P₁(2) = P(S₁⁽²⁾); P₂(2) = P(S₂⁽²⁾); …; P_n(2) = P(S_n⁽²⁾);

P₁(k) = P(S₁^(k)); P₂(k) = P(S₂^(k)); …; P_n(k) = P(S_n^(k)).

Легко заметить, что для каждого номера шага выполняется условие

P₁(k) + P₂(k) +…+ P_n(k) = 1.

Назовём эти вероятности вероятностями состояний.следовательно, задача будет звучать следующим образом: найти вероятности состояний системы для любого k.

Пример.Пусть имеется какая-то система, которая может находиться в любом из шести состояний. тогда процессы, происходящие в ней, можно изобразить либо в виде графика изменения состояния системы (рис. 7.9, а), либо в виде графа состояний системы (рис. 7.9, б).

а)

Рис. 7.9

Также процессы в системе можно изобразить в виде последовательности состояний: S₁, S₃, S₂, S₂, S₃, S₅, S₆, S₂.

Вероятность состояния на (k + 1)-м шаге зависит только от состояния на k-м шаге.

Для любого шага k существуют какие-то вероятности перехода системы из любого состояния в любое другое состояние, назовем эти вероятности переходными вероятностями марковской цепи.

Некоторые из этих вероятностей будут равны 0, если переход из одного состояния в другое невозможен за один шаг.

Марковская цепь называется однородной, если переходные состояния не зависят от номера шага, в противном случае она называется неоднородной.

Пусть имеется однородная марковская цепь и пусть система S имеет n возможных состояний: S₁, …, S_n. Пусть для каждого состояния известна вероятность перехода в другое состояние за один шаг, т.е. P_ij (из S_i в S_jза один шаг), тогда мы можем записать переходные вероятности в виде матрицы.

. (7.1)

По диагонали этой матрицы расположены вероятности того, что система переходит из состояния S_i в то же состояние S_i.

Пользуясь введенными ранее событиями S₁^(k), S₂^(k),…, S_n^(k) можно переходные вероятности записать как условные вероятности:

P_ij=P(S_j^(k)/S_i^k-1)

Очевидно, что сумма членов P_ij^k=P(S_j^(k)/S_i^k-1) в каждой строке матрицы (1) равна единице, поскольку события S₁^(k), S₂^(k),…, S_n^(k) образуют полную группу несовместных событий.

При рассмотрении марковских цепей, так же как и при анализе марковского случайного процесса, используются различные графы состояний (рис. 7.10).

Рис. 7.10

Данная система может находиться в любом из шести состояний, при этом P_ij – вероятность перехода системы из состояния S_i в состояние S_j. Для данной системы запишем уравнения, что система находилась в каком-либо состоянии и из него за время t не вышла:

В общем случае марковская цепь является неоднородной, т. е. вероятность P_ij меняется от шага к шагу. Предположим, что задана матрица вероятностей перехода на каждом шаге, тогда вероятность того, что система S на k-м шаге будет находиться в состоянии S_i, можно найти по формуле

Зная матрицу переходных вероятностей и начальное состояние системы, можно найти вероятности состояний P₁(k), P₂(k), …, P_n(k) после любого k-го шага. Пусть в начальный момент времени система находится в состоянии S_m. Тогда для t = 0

P₁(0)=0, P₂(0)=0,…, P_m(0)=1,…, P_n(0)=0

Найдем вероятности после первого шага. Из состояния S_m система перейдет в состояния S₁, S₂ и т.д. с вероятностями P_m₁, P_m₂, …, P_mm, … , P_mn. Тогда после первого шага вероятности будут равны

P₁(1) = P_m1; P₂(1) = P_m2, …, P_n(1) = P_mn (7.2)

Найдем вероятности состояния после второго шага: P₁(2), P₂(2), …, P_n(2). Будем вычислять эти вероятности по формуле полной вероятности с гипотезами:

.

Гипотезами будут следующие утверждения:

после первого шага система была в состоянии S₁-H₁;
после второго шага система была в состоянии S₂-H₂;
после n-го шага система была в состоянии S_n-H_n.

Вероятности гипотез известны из выражения (7.2). Условные вероятности перехода в состояние А при каждой гипотезе тоже известны и записаны в матрицы переходных состояний. Тогда по формуле полной вероятности получим:

Вероятность любого состояния после второго шага:

(7.3)

В формуле (7.3) суммируются все переходные вероятности P_ij, но учитываются только отличные от нуля. Вероятность любого состояния после k-го шага:

(7.4)

Таким образом, вероятность состояния после k-го шага определяется по рекуррентной формуле (7.4) через вероятности (k – 1)-го шага.

Задача 6. Задана матрица вероятностей перехода для цепи Маркова за один шаг. Найти матрицу перехода данной цепи за три шага.

Решение. Матрицей перехода системы называют матрицу, которая содержит все переходные вероятности этой системы:

В каждой строке матрицы помещены вероятности событий (перехода из состояния i в состояние j), которые образуют полную группу, поэтому сумма вероятностей этих событий равна единице:

Обозначим через p_ij(n) вероятность того, что в результате n шагов (испытаний) система перейдет из состояния i в состояние j. Например p₂₅(10) — вероятность перехода из второго состояния в пятое за десять шагов. Отметим, что при n=1 получаем переходные вероятности p_ij(1)=p_ij.

Перед нами поставлена задача: зная переходные вероятности p_ij, найти вероятности p_ij(n) перехода системы из состояния i в состояние j заn шагов. Для этого введем промежуточное (между iи j) состояние r. Другими словами, будем считать, что из первоначального состояния i за m шагов система перейдет в промежуточное состояние r с вероятностью p_ij(n-m), после чего, за оставшиеся n-m шагов из промежуточного состояния r она перейдет в конечное состояние j с вероятностью p_ij(n-m). По формуле полной вероятности получаем:

.

Эту формулу называют равенством Маркова. С помощью этой формулы можно найти все вероятности p_ij(n), а, следовательно, и саму матрицу P_n. Так как матричное исчисление ведет к цели быстрее, запишем вытекающее из полученной формулы матричное соотношение в общем виде P_n = P₁ⁿ.

Вычислим матрицу перехода цепи Маркова за три шага, используя полученную формулу:

Ответ: .

Для проверка решения можно использовать калькулятор умножения матриц.

Задача №1. Матрица вероятностей перехода цепи Маркова имеет вид:

.

Распределение по состояниям в момент времени t=0 определяется вектором:

π⁰=(0.5; 0.2; 0.3)

Найти:а) распределение по состояниям в моменты t=1,2,3,4.

в) стационарное распределение.

Источник