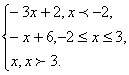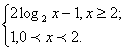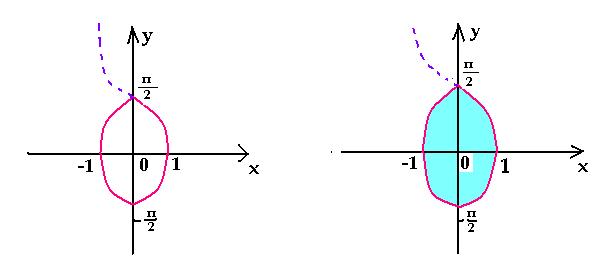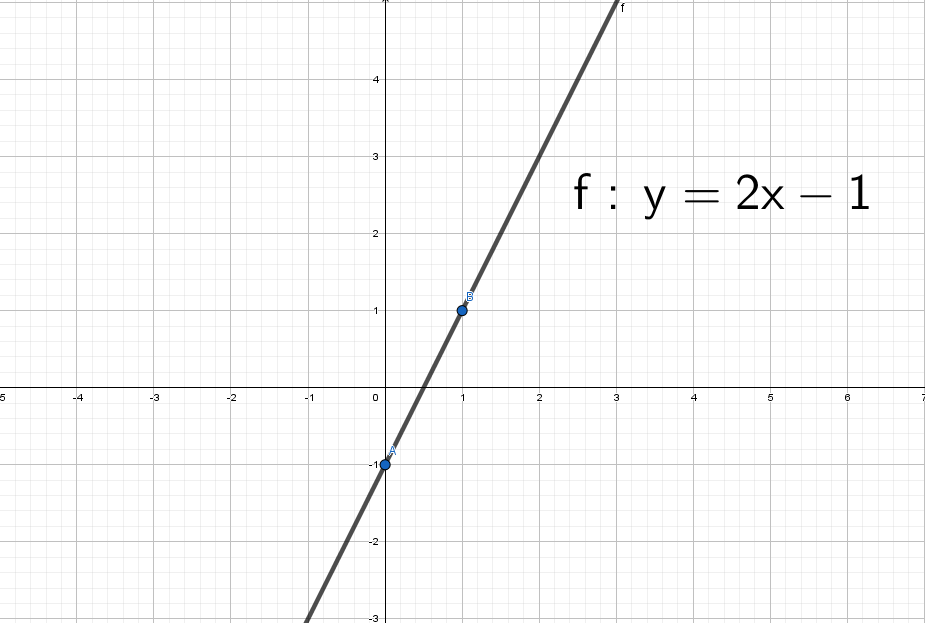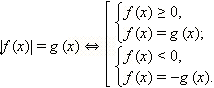Определение модуля
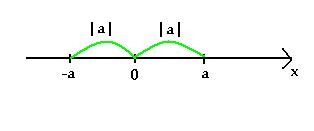
Алгебрагическое определение: | x |
=
Геометрическое определение: модулем
числа называется расстояние от точки,
изображающей это число, до начала отсчета.
Понятие модуля впервые вводится в 6 классе, в 7
классе рассматривается линейная функция и ее
график и уже можно показывать построение
несложных графиков функций, содержащих модуль.
Далее, по мере изучения различных функций, их
свойств, каждую такую тему можно заканчивать
рассмотрением более сложных графиков, в том
числе с модулем. В этой статье рассматриваются
основные приемы построения графиков таких
функций.
I. На алгебрагическом определении основан метод
«раскрытия модуля на промежутках».
Например: | x + 2 | = | x + 2 | =
метод можно применять при построении графиков
функций, содержащих один или более модулей.
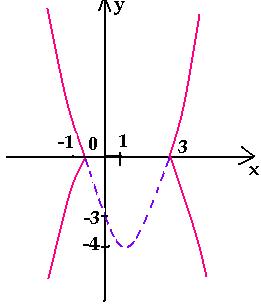
Например, построим график функции у = | x + 2 | –
2x + 1 , предварительно упростив ее.
у = у
=
Если модулей несколько, то каждый из них
раскрываем на промежутках относительно точек,
обращающих каждый из них в нуль. Например,
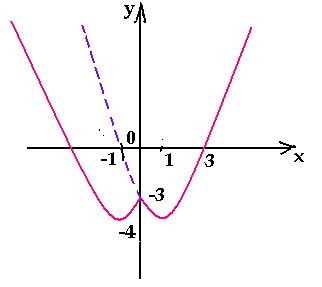
построим график функции у = | 3 – x | – x
+ | x + 2 | + 1.
1. Если х < – 2, то у = 3 – х – х
– (х + 2) + 1, у = – 3х + 2.
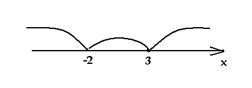
< х < 3, то у = 3 – х – х + х
+ 2 + 1, у = – х + 6.
3. Если х > 3, то у = – (3 – х) – х
+ х + 2 + 1, у = х.
записываем как кусочно-заданную:
у =
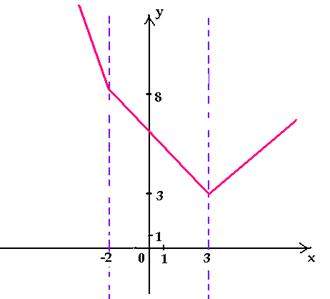
Подобно тому, как числовая прямая точками – 2 и 3
разбивается на промежутки, координатная
плоскость прямыми х = – 2 и х = 3
разбивается на части («полосы»), в каждой из
которых строим свой график. Заметим, что данная
функция непрерывна, поэтому на «границах» части
графика должны соединяться.
метод можно применять к функциям разных видов.
Например, построим график функции у = | log2
x – 1 | – log0,5 x.
Заметим, что х > 0.
1. Пусть log2x – 1 > 0, log2x >
1, x > 2, тогда у = log2 x – 1 +
log2 x; y = 2 log2 x – 1.
2. Пусть log2 x – 1 < 0, 0 < x < 2,
тогда у = – log2 x + 1 + log2 x; y
= 1.
Запишем функцию как кусочно-заданную:
у =
III. Рассмотрим некоторые частные случаи
функций, содержащих модуль.
1) у = | f(x) |.
По определению модуля имеем: | f(x) | =
Таким образом , для того, чтобы построить график
такой функции, необходимо взять часть графика,
лежащую не ниже оси абсцисс, а часть графика,
лежащую ниже этой оси отобразить относительно
нее в верхнюю полуплоскость. (Заметим, что «–»,
стоящий перед функцией означает симметричное
отображение графика относительно оси абсцисс).
Например, построим график функции у = | x2
– 2х – 3 |.
Построим сначала график функции у = х2
– 2х – 3. Графиком этой функции является
парабола, ветви которой направлены вверх.
Координаты ее вершины: х = 1, у = – 4. Точки
пересечения параболы с осями координат: (0; – 3); (–
1; 0); (3; 0). Далее выполняем отображение части
графика, лежащей в нижней полуплоскости,
относительно оси абсцисс.
2) у = f(| x |). Используем определение модуля: f(|
x |) =
Чтобы построить график такой функции строим
график функции у = f(x) и берем ту его
часть, где х > 0 (в правой полуплоскости).
Затем эту часть симметрично отображаем в левую
полуплоскость, где х < 0. (Заметим, что
построение графика функции f(– x) и
состоит в отображении части графика, лежащей в
правой полуплоскости в левую относительно оси
ординат).
Например, построим график функции у = х2
– 2| х | – 3. Сначала строим график функции у
= х2 – 2х – 3, далее выполняем
указанные преобразования.
3) Построим график функции y = | f(| x
|)|, например, y = | x2 – 2| х | – 3 |,
выполним последовательно преобразования,
рассмотренные в пунктах 2 и 1.
4. Рассмотрим зависимость | y | = f(x).
Ее нельзя назвать функцией, так как не
выполняется условие: каждому значению х должно
соответствовать единственное значение у.
Рассмотрим построение графика такой
зависимости (можно говорить «графика
уравнения»). Используем определение модуля: у
= f(x), если у > 0, – у = f(x),
y = – f(x), если у < 0
Получаем, чтобы построить такой график, сначала
строим график функции у = f(x) и
берем ту его часть, которая лежит в верхней
полуплоскости, где у > 0; чтобы
построить график в нижней полуплоскости (где у
< 0), нужно построенную часть отобразить
симметрично относительно оси абсцисс (знак «–»
перед функцией и означает такое отображение)
Например, построим график уравнения | y | = x2
– 2х – 3
Заметим, что графики, не относящиеся к
рассмотренным частным случаям, следует строить «
раскрывая модули на промежутках».
| x |
1 |
0 |
– 1 |
|
y |
0 |
|
|
IV. Приведем некоторые примеры
1. Построим график уравнения | y | = arccos| x
|.
2. Графическим способом можно решать и
неравенства с двумя переменными. Например,
решением неравенства | y | < arccos| x |
являются координаты точек закрашенной части
плоскости, включая границы.
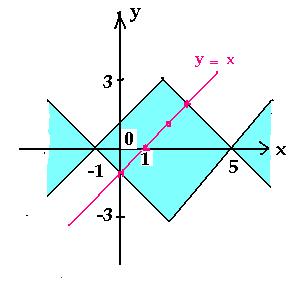
Решим еще одно задание, предлагавшееся на ЕГЭ:
найти все целочисленные решения неравенства | y
| < | | x – 2 | – 3 | (х0; у0),
для которых х0 = у0. Построим
сначала график уравнения | y | = | | x – 2 | –
3 |. Решением данного неравенства будут являться
координаты точек закрашенной части плоскости,
включая границы.
Пары чисел (х0; у0),
являющиеся решениями неравенства, для которых y0
= x0, являются координатами точек,
лежащих на прямой у = х. Выберем точки с
целыми координатами: (0; – 1); (1; 0); (2; 1); (3; 2), они и
будут являться решениями данной задачи.
3. Определить, сколько корней имеет уравнение | 3
– x | + log3| x | = 2 – x.
Запишем уравнение в виде | 3 – x | + x = log3|
x | + 2. В одной системе координат построим
графики функций y = | 3 – x | = x (1) и y
= log3| x | = 2 (2). Функцию (1) запишем как
кусочно-заданную, раскрывая модуль на
промежутках:
y =
График функции (2) построим, выполняя
отображение графика y = log3x + 2
относительно оси ординат ( один из рассмотренных
частных случаев ).
Графики имеют две общие точки, следовательно,
данное уравнение имеет два корня.
V. Для повторения материала, его закрепления
предлагаем выполнить следующие задания.
1. Постройте графики функций и уравнений: y =
| y | =
; y = | | 2 – x
| – 4 |; y = | x2 – 4 | x | + 3 |; y = + 1.
2. Решите графически уравнения c одной и двумя
переменными: | 3 – x | – 3 = 2| x | – x2;
| y | = 2| x | – x2; = | x – 2,5 | –1,5.
3. Решите графически неравенства с двумя
переменными: | y | > x24x + 3;
| x | + | y | < 3.
4. Решите графически систему уравнений:
5. Найдите все значения а, при каждом из которых
уравнение | x + a | + | | x – 3 | – 4 | = 1
имеет ровно два корня.
Пошаговое построение графиков.
«Навешивание» модулей на прямые, параболы, гиперболы.
Графики — самая наглядная тема по алгебре. Рисуя графики, можно творить, а если еще и сможешь задать уравнения своего творчества, то и учитель достойно это оценит.
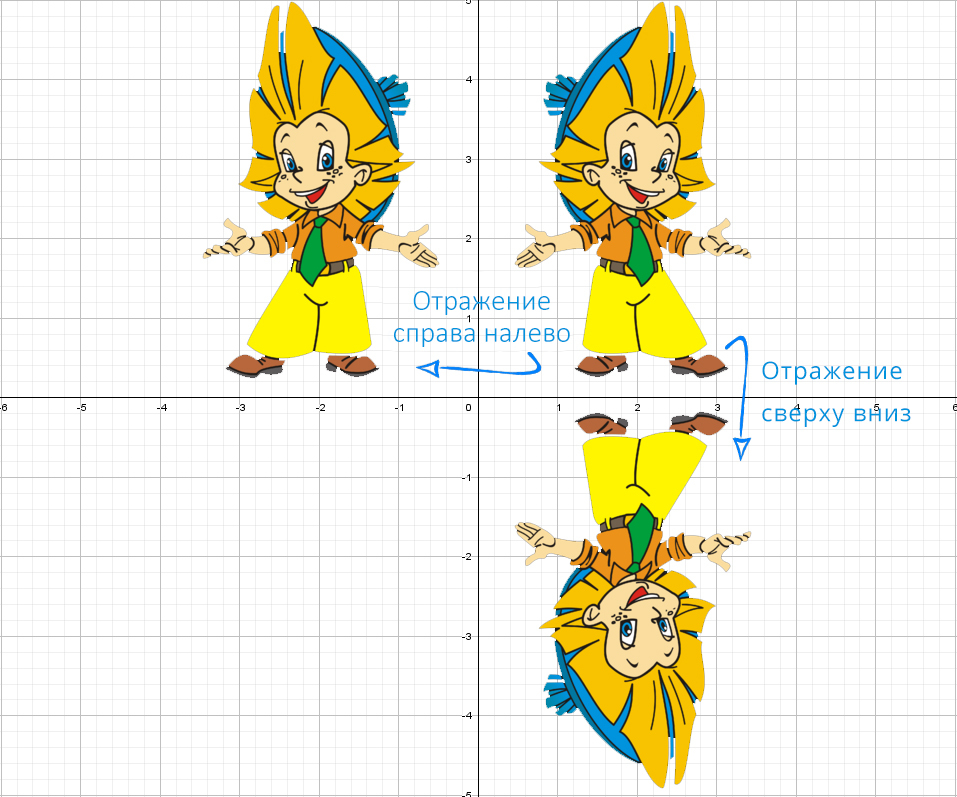
Для понимания друг друга введу немного «обзываний» системы координат:
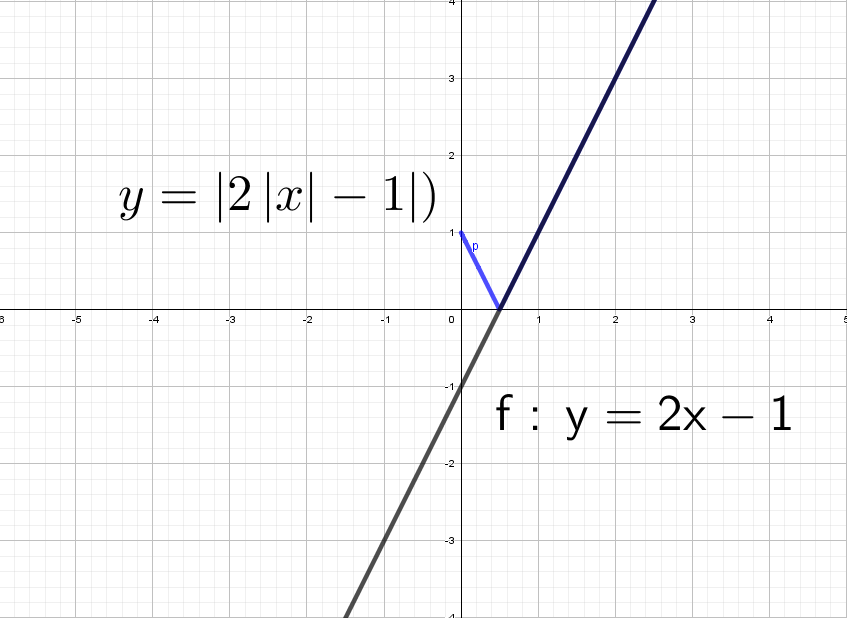
Для начала построим график прямой y = 2x − 1.
Не сомневаюсь, что ты помнишь. Я напомню себе, что через 2 точки можно провести одну прямую.
Возьмем значение X = 0 и Х = 1 и подставим в выражение y = 2x − 1, тогда соответственно Y = − 1 и Y = 1
Через данные две точки А = (0; −1) и B = (1; 1) проводим единственную прямую:
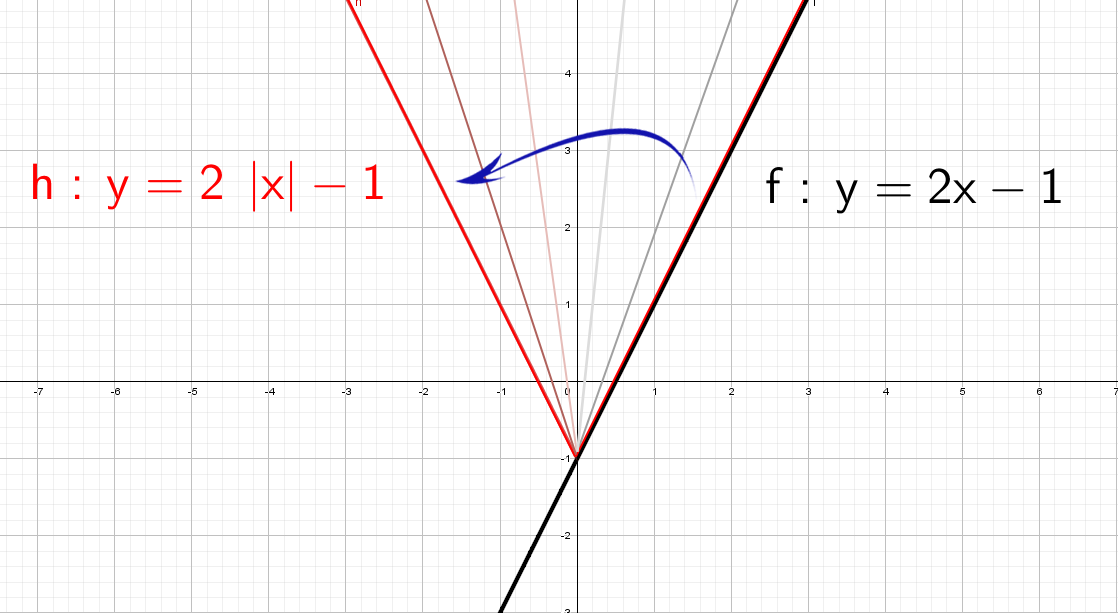
А если теперь добавить модуль y = |2x − 1|.
Модуль — это всегда положительное значение, получается, что «y» должен быть всегда положительным.
Значит, если модуль «надет» на весь график, то, что было в нижней части «−y», отразится в верхнюю (как будто сворачиваете лист по оси х и то, что было снизу, отпечатываете сверху).
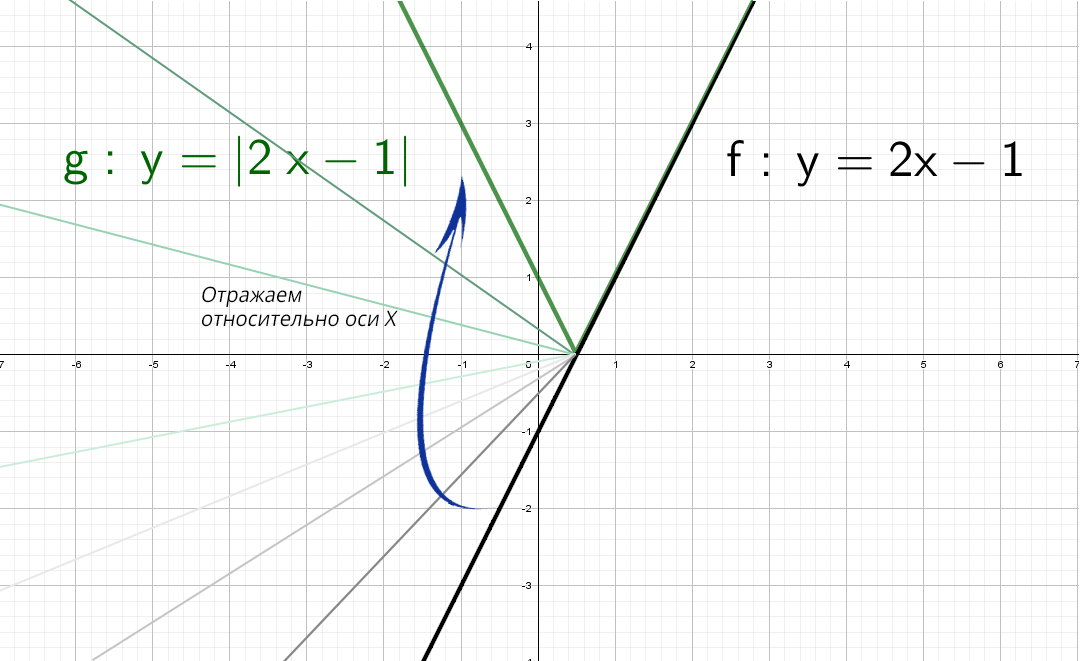
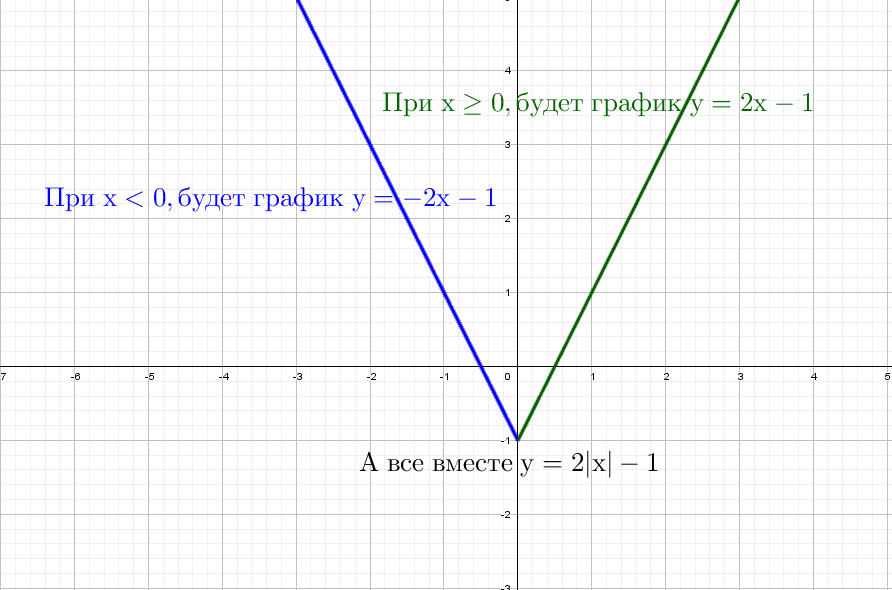
Красота! А как же будет выглядеть график, если надеть модуль только на «х»: y = 2|x| − 1?
Одна строчка рассуждений и рисуем:
Модуль на «x», тогда в этом случае x = −x, то есть все, что было в правой части, отражаем в левую. А то, что было в плоскости «−x», убираем.
Здесь отражаем относительно оси «y». Такая же галочка, только теперь через другую ось.
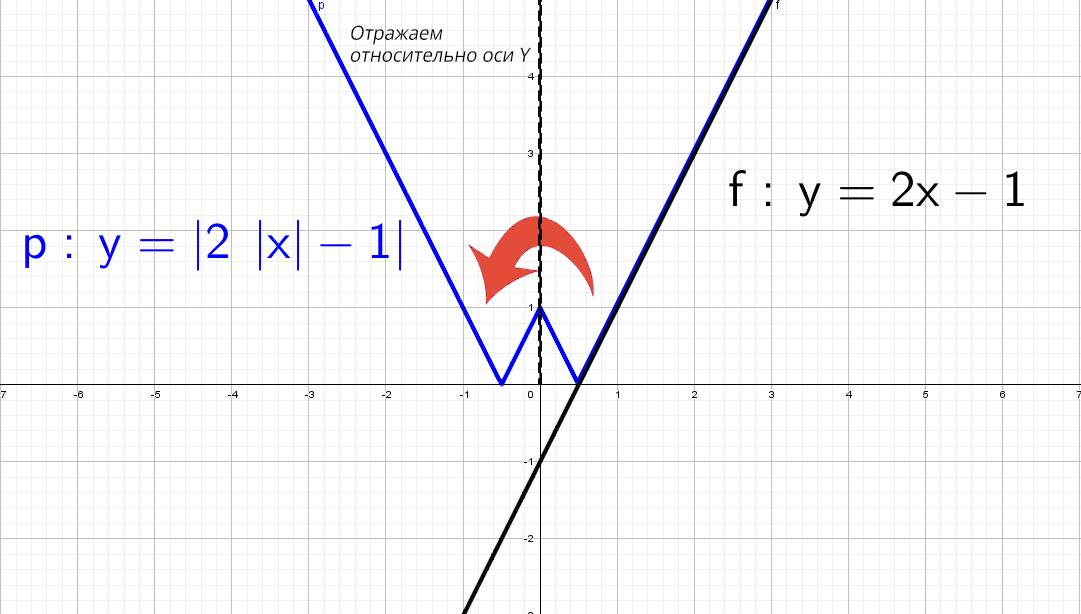
Смертельный номер: y = |2|x| − 1|.
Черную прямую y = 2x − 1 отражаем относительно оси Х, получим y = |2x − 1|. Но мы выяснили, что модуль на х влияет только на левую часть.
В правой части: y = |2x − 1| и y = |2|x| − 1| идентичны!
А после этого отражаем относительно оси «y» то, что мы получили справа налево:
Если ты человек амбициозный, то прямых тебе будет мало! Но то, что описано выше, работает на всех остальных графиках, значит делаем по аналогии.
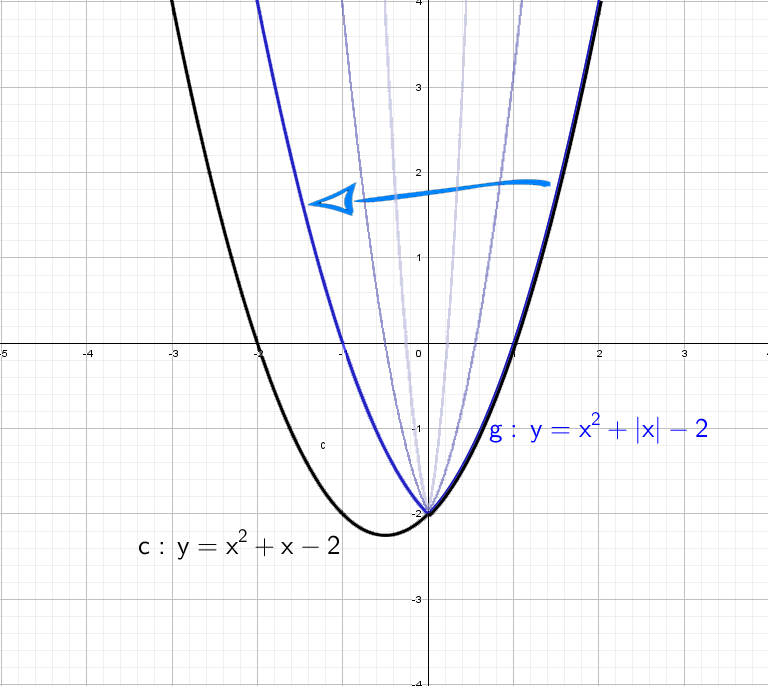
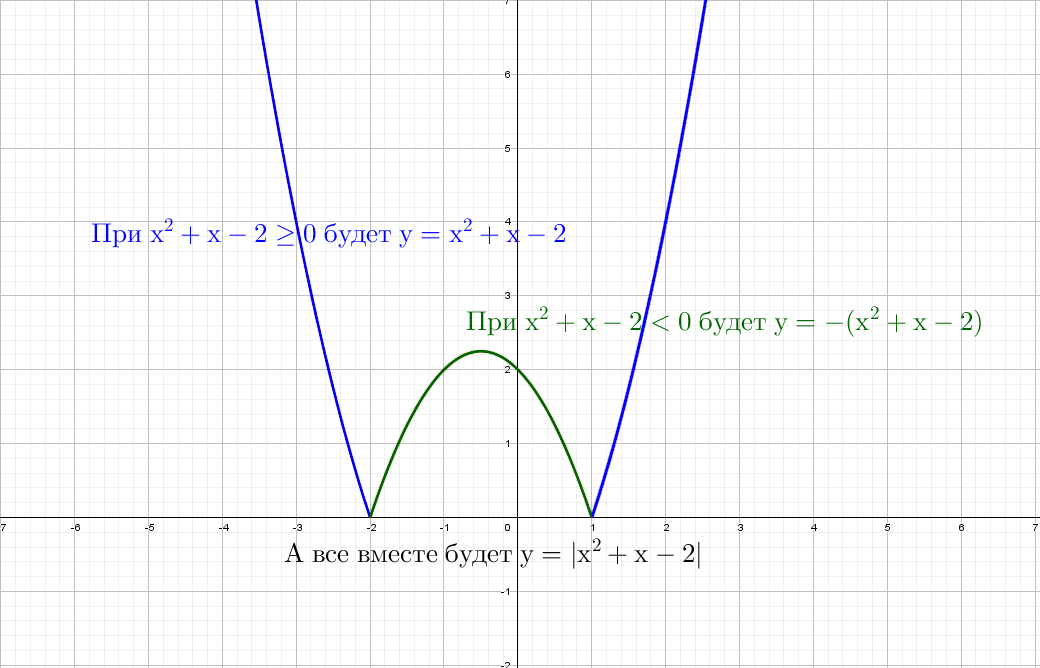
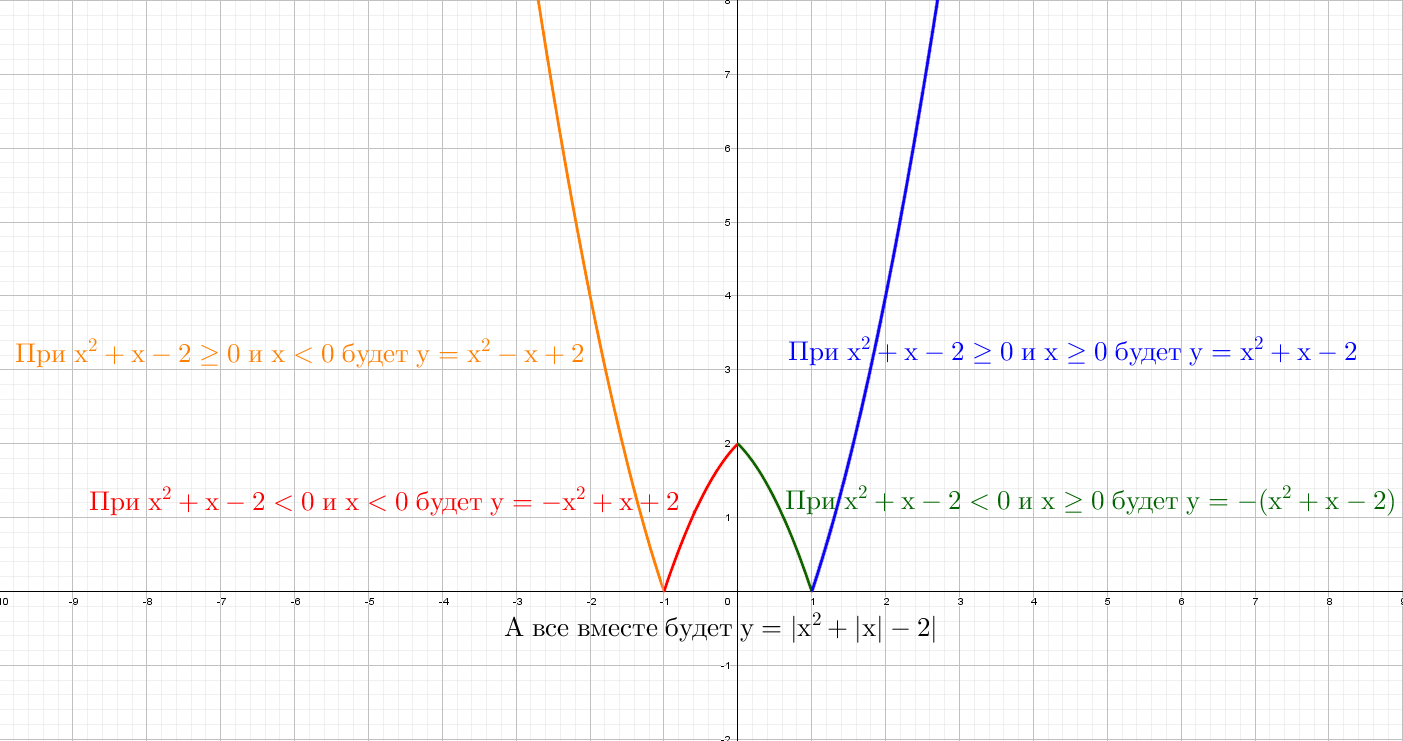
Разберем по винтикам параболу y = x² + x − 2. Точки пересечения с осью «x» получим с помощью дискриминанта: x₁ = 1 и x₂ = -2.
Можно найти вершину у параболы и взять пару точек для точного построения.
А как будет выглядеть график: y = |x²| + x − 2? Слышу: «Такого мы еще не проходили», а если подумаем? Модуль на x², он же и так всегда положителен, от модуля тут толку, как от стоп-сигнала зайцу − никакого.
При y = x² + |x| − 2 все так же стираем всю левую часть, и отражаем справа налево:
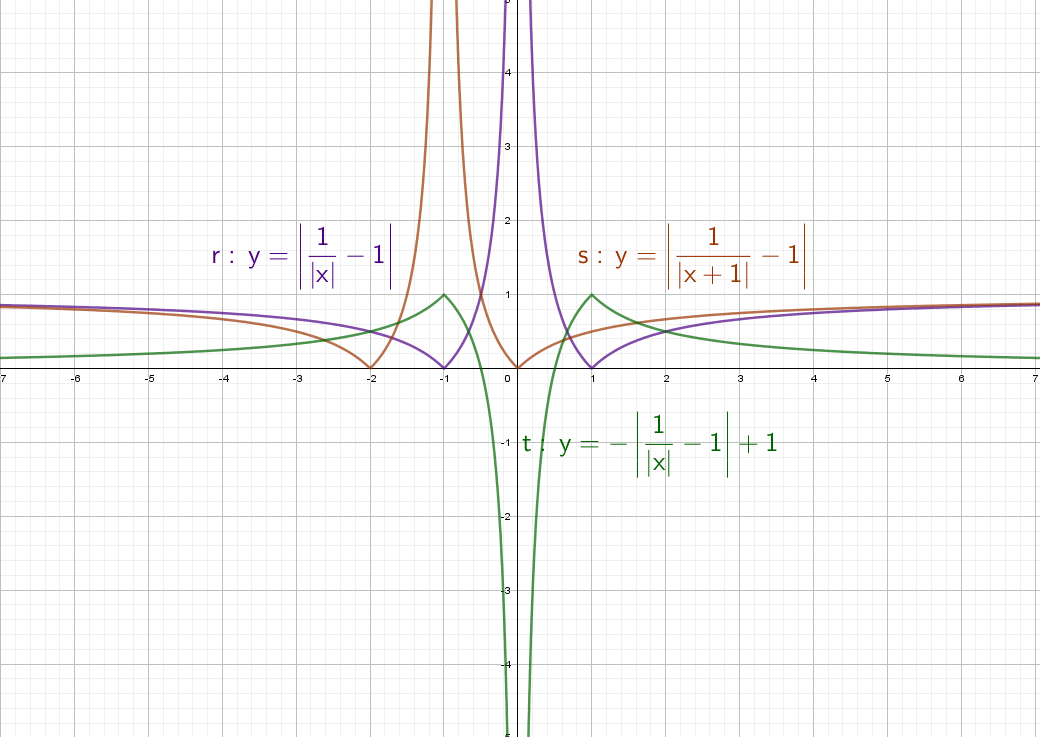
А дальше что мелочиться: рассмотри сразу остальные графики с модулем!
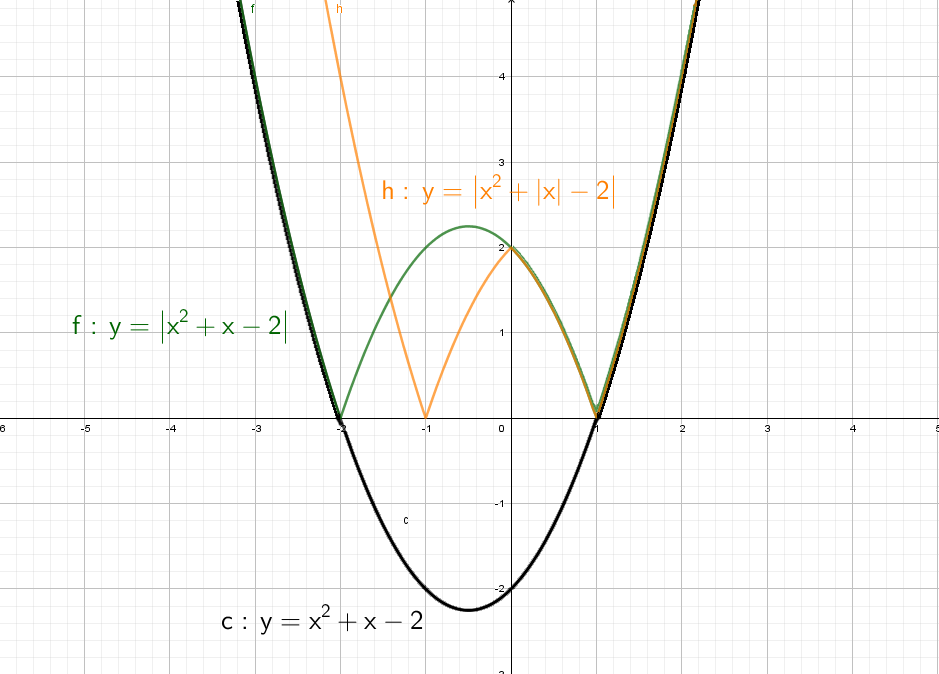
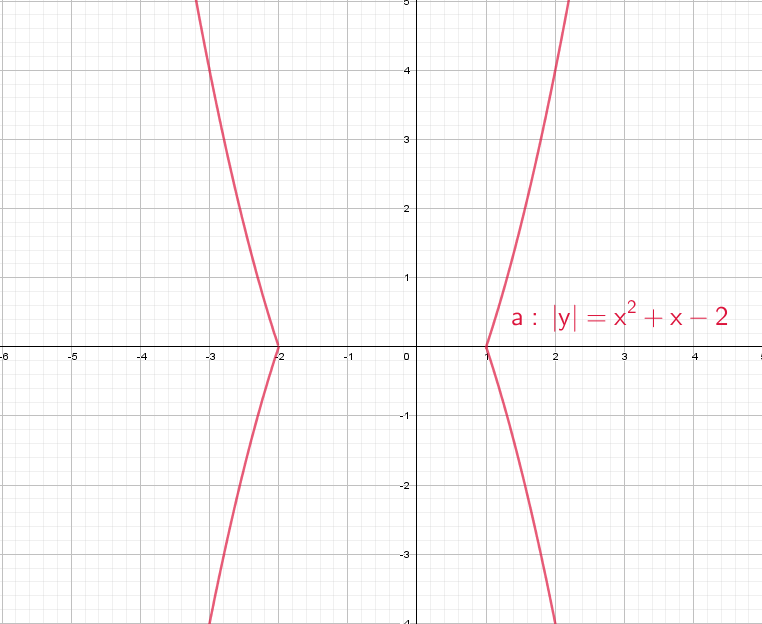
Следующий смертельный номер: |y| = x² + x − 2, подумай хорошенько, а еще лучше попробуй нарисовать сам.
При положительных значениях «y» от модуля нет смысла − уравнения y = x² + x − 2, а при «−y» ничего не меняется, будет так же y = x² + x − 2!
Рисуем параболу в верхней части системы координат (где у > 0), а затем отражаем вниз.
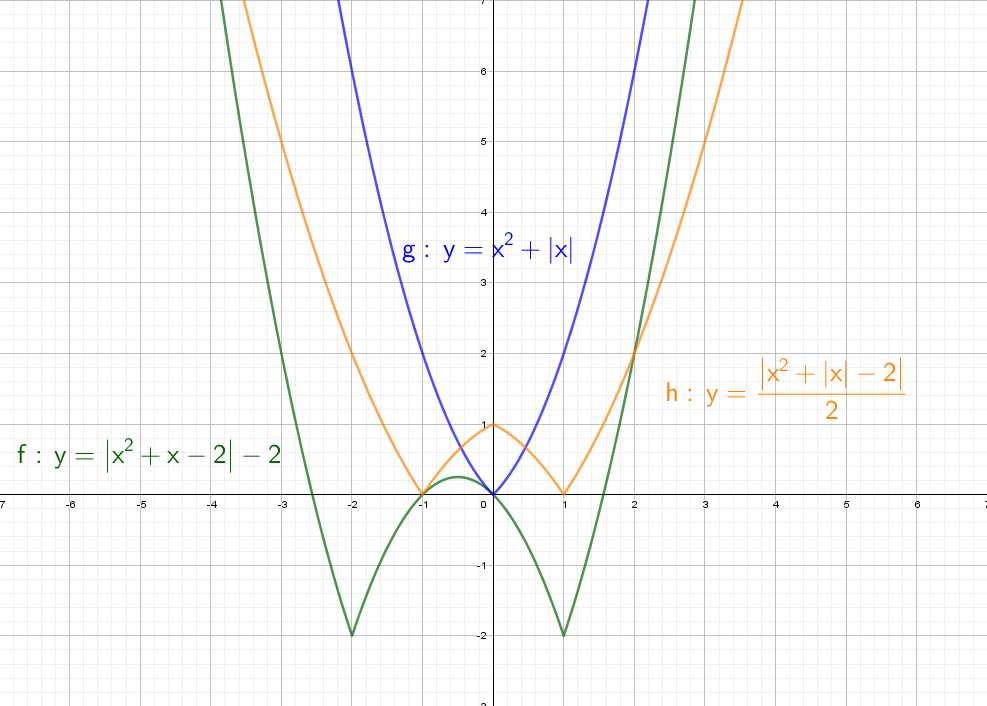
А теперь сразу комбо:
Cиний: похож на y = x² + |x| − 2, только поднят вверх. Строим график в правой части, а затем отражаем через ось Y влево.
Оранжевый: строим в правой части и отражаем относительно оси Х. Доходим до оси Y и отражаем все что было справа налево. Двойка в знаменателе показывает, что график будет «шире», расходится в бока он быстрее остальных.
Зеленый: Так же начинаем с правой части и отражаем относительно оси оси Y. Получается график y = |x² + x − 2|, но еще есть −2, поэтому опустим график на 2 вниз. Теперь параболы как бы отражается относительно Y = − 2.
Легкий и средний уровень позади, и настала пора выжать концентрацию на максимум, потому что дальше тебя ждут гиперболы, которые частенько встречаются во второй части ЕГЭ и ОГЭ.
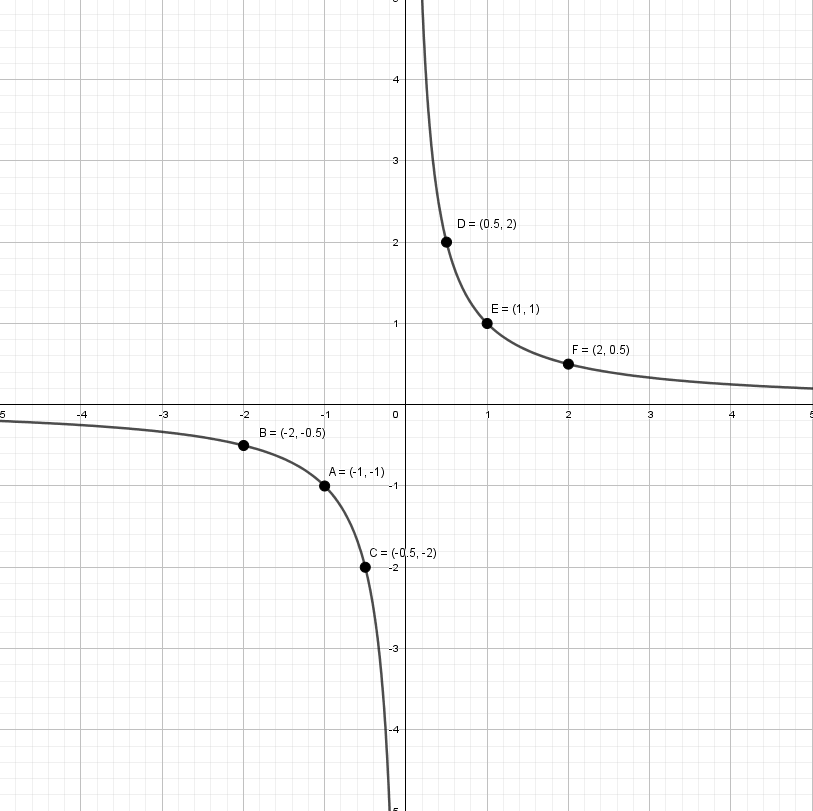
y = 1/x — простая гипербола, которую проще всего построить по точкам, 6-8 точек должно быть достаточно:
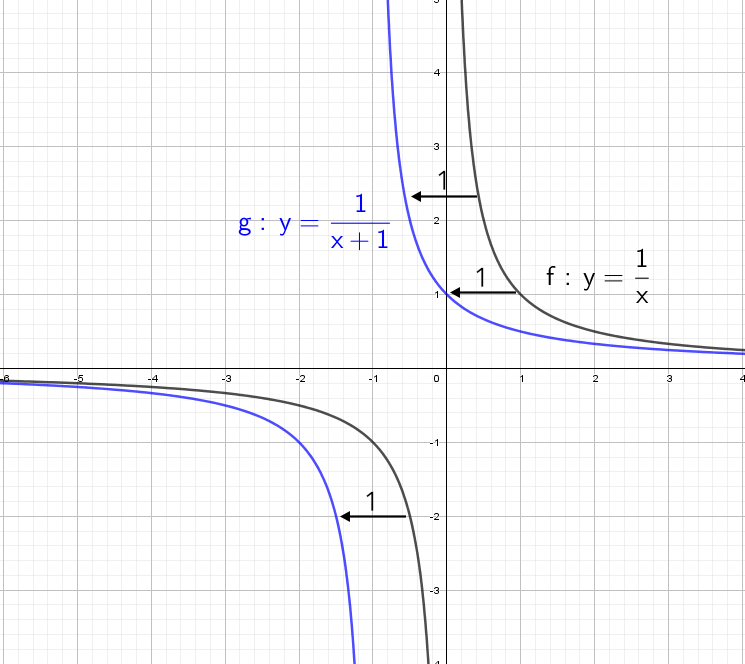
А что будет, если мы добавим в знаменателе «+1»? График сдвинется влево на единицу:
А что будет, если мы добавим в знаменателе «−1»? График сдвинется вправо на единицу.
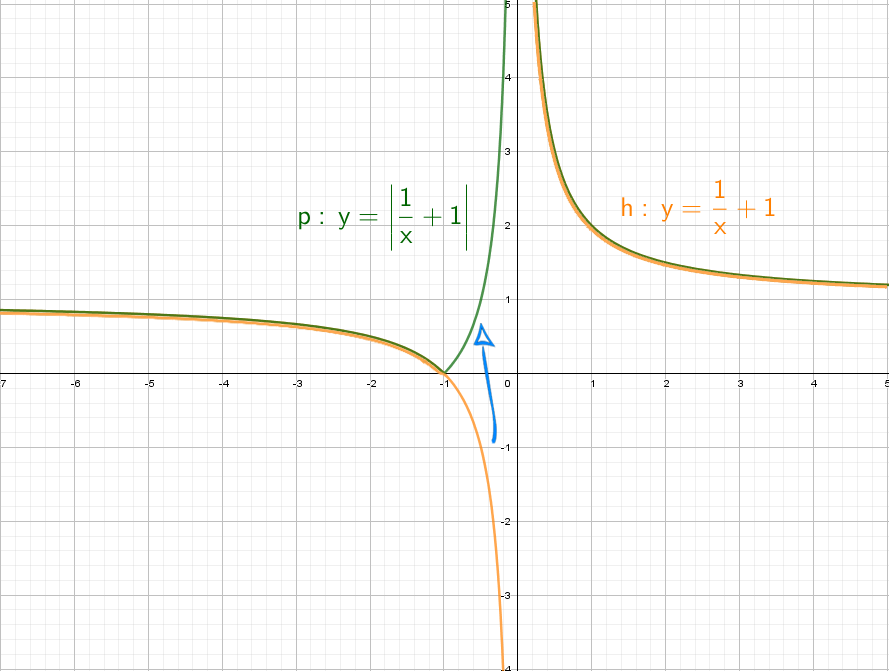
А если добавить отдельно «+1» y = (1/x) + 1? Конечно, график поднимется вверх на единицу!
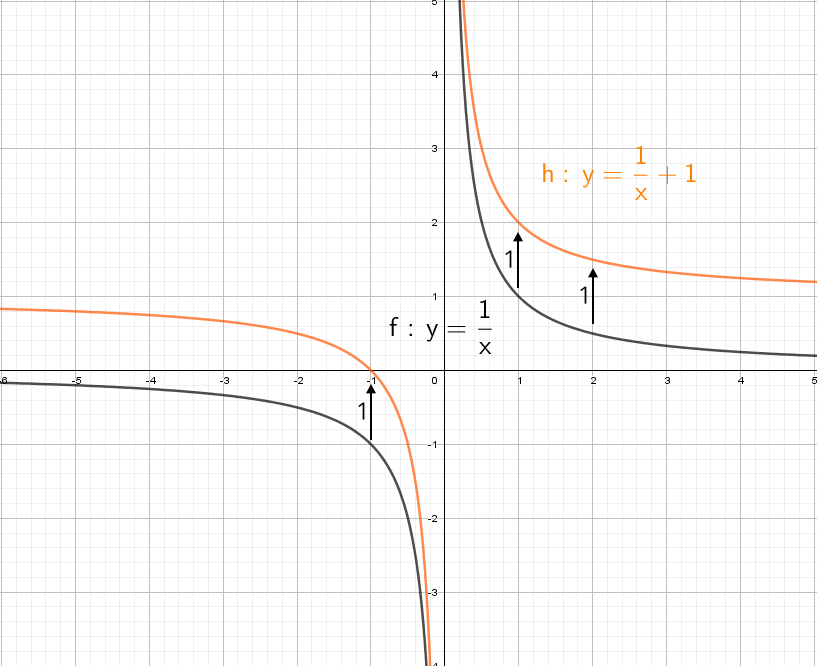
Теперь начнем «накручивать» модули: y = |1/x + 1| — отражаем все из нижней части в верхнюю.
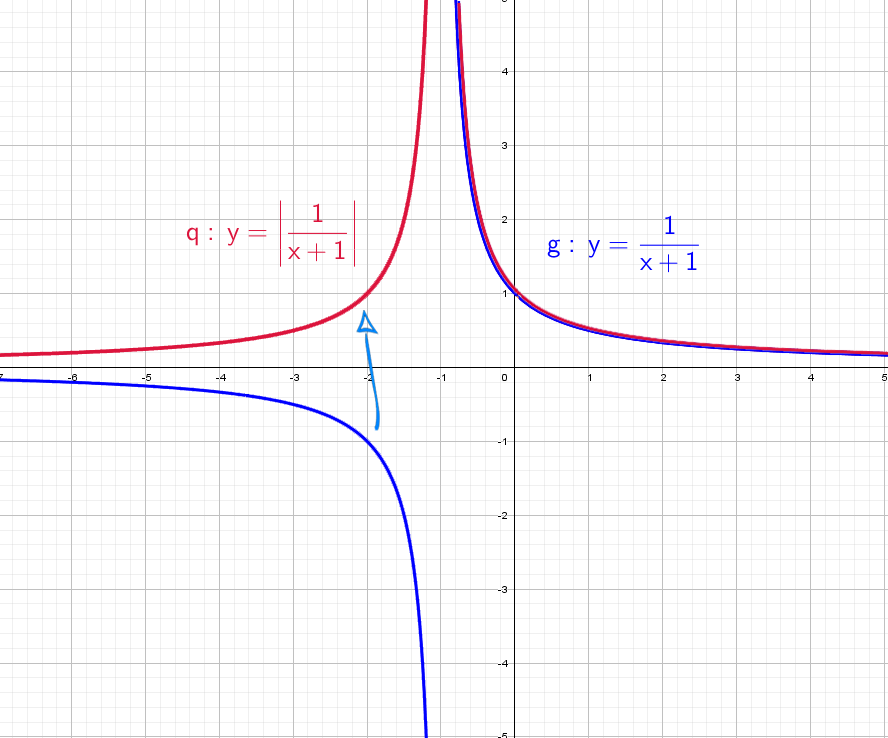
Возьмем другой модуль, мой амбициозный друг, раз ты дошел до этогог места: y = |1/(x + 1)|. Как и выше, когда модуль надет на всю функцию, мы отражаем снизу вверх.
Можно придумывать массу вариантов, но общий принцип остается для любого графика. Принципы повторим в выводах в конце статьи.
Фиолетовый: Вычитаем из дроби −1 и сдвигаем график вниз на единицу. Ставим модуль − отражаем все, что снизу вверх.
Оранжевый: Ставим +1 в знаменателе и график смещается влево на единицу. Вычитаем из дроби −1 и сдвигаем график вниз на единицу. А после этого ставим модуль − отражаем все, что снизу вверх.
Зеленый: Сначала получим фиолетовый график. После этого ставим «−» и отражаем график по горизонтали. Сгибаем лист по оси Х и переводим его вниз. Остается добавить +1, это значит, что его нужно поднять вверх на единицу.
Модули не так уж страшны, если еще вспомнить, что их можно раскрыть по определению:
И построить график, разбив его на кусочно-заданные функции.
Например для прямой:
Для параболы с одним модулем будет два кусочно-заданных графика:
C двумя модулями кусочно-заданных графиков будет четыре:
Выводы:
- Модуль — это не просто две палочки, а жизнерадостное, всегда положительное значение!
- Модулю без разницы находится он в прямой, параболе или еще где-то. Отражения происходят одни и те же.
- Любой нестандартный модуль можно разбить на кусочно-заданные функции, условия только вводятся на каждый модуль.
- Существует большое количество модулей, но парочку вариантов стоит запомнить, чтобы не строить по точкам:
- Если модуль «надет» на все выражение (например, y = |x² + x − 2|), то нижняя часть отражается наверх.
- Если модуль «надет» только на х (например, y = x² + |x| − 2), то правая часть графика отражается на левую часть. А «старая» левая часть стирается.
- Если модуль «надет» и на х, и на все выражение (например, y = |x² + |x| − 2|), то сначала отражаем график снизу вверх, после этого стираем полностью левую часть и отражаем справа налево.
- Если модуль «надет» на y (например, |y| = x² + x − 2), то мы оставляем верхнюю часть графика, нижнюю стираем. А после отражаем сверху вниз.
Будь в курсе новых статеек, видео и легкого математического юмора.
Знак модуля, пожалуй, одно из самых интересных явлений в математике. В связи с этим у многих школьников возникает вопрос, как строить графики функций, содержащих модуль. Давайте подробно разберем этот вопрос.
1. Построение графиков функций, содержащих модуль
Пример 1.
Построить график функции y = x2 – 8|x| + 12.
Решение.
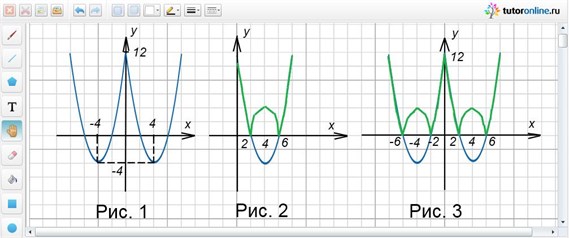
Определим четность функции. Значение для y(-x) совпадает со значением для y(x), поэтому данная функция четная. Тогда ее график симметричен относительно оси Oy. Строим график функции y = x2 – 8x + 12 для x ≥ 0 и симметрично отображаем график относительно Oy для отрицательных x (рис. 1).
Пример 2.
Следующий график вида y = |x2 – 8x + 12|.
– Какова область значений предложенной функции? (y ≥ 0).
– Как расположен график? (Над осью абсцисс или касаясь ее).
Это значит, что график функции получают следующим образом: строят график функции y = x2 – 8x + 12, оставляют часть графика, которая лежит над осью Ox, без изменений, а часть графика, которая лежит под осью абсцисс, симметрично отображают относительно оси Ox (рис. 2).
Пример 3.
Для построения графика функции y = |x2 – 8|x| + 12| проводят комбинацию преобразований:
y = x2 – 8x + 12 → y = x2 – 8|x| + 12 → y = |x2 – 8|x| + 12|.
Ответ: рисунок 3.
Рассмотренные преобразования справедливы для всех видов функций. Составим таблицу:
|
Функция |
Преобразование |
|
f(|x|) |
1) Для x ≥ 0, y = f(x) 2) Для x < 0 – преобразование симметрии относительно Oy графика y = f(x), для x ≥ 0 симметричные части графика из правой полуплоскости в левую |
|
|f(x)| |
1) Для f(x) ≥ 0, |f(x)| = f(x) 2) Для f(x) < 0, |f(x)| = -f(x) Симметричное отображение части графика из нижней полуплоскости в верхнюю относительно Ox |
|
|f(|x|)| |
f(x) → f(|x|) → |f(|x|)|. |
2. Построение графиков функций, содержащих в формуле «вложенные модули»
Мы уже познакомились с примерами квадратичной функции, содержащей модуль, а так же с общими правилами построения графиков функций вида y = f(|x|), y = |f(x)| и y = |f(|x|)|. Эти преобразования помогут нам при рассмотрении следующего примера.
СЛОЖНА-А-А 🙀 Ты же знаешь, что если не разобраться в теме сейчас, то потом придется исправлять оценки. Беги на бесплатное онлайн-занятие с репетитором (подробности тут + 🎁).
Пример 4.
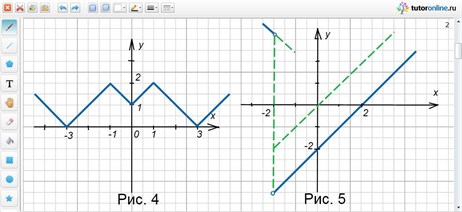
Рассмотрим функцию вида y = |2 – |1 – |x|||. Выражение, задающее функцию, содержит «вложенные модули».
Решение.
Воспользуемся методом геометрических преобразований.
Запишем цепочку последовательных преобразований и сделаем соответствующий чертеж (рис. 4):
y = x → y = |x| → y = -|x| → y = -|x| + 1 → y = |-|x| + 1|→ y = -|-|x| + 1|→ y = -|-|x| + 1| + 2 → y = |2 –|1 – |x|||.
Рассмотрим случаи, когда преобразования симметрии и параллельного переноса не являются основным приемом при построении графиков.
Пример 5.
Построить график функции вида y = (x2 – 4)/√(x + 2)2.
Решение.
Прежде чем строить график, преобразуем формулу, которой задана функция, и получим другое аналитическое задание функции (рис. 5).
y = (x2 – 4)/√(x + 2)2 = (x– 2)(x + 2)/|x + 2|.
Раскроем в знаменателе модуль:
При x > -2, y = x – 2, а при x < -2, y = -(x – 2).
Область определения D(y) = (-∞; -2)ᴗ(-2; +∞).
Область значений E(y) = (-4; +∞).
Точки, в которых график пересекает с оси координат: (0; -2) и (2; 0).
Функция убывает при всех x из интервала (-∞; -2), возрастает при x от -2 до +∞.
Здесь нам пришлось раскрывать знак модуля и строить график функции для каждого случая.
Пример 6.
Рассмотрим функцию y = |x + 1| – |x – 2|.
Решение.
Раскрывая знак модуля, необходимо рассмотреть всевозможную комбинацию знаков подмодульных выражений.
Возможны четыре случая:
{x + 1 – x + 2 = 3, при x ≥ -1 и x ≥ 2;
{-x – 1 + x – 2 = -3, при x < -1 и x < 2;
{x + 1 + x – 2 = 2x — 1, при x ≥ -1 и x < 2;
{-x – 1 – x + 2 = -2x + 1, при x < -1 и x ≥ 2 – пустое множество.
Тогда исходная функция будет иметь вид:
{3, при x ≥ 2;
y = {-3, при x < -1;
{2x – 1, при -1 ≤ x < 2.
Получили кусочно-заданную функцию, график которой изображен на рисунке 6.
3. Алгоритм построения графиков функций вида
y = a1|x – x1| + a2|x – x2| + … + an|x – xn| + ax + b.
В предыдущем примере было достаточно легко раскрыть знаки модуля. Если же сумм модулей больше, то рассмотреть всевозможные комбинации знаков подмодульных выражений проблематично. Как же в этом случае построить график функции?
Заметим, что графиком является ломаная, с вершинами в точках, имеющих абсциссы -1 и 2. При x = -1 и x = 2 подмодульные выражения равны нулю. Практическим путем мы приблизились к правилу построения таких графиков:
Графиком функции вида y = a1|x – x1| + a2|x – x2| + … + an|x – xn| + ax + b является ломаная с бесконечными крайними звеньями. Чтобы построить такую ломаную, достаточно знать все ее вершины (абсциссы вершин есть нули подмодульных выражений) и по одной контрольной точке на левом и правом бесконечных звеньях.
Задача.
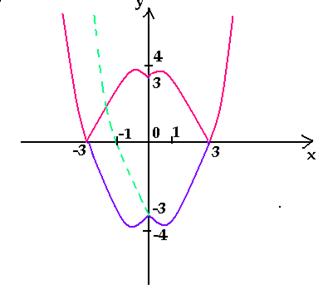
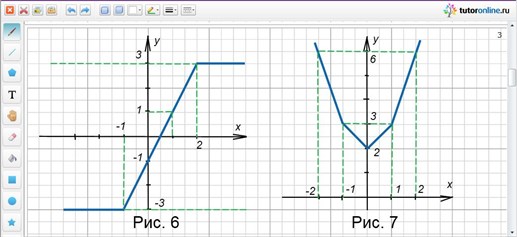
Построить график функции y = |x| + |x – 1| + |x + 1| и найти ее наименьшее значение.
Решение:
Нули подмодульных выражений: 0; -1; 1. Вершины ломаной (0; 2); (-1; 3); (1; 3). Контрольная точка справа (2; 6), слева (-2; 6). Строим график (рис. 7). min f(x) = 2.
Молодец! Раз ты дочитал это до конца, вероятно, ты все отлично усвоил. Но если вдруг что-то еще непонятно — попробуй онлайн-занятие с репетитором (подробности тут + 🎁).
Остались вопросы? Не знаете, как построить график функции с модулем?
Чтобы получить помощь репетитора – зарегистрируйтесь.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
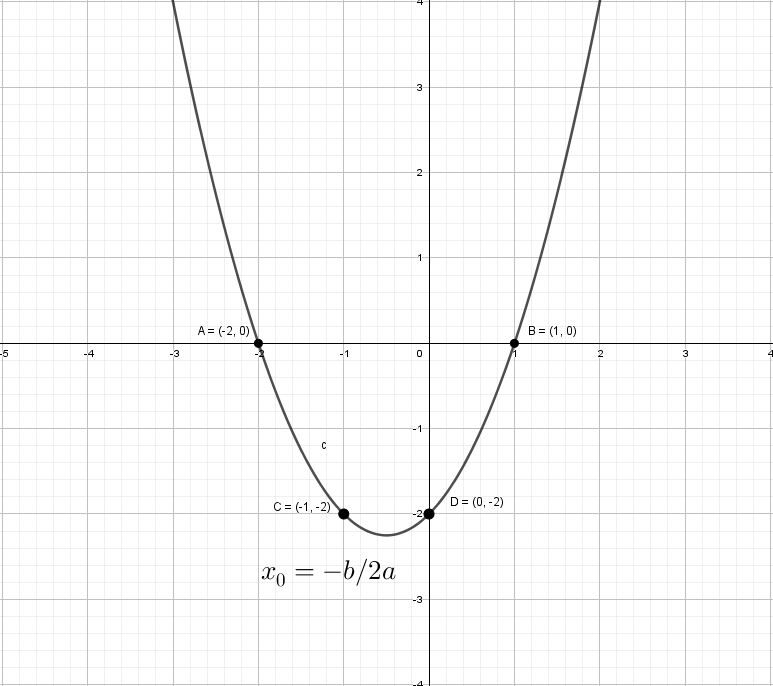
График квадратичной функции, содержащей модуль.
Функция, определяемая формулой у=ах²+вх+с, где х и у переменные, а параметры а, в и с – любые действительные числа, причём а≠0, называется квадратичной.
График функции у=ах²+вх+с есть парабола; осью симметрии параболы является прямая . При а>0 «ветви» параболы направлены вверх, при а<0 – вниз.
Чтобы построить график квадратичной функции, нужно:
1) найти координаты вершины параболы и отметить её в координатной плоскости;
2) построить ещё несколько точек, принадлежащих параболе;
3) соединить отмеченные точки плавной линией.
Определение: абсолютной величиной неотрицательного числа называется само это число, абсолютной величиной отрицательного числа называется противоположное ему положительное число.
Свойства: 1 .|a| ≥0, 3 .|a∙b|=|a|∙|b|,
2. |a|²= a², 4. |a/b|=|a|/|b|, b≠0
2. Построение графика квадратичной функции, содержащей переменную под знаком модуля.
На примере функции у= x ^2– 6х +5 рассмотрены всевозможные случаи расположения модуля.
у = |x 2 – 6х +5|
у = | х | 2 – 6х +5
у = х² – 6|х| +5
у = |х|² — 6|х|+5
у = |х² – 6х| +5
у = |х² – 6|х| +5|
у = x 2 -|6х + 5|
|y|= x 2 – 6х +5
Пример 1:Построим график функции у = |x 2 – 6х +5|.
Пользуясь определением модуля, рассмотрим два случая:
1) x 2– 6х +5≥ 0, тогда у= x 2– 6х +5.
Построим данную параболу. Выделим все точки параболы с неотрицательной ординатой.
2) x 2– 6х +5<0, тогда у= -(x 2– 6х +5) или -x 2+ 6х -5>0, y= -x 2+ 6х -5.
Построим график данной функции, и выделим все точки параболы с положительной ординатой. Все выделенные в обоих случаях точки образуют график функции у = |x 2 – 6х +5|.
.
Итак ,можно сделать вывод: чтобы получить график функции у = |x 2 -6х + 5|, нужно часть параболы, расположенной ниже оси Ох, зеркально отобразить относительно оси Ох .
Пример 2:Рассмотрим график функции у = |х|²– 6х +5.
Т. к. |х|²= х², то график функции у =|х|² — 6х +5 совпадет с графиком функции у = х² — 6х +5, не содержащей знак абсолютной величины.
.
Пример 3: Рассмотрим график функции у = х² – 6|х| +5.
Воспользуемся определением модуля числа.
Пусть x≥0, тогда y= х² — 6х +5.
Построим параболу у = х² — 6х +5 и обведём ту её часть, которая соответствует неотрицательным значениям х , т.е. часть, расположенную правее оси Оу.
2)Пусть x<0, тогда y= x² + 6х +5.
В той же координатной плоскости построим параболу у = х² +6х +5 и обведём ту её часть, которая соответствует отрицательным значениям х, т.е. часть, расположенную левее оси Оу. Обведённые части парабол вместе образуют график функции у = х² — 6|х| +5
Итак, можно сделать вывод: для построения графика функции у = х² – 6|х| +5. надо сохранить ту часть графика , точки которой находятся на оси Oy или справа от нее, и симметрично отобразить ее относительно оси Оy.
Пример 4: Рассмотрим график функции у = |х|² — 6|х|+5.
Т.к. |х|²= х², то график функции у = |х|² – 6|х| +5 совпадает с графиком функции у = х² – 6|х| +5, рассмотренном в примере 3.
Пример 5. Построим график функции у = |х² – 6х| +5.
Для этого построим сначала график функции у = х² — 6х. Чтобы получить из него график функции у = |х² — 6х|, нужно часть параболы, расположенную ниже оси х, заменить линией ей симметричной относительно оси х. Т.к. нам
Нужно построить график функции у = |х² — 6х| +5, то график рассмотренной нами функции у = |х² — 6х| нужно просто поднять по оси у на 5 единиц вверх.
Пример 6: Построим график функции у = |х² – 6|х| +5|.
Для этого сначала построим график функции у =х²- 6|х| +5. (см. пример 3).
Т. к. наша функция полностью находится под знаком модуля, то для того, чтобы построить график функции
у = |х² – 6|х| +5|, нужно часть параболы, расположенную ниже оси Ох, заменить линией ей симметричной относительно оси Ох.
Пример 7:Построим график функции у = x 2 -|6х + 5|.
Пользуясь определением модуля, рассмотрим два случая:
6х+5≥0, т.е. х ≥ -5∕6, , тогда функция примет вид у=x² — 6х -5.
Построим параболу и обведем ту часть , где x≥-5∕6,
6х+5<0, т.е. х < -5∕6, тогда функция принимает вид у=x² + 6х +5.
Построим эту параболу и обведем ту её часть, которая расположена левее точки с абсциссой х =-5∕6,
Обведенные в обоих случаях части парабол являются графиком данной функции.
Пример 8. |y|= x 2 – 6х +5
Равенство |y|= x 2 – 6х +5 не задает функции, т. к. при
x 2 – 6х +5 >0 имеем 2 значения y, соответствующих
данному значению x, а при x 2 – 6х +5 <0, ни одного такого
значения. График данного уравнения строится так:
Отбрасываем ту часть графика , которая лежит ниже оси
Ох, а оставшуюся часть симметрично отображаем
относительно оси Ох.
1)Для построения графика функции y = |f(x)| , надо сохранить ту часть графика функции y = f(x), точки которой находятся на оси Ох или выше оси Ох, и симметрично отразить относительно оси Ох ту часть графика функции y = f(x), которая расположена ниже оси Ох.
2) Для построения графика y = f(|x|) надо сохранить ту часть графика функции y = f(|x|), точки которой на оси Оу или справа от неё и симметрично отразить эту часть графика относительно оси Оу.
3) Чтобы построить график функции |y|= x 2 – 6х +5 нужно:
Отбросить ту часть графика , которая лежит ниже оси
Ох, а оставшуюся часть симметрично отобразить
относительно оси Ох
Используемая литература:
1.Математика. Алгебра. Функции. Анализ данных. 9 кл.: М.: Учеб. для общеобразоват. учреждений / Г. В. Дорофеев, С. Б. Суворова, Е. А. Бунимович, Л. В. Кузнецова, С. С. Минаева. 2. Курс высшей математики для техникумов. И. Ф. Суворов, Москва — 1967.
3. Математика. Алгебра и элементарные функции. М. И. Абрамович, М. Т. Стародубцев.
4. А.Г. Мордкович Книга для учителя. Беседы с учителями. Москва – «Оникс 21 век», «Мир и образование», 2005 г.
Готовимся к ОГЭ по математике, решаем задание 23 на построение графика функции с модулем. За это задание на экзамене можно получить максимум 2 балла.
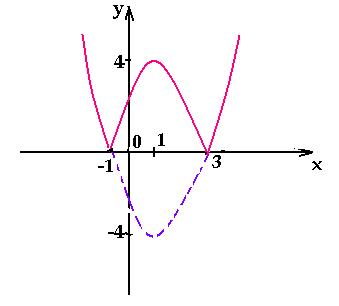
Постройте график функции y= |x 2 + 4x + 3|. Какое наибольшее число общих точек график данной функции может иметь с прямой параллельной оси абсцисс?
Чтобы построить график функции y= |x 2 + 4x + 3|, нужно сначала построить график функции y= x 2 + 4x + 3. Это квадратичная функция, график которой парабола с ветвями направленными вверх. Выделим квадрат двучлена чтобы найти вершину параболы: x 2 + 4x + 3 = (x 2 + 4x + 4) — 1 = (x + 2) 2 -1. Мы преобразовали функцию y = (x + 2) 2 — 1. Вершина параболы имеет координаты (-2;-1) и ось симметрию x = -2. Построим параболу по точкам. В таблице приведены значения для правой ветви. Левая ветвь строится симметрично.
Первая часть задания 23 из ОГЭ по математике выполнена, т.е. построен график квадратичной функции под модулем. Осталось определить — какое наибольшее число общих точек график данной функции может иметь с прямой параллельной OX:
- если проведем прямую y=0, то получаем 2 общие точки;
- если значения y находятся в промежутке (0;1), то 4 общие точки;
- если проведем прямую y =1, то мы видим 3 общие точки;
- если y>1, то 2 точки.

Данная статья посвящена решению примеров заданий 23 из ОГЭ по математике. В этих заданиях школьников обычно просят построить график той или иной функции, а затем указать, при каких значениях параметра этот график пересекается с неким другим графиком, касается его или же, к примеру, имеет с ним несколько точек пересечения. Ну и тому подобное. В данной статье вы найдёте разбор примеров решения заданий 23 из ОГЭ по математике от профессионального репетитора, на протяжении многих лет занимающегося подготовкой школьников к этому экзамену.
Примеры решения заданий 23 из ОГЭ по математике
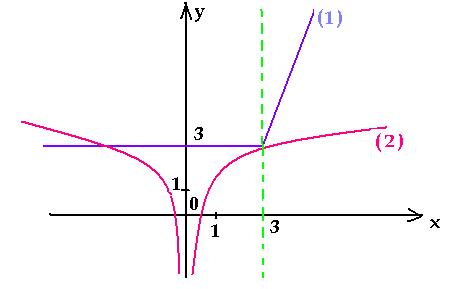
Пример 1. Постройте график функции
Определите, при каких значениях прямая имеет с графиком ровно одну общую точку.
Построение графика функции всегда нужно начинать с указания области определения этой функции. В данном случае ограничения на эту область задаются тем, что в знаменателе не должно быть нуля, потому что деление на нуль не имеет математического смысла. То есть областью определения данной функции являются все числа, за исключением 1. Записать это можно следующим образом:
После того, как мы указали область определения исходной функции, можно попробовать её упростить. Для этого вынесем минус в знаменателе за скобку и сократим. В результате получим следующее выражение:
График данной функции получается из графика функции путём её отражения относительно оси OX
и параллельного переноса всех точек на 0,25 единичного отрезка вниз. При этом мы должны удалить из этого графика точку , потому что она не входит в область определения исходной функции. То есть искомый график выглядит следующим образом:
Теперь отвечаем на главный вопрос задачи. Графиком функции является прямая, проходящая через начало координат. При этом в зависимости от коэффициента эта прямая имеет разный наклон относительно оси OX
. Когда это прямая имеет ровно одну общую точку с изображённым графиком? Только в двух случаях. Рассмотрим их по отдельности.
Первый случай
. Когда данная прямая касается изображённого графика. Это ситуация изображена на рисунке:
Сложность состоит в том, чтобы определить значения , при которых эта ситуация реализуется. Для решения этой задачи можно использовать несколько различных подходов. Используем наиболее типичный.
Суть в том, что в точке касания графики проходят через одну и ту же точку на координатной плоскости. Значит, в этой точке имеет место равенство:
Дискриминант последнего квадратного уравнения равен , и в зависимости от коэффициента он может быть:
- отрицательным, тогда корней у этого уравнения не будет, как не будет и точек пересечения соответствующей прямой с изображённым графиком;
- положительным, тогда корней будет два, а значит и точек пересечения будет две (этот случай нам также не подходит);
- равен нулю, именно этот случай соответствует касанию прямой с графиком, поскольку записанное уравнение в этом случае будет иметь только одно решение.
То есть , то есть . Соответствующие прямые как раз и изображены на рисунке выше.
Второй случай
. Не забываем, что точка с абсциссой не принадлежит нашему графику. Значит, открывается ещё одна возможность, когда прямая будет иметь с графиком ровно одну общую точку. Вот этот случай:
Для нахождения в этом случае подставляем координаты точки в уравнение прямой . В результате получаем .
Сразу отметим, что в область определения данной функции входят все числа: . Наша задача теперь, как это часто бывает при решении заданий 23 из ОГЭ по математике, состоит в том, чтобы построить график этой функции. Для тех кто не сталкивался ранее с подобными заданиями, это может показаться странным, но график данной функции можно построить из графика функции . Нужно только выделить в подмодульном выражении полный квадрат. Для этого проведём следующие преобразования:
Из последнего с помощью формулы «квадрат разности» получаем:
Построим сначала график функции . Этот график получается из графика функции путём его переноса на единичного отрезка вправо и на единичного отрезка вниз:
При этом нули функции равны 2 и -1. Что произойдёт с этой параболой, если взять модуль от всего выражения, стоящего справа? Все точки, лежащие ниже оси OX
(с отрицательными ординатами), отразятся вверх относительно оси OX
. В результате получится вот такой график:
Теперь, глядя на этот график, уже понятно, что максимальное число точек пересечения данного графика с линией, параллельной оси абсцисс, будет равно 4. В качестве примера можно взять прямую :
Вот так решаются задания 23 из ОГЭ по математике. Как я уже говорил, это довольно интересные задания, которые к тому же можно научиться решать по ясному и запоминающемуся алгоритму. И как только вы овладеете этим мастерством, все задачи 23 из ОГЭ по математике будут казаться вам простыми и даже очевидными. Это станет для вас ещё одним заветным ключиком, который поможет получить максимальный балл на экзамене. Так что желаю вам успехов в подготовке и удаче на экзамене!
Сергей Валерьевич
Разбор типовых вариантов заданий №23 ОГЭ по математике
Первый вариант задания
Постройте график функции
Алгоритм решения:
- Записываем ответ.
Решение:
1. Преобразуем функцию в зависимости от знака переменной х.
2. График функции заданных значениях х — часть параболы, ветви которой направлены вниз.
Вершина расположена в точке с координатами:
Найдем нули функции: График проходит через начало координат и точку (-2;-7).
Вершина ее находится в точке:
Определим нули параболы
3. Изображаем график функции на координатной плоскости:
4. Из построения легко видно, что прямая y = m имеет с графиком ровно две точки, когда проходит через вершину одной из парабол, образующих график данной функции.
Значит, две общие точки функция и прямая имеют при m = -2,25 или m = 12,25.
Ответ: -2,25; 12,25.
Второй вариант задания
Постройте график функции
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем формулу в зависимости от знака переменной х:
2. Графиком функции является парабола, ветви которой направлены вниз.
Вершина ее находится в точке:
Найдем нули функции: График проходит через начало координат и точку (0;4).
Графиком второй функции является парабола, ветви которой направлены вверх.
Вершина ее находится в точке:
Определим нули параболы
3. Изображаем график на координатной плоскости:
Из изображения видно, что прямая y= m имеет с графиком только две общих точки, когда m=-9 или m=4. На графике прямая изображена красной линией при каждом значении m.
Ответ: -9; 4.
Третий вариант задания
Постройте график функции
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем формулу функции в зависимости от знака переменной
2. Определяем вид функции и находим дополнительные точки для каждого участка графика.
График при — часть парабола, ветви которой направлены вниз. Потому как коэффициент а
=-1 – отрицательный.
Определим вершину параболы и
.
Вершина находится в точке (-3; 9).
Парабола проходит еще через точки (0;0) и (0;6).
Если , ветви параболы направлены вверх. Найдем вершину:
, (2; -4).
График проходит также через точки (0;0) и (0;4).
3. Строим искомый график:
Из построения видно, что прямая y=m имеет только 2 общие точки с графиком функции в случаях, когда m=-4 или m=9. На рисунке прямые изображены красным цветом.
Ответ: -4; 9.
Четвертый вариант задания
Постройте график функции
Определите, при каких значениях k прямая у = kx не имеет с графиком общих точек.
Алгоритм решения:
- Строим график.
- Записываем ответ.
Решение:
1. Если x
Дробь, получившаяся в результате, определена . График представляет собой часть гиперболы.
Точки для построения графика:
3. Построим график заданной функции:
4. Прямая y=kx не имеет общих точек с графиком, при k=-1; 0 и 1, потому как тогда прямая проходит через точки, не входящие в область определения заданной функции.
На графике прямые для k=-1; 1изображены красным.
Ответ: -1; 0; 1.
Пятый вариант задания
Постройте график функции
Определите, при каких значениях k прямая y = kx не имеет с графиком общих точек.
Алгоритм решения:
- Раскрываем модуль и преобразовываем формул функции.
- Определяем вид функции на каждом промежутке и находим дополнительные точки графика.
- Строим график.
- Определяем искомые значения k.
- Записываем ответ.
Модуль — одна из тех вещей, о которых вроде-бы все слышали, но в действительности никто нормально не понимает. Поэтому сегодня будет большой урок, посвящённый решению уравнений с модулями.
Сразу скажу: урок будет несложный. И вообще модули — вообще тема относительно несложная. «Да конечно, несложная! У меня от неё мозг разрывается!» — скажут многие ученики, но все эти разрывы мозга происходят из-за того, что у большинства людей в голове не знания, а какая-то хрень. И цель этого урока — превратить хрень в знания.:)
Немного теории
Итак, поехали. Начнём с самого важного: что такое модуль? Напомню, что модуль числа — это просто то же самое число, но взятое без знака «минус». Т.е., например, $left| -5 right|=5$. Или $left| -129,5 right|=129,5$.
Вот так всё просто? Да, просто. А чему тогда равен модуль положительного числа? Тут ещё проще: модуль положительного числа равен самому этому числу: $left| 5 right|=5$; $left| 129,5 right|=129,5$ и т.д.
Получается любопытная вещь: разные числа могут иметь один тот же модуль. Например: $left| -5 right|=left| 5 right|=5$; $left| -129,5 right|=left| 129,5 right|=129,5$. Нетрудно заметить, что это за числа, у которых модули одинаковые: эти числа противоположны. Таким образом, отметим для себя, что модули противоположных чисел равны:
[left| -a right|=left| a right|]
Ещё один важный факт: модуль никогда не бывает отрицательным
. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.
Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:
Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.
Таким образом, если рассмотреть функцию $y=left| x right|$ и попробовать нарисовать её график, то получится вот такая «галка»:
График модуля и пример решения уравнения
Из этой картинки сразу видно, что $left| -m right|=left| m right|$, а график модуля никогда не опускается ниже оси абсцисс. Но это ещё не всё: красной линией отмечена прямая $y=a$, которая при положительных $a$ даёт нам сразу два корня: ${{x}_{1}}$ и ${{x}_{2}}$, но об этом мы поговорим позже.:)
Помимо чисто алгебраического определения, есть геометрическое. Допустим, есть две точки на числовой прямой: ${{x}_{1}}$ и ${{x}_{2}}$. В этом случае выражение $left| {{x}_{1}}-{{x}_{2}} right|$ — это просто расстояние между указанными точками. Или, если угодно, длина отрезка, соединяющего эти точки:
Модуль — это расстояние между точками на числовой прямой
Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)
Основная формула
Ну хорошо, с определением разобрались. Но легче-то от этого не стало. Как решать уравнения, содержащие этот самый модуль?
Спокойствие, только спокойствие. Начнём с самых простых вещей. Рассмотрим что-нибудь типа такого:
[left| x right|=3]
Итак, модуль$x$ равен 3. Чему может быть равен $x$? Ну, судя по определению, нас вполне устроит $x=3$. Действительно:
[left| 3 right|=3]
А есть ли другие числа? Кэп как бы намекает, что есть. Например, $x=-3$ — для него тоже $left| -3 right|=3$, т.е. требуемое равенство выполняется.
Так может, если поискать, подумать, мы найдём ещё числа? А вот обломитесь: больше чисел нет. Уравнение $left| x right|=3$ имеет лишь два корня: $x=3$ и $x=-3$.
Теперь немного усложним задачу. Пусть вместо переменной $x$ под знаком модуля тусуется функция $fleft(x right)$, а справа вместо тройки поставим произвольное число $a$. Получим уравнение:
[left| fleft(x right) right|=a]
Ну и как такое решать? Напомню: $fleft(x right)$ — произвольная функция, $a$ — любое число. Т.е. вообще любое! Например:
[left| 2x+1 right|=5]
[left| 10x-5 right|=-65]
Обратим внимание на второе уравнение. Про него сразу можно сказать: корней у него нет. Почему? Всё правильно: потому что в нём требуется, чтобы модуль был равен отрицательному числу, чего никогда не бывает, поскольку мы уже знаем, что модуль — число всегда положительное или в крайнем случае ноль.
А вот с первым уравнением всё веселее. Тут два варианта: либо под знаком модуля стоит положительное выражение, и тогда$left| 2x+1 right|=2x+1$, либо это выражение всё-таки отрицательное, и тогда $left| 2x+1 right|=-left(2x+1 right)=-2x-1$. В первом случае наше уравнение перепишется так:
[left| 2x+1 right|=5Rightarrow 2x+1=5]
И внезапно получается, что подмодульное выражение $2x+1$ действительно положительно — оно равно числу 5. Т.е. мы можем спокойно решать это уравнение — полученный корень будет кусочком ответа:
Особо недоверчивые могут попробовать подставить найденный корень в исходное уравнение и убедиться, что действительно под модулем будет положительное число.
Теперь разберём случай отрицательного подмодульного выражения:
[left{ begin{align}& left| 2x+1 right|=5 & 2x+1 lt 0 end{align} right.Rightarrow -2x-1=5Rightarrow 2x+1=-5]
Опа! Снова всё чётко: мы предположили, что $2x+1 lt 0$, и в результате получили, что $2x+1=-5$ — действительно, это выражение меньше нуля. Решаем полученное уравнение, при этом уже точно зная, что найденный корень нас устроит:
Итого мы вновь получили два ответа: $x=2$ и $x=3$. Да, объём вычислений оказался малость побольше, чем в совсем уж простом уравнении $left| x right|=3$, но принципиально ничего не изменилось. Так может, существует какой-то универсальный алгоритм?
Да, такой алгоритм существует. И сейчас мы его разберём.
Избавление от знака модуля
Пусть нам дано уравнение $left| fleft(x right) right|=a$, причём $age 0$ (иначе, как мы уже знаем, корней нет). Тогда можно избавиться от знака модуля по следующему правилу:
[left| fleft(x right) right|=aRightarrow fleft(x right)=pm a]
Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого
[left| 5x+4 right|=10Rightarrow 5x+4=pm 10]
Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:
[begin{align}& 5x+4=10Rightarrow 5x=6Rightarrow x=frac{6}{5}=1,2; & 5x+4=-10Rightarrow 5x=-14Rightarrow x=-frac{14}{5}=-2,8. end{align}]
Вот и всё! Получили два корня: $x=1,2$ и $x=-2,8$. Всё решение заняло буквально две строчки.
Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:
[left| 7-5x right|=13]
Опять раскрываем модуль с плюсом и минусом:
[begin{align}& 7-5x=13Rightarrow -5x=6Rightarrow x=-frac{6}{5}=-1,2; & 7-5x=-13Rightarrow -5x=-20Rightarrow x=4. end{align}]
Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.
Случай переменной правой части
А теперь рассмотрим вот такое уравнение:
[left| 3x-2 right|=2x]
Это уравнение принципиально отличается от всех предыдущих. Чем? А тем, что справа от знака равенства стоит выражение $2x$ — и мы не можем заранее знать, положительное оно или отрицательное.
Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней
— мы уже знаем, что модуль не может быть равен отрицательному числу.
А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».
Таким образом, сформулируем правило для произвольных функций $fleft(x right)$ и $gleft(x right)$ :
[left| fleft(x right) right|=gleft(x right)Rightarrow left{ begin{align}& fleft(x right)=pm gleft(x right), & gleft(x right)ge 0. end{align} right.]
Применительно к нашему уравнению получим:
[left| 3x-2 right|=2xRightarrow left{ begin{align}& 3x-2=pm 2x, & 2xge 0. end{align} right.]
Ну, с требованием $2xge 0$ мы как-нибудь справимся. В конце концов, можно тупо подставить корни, которые мы получим из первого уравнения, и проверить: выполняется неравенство или нет.
Поэтому решим-ка само уравнение:
[begin{align}& 3x-2=2Rightarrow 3x=4Rightarrow x=frac{4}{3}; & 3x-2=-2Rightarrow 3x=0Rightarrow x=0. end{align}]
Ну и какой их этих двух корней удовлетворяет требованию $2xge 0$? Да оба! Поэтому в ответ пойдут два числа: $x={4}/{3};$ и $x=0$. Вот и всё решение.:)
Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}]
Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:
[left| fleft(x right) right|=gleft(x right)]
И решается оно точно так же:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}Rightarrow left{ begin{align}& {{x}^{3}}-3{{x}^{2}}+x=pm left(x-{{x}^{3}} right), & x-{{x}^{3}}ge 0. end{align} right.]
С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:
[{{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}]
Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}; & 2{{x}^{3}}-3{{x}^{2}}=0; end{align}]
Выносим общий множитель ${{x}^{2}}$ за скобку и получаем очень простое уравнение:
[{{x}^{2}}left(2x-3 right)=0Rightarrow left[ begin{align}& {{x}^{2}}=0 & 2x-3=0 end{align} right.]
[{{x}_{1}}=0;quad {{x}_{2}}=frac{3}{2}=1,5.]
Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.
Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=-left(x-{{x}^{3}} right); & {{x}^{3}}-3{{x}^{2}}+x=-x+{{x}^{3}}; & -3{{x}^{2}}+2x=0; & xleft(-3x+2 right)=0. end{align}]
Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:
[left[ begin{align}& x=0 & -3x+2=0 end{align} right.]
Ну вот мы получили три корня: $x=0$, $x=1,5$ и $x={2}/{3};$. Ну и что из этого набора пойдёт в окончательный ответ? Для этого вспомним, что у нас есть дополнительное ограничение в виде неравенства:
Как учесть это требование? Да просто подставим найденные корни и проверим: выполняется неравенство при этих $x$ или нет. Имеем:
[begin{align}& x=0Rightarrow x-{{x}^{3}}=0-0=0ge 0; & x=1,5Rightarrow x-{{x}^{3}}=1,5-{{1,5}^{3}} lt 0; & x=frac{2}{3}Rightarrow x-{{x}^{3}}=frac{2}{3}-frac{8}{27}=frac{10}{27}ge 0; end{align}]
Таким образом, корень $x=1,5$ нас не устраивает. И в ответ пойдут лишь два корня:
[{{x}_{1}}=0;quad {{x}_{2}}=frac{2}{3}.]
Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.
Уравнения с двумя модулями
До сих пор мы изучали лишь самые простые уравнения — там был один модуль и что-то ещё. Это «что-то ещё» мы отправляли в другую часть неравенства, подальше от модуля, чтобы в итоге всё свелось к уравнению вида $left| fleft(x right) right|=gleft(x right)$ или даже более простому $left| fleft(x right) right|=a$.
Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:
[left| fleft(x right) right|=left| gleft(x right) right|]
Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.
Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:
[left| fleft(x right) right|=left| gleft(x right) right|Rightarrow fleft(x right)=pm gleft(x right)]
Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.
Давайте попробуем решать вот такую задачу:
[left| 2x+3 right|=left| 2x-7 right|]
Элементарно, Ватсон! Раскрываем модули:
[left| 2x+3 right|=left| 2x-7 right|Rightarrow 2x+3=pm left(2x-7 right)]
Рассмотрим отдельно каждый случай:
[begin{align}& 2x+3=2x-7Rightarrow 3=-7Rightarrow emptyset ; & 2x+3=-left(2x-7 right)Rightarrow 2x+3=-2x+7. end{align}]
В первом уравнении корней нет. Потому что когда это $3=-7$? При каких значениях $x$? «Какой ещё нафиг $x$? Ты обкурился? Там вообще нет $x$» — скажете вы. И будете правы. Мы получили равенство, не зависящее от переменной $x$, и при этом само равенство — неверное. Потому и нет корней.:)
Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:
Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)
В итоге окончательный ответ: $x=1$.
Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|]
Опять у нас уравнение вида $left| fleft(x right) right|=left| gleft(x right) right|$. Поэтому сразу переписываем его, раскрывая знак модуля:
[{{x}^{2}}-3x+2=pm left(x-1 right)]
Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:
Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми.
Но ведь ничто не мешает нам переписать исходное уравнение следующим образом:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|Rightarrow left| {{x}^{2}}-3x+2 right|=left| x-1 right|]
Что произошло? Да ничего особенного: просто поменяли левую и правую часть местами. Мелочь, которая в итоге немного упростит нам жизнь.:)
В общем, решаем это уравнение, рассматривая варианты с плюсом и с минусом:
[begin{align}& {{x}^{2}}-3x+2=x-1Rightarrow {{x}^{2}}-4x+3=0; & {{x}^{2}}-3x+2=-left(x-1 right)Rightarrow {{x}^{2}}-2x+1=0. end{align}]
Первое уравнение имеет корни $x=3$ и $x=1$. Второе вообще является точным квадратом:
[{{x}^{2}}-2x+1={{left(x-1 right)}^{2}}]
Поэтому у него единственный корень: $x=1$. Но этот корень мы уже получали ранее. Таким образом, в итоговый ответ пойдут лишь два числа:
[{{x}_{1}}=3;quad {{x}_{2}}=1.]
Миссия выполнена! Можно взять с полки и скушать пирожок. Там их 2, ваш средний.:)
Важное замечание
. Наличие одинаковых корней при разных вариантах раскрытия модуля означает, что исходные многочлены раскладываются на множители, и среди этих множителей обязательно будет общий. Действительно:[begin{align}& left| x-1 right|=left| {{x}^{2}}-3x+2 right|; & left| x-1 right|=left| left(x-1 right)left(x-2 right) right|. end{align}]
Одно из свойств модуля: $left| acdot b right|=left| a right|cdot left| b right|$ (т.е. модуль произведения равен произведению модулей), поэтому исходное уравнение можно переписать так:
[left| x-1 right|=left| x-1 right|cdot left| x-2 right|]
Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:
[begin{align}& left| x-1 right|=left| x-1 right|cdot left| x-2 right|; & left| x-1 right|-left| x-1 right|cdot left| x-2 right|=0; & left| x-1 right|cdot left(1-left| x-2 right| right)=0. end{align}]
Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:
[left[ begin{align}& left| x-1 right|=0, & left| x-2 right|=1. end{align} right.]
Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)
Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)
Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.
Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.
Итак, уравнение:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0]
Нет, это не опечатка: между модулями именно плюс. И нам нужно найти, при каких $x$ сумма двух модулей равна нулю.:)
В чём вообще проблема? А проблема в том, что каждый модуль — число положительное, либо в крайнем случае ноль. А что будет, если сложить два положительных числа? Очевидно, снова положительное число:
[begin{align}& 5+7=12 gt 0; & 0,004+0,0001=0,0041 gt 0; & 5+0=5 gt 0. end{align}]
Последняя строчка может натолкнуть на мысль: единственный случай, когда сумма модулей равна нулю — это если каждый модуль будет равен нулю:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0Rightarrow left{ begin{align}& left| x-{{x}^{3}} right|=0, & left| {{x}^{2}}+x-2 right|=0. end{align} right.]
А когда модуль равен нулю? Только в одном случае — когда подмодульное выражение равно нулю:
[{{x}^{2}}+x-2=0Rightarrow left(x+2 right)left(x-1 right)=0Rightarrow left[ begin{align}& x=-2 & x=1 end{align} right.]
Таким образом, у нас есть три точки, в которых обнуляется первый модуль: 0, 1 и −1; а также две точки, в которых обнуляется второй модуль: −2 и 1. Однако нам нужно, чтобы оба модуля обнулялись одновременно, поэтому среди найденных чисел нужно выбрать те, которые входят в оба набора. Очевидно, такое число лишь одно: $x=1$ — это и будет окончательным ответом.
Метод расщепления
Что ж, мы уже рассмотрели кучу задач и изучили множество приёмов. Думаете, на этом всё? А вот и нет! Сейчас мы рассмотрим заключительный приём — и одновременно самый важный. Речь пойдёт о расщеплении уравнений с модулем. О чём вообще пойдёт речь? Давайте вернёмся немного назад и рассмотрим какое-нибудь простое уравнение. Например, это:
[left| 3x-5 right|=5-3x]
В принципе, мы уже знаем, как решать такое уравнение, потому что это стандартная конструкция вида $left| fleft(x right) right|=gleft(x right)$. Но попробуем взглянуть на это уравнение немного под другим углом. Точнее, рассмотрим выражение, стоящее под знаком модуля. Напомню, что модуль любого числа может быть равен самому числу, а может быть противоположен этому числу:
[left| a right|=left{ begin{align}& a,quad age 0, & -a,quad a lt 0. end{align} right.]
Собственно, в этой неоднозначности и состоит вся проблема: поскольку число под модулем меняется (оно зависит от переменной), нам неясно — положительное оно или отрицательное.
Но что если изначально потребовать, чтобы это число было положительным? Например, потребуем, чтобы $3x-5 gt 0$ — в этом случае мы гарантированно получим положительное число под знаком модуля, и от этого самого модуля можно полностью избавиться:
Таким образом, наше уравнение превратится в линейное, которое легко решается:
Правда, все эти размышления имеют смысл только при условии $3x-5 gt 0$ — мы сами ввели это требование, дабы однозначно раскрыть модуль. Поэтому давайте подставим найденный $x=frac{5}{3}$ в это условие и проверим:
Получается, что при указанном значении $x$ наше требование не выполняется, т.к. выражение оказалось равно нулю, а нам нужно, чтобы оно было строго больше нуля. Печалька.:(
Но ничего страшного! Ведь есть ещё вариант $3x-5 lt 0$. Более того: есть ещё и случай $3x-5=0$ — это тоже нужно рассмотреть, иначе решение будет неполным. Итак, рассмотрим случай $3x-5 lt 0$:
Очевидно, что в модуль раскроется со знаком «минус». Но тогда возникает странная ситуация: и слева, и справа в исходном уравнении будет торчать одно и то же выражение:
Интересно, при каких таких $x$ выражение $5-3x$ будет равно выражению $5-3x$? От таких уравнений даже Капитан очевидность подавился бы слюной, но мы-то знаем: это уравнение является тождеством, т.е. оно верно при любых значениях переменной!
А это значит, что нас устроят любые $x$. Вместе с тем у нас есть ограничение:
Другими словами, ответом будет не какое-то отдельное число, а целый интервал:
Наконец, осталось рассмотреть ещё один случай: $3x-5=0$. Тут всё просто: под модулем будет ноль, а модуль нуля тоже равен нулю (это прямо следует из определения):
Но тогда исходное уравнение $left| 3x-5 right|=5-3x$ перепишется следующим образом:
Этот корень мы уже получали выше, когда рассматривали случай $3x-5 gt 0$. Более того, это корень является решением уравнения $3x-5=0$ — это ограничение, которое мы сами же и ввели, чтобы обнулить модуль.:)
Таким образом, помимо интервала нас устроит ещё и число, лежащее на самом конце этого интервала:
Объединение корней в уравнениях с модулем
Итого окончательный ответ: $xin left(-infty ;frac{5}{3} right]$. Не очень-то привычно видеть такую хрень в ответе к довольно простому (по сути — линейному) уравнению с модулем, правда? Что ж, привыкайте: в том и состоит сложность модуля, что ответы в таких уравнениях могут оказаться совершенно непредсказуемыми.
Куда важнее другое: мы только что разобрали универсальный алгоритм решения уравнения с модуляем! И состоит этот алгоритм из следующих шагов:
- Приравнять каждый модуль, имеющийся в уравнении, к нулю. Получим несколько уравнений;
- Решить все эти уравнения и отметить корни на числовой прямой. В результате прямая разобьётся на несколько интервалов, на каждом из которых все модули однозначно раскрываются;
- Решить исходное уравнение для каждого интервала и объединить полученные ответы.
Вот и всё! Остаётся лишь один вопрос: куда девать сами корни, полученные на 1-м шаге? Допустим, у нас получилось два корня: $x=1$ и $x=5$. Они разобьют числовую прямую на 3 куска:
Разбиение числовой оси на интервалы с помощью точек
Ну и какие тут интервалы? Понятно, что их три:
- Самый левый: $x lt 1$ — сама единица в интервал не входит;
- Центральный: $1le x lt 5$ — вот тут единица в интервал входит, однако не входит пятёрка;
- Самый правый: $xge 5$ — пятёрка входит только сюда!
Я думаю, вы уже поняли закономерность. Каждый интервал включает в себя левый конец и не включает правый.
На первый взгляд, такая запись может показаться неудобной, нелогичной и вообще какой-то бредовой. Но поверьте: после небольшой тренировки вы обнаружите, что именно такой подход наиболее надёжен и при этом не мешает однозначно раскрывать модули. Лучше уж использовать такую схему, чем каждый раз думать: отдавать левый/правый конец в текущий интервал или «перекидывать» его в следующий.
Модуль — одна из тех вещей, о которых вроде-бы все слышали, но в действительности никто нормально не понимает. Поэтому сегодня будет большой урок, посвящённый решению уравнений с модулями.
Сразу скажу: урок будет несложный. И вообще модули — вообще тема относительно несложная. «Да конечно, несложная! У меня от неё мозг разрывается!» — скажут многие ученики, но все эти разрывы мозга происходят из-за того, что у большинства людей в голове не знания, а какая-то хрень. И цель этого урока — превратить хрень в знания.:)
Немного теории
Итак, поехали. Начнём с самого важного: что такое модуль? Напомню, что модуль числа — это просто то же самое число, но взятое без знака «минус». Т.е., например, $left| -5 right|=5$. Или $left| -129,5 right|=129,5$.
Вот так всё просто? Да, просто. А чему тогда равен модуль положительного числа? Тут ещё проще: модуль положительного числа равен самому этому числу: $left| 5 right|=5$; $left| 129,5 right|=129,5$ и т.д.
Получается любопытная вещь: разные числа могут иметь один тот же модуль. Например: $left| -5 right|=left| 5 right|=5$; $left| -129,5 right|=left| 129,5 right|=129,5$. Нетрудно заметить, что это за числа, у которых модули одинаковые: эти числа противоположны. Таким образом, отметим для себя, что модули противоположных чисел равны:
[left| -a right|=left| a right|]
Ещё один важный факт: модуль никогда не бывает отрицательным
. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.
Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:
Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.
Таким образом, если рассмотреть функцию $y=left| x right|$ и попробовать нарисовать её график, то получится вот такая «галка»:
График модуля и пример решения уравнения
Из этой картинки сразу видно, что $left| -m right|=left| m right|$, а график модуля никогда не опускается ниже оси абсцисс. Но это ещё не всё: красной линией отмечена прямая $y=a$, которая при положительных $a$ даёт нам сразу два корня: ${{x}_{1}}$ и ${{x}_{2}}$, но об этом мы поговорим позже.:)
Помимо чисто алгебраического определения, есть геометрическое. Допустим, есть две точки на числовой прямой: ${{x}_{1}}$ и ${{x}_{2}}$. В этом случае выражение $left| {{x}_{1}}-{{x}_{2}} right|$ — это просто расстояние между указанными точками. Или, если угодно, длина отрезка, соединяющего эти точки:
Модуль — это расстояние между точками на числовой прямой
Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)
Основная формула
Ну хорошо, с определением разобрались. Но легче-то от этого не стало. Как решать уравнения, содержащие этот самый модуль?
Спокойствие, только спокойствие. Начнём с самых простых вещей. Рассмотрим что-нибудь типа такого:
[left| x right|=3]
Итак, модуль$x$ равен 3. Чему может быть равен $x$? Ну, судя по определению, нас вполне устроит $x=3$. Действительно:
[left| 3 right|=3]
А есть ли другие числа? Кэп как бы намекает, что есть. Например, $x=-3$ — для него тоже $left| -3 right|=3$, т.е. требуемое равенство выполняется.
Так может, если поискать, подумать, мы найдём ещё числа? А вот обломитесь: больше чисел нет. Уравнение $left| x right|=3$ имеет лишь два корня: $x=3$ и $x=-3$.
Теперь немного усложним задачу. Пусть вместо переменной $x$ под знаком модуля тусуется функция $fleft(x right)$, а справа вместо тройки поставим произвольное число $a$. Получим уравнение:
[left| fleft(x right) right|=a]
Ну и как такое решать? Напомню: $fleft(x right)$ — произвольная функция, $a$ — любое число. Т.е. вообще любое! Например:
[left| 2x+1 right|=5]
[left| 10x-5 right|=-65]
Обратим внимание на второе уравнение. Про него сразу можно сказать: корней у него нет. Почему? Всё правильно: потому что в нём требуется, чтобы модуль был равен отрицательному числу, чего никогда не бывает, поскольку мы уже знаем, что модуль — число всегда положительное или в крайнем случае ноль.
А вот с первым уравнением всё веселее. Тут два варианта: либо под знаком модуля стоит положительное выражение, и тогда$left| 2x+1 right|=2x+1$, либо это выражение всё-таки отрицательное, и тогда $left| 2x+1 right|=-left(2x+1 right)=-2x-1$. В первом случае наше уравнение перепишется так:
[left| 2x+1 right|=5Rightarrow 2x+1=5]
И внезапно получается, что подмодульное выражение $2x+1$ действительно положительно — оно равно числу 5. Т.е. мы можем спокойно решать это уравнение — полученный корень будет кусочком ответа:
Особо недоверчивые могут попробовать подставить найденный корень в исходное уравнение и убедиться, что действительно под модулем будет положительное число.
Теперь разберём случай отрицательного подмодульного выражения:
[left{ begin{align}& left| 2x+1 right|=5 & 2x+1 lt 0 end{align} right.Rightarrow -2x-1=5Rightarrow 2x+1=-5]
Опа! Снова всё чётко: мы предположили, что $2x+1 lt 0$, и в результате получили, что $2x+1=-5$ — действительно, это выражение меньше нуля. Решаем полученное уравнение, при этом уже точно зная, что найденный корень нас устроит:
Итого мы вновь получили два ответа: $x=2$ и $x=3$. Да, объём вычислений оказался малость побольше, чем в совсем уж простом уравнении $left| x right|=3$, но принципиально ничего не изменилось. Так может, существует какой-то универсальный алгоритм?
Да, такой алгоритм существует. И сейчас мы его разберём.
Избавление от знака модуля
Пусть нам дано уравнение $left| fleft(x right) right|=a$, причём $age 0$ (иначе, как мы уже знаем, корней нет). Тогда можно избавиться от знака модуля по следующему правилу:
[left| fleft(x right) right|=aRightarrow fleft(x right)=pm a]
Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого
[left| 5x+4 right|=10Rightarrow 5x+4=pm 10]
Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:
[begin{align}& 5x+4=10Rightarrow 5x=6Rightarrow x=frac{6}{5}=1,2; & 5x+4=-10Rightarrow 5x=-14Rightarrow x=-frac{14}{5}=-2,8. end{align}]
Вот и всё! Получили два корня: $x=1,2$ и $x=-2,8$. Всё решение заняло буквально две строчки.
Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:
[left| 7-5x right|=13]
Опять раскрываем модуль с плюсом и минусом:
[begin{align}& 7-5x=13Rightarrow -5x=6Rightarrow x=-frac{6}{5}=-1,2; & 7-5x=-13Rightarrow -5x=-20Rightarrow x=4. end{align}]
Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.
Случай переменной правой части
А теперь рассмотрим вот такое уравнение:
[left| 3x-2 right|=2x]
Это уравнение принципиально отличается от всех предыдущих. Чем? А тем, что справа от знака равенства стоит выражение $2x$ — и мы не можем заранее знать, положительное оно или отрицательное.
Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней
— мы уже знаем, что модуль не может быть равен отрицательному числу.
А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».
Таким образом, сформулируем правило для произвольных функций $fleft(x right)$ и $gleft(x right)$ :
[left| fleft(x right) right|=gleft(x right)Rightarrow left{ begin{align}& fleft(x right)=pm gleft(x right), & gleft(x right)ge 0. end{align} right.]
Применительно к нашему уравнению получим:
[left| 3x-2 right|=2xRightarrow left{ begin{align}& 3x-2=pm 2x, & 2xge 0. end{align} right.]
Ну, с требованием $2xge 0$ мы как-нибудь справимся. В конце концов, можно тупо подставить корни, которые мы получим из первого уравнения, и проверить: выполняется неравенство или нет.
Поэтому решим-ка само уравнение:
[begin{align}& 3x-2=2Rightarrow 3x=4Rightarrow x=frac{4}{3}; & 3x-2=-2Rightarrow 3x=0Rightarrow x=0. end{align}]
Ну и какой их этих двух корней удовлетворяет требованию $2xge 0$? Да оба! Поэтому в ответ пойдут два числа: $x={4}/{3};$ и $x=0$. Вот и всё решение.:)
Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}]
Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:
[left| fleft(x right) right|=gleft(x right)]
И решается оно точно так же:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}Rightarrow left{ begin{align}& {{x}^{3}}-3{{x}^{2}}+x=pm left(x-{{x}^{3}} right), & x-{{x}^{3}}ge 0. end{align} right.]
С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:
[{{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}]
Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}; & 2{{x}^{3}}-3{{x}^{2}}=0; end{align}]
Выносим общий множитель ${{x}^{2}}$ за скобку и получаем очень простое уравнение:
[{{x}^{2}}left(2x-3 right)=0Rightarrow left[ begin{align}& {{x}^{2}}=0 & 2x-3=0 end{align} right.]
[{{x}_{1}}=0;quad {{x}_{2}}=frac{3}{2}=1,5.]
Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.
Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=-left(x-{{x}^{3}} right); & {{x}^{3}}-3{{x}^{2}}+x=-x+{{x}^{3}}; & -3{{x}^{2}}+2x=0; & xleft(-3x+2 right)=0. end{align}]
Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:
[left[ begin{align}& x=0 & -3x+2=0 end{align} right.]
Ну вот мы получили три корня: $x=0$, $x=1,5$ и $x={2}/{3};$. Ну и что из этого набора пойдёт в окончательный ответ? Для этого вспомним, что у нас есть дополнительное ограничение в виде неравенства:
Как учесть это требование? Да просто подставим найденные корни и проверим: выполняется неравенство при этих $x$ или нет. Имеем:
[begin{align}& x=0Rightarrow x-{{x}^{3}}=0-0=0ge 0; & x=1,5Rightarrow x-{{x}^{3}}=1,5-{{1,5}^{3}} lt 0; & x=frac{2}{3}Rightarrow x-{{x}^{3}}=frac{2}{3}-frac{8}{27}=frac{10}{27}ge 0; end{align}]
Таким образом, корень $x=1,5$ нас не устраивает. И в ответ пойдут лишь два корня:
[{{x}_{1}}=0;quad {{x}_{2}}=frac{2}{3}.]
Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.
Уравнения с двумя модулями
До сих пор мы изучали лишь самые простые уравнения — там был один модуль и что-то ещё. Это «что-то ещё» мы отправляли в другую часть неравенства, подальше от модуля, чтобы в итоге всё свелось к уравнению вида $left| fleft(x right) right|=gleft(x right)$ или даже более простому $left| fleft(x right) right|=a$.
Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:
[left| fleft(x right) right|=left| gleft(x right) right|]
Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.
Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:
[left| fleft(x right) right|=left| gleft(x right) right|Rightarrow fleft(x right)=pm gleft(x right)]
Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.
Давайте попробуем решать вот такую задачу:
[left| 2x+3 right|=left| 2x-7 right|]
Элементарно, Ватсон! Раскрываем модули:
[left| 2x+3 right|=left| 2x-7 right|Rightarrow 2x+3=pm left(2x-7 right)]
Рассмотрим отдельно каждый случай:
[begin{align}& 2x+3=2x-7Rightarrow 3=-7Rightarrow emptyset ; & 2x+3=-left(2x-7 right)Rightarrow 2x+3=-2x+7. end{align}]
В первом уравнении корней нет. Потому что когда это $3=-7$? При каких значениях $x$? «Какой ещё нафиг $x$? Ты обкурился? Там вообще нет $x$» — скажете вы. И будете правы. Мы получили равенство, не зависящее от переменной $x$, и при этом само равенство — неверное. Потому и нет корней.:)
Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:
Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)
В итоге окончательный ответ: $x=1$.
Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|]
Опять у нас уравнение вида $left| fleft(x right) right|=left| gleft(x right) right|$. Поэтому сразу переписываем его, раскрывая знак модуля:
[{{x}^{2}}-3x+2=pm left(x-1 right)]
Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:
Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми.
Но ведь ничто не мешает нам переписать исходное уравнение следующим образом:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|Rightarrow left| {{x}^{2}}-3x+2 right|=left| x-1 right|]
Что произошло? Да ничего особенного: просто поменяли левую и правую часть местами. Мелочь, которая в итоге немного упростит нам жизнь.:)
В общем, решаем это уравнение, рассматривая варианты с плюсом и с минусом:
[begin{align}& {{x}^{2}}-3x+2=x-1Rightarrow {{x}^{2}}-4x+3=0; & {{x}^{2}}-3x+2=-left(x-1 right)Rightarrow {{x}^{2}}-2x+1=0. end{align}]
Первое уравнение имеет корни $x=3$ и $x=1$. Второе вообще является точным квадратом:
[{{x}^{2}}-2x+1={{left(x-1 right)}^{2}}]
Поэтому у него единственный корень: $x=1$. Но этот корень мы уже получали ранее. Таким образом, в итоговый ответ пойдут лишь два числа:
[{{x}_{1}}=3;quad {{x}_{2}}=1.]
Миссия выполнена! Можно взять с полки и скушать пирожок. Там их 2, ваш средний.:)
Важное замечание
. Наличие одинаковых корней при разных вариантах раскрытия модуля означает, что исходные многочлены раскладываются на множители, и среди этих множителей обязательно будет общий. Действительно:[begin{align}& left| x-1 right|=left| {{x}^{2}}-3x+2 right|; & left| x-1 right|=left| left(x-1 right)left(x-2 right) right|. end{align}]
Одно из свойств модуля: $left| acdot b right|=left| a right|cdot left| b right|$ (т.е. модуль произведения равен произведению модулей), поэтому исходное уравнение можно переписать так:
[left| x-1 right|=left| x-1 right|cdot left| x-2 right|]
Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:
[begin{align}& left| x-1 right|=left| x-1 right|cdot left| x-2 right|; & left| x-1 right|-left| x-1 right|cdot left| x-2 right|=0; & left| x-1 right|cdot left(1-left| x-2 right| right)=0. end{align}]
Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:
[left[ begin{align}& left| x-1 right|=0, & left| x-2 right|=1. end{align} right.]
Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)
Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)
Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.
Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.
Итак, уравнение:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0]
Нет, это не опечатка: между модулями именно плюс. И нам нужно найти, при каких $x$ сумма двух модулей равна нулю.:)
В чём вообще проблема? А проблема в том, что каждый модуль — число положительное, либо в крайнем случае ноль. А что будет, если сложить два положительных числа? Очевидно, снова положительное число:
[begin{align}& 5+7=12 gt 0; & 0,004+0,0001=0,0041 gt 0; & 5+0=5 gt 0. end{align}]
Последняя строчка может натолкнуть на мысль: единственный случай, когда сумма модулей равна нулю — это если каждый модуль будет равен нулю:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0Rightarrow left{ begin{align}& left| x-{{x}^{3}} right|=0, & left| {{x}^{2}}+x-2 right|=0. end{align} right.]
А когда модуль равен нулю? Только в одном случае — когда подмодульное выражение равно нулю:
[{{x}^{2}}+x-2=0Rightarrow left(x+2 right)left(x-1 right)=0Rightarrow left[ begin{align}& x=-2 & x=1 end{align} right.]
Таким образом, у нас есть три точки, в которых обнуляется первый модуль: 0, 1 и −1; а также две точки, в которых обнуляется второй модуль: −2 и 1. Однако нам нужно, чтобы оба модуля обнулялись одновременно, поэтому среди найденных чисел нужно выбрать те, которые входят в оба набора. Очевидно, такое число лишь одно: $x=1$ — это и будет окончательным ответом.
Метод расщепления
Что ж, мы уже рассмотрели кучу задач и изучили множество приёмов. Думаете, на этом всё? А вот и нет! Сейчас мы рассмотрим заключительный приём — и одновременно самый важный. Речь пойдёт о расщеплении уравнений с модулем. О чём вообще пойдёт речь? Давайте вернёмся немного назад и рассмотрим какое-нибудь простое уравнение. Например, это:
[left| 3x-5 right|=5-3x]
В принципе, мы уже знаем, как решать такое уравнение, потому что это стандартная конструкция вида $left| fleft(x right) right|=gleft(x right)$. Но попробуем взглянуть на это уравнение немного под другим углом. Точнее, рассмотрим выражение, стоящее под знаком модуля. Напомню, что модуль любого числа может быть равен самому числу, а может быть противоположен этому числу:
[left| a right|=left{ begin{align}& a,quad age 0, & -a,quad a lt 0. end{align} right.]
Собственно, в этой неоднозначности и состоит вся проблема: поскольку число под модулем меняется (оно зависит от переменной), нам неясно — положительное оно или отрицательное.
Но что если изначально потребовать, чтобы это число было положительным? Например, потребуем, чтобы $3x-5 gt 0$ — в этом случае мы гарантированно получим положительное число под знаком модуля, и от этого самого модуля можно полностью избавиться:
Таким образом, наше уравнение превратится в линейное, которое легко решается:
Правда, все эти размышления имеют смысл только при условии $3x-5 gt 0$ — мы сами ввели это требование, дабы однозначно раскрыть модуль. Поэтому давайте подставим найденный $x=frac{5}{3}$ в это условие и проверим:
Получается, что при указанном значении $x$ наше требование не выполняется, т.к. выражение оказалось равно нулю, а нам нужно, чтобы оно было строго больше нуля. Печалька.:(
Но ничего страшного! Ведь есть ещё вариант $3x-5 lt 0$. Более того: есть ещё и случай $3x-5=0$ — это тоже нужно рассмотреть, иначе решение будет неполным. Итак, рассмотрим случай $3x-5 lt 0$:
Очевидно, что в модуль раскроется со знаком «минус». Но тогда возникает странная ситуация: и слева, и справа в исходном уравнении будет торчать одно и то же выражение:
Интересно, при каких таких $x$ выражение $5-3x$ будет равно выражению $5-3x$? От таких уравнений даже Капитан очевидность подавился бы слюной, но мы-то знаем: это уравнение является тождеством, т.е. оно верно при любых значениях переменной!
А это значит, что нас устроят любые $x$. Вместе с тем у нас есть ограничение:
Другими словами, ответом будет не какое-то отдельное число, а целый интервал:
Наконец, осталось рассмотреть ещё один случай: $3x-5=0$. Тут всё просто: под модулем будет ноль, а модуль нуля тоже равен нулю (это прямо следует из определения):
Но тогда исходное уравнение $left| 3x-5 right|=5-3x$ перепишется следующим образом:
Этот корень мы уже получали выше, когда рассматривали случай $3x-5 gt 0$. Более того, это корень является решением уравнения $3x-5=0$ — это ограничение, которое мы сами же и ввели, чтобы обнулить модуль.:)
Таким образом, помимо интервала нас устроит ещё и число, лежащее на самом конце этого интервала:
Объединение корней в уравнениях с модулем
Итого окончательный ответ: $xin left(-infty ;frac{5}{3} right]$. Не очень-то привычно видеть такую хрень в ответе к довольно простому (по сути — линейному) уравнению с модулем, правда? Что ж, привыкайте: в том и состоит сложность модуля, что ответы в таких уравнениях могут оказаться совершенно непредсказуемыми.
Куда важнее другое: мы только что разобрали универсальный алгоритм решения уравнения с модуляем! И состоит этот алгоритм из следующих шагов:
- Приравнять каждый модуль, имеющийся в уравнении, к нулю. Получим несколько уравнений;
- Решить все эти уравнения и отметить корни на числовой прямой. В результате прямая разобьётся на несколько интервалов, на каждом из которых все модули однозначно раскрываются;
- Решить исходное уравнение для каждого интервала и объединить полученные ответы.
Вот и всё! Остаётся лишь один вопрос: куда девать сами корни, полученные на 1-м шаге? Допустим, у нас получилось два корня: $x=1$ и $x=5$. Они разобьют числовую прямую на 3 куска:
Разбиение числовой оси на интервалы с помощью точек
Ну и какие тут интервалы? Понятно, что их три:
- Самый левый: $x lt 1$ — сама единица в интервал не входит;
- Центральный: $1le x lt 5$ — вот тут единица в интервал входит, однако не входит пятёрка;
- Самый правый: $xge 5$ — пятёрка входит только сюда!
Я думаю, вы уже поняли закономерность. Каждый интервал включает в себя левый конец и не включает правый.
На первый взгляд, такая запись может показаться неудобной, нелогичной и вообще какой-то бредовой. Но поверьте: после небольшой тренировки вы обнаружите, что именно такой подход наиболее надёжен и при этом не мешает однозначно раскрывать модули. Лучше уж использовать такую схему, чем каждый раз думать: отдавать левый/правый конец в текущий интервал или «перекидывать» его в следующий.
Готовимся к ОГЭ по математике, решаем задание 23 на построение графика функции с модулем. За это задание на экзамене можно получить максимум 2 балла.
Постройте график функции y= |x 2 + 4x + 3|. Какое наибольшее число общих точек график данной функции может иметь с прямой параллельной оси абсцисс?
Чтобы построить график функции y= |x 2 + 4x + 3|, нужно сначала построить график функции y= x 2 + 4x + 3. Это квадратичная функция, график которой парабола с ветвями направленными вверх. Выделим квадрат двучлена чтобы найти вершину параболы: x 2 + 4x + 3 = (x 2 + 4x + 4) — 1 = (x + 2) 2 -1. Мы преобразовали функцию y = (x + 2) 2 — 1. Вершина параболы имеет координаты (-2;-1) и ось симметрию x = -2. Построим параболу по точкам. В таблице приведены значения для правой ветви. Левая ветвь строится симметрично.
Первая часть задания 23 из ОГЭ по математике выполнена, т.е. построен график квадратичной функции под модулем. Осталось определить — какое наибольшее число общих точек график данной функции может иметь с прямой параллельной OX:
- если проведем прямую y=0, то получаем 2 общие точки;
- если значения y находятся в промежутке (0;1), то 4 общие точки;
- если проведем прямую y =1, то мы видим 3 общие точки;
- если y>1, то 2 точки.

Данная статья посвящена решению примеров заданий 23 из ОГЭ по математике. В этих заданиях школьников обычно просят построить график той или иной функции, а затем указать, при каких значениях параметра этот график пересекается с неким другим графиком, касается его или же, к примеру, имеет с ним несколько точек пересечения. Ну и тому подобное. В данной статье вы найдёте разбор примеров решения заданий 23 из ОГЭ по математике от профессионального репетитора, на протяжении многих лет занимающегося подготовкой школьников к этому экзамену.
Примеры решения заданий 23 из ОГЭ по математике
Пример 1. Постройте график функции
Определите, при каких значениях прямая имеет с графиком ровно одну общую точку.
Построение графика функции всегда нужно начинать с указания области определения этой функции. В данном случае ограничения на эту область задаются тем, что в знаменателе не должно быть нуля, потому что деление на нуль не имеет математического смысла. То есть областью определения данной функции являются все числа, за исключением 1. Записать это можно следующим образом:
После того, как мы указали область определения исходной функции, можно попробовать её упростить. Для этого вынесем минус в знаменателе за скобку и сократим. В результате получим следующее выражение:
График данной функции получается из графика функции путём её отражения относительно оси OX
и параллельного переноса всех точек на 0,25 единичного отрезка вниз. При этом мы должны удалить из этого графика точку , потому что она не входит в область определения исходной функции. То есть искомый график выглядит следующим образом:
Теперь отвечаем на главный вопрос задачи. Графиком функции является прямая, проходящая через начало координат. При этом в зависимости от коэффициента эта прямая имеет разный наклон относительно оси OX
. Когда это прямая имеет ровно одну общую точку с изображённым графиком? Только в двух случаях. Рассмотрим их по отдельности.
Первый случай
. Когда данная прямая касается изображённого графика. Это ситуация изображена на рисунке:
Сложность состоит в том, чтобы определить значения , при которых эта ситуация реализуется. Для решения этой задачи можно использовать несколько различных подходов. Используем наиболее типичный.
Суть в том, что в точке касания графики проходят через одну и ту же точку на координатной плоскости. Значит, в этой точке имеет место равенство:
Дискриминант последнего квадратного уравнения равен , и в зависимости от коэффициента он может быть:
- отрицательным, тогда корней у этого уравнения не будет, как не будет и точек пересечения соответствующей прямой с изображённым графиком;
- положительным, тогда корней будет два, а значит и точек пересечения будет две (этот случай нам также не подходит);
- равен нулю, именно этот случай соответствует касанию прямой с графиком, поскольку записанное уравнение в этом случае будет иметь только одно решение.
То есть , то есть . Соответствующие прямые как раз и изображены на рисунке выше.
Второй случай
. Не забываем, что точка с абсциссой не принадлежит нашему графику. Значит, открывается ещё одна возможность, когда прямая будет иметь с графиком ровно одну общую точку. Вот этот случай:
Для нахождения в этом случае подставляем координаты точки в уравнение прямой . В результате получаем .
Сразу отметим, что в область определения данной функции входят все числа: . Наша задача теперь, как это часто бывает при решении заданий 23 из ОГЭ по математике, состоит в том, чтобы построить график этой функции. Для тех кто не сталкивался ранее с подобными заданиями, это может показаться странным, но график данной функции можно построить из графика функции . Нужно только выделить в подмодульном выражении полный квадрат. Для этого проведём следующие преобразования:
Из последнего с помощью формулы «квадрат разности» получаем:
Построим сначала график функции . Этот график получается из графика функции путём его переноса на единичного отрезка вправо и на единичного отрезка вниз:
При этом нули функции равны 2 и -1. Что произойдёт с этой параболой, если взять модуль от всего выражения, стоящего справа? Все точки, лежащие ниже оси OX
(с отрицательными ординатами), отразятся вверх относительно оси OX
. В результате получится вот такой график:
Теперь, глядя на этот график, уже понятно, что максимальное число точек пересечения данного графика с линией, параллельной оси абсцисс, будет равно 4. В качестве примера можно взять прямую :
Вот так решаются задания 23 из ОГЭ по математике. Как я уже говорил, это довольно интересные задания, которые к тому же можно научиться решать по ясному и запоминающемуся алгоритму. И как только вы овладеете этим мастерством, все задачи 23 из ОГЭ по математике будут казаться вам простыми и даже очевидными. Это станет для вас ещё одним заветным ключиком, который поможет получить максимальный балл на экзамене. Так что желаю вам успехов в подготовке и удаче на экзамене!
Сергей Валерьевич
Разбор типовых вариантов заданий №23 ОГЭ по математике
Первый вариант задания
Постройте график функции
Алгоритм решения:
- Записываем ответ.
Решение:
1. Преобразуем функцию в зависимости от знака переменной х.
2. График функции заданных значениях х — часть параболы, ветви которой направлены вниз.
Вершина расположена в точке с координатами:
Найдем нули функции: График проходит через начало координат и точку (-2;-7).
Графиком второй функции является парабола, ветви которой направлены вверх.
Вершина ее находится в точке:
Определим нули параболы
3. Изображаем график функции на координатной плоскости:
4. Из построения легко видно, что прямая y = m имеет с графиком ровно две точки, когда проходит через вершину одной из парабол, образующих график данной функции.
Значит, две общие точки функция и прямая имеют при m = -2,25 или m = 12,25.
Ответ: -2,25; 12,25.
Второй вариант задания
Постройте график функции
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем формулу в зависимости от знака переменной х:
2. Графиком функции является парабола, ветви которой направлены вниз.
Вершина ее находится в точке:
Найдем нули функции: График проходит через начало координат и точку (0;4).
Графиком второй функции является парабола, ветви которой направлены вверх.
Вершина ее находится в точке:
Определим нули параболы
3. Изображаем график на координатной плоскости:
Из изображения видно, что прямая y= m имеет с графиком только две общих точки, когда m=-9 или m=4. На графике прямая изображена красной линией при каждом значении m.
Ответ: -9; 4.
Третий вариант задания
Постройте график функции
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем формулу функции в зависимости от знака переменной
2. Определяем вид функции и находим дополнительные точки для каждого участка графика.
График при — часть парабола, ветви которой направлены вниз. Потому как коэффициент а
=-1 – отрицательный.
Определим вершину параболы и
.
Вершина находится в точке (-3; 9).
Парабола проходит еще через точки (0;0) и (0;6).
Если , ветви параболы направлены вверх. Найдем вершину:
, (2; -4).
График проходит также через точки (0;0) и (0;4).
3. Строим искомый график:
Из построения видно, что прямая y=m имеет только 2 общие точки с графиком функции в случаях, когда m=-4 или m=9. На рисунке прямые изображены красным цветом.
Ответ: -4; 9.
Четвертый вариант задания
Постройте график функции
Определите, при каких значениях k прямая у = kx не имеет с графиком общих точек.
Алгоритм решения:
- Строим график.
- Записываем ответ.
Решение:
1. Если x
Дробь, получившаяся в результате, определена . График представляет собой часть гиперболы.
Точки для построения графика:
3. Построим график заданной функции:
4. Прямая y=kx не имеет общих точек с графиком, при k=-1; 0 и 1, потому как тогда прямая проходит через точки, не входящие в область определения заданной функции.
На графике прямые для k=-1; 1изображены красным.
Ответ: -1; 0; 1.
Пятый вариант задания
Постройте график функции
Определите, при каких значениях k прямая y = kx не имеет с графиком общих точек.
Алгоритм решения:
- Раскрываем модуль и преобразовываем формул функции.
- Определяем вид функции на каждом промежутке и находим дополнительные точки графика.
- Строим график.
- Определяем искомые значения k.
- Записываем ответ.
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Задание 22 № 75
Постройте график функции и определите, при каких значениях параметра c прямая
имеет с графиком ровно одну общую точку.
Источник: ГИА по математике 28.05.2013. Основная волна. Вариант 1301.
2
Постройте график функции и найдите все значение k, при которых прямая
имеет с графиком данной функции ровно одну общую точку.
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(1 вар)
3
Постройте график функции и найдите все значения a, при которых прямая
не имеет с графиком данной функции общих точек.
Источник: ГИА-2013. Математика. Диагностическая работа № 2.(5 вар)
4
Постройте график функции и определите, при каких значениях c прямая
имеет с графиком три общие точки.
Источник: ГИА-2013. Математика. Тренировочная работа № 2.(1 вар)
5
Постройте график функции и найдите значения m, при которых прямая
имеет с ним ровно две общие точки.
Источник: ГИА-2013. Математика. Пробные варианты от ФИПИ (1 вар.)
Пройти тестирование по этим заданиям
Разбор типовых вариантов заданий №23 ОГЭ по математике
Первый вариант задания
Постройте график функции
Алгоритм решения:
- Записываем ответ.
Решение:
1. Преобразуем функцию в зависимости от знака переменной х.
2. График функции заданных значениях х — часть параболы, ветви которой направлены вниз.
Вершина расположена в точке с координатами:
Найдем нули функции: График проходит через начало координат и точку (-2;-7).
Вершина ее находится в точке:
Определим нули параболы
3. Изображаем график функции на координатной плоскости:
4. Из построения легко видно, что прямая y = m имеет с графиком ровно две точки, когда проходит через вершину одной из парабол, образующих график данной функции.
Значит, две общие точки функция и прямая имеют при m = -2,25 или m = 12,25.
Ответ: -2,25; 12,25.
Второй вариант задания
Постройте график функции
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем формулу в зависимости от знака переменной х:
2. Графиком функции является парабола, ветви которой направлены вниз.
Вершина ее находится в точке:
Найдем нули функции: График проходит через начало координат и точку (0;4).
Графиком второй функции является парабола, ветви которой направлены вверх.
Вершина ее находится в точке:
Определим нули параболы
3. Изображаем график на координатной плоскости:
Из изображения видно, что прямая y= m имеет с графиком только две общих точки, когда m=-9 или m=4. На графике прямая изображена красной линией при каждом значении m.
Ответ: -9; 4.
Третий вариант задания
Постройте график функции
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем формулу функции в зависимости от знака переменной
2. Определяем вид функции и находим дополнительные точки для каждого участка графика.
График при — часть парабола, ветви которой направлены вниз. Потому как коэффициент а
=-1 – отрицательный.
Определим вершину параболы и
.
Вершина находится в точке (-3; 9).
Парабола проходит еще через точки (0;0) и (0;6).
Если , ветви параболы направлены вверх. Найдем вершину:
, (2; -4).
График проходит также через точки (0;0) и (0;4).
3. Строим искомый график:
Из построения видно, что прямая y=m имеет только 2 общие точки с графиком функции в случаях, когда m=-4 или m=9. На рисунке прямые изображены красным цветом.
Ответ: -4; 9.
Четвертый вариант задания
Постройте график функции
Определите, при каких значениях k прямая у = kx не имеет с графиком общих точек.
Алгоритм решения:
- Строим график.
- Записываем ответ.
Решение:
1. Если x
Дробь, получившаяся в результате, определена . График представляет собой часть гиперболы.
Точки для построения графика:
3. Построим график заданной функции:
4. Прямая y=kx не имеет общих точек с графиком, при k=-1; 0 и 1, потому как тогда прямая проходит через точки, не входящие в область определения заданной функции.
На графике прямые для k=-1; 1изображены красным.
Ответ: -1; 0; 1.
Пятый вариант задания
Постройте график функции
Определите, при каких значениях k прямая y = kx не имеет с графиком общих точек.
Алгоритм решения:
- Раскрываем модуль и преобразовываем формул функции.
- Определяем вид функции на каждом промежутке и находим дополнительные точки графика.
- Строим график.
- Определяем искомые значения k.
- Записываем ответ.
Готовимся к ОГЭ по математике, решаем задание 23 на построение графика функции с модулем. За это задание на экзамене можно получить максимум 2 балла.
Постройте график функции y= |x 2 + 4x + 3|. Какое наибольшее число общих точек график данной функции может иметь с прямой параллельной оси абсцисс?
Чтобы построить график функции y= |x 2 + 4x + 3|, нужно сначала построить график функции y= x 2 + 4x + 3. Это квадратичная функция, график которой парабола с ветвями направленными вверх. Выделим квадрат двучлена чтобы найти вершину параболы: x 2 + 4x + 3 = (x 2 + 4x + 4) — 1 = (x + 2) 2 -1. Мы преобразовали функцию y = (x + 2) 2 — 1. Вершина параболы имеет координаты (-2;-1) и ось симметрию x = -2. Построим параболу по точкам. В таблице приведены значения для правой ветви. Левая ветвь строится симметрично.
Первая часть задания 23 из ОГЭ по математике выполнена, т.е. построен график квадратичной функции под модулем. Осталось определить — какое наибольшее число общих точек график данной функции может иметь с прямой параллельной OX:
- если проведем прямую y=0, то получаем 2 общие точки;
- если значения y находятся в промежутке (0;1), то 4 общие точки;
- если проведем прямую y =1, то мы видим 3 общие точки;
- если y>1, то 2 точки.

Данная статья посвящена решению примеров заданий 23 из ОГЭ по математике. В этих заданиях школьников обычно просят построить график той или иной функции, а затем указать, при каких значениях параметра этот график пересекается с неким другим графиком, касается его или же, к примеру, имеет с ним несколько точек пересечения. Ну и тому подобное. В данной статье вы найдёте разбор примеров решения заданий 23 из ОГЭ по математике от профессионального репетитора, на протяжении многих лет занимающегося подготовкой школьников к этому экзамену.
Примеры решения заданий 23 из ОГЭ по математике
Пример 1. Постройте график функции
Определите, при каких значениях прямая имеет с графиком ровно одну общую точку.
Построение графика функции всегда нужно начинать с указания области определения этой функции. В данном случае ограничения на эту область задаются тем, что в знаменателе не должно быть нуля, потому что деление на нуль не имеет математического смысла. То есть областью определения данной функции являются все числа, за исключением 1. Записать это можно следующим образом:
После того, как мы указали область определения исходной функции, можно попробовать её упростить. Для этого вынесем минус в знаменателе за скобку и сократим. В результате получим следующее выражение:
График данной функции получается из графика функции путём её отражения относительно оси OX
и параллельного переноса всех точек на 0,25 единичного отрезка вниз. При этом мы должны удалить из этого графика точку , потому что она не входит в область определения исходной функции. То есть искомый график выглядит следующим образом:
Теперь отвечаем на главный вопрос задачи. Графиком функции является прямая, проходящая через начало координат. При этом в зависимости от коэффициента эта прямая имеет разный наклон относительно оси OX
. Когда это прямая имеет ровно одну общую точку с изображённым графиком? Только в двух случаях. Рассмотрим их по отдельности.
Первый случай
. Когда данная прямая касается изображённого графика. Это ситуация изображена на рисунке:
Сложность состоит в том, чтобы определить значения , при которых эта ситуация реализуется. Для решения этой задачи можно использовать несколько различных подходов. Используем наиболее типичный.
Суть в том, что в точке касания графики проходят через одну и ту же точку на координатной плоскости. Значит, в этой точке имеет место равенство:
Дискриминант последнего квадратного уравнения равен , и в зависимости от коэффициента он может быть:
- отрицательным, тогда корней у этого уравнения не будет, как не будет и точек пересечения соответствующей прямой с изображённым графиком;
- положительным, тогда корней будет два, а значит и точек пересечения будет две (этот случай нам также не подходит);
- равен нулю, именно этот случай соответствует касанию прямой с графиком, поскольку записанное уравнение в этом случае будет иметь только одно решение.
То есть , то есть . Соответствующие прямые как раз и изображены на рисунке выше.
Второй случай
. Не забываем, что точка с абсциссой не принадлежит нашему графику. Значит, открывается ещё одна возможность, когда прямая будет иметь с графиком ровно одну общую точку. Вот этот случай:
Для нахождения в этом случае подставляем координаты точки в уравнение прямой . В результате получаем .
Сразу отметим, что в область определения данной функции входят все числа: . Наша задача теперь, как это часто бывает при решении заданий 23 из ОГЭ по математике, состоит в том, чтобы построить график этой функции. Для тех кто не сталкивался ранее с подобными заданиями, это может показаться странным, но график данной функции можно построить из графика функции . Нужно только выделить в подмодульном выражении полный квадрат. Для этого проведём следующие преобразования:
Из последнего с помощью формулы «квадрат разности» получаем:
Построим сначала график функции . Этот график получается из графика функции путём его переноса на единичного отрезка вправо и на единичного отрезка вниз:
При этом нули функции равны 2 и -1. Что произойдёт с этой параболой, если взять модуль от всего выражения, стоящего справа? Все точки, лежащие ниже оси OX
(с отрицательными ординатами), отразятся вверх относительно оси OX
. В результате получится вот такой график:
Теперь, глядя на этот график, уже понятно, что максимальное число точек пересечения данного графика с линией, параллельной оси абсцисс, будет равно 4. В качестве примера можно взять прямую :
Вот так решаются задания 23 из ОГЭ по математике. Как я уже говорил, это довольно интересные задания, которые к тому же можно научиться решать по ясному и запоминающемуся алгоритму. И как только вы овладеете этим мастерством, все задачи 23 из ОГЭ по математике будут казаться вам простыми и даже очевидными. Это станет для вас ещё одним заветным ключиком, который поможет получить максимальный балл на экзамене. Так что желаю вам успехов в подготовке и удаче на экзамене!
Сергей Валерьевич
Модуль — одна из тех вещей, о которых вроде-бы все слышали, но в действительности никто нормально не понимает. Поэтому сегодня будет большой урок, посвящённый решению уравнений с модулями.
Сразу скажу: урок будет несложный. И вообще модули — вообще тема относительно несложная. «Да конечно, несложная! У меня от неё мозг разрывается!» — скажут многие ученики, но все эти разрывы мозга происходят из-за того, что у большинства людей в голове не знания, а какая-то хрень. И цель этого урока — превратить хрень в знания.:)
Немного теории
Итак, поехали. Начнём с самого важного: что такое модуль? Напомню, что модуль числа — это просто то же самое число, но взятое без знака «минус». Т.е., например, $left| -5 right|=5$. Или $left| -129,5 right|=129,5$.
Вот так всё просто? Да, просто. А чему тогда равен модуль положительного числа? Тут ещё проще: модуль положительного числа равен самому этому числу: $left| 5 right|=5$; $left| 129,5 right|=129,5$ и т.д.
Получается любопытная вещь: разные числа могут иметь один тот же модуль. Например: $left| -5 right|=left| 5 right|=5$; $left| -129,5 right|=left| 129,5 right|=129,5$. Нетрудно заметить, что это за числа, у которых модули одинаковые: эти числа противоположны. Таким образом, отметим для себя, что модули противоположных чисел равны:
[left| -a right|=left| a right|]
Ещё один важный факт: модуль никогда не бывает отрицательным
. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.
Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:
Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.
Таким образом, если рассмотреть функцию $y=left| x right|$ и попробовать нарисовать её график, то получится вот такая «галка»:
График модуля и пример решения уравнения
Из этой картинки сразу видно, что $left| -m right|=left| m right|$, а график модуля никогда не опускается ниже оси абсцисс. Но это ещё не всё: красной линией отмечена прямая $y=a$, которая при положительных $a$ даёт нам сразу два корня: ${{x}_{1}}$ и ${{x}_{2}}$, но об этом мы поговорим позже.:)
Помимо чисто алгебраического определения, есть геометрическое. Допустим, есть две точки на числовой прямой: ${{x}_{1}}$ и ${{x}_{2}}$. В этом случае выражение $left| {{x}_{1}}-{{x}_{2}} right|$ — это просто расстояние между указанными точками. Или, если угодно, длина отрезка, соединяющего эти точки:
Модуль — это расстояние между точками на числовой прямой
Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)
Основная формула
Ну хорошо, с определением разобрались. Но легче-то от этого не стало. Как решать уравнения, содержащие этот самый модуль?
Спокойствие, только спокойствие. Начнём с самых простых вещей. Рассмотрим что-нибудь типа такого:
[left| x right|=3]
Итак, модуль$x$ равен 3. Чему может быть равен $x$? Ну, судя по определению, нас вполне устроит $x=3$. Действительно:
[left| 3 right|=3]
А есть ли другие числа? Кэп как бы намекает, что есть. Например, $x=-3$ — для него тоже $left| -3 right|=3$, т.е. требуемое равенство выполняется.
Так может, если поискать, подумать, мы найдём ещё числа? А вот обломитесь: больше чисел нет. Уравнение $left| x right|=3$ имеет лишь два корня: $x=3$ и $x=-3$.
Теперь немного усложним задачу. Пусть вместо переменной $x$ под знаком модуля тусуется функция $fleft(x right)$, а справа вместо тройки поставим произвольное число $a$. Получим уравнение:
[left| fleft(x right) right|=a]
Ну и как такое решать? Напомню: $fleft(x right)$ — произвольная функция, $a$ — любое число. Т.е. вообще любое! Например:
[left| 2x+1 right|=5]
[left| 10x-5 right|=-65]
Обратим внимание на второе уравнение. Про него сразу можно сказать: корней у него нет. Почему? Всё правильно: потому что в нём требуется, чтобы модуль был равен отрицательному числу, чего никогда не бывает, поскольку мы уже знаем, что модуль — число всегда положительное или в крайнем случае ноль.
А вот с первым уравнением всё веселее. Тут два варианта: либо под знаком модуля стоит положительное выражение, и тогда$left| 2x+1 right|=2x+1$, либо это выражение всё-таки отрицательное, и тогда $left| 2x+1 right|=-left(2x+1 right)=-2x-1$. В первом случае наше уравнение перепишется так:
[left| 2x+1 right|=5Rightarrow 2x+1=5]
И внезапно получается, что подмодульное выражение $2x+1$ действительно положительно — оно равно числу 5. Т.е. мы можем спокойно решать это уравнение — полученный корень будет кусочком ответа:
Особо недоверчивые могут попробовать подставить найденный корень в исходное уравнение и убедиться, что действительно под модулем будет положительное число.
Теперь разберём случай отрицательного подмодульного выражения:
[left{ begin{align}& left| 2x+1 right|=5 & 2x+1 lt 0 end{align} right.Rightarrow -2x-1=5Rightarrow 2x+1=-5]
Опа! Снова всё чётко: мы предположили, что $2x+1 lt 0$, и в результате получили, что $2x+1=-5$ — действительно, это выражение меньше нуля. Решаем полученное уравнение, при этом уже точно зная, что найденный корень нас устроит:
Итого мы вновь получили два ответа: $x=2$ и $x=3$. Да, объём вычислений оказался малость побольше, чем в совсем уж простом уравнении $left| x right|=3$, но принципиально ничего не изменилось. Так может, существует какой-то универсальный алгоритм?
Да, такой алгоритм существует. И сейчас мы его разберём.
Избавление от знака модуля
Пусть нам дано уравнение $left| fleft(x right) right|=a$, причём $age 0$ (иначе, как мы уже знаем, корней нет). Тогда можно избавиться от знака модуля по следующему правилу:
[left| fleft(x right) right|=aRightarrow fleft(x right)=pm a]
Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого
[left| 5x+4 right|=10Rightarrow 5x+4=pm 10]
Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:
[begin{align}& 5x+4=10Rightarrow 5x=6Rightarrow x=frac{6}{5}=1,2; & 5x+4=-10Rightarrow 5x=-14Rightarrow x=-frac{14}{5}=-2,8. end{align}]
Вот и всё! Получили два корня: $x=1,2$ и $x=-2,8$. Всё решение заняло буквально две строчки.
Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:
[left| 7-5x right|=13]
Опять раскрываем модуль с плюсом и минусом:
[begin{align}& 7-5x=13Rightarrow -5x=6Rightarrow x=-frac{6}{5}=-1,2; & 7-5x=-13Rightarrow -5x=-20Rightarrow x=4. end{align}]
Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.
Случай переменной правой части
А теперь рассмотрим вот такое уравнение:
[left| 3x-2 right|=2x]
Это уравнение принципиально отличается от всех предыдущих. Чем? А тем, что справа от знака равенства стоит выражение $2x$ — и мы не можем заранее знать, положительное оно или отрицательное.
Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней
— мы уже знаем, что модуль не может быть равен отрицательному числу.
А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».
Таким образом, сформулируем правило для произвольных функций $fleft(x right)$ и $gleft(x right)$ :
[left| fleft(x right) right|=gleft(x right)Rightarrow left{ begin{align}& fleft(x right)=pm gleft(x right), & gleft(x right)ge 0. end{align} right.]
Применительно к нашему уравнению получим:
[left| 3x-2 right|=2xRightarrow left{ begin{align}& 3x-2=pm 2x, & 2xge 0. end{align} right.]
Ну, с требованием $2xge 0$ мы как-нибудь справимся. В конце концов, можно тупо подставить корни, которые мы получим из первого уравнения, и проверить: выполняется неравенство или нет.
Поэтому решим-ка само уравнение:
[begin{align}& 3x-2=2Rightarrow 3x=4Rightarrow x=frac{4}{3}; & 3x-2=-2Rightarrow 3x=0Rightarrow x=0. end{align}]
Ну и какой их этих двух корней удовлетворяет требованию $2xge 0$? Да оба! Поэтому в ответ пойдут два числа: $x={4}/{3};$ и $x=0$. Вот и всё решение.:)
Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}]
Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:
[left| fleft(x right) right|=gleft(x right)]
И решается оно точно так же:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}Rightarrow left{ begin{align}& {{x}^{3}}-3{{x}^{2}}+x=pm left(x-{{x}^{3}} right), & x-{{x}^{3}}ge 0. end{align} right.]
С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:
[{{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}]
Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}; & 2{{x}^{3}}-3{{x}^{2}}=0; end{align}]
Выносим общий множитель ${{x}^{2}}$ за скобку и получаем очень простое уравнение:
[{{x}^{2}}left(2x-3 right)=0Rightarrow left[ begin{align}& {{x}^{2}}=0 & 2x-3=0 end{align} right.]
[{{x}_{1}}=0;quad {{x}_{2}}=frac{3}{2}=1,5.]
Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.
Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=-left(x-{{x}^{3}} right); & {{x}^{3}}-3{{x}^{2}}+x=-x+{{x}^{3}}; & -3{{x}^{2}}+2x=0; & xleft(-3x+2 right)=0. end{align}]
Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:
[left[ begin{align}& x=0 & -3x+2=0 end{align} right.]
Ну вот мы получили три корня: $x=0$, $x=1,5$ и $x={2}/{3};$. Ну и что из этого набора пойдёт в окончательный ответ? Для этого вспомним, что у нас есть дополнительное ограничение в виде неравенства:
Как учесть это требование? Да просто подставим найденные корни и проверим: выполняется неравенство при этих $x$ или нет. Имеем:
[begin{align}& x=0Rightarrow x-{{x}^{3}}=0-0=0ge 0; & x=1,5Rightarrow x-{{x}^{3}}=1,5-{{1,5}^{3}} lt 0; & x=frac{2}{3}Rightarrow x-{{x}^{3}}=frac{2}{3}-frac{8}{27}=frac{10}{27}ge 0; end{align}]
Таким образом, корень $x=1,5$ нас не устраивает. И в ответ пойдут лишь два корня:
[{{x}_{1}}=0;quad {{x}_{2}}=frac{2}{3}.]
Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.
Уравнения с двумя модулями
До сих пор мы изучали лишь самые простые уравнения — там был один модуль и что-то ещё. Это «что-то ещё» мы отправляли в другую часть неравенства, подальше от модуля, чтобы в итоге всё свелось к уравнению вида $left| fleft(x right) right|=gleft(x right)$ или даже более простому $left| fleft(x right) right|=a$.
Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:
[left| fleft(x right) right|=left| gleft(x right) right|]
Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.
Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:
[left| fleft(x right) right|=left| gleft(x right) right|Rightarrow fleft(x right)=pm gleft(x right)]
Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.
Давайте попробуем решать вот такую задачу:
[left| 2x+3 right|=left| 2x-7 right|]
Элементарно, Ватсон! Раскрываем модули:
[left| 2x+3 right|=left| 2x-7 right|Rightarrow 2x+3=pm left(2x-7 right)]
Рассмотрим отдельно каждый случай:
[begin{align}& 2x+3=2x-7Rightarrow 3=-7Rightarrow emptyset ; & 2x+3=-left(2x-7 right)Rightarrow 2x+3=-2x+7. end{align}]
В первом уравнении корней нет. Потому что когда это $3=-7$? При каких значениях $x$? «Какой ещё нафиг $x$? Ты обкурился? Там вообще нет $x$» — скажете вы. И будете правы. Мы получили равенство, не зависящее от переменной $x$, и при этом само равенство — неверное. Потому и нет корней.:)
Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:
Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)
В итоге окончательный ответ: $x=1$.
Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|]
Опять у нас уравнение вида $left| fleft(x right) right|=left| gleft(x right) right|$. Поэтому сразу переписываем его, раскрывая знак модуля:
[{{x}^{2}}-3x+2=pm left(x-1 right)]
Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:
Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми.
Но ведь ничто не мешает нам переписать исходное уравнение следующим образом:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|Rightarrow left| {{x}^{2}}-3x+2 right|=left| x-1 right|]
Что произошло? Да ничего особенного: просто поменяли левую и правую часть местами. Мелочь, которая в итоге немного упростит нам жизнь.:)
В общем, решаем это уравнение, рассматривая варианты с плюсом и с минусом:
[begin{align}& {{x}^{2}}-3x+2=x-1Rightarrow {{x}^{2}}-4x+3=0; & {{x}^{2}}-3x+2=-left(x-1 right)Rightarrow {{x}^{2}}-2x+1=0. end{align}]
Первое уравнение имеет корни $x=3$ и $x=1$. Второе вообще является точным квадратом:
[{{x}^{2}}-2x+1={{left(x-1 right)}^{2}}]
Поэтому у него единственный корень: $x=1$. Но этот корень мы уже получали ранее. Таким образом, в итоговый ответ пойдут лишь два числа:
[{{x}_{1}}=3;quad {{x}_{2}}=1.]
Миссия выполнена! Можно взять с полки и скушать пирожок. Там их 2, ваш средний.:)
Важное замечание
. Наличие одинаковых корней при разных вариантах раскрытия модуля означает, что исходные многочлены раскладываются на множители, и среди этих множителей обязательно будет общий. Действительно:[begin{align}& left| x-1 right|=left| {{x}^{2}}-3x+2 right|; & left| x-1 right|=left| left(x-1 right)left(x-2 right) right|. end{align}]
Одно из свойств модуля: $left| acdot b right|=left| a right|cdot left| b right|$ (т.е. модуль произведения равен произведению модулей), поэтому исходное уравнение можно переписать так:
[left| x-1 right|=left| x-1 right|cdot left| x-2 right|]
Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:
[begin{align}& left| x-1 right|=left| x-1 right|cdot left| x-2 right|; & left| x-1 right|-left| x-1 right|cdot left| x-2 right|=0; & left| x-1 right|cdot left(1-left| x-2 right| right)=0. end{align}]
Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:
[left[ begin{align}& left| x-1 right|=0, & left| x-2 right|=1. end{align} right.]
Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)
Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)
Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.
Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.
Итак, уравнение:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0]
Нет, это не опечатка: между модулями именно плюс. И нам нужно найти, при каких $x$ сумма двух модулей равна нулю.:)
В чём вообще проблема? А проблема в том, что каждый модуль — число положительное, либо в крайнем случае ноль. А что будет, если сложить два положительных числа? Очевидно, снова положительное число:
[begin{align}& 5+7=12 gt 0; & 0,004+0,0001=0,0041 gt 0; & 5+0=5 gt 0. end{align}]
Последняя строчка может натолкнуть на мысль: единственный случай, когда сумма модулей равна нулю — это если каждый модуль будет равен нулю:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0Rightarrow left{ begin{align}& left| x-{{x}^{3}} right|=0, & left| {{x}^{2}}+x-2 right|=0. end{align} right.]
А когда модуль равен нулю? Только в одном случае — когда подмодульное выражение равно нулю:
[{{x}^{2}}+x-2=0Rightarrow left(x+2 right)left(x-1 right)=0Rightarrow left[ begin{align}& x=-2 & x=1 end{align} right.]
Таким образом, у нас есть три точки, в которых обнуляется первый модуль: 0, 1 и −1; а также две точки, в которых обнуляется второй модуль: −2 и 1. Однако нам нужно, чтобы оба модуля обнулялись одновременно, поэтому среди найденных чисел нужно выбрать те, которые входят в оба набора. Очевидно, такое число лишь одно: $x=1$ — это и будет окончательным ответом.
Метод расщепления
Что ж, мы уже рассмотрели кучу задач и изучили множество приёмов. Думаете, на этом всё? А вот и нет! Сейчас мы рассмотрим заключительный приём — и одновременно самый важный. Речь пойдёт о расщеплении уравнений с модулем. О чём вообще пойдёт речь? Давайте вернёмся немного назад и рассмотрим какое-нибудь простое уравнение. Например, это:
[left| 3x-5 right|=5-3x]
В принципе, мы уже знаем, как решать такое уравнение, потому что это стандартная конструкция вида $left| fleft(x right) right|=gleft(x right)$. Но попробуем взглянуть на это уравнение немного под другим углом. Точнее, рассмотрим выражение, стоящее под знаком модуля. Напомню, что модуль любого числа может быть равен самому числу, а может быть противоположен этому числу:
[left| a right|=left{ begin{align}& a,quad age 0, & -a,quad a lt 0. end{align} right.]
Собственно, в этой неоднозначности и состоит вся проблема: поскольку число под модулем меняется (оно зависит от переменной), нам неясно — положительное оно или отрицательное.
Но что если изначально потребовать, чтобы это число было положительным? Например, потребуем, чтобы $3x-5 gt 0$ — в этом случае мы гарантированно получим положительное число под знаком модуля, и от этого самого модуля можно полностью избавиться:
Таким образом, наше уравнение превратится в линейное, которое легко решается:
Правда, все эти размышления имеют смысл только при условии $3x-5 gt 0$ — мы сами ввели это требование, дабы однозначно раскрыть модуль. Поэтому давайте подставим найденный $x=frac{5}{3}$ в это условие и проверим:
Получается, что при указанном значении $x$ наше требование не выполняется, т.к. выражение оказалось равно нулю, а нам нужно, чтобы оно было строго больше нуля. Печалька.:(
Но ничего страшного! Ведь есть ещё вариант $3x-5 lt 0$. Более того: есть ещё и случай $3x-5=0$ — это тоже нужно рассмотреть, иначе решение будет неполным. Итак, рассмотрим случай $3x-5 lt 0$:
Очевидно, что в модуль раскроется со знаком «минус». Но тогда возникает странная ситуация: и слева, и справа в исходном уравнении будет торчать одно и то же выражение:
Интересно, при каких таких $x$ выражение $5-3x$ будет равно выражению $5-3x$? От таких уравнений даже Капитан очевидность подавился бы слюной, но мы-то знаем: это уравнение является тождеством, т.е. оно верно при любых значениях переменной!
А это значит, что нас устроят любые $x$. Вместе с тем у нас есть ограничение:
Другими словами, ответом будет не какое-то отдельное число, а целый интервал:
Наконец, осталось рассмотреть ещё один случай: $3x-5=0$. Тут всё просто: под модулем будет ноль, а модуль нуля тоже равен нулю (это прямо следует из определения):
Но тогда исходное уравнение $left| 3x-5 right|=5-3x$ перепишется следующим образом:
Этот корень мы уже получали выше, когда рассматривали случай $3x-5 gt 0$. Более того, это корень является решением уравнения $3x-5=0$ — это ограничение, которое мы сами же и ввели, чтобы обнулить модуль.:)
Таким образом, помимо интервала нас устроит ещё и число, лежащее на самом конце этого интервала:
Объединение корней в уравнениях с модулем
Итого окончательный ответ: $xin left(-infty ;frac{5}{3} right]$. Не очень-то привычно видеть такую хрень в ответе к довольно простому (по сути — линейному) уравнению с модулем, правда? Что ж, привыкайте: в том и состоит сложность модуля, что ответы в таких уравнениях могут оказаться совершенно непредсказуемыми.
Куда важнее другое: мы только что разобрали универсальный алгоритм решения уравнения с модуляем! И состоит этот алгоритм из следующих шагов:
- Приравнять каждый модуль, имеющийся в уравнении, к нулю. Получим несколько уравнений;
- Решить все эти уравнения и отметить корни на числовой прямой. В результате прямая разобьётся на несколько интервалов, на каждом из которых все модули однозначно раскрываются;
- Решить исходное уравнение для каждого интервала и объединить полученные ответы.
Вот и всё! Остаётся лишь один вопрос: куда девать сами корни, полученные на 1-м шаге? Допустим, у нас получилось два корня: $x=1$ и $x=5$. Они разобьют числовую прямую на 3 куска:
Разбиение числовой оси на интервалы с помощью точек
Ну и какие тут интервалы? Понятно, что их три:
- Самый левый: $x lt 1$ — сама единица в интервал не входит;
- Центральный: $1le x lt 5$ — вот тут единица в интервал входит, однако не входит пятёрка;
- Самый правый: $xge 5$ — пятёрка входит только сюда!
Я думаю, вы уже поняли закономерность. Каждый интервал включает в себя левый конец и не включает правый.
На первый взгляд, такая запись может показаться неудобной, нелогичной и вообще какой-то бредовой. Но поверьте: после небольшой тренировки вы обнаружите, что именно такой подход наиболее надёжен и при этом не мешает однозначно раскрывать модули. Лучше уж использовать такую схему, чем каждый раз думать: отдавать левый/правый конец в текущий интервал или «перекидывать» его в следующий.
Модуль — одна из тех вещей, о которых вроде-бы все слышали, но в действительности никто нормально не понимает. Поэтому сегодня будет большой урок, посвящённый решению уравнений с модулями.
Сразу скажу: урок будет несложный. И вообще модули — вообще тема относительно несложная. «Да конечно, несложная! У меня от неё мозг разрывается!» — скажут многие ученики, но все эти разрывы мозга происходят из-за того, что у большинства людей в голове не знания, а какая-то хрень. И цель этого урока — превратить хрень в знания.:)
Немного теории
Итак, поехали. Начнём с самого важного: что такое модуль? Напомню, что модуль числа — это просто то же самое число, но взятое без знака «минус». Т.е., например, $left| -5 right|=5$. Или $left| -129,5 right|=129,5$.
Вот так всё просто? Да, просто. А чему тогда равен модуль положительного числа? Тут ещё проще: модуль положительного числа равен самому этому числу: $left| 5 right|=5$; $left| 129,5 right|=129,5$ и т.д.
Получается любопытная вещь: разные числа могут иметь один тот же модуль. Например: $left| -5 right|=left| 5 right|=5$; $left| -129,5 right|=left| 129,5 right|=129,5$. Нетрудно заметить, что это за числа, у которых модули одинаковые: эти числа противоположны. Таким образом, отметим для себя, что модули противоположных чисел равны:
[left| -a right|=left| a right|]
Ещё один важный факт: модуль никогда не бывает отрицательным
. Какое бы число мы ни взяли — хоть положительное, хоть отрицательное — его модуль всегда оказывается положительным (или в крайнем случае нулём). Именно поэтому модуль часто называют абсолютной величиной числа.
Кроме того, если объединить определение модуля для положительного и отрицательного числа, то получим глобальное определение модуля для всех чисел. А именно: модуль числа равен самому этому числу, если число положительное (или ноль), либо равен противоположному числу, если число отрицательное. Можно записать это в виде формулы:
Ещё есть модуль нуля, но он всегда равен нулю. Кроме того, ноль — единственное число, которое не имеет противоположного.
Таким образом, если рассмотреть функцию $y=left| x right|$ и попробовать нарисовать её график, то получится вот такая «галка»:
График модуля и пример решения уравнения
Из этой картинки сразу видно, что $left| -m right|=left| m right|$, а график модуля никогда не опускается ниже оси абсцисс. Но это ещё не всё: красной линией отмечена прямая $y=a$, которая при положительных $a$ даёт нам сразу два корня: ${{x}_{1}}$ и ${{x}_{2}}$, но об этом мы поговорим позже.:)
Помимо чисто алгебраического определения, есть геометрическое. Допустим, есть две точки на числовой прямой: ${{x}_{1}}$ и ${{x}_{2}}$. В этом случае выражение $left| {{x}_{1}}-{{x}_{2}} right|$ — это просто расстояние между указанными точками. Или, если угодно, длина отрезка, соединяющего эти точки:
Модуль — это расстояние между точками на числовой прямой
Из этого определения также следует, что модуль всегда неотрицателен. Но хватит определений и теории — перейдём к настоящим уравнениям.:)
Основная формула
Ну хорошо, с определением разобрались. Но легче-то от этого не стало. Как решать уравнения, содержащие этот самый модуль?
Спокойствие, только спокойствие. Начнём с самых простых вещей. Рассмотрим что-нибудь типа такого:
[left| x right|=3]
Итак, модуль$x$ равен 3. Чему может быть равен $x$? Ну, судя по определению, нас вполне устроит $x=3$. Действительно:
[left| 3 right|=3]
А есть ли другие числа? Кэп как бы намекает, что есть. Например, $x=-3$ — для него тоже $left| -3 right|=3$, т.е. требуемое равенство выполняется.
Так может, если поискать, подумать, мы найдём ещё числа? А вот обломитесь: больше чисел нет. Уравнение $left| x right|=3$ имеет лишь два корня: $x=3$ и $x=-3$.
Теперь немного усложним задачу. Пусть вместо переменной $x$ под знаком модуля тусуется функция $fleft(x right)$, а справа вместо тройки поставим произвольное число $a$. Получим уравнение:
[left| fleft(x right) right|=a]
Ну и как такое решать? Напомню: $fleft(x right)$ — произвольная функция, $a$ — любое число. Т.е. вообще любое! Например:
[left| 2x+1 right|=5]
[left| 10x-5 right|=-65]
Обратим внимание на второе уравнение. Про него сразу можно сказать: корней у него нет. Почему? Всё правильно: потому что в нём требуется, чтобы модуль был равен отрицательному числу, чего никогда не бывает, поскольку мы уже знаем, что модуль — число всегда положительное или в крайнем случае ноль.
А вот с первым уравнением всё веселее. Тут два варианта: либо под знаком модуля стоит положительное выражение, и тогда$left| 2x+1 right|=2x+1$, либо это выражение всё-таки отрицательное, и тогда $left| 2x+1 right|=-left(2x+1 right)=-2x-1$. В первом случае наше уравнение перепишется так:
[left| 2x+1 right|=5Rightarrow 2x+1=5]
И внезапно получается, что подмодульное выражение $2x+1$ действительно положительно — оно равно числу 5. Т.е. мы можем спокойно решать это уравнение — полученный корень будет кусочком ответа:
Особо недоверчивые могут попробовать подставить найденный корень в исходное уравнение и убедиться, что действительно под модулем будет положительное число.
Теперь разберём случай отрицательного подмодульного выражения:
[left{ begin{align}& left| 2x+1 right|=5 & 2x+1 lt 0 end{align} right.Rightarrow -2x-1=5Rightarrow 2x+1=-5]
Опа! Снова всё чётко: мы предположили, что $2x+1 lt 0$, и в результате получили, что $2x+1=-5$ — действительно, это выражение меньше нуля. Решаем полученное уравнение, при этом уже точно зная, что найденный корень нас устроит:
Итого мы вновь получили два ответа: $x=2$ и $x=3$. Да, объём вычислений оказался малость побольше, чем в совсем уж простом уравнении $left| x right|=3$, но принципиально ничего не изменилось. Так может, существует какой-то универсальный алгоритм?
Да, такой алгоритм существует. И сейчас мы его разберём.
Избавление от знака модуля
Пусть нам дано уравнение $left| fleft(x right) right|=a$, причём $age 0$ (иначе, как мы уже знаем, корней нет). Тогда можно избавиться от знака модуля по следующему правилу:
[left| fleft(x right) right|=aRightarrow fleft(x right)=pm a]
Таким образом, наше уравнение с модулем распадается на два, но уже без модуля. Вот и вся технология! Попробуем решить парочку уравнений. Начнём вот с такого
[left| 5x+4 right|=10Rightarrow 5x+4=pm 10]
Отдельно рассмотрим, когда справа стоит десятка с плюсом, и отдельно — когда с минусом. Имеем:
[begin{align}& 5x+4=10Rightarrow 5x=6Rightarrow x=frac{6}{5}=1,2; & 5x+4=-10Rightarrow 5x=-14Rightarrow x=-frac{14}{5}=-2,8. end{align}]
Вот и всё! Получили два корня: $x=1,2$ и $x=-2,8$. Всё решение заняло буквально две строчки.
Ок, не вопрос, давайте рассмотрим что-нибудь чуть посерьёзнее:
[left| 7-5x right|=13]
Опять раскрываем модуль с плюсом и минусом:
[begin{align}& 7-5x=13Rightarrow -5x=6Rightarrow x=-frac{6}{5}=-1,2; & 7-5x=-13Rightarrow -5x=-20Rightarrow x=4. end{align}]
Опять пара строчек — и ответ готов! Как я и говорил, в модулях нет ничего сложного. Нужно лишь запомнить несколько правил. Поэтому идём дальше и приступаем с действительно более сложным задачам.
Случай переменной правой части
А теперь рассмотрим вот такое уравнение:
[left| 3x-2 right|=2x]
Это уравнение принципиально отличается от всех предыдущих. Чем? А тем, что справа от знака равенства стоит выражение $2x$ — и мы не можем заранее знать, положительное оно или отрицательное.
Как быть в таком случае? Во-первых, надо раз и навсегда понять, что если правая часть уравнения окажется отрицательной, то уравнение не будет иметь корней
— мы уже знаем, что модуль не может быть равен отрицательному числу.
А во-вторых, если права часть всё-таки положительна (или равна нулю), то можно действовать точно так же, как раньше: просто раскрыть модуль отдельно со знаком «плюс» и отдельно — со знаком «минус».
Таким образом, сформулируем правило для произвольных функций $fleft(x right)$ и $gleft(x right)$ :
[left| fleft(x right) right|=gleft(x right)Rightarrow left{ begin{align}& fleft(x right)=pm gleft(x right), & gleft(x right)ge 0. end{align} right.]
Применительно к нашему уравнению получим:
[left| 3x-2 right|=2xRightarrow left{ begin{align}& 3x-2=pm 2x, & 2xge 0. end{align} right.]
Ну, с требованием $2xge 0$ мы как-нибудь справимся. В конце концов, можно тупо подставить корни, которые мы получим из первого уравнения, и проверить: выполняется неравенство или нет.
Поэтому решим-ка само уравнение:
[begin{align}& 3x-2=2Rightarrow 3x=4Rightarrow x=frac{4}{3}; & 3x-2=-2Rightarrow 3x=0Rightarrow x=0. end{align}]
Ну и какой их этих двух корней удовлетворяет требованию $2xge 0$? Да оба! Поэтому в ответ пойдут два числа: $x={4}/{3};$ и $x=0$. Вот и всё решение.:)
Подозреваю, что кто-то из учеников уже начал скучать? Что ж, рассмотрим ещё более сложное уравнение:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}]
Хоть оно и выглядит злобно, по факту это всё то же самое уравнение вида «модуль равен функции»:
[left| fleft(x right) right|=gleft(x right)]
И решается оно точно так же:
[left| {{x}^{3}}-3{{x}^{2}}+x right|=x-{{x}^{3}}Rightarrow left{ begin{align}& {{x}^{3}}-3{{x}^{2}}+x=pm left(x-{{x}^{3}} right), & x-{{x}^{3}}ge 0. end{align} right.]
С неравенством мы потом разберёмся — оно какое-то уж слишком злобное (на самом деле простое, но мы его решать не будем). Пока лучше займёмся полученными уравнениями. Рассмотрим первый случай — это когда модуль раскрывается со знаком «плюс»:
[{{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}]
Ну, тут и ежу понятно, что нужно всё собрать слева, привести подобные и посмотреть, что получится. А получится вот что:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=x-{{x}^{3}}; & 2{{x}^{3}}-3{{x}^{2}}=0; end{align}]
Выносим общий множитель ${{x}^{2}}$ за скобку и получаем очень простое уравнение:
[{{x}^{2}}left(2x-3 right)=0Rightarrow left[ begin{align}& {{x}^{2}}=0 & 2x-3=0 end{align} right.]
[{{x}_{1}}=0;quad {{x}_{2}}=frac{3}{2}=1,5.]
Тут мы воспользовались важным свойством произведения, ради которого мы и раскладывали исходный многочлен на множители: произведение равно нулю, когда хотя бы один из множителей равен нулю.
Теперь точно так же разберёмся со вторым уравнением, которое получается при раскрытии модуля со знаком «минус»:
[begin{align}& {{x}^{3}}-3{{x}^{2}}+x=-left(x-{{x}^{3}} right); & {{x}^{3}}-3{{x}^{2}}+x=-x+{{x}^{3}}; & -3{{x}^{2}}+2x=0; & xleft(-3x+2 right)=0. end{align}]
Опять то же самое: произведение равно нулю, когда равен нулю хотя бы один из множителей. Имеем:
[left[ begin{align}& x=0 & -3x+2=0 end{align} right.]
Ну вот мы получили три корня: $x=0$, $x=1,5$ и $x={2}/{3};$. Ну и что из этого набора пойдёт в окончательный ответ? Для этого вспомним, что у нас есть дополнительное ограничение в виде неравенства:
Как учесть это требование? Да просто подставим найденные корни и проверим: выполняется неравенство при этих $x$ или нет. Имеем:
[begin{align}& x=0Rightarrow x-{{x}^{3}}=0-0=0ge 0; & x=1,5Rightarrow x-{{x}^{3}}=1,5-{{1,5}^{3}} lt 0; & x=frac{2}{3}Rightarrow x-{{x}^{3}}=frac{2}{3}-frac{8}{27}=frac{10}{27}ge 0; end{align}]
Таким образом, корень $x=1,5$ нас не устраивает. И в ответ пойдут лишь два корня:
[{{x}_{1}}=0;quad {{x}_{2}}=frac{2}{3}.]
Как видите, даже в этом случае ничего сложного не было — уравнения с модулями всегда решаются по алгоритму. Нужно лишь хорошо разбираться в многочленах и неравенствах. Поэтому переходим к более сложным задачам — там уже будет не один, а два модуля.
Уравнения с двумя модулями
До сих пор мы изучали лишь самые простые уравнения — там был один модуль и что-то ещё. Это «что-то ещё» мы отправляли в другую часть неравенства, подальше от модуля, чтобы в итоге всё свелось к уравнению вида $left| fleft(x right) right|=gleft(x right)$ или даже более простому $left| fleft(x right) right|=a$.
Но детский сад закончился — пора рассмотреть что-нибудь посерьёзнее. Начнём с уравнений вот такого типа:
[left| fleft(x right) right|=left| gleft(x right) right|]
Это уравнение вида «модуль равен модулю». Принципиально важным моментом является отсутствие других слагаемых и множителей: только один модуль слева, ещё один модуль справа — и ничего более.
Кто-нибудь сейчас подумает, что такие уравнения решаются сложнее, чем то, что мы изучали до сих пор. А вот и нет: эти уравнения решаются даже проще. Вот формула:
[left| fleft(x right) right|=left| gleft(x right) right|Rightarrow fleft(x right)=pm gleft(x right)]
Всё! Мы просто приравниваем подмодульные выражения, ставя перед одним из них знак «плюс-минус». А затем решаем полученные два уравнения — и корни готовы! Никаких дополнительных ограничений, никаких неравенств и т.д. Всё очень просто.
Давайте попробуем решать вот такую задачу:
[left| 2x+3 right|=left| 2x-7 right|]
Элементарно, Ватсон! Раскрываем модули:
[left| 2x+3 right|=left| 2x-7 right|Rightarrow 2x+3=pm left(2x-7 right)]
Рассмотрим отдельно каждый случай:
[begin{align}& 2x+3=2x-7Rightarrow 3=-7Rightarrow emptyset ; & 2x+3=-left(2x-7 right)Rightarrow 2x+3=-2x+7. end{align}]
В первом уравнении корней нет. Потому что когда это $3=-7$? При каких значениях $x$? «Какой ещё нафиг $x$? Ты обкурился? Там вообще нет $x$» — скажете вы. И будете правы. Мы получили равенство, не зависящее от переменной $x$, и при этом само равенство — неверное. Потому и нет корней.:)
Со вторым уравнением всё чуть интереснее, но тоже очень и очень просто:
Как видим, всё решилось буквально в пару строчек — другого от линейного уравнения мы и не ожидали.:)
В итоге окончательный ответ: $x=1$.
Ну как? Сложно? Конечно, нет. Попробуем что-нибудь ещё:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|]
Опять у нас уравнение вида $left| fleft(x right) right|=left| gleft(x right) right|$. Поэтому сразу переписываем его, раскрывая знак модуля:
[{{x}^{2}}-3x+2=pm left(x-1 right)]
Возможно, кто-то сейчас спросит: «Эй, что за бред? Почему «плюс-минус» стоит у правого выражения, а не у левого?» Спокойно, сейчас всё объясню. Действительно, по-хорошему мы должны были переписать наше уравнение следующим образом:
Затем нужно раскрыть скобки, перенести все слагаемые в одну сторону от знака равенства (поскольку уравнение, очевидно, в обоих случаях будет квадратным), ну и дальше отыскать корни. Но согласитесь: когда «плюс-минус» стоит перед тремя слагаемыми (особенно когда одно из этих слагаемых — квадратное выражение), это как-то более сложно выглядит, нежели ситуация, когда «плюс-минус» стоит лишь перед двумя слагаемыми.
Но ведь ничто не мешает нам переписать исходное уравнение следующим образом:
[left| x-1 right|=left| {{x}^{2}}-3x+2 right|Rightarrow left| {{x}^{2}}-3x+2 right|=left| x-1 right|]
Что произошло? Да ничего особенного: просто поменяли левую и правую часть местами. Мелочь, которая в итоге немного упростит нам жизнь.:)
В общем, решаем это уравнение, рассматривая варианты с плюсом и с минусом:
[begin{align}& {{x}^{2}}-3x+2=x-1Rightarrow {{x}^{2}}-4x+3=0; & {{x}^{2}}-3x+2=-left(x-1 right)Rightarrow {{x}^{2}}-2x+1=0. end{align}]
Первое уравнение имеет корни $x=3$ и $x=1$. Второе вообще является точным квадратом:
[{{x}^{2}}-2x+1={{left(x-1 right)}^{2}}]
Поэтому у него единственный корень: $x=1$. Но этот корень мы уже получали ранее. Таким образом, в итоговый ответ пойдут лишь два числа:
[{{x}_{1}}=3;quad {{x}_{2}}=1.]
Миссия выполнена! Можно взять с полки и скушать пирожок. Там их 2, ваш средний.:)
Важное замечание
. Наличие одинаковых корней при разных вариантах раскрытия модуля означает, что исходные многочлены раскладываются на множители, и среди этих множителей обязательно будет общий. Действительно:[begin{align}& left| x-1 right|=left| {{x}^{2}}-3x+2 right|; & left| x-1 right|=left| left(x-1 right)left(x-2 right) right|. end{align}]
Одно из свойств модуля: $left| acdot b right|=left| a right|cdot left| b right|$ (т.е. модуль произведения равен произведению модулей), поэтому исходное уравнение можно переписать так:
[left| x-1 right|=left| x-1 right|cdot left| x-2 right|]
Как видим, у нас действительно возник общий множитель. Теперь, если собрать все модули с одной стороны, то можно вынести этот множитель за скобку:
[begin{align}& left| x-1 right|=left| x-1 right|cdot left| x-2 right|; & left| x-1 right|-left| x-1 right|cdot left| x-2 right|=0; & left| x-1 right|cdot left(1-left| x-2 right| right)=0. end{align}]
Ну а теперь вспоминаем, что произведение равно нулю, когда хотя бы один из множителей равен нулю:
[left[ begin{align}& left| x-1 right|=0, & left| x-2 right|=1. end{align} right.]
Таким образом, исходное уравнение с двумя модулями свелось к двум простейшим уравнениям, о которых мы говорили в самом начале урока. Такие уравнения решаются буквально в пару строчек.:)
Данное замечание, возможно, покажется излишне сложным и неприменимым на практике. Однако в реальности вам могут встретиться куда более сложные задачи, нежели те, что мы сегодня разбираем. В них модули могут комбинироваться с многочленами, арифметическими корнями, логарифмами и т.д. И в таких ситуациях возможность понизить общую степень уравнения путём вынесения чего-либо за скобку может оказаться очень и очень кстати.:)
Теперь хотелось бы разобрать ещё одно уравнение, которое на первый взгляд может показаться бредовым. На нём «залипают» многие ученики — даже те, которые считают, что хорошо разобрались в модулях.
Тем не менее, это уравнение решается даже проще, чем то, что мы рассматривали ранее. И если вы поймёте почему, то получите ещё один приём для быстрого решения уравнений с модулями.
Итак, уравнение:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0]
Нет, это не опечатка: между модулями именно плюс. И нам нужно найти, при каких $x$ сумма двух модулей равна нулю.:)
В чём вообще проблема? А проблема в том, что каждый модуль — число положительное, либо в крайнем случае ноль. А что будет, если сложить два положительных числа? Очевидно, снова положительное число:
[begin{align}& 5+7=12 gt 0; & 0,004+0,0001=0,0041 gt 0; & 5+0=5 gt 0. end{align}]
Последняя строчка может натолкнуть на мысль: единственный случай, когда сумма модулей равна нулю — это если каждый модуль будет равен нулю:
[left| x-{{x}^{3}} right|+left| {{x}^{2}}+x-2 right|=0Rightarrow left{ begin{align}& left| x-{{x}^{3}} right|=0, & left| {{x}^{2}}+x-2 right|=0. end{align} right.]
А когда модуль равен нулю? Только в одном случае — когда подмодульное выражение равно нулю:
[{{x}^{2}}+x-2=0Rightarrow left(x+2 right)left(x-1 right)=0Rightarrow left[ begin{align}& x=-2 & x=1 end{align} right.]
Таким образом, у нас есть три точки, в которых обнуляется первый модуль: 0, 1 и −1; а также две точки, в которых обнуляется второй модуль: −2 и 1. Однако нам нужно, чтобы оба модуля обнулялись одновременно, поэтому среди найденных чисел нужно выбрать те, которые входят в оба набора. Очевидно, такое число лишь одно: $x=1$ — это и будет окончательным ответом.
Метод расщепления
Что ж, мы уже рассмотрели кучу задач и изучили множество приёмов. Думаете, на этом всё? А вот и нет! Сейчас мы рассмотрим заключительный приём — и одновременно самый важный. Речь пойдёт о расщеплении уравнений с модулем. О чём вообще пойдёт речь? Давайте вернёмся немного назад и рассмотрим какое-нибудь простое уравнение. Например, это:
[left| 3x-5 right|=5-3x]
В принципе, мы уже знаем, как решать такое уравнение, потому что это стандартная конструкция вида $left| fleft(x right) right|=gleft(x right)$. Но попробуем взглянуть на это уравнение немного под другим углом. Точнее, рассмотрим выражение, стоящее под знаком модуля. Напомню, что модуль любого числа может быть равен самому числу, а может быть противоположен этому числу:
[left| a right|=left{ begin{align}& a,quad age 0, & -a,quad a lt 0. end{align} right.]
Собственно, в этой неоднозначности и состоит вся проблема: поскольку число под модулем меняется (оно зависит от переменной), нам неясно — положительное оно или отрицательное.
Но что если изначально потребовать, чтобы это число было положительным? Например, потребуем, чтобы $3x-5 gt 0$ — в этом случае мы гарантированно получим положительное число под знаком модуля, и от этого самого модуля можно полностью избавиться:
Таким образом, наше уравнение превратится в линейное, которое легко решается:
Правда, все эти размышления имеют смысл только при условии $3x-5 gt 0$ — мы сами ввели это требование, дабы однозначно раскрыть модуль. Поэтому давайте подставим найденный $x=frac{5}{3}$ в это условие и проверим:
Получается, что при указанном значении $x$ наше требование не выполняется, т.к. выражение оказалось равно нулю, а нам нужно, чтобы оно было строго больше нуля. Печалька.:(
Но ничего страшного! Ведь есть ещё вариант $3x-5 lt 0$. Более того: есть ещё и случай $3x-5=0$ — это тоже нужно рассмотреть, иначе решение будет неполным. Итак, рассмотрим случай $3x-5 lt 0$:
Очевидно, что в модуль раскроется со знаком «минус». Но тогда возникает странная ситуация: и слева, и справа в исходном уравнении будет торчать одно и то же выражение:
Интересно, при каких таких $x$ выражение $5-3x$ будет равно выражению $5-3x$? От таких уравнений даже Капитан очевидность подавился бы слюной, но мы-то знаем: это уравнение является тождеством, т.е. оно верно при любых значениях переменной!
А это значит, что нас устроят любые $x$. Вместе с тем у нас есть ограничение:
Другими словами, ответом будет не какое-то отдельное число, а целый интервал:
Наконец, осталось рассмотреть ещё один случай: $3x-5=0$. Тут всё просто: под модулем будет ноль, а модуль нуля тоже равен нулю (это прямо следует из определения):
Но тогда исходное уравнение $left| 3x-5 right|=5-3x$ перепишется следующим образом:
Этот корень мы уже получали выше, когда рассматривали случай $3x-5 gt 0$. Более того, это корень является решением уравнения $3x-5=0$ — это ограничение, которое мы сами же и ввели, чтобы обнулить модуль.:)
Таким образом, помимо интервала нас устроит ещё и число, лежащее на самом конце этого интервала:
Объединение корней в уравнениях с модулем
Итого окончательный ответ: $xin left(-infty ;frac{5}{3} right]$. Не очень-то привычно видеть такую хрень в ответе к довольно простому (по сути — линейному) уравнению с модулем, правда? Что ж, привыкайте: в том и состоит сложность модуля, что ответы в таких уравнениях могут оказаться совершенно непредсказуемыми.
Куда важнее другое: мы только что разобрали универсальный алгоритм решения уравнения с модуляем! И состоит этот алгоритм из следующих шагов:
- Приравнять каждый модуль, имеющийся в уравнении, к нулю. Получим несколько уравнений;
- Решить все эти уравнения и отметить корни на числовой прямой. В результате прямая разобьётся на несколько интервалов, на каждом из которых все модули однозначно раскрываются;
- Решить исходное уравнение для каждого интервала и объединить полученные ответы.
Вот и всё! Остаётся лишь один вопрос: куда девать сами корни, полученные на 1-м шаге? Допустим, у нас получилось два корня: $x=1$ и $x=5$. Они разобьют числовую прямую на 3 куска:
Разбиение числовой оси на интервалы с помощью точек
Ну и какие тут интервалы? Понятно, что их три:
- Самый левый: $x lt 1$ — сама единица в интервал не входит;
- Центральный: $1le x lt 5$ — вот тут единица в интервал входит, однако не входит пятёрка;
- Самый правый: $xge 5$ — пятёрка входит только сюда!
Я думаю, вы уже поняли закономерность. Каждый интервал включает в себя левый конец и не включает правый.
На первый взгляд, такая запись может показаться неудобной, нелогичной и вообще какой-то бредовой. Но поверьте: после небольшой тренировки вы обнаружите, что именно такой подход наиболее надёжен и при этом не мешает однозначно раскрывать модули. Лучше уж использовать такую схему, чем каждый раз думать: отдавать левый/правый конец в текущий интервал или «перекидывать» его в следующий.
Разбор типовых вариантов заданий №23 ОГЭ по математике
Первый вариант задания
Постройте график функции
Алгоритм решения:
- Записываем ответ.
Решение:
1. Преобразуем функцию в зависимости от знака переменной х.
2. График функции заданных значениях х — часть параболы, ветви которой направлены вниз.
Вершина расположена в точке с координатами:
Найдем нули функции: График проходит через начало координат и точку (-2;-7).
Вершина ее находится в точке:
Определим нули параболы
3. Изображаем график функции на координатной плоскости:
4. Из построения легко видно, что прямая y = m имеет с графиком ровно две точки, когда проходит через вершину одной из парабол, образующих график данной функции.
Значит, две общие точки функция и прямая имеют при m = -2,25 или m = 12,25.
Ответ: -2,25; 12,25.
Второй вариант задания
Постройте график функции
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем формулу в зависимости от знака переменной х:
2. Графиком функции является парабола, ветви которой направлены вниз.
Вершина ее находится в точке:
Найдем нули функции: График проходит через начало координат и точку (0;4).
Графиком второй функции является парабола, ветви которой направлены вверх.
Вершина ее находится в точке:
Определим нули параболы
3. Изображаем график на координатной плоскости:
Из изображения видно, что прямая y= m имеет с графиком только две общих точки, когда m=-9 или m=4. На графике прямая изображена красной линией при каждом значении m.
Ответ: -9; 4.
Третий вариант задания
Постройте график функции
Определите, при каких значениях m прямая y = m имеет с графиком ровно две общие точки.
Алгоритм решения:
- Преобразуем формулу, которая задает функцию.
- Определяем вид и характерные точки функции на каждом промежутке.
- Изображаем график на координатной плоскости.
- Делаем вывод относительно количества точек пересечения.
- Записываем ответ.
Решение:
1. Преобразуем формулу функции в зависимости от знака переменной
2. Определяем вид функции и находим дополнительные точки для каждого участка графика.
График при — часть парабола, ветви которой направлены вниз. Потому как коэффициент а
=-1 – отрицательный.
Определим вершину параболы и
.
Вершина находится в точке (-3; 9).
Парабола проходит еще через точки (0;0) и (0;6).
Если , ветви параболы направлены вверх. Найдем вершину:
, (2; -4).
График проходит также через точки (0;0) и (0;4).
3. Строим искомый график:
Из построения видно, что прямая y=m имеет только 2 общие точки с графиком функции в случаях, когда m=-4 или m=9. На рисунке прямые изображены красным цветом.
Ответ: -4; 9.
Четвертый вариант задания
Постройте график функции
Определите, при каких значениях k прямая у = kx не имеет с графиком общих точек.
Алгоритм решения:
- Строим график.
- Записываем ответ.
Решение:
1. Если x
Дробь, получившаяся в результате, определена . График представляет собой часть гиперболы.
Точки для построения графика:
3. Построим график заданной функции:
4. Прямая y=kx не имеет общих точек с графиком, при k=-1; 0 и 1, потому как тогда прямая проходит через точки, не входящие в область определения заданной функции.
На графике прямые для k=-1; 1изображены красным.
Ответ: -1; 0; 1.
Пятый вариант задания
Постройте график функции
Определите, при каких значениях k прямая y = kx не имеет с графиком общих точек.
Алгоритм решения:
- Раскрываем модуль и преобразовываем формул функции.
- Определяем вид функции на каждом промежутке и находим дополнительные точки графика.
- Строим график.
- Определяем искомые значения k.
- Записываем ответ.
Данная статья посвящена решению примеров заданий 23 из ОГЭ по математике. В этих заданиях школьников обычно просят построить график той или иной функции, а затем указать, при каких значениях параметра этот график пересекается с неким другим графиком, касается его или же, к примеру, имеет с ним несколько точек пересечения. Ну и тому подобное. В данной статье вы найдёте разбор примеров решения заданий 23 из ОГЭ по математике от профессионального репетитора, на протяжении многих лет занимающегося подготовкой школьников к этому экзамену.
Примеры решения заданий 23 из ОГЭ по математике
Пример 1. Постройте график функции
Определите, при каких значениях прямая имеет с графиком ровно одну общую точку.
Построение графика функции всегда нужно начинать с указания области определения этой функции. В данном случае ограничения на эту область задаются тем, что в знаменателе не должно быть нуля, потому что деление на нуль не имеет математического смысла. То есть областью определения данной функции являются все числа, за исключением 1. Записать это можно следующим образом:
После того, как мы указали область определения исходной функции, можно попробовать её упростить. Для этого вынесем минус в знаменателе за скобку и сократим. В результате получим следующее выражение:
График данной функции получается из графика функции путём её отражения относительно оси OX
и параллельного переноса всех точек на 0,25 единичного отрезка вниз. При этом мы должны удалить из этого графика точку , потому что она не входит в область определения исходной функции. То есть искомый график выглядит следующим образом:
Теперь отвечаем на главный вопрос задачи. Графиком функции является прямая, проходящая через начало координат. При этом в зависимости от коэффициента эта прямая имеет разный наклон относительно оси OX
. Когда это прямая имеет ровно одну общую точку с изображённым графиком? Только в двух случаях. Рассмотрим их по отдельности.
Первый случай
. Когда данная прямая касается изображённого графика. Это ситуация изображена на рисунке:
Сложность состоит в том, чтобы определить значения , при которых эта ситуация реализуется. Для решения этой задачи можно использовать несколько различных подходов. Используем наиболее типичный.
Суть в том, что в точке касания графики проходят через одну и ту же точку на координатной плоскости. Значит, в этой точке имеет место равенство:
Дискриминант последнего квадратного уравнения равен , и в зависимости от коэффициента он может быть:
- отрицательным, тогда корней у этого уравнения не будет, как не будет и точек пересечения соответствующей прямой с изображённым графиком;
- положительным, тогда корней будет два, а значит и точек пересечения будет две (этот случай нам также не подходит);
- равен нулю, именно этот случай соответствует касанию прямой с графиком, поскольку записанное уравнение в этом случае будет иметь только одно решение.
То есть , то есть . Соответствующие прямые как раз и изображены на рисунке выше.
Второй случай
. Не забываем, что точка с абсциссой не принадлежит нашему графику. Значит, открывается ещё одна возможность, когда прямая будет иметь с графиком ровно одну общую точку. Вот этот случай:
Для нахождения в этом случае подставляем координаты точки в уравнение прямой . В результате получаем .
Сразу отметим, что в область определения данной функции входят все числа: . Наша задача теперь, как это часто бывает при решении заданий 23 из ОГЭ по математике, состоит в том, чтобы построить график этой функции. Для тех кто не сталкивался ранее с подобными заданиями, это может показаться странным, но график данной функции можно построить из графика функции . Нужно только выделить в подмодульном выражении полный квадрат. Для этого проведём следующие преобразования:
Из последнего с помощью формулы «квадрат разности» получаем:
Построим сначала график функции . Этот график получается из графика функции путём его переноса на единичного отрезка вправо и на единичного отрезка вниз:
При этом нули функции равны 2 и -1. Что произойдёт с этой параболой, если взять модуль от всего выражения, стоящего справа? Все точки, лежащие ниже оси OX
(с отрицательными ординатами), отразятся вверх относительно оси OX
. В результате получится вот такой график:
Теперь, глядя на этот график, уже понятно, что максимальное число точек пересечения данного графика с линией, параллельной оси абсцисс, будет равно 4. В качестве примера можно взять прямую :
Вот так решаются задания 23 из ОГЭ по математике. Как я уже говорил, это довольно интересные задания, которые к тому же можно научиться решать по ясному и запоминающемуся алгоритму. И как только вы овладеете этим мастерством, все задачи 23 из ОГЭ по математике будут казаться вам простыми и даже очевидными. Это станет для вас ещё одним заветным ключиком, который поможет получить максимальный балл на экзамене. Так что желаю вам успехов в подготовке и удаче на экзамене!
Сергей Валерьевич
Готовимся к ОГЭ по математике, решаем задание 23 на построение графика функции с модулем. За это задание на экзамене можно получить максимум 2 балла.
Постройте график функции y= |x 2 + 4x + 3|. Какое наибольшее число общих точек график данной функции может иметь с прямой параллельной оси абсцисс?
Чтобы построить график функции y= |x 2 + 4x + 3|, нужно сначала построить график функции y= x 2 + 4x + 3. Это квадратичная функция, график которой парабола с ветвями направленными вверх. Выделим квадрат двучлена чтобы найти вершину параболы: x 2 + 4x + 3 = (x 2 + 4x + 4) — 1 = (x + 2) 2 -1. Мы преобразовали функцию y = (x + 2) 2 — 1. Вершина параболы имеет координаты (-2;-1) и ось симметрию x = -2. Построим параболу по точкам. В таблице приведены значения для правой ветви. Левая ветвь строится симметрично.
Первая часть задания 23 из ОГЭ по математике выполнена, т.е. построен график квадратичной функции под модулем. Осталось определить — какое наибольшее число общих точек график данной функции может иметь с прямой параллельной OX:
- если проведем прямую y=0, то получаем 2 общие точки;
- если значения y находятся в промежутке (0;1), то 4 общие точки;
- если проведем прямую y =1, то мы видим 3 общие точки;
- если y>1, то 2 точки.